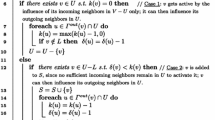Discovering Small Target Sets in Social Networks: A Fast and Effective Algorithm

Abstract

Given a network represented by a graph $G=(V,E)$, we consider a dynamical process of influence diffusion in G that evolves as follows: Initially only the nodes of a given $S\subseteq V$ are influenced; subsequently, at each round, the set of influenced nodes is augmented by all the nodes in the network that have a sufficiently large number of already influenced neighbors. The question is to determine a small subset of nodes S (a target set) that can influence the whole network. This is a widely studied problem that abstracts many phenomena in the social, economic, biological, and physical sciences. It is known that the above optimization problem is hard to approximate within a factor of $2^{\log ^{1-\epsilon }|V|}$, for any $\epsilon >0$. In this paper, we present a fast and surprisingly simple algorithm that exhibits the following features: (1) when applied to trees, cycles, or complete graphs, it always produces an optimal solution (i.e, a minimum size target set); (2) when applied to arbitrary networks, it always produces a solution of cardinality which improves on previously known upper bounds; (3) when applied to real-life networks, it always produces solutions that substantially outperform the ones obtained by previously published algorithms (for which no proof of optimality or performance guarantee is known in any class of graphs).

1 Introduction

Social networks have been extensively investigated by student of the social science for decades (see, e.g., [39]). Modern large scale online social networks, like Facebook and LinkedIn, have made available huge amount of data, thus leading to many applications of online social networks, and also to the articulation and exploration of many interesting research questions. A large part of such studies regards the analysis of social influence diffusion in networks of people. Social influence is the process by which individuals adjust their opinions, revise their beliefs, or change their behaviors as a result of interactions with other people [11]. It has not escaped the attention of advertisers that the process of social influence can be exploited in viral marketing [31]. Viral marketing refers to the spread of information about products and behaviors, and their adoption by people. According to Lately [28], “the traditional broadcast model of advertising-one-way, one-to-many, read-only is increasingly being superseded by a vision of marketing that wants, and expects, consumers to spread the word themselves”. For what interests us, the intent of maximizing the spread of viral information across a network naturally suggests many interesting optimization problems. Some of them were first articulated in the seminal papers [26, 27]. The recent monograph [7, 37] contains an excellent description of the area. See also [32, 42] In the next section, we will explain and motivate our model of information diffusion, state the problem we are investigating, describe our results, and discuss how they relate to the existing literature.

1.1 The Model

Let $G = (V,E)$ be a graph modeling the network. We denote by $\Gamma _G(v)$ and by $d_G(v)=|\Gamma _G(v)|$, respectively, the neighborhood and the degree of the vertex v in G. Let $t: V \rightarrow {\mathbb {N}}_0=\{0,1, \ldots \}$ be a function assigning thresholds to the vertices of G. For each node $v\in V$, the value t(v) quantifies how hard it is to influence node v, in the sense that easy-to-influence elements of the network have “low” threshold values, and hard-to-influence elements have “high” threshold values [25].

Definition 1

Let $G=(V,E)$ be a graph with threshold function $t: V \longrightarrow {\mathbb {N}}_0$ and $S\subseteq V$. An activation process in G starting at S is a sequence of vertex subsets ${\mathsf{Active}}_G[S,0] \subseteq {\mathsf{Active}}_G[S,1] \subseteq \ldots \subseteq {\mathsf{Active}}_G[S,\ell ] \subseteq \ldots \subseteq V$ of vertex subsets, with ${\mathsf{Active}}_G[S,0] = S$ and

$$\begin{aligned} {\mathsf{Active}}_G[S,\ell ] = {\mathsf{Active}}_G[S,\ell -1]\cup \Big \{u :\, \big |\Gamma _G(u)\cap {\mathsf{Active}}_G[S,\ell - 1]\big |\ge t(u)\Big \}, \text{ for } \ell \ge 1. \end{aligned}$$

A target set for G is set $S\subseteq V$ such that ${\mathsf{Active}}_G[S,\lambda ]=V$ for some $\lambda \ge 0$

In words, at each round $\ell$ the set of active nodes is augmented by the set of nodes u that have a number of already activated neighbors greater or equal to u’s threshold t(u). The vertex v is said to be activated at round $\ell >0$ if $v \in {\mathsf{Active}}_G[S,\ell ]{\setminus } {\mathsf{Active}}_G[S,\ell - 1]$.

In the rest of the paper we will omit the subscript G whenever the graph G is clear from the context.

Example 1

Consider the tree T in Fig. 1. The number inside each circle is the vertex threshold. A possible target set for T is $S=\{v_1, v_5, v_7\}$. Indeed we have

$$\begin{aligned} {\mathsf{Active}}[S,0]= & {} S=\{v_1, v_5, v_7\},\\ {\mathsf{Active}}[S,1]= & {} S\cup \{v_2,v_3,v_4,v_6,v_8,v_9\},\\ {\mathsf{Active}}[S,2]= & {} {\mathsf{Active}}[S,1]\cup \{ v_{10} \} =V. \end{aligned}$$

Fig. 1

A tree with vertex set $V=\{v_1, v_2,\ldots , v_{10}\}$ where the number inside each circle is the vertex threshold. A target set is $S=\{v_1, v_5, v_7\}$

The problem we study in this paper is defined as follows:

• Target Set Selection (TSS). Instance: A network $G=(V,E)$, thresholds $t:V\rightarrow {\mathbb {N}}_0$. Problem: Find a target set $S\subseteq V$ of minimum size for G.

1.2 The Context and Our Results

The Target Set Selection Problem has roots in the general study of the spread of influence in Social Networks (see [7, 22] and references quoted therein). For instance, in the area of viral marketing [21], companies want to promote products or behaviors might initially try to target and convince a few individuals who, by word-of-mouth, can trigger a cascade of influence in the network leading to an adoption of the products by a much larger number of individuals. Recently, viral marketing has been also recognised as an important tool in the communication strategies of politicians [4, 29, 38].

The first authors to study problems of spread of influence in networks from an algorithmic point of view were Kempe et al. [26, 27]. However, they were mostly interested in networks with randomly chosen thresholds. Chen [6] studied the following minimization problem: Given a graph G and fixed arbitrary thresholds t(v), $\forall \,\, v\in V$, find a target set of minimum size that eventually activates all (or a fixed fraction of) nodes of G. He proved a strong inapproximability result that makes unlikely the existence of an algorithm with approximation factor better than $O(2^{\log ^{1-\epsilon }|V|})$. Chen’s result stimulated a series of papers [1,2,3, 5, 8,9,10, 12,13,14, 16,17,19, 23, 24, 34, 35, 41, 43] that isolated interesting cases in which the problem (and variants thereof) become tractable. A notable absence from the literature on the topic (with the exception of Thang et al. [36] and Shakarian et al. [20]) are algorithms for the Target Set Selection Problem that work for arbitrary graphs. This is probably due to the previously quoted strong inapproximability result of Chen [6], that seems to suggest that the problem is hopeless. Providing such an algorithm for general graphs, evaluating its performances and esperimentally validating it on real-life networks, is the main objective of this paper.

1.2.1 Our Results

In this paper, we present a fast and simple algorithm that exhibits the following series of interesting features:

(1):

It always produces an optimal solution (i.e, a minimum size subset of nodes that influence the whole network) in case G is either a tree, a cycle, or a complete graph. These results were previously obtained in [6, 34] by means of different ad-hoc algorithms.

(2):

For general networks, our algorithm always produces a target set whose cardinality is smaller than $\sum _{v\in V} \min \left( 1,\frac{t(v)}{d(v) +1}\right)$. Our result improves on the corresponding results of Ackerman et al. [15] and Centeno et al. [1];

(3):

In real-life networks our algorithm produces solutions that outperform the ones obtained using the algorithms presented in the papers [20, 36], for which, however, no proof of optimality or performance guarantee is known in any class of graphs. The data sets we use, to experimentally validate our algorithm, include those considered in [20, 36].

It is worthwhile to remark that our algorithm, when executed on a graph G for which the thresholds t(v) have been set equal to the nodes degree d(v), for each $v\in V$, it outputs a vertex cover of G, (since in that particular case a target set of G is, indeed, a vertex cover of G). Therefore, our algorithm appears to be a new algorithm, to the best of our knowledge, to compute the vertex cover of graphs (notice that our algorithm differs from the classical algorithm that computes a vertex cover by iteratively deleting a vertex of maximum degree in the graph). We plan to investigate elsewhere the theoretical performances of our algorithm (i.e., its approximation factor); computational experiments suggest that it performs surprisingly well in practice.

2 The TSS Algorithm

In this section we present our algorithm for the TSS problem. The strategies commonly proposed in the literature to solve the TSS problem are mostly additive (e.g., [26, 27]), in that they focus on the addition of very influential nodes (according to some measure of node influence, such as the node degree) to a current solution S until it becomes a target set. In this work, we study a subtractive algorithm, given in Algorithm 1, which iteratively prunes nodes from the graph (and therefore, from the set of candidates to be part of the target set). The pruning is done according to a designed rule that tries to balance between the capability of a node to influence other nodes and its “easiness” (or hardness) to be influenced by other nodes.

At each iteration, if no extremal condition (e.g., Case 1 or 2) occurs, then Case 3 holds and a vertex is selected to be discarded; such a vertex is chosen as to maximize a properly chosen function that, for each node, is directly proportional to its remaining threshold and inversely proportional to its degree (see line 17). When a node v is removed from the graph, its neighbors update their degree accordingly (see lines 18–20). Consequently, during the deletion process, some vertex v in the surviving graph may remain with less neighbors than its threshold (Case 2); in such a case v must be necessarily added to the current solution set S (see line 13) since there is no possibility to activate v through its neighbors. Coherently, its neighbors’ thresholds are decreased by 1, since they receive v’s influence (see lines 14–15). Once a node is added to S, it is deleted from the graph, like in the Case 3 above.

It can also happen that the surviving graph contains a vertex v whose threshold has been decreased down to 0 (which means that the current set of nodes in S are able to activate v); in such a case (Case 1), v is deleted from the graph and its neighbors’ thresholds are decreased by 1, since they will receive v’s influence once v activates (see lines 9–10).

A possible execution of the algorithm TSS on the graph in Fig. 1 is described below and summarized in Table 1. Before starting the deletion process, the algorithm initializes the target set S to the empty set and a set U (used to keep the surviving nodes of G) to V, moreover it also exploits three variables for each node:

• ${\delta }(v)$ which is initialized to the degree of node v,

• k(v) which is initialized to threshold of node v, and

• N(v) which is initialized to the set of neighbors of node v.

The algorithm proceeds as follows:

Iteration 1 If no node in U has threshold either equal to 0 or larger than the degree, then Case 3 of the algorithm occurs and a node is selected according to condition at line 17 of the algorithm. All the leaves of the tree in Fig. 1 satisfy this condition, therefore the algorithm arbitrary chooses one of them.¹ Let $v_{10}$ be the selected vertex. Hence, $v_{10}$ is removed. As a consequence $v_6$ will not count on $v_{10}$ for being influenced in the future (the value ${\delta }(v_6)$, which denotes the degree of $v_6$ restricted to the nodes belonging to the residual graph, is decreased by 1).

Iteration 2 and 3 Case 3 is applied to nodes $v_9$ and $v_8$ and the value ${\delta }(v_7)$ is updated accordingly.

Table 1 An example of execution of TSS(G) on the graph T in Fig. 1

Iteration 4 In the residual graph, node $v_7$ has fewer neighbors than its threshold (i.e., ${\delta }(v_7) = 1 < 2 = k(v_7)$) and Case 2 of the algorithm occurs (notice that no node has threshold equal to 0). Hence, $v_7$ is selected and added to the target set S. As a consequence, $v_7$ is removed and the threshold of its neighbor $v_1$ is decreased by 1 (since it will receive $v_7$’s influence).

Iteration 5 Case 3 applies to node $v_6$.

Iteration 6 Case 2 applies to node $v_5$.

Iteration 7 The residual threshold of node $v_4$ is now 0 (e.g., the nodes which are already in S see Case 2 suffice to activate $v_4$). Hence, Case 1 occurs and $v_4$ is removed from the graph, the threshold of its neighbor $v_1$ is decreased by 1 (since once $v_4$ activates, $v_1$ will receive $v_4$’s influence).

Iteration 8 and 9 Case 3 applies to nodes $v_3$ and $v_2$.

Iteration 10 Case 2 applies to node $v_1$.

The algorithm outputs the set S which contains the nodes that were selected on the occurrences of Cases 2. In our example the output is $S=\{v_1,v_5,v_7\}$ which, as showed in Example 1, is a target set for T.

In the rest of the paper, we use the following notation. We denote by n the number of nodes in G, that is, $n=|V|$. Moreover we denote:

• By $v_i$ the vertex that is selected during the $n-i+1$th iteration of the while loop in TSS(G), for $i=n,\ldots ,1$;

• by G(i) the graph induced by $V_i=\{v_{i},\ldots ,v_1\}$

• by $\delta _i(v)$ the value of $\delta (v)$ as updated at the beginning of the $(n-i+1)$th iteration of the while loop in TSS(G).

• by $N_i(v)$ the set N(v) as updated at the beginning of the $(n-i+1)$th iteration of the while loop in TSS(G), and

• by $k_i(v)$ the value of k(v) as updated at the beginning of the $(n-i+1)$th iteration of the while loop in TSS(G).

For the initial value $i=n$, the above values are those of the input graph G, that is: $G(n)=G$, $\delta _n(v)=d(v)$, $N_n(v)=\Gamma (v)$, $k_n(v)=t(v)$, for each vertex v of G.

We start with two technical Lemmata which will be useful in the rest of the paper.

Lemma 1

Consider a graph G. For any $i=n,\ldots ,1$ and $u\in V_i$, it holds that

$$\begin{aligned} \Gamma _{G(i)}(u)=N_i(u) \text{ and } \quad d_{G(i)}(u)=\delta _i(u). \end{aligned}$$

(1)

Proof

For $i=n$ we have $d_{G(n)}(u)=d_G(u)=\delta _n(u)$ and $\Gamma _{G(n)}(u)=\Gamma _{G}(u)=N_n(u)$ for any $u\in V_n=V$.

Suppose now that the equalities hold for some $i\le n$. The graph $G(i-1)$ corresponds to the subgraph of G(i) induced by $V_{i-1}=V_i-\{v_i\}$. Hence

$$\begin{aligned} \Gamma _{G(i-1)}(u)=\Gamma _{G(i)}(u)-\{v_i\}, \end{aligned}$$

and

$$\begin{aligned} d_{G(i-1)}(u)={\left\{ \begin{array}{ll}{d_{G(i)}(u)-1}&{}{\text{ if }u\in \Gamma _{G(i)}(v_i),}\\ {d_{G(i)}(u)}&{}{\text{ otherwise. }}\end{array}\right. } \end{aligned}$$

We deduce that the desired equalities hold for $i-1$ by noticing that the algorithm uses the same rules to get

$$\begin{aligned} N_{i-1}(u)=N_i(u)-\{v_i\} \end{aligned}$$

and

$$\begin{aligned} \delta _{i-1}(u)={\left\{ \begin{array}{ll}{\delta _{i}(u)-1}&{}{ \text{ if }u\in N_i(v_i)=\Gamma _{G(i)}(v_i),}\\ {\delta _{i}(u)}&{}{\text{ otherwise }.}\end{array}\right. } \end{aligned}$$

$\square$

Lemma 2

For any $i>1$, if $S^{(i-1)}$ is a target set for $G(i-1)$ with thresholds $k_{i-1}(u)$, for $u\in V_{i-1}$, then

$$\begin{aligned} S^{(i)}={\left\{ \begin{array}{ll}{S^{(i-1)}\cup \{v_i\}}&{}{\text{ if }k_i(v_i)>\delta _i(v_i)}\\ {S^{(i-1)}}&{}{\text{ otherwise }}\end{array}\right. } \end{aligned}$$

(2)

is a target set for G(i) with thresholds $k_i(u)$, for $u\in V_{i}$.

Proof

Let us first notice that, according to the algorithm TSS, for each $u\in V_{i-1}$ we have

$$\begin{aligned} k_{i-1}(u)={\left\{ \begin{array}{ll}{\max (k_i(u)-1,0)}&{}{\text{ if }u\in N_i(v_i) \hbox { and } (k_i(v_i)=0 \quad \hbox {or}\quad k_i(v_i)>\delta _i(v_i))}\\ {k_i(u)}&{}{\hbox {otherwise.}}\end{array}\right. }\nonumber \\ \end{aligned}$$

(3)

• (1) If $k_i(v_i)=0$, then $v_i\in {\mathsf{Active}}_{G(i)}[S^{(i)},1]$ whatever $S^{(i)}\subseteq V_i-\{v_i\}$. Hence, by the Eq. (3), any target set $S^{(i-1)}$ for $G(i-1)$ is also a target set for G(i).

• (2) If $k_i(v_i)>\delta _i(v_i)$ then $S^{(i)}=S^{(i-1)}\cup \{v_i\}$ and $k_{i-1}(u)=k_i(u)-1$ for each $u\in N_i(v_i)$. It follows that for any $\ell \ge 0$,

  $$\begin{aligned} {\mathsf{Active}}_{G(i)}[S^{(i-1)}\cup \{v_i\},\ell ]-\{v_i\}={\mathsf{Active}}_{G(i-1)}[S^{(i-1)},\ell ]. \end{aligned}$$

  Hence, ${\mathsf{Active}}_{G(i)}[S^{(i)},\ell ]={\mathsf{Active}}_{G(i-1)}[S^{(i-1)},\ell ]\cup \{v_i\}.$

• (3) Let now $1\le k_i(v_i)\le \delta _i(v_i)$. We have that $k_{i-1}(u)=k_i(u)$ for each $u\in V_{i-1}$. If $S^{(i-1)}$ is a target set for $G(i-1)$, by definition there exists an integer $\lambda$ such that ${\mathsf{Active}}_{G(i-1)}[S^{(i-1)},\lambda ]=V_{i-1}$. We then have $V_{i-1}\subseteq {\mathsf{Active}}_{G(i)}[S^{(i-1)},\lambda ]$ which implies ${\mathsf{Active}}_{G(i)}[S^{(i-1)},\lambda +1]=V_i$. $\square$

We can now prove the main result of this section.

Theorem 1

For any graph G and threshold function t, the algorithm TSS(G) outputs a target set for G.

Proof

Let S be the output of the algorithm TSS(G). We show that for each $i=1,\ldots ,n$ the set $S\cap \{v_{i},\ldots ,v_1\}$ is a target set for the graph G(i), assuming that each vertex u in G(i) has threshold $k_i(u)$. The proof is by induction on the number i of nodes of G(i).

If $i=1$ then the unique vertex $v_1$ in G(1) either has threshold $k_1(v_1)=0$ and $S\cap \{v_1\}=\emptyset$ or the vertex has positive threshold $k_1(v_1)>{\delta }_1(v_1)=0$ and $S\cap \{v_1\}=\{v_1\}$.

Consider now $i>1$ and suppose the algorithm be correct on $G(i-1)$, that is, $S\cap \{v_{i-1},\ldots ,v_1\}$ is a target set for $G(i-1)$ with threshold function $k_{i-1}$. We notice that in each among Cases 1, 2 and 3, the algorithm updates the thresholds and the target set according to Lemma 2. Hence, the algorithm is correct on G(i) with threshold function $k_i$. The theorem follows since $G(n)=G$. $\square$

It is possible to see that the TSS algorithm can be implemented in such a way to run in $O(|E|\log |V|)$ time. Indeed we need to process the nodes $v\in V$ according to the metric $t(v)/(d(v)(d(v)+1))$, and the updates that follow each processed node $v\in V$ involve at most the d(v) neighbors of v.

3 Estimating the Size of the Solution

In this section we prove an upper bound on the size of the target set obtained by the algorithm TSS(G) for any input graph G. Our bound, given in Theorem 2, improves on the bound $\sum _{v\in V} \min \left( 1,\frac{t(v)}{d(v) +1}\right)$ given in [1, 15]. Moreover, the result in [1] is based on the probabilistic method and an effective algorithm results only by applying suitable derandomization steps.

Theorem 2

Let G be a connected graph with at least 3 nodes and threshold function $t:V\rightarrow {\mathbb {N}}_0$. The algorithm TSS(G) outputs a target set S of size

$$\begin{aligned} |S|\le \sum _{v \in \{u\,|\, u\in V^{(2)}\, \vee \, t(u)\ne 1\}}\min \left( 1,\frac{t(v)}{d^{(2)}(v){+}1}\right) , \end{aligned}$$

(4)

where $V^{(2)}=\{v \, |\, v\in V,\, d(v)\ge 2\}$ and $d^{(2)}(v)=|\{u\in \Gamma (v) \, |\, u\in V^{(2)} \, \vee \, t(u)\ne 1\}|$.

Proof

For each $i=1,\ldots , n$, define

• (a) $\delta ^{(2)}_i(v)=|\{u\in N_i(v) \, |\, u\in V^{(2)} \, \vee \, t(u)\ne 1\}|$;

• (b) $I_i=\left\{ v \,{|}\, v\in V_i-V^{(2)}, \, k_i(v)>\delta _i(v) \right\}$,

• (c) $W(G(i))=\sum _{v \in V_i \cap V^{(2)}} \min \left( 1,\frac{k_i(v)}{\delta ^{(2)}_i(v)+1}.\right) +|I_i|.$

We prove that

$$\begin{aligned} |S\cap V_i|\le W(G(i)), \end{aligned}$$

(5)

for each $i=1,\ldots , n$. The bound (4) on S follows recalling that $G(n)=G$ and

$$\begin{aligned} I_n=\left\{ v \,{|}\, v\not \in V^{(2)},\, t(v)= k (v)> {\delta }(v)=d(v)=1 \right\} . \end{aligned}$$

The proof is by induction on i. If $i=1$, the claim follows noticing that

$$\begin{aligned} |S\cap \{v_1\}|={\left\{ \begin{array}{ll}{0}&{}{\text{ if }k_1(v_1)=0}\\ {1}&{}{\text{ if }k_1(v_1)\ge 1}\end{array}\right. } \text{ and } \quad W(G(1))={\left\{ \begin{array}{ll}{0}&{}{\text{ if }k_1(v_1)=0 \text{ and } v_1{\in } V^{(2)}}\\ {1}&{}{\text{ otherwise. }}\end{array}\right. } \end{aligned}$$

Assume now (5) holds for $i-1\ge 1$, and consider G(i) and the node $v_{i}$. We have

$$\begin{aligned} |S\cap \{v_{i},\ldots ,v_1\}|=|S\cap \{v_i\}|+|S\cap \{v_{i-1},\ldots ,v_1\}|\le |S\cap \{v_i\}|+W(G(i-1)). \end{aligned}$$

We show now that

$$\begin{aligned} W(G(i))\ge W(G(i-1)) +|S\cap \{v_i\}|. \end{aligned}$$

We first notice that $W(G(i))-W(G(i-1))$ can be written as

$$\begin{aligned}&\sum _{v\in V_i \cap V^{(2)}} \min \left( 1,\frac{k_i(v)}{\delta ^{(2)}_i(v)+1}\right) +|I_i|-\sum _{v\in V_{i-1} \cap V^{(2)}} \min \left( 1,\frac{k_{i-1}(v)}{\delta ^{(2)}_{i-1}(v)+1}\right) -|I_{i-1}| \end{aligned}$$

We notice that $k_i(v)-1\le k_{i-1}(v)\le k_i(v)$ and $\delta _i(v)-1\le \delta _{i-1}(v)\le \delta _i(v)$, for each neighbor v of $v_i$ in G(i), and that threshold and degree remain unchanged for each other node in $G(i-1)$. Therefore, we get

$$\begin{aligned}&W(G(i))-W(G(i-1))\ge |I_i| - |I_{i-1}|\nonumber \\&\quad +{\mathop {\mathop {\sum }\limits _{v\in N_{i}(v_i) \cap V^{(2)}}}\limits _{k_i(v)\le \delta ^{(2)}_i(v)}} \left( \frac{k_i(v)}{\delta ^{(2)}_i(v)+1}- \frac{k_{i-1}(v)}{\delta ^{(2)}_{i-1}(v)+1}\right) \nonumber \\&\quad + {\left\{ \begin{array}{ll} \min \left( 1,\frac{k_{i}(v_i)}{\delta ^{(2)}_{i}(v_i)+1}\right) &{}\quad {\text{ if }d(v_i)\ge 2} \\ 0 &{}\text{ otherwise }. \end{array}\right. } \end{aligned}$$

(6)

We distinguish three cases according to those in the algorithm TSS(G).

• (I) Suppose that Case 1 of the Algorithm TSS holds; i.e. $k_i(v_i)=0$. Recall that the Algorithm TSS(G) updates the the values of ${\delta }(u)$ and k(u) for each node in $V_i$ as follows:

  $$\begin{aligned} {\delta }_{i-1}(u){=}{\left\{ \begin{array}{ll}{{\delta }_{i}(u){-}1}&{}{\text{ if }u {\in } N(v_i)}\\ {{\delta }_{i}(u) }&{}{\text{ otherwise, }}\end{array}\right. }k_{i-1}(u){=}{\left\{ \begin{array}{ll}{k_{i}(u){-}1}&{}{\text{ if }u {\in } N(v_i), k_i(u){>}0}\\ {k_{i}(u) }&{}{\text{ otherwise. }}\end{array}\right. }\nonumber \\ \end{aligned}$$

  (7)

  By (b), (7) and being $k_i(v_i)=0$, we immediately get $I_{i-1}= I_{i}$. Hence, from (6) we have

  $$\begin{aligned}&W(G(i))-W(G(i-1))\ge {\mathop {\mathop {\sum }\limits _{v\in N_{i}(v_i) \cap V^{(2)}}}\limits _{k_i(v)\le \delta ^{(2)}_i(v)}} \left( \frac{k_i(v)}{\delta ^{(2)}_i(v)+1}- \frac{k_{i-1}(v)}{\delta ^{(2)}_{i-1}(v)+1}\right) \ge 0, \end{aligned}$$

  where the last inequality is implied by (7). Since we know that in Case 1 the selected node $v_i$ is not part of S, we get the desired inequality $W(G(i))-W(G(i-1))\ge |S\cap \{v_{i}\}|$.

• (II) Suppose that Case 2 of the algorithm holds; i.e. $k_i(v_i)\ge \delta _i(v_i)+1$ and $k(v)>0$ for each $v\in V_i$. The Algorithm TSS(G) updates the values of ${\delta }(u)$ and k(u) for each node $u\in V_{i-1}$ as in (7). Hence, we have

  $$\begin{aligned} I_{i-1}={\left\{ \begin{array}{ll}{I_i}&{}{\text{ if }d(v_i)\ge 2}\\ {I_i-\{v_i\}}&{}{{ \text{ otherwise }}}\end{array}\right. } \end{aligned}$$

  and, using this case assumption, Eq. (6) becomes

  $$\begin{aligned} W(G(i))-W(G(i-1))\ge 1+{\mathop {\mathop {\sum }\limits _{v\in N_{i}(v_i) \cap V^{(2)}}}\limits _{k_i(v)\le \delta ^{(2)}_i(v)}} \left( \frac{k_i(v)}{\delta ^{(2)}_i(v)+1}-\frac{k_{i-1}(v)}{\delta ^{(2)}_{i-1}(v)+1}\right) \ge 1. \end{aligned}$$

  Since in Case 2 $v_i$ is part of the output S, we get $W(G(i))-W(G(i-1))\ge 1=|S\cap \{v_{i}\}|$.

• (III) Suppose that Case 3 of the algorithm holds. We know that:

  • (i) $1\le k_i(v)\le {\delta }_i(v)$, for each $v \in V_i$;

  • (ii) $I_i=\emptyset$—by (i) above;

  • (iii) $\frac{k_i(v_i)}{{\delta }_i(v_i)(\delta _i(v_i)+1)}\ge \frac{k_i(v)}{{\delta }_i(v)({\delta }_i(v)+1)}$, for each $v\in V_i$;

  • (iv) for each $v\in V_{i-1}$, $k_{i-1}(u)=k_{i}(u)$ and ${\delta }_{i-1}(u)={\left\{ \begin{array}{ll}{{\delta }_{i}(u){-}1}&{}{\text{ if }u {\in } N(v_i)}\\ {{\delta }_{i}(u) }&{}{\text{ otherwise. }}\end{array}\right. }$

We distinguish three cases on the value of $d(v_i)$ and $\delta _i(v_i)$:

• Suppose first $d(v_i)\ge \delta _i(v_i) \ge 2$. We have $\delta _i(v)\ge 2$, for each $\ v \in V_i$. Otherwise, by (i) we would get $\delta _i(v)=k_i(v)=1$ and, as a consequence

  $$\begin{aligned} \frac{k_i(v)}{\delta _i(v)(\delta _i(v)+1)}=1/2, \text{ while } \frac{k_i(v_i)}{\delta _i(v_i)(\delta _i(v_i)+1)} \le \frac{1}{\delta _i(v_i)+1} \le 1/3, \end{aligned}$$

  contradicting (iii). Therefore, by (b) $I_{i-1}=\emptyset$ and $\delta ^{(2)}_i(v)= \delta _i(v)$, for each $v \in V_i$. This, (ii), and (6) imply

  $$\begin{aligned} W(G(i))-W(G(i-1))\ge & {} {\mathop {\mathop {\sum }\limits _{v\in N_{i}(v_i) }}\limits _{k_i(v)\le \delta _i(v)}}\left( \frac{k_i(v)}{\delta _i(v)+1} - \frac{k_{i}(v)}{\delta _{i}(v)} \right) + \frac{k_{i}(v_i)}{\delta _{i}(v_i)+1}\\= & {} \frac{k_{i}(v_i)}{\delta _{i}(v_i)+1} - {\mathop {\mathop {\sum }\limits _{v\in N_{i}(v_i)}}\limits _{k_i(v)\le \delta _i(v)}} \frac{k_i(v)}{\delta _i(v)(\delta _i(v)+1)}. \end{aligned}$$

  As a consequence, by using (iii) and recalling that $v_i\notin S$ we get

  $$\begin{aligned} W(G(i))-W(G(i-1))\ge \frac{k_i(v_i)}{\delta _i(v_i)+1}-\frac{k_{i}(v_i)}{\delta _{i}(v_i)+1} = 0 =|S\cap \{v_{i}\}|. \end{aligned}$$

• Assume now $d(v_i)\ge 2$ and $\delta _i(v_i) = 1$. Let u be the neighbor of $v_i$ in G(i).

  If $d(u) \ge 2,$ then $u\notin I_{i-1}$ and, by (ii), $I_{i-1}=I_i=\emptyset .$ By (6), we obtain

  $$\begin{aligned} W(G(i)){-}W(G(i-1))\ge & {} \left( \frac{k_i(u)}{\delta ^{(2)}_i(u)+1}-\frac{k_{i-1}(u)}{\delta ^{(2)}_{i-1}(u)+1}\right) \\&+\min \left( 1,\frac{k_{i}(v_i)}{\delta ^{(2)}_{i}(v_i)+1}\right) \\= & {} \left( \frac{k_i(u)}{\delta ^{(2)}_i(u)+1}{-}\frac{k_{i}(u)}{\delta ^{(2)}_{i}(u)}\right) {+}1/2\\= & {} 1/2-\frac{k_i(u)}{\delta ^{(2)}_i(u)(\delta ^{(2)}_i(u)+1)}\\\ge & {} 1/2-\frac{1}{\delta ^{(2)}_i(u)+1}\ge 0 =|S\cap \{v_{i}\}|. \end{aligned}$$

  If $d(u) =1$ then by (i) $1 \le k_i(u)\le t(u) \le d(u)$ and we have $t(u)=1$. Moreover, by (iv) ${\delta }_{i-1}(u)=0$, ${\delta }^{(2)}_i(v_i)=0$ and $k_{i-1}(u)=k_{i}(u)\ge 1$. Hence $u\in I_{i-1}.$ Recalling that $I_i=\emptyset$, we get $I_{i-1}=\{u\}.$ As a consequence, (6) becomes

  $$\begin{aligned} W(G(i))-W(G(i-1))\ge & {} |I_i|- |I_{i-1}|+ 0 +\min \left( 1,\frac{k_{i}(v_i)}{\delta ^{(2)}_{i}(v_i)+1}\right) \\= & {} 0 = |S\cap \{v_{i}\}|. \end{aligned}$$

• Suppose finally $d(v_i)=1$. Let u be the unique neighbor of $v_i$ in G(i)

  If $d(u)\ge 2$, then $u\notin I_{i-1}$ and, by (ii), $I_{i-1}=I_i=\emptyset .$ Moreover, by (i) we know that $1 \le k_i(v_i)\le t(v_i) \le d(v_i)$ and we have $t(v_i)=1$. Hence $\delta ^{(2)}_i(u)=\delta ^{(2)}_{i-1}(u)$. By (6), we obtain

  $$\begin{aligned} W(G(i)){-}W(G(i{-}1))\ge 0+ \left( \frac{k_i(u)}{\delta ^{(2)}_i(u)+1}-\frac{k_{i-1}(u)}{\delta ^{(2)}_{i-1}(u)+1}\right) = 0 =|S\cap \{v_{i}\}|. \end{aligned}$$

  Finally, the case $d(u)\le 1$ can hold only if the input graph G has a connected component consisting of two nodes. This is excluded by the theorem hypothesis.$\square$

Remark 1

We stress that the bound in Theorem 2 improves on the previously known bound $\sum _{v\in V} \min \left( 1, t(v)/(d(v)+1)\right)$ given in [1, 15]. Indeed we can show that that for any graph it holds that

$$\begin{aligned} \sum _{v \in \{u\,|\, u\in V^{(2)}\, \vee \, t(u)\ne 1\}}\min \left( 1,\frac{t(v)}{d^{(2)}(v){+}1}\right) \le \sum _{v\in V} \min \left( 1, \frac{t(v)}{d(v)+1} \right) . \end{aligned}$$

(8)

In order to prove (8), we first notice that the difference between the two bounds can be written as,

$$\begin{aligned}&\sum _{v\in V} \min \left( 1, \frac{t(v)}{d(v)+1} \right) - \sum _{v \in \{u\,|\, u\in V^{(2)}\, \vee \, t(u)\ne 1\}}\min \left( 1,\frac{t(v)}{d^{(2)}(v){+}1}\right) \\&\quad =\sum _{v\in V^{(2)}} \min \left( 1, \frac{t(v)}{d(v){+}1} \right) {+}\sum _{v\notin V^{(2)}} \min \left( 1, \frac{t(v)}{2} \right) \\&\qquad - \sum _{v\in V^{(2)}} \min \left( 1,\frac{t(v)}{d^{(2)}(v){+}1}\right) {+}{\mathop {\mathop {\sum }\limits _{v\notin V^{(2)}}}\limits _{t(v)>1}}{1}\\&\quad = \sum _{v\in V^{(2)}} \min \left( 1, \frac{t(v)}{d(v){+}1} \right) {+}{\mathop {\mathop {\sum }\limits _{v \notin V^{(2)}}}\limits _{t(v)=1}}{1/2}- \sum _{v\in V^{(2)}} \min \left( 1,\frac{t(v)}{d^{(2)}(v){+}1}\right) \\&\quad \ge {\mathop {\mathop {\sum }\limits _{v\in V^{(2)}}}\limits _{t(v)\le d(v)}}\frac{t(v)}{d(v)+1} +{\mathop {\mathop {\sum }\limits _{v \notin V^{(2)}}}\limits _{t(v)=1}}{1/2} -{\mathop {\mathop {\sum }\limits _{v\in V^{(2)}}}\limits _{t(v)\le d(v)}}\min \left( 1,\frac{t(v)}{d^{(2)}(v) +1}\right) \\&\quad \ge {\mathop {\mathop {\sum }\limits _{v\in V^{(2)}}}\limits _{t(v)\le d(v)}}\left( \frac{t(v)}{d(v)+1} + {\frac{d(v)-d^{(2)}(v)}{2}} \right) -{\mathop {\mathop {\sum }\limits _{v\in V^{(2)}}}\limits _{t(v)\le d(v)}}\min \left( 1,\frac{t(v)}{d^{(2)}(v) +1}\right) , \end{aligned}$$

where the last inequality is due to the fact that

$$\begin{aligned} {\mathop {\mathop {\sum }\limits _{v \notin V^{(2)}}}\limits _{t(v)=1}}{1/2} = \sum _{v\in V^{(2)} } {\frac{d(v)-d^{(2)}(v)}{2}} \ge {\mathop {\mathop {\sum }\limits _{v\in V^{(2)}}}\limits _{t(v)\le d(v)}}{\frac{d(v)-d^{(2)}(v)}{2}} \end{aligned}$$

that is, we are aggregating the contribution of each node, having both degree and threshold equal to 1, to that of its unique neighbor.

Now let us consider the contribution of each $v \in V^{(2)}$, such that $t(v)\le d(v)$, to the equation above. If $d(v)=d^{(2)}(v)$, then clearly the contribution of v is zero. If $d(v)-d^{(2)}(v)\ge 2$ then the contribution of v is

$$\begin{aligned} \frac{t(v)}{d(v)+1} + {\frac{d(v)-d^{(2)}(v)}{2}} - \min \left( 1,\frac{t(v)}{d^{(2)}(v) +1}\right) \ge \frac{t(v)}{d(v)+1}+1-1\ge 0 \end{aligned}$$

Finally, if $d(v)-d^{(2)}(v)=1$ we have

$$\begin{aligned}&\frac{t(v)}{d(v)+1} + {1/2} - \min \left( 1,\frac{t(v)}{d(v)}\right) =\frac{t(v)}{d(v)+1} + {1/2} - \frac{t(v)}{d(v)}\\&\quad = \frac{2(d(v)-t(v))}{2d(v)(d(v)+1)} \ge 0. \end{aligned}$$

In each case the contribution of v is non negative and (8) holds.

Furthermore, it is worth to notice that our bound can give a dramatic improvement with respect to one in [1, 15]. As an example, consider the star graph on n nodes with center c given in Fig. 2. The node thresholds are equal equal to 1 for each leaf node and equal to $t(c)\le n$ for the center node c. The ratio of the bound in [1, 15] to the one in this paper is

$$\begin{aligned} \frac{\sum _{v\in V} \min \left( 1, \frac{t(v)}{(d(v)+1)} \right) }{\sum _{v \in \{u\,|\, u\in V^{(2)}\, \vee \, t(u)\ne 1\}}\min \left( 1,\frac{t(v)}{d^{(2)}(v){+}1}\right) } = \frac{\frac{t(c)}{n}+\frac{n-1}{2}}{1+0}\ge \frac{n-1}{2}. \end{aligned}$$

Fig. 2

A star graph with n nodes. The bound in [1, 15] provides a target set of size $\frac{t(c)}{n}+\frac{n-1}{2}$ while the bound in Theorem 2 is 1. In this specific case the bound of Theorem 2 is tight, the optimal target set consists of the center node c

4 Optimality Cases

In this section, we prove that our algorithm TSS provides a unified setting for several results, obtained in the literature by means of different ad hoc algorithms. Trees, cycles and cliques are among the few cases known to admit optimal polynomial time algorithms for the TSS problem [6, 34]. In the following, we prove that our algorithm TSS provides the first unifying setting for all these cases.

Theorem 3

The algorithm TSS(T) returns an optimal solution whenever the input graph T is a tree.

Proof

Let $T=(V,E)$ and $n=|V|$. We recall that for $i=1,\ldots ,n$: $v_i$ denotes the node selected during the $n-i+1$th iteration of the while loop in TSS, T(i) is the forest induced by the set $V_i=\{v_{i},\ldots ,v_1\}$, and $\delta _i(v)$ and $k_i(v)$ are the degree and threshold of v, for $v\in V_i$. Let S be the target set produced by the algorithm TSS(T). We prove by induction on i that

$$\begin{aligned} |S\cap \{v_{i},\ldots ,v_1\}|=|S^*_i|, \end{aligned}$$

(9)

where $S^*_i$ represents an optimal target set for the forest T(i) with threshold function $k_i$. For $i=1$, it is immediate that for the only node $v_1$ in F(1) one has

$$\begin{aligned} S\cap \{v_1\} = S^*_1 = {\left\{ \begin{array}{ll}{\emptyset } &{}\quad {\text{ if }k_1(v_1)=0}\\ {\{v_1\}}&{}\quad {\text{ otherwise. } }\end{array}\right. } \end{aligned}$$

Suppose now (9) true for $i-1$ and consider the tree T(i) and the selected node $v_i$.

• 1. Assume first that $k_i(v_i)=0$. We get

  $$\begin{aligned} |S\cap \{v_{i},\ldots ,v_1\}|=|S\cap \{v_{i-1},\ldots ,v_1\}|=|S^*_{i-1}|\le |S^*_{i}| \end{aligned}$$

  and the equality (9) holds for i.

• 2. Assume now that $k_i(v_i)\ge \delta _i(v_i)+1$. Clearly, any solution for T(i) must include node $v_i$, otherwise it cannot be activated. This implies that

  $$\begin{aligned} |S^*_i|=1+|S^*_{i-1}|=1+ |S\cap \{v_{i-1},\ldots ,v_1\}|=|S\cap \{v_{i},\ldots ,v_1\}| \end{aligned}$$

  and (9) holds for i.

• 3. Finally, suppose that $v_i=\mathtt{argmax}_{i\ge j\ge 1}\left\{ {k_i(v_j)}/{(\delta _i(v_j)(\delta _i(v_j)+1))}\right\}$ (cfr. line 21 of the algorithm). In this case each leaf $v_j$ in T(i) has

  $$\begin{aligned} \frac{k_i(v_\ell )}{\delta _i(v_\ell )(\delta _i(v_\ell )+1)}= \frac{1}{2} \end{aligned}$$

  while each internal node $v_\ell$ has

  $$\begin{aligned} \frac{k_i(v_\ell )}{\delta _i(v_\ell )(\delta _i(v_\ell )+1)}\le \frac{1}{\delta _i(v_\ell )+1}\le \frac{1}{3}. \end{aligned}$$

  Hence, the node $v_i$ must be a leaf in T(i) and has $k_i(v_i)=\delta _i(v_i)=1$. Hence $|S\cap \{v_{i},\ldots ,v_1\}|=|S\cap \{v_{i-1},\ldots ,v_1\}|=|S^*_{i-1}|\le |S^*_{i}|$. $\square$

Theorem 4

The algorithm TSS(C) outputs an optimal solution whenever the input graph C is a cycle.

Proof

If the first selected node $v_n$ has threshold 0 then clearly $v_n\not \in S^*$ for any optimal solution $S^*$.

If the threshold of $v_n$ is larger than its degree then clearly $v_n\in S^*$ for any optimal solution $S^*$. In both cases $v_n\in {\mathsf{Active}}[S^*,1]$ and its neighbors can use $v_n$’s influence; that is, the algorithm correctly sets $k_{n-1}=\max (k_n -1,0)$ for these two nodes.

If threshold of each node $v\in V$ is $1\le t(v)\le d(v)$, we get that during the first iteration of the algorithm TSS(C), the selected node $v_n$ satisfies Case 3 and has $t(v_n)=2$ if at least one of the nodes in C has threshold 2, otherwise $t(v_n)=1$. Moreover, it is not difficult to see that there exists an optimal solution $S^*$ for C such that $S^*\cap \{ v_n\}=\emptyset$.

In each case, the result follows by Theorem , since the remaining graph is a path on nodes $v_{n-1},\ldots , v_1$. $\square$

Theorem 5

Let $K=(V,E)$ be a clique with $V= \{u_1,\ldots , u_n\}$ and $t(u_1)\le \cdots \le t(u_{n-m})< n \le t(u_{n-m+1})\le \cdots \le t(u_n)$. The algorithm TSS(K) outputs an optimal target set of size

(10)

Proof

It is well known that there exists an optimal target set $S^*$ consisting of the $|S^*|$ nodes of higher threshold [34]. Being $S^*$ a target set, we know that each node in the graph K must activate. Therefore, for each $u\in V$ there exists some iteration $i\ge 0$ such that $u\in {\mathsf{Active}}[S,i]$. Assume $V= \{u_1,\ldots , u_n\}$ and

$$\begin{aligned} t(u_1)\le \cdots \le t(u_{n-m})< n \le t(u_{n-m+1})\le \cdots \le t(u_n). \end{aligned}$$

Since the thresholds are non decreasing with the node index, it follows that:

• for each $j\ge n-m+1$, the node $u_j$ has threshold $t(u_j)\ge n$ and $u_j\in S^*$ must hold. Hence, $|S^*|\ge m$;

• for each $j\le n-|S^*|$, the node $u_j$ activates if it gets, in addition to the influence of its m neighbors with threshold larger than $n-1$, the influence of at least $t(u_j)-m$ other neighbors, hence we have that

  $$\begin{aligned} t(u_j)-m\le j-1+(|S^*|-m) \end{aligned}$$

  must hold;

• for each $j=n-|S^*|+1, \ldots , n-m$, we have

  $$\begin{aligned} t(u_j)-m-j+1\le (n-1) - m - (n-|S^*|+1) +1=|S^*|-m +1. \end{aligned}$$

Summarizing, we get,

$$\begin{aligned} |S^*|\ge m + \quad \max _{{1\le j\le n-m}}\max \left( t(u_j) -m -j +1,0\right) . \end{aligned}$$

We show now that the algorithm TSS outputs a target set S whose size is upper bounded by the value in (10). Notice that, in general, the output S does not consist of the nodes having the highest thresholds.

Consider the residual graph $K(i)=(V_i,E_i)$, for some $1\le i\le n$. It is easy to see that for any $u_j, u_s\in V_i$ it holds

• (1) $\delta _i(u_j)=i$;

• (2) if $j<s$ then $k_i(u_j)\le k_i(u_s)$;

• (3) if $t(u_j) \ge n$ then $k_i(u_j) \ge i$,

• (4) if $t(u_j) < n$ then $k_i(u_j) \le i$.

W.l.o.g. we assume that at any iteration of algorithm TSS if the node to be selected is not unique then the tie is broken as follows (cfr. point 2) above):

• (i) If Case 1 holds then the selected node is the one with the lowest index,

• (ii) if either Case 2 or Case 3 occurs then the selected node is the one with the largest index.

Clearly, this implies that K(i) contains i nodes with consecutive indices among $u_1,\ldots ,u_n$, that is,

$$\begin{aligned} V_i=\left\{ u_{\ell _i},u_{\ell _i+1},\ldots ,u_{r_i}\right\} \end{aligned}$$

(11)

for some $\ell _i\ge 1$ and $r_i=\ell _i+i-1$.

Let $h=n-m$. We shall prove by induction on i that, for each $i=n,\ldots , 1$, at the beginning of the $n-i+1$th iteration of the while loop in TSS(K), it holds

$$\begin{aligned} |S\cap V_i| \le {\left\{ \begin{array}{ll} {(r_i-h)+\max _{\begin{array}{c} \ell _i \le j \le h \end{array}} \max ( k_i(u_j)-(r_i-h)-j+\ell _i, \, 0)} &{} { \text{ if } r_i > h,}\\ {\max _{\begin{array}{c} \ell _i \le j \le r_i \end{array} } \max (k_i(u_j)-j+\ell _i ,\, 0)}&{ \text{ if } r_i \le h.} \end{array}\right. }\nonumber \\ \end{aligned}$$

(12)

The upper bound (10) follows when $i=n$; indeed $K(n)=K$ and $|S|=|S\cap V(n)|$.

For $i=1$, K(1) is induced by only one node, let say u, and

$$\begin{aligned} |S\cap \{u\}| = {\left\{ \begin{array}{ll} {1} &{}\quad {\text{ if }k_1(u)\ge 1,} \\ {0} &{} \quad {\text{ if }k_1(u)=0.} \end{array}\right. } \end{aligned}$$

proving that the bound holds in this case.

Suppose now (12) true for some $i-1\ge 1$ and consider the $n-i+1$th iteration of the algorithm TSS. Let v be the node selected by algorithm TSS at the $n-i+1$th iteration. We distinguish three cases according to the cases of the algorithm TSS(G).

Case 1: $k_{i}(v)=0$ By (i) and (11), one has $v=u_{\ell _i}$, $\ell _{i-1}=\ell _i+1$ and $r_{i-1}=r_i$. Moreover, $k_{i}(u_j)=k_{i-1}(u_j)+1$ for each $u_j\in V_{i-1}$. Hence,

$$\begin{aligned}&|S\cap V_i| = |S\cap V_{i-1}|\\&\quad \le {\left\{ \begin{array}{ll} {(r_i{-}h)+\max _{\begin{array}{c} \ell _i+1 \le j \le h \end{array}} \max ( k_{i-1}(u_j){-}(r_i{-}h){-}j+\ell _i{+}1,\, 0)} &{}\quad {\text{ if }r_i> h,}\\ {\max _{\begin{array}{c} \ell +1 \le j \le r \end{array} } \max (k_{i-1}(u_j)-j+\ell +1,\, 0)}&\quad {\text{ if }r_i \le h,} \end{array}\right. }\\&\quad = {\left\{ \begin{array}{ll} {(r_i-h)+\max _{\begin{array}{c} \ell _i \le j \le h \end{array}} \max (k_{i}(u_j)-(r_i-h)-j+\ell _i,0)}&{}\quad {\text{ if }r_i > h,}\\ {\max _{\begin{array}{c} \ell \le j \le r \end{array} } \max (k_{i}(u_j)-j+\ell , 0)}&\quad {\text{ if }r \le h.} \end{array}\right. } \end{aligned}$$

Case 2: ${k_{i}(v)>\delta _{i}(v)}$ By (ii) and (11) we have $v=u_{r_i}$, $\ell _i=\ell _{i-1}$, $r_{i-1}=r_i-1$. Moreover, $k_{i}(u_j)=k_{i-1}(u_j)+1$ for each $u_j\in V_{i-1}$. Recalling relations (3) and (4), we have

$$\begin{aligned}&|S\cap V_i| = 1+|S\cap V_{i-1}|\\&\quad \le 1{+} {\left\{ \begin{array}{ll} (r_{i-1}-h){+}\max _{\begin{array}{c} \ell _{i-1} \le j \le h \end{array}} \max (k_{i-1}(u_j)-(r_{i-1}-h)-j+\ell _{i-1},\, 0) &{}\text{ if }r_{i-1}\le h,\\ \max _{\begin{array}{c} \ell _{i-1} \le j \le r_{i-1} \end{array} } \max (k_{i-1}(u_j)-j+\ell _{i-1},\, 0)&\text{ if }r_{i-1} {\le } h, \end{array}\right. } \\&\quad = {\left\{ \begin{array}{ll} {(r_i{-}h)+\max _{\begin{array}{c} \ell _i \le j \le h \end{array}} \max (k_{i-1}(u_j)+1-(r_i-h)-j+\ell _i,\, 0)} &{}\quad {\text{ if }r_i-1 \le h,}\\ {\max _{\begin{array}{c} \ell \le j \le r_i-1 \end{array} } \max (k_{i-1}(u_j)+1-j+\ell _i ,\, 1) }&\quad { \text{ if }r_i-1 \le h.} \end{array}\right. } \\&\quad ={\left\{ \begin{array}{ll} {(r_i-h)+\max \{0,\max _{\begin{array}{c} \ell _i \le j \le h \end{array}} k_{i}(u_j)-(r_i-h)-j+\ell _i\}} &{}\quad { \text{ if }r_i > h,}\\ {\max \{0,\max _{\begin{array}{c} \ell _i \le j \le r_i \end{array} } k_{i}(u_j)-j+\ell _i \}}&\quad { \text{ if }r_i \le h.} \end{array}\right. } \end{aligned}$$

Case 3: $0<k_{i}(v)\le \delta _{i}(v)$ By (ii) and (11) we have $v=u_{r_i}$, $\ell _i=\ell _{i-1}$, $r_{i-1}=r_i-1$. Moreover, $k_{i}(u_j)=k_{i-1}(u_j)$ for each $u_j\in V_{i-1}$. Recalling that by (3) and (4) we have $t(u_r) <n$, which implies $r_i\le h$, we have

$$\begin{aligned} |S\cap V_i|= & {} |S\cap V_{i-1}| \le \max _{\begin{array}{c} \ell _{i-1} \le j \le r_{i-1} \end{array} } \max (k_{i-1}(u_j)-j+\ell _{i-1}, \, 0) \\\le & {} \max _{\begin{array}{c} \ell _i \le j \le r_i-1 \end{array} } \max (k_{i}(u_j)-j+\ell _i, \, 0) \\\le & {} \max _{\begin{array}{c} \ell _i \le j \le r_i \end{array} } \max (k_{i}(u_j)-j+\ell _i, \, 0). \end{aligned}$$

$\square$

5 Computational Experiments

We have extensively tested our algorithm TSS(G) both on random graphs and on real-world data sets, and we found that our algorithm performs surprisingly well in practice. This seems to suggest that the otherwise important inapproximability result of Chen [6] refers to rare or artificial cases.

5.1 Random Graphs

The first set of tests was done in order to compare the results of our algorithm to the exact solutions, found by formulating the problem as an 0-1 Integer Linear Programming (ILP) problem. Although the ILP approach provides the optimal solution, it fails to return the solution in a reasonable time (i.e., days) already for moderate size networks. We applied both our algorithm and the ILP algorithm to random graphs with up to 50 nodes. Figure 3 depicts the results on Random Graphs G(n, p) on n nodes (any possible edge occurs independently with probability $0< p < 1$). The two plots report the results obtained for $n=30$ and $n=50$. For each plot the value of the p parameter appears along the X-axis, while the size of the solution appears along the Y-axis. Results on intermediates sizes exhibit similar behaviors. Our algorithm produced target sets of size close to the optimal (see Fig. 3); for several instances it found an optimal solution.

Fig. 3

Experiments for random graphs G(n, p) on n nodes (any possible edge occurs independently with probability $0< p < 1$). a $n=30$, b $n=50$ with $p\in \{10/100, 20/100,\ldots , 90/100\}$. For each node the threshold was fixed to a random value between 1 and the node degree

5.2 Large Real-Life Networks

We performed experiments on several real social networks of various sizes from the Stanford Large Network Data set Collection (SNAP) [30] and the Social Computing Data Repository at Arizona State University [40]. The data sets we considered include both networks for which small target sets exist and networks needing larger target sets (due to the existence of communities, i.e., tightly connected disjoint groups of nodes that appear to delay the diffusion process).

Test Network Experiments have been conducted on the following networks:

• BlogCatalog [40]: a friendship network crawled from BlogCatalog, a social blog directory website which manages the bloggers and their blogs. It has 88,784 nodes and 4,186,390 edges. Each node represents a blogger and the network contains an edge (u, v) if blogger u is friend of blogger v.

• BlogCatalog2 [40]: a friendship network crawled from BlogCatalog. It has 97,884 nodes and 2,043,701 edges.

• BlogCatalog3 [40]: a friendship network crawled from BlogCatalog. It has 10,312 nodes and 333,983 edges.

• BuzzNet [40]: BuzzNet is a photo, journal, and video-sharing social media network. It has 101,168 nodes and 4,284,534 edges.

• CA-AstroPh[30]: A collaboration network of Arxiv ASTRO-PH (Astro Physics). It has 18,772 nodes and 198,110 edges. Each node represents an author and the network contains an edge (u, v) if an author u co-authored a paper with author v.

• ca-CondMath [30] A collaboration network of Arxiv COND-MAT (Condense Matter Physics). It has 23,133 nodes and 93,497 edges.

• ca-GrQc [30]: A collaboration network of Arxiv GR-QC (General Relativity and Quantum Cosmology), It has 5,242 nodes and 14,496 edges.

• ca-HepPh [30]: A collaboration network of Arxiv HEP-PH (High Energy Physics-Phenomenology), it covers papers from January 1993 to April 2003. It has 10,008 nodes and 118,521 edges.

• ca-HepTh [30]: A collaboration network of HEP-TH (High Energy Physics-Theory) It has 9,877 nodes and 25,998 edges.

• Delicious [40]: A friendship network crawled on Delicious, a social bookmarking web service for storing, sharing, and discovering web bookmarks. It has 103,144 nodes and 1,419,519 edges.

• Douban [40]: A friendship network crawled on Douban.com, a Chinese website providing user review and recommendations for movies, books, and music. It has 154,907 nodes and 654,188 edges.

• Lastfm [40]: Last.fm is a music website, founded in UK in 2002. It has claimed over 40 million active users based in more than 190 countries. It has 108,493 nodes and 5,115,300 edges.

• Livemocha [40]: Livemocha is the world’s largest online language learning community, offering free and paid online language courses in 35 languages to more than 6 million members from over 200 countries around the world. It has 104,438 nodes and 2,196,188 edges.

• YouTube2 [30]: is a data set crawled from YouTube, the video-sharing web site that includes a social network. In the Youtube social network, users form friendship each other and users can create groups which other users can join. It contains 1,138,499 users and 2,990,443 edges.

The main characteristics of the studied networks are shown in Table  2. In particular, for each network we report the maximum degree, the diameter, the size of the largest connected component (LCC), the number of triangles, the clustering coefficient and the network modularity [33].

Table 2 Networks parameters

The competing algorithms We compare the performance of our algorithm TSS toward that of the best, to our knowledge, computationally feasible algorithms in the literature. Namely, we compare to Algorithm TIP_DECOMP recently presented in [36], in which nodes minimizing the difference between degree and threshold are pruned from the graph until a “core” set is produced. We also compare our algorithm to the VirAds algorithm presented in [20]. Finally, we compare to an (enhanced) Greedy strategy (given in Algorithm 2), in which nodes of maximum degree are iteratively inserted in the target set and pruned from the graph. Nodes that remains with zero threshold are simply eliminated from the graph, until no node remains.

Fig. 4

BlogCatalog [40]

Fig. 5

BlogCatalog2 [40]

Fig. 6

BlogCatalog3 [40]

Fig. 7

BuzzNet [40]

Fig. 8

CA-Astro-Ph [30]

Fig. 9

Ca-CondMat [30]

Fig. 10

CA-GR-QC [30]

Fig. 11

CA-HepPh [30]

Fig. 12

Ca-HepTh [30]

Fig. 13

Delicious [40]

Fig. 14

Douban [40]

Fig. 15

Lastfm [40]

Fig. 16

Livemocha [40]

Fig. 17

YouTube2 [30]

The worst case computational complexities of the four considered algorithms are similar. TSS, Greedy, and TIP_DECOMP require $O(|E|\log |V|)$ time, while VirAds requires $O(|V|^2 \times (|V|+|E|)$ time. We do not report here the actual running times measured during the experiments since they are very much machine-and-implementation dependent. However, we observed that all algorithms are computationally feasible and require comparable times.

Thresholds values According to the scenario considered in [36], in our experiments the thresholds are constant among all vertices (precisely the constant value is an integer in the interval [1, 10] and for each vertex v the threshold t(v) is set as $min\{t, d(v)\}$ where $t = 1,2,\ldots ,10$.

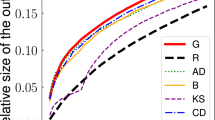
Results Figures 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 and 17 depict the experimental results on large real-life networks. For each network the results are reported in a separated plot. For each plot the value of the threshold parameter appears along the X-axis, while the size of the solution appears along the Y-axis. For each dataset, we compare the performance of our algorithm TSS to the algorithm TIP_DECOMP [36], to the algorithm VirAds [20], and to the Greedy strategy.

All test results consistently show that the TSS algorithm we introduce in this paper presents the best performances on all the considered networks, while none among TIP_DECOMP, VirAds, and Greedy is always better than the other two.

Additional analysis of the performance of the TSS algorithm and some of its variants has been presented in [19]. There, it has also shown that the algorithm performances are good even in complex scenarios, namely with random or degree-proportional thresholds.

6 Concluding Remarks

We presented a simple algorithm to find small sets of nodes that influence a whole network, where the dynamic that governs the spread of influence in the network is given in Definition 1. In spite of its simplicity, our algorithm is optimal for several classes of graphs, it improves on the general upper bound given in [1] on the cardinality of a minimal influencing set, and outperforms, on real life networks, the performances of known algorithms for the same problem. There are many possible ways of extending our work. We would be especially interested in discovering additional interesting classes of graphs for which our algorithm is optimal (we conjecture that this is indeed the case).