Quick but Odd Growth of Cacti

Abstract

Let ${\mathcal {F}}$ be a family of graphs. Given an n-vertex input graph G and a positive integer k, testing whether G has a vertex subset S of size at most k, such that $G-S$ belongs to ${\mathcal {F}}$, is a prototype vertex deletion problem. These type of problems have attracted a lot of attention in recent times in the domain of parameterized complexity. In this paper, we study two such problems; when ${\mathcal {F}}$ is either the family of forests of cacti or the family of forests of odd-cacti. A graph H is called a forest of cacti if every pair of cycles in H intersect on at most one vertex. Furthermore, a forest of cacti H is called a forest of odd cacti, if every cycle of H is of odd length. Let us denote by ${\mathcal {C}}$ and ${{\mathcal {C}}}_\mathsf{odd}$, the families of forests of cacti and forests of odd cacti, respectively. The vertex deletion problems corresponding to ${\mathcal {C}}$ and ${{\mathcal {C}}}_\mathsf{odd}$ are called Diamond Hitting Set and Even Cycle Transversal, respectively. In this paper we design randomized algorithms with worst case run time $12^k n^{\mathcal {O}(1)}$ for both these problems. Our algorithms considerably improve the running time for Diamond Hitting Set and Even Cycle Transversal, compared to what is known about them.

1 Introduction

In the field of parameterized graph algorithms, vertex (edge) deletion (addition, editing) problems constitute a considerable fraction. In particular, let ${\mathcal {F}}$ be a family of graphs. Given an input graph G and a positive integer k, testing whether G has a subset of at most k vertices (edges) S, such that $G- S$ belongs to ${\mathcal {F}}$, is a prototype vertex (edge) deletion problem. Many well known problems in parameterized complexity can be phrased in this language. For example, if ${\mathcal {F}}$ is the family of edgeless graphs, or forests, or bipartite graphs, then the vertex deletion problems to convert the input graph into a graph in ${\mathcal {F}}$ are Vertex Cover, Feedback Vertex Set, and Odd Cycle Transversal, respectively. Most of these problems are NP-complete due to a classic result by Lewis and Yannakakis [19], and naturally a candidate for parameterized study (with respect to solution size). Vertex Cover, Feedback Vertex Set and Odd Cycle Transversal are some of the most well studied problems in the domain of parameterized complexity. These problems have led to identification of several new techniques and ideas in the field.

Recent years have seen a plethora of results around vertex and edge deletion problems, in the domain of parameterized complexity [4, 5, 11,12,13, 15, 16]. In this paper, we continue this line of research and study two vertex deletion problems. In particular we study the problem of deleting vertices to get a cactus or an odd cactus graph. A graph H is called a cactus graph if H is connected and every pair of cycles in H intersect on at most one vertex. Furthermore, a cactus graph H is called an odd cactus graph, if every cycle of H is of odd length. A graph is called a forest of cacti if every component of the graph is a cacti. Let us denote by ${\mathcal {C}}$ and ${{\mathcal {C}}}_\mathsf{odd}$, the families of forests of cacti and forests of odd cacti, respectively. The vertex deletion problems corresponding to ${\mathcal {C}}$ and ${{\mathcal {C}}}_\mathsf{odd}$ are called Diamond Hitting Set and Even Cycle Transversal, respectively. It is important to note here that the name of deleting vertices to get into ${{\mathcal {C}}}_\mathsf{odd}$ is called Even Cycle Transversal, because it is equivalent to deleting a vertex subset S of size at most k such that $G- S$ does not have any cycle of even length. The problem of deleting vertices to get into ${{\mathcal {C}}}$ is called Diamond Hitting Set, because, it is equivalent to deleting a vertex subset S of size at most k such that $G- S$ does not contain diamond as a subgraph (see Definition 3 for the definition of diamond). More precisely, we study the following problems in the realm of parameterized complexity.

Parameterized complexity has two major subareas—fixed parameter tractability (FPT) and kernelization. A parameterized problem $\varPi$ is a subset of $\varSigma ^*\times {\mathbb N}$, where $\varSigma$ is a finite alphabet and ${\mathbb N}$ is the set of natural numbers. We say that a parameterized problem $\varPi$ is fixed parameter tractable, if there is an algorithm solving the problem $\varPi$, which on input (x, k) runs in time $f(k)\vert x\vert ^{{\mathcal O}(1)}$, where f is an arbitrary function and $\vert x\vert$ is the length of x. A kernelization algorithm for a parameterized problem $\varPi$ is a polynomial time algorithm (computable function) $A~:~ \varSigma ^*\times {\mathbb N}\rightarrow \varSigma ^*\times {\mathbb N}$ such that $(x,k)\in \varPi$ if and only if $(x',k')=A((x,k))\in \varPi$ and $\vert x'\vert +k'\le g(k)$ where g is a computable function. For a broader overview about parameterized complexity we refer to monographs [6, 8].

It needs to be mentioned that, in this paper, we refer to multigraphs (which may have parallel edges) as graphs. While Odd Cycle Transversal is one of the most well studied problem in the realm of parameterized complexity, there is only one article about Even Cycle Transversal in the literature. The structure of a graph without even cycles, or without cycles of length 0 modulo p for some positive integer p, is simple. Thomassen [21] showed that such graphs have treewidth at most f(p). Misra et al. [20] used the structural properties of odd cactus graphs to design an algorithm for Even Cycle Transversal with running time $50^k n^{{\mathcal O}(1)}$. They also give an ${\mathcal O}(k^2)$ kernel for the problem. On the other hand the family ${\mathcal {C}}$ of forests of cacti can be characterised by a single excluded minor. In particular, let $\varTheta$ be a graph on two vertices that have three parallel edges, then a graph $H\in {{\mathcal {C}}}$ if and only if H does not contain $\varTheta$ as a minor. Since $\varTheta$ is a connected planar graph we obtain a $c^kn^{{\mathcal O}(1)}$ time algorithm as a corollary to the main results in [11, 15, 16]. However, the exact value of c is not given in any of these algorithms as all of them use a protrusion subroutine [3]. The problem also has a ${\mathcal O}(k^2 \log ^{3/2} k)$ kernel [10]. It should also be noted that Diamond Hitting Set and Even Cycle Transversal admit approximation algorithms with factor 9 and 10, respectively [9, 20].

Our main theorems are the following.

Theorem 1

There is a randomized algorithm for Even Cycle Transversal with worst case run time ${\mathcal O}(12^k nm(n+m))$, where n and m are the number of vertices and edges in the input graph, respectively. The algorithm outputs No if the input is a No instance and for a Yes instance, with probability at least $1-\frac{1}{e}$, returns a solution.

Theorem 2

There is a randomized algorithm for Diamond Hitting Set with worst case run time $12^k n^{\mathcal {O}(1)}$, where n is the number of vertices in the input graph. The algorithm outputs No if the input is a No instance and for a Yes instance, with probability at least $1-\frac{1}{e}$, returns a solution.

Two other related problems studied in the literature are Treewidth-2-Vertex Deletion and Outerplanar Vertex Deletion. In both the problems, the input is an n-vertex graph G and a positive integer k, and the objective is to delete at most k vertices to get a graph of treewidth 2 (in other words a $K_4$-minor free graph) in case of Treewidth-2-Vertex Deletion and an outerplanar graph (in other words a graph without $K_4$ and $K_{2,3}$ as minors) in case of Outerplanar Vertex Deletion. Recall that in Diamond Hitting Set we are looking for a vertex subset of size at most k which hits all $\varTheta$-minors of the input graph. In Treewidth-2-Vertex Deletion and Outerplanar Vertex Deletion, we are looking for a vertex subset of size at most k, which hits all $K_4$-minors and $\{K_4, K_{2,3}\}$-minors of the input graph, respectively. Kim et al. [17] showed that there exists an algorithm for Treewidth-2-Vertex Deletion running in time $2^{{\mathcal O}(k)} n^{{\mathcal O}(1)}$. Again, this algorithm uses a protrusion subroutine similar to that in [3], but adapted according to the need of the problem, and therefore the exact value in the exponent of the running time is not known. It follows from the later work of Fomin et al. [11] that both the problems have algorithms running in time $2^{{\mathcal O}(k)} n^{{\mathcal O}(1)}$, because they are special cases of Planar ${{\mathcal {F}}}$-Deletion.

Our Methods. Our algorithms use the same methodology that is used for the $4^k n^{{\mathcal O}(1)}$ time algorithm for Feedback Vertex Set [2], and its generalization to Planar ${\mathcal {F}}$ Deletion [11]. In both our algorithms, we start by applying some reduction rules to the given instance. After this, we show that the number of edges incident with any solution S of our problems, is a constant fraction to the total number of edges in the graph. This counting lemma is our main technical contribution. We also observe that the analysis for the counting lemma is tight for an infinite family of graphs and thus the analysis of our randomized algorithms cannot be improved. It is in the same spirit as finding an infinite family of instances for which an approximation algorithm achieves its approximation ratio.

To apply our reduction rules in a way that the ratio between the number of edges incident with a solution S of the problem and the total number of edges in the input graph is as small as possible, we study a more general problem than Even Cycle Transversal, which we call Parity Even Cycle Transversal. In this problem we are given a graph G and a weight function $w:E(G)\rightarrow \{0,1\}$ and the objective is to delete a subset S of vertices of size at most k such that in $G- S$ there is no cycle whose weight sum is even. Observe that if w assigns one to every edge then it is same as Even Cycle Transversal.

2 Preliminaries

For a function $f~:~D\rightarrow R$ and $y\in R$, we use $f^{-1}(y)$ to denote the set $\{x\in D~\vert ~f(x)=y\}$. For a set U that is the disjoint union of subsets $U_1, U_2,\ldots , U_t$, we write $U= \biguplus _{1 \le i\le t} U_i$.

Fact 1

For any $n \in {\mathbb N}$, $(1-\frac{1}{n})^n \le \frac{1}{e}$.

We denote a graph as G, and its vertex set and edge set as V(G) and E(G), respectively. It is possible that there are parallel edges between two vertices of a graph. The degree of a vertex $v \in V(G)$, denoted by $d_G(v)$, is the number of edges incident with v. The neighbourhood of v, denoted by $N_G(v)$, is the set of vertices that have at least one edge incident with v. For a subset of vertices S, we use G[S] and $G-S$ to denote the subgraphs of G induced by S and $V(G)\setminus S$, respectively. An edge between two vertices $u,v \in V(G)$ is denoted by (u, v), while a path between u, v is denoted by [u, v]. If a sequence of vertices $v_1,\ldots , v_t$ or edges $e_1, \ldots , e_t$ form a path, then we also denote this path by $[v_1,\ldots , v_t]$ and $[e_1, \ldots e_t]$, respectively. For a path/cycle Q, we use E(Q) to denote the set of edges in the path/cycle Q. Given two subsets $V_1,V_2 \subseteq V(G)$, $E(V_1,V_2)$ denotes the set of edges in E(G) that have one end point in $V_1$ and the other in $V_2$. For a vertex $v\in V(G)$ and subset $V'\subseteq V(G)\setminus \{v\}$ we use $E(v,V')$ to denote the edge set $E(\{v\},V')$. The subdivision of an edge $e = (u,v)$ of a graph G results in a graph $G'$, which contains a new vertex w, and where the edge e is replaced by two new edges (u, w) and (w, v). A graph $\hat{G}$ is a subdivision of a graph G if there is a sequence of graphs $(G_1,G_2,\ldots , G_t)$, with $G_1 = G$ and $G_t = \hat{G}$, where for each $1< i \le t$, $G_i$ is obtained by the subdivision of an edge of $G_{i-1}$.

For a graph G, we say a vertex $v\in V(G)$ is a cut vertex if $G - \{v\}$ has more components than G. A connected graph $G'$ is called a biconnected graph if the graph $G'$ does not contain any cut vertex. A block of a graph G is a maximal biconnected subgraph of G.

Definition 1

(Block-Cut Vertex Tree) Let G be a connected graph, C be the set of cut vertices of G and ${{\mathcal {B}}}$ be the set of blocks of G. The block-cut vertex tree H of G has vertex set $C\cup {{\mathcal {B}}}$ and $E(H)=\{(c,B)~|~c\in C, B\in {{\mathcal {B}}}, c\in V(B)\}$.

In fact it is known that block-cut vertex tree of a graph is indeed a tree [7]. Now we explain how to construct a block decomposition tree of a connected graph. Let H be a block-cut vertex tree of a connected graph G. Let C be the set of cut vertices of G and ${{\mathcal {B}}}$ be the set of blocks of G. We arbitrarily root the tree H at a root $B_r$, where $B_r\in {{\mathcal {B}}}$. Now a block decomposition tree ${{\mathcal {T}}}$ of G has vertex set ${{\mathcal {B}}}$ and $(B_1,B_2)\in E({{\mathcal {T}}})$ if $V(B_1)\cap V(B_2)\ne \emptyset$ (in other words $B_1$ and $B_2$ share a cut vertex of G) and $B_1$ is an ancestor of $B_2$ in H. In other words, ${{\mathcal {T}}}$ is obtained from H by contracting the set of edges $\{(c,B)~|~c\in C, B\in {{\mathcal {B}}}, B \text{ is } \text{ the } \text{ parent } \text{ of }$c$\text{ in } H\}$. Thus ${{\mathcal {T}}}$ is indeed a tree. See Fig. 1 for an illustration of block decomposition tree of a graph. A block decomposition tree of a graph can be built in linear time [14].

Fig. 1

The leftmost figure is a graph G with blocks $B_1,B_2,B_3,B_4$ and $B_5$. The cut vertices in G are $c_1,c_2,c_3$ and $c_4$. The middle figure is the block-cut vertex tree H of G. The rightmost figure is a block decomposition tree ${{\mathcal {T}}}$ of G constructed from H rooted at $B_1$

Lemma 1

Let T be a tree. Let $V_1=\{v\in V(T)~\vert ~d_T(v)=1\}$, $V_2=\{v\in V(T)~\vert ~d_T(v)=2\}$ and $V_3=\{v\in V(T)~\vert ~d_T(v)\ge 3\}$. Then $\sum _{v\in V_3} d_T(v) \le 3 \vert V_1 \vert$.

Proof

We know that $\vert V(T) \vert = \vert V_1 \vert + \vert V_2 \vert + \vert V_3 \vert$. Also, $\varSigma _{v \in V(T)} d_{T}(v) = 2 \vert E(T) \vert = 2(\vert V(T) \vert - 1)$. Now, $\varSigma _{v \in V(T)} d_{T}(v) = \varSigma _{v \in V_1} d_{T}(v) + \varSigma _{v \in V_2} d_T(v) + \varSigma _{v \in V_3} d_{T}(v) \ge \vert V_1 \vert + 2\vert V_2 \vert + 3 \vert V_3 \vert$. Using the two equations we get that $\vert V_3 \vert \le \vert V_1 \vert - 2 \le \vert V_1 \vert$. This also means $\varSigma _{v \in V_3} d_{T}(v) = 2(\vert V_1 \vert + \vert V_2\vert + \vert V_3 \vert - 1) -(\vert V_1 \vert + 2 \vert V_2 \vert ) \le \vert V_1\vert + 2 \vert V_3 \vert$. Using the bound of $\vert V_3 \vert$, $\varSigma _{v \in V_3} d_{T}(v) \le 3 \vert V_1 \vert$. $\square$

Definition 2

A cactus graph is a connected graph where any two cycles have at most one vertex in common. Equivalently, every edge of the graph belongs to at most one cycle. Another equivalent definition is that any block of a cactus graph can be either a cycle or an edge. A graph where every component is a cactus graph is called a forest of cacti.

Definition 3

Let $\varTheta$ be a graph on a pair of vertices $\{u,v\}$ that have 3 parallel edges between them. A graph is called a diamond graph if it is obtained by a number of subdivisions of $\varTheta$.

The following proposition characterizes the class of forests of cacti.

Proposition 1

(Fiorini et. al.[9]) A graph is a forest of cacti if and only if it does not have a diamond as a subgraph.

The definition of diamond graphs and the characterisation of forests of cacti have been taken from [9]. Please refer to [7] for further details on notations and definitions in graph theory.

3 Counting Lemma

In this section, we consider a graph G which has a set S, the deletion of which results in a cactus graph. Moreover, we assume that each vertex of the cactus graph $G-S$ has at least three distinct neighbors in G or shares at least two edges with S. Then, it is possible to bound the number of edges in $E(G-S)$ by the number of edges in $E(S,V(G)\setminus S)$. In fact, we exhibit a family of graphs where this bound is tight, up to a constant difference.

Lemma 2

Let G be a graph and $S\subseteq V(G)$ such that $G-S$ is a cactus graph and for all $v\in V(G)\setminus S$ one of the following two conditions holds:

• 1. v has at least 3 distinct neighbors in G, or

• 2. there are at least two edges in E(v, S)

Then $\vert E(G-S)\vert \le 5\vert E(S,V(G) \setminus S) \vert$.

Proof

Let $G'=G-S$. We know that $G'$ is a cactus graph. Let ${{\mathcal {T}}}$ be the block decomposition tree of $G'$ rooted at a vertex of degree one. Throughout the proof, for a block X of $G'$, we represent the corresponding vertex in ${\mathcal {T}}$ as $t_X$. Let $B= E(G')$ and $C=E(S,V(G)\setminus S)$. We need to show that $\vert B \vert \le 5 \vert C \vert$.

Since $G'$ is a cactus graph, by Proposition 1, there cannot be three parallel edges between two vertices of $G'$. Towards the proof, we first define some notations. Let X be a block that is an edge or a cycle of length 2 in $G'$, and such that $t_X$ has only one child $t_Y$, which is a leaf node in ${{\mathcal {T}}}$. Then we say that the blocks X and Y of $G'$ together form a super block. If blocks X and Y form a super block Z, where $t_Y$ is a leaf node, then by parent of the super block Z, we mean the parent of $t_X$ in ${{\mathcal {T}}}$. All other blocks, which are not part of any super block, are called normal blocks. By size of a (super/normal) block Z, denoted by $\mathsf{size}(Z)$, we mean the number of edges in the block Z. To bound the number of edges in $G'$ it is enough to bound the total number of edges in super blocks and normal blocks. Let ${{\mathcal {B}}}_{\ell }$ be the set containing all super blocks and normal blocks which correspond to leaves in ${{\mathcal {T}}}$. Let ${{\mathcal {B}}}_n$ be the set of normal blocks which are not part of ${{\mathcal {B}}}_{\ell }$. Now we define $B_{\ell }$ as the set of edges in the (normal/super) blocks which are part of ${{\mathcal {B}}}_{\ell }$, and $B_n$ as the set of edges in the normal blocks which are part of ${{\mathcal {B}}}_{n}$. To bound the cardinality of B, it is enough to bound the cardinality of $B_{\ell }$ and $B_n$, individually. We partition the edges in C as follows. We say an edge $e\in C$ is incident with a (super/normal) block Z if it is incident with a vertex u in Z, which is not the cut vertex shared with the parent of Z. We use $E_Z$ to denote the set of edges in C, which are incident with the (super/normal) block Z. Let $C_{\ell }$ be the set of edges in C which are incident with (super/normal) blocks in ${{\mathcal {B}}}_{\ell }$. Similarly, let $C_{n}$ be the set of edges in C which are incident with blocks in ${{\mathcal {B}}}_{n}$. Let $r_i$ be the number of blocks of size i in ${{\mathcal {B}}}_{\ell }$. Let $B_{\ell }^{(i)}$ be the set of edges in blocks of size i in ${{\mathcal {B}}}_{\ell }$. Let $C_{\ell }^{(i)}$ be the set of edges in $C_{\ell }$ which are incident with blocks of size i in ${{\mathcal {B}}}_{\ell }$. Notice that $B_{\ell }=\biguplus _{1 \le i \le n} B_{\ell }^{(i)}$ and $C_{\ell }=\biguplus _{1 \le i \le n} C_{\ell }^{(i)}$.

Claim 1

$r_i\le \frac{\vert C_{\ell }^{(i)}\vert }{2}$ for $i\le 4$ and $r_i\le \frac{\vert C_{\ell }^{(i)}\vert }{i-3}$ for $i\ge 5$.

Proof

Bound on $r_1$ Let X be a block of size one in ${{\mathcal {B}}}_\ell$. That is, the block X is a single edge (x, y) and there is a vertex in $\{x,y\}$ which has degree one in $G'$. Let x be the degree one vertex. By our assumption at least 2 edges in $C_{\ell }^{(1)}$ are incident with x. This implies that $\vert E_X \vert \ge 2$. Thus we have that $\vert C_{\ell }^{(1)}\vert = \sum _{\{X: \mathsf{size}(X)=1\}} \vert E_X \vert \ge 2 r_1$. Hence $r_1\le \frac{\vert C_{\ell }^{(1)}\vert }{2}$.

Bound on $r_2$ Let X be a block of size two in ${{\mathcal {B}}}_\ell$. If X is a normal block, then the block X is a cycle y, x, y of length 2. Since X is a leaf block, there is a vertex in X which is not a cut vertex in $G'$. Let x be the vertex in X such that x is not a cut vertex. This implies that $N_{G'}(x)=\{y\}$. Thus, by our assumption, either $\vert E(x,S)\vert \ge 2$ or x has two neighbors in S. In either case, $\vert E(x,S)\vert \ge 2$. That is, $\vert E_X \vert \ge 2$. If X is a super block, then X consists of two blocks Y and Z of size 1 each, such that $t_Y$ has only one child $t_Z$ and $t_Z$ is a leaf node in ${{\mathcal {T}}}$. Let $Z=(x,y)$ be such that x has degree one in $G'$. Thus, by our assumption, we can conclude that $\vert E(x,S)\vert \ge 2$. That is, $\vert E_X \vert \ge 2$. Thus, we have that $\vert C_{\ell }^{(2)}\vert = \sum _{\{X: \mathsf{size}(X)=2\}} \vert E_X \vert \ge 2 r_2$. Hence, $r_2\le \frac{\vert C_{\ell }^{(2)}\vert }{2}$.

Bound on $r_3$ Let X be a (super/normal) block of size three in ${{\mathcal {B}}}_\ell$. That is, either the block X is a cycle x, y, z, x of length 3, or it is a super block consisting of two blocks, where one of them is a cycle of length 2 and the other is an edge. If X is a cycle x, y, z, x, then $t_X$ is a leaf in ${{\mathcal {T}}}$. Let z be the only cut vertex in $\{x,y,z\}$. This implies that the degrees of x and y are exactly 2 in $G'$. Thus, by our assumption, $\vert E(x,S) \vert \ge 1$ and $\vert E(y,S) \vert \ge 1$. This implies that $\vert E_X\vert \ge 2$.

Suppose X is a super block. Then X consists of a cycle x, y, x and an edge (y, z). In this case, only one vertex, either x or z, will be shared with the parent of X and all other vertices will not have a neighbor in $V(G')\setminus X$. Suppose x is the shared vertex with the parent of the block X. Then, the number of distinct neighbors of y and z in $G'$ is exactly 2 and 1, respectively. This implies that $\vert E(y,S)\vert \ge 1$ and $\vert E(z,S)\vert \ge 2$. Consequently, $\vert E_X\vert \ge 3$. By a similar argument, we can show that if z is the shared vertex of the super block X with its parent, then $\vert E_X\vert \ge 3$. Thus, we have that $\vert C_{\ell }^{(3)}\vert = \sum _{\{X: \mathsf{size}(X)=3 \}} \vert E_X \vert \ge 2 r_3$. Hence, $r_3\le \frac{\vert C_{\ell }^{(3)}\vert }{2}$.

Bound on $r_4$ Let X be a (super/normal) block of size four in ${{\mathcal {B}}}_\ell$. That is, either the block X is a cycle of length 4 or it is a super block consisting of two blocks. If X is a cycle of length 4, then $t_X$ is a leaf in ${{\mathcal {T}}}$. This implies that the degree of every vertex in X, except the cut vertex shared with the parent block, is exactly 2 in $G'$. This implies that $\vert E_X\vert \ge 3$.

Suppose X is a super block consisting of two blocks Y and Z, where the size of Y is at most 2 and $t_Z$ is a leaf node in ${{\mathcal {T}}}$. If $\mathsf{size}(Y)=1$, then Z is a cycle of length 3. This implies that at least two vertices in Z have degree exactly 2 in $G'$. Thus, by our assumption, $\vert E_Z\vert \ge 2$ and this implies that $\vert E_X\vert \ge 2$.

If $\mathsf{size}(Y)=2$, then both Y and Z are cycles of length 2. Let x, y, x be the block Y and y, z, y be the block Z. Thus, the number of distinct neighbors of y and z in $G'$ is 2 and 1, respectively. By our assumption, this implies that $\vert E(y,S)\vert \ge 1$ and $\vert E(z,S)\vert \ge 2$. Thus, we have that $\vert E_X\vert \ge 3$. Hence, we conclude that $\vert C_{\ell }^{(4)}\vert = \sum _{\{X: \mathsf{size}(X)=4\}}\vert E_X \vert \ge 2 r_4$. This means, $r_4\le \frac{\vert C_{\ell }^{(4)}\vert }{2}$.

Bound on $r_i$ for $i\ge 5$ Let X be a (super/normal) block of size at least five in ${{\mathcal {B}}}_\ell$. That is, either the block X is a cycle of length i, or it is a super block consisting of two blocks Y and Z such that Z is a cycle of length at least $i-2$ and $t_Z$ is a leaf in ${{\mathcal {T}}}$. In either case, X contains at least $i-3$ vertices (excluding the cut vertex shared with the parent block) having exactly 2 distinct neighbors in $G'$. This implies that $\vert E_X\vert \ge i-3$. Hence, we have that $\vert C_{\ell }^{(i)}\vert = \sum _{\{X: \mathsf{size}(X)=i\}} \vert E_X \vert \ge (i-3) r_i$. Thus, $r_i\le \frac{\vert C_{\ell }^{(i)}\vert }{i-3}$. $\square$

Now we can bound the cardinality of $B_{\ell }$. Let ${C}_{\ell }^{\scriptscriptstyle {(\le 4)}}=\bigcup _{i\le 4} {C}_{\ell }^{(i)}$ and ${C}_{\ell }^{\scriptscriptstyle {(\ge 5)}}=\bigcup _{i\ge 5} {C}_{\ell }^{(i)}$.

$$\begin{aligned} \vert {B}_{\ell }\vert =\sum _i \vert {B}_{\ell }^{(i)}\vert= & {} \sum _i i\cdot r_i \nonumber \\\le & {} 2\left| {C}_{\ell }^{\scriptscriptstyle {(\le 4)}}\right| +\sum _{i\ge 5 } \frac{i}{i-3} \left| {C}_{\ell }^{(i)}\right| \qquad (\text{ By } \text{ Claim }~1) \end{aligned}$$

(1)

$$\begin{aligned}\le & {} 2\left| {C}_{\ell }^{\scriptscriptstyle {(\le 4)}}\right| + \frac{5}{2} \left| {C}_{\ell }^{\scriptscriptstyle {(\ge 5)}}\right| \end{aligned}$$

(2)

What remains is to bound the cardinality of $B_n$. Let ${{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$ be the set of blocks in ${{\mathcal {B}}}_n$ such that the corresponding nodes in ${{\mathcal {T}}}$ have degree at least 3. That is,

$$\begin{aligned} {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}=\{X\in {{\mathcal {B}}}_n~\vert ~ d_{{\mathcal {T}}}(t_X)\ge 3\}. \end{aligned}$$

Let ${B}_n^{\scriptscriptstyle {(\ge 3)}}$ be the set of edges present in the blocks in ${{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$. We first bound the cardinality of ${B}_n^{\scriptscriptstyle {(\ge 3)}}$ and then the cardinality of ${B}_n \setminus {B}_n^{\scriptscriptstyle {(\ge 3)}}$. For a set $X\subseteq V(G')$ let $\mathsf{numcut}_X$ and $\mathsf{numnoncut}_X$ denote the number of cut vertices and non-cut vertices in X, respectively.

$$\begin{aligned} \vert {B}_n^{\scriptscriptstyle {(\ge 3)}} \vert\le & {} \sum _{X\in {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}} \vert X \vert \nonumber \\= & {} \sum _{X\in {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}}\mathsf{numcut}_X+ \mathsf{numnoncut}_X \end{aligned}$$

(3)

The first inequality follows from the fact that the number of edges in a block of a cactus graph is at most the number of vertices in the block. The quantity $\sum _{X\in {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}} \mathsf{numcut}_X$, is at most $\sum _{X\in {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}} d_{{\mathcal {T}}} (t_X)$. This is bounded by three times the number of leaves in ${{\mathcal {T}}}$ (by Lemma 1). Thus by Claim 1, we have the following equation.

$$\begin{aligned} \sum _{X\in {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}} \mathsf{numcut}_X\le & {} \frac{3}{2}\left| {C}_{\ell }^{\scriptscriptstyle {(\le 4)}}\right| + \frac{3}{2} \left| {C}_{\ell }^{\scriptscriptstyle {(\ge 5)}}\right| \end{aligned}$$

(4)

Let $C_n^{\scriptscriptstyle {\ge 3}}$ be the set of edges in $C_n$ which are incident with blocks in ${{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$, and $C_n^{\scriptscriptstyle {\le 2}}$ be the set of edges in $C_n$ which are incident with blocks in ${{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$. For each non-cut vertex x in the block $X\in {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$, there is at least one edge from ${C}_n^{\scriptscriptstyle {(\ge 3)}}$ which is incident with x. This implies the following.

$$\begin{aligned} \sum _{X\in {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}} \mathsf{numnoncut}_X \le \left| C_n^{\scriptscriptstyle {(\ge 3)}} \right| \end{aligned}$$

(5)

Applying Eqs. 4, 5 in Eq. 3, we get the following equation.

$$\begin{aligned} \vert { B}_n^{\scriptscriptstyle {(\ge 3)}} \vert\le & {} \frac{3}{2}\left| {C}_{\ell }^{\scriptscriptstyle {(\le 4)}}\right| + \frac{3}{2} \left| {C}_{\ell }^{\scriptscriptstyle {(\ge 5)}}\right| + \left| C_n^{\scriptscriptstyle {(\ge 3)}} \right| \end{aligned}$$

(6)

Fig. 2

A schematic diagram, when a block X of size at most 2 has only one child which is a super block composed of $Y_1$ and $Y_2$. Here the dotted edges belongs to $E(S,V(G)\setminus S)$

Now we bound the cardinality of ${ B}_n \setminus {B}_n^{\scriptscriptstyle {(\ge 3)}}$. First, we bound the number of edges in the blocks in ${{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$ which are not incident with any edge in $C_n$. Let X be a block in ${{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$, such that there is no edge from $C_n$ incident with it. Since $t_X$ has degree 2 in ${{\mathcal {T}}}$, the number of cut vertices in X is 2. Now, we claim that $\mathsf{size}(X)\le 2$. Suppose not. Then there is a vertex x in X such that the degree of x in $G'$ is two. Thus, by our assumption, x is incident with an edge from $C_n$. This contradicts the fact that no edge from $C_n$ is incident with X. Since X is a block in ${{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$, we have that $t_X$ has only one child. Let the child of $t_X$ be $t_Y$. Now we have the following claim.

Fig. 3

A schematic diagram, when a block X of size at most 2 has only one child Y such that $size(Y)\le 2$ and $d_{{\mathcal {T}}}(t_Y)=2$. Here the dotted edges belongs to $E(S,V(G)\setminus S)$

Claim 2

Either $d_{{\mathcal {T}}}(t_Y)\ge 3$ or $Y\in {{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\le 3)}}$ such that there is an edge from $C_n^{\scriptscriptstyle {(\le 2)}}$ incident with Y.

Proof

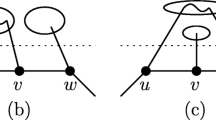
Towards the claim, we first show that $Y\notin {{\mathcal {B}}}_{\ell }$. Suppose not. If Y is a normal block in ${{\mathcal {B}}}_{\ell }$, then X and Y together will form a super block and it contradicts the fact that $X\in {{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$. Suppose Y is a super block in ${{\mathcal {B}}}_{\ell }$. Let $Y_1$ and $Y_2$ be two blocks such that they together form the super block Y. By the definition of super block either $t_{Y_1}$ or $t_{Y_2}$ is a leaf in ${{\mathcal {T}}}$. Without loss of generality assume that $t_{Y_2}$ is a leaf in ${{\mathcal {T}}}$ (see Fig. 2). Consider the vertex x shared by the blocks X and $Y_1$. The number of neighbors of x in $G'$ is 2. Thus, by our assumption, x is incident with a vertex in $C_n$. This contradicts the fact that X is a block in ${{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$ which is not incident with any edge in $C_n$. Now to prove the claim the only case remaining is $Y\in {{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$ and there is no edge from $C_n^{\scriptscriptstyle {(\le 2)}}$ incident with Y (see Fig. 3). Then, the size of Y is at most 2. Consider the vertex x shared by the blocks X and Y. The number of neighbors of x in $G'$ is 2. Thus by our assumption x is incident with a vertex in $C_n$. This contradicts the fact that X be a block in ${{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$ which is not incident with any edge in $C_n$. This proves the claim. $\square$

Using Claim 2 we can show that the total number of edges in the blocks in ${{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$ which are not incident with any edge in $C_n$ is bounded by

$$\begin{aligned} 2 \left( \left| {{\mathcal {C}}}_n^{\scriptscriptstyle {(\le 2)}}\right| + \sum _{\begin{array}{c} \{t\in V({{\mathcal {T}}}):\\ d_{{\mathcal {T}}}(t)\ge 3\} \end{array}} 1 \right)\le & {} 2\left| {{\mathcal {C}}}_n^{\scriptscriptstyle {(\le 2)}} \right| + 2\sum _{i} r_i \nonumber \\\le & {} 2\vert {{\mathcal {C}}}_n^{\scriptscriptstyle {(\le 2)}} \vert + \left| {C}_{\ell }^{\scriptscriptstyle {(\le 4)}}\right| + \left| {C}_{\ell }^{\scriptscriptstyle {(\ge 5)}}\right| \quad (\text{ By } \text{ Claim }~1). \end{aligned}$$

(7)

Now, we bound the number of edges in the blocks in ${{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$ which are incident with some edges in $C_n$. Let X be a such a block. If the size of X is at most two, then there is at least one edge from ${{\mathcal {C}}}_n^{\scriptscriptstyle {(\le 2)}}$ which is incident with X. If the size of X is at least $i\ge 3$, then there are $i-2$ vertices in X such that each of these vertices will have only two neighbors in $G'$. By our assumption, this implies that there are at least $i-2$ edges from ${{\mathcal {C}}}_n^{\scriptscriptstyle {(\le 2)}}$ which are incident with X. Thus, the total number of edges, in the blocks in ${{\mathcal {B}}}_n \setminus {{\mathcal {B}}}_n^{\scriptscriptstyle {(\ge 3)}}$, which are incident with some edges in $C_n$, is bounded by $3 \vert {{\mathcal {C}}}_n^{\scriptscriptstyle {(\le 2)}} \vert$. Hence,

$$\begin{aligned} \left| B_n \setminus B_n^{\scriptscriptstyle {(\ge 3)}}\right|\le & {} 5\left| {{\mathcal {C}}}_n^{\scriptscriptstyle {(\le 2)}} \right| + \left| {C}_{\ell }^{\scriptscriptstyle {(\le 4)}}\right| + \left| {C}_{\ell }^{\scriptscriptstyle {(\ge 5)}}\right| . \end{aligned}$$

(8)

Hence,

$$\begin{aligned} \vert B \vert= & {} \left| B_{\ell }\right| + \left| B_n^{\scriptscriptstyle {(\ge 3)}}\right| + \left| B_n \setminus B_n^{\scriptscriptstyle {(\ge 3)}}\right| \\\le & {} \frac{9}{2}\left| {C}_{\ell }^{\scriptscriptstyle {(\le 4)}}\right| + 5 \left| {C}_{\ell }^{\scriptscriptstyle {(\ge 5)}}\right| + 5\left| {{\mathcal {C}}}_n^{\scriptscriptstyle {(\le 2)}} \right| + \left| {C}_{n}^{\scriptscriptstyle {(\ge 3)}}\right| \qquad (\text{ By } \text{ Eqs. }~2,~6 \text{ and }~8) \\\le & {} 5 \vert C \vert . \end{aligned}$$

This completes the proof of the Lemma. $\square$

Fig. 4

A tight example of Lemma 2. Here $S=\{s\}$

The bound given in Lemma 2 is in fact tight. Given a graph G and a set $S \subseteq V(G)$ such that the assumptions of Lemma 2 hold, consider the edge sets $B = E(G-S)$ and $C = E(S,V(G)\setminus S)$. Figure 4 represents a family where for every pair of consecutively occurring triangle and double parallel edges in the cactus, there is an edge in C. On the other hand, except for the three edges $e_1,e_2$ and $e_3$ in C, each other edge is incident to a distinct triangle. Thus, $\vert B \vert = 5(\vert C \vert -3)$. Hence, this is a family of tight instances.

4 Algorithm for Even Cycle Transversal

In this section, we give a randomized FPT algorithm for Even Cycle Transversal. In other words, the algorithm runs in FPT time and if there is a solution of size at most k, then with high probability the algorithm will return a solution of size at most k for Even Cycle Transversal. The following problem is a generalization of Even Cycle Transversal.

We call a cycle C an even-parity (odd-parity) cycle if $\varSigma _{e \in E(C)} w(e) = 0 \mod 2$ ($\varSigma _{e \in E(C} w(e) = 1 \mod 2$), respectively. For compactness of notation, we define the function $\mathsf{parity}: 2^{E(G)} \rightarrow \{0,1\}$, where for an edge set $E' \subseteq E(G)$, $\mathsf{parity}(E') = \varSigma _{e \in E'} w(e) \mod 2$. In other words, for an even-parity (odd-parity) cycle C, $\mathsf{parity}(E(C)) = 0$ ($\mathsf{parity}(E(C))= 1$), respectively. This should not be confused with cycles of even or odd length, since we will refer to these cycles simply as even and odd cycles.

In what follows, we give a randomized FPT algorithm for Parity Even Cycle Transversal, that runs in ${\mathcal O}(12^k m + nm(n+m))$ worst case time, where m is the number of edges in the input graph. Our algorithm will compute a vertex subset X of size at most k and returns it as a solution if it is indeed a solution and otherwise returns No. First, we apply some reduction rules on the input graph. A reduction rule reduces an instance $(I_1,k)$ of a problem $\varPi$ to another instance $(I_2,k')$ of $\varPi$. The reduction rule is safe when $(I_1,k)$ is a Yes instance if and only if $(I_2,k')$ is a Yes instance. Applying a reduction rule on an input graph is also termed as reducing the graph, and the resultant graph is termed as the reduced graph. Let G be the input graph. Our algorithm will set $X{:}{=}\emptyset$ initially. After the reduction rules have been exhaustively applied on the input graph G, we show that for every solution at least $\frac{1}{6}$ fraction of edges is incident with the vertices of the solution. Let $G'$ be the reduced graph. Then our algorithm picks an edge and its endpoint (say v) at random, puts the vertex into X. Then again we apply reduction rules exhaustively on $G'-\{v\}$ such that in the reduced graph for every solution at least $\frac{1}{6}$ fraction of edges is incident with the vertices of the solution. Again our algorithm picks an edge and its endpoint at random, puts the vertex into X. The algorithm continues the above process (i.e, applying reduction rules on the graph, randomly picking an edge and choosing one of its end points) k times or until the reduced graph is empty. If there is a solution of size at most k in G, then this procedure outputs a solution (that is, X is indeed a solution) with probability at least $12^{-k}$. Then by repeating this procedure $12^k$ times, we obtain constant success probability.

Now, we describe the reduction rules for Parity Even Cycle Transversal and prove their safeness.

Reduction Rule 1

If there is a vertex v in G which is not part of any even-parity cycle, then delete v from G.

Lemma 3

Reduction Rule 1 is safe.

Proof

Suppose we delete v from G. If C is an even-parity cycle of G, it is still an even-parity cycle of $G - \{v\}$. Similarly, if there is an even-parity cycle $C'$ in $G - \{v\}$, then $C'$ is also an even-parity cycle in G. Now, Suppose (G, k) is a Yes instance of Parity Even Cycle Transversal. Let S be a solution of size at most k for G. Since $G-\{v\}$ is a subgraph of G and S is a solution for G, we have that $S\setminus \{v\}$ is a solution for the reduced graph $G - \{v\}$ as well. Therefore, $(G - \{v\},k)$ is also a Yes instance of Parity Even Cycle Transversal.

Conversely, suppose the reduced instance is a Yes instance. Suppose $S'$ is a solution of size at most k for $G - \{v\}$. Then, $S'$ hits all even-parity cycles of $G - \{v\}$. This means, that $S'$ also hits all even-parity cycles of G, and therefore $S'$ is a solution in G. Thus, (G, k) is a Yes instance of Parity Even Cycle Transversal. $\square$

Lemma 4

There is an algorithm which, given a graph G and $w~:~E(G)\rightarrow \{0,1\}$, runs in time ${\mathcal O}(\vert E(G)\vert (\vert V(G)\vert +\vert E(G)\vert ) )$ and outputs all vertices in G that are not part of any even-parity cycle.

Proof

It is known that there is an algorithm ${{\mathcal {A}}}$, which takes as input a graph H, and two vertices $s,t\in V(H)$, and checks whether there is an odd length path from s to t in time ${\mathcal O}(\vert V(H)\vert +\vert E(H)\vert )$ [1, 18]. We use algorithm ${{\mathcal {A}}}$ to design an algorithm ${{\mathcal {A}}}'$ mentioned in the lemma. We construct, from the given graph G and edge-weight function w, a graph $\hat{G}$ without edge weights. This is done by subdividing every edge of weight 0. Notice that $V(G)\subseteq V({\hat{G}})$. By this reduction, any vertex in V(G) belongs to an even-parity cycle in G if and only if it belongs to an even cycle in $\hat{G}$. Now, for each edge $(u,v)\in E({\hat{G}})$, run algorithm ${{\mathcal {A}}}$, and check whether there is an odd length path from v to u in the graph $\hat{G}-\{(v,u)\}$ and marks both u and v if there is an odd length path. Then algorithm ${{\mathcal {A}}}'$ return all the unmarked vertices from V(G). The running time of the algorithm ${{\mathcal {A}}}'$ is ${\mathcal O}(\vert E(G)\vert (\vert V(G)\vert +\vert E(G)\vert ) )$. $\square$

Reduction Rule 2

Let [x, y, z] be a path in G and the degree of y be exactly 2. Then delete y from G and add a new edge $e_1 = (x,z)$ with weight $w(e_1) = w((x,y)) + w((y,z)) \mod 2$ (see Fig. 5).

Fig. 5

Reduction rule 2. Here the weight of new edge (x, z) is $w((x,z))=(w((x,y))+w((y,z)) \mod 2$

Lemma 5

Reduction Rule 2 is safe.

Proof

Suppose C is a cycle of parity p in G, which contains the vertex y. Then, since $d_G (y)=2$, C must contain the path [x, y, z]. In the reduced graph $G'$, C is reduced to a cycle $C'$ which contains the edge $e_1=(x,z)$. By definition of $w(e_1)$, the parity of the reduced cycle is still p. On the other hand, if $C'$ is a cycle of parity p in the reduced graph $G'$, and $C'$ does not contain the new edge $e_1$, then $C'$ is a cycle of the original graph G. Otherwise, there is a corresponding cycle C in G, which contains the path [x, y, z] instead of the newly added edge $e_1$. Again, by definition of $w(e_1)$, the parities of $C'$ and C are the same.

Now, suppose (G, k) is a Yes instance for Parity Even Cycle Transversal. Let S be a solution set in G. Then S hits all even-parity cycles of G. We have argued that any cycle in G that contains y also contains x and z. Thus, if y was contained in S, then $S \cup \{x\} \setminus \{y\}$ is also a solution that hits all even-parity cycles of G. Since the parities of cycles are preserved by this reduction, it implies that $S \cup \{x\} \setminus \{y\}$ is a solution that hits all even-parity cycles of the reduced graph, and that the reduced instance is also a Yes instance.

Conversely, suppose the reduced instance is a Yes instance. let $S'$ be a solution set of $G'$. We will show that $S'$ is also a solution for G. Suppose there is an even-parity cycle C in G, that is not hit by $S'$, then this cycle must have the vertex y. This implies that the cycle must have the path [x, y, z]. Let $P = C - \{y\}$. Look at the cycle $C'$ formed by the set of edges $E(P) \cup \{e_1\}$ in $G'$. This is also an even-parity cycle which is not hit by $S'$. This contradicts the fact that $S'$ is a solution set of $G'$. Thus, (G, k) must be a Yes instance of Parity Even Cycle Transversal.

Reduction Rule 3

Let x, y be two vertices with two parallel edges $e_1$ and $e_2$. Let $w(e_1)=1, w(e_2)=0$. Further, $e_3=(y,z)$ is an edge in G, with $z \ne x$, and $d_G(y) = 3$. Then delete y from the graph G and add two new edges $f_1, f_0 = (x,z)$. Define $w(f_1) = 1$ and $w(f_0) = 0$ (see Fig. 6).

Fig. 6

Reduction rule 3

Lemma 6

Reduction Rule 3 is safe.

Proof

Suppose (G, k) is a Yes instance. Let S be a solution for (G, k). If S contains y, then the set $S \cup \{x\} \setminus \{y\}$ is also a solution for (G, k), because any even-parity cycle that passes through y also passes through x. So, we assume that the solution set S does not contain y. Now we claim that S is also a solution for $(G',k)$. Let $C'$ be an even-parity cycle in $G'$. If $C'$ does not contain $f_1$ or $f_0$, then $C'$ is also an even-parity cycle in G and hence $V(C')\cap S \ne \emptyset$. Now, suppose $E(C')\cap \{f_0,f_1\}\ne \emptyset$. Since $C'$ is an even-parity cycle, $\{f_0,f_1\} \nsubseteq E(C')$. Let $f_i \in E(C')$, where $i\in \{0,1\}$. Let $j\in \{1,2\}$ such that $w(e_j)+w(e_3)=w(f_i) \mod 2$. We define C to be the cycle in G formed by the edges $(E(C') \cup \{e_j,e_3\})\setminus \{f_i\}$. Since $C'$ is an even-parity cycle, $E(C)=(E(C') \cup \{e_j,e_3\})\setminus \{f_i\}$, and $w(e_j)+w(e_3)=w(f_i) \mod 2$, we have that C is an even-parity cycle in G and $V(C)\setminus \{y\}=V(C')$. Since S is a solution for (G, k) not containing y, $V(C')\cap S=V(C)\cap S \ne \emptyset$. Hence S is a solution for $(G',k)$.

Suppose $(G',k)$ is a Yes instance. Let $S'$ be a solution for $(G',k)$. We will show that $S'$ is also a solution for (G, k). Let C be an even-parity cycle of G. If V(C) does not contain y, then C is also an even-parity cycle in $G'$. This implies that $V(C)\cap S'\ne \emptyset$. Now, suppose $y\in V(C)$. Since C is an even-parity cycle and $y\in V(C)$, there exists $i\in \{1,2\}$, such that $\{e_i,e_3\}\subseteq E(C)$ and $e_j\notin E(C)$, where $j \in \{1,2\}\setminus \{i\}$. Let $r=w(e_i)+w(e_3)\mod 2$. We define $C'$ to be the cycle in $G'$ formed by the edges $(E(C)\cup \{f_r\})\setminus \{e_i,e_3\}$. Since C is an even-parity cycle, $C'$ is also an even-parity cycle. This implies that $V(C)\cap S'= V(C')\cap S \ne \emptyset$. This completes the proof of the lemma. $\square$

Reduction Rule 4

Let $\{x_1,y\}$ be a pair of vertices that have two parallel edges $e_1$ and $e_2$, with $w(e_1)=1, w(e_2)=0$. Let there be another vertex $x_2 \ne x_1$ such that $\{x_2,y\}$ have two parallel edges $e_3$ and $e_4$. It also holds that $w(e_3)=1, w(e_4)=0$. Let $d_G(y)=4$. Then delete y from G and add two new parallel edges $f_1$, $f_0$ between $x_1$ and $x_2$. We define $w(f_1) = 1$ and $w(f_0) = 0$ (see Fig. 7).

Lemma 7

Reduction Rule 4 is safe.

Fig. 7

Reduction rule 4

Proof

Suppose (G, k) is a Yes instance. Let S be a solution for (G, k). If S contains y, then the set $S \cup \{x\} \setminus \{y\}$ is also a solution for (G, k), because any even-parity cycle that passes through y also passes through x. So, we assume that the solution set S does not contain y. Now we claim that S is also a solution for $(G',k)$. Let $C'$ be an even-parity cycle in $G'$. If $C'$ does not contain $f_1$ or $f_0$, then $C'$ is also an even-parity cycle in G and hence $V(C')\cap S \ne \emptyset$. Now, suppose $E(C')\cap \{f_0,f_1\}\ne \emptyset$. Since $C'$ is an even-parity cycle, $\{f_0,f_1\} \nsubseteq E(C')$. So there is exactly one $i \in \{0,1\}$ such that $f_i \in E(C')$. Let $j\in \{1,2\}$ and $j'\in \{3,4\}$ such that $w(e_j)+w(e_{j'})=w(f_i) \mod 2$. We define C to be the cycle in G formed by the edges $(E(C') \cup \{e_j,e_{j'}\})\setminus \{f_i\}$. Since $C'$ is an even-parity cycle, $E(C)=(E(C') \cup \{e_j,e_{j'}\})\setminus \{f_i\}$, and $w(e_j)+w(e_{j'})=w(f_i) \mod 2$, we have that C is an even-parity cycle in G and $V(C)\setminus \{y\}=V(C')$. Since S is a solution for (G, k) not containing y, $V(C')\cap S=V(C)\cap S \ne \emptyset$. Hence S is a solution for $(G',k)$.

Suppose $(G',k)$ is a Yes instance. Let $S'$ be a solution for $(G',k)$. We will show that $S'$ is also a solution for (G, k). Let C be an even-parity cycle of G. If V(C) does not contain y, then C is also an even-parity cycle in $G'$. This implies that $V(C)\cap S'\ne \emptyset$. Now, suppose $y\in V(C)$. Since C is an even-parity cycle and $y\in V(C)$, there exist $i\in \{1,2\}$ and $j\in \{3,4\}$, such that $\{e_i,e_{j}\}\subseteq E(C)$ and $e_{i'},e_{j'}\notin E(C)$, where $i' \in \{1,2\}\setminus \{i\}$ and $j' \in \{3,4\}\setminus \{j\}$. Let $r=w(e_i)+w(e_j)\mod 2$. We define $C'$ to be the cycle in $G'$ formed by the edges $(E(C)\cup \{f_r\})\setminus \{e_i,e_j\}$. Since C is an even-parity cycle, $C'$ is also an even-parity cycle. This implies that $V(C)\cap S'= V(C')\cap S \ne \emptyset$. This completes the proof of the lemma. $\square$

In our algorithm, in all steps we apply Reduction Rules 1, 2, 3 and 4 exhaustively as long as they are applicable. The resultant graph is called a reduced graph.

Observation 1

Let (G, k) be an instance of Parity Even Cycle Transversal and $(G',k)$ be the instance obtained after applying Reduction Rules 1, 2, 3 and 4. Then if S is a solution for $(G',k)$, then S is a solution for (G, k).

The proof of Observation 1 follows from the Lemmata 3, 5, 6 and 7.

We give the definition of an odd-parity (even-parity) cactus graph and relate it to Parity Even Cycle Transversal, respectively.

Definition 4

A cactus graph, where the edges have weights from $\{0,1\}$, is an odd-parity (even-parity) cactus graph when every block of the graph is either an odd-parity (even-parity) cycle, or an edge, respectively.

Lemma 8

Let G be a connected graph and $w:E(G) \rightarrow \{0,1\}$ be a weight function on the edges. The graph G does not contain any cycle C with $\mathsf{parity}(C) = 0$ if and only if G is an odd-parity cactus graph.

Proof

Suppose G does not contain any even-parity cycle. Then every cycle in G must be of odd-parity. Thus, if G was a cactus graph then it must be an odd-parity cactus graph. Suppose G is not a cactus graph. Then, by Proposition 1, there is a diamond D in G. Let the diamond be defined at the vertex pair $\{u,v\}$ by the three disjoint paths $P_1, P_2, P_3$. Let $\mathsf{parity}(P_1)=p_1, \mathsf{parity}(P_2)=p_2, \mathsf{parity}(P_3)=p_3$. By Pigeonhole Principle, at least two among $P_1,P_2$ and $P_3$ must have the same parity. Without loss of generality, let $P_1$ and $P_2$ have the same parity. Then the cycle $[P_1uP_2v]$ is of even parity, which is a contradiction to the assumption on G. Hence, G must be an odd-parity cactus graph.

Conversely, suppose G is an odd-parity cactus graph. Then there is a block decomposition of G where every block is either an odd-parity cycle or an edge. By definition of a block, any cycle C of G must be contained completely inside a block. This implies that there are no even-parity cycles in G. $\square$

Let G be a graph and let S be a set of vertices that hits all even-parity cycles in G. Then each component of $G -S$ does not contain an even-parity cycle. By Lemma 8, it follows that $G-S$ is a forest of odd-parity cacti.

Observation 2

Let G be a reduced graph for Parity Even Cycle Transversal and S be a solution for Parity Even Cycle Transversal in G. Then, for each connected component C of $G-S$, $G[V(C) \cup S]$ and S satisfy the conditions of Lemma 2.

Proof

Let $v \in C$ be a vertex that does not have at least three distinct neighbours in G. Suppose there is at most one edge in E(v, S). Also note that v cannot have one neighbour in V(C) with at least two parallel edges of the same parity: this would mean that two parallel edges of the same parity form an even-parity cycle. Also, notice that if v has one neighbour with at least three parallel edges, then by pigeonhole principle, at least two of the parallel edges are of the same parity. Since Reduction Rule 1 does not apply any more, v must have exactly two distinct neighbours. Since Reduction Rules 2, 3 and 4 are no longer applicable, a vertex with exactly two distinct neighbours does not exist in the reduced graph. This is a contradiction. Thus, in the reduced instance, every vertex in C satisfies the conditions of Lemma 2. $\square$

Now, we are ready to describe the algorithm for Parity Even Cycle Transversal. Informally, the algorithm runs for $12^k$ rounds. In each round, a vertex subset of size at most k is obtained. We show that, given a Yes instance, with high probability there is at least one round where the constructed vertex subset is a solution set for Parity Even Cycle Transversal. A No instance is always detected correctly by the algorithm.

Theorem 3

Parity Even Cycle Transversal has a randomized algorithm with worst case run time ${\mathcal O}(12^k nm(n+m))$, where n and m are the number of vertices and edges in the input graph, respectively. The algorithm outputs No if the input is a No instance and for a Yes instance, with probability $1-\frac{1}{e}$, returns a solution.

Proof

Let (G, k) be the input instance. Our algorithm runs a procedure (call it procedure ${{\mathcal {Q}}}$) $12^k$ times. The procedure Q has at most k iterative steps and is as follows: We set $S {:}{=} \emptyset$ and $G'{:}{=}G$ to start with. We apply Reduction Rules 1, 2, 3 and 4 to the graph $G'$ as long as we can. If the reduced graph $G''$ is non-empty, we pick an edge $e=(u,v) \in E(G'')$ uniformly at random and then, with equal probability, we pick one of the two endpoints (say the vertex picked is v). In other words, we pick a vertex with probability proportional to its degree. Now we set $S{:}{=}S \cup \{v\}$ and $G'{:}{=}G''-\{v\}$. We do this for at most k steps, stopping whenever the graph becomes empty. Notice that the algorithm could stop if the graph becomes empty after applying the reduction rules exhaustively. Then we check if the constructed set S is a solution set of Parity Even Cycle Transversal for the input graph G. Note that recognizing a forest of odd-parity cacti is equivalent to building a block-decomposition and checking if each block is an odd-parity cycle or an edge – this step can be performed in linear time [14]. If all the $12^k$ executions of procedure Q fail to find out a solution, then the algorithm will output No.

Now we analyse the success probability of the algorithm. For any $i\in \{0,\ldots ,k\}$, let $S_i$ be the set of vertices obtained at the end of step i. Consider the step $i+1$, where $i\in \{0,\ldots ,k-1\}$. Let $G_{i+1}$ be the reduced graph in step $i+1$. By Observation 1, if D is solution of cardinality at most $k-i$ for $(G_{i+1},k-i)$, then $S_i\cup D$ is a solution for (G, k). Suppose there is a solution $S^*_{k-i}$ of size at most $k-i$ in $G_{i+1}$. By Observation 2, for each component C of $G_{i+1}-S^*_{k-i}$, $G_{i+1}[V(C)\cup S^*_{k-i}]$ and $S^*_{k-i}$ satisfy the conditions of Lemma 2. By the conditions of Lemma 2, for each component C of $G_{i+1}-S^*_{k-i}$, $\vert E(C) \vert \le \frac{5}{6} \vert E(G_{i+1}[V(C)\cup S^*_{k-i}]) \vert$. This implies that $\vert E(G_{i+1}-S^*_{k-i}) \vert \le \frac{5}{6} \vert E(G_{i+1}) \vert$. The algorithm chooses a vertex in step $i+1$ using a random process. We say that the vertex chosen by the algorithm in step $i+1$ is good if the algorithm chooses a vertex from $S^*_{k-i}$. Since $\vert E(G_{i+1}-S^*_{k-i}) \vert \le \frac{5}{6} \vert E(G_{i+1}) \vert$, the probability that an edge incident with a vertex from $S^*_{k-i}$, is picked uniformly at random in step $i+1$, is at least $\frac{1}{6}$. Once we have picked this edge, the probability that we choose an end point of the edge that belongs to $S^*_{k-i}$ is at least $\frac{1}{2}$. Therefore, the probability that a good vertex is chosen in step $i+1$ is at least $\frac{1}{2}\cdot \frac{1}{6}= \frac{1}{12}$. We succeed in finding a solution set S for Parity Even Cycle Transversal if every step picks a good vertex in that step. Thus, the probability of failure in the k-step procedure is at most $1 - (\frac{1}{12})^k$. We repeat the procedure Q $12^k$ times. The probability of failure of this many-round procedure is the probability that procedure Q fails in all the $12^k$ executions, which is at most $\left( 1 - \left( \frac{1}{12}\right) ^k\right) ^{12^k} \le \frac{1}{e}$ (by Fact 1).

Now we prove the claimed running time. By Lemma 4 we can identify and apply Reduction Rule 1 in time ${\mathcal O}(m(n+m))$. Notice that checking whether any of Reduction Rules 2, 3 and 4, is applicable, takes ${\mathcal O}(m)$ time and these reduction rules can be applied in constant time. Since each application of a reduction rule reduces the number of vertices by at least one, the total number of times these reduction rules are applicable in the procedure Q is at most n. Thus, the total time spent for applying Reduction Rules in the procedure Q is ${\mathcal O}(nm(n+m))$. Moreover, in each iteration of procedure Q, we pick an edge and one of its endpoints in ${\mathcal O}(m)$ time. Therefore, over k iterations, we spend ${\mathcal O}(km)$ time picking edges and a corresponding endpoint. This means that one execution of procedure Q takes time ${\mathcal O}(nm(n+m)+km)={\mathcal O}(nm(n+m))$. There are $12^k$ executions which makes the total running time to be ${\mathcal O}(12^k nm(n+m))$. $\square$

Corollary 1

Even Cycle Transversal has a randomized algorithm with worst case run time ${\mathcal O}(12^k nm(n+m))$, where n and m are the number of vertices and edges in the input graph, respectively. The algorithm outputs No if the input is a No instance and for a Yes instance, with probability $1-\frac{1}{e}$, returns a solution.

5 Algorithm for Diamond Hitting Set

In this section, we give a randomized FPT algorithm for Diamond Hitting Set. It was shown in [9] that there is a set of safe reduction rules that can be applied to reduce the input graph to a graph with certain properties.

Proposition 2

(Fiorini et. al. [9]) There is a polynomial time algorithm which takes a graph H as input and outputs a graph $H'$ such that (i) the cardinalities of minimum diamond hitting sets of H and $H'$ are the same, (ii) every vertex of $H'$ either has at least three distinct neighbours or is incident with three parallel edges, (iii) $V(H')\subseteq V(H)$, and (iv) if $S'$ is a diamond hitting set of $H'$, then $S'$ is a diamond hitting set of H as well.

Proposition 2 follows from the work of Fiorini et. al. [9]. In Section 3 of [9], two reduction rules are defined to get the graph $H'$, where $H'$ is a minor of H (i.e, $H'$ is obtained from a subgraph of H, by a series of edge contractions) and property (ii) of Proposition 2 is mentioned. The property (iv) of Proposition 2 is mentioned in Section 4 of [9]. We call the output of the algorithm mentioned in Proposition 2 as reduced graph of Diamond Hitting Set.

Observation 3

Let G be a reduced graph for Diamond Hitting Set and S be a solution in G. Then, for each connected component C in $G-S$, $G[V(C) \cup S]$ and S satisfy the conditions of Lemma 2.

Proof

Let G be the reduced instance. Given a diamond-hitting set S, Proposition 1 shows that $G-S$ must be a forest of cacti. Thus, for each component C of $G-S$, C is a cactus graph. Let $v \in C$ be a vertex that does not have at least three distinct neighbours. Then, v must have at least three parallel edges with a neighbour u. Since there are no diamonds in C, it must be the case that $u \in S$ and therefore, there are at least two edges in E(v, S). Thus, in the reduced instance, every vertex in C satisfies the conditions of Lemma 2. $\square$

Now, we can design an algorithm for Diamond Hitting Set, that is very similar to the algorithm for Parity Even Cycle Transversal. The algorithm runs for $12^k$ rounds. In each round, a set of size at most k is obtained. We show that, for a Yes instance, with high probability there is at least one round where the constructed set is a solution set for Diamond Hitting Set. The algorithm detects No instances correctly.

Theorem 4

Diamond Hitting Set has a randomized algorithm with worst case running time $12^k n^{\mathcal {O}(1)}$, where n is the number of vertices in the input graph. The algorithm outputs No if the input is a No instance and for a Yes instance, with probability $1-\frac{1}{e}$, returns a solution.

Proof

(proof sketch) The algorithm is similar in description to the algorithm mentioned in the proof of Theorem 3. In this algorithm, instead of applying Reduction Rules 1, 2, 3 and 4, we exhaustively apply the reduction algorithm mentioned in Proposition 2 and check whether the constructed set is a diamond hitting set of G. The correctness of the algorithm follows from arguments similar to those given in the proof of Theorem 3; in the arguments we replace Observation 1 with property (iv) of Proposition 2 and Observation 2 with Observation 3. The claimed bound on the running time can be proved by using arguments similar to that used in the proof of Theorem 3. $\square$

6 Conclusion

In this work we designed randomized algorithms for Even Cycle Transversal and Diamond Hitting Set with worst case run time $12^k n^{\mathcal {O}(1)}$. It is natural to ask whether we can get fast deterministic algorithms for these problems. Another question is to find Strong Exponential Time Hypothesis based lower bounds on the base of the exponent in the running time for Even Cycle Transversal and Diamond Hitting Set.