Optimistically tuning synchronous byzantine consensus: another win for null messages

“I am prepared for the worst, but hope for the best”

Benjamin Disraeli [9]

Abstract

Modular methods that transform Byzantine consensus protocols for the synchronous model into ones that are fast and communication efficient in failure-free executions are presented. Small and short protocol segments called layers are custom designed to act as a highly efficient preliminary stage that solves Consensus if no failures occur. When composed with a Byzantine consensus protocol of choice, they allow considerable control over the tradeoff in the combined protocol’s behavior in the presence of failures and its performance in their absence. In failure-free executions, they are more efficient than all existing Byzantine consensus protocols. In the presence of failures, they incur a small cost over the complexity of the original consensus protocol being transformed. A key ingredient underlying the efficiency of the new layers is the judicious use of null messages for broadcasting information in failure-free runs. In particular, the notion of a silent validation round, which implements such a broadcast, is defined and used in several ways.

1 Introduction

Byzantine-faulty processes are able collude arbitrarily and can, in particular, send arbitrary messages. Consequently, tolerating Byzantine failures can be costly. In their seminal paper [38] Pease, Shostak and Lamport defined the Byzantine consensus problem (originally called Interactive Consistency), and presented a protocol in which processes send $\varOmega (n^t)$ bits of information to each other, and decide at the end of $t+1$ synchronous rounds. (n is the number of processes, and $t<n/3$ is a bound on the number of faults that the protocol tolerates.) While the complexity of Byzantine Consensus protocols has been reduced in the four decades since then, it is still much higher than that of solving Consensus in the crash failure model and in other benign models. Since faulty processors can lie arbitrarily, messages in the Byzantine model carry significantly less useful information. The contents of a message cannot be trusted, and so even when no failures occur, just the a priori possibility of failures significantly complicates protocols. Of course, communication is not completely useless in the Byzantine model, since a process can derive useful conclusions when it receives many messages stating the same fact. Indeed, Consensus protocols in this model use many more messages than ones in less malicious settings such as the authenticated Byzantine or crash models. (In the absence of signatures, Byzantine processes can readily lie about what other processes sent them.)

Whereas the damage that malicious cyber attacks may cause is considerable and tolerating Byzantine faults is important, in many settings such faults are typically rare. Consequently, paying a high premium for fault-tolerance even when failures do not occur is clearly undesirable. Dolev et al. [11], introduced “early stopping” solutions whose complexity depends in an adaptive manner on the number of actual failures f in an execution. In many settings, however, executions in which no failures occur, i.e., where $f=0$, are much more prevalent than ones with $f\ge 1$. This paper shows that Consensus protocols can be tuned to be extremely efficient in failure-free executions, with no significant effect on their complexity when failures do occur.

One way to reduce the number of messages sent by a protocol is to use synchrony to our advantage. For example, it is possible to encode information by the time, or round number, in which a message is sent. This trades $2^k$ rounds in exchange for saving k bits, which is rather costly. A more effective way to exploit synchrony is by using null messages. In a synchronous message-passing model with reliable links, the fact that no message is received implies that none was sent. Lamport argued that this provides a natural way to transmit information by not sending a message [29]. He considered not sending a message as a form of sending a null message, which is received once the bound on transmission time is reached. The advantage of sending a null message over sending a very short message is considerable. Preparing and sending an explicit message incurs costs in memory, computation and bandwidth. Indeed, using the popular IEEE 802.3 standard [23], for example, requires more than 690 bits of traffic even for a message with single bit content. (IEEE 802.3 Ethernet is the most widely used link-layer protocol.) A natural question then becomes how to utilize null messages effectively in protocol design.

In this paper, we define a new primitive based on null messages, which is called a silent validation round (svr). It allows all processes to detect that a certain milestone (a global property of interest) has been reached. As we show, in failure-free runs this can be used to provide useful information and allow progress at a cost of a single round, and no communication costs whatsoever. In essence, an svr “sends” a quadratic number of null messages to achieve an all-to-all broadcast among the processes. By extensively using null messages and svrs, we design elegant layers consisting of three or four rounds that can be used to modify any Consensus protocol to be very quick and efficient in failure-free executions. In executions with failures, the tuned protocol maintains similar complexity to the original protocol.

This work makes two different, but complementary, types of contributions. First, from an algorithmic perspective, the tuning layers.

• We provide a general transformation for Consensus protocols that, in failure-free runs, decides optimally fast (after 2 rounds), and requires a factor of $\varOmega (n)$ less communication than the best previously-known optimally fast protocol.

• We provide a second general transformation that results in better communication costs in failure-free runs than any known protocol. Its communication complexity (bits and messages) in failure-free runs is a factor of 24 better than the next best protocol. Moreover, our protocol decides after 3 rounds, whereas the previous protocol requires up to 8.

• In addition to providing exceptional efficiency in failure-free rounds, our transformations allow the designer to choose any protocol of her liking to execute in case failures do occur. In this manner, she can determine the most suitable complexity tradeoffs for the latter case.

Second, from the perspective of principles and techniques for protocol design, this work initiates an investigation of how null messages can be used effectively in the Byzantine model. To this end,

• We present methods for using null messages in a Byzantine setting.

• In particular, we present and formalize the notion of a silent validation round. svr is a powerful tool for failure-free optimization.

• The power of the above techniques is demonstrated by their successful use in the design of our new efficient Consensus protocols.

1.1 Related work

Optimizing for specific cases of interest is a well known concept. Indeed, Hadzilacos and Halpern in [20] use the term cautiously optimistic to describe protocols that assume failure-free operation, but provide mechanisms to handle failures if they do occur. The fast-path slow-path approach was originally applied in the shared-memory domain by Lamport [30]. Additional examples in the shared-memory domain can be found in, e.g., [25, 39]. In message-passing systems, optimizing for failure-free executions plays a significant role in various problems [13, 19, 27, 31, 33], as well as in well-known practical solutions to the state replication problem (e.g., [6, 26]).

Null messages are particularly useful for optimizing the communication costs of failure-free executions. In a previous work [18], we used null messages for a different problem—Atomic Commitment—in the more benign crash failure model. In this setting, [18] identified the silent choir pattern in which a set of (possibly faulty) processes refrain from sending a message to a given process. A silent choir was shown to be the only way in which the process can gain knowledge regarding certain facts about another process without an explicit message chain between the two. In this work we tackle the more challenging Byzantine-failure model, in which the message patterns necessary for knowledge gain are substantially different than those in the crash-failure model. We focus on the popular Consensus problem and provide general primitives for using null messages efficiently.

Hadzilacos and Halpern [21] studied efficient solutions to the Byzantine Agreement problem (BA) in a variety of failure models, ranging from crash to Byzantine failures. Their work makes extensive and judicious use of null messages to obtain protocols that are message-optimal in failure-free runs. In particular, [21] uses null messages in a flexible manner to encode different facts in different rounds, and even to report different values to different processes in the same round. For the Byzantine model, their Byzantine Agreement protocol achieves the tight bound of $n(t+1)/4$ messages in failure-free executions, but requires more than t rounds to halt. While Consensus can be solved by simply invoking n instances of their BA protocol, this does not provide an efficient solution to Consensus.

Dolev et al. [11], introduced the concept of “early stopping” protocols, whose complexity is adaptive to the number of actual failures f in an execution. Such protocols for Consensus often decide after $\min \{ t + 1, f + 2\}$ rounds [1, 11, 34, 37]. These solutions provide a form of graceful performance degradation as the number of failures increases. In many early stopping protocols, failure-free executions incur complexity costs in order to ensure that executions with failures would decide early as well. In particular, all of the early-stopping protocols cited above cost $\varOmega (n^3)$ bits in failure-free runs, compared to our O(nt) bits.

Our solutions come in the form of short modular layers similar in spirit to the short and elegant layer used by Turpin and Coan [40], which provided a general transformation of binary Consensus protocols into multi-valued ones.

The remainder of the paper is organized as follows. The next section formally defines our system model. In Sect. 3 we provide efficient techniques for using null messages to convey information in Byzantine synchronous message-passing systems. Section 4 applies the methods from Sect. 3 to design short layers for Byzantine Consensus. It starts by presenting two layers for binary Consensus, and shows how to modify them to handle a multi-valued Consensus. Finally, concluding remarks are discussed in Sect. 5. Proofs of all statements appear either in the main text or in the Appendix.

2 Model and preliminaries

2.1 Consensus

Reaching agreement on values is a fundamental problem in distributed systems. While voting is a natural mechanism for this purpose, it is not implementable when failures are possible. The Byzantine Consensus problem (originally called Interactive Consistency) was defined in the seminal paper of Pease, Shostak and Lamport [38] in 1980. Broadly speaking, Byzantine Consensus considers the problem of reaching agreement among a group of n parties, up to t of which can be Byzantine faults and deviate from the protocol arbitrarily. Pease, Shostak and Lamport presented a protocol that solves the problem in $t+1$ rounds whenever $n>3t$, and proved that no solution for $n\le 3t$ exists [32, 38]. Fischer and Lynch later showed that $t+1$ rounds are necessary in the worst-case run of any Byzantine Consensus protocol [16]. In the original solution of [32, 38], processes never decide before the end of $t+1$ rounds. Moreover, each process sends an exponential number of bits of information (and performs an exponential amount of computation) in every execution. The authors leave as an open problem the design of more efficient solutions to Byzantine Consensus, and the quest for efficient solutions to this problem has received a great deal of attention over the last four decades. For a recent partial survey, see [1].

In this paper we use the standard definition for the Consensus problem. Each process i starts with some initial proposal $v_i\in V$, and all correct processes need to reach a common decision. All runs of a Consensus protocol are required to satisfy the following conditions:

${\textsc {Consensus}}$

Decision :

Every correct process must eventually decide,

Agreement :

All correct processes make the same decision, and

Validity :

If all correct processes have the same initial proposal, then all correct processes decide on this value.

When $V=\{0,1\}$ the problem is called binary Consensus, and when $|V|>2$ we refer to it as multi-valued Consensus. A Byzantine Consensus protocol is a Consensus protocol that can tolerate up to t Byzantine failures per run.

2.2 Model of computation

We consider the standard synchronous message-passing model for Byzantine failures (without signatures). We assume a set ${\mathbb {P}}=\{0,1,\ldots ,n-1\}$ of $n> 2$ processes. Each pair of processes is connected by a two-way communication link, and for each message the receiver knows the identity of the sender. All processes share a discrete global clock that starts at time 0 and advances by increments of one. At any given time $m\ge 0$, each process is in a well-defined local state. For simplicity, we assume that the local state of each process i at a given point consists of its initial proposal $v_i$, the current time m, and the finite sequence of the actions that i has performed up to that time (including the messages it has sent) as well as the messages that process i has received so far. In particular, its local state at time 0 has the form $(v_i,0,\{ \} )$.

A protocol ${\mathcal {P}}$ specifies what messages a process should send and what decisions it should take, as a deterministic function of its local state. Communication in the system proceeds in a sequence of rounds, with round $m+1$ taking place between time m and time $m+1$, for $m\ge 0$. A message sent from a process i to j at time m will reach j by time $m+1$. We think of such a message as being sent in round $m+1$, and as being received in the same round. In a given execution, a process is either correct or faulty. Correct processes faithfully follow the protocol. In contrast, faulty processes may deviate from the protocol in an arbitrary manner. In particular, a faulty process can act maliciously and send bogus messages in an attempt to sabotage the correct operation of the system.

We will consider the design of protocols that are required to withstand up to t failures. Given $1\le t<n$, we denote by $\gamma ^t$ the model described above in which it is guaranteed that no more than t processes are faulty in any given run. We assume that a protocol ${\mathcal {P}}$ has access to the values of n and t, typically passed to ${\mathcal {P}}$ as parameters.

A run is a description of a (possibly infinite) execution of the system. We call a set of runs R a system. We will be interested in systems of the form $R_{{\mathcal {P}}}=R({{\mathcal {P}}},\gamma ^t)$ consisting of all runs of a given protocol ${\mathcal {P}}$ in which no more than t processes are faulty. Observe that a protocol ${\mathcal {P}}$ solves Consensus in the model $\gamma ^t$ if and only if every run of $R_{{\mathcal {P}}}$ satisfies the Decision, Agreement and Validity conditions described above. Given a run r and a time m, we denote the local state of process i at time m in run r by $r_i(m)$. Notice that a process i can be in the same local state in different runs of the same protocol. But $r_i(m)=r'_i(m')$ can hold only if $m=m'$ since the current time m is represented in the local state.

2.3 Indistinguishability and knowledge

Our analysis makes limited use of the theory of knowledge in distributed systems. This section introduces just enough of the theory of knowledge to support the analysis in this paper. More details can be found, e.g., in [14]. The formal definitions reviewed in this section are used only in Theorem 1 and in the proofs in the appendix. The reader can safely skip this section in a first reading.

Two runs r and $r'$ are said to be indistinguishable to process i at time m if $r_i(m)=r'_i(m)$. We denote this by $r\approx _{i}^{m}r'$. Notice that since we assume that correct processes follow deterministic protocols, if $r\approx _{i}^{m}r'$ then a correct process i is guaranteed to perform the same actions at time m in both r and $r'$.

Problem specifications typically impose restrictions on actions, based on properties of the run. Moreover, since the actions that a correct process performs are a function of its local state, the restrictions can depend on properties of other runs as well. For example, the Agreement condition implies that a correct process i cannot decide on v at time m in a run r if there is an indistinguishable run $r'\approx _{i}^{m}r$ in which some correct process decides on $u\ne v$. Similarly, by the Validity condition a correct process i cannot decide on v if there is a run $r'$ that is indistinguishable from r (to i at time m) in which all correct processes have the same initial proposal $v'\ne v$. These examples illustrate how indistinguishability might inhibit actions — performing an action might be prohibited because of what may be true at indistinguishable runs.

Rather than considering when actions are prohibited, we can choose to consider what is required in order for an action to be allowed by the specification. To this end, we can view the Agreement condition as implying that a correct process i is allowed to decide on v at time m in r only if in every run $r'\approx _{i}^{m}r$ there is no correct process that decides otherwise. This is much stronger than stating that no correct process decides otherwise in the run r itself, of course. Roughly speaking, the stronger statement is true because at time m process i cannot tell whether it is in r or in any of the runs $r'\approx _{i}^{m}r$. When this condition holds, we say that i knows that no correct process decides otherwise. Generally, it will be convenient to define the dual of indistinguishability, i.e., what is true at all indistinguishable runs, as what the process knows. More formally, following in the spirit of [14, 22], we proceed to define knowledge in our distributed systems as follows.

Definition 1

(Knowledge) Fix a system R, a run $r\in R$, a process i and a fact $\varphi$. We say that $K_i\varphi$ (which we read as “process i knows $\varphi$”) holds at time m in r iff $\varphi$ is true of all runs $r'\in R$ such that $r'\approx _{i}^{m}r$.

We use Boolean operators such as $\lnot$ (Not), $\wedge$ (And), and $\vee$ (Or) freely in the sequel. Notice that knowledge is defined with respect to a given system R. Often, the system is clear from context and is not stated explicitly. Definition 1 immediately implies the so-called Knowledge property: If $K_i\varphi$ holds at (any) time m in r, then r satisfies $\varphi$.

Our analysis will involve, in part, i-local facts, which are facts about the local states of a process i. Formally, a fact $\varphi _i$ is an i-local fact in a system R if there is a set $Z_i$ of local states of i such that $\varphi _i$ holds if and only if i’s local state is a member of $Z_i$. Examples of i-local facts are “$v_i=x$” (i’s initial proposal is x), “i received message $\mu$ from j” (in the current run), and “i has decided v” (in the current run).

3 Using null messages

Recall that sending a null message is, in general, considerably cheaper than sending an explicit message. But what information can a null message convey? In a reliable synchronous model, a process j that does not receive a message from i is guaranteed that i purposely sent j a null message. Moreover, if i’s protocol is such that a null message would be sent only if some condition holds, then j is informed by i’s null message that the condition holds. If processes can fail, then a null message can result from the fact that i is faulty, regardless of what its protocol specifies. Consequently, the only information that j learns from i’s null message arrives is that if i is correct then the condition holds. In the crash failure model, explicit (non-null) messages are only ever sent according to the protocol. This makes null messages qualitatively different from explicit messages in the crash model, as discussed by [18]. In the Byzantine model, however, faulty processes may send arbitrary messages. Consequently, the only information that j learns from an explicit message $\mu$ it receives from i in this model is that if i is correct then the conditions under which the protocol specifies that i should send $\mu$ holds. Essentially, in the Byzantine model the status of a null message is similar to that of an explicit message. This is not because null messages are promoted in the Byzantine case, but rather because the information content of explicit messages is demoted there. (In the authenticated model [12], signed messages are no longer similar to null messages.)

Suppose that a given process j receives from every process i a message reporting an i-local fact $\varphi _i$. Then, as discussed above, j learns that the $\varphi _i$’s of all correct processes i are true. Although j’s uncertainty regarding the identity of the correct processes may cause it to be unsure which of these facts holds, the information obtained in this manner can still be valuable. The success of a protocol in the Byzantine model is typically defined in terms of events that take place at correct processes (after all, the protocol does not control the faulty processes). In Consensus, for example, the three conditions of Decision, Agreement and Validity are all stated in terms of the correct processes. Indeed, a process may be able to terminate in Consensus once it discovers that every correct process has all of the information it needs in order to decide.

Coordinated use of null messages by many processes gives rise to a powerful primitive. We use a silent round, involving no communication, as an efficient tool for detecting global system properties about the correct processes, and will be especially useful in failure-free runs. We proceed as follows.

Definition 2

For every $i\in {\mathbb {P}}$, let $\varphi _i$ be an i-local fact in the system $R_{{\mathcal {P}}}=R({\mathcal {P}},\gamma ^t)$. Denote ${\bar{\varphi }_{c}^{}}\triangleq \bigwedge \limits _{\tiny {\text {correct}}\ i }\!\!\varphi _i$ , and fix some time $m\ge 0$. A protocol ${\mathcal {P}}$ is said to implement a silent validation round for ${\bar{\varphi }_{c}^{}}$ (denoted by ${\textsf {svr}({\bar{\varphi }_{c}^{}})}$) in round $m+1$ if in every run $r\in R_{{\mathcal {P}}}$, each correct $i\in {\mathbb {P}}$ sends messages to everyone in round $m+1$ in case $\varphi _i$ does not hold at time m, and sends no message to anyone in round $m+1$ if $\varphi _i$ does hold.

The fact ${\bar{\varphi }_{c}^{}}$ states that for every correct process i (in the current run) the fact $\varphi _i$ holds. Clearly, its truth depends on the identity of the correct processes which, in turn, is determined by the run. By design, silent validation rounds satisfy the following:

Theorem 1

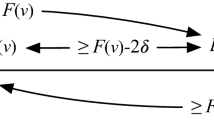
Assume that ${\mathcal {P}}$ implements an ${\textsf {svr}({\bar{\varphi }_{c}^{}})}$ in round $m+1$, and fix a run r of  ${\mathcal {P}}\!$. A process j that receives no messages whatsoever in round $m+1$ knows at time $m+1$ that ${\bar{\varphi }_{c}^{}}$ was true at time m.

Proof

Suppose that the assumptions hold and j does not receive any round $m+1$ message in a run $r\in R_{{\mathcal {P}}}$. We need to show that, at time $m+1$ in r, process j knows that ${\bar{\varphi }_{c}^{}}$ was true at time m. Fix a run $r'\in R_{{\mathcal {P}}}$ such that $r'\approx _{j}^{m+1}r$ (i.e., $r'$ is j-indistinguishable from r at time $m+1$). It follows that j does not receive any round $m+1$ message in $r'$ (otherwise it would distinguish $r'$ from r). Since j receives no round $m+1$ messages in $r'$, no correct process sends j any message in round $m+1$ of $r'$. Given that ${\mathcal {P}}$ implements an ${\textsf {svr}({\bar{\varphi }_{c}^{}})}$ in round $m+1$, we have by Definition 2 that $\varphi _i$ holds at time m in $r'$ for all correct $i\in {\mathbb {P}}$. Consequently, ${\bar{\varphi }_{c}^{}}$ also holds at time m in $r'$. Since this is true for every run $r'\approx _{j}^{m+1}r$, we have by Definition 1 that j knows at time $m+1$ in r that ${\bar{\varphi }_{c}^{}}$ was true at time m. $\square$

We shall refer to properties of the form ${\bar{\varphi }_{c}^{}}$ as global milestones. Knowing that a global milestone has been reached is often valuable in distributed protocols. For example, in many popular Consensus protocols, the processes maintain a local estimate of the decision value. Once the estimates of all correct processes are the same, the decision value is determined. The fact that all estimates are the same corresponds to a global milestone. As we will see later on, this global milestone can be detected by all correct processes, following a properly designed silent validation round. Existing protocols in the literature often employ other means to detect global milestones. Indeed, a variety of fault-tolerant protocols use long silent phases consisting of more than t rounds to verify that a specific milestone has been reached (e.g., [2, 19, 21]). The time complexity of these protocols can easily be reduced if the multi-round phase is replaced by a single-round svr.

While silent validation rounds have not been defined explicitly before, they have implicitly appeared in several distributed protocols in the literature. One interesting application of this technique is in broadcast-based protocols for radio networks, where such rounds are used to overcome possible malicious behavior (see, e.g., [8, 17]). Moreover, the Atomic Commitment protocols in [18] use silent validation rounds to gain communication efficiency. We remark that although silent validation rounds can sometimes convey the global information ${\bar{\varphi }_{c}^{}}$ practically for free, it is clear that they might induce high costs when ${\bar{\varphi }_{c}^{}}$ does not hold. This is inherent in using null messages effectively. At best, such use will shift costs among executions; it does not eliminate them totally (cf. [18]). As shown in Sect. 4, silent validation can allow us to reduce the communication costs of Consensus considerably in failure-free runs.

We use null messages in Sect. 4 in two additional manners:

Encoding a fixed value A trivial way to benefit from null messages is by having i encode a specific value (say 1) by a null message. If i encodes the same value by null messages in its communications to all processes, then the cost of reporting its value greatly improves (over not using null messages) in the best case, but no real gain is made in the worst case, in which its value differs from the chosen one. The worst-case performance can often be improved by using null messages to represent different values, in a manner that depends on the recipient. Thus, for example, in binary Consensus, process i could use null messages to report 0 to one half of the processes (sending an explicit message to the other half), and reverse the role of null messages in reporting 1. Doing so allows i to broadcast its value using n/2 messages in every case. (This idea is not new; see [2, 21] for such a use of null messages).

On-the-fly endcoding A null message from j to i need not be restricted to encoding an a priori fixed value. In fact, it is possible for a null message from j to i to refer to different values in distinct runs of the same protocol. In our protocols, there are typically processes that belong to a committee that collects initial proposals, and recommends a decision value. If a process i reports a value v to such a committee member j, then j sends i a null message to encode a recommendation of v (and an explicit message to encode recommendations of values $v'\ne v$). A null message from j to i thus dynamically encodes a value whose identity is based on their past communication.

4 Improving Byzantine consensus protocols

We now use the insights from Sect. 3 to design a method for improving Byzantine Consensus protocols. We use a modular approach, in which the protocol designer is free to choose a Byzantine Consensus protocol of her liking (which we refer to as the base protocol). If no failures occur, a very short and efficient protocol layer is executed and Consensus is achieved with relative ease. Execution reverts to the base protocol if failures prevent the layer from reaching Consensus quickly. This affords the designer with the best of both worlds—excellent behavior in the failure-free runs, and execution of a base protocol with the properties that the designer favors most when failures do occur. Crucially, when failures occur, executing the optimizing layer adds a negligible cost to runs of the base protocol. In a similar manner, Turpin and Coan used a layer to convert binary Consensus protocols into multi-valued ones [40].

One may argue that it is preferable in many applications to have a Consensus algorithm decide on the majority value (i.e., produce a fair vote). The possibility of failures makes this impossible in general, and the specification of Consensus can be viewed as an approximation of voting. Interestingly, all of our solutions have the additional quality that they emulate a fair voting mechanism in the absence of failures. I.e., they decide on the majority values in binary Consensus, and on a plurality value in multi-valued Consensus.

Throughout this section we use the following notations. Given a protocol ${\mathcal {P}}$ and a layer L, we denote the composition of L and ${\mathcal {P}}$ by $L\odot {\mathcal {P}}$. In figures depicting a layer we use a to mark a command that is the only operation the process performs in the current round, if the execution is failure free. Moreover, we depict the call to the base protocol by painting a box around the base protocol (see, e.g., line 28 of Algorithm 1). We start by presenting two optimizing layers for binary Consensus, followed by extensions that modify them to handle multi-valued Consensus.

4.1 Better time-optimal solutions to consensus

There is a well known lower bound stating that Byzantine Consensus protocols require 2 rounds of communication prior to deciding in failure-free executions [11, 24]. Our first layer is $\textsc {GreatSanhedrin}$ ($\textsc {GtSn}$ for short). In failure-free runs, this layer decides optimally fast (at time 2), and uses significantly fewer messages than any previously known protocol.

Roughly speaking, $\textsc {GreatSanhedrin}$ works as follows: (See Algorithm 1 for the pseudocode.) A large committee, consisting of $2t+1$ processes (which we call the Sanhedrin),¹ is defined a priori. We use $\left\{ 0,1,\ldots ,2t\right\}$ in Algorithm 1. In the first round, every process informs each member of the Sanhedrin of its initial proposal. Every Sanhedrin member j computes the majority of the values it received, which then serves as its recommendation. ($MAJ (\mathtt {values}_j)$ denotes the majority of values received by j on line 11 of Algorithm 1. It evaluates to 1 in case of a tie.) In the second round, j informs all processes of its recommendation. A process that receives a unanimous recommendation from the Sanhedrin in the second round decides on this recommendation at time 2, and sends no messages in the third round. A process that receives a recommendation for more than one value will, in the third round, broadcast a !‘help! message to alert everyone that it does not know what to decide. Any process that receives a !‘help! message in the third round will participate in an instance of the base Consensus protocol, starting from time 3 (i.e., from the fourth round on). The value used by a process in the base protocol, denoted by $est _i$, is determined at time 2.

Following the principles discussed in Sect. 3, processes convey certain values using null messages, rather than by explicit messages. Specifically, in the first round a process will use a null message to encode a fixed value for every intended recipient. This is done in a balanced manner, to improve the worst-case complexity. In the second round a Sanhedrin member encodes values “on-the-fly” by null messages. Namely, a null message will be sent from a Sanhedrin member to process i in order to encode that the value recommended by the Sanhedrin member equals the value that i proposed. An explicit message is sent if the recommendation differs from i’s proposal. The third round forms a silent validation round (Definition 2) for the global fact “all correct processes have decided.”

In failure-free executions, all members of the Sanhedrin receive the same messages in the first round, and make unanimous recommendations. Consequently, all processes decide at time 2, are silent in the third round, and halt at time 3. In addition to deciding at time 2 in failure-free runs (which is optimal), $\textsc {GtSn}$ also does so with roughly 2nt bits. (Correct processes only ever send single-bit messages). All previously known time-optimal protocols send $\varOmega (n^3)$ bits (e.g., [1, 11, 34, 37]). We note that these solutions were designed to ensure early stopping, and were not designed to optimize failure-free executions. Optimizing explicitly for the failure-free case, where the actual number of faults is $f=0$, yields greater efficiency. Using $\textsc {GtSn}$ improves on the state-of-the-art by a factor of $n^2/t >n$. Notice that this improvement in the failure-free case does not impose substantial costs in case failures do occur. The layer adds only three rounds and $O(n^2)$ bits of communication, which does not affect the asymptotic complexity of any known base protocol. Thus, a designer can ensure optimally fast and highly efficient majority voting in failure-free runs, while reverting to her protocol of choice at a negligible cost in case failures occur.

Theorem 2

Let $k\ge 3$ and let $\mathtt {Base}$ be a binary Consensus protocol for $n>kt$. Then $\textsc {GtSn}\odot \mathtt {Base}$ yields a binary Consensus protocol for $n>kt$ in which

• 1. In failure-free runs decisions occur after 2 rounds and at most $2n(t+1)$ bits are communicated, while

• 2. When failures cause $\mathtt {Base}$ to be invoked, at most $2n(t+1)+n^2$ bits are sent by correct processes, and 3 rounds elapse before control reverts to $\mathtt {Base}$.

• 3. In failure-free runs, the composed protocol decides on the majority value.

Sketch of Proof

 ² When all correct processes decide in the course of the base protocol phase, correctness follows from the base protocol’s guarantees. When all correct processes decide early (at time 2), then they all decide according to the same unanimous recommendation in line 18; two unanimous recommendations cannot conflict. So again, Consensus is satisfied.

Finally, suppose that a correct process i decides on v early (in line 18) but another correct process j is unable to decide at that time. Observe that i decided in line 18 due to a unanimous recommendation on v. The unanimous recommendation on v implies that all correct Sanhedrin members (at least $t+1$) recommended v in the second round and that all processes have received these recommendations by time 2. Therefore, all correct processes set their estimations to v in lines 18 and 21. Moreover, the protocol implements a silent validation round for the global fact “all correct processes have decided” in the third round. Thus, by Theorem 1 and line 26, a correct process participates in the base protocol unless it knows at time 3 that all correct processes have decided already. This ensures that all correct processes (decided or undecided) will participate in the base protocol phase, and as they all propose the same estimate v, the consensus value of the base protocol is v. Therefore, j will decide on v in agreement with i’s decision. Finally, establishing the bit count and failure-free majority voting claims (1)–(3) is rather straightforward.

Theorem 2 is stated with respect to protocols $\mathtt {Base}$ that solve Consensus for $n>kt$ (as do later Theorems in the paper). This makes the result more general than a statement for every protocol that solves Consensus for $n>3t$, since there are multiple Byzantine Consensus protocols in the literature whose resilence is worse than $n>3t$. Thus, for example, Theorem 2 implies that $\textsc {GtSn}$ can be used to optimize Algorithm B of [3], which solves binary Consensus for $n>4t$.

4.2 Halving the message costs

Our second layer, called $\textsc {SmallCouncil}$ (denoted $\textsc {SlCl}$ for short), uses an extra silent validation round to further reduce the comunication costs in failure-free runs to approximately nt bits. This allows the protocol designer to emulate majority voting in failure-free runs with half of the number bits at the price of a single additional round compared to $\textsc {GtSn}$. Algorithm 2 presents the full pseudocode. The ideas underlying the design of $\textsc {SlCl}$ are similar to those of $\textsc {GtSn}$.

A committee of $t+1$ processes (this time called the Council ) is defined a priori. In the first round, all processes report their initial proposals to the Council. Each Council member then calculates the majority value among the reported votes, and sends a recommendation to all processes accordingly. At time 2, a process that received a unanimous recommendation from the Council sets its estimation to be that recommendation and remains silent in the third round. Otherwise (if it receives conflicting recommendations), it sets its estimation to be its initial proposal, and broadcasts an $\overline{{ err}}$ message to alert all of the problem. A process that receives no $\overline{{ err}}$ message in the third round decides at time 3 on its estimation. If it does receive a third round $\overline{{ err}}$ message, then it broadcasts a !‘help! message to alert everyone that it does not know what to decide. Any process that receives a !‘help! message in the fourth round will participate in an instance of the base protocol, starting from time 4. The process uses its estimation value as a proposal in the base protocol.

In terms of communication, in this layer, both the third and fourth rounds serve as silent validation rounds. The third round is an svr for the global fact “all correct processes have received a unanimous recommendation,” and the fourth for “all correct processes have decided.”

Theorem 3

Let $k\ge 3$ and let $\mathtt {Base}$ be a binary Consensus protocol for $n>kt$. Then $\textsc {SlCl}\odot \mathtt {Base}$ yields a binary Consensus protocol in which

• 1. In failure-free runs, decisions occur after 3 rounds and at most $n(t+1.5)$ bits are communicated, while

• 2. When failures cause $\mathtt {Base}$ to be invoked, at most $n(t+1.5)+2n^2$ bits are sent by correct processes, and 4 rounds elapse before control reverts to $\mathtt {Base}$.

• 3. In failure-free runs, the composed protocol decides on the majority value.

The bit complexity of the $\textsc {SmallCouncil}$ layer is 4 times the best-known lower bound of $\varOmega (nt/4)$ bits for this case from [10, 21]. The best previously-known communication behavior is by the Early Stopping Phase King protocol of [5], which requires up to $8n^2$ bits and takes up to 8 rounds to decide in failure-free runs. Our $\textsc {SlCl}$ layer achieves a 24-fold improvement in bit complexity, while also reducing the decision time (from 8 to 3 rounds). Moreover, the Phase King protocol (and the like) are far from emulating majority in failure-free runs. Even in failure-free executions, the King’s proposal typically wins. Finally, in problematic cases involving failures, $\textsc {SlCl}$ adds only 4 rounds and fewer than $3 n^2$ bits to the complexity of the run. Consequently, as for $\textsc {GtSn}$, prepending $\textsc {SlCl}$ does not change the asymptotic complexity of any possible base protocol.

Prepending a $\textsc {GtSn}$ or a $\textsc {SlCl}$ layer to existing protocols is simple to realize and gives rise to a rich family of Byzantine Consensus protocols with desirable properties. For example, a designer that seeks time-optimal and cheap failure-free behavior, together with fast decisions in case of failures, can compose $\textsc {GtSn}$ onto the protocol of [1]. This yields excellent failure-free behavior (optimally fast decision in 2 rounds, high efficiency, and majority voting emulation), while ensuring that fault-laden executions decide within $f+5$ rounds (at a high polynomial bit cost in the worst case), where $f>0$ is the number of actual failures in an execution. A designer wishing to optimize communication could compose $\textsc {GtSn}$ onto the Early Stopping Phase King protocol of [5]. In a failure-free execution, this implements a majority vote within three rounds, using the lowest known communication complexity. In the presence of failures, it becomes somewhat slower but remains efficient, deciding within $4(f+3)$ rounds and using at most $n^2(4f+6)$ bits of communication.

4.3 Multi-valued consensus

So far we have dealt with binary Consensus. Recall that in multi-valued Consensus $|V|>2$. Hence, the benefit of encoding specific values by null messages is reduced (linearly) as the size of the set V of values grows. Fortunately, the more subtle uses of null messages for reporting values “on the fly,” and for performing silent validation rounds do not depend on |V| in a similar fashion. As it turns out, the techniques used above in the binary case can still provide significant benefits for multi-valued Consensus.

Layers $\textsc {GtSn}^{ mv }$ and $\textsc {SlCl}^{ mv }$, which handle multi-valued Consensus, differ from $\textsc {GtSn}$ and $\textsc {SlCl}$ in two minor ways. One is that the majority computation on line 11 of the original layers is replaced by a plurality computation. The other difference is even smaller. For ease of exposition, null messages are used in the first rounds of the new layers to encode a single, fixed, proposed value (the most likely one, say). No further changes are needed. As for the binary case, efficiency is obtained by using the techniques in Sect. 3 for employing null messages. Algorithm 3 below presents $\textsc {SlCl}^{ mv }$ while the pseudocode of $\textsc {GtSn}^{ mv }$ appears in Algorithm 4 in Appendix A. Properties of the multi-valued layers are summarized by:

Theorem 4

Let $k\ge 3$, and let $\mathtt {Base}$ be a multi-valued Consensus protocol for $n>kt$. Then composing each of $\textsc {GtSn}^{ mv }$ and $\textsc {SlCl}^{ mv }$ with $\mathtt {Base}$ yields a multi-valued Consensus protocol. Moreover,

• 1. In failure-free runs of $\textsc {GtSn}^{ mv }$ (resp. $\textsc {SlCl}^{ mv }$) decisions occur after 2 (resp. 3) rounds, and at most $4n(t+1)\log _2|V|$ (resp. $2n(t+1)\log _2|V|$) bits are communicated, while

• 2. When failures cause $\mathtt {Base}$ to be invoked, at most $4n(t+1)\log _2|V|+n^2$ (resp. $2n(t+1)\log _2|V|+2n^2$) bits are sent in total by correct processes, and 3 (resp. 4) rounds elapse before control reverts to $\mathtt {Base}$.

• 3. In a failure-free run, both protocols are guaranteed to decide on a plurality value.

Previous time-optimal multi-valued Consensus protocols send $\varOmega (n^3\log _2|V|)$ bits in their failure-free runs (e.g., [1]). Hence, just as in the case of binary Consensus, our layers offer a factor of $\varOmega (n)$ improvement in communication complexity for failure-free executions. For protocols that are not time optimal, the Turpin and Coan approach [40], when combined with the (binary) Early Stopping Phase King protocol (ESPK), is the most efficient previously known solution. It transmits as many as $n^2\log _2|V|+9n^2$ bits in failure-free runs, and can require as many as 10 rounds to decide when no failure occurs. Our $\textsc {SlCl}^{ mv }$ layer guarantees slightly better communication complexity (roughly by a factor of n/t) and faster decision time (3 rounds instead of 10) in failure-free runs.

Contrary to the situation for binary Consensus, in multi-valued Consensus it is often impossible to guarantee that the correct processes will decide on a valid proposal (i.e., on a value proposed by a correct process). Indeed, [36] shows the impossibility whenever $t\cdot |V|\ge n$. This is typically handled by allowing decisions on a default value ‘$\bot$’ (so that the set of possible decision values is $V\cup \{\bot \}$). While deciding on the default value provides a consistent outcome for the correct processes, it does not provide much shared information about the proposed values. Many protocols for multi-valued Consensus are designed to opt for the default value unless an overwhelming number of values are the same. This is true even for the popular reduction from multi-valued to binary Consensus by Turpin and Coan in [40]. Both of our layers for multi-valued Consensus ensure that, in failure-free executions, the processes always decide on a valid plurality value, and not on the default value ‘$\bot$.’

4.4 Redundant executions

The layers we have introduced all guarantee that Consensus is obtained in failure-free executions without the base protocol ever being called into action. In other executions, if any of the correct processes reverts to the base protocol in order to determine its decision value, it first alerts all correct processes, and they all participate in the execution of the base protocol. There is a third possibility, in which all correct processes have decided, but a malicious process falsely alerts some of the correct processes. This can initiate an execution of the base protocol in which fewer than $n-t$ correct processes participate. We will refer to the executions of the base protocol in this case as redundant executions. Since the correctness of the base protocol may rely on the existence of sufficiently many correct participants, such an execution might, in general, fail to satisfy the conditions for Consensus. Crucially, since all correct processes have aleady decided within the prepended layer, the base protocol does not affect any of their decisions. Consequently, the redundant execution does not affect the correctness of our solution. (Hence the name redundant.) It can, however, affect the communication costs and halting times in redundant executions.

In most popular Consensus protocols in the literature, redundant executions, in which a subset of the processes are initially crashed and at most t act maliciously, do not have greater time and communication costs than “standard” executions of the protocol. If the protocol designer chooses to use a (base) Consensus protocol ${\mathcal {P}}$ for which redundant executions may be costly, she can often slightly modify the protocol to alleviate this cost. For example, recall that a correct process i participates in a redundant execution only if it has decided before entering the base protocol. All of our layers ensure that, in this case, all correct processes participating in the protocol propose the same value as i does. The designer can therefore make a correct process that has decided before entering ${\mathcal {P}}$ simply stop executing ${\mathcal {P}}$ once it observes a scenario that is inconsistent with all correct processes proposing the same initial proposal as its own. Another possibility is simply monitoring the costs. A process that participates in the base protocol monitors the time elapsed and the amount of messages it has sent. If any of these exceeds the worst-case cost for the base protocol with all correct processes participating, the process can safely halt. The execution is redundant.

A comment on randomized Consensus A popular approach to achieve efficiency is by using randomized algorithms. While such solutions do not satisfy the standard definition of Consensus, they typically offer reduced complexity in expectation. Our deterministic layers can be used to tune the performance of these algorithms, just as they do for deterministic ones. Prepending our layers to a randomized algorithm yields outstanding deterministic performance in failure-free runs, while preserving their randomized guarantees for runs with failures. Clearly, redundant executions are still possible, and all of the above applies to randomized algorithms as well. For example, consider using the randomized algorithm of Feldman and Micali [15] as the base protocol ${\mathcal {P}}$. In this case, redundant executions of ${\mathcal {P}}$ do not incur higher costs than “standard” executions. Moreover, as suggested above, the designer can make a correct process i that has decided before entering ${\mathcal {P}}$ simply stop executing ${\mathcal {P}}$ once it observes a scenario that is inconsistent with all correct processes proposing i’s decision value. In this case, redundant executions of ${\mathcal {P}}$ would halt after a single round.

5 Discussion

We have offered a modular approach to tuning the performance of Byzantine Consensus protocols. Short protocols, called layers solve Consensus efficiently in the absence of failures, and transfer control to a chosen base protocol when failures do occur. Focusing on the failure-free case offers advantages over the more common approach of early stopping advocated by [11]. The optimal decision time for Consensus in the absence of failures is known to be two rounds. While the most efficient protocols that decide optimally fast in this case has been early stopping protocols, and they required $\varTheta (n^3)$ bits of communication. The GreatSanhedrin layer, in comparison, improves on this by a factor of $\varOmega (n^2/t)$.

If we relax the constraint of deciding in two rounds, while the lower bound on the number of bits required to reach Consensus in failure-free executions is $\sim \! nt/4$ [10, 21], the best previously known upper bound was $8n^2$ [5]. The SmallCouncil layer improves this by a multiplicative factor of 24, while reducing the decision time from 8 to 3 rounds. A factor of 4 gap remains, and closing this gap is an open problem. If the tight bound is better than the nt messages of $\textsc {SmallCouncil}{}$, it will be interesting to see whether the techniques that we have identified suffice, or whether new techniques will be required.

A central tool driving the communication efficiency of our solutions has been the use of null messages to convey information. In a previous work, null messages were used for this purpose in the crash-failure model [18]. Unfortunately, the main theorem there does not apply to the Byzantine model, since there are essential differences in the way in which information flows in benign models and in Byzantine models. In the former, messages are only ever sent according to the protocol, in contrast to models with potentially maliscious failures. In fact, the Byzantine model is, in a sense, more favorable for using null messages than the crash-failure model is: While receiving a null message is less persuasive than receiving an explicit one in the crash model, the two are equally persuasive in the Byzantine case. This is not because null messages are more informative in the latter, but rather because explicit messages are less informative there.

We identified a primitive, called a silent validation round (svr), which allows all processes to detect a global property regarding all correct processes, using a single silent round. As the use of such silent rounds in our layers shows, this is an effective primitive for coordination in distributed protocols for the Byzantine setting. It would be interesting to explore the use of silent validation rounds for other models and applications. For example, the Bitcoin blockchain setting is one in which timing and synchrony play a central role, while participants cannot be trusted. Indeed, the set of participants in such settings is not fixed and is in general even unknown [35]. Silent validation rounds can inform all processes about the state of all correct participants, without even knowing who the participants are.

In a broader sense, there is a key principle underlying our techniques here and in [18]. In asynchronous systems, information flows only via message chains [7, 28]. Synchronous systems, however, allow information to flow in many (sometimes complicated) different patterns. Syncausality and the centipede pattern of [4] facilitate coordination in reliable systems, while silent choirs can be used effectively when failures are limited to crashing [18]. In this paper, we identified the svr pattern as an efficient means to broadcast global milestones in the Byzantine setting. This is another testimony for the power of timing and silence in distributed computing.

Appendices

Multi-valued variants

In multi-valued Consensus, the decision value domain is commonly defined as $V\cup \{ \bot \}$, where $\bot$ is some default value. A key technical difference between the two Consensus problems is that in the multi-valued case it is sometimes impossible to guarantee that processes decide on a value proposed by a correct process. More precisely, if $\frac{n}{|V|}\le t$ then it is impossible to guarantee that in every execution, all processes decide on some correct proposal.

Many multivalued Byzantine protocols circumvent this issue by having a strong tendency to decide on the default value $\bot$. (These protocols decide $\bot$ in all runs, except when there is a value v that is proposed by at least $n-t$ processes.) In a practical sense, deciding on $\bot$ often means a “no-op” or a “blank” result. As stated in Theorem 4(3), our multivalued layers do not produce this effect. On the contrary, they allow a designer to improve her solution’s time and communication costs while also emulating a fair voting mechanism (plurality) in failure-free runs. Formally, the plurality function $PLUR (\cdot ): V^n\rightarrow V$ is defined as

$$\begin{aligned} PLUR (\mathbf{v} )\triangleq \text {most common}\ v\ \text {in}\ \mathbf{v} . \end{aligned}$$

If several values are tied for the most common value, $PLUR (\mathbf{v} )$ is the minimal such value.

While implementing plurality voting in is desirable in most cases, it may also be desirable not to decide on values that no correct process proposed and to decide on ‘$\bot$’ (no-op) in that case instead. If the designer wishes to guarantee this “correct decision” criteria, she can replace normal plurality with the t-thresholded plurality function $t PLUR (\cdot ): V^n\rightarrow V\cup \{\bot \}$, which we define as

$$\begin{aligned} t PLUR (\mathbf{v} )\triangleq \left\{ \begin{array}{l} \begin{array}{ll} \bot &{} \qquad \text {if no value in}\ \mathbf{v} \ \text {has more}\\ &{} \qquad \text {than}\ t\ \text {occurrences} \\ \end{array} \\ \text {most common}\ v\ \text {in}\ \mathbf{v} \quad \text {otherwise}\\ \end{array}\right\} . \end{aligned}$$

A Consensus protocol that guarantees the “correct decision” criteria in every execution, and emulates t-thresholded plurality in failure-free runs, conforms with plurality as much as possible in these runs.

Algorithms 4 and 3 present $\textsc {GtSn}^{ mv }$ and $\textsc {SlCl}^{ mv }$, which are slight modifications of the layers presented in Sects. 4.1 and 4.2 that handle multi-valued Consensus. As stated before, this is achievable due to the generality of the techniques from Sect. 3 in employing null messages. The new layers differ from the original ones in two minor ways. One is that the majority computation on line 11 of the original layers is replaced by a plurality computation. The other difference is even smaller. For ease of exposition, null messages are used in the first round to encode a single, fixed, proposed value (e.g., the most likely one). No further changes are needed. We remark that in the first round of the layers for binary Consensus we bounded the worst-case message complexity by sending null messages to half of the recipients both when proposing 0 and when proposing 1. It is clearly possible to use null messages selectively for different values in the multi-valued case. But as |V| grows, the advantage of doing so diminishes.

Correctness proofs for the protocols

The Proofs of Theorems 2 and 3 make use of the following lemma:

Lemma 1

Fix a run r of $\textsc {GtSn}\odot \mathtt {Base}$ (resp. $\textsc {SlCl}\odot \mathtt {Base}$). If a correct process i does not decide at time 2 (resp. 3), then all the correct processes participate in the $\mathtt {Base}$ phase from time 3 on (resp. 4 on).

Proof

Let r and i satisfy the assumptions, and let j be a correct process in r. Denote by $\texttt {all}\_\texttt {decided}$ the fact “all correct processes have decided”. Then, line 18 of $\textsc {GtSn}$ (resp. line 23 of $\textsc {SlCl}$) implements an svr(all_decided) in the third round (resp. in the fourth round). Suitably, line 25 (resp. line 26) dictates that j halts and does not participate in the base protocol only if j received no third round (resp. fourth round) messages whatsoever. By line 25 (resp. 26) and Theorem 1 we have that j participates in the base protocol unless it knows at time 3 (resp. time 4) that $\texttt {all}\_\texttt {decided}$ was true at time 2 (resp. 3). Since i does not decide at time 2 (resp. 3) in r, then $\texttt {all}\_\texttt {decided}$ is not true at time 2 (resp. 3). By the knowledge property, j does not know that $\texttt {all}\_\texttt {decided}$ was true at time 2 (resp. 3), because it is false. Consequently, no correct process j halts at time 3 (resp. 4) in r, and they all participate in the $\mathtt {Base.Protocol}$ phase from time 3 (resp. 4) on. $\square$

We now turn to prove the algorithm properties stated in Theorems 2–4. While, for ease of exposition, the Algorithms include messages sent from a process to itself, the analysis will assume that these are implemented without explicit messages being sent.

Theorem 2

Let $k\ge 3$ and let $\mathtt {Base}$ be a binary Consensus protocol for $n>kt$. Then $\textsc {GtSn}\odot \mathtt {Base}$ yields a binary Consensus protocol in which

• 1. In failure-free runs decisions occur after 2 rounds and at most $2n(t+1)$ bits are communicated, while

• 2. When failures cause $\mathtt {Base}$ to be invoked, at most $2n(t+1)+n^2$ bits are sent by correct processes, and 3 rounds elapse before control reverts to $\mathtt {Base}$.

• 3. In failure-free runs, the composed protocol decides on the majority value.

Proof

We now prove that $\textsc {GtSn}\odot \mathtt {Base}$ is a binary Consensus protocol. Fix a run r of $\textsc {GtSn}\odot \mathtt {Base}$. We show that r satisfies Decision, Validity and Agreement:

Decision Let i be a correct process in r. If i decides at time 2 we are done. If it doesn’t, then by Lemma 1 all correct processes participate in the $\mathtt {Base}$ phase. By the Decision property of the $\mathtt {Base}$ protocol, process i completes the execution of line 28 and decides on line 30.

Validity Let i be a correct process in r and assume that all correct processes propose the same value v. Recall that, since $n>3t$ by assumption, the correct processes consist of a strict majority. By the pigeonhole principle, at least $t+1$ Sanhedrin members are correct. These correct Sanhedrin members follow the protocol on lines 06–11 and compute the majority of votes reported to them, which is v, thus, they recommend v to all by lines 12–16. Thereafter, by time 2, every correct process receives at least those $t+1$ recommendations on v and sets its estimation to v either by line 18 (in case of a unanimous recommendation), or by line 21. If i decides at time 2, it decides on its estimation v by line 18, and we are done. Assume it didn’t, then by Lemma 1i and all other correct process participate in the base protocol on line 28. As we have shown, the estimation of all correct processes is set to v on lines 18 and 21. Thus, all correct processes enter the base protocol with a proposal of v. From Validity of the base protocol, this ensures that i performs $\textsf {dec}\leftarrow v$ on line 28 and decides on v in line 30.

Agreement Let i and j be correct processes in r. Assume w.l.o.g. that i decides no later than j. If i does not decide at time 2 then both it and j participate in the base protocol and decide according to it. In particular, their decisions satisfy Agreement. Let us assume that i decides at time 2 on v. Specifically, line 18 is the only line in which a correct process decides at time 2. A correct process (such as i) decides in line 18 iff it received a unanimous recommendation on v. Recall that every unanimous recommendation includes a report of at least $t+1$ correct processes. It follows that every correct process receives at least $t+1$ recommendations on v and therefore sets its estimation to v in lines 18 or 21. Moreover, since no unanimous recommendation on $u\ne v$ is possible, if j also decides at time 2, then it decides on v as well, and Agreement holds. If j does not decide at time 2, then, by Lemma 1, all correct processes participate in the $\mathtt {Base.Protocol}$ phase. And, since all correct processes fixed their estimations to v at time 2, they all enter the base protocol with $est =v$. The Validity of the base protocol ensures that j will decide v in line 30, upholding Agreement.

• 1. In a failure-free run at time 0 every process transmits its proposal to half of the Sanhedrin by silence and the other half by messages. Sanhedrin members have one less message to send in half the cases (to themselves), thus at most $n\lceil (2t+1)/2\rceil -\lfloor (2t+1)/2\rfloor \le n(t+1)$ bits are sent in total during the first round. Since no failures occur $MAJ (\texttt {values}_j)$ is the same for every Sanhedrin member $j\in \{0,\ldots ,2t\}$ and they all recommend the same value $v= MAJ (\texttt {values})$. At time 1, by lines 12–16, Sanhedrin members send their recommendations on v to at least half of the processes by silence and the other part by messages. Thus, the Sanhedrin sends at most a total of $(2t+1)\lceil (n-1)/2\rceil \le n(t+1)$ bits in the second round. The unanimous recommendation of the second round causes every $i\in {\mathbb {P}}$ to decide v at time 2 by line 18, remain silent in the third round and halt at time 3 by line 26.

• 2. Again, correct processes send their proposals to the Sanhedrin at a cost of at most $n(t+1)$ bits in the first round, and correct Sanhedrin members send their recommendations to processes with a total cost of at most $n(t+1)$ bits in the second round. The difference lays in the third round, when correct processes may not receive a unanimous recommendation and would therefore send !‘help! messages (that can be implemented using a single bit) by line 24. This costs in the worst case $n(n-1)$ bits. After this, all remaining communication is due to the base protocol.

• 3. In a failure-free run, all processes transmit their proposals according to protocol at time 0 and a Sanhedrin member calculates its majority at time 1 on lines 06–11. The majority value v is unique and therefore all Sanhedrin members send the same recommendations of v by lines 12–16 at time 1. All processes receive the unanimous recommendation on v by time 2 and therefore decide on it in line 18.

$\square$

Theorem 3

Let $k\ge 3$ and let $\mathtt {Base}$ be a binary Consensus protocol for $n>kt$. Then $\textsc {SlCl}\odot \mathtt {Base}$ yields a binary Consensus protocol in which

• 1. In failure-free runs, decisions occur after 3 rounds and at most $n(t+1.5)$ bits are communicated, while

• 2. When failures cause $\mathtt {Base}$ to be invoked, at most $n(t+1.5)+2n^2$ bits are sent by correct processes, and 4 rounds elapse before control reverts to $\mathtt {Base}$.

• 3. In failure-free runs, the composed protocol decides on the majority value.

Proof

We now prove that $\textsc {SlCl}\odot \mathtt {Base}$ is a binary Consensus protocol. Fix a run r of $\textsc {SlCl}\odot \mathtt {Base}$. We show that r satisfies Decision, Validity and Agreement:

Decision Let i be a correct process in r. If i decides at time 3 we are done. If it doesn’t, then by Lemma 1 all correct processes participate in the base protocol. By the Decision property of the base protocol, process i completes the execution of line 29 and decides on line 31.

Validity Let i be a correct process in r and assume that all correct processes propose the same value v. Recall that, since $n>3t$ by assumption, the correct processes consist of a strict majority. By the pigeonhole principle, at least one process $j_c\in \left\{ 0,1,2,\ldots ,t\right\}$ is correct. Process $j_c$ follows the protocol and at time 1 on lines 06–11 it computes the majority of votes as reported to it. This value is v, obviously. Consequently, by lines 12–16 $j_c$ recommends v in the second round. Thereafter, at time 2 every correct process receives $j_c$’s recommendation on v and therefore sets its estimation to v ($est \leftarrow v$), either in line 18 due to a unanimous recommendation, or in line 20 because its own initial proposal is v. If i decides at time 3, by line 23 it decides on its estimation, which we have established is v. The only other option for i to decide is on line 31 by using the base protocol. It remains to show that if i decides using the base protocol, then its decision is also v. Assume that i decides using the base protocol. Since i is a correct process that does not decide at time 3, by Lemma 1 all correct processes participate in the base protocol. As we have shown, the estimation of every correct process is set to v at time 2 by lines 18 and 20, and so all correct processes enter the base protocol on line 29 at time 4 with the proposal v. The Validity of the base protocol ensures that i sets $\textsf {dec}\leftarrow v$ on line 29 and that i decides v on line 31. Hence, we are done.

Agreement Let i and j be correct processes in r. Assume w.l.o.g. that i decides no later than j. If i does not decide at time 3 then both it and j participate in the base protocol and decide according to it. In particular, their decisions satisfy Agreement. Let’s assume that i decides at time 3 on a value v. The third round of layer $\textsc {SlCl}$ (line 21), implements a silent validation round for the global fact ${\bar{\varphi }_{c}^{}}\triangleq$“a unanimous recommendation was received by all correct processes.” The svr information transfer guarantees of Theorem 1 and line 22 at time 3, imply that i decides at time 3 only if ${\bar{\varphi }_{c}^{}}$ was true at time 2. In particular,if i decides in line 23, then it decides on its estimate value ($est _{i}=v$). Recall that every unanimous recommendation includes at least one correct process’ recommendation which it recommended to all. It follows that if two correct processes receive unanimous recommendations, then these recommendations are the same. Thus, the ${\textsf {svr}({\bar{\varphi }_{c}^{}})}$ in the third round informs i that all correct processes have their estimations set to v. If j also decides at time 3 (in line 23), then it decides on its estimation v, and Agreement holds. If j does not decide at time 3, then, by Lemma 1, all correct processes participate in base protocol. Moreover, since all correct processes have the same estimate v, they all propose v to the base protocol in line 29. Validity of the base protocol guarantees that $\textsf {dec}\leftarrow v$ in line 29 and j decides v by line 31, ensuring Agreement.

• 1. In a failure-free run at time 0 every process transmits its proposal to half of the Council by silence and to the other half by messages. Council members have one less message to send in half the cases (to themselves), thus at most a total of $n\lceil (t+1)/2\rceil -\lfloor (t+1)/2\rfloor \le n(t+2)/2 -t/2$ bits are sent during the first round. Since no failures occur $MAJ (\texttt {values}_j)$ is the same for every Council member $j\in \{0,\ldots ,t\}$ and they all recommend the same value $v= MAJ (\texttt {values})$. At time 1, lines 12–16, Council members send their recommendation on v to at least half of the processes by silence and to the other part by messages. Thus, sending at most a total of $(t+1)\lceil (n-1)/2\rceil \le n(t+1)/2$ bits in the second round. The unanimous recommendation on v of the second round causes every $i\in {\mathbb {P}}$ to set its estimate to $est _i\leftarrow v$ at time 2, and remain silent in the third round. Thus, in a failure-free run, no message is sent in the third round. At time 3, no message is received and in particular no ‘$\overline{{ err}}$’ message, therefore, every process decides on its estimate, remains quiet in the fourth round and halts at time 4. In conclusion, the total number of messages/bits sent in a failure-free run of $\textsc {SlCl}\odot \mathtt {Base}$ is at most $n(t+2)/2 -t/2 + n(t+1)/2<n(t+1.5)$.

• 2. Again, correct processes send their proposals to the Council at a total cost of at most $n(t+2)/2 -t/2$ bits in the first round, and correct Council members send their recommendations to processes with a total cost of at most $n(t+1)/2$ bits in the second round. The difference lies in the third and fourth rounds, when correct processes may not receive a unanimous recommendation and would therefore send ‘$\overline{{ err}}$’ messages by line 21 in the third round and !‘help! messages by line 25 in the fourth round (each message can be implemented using a single bit). In the worst case, this adds a total cost of $2n(n-1)$ bits in the third and fourth rounds. After this, starting at time 4, all remaining communication is due to the base protocol.

• 3. In a failure-free run, all processes transmit their proposals according to protocol at time 0. A Council member calculates the correct majority value v at time 1 on lines 06–11. The majority value v is unique and therefore all Council members send the same recommendation v at time 1 by lines 12–16. All processes receive the unanimous recommendation on v by time 2 and therefore set their estimation to v by line 18 and remain silent. In the third round, no messages are sent in a failure-free run, in particular no ‘$\overline{{ err}}$’ messages. Therefore, every process decides in line 23 on its estimate v which is the majority value.

$\square$

Theorem 4

Let $k\ge 3$, and let $\mathtt {Base}$ be a multi-valued Consensus protocol for $n>kt$. Then composing each of $\textsc {GtSn}^{ mv }$ and $\textsc {SlCl}^{ mv }$ with $\mathtt {Base}$ yields a multi-valued Consensus protocol. Moreover,

• 1. In failure-free runs of $\textsc {GtSn}^{ mv }$ (resp. $\textsc {SlCl}^{ mv }$) decisions occur after 2 (resp. 3) rounds, and at most $4n(t+1)\log _2|V|$ (resp. $2n(t+1)\log _2|V|$) bits are communicated, while

• 2. When failures cause $\mathtt {Base}$ to be invoked, at most $4n(t+1)\log _2|V|+n^2$ (resp. $2n(t+1)\log _2|V|+2n^2$) bits are sent in total by correct processes, and 3 (resp. 4) rounds elapse before control reverts to $\mathtt {Base}$.

• 3. In a failure-free run, both protocols are guaranteed to decide on a plurality value.

Proving $\textsc {GtSn}^{ mv }\odot \mathtt {Base}$ (resp. $\textsc {SlCl}^{ mv }\odot \mathtt {Base}$) is a Consensus protocol stems directly from the proof for $\textsc {GtSn}\odot \mathtt {Base}$ in Theorem 2 (resp. $\textsc {SlCl}\odot \mathtt {Base}$ in Theorem 3). The only minor modification is in Validity, replacing majority with plurality. However, since when all correct processes propose the same value v both plurality and majority have the same result, this modification is insignificant. Hence, Validity is maintained for the multi-valued as well. We are thus left only with proving the rest:

Proof

(for $\textsc {GreatSanhedrin}^{ mv }\odot \mathtt {Base}$)

• 1. In a failure-free run at time 0 every process transmits its proposal to all Sanhedrin members by messages or silence (a messages can encode any value by at most $\log _2|V|$ bits). Sanhedrin members have one less message to send (to themselves). A message encodes a value by $\log _2|V|$ bits. Thus a total of at most $(n-1)(2t+1)\log _2|V|$ bits are sent during the first round. Since no failures occur $PLUR (\texttt {values}_j)$ is the same for every Sanhedrin member $j\in \{0,\ldots ,2t\}$ and they all recommend the same value $v= PLUR (\texttt {values})$. At time 1, Sanhedrin members send their recommendations of v to all processes. Thus, sending at most $(2t+1)(n-1)\log _2|V|$ bits in the second round. The unanimous recommendation of the second round causes every $i\in {\mathbb {P}}$ to decide v at time 2 by line 17, remain silent during the third round and halt at time 3 by line 25.

• 2. Again, correct processes send their proposals to the Sanhedrin at a total cost of at most $(n-1)(2t+1)\log _2|V|$ bits in the first round, and correct Sanhedrin members send their recommendations to processes with a cost of at most $(2t+1)(n-1)\log _2|V|$ bits in the second round. The difference lies in the third round, when correct processes may not receive a unanimous recommendation and would therefore send !‘help! messages (that can be implemented using a single bit) by line 23. This costs in the worst case $n(n-1)$ bits. After this, all remaining communication is due to the base protocol.

• 3. In a failure-free run, all processes transmit their proposals according to protocol at time 0 and a Sanhedrin member calculates their plurality at time 1 on lines 05–10. The plurality value v is unique (a known tie-breaker exists), and therefore all Sanhedrin members send the same recommendations on v by lines 11–15 at time 1. All processes receive the unanimous recommendation on v by time 2 and therefore decide on it in line 17.

$\square$

Proof

(for $\textsc {SmallCouncil}^{ mv }\odot \mathtt {Base}$)

• 1. In a failure-free run at time 0 every process sends its proposal to the Council by an explicit or a null messages (an explicit message can encode any value by at most $\log _2|V|$ bits). Council members have one less message to send (to themselves), thus at most $(n-1)(t+1)\log _2|V|$ bits are sent during the first round. Since no failures occur $PLUR (\texttt {values}_j)$ is the same for every Council member $j\in \{0,\ldots ,t\}$ and they all recommend the same value $v= PLUR (\texttt {values})$. At time 1, lines 10–15, Council members send their recommendation of v to all the processes. Thus, the number of bits sent in the second round is at most $(t+1)(n-1)\log _2|V|$. The unanimous recommendation of v in the second round causes every $i\in {\mathbb {P}}$ to set its estimate to $est _i\leftarrow v$ at time 2, and remain silent during the third round. Thus, in a failure-free run, no message is sent in the third round. At time 3, no message is received and in particular no ‘$\overline{{ err}}$’ message, therefore, every process decides on its estimate, remains quiet in the fourth round and halts at time 4.

• 2. Again, correct processes send their proposals to the Council at a total cost of at most $(n-1)(t+1)\log _2|V|$ bits in the first round, and correct Council members send their recommendations to processes with a total cost of at most $(t+1)(n-1)\log _2|V|$ bits in the second round. The difference lies in the third and fourth rounds, when correct processes might not receive a unanimous recommendation and would therefore send ‘$\overline{{ err}}$’ messages by line 20 in the third round and !‘help! messages by line 24 in the fourth round (each of these messages can be implemented using a single bit). In the worst case, this adds a total cost of $2n(n-1)$ bits in the third and fourth rounds. After this, starting at time 4, all remaining communication is due to the base protocol.

• 3. In a failure-free run, all processes transmit their proposals according to protocol at time 0 and a Council member calculates their plurality at time 1 (on lines 05–10). The plurality value v is unique (a known tie-breaker exists), and therefore all Council members send the same recommendations of v by lines 11–15 at time 1. All processes receive the unanimous recommendation of v by time 2 and by line 17 set their estimate to v and remain silent. Thereafter, at time 3 by line 22 the processes decide on v.

$\square$