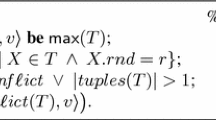On the uncontended complexity of anonymous agreement

Abstract

In this paper, we study uncontended complexity of anonymous k-set agreement algorithms, counting the number of memory locations used and the number of memory updates performed in operations that encounter no contention. We assume that in contention-free executions of a k-set agreement algorithm, only “fast” read and write operations are performed, and more expensive synchronization primitives, such as CAS, are only used when contention is detected. We call such concurrent implementations interval-solo-fast and derive the first nontrivial tight bounds on space complexity of anonymous interval-solo-fast k-set agreement.

1 Introduction

One of the central distributed abstractions is k -set agreement [7], where a collection of processes propose their private inputs, and each process must output one of the proposed inputs, so that at most k distinct values are output. By bounding the uncertainty about the inputs, a k-set agreement protocol can be used to implement k generic replicated services in a consistent and fault-tolerant way [11, 16]. Therefore, complexity of set agreement protocols has become one of the most important topics in the theory of distributed computing.

It is known that 1-set agreement, under the original name of consensus, cannot be solved in an asynchronous read-write shared memory system in a deterministic and fault-tolerant way [10, 21]. More generally, k-set agreement cannot be solved using read-write shared memory as long as k or more processes can fail by crashing (prematurely halting their computations) [3, 18, 24]. In particular, k-set agreement cannot be solved in the wait-free manner [16], i.e., tolerating up to $n-1$ faulty processes, where n is the number of processes in the system. These impossibility results stem from the difficulty of handling contended executions: process concurrently accessing shared data may not be able to distinguish executions in which conflicting decisions must be taken.

To circumvent the above impossibilities, we should thus use stronger (and more expensive) synchronization primitives, such as compare-and-swap. One way to decrease the overall costs is to require that a process invokes such primitives only if in the presence of interval contention, i.e., when its propose operation is concurrent with the propose operation of another process. In contention-free executions, only cheaper read and write primitives are used. We call a wait-free algorithm with these properties interval-solo-fast.

Ideally, interval-solo-fast algorithms should have an optimized behavior in uncontended executions, as they are believed to be common in practice [22]. It is therefore natural to explore the uncontended complexity of set agreement algorithms: how many memory operations (reads and writes) need to be performed and how many distinct memory locations need to be accessed in the absence of interval contention?

In general, interval-solo-fast consensus and, thus, k-set agreement for any $k\ge 1$, can be solved with only constant uncontended complexity [22]. To make the problem nontrivial, we restrict our study to anonymous consensus algorithms, i.e., algorithms not using process identifiers and, thus, programming all processes identically. Besides intellectual curiosity, there are practical reasons to study anonymous algorithms in the shared memory model, discussed in [14].

Our results. On the lower-bound side, we show that any anonymous interval-solo-fast k-set agreement algorithm exhibits non-trivial uncontended complexity that depends on n, the number of processes, k, the degree of agreement, and m, the cardinality of the set V of all input values that are allowed to be proposed. More precisely, we show that the space complexity of a propose operation is in $\Omega (\min (\sqrt{n/k},\log {(m/k)}/\log {\log {(m/k)}}))$. Also, if the algorithm uses less than $\Gamma ^{-1}(m/k)$ memory locations, where $\Gamma ^{-1}$ is the inverse of the factorial function, we show that, in the worst case, a propose operation running solo, i.e., without any other process invoking propose, must write to $\Omega (\min (\sqrt{n/k},\log {(m/k)}/\log {\log {(m/k)}}))$ distinct memory locations. This metric, which we call solo-write complexity, is upper-bounded by the step complexity of the algorithm, i.e., the worst-case number of all primitive operations applied to shared memory locations by an individual propose operation. In the special case of input-oblivious algorithms, where the sequence of memory locations written in a solo execution does not depend on the input value, we derive a stronger lower bound of $\Omega (\sqrt{n/k})$ on solo-write complexity. Our proof only requires the algorithm to ensure that operations terminate in solo executions, so the lower bounds also hold for abortable [2, 15] and obstruction-free [17] implementations.¹

We then show that our lower bound is tight. Our matching interval solo-fast k-set agreement algorithm is based on our novel k -value-splitter abstraction, extending the classical splitter mechanism [5, 20, 23]. The abstraction is interesting in its own right. Informally, a k-value-splitter exports a single operation split that takes a value in a value set V as a parameter and returns a boolean response so that (1) if $\textit{split}(v)$ completes before any other $\textit{split}$ operation starts, then it returns $\textit{true}$, and (2) the number of distinct inputs of operations that returned $\textit{true}$ is at most k.

We describe a transformation of a k-value-splitter into an anonymous and interval-solo-fast k-set agreement algorithm, incurring only a constant overhead with respect to the k-value-splitter complexity.

Then we present two value-splitter read-write implementations. The first algorithm is a novel anonymous and input-oblivious implementation of a k-value-splitter that exhibits $O(\sqrt{n/k})$ space and solo-write complexity. The second (not input-oblivious) algorithm exhibits $O(\log {(m/k)}/\log {\log {(m/k)}})$ space and solo-write complexity. The two implementations, combined with our value-splitter-based k-set agreement algorithm, provide the desired $O(\min (\sqrt{n/k},\log {(m/k)}/\log {\log {(m/k)}}))$ upper bound.

Our results are summarized in Table 1. It is interesting to notice that, for the case of consensus ($k=1$), the step complexities are O(n) for the first algorithm and $O(\log {m}/\log {\log {m}})$ for the second one. Aspnes and Ellen [1] showed that any anonymous consensus protocol has to execute $\Omega (\min (n,\log {m}/\log {\log {m}}))$ steps in solo executions. Thus, our consensus algorithms also have asymptotically optimal step complexity.

Table 1 Space and solo-write complexity for anonymous interval-solo-fast k-set agreement

Overall, our results imply the first nontrivial tight lower bound on the space complexity for general k-set agreement known so far, complementing the recent $\Omega (n)$ bound on the space complexity of solo-terminating anonymous consensus [12]. In the case of binary consensus, where the set of possible input values is of size 2, our constant-space consensus algorithm exhibits a linear gap between algorithms adapting to interval contention vs. step contention. The gap is derived from the bound proved in [26] : any solo terminating binary consensus algorithm uses at least $n-1$ read/write base objects (usually called registers). This result also holds if the algorithm can use the identifiers of the processes. In the case of multi-valued consensus, our results also show that there is an inherent gap between anonymous and non-anonymous consensus algorithms: regardless of the number of possible inputs, non-anonymous consensus has constant uncontended complexity [22].

2 Related work

The idea of optimizing concurrent algorithms for uncontended executions was suggested by Lamport in his “fast” mutual exclusion algorithm [20]. The term solo-fast was introduced by Attiya et al. [2] to denote implementations that in absence of step contention only apply reads and writes. Informally, an operation performed by a process encounters step contention if another process takes steps in the operation’s interval. To avoid confusion, in the following we rename these algorithms step-solo-fast.

Fich et al. [9] have shown that any solo-terminating (and, as a result, obstruction-free) read-write (non-anonymous) consensus protocol must use $\Omega (\sqrt{n})$ memory locations. Gelashvili [12] proved a stronger $\Omega (n)$ lower bound for the anonymous case. Zhu [26] proved this lower bound for the more general non-anonymous case. Attiya et al. [2] showed that any step-solo-fast either use $\Omega (\sqrt{n})$ space or incur $\Omega (\sqrt{n})$ memory stalls per operation. No obstruction-free or step-solo-fast algorithm matching these lower bounds is known so far: existing algorithms typically expose O(n) space complexity. These lower bounds focus on step contention and do not extend to uncontended executions, where no interval contention is encountered. In [8], an $\Omega (\sqrt{n/k})$ space-complexity bound for anonymous obstruction-free k-set agreement was derived, but, given the $\Theta (n)$ bound established in [12] for obstruction-free consensus, we conjecture that the space complexity of k-set agreement is $\Omega (n-k)$, matching the recent algorithm by Bouzid et al. [4].

Our k -value-splitter abstraction is inspired by the splitter mechanism in [5, 23], originally suggested by Lamport [20]. Unlike the splitter object, more than one process can return true but only if these processes propose at most k distinct input values. The idea of adapting the outputs of an algorithm to the number of distinct inputs was originally proposed by Yang et al. [25]. In the case of $k=1$, we can implement a 1-value splitter using a conflict-detector object [1] plus a constant number of registers. The novel input-oblivious value-splitter implementation we present is inspired by the obstruction-free leader election algorithm recently proposed by Giakkoupis et al. [13].

This paper generalizes our recent bounds for anonymous consensus presented in [6].

Roadmap The rest of the paper is organized as follows. We give preliminary definitions in Sect. 3. We present our lower bound in Sect. 4 and our upper bound in Sect. 5. We conclude the paper in Sect. 6.

3 Preliminaries

The model of computation We consider a standard asynchronous shared-memory model in which $n>1$ processes communicate by applying atomic (or linearizable [19]) operations on shared variables, called base objects. We assume every base object maintains a state and exports a subset of the Read, Write and Compare-And-Swap (CAS) operations. $\textit{Read}(R)$ returns the value of R, and $\textit{Write}(R,v)$ sets the state of R to v. $\textit{CAS}(R,e,v)$ checks if the state of R is e and, if so, sets the state of R to v and returns $\textit{true}$; otherwise, the state remains unchanged and $\textit{false}$ is returned.

A register is a base object that exports only the Read and Write operations.

Algorithms and executions To implement a (high-level) object from a set of base objects, processes follow an algorithm ${\mathcal {A}}$, associating each process p with a deterministic automaton ${\mathcal {A}}_p$. To avoid confusion between the base objects and the implemented one, we reserve the term operation for the object being implemented and we call primitives the operations on base objects. We say that an operation is performed on a high-level object and that a primitive is applied to a base object.

Each process has a local state that consists of the values stored in its local variables and a programme counter.

A configuration specifies the state of each base object and the local state of each process at one moment. In an initial configuration, all base objects have the initial values specified by the algorithm and all processes are in their initial states.

A process is active if an operation has been invoked by the process but the operation has not yet produced a matching response; otherwise the process is called idle. We assume that an operation can only be invoked by an idle process and only active processes take steps. A configuration is quiescent if every process is idle in it.

An execution fragment of an algorithm is a (possibly infinite) sequence $C_{1},\phi _1,\ldots , C_{i},\phi _{i},\ldots$ of configurations alternating with steps, where each step is the application of a primitive $\phi _i$ to some base object in configuration $C_i$ resulting in configuration $C_{i+1}$. For any finite execution fragment $\alpha$ ending with configuration C and any execution fragment $\alpha ^\prime$ starting at C, the execution $\alpha \alpha ^\prime$ is the concatenation of $\alpha$ and $\alpha ^\prime$; in this case $\alpha ^\prime$ is called an extension of $\alpha$. An execution is an execution fragment starting from the initial configuration $C_0$.

In an infinite execution, a process is correct if it takes an infinite number of steps or is idle from some point on. Otherwise, the process is called crashed. A crashed process is active.

In a solo execution, only one process takes steps. An operation invoked by a process in a given execution is completed if its invocation is followed by a matching response. An operation invoked by a process p in an execution E is uncontended if no process other than p is active between its invocation and response. We also say that p executes its operation in the absence of interval contention.

Finally, we say that an operation executes in the absence of step contention if all the steps of the operation are contiguous in the execution.

k-set agreement The k -set agreement [7] object exports one operation $\textit{propose}(v)$, where v is an input taken from some domain V ($|V|\ge k+1$). The output values must satisfy the following properties:

• k -Agreement: the set of all output values contains at most k distinct values.

• Validity: every output value is one of the input values.

In the special case of $k=1$, 1-set agreement is called consensus.

Properties of algorithms An algorithm is wait-free if in every execution, each correct process completes each of its operation in a finite number of its own steps [16].

A wait-free algorithm is interval-solo-fast if, in the absence of interval contention, a process only applies read and write primitives.

An algorithm is input-oblivious if a process accesses the same sequence of base objects in any solo execution of the algorithm, regardless of its input.

An algorithm ${\mathcal {A}}$ is anonymous if ${\mathcal {A}}_p$ does not depend on p, i.e., the algorithm programs the processes identically, regardless of their identifiers.

In this paper we are concerned with two complexity metrics: space complexity, i.e., the number of base objects an algorithm uses, and solo-write complexity, i.e., the maximal number of writes performed in a solo execution of a single operation of an algorithm, taken over all possible input values. Note that solo-write complexity is upper-bounded by the step complexity of the algorithm, i.e., the number of base-object accesses a single operation may perform.

4 Lower bounds for interval-solo-fast k-set agreement

Consider any n-process anonymous implementation of interval-solo-fast k-set agreement with a set V of input values, where $|V|=m\ge k+1$. In this section, we show that the uncontended space complexity of this implementation must be $\Omega (\min (\sqrt{n/k},\log {(m/k)}/\log {\log {(m/k)}}))$. Moreover, if the space complexity is less than $\Gamma ^{-1}(m/k)$, where $\Gamma ^{-1}$ is the inverse of the factorial function ($\Gamma (x)=x!$), then the implementation must have an execution in which some propose operation, running solo, performs $\Omega (\min (\sqrt{n/k},\log {(m/k)}/\log {\log {(m/k)}}))$ writes on distinct base objects.

We also show that in the special case when the implementation is input-oblivious, the bounds on uncontended space complexity and solo-write complexity become $\Omega (\sqrt{n/k})$.

Overview of the proof Assume that there exists an interval-solo-fast anonymous k-set agreement algorithm ${\mathcal {A}}$ that uses at most b distinct base objects with $b{<}\min (\sqrt{n/k},\Gamma ^{-1}(m/k))$. Recall that $\Gamma ^{-1}(x)\in \Theta (\log {x}/\log {\log {x}})$.

By the way of contradiction, we are going to show that the algorithm must have an execution in which $k+1$ different values are returned.

To this aim, we are going to iteratively construct an execution of ${\mathcal {A}}$ which is, for every process p, indistinguishable from an execution in which p runs solo. Since the implementation is interval-solo-fast, no process applies primitives other than reads and writes in the constructed execution. Also, there are $k+1$ processes that complete their operations, and each of these processes decides on its distinct input value, establishing a contradiction. We use the remaining processes to hide contention by covering registers written by the $k+1$ deciding processes: when reading such a register, a deciding process should obtain the value it previously wrote. These processes are clones of deciding processes. In particular, a clone of a process p in the execution is a process with the same input as p which proceeds in lockstep with p, reading and writing the same values as p, until immediately before some write to a base object. For each base object written by a deciding process p, we let some clones of p poised to write to this base object to later rewrite the value written by p.

Selecting “confusing” inputs Let $C_0$ be the initial configuration of ${\mathcal {A}}$. For each $u\in V$, let $\alpha _u$ denote the execution of ${\mathcal {A}}$ in which a process, starting from $C_0$, invokes $\textit{propose}(u)$ and runs solo until the operation completes. Since the algorithm is anonymous, $\alpha _v$ does not depend on the process identifier.

For a given $u\in V$, consider the sequence of base objects written in $\alpha _u$, ordered by the times they are first written in $\alpha _u$. For our proof to work there must be a set U of $k+1$ distinct values such that the sequences of base objects, put in the order of the times they are first written in executions $\alpha _{u}$, $u\in U$, are prefix-related: for each two such sequences, one is a prefix of the other.

For an input-oblivious algorithm, all these sequences are identical, regardless of the relation between m and b. Thus U can be any set of $k+1$ distinct input values.

For non input-oblivious algorithms, the existence of such $k+1$ distinct values is implied by the condition $b<\Gamma ^{-1}(m/k)$. There are m possible input values u (and, thus, possible executions $\alpha _u$), and at most b! possible orders in which b base objects can be written for the first time in executions $\alpha _u$, $u\in V$. Using the fact that $b<\Gamma ^{-1}(m/k)$ and, thus, $b! <m/k$, we are going to show that there exists a set of $k+1$ distinct values such that the sequences of base objects, put in the order of the times they are first written in executions $\alpha _{u}$, $u\in U$, are prefix-related.

Indeed, let $f_u : \{1,\ldots ,b\} \rightarrow \{1,\ldots ,b\}\cup \{\bot \}$ be defined as follows: $f_u(1)$ is the first register written in $\alpha _u$, and for each $i=2,\ldots ,b$, $f_u(i)$ is the first register written in $\alpha _u$ that does not appear in $\{f(1),\ldots ,f(i-1)\}$, or $\bot$ if there is no such register. Note that, by the definition, for each $f_u$, there exists $j\in \{1,\ldots ,b\}$, such that for all $i=1,\ldots ,j$, $f_u(i)\ne \bot$ and for all $i=j+1,\ldots ,b$, $f_u(i)=\bot$. We say that $f_u$ is a prefix of $f_v$ if for each $i=1,\ldots ,b$, $f_u(i)\ne \bot \Rightarrow f_u(i)=f_v(i)$.

Lemma 1

If $b<\Gamma ^{-1}(m/k)$, where $m=|V|$, then there exists $U \subseteq V$ such that $|U|=k+1$ and for all $u,v\in U$, either $f_u$ is a prefix of $f_v$ or vice versa.

Proof

Consider an injective function $g: \{1,\ldots ,b\} \rightarrow \{1,\ldots ,b\}$. Note that there are exactly b! such functions. Since $b! <m/k$, there must be an injective function $g: \{1,\ldots ,b\} \rightarrow \{1,\ldots ,b\}$ and a set $U\subseteq V$ of size $k+1$ such that for each $u\in U$, $f_u$ is a prefix of g. Thus, for all $u,v\in U$, both $f_u$ and $f_v$ are prefixes of g, and, hence, have that either $f_u$ is a prefix of $f_v$ or vice versa. $\square$

Lower bound For the rest of the proof, let U be a set of inputs in V such that $|U|=k+1$ and for all $u,v\in U$, either $f_u$ is a prefix of $f_v$ or vice versa. Let $\rho =r_1,\ldots ,r_b$ be a sequence of base objects such that for each $u\in U$, the sequence of base objects, ordered by the times they are first written in $\alpha _u$ is a prefix of $\rho$: $\forall i=1,\ldots ,b$, $f_u(i)\in \{r_i,\bot \}$. Let $t\le b$ be the length of the longest such sequence.

For each $u{\in }U$, we write $\alpha _u{=}\alpha _{0,u}\beta _{1,u}\alpha _{1,u}\cdots \beta _{s_u,u}\alpha _{s_u,u}$, where $s_u\le t$ and for each $i=1,\ldots ,s_u$, $\beta _{i,u}$ is the first write to $r_i$ in $\alpha _u$.

Assume, without loss of generality, that $U=\{0,\ldots ,k\}$ and fix a set of $k+1$ distinct processes $\{p_0,\ldots ,p_k\}$. Remember that two configurations are indistinguishable to a process, if the process has the same state in both configurations.

For $i\in \{0,\ldots ,t\}$, we say that a configuration $D_i=C_0\gamma _i$ is i -confusing if:

• at most $k(1+\sum _{j=0}^{i-1}j)+1$ processes take steps in $\gamma _i$,

• for each $u\in U$, $D_i$ is indistinguishable for $p_u$ from $C_o\alpha _{0,u}\beta _{1,u}\alpha _{1,u}\cdots \beta _{\ell _i,u} \alpha _{\ell _i,u}$, where $\ell _i=\min (s_u,i)$, and

• there exists a process $p_u$, $u\in U$, such that the states of the shared memory in $D_i$ and $C_o\alpha _{0,u}\beta _{1,u} \alpha _{1,u}\cdots \beta _{\ell _i,u}\alpha _{\ell _i,u}$ are the same.

Lemma 2

For each $i=0,\ldots ,t$, if $n\ge k(1+\sum _{j=0}^{i-1}j)+1$, then ${\mathcal {A}}$ has an i-confusing configuration.

Proof

In the base case $i{=}0$, we take $D_0$ to be $C_0\alpha _{0,0}\cdots \alpha _{0,k}$. The execution $\alpha _{0,0}\cdots \alpha _{0,k}$ is read-only and, thus, $D_0$ is, for every process $p_u$, $u\in U$, starting with input u, indistinguishable from $C_0\alpha _{0,u}$. Note that at most $k+1$ processes take steps in $\alpha _{0,0}\cdots \alpha _{0,k}$ and the state of the memory in $D_0$ is the same as in any $C_0\alpha _{0,u}$ for each $u\in U$.

Suppose now that the claim holds for $0,\ldots ,i-1$, and let $D_{i-1}=C_0\gamma _{i-1}$ be a $(i-1)$-confusing configuration. We can construct $\gamma _{i-1}'$ which is exactly like $\gamma _{i-1}$, except that for each register $r_m\in \{r_1,\ldots ,r_{i-1}\}$ and each $u\in U$, whenever $p_u$ performs its last write to $r_m$ in $\gamma _{i-1}$ (if it does), we introduce a distinct clone of $p_u$ that is stopped just before performing this write. We make an exception for $p_u$ that satisfies the third condition on the $(i-1)$-confusing configuration $D_{i-1}$—for this process we do not add clones.

Since no $p_u$ can distinguish $C_0\gamma _{i-1}$ from $C_0\alpha _{0,u}\beta _{1,u}\alpha _{1,u}\cdots \beta _{\ell _{i-1},u}\alpha _{\ell _{i-1},u}$, where $\ell _{i-1}=\min (s_u,i-1)$, and one of the processes $p_u$ does not require clones in the constructed execution, the number of clones we add is at most $k(i-1)$. Since we have at least $k(1+\sum _{j=0}^{i-1}j)+1$ processes and at most $k(1+\sum _{j=0}^{i-2}j)+1$ of them are involved in $\gamma _{i-1}$, we can indeed add $k(i-1)$ such clones.

Note that for each $u\in U$, either $i-1 \ge s_u$ and $p_u$ has terminated its operation by outputting its own input u, or $i-1 < s_u$ and the next step $p_u$ is about to perform in $C_0\gamma _{i-1}'$ is the write $\beta _{i,u}$ on $r_i$.

Now we extend $\gamma _{i-1}'$ to construct $\gamma _i$ as follows. Take any not yet terminated $p_u$, and let it perform the write $\beta _{i,u}$. Then we let every clone of $p_u$ (if any) perform its write on one of the registers written by $p_u$ in $\gamma _{i-1}$. Let $\tau _{i,u}$ be this block write by the clones and $C_0\gamma _{i-1}'\beta _{i,u}\tau _{i,u}$ be the resulting configuration. Note that $p_u$ cannot distinguish $C_0\gamma _{i-1}'\beta _{i,u}\tau _{i,u}$ from $C_0\alpha _{0,u}\beta _{1,u}\cdots \alpha _{i-1,u}\beta _{i,u}$ if it runs solo from these two configurations. Thus, we extend the execution to obtain $C_0\gamma _{i-1}'\beta _{i,u}\tau _{i,u}\alpha _{i,u}$ that is indistinguishable for $p_u$ from $C_0\alpha _{0,u}\beta _{1,u}\alpha _{1,u}\cdots \beta _{i,u}\alpha _{i,u}$.

By performing this procedure for every process that has not yet terminated in $C_0\gamma _{i-1}'$, one by one, starting from the process that was the last to write in $\gamma _{i-1}$, we obtain $\gamma _i$ such that (1) $\gamma _i$ involves at most $k(1+\sum _{j=0}^{i-2}j)+1+k(i-1)=k(1+\sum _{j=0}^{i-1}j)+1$ processes, (2) for every $p_u$, $u\in U$, $C_0\gamma _{i}$ is indistinguishable from $C_0\alpha _{0,u}\beta _{1,u}\alpha _{1,u}\cdots \beta _{\ell _{i},u}\alpha _{\ell _{i},u}$, and (3) if $p_u$ is the last process to perform its writes in $\gamma _i$, then the states of registers $r_1,\ldots ,r_i$ (and, thus, of the memory, as these are the only registers modified in these executions) in $C_0\gamma _i$ and $C_0\alpha _{0,u}\beta _{1,u}\alpha _{1,u}\cdots \beta _{i,u}\alpha _{i,u}$ are identical. Thus, $D_i =C_0\gamma _i$ is an i-confusing configuration. $\square$

Now we are ready to prove our lower bound:

Theorem 3

Any n-process m-valued interval-solo-fast anonymous k-set agreement algorithm must have space complexity in $\Omega (\min (\sqrt{n/k},\log {(m/}k)/\log {\log {(m/k)}}))$. If the algorithm uses fewer than $\Gamma ^{-1}(m/k)$ registers then it has solo-write complexity in $\Omega (\min (\sqrt{n/k},\log {(m/k)}/\log {\log {(m/k)}}))$. If the algorithm is input-oblivious, then its space and solo-write complexities are in $\Omega (\sqrt{n/k)})$.

Proof

Suppose, by contradiction, that an n-process m-valued interval-solo-fast anonymous k-set agreement algorithm uses at most b base objects such that $b\le \sqrt{n/k}$ and either $b<\Gamma ^{-1}{(m/k)}$ or the algorithm is input-oblivious.

Then, $n\ge k(1+\frac{b^2-b}{2})+1$ and by Lemma 2, there exists a t-confusing configuration $D_t$ for some $t\le b$. There exists $U\subseteq V$, such that no process $p_u$, $u\in U$, can distinguish $D_t$ from $C_0\alpha _{0,u}\beta _{1,u}\alpha _{1,u}\cdots \beta _{\ell _{t},u}\alpha _{\ell _{t},u}$ and, since $s_u\le t$, $\ell _{i,t}=\min (s_u,t)=s_u$, we derive that no $p_u$ can distinguish $D_t$ from $C_0\alpha _u$ and, thus, every $p_u$ must terminate by outputting u in $D_t$. Hence, we obtain a contradiction by constructing an execution of ${\mathcal {A}}$ in which $k+1$ different values are decided. Thus, it must hold that either $b\ge \Gamma ^{-1}{(m/k)}$ or $b>\sqrt{n/k}$, which gives space complexity at least $\min (\sqrt{n/k},\Gamma ^{-1}(m/k))\in \Omega (\min (\sqrt{n/k},\log {(m/k)}/\log {\log {(m/k)}}))$. Moreover, if $b< \Gamma ^{-1}{(m/k)}$, we get solo-write complexity in $\Omega (\min (\sqrt{n/k},\log {(m/k)}/\log {\log {(m/k)}}))$.

If the algorithm is input-oblivious, we get both space and solo-write complexity in $\Omega (\sqrt{n/k})$. $\square$

5 Optimal interval-solo-fast k-set agreement

In this section we present an algorithm that implements interval-solo-fast k-set agreement. This algorithm can be seen as a generalization the splitter-based consensus algorithm in [22], where we replace the splitter object with the k -value-splitter object that we introduce in this paper.

5.1 k-Value-splitters

A splitter provides processes with a single operation $\textit{split}()$ that returns a boolean response, so that (i) if a process runs solo, it must obtain $\textit{true}$ and (ii) $\textit{true}$ is returned to at most one process.

A k-value-splitter exports a single operation $\textit{split}(v)$ ($v\in V$, for some input domain V) and relaxes property (ii) of splitters by allowing multiple processes to obtain $\textit{true}$ but for no more than k different input values. Note that, unlike conventional splitters [5, 20, 23], the conditions restricting the outputs of a k-value-splitter are based on distinct values, rather than distinct processes. Besides, as we are interested in solving k-set agreement, we introduce a generalized abstraction using parameter k.

More formally:

Definition 4

A k-value-splitter supports a single operation split(v), taking as input a value v in some domain V, that returns a boolean and, in any given execution, ensures the following properties:

• 1. Solo execution If a $\textit{split}$ operation completes before any other $\textit{split}$ operation is invoked, then it returns $\textit{true}$, and

• 2. k-VS-agreement If S is the set of the inputs of the $split$ operations that return true, then $|S| \le k$.

We use a k-value-splitter object to construct an anonymous k-set agreement algorithm. The algorithm incurs only a constant overhead with respect to the implementation of the k-value-splitter it uses and is interval-solo-fast assuming that the underlying k-value-splitter is interval-solo-fast.

Then we describe two anonymous interval-solo-fast implementations of a k-value-splitter. The first one is input-oblivious and exhibits $O(\sqrt{n/k})$ solo-write and space complexity, regardless of the number m of possible inputs. The second one exhibits complexities $O(\log {(m/k)}/\log {\log {(m/k)}})$, regardless of the number of processes n. The two algorithms provide a matching upper bound to our $\Omega (\min (\sqrt{2n/k},\log {(m/k)}/\log {\log {(m/k)}}))$ lower bound.

5.2 k-set agreement using k-value-splitter

The pseudocode of our k-set agreement algorithm is given in Algorithm 1. A value decided by the k-set agreement is written in a variable D, initially $\bot \notin V$. The first steps by a process p are to check if D stores a non-$\bot$ value and if so, return this value. Otherwise, the process accesses the k-value-splitter object $\textit{KVS}$.

If it obtains $\textit{true}$ from its invocation of $\textit{KVS}.\textit{split}(v)$, p writes its input value v in a register F. Then, it reads a register Z to check if some other process has detected contention. If the value of Z is $\textit{false}$ (no contention) p decides its own value. Before returning the decided value, process p writes it in D. The write primitives on F and D, with a read of Z in between, are intended to ensure that either process p detects that some other process is around and resorts to applying a CAS primitive on D, or the contending process adopts the input value of p.

If p obtains $\textit{false}$ from the value-splitter, it sets Z to $\textit{true}$ (contention is detected). Recall that this may happen if more than one process accessed the value-splitter, regardless of their input values. Then, p reads register F and, if F stores a non-$\bot$ value, adopts the value as its current proposal. Finally, it applies the CAS primitive on D with its proposal and decides the value read in D.

Notice that, assuming that the k-value-splitter is interval-solo-fast, a process running in the absence of interval contention reaches a decision applying only reads and writes.

In the following we prove that Algorithm 1 indeed implements interval-solo-fast k-set agreement, assuming that $\textit{KVS}$ is an interval-solo-fast implementation of a k-value-splitter. We show that such implementations exist in the next subsection.

Correctness and complexity of Algorithm 1

Lemma 5

(Agreement) No more than k different values are returned.

Proof

Given that only values stored in D can be returned, it is sufficient to show that at most k values can be stored in D.

By the algorithm D is updated in lines 12 and 5. Note that, since a CAS succeeds in updating the value of D in line 12 only if D contains $\bot$ and, since D is updated with a non-$\bot$ value in V, at most one process may succeed with its CAS. D is updated at line 5 only if the corresponding process obtains $\textit{true}$ from the k-value-splitter. By the k-VS-Agreement property of k-value-splitters, at most k distinct values can be written in D in line 5.

Thus, the only possibility for $k+1$ different values to be stored in D is when one process, say p, applies a CAS in line 12 and updates D with a value v and other processes write k distinct values in D in line 5. Assume by contradiction that it is true.

Note that p must have obtained $\textit{false}$ from the k-value-splitter, otherwise at most $k-1$ other values could be written in D in line 5, by the k-VS-Agreement property of k-value-splitters. Thus, before applying CAS on D, p has read F in line 10. Since the values written in F are the k values written in D, at line 5, p has read $\bot$ in F. In the other case, p will adopt the value in F and will apply the CAS with this value, so only k values will be stored in D.

Then p reads F before any other process writes to it. By the algorithm, p has previously set the “contention flag” Z to $\textit{true}$ in line 9. Therefore, after any writing in F, a process must find Z set to $\textit{true}$ (“contention is detected”) and resort to CAS instead of writing in D in line 5—a contradiction. $\square$

Lemma 6

Algorithm 1 is interval-solo-fast.

Proof

If a process p invokes its $\textit{propose}$ operation and finds a non-$\bot$ value in D, then p returns after having applied a single read on D, so the claim follows.

Otherwise, suppose that p initially finds $D=\bot$ and applies the CAS primitive (line 12). We show that there is an operation that overlaps with the $\textit{propose}$ of p.

By inspecting the pseudo-code, it is easy to see that p applies the CAS primitive only if (1) it has read $Z=\textit{true}$ (line 4) or (2) it has obtained $\textit{false}$ from $\textit{KVS}$. In both cases another process q previously invoked a $\textit{propose}$ operation.

By the algorithm, before completing its operation, q either writes its decided (non-$\bot$) value in D (line 5) or tries to update D with its decided value using CAS (line 12), which fails only if D already contains a non-$\bot$ value. Given that p has initially found $\bot$ in D, we deduce that the operation of q has not completed before the operation of p has started. Thus, the two operations overlap. The assumption that the value-splitter is interval-solo-fast and the fact the algorithm contains no loops or waiting statements, implies the claim. $\square$

Lemmata 5 and 6 imply:

Theorem 7

If $\textit{KVS}$ is an interval-solo-fast implementation of a k-value-splitter, with a space complexity b and a solo-write complexity s, then Algorithm 1 implements interval-solo-fast k-set agreement with space complexity $b+3$ and solo-write complexity $s+2$.

The complexity claims follow directly from the pseudo-code.

5.3 Interval-solo-fast k-value-splitter implementations

Input-oblivious value-splitter Algorithm 2 describes our anonymous and input-oblivious implementation of a k-value-splitter. The algorithm only uses an array R of b registers where $b^2-3b+4 > (2n-2)/k$ and is, trivially, interval-solo-fast. Thus, by Theorem 3, the space complexity of our interval-solo-fast consensus algorithm is asymptotically optimal.

In the algorithm, a process p performing operation $\textit{split}(v)$ tries to write its input value to registers $R[0],\ldots ,R[b-1]$. Each time, before writing to R[i], p reads $i+1$ registers : it verifies that $R[0],\ldots ,R[i-1]$ store v and that R[i] still stores the initial value $\bot$. If this is not the case, i.e., either another $\textit{split}$ operation has previously completed or there is a concurrent one, the operation returns $\textit{false}$. After the last write to $R[b-1]$, the operation returns $\textit{true}$. Note that several processes proposing the same value and executing in lock-step may return $\textit{true}$.

Note also that the solo-write complexity of Algorithm 2 is $b=O(\sqrt{n/k})$. Since, for $i =1$ to b, in the ith iteration, a process reads i registers, the algorithm also has step complexity of O(n / k) which has been shown to be optimal for the case $k=1$ [1].

Fig. 1

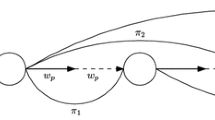
Execution for Lemma 8, assuming that $q_0,\ldots ,q_k$ read R[l] in that order

The following lemma will be instrumental in showing that Algorithm 2 satisfies the k-VS-Agreement property.

Lemma 8

Let $\gamma$ be an execution and let $i \in \{1, \dots , b-1\}$. Suppose $k+1$ processes $q_0, \dots , q_k$ write distinct values $u_0, \dots , u_k$ to $R[i+1]$ during $\gamma$. Then, there exists a set $P_i$ of processes such that:

• $|P_i|=i\cdot k$,

• $q_i \notin P$,

• at the configuration that immediately succeeds the last write primitive applied by processes in $P_i$, $R[i+1]=\bot$;

• $\gamma$ passes through a configuration C in which $R[i] \ne \bot$ in C and each process in $P_i$ applies a write primitive after C.

Proof

Fix an i such that $0<i< b-1$ and let $Q=\{q_0,\ldots ,q_k\}$ be $k+1$ distinct processes that write distinct values $\{u_0,\ldots ,u_k\}$ in $R[i+1]$ in an execution $\gamma$. By the pseudocode of Algorithm 2, these processes also write in R[i]. Before writing in $R[i+1]$, a process makes sure that $R[0],R[1],\ldots ,R[i]$ contain its own input value (lines 4, 5), and $R[i+1]$ contains the initial value $\bot$ (line 8).

Let C be the configuration immediately before the first read by a process in Q after it writes in R[i]. By definition $R[i] \ne \bot$ in C. Let $C'$ be the configuration immediately after the last process in Q performs its read of $R[i+1]$ before writing to it in $\gamma$. By the algorithm, the write in $R[i+1]$ by any $q_j$ follows $C'$ in $\gamma$.

For a given l, $0 \le l < i$, consider the order of the $k+1$ read operations on R[l] executed by processes in Q after their writes on R[i]. Assume, without loss of generality, that the order is $q_0$, $\ldots$, $q_k$. Also, since for each $h=1$,$\ldots$, k $q_{h-1}$ reads $u_{h-1}$ in R[l] and $q_h$ reads $u_h$ in R[l], there must be a process $p_{h,l}$ that writes $u_h$ in $R[\ell ]$ between these two read operations. We show that this is the last write of $p_{h,l}$ in $\gamma$. Indeed, before performing the next write (on $R[l+1]$), $p_{h,l}$ reads $R[l+1]$. Since the write by $p_{h,l}$ follows the read on R[l] by process $q_{h-1}$, by the algorithm, $q_{h-1}$ has previously written $u_{h-1}\ne \bot$ in R[i] and, thus, in $R[l+1]$. Hence, in the configuration immediately before the write in R[l] by $p_{h,l}$ we have $R[l+1]\ne \bot$. The check in line 8 implies that $p_{h,l}$ cannot write to any register after R[l]. Note that all these processes $p_{h,l}$ must be distinct from any $q_j$: otherwise, we contradict the fact that every $q_j$ writes in R[i], $i>l$. Note that $p_{h,l}$ is different from any $p_{h',l'}$ if $h' \ne h$ or $l \ne l'$. Thus, there are $i\cdot k$ such processes: one for each register R[l], $0\le l<i$, and each h, $1\le h \le k$.

Finally, since the last write primitive of $p_{h,l}$ precedes configuration $C'$, at the configuration immediately after this write $R[i+1]$ stores the initial value. This is illustrated in Fig. 1.

Moreover, since the last write of $p_{h,l}$ happens after a read by a process in Q, it is applied after the configuration C.

Thus, the set $P_i$ of $i\cdot k$ processes $p_{h,l}$, $l=0,\ldots ,i-1$, and $h = 1, \ldots k$, satisfies the conditions of the lemma. $\square$

Lemma 9

(k -VS-Agreement) Invocations of $\textit{split}(v)$ return true for at most k distinct values.

Proof

Suppose, by contradiction, that $k+1$ invocations of $\textit{split}$ performed by processes $q_0,\ldots ,q_k$ with distinct values $\{u_0,\ldots ,u_k\}$ return true. Recall that before returning $\textit{true}$, a process $q_j$ has to write its input value $u_j$ in all b registers. For each $i=1,\ldots b-2$, let $P_i$ be the $i\cdot k$ processes, satisfying the conditions specified by Lemma 8.

Consider any two sets $P_i$, $P_l$, $0<i< l < b-1$. We show that $P_i \cap P_l = \emptyset$. Indeed, by the definition of $P_i$, in the configuration when the processes in $P_i$ have completed all their writes, $R[i+1]$ stores $\bot$ and, by the algorithm, since $l>i$, R[l] also stores $\bot$. But, by the definition of $P_l$, each process in $P_l$ has applied a write primitive after a configuration where $R[l] \ne \bot$. Thus, $P_i$ and $P_l$ are disjoint.

Recall that each $q_j$, $j \in \{0, \ldots , k\}$, writes to $R[b-1]$ and, thus, does not belong to $\cup _{i=1}^{b-2} P_i$. Hence, the total number of processes must be at least $k+1+\sum _{i=1}^{b-2} ik = k+1+k\frac{b^2-3b+2}{2}$, which contradicts the assumption that that $b^2-3b+4 >\frac{2n-2}{k}$. $\square$

Lemma 10

(Wait-freedom) In every execution, each correct process completes its $\textit{split}$ operation in a finite number of its own steps.

Proof

By the pseudo-code of Algorithm 2 the value of Lastwritten at the beginning of the ith iteration of the while loop is equal to $i-2$ (lines 1 and 10). Then, by the exit condition of the while loop, this is executed at most $b+1$ times. Similarly the for loop is executed a finite number of times. Then, a correct process either returns a response on line 5 or on line 8, or after at most $b+1$ iterations of the while loop. $\square$

Theorem 11

Algorithm 2 is an interval-solo-fast anonymous input-oblivious implementation of a k-value-splitter with solo-write and space complexities in $O(\sqrt{n/k})$.

Proof

Since only read-write registers are used and the $\textit{split}$ operation is wait-free by Lemma 10, the algorithm is trivially interval-solo-fast.

By Lemma 9, the algorithm satisfies the k -VS-Agreement property. We prove in the following that the Solo Execution property is also satisfied. Consider any solo execution $\gamma$ in which a $\textit{split}(v)$ by a process p completes and suppose, by contradiction, that the operation returns false. By inspecting the pseudocode, it is easy to see that the value of $\textit{Lastwritten}$ is equal to the index of the last register p wrote or to $-1$ if no such writes took place. To return false p must have either read a value different from its input (line 5) or a value different from $\bot$ in a register p has not yet written (line 8). But this contradicts the fact that $\gamma$ is a solo execution. Thus, the algorithm satisfies the Solo Execution property. $\square$

Non-input-oblivious k -value-splitter We now describe an anonymous k-value-splitter algorithm that exhibits $O(\log (m/k)/\log {\log {(m/k)}})$ complexity. The algorithm uses an array R of b registers, where $b!= \lceil m/k \rceil$. The values set is partitioned into $l=\lceil m/k \rceil$ subsets $V_1$, $\ldots$, $V_l$; the size of each subset is at most k. A unique permutation $\pi _{j}$ of the registers in R is associated to each value subset $V_j$ for each $j \in \{1,\dots , l\}$. The permutation is used as the order in which the processes access the registers during the execution of split(v) with $v\in V_j$. Therefore, the algorithm is not input-oblivious.

In its i-th access, a process executing split(v) with $v \in V_j$ first reads register $R[\pi _{j}(i)]$; if $\bot$ is read, the process writes v to it; If a value $v'\ne v$ is read, it returns false (contention is detected). If the process succeeds in writing v in all registers, it returns true. The algorithm is also trivially anonymous and interval-solo-fast.

Theorem 12

Algorithm 3 implements anonymous interval-solo-fast m-valued k-value-splitter with solo-write and space complexity in $O(\log {(m/k)}/\log {\log {(m/k)}})$.

Proof

If an operation $\textit{split}(v)$ runs solo, then no value other than v can be found in any register (line 2). Thus the Solo Execution property is ensured.

Suppose, by contradiction, that $k+1$ $\textit{split}()$ operations with distinct values return true. Among these $k+1$ values, there are two distinct values, v and $v'$ that belong to two distinct subsets, respectively $V_i$ and $V_h$. Let $j,\ell$ be two indexes in $\{1,\ldots ,b\}$ such that j appears before $\ell$ in $\pi _i$ but $\ell$ appears before j in $\pi _{h}$. By the algorithm, before returning true, $p_{v}$ and $p_{v'}$ have read, respectively, v and $v'$ in both R[j] and $R[\ell ]$.

Without loss of generality, let v be written to R[j] before $v'$ is written to $R[\ell ]$. By the algorithm, before any process performing $\textit{split}(v')$ reads R[j] in line 2 (and, thus, writes $v'$ to R[j] in line 3), $v'$ has been written to $R[\ell ]$, and, by the assumption, v has been written to R[j]. Hence, the process will not find $\bot$ in R[j] and will not write to R[j]—a contradiction. Therefore, the algorithm satisfies the k-VS-Agreement property.

Since every operation performs b writes and b reads, where $b!=\lceil m/k \rceil$, the step and space complexities of the algorithm are $O(\log {(m/k)}/\log {\log {(m/k)}})$. $\square$

6 Concluding remarks

In this paper, we present matching lower and upper bounds $\Theta (\min (\sqrt{n/k},\log {(m/k)}/\log {\log {(m/k)}}))$ on the space complexity of anonymous interval-solo-fast k-set agreement implementations. If the implementation uses less than $\Gamma ^{-1}(m/k)$ registers, then its solo-write complexity must be $\Omega (\min (\sqrt{n/k},\log {(m/k)}/\log {\log {(m/k)}}))$. If the implementation is input-oblivious, its solo-write complexity is $\Omega (\sqrt{n/k})$. Our matching interval-solo-fast k-set implementation exhibit solo-write complexity (and, thus, uncontended space complexity) of $O(\min (\sqrt{n/k},\log {(m/k)}/ \log {\log {(m/k)}}))$. Our results imply the first non-trivial tight bound for general k-set agreement.

The proof of our lower bound is based on constructing executions in which no process is aware of interval contention and, thus, the lower bounds also apply to abortable [2, 15] k-set agreement algorithms, where operations are allowed to return a specific abort response when interval contention is detected, and be-reinvoked later. An interesting open question is whether a matching abortable k-set agreement algorithm can be found.