Abstract
We study the dynamics of symmetric and asymmetric spin-glass models of size N. The analysis is in terms of the double empirical process: this contains both the spins, and the field felt by each spin, at a particular time (without any knowledge of the correlation history). It is demonstrated that in the large N limit, the dynamics of the double empirical process becomes deterministic and autonomous over finite time intervals. This does not contradict the well-known fact that SK spin-glass dynamics is non-Markovian (in the large N limit) because the empirical process has a topology that does not discern correlations in individual spins at different times. In the large N limit, the evolution of the density of the double empirical process approaches a nonlocal autonomous PDE operator \(\Phi _t\). Because the emergent dynamics is autonomous, in future work one will be able to apply PDE techniques to analyze bifurcations in \(\Phi _t\). Preliminary numerical results for the SK Glauber dynamics suggest that the ‘glassy dynamical phase transition’ occurs when a stable fixed point of the flow operator \(\Phi _t\) destabilizes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper studies the emergent dynamics of mean-field non-spherical spin-glasses. At low temperature, spin-glass systems are characterized by slow emergent timescales that typically diverge with the system size (see [41, 44, 62] for good surveys of known results). Probably the most famous mean-field spin glass model is that of Sherrington and Kirkpatrick [58]. It is widely known in the physics community that the SK spin glass undergoes a ‘dynamical phase transition’ as the temperature is lowered [4, 5, 41, 62]. Essentially what this means is that the average correlation-in-time of spins does not go to zero as time progresses: that is, some spins get locked into particular states and flip extremely rarely. Although there has been much progress in the study of spin glass dynamics [9, 10, 40], a rigorous proof of a dynamical phase transition in the original SK spin glass model remains elusive. More precisely, although it is known that the time to equilibrium is O(1) when the temperature \(\beta ^{-1}\) is high [8, 33], there is lacking a proof that the time-to-equilibrium diverges with N when \(\beta \) is large (to the best of this author’s knowledge). Furthermore it is well-established that the equilibrium SK Spin-Glass system undergoes a ‘Replica Symmetry Breaking’ phase transition as \(\beta \) increases [39, 55, 64], and this leads many scholars to expect that a phase transition should also be manifest in the initial dynamics. The equilibrium ‘Replica Symmetry Breaking’ transition is characterized by the distribution of the overlap between two independent replica not concentrating at 0, but possessing a continuous density over an interval away from zero [53, 65]. A major reason for the lack of a rigorous characterization of the dynamical phase transition (as emphasized by Ben Arous [5] and Guionnet [41]) is that the existing large N emergent equations are not autonomous and very difficult to analyze rigorously. This paper takes steps towards this goal by deriving an autonomous PDE for the emergent (large N) dynamics: this PDE should be more amenable to a bifurcation analysis (to be performed in future work) than the existing nonautonomous delay equations [9, 37]. These results are also of great relevance to the dynamics of asymmetric spin glass models, which have seen a resurgence of interest in neuroscience in recent years [24, 26, 28,29,30, 32, 47].
This paper determines the emergent dynamics of M ‘replica’ spin glass systems started at initial conditions that are independent of the connections. ‘Replicas’ means that we take identical copies of the same static connection topology \({\mathbf {J}}\), and conditionally on \({\mathbf {J}}\), run independent and identically-distributed jump-Markov stochastic processes on each replica. As noted above, Replicas are known to shed a lot of insight into the rich tree-like structure of ‘pure states’ that emerge in the static SK spin glass at low temperature [39, 53, 55, 64, 65], and it is thus reasonable to conjecture that replicas will shed much insight into the dynamical phase transition. Indeed Ben Arous and Jagannath [6] use the overlap of two replicas to determine bounds on the spectral gap determining the rate of convergence to equilibrium of mean-field spin glasses. Writing \({\mathcal {E}} = \lbrace -1,1 \rbrace \), the spins flip between \(-1\) and 1 at rate \(c(\sigma ^{i,j}_t,G_t^{i,j})\) for some general function \(c: \lbrace -1,1\rbrace \times {\mathbb {R}} \rightarrow {\mathbb {R}}^+\), where the field felt by the spin is written as
and \({\mathbf {J}} = \lbrace J^{jk} \rbrace _{1\le j \le k \le N}\) are i.i.d. centered Gaussian variables with a specified level of symmetry. For Glauber dynamics for the SK spin glass [53], the connections are symmetric (i.e. \(J^{jk} = J^{kj}\)) and the dynamics is reversible, with c taking the form [38],
where h is a constant known as the magnetization, and \(\beta ^{-1}\) is the temperature. In this case, the spin-glass dynamics are reversible with respect to the following Gibbs Measure
where \(\rho ^N_{{\mathbf {J}}}\) is a normalizing factor, often called the free energy, given by
For further details on the equilibrium Gibbs measure, see the reviews in [13, 55, 65]. It is known that as \(\beta \) increases from 0, a sharp transition occurs, where the convergence to equilibrium bifurcates from being O(1) in time, to timescales that diverge in N [5, 44].
One of the novelties of this paper is to study the emergent properties of the double empirical process \(({\hat{\mu }}^N_t(\varvec{\sigma },{\mathbf {G}}))_{t\ge 0}\), which contains information on the distribution of the spins and fields, without knowledge of the ‘history’ of each spin and field. Formally, \({\hat{\mu }}^N(\varvec{\sigma },{\mathbf {G}})\) is a càdlàg \({\mathcal {P}}\)-valued process (where \({\mathcal {P}}={\mathcal {M}}^+_1( {\mathcal {E}}^M \times {\mathbb {R}}^M)\)), i.e.
where \(\lbrace \sigma ^{i,j}_t \rbrace \) is the solution of the jump Markov Process, and the fields are defined in (1).
We now overview some of the existing literature on the dynamics of the SK spin glass. In the physics literature, averaging over quenched disorder been used to derive limiting equations for the correlation functions [22, 42, 48, 49, 53, 59,60,61]. The first rigorous mathematical results were obtained in the seminal work of Ben Arous and Guionnet [9, 11] (these results were for a similar ‘soft-spin’ model driven by Brownian Motions). Guionnet [40] expanded on this work to prove that in the soft SK spin glass started at i.i.d initial conditions, the dynamics of the empirical measure converges to a unique limit, with no restriction on time or temperature. Grunwald [37, 38] obtained analogous equations for the limiting dynamics of the pathwise empirical measure for the jump-Markov system studied in this paper. More recent work by Ben Arous, Dembo and Guionnet has rigorously established the Cugliandolo-Kurchan [22] / Crisanti-Horner-Sommers [21] equations for spherical spin glasses using Gaussian concentration inequalities [10]. A recent preprint of Dembo, Lubetzky and Zeitouni has established universality for asymmetric spin glass dynamics, extending the work of Ben Arous and Guionnet to non-Gaussian connections, with no restriction on time or temperature [24].
In the papers cited above, the emergent large N dynamics is non-autonomous: that is, one needs to know the full history of the emergent variable (either the empirical measure, or correlation / response functions) upto time t to predict the dynamics upto time \(t+\delta t\). In the early work of Ben Arous, Guionnet and Grunwald [9, 11, 37, 40], the emergent variable is the pathwise empirical measure. This is an extremely rich object because it ‘knows’ about average correlations in individual spins at different times. Ben Arous and Guionnet [9] demonstrated that the limiting dynamics of the pathwise empirical measure is the law of a complicated implicit delayed stochastic differential equation. In the later work of Ben Arous, Dembo and Guionnet on spherical spin glasses, a simpler set of emergent variables was used: the correlation and response functions [4, 10] (this formalism is frequently used by physicists [22, 42, 53]). In the \(p=2\) case, the resultant equations are autonomous, and this allowed them to rigorously prove that there is a dynamical phase transition [4].
There is still lacking a rigorous characterization of the dynamical phase transition in the non-spherical SK model. As has been emphasized by Ben Arous [5] and Guionnet [41], a fundamental difficulty is that all of the known emergent equations are non-autonomous (that is, they are either delay integro-differential equations, or an implicit delayed SDE [9, 37]). A major reason that the emergent equations are not autonomous is that the emergent object studied by [9, 37] - the pathwise empirical measure - carries too much information, because it knows about the history of the spin-flipping. This is why this paper focuses on determining the limiting dynamics of a different order parameter: the double empirical process (as defined in (5)-(7)) that cannot discern time-correlations in individual spins. The empirical process carries more information about the system than that of Ben Arous, Guionnet [9, 11, 40] and Grunwald [37] insofar as it contains information about overlaps between different replicas, but less information insofar as it does not know about correlations-in-time of individual spins. The chief advantage of working with this order parameter is that the dynamics becomes autonomous in the large N limit, just as in classical methods for studying the empirical process in interacting particle systems [23, 63]. One can now apply the apparatus of PDEs to the limiting equations to study the bifurcation of the fixed points. Indeed preliminary analytic work has identified that there is a bifurcation in the fixed point of the flow (31) for SK Glauber dynamics, and 2 replica (see Remark 2.5).
Many recent applications of dynamical spin glass theory have been in neuroscience, being referred to as networks of balanced excitation and inhibition. Typically the connections in these networks are almost asymmetric, unlike in the original SK model. These applications include networks driven by white noise [14, 16, 17, 28,29,30,31, 66] and also deterministic disordered networks [1, 20, 26, 47]Footnote 1; the common element to all of these papers being the random connectivity of mean zero and high variance. It has been argued that the highly variable connectivity in the brain is a vital component to the emergent gamma rhythm [14]. Another important application of spin-glass theory has been the study of stochastic gradient descent algorithms [7, 54].
Our fundamental result is to show that as \(N\rightarrow \infty \), the empirical process converges to have a density given by a Mckean-Vlasov-type PDEFootnote 2 of the form, for \(\varvec{\alpha }\in {\mathcal {E}}^M\) and \({\mathbf {x}} \in {\mathbb {R}}^M\),
where \(\xi _t \in {\mathcal {M}}^+_1\big ({\mathcal {E}}^{M} \times {\mathbb {R}}^M\big )\) is the probability measure with density \(p_t\), \(\varvec{\alpha }[i]\) is the same as \(\varvec{\alpha }\), except that the \(i^{th}\) spin has a flipped sign. \({\mathbf {m}}^{\xi _t}\) and \({\mathbf {L}}^{\xi _t}\) are functions defined in Sect. 2.
In broad outline, our method of proof resembles that of Ben Arous and Guionnet [9] and Grunwald [37], insofar as (i) we freeze the interaction and (ii) study the Gaussian properties of the field variables. However our approach is different insofar as, after freezing the interaction, we do not use Girsanov’s Theorem to study a tilted system, but instead study the pathwise evolution of the empirical process over small time increments. This pathwise approach to the Large Deviations of interacting particle systems has been popular in recent years: being employed in the work of Budhiraja, Dupuis and colleagues [15], in this author’s work on interacting particle systems with a sparse random topology [52], and subsequent work in [18, 19, 31]. More precisely, we study the evolution over small time intervals of the expectation of test functions with respect to the double empirical measure: a method that has been applied to interacting particle systems in, for example, [45] and [51]. To understand the change in the fields \(\lbrace G^j_t\rbrace \) over a small increment in time, we use the law \(\gamma \) of the connections, conditioned on the value of the fields at that time step. It is fundamental to our proof that - essentially due to the Woodbury formula for the inverse of a matrix with a finite-rank perturbation - the conditional Gaussian density can be written as a function of the empirical measure \({\hat{\mu }}^N_t(\varvec{\sigma }, {\mathbf {G}}) = N^{-1}\sum _{j\in I_N} \delta _{(\varvec{\sigma }^j_t , {\mathbf {G}}^j_t)}\) and the local spin and field variables (see the analysis in Section 7.1).
Notation: Let \({\mathcal {E}} = \lbrace -1 ,1 \rbrace \). For any Polish Space \({\mathcal {X}}\), we let \({\mathcal {M}}^+_1({\mathcal {X}})\) denote all probability measures on \({\mathcal {X}}\), and \({\mathcal {D}}\big ( [0,T], {\mathcal {X}} \big )\) the Skorohod space of all \({\mathcal {X}}\)-valued càdlàg functions [12]. We always endow \({\mathcal {M}}^+_1({\mathcal {X}})\) with the topology of weak convergence. Let \({\mathcal {P}} := {\mathcal {M}}^+_1\big ({\mathcal {E}}^M \times {\mathbb {R}}^M\big )\) denote the set of all probability measures on \({\mathcal {E}}^M \times {\mathbb {R}}^M\), and define the subset
For any vector \({\mathbf {g}} \in {\mathbb {R}}^M\), \(\left\| {\mathbf {g}} \right\| \) is the Euclidean norm, and \(\left\| {\mathbf {g}} \right\| _{\infty }\) is the supremum norm. For any square matrix \({\mathbf {K}} \in {\mathbb {R}}^{m\times m}\), \(\left\| {\mathbf {K}} \right\| \) is the operator norm, i.e.
Let \(d_W\) be the Wasserstein Metric [34, 63] on \(\tilde{{\mathcal {P}}}\), i.e.
where the infimum is over all measures \(\eta \in {\mathcal {M}}^+_1\big ( {\mathcal {E}}^M\times {\mathbb {R}}^M \times {\mathcal {E}}^M\times {\mathbb {R}}^M\big )\) with marginals \(\beta \) (over the first two variables), and \(\zeta \) (over the second two variables). We let \({\mathcal {C}}([0,T],{\mathcal {X}})\) denote the space of all continuous functions from [0, T] to \({\mathcal {X}}\). \({\mathcal {B}}({\mathcal {X}})\) denotes the Borelian subsets.
The spins are indexed by \(I_N := \lbrace 1,2,\ldots , N\rbrace \), and the replicas by \(I_M := \lbrace 1,2,\ldots ,M\rbrace \). The typical indexing convention that we follow is \(\varvec{\sigma }^j_t = (\sigma ^{1,j}_t,\ldots ,\sigma ^{M,j}_t)^T \in {\mathcal {E}}^M\), and \(\varvec{\sigma }_t = (\sigma ^{i,j}_t)_{i \in I_M, j\in I_N} \in {\mathcal {E}}^{NM}\).
2 Outline of model and main result
Let \(\big (\Omega ,{{\mathcal {F}}}, ({\mathcal {F}}_t) , {\mathbb {P}}\big )\) be a filtered probability space containing the following random variables. The connections \(( J^{jk})_{j,k \in {\mathbb {Z}}}\) are centered Gaussian random variables, with joint law \(\gamma \in {\mathcal {M}}^+_1\big ({\mathbb {R}}^{{\mathbb {Z}}^+\times {\mathbb {Z}}^+}\big )\). To lighten the notation we assume that there are self-connections (one could easily extend the results of this paper to the case where there are no self-connections). Their covariance is taken to be of the form
The parameter \({\mathfrak {s}} \in [0,1]\) is a constant indicating the level of symmetry in the connections. In the case that \({\mathfrak {s}} = 1\), \(J^{jk} = J^{kj}\) identically, and in the case that \({\mathfrak {s}}=0\), \(J^{jk}\) is probabilistically independent of \(J^{kj}\). (One could easily extend these results to the case that \({\mathfrak {s}} \in [-1,0)\)). \(\lbrace J^{jk} \rbrace _{j,k \in {\mathbb {Z}}^+}\) are assumed to be \({\mathcal {F}}_0\)-measurable.
We take M replicas of the spins: this means that the connections \({\mathbf {J}}\) are the same across the different systems, but (conditionally on \({\mathbf {J}}\)) the spin-jumps in different systems are independent. Our reason for working with replicas is that, as discussed in the introduction, in the case of reversible dynamics, replicas are known to shed much light on the rich ‘tree-like’ structure of pure states in the equilibrium Gibbs measure [39, 53, 55, 56, 64]. If one wishes to avoid replicas, one could just take \(M=1\). The spins \( \big \lbrace \sigma ^{i,j}_{t} \big \rbrace _{j\in I_N , i \in I_M, t\ge 0 }\) constitute a system of jump Markov processes: i being the replica index, and j being the spin index. Spin (i, j) flips between states in \({\mathcal {E}} = \lbrace -1 , 1 \rbrace \) with intensity \(c(\sigma ^{i,j}_t,G^{i,j}_t)\) (where \(G^{i,j}_t = N^{-\frac{1}{2}}\sum _{k=1}^N J^{jk}\sigma ^{i,k}_t\)) for a function \(c: {\mathcal {E}}\times {\mathbb {R}} \rightarrow [0,\infty )\) for which we make the following assumptions:
-
c is strictly positive and uniformly bounded, i.e. for some constant \(c_1 > 0\),
$$\begin{aligned} \sup _{\sigma \in {\mathcal {E}}}\sup _{g\in {\mathbb {R}}}\big | \big (c(\sigma ,g) \big | \le c_1 \text { and }c(\sigma ,g) > 0. \end{aligned}$$(12) -
The following Lipschitz condition is assumed: for a constant \(c_L > 0\), for all \(\sigma \in {\mathcal {E}}\) and \(g_1,g_2 \in {\mathbb {R}}\),
$$\begin{aligned} \big | c\big (\sigma ,g_1\big )- c\big (\sigma ,g_2\big ) \big |&\le c_L \big | g_1 - g_2 \big | \end{aligned}$$(13)$$\begin{aligned} \big | \log c\big (\sigma ,g_1\big )- \log c\big (\sigma ,g_2\big ) \big |&\le c_L \big | g_1 - g_2 \big | . \end{aligned}$$(14) -
The following limits exist for \(\sigma = \pm 1\),
$$\begin{aligned} \lim _{g\rightarrow -\infty } c(\sigma ,g) \; \; , \; \; \lim _{g\rightarrow \infty } c(\sigma ,g). \end{aligned}$$(15) -
The log of c is bounded in the following way: there exists a constant \(C_g > 0\) such that
$$\begin{aligned} \sup _{\alpha \in {\mathcal {E}}}\big | \log c(\alpha ,g) \big | \le C_g \big | g \big |. \end{aligned}$$(16)
We note that the Glauber Dynamics for the reversible dynamics in (2) satisfy the above assumptions [35, 38].
To facilitate the proofs, we represent the stochasticity as a time-rescaled system of Poisson counting processes of unit intensity [27]. We thus define \(\lbrace Y^{i,j}(t) \rbrace _{i\in I_M , j \in {\mathbb {Z}}^+}\) to be independent Poisson processes, which are also independent of the disorder variables \(\lbrace J^{jk} \rbrace _{j,k \in {\mathbb {Z}}^+}\). We define the spin system \(\lbrace \sigma ^{i,j}_t \rbrace \) to be the unique solution of the following system of SDEs
where \(A\cdot x := (-1)^x\). Clearly \(\sigma ^{i,j}_t\) depends on N (for convenience this is omitted from the notation). The law of the initial condition \(\varvec{\sigma }_0\) is written as \(\mu _{0} \in {\mathcal {M}}^+_1\big ({\mathcal {E}}^{MN}\big )\). \(\mu _0\) is assumed to be independent of the disorder. Note that the forward Komolgorov equation describing the dynamics of the law \(P^N_{{\mathbf {J}}}(t) \in {\mathcal {M}}^+_1\big ({\mathcal {E}}^{MN}\big )\) of the spins at time t (conditioned on a realization \({\mathbf {J}}\) of the disorder) is [27]
where \(\varvec{\sigma }[i,j] \in {\mathcal {E}}^{MN}\) is the same as \(\varvec{\sigma }\), except that the spin with indices (i, j) has a flipped sign, and \({\hat{G}}^{i,j}_t = N^{-1/2}\sum _{k\in I_N, k\ne j}J^{jk}\sigma ^{i,k}_t - 2N^{-1/2}J^{jj}\sigma ^{i,j}_t\).
For some fixed constant \({\mathfrak {c}} > 0\), define the set
We assume that the initial condition is such that
Note that (20) is satisfied if \(\lbrace \varvec{\sigma }^j_0 \rbrace _{j\in I_N}\) are iid samples from some probability law \({\tilde{\mu }}_0 \in {\mathcal {M}}^+_1({\mathcal {E}}^M)\) that is such that
One would then find that (20) follows from Sanov’s Theorem [25]. For an arbitrary positive constant \(T>0\), we define
If \(\tau _N < T\), then the smallest eigenvalue of the overlap matrix \({\mathbf {K}}^{{\hat{\mu }}^N_{\tau _N}}\) (as defined in (24)) is less than or equal to \(\mathfrak {c}\). Intuitively, the stopping time is reached when the spins in different replicas are too similar. One expects that this is an extremely rare event, even on timescales diverging in N. See Remark 2.4. The main result of this paper is the following. We emphasize that these are ‘quenched’ results. ‘Annealing’ methods are not used in this paper.
Theorem 2.1
Fix \(T > 0\). There exists a flow operator \(\Phi : {\mathcal {P}} \rightarrow {\mathcal {C}}\big ([0,T],{\mathcal {P}} \big )\) written \(\Phi \cdot \mu := \lbrace \Phi _t\cdot \mu \rbrace _{t\ge 0}\) such that \(\Phi _0\cdot \mu = \mu \) and for any \(\epsilon > 0\)
The flow \(\Phi \) is specified in Sect. 2.1. It follows immediately from the Borel-Cantelli Theorem that \({\mathbb {P}}\) almost surely
2.1 Existence and uniqueness of the flow \(\Phi _t\)
In this section we define \(\Phi \cdot \mu \in {\mathcal {C}}\big ([0,T],{\mathcal {P}} \big )\), for any \(\mu \in {\mathcal {P}}\) such that \({\mathbb {E}}^{\mu (\sigma ,g)}\big [g^2\big ] <\infty \). We write \(\Phi \cdot \mu := \lbrace \Phi _t\cdot \mu \rbrace _{t\in [0,T]}\), where \(\Phi _t: {\mathcal {P}} \rightarrow {\mathcal {P}}\), and in the following we write \(\xi _t =\Phi _t \cdot \mu \).
Lemma 2.2
Fix \(T > 0\). For any \(\mu \in {\mathcal {P}} := {\mathcal {M}}^+_1\big ({\mathcal {E}}^M \times {\mathbb {R}}^M\big )\) such that \({\mathbb {E}}^{\mu (\sigma ,g)}\big [g^2\big ] <\infty \), there exists a unique set of measures \(\lbrace \xi _{t}\rbrace _{t\in [0,T]} \subset {\mathcal {P}}\) with the following characteristics
-
1.
For all \(t \in (0, T]\), \(\xi _t\) has a density in its second variable, i.e. \(d\xi _t(\varvec{\sigma },{\mathbf {x}}) = p_t(\varvec{\sigma },{\mathbf {x}})d{\mathbf {x}}\). \(p_t(\varvec{\sigma },{\mathbf {x}})\) is continuously differentiable in t, twice continuously differentiable in \({\mathbf {x}}\), and satisfies the system of equations (24)–(31).
-
2.
\(\xi _0 = \mu \), and for all \(t\in [0,T]\), \(t \rightarrow \xi _t\) is continuous.
For any \(\xi \in {\mathcal {P}}\) such that \({\mathbb {E}}^{\xi (\sigma ,g)}\big [\left\| g \right\| ^2\big ] <\infty \), define the \(M\times M\) coefficient matrices \(\lbrace {\mathbf {L}}^{\xi },\varvec{\kappa }^{\xi },\varvec{\upsilon }^{\xi },{\mathbf {K}}^{\xi }\rbrace \in {\mathbb {R}}^{M^2}\) to have the following elements,
For any \(\mu \in {\mathcal {P}}\), define \(\Lambda ^{\mu }\) to be the smallest eigenvalue of \({\mathbf {K}}^{\mu }\), i.e.
noting that the eigenvalues of \({\mathbf {K}}^{\mu }\) are real (since it is symmetric) and non-negative. To facilitate the following proofs (in particular, the existence and uniqueness of the solution to the PDE), we want the following functions \({\mathbf {m}}^{\xi }(\varvec{\sigma },{\mathbf {x}})\) and \({\mathbf {L}}^{\xi }\) to be uniformly Lipschitz for all \(\xi \in {\mathcal {P}}\). Indeed thanks to our definition of the stopping time \(\tau _N\), it does not matter how \({\mathbf {m}}^{\xi }\) is defined for \(\xi \) such that \(\Lambda ^{\xi } < {\mathfrak {c}}/2\), as long as \(\epsilon \) is sufficiently small. To this end, we choose a definition that ensures that \(\xi \rightarrow {\mathbf {H}}^{\xi }\) is uniformly Lipschitz, i.e.
Now define the vector field \({\mathbf {m}}^{\xi }(\varvec{\sigma },{\mathbf {x}}) : {\mathcal {P}}\times {\mathcal {E}}^M \times {\mathbb {R}}^M \rightarrow {\mathbb {R}}^M\) as follows
We can now write down the PDE that defines the density of \(\xi _t := \Phi _t(\mu )\). For some \(\varvec{\alpha }\in {\mathcal {E}}^M\) and \({\mathbf {x}}\in {\mathbb {R}}^M\), we write \(p_t(\varvec{\alpha },{\mathbf {x}})\) to be the density of \(\xi _t\) in its second variable, i.e. \(\xi _t\big (\varvec{\sigma }=\varvec{\alpha }, g^i \in [x^i,x^i+dx^i]\big ) := p_t(\varvec{\alpha },{\mathbf {x}}) dx^1 \ldots dx^M\). Write \(\varvec{\alpha }[i]\in {\mathcal {E}}^M\) to be almost identical to \(\varvec{\alpha }\), except that the \(i^{th}\) spin has a flipped sign. The evolution of the densities is governed by the following system of partial differential equations
Remark 2.3
We emphasize that the convergence result in Theorem 2.1 does not hold for the path-wise empirical measure, i.e.
endowed with the Skorohod topology on the set of càdlàg paths \({\mathcal {D}}\big ([0,T],{\mathcal {E}}^{M}\big )\) [27]. Indeed it is known that the limit of the pathwise empirical measure is non-Markovian, so the Markovian stochastic hybrid system with Fokker-Planck equation given by (31) is almost certainly not the limiting law for the pathwise empirical measure [9]. This does not mean that our result in Theorem 2.1 is inconsistent with the non-Markovian results in the work of Ben Arous, Guionnet and Grunwald [9, 37], since the topology in our theorem cannot discern correlations in particular spins at different times.
Remark 2.4
It seems plausible that for any temperature \(\beta > 0\) and any \(T > 0\), there exists \({\mathfrak {c}}\) such that
Perhaps one could prove this by demonstrating that the attracting manifold of the flow \(\Phi _t\) is such that all eigenvalues of \({\mathbf {K}}^{\xi _t}\) are strictly positive. One expects this to be true because of the presence of the diffusions in the PDE. However the author has not yet seen an easy proof of this.
Remark 2.5
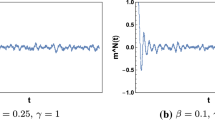
Suppose that the dynamics is reversible, with spin-flipping intensity given by (2), \(h = 0\) and the symmetry \({\mathfrak {s}}=1\). Preliminary numerical work by C.MacLaurinFootnote 3 has identified a family of fixed point solutions to (8) with two replicas (i.e. \(M=2\)). Let \(q \ge 0\) satisfy the implicit relationship
With the above definitions, the field distributions \(p(\varvec{\alpha }, \cdot )\) in the fixed point solution to (8) are weighted Gaussians. For \(h=0\), there is a bifurcation as \(\beta \) increases through 1 in the solutions to (32): for \(\beta \le 1\), \(q=0\) is the unique solution, but for \(\beta > 1\), it is no longer unique.
2.2 Proof outline
We discretize time into \((n+1)\) timesteps \(\lbrace t^{(n)}_a \rbrace _{0\le a \le n}\): writing \(\Delta = t^{(n)}_{a+1} - t^{(n)}_a = Tn^{-1}\). In Sect. 3 we use an argument that is reminiscent of Gronwall’s Inequality to demonstrate that if the action of the flow operator over the time interval \([t^{(n)}_a,t^{(n)}_{a+1}]\) corresponds to the dynamics of the empirical process to within an error of \(o(\Delta )\), then the supremum of the difference between the empirical process and the flow over the entire interval [0, T] must be small. We also introduce an approximate flow \(\Psi _t\), obtained by evaluating the coefficients in the PDE at \({\hat{\mu }}^N_t\) rather than \(\xi _t\). In subsequent sections it will be easier to compare \(\Psi _t\) to \({\hat{\mu }}^N_t\) than to compare \(\Phi _t\) to \({\hat{\mu }}^N_t\).
To accurately estimate the ‘average’ change in the fields \(G^{q,j}_{t^{(n)}_a} \rightarrow G^{q,j}_{t^{(n)}_{a+1}}\) we must perform a change-of-measure to a stochastic process \({\tilde{\sigma }}^{q,j}_{i,t}\) whose spin-flipping is independent of the connections. The reason for this change of measure is that now the changed fields \({\tilde{G}}^{i,j}_t := N^{-1/2}\sum _{k\in I_N}J^{jk}{\tilde{\sigma }}^{i,k}_t\) are Gaussian, and their incremental behavior can be accurately predicted by studying their covariance structure. In Sect. 4 we define \(C^N_{{\mathfrak {n}}}\) such processes \(\lbrace \tilde{\varvec{\sigma }}_{i,t} \rbrace _{1\le i \le C^N_{{\mathfrak {n}}}}\), and we demonstrate that the probability law of the original \({\mathcal {E}}^{MN}\)-valued process \(\varvec{\sigma }_t\) must be close to at least one of them using Girsanov’s Theorem. The partition of the path space \({\mathcal {D}}([0,T],{\mathcal {E}}^M)^N\) is implemented using a second, finer, discretization of time into \(\lbrace t^{(m)}_a \rbrace _{0\le a \le m}\), for some m which is an integer multiple of n. This finer partition of time is needed to ensure that the Girsanov exponent is sufficiently close to unity.
In Sect. 5 we demonstrate that the Wasserstein distance can be approximated arbitrarily well by taking the supremum of the difference in expectation of a finite set of smooth functions. Working now exclusively with the processes \(\tilde{\varvec{\sigma }}_{i,t}\), we Taylor expand the change in expectation of such functions from \(t^{(n)}_a\) to \(t^{(n)}_{a+1}\), for both the empirical measure and the flow operator \(\Phi _t\). The Taylor expansion implies that only the first two moments of the empirical measure and flow operator need to match in order that the change in the Wasserstein Distance is \(o(\Delta )\). There are two basic types of term in the difference of the Taylor Expansions: (i) terms that can be bounded using concentration inequalities for Poisson Processes \(\lbrace Y^{q,j}(t) \rbrace _{q\in I_M,j\in I_N}\), and (ii) terms that require the law \(\gamma \) of the Gaussian connections \(\lbrace J^{jk} \rbrace _{j,k \in I_N}\) to be accurately bounded.
In Sect. 6, we bound the terms (i) whose dynamics can be accurately predicted using the Law of Large numbers for Poisson Processes. These bounds typically involve concentration inequalities for compensated Poisson Processes (which are Martingales [2]). In Sect. 7, we bound the terms (ii), using the conditional Gaussian probability law \(\gamma _{\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}}}\) - obtained by taking the law \(\gamma \in {\mathcal {M}}^+_1({\mathbb {R}}^{N^2})\) of the connections \(\lbrace J^{jk} \rbrace _{j,k\in I_N}\) and conditioning on the values of the NM field variables \(\lbrace {\tilde{G}}^{q,j}_{t^{(n)}_a} \rbrace _{q\in I_M, j\in I_N}\). We demonstrate that the average change in the field terms \({\tilde{G}}^{q,j}_{t^{(n)}_{a+1}} - {\tilde{G}}^{q,j}_{t^{(n)}_a}\) is governed by the first and second moments of \(\gamma _{\varvec{\sigma },{\mathbf {G}}}\). The first moment ultimately leads to the term \({\mathbf {m}}^{\xi _t}\) in (31), and the second moment ultimately leads to the diffusion coefficient \(\sqrt{L^{\xi _t}_{ii}}\).
Before we commence the above plan, we require that the flow operator \(\Phi _t\) is well defined.
Proof of Lemma 2.2
We can interpret \(p_t\) as the marginal probability law of the solution of a nonlinear SDE driven by a Levy Process. [46] proved the existence and uniqueness of a solution to such an SDE in the case that the coefficients are uniformly Lipschitz functions of the probability law (with respect to the Wasserstein distance). By contrast, our coefficients \({\mathbf {m}}^{\xi _t}\) and \(\big ({\mathbf {L}}^{\xi _t}\big )^{1/2}\) (one must take the square root of the diffusion coefficient to obtain the coefficient of the stochastic integral) are only locally Lipschitz (see Lemma 2.6).
To get around this, one first uses [46] to show existence and uniqueness for an analogous system driven by uniformly Lipschitz coefficients \(\hat{{\mathbf {m}}}^{\xi _t}\) and \(\big \lbrace \big ({\hat{L}}_{ii}^{\xi _t}\big )^{1/2} \big \rbrace _{i\in I_M}\). These coefficients are taken to be identical to \({\mathbf {m}}^{\xi _t}\) and \((L_{ii}^{\xi _t})^{1/2} \) when \(\xi _t \in {\mathcal {D}}_{\epsilon }\), where
The solution is written as \(\xi _{\epsilon ,t}\). One then shows that for small enough \(\epsilon \), \(\xi _{\epsilon ,t} \in {\mathcal {D}}_{\epsilon }\) for all \(t\in [0,T]\). Once one has shown this, it must be that \(\xi _t := \xi _{\epsilon ,t}\) is the unique solution.
To do this, one can easily show (analogously to Lemma 3.6) that for all \(\epsilon > 0\), there exist constants \(C_1,C_2 > 0\) such that
The boundedness of \({\mathbb {E}}^{\xi _{\epsilon ,t}}[ (x^i)^2]\) then implies a lower bound for \({\hat{L}}^{\xi _{\epsilon ,t}}_{ii}\), since for any \(u > 0\), thanks to Chebyshev’s Inequality, \(\xi _{\epsilon ,t}(| x^i| \le u ) \ge 1 - {\mathbb {E}}^{\xi _{\epsilon ,t}}[(x^i)^2] u^{-2}\), and the continuity of c implies that \(\inf _{|x| \le u , \sigma \in {\mathcal {E}}}c(\sigma ,x) > 0\). Since \(\mu \rightarrow L^{\mu }_{ii}\) is uniformly Lipschitz, it must be that \(\mu \rightarrow \sqrt{L^{\mu }_{ii}}\) is uniformly Lipschitz over \({\mathcal {D}}_{\epsilon }\), since \(L^{\mu }_{ii}\) is bounded away from zero. \(\square \)
The above existence and uniqueness proof requires that the coefficients of the PDE in (31) are Lipschitz. This is noted in the follow Lemma.
Lemma 2.6
-
(i)
There exists a constant \(C_1>0\) such that for any \(\beta ,\zeta \in \tilde{{\mathcal {P}}}\),
$$\begin{aligned} \sup _{1\le p,q \le M} \big | L_{pq}^{\beta } - L^{\zeta }_{pq}\big | , \big | K_{pq}^{\beta } - K^{\zeta }_{pq}\big |&\le C_1 d_W(\beta ,\zeta ) \end{aligned}$$(33)$$\begin{aligned} \sup _{1\le p,q \le M} \big | \upsilon _{pq}^{\beta } - \upsilon ^{\zeta }_{pq}\big | , \big | \kappa _{pq}^{\beta } - \kappa ^{\zeta }_{pq}\big |&\le C_1\big (1 + {\mathbb {E}}^{\beta }\big [\left\| {\mathbf {x}} \right\| ^2\big ]^{\frac{1}{2}}\big )d_W(\beta ,\zeta ). \end{aligned}$$(34) -
(ii)
There is a constant \(C>0\) such that for all \(\beta ,\zeta \in \tilde{{\mathcal {P}}}\) such that \(\Lambda ^{\beta },\Lambda ^{\zeta } \ge {\mathfrak {c}}/2\), all \(\varvec{\alpha },\varvec{\sigma }\in {\mathcal {E}}^M\) and all \({\mathbf {x}},{\mathbf {g}} \in {\mathbb {R}}^M\),
$$\begin{aligned} \left\| {\mathbf {m}}^{\beta }(\varvec{\alpha },{\mathbf {x}}) - {\mathbf {m}}^{\zeta }(\varvec{\sigma },{\mathbf {g}}) \right\|&\le Cd_W(\beta ,\zeta )\big \lbrace 1 + \left\| {\mathbf {g}} \right\| + {\mathbb {E}}^{\zeta }\big [\left\| {\mathbf {g}} \right\| ^2\big ]^{\frac{1}{2}}\big \rbrace \nonumber \\&\quad + C\left\| \mathbf {x-{\mathbf {g}}} \right\| +C\big \lbrace 1 + {\mathbb {E}}^{\zeta }\big [\left\| {\mathbf {g}} \right\| ^2\big ]^{\frac{1}{2}}\big \rbrace \left\| \varvec{\alpha }-\varvec{\sigma } \right\| \end{aligned}$$(35)$$\begin{aligned} \left\| {\mathbf {m}}^{\beta }(\varvec{\alpha },{\mathbf {g}}) \right\|&\le C \left\| {\mathbf {g}} \right\| + C \big (1 + {\mathbb {E}}^{\beta }\big [\left\| {\mathbf {g}} \right\| ^2\big ]^{\frac{1}{2}} \big ). \end{aligned}$$(36)
Proof
Both results follow almost immediately from the definitions, since \(|c(\cdot ,\cdot )|\) is uniformly bounded, and \(|c(\alpha ,x) - c(\alpha ,g)| \le c_L |x-g|\). It follows from the definition in (29) that \(\xi \rightarrow H_{jk}^{\xi }\) is uniformly Lipschitz (for all indices \(j,k\in I_M\)), since (as noted in (i) of this lemma) \(\xi \rightarrow K_{jk}^{\xi }\) is uniformly Lipschitz. Furthermore \(\big | H_{jk}^{\xi } \big |\) is uniformly bounded, because \(| K^{\xi }_{jk}| \le 1\). \(\square \)
3 Organization of Proof of Theorem 2.1
This section lays the groundwork for the proof of Theorem 2.1, using an argument that is reminiscent of Gronwall’s Inequality. The ultimate aim of this section is to demonstrate that, if the change in the empirical process over a small increment \(\Delta \) in time is similar to the incremental change induced by the flow operator \(\Phi _\Delta \cdot {\hat{\mu }}^N_t\), then the distance \(\sup _{t\in [0,T]}d_W({\hat{\mu }}^N_t , \Phi _t\cdot {\hat{\mu }}^N)\) is \(O(\Delta ^2)\). Thus this section reduces the proof of Theorem 2.1, to the sufficient condition in Lemma 3.5. The rest of the paper is then oriented towards proving Lemma 3.5. The proofs of the lemmas stated just below are deferred to later in the section.
We will express the event in the statement of Theorem 2.1 as a union of \(a_N\) subevents, i.e.
As is noted in the following lemma, it will then suffice to show that the probability of each of the subevents \(\lbrace {\mathcal {A}}^N_j\rbrace \) is exponentially decaying.
Lemma 3.1
Suppose that events \(\lbrace {\mathcal {A}}^N_j \rbrace _{j=1}^{a_N}\) are such that \(\underset{N\rightarrow \infty }{{\overline{\lim }}}N^{-1}\log a_N = 0\). Then
Proof
Immediate from the definitions. \(\square \)
We now outline more precisely what these events are. First, we require that the matrix of connections is sufficiently regular. Let \({\mathbf {J}}_N\) be the \(N\times N\) matrix with (j, k) element equal to \(N^{-\frac{1}{2}}J^{jk}\). Define \({\mathcal {J}}_N\) to be the event
The following lemma notes that \({\mathcal {J}}_N\) is overwhelmingly likely.
Lemma 3.2
-
1.
$$\begin{aligned} \underset{N\rightarrow \infty }{{\overline{\lim }}}N^{-1}\log \gamma \big ( {\mathcal {J}}_N^c \big ) := \Lambda _J < 0. \end{aligned}$$(39)
-
2.
Also,
$$\begin{aligned} {\mathcal {J}}_N \subseteq \big \lbrace \text {For all }t\ge 0,\; {\hat{\mu }}^N_t \in {\mathcal {W}}_2 \big \rbrace . \end{aligned}$$(40)
Define the spaces of measures
Next we define a map \(\Psi : {\mathcal {W}}_{[0,T]} \rightarrow {\mathcal {C}}\big ( [0,T],{\mathcal {P}}\big )\), \(\Psi := (\Psi _t)_{t\in [0,T]}\), that is an approximation of the flow \(\Phi _t\), such that the coefficients of the PDE are evaluated at \({\hat{\mu }}^N_t\), rather than \(\xi _t\). More precisely, it is such that \(\Psi \cdot \mu _{[0,T]} := \eta _{[0,T]}\), and for \(t > 0\), \(\eta _t\) has density \(p_t\) satisfying the PDE
where \(\varvec{\alpha }[i] \in \mathcal {E}^M\) is the same as \(\varvec{\alpha }\in \mathcal {E}^M\), except that the \(i^{th}\) spin has a flipped sign.
We insist that \(\eta _0 = \mu _0\), and that \(t \rightarrow \eta _t\) is continuous. Write \(\Psi _t \cdot \mu _{[0,T]} := \eta _t\). One can easily check that \(\Psi \) is uniquely defined.
The following lemma states that \(\Psi \) is a good approximation of \(\Phi \). The second result in the lemma is necessary for us to be sure that we avoid the pathological situation of \(\Lambda ^{{\hat{\mu }}^N_t} \rightarrow 0\), which would mean that the coefficients in the PDE blowup (see the definition in (28)). Incidentally, this is precisely the reason that we require the stopping time \(\tau _N\) in (21).
Lemma 3.3
Define \({\tilde{d}}_T: {\mathcal {D}}\big ( [0,T], {\mathcal {P}}\big ) \times {\mathcal {D}}\big ( [0,T], {\mathcal {P}}\big ) \rightarrow {\mathbb {R}}^+\) to be
noting that \({\tilde{d}}_T\) does not metrize the Skorohod topology. For any \(\epsilon > 0\), there exists \(\delta > 0\) such that
Furthermore, there exists \(\delta _{{\mathfrak {c}}}\) such that for all \(\delta \le \delta _{{\mathfrak {c}}}\),
Next we discretize time, and also the flow \(\Psi _t\). We partition the time interval [0, T] into \( \lbrace t^{(n)}_b \rbrace _{b=0}^{n-1}\), with \(t^{(n)}_b = b\Delta \) and \(\Delta = T/n\). For any \(t\in [0,T]\), define \(t^{(n)} := \sup \lbrace t^{(n)}_b \; : t^{(n)}_b \le t \rbrace \). We write \(\Psi _b := \Psi _{t^{(n)}_b}\), \({\hat{\mu }}^N_b(\varvec{\sigma },{\mathbf {G}}) := {\hat{\mu }}^N_{t^{(n)}_b}\), \(\varvec{\sigma }_b := \varvec{\sigma }_{t^{(n)}_b}\).
We can now decompose the event in the statement of Theorem 2.1 into the following events. It follows from Lemma 3.3 that for any \({\tilde{\epsilon }} > 0\), there must exist \(\epsilon > 0\) such that
It is assumed that \(\epsilon \le \delta _{{\mathfrak {c}}}\), as defined in Lemma 3.3. Thanks to Lemma 3.1, for Theorem 2.1, to hold, it thus suffices to prove that some \(n\in {\mathbb {Z}}^+\),
(47) is demonstrated in Lemma 3.6, (48) is established in Lemma 3.7 and (50) is a consequence of Lemma 3.2.
In order that Theorem 2.1 is true, it thus only remains to prove (49). Define the events \(\lbrace {\mathcal {U}}^N_b \rbrace _{b=0}^{n-1}\), for a positive constant \({\mathfrak {u}} > 0\) (to be specified more precisely below - for the moment we note that \({\mathfrak {u}}\) will be chosen independently of n and N), and writing \({\tilde{\epsilon }} = \epsilon / 3\),
and observe that
We thus find from Lemma 3.1 that, in order that (49) holds, it suffices to prove that
We now make a further approximation to the operator \(\Psi _t\). For any \(\varvec{\sigma }\in {\mathcal {E}}^{MN}\) and \({\mathbf {G}} \in {\mathbb {R}}^{MN}\), define the random measure \(\xi _b(\varvec{\sigma },{\mathbf {G}}) \in {\mathcal {P}}\), which is such that \(\xi _b(\varvec{\sigma },{\mathbf {G}}) \simeq \Psi _{b+1}\cdot {\hat{\mu }}^N(\varvec{\sigma },{\mathbf {G}})\), as follows. Let \(\lbrace {\tilde{Y}}^p(t) \rbrace _{p\in I_M}\) be independent Poisson Counting Processes, and \(\lbrace {\tilde{W}}^p_t \rbrace _{p=1}^M\) independent Wiener Processes (they are also independent of the proceses \(Y^{p,j}(t)\) and connections \({\mathbf {J}}\) used to define the original system). Writing \({\hat{\mu }}^N_{b}(\varvec{\sigma },{\mathbf {G}})\) to be the law of random variables \((\varvec{\zeta }_0,{\mathbf {x}}_0)\), define \(\xi _b(\varvec{\sigma },{\mathbf {G}})\) to be the law of \((\varvec{\zeta }_{\Delta } , \mathbf {x}_{\Delta })\), where, recalling that \(A\cdot x := (-1)^x\), for each \(p\in I_M\),
and \(\Delta = T/n\). When the context is clear, we omit the argument of \(\xi _b\).
It follows from the facts that (i) \( d_{W}\big ( \Psi _{b+1}\cdot {\hat{\mu }}^N , {\hat{\mu }}^N_{b+1} \big ) \le d_{W}\big (\xi _b , {\hat{\mu }}^N_{b+1} \big ) +d_{W}\big ( \Psi _{b+1}\cdot {\hat{\mu }}^N, \xi _b\big ) \) and (ii) \(\exp ( {\mathfrak {u}} t^{(n)}_{b+1} / T -{\mathfrak {u}} ) \ge \exp ( {\mathfrak {u}} t^{(n)}_{b} / T + {\mathfrak {u}}\Delta / 2T -{\mathfrak {u}} ) + \exp ( {\mathfrak {u}} t^{(n)}_{b} / T-{\mathfrak {u}} ){\mathfrak {u}} \Delta / 2T\) (recalling that \(\Delta = t^{(n)}_{b+1} - t^{(n)}_b\)), that
We thus find that
Therefore (52) will be seen to be true once we demonstrate Lemmas 3.4 and 3.5.
Lemma 3.4
For any \({\tilde{\epsilon }} > 0\), for all sufficiently large n, and all b such that \(0\le b < n\),
Lemma 3.4 is proved later in this section.
Lemma 3.5
Suppose that for any \({\bar{\epsilon }} > 0\), for all sufficiently large n and all \(0\le b \le n-1\),
Then Theorem 2.1 must be true.
The rest of this paper is devoted to establishing Lemma 3.5. In the next section, Lemma 4.6 determines a sufficient condition for Lemma 3.5 to hold, in terms of processes \(\lbrace \tilde{\varvec{\sigma }}_{i,t} \rbrace \) whose spin-flipping is independent of the connections. The rest of the sections then prove that the condition of Lemma 4.6 must be satisfied.
3.1 Regularity of the connections: Proof of Lemma 3.2
Proof
We decompose \({\mathbf {J}}_N\) into a symmetric matrix and an i.i.d. matrix, i.e. \({\mathbf {J}}_N = N^{-1/2}\sqrt{{\mathfrak {s}}}\hat{{\mathbf {J}}}_N + N^{-1/2}\sqrt{1-{\mathfrak {s}}}\tilde{{\mathbf {J}}}_N +N^{-1/2}{\mathbf {D}}_N\). Here \({\mathbf {D}}_N\) is diagonal, \(\hat{{\mathbf {J}}}_N\) is symmetric and \(\tilde{{\mathbf {J}}}_N\) is neither symmetric nor anti-symmetric. The entries in all three matrices can be taken to be i.i.d of zero mean and unit variance (in the symmetric matrix the entries are i.i.d. apart from the symmetry \(J^{jk} = J^{kj}\)). A union-of-events bound implies that
For the last term, using Lemma 3.1
It is a standard result from random matrix theory [3] that
The last bound follows from recent results on the maximum eigenvalue of the Ginibre ensemble [57] ,
For (2), it may be observed that
as long as \({\mathcal {J}}_N\) holds. \(\square \)
3.2 Approximating flow \(\Psi _t\)
This section proves that \(\Psi _t\) is a good approximation to the flow \(\Phi _t\). We now prove Lemma 3.6, which implies that the operator \(\Psi \) is compact.
Lemma 3.6
There exists a constant \({\bar{C}} > 0\) such that for all \(\mu _{[0,T]} \in \hat{{\mathcal {W}}}_{[0,T]}\), and writing \(\eta _t = \Psi _t \cdot \mu _{[0,T]}\),
Proof
To implement the Wasserstein distance, we require a common probability space, and it is easiest to use the stochastic process with marginal probability laws given by (43). That is, \(\eta _t \in {\mathcal {P}}\) is the marginal law of the solution \((\varvec{\alpha }_t,{\mathbf {z}}_t)\) of the following stochastic hybrid system. Let \(\lbrace {\tilde{Y}}^p(t) \rbrace _{p\in I_M}\) be independent Poisson Counting Processes, and \(\lbrace {\tilde{W}}^p_t \rbrace _{p \in I_M}\) independent Wiener Processes (these processses are also independent of the Poisson processes \(\lbrace Y^{p,j}(t)\rbrace _{p \in I_M,j \in I_N}\) and connections \(\lbrace J^{jk} \rbrace _{j,k\in I_N}\) used to define the original system) and define for \(p\in I_M\),
and the initial random variables \((\varvec{\alpha }_0 , {\mathbf {x}}_0)\) are distributed according to \(\mu _0\). One easily checks that a unique solution exists to the above equation.
We first establish that there exists a constant \({\tilde{C}}\) such that
Thanks to Ito’s Lemma,
where \(D^{\mu _s}_{ij} =2 \sqrt{L^{\mu _s}_{ii}}\delta (i,j)\). It follows from (36) (and the Cauchy-Schwarz Inequality) that
The definition of \(\hat{{\mathcal {W}}}_{[0,T]}\) implies that \(\sup _{s\in [0,T]} {\mathbb {E}}^{\mu _s}[\left\| {\mathbf {g}} \right\| ^2] \le 3\), and it is immediate from the definition that \(|L_{ii}^{\mu _s}| \le c_1\). Thus taking expectations of both sides of (63), we obtain (62) as required.
An application of Gronwall’s Inequality to (62) implies that
which establishes the first identity, since (by definition) \( {\mathbb {E}}^{\mu _0}\big [\left\| {\mathbf {x}} \right\| ^2\big ] \le 3\). It remains to demonstrate uniform continuity. It follows from Ito’s Lemma that for all \(t > u\),
We thus find that, using the Cauchy-Schwarz inequality,
since \(|L_{ii}^{\mu _t}|\) is uniformly upperbounded by \(c_1\) (the uniform upperbound for the jump intensity). It follows from (36) that, using the inequality \((a+b)^2 \le 2a^2 + 2b^2\),
Thanks to the definition of \(\hat{{\mathcal {W}}}_{[0,T]}\), \( {\mathbb {E}}^{\mu _t}[ \left\| {\mathbf {x}} \right\| ^2 ] \le 3\). It therefore follows from (64) that there exists a constant \({\hat{C}}\) such that
Gronwall’s Inequality now implies that
and Jensen’s Inequality therefore implies that
The uniform bound \(c_1\) for the intensity of the spin-flipping implies that
The above two identities imply (59). \(\square \)
We now prove Lemma 3.3.
Proof
The second result in Lemma 3.6 implies that all elements of \(\Psi \cdot {\mathcal {W}}_{[0,T]}\) are uniformly continuous. The first result in Lemma 3.6 implies that the individual marginals \(\lbrace \eta _t \rbrace \) belong to the compact space of measures
(This space is compact thanks to Prokhorov’s Theorem). It thus follows from the generalized Arzela-Ascoli Theorem [36] that \(\Psi \cdot {\mathcal {W}}_{[0,T]}\) is compact in \({\mathcal {C}}([0,T],{\mathcal {P}})\) (this space being endowed with the supremum metric (44)).
Suppose for a contradiction that the lemma were not true. Then there would have to exist some \({\tilde{\epsilon }} > 0\) and some sequence \(\mu ^n \in \hat{{\mathcal {W}}}_2\) such that \({\tilde{d}}_T( \Psi \cdot \mu ^n , \mu ^n ) < n^{-1}\) and \({\tilde{d}}_T( \Phi \cdot \mu ^n_0 , \mu ^n ) \ge {\tilde{\epsilon }}\). The compactness of the space \(\Psi \cdot \hat{{\mathcal {W}}}_{[0,T]}\) means that \(\big ( \Psi \cdot \mu ^n \big )_{n\in {\mathbb {Z}}^+}\) must have a convergent subsequence \(\big ( \Psi \cdot \mu ^{p_n} \big )_{n\in {\mathbb {Z}}^+}\), converging to some \(\phi = (\phi _t)_{t\in [0,T]}\). Since \({\tilde{d}}_T( \Psi \cdot \mu ^n , \mu ^n ) < n^{-1}\), it must be that \(\mu ^{p_n} \rightarrow \phi \) as well. Since \(\Psi \) is continuous, \(\Psi \cdot \mu ^{p_n}\) also converges to \(\Psi \cdot \phi \). We thus find that \(\Psi \cdot \phi = \phi \). This implies that \(\phi = \Phi \cdot \phi _0\), and since \(\phi \ne \mu \), this contradicts the uniqueness of the fixed point \(\xi _t\) established in Lemma 2.2.
It remains to prove (46). First we note that for small enough \(\epsilon \), we are certain to avoid the pathological situation of \(\Lambda ^{\Phi _t\cdot {\hat{\mu }}^N} \rightarrow 0\) for \(t \le \tau _N\). This event would imply that \(\left\| ({\mathbf {K}}^{\xi _t})^{-1} \right\| \rightarrow \infty \) (and the PDE in (31) would no longer be accurate). Let \(\epsilon _{{\mathfrak {c}}}>0\) be the largest number such that
Such an \(\epsilon _{{\mathfrak {c}}}\) always exists because the map \(\Lambda ^{\mu }\) is continuous. We will thus assume (throughout the rest of this paper) that \(\epsilon \le \epsilon _{{\mathfrak {c}}}\), because in any case if the RHS of the following inequality is less than zero, then the LHS must be less than zero too, i.e.
With this choice of \(\epsilon \), we are assured that \({\mathbb {P}}\big ({\mathcal {Q}}_N^c\big ) = 0\) where
As long as \(\epsilon \le \epsilon _{{\mathfrak {c}}}\) (defined just above (71)), and \(\delta \) is chosen such that (45) is satisfied, then (46) must hold. \(\square \)
3.3 Proofs of the remaining Lemmas
Lemma 3.7
For any \(\epsilon > 0\), for all sufficiently large n,
Proof
It follows from the definition that
The renewal property of Poisson Processes implies that the following processes \(\lbrace Y^{q,j}_a(t) \rbrace _{q\in I_M, j \in I_N}\) are Poissonian:
Now as long as the event \({\mathcal {J}}_N\) holds,
Similarly, \(N^{-1}\sum _{j\in I_N, i\in I_M} \big | \sigma ^{i,j}_{s} - \sigma ^{i,j}_{b}\big | \le 2N^{-1}\sum _{j\in I_N, i\in I_M} Y_b^{i,j}(c_1 \Delta )\). Writing \({\bar{\epsilon }}\) to be such that \(\sqrt{12{\bar{\epsilon }}} + 2{\bar{\epsilon }} = \epsilon \), and noting that \(Y_b^{i,j}\) is non-decreasing, it thus suffices to prove that for any \({\bar{\epsilon }} >0 \),
Taking \(\Delta \) to be such that \(c_1\Delta \le {\bar{\epsilon }}/2\), it suffices to prove that
Since the \(\lbrace Y^{i,j} \rbrace _{i\in I_M, j\in I_N}\) are independent, and \({\mathbb {E}}\big [ N^{-1}\sum _{j\in I_N, i\in I_M} Y_b^{i,j}(c_1 \Delta )\big ] = Mc_1\Delta \), Sanov’s Theorem implies (76) [25]. \(\square \)
We now prove Lemma 3.4.
Proof
Let \(\eta _b \in {\mathcal {P}} \) to be the law of the same stochastic process as \(\xi _b(\varvec{\sigma },{\mathbf {G}})\), except that the law of the initial value at time \(t^{(n)}_b\) is given by \(\Psi _b \cdot {\hat{\mu }}^N\) rather than the empirical measure. More precisely, writing \(\Psi _b\cdot {\hat{\mu }}^N\) to be the law of random variables \((\varvec{\alpha }_b,{\mathbf {x}}_b)\), define \(\eta _b\) to be the law of \((\varvec{\beta }_{\Delta + t^{(n)}_b} ,{\mathbf {z}}_{\Delta + t^{(n)}_b})\), where, writing \(A\cdot x = (-1)^x\), for \(p\in I_M\), for \(t\ge t^{(n)}_b\),
Thanks to the fact that \(\exp ( {\mathfrak {u}} t^{(n)}_{b} / T + {\mathfrak {u}}\Delta / (2T) -{\mathfrak {u}} ) \ge \exp ( {\mathfrak {u}} t^{(n)}_{b} / T + {\mathfrak {u}}\Delta / 4T -{\mathfrak {u}} ) + \exp ( {\mathfrak {u}} t^{(n)}_{b} / T-{\mathfrak {u}} ){\mathfrak {u}} \Delta / 4T\), analogously to (55) we find that
Thanks to Lemma 3.1, it thus suffices for us to prove the following three inequalities,
for some \(\epsilon _0 > 0\),
It has already been proved in Lemma 3.7 that for any \(\epsilon _0\), for all large enough n (82) must hold.
Proof of (83)
We compare the stochastic processes (60)–(61) whose law is \(\Psi _{b+1}\cdot {\hat{\mu }}^N\) to the stochastic processes (78)–(79) whose law is \(\eta _b\). Notice that these processes have the same initial condition at time \(t^{(n)}_b\). Using Ito’s Lemma, for \(t \ge t^{(n)}_b\),
Analogously to the bound in (64), one easily establishes the following uniform bound for the moments
for some constant \(\breve{C}\). Using the Lipschitz inequality for \({\mathbf {m}}\) in Lemma 2.6, and making use of the uniform bound in (85), there exists a constant \(\grave{C}\) such that for all \(s \in [t^{(n)}_b , t^{(n)}_{b+1}]\),
Taking expectations of both sides of (84), employing the Cauchy-Schwarz Inequality, and assuming that \(\sup _{s\in [t^{(n)}_b,t^{(n)}_{b+1}]}d_W({\hat{\mu }}^N_s,{\hat{\mu }}^N_b) \le \epsilon _0\), we obtain that
Properties of the Poisson Process (see for example Lemma 8.1) dictate that \({\mathbb {E}}\big [\left\| \varvec{\alpha }_s - \varvec{\alpha }_b \right\| ^2\big ] \le 4 c_1\Delta \), as long as \(s-t^{(n)}_b \le \Delta \). Thus for all t such that \({\mathbb {E}}\big [\left\| {\mathbf {x}}_{t}-{\mathbf {z}}_t \right\| ^2\big ] \le \Delta \), it must hold that
We thus find from Gronwall’s Inequality that for any \({\bar{\epsilon }} > 0\), through choosing \(\epsilon _0\) to be sufficiently small, and n to be sufficiently large,
Using the compensated Poisson Process representation, we obtain that
using the fact that \(c(\cdot ,\cdot )\) is Lipschitz and bounded. Since the expectation in the last term goes to zero as \(\Delta \rightarrow 0\), it follows from (87) and (88) that for sufficiently large n,
We have thus established (83) and it remains to prove (81). Suppose that \(d_W\big ( \Psi _{b}\cdot {\hat{\mu }}^N, {\hat{\mu }}^N_b\big ) \le {\tilde{\epsilon }}\exp \big ( {\mathfrak {u}} t^{(n)}_{b} / T -{\mathfrak {u}} \big )\). The definition of the Wasserstein distance implies that for any \(\delta > 0\), there must exist a common probability space supporting the random variables \((\varvec{\zeta },{\mathbf {x}},\varvec{\beta },{\mathbf {z}})\), with \({\hat{\mu }}^N_b\) the law of \((\varvec{\zeta },{\mathbf {x}})\), and \(\Psi _b \cdot {\hat{\mu }}^N\) the law of \((\varvec{\beta },{\mathbf {z}})\), and such that
We append the mutually independent Poisson processes \(\lbrace {\tilde{Y}}^p(t) \rbrace _{p\in I_M}\) and Brownian motions \(\lbrace {\tilde{W}}^p_t \rbrace _{p\in I_M}\) to this same space, and define \((\varvec{\zeta }_{\Delta },{\mathbf {x}}_{\Delta })\) to satisfy (53)–(54) and \((\varvec{\beta }_{\Delta }, {\mathbf {z}}_{\Delta })\) to satisfy (78)–(79). We then observe using the triangle inequality that
Define \(v_p = \inf \big \lbrace c(\beta ^p,z^p),c(\zeta ^p,x^p) \big \rbrace \) and let \(\lbrace \breve{Y}^p,{\hat{Y}}^p, \grave{Y}^p\rbrace _{p\in I_M}\) be independent Poisson Processes. Using the additive property of Poisson Processes [27], we have the following representation
Hence (91) implies that
where \(c_1\) is the uniform upperbound for the jump rate, and \(c_L\) is the Lipschitz constant for c. Taking expectations of both sides, one finds that there exists a constant \({\bar{C}} > 0\) such that
We analogously find that for a constant \(C> 0\),
since the coefficients \({\mathbf {m}}\) and \({\mathbf {L}}\) are Lipschitz, as noted in Lemma 2.6. The above results (89)-(93) imply that there exists a constant \({\hat{C}} > 0\) such that
Thus as long as \({\mathfrak {u}}/4T > {\hat{C}}\), if \(d_W({\hat{\mu }}^N_b, \Psi _b\cdot {\hat{\mu }}^N) \le {\tilde{\epsilon }}\exp \big ( {\mathfrak {u}} t^{(n)}_{b} / T -{\mathfrak {u}} \big )\), it must be that \(d_{W}( \eta _b, \xi _b ) \le {\tilde{\epsilon }}\exp \big ( {\mathfrak {u}} t^{(n)}_{b} / T + {\mathfrak {u}}\Delta / 4T -{\mathfrak {u}} \big )\), which establishes (81). \(\square \)
4 Change of measure
It remains for us to prove Lemma 3.5. To do this, we must ‘separate’ the effects of the stochasticity and the disorder on the dynamics by defining new processes \(\tilde{\varvec{\sigma }}_{i,t}\) (with i belonging to an index set that grows polynomially in N) that are such that the spin-flipping is independent of the connections. However it will be seen that \(\tilde{\varvec{\sigma }}_{i,t}\) is an excellent approximation to the old process, as long as the empirical process lies in a small subset \({\mathcal {V}}^N_i\) of \({\mathcal {M}}^+_1\big ({\mathcal {D}}([0,T],{\mathcal {E}}^M\times {\mathbb {R}}^M)\big )\). The number of such subsets \(\lbrace {\mathcal {V}}^N_i \rbrace \) is polynomial in N: this polynomial growth will be dominated by the exponential decay of the probability bounds of subsequent sections. The fact that the new processes are independent of the connections will allow us to use a conditional Gaussian measure to accurately infer the evolution of the fields over a small time step (in Sect. 7). In order that we may employ Girsanov’s Theorem, it is essential that the processes \(\tilde{\varvec{\sigma }}_{i,t}\) are adapted to the filtration \({\mathcal {F}}_t\) as well. The main result of this section is Lemma 4.6: this lemma gives a sufficient condition in terms of the new processes \(\tilde{\varvec{\sigma }}_{i,t}\) for the condition of Lemma 3.5 to be satisfied.
4.1 Partition of the probability space
Define the pathwise empirical measure
The pathwise empirical measure will be used to partition the probability space. Before we partition \({\mathcal {M}}^+_1\big ({\mathcal {D}}([0,T],{\mathcal {E}}^M\times {\mathbb {R}}^M)\big )\), we must first partition the underlying state space \({\mathcal {E}}^{M} \times {\mathbb {R}}^M\). For some positive integer \({\mathfrak {n}}\), define the sets \(\lbrace D_i \rbrace _{0\le i \le {\mathfrak {n}}^2+1}\subset \mathcal {B}(\mathbb {R})\) as follows.
Next, let \(\lbrace {\tilde{D}}_i \rbrace _{1\le i \le C_{\mathfrak {n}}} \subset \mathcal {B}(\mathbb {R}^M)\) be such that for each i,
for integers \(\lbrace p^i_j \rbrace \). The sets are defined to be such that
Next we partition the path space
where \(\lbrace {\hat{D}}_i \rbrace \) are defined as follows. In constructing this partition, we require a more refined partition of the time interval [0, T] into \((m+1)\) time points \(\lbrace t^{(m)}_a \rbrace _{0\le a \le m}\): this is necessary for us to be able to control the Girsanov Exponent in the next section. It is assumed that m is an integer multiple of n (the integer dictating the number of time points in the previous section). Throughout this section, unless specified otherwise, for \(0\le a \le m\), we write \(\varvec{\sigma }_a := \varvec{\sigma }_{t^{(m)}_a}\). Each \({\hat{D}}_i \subset {\mathcal {D}}([0,T], {\mathcal {E}}^M \times {\mathbb {R}}^M)\) is nonempty, and of the form
for indices \(\lbrace q^i_a, r^i_a\rbrace _{0\le a \le m}\), \(1 \le q^i_a,r^i_a \le C_{\mathfrak {n}}\). The indices are chosen such that (i) \({\hat{D}}_i \cap {\hat{D}}_j = \emptyset \) if \(i\ne j\), (ii) \({\hat{D}}_i \ne \emptyset \) and (iii) (100) is satisfied. Let
Next, for a positive integer \(C^N_{{\mathfrak {n}}}\), make the partition
where each \({\mathcal {V}}^N_i\) is such that \(\mu \in {\mathcal {V}}^N_i\) if and only if (i) \(\mu \in \hat{{\mathcal {W}}}_2\) and (ii) for all \(1\le q,r \le {\hat{C}}_{{\mathfrak {n}}}\),
It is assumed that the indices are chosen such that (i) \({\mathcal {V}}^N_i \ne \emptyset \) and (ii) the partition is disjoint, i.e. \({\mathcal {V}}^N_i \cap {\mathcal {V}}^N_j = \emptyset \) if \(i\ne j\). The motivation for the scaling of \(N^{-1}\) for the mass of each set in (104) is that if \({\tilde{\mu }}^N \in {\mathcal {V}}^N_j\), then we will know the precise mass assigned to each set, since the empirical process can only assign a mass that is an integer multiple of \(N^{-1}\) to each set.
We next prove that the radius of the sets in the partition goes to zero uniformly, in the following sense.
Lemma 4.1
Define
For \(f\in {\mathfrak {U}}\), write \({\hat{f}} : {\mathcal {D}}([0,T],{\mathcal {E}}^M \times {\mathbb {R}}^M) \rightarrow {\mathbb {R}}\) to be \({\hat{f}}(\varvec{\alpha },{\mathbf {x}}) := f\big ( (\alpha ^q_{t^{(m)}_a})_{0\le a \le m, q\in I_M} , (x^q_{t^{(m)}_a})_{0\le a \le m, q\in I_M} \big )\). We find that for any \(m\ge 1\),
Proof
We notice that for any \(1\le i \le C^N_{{\mathfrak {n}}}\) and any \(\mu \in {\mathcal {V}}^N_i\),
using the fact that \({\mathcal {V}}^N_i \subset \hat{{\mathcal {W}}}_2\) (as defined in (102)). Thus the mass assigned to non-bounded sets goes to zero uniformly as \({\mathfrak {n}} \rightarrow 0\). Furthermore it can be seen from the definition in (99) that the radius of the bounded sets goes to zero uniformly as \({\mathfrak {n}}\rightarrow \infty \), which implies the lemma. \(\square \)
Next we observe that the number of sets in the partition is subexponential in N: this is an essential property, because it means that the partition size is dominated by the exponential decay of the probabilities in coming sections.
Lemma 4.2
For any \({\mathfrak {n}} \in {\mathbb {Z}}^+\),
Proof
We notice from (104) that each \({\mathcal {V}}^N_i\) can assign \((N+1)\) possible values to the mass of each set \({\hat{D}}_q \times {\hat{D}}_r \in \mathcal {D}([0,T],\mathcal {E}^M) \times \mathcal {D}([0,T],\mathbb {R}^M)\). Since here are \({\tilde{C}}_{{\mathfrak {n}}}^2\) such sets, the number of such \({\mathcal {V}}^N_i\) must be upperbounded by \((N+1)^{{\tilde{C}}^2_{{\mathfrak {n}}}}\). Since this is polynomial in N, we have established the lemma. \(\square \)
4.1.1 Definition of the approximating process
We are now in a position to define the adapted stochastic process \(\tilde{\varvec{\sigma }}_i\) (for each \(1\le i \le C^N_{{\mathfrak {n}}}\)), written \(\tilde{\varvec{\sigma }}_i := ({\tilde{\sigma }}^{q,j}_{i,t})_{q\in I_M, j\in I_N, t\in [0,T]}\). Write \(\tilde{{\mathcal {V}}}^N_{i,t} \subset {\mathcal {M}}^+_1\big ({\mathcal {D}}([0,t],{\mathcal {E}}^M)\big )\) to be the projection of the probability measures in \( {\mathcal {M}}^+_1\big ({\mathcal {D}}([0,T],{\mathcal {E}}^M \times {\mathbb {R}}^M)\big )\) onto their marginals over \({\mathcal {D}}([0,t],{\mathcal {E}}^M)\) - and define \({\mathcal {V}}^N_{i,t}\) to be the analogous projection onto the marginal over \({\mathcal {D}}([0,t],{\mathcal {E}}^M \times {\mathbb {R}}^M)\). We write the intensity of \({\tilde{\sigma }}^{q,j}_{i,t}\) as \(\tilde{{\mathfrak {G}}}^{q,j}_{i,t}\). We will choose the fields to be such that as long as \({\tilde{\mu }}^N_{[0,t]}(\tilde{\varvec{\sigma }}) := N^{-1}\sum _{j\in I_N}\delta _{\varvec{\sigma }^j_{[0,t]}} \in \tilde{{\mathcal {V}}}^N_{i,t}\), then necessarily \({\tilde{\mu }}^N_{[0,t]}(\tilde{\varvec{\sigma }}_i,\tilde{{\mathfrak {G}}}_i) \in {\mathcal {V}}^N_{i,t}\). This property is essential for us to be able to control the Girsanov Exponent in the next section.
We first find any set of paths \(\varvec{\alpha }_i\) and intensities \({\mathfrak {G}}_i\) that are such that their empirical process is in \({\mathcal {V}}^N_i\).
Lemma 4.3
For all large enough N, for each \(1\le i \le C^N_{{\mathfrak {n}}}\), there exists \(\varvec{\alpha }_i \in {\mathcal {D}}\big ([0,T],{\mathcal {E}}^M\big )^N\) and \({\mathfrak {G}}_i \in {\mathcal {D}}\big ([0,T],{\mathbb {R}}^M\big )^N\) such that
Proof
Let \(\breve{\pi }: {\mathcal {M}}^+_1\big ( {\mathcal {D}}([0,T],{\mathcal {E}}^M \times {\mathbb {R}}^M)\big ) \rightarrow {\mathcal {M}}^+_1\big ( {\mathcal {E}}^{MN(m+1)} \times {\mathbb {R}}^{MN(m+1)}\big )\) be the projection of a measure onto its marginal at times \(\lbrace t^{(m)}_a \rbrace _{0\le a \le m}\). Because empirical measures are dense in \( {\mathcal {M}}^+_1\big ( {\mathcal {E}}^{MN(m+1)} \times {\mathbb {R}}^{MN(m+1)}\big )\), for all large enough N, there must exist \(\tilde{\varvec{\alpha }}_i \in {\mathcal {E}}^{MN(m+1)}\), written \(\tilde{\varvec{\alpha }}_i := (\tilde{\varvec{\alpha }}_{i,a})_{0\le a \le m}\), and \(\tilde{{\mathfrak {G}}}_i \in {\mathbb {R}}^{MN(m+1)}\), written \(\tilde{{\mathfrak {G}}}_i := (\tilde{{\mathfrak {G}}}_{i,a})_{0\le a \le m}\) such that
We can now define \(\varvec{\alpha }_i := (\varvec{\alpha }_{i,t})_{t\in [0,T]} \in {\mathcal {D}}\big ([0,T],{\mathcal {E}}^{M}\big )^N\) and \({\mathfrak {G}}_{i} := ({\mathfrak {G}}_{i,t})_{t\in [0,T]} \in {\mathcal {D}}\big ([0,T],{\mathcal {E}}^M\big )^N\) as follows: for each \(0\le a \le m\),
\(\square \)
Next, we prove that if \({\tilde{\mu }}^N_{[0,t]}(\tilde{\varvec{\sigma }}) \in \tilde{{\mathcal {V}}}^N_{i,t}\), then we must be able to find a permutation of the intensities \(\lbrace {\mathfrak {G}}_{i,t}^j \rbrace \) that ensures that the associated empirical process is in \({\mathcal {V}}^N_{i}\). Define \({\mathfrak {P}}^N\) to be the set of all permutations on \(I_N\) (i.e. each member of \({\mathfrak {P}}^N\) is a bijective map \(I_N \rightarrow I_N\)).
Define the stopping time
Lemma 4.4
For any \(\tilde{\varvec{\sigma }}_i \in {\mathcal {D}}([0,T] , {\mathcal {E}}^M)^N\) and any \(t < {\tilde{\tau }}_i\), define \(\pi _{t,\tilde{\varvec{\sigma }}_i} \in {\mathfrak {P}}^N\) to be such that
\(\pi _{t,\tilde{\varvec{\sigma }}}\) is well-defined, but not uniquely defined. Furthermore \(\pi _{\cdot ,\cdot }{:}[0,T] \!\times \! \mathcal {D}([0,T] , \mathcal {E}^M)^N\) \(\rightarrow {\mathfrak {P}}^N\) is progressively-measurable
Proof
Write \(\breve{\varvec{\alpha }}_{i,t} := \varvec{\alpha }_{i,t\wedge {\tilde{\tau }}_i}\). We first claim that \(\breve{\pi }\cdot {\tilde{\mu }}^N(\tilde{\varvec{\sigma }}_i) = \breve{\pi }\cdot {\tilde{\mu }}^N(\breve{\varvec{\alpha }}_{i})\), as long as \(t < {\tilde{\tau }}_i\). This is because \({\mathcal {V}}^N_i\) specifies the mass of each set to an accuracy of \(N^{-1}\), but the mass assigned to any set by the empirical measure must also be a multiple of \(N^{-1}\). This means that we must be able to find a permutation such that (114115116) is satisfied. \(\square \)
We can now formally define the stochastic process \(\tilde{\varvec{\sigma }}_i\). First, \({\tilde{\sigma }}^{q,j}_{i,t}\) is ‘stopped’ once the empirical measure is no longer in \(\tilde{{\mathcal {V}}}^N_{i,t}\), i.e.
For all \(t\le {\tilde{\tau }}_i\), we stipulate that \({\tilde{\sigma }}^{q,j}_{i,t}\) satisfies the identity,
recalling that \(A\cdot x\) is defined to be \(-1^{x}\). Recall from (117) that \({\tilde{\sigma }}^{q,j}_t\) is defined to be stopped for \(t\ge {\tilde{\tau }}_i\).
Lemma 4.5
The stochastic processes \(\big \lbrace {\tilde{\sigma }}^{q,j}_{i,t} \big \rbrace _{j\in I_N,q\in I_M, t\in [0,T]}\) are uniquely well-defined and are adapted to the filtration \({\mathcal {F}}_t\). Also if \({\tilde{\tau }}_i > T\), then, writing \(\tilde{{\mathfrak {G}}}^{q,j}_{i,s} := {\mathfrak {G}}^{q,\pi _{s,\tilde{\varvec{\sigma }}}(j)}_{i,s}\) and \(\tilde{{\mathfrak {G}}}^{q,j}_{i} = (\tilde{{\mathfrak {G}}}^{q,j}_{i,s})_{s\in [0,T]}\), it must be that
Proof
This is immediate from the definitions. \(\square \)
4.2 Girsanov’s Theorem
In this section we demonstrate that the probability law of the original system \(\varvec{\sigma }_t\) can be well-approximated by the law of one of the processes \(\lbrace \tilde{\varvec{\sigma }}_{i,t} \rbrace _{1\le i \le C^N_{{\mathfrak {n}}}}\). The main result is Lemma 4.6: the implication of this lemma is that if we can show that the flow operator accurately describes the dynamics of the empirical processes generated by each of the \(\tilde{\varvec{\sigma }}_i\), then it must accurately describe the original empirical process as well.
Let \(R^N_{i} \in {\mathcal {M}}^+_1 \big ( {\mathcal {D}}\big ( [ 0 , T] , {\mathcal {E}}^{M} \big )^N \big )\) be the probability law of the processes \(\big \lbrace {\tilde{\sigma }}^{q,j}_{i,t} \big \rbrace _{j\in I_N,q\in I_M, t\in [0,T]}\). Define the stopping time \(\tau _i\) that is the analog of \({\tilde{\tau }}_i\) in (113), i.e.
Notice that, necessarily,
Let \(P^N_{{\mathbf {J}}} \in {\mathcal {M}}^+_1 \big ( {\mathcal {D}}\big ( [ 0 , T] , {\mathcal {E}}^{M} \big )^N \big )\) be the law of the original spin system \(\big \lbrace \sigma ^{q,j}_{i,t \wedge \tau _i \wedge T} \big \rbrace _{j\in I_N,q\in I_M, t\in [0,T]}\), conditioned on a realization of the connections \({\mathbf {J}}\), and stopped at time \(\tau _i\). Write
where \(\pi _{\cdot ,\cdot }\) is defined in Lemma 4.4. Define the Girsanov exponent
and we have defined \({\hat{\sigma }}^{i,j}_s\) to be the integer-valued nondecreasing càdlàg process specifying how many times that \(\sigma ^{i,j}_s\) has changed sign over the time period [0, s), i.e. \(\sigma ^{i,j}_s = \sigma ^{i,j}_0 \times (-1)^{{\hat{\sigma }}^{i,j}_s}\). It follows from Girsanov’s TheoremFootnote 4 [37, 43] that the Radon-Nikodym derivative satisfies
Write \({\tilde{G}}^{q,j}_{i,t} = N^{-1/2}\sum _{k\in I_N}J^{jk}{\tilde{\sigma }}^{q,k}_{i,t}\) and define \({\tilde{\tau }}_N\) to be the analog of (21),i.e.
Lemma 4.6
Suppose that for any \({\bar{\epsilon }} > 0\), there exists \(n_0 \in {\mathbb {Z}}^+\) such that for all \(n \ge n_0\), there exists \({\mathfrak {n}}_0(n) \in {\mathbb {Z}}^+\), such that for all \({\mathfrak {n}} \ge {\mathfrak {n}}_0(n)\), there exists \(m_0(n,{\mathfrak {n}})\) such that for all \(m\ge m(n,{\mathfrak {n}})\),
for some \({\mathfrak {k}} > 0\). Then the condition of Lemma 3.5 is satisfied, i.e. for any \({\tilde{\epsilon }} > 0\), for large enough \(n\in {\mathbb {Z}}^+\),
Proof
The event \({\mathcal {J}}_N\) necessarily implies that \({\tilde{\mu }}^N \in \hat{{\mathcal {W}}}_2\). We can thus apply a union-of-events bound to the partition in (103) to obtain that
noting that the constant \({\mathfrak {k}}\) is defined in (126). Noting that \(C^N_{{\mathfrak {n}}}\) is polynomial in N (as proved in Lemma 4.2), thanks to Lemma 3.1, it suffices to prove that each of the terms on the right hand side of (128) are exponentially decaying in N. Using the Radon-Nikodym derivative (124),
using the assumption (126) in the statement of the lemma. It thus remains to prove that
Notice that \({\tilde{\mu }}^N(\varvec{\sigma },{\mathbf {G}}) \in {\mathcal {V}}^N_i\) implies that \(\tau _i > T\). Recalling that \(\hat{{\mathfrak {G}}}^{q,j}_a := \hat{{\mathfrak {G}}}^{q,j}_{t^{(m)}_a}\) and \(\sigma ^{q,j}_a := \sigma ^{q,j}_{t^{(n)}_a}\), define the following time-discretized approximation of the Girsanov Exponent,
One expects the above approximation to be very accurate for large \(m \in {\mathbb {Z}}^+\) because
(The probability that \( {\hat{\sigma }}^{q,j}_{a+1} - {\hat{\sigma }}^{q,j}_a \ge 2\) is very small once the time interval \(Tm^{-1}\) is small). Thus to establish (129), it suffices to establish the follow two identities
We start by establishing (133). We observe from (130) that there exists a function \({\mathcal {H}}: {\mathcal {D}}\big ( [0,T], {\mathcal {E}}^M \times {\mathbb {R}}^M\big ) \rightarrow {\mathbb {R}}\) such that
Furthermore \({\mathcal {H}}\) is a function of the values of the variables at the times \(\lbrace t^{(m)}_a \rbrace _{0\le a \le m}\). Now if \({\tilde{\mu }}^N(\varvec{\sigma }, {\mathbf {G}}) \in {\mathcal {V}}^N_i\), then necessarily \({\tilde{\mu }}^N(\varvec{\sigma }, \hat{{\mathfrak {G}}}) \in {\mathcal {V}}^N_i\). It now follows from (i) the fact that the functions c and \(\log c\) are uniformly Lipschitz in their second argument and (ii) Lemma 4.1, that for large enough \({\mathfrak {n}}\), it must be that
We have thus established (133). It remains to establish (132). Write
We wish to split \(\Gamma ^N_i(\varvec{\sigma },{\mathbf {J}}) - {\tilde{\Gamma }}^N_i(\varvec{\sigma })\) into the sum of five terms and bound each term separately. First, using (131), we notice that the difference of the stochastic integral in \(\Gamma ^N_i(\varvec{\sigma },{\mathbf {J}})\) and its time-discretized equivalent in \({\tilde{\Gamma }}^N_i(\varvec{\sigma })\) is
Second, it is immediate from the definition that it is always the case that \(-{\mathfrak {n}} \le \hat{{\mathfrak {G}}}^{q,j}_s \le {\mathfrak {n}}\). In order that (132) is satisfied, it suffices to demonstrate the following identities,
We start with (135). The event \({\mathcal {J}}_N\) implies that \(N^{-1}\sum _{j\in I_N} \chi \lbrace |G^{q,j}_s| > {\mathfrak {n}} \rbrace \le 3{\mathfrak {n}}^{-2}\). Thus, since \(c(\cdot ,\cdot )\) is uniformly upperbounded by \(c_1\),
Since the right hand side goes to zero as \({\mathfrak {n}}\rightarrow \infty \), (135) follows from (ii) of Lemma 8.2, as long as \({\mathfrak {n}}\) is large enough.
(136) follows from the concentration inequality in (i) of Lemma 8.2, employing the facts that (i) \(|F^{q,j}_s|\) is uniformly upperbounded, and (ii) \({\hat{\sigma }}^{q,j}_t - \int _0^t c(\sigma ^{q,j}_s,G^{q,j}_s)ds\) is a compensated Poisson Process (a Martingale [2]).
For (137), the boundedness of \(c(\cdot ,\cdot )\) by \(c_1\) (in the first line), and Jensen’s Inequality (in the second line) imply that
using (i) the fact that \(\log c(\cdot ,\cdot )\) has Lipschitz constant \(c_L\) (in its second argument), and (ii) as long as the event \({\mathcal {J}}_N\) holds. Define the renewed Poisson Processes \(\lbrace Y^{q,j}_a(t) \rbrace _{q\in I_M, j \in I_N}\) to be
Now since the flipping intensity is uniformly upperbounded by \(c_1\), if \(t \le t^{(m)}_{a+1}\) then
Now \(t - t^{(m)} \le \delta \), where \(\delta = Tm^{-1}\). Jensen’s Inequality thus implies that
We thus find that there is a constant C such that
For large enough m, this probability is exponentially decaying, thanks to Lemma 8.1.
For (138), since the flipping rate is uniformly upperbounded by \(c_1\), there exists a constant \(C({\mathfrak {n}})\) such that \(F^{q,j}_s \le C({\mathfrak {n}})\). Thus by Chernoff’s Inequality,
for some constant \(v > 0\). To bound (141), we start by evaluating the integral conditionally on \({\mathcal {F}}_{t^{(m)}_{m-1}}\). Notice that \(\lbrace {\hat{Y}}^{q,j}_{m-1} \rbrace _{q\in I_M, j\in I_N}\) are independent of \({\mathcal {F}}_{t^{(m)}_{m-1}}\) (thanks to the renewal property of Poisson Processes). Also \({\hat{Y}}^{q,j}_a(c_1 \delta ) \chi \lbrace {\hat{Y}}^{q,j}_a(c_1 \delta ) \ge 2 \rbrace \le Y^{q,j}_a(c_1 \delta ) \chi \lbrace Y^{q,j}_a(c_1 \delta ) \ge 2 \rbrace \). We thus find that, for \(a= m-1\), and using the fact that \({\mathbb {P}}(Y^{q,j}_a(c_1 \delta ) = r) = \exp (-r\delta c_1)(\delta c_1)^r / (r!)\),
We take m to be large enough that
We then continue the argument, evaluating (141) conditionally on \({\mathcal {F}}_{t^{(m)}_{m-2}}\), then \({\mathcal {F}}_{t^{(m)}_{m-3}}\) ... and finally \({\mathcal {F}}_{t^{(m)}_0}\). We find that (141) must be less than or equal to \(\lbrace 1 + m^{-3/2} \rbrace ^{NM(m+1)}\exp \big (-\frac{N\mathfrak {k} v}{20C(\mathfrak {n})}\big )\). For large enough m, this must be exponentially decaying. We have established (138).
We see that (139) is a difference between an integral and its time-discretized approximation, and can easily be shown to be true for large enough m. \(\square \)
5 Taylor expansion of test functions
After the change of measure of the previous section, our task is easier, because now the spin-flipping intensity of \(\tilde{\varvec{\sigma }}_{i,t}\) is independent of the connections \({\mathbf {J}}\). This section (and the remainder of the paper) is oriented towards proving condition (126) of Lemma 4.6. This proof is accomplished through the comparison of the expectations of test functions, using the dual Kantorovich representation of the Wasserstein distance. We will Taylor expand the test functions to second order, and (in subsequent sections) demonstrate that the expectation with respect to the flow operator \(\Psi _t\) almost matches the expectation with respect to the empirical process.
Let \({\mathfrak {H}}\) be the set of all functions that are uniformly Lipschitz, i.e.
It follows from the Kantorovich-Rubinstein theorem [34] that
Our proofs only make use of a finite number of test functions: so we must demonstrate that the right hand side of the above equation can be approximated arbitrarily well by taking the supremum over a finite subset. Furthermore we require that the test functions are three-times differentiable in order that the expectations of stochastic fluctuations converge smoothly. Let \({\mathfrak {H}}_a\) be the set of all \(f \in {\mathfrak {H}}\) satisfying the following assumptions.
-
\(f(\varvec{\alpha },{\mathbf {x}}) = 0\) for \(\left\| {\mathbf {x}} \right\| \ge a\).
-
\(f(\varvec{\alpha },{\mathbf {x}}) = \chi \lbrace \varvec{\alpha }= \varvec{\beta }\rbrace {\bar{f}}({\mathbf {x}})\), for some fixed \(\varvec{\beta }\in {\mathcal {E}}^M\) and \({\bar{f}} \in {\mathcal {C}}^3({\mathbb {R}}^M)\).
-
Write the first, second and third order partial derivatives, in the second variable, as (respectively) \({\bar{f}}_j , {\bar{f}}_{jk} , {\bar{f}}_{jkl}\), for \(j,k,l \in I_M\). These are all assumed to be uniformly bounded by 1.
Lemma 5.1
For any \(\delta > 0\), there exists \(a \in {\mathbb {Z}}^+\) and a finite subset \(\bar{{\mathfrak {H}}}_a \subset {\mathfrak {H}}_a\) such that for all \(\mu ,\nu \in {\mathcal {W}}_2\),
Proof
For any \(\mu \in {\mathcal {W}}_2\), any \(f\in {\mathfrak {H}}\), and \(a > 0\),
Thus for any \(\delta >0\), for large enough a,
where \(\tilde{{\mathfrak {H}}}_a\) is the set of all \(f \in {\mathfrak {H}}\) such that \(f(\varvec{\alpha },{\mathbf {x}}) = 0\) if \(\left\| {\mathbf {x}} \right\| \ge a\). It remains to demonstrate that we can find a finite subset \(\bar{{\mathfrak {H}}}_a\) of \({\mathfrak {H}}_a\) such that
Since continuous functions on compact domains can be approximated arbitrarily well by smooth functions, it must be that
It follows from the Arzela-Ascoli Theorem that \({\mathfrak {H}}_a\) is compact. Thus we can find a finite cover of \({\mathfrak {H}}_a\) such that every function in \({\mathfrak {H}}_a\) is within \(\delta / 2\) of a function in the finite cover (relative to the supremum norm). \(\square \)
Now set \(\delta = \Delta {\bar{\epsilon }} / 2\), and let \(a \in {\mathbb {R}}^+\) and \({\mathfrak {h}}_a\) be such that for all \(\mu ,\nu \in \mathcal {W}_2\), \(d_W(\mu ,\nu ) \le \delta + \mathrm{a} \sup _{{\mathbf {f}}\in \bar{{\mathfrak {H}}}_a}\big \lbrace \big | {\mathbb {E}}^{\mu }[ f ] - {\mathbb {E}}^{\nu }[ f ] \big | \big \rbrace \). We write \({\mathfrak {F}} \subset {\mathcal {C}}^3({\mathbb {R}}^M)\) to be such that
and we define the pseudo-metricFootnote 5
Henceforth we drop the subscript \({\mathfrak {q}}\) from the processes \(\tilde{\varvec{\sigma }}_{{\mathfrak {q}},t}\) and \(\tilde{{\mathbf {G}}}_{{\mathfrak {q}},t}\). We find that for the condition (126) of Lemma 4.6 to be satisfied, it suffices for us to prove that for any \({\bar{\epsilon }}> 0\), for all sufficiently large n and all \(0\le b \le n-1\),
recalling that \({\tilde{G}}^{p,j}_t = N^{-1/2}\sum _{k\in I_N}J^{jk} {\tilde{\sigma }}^{p,k}_t\) and \(\xi _b(\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}})\) is the law of the random variables in (53)-(54). We emphasize that throughout the rest of this paper, \(\tilde{\varvec{\sigma }}_{b} := \tilde{\varvec{\sigma }}_{t^{(n)}_{b}}\): that is the subscript is with respect to the \(n+1\)-point time discretization. Write the first derivative of \(\phi \in {\mathfrak {F}}_{{\mathfrak {m}}}\) with respect to the \(j^{th}\) variable as \(\phi _j\), the second derivative of \(\phi \in {\mathfrak {F}}_{{\mathfrak {m}}}\) with respect to the \(j^{th}\) and \(k^{th}\) variables as \(\phi _{jk}\), and the third derivative as \(\phi _{jkl}\).
We enumerate \({\mathfrak {F}}\) as \({\mathfrak {F}} = \big \lbrace \phi ^a \big \rbrace _{a=1}^{|{\mathfrak {F}}|}\). For \(\varvec{\alpha }\in {\mathcal {E}}^M\), define
We first establish a more workable expression for \(R^{a,\varvec{\alpha }}_b\).
Lemma 5.2
Recall that \(\varvec{\alpha }[i] \in {\mathcal {E}}^M\) is the same as \(\varvec{\alpha }\), except that the \(i^{th}\) spin has a flipped sign.
Proof
Recall the definition of \(\xi _b(\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}})\), in terms of independent unit-intensity Poisson processes \(\lbrace {\tilde{Y}}^p(t)\rbrace _{p\in I_M}\) and independent Brownian motions \(\lbrace {\tilde{W}}^p_t \rbrace _{p\in I_M}\) in (53)-(54). We can then write \(R^{a,\varvec{\alpha }}_b\) as
and the expectation in (153) is taken with respect to the \(\tilde{{\mathbf {Y}}}\) and \(\tilde{{\mathbf {W}}}_{\Delta }\) random variables, holding \(\tilde{\varvec{\sigma }}_b\) and \(\tilde{{\mathbf {G}}}_b\) to be fixed, and \(A \cdot x := (-1)^x\). Write
Basic properties of the Poisson process - and recalling that the jump intensity c is uniformly upperbounded by \(c_1\) - imply that \({\mathbb {E}}[ X^j_{b+1} \; | \; \tilde{\varvec{\sigma }}_b, \tilde{{\mathbf {G}}}_b ] = O(\Delta ^2)\) [27] (one can see from the Komolgorov Forward equation (18) why this is true). We thus find that
Applying a Taylor expansion, and noting that the third order partial derivatives of \(\phi ^a\) are uniformly bounded, we obtain that
since \({\mathbb {E}}[ \Vert \tilde{{\mathbf {W}}}_{\Delta }\Vert ^3 ] = O\big ( (\Delta )^{3/2}\big )\). This implies the lemma. \(\square \)
Using a union-of-events bound, we obtain that
The implication of the above argument is that, in order that (149) is satisfied, and making use of Lemma 3.1, it suffices to prove the following lemma.
Lemma 5.3
In order that condition (126) of Lemma 4.6 is satisfied, it suffices to prove the following statement. For any \(\epsilon > 0\), there exists \(n_0\) such that for all \(n \ge n_0\), there exists \({\mathfrak {n}}_0 \in {\mathbb {Z}}^+\) such that for all \({\mathfrak {n}} \ge {\mathfrak {n}}_0\),
Substituting the expression for \(R^{a,\varvec{\alpha }}_{b+1}\) in Lemma 5.2, we find that the difference can be decomposed as
and \(\lbrace \beta ^i \rbrace _{i=1}^5\) are defined as follows (the dependence of \(\beta ^i\) on a has been neglected from the notation). Our aim is to decompose the difference into terms that can either be controlled with Poisson concentration inequalities or controlled with the Gaussian law of the connections. Here and below, \({\hat{\mu }}^N_b := {\hat{\mu }}^N_b(\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}})\). The term \(\beta ^1\) represents the leading order change in the two expectations due to jumps in the spins, while holding the field to be constant, i.e.
recalling that \(\varvec{\alpha }[i]\) is the same as \(\varvec{\alpha }\), except that the \(i^{th}\) element has a flipped sign.
The sum of the terms \(\beta ^2 + \beta ^3\) represents the leading order change in the two expectations due to changes in the field \(\tilde{{\mathbf {G}}}_t\), while holding the spin to be constant. A Taylor approximation is used: \(\beta ^2\) contains the linear terms, and \(\beta ^3\) the quadratic terms,
\(\beta ^4\) can be thought of as the average ‘cross-variation’ between the spins and the fields:
The term \(\beta ^5\) is the remainder, such that (158) holds identically. This means that
We further decompose \(\beta ^2\) and \(\beta ^3\) as follows. The terms \(\beta ^6\), \(\beta ^8\) and \(\beta ^9\) - to be outlined just below - will be bounded in Sect. 7 using the conditional Gaussian law of the connections. The term \(\tilde{{\mathbf {m}}}^j_b\) - to be outlined just below - is the mean of a conditional Gaussian expectation, and \(\tilde{{\mathbf {L}}}^{ij}_b\) is approximately half the conditional variance. Define the \(M\times M\) matrices \(\lbrace \tilde{{\mathbf {K}}}_b,\tilde{{\mathbf {L}}}_b,\tilde{\varvec{\kappa }}_b,\tilde{\varvec{\upsilon }}_b \rbrace \) to have the following elements: for \(p,q\in I_M\)
If \({\tilde{\tau }}_N > t^{(n)}_b\), \(\tilde{{\mathbf {K}}}_b\) is invertible, and we write \(\tilde{{\mathbf {H}}}_b = \tilde{{\mathbf {K}}}_b^{-1}\). For \(j\in I_N\), writing \(\tilde{\varvec{\sigma }}^j_b = \big (\sigma ^{1,j}_b,\ldots ,\sigma ^{M,j}_b\big )\), \(\tilde{{\mathbf {G}}}^j_b = \big ({\tilde{G}}^{1,j}_b,\ldots ,{\tilde{G}}^{M,j}_b \big )\) and \(\tilde{{\mathbf {m}}}^j_b = \big ({\tilde{m}}^{1,j}_b,\ldots ,{\tilde{m}}_b^{M,j}\big )\), we define
We can now further decompose \(\beta ^2\) as follows,
noting that \(m^{{\hat{\mu }}^N_b}\) is defined in (30). We further decompose \(\beta ^3(\varvec{\alpha },\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}}) \) as follows
We can now decompose the criteria of Lemma 5.3 into the following set of criteria.
Lemma 5.4
To prove Lemma 4.6 it suffices for us to show that for any \({\bar{\epsilon }} > 0\), there exists \(n_0\) such that for all \(n \ge n_0\), there exists \({\mathfrak {n}}_0 \in {\mathbb {Z}}^+\) such that for all \({\mathfrak {n}} \ge {\mathfrak {n}}_0\), for each i such that \(1 \le i \le 11\) (with \(i\ne 2,3\)), (recalling that \(\Delta = Tn^{-1}\))
Proof
The above analysis implies that for large enough n,
By Lemma 5.2, as long as \(\Delta \) is sufficiently small,
The Lemma now follows as a consequence of Lemma 3.1, since \(|{\mathfrak {F}}| < \infty \). \(\square \)
The nine bounds necessary for Lemma 5.4 are contained in the next two sections. They are split into two types: the terms directly requiring the law of the Gaussian connections (i.e. \(\beta ^6, \beta ^8, \beta ^9\)) are bounded in Sect. 7. The other six terms mostly require concentration inequalities for Poisson processes, and they are bounded in Sect. 6.
6 Stochastic bounds
This section is devoted to bounding the terms in Lemma 5.4 that do not directly require the law of the Gaussian connections (i.e. \(\gamma \)). The terms that are bounded in the first part of this section are \(\beta ^4\) (the ‘cross-variation’ of the spins and fields) and \(\beta ^5\) (the remainder after the Taylor Expansion). In the next subsection, the remaining terms \(\beta ^1,\beta ^7,\beta ^{10},\beta ^{11}\) are bounded: the bounding of these terms requires concentration inequalities for sums of compensated Poisson Processes. Throughout this section we omit the \({\mathfrak {q}}\) subscript from the stochastic process, writing \(\tilde{\varvec{\sigma }}_{{\mathfrak {q}},t} := \tilde{\varvec{\sigma }}_t\).
Throughout this section \(\varvec{\alpha }\in {\mathcal {E}}^M\) is a fixed constant. Define for \( u \ge 0\),
and notice that \(\lbrace Y_b^{i,j}(t) \rbrace _{i\in I_M,j\in I_N}\) are distributed as iid unit intensity Poisson Processes. Recalling that \(A\cdot x := (-1)^x\), it may be inferred from the definition in (118) that for \(t\ge t^{(n)}_b\),
Let \({\mathcal {I}}_N = \big \lbrace j\in I_N \; : \text { For some }i\in I_M \; , \; Y^{i,j}_b(c_1 \Delta ) \ge 1 \big \rbrace \), recalling that \(c_1\) is the uniform upper bound for the spin flipping rate. Clearly if \(j\notin {\mathcal {I}}_N\) then \(\tilde{\varvec{\sigma }}^j_b = \tilde{\varvec{\sigma }}^j_{b+1}\). Write \({\mathcal {I}}_N^c = \lbrace j\in I_N : j\notin {\mathcal {I}}_N \rbrace \). Splitting the indices as \(I_N = {\mathcal {I}}_N \cup {\mathcal {I}}_N^c\) is useful because the fields \(\lbrace {\tilde{G}}^{p,j}_{b+1} - {\tilde{G}}^{p,j}_b \rbrace _{j\in {\mathcal {I}}_N^c}\) are independent.
We start with a lemma concerning the average change in fields indexed by \({\mathcal {I}}_N\).
Lemma 6.1
There exists \(n_0 \in {\mathbb {Z}}^+\) and a constant \({\hat{C}}_{\gamma }\) such that for all \(n \ge n_0\),
Proof
Let \(\tilde{{\mathbf {J}}}_N\) be the \(|{\mathcal {I}}_N | \times |{\mathcal {I}}_N |\) square matrix with entries given by \(\lbrace N^{-1/2} J^{jk} \rbrace _{j,k \in {\mathcal {I}}_N}\). Let its operator norm be \(\left\| \tilde{{\mathbf {J}}}_N \right\| \). Observe that
Writing \({\hat{C}}_{\gamma } = 6\sqrt{2} c_1^{3/2}M(M+1)\), we observe that if \( \left\| \tilde{{\mathbf {J}}}_N \right\| \le 3\sqrt{c_1\Delta / 2}\) and \(N^{-1}\sum _{j\in {\mathcal {I}}_N}\chi \big \lbrace \text {For some }i\in I_M \; , {\tilde{\sigma }}^{i,j}_{b+1} \ne {\tilde{\sigma }}^{i,j}_b\big \rbrace \le c_1 \Delta ( M+1)\) then \(N^{-1}\sum _{j\in {\mathcal {I}}_N}\left\| {\tilde{G}}^{i,j}_{b+1} - {\tilde{G}}^{i,j}_b \right\| ^2 \le {\hat{C}}_{\gamma }\Delta ^{3/2}\). We thus find that,
It follows from basic properties of Poisson Processes (noted in Lemma 8.1) that the probability of the first term on the right hand side is exponentially decaying. It thus remains to prove that
Define \(\bar{{\mathbf {J}}}_N\) to be the \(|{\mathcal {I}}_N| \times |{\mathcal {I}}_N| \) square matrix with elements \(|{\mathcal {I}}_N|^{-\frac{1}{2}} J^{jk}\): that is, \(\bar{{\mathbf {J}}}_N =\sqrt{N} |{\mathcal {I}}_N|^{-\frac{1}{2}}\tilde{{\mathbf {J}}}_N\). This means that
Notice that the (random) indices in \({\mathcal {I}}_N\) are independent of the static connections \(\lbrace J^{jk} \rbrace _{j,k \in {\mathbb {Z}}^+}\) - since the Poisson Processes \(\lbrace Y^{i,j}(t)\rbrace \) are Markovian and independent of the static connections. We can now use known bounds on the dominant eigenvalue of random matrices (as noted in (3) of Lemma 3.2) to obtain that
as required, where the constant \(\Lambda _J\) is defined in Lemma 3.2. \(\square \)
We start with the bound of \(\beta ^4\) (which is defined in (160)): this can be thought of as the average ‘cross-variation’ between the spins and fields over the small time interval \(\Delta \).
Lemma 6.2
For any \({\bar{\epsilon }} > 0\), for sufficiently large n,
Proof
Now for some \(z > 0\),
By Lemma 8.1,
It remains to prove that the second term on the right-hand-side of (181) is negative. Thanks to the identity in (176), if \(Y^{i,j}_b(c_1 \Delta + z ) = 0\) for all \(i\in I_M\) then \(\tilde{\varvec{\sigma }}^j_{b+1} = \tilde{\varvec{\sigma }}^j_b\) and \(\chi \lbrace \tilde{\varvec{\sigma }}^{j}_{b+1} = \varvec{\alpha }\rbrace - \chi \lbrace \tilde{\varvec{\sigma }}^{j}_b = \varvec{\alpha }\rbrace = 0\). We thus have that
for \(\bar{{\mathbf {G}}}^j = \lambda _j \tilde{{\mathbf {G}}}^j_b + (1-\lambda _j)\tilde{{\mathbf {G}}}^j_{b+1}\), for some \(\lambda _j \in [0,1]\), by the Taylor Remainder Theorem. It follows from (182) that if \(|{\mathcal {I}}_N| < N{\bar{\epsilon }}\Delta / 4\), then since \(|\phi ^a| \le 1\), it must necessarily be the case that
as required. It thus suffices for us to prove that
Using a union-of-events bound,
where \(\tilde{{\mathbf {J}}}_N\) is the \(|{\mathcal {I}}_N | \times |{\mathcal {I}}_N |\) square matrix with entries given by \(\lbrace N^{-1/2} J^{jk} \rbrace _{j,k \in {\mathcal {I}}_N}\). Just as we proved in (180), for small enough \(\Delta \),
It thus suffices for us to prove that for \(\Delta \) sufficiently small,
To this end, we obtain from (183) that, since \(|\phi ^a_i | \le 1\), by the Cauchy-Schwarz Inequality,
Now if \( |{\mathcal {I}}_N| \le N (M c_1 \Delta + z)\) and \(\left\| \tilde{{\mathbf {J}}}_N \right\| \le 3 |{\mathcal {I}}_N|^{\frac{1}{2}}N^{-1/2} \le 3 (Mc_1 \Delta + z )^{\frac{1}{2}}\), it must be that, (since \(({\tilde{\sigma }}^{i,j}_{b+1} - {\tilde{\sigma }}^{i,j}_b)^2 \le 4\)),
We choose \(z = \Delta \), and find that (186) implies that
This means that for \(\Delta \) sufficiently small,
which implies (185), as required. \(\square \)
Lemma 6.3
For any \({\bar{\epsilon }} > 0\), for large enough n
Proof
Recall the definition of \(\beta ^5\):
If \(\sup _{i\in I_M}|{\tilde{G}}^{i,j}_{b+1} - {\tilde{G}}^{i,j}_b| \le (\Delta )^{2/5}\), then it follows from Taylor’s Theorem that
once n is sufficiently large (since \(\Delta = Tn^{-1}\)), and \(\hat{\mathbf {G}}^j\) is in the convex hull of \(\tilde{\mathbf {G}}^j_b\) and \(\tilde{\mathbf {G}}^j_{b+1}\). Write \({\tilde{I}}_N = \big \lbrace j\in I_N: \sup _{i\in I_M}|{\tilde{G}}^{i,j}_{b+1} - {\tilde{G}}^{i,j}_b| \le (\Delta )^{2/5}\big \rbrace \). Since the magnitude of \(\phi \) and its first three derivatives are all upperbounded by 1, it must be that there is a constant C such that
The previous two equations imply that
It thus suffices to prove that
To establish the above equation, it suffices in turn to prove that (writing \(\breve{\epsilon } = {\bar{\epsilon }} / 108\)),
and we recall that \({\mathcal {I}}_N^c = \lbrace j\in I_N : j\notin {\mathcal {I}}_N \rbrace \). Starting with (191), observe that
The probability of the right hand side is exponentially decaying (for large enough n), as a consequence of Lemma 6.1. The inequalities (192) and (193) are established in Lemma 6.4. \(\square \)
Lemma 6.4
For any \(\epsilon > 0\), for sufficiently large \(n\in {\mathbb {Z}}^+\) (and recalling that \(\Delta = T/n\)),
Proof
The proofs are very similar and so we only include the second result. It follows from Lemma 3.1 that
By Lemma 8.1, \(\underset{N\rightarrow \infty }{{\overline{\lim }}} N^{-1}\log {\mathbb {P}}\big (N^{-1} |{\mathcal {I}}_N| \notin [c_1\Delta / 2 , c_1 \Delta ( M+1)] \big ) < 0\) as required.
We write \({\tilde{H}}^{i,j} = {\tilde{G}}^{i,j}_{b+1} - {\tilde{G}}^{i,j}_b\). By Chernoff’s Inequality,
In the above expectation, \(\tilde{\varvec{\sigma }}\) (which determines the indices \({\mathcal {I}}_N\)) is independent of \({\mathbf {J}}\). Furthermore, conditionally on \(\tilde{\varvec{\sigma }}\), \({\tilde{G}}^{i,j}\) is independent of \({\tilde{G}}^{p,k}\) if \(j\ne k\) and \(j,k\in {\mathcal {I}}_N^c\). This last fact is immediate from the definition of the indices in \({\mathcal {I}}_N^c\): the coefficients of common edges are zero. We thus see that the conditional moments are
as long as \(N^{1}|{\mathcal {I}}_N | \le c_1 \Delta ( M+1)\). Standard Gaussian properties therefore dictate that as long as \(N^{-1} |{\mathcal {I}}_N| \le c_1 \Delta ( M+1)\), there exists a constant \(k > 0\) such that for all sufficiently small \(\Delta \),
This means that
For small enough \(\Delta \), the right hand side is exponentially decaying, as required. \(\square \)
6.1 Bounds using concentration inequalities for poisson processes
Lemma 6.5
For any \({\tilde{\epsilon }} > 0\), for all large enough n (and therefore small \(\Delta = T/n\)), we can find \({\mathfrak {n}}_0(n) \in {\mathbb {Z}}^+\) such that for all \({\mathfrak {n}} \ge {\mathfrak {n}}_0(n)\),
Proof
We prove that
The proof of the reverse inequality, i.e.
is analogous. One can decompose
where
Thanks to Lemma 4.1, for large enough \({\mathfrak {n}}\), if \({\tilde{\mu }}^N(\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}}) \in {\mathcal {V}}^N_{{\mathfrak {q}}}\) then necessarily
Suppose that \(\sum _{i\in I_M}Y_b^{i,j}\big ( c_1 \Delta \big ) \le 1\) (recall the definition in (175)). In this case, at most one of the spins \(\lbrace {\tilde{\sigma }}^{i,j}_s \rbrace _{i \in I_M}\) flips once over the time interval \([t^{(n)}_b , t^{(n)}_{b+1}]\). In this case,
Conversely if \(\sum _{i\in I_M}Y_b^{i,j}\big ( c_1 \Delta \big ) \ge 2\), then
We thus find that
The probability of each of the first two terms on the right hand side is exponentially decaying thanks to (i) of Lemma 8.2. For the third term, one easily shows that as long as the event \({\mathcal {J}}_N\) holds,
Thanks to (ii) of Lemma 8.1, one finds that the probability of the RHS of the above equation exceeding \({\tilde{\epsilon }}\Delta /8\) is exponentially decaying in N, once \(\Delta \) is small enough. For the last term on the RHS of (204), by Chernoff’s Inequality, for a constant \(u > 0\),
Now for any positive integer k, thanks to the renewal property of Poisson Processes,
since \(Y_b^{i,j}(c_1\Delta )\) is Poisson-distributed. We take n sufficiently large that \(c_1 \Delta \exp (4u) \le \exp (-u\tilde{\epsilon } / 16)\), and we obtain that
Summing the geometric series, the above can be made arbitrarily small by taking u to be large. Since the processes \(Y^{i,j}_b\) are independent, we find that the RHS of (205) is exponentially decaying in N, as required. \(\square \)
Lemma 6.6
For any \({\bar{\epsilon }}\), for all sufficiently large n,
Proof
Now since \(|\phi ^a_{ii}| \le 1\), \(\big \lbrace \big |\beta ^{11}(\varvec{\alpha },\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}})\big | \ge {\bar{\epsilon }}\Delta \big \rbrace \subseteq \big \lbrace \big | 2\Delta L^{{\hat{\mu }}^N_b}_{ii} - {\tilde{L}}^{ii}_b \big | \ge {\bar{\epsilon }}\Delta \big \rbrace \). The probability of this event is exponentially decaying, thanks to Lemma 6.7.
The proof of (207) is similar: one compares the definition of \(\tilde{{\mathbf {m}}}_b\) in (164) to the definition of \({\mathbf {m}}^{{\hat{\mu }}^N_b}\) in (30). Note that the condition \({\tilde{\tau }}_N > t^{(n)}_b\) implies that \(\tilde{{\mathbf {H}}}_b = {\mathbf {H}}^{{\hat{\mu }}^N_b}\) (see the definition in (29)) and also \(\tilde{\varvec{\upsilon }}_b = \varvec{\upsilon }^{{\hat{\mu }}^N_b}\). One therefore finds that
Thus
Now write
We now establish that
for sufficiently small \(\epsilon _0\), and sufficiently small \(\Delta \). Now \({\tilde{\tau }}_N > t^{(n)}_b\) implies that \(\left\| \tilde{{\mathbf {H}}}_b \right\| \le {\mathfrak {c}}^{-1}\), and the Cauchy-Schwarz Inequality (and also condition \({\mathcal {J}}_N\)) imply that \(| \upsilon _b^{pq} |^2 \le N^{-1}\sum _{j\in I_N}|G^{p,j}|^2 \le 3\). This means that \(\left\| \varvec{\upsilon }_b \right\| \) is bounded. Furthermore by Jensen’s Inequality \(\left( N^{-1}\sum _{j\in I_N} \left\| {\mathbf {G}}^j_b \right\| \right) ^2 \le N^{-1}\sum _{j\in I_N} \left\| {\mathbf {G}}^j_b \right\| ^2 \le 3M\) (as a consequence of \({\mathcal {J}}_N\)). The probability of \(({\mathcal {U}}^N)^c\) is exponentially decaying, thanks to Lemma 6.7. \(\square \)
Lemma 6.7
For any \(\epsilon _0 > 0\), there exists \(n_0 \in {\mathbb {Z}}^+\) such that for all \(n\ge n_0\), there exists \({\mathfrak {n}}_0(n)\) such that for all \({\mathfrak {n}} \ge {\mathfrak {n}}_0(n)\),
Proof
The proofs are almost identical, so we only prove (209). Recall from (26) and (163) that
By Lemma 3.1,
Now a union of events bound implies that
where
Now, by definition, \({\hat{\mu }}^N(\tilde{\varvec{\sigma }},\tilde{{\mathfrak {G}}}_{{\mathfrak {q}}}) \in {\mathcal {V}}^N_{{\mathfrak {q}}}\). Thus if \({\tilde{\mu }}^N(\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}}) \in {\mathcal {V}}^N_{{\mathfrak {q}}}\) as well, then since the radius of the set \({\mathcal {V}}^N_{{\mathfrak {q}}}\) goes to zero as \({\mathfrak {n}}\rightarrow \infty \), (as proved in Lemma 4.1), it must be that for sufficiently large \({\mathfrak {n}}\)
since
We similarly find that for large enough \({\mathfrak {n}}\),
Concerning the other term on the right hand side of (212),
We thus find that
Now \(\grave{\kappa }^{pq}\) is the sum of compensated Poisson Processes (which are Martingales), since, making use of the representation in (176),
Recalling that \(|\tilde{{\mathfrak {G}}}^{q,k}_{{\mathfrak {q}},t^{(n)}_b}| \le {\mathfrak {n}}\), it is therefore a consequence of Lemma 8.2 that
Since \({\tilde{\sigma }}^{p,k}_s = {\tilde{\sigma }}^{p,k}_b\) for all \(s\in [t^{(n)}_b , t^{(n)}_{b+1}]\) if \(Y^{p,k}_b(c_1\Delta ) = 0\), we similarly find that
for large enough n (recalling that \(\Delta = Tn^{-1}\)), thanks to Lemma 8.1 (ii). \(\square \)
Lemma 6.8
For any \({\bar{\epsilon }} > 0\), for large enough \(n\in {\mathbb {Z}}^+\),
Proof
Since \(\big | \phi ^a_{ip}(\tilde{{\mathbf {G}}}_b^{j})| \le 1\) by definition,
by Jensen’s Inequality. Thanks to the triangle inequality,
We thus find that
Since \({\tilde{\tau }}_N > t^{(n)}_b\), \(\left\| \tilde{{\mathbf {H}}}_b \right\| \le {\mathfrak {c}}^{-1}\). Since \(|{\tilde{\sigma }}^{i,j}_t | \le 1\), \(\left\| \tilde{\varvec{\sigma }}^j_b \right\| \le \sqrt{M}\). The event \({\mathcal {J}}_N\) implies-after an application of the Cauchy-Schwarz Inequality-that \(| {\tilde{\upsilon }}^{pq}_b| \le \sqrt{3}\) and \(| {\tilde{\kappa }}^{pq}_b | \le \sqrt{3} c_1\). Now
Lemma 6.7 implies that the probability of the following event not holding is exponentially decaying,
We can thus assume that the above events hold. Since \(| L_{pq}^{{\hat{\mu }}^N_b(\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}})}| \le c_1\) and
it must be that there exist positive constants \(C_1,C_2\) such that
We thus find that
as long as the event \({\mathcal {J}}_N\) holds. In conclusion, as long as the events \({\tilde{\tau }}_N \ge t^{(n)}_b\), \({\mathcal {J}}_N\) and (217) hold, it must be that
Clearly for small enough \(\Delta \), (215) must hold. \(\square \)
7 Using the Gaussian Law to estimate the field dynamics
In this section we continue the proof of Lemma 5.4: providing bounds for the terms \(\beta ^6(\varvec{\alpha },\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}}),\beta ^8(\varvec{\alpha },\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}}),\beta ^9(\varvec{\alpha },\tilde{\varvec{\sigma }},\tilde{{\mathbf {G}}})\). The bounding of these terms requires the law \(\gamma \) of the Gaussian connections \(\lbrace J^{jk} \rbrace _{j,k\in I_N}\). Recall that the processes \(\lbrace \tilde{\varvec{\sigma }}_i \rbrace _{1\le i \le C^N_{{\mathfrak {n}}}}\) are independent of the connections, and so conditioning on these processes does not affect the distribution of the connections. For fixed \(\tilde{\varvec{\sigma }}_b \in {\mathcal {E}}^{MN}\) and any \({\mathbf {g}} \in {\mathbb {R}}^{MN}\), let \(\gamma _{\tilde{\varvec{\sigma }}_b, {\mathbf {g}}} \in {\mathcal {M}}^+_1\big ({\mathbb {R}}^{N^2}\big )\) be the regular conditional probability distribution of the connections \({\mathbf {J}}\), conditionally on
Standard theory dictates that \(\gamma _{\tilde{\varvec{\sigma }}_b, {\mathbf {g}}}\) is Gaussian (see for instance Theorem A.1.3 in [50]). We start by determining expressions for the conditional mean and variance of \(\gamma _{\tilde{\varvec{\sigma }}_b, {\mathbf {g}}}\) in Sect. 7.1. We then use these expressions to bound \(\beta ^6, \beta ^8\) and \(\beta ^9\) in Sect. 7.2.
7.1 The Conditional mean and covariance
The main result of this section is Lemma 7.2: this lemma is crucial because it demonstrates that the conditional mean of the increment \({\tilde{G}}^{i,j}_{b+1} - {\tilde{G}}^{i,j}_b\) can be written as a function of the variables \(\lbrace \tilde{\varvec{\sigma }}^{j}_b, \tilde{\varvec{\sigma }}^{j}_{b+1},\tilde{{\mathbf {G}}}^{j}_b\rbrace \) and the empirical measure at time \(t^{(n)}_b\), i.e. \({\hat{\mu }}^N(\tilde{\varvec{\sigma }}_b,\tilde{{\mathbf {G}}}_b)\). This property allows us to obtain a closed expression for the dynamics of the empirical process. We also determine some bounds on the conditional variance matrix.
We write
Let \({\tilde{\gamma }}_{\tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1}}\in {\mathcal {M}}^+_1\big ({\mathbb {R}}^{2MN}\big )\) be the law of \(\lbrace \tilde{\mathbf {G}}_b , \tilde{\mathbf {F}}_b \rbrace \) under \(\gamma \) (for fixed \(\lbrace \tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1}\rbrace \)). Since the above definitions are linear, standard theory dictates that \({\tilde{\gamma }}_{\tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1}}\) is Gaussian. Next define \(\gamma _{\tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1},\tilde{{\mathbf {G}}}_b}^N \in {\mathcal {M}}^+_1\big ({\mathbb {R}}^{MN}\big )\) to be the law of \(\tilde{\mathbf {F}}_b\) under \({\tilde{\gamma }}_{\tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1}}\), conditionally on \(\tilde{{\mathbf {G}}}_b\). The rest of this section is devoted to finding tractable expressions for the mean and variance of \(\gamma _{\tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1},\tilde{{\mathbf {G}}}_b}^N\). We define the density of \(\gamma _{\tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1},\tilde{{\mathbf {G}}}_b}^N\) to be \(\grave{\Upsilon }_{\tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1},\tilde{{\mathbf {G}}}_b} \in {\mathcal {C}}\big ({\mathbb {R}}^{MN}\big )\).
Let \(\Upsilon ^N_{\tilde{\varvec{\sigma }}_b, \tilde{\varvec{\sigma }}_{b+1}} \in {\mathcal {C}}({\mathbb {R}}^{2MN}) \) be the Gaussian density of \(\lbrace {\tilde{G}}^{i,j}_b, \tilde{F}^{i,j}_{b}\rbrace _{j=1}^N\) under \(\gamma \), i.e.
and \(\bar{{\mathcal {K}}}_N\big (\tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1}\big )\) is the \(2NM \times 2NM\) covariance matrix of \(\big \lbrace {\tilde{G}}^{i,j}_b, {\tilde{F}}^{i,j}_b \big \rbrace _{i\in I_N,j \in I_N}\), i.e.
The contents of \(\bar{{\mathcal {K}}}_N\big (\tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1}\big )\) are the following \(MN \times MN\) square matrices, with the replica indices at the top, and the spin indices at the bottom, i.e. for \(i,m \in I_M\) and \(j,k \in I_N\),
Standard theory (see for instance Theorem A.1.3 in [50]) dictates that the density \(\grave{\Upsilon }^N_{\tilde{\varvec{\sigma }}_b \tilde{\varvec{\sigma }}_{b+1},\tilde{{\mathbf {G}}}_b}(\tilde{{\mathbf {F}}}_b) \) of \(\gamma _{\tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1},\tilde{{\mathbf {G}}}_b}\) assumes the form
Here \(\tilde{{\mathbf {m}}}_b(\tilde{\varvec{\sigma }}_{b},\tilde{\varvec{\sigma }}_{b+1},\tilde{{\mathbf {G}}}_b) := \lbrace {\tilde{m}}_b^{i,j}(\tilde{\varvec{\sigma }}_{b},\tilde{\varvec{\sigma }}_{b+1},\tilde{{\mathbf {G}}}_b) \rbrace _{(i,j)\in I_{M,N}}\) is the vector of conditional means of \(\lbrace F^{i,j}_{b+1} \rbrace \) i.e.
i.e. in the above \({\tilde{m}}^{i,j}_{b}\) is the element with index (i, j) in the above vector resulting from two matrix multiplications on the vector \(\tilde{{\mathbf {G}}}_b\). \({\mathcal {R}}_N\big (\tilde{\varvec{\sigma }}_{b},\tilde{\varvec{\sigma }}_{b+1}\big )\) is the \(MN\times MN\) conditional covariance matrix of \(\tilde{{\mathbf {F}}}_b\), i.e.
noting that \({\mathcal {L}}_N\) is an \(MN\times MN\) matrix.
Lemma 7.1
Recall that \(\left\| \cdot \right\| \) is the operator norm and the definition of \(\tilde{{\mathbf {L}}}_b\) in (162). We have the following bounds on \(NM \times NM\) square matrices
Proof
(230) is a known property of finite Gaussian systems: the conditional variance is always less than or equal to the variance. It follows from the fact that \({\mathcal {R}}_N\), \(\tilde{{\mathcal {K}}}_N\) and \({\mathcal {L}}_N\) are positive semi-definite.
For (231), write \(U^i_b = N^{-1}\sum _{l=1}^N \chi \big \lbrace {\tilde{\sigma }}^{i,l}_{b+1} \ne {\tilde{\sigma }}^{i,l}_b \big \rbrace \) and \({\mathfrak {a}} = ({\mathfrak {a}}^{i,j})_{i\in I_M, j\in I_N}\). Observe that
using the Cauchy-Schwarz Inequality, and the fact that since \(\big |\sigma ^{i,l}_{b+1} - \sigma ^{i,l}_b \big | \le 2\),
Now
by the (discrete) Jensen’s Inequality. We thus find that
which implies (231). The proofs of (232) and (233) are analogous to the proof of (ii) and are neglected. \(\square \)
Recall that the \(M\times M\) matrices \(\lbrace \tilde{{\mathbf {K}}}_b,\tilde{{\mathbf {L}}}_b,\tilde{\varvec{\kappa }}_b,\tilde{\varvec{\upsilon }}_b \rbrace \) were defined to have the following elements
We now determine a precise expression for the conditional mean. It is fundamental to the entire paper that \(\tilde{{\mathbf {m}}}^j \) can be written as a function purely of (i) ‘local variables’ (i.e. \(\tilde{{\mathbf {G}}}^j_b \), \(\tilde{\varvec{\sigma }}^j_b\) and \(\tilde{\varvec{\sigma }}^j_{b+1}\), and (ii) the empirical measure (i.e. via the definitions in (234)–(235)).
Lemma 7.2
Assume that \(\tilde{\varvec{\sigma }}_b \in {\mathcal {X}}^N\). (i) \(\tilde{{\mathbf {K}}}_b\) is invertible, and we write \(\tilde{{\mathbf {H}}}_b = \tilde{{\mathbf {K}}}_b^{-1}\). \(\left\| \tilde{{\mathbf {H}}}_b \right\| \le {\mathfrak {c}}^{-1}\).
(ii) Writing \(\tilde{\varvec{\sigma }}^j_b = \big (\sigma ^{1,j}_b,\ldots ,\sigma ^{M,j}_b\big )^T\), \(\tilde{{\mathbf {G}}}^j_b = \big ({\tilde{G}}^{1,j}_b,\ldots ,{\tilde{G}}^{M,j}_b \big )^T\) and \(\tilde{{\mathbf {m}}}^j_b = \big ({\tilde{m}}^{1,j}_b,\ldots ,{\tilde{m}}_b^{M,j}\big )^T\), we have that
Proof
The fact that \(\tilde{\varvec{\sigma }}_b \in {\mathcal {X}}^N\) implies that the \(M\times M\) square matrix \(\tilde{{\mathbf {K}}}_b\) (with elements defined in (234)) has eigenvalues greater than \({\mathfrak {c}}\). Since it is co-diagonal with its inverse, it must be that \(\left\| \tilde{{\mathbf {H}}}_b \right\| \le {\mathfrak {c}}^{-1}\). Lets first assume that \(\mathcal {K}_N(\tilde{\varvec{\sigma }}_b)\) is invertible. Let \({\mathbf {V}} = {\mathcal {K}}_N(\tilde{\varvec{\sigma }}_b)^{-1}\tilde{{\mathbf {G}}}_b\). Writing \({\mathbf {V}} = \big \lbrace V^{i,j} \big \rbrace _{i\in I_M, j \in I_N}\), it must be that
Substituting the identity in (223) we find that
Rearranging (238), we find that
where
In matrix/vector notation, this means that \({\mathbf {V}}^j =\tilde{{\mathbf {H}}}\tilde{{\mathbf {G}}}^j_b - {\mathfrak {s}}\tilde{{\mathbf {H}}}{\mathbf {Q}}\tilde{\varvec{\sigma }}^j_b\). Now using the identities in (225) and (227),
We add \({\tilde{\sigma }}_b^{p,j}\) to both sides of (238), and sum over j, obtaining that
Multiplying both sides of the above equation by \(\tilde{{\mathbf {H}}}_b\), we find that
Substituting this into (240), we find that, as required,
In reaching this expression we assumed that \(\mathcal {K}_N(\tilde{\varvec{\sigma }}_b)\) is invertible. In fact the above expression for the conditional mean must also be correct if the covariance matrix is not invertible. One can see this by adding \(\delta \mathbf {Id}\) to \(\mathcal {K}(\tilde{\varvec{\sigma }}_b)\), obtaining an expression for the conditional mean using similar methods, and then taking \(\delta \rightarrow 0\). \(\square \)
7.2 Bounding \(\beta ^6,\beta ^8,\beta ^9\)
These terms are defined in (166), (168) and (169). \(\beta ^6\) and \(\beta ^8\) concern the linear increments in the fields \({\tilde{G}}^{q,j}_{b+1} - {\tilde{G}}^{q,j}_n\), and \(\beta ^9\) concerns the quadratic increments in the fields.
Lemma 7.3
For any \({\bar{\epsilon }} > 0\), for all large enough n,
Proof
The proofs of the above two terms are very similar, thus we only prove (244).
Define \(R^{N}_{{\mathfrak {q}},\tilde{\varvec{\sigma }}_b} \in {\mathcal {M}}^+_1\big ( {\mathcal {D}}([t^{(n)}_b , T],{\mathcal {E}}^M)^N \big )\) to be the law of the stochastic process \(\tilde{\varvec{\sigma }}_{{\mathfrak {q}},t}\), conditioned on its value \(\tilde{\varvec{\sigma }}_{b}\) at time \(t^{(n)}_b\). (Recall the definition of this process in Sect. 4.2). As previously, we drop the subscript and write \(\tilde{\varvec{\sigma }}_{{\mathfrak {q}},t} := \tilde{\varvec{\sigma }}_t\). Define \(Q^N_{\tilde{\varvec{\sigma }}_b,\tilde{{\mathbf {G}}}_b}\) to be the regular conditional probability distribution of \(({\mathbf {J}}, \tilde{\varvec{\sigma }}_b)\), conditionally on both \(\tilde{\varvec{\sigma }}_b\) and \(\tilde{{\mathbf {G}}}_b\). Since \(\tilde{\varvec{\sigma }}_b\) and \({\mathbf {J}}\) are independent, we have that
Writing \({\mathcal {Z}}^N = \big \lbrace {\mathbf {g}} \in {\mathbb {R}}^{MN} \; : \sup _{i\in I_M}\sum _{j\in I_N}|g^{i,j}|^2 \le 3N \big \rbrace \), this means that
It thus suffices to prove that
For a constant \({\mathfrak {r}} > 0\), by Chernoff’s Inequality,
Under \(Q^N_{\tilde{\varvec{\sigma }}_b , \tilde{{\mathbf {G}}}_b}\), and conditionally on \(\tilde{\varvec{\sigma }}_{t}\),
is Gaussian and of zero mean, using the expression for the conditional mean in Lemma 7.2. The covariance can be upperbounded using (i) and (ii) in Lemma 7.1, i.e.
using the fact that \(|\phi ^a_i| \le 1\). We thus find that, using the formula for the moment-generating function of a Gaussian distribution,
We now choose \({\mathfrak {r}} = {\bar{\epsilon }} \Delta / \big (4M^2(1+{\mathfrak {s}})\big )\), which means that
We thus find from (249), (250), (251) and (252) that
This implies (248). The proof of (245) is analogous to the proof of (244). \(\square \)
Lemma 7.4
For any \({\bar{\epsilon }} > 0\), for all sufficiently large n
Proof
Taking conditional expectations (analogously to the proof of Lemma 7.3), it suffices to prove that
Thanks to Lemma 8.1, \(\underset{N\rightarrow \infty }{{\overline{\lim }}}N^{-1}\log {\mathbb {P}}\big (\sup _{q\in I_M}N^{-1}\sum _{l\in I_N} \chi \lbrace {\tilde{\sigma }}^{q,l}_{b+1} \ne {\tilde{\sigma }}^{q,l}_b \rbrace > (c_1 + 1)\Delta \big ) < 0\). We can thus assume henceforth that
By Chernoff’s Inequality, for a constant \(\mathfrak {r} > 0\),
We now bound the first of the expectations on the right hand side: the bound of the other is similar. Let \({\mathcal {O}}\) be an \(NM\times NM\) square matrix (indexed using the following double-indexed notation). The element of \({\mathcal {O}}\) with indices (i, j) , (p, k) (for \(i,p\in I_M \; , \; j,k\in I_N\)) is defined to be \({\mathfrak {r}}\delta (j,k)\phi ^a_{ip}(\tilde{{\mathbf {G}}}^{j}_b)\chi \lbrace \tilde{\varvec{\sigma }}^j_b= \varvec{\alpha }\rbrace \). Define \(\bar{{\mathcal {O}}} = \frac{1}{2}({\mathcal {O}} + {\mathcal {O}}^T)\). Under \(\gamma _{\tilde{\varvec{\sigma }}_b,\tilde{{\mathbf {G}}}_b}\), \(\big \lbrace {\tilde{G}}^{i,j}_{b+1} - {\tilde{G}}^{i,j}_b - {\tilde{m}}^{i,j}_b\big \rbrace _{i\in I_M,j\in I_N}\) are centered Gaussian variables, with their \(NM \times NM\) covariance matrix equal to \({\mathcal {R}}_N\big (\tilde{\varvec{\sigma }}_b , \tilde{\varvec{\sigma }}_{b+1}\big )\) (as defined in (228)). Gaussian arithmetic thus implies that
where \(\lbrace \lambda _j \rbrace _{j=1}^{MN}\) are the eigenvalues of the real symmetric matrix \({\mathcal {R}}_N(\tilde{\varvec{\sigma }}_{b},\tilde{\varvec{\sigma }}_{b+1})^{1/2} \bar{{\mathcal {O}}}{\mathcal {R}}_N(\tilde{\varvec{\sigma }}_{b},\tilde{\varvec{\sigma }}_{b+1})^{1/2} \) (assuming for the moment that the modulus of each of these eigenvalues is strictly less than one). We thus find that
where \(Z_u \in [1-\lambda _u, 1]\) if \(\lambda _u > 0\), else \(Z_u \in [1,1-\lambda _u]\) if \(\lambda _u < 0\), using the second-order Taylor Expansion of \(\log \) about 1. Now
(using Lemma 7.1, and writing \({\bar{C}} = 4M(1+{\mathfrak {s}}))\). It may be observed from the block diagonal structure of \(\bar{{\mathcal {O}}}\) (i.e. \(\bar{{\mathcal {O}}}\) is ‘diagonal’ with respect to the \(I_N\) indices) that
since \(\big | \phi ^a_{ip}(\tilde{{\mathbf {G}}}^{j}_b)\chi \lbrace \tilde{\varvec{\sigma }}^j_b= \varvec{\alpha }\rbrace \big | \le 1\), and utilizing the fact that the operator norm is upper-bounded by the Frobenius matrix norm.
We thus find that \(\lambda _j \le \frac{1}{2}\), as long as \(\frac{M{\mathfrak {r}}{\bar{C}}}{N}\sup _{q\in I_M}\sum _{l=1}^N \chi \big \lbrace {\tilde{\sigma }}^{q,l}_{b+1} \ne {\tilde{\sigma }}^{q,l}_b \big \rbrace \le \frac{1}{2}\), and this follows from our earlier assumption (256) as long as \(\Delta \) is small enough. This means that \(Z_j \ge 1/2\). Since
we find that (259) implies that
using (260) and (261). Now, noting the definition of \({\mathcal {R}}_N(\tilde{\varvec{\sigma }}_{b},\tilde{\varvec{\sigma }}_{b+1})\) in (228),
One can straightforwardly demonstrate that \(\mathrm{tr}\big (\bar{\mathcal {O}}\mathcal {L}_N(\tilde{\varvec{\sigma }}_b,\tilde{\varvec{\sigma }}_{b+1})\big ) \le \text {Const}\big (N\Delta ^2 + 1\big )\), for some constant. More precisely, one can use concentration inequalities to show that the probability of the above not holding is exponentially decaying.
Now substituting the definition of \(\tilde{{\mathcal {K}}}_N\) in (224),
One can easily demonstrate using Martingale concentration inequalities (similar to those in the Appendix) that there exists a constant \({\tilde{C}}\) such that for all \(n\in {\mathbb {Z}}^+\), if \(p\ne i\) then
Using the definition of \({\tilde{L}}\) in (162), and the fact that \(({\tilde{\sigma }}^{i,k}_{b+1} - {\tilde{\sigma }}^{i,k}_{b})^2 = 2{\tilde{\sigma }}^{i,k}_b({\tilde{\sigma }}^{i,k}_{b} - {\tilde{\sigma }}^{i,k}_{b+1})\) (since \({\tilde{\sigma }}^{i,k}_u \in \lbrace -1,1 \rbrace \)), we obtain that the probability that the following event does not hold is exponentially decaying in N,
In summary, we obtain from (256), (258), (262), (263) and (264) that
This clearly implies (255) (and therefore the lemma) as long as \(\Delta \) and \({\mathfrak {r}}\) are sufficiently small. \(\square \)
8 Appendix: Properties of poisson processes
The following lemma contains some standard results concerning Poisson counting processes [27]. The first three can be demonstrated using Chernoff’s Inequality, and the last is a standard formula.
Lemma 8.1
-
(i)
For any \(t \ge t^{(n)}_b\), and any \(i\in I_M, j\in I_N\),
$$\begin{aligned} {\mathbb {P}}\big ( {\tilde{\sigma }}^{i,j}_t \ne {\tilde{\sigma }}^{i,j}_b \big ) \le c_1 (t - t^{(n)}_b). \end{aligned}$$(265) -
(ii)
For any \(\epsilon > 0\),
$$\begin{aligned} \underset{N\rightarrow \infty }{{\overline{\lim }}}N^{-1}\log {\mathbb {P}}\left( N^{-1}\sum _{j\in I_N} \chi \left\{ \sum _{i\in I_M} Y^{i,j}_b( c_1 t)> 0 \right\} > (M c_1+\epsilon ) t \right) < 0\nonumber \\ \end{aligned}$$(266) -
(iii)
For any \(\epsilon \in (0, c_1)\),
$$\begin{aligned} \underset{N\rightarrow \infty }{{\overline{\lim }}}N^{-1} \log {\mathbb {P}}\left( N^{-1}\sum _{j\in I_N} \chi \left\{ \sum _{i \in I_M} Y^{i,j}_b( c_1 t) > 0 \right\}< (c_1-\epsilon ) t \right) < 0\nonumber \\ \end{aligned}$$(267) -
(iv)
For any \(u,x> 0\),
$$\begin{aligned} {\mathbb {E}}\big [\exp \big (uY^{i,j}(x t) \big ) \big ] = \exp \big (x t \lbrace e^u - 1 \rbrace \big ). \end{aligned}$$(268)
The following general lemma yields a concentration inequality for compensated Poisson Processes.
Lemma 8.2
Suppose that \(\lbrace u^{q,j}_s , v^{q,j}_t \rbrace _{j\in I_N}\) are adapted càdlàg stochastic processes, with \(u^{q,j}_t \ge 0\) and that
Assume that \( u^{q,j}_t \le u_{max}\) for some constant \(u_{max}\).
-
(i)
Suppose that \(| v^{q,j}_t | \le v_{max}\) for some constant \(v_{max}\). Then there exists \(z_0\) and a constant C such that for all \(z \in [0,z_0]\),
$$\begin{aligned} {\mathbb {P}}\left( \sup _{t\in [0,x]}\sum _{j\in I_N,q\in I_M}X^{q,j}_t \ge Nz \right) \le \exp \left( -NCz^2 / x^2 \right) \end{aligned}$$(271) -
(ii)
Suppose that \(N^{-1}\sup _{t\in [0,T]}\sum _{j\in I_N}\chi \lbrace v^{q,j}_t \ne 0 \rbrace \exp (v^{q,j}_t) \le C\). Then for all \(z > 0\),
$$\begin{aligned} \sup _{q\in I_M}{\mathbb {P}}\left( \sup _{t\in [0,x]}\sum _{j\in I_N}X^{q,j}_t \ge Nz \right) \le \exp \left( Nu_{max}xC-Nz\right) . \end{aligned}$$(272)
Proof
Now since the exponential function is increasing, for a constant \(y > 0\),
by Doob’s Submartingale Inequality, and using the fact that the compensated Poisson Process \(X^{q,j}_t\) is a Martingale [2]. Choose y to be such that \(\exp (y v_{max}) \le 2\). We now demonstrate that
First notice that, since the functions are càdlàg,
We then find that, for \(t\in [0,x)\),
using the expression for the Poisson moment in (268). Now since \(\exp (yv^{q,j}_t) \le 2\), Taylor’s Theorem implies that \(\exp (yv^{q,j}_t)-1 \le yv^{q,j}_t + (yv^{q,j}_t)^2\). On taking \(h\rightarrow 0\), we thus obtain that
Gronwall’s Inequality thus implies (275). We now choose \(y= \min \big \lbrace z / (2Mx u_{max}v_{max}^2)),( \log 2) / v_{max} \big \rbrace \) and we have obtained (i). (ii) follows analogously. \(\square \)
Notes
One should be able to adapt the methods of this paper to this setting.
Private communication.
A quick way to see why this formula holds is to note that the probability of a jump occurring over a small time interval is approximately exponentially distributed, i.e. \({\mathbb {P}}(|\sigma ^{i,j}_{\Delta } - \sigma ^{i,j}_0| > 0 \big ) \simeq c(\sigma ^{i,j}_0, G^{i,j}_0)\exp \big (-\Delta c(\sigma ^{i,j}_0, G^{i,j}_0)\big )\). Taking the ratio of two such densities, multiplying over many time intervals, and then taking \(\Delta \rightarrow 0\), we obtain the formula (124).
This satisfies all of the axioms of a metric, except that \(d_K(\mu ,\nu )=0\) does not necessarily imply that \(\mu =\nu \).
References
Aljadeff, J., Stern, M., Sharpee, T.: Transition to chaos in random networks with cell-type-specific connectivity. Phys. Rev. Lett. 114(8) (2015)
Anderson, D.F., Kurtz, T.G.: Stochastic Analysis of Biochemical Systems. Springer, Berlin (2015)
Anderson, G.W., Guionnet, A., Zeitouni, O.: An Introduction to Random Matrices. Cambridge University Press, Cambridge (2011)
Arous, G.B., Dembo, A., Guionnet, A.: Aging of spherical spin glasses. Probab. Theory Relat. Fields 120(1), 1–67 (2001)
Arous, G.B.: Aging and spin-glass dynamics. In Proceedings of the International Congress of Mathematicians, volume III, pages 3–14. Higher Ed. Press, (2003)
Arous, G.B., Jagannath, A.: Spectral aap estimates in mean field spin glasses. Commun. Math. Phys. 361, 1–52 (2018)
Baity-Jesi, M., Sagun, L., Geiger, M., Spigler, S., Arous, G.B., Cammarota, C., LeCun, Y., Wyart, M., Biroli, G.: Comparing Dynamics: Deep Neural Networks versus Glassy Systems. (2018)
Bauerschmidt, R., Bodineau, T.: A very simple proof of the LSI for high temperature spin systems. J. Funct. Anal. 276(8), 2582–2588 (2019)
Ben-Arous, G., Guionnet, A.: Large deviations for Langevin spin glass dynamics. Probab. Theory Relat. Fields 102(4), 455–509 (1995)
Ben-Arous, G., Dembo, A., Guionnet, A.: Cugliandolo-Kurchan equations for dynamics of spin-glasses. Probab. Theory Relat. Fields 136(4), 619–660 (2006)
Arous, G.B., Guionnet, A.: Langevin Dynamics for Sherrington-Kirkpatrick Spin Glasses. In Anton Bovier and P Picco, editors, Mathematical Aspects of Spin Glasses and Neural Networks. Birkhauser, 1 edition, (1998)
Billingsley, P.: Convergence of Probability Measures. Wiley, New York (1999)
Bolthausen, E., Bovier, A.: Spin Glasses, vol. 2084. Springer (2007)
Brunel, N., Wang, X.-J.: What Determines the Frequency of Fast Network Oscillations With Irregular Neural Discharges? I. Synaptic Dynamics and Excitation-Inhibition Balance. J. Neurophysiol. 90, 415–430 (2003)
Budhiraja, A., Dupuis, P., Fischer, M.: Large deviation properties of weakly interacting processes via weak convergence methods. Annals Probab. 40(1), 74–102 (2012)
Cabana, T., Touboul, J.: Large deviations, Dynamics and phase transitions in large stochastic and disordered neural networks. J. Stat. Phys. 153(2), 211–269 (2013)
Cessac, B., Doyon, B., Quoy, M., Samuelides, M.: Mean-field equations , bifurcation map and route to chaos in discrete time neural networks. Physica D 74, 24–44 (1994)
Coghi, M., Deuschel, J-D., Friz, P., Maurelli, M.: Pathwise McKean-Vlasov Theory. 1–41, (2018)
Coppini, F., Dietert, H., Giacomin, G.: A law of large numbers and large deviations for interacting diffusions on Erdos-Rényi graphs. Stoch. Dyn. 20(02), 2050010 (2019)
Crisanti, A., Sompolinsky, H.: Path integral approach to random neural networks. Phys. Rev. E 98(6), 1–20 (2018)
Crisanti, A., Horner, H., Sommers, H.J.: The spherical p-spin interaction spin-glass model. Z. Phys. B: Condens. Matter 92(2), 257–271 (1993)
Cugliandolo, L.F., Kurchan, J.: On the out-of-equilibrium relaxation of the Sherrington-Kirkpatrick model. J. Phys. A: Math. Gen. 27(17), 5749–5772 (1994)
Dawson, D., Gartner, J.: Large Deviations, Free Energy Functional and Quasi-Potential for a Mean Field Model of Interacting Diffusions. American Mathematical Society, (1989)
Dembo, A., Lubetzky, E., Zeitouni, O.: Universality for langevin spin glass dynamics. Arxiv Preprint 1, 1–18 (2019)
Dembo, A., Zeitouni, O.: Large Deviations Techniques and Applications, 2nd edn. Springer, Berlin (1998)
Doiron, B., Litwin-Kumar, A., Rosenbaum, R., Ocker, G., Josic, K.: The mechanics of state dependent neural correlations. Nat. Neurosci. 19(3), 383–393 (2016)
Ethier, S., Kurtz, T.: Markov Processes. Characterization and Convergence. Wiley Series in Probability and Mathematical Statistics, (1986)
Fasoli, D., Faugeras, O., Panzeri, S.: A Formalism for Evaluating Analytically the Cross-Correlation Structure of a Firing-Rate Network Model. J. Math. Neurosc. 5(1), 1–53 (2015)
Fasoli, D., Panzeri, S.: Stationary-state statistics of a binary neural network model with quenched disorder. Entropy 21(7), 1–30 (2019)
Faugeras, O., MacLaurin, J.: Asymptotic description of neural networks with correlated synaptic weights. Entropy 17(7), 4701–4743 (2015)
Faugeras, O., Maclaurin, J., Tanré, E.: A large deviation principle governing the thermodynamic limit of a network of Hopfield neurons with correlated synaptic weights. Archiv Preprint, (2019)
Faugeras, O., Soret, E., Tanré, E.: Asymptotic behaviour of a network of neurons with random linear interactions. Preprint HAL Id : hal-01986927, (2019)
Gheissari, R., Jagannath, A.: On the spectral gap of spherical spin glass dynamics. Annales de l’Institut Henri Poincaré, Probab. et Stat. 5(2), 1–21 (2019)
Gibbs, A.L., Su, F.E.: On choosing and bounding probability metrics. Int. Stat. Rev. 70(3), 419–435 (2002)
Glauber, R.J.: Time-dependent statistics of the Ising model. J. Math. Phys. 4(2), 294–307 (1963)
Green, J.W., Valentine, F.A.: On the Arzela-Ascoli Theorem. Math. Mag. 34(4), 199–202 (1961)
Grunwald, M.: Sanov results for Glauber spin-glass dynamics. Probab. Theory Relat. Fields 106, 187–232 (1996)
Grunwald, M.: Sherrington-Kirkpatrick Spin-Glass Dynamics. In: Bovier, Anton, Picco, Pierre (eds.) Mathematical Aspects of Spin Glasses. Birkhauser, Basel (1998)
Guerra, F.: Broken replica symmetry bounds in the mean field spin glass model. Commun. Math. Phys. 233(1), 1–12 (2003)
Guionnet, A.: Averaged and quenched propagation of chaos for spin glass dynamics. Probab. Theory Relat. Fields 109, 183–215 (1997)
Guionnet, A.: Dynamics for Spherical Models of Spin-Glass and Aging. In: Bolthausen, Erwin, Bovier, Anton (eds.) Spin Glasses. Springer, Berlin (2007)
Houghton, A., Jain, S., Young, A.P.: Role of initial conditions in the mean-field theory of spin-glass dynamics. Phys. Rev. B 28(5), 2630 (1983)
Jacod, J., Shiryaev, A.N.: Limit Theorem for Stochastic Processes, 2nd edn. Springer, New York (2002)
Jagannath, A.: Dynamics of mean field spin glasses on short and long timescales. Journal of Mathematical Physics 60(8) (2019)
Jourdain, B., Meleard, S.: Propagation of chaos and fluctuations for a moderate model with smooth initial data. Annales De L’I.H.P., Section B, 34(6), (1998)
Jourdain, B., Méléard, S., Woyczynski, W.: Nonlinear SDEs driven by Lévy processes and related PDEs. Alea 4, 1–28 (2007)
Kadmon, J., Sompolinsky, H.: Transition to chaos in random neuronal networks. Phys. Rev. X 5(4), 1–28 (2015)
Laughton, S.N., Coolen, A.C.C., Sherrington, D.: Order-Parameter Flow in the SK Spin-Glass II : Inclusion of Microscopic Memory Effects. Journal of Physics A: Mathematical and General 29(4), 763 (1996)
Laughton, S.N., Sherrington, D.: Dynamical Replica Theory for Disordered Spin Systems. Phys. Rev. B 2, 1–7 (1996)
Lindgren, George, Rootzen, Holger, Sandsten, Maria: Stationary Stochastic Processes for Scientists and Engineers. Chapman Hall, London (2013)
Lucon, E., Stannat, W.: Mean field limit for disordered diffusions with singular interactions 1. Annals Appl. Probab. 24(5), 1946–1993 (2014)
Maclaurin, J.: Large Deviations of a Network of Interacting Particles with Sparse Random Connections. arXiv preprintarXiv:1607.05471, (2018)
Mezard, M., Parisi, G., Virasoro, M.A., editors: Spin Glass Theory and Beyond. World Scientific, (1987)
Montanari, A.: Optimization of the Sherrington-Kirkpatrick Hamiltonian. 1–27, (2019)
Panchenko, D.: The Sherrington-Kirkpatrick Model. Springer, Berlin (2013)
Parisi, G.: Infinite number of order parameters for spin-glasses. Phys. Rev. Lett. 43(23), 1754 (1979)
Poplavskyi, M., Tribe, R., Zaboronski, O.: On the distribution of the largest real eigenvalue for the real ginibre ensemble. Annals Appl. Probab. 27(3), 1395–1413 (2017)
Sherrington, D., Kirkpatrick, S.: Solvable model of a spin-glass. Phys. Rev. Lett. 35(26), 1792 (1975)
Sommers, Hans-Jurgen: Path-integral approach to ising spin-glass. Dynamics. 58(12), 1268–1271 (1987)
Sompolinsky, H.: Time-dependent order parameters in spin-glasses. Phys. Rev. Lett. 47(13), 935–938 (1981)
Sompolinsky, H., Zippelius, A.: Dynamic Theory of the Spin-Glass Phase. Phys. Rev. Lett. 47(5), 359–362 (1981)
Stein, D.L., Newman, C.M.: Spin Glasses and Complexity. Princeton University Press, New Jersy (2013)
Sznitman, A-S.: Topics in Propagation of Chaos. In P.L Henneguin, editor, Lecture Notes in Mathematics. Ecole d’Ete de Probabilites de Saint-Flour XIX - 1989. Springer-Verlag, (1989)
Talagrand, M.: The Parisi formula. Ann. Math. 163(1), 221–263 (2006)
Talagrand, M.: Mean Field Models for Spin Glasses: Advanced Replica-Symmetry and Low Temperature. Springer, Berlin (2011)
Wainrib, G., Touboul, J.: Topological and dynamical complexity of random neural networks. Phys. Rev. Lett. 110(11), 1–4 (2013)
Acknowledgements
Much thanks to Colin MacLaurin (U. Queensland) for obtaining some preliminary numerical results that were incorporated into the introduction. Much thanks also to Gerard Ben Arous (NYU), David Shirokoff (NJIT), Victor Matveev (NJIT), Bruno Cessac (INRIA) and Etienne Tanre (INRIA) for interesting discussions and very helpful feedback.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
MacLaurin, J. An emergent autonomous flow for mean-field spin glasses. Probab. Theory Relat. Fields 180, 365–438 (2021). https://doi.org/10.1007/s00440-021-01040-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-021-01040-w