Introduction

With the completion the 1000 Genomes Project (Genomes Project et al. 2015), an unprecedented wealth of knowledge has been accumulated for understanding the variations at the human DNA level. However, little of this DNA-level knowledge has been translated into understanding the mechanisms of human diseases. Gene expression quantitative trait locus (eQTL) mapping is one of the most promising approaches to fill this gap, which aims to explore the genetic basis of gene expression (Cookson et al. 2009). Among the eQTL techniques, cis-eQTL mapping is the most commonly used technique to map local eQTLs on the same chromosome of the gene. To date, many statistical methods for eQTL mapping have been developed, however, the modeling of imprinting is typically ignored in these methods.

Imprinting is a type of parent-of-origin effect (POE) that the expression of certain genes depends on their allelic parent-of-origin. As such, the same alleles transmitted from the mother have different expression levels on transcripts compared with those transmitted from the father. Consequently, the influences on the phenotype between the two types of heterozygotes are different, as so-called parent-of-origin effect (POE). There are at least 80 imprinted genes discovered in humans, many of which are involved in embryonic and placental growth and development (Perry et al. 2014). Studies have suggested that POE is an important contributor to phenotypic variation in human complex diseases and may explain some of the “hidden” heritability. An earlier study showed that for type II diabetes, a variant of SNP rs2334499 in chromosome region 11p15 was protective when maternally transmitted, whereas it conferred risk when paternally transmitted (Kong et al. 2009). Important roles of POEs are also implicated in type I diabetes, breast cancer and other carcinomas (Kong et al. 2009; Wallace et al. 2010). In the past few years, there were few approaches that modeled POEs while searching for eQTLs with RNA-seq data. The only report was from a study recently conducted by Zhabotynsky et al. which proposed to jointly model genetic effect and POE focusing on modeling the allele specific expression (ASE) (Zhabotynsky et al. 2019).

In recent years, the inclusion of dominance in animal genomic models has been proposed by several researchers (Duenk et al. 2017; Ertl et al. 2014; Su et al. 2012; Xiang et al. 2018). From the theory of quantitative genetics, statistical additive genetic effects are obtained from average allele substitution effects, whereas dominance genetic effects reflect the deviation of the genotypic values of the heterozygotes and the expected midpoint of the two homozygotes. In quantitative genetics, the partition of the variance in statistical components is due to additivity. Dominance does not reflect the biological effect of the genes, but it is most useful for prediction, selection, and evolution (Huang and Mackay 2016).

Multi-collinearity, however, is an important issue arising from modeling multiple genetic effects. To achieve straightforward model selection and variance component analysis, uncorrelated estimation of the additive and dominance effects is necessary. To achieve this goal, in our study, we developed an orthogonal model to jointly evaluate the effect from both additive and dominance genetic effects along with the detection of POE in eQTL mapping for RNA sequencing read count data. To evaluate gene expression levels, RNA sequencing (RNA-seq) technology has recently become a widely used high-throughput technology to assess the gene expression abundance, especially in discovery of novel eQTLs (Ellis et al. 2013).

Genetic imprinting affects complex diseases through regulating the gene expression and can reveal an important component of heritable variation that remains “hidden” in traditional complex trait studies. In this study, we hypothesized that POEs contribute to regulating gene expression along with the main allelic effect (i.e., additive and dominance effects) from the gene. Accordingly, we developed a statistical framework to test the main allelic effects of the candidate eQTLs along with the detection of POE with a natural model and an orthogonal model. Intensive simulations were conducted to evaluate the methods. We also applied the methods to an existing HapMap project trio dataset to validate the reported imprinting genes and identify novel cis-eQTLs for these genes.

Methods

The stat-POE and func-POE methods

Our methods were developed from a basic model of eQTL mapping of a single gene with RNA-seq data that are read counts. Therefore, we consider a single gene and study the association of its expression with the \(j\)th candidate eQTL. Let \({y}_{i}\) be the total read counts mapped to this gene in the ith sample, where \(i=1,\dots ,n\) and n is the sample size. We model \({y}_{i}\) using the negative binomial(NB) distribution as they are sparse count data. The NB distribution allows over-dispersion (the variance exceeds the mean) estimation. Let \({f}_{\mathrm{N}\mathrm{B}}({y}_{i};{\mu }_{i},\phi )\) be the probability mass function for a NB distribution with mean \({\mu }_{i}\) and dispersion parameter \(\phi \):

$${f}_{\mathrm{N}\mathrm{B}}({y}_{i};{\mu }_{i},\phi )=\frac{\Gamma ({y}_{i}+1/\phi )}{{y}_{i}!\Gamma (1/\phi )}{\left(\frac{1}{1+\phi {\mu }_{i}}\right)}^{1/\phi }{\left(\frac{\phi {\mu }_{i}}{1+\phi {\mu }_{i}}\right)}^{{y}_{i}},{y}_{i}=\mathrm{0,1}, 2, \dots $$
(1)

where \(\Gamma (\cdot )\) is the gamma function. It’s easy to find that the variance \(\mathrm{V}\mathrm{a}\mathrm{r}({y}_{i})={\mu }_{i}+\phi {\mu }_{i}^{2}\), in which \(\phi {\mu }_{i}^{2}\) is the over-dispersion part. As the over-dispersion parameter \(\phi \) converges to \(0\), \({f}_{NB}({y}_{i};{\mu }_{i},\phi )\) converges to \({f}_{p}({y}_{i};{\mu }_{i})={\mu }_{i}^{{y}_{i}}{e}^{-{\mu }_{i}}/{y}_{i}!\), which is the probability mass function for Poisson distribution with mean parameter \({\mu }_{i}\). Let \({\mathbf{X}}_{i}\) be a set of \(p\) covariates and \({\varvec{\beta}}=({\beta }_{1},\dots ,{\beta }_{p}){^{\prime}}\) be the regression coefficients, and \({{\varvec{\beta}}}_{G}=(R,a,d, l){^{\prime}}\) be the genetic effects from genotypes (\(G\)) of the eQTL on \(Y\), where \(R\) is the baseline, \(a\), \(d\) and \(l\) are the additive, dominance and imprinting effects from \(G\), respectively. The covariate effect of \(G={G}_{i}\) and covariates \(\mathbf{X}={\mathbf{x}}_{i}\) on the gene expression, can be formulated through the following log-linear regression model

$$\mathrm{l}\mathrm{o}\mathrm{g}({\mu }_{i})={\varvec{\beta}}{^{\prime}}{\mathbf{x}}_{i}+\omega ({G}_{i},{{\varvec{\beta}}}_{G}),$$
(2)

where \(\omega ({G}_{i},{{\varvec{\beta}}}_{G})\) is the function reflecting the genetic effects.

For a bi-allelic locus, let the major and minor alleles of the \(j\)th candidate eQTL as \({A}_{1}\) and \({A}_{2}\), respectively. The genotype G takes four possible values \({\overrightarrow{A}}_{1}{A}_{1},\)\({\overrightarrow{A}}_{1}{A}_{2}\), \({\overrightarrow{A}}_{2}{A}_{1}\) and \({\overrightarrow{A}}_{2}{A}_{2},\), the first allele of which with arrow denotes the paternal allele and the second allele denotes the one originated from the maternal side. We use \({p}_{11},{p}_{12},{p}_{21}\) and \({p}_{22}\) to denote genotype frequencies in the population, and use \(M\) to denote the number of variant allele \({A}_{2}\), which takes values of \(0, 1, 1\) and \(2\) for the four genotypes separately. \(\overline{M}=1+{p}_{22}-{p}_{11}\) and \(V=({p}_{11}+{p}_{22})-({p}_{11}-{p}_{22}{)}^{2}\) are the mean and variance of \(M\).

For estimation of the genetic effects, there are different methods we can epress the genetic effect function \(\omega ({G}_{i},{{\varvec{\beta}}}_{G})\). Early in 2013, we proposed a unified orthogonal framework to model genetic variants displaying imprinting effects for quantitative traits (Xiao et al. 2013). We proposed two related methods for identifying genetic variants influences on quantitative traits with different characteristics, the statistical and functional POE methods. The statistical POE method in Xiao et al. (2013) was claimed to be partially orthogonal and allows for imprinting effect detection while maintaining sufficient power for main allelic effects (i.e., the additive and dominance effects) in certain conditions. Motivated by that study, we here develop \(\omega ({G}_{i},{{\varvec{\beta}}}_{G})\) in a population-referenced formulation with an orthogonal model, termed Stat-POE model, generated from reparameterization procedure:

$$\omega \left({G}_{i},{{\varvec{\beta}}}_{G}\right)=\left\{\begin{array}{cc}\begin{array}{c}R-\overline{M}a-2{p}_{22}\left({p}_{12}+{p}_{21}\right)d/V,\\ R+\left(1-\overline{M}\right)a+4{p}_{11}{p}_{22}d/V-2{p}_{21}l/\left({p}_{12}+{p}_{21}\right),\end{array}& \begin{array}{c}\,\,\mathrm{i}\mathrm{f} \,\,{G}_{i}={\overrightarrow{A}}_{1}{A}_{1}\\ \,\,\mathrm{i}\mathrm{f} \,\,{G}_{i}={\overrightarrow{A}}_{1}{A}_{2}\end{array}\\ \begin{array}{c}R+\left(1-\overline{M}\right)a+4{p}_{11}{p}_{22}d/V+2{p}_{12}l/\left({p}_{12}+{p}_{21}\right),\\ R+\left(2-\overline{M}\right)a-2{p}_{11}\left({p}_{12}+{p}_{21}\right)d/V, \end{array}& \begin{array}{c}\,\,\mathrm{i}\mathrm{f}\,\, {G}_{i}={\overrightarrow{A}}_{2}{A}_{1}\\ \,\,\mathrm{i}\mathrm{f} \,\,{G}_{i}={\overrightarrow{A}}_{2}{A}_{2}\end{array}\end{array}\right.$$
(3)

With the orthogonality property, this model allows for un-correlated estimation of the genetic effects including the additive, dominance and imprinting effects. Such orthogonal model also enables straightforward model comparison with nested genetic models (Alvarez-Castro and Carlborg 2007). Note that we continued to use the same terminology of the Stat-POE model as what we used in Xiao et al., 2013, although the Stat-POE model in this study as shown in Eq. (3) is a newly proposed model that is fully orthogonal.

For a functional model without the orthogonalization property but with a POE component, the genetic effect function \(\omega ({G}_{i},{{\varvec{\beta}}}_{G})\) can be expressed as

$$\omega \left({G}_{i},{{\varvec{\beta}}}_{G}\right)=\left\{\begin{array}{cc}\begin{array}{c}R\\ R+a+d-l, \end{array}& \begin{array}{c} \,\,\mathrm{i}\mathrm{f}\,\,{ G}_{i}={\overrightarrow{A}}_{1}{A}_{1}\\ \,\,\mathrm{i}\mathrm{f} \,\,{G}_{i}={\overrightarrow{A}}_{1}{A}_{2}\end{array}\\ \begin{array}{c}R+a+d+l,\\ R+2a, \end{array}& \begin{array}{c} \,\,\mathrm{i}\mathrm{f}\,\, {G}_{i}={\overrightarrow{A}}_{2}{A}_{1}\\ \,\,\mathrm{i}\mathrm{f} \,\,{G}_{i}={\overrightarrow{A}}_{2}{A}_{2}\end{array}\end{array}\right.$$
(4)

from which we obtain

$$\begin{array}{c}a=\frac{1}{2}\mathrm{l}\mathrm{o}\mathrm{g}\left({\mu }_{i{\overrightarrow{A}}_{2}{A}_{2}}/{\mu }_{i{\overrightarrow{A}}_{1}{A}_{1}}\right),\\ d=\frac{1}{2}\log\left(\frac{{\mu }_{i{\overrightarrow{A}}_{1}{A}_{2}}+{{\mu }_{i}}_{{\overrightarrow{A}}_{2}{A}_{1}}}{{{\mu }_{i}}_{{\overrightarrow{A}}_{2}{A}_{2}}+{{\mu }_{i}}_{{\overrightarrow{A}}_{1}{A}_{1}}}\right)\\ l=\frac{1}{2}\mathrm{l}\mathrm{o}\mathrm{g}\left({\mu }_{i{\overrightarrow{A}}_{2}{A}_{1}}/{\mu }_{i{\overrightarrow{A}}_{1}{A}_{2}}\right),\end{array},$$
(5)

where \({\mu }_{i{A}_{1}{A}_{1}},{\mu }_{i{A}_{1}{A}_{2}},{\mu }_{i{A}_{2}{A}_{1}}\) and \({\mu }_{i{A}_{2}{A}_{2}}\) are the underlying means of the read counts for subjects with the four genotypes, respectively. The additive effect \(a\) measures the average fold change of gene expression between the two homozygotes; the dominance effect \(d\) measures the deviation of the heterozygotes from its additive expectation; and the imprinting effect \(l\) reflects the different effect from the two types of heterozygotes. Following the notations in Alvarez-Castro and Carlborg (2007), the model in Eq. (5) is defined as a functional POE (Func-POE) model, or a natural model since it uses natural effects of allele substitutions as parameters, mainly focusing on the biological properties (Alvarez-Castro and Carlborg 2007).

The general orthogonal and functional models have presented different properties for various application scopes in detecting epistasis, gene environment interactions and parent-of-origin effects in quantitative traits and qulitative traits (Ma et al. 2012; Xiao et al. 2013, 2014).

Parameter estimation and hypothesis testing

To estimate the genetic effects and POE, we can write the likelihood based on the data \(\left({y}_{i},{X}_{i},{G}_{i}\right)\)\(\left(i=\mathrm{1, 2},...N\right)\) as

$$L({\varvec{\beta}},{{\varvec{\beta}}}_{G},\phi ;\{{y}_{i},{\mathbf{x}}_{i}{\}}_{i=1}^{N})=\prod_{i=1}^{N}{f}_{NB}({y}_{i};{\mu }_{i}({\varvec{\beta}},{{\varvec{\beta}}}_{G}),\phi {)}^{{I}_{NB}({y}_{1},\dots ,{y}_{N})}{f}_{P}({y}_{i};{\mu }_{i}({\varvec{\beta}},{{\varvec{\beta}}}_{G}){)}^{1-{I}_{NB}({y}_{1},\dots ,{y}_{N})},$$
(6)

where \({I}_{NB}({y}_{1},\dots ,{y}_{N})\) is an indicator function which is equal to \(1\) if a negative binomial distribution is used and \(0\) if a Poisson distribution is used.

With Eq. 2.4, the maximum likelihood estimator (MLE) of the model parameters \(({{\varvec{\beta}}}_{\phi },{{\varvec{\beta}}}_{G})\) with \({{\varvec{\beta}}}_{\phi }\triangleq ({\varvec{\beta}}\boldsymbol{^{\prime}},\phi ){^{\prime}}\) can be estimated by the following iterative procedure.

  1. 1.

    Initialization: we first fit a null model using Poisson regression using the covariate \({\mathbf{X}}_{i}\), and estimate \({\varvec{\beta}}\), using a Newton–Raphson optimization algorithm based on formulas given in Appendix A.1. Subsequently, a score test is conducted for the over-dispersion parameter \(\phi \) where the hypothesis testing procedure is illustrated in Appendix A.2. If the p value of the score test is smaller than a cutoff value, e.g., \(\alpha =0.05\), we estimate a negative binomial regression model for which the regression parameters are denoted \({{\varvec{\beta}}}_{\phi }\). The details of the iterative formulas for estinating \({\varvec{\beta}}\) and \(\phi \) are given in (A.10) and (A.11) in Appendix A.3, which are based on the iteratively re-weighted least squares method (Green 1984) and the Newton–Raphson iterative method, respectively.

  2. 2.

    Iteration: (a) given \({\varvec{\beta}}\) or \({{\varvec{\beta}}}_{\phi }\), we estimate \({{\varvec{\beta}}}_{G}\) by the Newton–Raphson method illustrated in Appendix B; (b). Given \({{\varvec{\beta}}}_{G}\), we estimate \({\varvec{\beta}}\) by a Poisson regression with offsets \(\omega ({G}_{i},{{\varvec{\beta}}}_{G})\), or estimate \({{\varvec{\beta}}}_{\phi }\) by a negative binomial regression with offsets \(\omega ({G}_{i},{{\varvec{\beta}}}_{G})\). The estimation for \({\varvec{\beta}}\) under the Poisson regresion is the same as that in the initialization step with the first and second derivatives given in Appendix B.6 for the Stat-POE model and Appendix B.8 for the Func-POE model, respectively. Under the negative binomial regression, the estimation method for \({{\varvec{\beta}}}_{\phi }\) described in the the initialization step is also used here with the detailed forlumas given in Appendix B.5 for the Stat-POE model and in Appendix B.7 for the Func-POE model, respectively.

  3. 3.

    Termination: until iterate steps (1) and (2) estimate of all the parameters converge.

To assess whether each covariate in the model is significant on the read counts of the gene expression, statistical hypothesis testing will be performed. We constructed three testing methods including the likelihood ratio test (LRT), score test and Wald test as follows. For example, the of additive effect was tested using the hypotheses

$${H}_{0}:a=0\,\, {\text{vs}}\,\,\, {H}_{1}:a\ne 0.$$
(7)

Denote \({\varvec{\theta}}=({{\varvec{\beta}}}_{\phi }^{^{\prime}},{{\varvec{\beta}}}_{G}^{^{\prime}}){^{\prime}}\) for the Negative Binomial (NB) regression, or \({\varvec{\theta}}=({\varvec{\beta}}{^{\prime}},{{\varvec{\beta}}}_{G}^{^{\prime}}){^{\prime}}\) for the Poisson regression, the unrestricted MLE and restricted MLE under (Appendix D.1) obtained by the algorithm given in the above section are denoted as \(\widehat{{\varvec{\theta}}}\) and \(\hat{\tilde{\theta}},\) respectively. Without loss of generality, we put the parameter \(a\) in the first position of \({\varvec{\theta}}\) and denote the other parameters as \(\xi \), i.e. \({\varvec{\theta}}=(a,\xi {^{\prime}}){^{\prime}}\). Then the score function for \({\varvec{\theta}}\) is \(U({\varvec{\theta}})=\left[\begin{array}{l}\frac{\partial l({\varvec{\theta}})}{\partial a}\\ \frac{\partial l({\varvec{\theta}})}{\partial \xi }\end{array}\right]\), and the expected fisher information matrix is \(I({\varvec{\theta}})=-\mathrm{E}\left[ \begin{array}{ll} \frac{{\partial }^{2}l({\varvec{\theta}})}{\partial {a}^{2}}& \frac{{\partial }^{2}l({\varvec{\theta}})}{\partial a\partial \xi {^{\prime}}}\\ \frac{{\partial }^{2}l({\varvec{\theta}})}{\partial \xi \partial a} & \frac{{\partial }^{2}l({\varvec{\theta}})}{\partial {a}^{2}}\end{array}\right]\)\(\triangleq \left[\begin{array}{ll}{I}_{aa}({\varvec{\theta}})& {I}_{a\xi }({\varvec{\theta}})\\ {I}_{\xi a}({\varvec{\theta}})& {I}_{\xi \xi }({\varvec{\theta}})\end{array}\right]\), where \(l({\varvec{\theta}})\) is the log-likelihood function given as in Appendix B.1 for NB regression and the Stat-POE model, in Appendix B.2 for Poisson regression and statistical model, in Appendix B.3 for NB regression and the Func-POE model, and in Appendix B.4 for Poisson regression and the Func-POE model. The formulas of \(U({\varvec{\theta}})\) and \(I({\varvec{\theta}})\) are given in Appendix C. The LRT statistic is

$${T}_{L}=2[l(\widehat{{\varvec{\theta}}})-l()].$$
(8)

According to the theory from Rao (2005), in our statistical setting, the score test statistic is defined as

$${T}_{S}={\left(\frac{\partial l({\varvec{\theta}})}{\partial a}\right)}^{2}{|}_{\hat{\tilde{\theta}}}{J}_{aa}({\varvec{\theta}}){|}_{\hat{\tilde{\theta}}}.$$
(9)

where \({J}_{\mathrm{a}\mathrm{a}}({\varvec{\theta}})=({I}_{aa}({\varvec{\theta}})-{I}_{a\xi }({\varvec{\theta}}){I}_{\xi \xi }^{-1}({\varvec{\theta}}){I}_{\xi a}({\varvec{\theta}}){)}^{-1}\).

Moreover, the Wald test statistic is defined by:

$${T}_{W}=\frac{{\widehat{a}}^{2}}{{J}_{aa}({\varvec{\theta}}){|}_{\widehat{{\varvec{\theta}}}}}.$$
(10)

Under \({H}_{0}\), the statistics \({T}_{L}\), \({T}_{S}\), and \({T}_{W}\) all converge to \({\chi }_{1-}^{2}\) distributions. For a given significance level \(\alpha \), we reject \({H}_{0}\) when the observed value of the statistics are greater than \({\chi }_{\mathrm{1,1}-\alpha }^{2}\). The process of the hypothesis testing for the other parameters can be implemented in a similar manner.

Simulations

To evaluate the performance of the proposed statistical methods in eQTL mapping with RNA-seq data, we carried out extensive simulation studies in realistic settings. First, we compared the statistical power of the Stat-POE and Func-POE methods in detecting the main allelic effects (i.e., the additive and dominance effects) and POE. We simulated \({y}_{i}\), the total number of read counts of a gene in the ith sample as being generated from a negative binomial distribution with \({\mu }_{iG}= \mathrm{e}\mathrm{x}\mathrm{p}\left(0.1{x}_{i}+\omega \left({G}_{i},{\beta }_{G}\right)\right)\). The over-dispersion parameter \(=0.2\) and the covariate X was a continuous variable \(\mathbf{X}\sim \mathrm{N}(\mathrm{0,1})\). To evaluate the performance of the methods in estimating both genetic effects and over-dispersion, we generated data with different sample sizes N = 50, 100, 200 and 500, respectively. Hardy–Weinberg Equilibrium (HWE) proportion was used so that the genotype frequencies in the samples were set at [p11, p12, p21, p22] = [0.36, 0.24, 0.24, 0.16]. In addition to the main scenarios of HWE proportions, non-HWE genotype proportions were also simulated that the proportions of two heterozygotes were different, [p12, p21] = [0.20, 0.28] or [p12, p21] = [0.28, 0.20]. The over-dispersion parameter was set at empirical values that was 0.2 or 0.5. The additive effect α and dominance effect δ were both fixed at values of log (1.2) where the values of 1.2 reflected the fold change of the logarithm mean shift of the genotypic values, referring to Eq. (5). The POE parameter ι was set at log (1.1) or log (1.2), respectively.

Each simulation was replicated 500 times to evaluate the performance of the Stat-POE and Func-POE methods. Relative bias and mean square of errors (MSE) were calculated for each parameter in the different scenarios to evaluate the estimation accuracy. The estimation relative bias was defined as the difference between estimated value and the true parameter value and then divided by the true parameter value. We also used simulated data to quantify the statistical power and Type I error rates of the methods. To illustrate the performance of the proposed methods in detecting genetic effect terms and POE, the statistical power was calculated using a range of different critical values. Type I error was calculated under the null model where there was no genetic effect or POE for the three testing methods, the LRT, Wald and score tests.

Application to a HapMap RNA-seq dataset

Datasets

We used an RNA-seq dataset from 30 HapMap Caucasian samples obtained from the NCBI Bioproject (PRJNA385599). The samples were collected from lymphoblastoid cell lines from 15 males and 15 females. For most of these samples, the RNA reads were 150 bp paired-end reads, with an additional run with 75 bp paired-end reads. The median of the total number of reads for these 30 samples was approximately 20 million. All of these reads were mapped to hg38 human reference genome using Tophat2 (Zhabotynsky et al. 2019).

Since all of these samples were from children of family trios, the parents of these children were also part of the samples included in the 1000 Genomes Project (2012). For these 30 trios, the HapMap project genotyped about 3.9 million SNPs. Genotyping data of the 30 trios were used to obtain the phased genotype of the children. The phasing and imputation of these 30 trios were conducted by Zhabotynsky et al.’s study, from where the phased and imputed genotypes in our study were directly obtained (Zhabotynsky et al. 2019). Briefly, SHAPEIT2 (Delaneau et al. 2014) was used for phasing and IMPUTE2 (Howie et al. 2012) was used for imputation against the 1000 Genome reference panel containing 2504 individuals and ~ 82 million SNPs. Based on the phased and imputed SNPs, we had 6,211,048 imputed SNPs of high confidence in total, the ones with at least one heterozygote in the sample which were all informative.

Identification of imprinted genes and genes with dominance effect

We selected 22 known imprinted genes based on the list reported by a recent publication (Jadhav et al. 2019). These genes were selected because they had abundant expression in the 30 samples. The genes and related information are listed in Supplementary Table 1. For each potential imprinting gene, all SNPs in the gene coding region were defined as candidate cis-eQTLs. For each SNP and gene expression pair, the Stat-POE method was applied to detect candidate cis-eQTLs with additive, dominance and POE effects. Four covariates were adjusted in the model including the total read counts per individual and the first three principal components computed from the matrix of normalized expression to remove the effect from potential confounders. In all of the above hypothesis testing, the Benjamini–Hochberg (BH) method was used for multiple comparisons to adjust the p-values obtained from the LRTs (Benjamini and Hochberg 1995). We tested the POE of the previously reported imprinted genes in Supplementary Table 1 to evaluate the performance of our methods. For novel discovery of genetic effects of these potential imprinting genes, we tested the additive and dominance effects simultaneously.

Results

Simulations

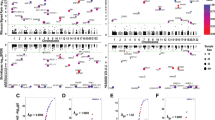
The statistical power of the Stat-POE and Func-POE methods was investigated for POE at two scenarios with different levels of POE: (a) a small POE with ι = log(1.1) and (b) a moderate POE with ι = log(1.2). The results are shown in Figs. 1, 2 for these two scenarios, respectively. In both scenarios, the additive and dominance effects were fixed at log (1.2). In the simulations, to demonstrate the desirable performance of the Stat-POE method when the effect size was relatively too small to detect, we evaluated the methods at a fixed and small fold change in both overall allelic effects (i.e., additive and dominance effects). Consequently, even at a sample size of 50 with moderate over-dispersion (ϕ = 0.2), the Stat-POE method presented around 70.8% power to detect genetic effect at 1.2-fold change in additive effect, corresponding to an effect size of log(1.2) = 0.18 (Fig. 1). To detect POE at the fold change of 1.2, the Stat-POE and Func-POE methods both reached a statistical power of 83% with a reasonable sample size of 100 (Fig. 2). Even with a very small effect size from POE at a fold change of 1.1, corresponding to an effect size of log (1.1) = 0.10, the methods yielded 61% power when the sample size was 200, and 91% when the sample size was 500 (Fig. 1). As expected, the Stat-POE method yielded the same power in detecting POE but a more desirable power in detecting main genetic effects compared to the Func-POE model (Figs. 1, 2). We also simulated the proportion of non-HWE that genotype frequencies of the two heterozygotes are unequal. The Stat-POE model always outperformed the Func-POE model in detecting additive effects, though it is not always the case for detection of the dominance effect (Supplementary Figs. 1, 2). In conclusion, the Stat-POE method outperformed the Func-POE method in most simulation scenarios and these two methods all achieved sufficient power for detection of POEs with a practical sample size for family data (N = 100).

Fig. 1
figure 1

Statistical power to detect additive, dominance and POE effect when a–c overdispersion φ = 0.2 and d–eφ = 0.5 for various samples sizes, using Stat-POE model (stat) or Func-POE model (func).The covariate coefficient \(\beta =0.1\), the sample size (n) was set at 50, 100, 200 and 500, respectively. Addi additive effect, domi dominant effect, impr imprinting effect, stat statistical model, func functional model. The additive effect α = log(1.2), dominant effect δ = log(1.2), imprinting effect ι = log(1.1). The genotype frequencies in the samples were set at [p11, p12, p21, p22] = [0.36, 0.24, 0.24, 0.16]. Score test results are shown

Full size image
Fig. 2
figure 2

Statistical power to detect additive, dominance and POE effect when a–c overdispersion φ = 0.2 and d–eφ = 0.5 for various samples sizes, using Stat-POE model (stat) or Func-POE model (func).The covariate coefficient \(\beta =0.1\), the sample size (n) was set at 50, 100, 200 and 500, respectively. Addi additive effect, domi dominant effect, impr imprinting effect, stat statistical model, func functional model. The additive effect α = log(1.2), dominant effect δ = log(1.2), imprinting effect ι = log(1.2). The genotype frequencies in the samples were set at [p11, p12, p21, p22] = [0.36, 0.24, 0.24, 0.16]. Score test results were shown

Full size image

With the simulated data, we also evaluated the estimation bias for all the parameters \(\left(\beta ,{\beta }_{G},\right)\) estimated from the Stat-POE model. Table 1 shows that the estimation of all genetic effects achieved higher accuracy when sample size increased. Interestingly, the estimation of the covariate coefficient \(\beta \) and over-dispersion parameter \(\phi\) was not notably affected by the sample sizes. Also, the estimation of genetic effects was not obviously affected by the value of the over-dispersion parameter. These results revealed the accurate and robust estimation of the covariates and over-dispersion parameters determined using the Stat-POE model. Moreover, large sample sizes and small over-dispersion ensured better overall performance of the proposed methods.

Table 1 Simulation results with different sample sizes
Full size table

We observed the global trend of the type I error approaching the nominal level for all tests of both Stat-POE and Func-POE methods when sample size increases. The overall type I error rate of the LRT was closer to the nominal level than were the rates for the score and Wald tests (Table 2). Although there were slightly inflated false positives in detecting genetic effect and POEs when sample sizes were small, the type I error rates were close to nominal levels for relatively large sample sizes. Also, the score test achieved approximately equivalent performance with the LR tests given large sample sizes (for example, when ϕ = 0.5, N = 500). Notably, the type I errors for detecting the genetic effects was comparable between the Stat-POE and Func-POE models in most scenarios.

Table 2 Type I error of the methods in detecting genetic effects
Full size table

Real data application to HapMap parent–child trio data

Using 30 children of the family trios from the HapMap project, we applied the proposed Stat-POE methods to estimate the additive and imprinting effects for 22 genes with previous evidence of imprinting. These selected genes were identified as imprinted genes using 296 phased trios from the 1000 Genomes Project and the Genome of the Netherlands participants (Jadhav et al. 2019).

With the proposed Stat-POE method, we identified 33 significant cis-eQTLs (with adjusted p values in additive effects < 0.05) for seven genes (LPAR6, RB1, PXDC1, IGF1R, AC069277.2, IGF2BP3 and SNRPN) (Supplementary Table 2). Among them, most candidate cis-eQTLs presented maternal expression pattern in regulating the gene expression. In addition, we identified six genes with significant imprinting effects, which were LPAR6, PER3, RB1, PXDC, IGF1R and IGF2BP3 with adjusted p values < 0.05 (Table 3). Among the significantly imprinting genes, the gene expression of LPAR6 and IGF1R had significant regulation from the candidate cis-eQTLs rs11633209, rs728075 and rs7329291 in additive effect (adjusted p values = 1.96 × 10–66, 3.57 × 10–64 and 3.57 × 10–64). Interestingly, we also discovered two novel genes that presented significant dominance effect in gene expression (Table 4), including RB1 from multiple candidate cis-eQTLs (adjusted p value = 3.02 × 10–80) and IGF1R from SNP rs4965238 (adjusted p value = 1.37 × 10–67). Among the identified genes presenting dominance effect in eQTL mapping, the RB1 gene located on chromosome 13 was a tumor suppressor gene, the mutation inactivation of which has been found to be the cause of human cancer (Chinnam and Goodrich 2011). It was also found to be an imprinting gene earlier in 2009 (Kanber et al. 2009). Interesting, IGF1R was the only gene that presented both dominance effect and imprinting effect from the candidate cis-eQTL rs4965238 (Table 4).

Table 3 A list of genes with potential imprinting effects (p values < 0.05)
Full size table
Table 4 A list of genes with potential dominance effects (p values < 0.05)
Full size table

In conclusion, our real data application validated several existing imprinting genes. Additionally, we mapped candidate eQTLs for these imprinted genes using our proposed methods. More interestingly, we discovered that a few genes presented significant dominance effect which might be involved in tumorigenesis.

Discussion

This article stands on recent advances in genetic modeling for carrying out new methodological developments to the aid of the analysis of eQTL mapping with genetic imprinting detection. We developed two statistical methods. The Stat-POE model provides a solution that allows for additive-by-dominance genetic effects for cis-eQTL mapping with RNA-seq data. The Func-POE is an alternative method which focuses on biological interpretations. We demonstrated the desirable power and preserved Type I error of the methods in most scenarios with un-biased estimation of the genetic effects and over-dispersion of the RNA-seq data. The application to the HapMap project validated previously reported imprinting genes and discovered significant cis-eQTLs for these imprinted genes. More interestingly, we identified two novel imprinting genes with significant dominance effect.

In the parameter estimation and hypothesis testing, we implemented the Stat-POE and Func-POE with three different tests, including the LRT, score and Wald tests. Among these three tests, the score and Wald tests are known to have poorer performance and less reliable results with small sample sizes by comparing to LRT (Table 2). From theory and our simulations (results not shown), the score test usually outperformed the other two in statistical power. To achieve a well-balanced Type I error and statistical power in detecting these genetic effects, we will suggest users to use the LRT when sample sizes are relatively small and score test otherwise.

We developed two imprinting effect models with RNA-seq data, including the Stat-POE model and Func-POE model both of which are appropriate for estimation of the genetic effects. The commonly used functional approach (i.e., Func-POE) is based on the observed genotype instead of the population frequencies therefore the results from which are easier to interpret. The disadvantage is that the functional model generates non-orthogonal estimates of regression coefficients when dominance components are included in the model. In contrast, parameters from application of the Stat-POE model describe the variance components rather than allele substitution effects, so may be seen to be having a less clear interpretation but it renders more straightforward model selection. Indeed, these two models can be transformed to each other in the estimates of the parameters, but the test statistics varied in formulas. (Xiao et al. 2013 Text S5). As a result, the orthogonal model is presenting better power than the functional model especially in detecting additive effect. To be noted, since the parameters are different biological properties and interpretations in the two models, the comparison of these two models should be understood in terms of the comparison of testing a genetic effect and/or the imprinting effects when the effect is existing, instead of the concrete values of the parameters. For example the orthogonal model presented increased power than the functional model when additive effect exists (Xiao et al. 2014).

Several alternative imprinting effect testing methods have been described in previous literature (Álvarez-Castro 2014; Palowitch et al. 2018; Wolf and Cheverud 2009; Xiao et al. 2013). The Xiao et al. (2013) was indeed the initial attempt of our reseach team to implement imprinting effect detection with a one-locus orthogonal model which provided both statistical (i.e., population-referenced) and functional (which are not population-referenced) formulations of the genetic effects. This imprinting model was shown to be orthogonal in certain conditions. Then Álvarez-Castro (2014) provided a formula similar to the model in our method (Eq. 3) for imprinting detection which was claimed to be fully orthogonal. However, their model in formula (10) was not completely accurate (might be due to typo or some other reasons). The developments by Wolf and Cheverud (2009) proposed a two-locus model that included epistatic interactions involving imprinting effects. They also provided a model (Wolf and Cheverud 2009, Appendix 2) with an explicit imprinting parameter that is orthogonal under the Hardy–Weinberg proportions. Nevertheless, none of the above methods provides explicit expressions for performing variance decompositions or addressing the hypothesis testing problems. In a more recent article of Palowitch et al. (2018), eQTL analyses were performed using a non-linear regression model for log-transformed expression, termed ACME (Additive Contributions, Multiplicative Error), assuming additive allelic effects on the original expression scale. Their count-based modeling approach through some transformations of expression is different from the traditional Poisson or NB generalized linear models for the count-based RNA-seq data. Also, it lacks the ability to test the imprinting effect and overdispersion of the RNA-seq data hence it cannot be fairly compared to our methods. It is worthwhile noticing that none of the above methods have been implemented the coding to be used with RNA-seq data for eQTL mapping.

This is the first time the performance of the natural and orthogonal (NOIA) models have been evaluated in RNA-seq data analyses. The NOIA method was proposed by Alvarez-Castro et al. in 2007 (Alvarez-Castro and Carlborg 2007) which was composed by a one-locus functional model and statistical/orthogonal model, with which we have extensively implemented to the estimation of statistical epistasis, gene-environmental interactions and imprinting effect in genotype–phenotype mapping for quantitative traits and qualitative traits (Ma et al. 2012; Xiao et al. 2013, 2014). It has been shown that the one-locus statistical model was orthogonal independent of whether HWE was satisfied or not for quantitative trait analysis (Alvarez-Castro and Carlborg 2007). The conclusion can be straightforwardly extended to the NB or Poisson regressions in our study after implementation of the imprinting effect detection. Through implementing the developed methods in RNA-seq data, we provide new insights into eQTL mapping with powerful accurate estimation of genetic effects, covariates and over-dispersion parameters, especially that the proposed Stat-POE model allows uncorrelated estimation of the genetic effects.

We also investigated the parameter estimation and hypothesis testing of the two models with NB regression and Poisson regression assumption of the read counts for different application scope (results not shown). NB regression is suggested when the over-dispersion is relatively large and Poisson regression is suggested to be used for small over-dispersion. For observed RNA-seq data with excessive zeros, for example, when estimated \({\mu }_{{\overrightarrow{A}}_{1}{A}_{2}}\) or \({\mu }_{{\overrightarrow{A}}_{2}{A}_{1}}\) in Eq. (5) equals to zero, we suggest adding one to the read counts to satisfy the hypothesis of data distribution. Fitting a zero-inflated Poisson regression is another promising direction to address such problems, which warrants a future research goal.

Still, this study has several limitations. First, family data such as trios are needed to obtain the genotypes of heterozygotes in the offspring. Imputation-based approaches might be useful for haplotype-based inference of the phase of the heterozygotes, such as BEAGLE (Browning and Browning 2009). Second, borrowing information from the whole samples will allow for more accurate modeling of the RNA-seq data. A third important direction would be incorporating the testing of allele specific gene expression (ASE) as conducted in Zhabotynsky’s work so that we can extend our work to model both ASE and POE for candidate cis-eQTLs (Zhabotynsky et al. 2019). The decreased cost of RNA-seq technology and future studies in methodology are warranted to achieve a more powerful estimation of decomposed variance from different genetic components.