Abstract
Previous research has shown that null numerosity can be processed as a numerical entity that is represented together with non-null numerosities on the same magnitude system. The present study examined which conditions enable perceiving nonsymbolic (i.e., an empty set) and symbolic (i.e., 0) representations of null numerosity as a numerical entity, using distance and end effects. In Experiment 1, participants performed magnitude comparisons of notation homogeneous pairs (both numerosities appeared in nonsymbolic or symbolic format), as well as heterogeneous pairs (a nonsymbolic numerosity versus a symbolic one). Comparisons to 0 resulted in faster responses and an attenuated distance effect in all conditions, whereas comparisons to an empty set produced such effects only in the nonsymbolic and symbolic homogeneous conditions. In Experiments 2 and 3, participants performed same/different numerosity judgments with heterogeneous pairs. A distance effect emerged for "different" judgments of 0 and sets of 1 to 9 dots, but not for those with an empty set versus digits 1–9. These findings indicate that perceiving an empty set, but not 0, as a numerical entity is determined by notation homogeneity and task requirements.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
A prevailing conception in various models of number representation is that numbers are represented along an ordered continuum of magnitudes, metaphorically referred to as the “mental number line” (e.g., Dehaene, 1992; Gallistel & Gelman, 2000; Verguts et al., 2005). This notion of such a numerical magnitude system is supported by several behavioral and neural effects which are considered markers for numeric representation, including the distance and end effects. The distance effect (Moyer & Landauer, 1967) describes faster responses and fewer errors observed when tasked with comparing numbers that are farther apart than closer together. For instance, responses should be faster for comparing 2 versus 8 (i.e., distance 6) than 2 versus 3 (i.e., distance 1). The end effect describes the phenomenon of faster responses received when comparing magnitudes among number pairs containing the lower or upper end-value in a set, versus comparing non-end-value pairs with the same intrapair distance (Banks, 1977; Leth-Steensen & Marley, 2000). For example, if only single digits are included in an experimental set, then, for any given intrapair distance, comparisons that involve the lower end-value of “1” (e.g., 1 vs. 4) tend to be responded to faster than comparisons utilizing the set’s middle range values (e.g., 4 vs. 7).
The end effect can also characterize responses to comparisons of episodic or semantic end-values. An episodic end-value serves as the smallest or largest member of a given experimental stimuli set during a magnitude comparison task (Pinhas et al., 2015); in such a task, number values are processed intentionally as part of the task demands (e.g., Banks, 1977; Leth-Steensen & Marley, 2000). In contrast, semantic end-values are numbers ‘tagged’ in long-term memory as "the smallest" based on prior life experience, causing them to develop this special status. Such tagging has been shown for 0 and for 1 (in the absence of 0), but not for 2, under conditions of automatic processing (i.e., when number value processing was not required by the task); participants automatically process only numbers typically experienced in daily life as being the smallest end-values (Pinhas & Tzelgov, 2012; Pinhas et al., 2015). It is also relevant to note that the distance and end effects interact, so that distance effects obtained for comparisons to an end-value are usually attenuated relative to distance effects obtained for pairs lacking an end-value (e.g., Leth-Steensen & Marley, 2000; Pinhas & Tzelgov, 2012).
Models of number representation refer to the fact that numbers can be presented in both nonsymbolic forms (e.g., an array of seven dots, a sequence of four tones) and symbolic forms (e.g., spoken or written number words, Arabic digits). However, there is a general dispute in the literature concerning the extent to which form impacts mental representation (e.g., Cohen Kadosh & Walsh, 2009). Some models postulate that symbolic information activates both the verbal and nonverbal codes of the symbol, the latter referring to the quantity the symbol stands for. For example, digit processing has been suggested to activate two systems: the verbal word frame (i.e., name of the number) and the magnitude representation system (i.e., quantity), while both systems activate the visual Arabic digit name form (Dehaene & Cohen, 1995). Nonsymbolic magnitudes are considered to directly activate the magnitude system via a single process and therefore result in faster processing compared to symbolic magnitudes (e.g., Dehaene, 1992; Dehaene & Cohen, 1995).
The mental representation of nonsymbolic quantities is a controversial topic in numerical cognition due to the fact that changing the value of a presented numerosity always changes its perceptual features as well. Therefore, it is debatable whether processing nonsymbolic numerosities is affected by changes in their continuous perceptual features (e.g., total surface area, density) or in the numerical value of the set. Some approaches assume that only perceptual features of nonsymbolic numerical stimuli are processed (Clearfield & Mix, 1999, 2001), while others argue that the stimuli's numerosity is processed as well (Feigenson et al., 2004; Gebuis & Reynvoet, 2011, 2012; Xu & Spelke, 2000). For example, previous developmental studies found that while looking at sets of objects, infants respond to changes in spatial extent (e.g., accumulated surface area and density) rather than changes in the number of objects (Clearfield & Mix, 1999, 2001). However, Xu and Spelke (2000) showed that infants discriminate between nonsymbolic numerosities, which goes beyond the perceptual properties of numerosity. It was further shown that infants’ number discrimination abilities are ratio-dependent, in accordance with Weber’s law. Such ratio dependence is often explained by assuming a logarithmic compression of the numerical magnitude’s representations (e.g., Feigenson et al., 2004). Moreover, recent studies assume that numerical judgments are based on processing both the discrete number of objects, as well as other continuous perceptual features of the stimuli (e.g., Gebuis & Reynvoet, 2011, 2012; Leibovich et al., 2017). This assumption is supported by recent neuroimaging data revealing that both numerical and nonnumerical regions of the brain are activated during a nonsymbolic judgment task (e.g., Leibovich & Ansari, 2017).
Is null numerosity represented as a numerical entity?
Not all researchers agree that zero is represented as a numerical entity, or, in other words, that it is represented as part of the same magnitude system together with other numerosities. For example, Brysbaert (1995) found that the processing time of an integer between 1 and 99 is a logarithmic function of the number magnitude, its frequency, and sometimes the syllable length of the number name. However, reading times for zero were slower than expected by this function, suggesting that the magnitude system is inclusive of integers 1 to 99, while 0 is represented separately. Brysbaert's suggestion is consistent with findings that because zero's parity status is less understood, it is represented separately from the numerical magnitude system (Fias, 2001; Nuerk et al., 2004). However, as mentioned above, we found in our previous research that, similar to 1, 0 is automatically perceived as the smallest end-value of the magnitude system as a byproduct of the end effect (Pinhas & Tzelgov, 2012; see also Pinhas et al., 2015). Similarly, Fischer and Rottmann (2005) found that the distance effect for comparisons to 0 is evident with positive integers, but not with negative integers; they concluded that 0 is represented as the smallest entity of the magnitude system. Furthermore, like other small integers, 0 was associated with the left side of space in a parity judgment task (Dehaene & Changeux, 1993). Notwithstanding, another interpretation of these results may be that 0 is perceived as a unique numerical entity and, therefore, it is represented separately from other numerical entities (Fias, 2001; Nuerk et al., 2004).
Similar to studies testing the symbolic form of null numerosity, we recently found that perceiving the nonsymbolic form of null numerosity as a numerical entity is context dependent (Zaks-Ohayon et al., 2021). In this study, we tested the representation of empty sets contrasted with sets of 1 to 9 dots, using the numerical comparison task. In Experiment 1, we manipulated the task instructions (i.e., "Choose the frame that contains more/less dots") so that participants would have to respond to the empty set and could not ignore it. In Experiment 2, we manipulated the task instructions by presenting different descriptions of the experimental numerical range (i.e., "You will be presented with sets of 0/1 to 9 dots") and participants were asked to choose the frame that contains more dots. The results of both experiments revealed (via end effect) that comparisons to empty sets were responded to faster than comparisons of non-empty sets. Furthermore, both types of comparisons produced distance effects, though they were attenuated for comparisons to empty sets. In Experiment 3, we manipulated the response mode so that two groups of participants responded to target location (using a key press/vocally), while the third group responded vocally to target color. Comparisons to empty sets resulted in distance effects only when responding to target location, irrespective of the response mode, indicating that triggering the activation of the spatial association between numbers and space is crucial for representing empty sets as numerical entities. Moreover, we established that the distance and end effects are adequate to determine such a representation (Zaks-Ohayon et al., 2021; see also, Pinhas et al., 2015; Pinhas & Tzelgov, 2012).
Children's representation of null numerosity
The understanding of zero in symbolic and nonsymbolic formats has also been studied among infants and children. Wellman and Miller (1986) found that younger children were less successful in a variety of numerical tasks involving zero compared to their performance with other small numbers. The authors suggested that the understanding of zero develops gradually. First, children acquire some familiarity with the name and the symbol of zero. Next, they understand that zero represents a unique numerical value. Finally, zero's relation to other small numbers is realized. Before the last phase, the number 1 is still considered to be the smallest number (however see Bialystok & Codd, 2000). In addition, Wynn and Chiang (1998) found that eight-month-old infants show no numerical expectation about the outcome of an operation that yields a result of zero items, though infants clearly distinguish between different small numbers of objects. However, it was shown that 12-month-old infants point to an empty location in which a desired object is missing, as a way of making an adult understand their request for it (similar to their use of pointing to present objects). The same use of pointing as a way of communicating about absent objects was not found in chimpanzees (Liszkowski et al., 2009).
Furthermore, a study by Merritt and Brannon (2013) examined whether young children understand the concept of null numerosity before acquiring the symbolic concept of “zero”. The authors used a numerical ordering task and found that both children and adults show distance effects for comparisons of dot arrays (varying in magnitude) with empty sets. Moreover, children aged four years old, who had not yet acquired the concept of zero, could not place it in its correct order but did show a distance effect for comparisons to empty sets. Merritt and Brannon concluded that this result was due to the fact that children represent null numerosity on the same mental continuum of non-null numerosities.
Nonhuman animals representation of null numerosity
Additional research provides evidence suggesting that nonhuman animals can also represent the numerical entity of zero. A study by Biro and Matsuzawa (2001) demonstrated that a chimpanzee that had previous training with the digits 1–9 was able to further acquire the representation of 0, although after the learning phase, there was still confusion between 0 and 1. In addition, grey parrots (e.g., Pepperberg, 2006; Pepperberg & Gordon, 2005) and Rhesus monkeys (Merrit, Rughani, & Brannon, 2009) demonstrated understanding that non-empty sets represent larger quantities than empty sets. For example, Merritt et al. (2009) presented Rhesus monkeys with a nonsymbolic magnitude (i.e., dot array) comparison task with pairs of stimuli generated from the numerosities zero (presented as an empty set) to nine. A distance effect was found for comparisons of dot arrays with empty sets, consistent with the notion that a null numerosity is represented as the smallest end-value of the magnitude system. Additionally, a recent study by Howard et al. (2018) found that after a learning period, honeybees could judge an empty set was "less" than a set with one object (i.e., one dot).
Moreover, two other studies performed single-cell recordings of the ventral parietal area and prefrontal cortex of monkeys (i.e., Macaca fuscata and Macaca mulatta) while they performed numerosity matching tasks that included empty sets and nonsymbolic numerosities (1–4) (Okuyama et al., 2015; Ramirez-Cardenas et al., 2016, see also Beran, Perdue, & Evans, 2015) and reported selective activations in response to empty sets. Accordingly, selective neurons coded empty sets in two different forms: 1) a discrete activation pattern of "empty set" versus "non-empty set", showing increased activity selective to empty sets and only weak activity to other numerosities, and 2) a continuous pattern of activation that peaked with empty sets and showed a gradual decrease to successively larger numerosities. This latter type of coding confirms that null numerosity can be responded to in relation to the non-null numerosity within the pair, possibly reflecting an analog comparison process that results in a distance effect (Okuyama et al., 2015; Ramirez-Cardenas et al., 2016).
The present study
In consideration of the previous findings regarding the representation of null numerosity, the main purpose of the present study was to explore under which conditions nonsymbolic (i.e., empty set) and symbolic (i.e., Arabic number “0”) formats of null numerosity are perceived as a numerical entity, as contrasted with other numerical entities. Because our main focus was determining the numeric status of null numerosity, we chose to contrast it with other numerosities while forgoing further examination of the well-established and well-studied relations between other numerosities. We hypothesized that if null numerosity is perceived as a numerical entity, then it should be represented on the same mental scale together with other non-null numerical entities. Further, similar to our previous studies on null numerosity, we used the presence of the distance and end effects in comparisons to null numerosity as a marker for numeric representation (Pinhas & Tzelgov, 2012; Pinhas et al., 2015; Zaks-Ohayon et al., 2021). Accordingly, we designed three experiments testing the mental representation of an empty set as contrasted with 0. In Experiment 1, participants performed magnitude comparisons between pairs of symbolic, nonsymbolic, and heterogeneous (nonsymbolic vs. symbolic) numerosities. In Experiments 2 and 3, participants performed same/different judgments on heterogeneous pairs of numerosities. This allowed us to directly examine whether empty sets are perceived as 0 by forcing participants to decide if both of the stimuli (i.e., empty set and 0) represent the same numerical value.
Based on prior studies, we predicted end effects for null numerosity comparisons (i.e., empty set or 0). That is, we predicted faster responses for comparisons involving null numerosities than for comparisons involving non-end numbers. The presence of end effects for null numerosity comparisons would indicate that null numerosity differs from non-null numerosity; however, to examine whether this difference indeed stems from null numerosity’s ordinal status, and not from its perceptual (or other) prominence, the distance effect can be utilized. We predicted attenuated distance effects in pairs that contained an empty set or 0, indicating that both nonsymbolic and symbolic notations of null numerosity are perceived as the smallest end-value of the magnitude system. Alternatively, if no distance effects would be obtained for comparisons to null numerosity, it would presumably suggest that null numerosity is perceived as “nothing,” and is not processed as a numerical entity.
It is well established that the context in which numerical entities are presented may affect their representation. Context can be modified by manipulating the numerical range (e.g., Pinhas et al., 2013), task instructions (e.g., Bächtold et al., 1998), or the spatial position of the stimuli (e.g., Fischer et al., , 2009, 2010; Notebaert et al., 2006; Shaki & Fischer, 2008). In a related vein, given the perceptual differences between an empty set that is presented as “nothing” (i.e., an empty frame), and the digit 0, which is presented as “something” (i.e., a symbol), the presence of distance effects for comparisons to null numerosity may depend on the format in which null numerosity is presented. In light of these factors, we hypothesized that manipulating the homogeneity of the format of the stimuli set may be crucial for perceiving an empty set as the numerical entity of 0. Accordingly, in conditions in which the stimuli set was homogeneous (i.e., symbolic or nonsymbolic stimuli), null numerosity (empty set or 0) was expected to be perceived as a numerical entity of an absence of a quantity, and comparisons to null numerosity were expected to produce distance effects. In contrast, under heterogeneous stimuli presentations (i.e., presenting a symbolic and a nonsymbolic stimulus), we conjectured that variability in the stimuli’s notation would presumably increase the perceptual dominance of empty sets. As digits are expected to be compared to framed dot arrays under such conditions, when a digit is contrasted with an empty frame, the latter is referred to as “nothing,” whereas when 0 is compared to sets of dots, we anticipated it would be considered as a numerical entity because two frames that contain “something” are being compared. Hence, comparisons to 0, but not to empty sets, were predicted to result in distance effects under a notation heterogeneous context.
Experiment 1
This experiment examined the conditions that allow perceiving null numerosity as a numerical entity represented on the same mental scale as other non-null numerosities. For that purpose, participants performed a magnitude comparison task in three different blocked formats: (a) nonsymbolic (i.e., pairs of sets of dots and pairs of a set of dots vs. an empty set), (b) symbolic (i.e., pairs of digits including comparisons to 0), and (c) mixed (i.e., a pair of a set of dots vs. a digit and an empty set vs. a digit). Thus, in each block, participants were presented with both comparisons to null numerosity (i.e., an empty set or 0, depending on the block’s format) and comparisons between non-null numerosities. We predicted that comparisons to null numerosity would respond to faster than comparisons of non-null numerosities across notation blocks, consistent with the end effect. In addition, we predicted that the distance effect would be attenuated for pairs including an empty set or 0. Such patterns of results across formats would indicate that both nonsymbolic and symbolic notations of null numerosity are perceived as the smallest end-value of the magnitude system. Moreover, due to the complexity of comparisons in the heterogeneous block (i.e., the mixed block), which required participants to compare two different natured pair members, we expected that response latencies would be longer in this block compared to the homogeneous blocks. Finally, we expected that an empty set would not be perceived as numerical entity under the heterogeneous block, and, thus, comparisons between empty sets and digits would not result in a distance effect.
Methods
Participants Twenty-four students from Ben-Gurion University of the Negev (13 females; aged 22–28 years old, Mage = 24.00 years) participated in the experiment in partial fulfillment of course requirements. All participants provided written informed consent, and the study protocol had been previously approved by the university’s Institutional Review Board, prior to beginning the experiment.
Apparatus and stimuli The experiment was conducted using Intel core i5 computers with 17-inch monitors. Stimuli were generated using MATLAB R2010 software (The MathWorks Inc., Natick, MA) and presented using E-prime 2 software (Schneider, Eschman, & Zuccolotto, 2002). The stimulus set included pairs of numerical values from 0 to 9, presented in a symbolic fashion or a nonsymbolic fashion, which consisted of sets of black dots (see Fig. 1).
Examples of stimuli (null numerosity and other comparisons) in each of the blocks presented in Experiment 1
The location of the dots in the frame and their diameter varied between pictures. Each pair was generated in three congruency conditions to prevent numerical discrimination on the basis of visual cues. The conditions were: (1) congruent, in which the larger numerosity consisted of the larger surface area, (2) incongruent, in which the larger numerosity consisted of the smaller surface area, and (3) neutral, in which the surface area was identical for both numerosities. All pictures were sized 3 × 3 inches, framed in black with a grey background. Other visual properties—area extended by a stimulus, dot diameter, and dot density—were randomized (for further explanation see Gebuis & Reynvoet, 2011). The symbolic stimuli were black digits written in Times New Roman font, sized 0.5 × 0.5 inches, and presented in the middle of the picture frame.
Following our previous research on zero (Pinhas & Tzelgov, 2012; Pinhas et al., 2015), the distance effect in this study was examined by providing comparisons of null numerosity (i.e., empty set or 0) and non-null numerosities (i.e., sets of 1 to 9 dots), with no regard to specific non-null values (therefore, processing differences between non-null numerosity values were not examined). In distinction to the procedure by which distance effects are usually tested by averaging all the data for each intrapair distance level (e.g. responses to the pairs (2 5), (3 6), and (6 9) can all be averaged to an intrapair distance of 3), comparisons involving null numerosity utilize only one number at each intrapair distance level. For example, comparing null numerosity and the numerosity of 3 results in the intrapair distance of 3. To contrast comparisons involving null numerosity to comparisons involving non-null numerosities, our study methodology designed the latter to follow the same logic, with only one pair fitting each intrapair distance level (i.e., “pure comparisons”, Pinhas & Tzelgov, 2012).
Accordingly, pairs were designed so that each included a smaller numerosity (i.e., 0, 1, 2, or 3), and the intrapair distance to the larger numerosity in the pair was 1 to 6 (24 pairs in total). The proportion between pairs that included null numerosity (18 repetitions × 6 distances = 108 pairs) and those who did not (6 repetitions × 6 distances × 3 congruency conditions = 108 pairs) was 1:1. Each numerosity appeared once on the left and once on the right so that each notation block was comprised of 432 trials, totaling 1,296 trials in the experiment (i.e., 108 pairs × 2 comparison types × 2 right/left side × 3 notation blocks = 1,296 trials).
Procedure The experiment was conducted separately with each participant, who sat on a chair about 50 cm from the computer screen, with their index fingers on the response keys of a standard QWERTY keyboard. They were instructed to respond as quickly and as accurately as possible by pressing the right key (“L”) if the larger numerosity was presented on the right side, and the left key (“A”) if the larger numerosity was presented on the left side. A short rest break was given after every 120 trials. Each trial started with a fixation cross that appeared at the center of the screen for 200 ms, followed by the target stimuli for 500 ms, and then a blank screen that appeared for 500 ms. Trials were randomly ordered. The experiment started with five training trials.
Pairs were presented in three experimental blocks. In the nonsymbolic block, each pair consisted of two sets of dot arrays. In the symbolic block, each pair consisted of two digits. In the mixed block, pairs were made up of a dot array and a digit (Fig. 1). Order of blocks was counterbalanced across participants.
Analysis All data were analyzed using STATISTICA 12 software (StatSoft, 2013). In all the experiments, follow-up analyses (e.g., contrasts, linear trends) were computed according to the non-pooled error term approach for repeated-measures designs (e.g., Keppel, 1991; Maxwell & Delaney, 2017).
Additionally, we conducted t test Bayesian analyses for specific hypotheses (i.e., with 1 df in the F’s numerator), to determine the likelihood of the alternative over the null hypotheses. This was conducted using the “Bayesian t test calculator for accepting and rejecting the null hypothesis” (Rouder, Spekman, Sun, Morey & Iverson, 2009). An increase in the value of the Bayes Factor (BF) reflects an increase in the likelihood of one hypothesis over the other. Typical evidence categories for BF values are: 1–3 = anecdotal, 3–10 = substantial, 10–30 = strong, 30–100 = very strong, > 100 = decisive (Jeffreys, 1961).
Results
The mean reaction time (RT) of correct responses (about 97% of the data) was first submitted to a three-way analysis of variance (ANOVA) with block type (symbolic, nonsymbolic, and mixed), comparison type (comparisons to null numerosity, other comparisons), and distance (1, 2, 3, 4, 5, and 6) as within-participants variables. Block and comparison types were categorial factors, whereas distance was a numerical factor. One participant was excluded due to high error rates. There was a main effect of block type, F(2, 44) = 38.04, MSE = 2,888, p < 0.001, η2p = 0.63 (mean RT of 400 ms, 382 ms, and 422 ms in the symbolic, nonsymbolic, and mixed blocks, respectively). Additionally, responses were faster for comparisons to null numerosity (388 ms) than for other comparisons (416 ms), F(1, 22) = 160, MSE = 1,106, p < 0.001, η2p = 0.87, and there was also a main effect of distance, F(5, 110) = 81.18, MSE = 299, p < 0.001, η2p = 0.78. All two-way interactions were significant: block × distance, F(10, 220) = 7.08, MSE = 157, p < 0.005, η2p = 0.24; block × comparison type, F(2, 44) = 9.05, MSE = 459, p < 0.001, η2p = 0.29; and comparison type × distance, F(5, 110) = 1.76, MSE = 167, p < 0.001, η2p = 0.09.
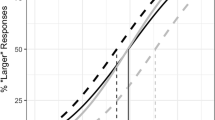
Moreover, as predicted, the three-way interaction of block × comparison type × distance was significant, F(10, 220) = 6.7, MSE = 186, p = 0.005, η2p = 0.31 (see Fig. 2).
Mean RT of correct responses as a function of block, comparison type, and distance in Experiment 1. Vertical bars denote ± standard errors
In light of our hypothesis that an empty set would be perceived differently from 0 under heterogeneous formats, and considering that the heterogeneous block provided two types of comparisons to null numerosity (i.e., digit vs. empty set; set of dots vs. 0), we further deconstructed the triple interaction as follows. First, we analyzed the homogeneous blocks, finding that the linear trends of distance (Pinhas et al., 2012) at each block and pair type combination revealed significant distance effects for both comparisons to 0, F(1, 22) = 42.089, MSE = 551, p < 0.001, η2p = 0.55, and other comparisons, F(1, 22) = 68.351, MSE = 63, p < 0.001, η2p = 0.76, in the symbolic block. In line with our predictions, the former’s distance effect was attenuated compared to the latter’s, as reflected in differences in the effect sizes of the linear trends. Consistently, there was also a significant difference between these two linear trends, F(1, 22) = 13.78, MSE = 148, p = 0.011, η2p = 0.37. A similar pattern emerged in the nonsymbolic block for comparisons to null numerosity, F(1, 22) = 61.39, MSE = 194, p < 0.001, η2p = 0.28, and other comparisons, F(1, 22) = 75.31, MSE = 549, p < 0.001, η2p = 0.77. Again, the two linear trends significantly differed from one another, F(1, 22) = 17.63, MSE = 251, p < 0.001, η2p = 0.43.Footnote 1
Next, we proceeded to examine the heterogeneous block. We separately analyzed the two types of comparisons to a null numerosity in the mixed block: (a) empty set versus a digit, and (b) 0 versus set of dots. A two-way repeated-measures ANOVA with null numerosity format (symbolic, nonsymbolic) and distance (1–6) as within-participants variables on the mean RT of correct responses revealed faster responses for comparisons between a digit with an empty set (396 ms) than for comparisons between a dot array with 0 (427 ms), F(1, 22) = 93.4, MSE = 699, p < 0.001, η2p = 0.82. Furthermore, the main effect of distance was significant, F(5, 55) = 41.7, MSE = 198, p < 0.001, η2p = 0.78. In addition, a significant interaction between null numerosity format and distance, F(5, 110) = 38.6, MSE = 365, p < 0.001, η2p = 0.65, indicated significantly different linear patterns for comparisons between 0 and a set of dots than an empty set and a digit, F(1, 22) = 41.41, MSE = 1,161, p < 0.001, η2p = 0.68, BF10 = 5,401 (see Fig. 3). Hence, the Bayes factor of this difference was decisively (i.e., 5,401 times more likely) in favor of the alternative hypothesis, indicating that the distance effects obtained for comparisons to 0 and to empty sets in the mixed block differed. This was contrary to the null hypothesis, according to which both observations of the distance effects belong to the same distribution. Moreover, an additional follow-up linear trend analysis on the interaction revealed that while there was a significant distance effect for comparisons between 0 and a set of dots, F(1, 22) = 25.54, MSE = 440, p < 0.001, η2p = 0.54, BF10 = 601, there was no distance effect for comparisons between an empty set and a digit, F(1, 22) = 0.976, MSE = 699, p = 0.751, BF01 = 3.02. Overall, these findings seem to indicate that under heterogeneous conditions, the representation of empty sets differs from the representation of 0.
Another interesting finding was that comparisons between 0 and 1 in the symbolic condition, as well as comparisons between 0 and 1 dot in the mixed condition, elicited substantially longer average RTs (480 ms) than comparisons of other adjacent quantities (380 ms), suggesting that such comparisons involve a considerable cognitive load.
Discussion
Consistent with our predictions, the results of Experiment 1 showed that in format-homogeneous pairs, comparisons to null numerosity (presented as 0 or an empty set) produced shorter RTs, consistent with the end effect. In addition, comparisons to null numerosity in format-homogeneous pairs resulted in an attenuated distance effect. Together, the end and distance effects, which serve as indicators of numeric processing (Pinhas & Tzelgov, 2012; Pinhas et al., 2015; Zaks-Ohayon et al., 2021) and were found for the homogeneous blocks, appear to indicate that null numerosity was perceived as the smallest end-value in the set, under these conditions. Alternatively, it may be argued that the attenuation of the distance effect in comparisons to null numerosity is less attributable to the perception of null numerosity as a numeric entity, but rather to the sole activation of the non-null numerosity within the pair, which in such type of comparisons corresponds to the intrapair distance. However, this argument can be refuted: if only the non-null numerosity within the pair was activated, then RTs should have increased with the increase in the non-null numerosity, confirming the size effect (e.g., Moyer & Landauer, 1967; Pinhas et al., 2010; Verguts et al., 2005), and reflecting the opposite pattern obtained for the distance effect. Hence, the distance effects obtained in comparisons to null numerosity presumably reflect the activation and comparison of two numerical entities.Footnote 2
As to the findings of the mixed block, as predicted, comparisons of 0 with dot arrays resulted in a distance effect, whereas the only condition in which comparisons to null numerosity did not produce a distance effect was when an empty set was compared with a digit. Therefore, the results of Experiment 1 suggest that format-homogeneity is important for perceiving an empty set as 0. In such conditions, comparing two stimuli with the same format (i.e., nonsymbolic/symbolic) is relatively easy because it does not require an additional "translation" from one format to another. However, in the mixed block trials, participants were exposed to both nonsymbolic and symbolic numerosities. Consistently, RTs were longer in the mixed block than in the two homogeneous blocks, suggesting a higher level of difficulty in the former. Still, format-heterogeneous comparisons of an array of dots with 0 produced a distance effect, meaning that the translation from one numerical format to the other occurred. In contrast, it seems that in format-heterogeneous comparisons of an empty set to digits, such translation was not applied, as indicated by the lack of a distance effect in such pairs. This difference suggests that when a digit was compared to an empty set, the empty set was perceived as “nothing”. Another possible explanation for the lack of a distance effect in comparisons between an empty set and a digit in the mixed block may be attributed to a perceptual strategy of “if the pair includes an empty set, then choose the other stimulus”. However, we believe that this explanation is unlikely because if so, then such a strategy should have also been applied in the case of comparisons to empty sets in the homogeneous blocks (which produced distance effects). Accordingly, taken together the findings of Experiment 1, format homogeneity seems crucial for perceiving an empty set as a numerical entity that can be represented on the same scale as other non-null numerical entities, similar to 0.
Experiment 2
It was previously argued that distance effects might reflect decision-making processes rather than numerical magnitude representations (e.g., Van Opstal et al., 2008). Therefore, in Experiments 2 and 3, we aimed to test whether the differences obtained between the two formats of null numerosity in Experiment 1 would be replicated with another paradigm. Moreover, previous studies revealed distance effects for both numerical and non-numerical comparisons (e.g., Cohen Kadosh et al., 2008). Hence, in Experiments 2 and 3, we used the same/different task, thought by some researchers to directly address numerical magnitude representations (e.g., Defever, Sasanguie, Vanderwaetere, & Reynvoet, 2012; Dehaene & Akhavein, 1995; but see Cohen, 2009).
The same/different paradigm consists of a simultaneous presentation of two stimuli and the task to determine whether they are identical in a pre-specified stimulus dimension. For instance, in a study by Ganor-Stern and Tzelgov (2008), the digits differed in their numerical values, as well as in their physical size (given the use of different symbolic notations). The results revealed distance effects in both numerical and physical same/different judgments, indicating that the numerical values were processed automatically (i.e., even when their processing was task-irrelevant). These findings are consistent with a previous study by Dehaene and Akhavein (1995), showing an automatic processing of number values in same/different physical and numerical judgments of pairs of digits and number words.
In Experiment 2, participants performed the same/different task with format-heterogeneous pairs that included a dot array and a digit or an empty set and a digit. They were asked to determine whether the two stimuli were numerically the same or different. Cohen (2009) postulated that when using the same/different task with homogeneous Arabic numbers, participants may respond to the visual similarity of the digits rather than to their numerical values. However, here, we used only mixed-notation stimuli, therefore, responses could not be attributed to visual similarity. We predicted that pairs with different numerical values would be more easily responded to than pairs with the same numerical value (e.g., Cohen, 2009; Dehaene & Akhavein, 1995; Ganor-Stern & Tzelgov, 2008). Moreover, we were particularly interested in responses to pairs that contained 0 and an empty set because they capture a participant’s answer to the question "Do 0 and an empty set represent the same numerical value?" If the results would reveal that responses to these pairs produce similar patterns as responses to other “same” pairs, it would imply that an empty set is represented as 0. Otherwise, it would suggest that under this context, an empty set is not represented as equivalent to 0.
Methods
Participants Fifty students from Ariel University (40 females; aged 20–26 years old, Mage = 23.46 years), randomly assigned to two equally sized groups, participated in the experiment for partial fulfillment of course requirements. All participants provided written informed consent, and the study protocol had been previously approved by the university’s Institutional Review Board, prior to beginning the experiment.
Apparatus and stimuli The stimulus set composed of heterogeneous pairs and was identical to the heterogeneous pairs used in the mixed block of Experiment 1. For “same” pairs, null numerosity was presented as an empty set and paired with a frame that contained the digit 0. Similarly, “same” pairs were generated for all other numerosities from 1 to 9, totaling 10 pairs. Each “same” pair contained two stimuli that varied in notation (nonsymbolic versus symbolic), but had the same numerosity. As for “different” pairs, which contained two stimuli that varied both in notation and numerosity, four different types of comparisons were generated in each block: (1) comparisons to null numerosity (i.e., represented by an empty set or 0, compared with the numerosities 1–6); (2) comparisons to one (represented by a single dot or 1, compared with the numerosities 2–7); (3) comparisons to two (represented by a pair of dots or 2, compared with the numerosities 3–8); and (4) comparisons to three (represented by a triad of dots or 3, compared with the numerosities 4–9). Thus, all “different” pairs produced the intrapair distance of 1 to 6. Each “different” pair was generated twice, differing in the notation of each pair member (e.g., the digit 2 compared to three dots; the digit 3 compared to two dots), creating a total of 48 pairs. The proportion of same and different trials was 1:1. Thus, 24 trials were presented for each same pair (24 repetitions × 10 numerosities = 240 pairs), and five trials for each different pair (5 repetitions × 48 pairs = 240 pairs). There were 960 trials in total, given that each number appeared once on the left and once on the right.
Procedure Participants were assigned randomly to one of two groups. One group was instructed to press the right key (“L”) if the numerosities presented on the screen had the same numerical value, and the left key (“A”) if they had different numerical value. The second group of participants was instructed by an opposite response-rule mapping, that is, pressing the right key (“L”) for a "different" response, and the left key (“A”) for a "same" response. A short rest break was given after every 96 trials. Each trial started with a fixation cross that appeared at the center of the screen for 250 ms, followed by the target stimuli that appeared for 500 ms, followed by a blank screen that did not disappear until a response was received. Finally, an inter-trial-interval (ITI) of a blank screen appeared for 500 ms before the next trial began. Trials were randomly ordered. The experiment started with five training trials.
All other details of the methodology were identical to Experiment 1.
Results
We first contrasted the mean RTs of the correct (93% of the data2) same versus different responses by a t test for dependent samples, revealing significantly faster responses for different (870 ms) than for same responses (1186 ms,), t(98) = -5.624, SD = 193.165, p < 0.001. This result indicates that it was easier for participants to determine the pair members differed from one another numerically than were the same.
Next, RTs in the “different” condition were submitted to a two-way repeated measures ANOVA with comparison type (digit to an empty set, non-empty set to 0, other comparisons) and distance (1, 2, 3, 4, 5, 6) as within-participants variables. The mean RTs of this ANOVA are summarized in Fig. 4a. The results revealed a main effect for comparison type, F(2, 96) = 12.15, MSE = 19,388, p < 0.001, η2p = 0.20. As predicted, planned comparisons demonstrated significantly faster responses for comparisons of empty sets versus digits (818 ms) than for comparisons of 0 versus non-empty sets (903 ms), F(1, 48) = 19.29, MSE = 24,180, p < 0.001, η2p = 0.28, BF10 = 346. However, there was no difference between the two pair types of null numerosity (i.e., empty set, 0) and non-null numerosities (i.e., other comparisons; 861 ms), F(1, 48) = 0.34, MSE = 14,594, p = 0.56, BF01 = 5.489. Moreover, the main effect of distance was significant, F(5, 240) = 3.59, MSE = 24,468, p < 0.005, η2p = 0.12, so that RTs linearly decreased with the increase in the intrapair distance, F(1, 48) = 2.73, MSE = 39,816, p < 0.005, η2p = 0.10. No significant interaction emerged between comparison type and distance, F(10, 480) = 1.03, MSE = 23,487, p = 0.410.
Finally, a third analysis was conducted on "same" responses, using a one-way repeated measures ANOVA with the presented numerosity (1, 2, 3, 4, 5, 6, 7, 8, 9) as a within-participants variable. The effect of the presented numerosity was significant, F(9,432) = 74.94, MSE = 101,549, p < 0.001, η2p = 0.61, demonstrating a significant linear increase in RTs with the increase in the presented numerosity, F(1, 48) = 91.47, MSE = 676,101, p < 0.001, η2p = 0.65 (see Fig. 5A). Moreover, visual inspection of the data revealed that comparisons between 0 and an empty set were slower than the "same" responses to other small numbers. To explore this pattern, we compared the RTs for "same" responses to the numerosities of 0 versus 1. This comparison was significant, F(1, 48) = 7.942, MSE = 8,108, p = 0.016, η2p = 0.13, BF10 = 6.238, possibly suggesting that an empty set was not perceived as a small numerosity, similarly to one, but rather as a unique member of the set.
Discussion
In Experiment 2, we investigated the nonsymbolic and symbolic representations of null numerosity using the same/different task, considered by some researchers to reflect a more direct assessment of the mental representation of numerical magnitudes (e.g., Defever et al., 2012; Dehaene & Akhavein, 1995). We replicated previous data demonstrating faster responses to "same" than "different" numerosities (Cohen, 2009; Defever et al., 2012; Dehaene & Akhavein, 1995 Ganor-Stern & Tzelgov, 2008). Moreover, response patterns to "same" pairs revealed an increase in RTs as a function of the increase in the presented numerosity, with extremely long latencies in the large numbers of the set. Such patterns are consistent with the size effect (e.g., Moyer & Landauer, 1967; Pinhas et al., 2010; Verguts et al., 2005) and resemble the process of counting, indicating that participants used counting to validate their judgments. Another support for this claim could be the difference in the response latencies between same and different judgments. While determining that the pair members were numerically different was a relatively fast process, the determination that they were the same took longer perhaps due to a strategy of counting to validate the response.
Most interestingly, "different" responses for comparisons of 0 versus dot arrays were the slowest, whereas those of empty sets versus digits were the fastest. These obtained differences between the two formats of null numerosity (across distance levels) may suggest that in heterogeneous format conditions, 0 is treated differently than empty sets, consistent with the findings in the mixed notation block of Experiment 1, using the numerical comparison task. On the other hand, “different” responses to the various comparison types in Experiment 2 were not modulated by distance. Instead, the distance effect was obtained across all pair types. Given these findings, and the fact that the current design allowed participants an unlimited time to respond, it is possible that their responses reflected decisions based on intentional strategies instead of more intuitive response processes. To test this possibility, Experiment 3 replicated Experiment 2 in all aspects other than limiting the response timeframe to 1000 ms from stimulus onset.
Experiment 3
Methods
Participants Fifty students from Ben-Gurion University of the Negev (29 females; aged 21–29 years old, Mage = 23.30 years), randomly assigned to two equal groups, participated in the experiment for partial fulfillment of course requirements. All participants gave written informed consent, and the study protocol had been previously approved by the university’s Institutional Review Board, prior to beginning the experiment.
Apparatus and stimuli The apparatus and the stimuli were identical to those used in Experiment 2.
Procedure The procedure differed from the one used in Experiment 2 only by limiting the response timeframe to 1000 ms from stimulus onset. Accordingly, each trial started with a fixation cross that appeared at the center of the screen for 250 ms, followed by the target stimuli that appeared for 500 ms, followed by a blank screen that appeared for 500 ms or less if a response was already made. A lack of response was considered as an incorrect response. Participants were able to respond during the 500 ms when the target stimuli were presented on the screen or in the following 500 ms of a blank screen. Finally, an ITI of a blank screen appeared for 500 ms before the next trial began.
Results
Mean RTs of correct responses (91% of the data2) were first submitted to a t-test for dependent samples, to establish a difference between correct "same" and "different" responses. As in Experiment 2, there was a significant difference between RTs for different (671 ms) and same (944 ms) responses, t(92) = -4.67, SD = 198.195, p < 0.001.
Next, responses in the “different” condition were submitted to a two-way repeated measures ANOVA with comparison type (empty set, 0, other comparisons) and distance (1, 2, 3, 4, 5, 6) as within-participants variables. The mean RTs of this ANOVA are summarized in Fig. 4b. As in Experiment 2, the results revealed a main effect for comparison type, F(2, 96) = 13.99, MSE = 18,110, p < 0.001, η2p = 0.22. Planned contrasts confirmed that responses were faster for comparisons to an empty set (572 ms) than for comparisons to 0 (659 ms), F(1, 48) = 26.09, MSE = 19,429, p < 0.001, η2p = 0.35, BF10 = 3,225, whereas no significant difference was found between the two types of comparisons to null numerosity (i.e., empty set, 0) and other comparisons (620 ms), F(1, 48) = 0.004, MSE = 16,791, p = 0.942, BF01 = 6.427. Moreover, a significant main effect of distance, F (5, 240) = 3.03, MSE = 23,668, p = 0.011, η2p = 0.05, revealed the expected linear decrease in RTs with the increase in the intrapair distance, F(1, 48) = 3.23, MSE = 37,618, p = 0.015, η2p = 0.13. The interaction between distance and comparison type was not significant, F(10, 480) = 1.02, MSE = 21,969, p = 0.434.
Finally, a third analysis was conducted on "same" responses, using a one-way repeated measures ANOVA with the presented numerosity (1, 2, 3, 4, 5, 6, 7, 8, 9) as a within-participants variable. A significant effect for the presented numerosity, F(9, 432) = 26.934, MSE = 3,920, p < 0.001, η2p = 0.61, demonstrated a significant linear increase in RTs with the increase in the presented numerosity, F(1, 48) = 91.47, MSE = 676,101, p < 0.001, η2p = 0.35 (see Fig. 5B). As in Experiment 2, a visual inspection of the data revealed that comparisons between 0 and an empty set were slower than "same" responses to other small numbers. To explore this pattern, we compared the RTs for "same" responses to the numerosities of 0 versus 1. This comparison was significant, F(1, 48) = 8.295, MSE = 676,101, p = 0.018, η2p = 0.15, BF10 = 7.175, possibly suggesting that an empty set was not perceived as a small numerosity, similarly to one, but rather as a unique member of the set.
Discussion
The only difference between Experiments 2 and 3 was limiting participants' response time to up to 1000 ms from stimulus onset. This was done to test whether responses would seem to reflect less calculated processes and/or intentional strategies. However, the emerging picture suggests that though limiting participants’ response time resulted in faster responses overall, the findings of Experiment 2 were fully replicated.
First, the results revealed a difference between same and different pairs in both Experiments 2 and 3, implying it was easier to classify two numerosities as different than as the same. This may be attributed to the fact that it takes more time to confirm similarity than to detect change (Cohen, 2009; Defever et al., 2012; Dehaene & Akhavein, 1995; Ganor-Stern & Tzelgov, 2008). Moreover, similar to the results of the distance effect found with the magnitude comparison task in Experiment 1, it seemed easier to classify different numerical magnitudes as the intrapair distance increased. This pattern may be explained by the increasing representational overlap between numerical magnitudes of close numerosities (e.g., Dehaene, 2003; Gallistel & Gelman, 1992; Moyer & Landauer, 1967; Van Opstal & Verguts, 2011).
Most interestingly, when exposed to pairs that contained different numerosities, the overall latencies (i.e., across distance levels) of the two types of comparisons to null numerosity varied dramatically, with comparisons to an empty set being responded to much faster than comparisons to 0. On the other hand, the distance effect for “different” responses was observed across all three comparison types and was not modulated by the various comparisons. These findings of distance effects in Experiments 2 and 3, which are considered as indicators for numerical representation, imply that under the context of the same/different task, both 0 and an empty set are represented as numerical entities. However, in both experiments, “different” responses to pairs that contained 0 elicited the longest RTs, indicating these were the "hardest" decisions (contrary to the prediction of the end effect) while pairs that contained empty sets had the shortest RTs, as expected by the end effect, indicating these were the “easiest” decisions. This finding demonstrates a differential processing for both types of null numerosity formats. It seems that when exposed to 0, that is, a digit, a full processing of the numerical meaning of the digit symbol needs to take place (Dehaene & Cohen, 1995; Verguts & Fias, 2004, 2008). According to some models of number representation, digits are mentally represented by the quantities with which they are associated. Thus, when exposed to a given digit, it is directly translated into its numerical value (e.g., Dehaene, 1992; Dehaene & Cohen, 1995).
However, in contrast to the mental translation process that occurs for digits other than 0, which all represent a given quantity, in the case of 0, such a translation process may have led to an informational conflict (e.g., Botvinick et al., 2001; Cohen et al., 1990; Entel et al., 2015; Levin & Tzelgov, 2016). Such a conflict may occur because 0 stands for a cardinal meaning of “nothing,” and yet the frame contained a digit; thus, it was not empty. Conflicts usually result in longer RTs, as occurred in “different” trials with 0 in both Experiments 2 and 3. Furthermore, this informational conflict, which is “built into” the notion of a symbol that represents “nothing,” possibly even exceeds in the context of heterogeneous notations in the case when 0 appears together with an empty set. “Different” pairs of empty sets versus digits did not involve any conflicts because “nothing” (i.e., an empty frame) was always compared to “something” (i.e., a non-zero digit), respectively, and thus, they resulted in the shortest latencies. Together, these findings point to the unique case of 0 as a numerical entity.
In both Experiments 2 and 3, responses to pairs containing a digit and a dot array that correspond to the same numerical value resulted in an increased RT with the increase in numerosity. This is consistent with previous findings regarding a size effect (e.g., Moyer & Landauer, 1967; Pinhas et al., 2010; Verguts et al., 2005) or a counting process. Counting is usually characterized by an increase in latency as a function of the increase in the counted number, due to the cognitive load that increases with the requirement to hold more objects in working memory (e.g., Gallistel & Gelman, 1992). Moreover, a subitizing effect is evident in such conditions. Previous studies involving nonsymbolic numerical stimuli demonstrated in enumeration tasks the phenomenon of subitizing, that is, rapid and accurate responses for small numerosities within the range of 1–4 (Kaufman, Lord, Reese, & Volkmann, 1949).
Notwithstanding, the most interesting finding under this condition was that “same” responses to pairs containing 0 and an empty set took longer than “same” pairs of other small numerosities, which is inconsistent with what one would expect according to the size effect. Hence, similar to “different” responses for pairs involving 0, this finding seems to reflect an informational conflict (e.g., Botvinick et al., 2001; Cohen et al., 1990; Entel et al., 2015; Levin & Tzelgov, 2016). It may also imply that the presented context affects the potential connection between 0 and an empty set, and that it determines whether each of these representations of null numerosity would be represented as part of the magnitude system (Dehaene & Changeux, 1993; Fischer & Rottmann, 2005; Pinhas et al., 2015; Pinhas & Tzelgov, 2012).
General discussion
In this study, we examined the conditions that allow representing null numerosity as part of the mental magnitude system using distance and end effects as indicators of numeric processing. To that end, we conducted a series of experiments that could be divided into two parts. In the first part (Experiment 1), we used a magnitude comparison task and manipulated notation homogeneity. We compared the representation of homogeneous pairs of stimuli (i.e., both members of the pair appeared in symbolic or nonsymbolic notation) with that of heterogeneous pairs (i.e., mixed notation). We found that in magnitude judgment tasks, the homogeneity of the stimuli notation is crucial for perceiving null numerosity (i.e., both an empty set and 0) as the smallest entity of the magnitude system. In the second part of the present research (Experiments 2–3), we used same/different judgments with a heterogeneous stimulus set that included only pairs with mixed notations. Overall, “different” responses for pairs containing an empty set were responded to in a dissimilar way than those containing 0, although distance effects were apparent across comparisons of null and non-null numerosities, indicating that both manifestations of null numerosity were represented as part of the numerical magnitude system.
An inconsistency that emerged in the current findings was that notation heterogeneous numerical comparisons (i.e., the mixed block in Experiment 1) which included an empty set, resulted in a null effect for distance, while judgments that involved 0 resulted in a distance effect. In contrast, in Experiments 2 and 3, “different” responses for heterogeneous pairs emerged with distance effects across comparison types, while responses to the various comparison types were not modulated by distance. One possible explanation for this inconsistency could be that, when conducting numerical judgments that require determination of which of two frames contain more dots, a frame that contains nothing represents an empty set while a frame with the digit 0 represents “something”—namely a (null) quantity (Zaks-Ohayon, et.al., 2021). However, when requested to determine whether the frames contained the same or different numerosity, participants were actually forced to represent the empty set in a numerical manner, which in turn resulted in distance effects that were not modulated by the specific comparison type. These findings demonstrate that the task requirements influence numeric processing, mainly in perceptual tasks, such as same/different judgments (e.g., Pinhas et al., 2013; Fischer et al., 2009; Fischer et al., 2010; Notebaert et al., 2006; Shaki & Fischer, 2008; Zaks-Ohayon, et.al., 2021; Ratinckx et al., 2005).
In a related vein, the findings of Experiments 2 and 3, in both the “same” and “different” conditions, demonstrate a distinctive processing for 0 and an empty set. Accordingly, while both a frame that contained 0 and an empty frame were aimed at representing null numerosity, they were not perceived identically. The empty frame had nothing inside of it and it represented null numerosity, so its perceptual and conceptual meanings were compatible; therefore, RTs for “different” trials containing an empty set were faster (consistent with the end effect) and it was easier to decide how to respond to it. In contrast, while the conceptual meaning of 0 was also of null numerosity, the frame was not empty, and it did contain something (i.e., the digit 0), resulting in relatively slower responses for both “same” and “different” trials containing 0. This may be analogous to the informational conflict that occurs in the Stroop effect (e.g., Botvinick et al., 2001; Cohen et al., 1990; Entel et al., 2015; Levin & Tzelgov, 2016). In the classical Stroop task, such an informational conflict refers to the activation of two color names in an incongruent stimulus, leading to longer latencies. Similarly, two different concepts were activated in the case of”0″ presented within a frame: a non-numerical concept of “nothing,” versus a numerical concept of “null numerosity” (i.e., “something”), resulting in longer latencies. This observation may be better understood in light of a previous eye-tracking study, in which it was determined that visual similarity is stronger than semantic similarity in visual search tasks. Findings revealed that in an environment full of distractions, it is more likely to associate two numbers with visual similarity than with semantic similarity (Godwin et al., 2014). Similarly, although the semantic connection between 0 and an empty set may be strong, these two stimuli may have been perceived differently due to their dramatic visual differences.
Moreover, it is possible that due to the fact that number processing involves the activation of different systems that connect the symbolic form, the verbal representation, and the magnitude system (Dehaene & Cohen, 1995), the representation of 0 has a unique status. It has a verbal code (i.e., the word zero) and a symbolic code (i.e., the digit 0), but it is not connected to a certain quantity, but rather, to a lack of it. This model may also explain our findings of longer RTs when responding to 0 than to empty sets because it assumes that nonsymbolic magnitudes are compared analogically, whereas symbolic magnitudes require an additional process of digit-quantity mapping that takes more time.
Overall, the current findings demonstrate the inherent conflict in processing the digit 0 as a number. In addition, they establish the understanding that an empty set is represented differently from 0, and that it can be represented as part of the magnitude system, as indicated by distance and end effects that emerge only under specific conditions. It has been argued that the perception of the concept of zero is hierarchical. Accordingly, when initially exposed, an empty set is perceived as “nothing”. Then, to associate an empty set with “zero”, one must realize that null numerosity could be “something” in a numeric fashion (Nieder, 2016). Consistent with this idea, it is possible that homogeneous presentations, in which all stimuli are presented in the same manner, create a context in which empty sets could be perceived as a numerical entity. In contrast, heterogeneous numerical comparisons of null numerosity (as presented in the mixed block of Experiment 1) lacked the conditions that allowed proceeding from the perception of an empty set as “nothing” to representing it as a numerical entity that corresponds to null numerosity.
Another aspect of the described conflict could be that two correlated (but not identical) features characterize numbers: ordinality and cardinality. Ordinality refers to the location of the number in the magnitude system in terms of its serial position in the ordered numbers sequence. For example, three comes after two and before four (e.g., Fias et al., 2007; Kaufmann, Vogel, Starke, & Schocke, 2009). Whereas the cardinality of a number refers to the actual quantity it represents (i.e., the number of elements in the set; for example, “there are three apples”; e.g., Cooper, 1984; Dehaene & Changeux, 1993), task requirements may lead to mental representations emphasizing ordinality or cardinality. This may apply to the tasks used in the current study. In Experiment 1, we used a magnitude comparison task that is known to focus on the ordinal status of the presented numbers (Fias et al., 2007; Kaufmann et al., 2009). In other words, determining which of two numerosities is larger requires referring to their order. This is enabled through ordering the numerosities and answering the question "which comes first?" without necessarily accessing the information regarding the quantity that each numerosity represents. The ordinal status of 0 and an empty set (perceived as a numerical entity) is identical because both correspond to the smallest numerical entity. Therefore, homogeneous notation conditions that include pairs of stimuli in the same format (be it symbolic or nonsymbolic) result in end effects. Only when the stimuli are in an identical format can the ordinality of both numerosities be directly compared.
Another possible explanation for the different patterns obtained for symbolic and nonsymbolic formats of null numerosity may be that numbers are mentally manipulated to match the required mental operation, as argued in Dehaene's triple-code model (Dehaene, 1992). When conducting magnitude comparisons in nonsymbolic formats, an analogue magnitude representation is used (Dehaene, 1992; Dehaene et al., 2003). However, symbolic formats may differ in different tasks (see Campbell, 1994). Numerical same/different judgments rely on different forms of representation and may require a "translation" of the presented stimuli to a symbolic fashion to determine their similarity (Dehaene, 1992). In this light, it may be that the homogeneous blocks of Experiment 1 encouraged perceiving 0 and empty sets as numerical entities because the judgment was ordinal, and thus, as we previously asserted, ordinal judgments of homogeneous stimuli resulted in distance effects that reflected numerical representations.
In contrast, under heterogeneous notation conditions, it seems that to determine the correct response, accessing the actual value of the given numerosity of both quantities represented was crucial for the judgment (i.e., processing cardinality; Cooper, 1984; Dehaene & Changeux, 1993). Therefore, we believe that the differences in our findings regarding the end effect resulted from the fact that, in homogeneous notation conditions, participants performed magnitude comparisons — a task that focuses on the ordinal status of the stimuli; therefore, comparisons to both 0 and empty sets resulted in end effects. It is noteworthy that when null numerosity was included in the experimental set, it had a given ordered position, similar to all other numerosities. However, when the focus was on the cardinal status, as happened in heterogeneous notation conditions (i.e., mixed block of Experiment 1), end effects were not evident for comparisons to 0 and empty sets. This is probably because, in contrast to all other numerosities, no matter what cardinal value they represented, 0 and empty sets represented null quantity.
Lastly, across all of our paradigms and experiments, comparisons between null numerosity (i.e., an empty set/0) and the numerosity one (i.e., one dot/1) resulted in longer RTs than with other pairs possessing an intrapair distance of 1. This result is consistent with our previous studies on null numerosity (Pinhas & Tzelgov, 2012; Pinhas et al., 2015; Zaks-Ohayon et al., 2021), and may be explained by the fact that both of these numerosities represent semantic lower end-values, causing their comparisons to be the “hardest”.
In conclusion, our findings demonstrate that notation homogeneity and task requirements determine whether an empty set and 0 will be processed as numerical entities, and accordingly, represented as members of the magnitude system, as indicated by the presence of distance and end effects. Future research is encouraged to examine whether other aspects of stimulus homogeneity besides notation allow perceiving null numerosity as a numerical entity.
Ethical approval
Our study was conducted in compliance with ethical standards. All participants gave informed consent to participate in the study, and there was no conflict of interest to declare. No animals were used in the study and all procedures performed involving human participants were in accordance with the ethical standards of the institutional research committee and with the 1964 Declaration of Helsinki and its later amendments, or comparable ethical standards.
Notes
Furthermore, visual inspection of the data in the symbolic block (see Figure 2, left panel) suggests that the distance effect found for comparisons to empty sets may stem from a significant linear decrease primarily explained by the RT difference between an intrapair distance of 1 and all other intrapair distances, instead of reflecting a gradual linear decrease with the increase in the intrapair distance. An intrapair distance of 1 in comparisons to null numerosity corresponds to a comparison between two semantic end-values, that is, 0 and 1. Such a comparison may be conflicting, thus resulting in longer RTs (Pinhas et al., 2015; Pinhas & Tzelgov, 2012). To examine this impression statistically, we reanalyzed both comparisons to null numerosity and other comparisons in each of the homogeneous blocks excluding an intrapair distance of 1. In each of these four conditions, we examined the significance of the linear trend to evaluate the presence of a distance effect. Comparisons to null numerosity resulted in significant linear trends in both the symbolic block, F(1, 23) = 12.48, MSE = 88.21, p = .004, η2p = .27, and nonsymbolic block, F(1, 23) = 71.12, MSE = 61.88, p < .001, η2p = .82. Similarly, significant linear trends were obtained for other comparisons in the symbolic block, F(1, 23) = 8.17, MSE = 206, p < .001, η2p = .09) and nonsymbolic block, F(1, 23) = 54.46, MSE = 371, p < .001, η2p = .48.
The error rate analyses in the same/different tasks of both Experiments 2 and 3 indicated an increase in the error rates as a function of an increase in the presented numerosity for “same” responses. These findings reflect the inaccuracy of the estimation process in larger quantities. “Different” responses rarely resulted in errors and, thus, their analyses did not result in significant effects. Accordingly, the error rate analyses revealed no speed-accuracy trade-offs or significant effects. Therefore, for the sake of brevity, they were not reported.
References
Bächtold, D., Baumüller, M., & Brugger, P. (1998). Stimulus-response compatibility in representational space. Neuropsychologia, 36(8), 731–735.
Banks, W. P. (1977). Encoding and processing of symbolic information in comparative judgments. The Psychology of Learning and Motivation, 11, 101–159.
Beran, M. J., Perdue, B. M., & Evans, T. A. (2015). Monkey mathematical abilities. The Oxford Handbook of Numerical Cognition (pp. 237–257). Oxford, UK: University Press.
Bialystok, E., & Codd, J. (2000). Representing quantity beyond whole numbers: Some, none, and part. Canadian Journal of Experimental Psychology/Revue Canadienne De Psychologie Expérimentale, 54, 117–128.
Biro, D., & Matsuzawa, T. (2001). Use of numerical symbols by the chimpanzee (Pan troglodytes): Cardinals, ordinals, and the introduction of zero. Animal Cognition, 4, 193–199.
Botvinick, M. M., Braver, T. S., Barch, D. M., Carter, C. S., & Cohen, J. D. (2001). Conflict monitoring and cognitive control. Psychological Review, 108, 624–652.
Brysbaert, M. (1995). Arabic number reading: On the nature of the numerical scale and the origin of phonological recoding. Journal of Experimental Psychology: General, 124, 434–452.
Butterworth, B., Zorzi, M., Girelli, L., & Jonckheere, A. (2001). Storage and retrieval of addition facts: The role of number comparison. The Quarterly Journal of Experimental Psychology: Section A, 54, 1005–1029.
Campbell, J. I. (1994). Architectures for numerical cognition. Cognition, 53(1), 1–44.
Campbell, J. I. D., & Metcalfe, A. W. S. (2007). Numeral format and arithmetic rules. European Journal of Cognitive Psychology, 19, 335–355.
Clearfield, M. W., & Mix, K. S. (1999). Number versus contour length in infants’ discrimination of small visual sets. Psychological Science, 10, 408–411.
Clearfield, M. W., & Mix, K. S. (2001). Amount versus number: Infants’ use of area and contour length to discriminate small sets. Journal of Cognition and Development, 2, 243–260.
Cohen, D. J. (2009). Integers do not automatically activate their quantity representation. Psychonomic Bulletin & Review, 16, 332–336.
Cohen, J. D., Dunbar, K., & McClelland, J. L. (1990). On the control of automatic processes: A parallel distributed processing account of the Stroop effect. Psychological Review, 97, 332–361.
Cohen Kadosh, R., Brodsky, W., Levin, M., & Henik, A. (2008). Mental representation: What can pitch tell us about the distance effect? Cortex, 44, 470–477.
Cohen Kadosh, R., & Walsh, V. (2009). Numerical representation in the parietal lobes: Abstract or not abstract? Behavioral and Brain Sciences, 32, 313–328.
Cooper Jr, R. G. (1984). Early number development. In Origins of cognitive skills: The eighteenth annual Carnegie symposium on cognition (pp. 157–192). Erlbaum.
Defever, E., Sasanguie, D., Vandewaetere, M., & Reynvoet, B. (2012). What can the same–different task tell us about the development of magnitude representations? Acta Psychologica, 140, 35–42.
Dehaene, S. (1992). Varieties of numerical abilities. Cognition, 44, 1–42.
Dehaene, S. (2003). The neural basis of the Weber-Fechner law: A logarithmic mental number line. Trends in Cognitive Sciences, 7, 145–147.
Dehaene, S., & Akhavein, R. (1995). Attention, automaticity, and levels of representation in number processing. Journal of Experimental Psychology: Learning, Memory, and Cognition, 21, 314–326.
Dehaene, S., & Changeux, J. (1993). Development of elementary numerical abilities: A neuronal model. Journal of Cognitive Neuroscience, 5, 390–407.
Dehaene, S., & Cohen, L. (1995). Towards an anatomical and functional model of number processing. Mathematical Cognition, 1, 83–120.
Dehaene, S., Piazza, M., Pinel, P., & Cohen, L. (2003). Three parietal circuits for number processing. Cognitive Neuropsychology, 20, 487–506.
Entel, O., Tzelgov, J., Bereby-Meyer, Y., & Shahar, N. (2015). Exploring relations between task conflict and informational conflict in the Stroop task. Psychological Research Psychologische Forschung, 79, 913–927.
Feigenson, L., Dehaene, S., & Spelke, E. (2004). Core systems of number. Trends in Cognitive Sciences, 8, 307–314.
Fias, W. (2001). Two routes for the processing of verbal numbers: Evidence from the SNARC effect. Psychological Research Psychologische Forschung, 65, 250–259.
Fias, W., Lammertyn, J., Caessens, B., & Orban, G. A. (2007). Processing of abstract ordinal knowledge in the horizontal segment of the intraparietal sulcus. Journal of Neuroscience, 27, 8952–8956.
Fischer, M. H., Mills, R. A., & Shaki, S. (2010). How to cook a SNARC: Number placement in text rapidly changes spatial-numerical associations. Brain and Cognition, 72(3), 333–336.
Fischer, M. H., Shaki, S., & Cruise, A. (2009). It takes just one word to quash a SNARC. Experimental Psychology, 56(5), 361–366.
Gallistel, C. R., & Gelman, R. (1992). Preverbal and verbal counting and computation. Cognition, 44, 43–74.
Gallistel, C. R., & Gelman, R. (2000). Non-verbal numerical cognition: From reals to integers. Trends in Cognitive Sciences, 4, 59–65.
Gebuis, T., & Reynvoet, B. (2011). Generating nonsymbolic number stimuli. Behavior Research Methods, 43, 981–986.
Gebuis, T., & Reynvoet, B. (2012). The interplay between nonsymbolic number and its continuous visual properties. Journal of Experimental Psychology: General, 141, 642648-.
Godwin, H. J., Hout, M. C., & Menneer, T. (2014). Visual similarity is stronger than semantic similarity in guiding visual search for numbers. Psychonomic Bulletin & Review, 21, 689–695.
Groen, G. J., & Parkman, J. M. (1972). A chronometric analysis of simple addition. Psychological Review, 79(4), 329–343.
Howard, S. R., Avarguès-Weber, A., Garcia, J. E., Greentree, A. D., & Dyer, A. G. (2018). Numerical ordering of zero in honey bees. Science, 360, 1124–1126.
Jeffreys, H. (1961). Theory of probability . Oxford University Press.
Kaufmann, L., Vogel, S. E., Starke, M., Kremser, C., & Schocke, M. (2009). Numerical and non-numerical ordinality processing in children with and without developmental dyscalculia: Evidence from fMRI. Cognitive Development, 24, 486–494.
Keppel, G. (1991). Design and analysis: A researcher's handbook Prentice-Hall, Inc.
Leibovich, T., & Ansari, D. (2017). Accumulation of non-numerical evidence during nonsymbolic number processing in the brain: An fmri study. Human Brain Mapping, 38, 4908–4921.
Leibovich, T., Katzin, N., Harel, M., & Henik, A. (2017). From “sense of number” to “sense of magnitude”: The role of continuous magnitudes in numerical cognition. Behavioral and Brain Sciences, 40, e164.
Leth-Steensen, C., & Marley, A. (2000). A model of response time effects in symbolic comparison. Psychological Review, 107, 62–100.
Levin, Y., & Tzelgov, J. (2016). What Klein’s “semantic gradient” does and does not really show: Decomposing Stroop interference into task and informational conflict components. Frontiers in Psychology, 7, 249.
Liszkowski, U., Schäfer, M., Carpenter, M., & Tomasello, M. (2009). Prelinguistic infants, but not chimpanzees, communicate about absent entities. Psychological Science, 20, 654–660.
Maxwell, S. E., Delaney, H. D., & Kelley, K. (2017). Designing experiments and analyzing data: A model comparison perspective (3rd ed.). Routledge.
Meck, W. H., & Church, R. M. (1983). A mode control model of counting and timing processes. Journal of Experimental Psychology: Animal Behavior Processes, 9, 320–334.
Merritt, D. J., & Brannon, E. M. (2013). Nothing to it: Precursors to a zero concept in preschoolers. Behavioural Processes, 93, 91–97.
Merritt, D. J., Rugani, R., & Brannon, E. M. (2009). Empty sets as part of the numerical continuum: Conceptual precursors to the zero concept in rhesus monkeys. Journal of Experimental Psychology: General, 138, 258–269.
Moyer, R. S., & Landauer, T. K. (1967). Time required for judgements of numerical inequality. Nature, 215, 1519–1520.
Nieder, A. (2018). Honey bees zero in on the empty set. Science, 360, 1069–1070.
Notebaert, W., Gevers, W., Verguts, T., & Fias, W. (2006). Shared spatial representations for numbers and space: The reversal of the SNARC and the Simon effects. Journal of Experimental Psychology: Human Perception and Performance, 32(5), 1197.
Nuerk, H., Iversen, W., & Willmes, K. (2004). Notational modulation of the SNARC and the MARC (linguistic markedness of response codes) effect. Quarterly Journal of Experimental Psychology Section A, 57, 835–863.
Okuyama, S., Kuki, T., & Mushiake, H. (2015). Representation of the numerosity ‘zero’ in the parietal cortex of the monkey. Scientific Reports, 5, 10059.
Pepperberg, I. M. (2006). Grey parrot numerical competence: A review. Animal Cognition, 9, 377–391.
Pepperberg, I. M., & Gordon, J. D. (2005). Number comprehension by a grey parrot (Psittacus erithacus), including a zero-like concept. Journal of Comparative Psychology, 119, 197–209.
Pinhas, M., Buchman, C., Lavro, D., Mesika, D., Tzelgov, J., & Berger, A. (2015). The neural signatures of processing semantic end values in automatic number comparisons. Frontiers in Human Neuroscience, 9, 645.
Pinhas, M., Pothos, E. M., & Tzelgov, J. (2013). Zooming in and out from the mental number line: Evidence for a number range effect. Journal of Experimental Psychology: Learning, Memory, and Cognition, 39(3), 972.
Pinhas, M., & Tzelgov, J. (2012). Expanding on the mental number line: Zero is perceived as the “smallest.” Journal of Experimental Psychology: Learning, Memory, and Cognition, 38(5), 1187–1205.
Pinhas, M., Tzelgov, J., & Ganor-Stern, D. (2012). Estimating linear effects in ANOVA designs: The easy way. Behavior Research Methods, 44(3), 788–794.
Pinhas, M., Tzelgov, J., & Guata-Yaakobi, I. (2010). Exploring the mental number line via the size congruity effect. Canadian Journal of Experimental Psychology, 64(3), 221–225.
Ramirez-Cardenas, A., Moskaleva, M., & Nieder, A. (2016). Neuronal representation of numerosity zero in the primate parieto-frontal number network. Current Biology, 26, 1285–1294.
Ratinckx, E., Brysbaert, M., & Fias, W. (2005). Naming two-digit Arabic numerals: Evidence from masked priming studies. Journal of Experimental Psychology: Human Perception and Performance, 31(5), 1150.
Robson, D. S. (1959). A simple method for constructing orthogonal polynomials when the independent variable is unequally spaced. Biometrics, 15, 187–191.
Rouder, J. N., Speckman, P. L., Sun, D., Morey, R. D., & Iverson, G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic bulletin & review, 16(2), 225–237.
Schneider, W., Eschman, A., & Zuccolotto, A. (2002). E-Prime: User's guide. Psychology Software Incorporated.
Semenza, C., Grana, A., & Girelli, L. (2006). On knowing about nothing: The processing of zero in single-and multi-digit multiplication. Aphasiology, 20, 1105–1111.
Shaki, S., & Fischer, M. H. (2008). Reading space into numbers–a cross-linguistic comparison of the SNARC effect. Cognition, 108(2), 590–599.
Tzelgov, J., & Ganor-Stern, D. (2005). Automaticity in processing ordinal information. In J. I. D. Campbell (Ed.), Handbook of mathematical cognition (pp. 55–67). Psychology Press.
Van Opstal, F., Gevers, W., De Moor, W., & Verguts, T. (2008). Dissecting the symbolic distance effect: Comparison and priming effects in numerical and nonnumerical orders. Psychonomic Bulletin & Review, 15, 419–425.
Van Opstal, F., & Verguts, T. (2011). The origins of the numerical distance effect: The same–different task. Journal of Cognitive Psychology, 23, 112–120.
Van Opstal, F., & Verguts, T. (2013). Is there a generalized magnitude system in the brain? Behavioral, neuroimaging, and computational evidence. Frontiers in Psychology, 4, 435.
Varma, S., & Schwartz, D. L. (2011). The mental representation of integers: An abstract-to-concrete shift in the understanding of mathematical concepts. Cognition, 121, 363–385.
Verguts, T., & Fias, W. (2004). Representation of number in animals and humans: A neural model. Journal of Cognitive Neuroscience, 16, 1493–1504.
Verguts, T., & Fias, W. (2008). Symbolic and nonsymbolic pathways of number processing. Philosophical Psychology, 21, 539–554.
Verguts, T., Fias, W., & Stevens, M. (2005). A model of exact small-number representation. Psychonomic Bulletin & Review, 12, 66–80.
Wellman, H. M., & Miller, K. F. (1986). Thinking about nothing: Development of concepts of zero. British Journal of Developmental Psychology, 4, 31–42.
Wynn, K., & Chiang, W. (1998). Limits to infants’ knowledge of objects: The case of magical appearance. Psychological Science, 9, 448–455.
Xu, F., & Spelke, E. S. (2000). Large number discrimination in 6-month-old infants. Cognition, 74, B1–B11.
Zaks-Ohayon, R., Pinhas, M., & Tzelgov, J. (2021). On the indicators for perceiving empty sets as zero. Acta Psychologica, 213, 103237. https://doi.org/10.1016/j.actpsy.2020.103237.
Acknowledgements
This study was carried out by the first author under the supervision of the second and third authors in partial fulfillment of the PhD requirements at Ben-Gurion University of the Negev. This research was supported by the Israel Science Foundation Grant no. 1799/12 awarded to the Center for the Study of the Neurocognitive Basis of Numerical Cognition, and Grant no. 1348/18 awarded to MP.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zaks-Ohayon, R., Pinhas, M. & Tzelgov, J. Nonsymbolic and symbolic representations of null numerosity. Psychological Research 86, 386–403 (2022). https://doi.org/10.1007/s00426-021-01515-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00426-021-01515-4