Bursting hierarchy in an adaptive exponential integrate-and-fire network synchronization

Abstract

Neuronal network synchronization has received wide interest. In the present manuscript, we study the influence of initial membrane potentials together with network topology on bursting synchronization, in particular the sequential order of stabilized bursting among neurons. We find a hierarchical phenomenon on their bursting order. With a focus on situations where network coupling advances spiking times of neurons, we grade neurons into different layers. Together with the neuronal network structure, we construct directed graphs to indicate bursting propagation between different layers. More explicitly, neurons in upper layers burst earlier than those in lower layers. More interestingly, we find that among the same layer, bursting order of neurons is mainly associated with the number of neurons they connected to the upper layer; more stimuli lead to earlier bursting. Receiving effectively the same stimuli from the upper layer, we observe neurons with fewer connections would burst earlier.

1 Introduction

The study of brain rhythms and synchronization of oscillatory activity has attracted substantial attention. In the brain, there is abundant experimental evidence of neuronal synchronization, which is associated with cognitive processes, such as visual cognition (Tallon-Baudry 2009), memory formation (Axmacher et al. 2006) and directed attention (Missonnier et al. 2006). Two typical rhythm synchronizations of coupled neurons are spiking synchronization which is equivalent to phase synchronization and bursting synchronization which characterizes temporal patterns between phase onset or offset times across neurons. Bursting synchronization occurs more often than spiking synchronization in neuronal networks (Shi and Lu 2007) and is widely viewed as a hallmark of seizures (Bergman and Deuschl 2002). Moreover, compared to single spikes, bursts of spikes in the nervous system allow neurons to enhance information transmission (Naud and Sprekeler 2018).

Based on some physiological experiments, a number of mathematical models have been developed to describe neuronal activity and bursting in various networks, such as the Hudgkin–Huxley model (Hodgkin and Huxley 1990) and its simplified versions including the leaky integrate-and-fire neuron models, Izhikevich neuron models, and the adaptive exponential integrate-and-fire neuron model (aEIF) (Lu et al. 2020; Izhikevich 2003; Stein 1965; Tsigkri-DeSmedt 2018; Brette and Gerstner 2005; Protachevicz et al. 2018). In particular, the aEIF model has an exponential spiking mechanism combined with adaptation (Brette and Gerstner 2005) which has been shown to predict with high accuracy the spike timing of real pyramidal neurons under noisy current injection (Jolivet et al. 2007; Clopath et al. 2007; Naud et al. 2008). Moreover, based on the aEIF model, Borges et al. (2017) verified that bursting synchronization was more robust than spiking synchronization.

The spike timing within bursts is suggested to be an important factor in providing efficient and reliable information transmission between neurons (Szücs et al. 2005). It has been suggested that spatiotemporal chaos of neurons can be tamed by synaptic strength and results as ordered bursting synchronization (Wang et al. 2007). Here we study the spatiotemporal patterns of burst synchronization by means of an aEIF neural model, in particular the bursting order of neurons and its association with network structures and initial membrane potentials. With a focus on situations where neuronal network coupling advances spiking times of all neurons, we grade neurons into different layers and find bursting hierarchy. Among the same layer, we find that neurons receiving more stimuli (i.e., affected by more connected neurons) from the upper layer would burst earlier; providing that neurons receive effectively the same stimuli from the upper layer, those with fewer connections would bust earlier.

The manuscript is organized as follows: Sect. 2 describes the aEIF neuronal network model. Effects of initial membrane potentials on network synchronization and bursting hierarchy among neurons are investigated in Sect. 3 for regular networks and small-world networks. Conclusion are given in Sect. 4.

2 Neuronal network model

In this section, we first introduce the aEIF model and show parameter space giving bursting and spiking synchronization patterns in Sect. 2.1 and then introduce the network model in Sect. 2.2.

2.1 The aEIF model

The aEIF model is a two-dimensional spiking neuron model given by the following differential equations (Brette and Gerstner 2005):

$$\begin{aligned} \left\{ \begin{aligned} C\frac{\mathrm{d}V}{\mathrm{d}t}&=-g_{L}(V-E_{L})+g_{L}\triangle _{T}\exp \left( \frac{V-V_{T}}{\triangle _{T}}\right) \\&\qquad -w+I,\\ \tau _{w}\frac{\mathrm{d}w}{\mathrm{d}t}&= a(V-E_{L})-w, \end{aligned} \right. \end{aligned}$$

(1)

where parameters are related to physiological quantities: V(t) is the membrane potential, w is the adaptation current, I is the injected current, C is the membrane capacitance, $g_{L}$ is the leak conductance, $E_{L}$ is the resting potential, $V_{T}$ is the threshold potential, $\triangle _{T}$ is the slope factor, $\tau _{w}$ is the time constant and a is the level of threshold adaptation. Due to the exponential term, when the membrane potential V is high enough, the trajectory will quickly diverge. When V(t) reaches the threshold $V_T$, the membrane potential V is reset to $V_{r}$ (referred as the reset potential) and the adaptation current w is increased by b as in Touboul and Brette (2008):

$$\begin{aligned} \left\{ \begin{aligned} V&\rightarrow V_{r},\\ w&\rightarrow w+b. \end{aligned}\right. \end{aligned}$$

In this aEIF model, many different firing patterns could occur including tonic spiking, regular bursting and adaptation (Borges et al. 2017; Touboul 2008). In this manuscript we focus on regular bursting, i.e., the potential converges to a stable spiking cycle containing a specific number of spikes, and there will be a quiescent period before spiking sequence occurs regularly (Touboul 2008). It is known that the injected current I and reset potential $V_r$ play important roles in generating different firing patterns, as the magnitude of I will affect the position of V-nullcline and w-nullcline of Eq. (1) (Borges et al. 2017; Touboul 2008). We mainly consider influence of reset potential $V_{r}$ and injected current I when fixing other parameters $C=281.0~\hbox {pF}, g_{L}=30.0~\hbox {nS}, E_{L}=-70.6~\hbox {mV}, V_{T}=-50.4~\hbox {mV}, \triangle _{T}=2~\hbox {mV}, \tau _{w}=20~\hbox {ms}, a=4~\hbox {nA}, b=0.5~\hbox {nA}$, as used previously (Touboul and Brette 2008).

Fig. 1

a shows the parameter space of the reset potential $V_{r}$ and input current I for two firing patterns. Bursting pattern (type I, $\hbox {CV}\ge 0.5$) and spiking pattern (type II, $\hbox {CV}<0.5$) are separated by the red line. b, c show examples of spiking (type I) and bursting (type II) patterns, respectively, indicated by red stars given in a in each region with CV values indicated in each panel; (b1, c1) show the time evolution of membrane potential (V) with zoom in (b2, c2) for a small time window; (b3, c3) show corresponding trajectories in V-w phase; the trajectory in (b3) converges to a stable spiking cycle containing 3 spikes, while the trajectory in (c3) converges to a limit spiking cycle containing only one spike; red and black dashed curves in (b3, c3) represent the V-nullcline and w-nullcline of Eq. (1), respectively. For visual display of curves in b, c we fix $V_{T}=0~\hbox {mV}$, and set $I=0.66~\hbox {nA}$, $V_r=-44~\hbox {mV}$ in b, and $I=0.70~\hbox {nA}$, $V_r=-57~\hbox {mV}$ in c

We employ coefficient of variation (CV) of neuronal interspike intervals (ISI) (Ostojic 2011) to distinguish different firing patterns:

$$\begin{aligned} \hbox {CV}=\frac{\sigma _{\mathrm{ISI}}}{\overline{\hbox {ISI}}}, \end{aligned}$$

(2)

where $\sigma _{\mathrm{ISI}}$ is the standard deviation of $\hbox {ISI}$ normalized by their mean $\overline{\hbox {ISI}}$. If $\hbox {CV}<0.5$, the neuron fires in a spiking pattern; while $\hbox {CV}\ge 0.5$, it fires in a bursting pattern (Borges et al. 2017). Figure 1a shows two types of firing in $V_r$-I parameter space according to $\hbox {CV}$ given in Eq. (2). When the reset membrane potential $V_r$ is small, spiking patterns occur, whereas when $V_r$ is large, bursting patterns occur (Touboul and Brette 2008; Touboul 2008). Figure 1b, c shows examples of tonic spiking and regular bursting patterns; in the bursting pattern, it fires 3 spikes per burst. With an input current, the neuron keeps a periodic firing pattern after a certain period of adjustment as seen from trajectories shown in Fig. 1b3, c3.

2.2 aEIF neuronal network model and synchronization

Next, we consider the aEIF neuronal network coupled through chemical synapses via the following differential equations (Borges et al. 2017):

$$\begin{aligned} \left\{ \begin{aligned} C\frac{\mathrm{d}V_{i}}{\mathrm{d}t}&=-g_{L}(V_{i}-E_{L})+g_{L}\triangle _{T}\exp \left( \frac{V_{i}-V_{T}}{\triangle _{T}}\right) \\&\qquad -w_{i}+I+(V_{\mathrm{REV}}-V_{i})\sum _{j=1}^{N}M_{ij}g_{j},\\ \tau _{w}\frac{\mathrm{d}w_{i}}{\mathrm{d}t}&=a(V_{i}-E_{L})-w_{i},\\ \tau _{g}\frac{\mathrm{d}g_{i}}{\mathrm{d}t}&=-g_{i}, \end{aligned} \right. \end{aligned}$$

(3)

where $V_{i}, w_i, g_i$ represent the membrane potential, adaptation current and synaptic conductance of neuron i, $V_{\mathrm{REV}}$ is the synaptic reversal potential, $\tau _{g}$ is the synaptic time constant, M is the adjacency matrix with elements $M_{ij}=1$ or 0 depending on whether or not there exists coupling between neurons i and j. The synaptic conductance decays exponentially with a synaptic time constant $\tau _g$. Parameters $\tau _w,a$ and $E_L$ are set as in the single neuron model in Sect. 2.1. We consider the connectivity between neurons is given by excitatory synapses. When $V_{i}$ reaches the threshold $V_T$ for some neuron i, its state variables are updated as follows (Protachevicz et al. 2019):

$$\begin{aligned} \left\{ \begin{aligned} V_{i}&\rightarrow V_{r},\\ w_{i}&\rightarrow w_{i}+b,\\ g_{i}&\rightarrow g_{i}+g_{\mathrm{exc}}, \end{aligned} \right. \end{aligned}$$

(4)

where $g_{\mathrm{exc}}=0.05~\hbox {nS}$ as used previously (Protachevicz et al. 2019) unless otherwise stated.

Equation (3) indicates that in addition to the external input current I, synaptic current is also generated by interactions between neurons. Thus, in a network of N neurons, the total current affecting neuron i reads as:

$$\begin{aligned} I^{i}_{\mathrm{total}}(t):=-w_{i}+I+(V_{\mathrm{REV}}-V_{i})\sum _{j=1}^{N}M_{ij}g_{j}. \end{aligned}$$

We take the same choice of single neuron aEIF model parameters as in Sect. 2.1, fix $\tau _{g}=2.728~\hbox {ms}$, $V_{\mathrm{REV}}=0~\hbox {mV}$ (Protachevicz et al. 2019), and set initial values of $w_i(0)=0~\hbox {nA}$ and $g_i(0)=0~\hbox {nS}$. Moreover, we fix $I=0.66~\hbox {nA}$ which will generate consecutive action potentials, and fix $V_r=-44~\hbox {mV}$. Firing patterns with 3 spikes per burst are robust for the input current I when $V_r>-45~\hbox {mV}$ as seen from Fig. 1a. We use these model parameters throughout the manuscript unless otherwise stated and study the effect of initial potentials $V_i$ on bursting synchronization.

2.2.1 Synchronization parameter

We introduce a synchronization parameter which focuses on the bursting patterns with specifically K spikes per burst. We record the time of each spike and denote as $T_{i}(m)$ for the m-th spike of neuron i. In particular, we denote $T_{i}^{n,j}:=T_{i}(j+K(n-1))$ for the j-th spiking time ($j=1,2,\ldots ,K$) at the n-th burst for neuron i. We then calculate the standard deviation of $T_i^{n,j}$ between neurons and refer to it as $\sigma _{n,j}$, i.e.,

$$\begin{aligned} \sigma _{n,j}:=\sqrt{\frac{\frac{1}{N}{\sum _{i=0}^{N-1}\left( T_i^{n,j}\right) ^2}-\left( \frac{1}{N}{\sum _{i=0}^{N-1}T_i^{n,j}}\right) ^2}{N-1}} \end{aligned}$$

where N is the number of neurons in the network. We then define the synchronization parameter at the n-th burst (with K spikes) as the average of standard deviations $\sigma _{n,j}$:

$$\begin{aligned} \delta (n):=\frac{1}{K}\sum _{j=1}^{K}\sigma _{n,j}. \end{aligned}$$

This synchronization parameter is adapted from Zheng and Lu (2008). For the model parameters we focus, the system generates regular bursts with 3 spikes per burst, i.e., $K=3$. Moreover, when the synchronization parameter $\delta (n)$ stabilizes, we define the stabilized synchronization parameter of the network as $\delta :=\lim _{n\rightarrow +\infty }\delta (n)$. Smaller $\delta$ indicates more clustered spiking times and higher synchronization of neurons.

2.2.2 Spiking time difference

In order to quantify the effect of network coupling on bursting, for each neuron i, we calculate its j-th spiking time $T_i(j)$ in a coupled network with an adjacency matrix M and also the spiking time ${\hat{T}}_i(j)$ in the same scenario except that the network is uncoupled (i.e., the adjacency matrix elements $M_{i,j}=0$). We then calculate the spiking time difference $\hbox {TD}_i(j):=T_i(j)-{\hat{T}}_i(j)$ of each neuron i between coupled and uncoupled networks as sketched in Fig. 2. Note that for spikes in the same burst, their corresponding spiking time difference would be the same. A spiking time difference $\hbox {TD}_i(j)<0$ (resp. $>0$) of one neuron indicates that the network connections advance (resp. delay) the response of its action potential, while $\hbox {TD}_i(j)=0$ indicates that network connections have effectively no effect on its spiking time. Once the firing pattern and corresponding inter-burst period of neurons in the network are stabilized, $\hbox {TD}_i(j)$ keeps constant and we denote this stabilized time difference as $\hbox {TD}_i:=\lim _{j\rightarrow +\infty }\hbox {TD}_i(j)$. We use $\hbox {TD}_i(j)$ and $\hbox {TD}_i$ for the j-th and stabilized spiking time difference of each neuron i, and we drop the subscript i sometimes without ambiguity.

Fig. 2

Illustration of spiking time difference $\hbox {TD}_i(j)=T_i(j)-{\hat{T}}_i(j)$ of a neuron i at its j-th spike where $T_i(j)$ and ${\hat{T}}_i(j)$ are calculated from time series in a coupled (blue) or uncoupled (orange) network for the i-th neuron at its j-th spike, respectively

3 Results

We first investigate in Sects. 3.1 and 3.2 the influence of initial membrane potentials on network synchronization in regular networks where each neuron is connected to an equal number of neighbors. Giving identical initial potentials in a regular network, all neurons would evolve identically the same and thus spike at the same time, thus giving synchronization parameter $\delta =0~\hbox {ms}$. In contrast, for neurons with different initial potentials, different spiking times could occur. With the calculation of spiking time difference, we find bursting hierarchy among neurons. We then examine this bursting hierarchy phenomenon in small-world networks in Sect. 3.3 and discuss the bursting sequence order in relation with degree and initial membrane potentials of neurons within the same layer in the hierarchic structure.

3.1 Influence of initial potentials on synchronization

To investigate the interaction between neurons in the coupled neuronal network, we start with a toy model of two neurons. Without loss of generality, we consider two initial membrane potentials $V_0\ge V_1$. Figure 3 shows the stabilized synchronization parameter $\delta$ for various $V_{0,1}$ and updated synaptic conductance $g_{\mathrm{exc}}$ which effectively gives different coupling strength between neurons.

When the updated synaptic conductance $g_{\mathrm{exc}}=0~\hbox {nS}$, two neurons with initial synaptic conductances $g_{0,1}(0)=0~\hbox {nS}$ are uncoupled. In this case, two neurons evolve independently; the neuron with a larger initial potential would burst earlier. Thus the stabilized synchronization parameter $\delta$ increases with the initial potential difference $V_0-V_1$ as shown in Fig. 3a. For positive $g_{\mathrm{exc}}$, neural interactions may play a role in their bursting synchronization. From Fig. 3a–d we observe that a higher interaction strength $g_{\mathrm{exc}}$ gives a lower stabilized synchronization parameter $\delta$ providing that the difference between the two initial potentials is sufficiently large. Figure 3e shows examples of spiking sequences for two initial potentials $V_0=-60~\hbox {mV}$ and $V_1=-70.6~\hbox {mV}$ (i.e., $V_0-V_1=10.6~\hbox {mV}$) with different $g_{\mathrm{exc}}$; the spiking of neuron 1 is advanced and closer to the spiking of neuron 0 for $g_{\mathrm{exc}}=0.05~\hbox {nS}$ or $0.5~\hbox {nS}$, compared to the uncoupled case ($g_{\mathrm{exc}}=0~\hbox {nS}$), indicating the effect of coupling on bursting synchronization. In this coupled example, neuron 0 spikes first, updates its synaptic conductance via Eq. (4) once its potential reaches the threshold $V_T$, and then the updated synaptic conductance tries to affect neuron 1 to burst via coupling term in Eq. (3); when bursting synchronization is stabilized, bursting time difference between neurons remains constant.

Moreover, we observed in Fig. 3b, c that the stabilized synchronization parameter $\delta$ increases with the initial potential difference $V_0-V_1$ to a saturate value denoted as $\delta _c$. This saturated stabilized synchronization parameter $\delta _c$ is independent of $V_{0,1}$, but is expected to be reduced with increasing coupling strength $g_{\mathrm{exc}}$ as higher $g_{\mathrm{exc}}$ enhance neural synchronization by comparing Fig. 3b, c. Note that spiking of neurons could be evoked by its own dynamics with or without interactions with others. The insets in Fig. 3b, c show that when $V_0-V_1$ is small, $\delta (1)\approx \delta$, i.e., the synchronization parameter at the first burst is close to the stabilized synchronization parameter, indicating that the first bursting state is already close to the stabilized bursting state, and coupling has little effects on its synchronization. In contrast, when $V_0-V_1$ is sufficiently large (where $\delta _c$ is reached), the synchronization parameter at the first burst $\delta (1)$ is much larger than the stabilized synchronization parameter $\delta =\delta _c$ and the larger $V_0-V_1$ the larger $\delta (1)$; with the coupling effect, two neurons evolve to reach stabilized synchronization parameter $\delta =\delta _c$. These results suggest that when $V_0-V_1$ is sufficiently large such that $\delta _c$ is reached, coupling plays a role in synchronization.

To better understand the saturation of the stabilized synchronization parameter, we show in Fig. 3f examples of spiking sequences for three different initial potentials where $\delta$ is saturated giving $g_{\mathrm{exc}}=0.05~\hbox {nS}$. We note that with a larger $V_0$, neuron 0 spikes earlier and affects neuron 1 to spike via the given coupling strength $g_{\mathrm{exc}}$, and the state of locked phase shifts for different $V_{0,1}$ while the relative spiking time difference between two neurons remain the same after the state is stabilized; this gives the same stabilized synchronization parameter $\delta$ for different $V_0$. We remark here that two neurons could be more clustered with a higher coupling strength $g_{\mathrm{exc}}$ as seen from Fig. 3e. Moreover, by the definition of synchronization parameter, in this two-neuron model, with equal spiking time difference of three spikes in each burst between two neurons, $\delta$ reads as a half of the corresponding spiking time difference of two neurons; in this example, neuron 1 bursts $3~\hbox {ms}$ behind neuron 0 when stabilized, giving $\delta =1.5~\hbox {ms}$.

Fig. 3

Stabilized synchronization parameter $\delta$ in a model with two neurons. a–c show the stabilized synchronization parameter as a function of initial potential difference $V_0-V_1$ for three different initial membrane potential $V_0$ as indicated when updated synaptic conductance $g_{\mathrm{exc}}=0$ (a), $0.05~\hbox {nS}$ (b) or $g_{\mathrm{exc}}=0.5~\hbox {nS}$ (c). The insert panels in b, c show the synchronization parameter for the first burst $\delta (1)$ and stabilized synchronization parameter $\delta$ for $V_0=-60~\hbox {mV}$. d shows the stabilized synchronization parameter $\delta$ of two neurons decreases with the updated synaptic conductance $g_{\mathrm{exc}}$ in the range considered, giving initial potentials $V_0=-60~\hbox {mV}$ and $V_1=-70.6~\hbox {mV}$. e shows the stabilized spiking sequences of two neurons with initial potentials $V_0=-60~\hbox {mV}$ and $V_1=-70.6~\hbox {mV}$ (i.e., $V_0-V_1=10.6~\hbox {mV}$) for three updated synaptic conductance $g_{\mathrm{exc}}$ as indicated. f shows the spiking sequences of two neurons with initial potentials $V_{0,1}$ (where the stabilized synchronization parameter $\delta$ is reached) for a updated synaptic conductance $g_{\mathrm{exc}}=0.05~\hbox {nS}$. The inset shows the zoom in of the indicated time window. Note in e, f neuron index is shifted to avoid overlaid for visualization effects

Next, we investigate effects of initial potentials on neuronal synchronization in regular networks with more neurons. We start with a simple case where initial membrane potentials are the same except for one neuron, say neuron 0 with initial potential $V_0$ and $V_0>V_i,i\ne 0$ as in the two-neuron model. Figure 4b shows the stabilized synchronization parameter $\delta$ for various $V_0$, while other initial potentials are $V_i=-70.6~\hbox {mV}, i\ne 0$ (the same as resting potential $E_L$) in a regular network of 7 neurons as shown in Fig. 4a. In this example, as $V_0$ is the largest initial potential, neuron 0 would spike first; when $V_0(t)$ reaches the threshold $V_T$, variables $V_0,w_0,g_0$ are updated; in particular $g_0$ is increased by $g_{\mathrm{exc}}$ which indicates a stronger interaction with neurons (i.e., neurons $\{1,2,5,6\}$ connected to it.

In this example, we observe from Fig. 4 that when $V_0<-61~mV$, the stabilized synchronization parameter $\delta$ exhibit approximately linear increase with $V_0$. When $V_0$ increases, the initial potential difference $V_0-V_i$ increases as well. While for larger $V_0$ ($V_0>-61~\hbox {mV}$, i.e., larger $V_0-V_1$), $\delta$ is saturated and keeps unchanged when increasing $V_0$. This is similar to the saturation observed in the two-neuron example in Fig. 3. These results suggest that in neuronal networks, the stabilized synchronization parameter $\delta$ could be saturated when initial potential difference is large enough.

Fig. 4

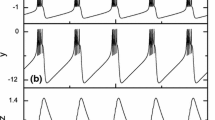
a shows a regular network of 7 neurons where each neuron is connected to its nearest 4 neighbors. b shows stabilized synchronization parameter $\delta$ when varying initial membrane potential $V_0$ in the regular network (a). c shows the evolution of synchronization parameter $\delta (n)$ for initial membrane potential $V_0$. d1–f2 show raster plots excitatory neurons at $n=1$ and $n=100$ for different $V_0$. Other initial potentials $V_i=-70.6~\hbox {mV}$ the same as the resting potential and the updated synaptic conductance $g_{\mathrm{exc}}=0.05~\hbox {nS}$. Note that black lines highlight the same spiking times of neurons. Also note that the width of each burst is the same for different $V_0$

Figure 4c shows the evolution of the synchronization parameter $\delta (n)$ for different $V_0$ and Fig. 4d1–f2 illustrates the transition of bursting patterns shown as raster plots from the first burst (i.e., $n=1$) to the stabilized burst (at $n=100$) for three different initial potentials $V_0$. We note that for $V_0=-67~\hbox {mV}$ which is close to others $V_i=-70.6~\hbox {mV}$, the first burst is already stabilized and no difference is observed on two raster plots (see Fig. 4f1, f2); for $V_0=-63~\hbox {mV}$, a small change of spiking time difference between neurons is observed from the first (at $n=1$) to stabilized bursts (at $n=100$) in Fig. 4e1, e2; for $V_0=-52$ (where $V_0-V_1$ is large and $\delta$ is saturated as seen from Fig. 4b), the first bursting pattern in Fig. 4d1 is far different to the stabilized burst in Fig. 4d2. Note that for all three different $V_0$, neuron 0 which has the largest initial potential bursts first, and then tries to affect other neurons to burst with the given coupling strength. This is similar to two-neuron model, when initial potential difference is larger (in particular when $\delta$ is stabilized), larger transition from the first to the stabilized burst would be expected, whereas when initial potential difference is small (before $\delta$ is saturated), $\delta (1)\approx \delta$. These suggest that synchronization parameter $\delta$ stabilizes faster for smaller $V_0$ (i.e., smaller initial potential difference $V_0-V_i (i\ne 0)$), as shown in Fig. 4c.

Moreover, we observe in Fig. 4d2, e2 that neurons with the same initial membrane potentials could burst at different times by neuronal network connections. Here, neuron 0 has the largest initial potential and generates the action potential first. Once updating its variables, neuron 0 affects its neighboring neurons $\{1,2,5,6\}$ via coupling and results different bursting time to neurons $\{3,4\}$ as seen in Fig. 4d2, e2. In particular, we calculate the spiking time difference $\hbox {TD}$ for all neurons. When $V_0=-67~\hbox {mV}$, $\hbox {TD}_i=0$ for all i, meaning neurons burst as effectively independent neurons, and equal initial potentials of neurons burst at the same time. When $V_0=-63~\hbox {mV}$, $\hbox {TD}_{0,3,4}=0$, whereas $\hbox {TD}_{1,2,5,6}<0$ which is consistent with neurons $\{1,2,5,6\}$ burst earlier than neurons $\{3,4\}$, though they have the same initial potentials. When $V_0=-52~\hbox {mV}$, $\hbox {TD}_0=0$ and $\hbox {TD}_i<0$ for all $i\ne 0$, meaning that the bursting time of neurons is advanced except for neuron 0 due to network connections. We remark here when $V_0>-61~\hbox {mV}$ the stabilized synchronization parameter $\delta$ is saturated as seen from Fig. 4b, and similar to the two-neuron model in Fig. 3f that for different initial potentials $V_0>-61~\hbox {mV}$, the stabilized bursting states shift forward or backward and the relative states of phase locking remain the same.

3.2 Bursting hierarchy in regular networks

We next consider more general initial membrane potentials of neurons. With some arbitrary neuron initial potentials for the same network structure as in Fig. 4a, we find more variety of phase locking states. Examples are shown in Fig. 5 (cases 1–3) and Fig. 6 (cases 4–6), and their initial potential and corresponding stabilized synchronization parameters $\delta$ are given in Table 1.

In both cases 1 and 2, neuron 6 which has the largest initial potential, generates action potential first (Fig. 7a). Moreover, we note that neuron 6 has $\hbox {TD}_6(k)=0$ for all spikes (Fig. 7c), indicating that neuron 6 spikes as its own independent spiking pattern, unaffected by the network, and $\hbox {TD}_i<0$ for all other neurons $i\ne 6$, suggesting that spiking times of these neurons are advanced due to network connections. We consider this as neuron 6 sends stimuli to other neurons connected to it and affects their spiking times. This is similar to simple examples in Sect. 3.1. We remark here cases 1 and 2 share the same largest initial potential and the same locked phase though they have other different initial potentials. These suggest that neuron 6 dominates network interactions and bursting propagation. Similarly, neuron 2 in case 3 which has the largest membrane potential and $\hbox {TD}_2(k)=0$ for all spikes, dominates the bursting propagation in the regular network.

Table 1 Initial membrane potential values $V_i$ (in unit of mV) of each neuron i in a regular network of 7 neurons shown in Fig. 4a, and the corresponding stabilized synchronization parameter $\delta ~(\hbox {ms})$

Fig. 5

a, b show locked phases for cases 1–3. Note that black (red) lines highlight the same (different) time of neurons. c shows the spiking time difference $\hbox {TD}(k)$ for each neuron in the network when comparing with neurons in the uncoupled network using the same initial membrane potentials as given in case 1 in Table 1. d shows stabilized time difference TD for all 7 neurons in cases 1–3. Note that $\hbox {TD}_6=0.8~\hbox {ms}$ in case 3. e, f show bursting propagation graphs from primary to tertiary neurons in cases 1–3. The network coupling structures are the same as in Fig. 4a

Inspired by the dominant role of neuron 6 (resp. neuron 2) in bursting from cases 1 and 2 (resp. case 3), we grade neurons into different layers. More precisely, neurons with large initial potentials together with $|\hbox {TD} |$ sufficiently small are graded as primary neurons, such as neuron 6 in case 1. We remark here that the neuron with second largest membrane potential and $\hbox {TD}\approx 0$ (say $|\hbox {TD} |<0.1~\hbox {ms}$) is also graded as a primary neuron, but not neurons with relatively low initial potentials and $\hbox {TD}=0$. We grade neurons connected to primary ones as secondary neurons and among the remaining neurons, those connected to secondary neurons are graded as tertiary neurons, etc.

Neurons in upper layers burst earlier than those in lower layers as seen from Fig. 5. Based on neurons network structure and ignoring interactions of neurons within the same layer, we construct a bursting propagation graph as in Fig. 5e, f to indicate the propagation of bursts from layers to layers. Such bursting propagation graph gives a coarse bursting order of neurons.

For neurons in the same layer, they may or may not burst at the same time. We now study bursting order of neurons within the same layer in more details. In case 1, secondary neurons $\{0, 5\}$ burst at the same time as seen from Fig. 5a. We interpret this from the bursting propagation graph in Fig. 5e that secondary neurons $\{0,5\}$ share the same connected primary neuron and propagate to the same number of tertiary neurons. We remark that neurons $\{0,5\}$ burst at slightly later time compared to secondary neurons $\{1,4\}$. This might be complicated combined effects from coupling to non-primary neurons and might be due to more connections within the same secondary layer for neurons $\{0,5\}$ compared to neurons $\{1,4\}$. Moreover, tertiary neurons $\{2,3\}$ in case 1 burst at the same time because the bursting times of their upper-layer neurons are equivalently the same. Note that tertiary neurons $\{5,6\}$ in case 3 burst at different times with effectively the same stimuli from secondary neurons. This is probably due to $\hbox {TD}_6=0.8~\hbox {ms}>0$ in case 3 which indicates a short delay in spiking though it has a relatively large initial potential. These suggest that bursting hierarchy of neurons as well as locked phases of neurons can be understood largely from bursting propagation graph in particular when $\hbox {TD}\le 0$ for all neurons.

In cases 1–3, there is only one primary neuron. With different initial membrane potentials, we may have two or more primary neurons. We consider situations with two primary neurons in the same regular network as in Fig. 4a; more primary neurons could be studied similarly. In particular we focus on situations with $\hbox {TD}\lesssim 0$ for all neurons. For the network structure in Fig. 4a, there are three topologically different bursting propagation graphs with two primary neurons as shown in Fig. 6c1–c3: (1) two primary neurons are connected in the network, and all neurons are graded into three layers; (2) two primary neurons are connected in the network, and all neurons are graded into two layers; (3) two primary neurons are not directly connected in the network. Figure 6a1–a3 shows examples of locked phases with corresponding model parameters given as cases 4–6 in Table 1 and bursting propagation graphs in Fig. 6c1–c3, respectively. The bursting propagation graphs are constructed based on network connection and stabilized spiking time difference $\hbox {TD}$ shown in Fig. 6b.

Similarly, bursts are initiated in primary neurons, which propagate to secondary and then tertiary neurons. Neurons within the same layer of neurons may burst at different times. In case 4, for the two primary neurons $\{0,6\}$, neuron 0 which has a larger initial potential than neuron 6, bursts earlier than neuron 6. Secondary neurons $\{1,5\}$ burst at the same time as they are both stimulated from two primary neurons $\{0,6\}$ and propagate to the same tertiary neuron. Secondary neuron 2 receives stimulus from its primary neuron 0 earlier than secondary neuron 4 receiving stimulus from its primary neuron 6, and bursts earlier. Similarly, comparing secondary neurons $\{5,6\}$ (which is connected to primary neuron 4) and neurons $\{0,1\}$ (which is connected to primary neuron 2) in case 5, their primary neuron 4 bursts earlier than primary neuron 2 and secondary neurons $\{5,6\}$ burst earlier than neurons $\{0,1\}$; see Fig. 6a2, c2. In case 6, secondary neurons $\{1,2,5\}$ receiving stimuli from both primary neuron $\{0,3\}$ burst earlier than secondary neurons $\{4,6\}$ which receive stimulus from only one primary neuron as seen in Fig. 6a3, c3.

Fig. 6

a1–a3 show raster plots of locked phases; black (red) lines highlight the same (different) spiking time. b shows the stabilized spiking time difference $\hbox {TD}$ for all neurons in cases 4–6. c1–c3 show the corresponding bursting propagation graphs. Network coupling structures are the same as in Fig. 4a. Initial membrane potentials in each case are given in Table 1

These results suggest that earlier bursting of neurons would stimulate and promote neurons connected to it in the next layer to burst earlier. Receiving stimuli from more upper-layer neurons would promote neurons to burst earlier as well. Moreover, we note that with the same number of neurons in the regular network, the stabilized synchronization parameters (see Table 1) are lower with fewer layers in bursting propagation graphs; this is consistent with that more clustered spiking would lead to higher synchronization.

3.3 Bursting hierarchy in small-world networks

In this subsection, we consider small-world networks which are more realistically simulated neuronal networks (Rubinov and Sporns 2010). For simplicity, we focus on situations where $\hbox {TD}\lesssim 0$ for all neurons; this usually occurs when the initial potentials of primary neurons are far away from others. Figure 7a1, b1 shows two examples of small-world networks with 7 and 9 neurons, respectively (referred as cases 7–8). These small-world networks are constructed from regular network models with 4 nearest neighbors and each connection is rewired with probability 0.5. Similar to cases in regular networks, we construct bursting propagation graphs as shown in Fig. 7a3, b3, based on neuronal initial potentials (listed in Table 2), neuronal network, and their spiking time difference $\hbox {TD}$. As expected, primary neurons burst first and propagate to the secondary, and then tertiary neurons.

Fig. 7

a1, b1 show the topological structure of small-world networks with 7 and 9 neurons as cases 7 and 8, respectively. a2, b2 show spiking time difference $\hbox {TD}(k)$ compared to neurons in uncoupled network with the same initial membrane potentials given in Table 2. Note that the $\hbox {TD}_{5,7}(k)$ curves are overlapped. a3, b3 show corresponding bursting propagation graphs. a4, b4 show raster plots of locked phases; black (red) lines highlight the same (different) spiking times

To examine the influence of upper-layer neurons on one neuron, we count the number of those upper-layer neurons connected to it from the bursting propagation graph and denote the number as $\hbox {dr}$ (listed in Table 2). We note that tertiary neurons $\{2,8\}$ in case 8 receive stimuli from 3 secondary neurons (i.e., $\hbox {dr}_{2,8}=3$), which is larger than $\hbox {dr}_0=2$ for neuron 0. Figure 7b4 shows that neurons $\{2,8\}$ burst earlier than neuron 0. This agrees with that neurons receiving more stimuli from upper layer would burst earlier.

In both cases 7 and 8, there is only one primary neuron, meaning secondary neurons receive stimulus from the primary neuron equally. However, we observe different bursting times among secondary neurons from Fig. 7a4, b4. In contrast to regular networks, neurons in small-world networks may have different degrees. We consider the potential influence of the connection degree in bursting times and list their degrees as d in Table 2. In case 7, secondary neurons have the degree order $d_4<d_{3,5}<d_{1,2}$. Interestingly, we note that secondary neurons burst sequentially consistent with their degree order in case 7. Such consistency between connection degrees and bursting hierarchy is also observed for secondary neurons in case 8. For these secondary neurons, they all connected to the same primary neuron, thus we consider the effect from primary neuron on their spiking is the same; the slightly different spiking times within secondary neurons might be the minor effects of interactions with other neurons (except the primary neuron). We remark here that neurons with the same degree do not necessary burst at the same time. For instance, tertiary neurons 2 and 8 in case 8, have the same degree ($d_{2,8}=3$) and are connected to secondary neurons $\{1,3,7\}$ and $\{1,3,4\}$, respectively, from Fig. 7b3; this might be that secondary neuron 7 bursts earlier than neuron 4, and promotes neuron 2 (which is connected to neuron 7) to burst earlier than neuron 8 (which is connected to neuron 4).

Table 2 Initial membrane potential values $V_i$ (in unit of mV), degree $d_i$, and connected neuron number $\hbox {dr}_i$ from upper layer based on the bursting propagation graphs in Fig. 7 for each neuron i

We next examine small-world networks with large number of neurons. Figure 8 shows an example of a small-world network with 20 neurons. With some chosen initial membrane potentials, the constructed bursting propagation graph and simulated locked phase are shown in Fig. 8b, c. We observe that the upper-layer neurons burst earlier than lower-layer neurons. In this example, all the secondary neurons are connected to the only primary neuron. We list the degree of secondary neurons in ascending order in Table 3. Combined with Fig. 8, we note that neurons with smaller degree burst earlier. Tertiary neurons are more complex than secondary neurons, as they may connect to different groups of upper-layer neurons and may also have different connection degrees. In this example, tertiary neurons have 4 different $\hbox {dr}$, as given in Table 4. Neuron 19 receives stimulus from only one secondary neuron (with $\hbox {dr}_{19}=1$), and bursts latest among the tertiary neurons. Neurons $\{5,10\}$ have $\hbox {dr}_{5,10}=5$ and both connect to secondary neuron $\{6,9,12,14,17\}$. Neuron 5 bursts earlier than neuron 10 which is consistent with their connection degree order $d_5<d_{10}$. Neurons $\{2,4,8,11,16,18\}$ receive stimuli from equal number of secondary neurons (though not necessary the same group); similar for neurons $\{0,7,1,3\}$. In particular, neurons $\{2,4\}$ share the same group of connected secondary neurons (and similarly neurons $\{5,10\}$); their bursting order is consistent with their degree. Neurons $\{11,16\}$ (similarly neurons $\{2,8\}$) connect to the same number but different groups of secondary neurons. For instance, neuron 11 receives stimuli from $\{9,14,15\}$, while neuron 16 receives stimuli from $\{12,14,15\}$; earlier bursting of neuron 12 than neuron 9 together with $d_{16}<d_{11}$ leads to earlier bursting of neuron 16 than neuron 11.

Fig. 8

a A small-world network of 20 neurons. b Bursting propagation graph of a large small-world network given in a. c Raster plot of locked phase in this small-world network; only first spiking times in the burst are shown for visual effects; black (red) lines highlight the same (different) spiking times

Table 3 Degree ($d_i$) and bursting order in a small-world network given in Fig. 8a for each secondary neuron i

These results suggest that neurons with more stimuli (here larger $\hbox {dr}$) would burst earlier than others in the same layer. For neurons in the same layer receiving effectively the same stimuli (i.e., two neurons share effectively the same bursting time of connected upper-layer neurons), those with smaller degree would then burst earlier. For neurons in the same layer receiving the same number of stimuli and having the same degree, those receive stimuli earlier (e.g., connected upper-layer neurons burst earlier) would burst earlier.

Table 4 Degree of tertiary neurons $d_i$, received number $\hbox {dr}_i$ from upper-layer neurons base on the bursting propagation graph Fig. 8b, and bursting order for each tertiary neuron in a small-world network given in Fig. 8a

4 Conclusion

In this manuscript, we study bursting synchronization and the corresponding locked phases of steady bursting patterns in the aEIF neuronal network model. In particular, we focus on influence from initial membrane potentials, together with network connections. Our simulations suggest that bursting synchronization could be saturated when the initial potential difference is sufficiently large by coupling. In order to measure the effect of network coupling on neuron bursting rhythm, we calculate the spiking time difference $\hbox {TD}$ between coupled and uncoupled networks with the same initial potentials. We focus on cases where $\hbox {TD}\lesssim 0$. Combined with raster plots of locked phases, we find that the neurons which have the highest initial potential always bursts first and their $\hbox {TD}$ is approximately equal to 0. We grade neurons in the network as primary, secondary and tertiary neurons etc, and construct corresponding bursting propagation graphs; neurons in the upper layer burst earlier than those in lower layers. Moreover, our simulation results suggest that among the same layer: (1) neurons receive more stimuli (larger $\hbox {dr}$) from upper-layer neurons would burst earlier; this is consistent with that the onset of synchrony depends on the number of signals received by each neuron (Belykh et al. 2005; 2) with effectively the same stimuli from upper layers, neurons with smaller degree would then burst earlier; (3) for neurons receiving the same number of stimuli from upper layer and have the same degree, neurons would burst earlier if their connected upper-layer neurons burst earlier.

For large networks, neurons may receive the same number but different groups of stimuli from upper layer and have different connection degree; such as neurons $\{2, 8\}$ in the small-world network (Fig. 8 and Table 4). In this case neuron 2 receives stimuli from $\{6,12,15\}$, whereas neuron 8 receive stimuli from $\{6,9,15\}$; besides the common upper-layer neurons $\{6,15\}$, neuron 2 is connected to the upper-layer neuron 12 which bursts earlier than neuron 9; however neuron 2 has larger degree than neuron 8 (i.e., $d_2>d_8$); the combined influence of degree and the upper-layer neurons in such cases remain unclear in determining their bursting hierarchy.

Our results are mainly based on $\hbox {TD}\lesssim 0$, and this situation occurs when initial potentials of neurons are relatively scattered, or large initial potentials are close to each other. In cases with $\hbox {TD}>0$ for some neurons (i.e., network connections effectively delay neurons to burst), how to determine primary neurons and bursting propagation graph remain to be investigated in the near future.

Previous studies show that increasing the number of network connections can enhance synchronization (Fink 2016). They consider heuristically that with more connections, the average shortest path length decreases, which enhances information transmission within a network, thereby enhancing synchrony. Using our bursting propagation graph, we could explain this as follows: with an equally fixed number of neurons, networks with more connections would lead to fewer layers, and neurons in the same layer burst at similar times; thus, smaller synchronization parameter $\delta$ would be expected with fewer layers. In our regular network cases, we do observe fewer layers (e.g., cases 5 and 6) in the bursting propagation graphs have smaller synchronization parameter (given in Table 1).

Last but not least, the model we consider focuses on connection given by excitatory synapses. However, there are also inhibitory synapses (Protachevicz et al. 2019, 2020) that inhibit the next neuron to generate the action potential. It would be interesting to extend our model with inclusion of both excitatory and inhibitory synapses to examine the influence of initial membrane potentials on the phase locking as well as bursting hierarchy of neurons.