1 Introduction

In recent years, high demand has been observed for using composite materials in different sciences and engineering systems to have more resistance to fatigue, high strength-to-weight ratio, and low damping factor in structural components. Laminated Composite Beams (LCB) are exciting because of their high strength under severe loading and wide application in engineering. The dynamic behavior of the LCB becomes more significant to capture their real response and obtain their structural properties. The natural frequency response of LCB, because of their nonlinear behavior is obtained is very important. The governing dynamic equation of beams and palates are nonlinear partial differential equations in space and time with different boundary conditions. There are a lot of challenges to finding an analytical solution for nonlinear partial differential equations. Usually, numerical methods have been applied to nonlinear problems because of the hard work to prepare analytical solutions. In recent years, scientists have worked on analytical and semi-analytical solutions for nonlinear engineering problems. Recently, many different approaches have been proposed and developed to achieve the approximate solutions of nonlinear partial differential equations such as: harmonic balance method [1], the energy balance method [2], the Hamiltonian approach [3], the max–min approach [4, 5], Homotopy perturbation method [6], the variational iteration method [7] and other related approaches [8,9,10,11,12,13]. Beam theory is classified into the following categories: 1) Euler–Bernoulli beam theory 2) first shear-order deformation beam theory 3) higher-order shear deformation beam theory. The assumption in the Euler–Bernoulli beams makes it acceptable for thin beams, not tick beams.

A comprehensive and methodical explanation of asymptotic techniques in the theory of plates and shells is provided by Awrejcewicz [14]. The fundamental ideas of asymptotics and their applications, as well as more contemporary and conventional methods like the composite equations approach and regular and singular perturbations, are the key components.

Gao and Krysko et al. [15] worked on the asymptotic methods among the theoretical techniques used to solve several practical mathematics, physics, and technology problems. These techniques frequently yield results that improve the efficiency of numerical evaluation algorithms.

The nonlinear dynamics of non-homogeneous beams with a material optimally distributed along the beam's length and height were studied by Krysko et al. [16]. The maximum stiffness of a beam microstructure was obtained by topological optimization for the specified boundary and loading circumstances, which served as the study's starting point. Consequently, a beam with an optimal microstructure that displayed non-homogeneity along the thickness and length of the beam was obtained.

Bhimaraddi and Chandrashekhara [17] studied the modeling of laminated beams by considering the parabolic shear deformation theory. They had prepared numerical results of the natural frequency of the beams. Zhen and Wanji [13] used displacement-based theories to analyze the free vibration of laminated beams. They tried to apply the Hamiltonian principles to achieve the dynamic governing equation. Aydogdu [18] studied a new higher-order shear deformable laminated composite plate. Girhammar [19] worked on the simplified static procedure for analyzing and designing composite beams with interlayer slips. Emam and Nayfeh [20] studied the exact solution of post-buckling analysis of laminated composite beams with different boundary conditions. Malekzadeh and Vosoghi [21] considered the nonlinear vibration of symmetric angle-ply laminated thin beams on a nonlinear elastic foundation with elastically restrained against rotation edges.

In this study, it has tried to develop the nonlinear governing equation of LCB by using Galerkin Method to find the effects of nonlinear parameters and of the axial force on the frequency of the beam. The nonlinear ordinary–differential equation is in the time domain only. The main objective of this paper is to propose a new so called Max–Min Approach (MMA) that can be used and apply for serious nonlinear problems in LCB to assess the nonlinear frequency of the problems. The accuracy of the solution has been verified with the numerical solution. The effects of essential parameters are also considered as shown graphically.

The paper has 5 sections. After the Introduction in the Sect. 2, the mathematical model and the governing equation of free vibration of a LCB on elastic foundation is introduced. Analyzing the simplified second-order strong nonlinear equation the conditions for the nonlinear beam buckling and post-buckling are determined. In Sect. 3, the new MMA for frequency calculation is considered. The general method is adopted for LCB. In Sect. 4, the results for the simple supported and clamped–clamped beams are obtained. The dependence of the frequency on axial force and parameters of elastic foundation are discussed. The results are compared with numerical and previously published analytic results. The paper ends with Conclusions.

2 Governing equation

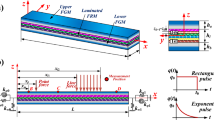
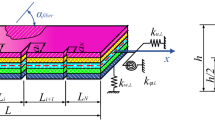
The plot of a laminated composite beam (LCB) on a nonlinear layer is shown in Fig. 1. The linear and shear layers are present in the straight laminated beam. The beam has three dimensions: length (L), width (b), and thickness (h). Coordinate along the axis of the beam is \(\widetilde{x}\) and in the direction of the thickness of the beam is \(\hat{Z}\). On the beam, a compressive axial force \(\hat{P}\) acts. It causes transversal-axial coupled vibrations.

Fig. 1
figure 1

The LCB with simply supported end conditions

Full size image

According to [22] and the Euler–Bernoulli’s beam theory, the transverse response of geometrically nonlinear composite fixed–fixed beam accounting for its mid-plane stretching is

$$\rho A\frac{{\partial }^{2}\widetilde{w}}{\partial {\widetilde{t}}^{2}}+b\widetilde{D}\frac{{\partial }^{4}\widetilde{w}}{\partial {\widetilde{x}}^{4}}+\frac{{\partial }^{2}\widetilde{w}}{\partial {\widetilde{x}}^{2}}\left[\begin{array}{c}\widetilde{P}-\widetilde{B}{\int }_{0}^{l}{\left(\frac{\partial \widetilde{w}}{\partial \widetilde{x}}\right)}^{2}\text{d}\widetilde{x}\\ -\widetilde{\Lambda }\left(\frac{\partial \widetilde{w}}{\partial \widetilde{x}}\left(l,\widetilde{t}\right)-\frac{\partial \widetilde{w}}{\partial \widetilde{x}}\left(0,\widetilde{t}\right)\right)\end{array}\right]={\widetilde{F}}_{w}$$
(1)

with

$$\widetilde{D}={D}_{11}-\frac{{B}_{11}^{2}}{{A}_{11}}, \widetilde{B}=\frac{b}{2l}{A}_{11}, \widetilde{\Lambda }=\frac{b}{l}{B}_{11}$$
(2)

where A11, B11 and D11 are axial, coupling and bending stiffness

$${A}_{11}=\sum_{k=1}^{N}{Q}_{11k}({\widetilde{Z}}_{k}-{\widetilde{Z}}_{k-1}), {B}_{11}=\frac{1}{2} \sum_{k=1}^{N}{Q}_{11k}({\widetilde{Z}}_{k}^{2}-{\widetilde{Z}}_{k-1}^{2}), {D}_{11}= \frac{1}{3} \sum_{k=1}^{N}{Q}_{11k}({\widetilde{Z}}_{k}^{3}-{\widetilde{Z}}_{k-1}^{3})$$
(3)

\({Q}_{11k}\) and \({\widetilde{Z}}_{k}\) is the reduced-transformed stiffness and height of the kth lamina, \(\rho A\) is mass per unit length, \(\widetilde{t}\) is time, \(\widetilde{w}\) is transversal displacement of the beam along the \(\hat{Z}\) coordinate and \({\widetilde{F}}_{w}\) is the distributed transverse force. Let us consider the LCB settled on the Winkler–Pasternak elastic foundation with load–displacement relationship

$${\widetilde{F}}_{w}={\widetilde{k}}_{S}\frac{{\partial }^{2}\widetilde{w}}{\partial {\widetilde{x}}^{2}}-\sum_{i=1}^{n}{\widetilde{k}}_{i}{\widetilde{w}}^{2i-1}$$
(4)

where \(\widetilde{k}\) i are linear and nonlinear coefficients of Winkler elastic foundation and \(\widetilde{k}\) S is the Pasternak coefficient of the shearing layer. Substituting (4) into (1), a nonlinear dimensionless partial differential equation is obtained

$$\rho A\frac{{\partial }^{2}\widetilde{w}}{\partial {\widetilde{t}}^{2}}+b\widetilde{D}\frac{{\partial }^{4}\widetilde{w}}{\partial {\widetilde{x}}^{4}}+\frac{{\partial }^{2}\widetilde{w}}{\partial {\widetilde{x}}^{2}}\left[\begin{array}{c}\widetilde{P}-\widetilde{B}{\int }_{0}^{l}{\left(\frac{\partial \widetilde{w}}{\partial \widetilde{x}}\right)}^{2}d\widetilde{x}-{\widetilde{k}}_{s}\\ -\widetilde{\Lambda }\left(\frac{\partial \widetilde{w}}{\partial \widetilde{x}}\left(l,\widetilde{t}\right)-\frac{\partial \widetilde{w}}{\partial \widetilde{x}}\left(0,\widetilde{t}\right)\right)\end{array}\right]+\sum_{i=1}^{n}{\widetilde{k}}_{i}{\widetilde{w}}^{2i-1}=0$$
(5)

By introducing the non-dimensional variables

$$x=\frac{\widetilde{x}}{l}, w=\frac{\widetilde{w}}{l}, t=\widetilde{t}\sqrt{\frac{b\widetilde{D}}{\rho A{l}^{4}}}$$
(6)

into (5), the dimensionless partial differential equation of free vibration of an asymmetrically LCB, as is suggested in [23], yields

$$\frac{{\partial }^{2}w}{\partial {t}^{2}}+\frac{{\partial }^{4}w}{\partial {x}^{4}}+\frac{{\partial }^{2}w}{\partial {x}^{2}}\left[\begin{array}{c}P-B \int^1_0{\left(\frac{\partial w}{\partial x}\right)}^{2}dx\\ -\Lambda \left(\frac{\partial w}{\partial x}\left(\text{1,0}\right)-\frac{\partial w}{\partial x}(0,t)\right)\end{array}\right]+\sum_{i=1}^{n}{k}_{i}{w}^{2i-1}-{k}_{s}\frac{{\partial }^{2}w}{\partial {x}^{2}}=0$$
(7)

where \(r=\sqrt{\frac{b\widetilde{D}}{2l\widetilde{B}}}\) is the gyration ration of the cross section, and the dimensionless parameters

$$P=\frac{\widetilde{P}{l}^{2}}{b\widetilde{D}}, \frac{1}{B}=2\left(\frac{r}{l}\right), {k}_{S}=\frac{{\widetilde{k}}_{S}{l}^{2}}{b\widetilde{D}},\Lambda =\frac{\widetilde{\Lambda }{l}^{3}}{b\widetilde{D}}, {k}_{i}=\frac{{\widetilde{k}}_{i}{l}^{2(i+1)}}{b\widetilde{D}}$$
(8)

For i = 3 Eq. (7) transforms into the cubic one presented in [24].

REMARK: Equation (7) is similar to the governing equation of a beam composed of an isotropic material with equivalent stiffness EA=\(\widetilde{B}/2l\) and bending stiffness EI = b \(\widetilde{D}.\) For the asymmetric laminate not only \(\widetilde{D}\) but also the coupling stiffness \(\widetilde{B}\) and therefore \(\widetilde{\Lambda }\) differ from zero and therefore \(\widetilde{\Lambda }\) also exist.

Assuming w(x,t) = ϕ(x)W(t) where ϕ(x) is the first eigenmode of the beam and using the Ritz method, the governing equation of motion follows as

$$\frac{{d}^{2}W\left(t\right)}{d{t}^{2}}+\left[{a}_{1}+\left(P-{k}_{s}\right){a}_{2}+{k}_{1}\right]W\left(t\right)+{a}_{5}W(t{)}^{2}+({k}_{2}{a}_{6}+{a}_{7})W(t{)}^{3}+\sum_{i=3}^{n}{k}_{i}{a}_{i+5}W(t{)}^{2i-1}=0$$
(9)

where αi are presented in Appendix 1. The initial conditions are as follows

$$W\left(0\right)=A, \frac{\text{d}W(0)}{dt}=0$$
(10)

where A denotes the non-dimensional initial amplitude of oscillation. The coefficient a5 exists for the unsymmetrical laminated beam and is zero for isotropic and symmetrically laminated ones. The existence of the quadratic term causes the difference in analysis of nonlinear vibrations for symmetrically and unsymmetrically laminated beams.

From Eq. (9), the post-buckling load–deflection relation of the LCB can be derived as follows

$${P}_{\text{NL}}=-\frac{{a}_{1}+{k}_{1}-{k}_{s}{a}_{2}+{a}_{5}W+\left({k}_{2}{a}_{6}+{a}_{7}\right){W}^{2}+\sum_{i=3}^{n}{k}_{i}{a}_{i+5}{W}^{2i-2}}{{a}_{2}}$$
(11)

where W = W(t). By neglecting the contribution of W in Eq. (11), the linear buckling load can be obtained as

$${P}_{L}={P}_{cr}=-\frac{{a}_{1}+{k}_{1}-{k}_{s}{a}_{2}}{{a}_{2}}$$
(12)

Comparing the buckling load in the nonlinear system with the linear case gives

$$\frac{{P}_{\text{NL}}}{{P}_{L}}=1+\frac{{a}_{6}+{a}_{5}W+{a}_{7}{W}^{2}}{{a}_{1}+{a}_{3}+{a}_{4}},$$
$$\frac{{P}_{\text{NL}}}{{P}_{L}}=1+\frac{{a}_{5}W+\left({k}_{2}{a}_{6}+{a}_{7}\right){W}^{2}+\sum_{i=3}^{n}{k}_{i}{a}_{i+5}{W}^{2i-2}}{{a}_{1}+{k}_{1}-{k}_{s}{a}_{2}}$$
(13)

Due to nonlinearity, the buckling load increases: the higher the nonlinearity of foundation, the higher the value of the buckling force in comparison to the linear case.

3 The max–min approach (MMA) in nonlinear LCB

Equation (4) is a second-order differential equation with strong polynomial nonlinearity. To obtain the exact frequency of vibration of (9) is not an easy task. Because of that the method for approximate value calculation is developed. The method is based on the Max–Min Approach (MMA) [5].

3.1 Generalization of the MMA in solving second-order nonlinear differential equation

Let us rewrite Eq. (9) in the general form of a nonlinear oscillator

$$\ddot{v}+ v f(v)=0, v(0)=A, \dot{v}(0)=0$$
(14)

where \(f\left( v \right)\) is a non-negative function of variable v. The trial solution of (9) is assumed in the form of a periodical function:

$$v(t)=A cos(\omega t),$$
(15)

where \(\omega\) is an unknown frequency (needs to be determined).

According to MMA [5] two assumptions are introduced:

1. The square of frequency, \({\omega }^{2}\), is never less than the square of frequency \({f}_{min}\) of the solution

$${v}_{1}\left(t\right)=A\mathit{cos}\left(\sqrt{{f}_{\text{min}}}\right)$$
(16)

for the following linear oscillator

$$\ddot{v}+v{f}_{\text{min} }=0, v\left(0\right)=A , \dot{v}\left(0\right) =0$$
(17)

where \(f_{\min }\) is the minimum value of the function \(f\left( v \right)\).

2. In addition, \(\omega^{2}\) never exceeds the square of the frequency \({f}_{\text{max}}\) of the solution

$${v}_{1}\left(t\right)=A\mathit{cos}(\sqrt{{f}_{max}}t)$$
(18)

By substituting it to the general nonlinear equation, it becomes

$$\ddot{v}+v{f}_{\text{max} }=0, v\left(0\right)=A , \dot{v}\left(0\right) =0$$
(19)

where \({f}_{\text{max}}\) is the maximum value of the function \(f\left(v\right)\).

Hence, it yields,

$${\frac{{f}_{\text{min}}}{1}<\omega }^{2}<\frac{{ f}_{\text{max}}}{1}$$
(20)

According to He Chentian interpolation [5], we obtain

$${\omega }^{2}=\frac{m{f}_{\text{min}}+n{ f}_{\text{max}}}{m+n},$$
(21)

or

$${\omega }^{2}=\sqrt{\frac{{f}_{\text{max}}+{k f}_{\text{max}}}{1+k}}$$
(22)

where \(m\) and \(n\) are weighting factors, and \(k = {n \mathord{\left/ {\vphantom {n m}} \right. \kern-0pt} m}\). So the solution of Eq. (19) can be expressed as

$$v\left(t\right)=A \text{cos}\sqrt{\frac{{f}_{\text{min}}+{k f}_{\text{max}}}{1+k}}t$$
(23)

The value of \(k\) can be approximately determined by various approximate methods (for example, see [8, 9]). Among others, hereby we use the residual method. Substituting (23) into (9) gives the following residual

$$R\left(t;k\right)=-{\omega }^{2}A\text{cos}(\omega t)+\left(A\text{cos}(\omega t)\right)\cdot f\left(A\text{cos}(\omega t)\right)$$
(24)

where \(\omega\) is given with (22). If, by chance, Eq. (23) is the exact solution, then \(R(t;k)\) is vanishing completely. Since our approach is only an approximation to the exact solution, we set

$${\int }_{0}^{T}R(t;k) \text{cos}\left(\sqrt{\frac{{f}_{min}+{k f}_{max}}{1+k}} t\right)\text{d}t=0$$
(25)

where \(T = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \omega }} \right. \kern-0pt} \omega }\). Solving the above equation the coefficient k is computed

$$k=\frac{{f}_{\text{max}}-{f}_{\text{max}}}{1-\sqrt{\frac{A}{\pi }{\int }_{0}^{\pi }\left({cos}^{2}x . f\left(A\text{cos} x\right)\right)\text{d}x}}$$
(26)

Substituting (26) into (22) the frequency, as the function of the initial amplitude A is determined.

3.2 Application of the MMA for frequency determination in LCB with polynomial nonlinearity

For approximate solving of Eq. (9) the aforementioned MMA procedure is adopted. For simplification the governing Eq. (9) is rewritten in the form

$$\frac{{d}^{2}W(t)}{d{t}^{2}}+{\beta }_{1}W\left(t\right)+{\beta }_{2}W{\left(t\right)}^{2}+{\beta }_{3}W{\left(t\right)}^{3}+\sum_{i=3}^{n}{\beta }_{2i-1}W(t{)}^{2i-1}=0$$
(27)

where

$${\beta }_{1}={a}_{1}+\left(P-{k}_{s}\right){a}_{2}+{k}_{1}, {\beta }_{2}={a}_{5}, {\beta }_{3}={k}_{2}{a}_{6}+{a}_{7}$$
$${\beta }_{2i-1}={k}_{i}{a}_{i+5} \text{for }i\hspace{0.17em}=\hspace{0.17em}3, 4,\dots n$$
(28)

The trial solution of (27) is assumed in the form

$$W\left(t\right)=A\text{cos}(\omega t)$$
(29)

where \(\omega\) is the unknown frequency. According to (20) the frequency of vibration in (29) is varying in the interval

$${\beta }_{1}<{\omega }^{2}<{\beta }_{1}+{\beta }_{2}A+{\beta }_{3}{A}^{2}+\sum_{i=3}^{n}{\beta }_{2i-1}{A}^{2i-2}$$
(30)

where

$${\omega }_{\text{min}}={\beta }_{1}, {\omega }_{\text{max}}={\beta }_{1}+{\beta }_{2}A+{\beta }_{3}{A}^{2}+\sum_{i=3}^{n}{\beta }_{2i-1}{A}^{2i-2}$$

According to the Chengtian’s inequality (21) and (22), we have

$${\omega }^{2}=\frac{m{\beta }_{1}+n\left({\beta }_{1}+{\beta }_{2}A+{\beta }_{3}{A}^{2}+\sum_{i=3}^{n}{\beta }_{2i-1}{A}^{2i-2}\right)}{m+n}$$
(31)

where m and n are weighting factors. Introducing \(k = {n \mathord{\left/ {\vphantom {n {m + n}}} \right. \kern-0pt} {m + n}}\) the frequency is approximated as

$$\omega =\sqrt{{\beta }_{1}+k\left({\beta }_{2}A+{\beta }_{3}{A}^{2}+\sum_{i=3}^{n}{\beta }_{2i-1}{A}^{2i-2}\right)}$$
(32)

Using (31), the approximate solution reads

$$W\left(t\right)=A\text{cos}\left(t\sqrt{{\beta }_{1}+k\left({\beta }_{2}A+{\beta }_{3}{A}^{2}+\sum_{i=3}^{n}{\beta }_{2i-1}{A}^{2i-2}\right)}\right)$$
(33)

In view of the approximate solution (33), Eq. (27) is rewritten in the form

$$\frac{{d}^{2}W}{d{t}^{2}}+{(\beta }_{1}+k\left({\beta }_{2}A+{\beta }_{3}{A}^{2}\right)W=k\left({\beta }_{2}A+{\beta }_{3}{A}^{2}+\sum_{i=3}^{n}{\beta }_{2i-1}{A}^{2i-2}\right)W-{\beta }_{2}{W}^{2}$$
$$-{\beta }_{3}{W}^{3}-\sum_{i=3}^{n}{\beta }_{2i-1}W(t{)}^{2i-1}$$
(34)

REMARK: If the expression (28) is the exact solution of (27), the right side of (35) completely vanishes.

Considering our approach which is just an approximation one, we set

$$\int^{T/4}_0(k\left({\beta }_{2}A+{\beta }_{3}{A}^{2}+\sum_{i=3}^{n}{\beta }_{2i-1}{A}^{2i-2}\right)W-{\beta }_{2}{W}^{2}-{\beta }_{3}{W}^{3}-\sum_{i=3}^{n}{\beta }_{2i-1}W\left(t{)}^{2i-1}\right)\text{cos}\left(\omega t\right)dt=0$$
(35)

where \(T = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \omega }} \right. \kern-0pt} \omega }\). Solving the above equation, we obtain

$$\begin{gathered} k = \frac{{9\,a\,\beta_{3} \,\pi + 32\,\beta_{2} }}{{12\,a\,\beta_{3} \,\pi + 12\,\beta_{2} \,\pi }}\;\;\;k = \frac{1}{{\beta_{2} + \beta_{3} A + \mathop \sum \nolimits_{i = 3}^{n} \beta_{2i - 1} A^{2i - 3} }}\left( {\frac{{8\beta_{2} }}{3\pi } + \frac{{3\beta_{3} A}}{4} + \mathop \sum \limits_{i = 3}^{n} \beta_{2i - 1} A^{2i - 3} C_{2i} } \right) \hfill \\ k = \frac{{9A\beta_{3} \pi + 32\beta_{2} }}{{12A\beta_{3} \pi + 12\beta_{2} }} \hfill \\ \end{gathered}$$
(36)

where

$$C_{2i} = 4\mathop \smallint \limits_{0}^{\frac{T}{4}} \cos^{2i} \left( {\omega t} \right){\text{d}}t$$

Substituting (32) into (26), the MMA frequency follows

$$\omega =\sqrt{{\beta }_{1}+\frac{8}{3}\frac{{\beta }_{2}A}{\pi }+\frac{3}{4}{\beta }_{3}{A}^{2}+\sum_{i=3}^{n}{\beta }_{2i-1}{A}^{2i-2}{C}_{2i}}$$
(37)

Hence, the approximate solution is readily

$$W\left(t\right)=A\text{cos}\left(t\sqrt{{\beta }_{1}+\frac{8}{3}\frac{{\beta }_{2}A}{\pi }+\frac{3}{4}{\beta }_{3}{A}^{2}+\sum_{i=3}^{n}{\beta }_{2i-1}{A}^{2i-2}{C}_{2i}}\right)$$
(38)

Comparing the frequency (38) of the nonlinear equation with the frequency of the linear system (\(\omega =\sqrt{{\beta }_{1}}\)) the co called ‘nonlinear to linear frequency ratio’ follows

$$\frac{{\omega }_{\text{NL}}}{{\omega }_{L}}=\sqrt{1+\frac{8}{3}\frac{{\beta }_{2}A}{{\beta }_{1}\pi }+\frac{3{\beta }_{3}{A}^{2}}{4{\beta }_{1}}+\sum_{i=3}^{n}\frac{{\beta }_{2i-1}}{{\beta }_{1}}{A}^{2i-2}{C}_{2i}}$$
(39)

For the case when the order of nonlinearity of the foundation is up to cubic order, the frequency ratio modifies into

$$\frac{{\omega }_{\text{NL}}}{{\omega }_{L}}=\sqrt{1+\frac{8}{3}\frac{{\beta }_{2}A}{{\beta }_{1}\pi }+\frac{3{\beta }_{3}{A}^{2}}{4{\beta }_{1}}}$$
(40)

i.e. by substituting (28)

$$\frac{{\omega }_{NL}}{{\omega }_{L}}=\sqrt{1+\frac{8}{3}\frac{{a}_{5}A}{{(a}_{1}+\left(P-{k}_{s}\right){a}_{2}+{k}_{1})\pi }+\frac{3({k}_{2}{a}_{6}+{a}_{7}){A}^{2}}{4({a}_{1}+\left(P-{k}_{s}\right){a}_{2}+{k}_{1})}}$$
(41)

The frequency ratio is the function of the initial amplitude but also of the intensity of the axial force P and parameters of the elastic foundation k1, k2 and ks.

4 Results and discussion

In this paper, Max–Min approach (MMA) is implemented to achieve a high accurate analytical solution for nonlinear vibration of Simply-Supported (S–S) and Clamped–Clamped (C–C) Euler–Bernoulli beams fixed at one end subjected to the axial loads. Lewandowski [25] gave for simply supported beam that \(A=\delta /\sqrt{12}\) and \(A={w}^{*}\left(\frac{1}{2}\right)\delta /\sqrt{12}\) for the clamped—clamped beam where \(\delta\) is the maximum amplitude parameter and \({w}^{*}\left(\frac{1}{2}\right)\) is the middle deflection of the first mode of beam. In Tables 1 and 2, the nonlinear to linear frequencies ratio (41) for the system of the S–S and C–C beams is tabulated. The results are compared for different values of initial amplitude A. The effects of \(\delta\) on the ratio of nonlinear to the linear frequency of the simply-supported beams and clamped–clamped beams are shown. It is notable to mention that Azrar [26] and Lewandowski [25] do not consider the mid-plane effect in their study; therefore, in the large amplitudes, the ratio of nonlinear to linear frequency increases. Numerical results were carried out by using Runge–Kutta method (RKM) and compared with MMA solution.

Table 1 Nonlinear frequency to linear frequency (\({{\omega_{{{\text{NL}}}} } \mathord{\left/ {\vphantom {{\omega_{{{\text{NL}}}} } {\omega_{L} }}} \right. \kern-0pt} {\omega_{L} }}\)) of simply-supported beams
Full size table
Table 2 Nonlner frequency to linear frequency (\({{\omega_{NL} } \mathord{\left/ {\vphantom {{\omega_{NL} } {\omega_{L} }}} \right. \kern-0pt} {\omega_{L} }}\)) of Clamped–Clamped Beams
Full size table

Figure 2 shows the displacement versus time variation obtained analytically, by using equation \(W\left(t\right)=A\text{cos}\left(t\sqrt{{\beta }_{1}+\frac{8}{3}\frac{{\beta }_{2}A}{\pi }+\frac{3}{4}{\beta }_{3}{A}^{2}}\right)\) and numerically, applying the RKM for solving the equation \(\frac{{d}^{2}W(t)}{d{t}^{2}}+{\beta }_{1}W\left(t\right)+{\beta }_{2}W{\left(t\right)}^{2}+{\beta }_{3}W{\left(t\right)}^{3}\) with initial conditions (5) and parameters (23), where k1 = k2 = ks = 1. It is observed that the motion is periodical and dependent on initial conditions. In addition, good agreement between analytical and numerical solutions for both type of beams, the simple supported and the clamped–clamped ones, are found.

Fig. 2
figure 2

Comparison of MMA analytical (full line) and RKM numerical (dotted line) W(t) versus time solutions for: simply supported (S–S) beam (red line) and Clamped–Clamped (C–C) beam (blue line)

Full size image

Using the relation (36), the influence of k1 on the nonlinear to linear frequency ratio (ωNL/ωL) versus amplitude of vibration A for simply supported beam is shown in Fig. 3. It is obtained that frequency ratio has the tendency of increase with increasing of the initial amplitude A. The increase is faster for smaller values of k1 than for higher ones.

Fig. 3
figure 3

Influence of k1 on nonlinear to linear frequency rate versus amplitude variation

Full size image

In Fig. 4, the influence of the coefficient of nonlinear elastic term k2 on the frequency (41) is shown. The frequency ratio is increasing with amplitude A: the higher is the value of k2, the frequency increase is higher.

Fig. 4
figure 4

The effect of k2 on nonlinear to linear frequency ratio for different amplitudes

Full size image

The shear coefficient kS has also an influence on the frequency ratio – amplitude relation (36). The effect of kS is the following: for higher the kS the faster is the frequency – versus amplitude increase (Fig. 5).

Fig. 5
figure 5

The effect of kS on nonlinear to linear frequency ratio for different amplitudes

Full size image

Figure 6 shows the effects of different axial loads on the nonlinear to linear frequency ratio versus amplitude of the clamped–clamped beam. It is obtained that the frequency ratio increases with increasing of the amplitude A. The higher is the value of the axial force, the frequency ratio increase is slower.

Fig. 6
figure 6

The effect of the axial force P on nonlinear to linear frequency ration for different amplitudes

Full size image

5 Conclusions

In this paper, vibrations of the asymmetric laminated composite beam (LCB) subjected to axial load and settled on Winkler–Pasternak elastic foundation are investigated. The Max–Min Approach (MMA) is adopted for providing of analytical solutions for axially loaded Euler Bernoulli beams under two different boundary conditions: (i) Simply-Supported (S–S), and (ii) Clamped–Clamped (C–C). The beam is settled on the Winkler–Pasternak foundation, where the nonlinearity is of polynomial type. The following is concluded:

  1. 1.

    In the beam with weak nonlinearity the value of linear elastic term has the dominant influence on the frequency of vibration. Thus, the higher is the parameter k1 of the linear term, the nonlinear to linear frequency ratio is almost 1. The difference is negligible.

  2. 2.

    However, if the nonlinearity in the beam is strong, the nonlinear frequency differs from the linear one significantly. The higher are the values of coefficients of nonlinearity k2, k3,…kn, the increase in the nonlinear frequency versus the linear one is faster. The same conclusion is valid for the shear coefficient kS.

  3. 3.

    In contrary, for increasing of the axial force P the ratio of the nonlinear to linear frequency is reducing and for sufficiently high value it tends to 1.

  4. 4.

    The MMA procedure is suitable for solving the differential equation with strong nonlinear polynomial displacement. The approximate solution is in good agreement with the exact numerically obtained one.

Finally, it is found that the suggested MMA method is suitable for application, in general, for solving strong nonlinear partial differential equations. It would be a good procedure for vibration analysis of beams with any other type of boundary conditions, too.