Analytical solution for contact and crack problem ın homogeneous half-plane

Abstract

In this study, the frictionless contact and crack problem of an elastic homogeneous semi-infinite plane has been investigated according to the elasticity theory. The problem has been solved as a superposition of the separate solutions of the contact and crack problem. The aim of this study is to find sub-punch stress distributions and stress intensity factors due to opening mode and shear mode for different loading conditions and geometric sizes. There are two rigid punches on the semi-infinite plane and P and Q loads are transferred to the semi-infinite plane by these punches. Problem has been considered as plain strain because of the geometry of the problem. The effect of the mass forces has not been included, the stress and displacement expressions to be used for the contact problem have been obtained by using Navier equations and Fourier integral transformation technique, and the boundary conditions determined for the problem has been applied. The equations to be used for the crack problem have been specified and the boundary conditions for the crack problem have been applied to these equations. The problem has been reduced to an integral equation system consisting of four singular integral equations where contact stresses and crack displacements are unknown. Numerical solution of the integral equation system has been realized by using Jacobi polynomials. Numerical results on sub-punch stress distributions and stress intensity factors have been obtained for different loading conditions, geometric sizes and presented by graphics.

1 Introduction

Contact problems have found many application areas in engineering structures. Examples of these application areas are highways, railways, airport runways, fuel tanks, spherical and cylindrical balls and cylindrical shafts. Elementary theory is inadequate in solving the stress and strain problem in engineering structures. Therefore, there is a need for the theory of elasticity. Although the expressions of elasticity are long and complex, with the developing numerical methods and computer technology, the solution of contact and crack problems has become easier and many studies have been made possible.

Many studies have been done on contact problems for various materials. First study on contact problems in homogeneous materials was put forward by Heinrich Hertz [23] and he maintained the theory for elastic bodies and frictionless surfaces. Erdoğan [19] proposed a method for solving the system of singular integral equations encountered in complex boundary value problems in rigid body mechanics and potential theory. The problem of symmetrical contact for elastic strips with different properties were discussed by Adams and Bogy [1]. Shield and Bogy [43] examined the contact problem of the layer that sits on an elastic semi-infinite plane and is pressed with a rigid punch. Papadopoulos et al. [39] studied about a finite element algorithm for the static solution of two-dimensional frictionless contact problems involving bodies undergoing arbitrarily large motions and deformations. Elsharkawy [18] investigated the frictional contact problem in an elastics half-plane covered with thin elastic layers. Ma and Korsunsky [33] (2006) studied the contact problem in the elastic half-plane covered with a thin layer on which the elastic punch, singular force and friction forces are affected. The continuous contact problem in the elastic half-plane covered with a functionally graded elastic layer was investigated by Ke and Wang [31]. El-Borgi et al. [14] examined the contact problem between the elastic functional graded layer and the homogeneous semi-infinite plane. Özşahin et al. [38] investigated the contact problem of composite elastic layer consisting of layers with different heights and elastic constants resting on two rigid flat punches. Chidlow and Teodorescu [8] studied about the two-dimensional frictionless contact problem of an inhomogeneous elastic composite layer under a rigid punch. Çömez and Erdöl [9] examined frictional contact problem of a rigid stamp and an elastic layer bonded to a homogeneous substrate. Birinci et al. [6] examined continuous and discontinuous cases of a contact problem for two elastic layers supported by a Winkler foundation using both analytical method and finite element method (FEM). El-Borgi and Çömez [16] studied the frictional contact problem of the graded layer that fits into a homogeneous semi-infinite plane and is loaded with a cylindrical rigid punch. Kaya et al. [29] used the finite element method (FEM) to address the problem of frictionless contact of a homogeneous layer that fits on an elastic semi-infinite plane and is loaded with three rigid flat punches.

Advances and research in materials science have led to the invention of materials that form the basis of the twenty-first century's high-tech field. However, with these developments, the need for materials with special characteristics has increased rapidly. The lack of a homogeneous material that provides high strength and thermal resistance, which is required especially in spacecraft, has led researchers to new searches. As a result of these researches, functionally graded materials (FGM) have emerged. The concept of FGM can be defined as a new material with metal/ceramic composition with graded structural functions. The metal in this material pair has toughness, electrical conductivity, and machinability; ceramic has low density, high strength and thermal resistance. In FGM, the material structure and properties change gradually/gradually within the material. With the advancing technology, many contact problems have been addressed for these materials. A receding contact axisymmetric problem between a functionally graded layer and a homogeneous substrate was studied by Rhimi et al. [41]. El-Borgi et al. [15] examined frictional receding contact plane problem between a functionally graded layer and a homogeneous substrate. Öner et al. [34] addressed analytical solution of a contact problem and comparison with the results from finite element method (FEM). The symmetrical double contact problem of functionally graded layers was examined by Liu et al. [32]. In the problem, using the Hankel integral transform method and matrix transfer method, the problem was transformed into two singular integral equation systems. A receding contact problem between a functionally graded layer and two homogeneous quarter planes was studied by Adıyaman et al. [3]. The continuous and discontinuous contact problem of a functionally graded layer resting on a rigid foundation was studied by Karabulut et al. [27]. Çömez [10] addressed the problem of frictional and non-friction contact of the functional graded layer seated on a rigid plane and loaded with a rigid cylindrical punch. The plane contact problem between a finite-thickness laterally graded solid and a rigid stamp of an arbitrary tip-profile was investigated by Arslan [4]. Kaya et al. [30] examined the continuous contact problem of two layers with different material properties, loaded with two rigid flat blocks and resting on a rigid plane using linear elasticity theory and the finite element method (FEM). The receding contact problems in functionally graded layered mediums were evaluated by means of different numerical solutions by Yaylacı et al. [46, 47]. Yaylacı et al. [46, 47] examined comparative study of analytical method, finite element method (FEM) and Multilayer Perceptron (MLP) for analysis of a contact problem. Yaylacı et al. [48] studied about evaluation of the contact problem of functionally graded layer resting on rigid foundation pressed via rigid punch by analytical and numerical (FEM and MLP) methods.

With the increase in studies in materials science, anisotropic materials that do not show the same mechanical properties all over the materials have emerged and many academic studies have been made on these materials. The frictionless receding contact problem between an anisotropic elastic layer and an anisotropic elastic half-plane was studied by Kahya et al. [26]. Akbarov et al. [2] examined dynamics of a system comprising an orthotropic layer and orthotropic half-plane under the action of an oscillating moving load. A semi-smooth newton method for orthotropic plasticity and frictional contact at finite strains was studied by Seitz et al. (2015). Hayashi et al. [24] addressed adhesive contact analysis for anisotropic materials considering surface stress and surface elasticity. On the analytical and finite element solution (FEM) of plane contact problem of a rigid cylindrical punch sliding over a functionally graded orthotropic medium was examined by Güler et al. [22]. Arslan [5] addressed frictional contact problem of an anisotropic laterally graded layer loaded by a sliding rigid stamp. Öner [35, 36] studied about two-dimensional frictionless contact analysis of an orthotropic layer under gravity. Frictionless contact mechanics of an orthotropic coating/isotropic substrate system was examined by Öner [35, 36]. Öner et al. [37] studied about double receding contact problem for two functionally graded layers pressed by a uniformly distributed load. Karabulut et al. [28] addressed continuous and discontinuous contact problem of a functionally graded (FG) orthotropic layer indented by a rigid cylindrical punch using FEM and analytical solution.

Because of very expensive losses associated with fractures, studies on crack problems were especially concentrated during the Second World War. Griffith [21] found that existing cracks in the material play an important role in the loss of strength. Studies are generally aimed at finding the maximum load that a structural member with cracks can carry and determining under which loading conditions the crack begins to grow. In recent years, great progress has been made in the theory of discollations and it has become easier to examine objects with cracks in them. The rapid progress of aviation and the establishment of the space industry have made studies in this direction more necessary. Kadıoğlu and Erdoğan [25] investigated the problem of cracks at the interface of overlapping orthotropic layers. Chen and Erdoğan [7] researched the problem of cracks on the surface of the homogeneous layer graded layer. El-Borgi et al. [17] addressed the problem of cracks in an infinite, functionally graded environment under thermo-mechanical loading. The problem of the crack between the homogeneous semi-infinite plane and the functionally graded layer was examined by Theotokoglou and Paulino [45]. Dağ [12] developed a new calculation method based on the equivalent area integral method for the Mod-I crack analysis of orthotropic functionally graded materials subjected to thermal stresses. Apatay (2010) addressed the problem of crack in frictional contact with rigid flat punch on a homogeneous layer. The crack problem in the frictional contact state of the functional graded layer sitting on a homogeneous semi-infinite plane was studied by Dağ et al. [13]. Romdhane et al. [40] examined the problem of cracks embedded in a functionally graded orthotropic layer sitting on a homogeneous layer, subjected to static normal and tangential surface loading. Talezadehlari et al. [44] investigated the frictional contact crack problem of the functional graded layer, which sits on a homogeneous substrate and loaded with a rigid punch. Punch profiles were taken as circular and flat and separate solutions were made. Sarıkaya and Dağ [42] investigated the crack problem in orthotropic elastic medium exposed to frictional contact with rigid flat punch.

When the literature studies are examined, it is seen that no problem is studied in the loading conditions and geometry in this study. This study will be a good guide for those who want to work on contact and crack problems. The author’s aim is addressing contact crack problem between two rigid flat punch and the semi-infinite plane. The problem is considered as plain strain state because dimension of the problem on z-axis is considered as a unit. By using Navier equations and Fourier integral transform techniques, general stress and displacement expressions to be used for the contact and crack problem of the semi-infinite plane has been obtained. The problem has been reduced to an integral equation system consisting of four singular integral equations by applying the specified boundary conditions for the crack and contact problem to the general equations, in which the contact stresses and crack displacements are unknown. The numerical solution of the integral equation system has been performed by using Jacobi polynomials.

2 Description and formulation of the problem

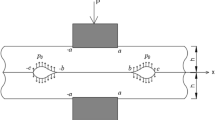
The singular loads are transferred to the homogeneous semi-infinite plane by means of punches in the form of P and Q. Problem is not symmetrical according to y axis. The punches contact the homogeneous semi-infinite plane at intervals [a, b] and [c, d], respectively. Crack depth is expressed with e and mass forces are neglected. The problem has been addressed without the effect of friction. In addition, it has been assumed that the thickness in the z-axis direction is a unit.

The problem has been solved as the superposition of two different problems in Fig. 1.

Fig. 1

Geometry of contact-crack problem between two rigid punch and semi-infinite plane

The crack problem can also be examined as the superposition of Problem 3 and Problem 4 in Fig. 2.

Fig. 2

Superposition of the Contact-Crack Problem as Problem 1 and Problem 2

If the mass forces are neglected, equilibrium equations for a two-dimensional elasticity problem are founded as:

$$\begin{gathered} \frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial\uptau _{xy} }}{\partial y} = 0 \hfill \\ \hfill \\ \end{gathered}$$

(1a)

$$\frac{{\partial \sigma_{y} }}{\partial y} + \frac{{\partial\uptau _{xy} }}{\partial x} = 0$$

(1b)

Using the stress components, displacement–strain relations and constitutive equations in the equilibrium equations, the stress relations are obtained as:

$$\sigma_{x} (x,y) =\uplambda e + 2\mu \left( {\frac{\partial u}{{\partial x}}} \right)$$

(2a)

$$\sigma_{y} (x,y) =\uplambda e + 2\mu \left( {\frac{\partial v}{{\partial y}}} \right)$$

(2b)

$$\uptau _{xy} = \mu \left\{ {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right\}$$

(2c)

The u and v in the expressions represent the displacements in the x and y directions, respectively. µ is the shear modulus of the homogeneous semi-infinite plane, e is the volume change ratio and λ is the Lâme constant. Lâme constant and volume change ratio are given as below, respectively:

$$\uplambda = \frac{{E\upnu }}{{(1 +\upnu )(1 - 2{\upnu )}}}$$

(3a)

$$e = \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}}$$

(3b)

$\nu$ is Poisson ratio in these expressions. If the necessary derivatives of the stress equations are taken and replaced by (1a) and (1b) in the equilibrium equations, Eqs. (4a) and (4b) obtained as:

$${(\lambda } + \mu )\left( {\frac{\partial e}{{\partial x}}} \right) + \mu {\nabla }^{2} u = 0$$

(4a)

$${(\lambda } + \mu )\left( {\frac{\partial e}{{\partial y}}} \right) + \mu {\nabla }^{2} v = 0$$

(4b)

$\nabla$ is partial differential operator and it is defined in two-dimensional problems as:

$$\nabla^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}$$

(5)

There is a situation where the size of the problem in one direction, the z-coordinate direction, is too large compared to the dimensions of the problem in the other two directions (x and y coordinate). Therefore plane strain state is valid for this problem. Navier equations mentioned above are valid for two-dimensional problems. As seen in the above expressions, Navier equations make the solution difficult as part of it forms a set of differential equations. To facilitate the solution, the Fourier integral transform is applied to the u and v displacement components and the Navier equations are transformed into a set of ordinary differential equations. Fourier transforms of the displacement expressions u and v:

$$u(x,y) = \frac{1}{2\pi }\int\limits_{{ - {\infty }}}^{{{ + \infty }}} {\upphi (\upxi ,y)e^{{i\upxi x}} d\upxi }$$

(6a)

$$v(x,y) = \frac{1}{2\pi }\int\limits_{{ - {\infty }}}^{{{ + \infty }}} {\uppsi (\upxi ,y)e^{{i\upxi x}} d\upxi }$$

(6b)

ξ is the Fourier transform variable. Inverse Fourier transforms of these expressions:

$$\upphi (\upxi ,y) = \int\limits_{{ - {\infty }}}^{{{ + \infty }}} {u(\upxi ,y)e^{{ - i\upxi x}} dx}$$

(7a)

$$\uppsi (\upxi ,y) = \int\limits_{{ - {\infty }}}^{{{ + \infty }}} {v(\upxi ,y)e^{{ - i\upxi x}} dx}$$

(7b)

When these equations are applied to Eqs. (4a) and (4b), a set of ordinary differential equations is formed as:

$$- (\uplambda + 2\mu )\upxi ^{2}\upphi + \mu\upphi ^{\prime\prime} + (\uplambda + \mu )i\upxi \uppsi ^{\prime} = 0$$

(8a)

$$(\uplambda + 2\mu )\uppsi ^{\prime\prime} -\upxi ^{2} \mu\uppsi + (\uplambda + \mu )i\upxi \upphi ^{\prime} = 0$$

(8b)

If the necessary definitions are made for the solution of this set of equations and converted to matrix format, the characteristic equation is obtained as:

$$s^{4} - 2\xi^{2} s^{2} + \xi^{4} = 0$$

(9)

The roots of this characteristic equation are obtained as $s_{1} = s_{2} = |\upxi |$ and $s_{3} = s_{4} = - |\upxi |$. In this case, the solution of the ordinary differential equation $\upphi (\upxi ,y)$ and $\uppsi (\upxi ,y)$ are obtained as:

$$\uppsi (\upxi ,y) = \left[ {A_{1} + A_{2} y} \right]e^{{ - |\upxi |y}} + \left[ {A_{3} + A_{4} y} \right]e^{{|\upxi |y}}$$

(10a)

$$\begin{aligned}\upphi (\upxi ,y) = & \left[ { - iA_{1} \frac{{|\upxi |}}{\upxi }e^{{ - |\upxi |y}} } \right] + \left[ {iA_{2} \left( {\frac{\kappa }{\upxi } - y\frac{{|\upxi |}}{\upxi }} \right)e^{{ - |\upxi |y}} } \right] \\ & + \left[ {iA_{3} \left( {\frac{{|\upxi |}}{\upxi }e^{{|\upxi |y}} } \right)} \right] + \left[ {iA_{4} \left( {\frac{\kappa }{\upxi } + y\frac{{|\upxi |}}{\upxi }} \right)e^{{|\upxi |y}} } \right] \\ \end{aligned}$$

(10b)

If these expressions are substituted in Eqs. (7a) and (7b), the displacement expressions of semi-infinite plane are obtained as:

$$u_{1} (x,y) = \frac{1}{2\pi }\int\limits_{{ - {\infty }}}^{{ + {\infty }}} {\left\{ {i\left[ { - A_{1} \frac{{|\upxi |}}{\upxi } + A_{2} \left( {\frac{\kappa }{\upxi } - \frac{{|\upxi |}}{\upxi }y} \right)} \right]e^{{ - |\upxi |y}} + i\left[ {A_{3} \frac{{|\upxi |}}{\upxi } + A_{4} \left( {\frac{\kappa }{\upxi } + \frac{{|\upxi |}}{\upxi }y} \right)} \right]e^{{|\upxi |y}} } \right\}} e^{i\xi x} d\xi$$

(11a)

$$v_{1} (x,y) = \frac{1}{2\pi }\int\limits_{{ - {\infty }}}^{{ + {\infty }}} {\left\{ {\left[ {A_{1} + A_{2} y} \right]e^{{ - |\upxi |y}} + \left[ {A_{3} + A_{4} y} \right]e^{{{|\xi }|y}} } \right\}e^{{i\upxi x}} } d\upxi$$

(11b)

Considering the vertical axis for the elastic semi-infinite plane, the displacements must be zero for y → -∞. When this condition is used, $A_{1}$ and $A_{2}$ will be equal to zero. If the displacement expressions are written in their places in the expressions (2a), (2b) and (2c), the stress relations of the homogeneous semi-infinite plane are as follows:

$$\sigma_{{x_{1} }} (x,y) = \frac{ - \mu }{{2\pi }}\int\limits_{{ - {\infty }}}^{{ + {\infty }}} {\left[ {2A_{3} |\upxi | + A_{4} \left( {(\kappa + 3) + 2|\upxi |y} \right)} \right]} e^{{|\upxi |y + i\upxi x}} d\upxi$$

(12a)

$$\sigma_{{y_{1} }} (x,y) = \frac{\mu }{2\pi }\int\limits_{{ - {\infty }}}^{{ + {\infty }}} {\left[ {2A_{3} |\upxi | + A_{4} \left( {(\kappa - 1) + 2|\upxi |y} \right)} \right]} e^{{|\upxi |y + i\upxi x}} d\upxi$$

(12b)

$$\uptau _{{xy_{1} }} (x,y) = \frac{\mu i}{{2\pi }}\int\limits_{{ - {\infty }}}^{{ + {\infty }}} {\left[ {2A_{3} |\upxi | + A_{4} \left[ {\frac{{{|\xi |}}}{\upxi }(\kappa + 1) + 2\upxi y} \right]} \right]} e^{{|\upxi |y + i\upxi x}} d\upxi$$

(12c)

Index 1 in these equations indicates that the equations belong to Problem 1 in Fig. 3. $\kappa$ is Kolosov constant and it is defined as $\kappa = 3 - 4\nu$ for plain strain situation.

Fig. 3

Crack Problem

3 Solution of contact problem

The boundary conditions for Problem 1 for y = 0 can be written as:

$$\sigma_{{y_{1} }} (x,0) = \left\{ {\begin{array}{*{20}c} { - p(x),} & {b < x < a} & {} \\ { - q(x),} & {c < x < d} & {} \\ {0,} & {other} & {} \\ \end{array} } \right\}$$

(13a)

$$\uptau _{{xy_{1} }} (x,0) = 0,\;\left( { - \infty < {\text{x}} < + \infty } \right)$$

(13b)

$$\frac{\partial }{\partial x}v_{1} (x,0) = 0,\;\;(b < x < a)$$

(13c)

$$\frac{\partial }{\partial x}v_{1} (x,0) = 0,\;(c < x < d)$$

(13d)

The equilibrium equations for the problem are as follows:

$$\int\limits_{b}^{a} {p(t)dt} = - P$$

(14a)

$$\int\limits_{c}^{d} {q(t)dt} = - Q$$

(14b)

The expressions p(x) and q(x) in the boundary conditions are the unknown contact stresses between punches and semi-infinite plane. When the boundary conditions (13a) and (13b) are applied to the stress expressions of the homogeneous semi-infinite plane and the inverse Fourier transforms of these equations are taken, two equations with two unknowns are obtained as:

$$2|\upxi |A_{3} + (\upkappa - 1)A_{4} = - \frac{1}{\mu }\int\limits_{b}^{a} {p(t)e^{{ - i\upxi t}} dt - } \frac{1}{\mu }\int\limits_{c}^{d} {q(t)e^{{ - i\upxi t}} dt}$$

(15a)

$$2|\upxi |A_{3} + \left[ {\frac{{|\upxi |}}{\upxi }(\kappa + 1)} \right]A_{4} = 0$$

(15b)

When this set of equations is solved, $A_{3}$ and $A_{4}$ coefficients are obtained. If these coefficients are written in the expression of the derivative of Eq. (11b) with respect to x, Eq. (12a), Eq. (12b), Eq. (12c) and integrals are converted to the interval (0, + ∞) and the closed integrals of stress and displacement expressions are taken, stress and displacement expressions are obtained as:

$$\begin{aligned} \sigma_{{x_{1} }} (x,y) = & \int\limits_{b}^{a} {p(t)dt\frac{1}{2\pi }\left[ {\frac{2( - y)}{{y^{2} + (t - x)^{2} }} + \frac{{2y\left[ {y^{2} - (t - x)^{2} } \right]}}{{y^{2} + (t - x)^{2} }}} \right]} \\ & + \int\limits_{c}^{d} {q(t)dt\frac{1}{2\pi }\left[ {\frac{2( - y)}{{y^{2} + (t - x)^{2} }} + \frac{{2y\left[ {y^{2} - (t - x)^{2} } \right]}}{{y^{2} + (t - x)^{2} }}} \right]} \\ \end{aligned}$$

(16a)

$$\begin{aligned} \sigma_{{y_{1} }} (x,y) = & \int\limits_{b}^{a} {p(t)dt\frac{1}{2\pi }\left[ {\frac{2y}{{y^{2} + (t - x)^{2} }} + \frac{{2y\left[ {y^{2} - (t - x)^{2} } \right]}}{{y^{2} + (t - x)^{2} }}} \right]} \\ & + \int\limits_{c}^{d} {q(t)dt\frac{1}{2\pi }\left[ {\frac{2y}{{y^{2} + (t - x)^{2} }} + \frac{{2y\left[ {y^{2} - (t - x)^{2} } \right]}}{{y^{2} + (t - x)^{2} }}} \right]} \\ \end{aligned}$$

(16b)

$$\uptau _{{xy_{1} }} (x,y) = \frac{1}{\pi }\int\limits_{b}^{a} {p(t)dt\left[ {\frac{{ - 2y^{2} (t - x)}}{{\left[ {y^{2} + (t - x)^{2} } \right]^{2} }}} \right]} + \frac{1}{\pi }\int\limits_{c}^{d} {q(t)dt\left[ {\frac{{ - 2y^{2} (t - x)}}{{\left[ {y^{2} + (t - x)^{2} } \right]^{2} }}} \right]}$$

(16c)

$$\begin{aligned} \frac{{\partial v_{1} (x,y)}}{\partial x} = & - \frac{1}{4\pi \mu }\int\limits_{b}^{a} {p(t)dt\left[ {\frac{{ - 4y^{2} (t - x)}}{{\left[ {y^{2} + (t - x)^{2} } \right]^{2} }} - (1 + \kappa )\frac{(t - x)}{{\left[ {y^{2} + (t - x)^{2} } \right]}}} \right]} \\ & - \frac{1}{4\pi \mu }\int\limits_{c}^{d} {q(t)dt\left[ {\frac{{ - 4y^{2} (t - x)}}{{\left[ {y^{2} + (t - x)^{2} } \right]^{2} }} - (1 + \kappa )\frac{(t - x)}{{\left[ {y^{2} + (t - x)^{2} } \right]}}} \right]} \\ \end{aligned}$$

(16d)

Since the closed integrals of the kernels of the integral equations are taken, the singularity that occurs in the integral equations is directly eliminated. Closed integration operations will also be applied to the crack problem.

4 Solution of crack problem

Stress and displacement expressions to be used for the crack problem:

For x > 0,

$$u_{3}^{x > 0} (x,y) = \frac{1}{2\pi }\int\limits_{{ - {\infty }}}^{{ + {\infty }}} {\left[ {\frac{{i|\upxi |}}{\upxi }B_{3} + (\frac{i\kappa }{\upxi } + \frac{{i|\upxi |}}{\upxi }x)B_{4} } \right]} e^{{ - |{\upxi |}x{ + }i\upxi y}} d\upxi$$

(17a)

$$v_{3}^{x > 0} (x,y) = \frac{1}{2\pi }\int\limits_{{ - {\infty }}}^{{ + {\infty }}} {\left( {B_{3} + B_{4} x} \right)} e^{{ - |{\upxi |}x{ + }i\upxi y}} d\upxi$$

(17b)

$$\sigma_{{x_{3} }}^{x > 0} (x,y) = - \frac{\mu i}{{2\pi }}\int\limits_{ - \infty }^{ + \infty } {\left[ {2{\upxi {\rm B}}_{3} + \left[ {(\kappa + 1)|\upxi | + 2\upxi ^{2} x} \right]\frac{{B_{4} }}{\upxi }} \right]} e^{{ - |\upxi |x + i\upxi y}} d\upxi$$

(17c)

$$\sigma_{{y_{3} }}^{x > 0} (x,y) = \frac{\mu i}{{2\pi }}\int\limits_{ - \infty }^{ + \infty } {\left[ {2\upxi B_{3} + \left[ { - (3 - \kappa )|\upxi | + 2\upxi ^{2} x} \right]\frac{{B_{4} }}{\upxi }} \right]} e^{{ - |\upxi |x + i\upxi y}} d\upxi$$

(17d)

$$\uptau _{{xy_{3} }}^{x > 0} (x,y) = \frac{ - \mu }{{2\pi }}\int\limits_{ - \infty }^{ + \infty } {\left[ {2|{\upxi |}B_{3} + \left[ {(\kappa - 1) + 2|{\upxi |}x} \right]B_{4} } \right]} e^{{ - |\upxi |x + i\upxi y}} d\upxi$$

(17e)

For x < 0,

$$u_{3}^{x < 0} (x,y) = \frac{1}{2\pi }\int\limits_{{ - {\infty }}}^{{ + {\infty }}} {\left[ { - \frac{{i|\upxi |}}{\upxi }B_{1} + (\frac{i\kappa }{\upxi } - \frac{{i|\upxi |}}{\upxi }x)B_{2} } \right]} e^{{|{\upxi |}x{ + }i\upxi y}} d\upxi$$

(18a)

$$v_{3}^{x < 0} (x,y) = \frac{1}{2\pi }\int\limits_{{ - {\infty }}}^{{ + {\infty }}} {\left( {B_{1} + B_{2} x} \right)} e^{{|{\upxi |}x{ + }i\upxi y}} d\upxi$$

(18b)

$$\sigma_{{x_{3} }}^{x < 0} (x,y) = \frac{\mu i}{{2\pi }}\int\limits_{ - \infty }^{ + \infty } {\left[ { - 2{\upxi {\rm B}}_{1} + \left[ {(\kappa + 1)|\upxi | - 2\upxi ^{2} x} \right]\frac{{B_{2} }}{\upxi }} \right]} e^{{|\upxi |x + i\upxi y}} d\upxi$$

(18c)

$$\sigma_{{y_{3} }}^{x < 0} (x,y) = \frac{ - \mu i}{{2\pi }}\int\limits_{ - \infty }^{ + \infty } {\left[ { - 2\upxi B_{1} + - \left[ {(3 - \kappa )|\upxi | + 2\upxi ^{2} x} \right]\frac{{B_{2} }}{\upxi }} \right]} e^{{|\upxi |x + i\upxi y}} d\upxi$$

(18d)

$$\uptau _{{xy_{3} }}^{x < 0} (x,y) = \frac{\mu }{2\pi }\int\limits_{ - \infty }^{ + \infty } {\left[ {2|{\upxi |}B_{1} + \left[ { - (\kappa - 1) + 2|{\upxi |}x} \right]B_{2} } \right]} e^{{|\upxi |x + i\upxi y}} d\upxi$$

(18e)

Boundary conditions for Problem 3 are as follows:

$$\sigma_{{x_{3} }}^{x > 0} (0,y) = \sigma_{{x_{3} }}^{x < 0} (0,y),\;\;\left( { - \infty < {\text{y}} < + \infty } \right)$$

(19a)

$$\uptau _{{xy_{3} }}^{x > 0} (0,y) =\uptau _{{xy_{3} }}^{x < 0} (0,y),\;( - \infty < {\text{y}} < + \infty )$$

(19b)

$$\frac{2\mu }{{\upkappa + 1}}\frac{\partial }{\partial y}\left( {u_{3}^{x > 0} (x,y) - u_{3}^{x < 0} (x,y)} \right) = \left\{ {\begin{array}{*{20}c} {f_{1} (y),} & {e < y < 0} \\ {0,} & {other} \\ \end{array} } \right\}$$

(19c)

$$\frac{2\mu }{{\upkappa + 1}}\frac{\partial }{\partial y}\left( {v_{3}^{x > 0} (x,y) - v_{3}^{x < 0} (x,y)} \right) = \left\{ {\begin{array}{*{20}c} {f_{2} (y),} & {e < y < 0} \\ {0,} & {other} \\ \end{array} } \right\}$$

(19d)

These expressions can be defined as functions of the horizontal and vertical displacement difference in the crack. If these boundary conditions are applied to stress and displacement expressions, four sets of equations with four unknowns are obtained as:

$$- 2{\upxi {\rm B}}_{1} + [(\kappa + 1)\frac{{|\upxi |}}{\upxi }]B_{2} + 2{\upxi {\rm B}}_{3} + [(\kappa + 1)\frac{{|\upxi |}}{\upxi }]B_{4} = 0$$

(20a)

$$2|\upxi |B_{1} + [ - (\kappa - 1)]B_{2} + 2|\upxi |B_{3} + (\kappa - 1)\upxi B_{4} = 0$$

(20b)

$$- |\upxi |B_{1} + \kappa B_{2} - |\upxi |B_{3} - \kappa B_{4} = \frac{\kappa + 1}{{2\mu }}\int\limits_{e}^{0} {f_{1} (t)e^{{ - i\upxi t}} dt}$$

(20c)

$$- i{\upxi {\rm B}}_{1} + i{\upxi {\rm B}}_{2} = \frac{\kappa + 1}{{2\mu }}\int\limits_{e}^{0} {f_{2} (t)e^{{ - i\upxi t}} dt}$$

(20d)

The coefficients $B_{1}$, $B_{2}$, $B_{3}$ and $B_{4}$ are obtained by solving these equations. If these coefficients are replaced in stress and displacement expressions and reduced to the intervals of integrals (0, + ∞) and closed integrals of stress and displacement expressions are taken as is done in the contact problem, stress and displacement expressions for problem 3 are obtained as:

$$\sigma_{{x_{3} }} (x,y) = - \frac{1}{\pi }\int\limits_{e}^{0} {f_{1} (t)dt} \left[ {\frac{{(y - t)\left[ {3x^{2} + (y - t)^{2} } \right]}}{{\left[ {x^{2} + (y - t)^{2} } \right]^{2} }}} \right] - \frac{1}{\pi }\int\limits_{e}^{0} {f_{2} (t)dt\left[ {\frac{{x\left[ { - x^{2} + (y - t)^{2} } \right]}}{{\left[ {x^{2} + (y - t)^{2} } \right]^{2} }}} \right]}$$

(21a)

$$\sigma_{{y_{3} }} (x,y) = \frac{1}{\pi }\int\limits_{e}^{0} {f_{1} (t)dt} \left[ {\frac{{(y - t)\left[ {x^{2} + (y - t)^{2} } \right]}}{{\left[ {x^{2} + (y - t)^{2} } \right]^{2} }}} \right] - \frac{1}{\pi }\int\limits_{e}^{0} {f_{2} (t)dt\left[ {\frac{{x\left[ {x^{2} + 3(y - t)^{2} } \right]}}{{\left[ {x^{2} + (y - t)^{2} } \right]^{2} }}} \right]}$$

(21b)

$$\uptau _{{xy_{3} }} (x,y) = \frac{1}{\pi }\int\limits_{e}^{0} {f_{1} (t)dt} \left[ {\frac{{x\left[ {x^{2} - (y - t)^{2} } \right]}}{{\left[ {x^{2} + (y - t)^{2} } \right]^{2} }}} \right] + \frac{1}{\pi }\int\limits_{e}^{0} {f_{2} (t)dt\left[ {\frac{{(y - t)\left[ {x^{2} - (y - t)^{2} } \right]}}{{\left[ {x^{2} + (y - t)^{2} } \right]^{2} }}} \right]}$$

(21c)

$$\begin{aligned} \frac{{\partial v_{3} (x,y)}}{\partial x} = & \frac{1}{4\mu \pi }\int\limits_{e}^{0} {f_{1} (t)dt} \left[ {\frac{{(1 - \kappa )x^{3} - x(3 +\upkappa )(y - t)^{2} }}{{\left[ {x^{2} + (y - t)^{2} } \right]^{2} }}} \right] \\ & + \frac{1}{4\mu \pi }\int\limits_{e}^{0} {f_{2} (t)dt} \left[ {\frac{{(1 - \kappa )x^{2} - (3 + \kappa )(y - t)^{2} }}{{\left[ {x^{2} + (y - t)^{2} } \right]^{2} }}} \right] \\ \end{aligned}$$

(21d)

The following equations must also be provided in order to solve the problem with the crack:

$$\sigma_{{y_{2} }} (x,0) = \sigma_{{y_{3} }} (x,0) + \sigma_{{y_{4} }} (x,0) = 0,\;\;\;\left( { - \infty < {\text{x}} < + \infty } \right)$$

(22a)

$$\uptau _{{xy_{2} }} (x,0) =\uptau _{{xy_{3} }} (x,0) +\uptau _{{xy_{4} }} (x,0) = 0,\;\;\left( { - \infty < {\text{x}} < + \infty } \right)$$

(22b)

The superscripts 2, 3 and 4 in these expressions show that the expressions belong to Problem 2, Problem 3 and Problem 4, respectively. When Eqs. (22a) and (22b) are applied, respectively:

$$\frac{1}{\pi }\int\limits_{e}^{0} {\frac{{( - t)(x^{2} - t^{2} )}}{{(x^{2} + t^{2} )^{2} }}} f_{1} (t)dt + \frac{1}{\pi }\int\limits_{e}^{0} {\frac{{x^{3} + 3xt^{2} }}{{(x^{2} + t^{2} )^{2} }}} f_{2} (t)dt + \frac{\mu }{2\pi }\int\limits_{ - \infty }^{ + \infty } {\left[ {2|\upxi |C_{1} + (\kappa - 1)C_{2} } \right]} e^{{i\upxi x}} d\upxi = 0$$

(23a)

$$\frac{1}{\pi }\int\limits_{e}^{0} {\frac{{x^{3} - xt^{2} }}{{(x^{2} + t^{2} )^{2} }}} f_{1} (t)dt + \frac{1}{\pi }\int\limits_{e}^{0} {\frac{{( - t)(x^{2} - t^{2} )}}{{(x^{2} + t^{2} )^{2} }}} f_{2} (t)dt + \frac{\mu i}{{2\pi }}\int\limits_{ - \infty }^{ + \infty } {\left[ {2\upxi C_{1} + (\kappa + 1)\frac{{|\upxi |}}{\upxi }C_{2} } \right]} e^{{i\upxi x}} d\upxi = 0$$

(23b)

As can be understood from Eqs. (23a) and (23b), the stress expressions for Problem 4 are the same as the displacement and stress expressions obtained for the contact problem in the first section, provided that the coefficients are different. When the inverse Fourier transforms of Eqs. (23a) and (23b) are taken, two equations with two unknowns emerge. With the solution of the equation set, the coefficients $C_{1}$ and $C_{2}$ are found. When these coefficients are replaced in stress and displacement expressions and the integrals are reduced to the interval (0, ∞) and closed integrals of stress and displacement expressions are taken, stress and displacement expressions for Problem 2 are obtained as:

$$\begin{aligned} \sigma_{{x_{2} }} (x,y) = & \frac{1}{\pi }\int\limits_{e}^{0} {f_{1} (t)dt} \left[ {\frac{{16yt(y + t)^{3} - 2(y + t)(y^{2} + 10yt + 3t^{2} )\left[ {(y + t)^{2} + x^{2} } \right]}}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right. \\ &\left. { + \frac{{(3y + 5t)\left[ {(y + t)^{2} + x^{2} } \right]^{2} }}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right] \\ &+ \frac{1}{\pi }\int\limits_{e}^{0} {f_{2} (t)dt\left[ {\frac{{16xyt(y + t)^{2} - 2x\left( {3t^{2} + 4yt - y^{2} } \right)\left[ {(y + t)^{2} + x^{2} } \right]}}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right.} \\ &\left. { - \frac{{x\left[ {(y + t)^{2} + x^{2} } \right]^{2} }}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right] \\ \end{aligned}$$

(24a)

$$\begin{aligned} \sigma _{{y_{2} }} (x,y) = & \frac{1}{\pi }\int\limits_{e}^{0} {f_{1} (t)dt} \left[ {\frac{{ - 16yt(y + t)^{3} - 2(y + t)\left( { - y^{2} - 6ty + t^{2} } \right)\left[ {(y + t)^{2} + x^{2} } \right]}}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right. \\ & \left. { - \frac{{( - y + t) + \left[ {(y + t)^{2} + x^{2} } \right]^{2} }}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right] \\ & + \frac{1}{\pi }\int\limits_{e}^{0} {f_{2} (t)dt} \left[ {\frac{{ - 16xyt(y + t)^{2} - 2x\left( {y^{2} + t^{2} } \right)\left[ {x^{2} + (y + t)^{2} } \right]}}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right. \\ & \left. { - \frac{{x\left[ {(y + t)^{2} + x^{2} } \right]^{2} }}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right] \\ \end{aligned}$$

(24b)

$$\begin{aligned} {\tau }_{{xy_{2} }} (x,y) = & \frac{1}{\pi }\int\limits_{e}^{0} {f_{1} (t)dt} \left[ {\frac{{ - 16xyt(y + t)^{2} - 2x\left( {4yt + y^{2} + t^{2} } \right)\left[ {(y + t)^{2} + x^{2} } \right]}}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right. \\ & \left. { - \frac{{x\left[ {(y + t)^{2} + x^{2} } \right]^{2} }}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right] \\ & + \frac{1}{\pi }\int\limits_{e}^{0} {f_{2} (t)dt} \left[ {\frac{{ - 16xyt(y + t)^{3} - 2(y + t)\left[ { - y^{2} + 6yt + t^{2} } \right][(y + t)^{2} + x^{2} ]}}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right. \\ & \left. { + \frac{{(t - y)\left[ {(y + t)^{2} + x^{2} } \right]^{2} }}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right] \\ \end{aligned}$$

(24c)

$$\begin{aligned} \frac{{\partial v_{2} }}{\partial x}(x,y) = & \frac{1}{4\mu \pi }\int\limits_{e}^{0} {f_{1} (t)dt} \left[ {\frac{{x\left[ {(\kappa + 3)\left( {y^{4} - 8yt^{3} } \right) - 6(\kappa + 8)y^{2} t^{2} } \right.}}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right. \\ & \left. { + \frac{{\left. {(\kappa - 1)x^{4} + 2(\kappa + 1)x^{2} \left( {y^{2} - t^{2} } \right) - (1 + 3\kappa )t^{4} + 8yt\left( {x^{2} - 2y^{2} } \right)} \right]}}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right] \\ & + \frac{1}{4\mu \pi }\int\limits_{e}^{0} {f_{2} (t)dt} \left[ {\frac{{(\kappa + 3)y^{5} + 2(\kappa + 1)x^{2} \left( {y^{3} + t^{3} } \right)}}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right. + \frac{{(\upkappa - 1)x^{4} (y - t) + 6(\kappa - 3)yx^{2} t(y + t)}}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }} \\ & \left. { + \frac{{2(9\kappa + 23)t^{2} y^{3} + 2(11\kappa + 21)t^{3} y^{2} + (13\kappa + 5)t^{4} y}}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }} + \frac{{(7\kappa + 21)ty^{4} + (1 + 3\kappa )t^{5} }}{{\left[ {(y + t)^{2} + x^{2} } \right]^{3} }}} \right] \\ \end{aligned}$$

(24d)

5 Numerical solution of ıntegral equations

Boundary conditions from which the p(t), q(t), f₁(t) and f₂(t) unknowns in the crack-contact problem are obtained as:

$$\sigma_{x} (0,y) = \sigma_{{x_{1} }} (0,y) + \sigma_{{x_{2} }} (0,y) = 0,\;\;\left( {{\text{e}} < {\text{y}} < 0} \right)$$

(25a)

$$\uptau _{xy} (0,y) =\uptau _{{xy_{1} }} (0,y) +\uptau _{{xy_{2} }} (0,y) = 0,\;\;\left( {{\text{e}} < {\text{y}} < 0} \right)$$

(25b)

$$\frac{\partial v(x,0)}{{\partial x}} = 0,\;\;\left( {{\text{b}} < {\text{x}} < {\text{a}}} \right)$$

(25c)

$$\frac{\partial v(x,0)}{{\partial x}} = 0,\;\;\left( {{\text{c}} < {\text{x}} < {\text{d}}} \right)$$

(25d)

If these boundary conditions are applied to the sum of expressions belonging to the derivative of stress and vertical displacement found for Problem 1 and Problem 2; Eqs. (26a), (26b), (26c) and (26d) are obtained as:

$$\begin{gathered} \frac{1}{\pi }\int\limits_{e}^{0} {\frac{{f_{1} (t_{1} )}}{{t_{1} - y_{1} }}dt_{1} + \frac{1}{\pi }\int\limits_{e}^{0} {f_{1} (t_{1} )K_{11} (t_{1} ,y_{1} )dt_{1} } } \hfill \\ + \frac{1}{\pi }\int\limits_{b}^{a} {p(t_{3} )K_{13} (t_{3} ,y_{1} )dt_{3} } \hfill \\ + \frac{1}{\pi }\int\limits_{c}^{d} {q(t_{4} )K_{14} (t_{4} ,y_{1} )dt_{4} } = 0\;\;\;\;\;\left( {{\text{e}} < {\text{y}}_{{1}} < 0} \right) \hfill \\ \end{gathered}$$

(26a)

$$\begin{gathered} \frac{1}{\pi }\int\limits_{e}^{0} {\frac{{f_{2} (t_{2} )}}{{t_{2} - y_{2} }}dt_{2} + \frac{1}{\pi }\int\limits_{e}^{0} {f_{2} (t_{2} )K_{22} (t_{2} ,y_{2} )dt_{2} } } \hfill \\ + \frac{1}{\pi }\int\limits_{b}^{a} {p(t_{3} )K_{23} (t_{3} ,y_{2} )dt_{3} } \hfill \\ + \frac{1}{\pi }\int\limits_{c}^{d} {q(t_{4} )K_{24} (t_{4} ,y_{2} )dt_{4} } = 0\;\;\;\;\;\left( {{\text{e}} < {\text{y}}_{{2}} < 0} \right) \hfill \\ \end{gathered}$$

(26b)

$$\begin{gathered} \frac{1}{\pi }\int\limits_{e}^{0} {f_{1} } \left( {t_{1} } \right)K_{31} \left( {t_{1} ,y_{3} } \right)dt_{1} + \frac{1}{\pi }\int\limits_{e}^{0} {f_{2} } \left( {t_{2} } \right)K_{32} \left( {t_{3} ,x_{3} } \right)dt_{2} \hfill \\ + \frac{1}{\pi }\int\limits_{b}^{a} {\frac{{p(t_{3} )}}{{t_{3} - x_{3} }}dt_{3} + \frac{1}{\pi }\int\limits_{c}^{d} {\frac{{q(t_{4} )}}{{t_{4} - x_{3} }}dt_{4} } } = 0\;\;\;\;\;\;\;\;\;\left( {{\text{b}} < {\text{x}}_{{3}} < {\text{a}}} \right) \hfill \\ \end{gathered}$$

(26c)

$$\begin{gathered} \frac{1}{\pi }\int\limits_{e}^{0} {f_{1} (t_{1} )K_{41} (t_{1} ,x_{4} )dt_{1} } + \frac{1}{\pi }\int\limits_{e}^{0} {f_{2} (t_{2} )K_{42} (t_{2} ,x_{4} )dt_{2} } \hfill \\ + \frac{1}{\pi }\int\limits_{b}^{a} {\frac{{p(t_{3} )}}{{t_{3} - x_{4} }}dt_{3} + \frac{1}{\pi }\int\limits_{c}^{d} {\frac{{q(t_{4} )}}{{t_{4} - x_{4} }}dt_{4} } } = 0\;\;\;\;\;\;\;\left( {{\text{c}} < {\text{x}}_{{4}} < {\text{d}}} \right) \hfill \\ \end{gathered}$$

(26d)

When the equilibrium equations are arranged as:

$$\int\limits_{b}^{a} {p(t_{3} )dt_{3} } = - P$$

(27a)

$$\int\limits_{c}^{d} {q(t_{4} )dt_{4} } = - Q$$

(27b)

Dimensionless quantities are be defined to be able to numerically solve integral equations as:

$$y_{1} = - \frac{e}{2}s_{1} + \frac{e}{2}$$

(28a)

$$y_{2} = - \frac{e}{2}s_{2} + \frac{e}{2}$$

(28b)

$$t_{1} = - \frac{e}{2}r_{1} + \frac{e}{2}$$

(28c)

$$t_{2} = - \frac{e}{2}r_{2} + \frac{e}{2}$$

(28d)

$$t_{3} = \frac{(a - b)}{2}r_{3} + \frac{a + b}{2}$$

(28e)

$$t_{4} = \frac{(d - c)}{2}r_{4} + \frac{d + c}{2}$$

(28f)

$$x_{3} = \frac{a - b}{2}s_{3} + \frac{a + b}{2}$$

(28g)

$$x_{4} = \frac{d - c}{2}s_{4} + \frac{d + c}{2}$$

(28h)

$$g_{1} (r_{1} ) = \frac{a - b}{P}f_{1} ( - \frac{e}{2}r_{1} + \frac{e}{2})$$

(28i)

$$g_{2} (r_{2} ) = \frac{a - b}{P}f_{2} ( - \frac{e}{2}r_{2} + \frac{e}{2})$$

(28j)

$$g_{3} (r_{3} ) = \frac{(a - b)}{P}P\left[ {\frac{a - b}{2}r_{3} + \frac{b + a}{2}} \right]$$

(28k)

$$g_{4} (r_{4} ) = \frac{a - b}{P}Q\left[ {\frac{d - c}{2}r_{4} + \frac{d + c}{2}} \right]$$

(28l)

In these expressions, g₁(r₁) and g₂(r₂) represent dimensionless quantities due to unknown stress intensity factors at the crack ends, g₃(r₃) and g₄(r₄) expressions indicate dimensionless quantities due to unknown contact stresses between punch and semi-infinite plane. When these dimensionless quantities are written in Eqs. (26a), (26b), (26c) and (26d), respectively:

$$\begin{gathered} - \frac{1}{\pi }\int\limits_{ - 1}^{1} {\frac{{g_{1} (r_{1} )}}{{r_{1} - s_{1} }}} dr_{1} + \int\limits_{ - 1}^{1} {M_{11} (r_{1} ,s_{1} )g_{1} (r_{1} )dr_{1} + \int\limits_{ - 1}^{1} {M_{13} (r_{3} ,s_{1} )g_{3} (r_{3} )dr_{3} } } \hfill \\ + \int\limits_{ - 1}^{1} {M_{14} (r_{4} ,s_{1} )g_{4} (r_{4} )dr_{4} } = 0 \hfill \\ \end{gathered}$$

(29a)

$$\begin{gathered} - \frac{1}{\pi }\int\limits_{ - 1}^{1} {\frac{{g_{2} (r_{2} )}}{{r_{2} - s_{2} }}} dr_{2} + \int\limits_{ - 1}^{1} {M_{22} (r_{2} ,s_{2} )g_{2} (r_{2} )dr_{2} + \int\limits_{ - 1}^{1} {M_{23} (r_{3} ,s_{2} )g_{3} (r_{3} )dr_{3} } } \hfill \\ + \int\limits_{ - 1}^{1} {M_{24} (r_{4} ,s_{2} )g_{4} (r_{4} )dr_{4} } = 0 \hfill \\ \end{gathered}$$

(29b)

$$\begin{gathered} \int\limits_{ - 1}^{1} {g_{1} (r_{1} )M_{31} (r_{1} ,s_{3} )dr_{1} + \int\limits_{ - 1}^{1} {g_{2} (r_{2} )M_{32} (r_{2} ,s_{3} )dr_{2} - \frac{1}{\pi }\int\limits_{ - 1}^{1} {\frac{{g_{3} (r_{3} )}}{{r_{3} - s_{3} }}dr_{3} } } } \hfill \\ + \frac{1}{\pi }\int\limits_{ - 1}^{1} {\frac{{g_{4} (r_{4} )}}{{\left[ {\frac{(d - c)}{2}r_{4} + \frac{d + c}{2}} \right] - \left[ {\frac{(b - a)}{2}s_{3} + \frac{b + a}{2}} \right]}}} \frac{d - c}{2}dr_{4} = 0 \hfill \\ \end{gathered}$$

(29c)

$$\begin{gathered} \int\limits_{ - 1}^{1} {g_{1} (r_{1} )M_{41} (r_{1} ,s_{4} )dr_{1} + \int\limits_{ - 1}^{1} {g_{2} (r_{2} )M_{42} (r_{2} ,s_{4} )dr_{2} } } \hfill \\ - \frac{1}{\pi }\int\limits_{ - 1}^{1} {\frac{{g_{3} (r_{3} )}}{{\left[ {\frac{a - b}{2}r_{3} + \frac{b + a}{2}} \right] - \left[ {\frac{d - c}{2}s_{4} + \frac{d + c}{2}} \right]}}\frac{a - b}{2}dr_{3} } + \frac{1}{\pi }\int\limits_{ - 1}^{1} {\frac{{g_{4} (r_{4} )}}{{r_{4} - s_{4} }}dr_{4} = 0} \hfill \\ \end{gathered}$$

(29d)

Numerical solution of integral equations is done with the help of Jacobi polynomials. Solution of integral equations are sought as:

$$g_{1} (r_{1} ) = (1 - r_{1} )^{{_{ - 1/2} }} \sum\limits_{n = 0}^{\infty } {A_{n} P_{n}^{( - 1/2,0)} (r_{1} )}$$

(30a)

$$g_{2} (r_{2} ) = (1 - r_{2} )^{ - 1/2} \sum\limits_{n = 0}^{\infty } {B_{n} P_{n}^{( - 1/2,0)} (r_{2} )}$$

(30b)

$$g_{3} (r_{3} ) = (1 - r_{3} )^{ - 1/2} (1 - r_{3} )^{ - 1/2} \sum\limits_{n = 0}^{\infty } {C_{n} P_{n}^{( - 1/2, - 1/2)} (r_{3} )}$$

(30c)

$$g_{4} (r_{4} ) = (1 - r_{4} )^{ - 1/2} (1 - r_{4} )^{ - 1/2} \sum\limits_{n = 0}^{\infty } {D_{n} P_{n}^{( - 1/2, - 1/2)} (r_{4} )}$$

(30d)

In these equations P_n Jacobi polynomial, A_n, B_n, C_n and D_n are unknown constants. When Eqs. (30a)-(30d) are written in Eqs. (29a)-(29d), 4N + 2 a linear equation is obtained that consists of 4N + 2 unknowns and 4N + 2 equations where g₁(r₁), g₂(r₂), g₃(r₃) and g₄(r₄) is unknown.

The first unknown constant in the expansion of with Jacobi polynomials defined in Eq. (30c) using Eq. (14a) and Eq. (28 k) is obtained as:

$$C_{0} = - {2 \mathord{\left/ {\vphantom {2 \pi }} \right. \kern-0pt} \pi }$$

(31a)

Similarly, the first unknown constant in the expansion of with Jacobi polynomials defined in Eq. (30d) using Eq. (14b) and Eq. (28 l) is obtained as:

$$D_{0} = {{2P} \mathord{\left/ {\vphantom {{2P} Q}} \right. \kern-0pt} Q}\pi$$

(31b)

When Eqs. (30a)-(30d), (30a), (30b) are written in Eqs. (29a) and (29d):

$$\begin{gathered} \sum\limits_{n = 0}^{N} {A_{n} \left\{ {\frac{{\Gamma ( - 1/2)\Gamma (n + 1)}}{{\pi \sqrt 2\Gamma (n + 1/2)}}F(n + 1, - n + \frac{1}{2};\frac{3}{2};\frac{{1 - s_{1} }}{2})} \right\}} \hfill \\ + \int\limits_{ - 1}^{1} {\left[ { - \frac{1}{\pi }\frac{e}{2}K_{11} \left( { - \frac{e}{2}r_{1} + \frac{e}{2}, - \frac{e}{2}s_{1} + \frac{e}{2}} \right)} \right]} (1 - r_{1} )^{ - 1/2} P_{n}^{( - 1/2,0)} (r_{1} )dr_{1} \hfill \\ + \sum\limits_{n = 1}^{N} {C_{n} \int\limits_{ - 1}^{1} {\left[ { - \frac{1}{\pi }\frac{a - b}{2}K_{13} \left[ {\frac{a - b}{2}r_{3} + \frac{b + a}{2}, - \frac{e}{2}s_{1} + \frac{e}{2}} \right]} \right]} } x(1 - r_{3} )^{ - 1/2} (1 + r_{3} )^{ - 1/2} P_{n}^{( - 1/2, - 1/2)} (r_{3} )dr_{3} \hfill \\ + \sum\limits_{n = 1}^{N} {D_{n} \int\limits_{ - 1}^{1} {\frac{1}{\pi }\frac{d - c}{2}K_{14} \left[ {\frac{d - c}{2}r_{4} + \frac{d + c}{2}, - \frac{e}{2}s_{1} + \frac{e}{2}} \right]} } x(1 - r_{4} )^{ - 1/2} (1 + r_{4} )^{ - 1/2} P_{n} (r_{4} )dr_{4} \hfill \\ = \frac{2}{\pi }\int\limits_{ - 1}^{1} {\left[ { - \frac{1}{\pi }\frac{a - b}{2}K_{13} \left[ {\frac{a - b}{2}r_{3} + \frac{a + b}{2},\frac{e}{2}s_{1} + \frac{e}{2}} \right]} \right]} x(1 - r_{3} )^{ - 1/2} (1 + r_{3} )^{ - 1/2} P_{0}^{( - 1/2, - 1/2)} (r_{3} )dr_{3} \hfill \\ + \left[ { - \frac{(a - b)2Q}{{(d - c)P\pi }}} \right]\int\limits_{ - 1}^{1} {\left[ {\frac{1}{\pi }\frac{(d - c)}{2}K_{14} \left[ {\frac{d - c}{2}r_{4} + \frac{d - c}{2},\frac{e}{2}s_{1} + \frac{e}{2}} \right]} \right]} \hfill\\ \;x(1 - r_{4} )^{ - 1/2} (1 - r_{4} )^{ - 1/2} P_{0}^{( - 1/2, - 1/2)} (r_{4} )dr_{4} \hfill \\ \end{gathered}$$

(32a)

$$\begin{gathered} \sum\limits_{n = 0}^{N} {B_{n} \left\{ {\frac{{\Gamma ( - 1/2)\Gamma (n + 1)}}{{\pi \sqrt 2\Gamma (n + 1/2)}}F(n + 1, - n + \frac{1}{2};\frac{3}{2};\frac{{1 - s_{2} }}{2})} \right\}} \hfill \\ + \int\limits_{ - 1}^{1} {\left[ { - \frac{1}{\pi }\frac{e}{2}K_{22} \left( { - \frac{e}{2}r_{2} + \frac{e}{2}, - \frac{e}{2}s_{2} + \frac{e}{2}} \right)} \right]} (1 - r_{2} )^{ - 1/2} P_{n}^{( - 1/2,0)} (r_{2} )dr_{2} \hfill \\ + \sum\limits_{n = 1}^{N} {C_{n} \int\limits_{ - 1}^{1} {\left[ { - \frac{1}{\pi }\frac{a - b}{2}K_{23} \left[ {\frac{a - b}{2}r_{3} + \frac{b + a}{2},\frac{e}{2}s_{2} + \frac{e}{2}} \right]} \right]} } (1 - r_{3} )^{ - 1/2} (1 + r_{3} )^{ - 1/2} P_{n}^{( - 1/2, - 1/2)} (r_{3} )dr_{3} \hfill \\ + \sum\limits_{n = 1}^{N} {D_{n} \int\limits_{ - 1}^{1} {\frac{1}{\pi }\frac{a - b}{2}K_{24} \left[ {\frac{d - c}{2}r_{4} + \frac{d + c}{2}, - \frac{e}{2}s_{2} + \frac{e}{2}} \right]} } x(1 - r_{4} )^{ - 1/2} (1 + r_{4} )^{ - 1/2} P_{n}^{( - 1/2, - 1/2)} (r_{4} )dr_{4} \hfill \\ = \left( { - \frac{2}{\pi }} \right)\int\limits_{ - 1}^{1} {\left[ { - \frac{1}{\pi }\frac{a - b}{2}K_{23} \left[ {\frac{a - b}{2}r_{3} + \frac{a + b}{2},\frac{e}{2}s_{2} + \frac{e}{2}} \right]} \right]} x(1 - r_{3} )^{ - 1/2} (1 + r_{3} )^{ - 1/2} P_{0}^{( - 1/2, - 1/2)} (r_{3} )dr_{3} \hfill \\ + \frac{2P}{{Q\pi }}\int\limits_{ - 1}^{1} {\left[ {\frac{1}{\pi }\frac{(a - b)}{2}K_{24} \left[ {\frac{a - b}{2}r_{4} + \frac{a + b}{2},\frac{e}{2}s_{2} + \frac{e}{2}} \right]} \right]} x(1 - r_{4} )^{ - 1/2} (1 + r_{4} )^{ - 1/2} P_{0}^{( - 1/2, - 1/2)} (r_{4} )dr_{4} \hfill \\ \end{gathered}$$

(32b)

$$\begin{gathered} \sum\limits_{n = 0}^{N} {A_{n} } \int\limits_{ - 1}^{1} {\left( { - \frac{1}{\pi }\frac{e}{2}K_{31} \left[ { - \frac{e}{2}r_{1} + \frac{e}{2},\frac{a - b}{2}s_{3} + \frac{b + a}{2}} \right]} \right)} \left( {1 - r_{1} } \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}} P_{n}^{{\left( {{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2},0} \right)}} \left( {r_{1} } \right)dr_{1} \hfill \\ + \sum\limits_{n = 0}^{N} {B_{n} \int\limits_{ - 1}^{1} {\left( { - \frac{1}{\pi }\frac{e}{2}K_{32} \left[ { - \frac{e}{2}r_{2} + \frac{e}{2},\frac{a - b}{2}s_{3} + \frac{b + a}{2}} \right]} \right)} } (1 - r_{2} )^{ - 1/2} P_{n}^{( - 1/2,0)} (r_{2} )dr_{2} \hfill \\ + \left( { - \frac{1}{2}} \right)\sum\limits_{n = 1}^{N} {C_{n} P_{n - 1}^{( - 1/2, - 1/2)} (s_{3} ) + \sum\limits_{n = 1}^{N} {D_{n} \int\limits_{ - 1}^{1} {\frac{1}{\pi }\left[ {\frac{1}{{\left( {\frac{d - c}{2}r_{4} + \frac{d + c}{2}} \right) - \left( {\frac{a - b}{2}s_{3} + \frac{b + a}{2}} \right)}}} \right]} } } \hfill \\ x\frac{d - c}{2}(1 - r_{4} )^{ - 1/2} (1 + r_{4} )^{ - 1/2} P_{n}^{( - 1/2, - 1/2)} (r_{4} )dr_{4} \hfill \\ = \left[ { - \frac{(a - b)2Q}{{(d - c)P\pi }}} \right]\int\limits_{ - 1}^{1} {\frac{1}{\pi }} \left[ {\frac{1}{{\left( {\frac{d - c}{2}r_{4} + \frac{d - c}{2}} \right) - \left( {\frac{a - b}{2}r_{4} + \frac{a + b}{2}} \right)}}} \right] \hfill \\ x\left( {\frac{d - c}{2}} \right)(1 - r_{4} )^{ - 1/2} (1 + r_{4} )^{ - 1/2} P_{0}^{( - 1/2, - 1/2)} (r_{4} )dr_{4} \hfill \\ \end{gathered}$$

(32c)

$$\begin{gathered} \sum\limits_{n = 0}^{N} {A_{n} \int\limits_{ - 1}^{1} {\left( { - \frac{1}{\pi }\frac{e}{2}K_{41} \left[ { - \frac{e}{2}r_{1} + \frac{e}{2},\frac{d - c}{2}s_{4} + \frac{d + c}{2}} \right]} \right)} } (1 - r_{1} )^{ - 1/2} P_{n}^{( - 1/2,0)} (r_{1} )dr_{1} \hfill \\ + \sum\limits_{n = 0}^{N} {B_{n} \int\limits_{ - 1}^{1} {\left( { - \frac{1}{\pi }\frac{e}{2}K_{42} \left[ { - \frac{e}{2}r_{2} + \frac{e}{2},\frac{d - c}{2}s_{4} + \frac{d + c}{2}} \right]} \right)} } (1 - r_{2} )^{ - 1/2} P_{n}^{( - 1/2,0)} (r_{2} )dr_{2} \hfill \\ + \frac{1}{\pi }\sum\limits_{n = 1}^{N} {C_{n} \int\limits_{ - 1}^{1} {\left[ {\frac{1}{{\left( {\frac{a - b}{2}r_{3} + \frac{a + b}{2}} \right) - \left( {\frac{d - c}{2}s_{4} + \frac{d + c}{2}} \right)}}} \right]} \left( {\frac{a - b}{2}} \right)(1 - r_{3} )^{ - 1/2} (1 + r_{3} )^{ - 1/2} } \hfill \\ xP_{n}^{( - 1/2, - 1/2)} (r_{3} )dr_{3} + \frac{1}{2}\sum\limits_{n = 1}^{N} {D_{n} } P_{n - 1}^{(1/2,1/2)} (s_{4} ) \hfill \\ = \frac{2}{\pi }\int\limits_{ - 1}^{1} {\left( { - \frac{1}{\pi }} \right)} \frac{1}{{\left( {\frac{a - b}{2}r_{3} + \frac{a + b}{2}} \right) - \left( {\frac{d - c}{2}s_{4} + \frac{d + c}{2}} \right)}}x\left( {\frac{b - a}{2}} \right)(1 - r_{3} )^{ - 1/2} (1 - r_{3} )^{ - 1/2} P_{0}^{( - 1/2, - 1/2)} (r_{3} )dr_{3} \hfill \\ \end{gathered}$$

(32d)

Г is the gamma function and F is the hypergeometric function. The roots of Jacobi polynomials in equations are defined as:

$$s_{1i} = s_{2i} = \cos \left( {\frac{\pi }{2}\left( {\frac{2i - 1}{{N + 1}}} \right)} \right)\;\;\;\;\;{\text{i}} = {1}, \ldots ..,{\text{N}} + {1}$$

(33a)

$$s_{3i} = s_{4i} = \cos \left( {\frac{\pi }{2}\left( {\frac{2i - 1}{N}} \right)} \right)\;\;\;\;\;\;\;{\text{i}} = {1}, \ldots ..,{\text{N}}$$

(33b)

6 Stress ıntensity factors

The Mod-I and Mod-II (opening and sliding mode) stress intensity factors at the crack tips can be defined as [20] and [11]:

$$k_{1} = \lim_{y \to e} \sqrt {2(y - e)\sigma_{x} (0,y)}$$

(34a)

$$k_{2} = \lim_{y \to e} \sqrt {2(y - e)\uptau _{xy} (0,y)}$$

(34b)

Normalized stress intensity factors are obtained as:

$$\frac{{k_{1} \sqrt { - e} }}{P} = \frac{ - e}{{a - b}}\sum\limits_{n = 0}^{N} {A_{n} P_{n}^{( - 1/2,0)} (1)}$$

(35a)

$$\frac{{k_{2} \sqrt { - e} }}{P} = \frac{ - e}{{a - b}}\sum\limits_{n = 0}^{N} {B_{n} P_{n}^{( - 1/2,0)} (1)}$$

(35b)

7 Numerical results

In this section, using the formulations given in the previous section, crack depth, punch widths, different loading conditions and the stress intensity factors at the crack tip depending on the variation of the distance between the punches and the crack and the stress distribution under the punch are examined. According to these parameters, numerical values are given as tables and graphs and the findings are examined.

In Fig. 4, the stress distributions formed under the punches according to the variation of the crack depth are given. As can be seen from the figure, it is seen that the change in crack depth does not have a significant effect on the sub-punch stress distributions.

Fig. 4

Sub-punch stress distribution in both punches according to the change of crack depth ($\kappa$ = 2, ν = 0.25, a/b = 0.5, c/b = -1, d/b = -1.5, P/Q = 2)

The effect of the change of P / Q ratio on sub-punch stress distributions is investigated in Fig. 5. As the P/Q ratio increased; although there is no significant change in the sub-punch stresses in the punch affected by the P load, there is a decrease in the sub-punch stresses in the punch affected by the Q load. The reason why there is no change in the sub-block stresses in the block affected by the P load; for example, when the load P increases by 2 times, the stresses increase by 2 times, but since the nondimensionalization of the contact stresses is done with P, P in the expression (p(x)/(P/b)) also increases by 2 times. Since the numerator and denominator have doubled, they simplify each other. For this reason, the stress distribution under the block does not change in the block affected by the P load.

Fig. 5

The sub-punch stress distribution in both punches according to the change of the P/Q ratio ($\kappa$ = 2, ν = 0.25, a/b = 0.5, c/b = -1, d/b = -1.5, e/b = -0.5)

The effect of the change in the width of the punch to which the Q load is applied on the stress distributions under the punches is examined in Fig. 6. As the width of the punch to which the Q load is applied increases, the sub-punch stresses occurring in the same punch decreases, while the sub-punch stresses occurring under the punch where the P load is applied do not cause a significant change.

Fig. 6

The sub-punch stress distribution in both punches according to the change of the punch width to which the Q load is applied ($\kappa$ = 2, ν = 0.25, P/Q = 0.25, a/b = 0.5, c/b = -1, e/b = -0.5)

The effect of P/Q ratio change on ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ is investigated in Table 1 and Fig. 7. When the table and figure are examined, as the P/Q ratio increases, ${k}_{1}\sqrt{-e}/P$ stress intensity factor decreases. When the P/Q ratio is lower than 0.379811, ${k}_{2}\sqrt{-e}/P$ stress intensity factor takes negative values. Therefore, ${k}_{2}\sqrt{-e}/P$ stress intensity factor takes positive values for P/Q = 0.5 and P/Q = 1.5, while it takes negative values for P/Q = 0.25.

Table 1 Change of ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ stress intensity factors for different P/Q ratio ($\kappa$ = 2, ν = 0.25, a/b = 0.5, c/b = −1, d/b = −1.5)

Fig. 7

Change of ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ stress intensity factors for different P/Q ratio ($\kappa$ = 2, ν = 0.25, a/b = 0.5, c/b = -1, d/b = -1.5)

In Table 2 and Fig. 8., the effect on the stress intensity factors ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ according to the change of P/Q ratio is examined when the punch positions and punch widths are the same. When the punches is not symmetrical, as the P/Q ratio increased ${k}_{1}\sqrt{-e}/P$ stress intensity factor decreases. As the e/b ratio, the crack depth, increases; ${k}_{1}\sqrt{-e}/P$ and absolute value of ${k}_{2}\sqrt{-e}/P$ increases. Also, for P/Q = 1, ${k}_{2}\sqrt{-e}/P$ value is found to be zero as expected.

Table 2 The change of the values of the ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ stress intensity factors for different P/Q ratios when the punch positions and punch widths are the same ($\kappa$ = 2, ν = 0.25, a/b = 0.5, c/b = −0.5, d/b = −1)

Fig. 8

The change of the values of the ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ stress intensity factors for different P/Q ratios when the punch positions and punch widths are the same ($\kappa$ = 2, ν = 0.25, a/b = 0.5, c/b = -0.5, d/b = -1)

In Table 3 and Fig. 9, the effect of the change of punch width to which the P load is applied on the stress intensity factors is examined. As the width of the punch applied on the P load increases; the effect of the P load on the crack will decrease according to the effect of the Q load on the crack and crack opening will occur. Therefore, as the width of this punch increases, ${k}_{1}\sqrt{-e}/P$ stress intensity factor increases. ${k}_{2}\sqrt{-e}/P$ stress intensity factor which take negative value decreases.

Table 3 The variation of the stress intensity factors ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ obtained for various values of the width of the punch on which the load P is applied ($\kappa$ = 2, ν = 0.25, P/Q = 4, c/b = −1, d/b = −1.5)

Fig. 9

The variation of the stress intensity factors ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ obtained for various values of the width of the punch on which the load P is applied ($\kappa$ = 2, ν = 0.25, a/b = 0.5, c/b = -0.5, d/b = -1)

In Table 4 and Fig. 10, the effect of the variation of the width of the punch on which the Q load is applied on the stress intensity factors obtained from the opening and shear modes is examined. As the width of this punch increases, ${k}_{1}\sqrt{-e}/P$ stress intensity factor decreases, ${k}_{2}\sqrt{-e}/P$ stress intensity factor increases.

Table 4 The variation of the stress intensity factors ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ obtained for various values of the width of the punch on which the load Q is applied ($\kappa$ = 2, ν = 0.25, P/Q = 0.25, a/b = 0.5, c/b = −1)

Fig. 10

The variation of the stress intensity factors ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ obtained for various values of the width of the punch on which the load Q is applied ($\kappa$ = 2, ν = 0.25, P/Q = 0.25, a/b = 0.5, c/b = -1)

In Table 5 and Fig. 11, the effect of the distance from the crack on the stress intensity factors of the punch to which the P load is applied is examined. As the punch moved away from the crack, the stress intensity factor ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ decreases. For a/b = 0.89, ${k}_{2}\sqrt{-e}/P$ stress intensity factor changes sign.

Table 5 The change of the ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ stress intensity factors obtained for various values of the distance from the crack of the punch on which the load P is applied ($\kappa$ = 2, ν = 0.25, P/Q = 4)

Fig. 11

The change of the ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ stress intensity factors obtained for various values of the distance from the crack of the punch on which the load P is applied ($\kappa$ = 2, ν = 0.25, P/Q = 4)

In Table 6 and Fig. 12, the effect of the change of the distance of the punch to which the Q load is applied to the crack on the stress intensity factors is examined. As the distance between the punch and the crack increases, ${k}_{1}\sqrt{-e}/P$ stress intensity factor decreases and ${k}_{2}\sqrt{-e}/P$ stress intensity factor increases.

Table 6 The change of the ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ stress intensity factors obtained for various values of the distance from the crack of the punch on which the load Q is applied ($\kappa$ = 2, ν = 0.25, P/Q = 0.25, a/b = 0.5)

Fig. 12

The change of the ${k}_{1}\sqrt{-e}/P$ and ${k}_{2}\sqrt{-e}/P$ stress intensity factors obtained for various values of the distance from the crack of the punch on which the load Q is applied ($\kappa$ = 2, ν = 0.25, P/Q = 0.25, a/b = 0.5)

8 Conclusion

There are three different modes for a crack in fracture mechanics. These are Mode I—opening mode (tensile stress perpendicular to the crack plane), Mode II—sliding mode (shear stress acting parallel to the crack plane and perpendicular to the crack front) and Mode III—tear mode (shear stress acting parallel to the crack plane and parallel to the crack front). The most important of these 3 modes is Mode I. In this study, Mode I and Mode II problems are valid for crack due to normal forces applied by the punch. As a result of the parametric analysis obtained at the end of the study, the effects of parameters such as punch width and punch position on the stress intensity multipliers obtained for these two modes, as well as their effects on the normal and shear stress distributions on the crack, are investigated.

The fact that the stress intensity factor ${k}_{1}\sqrt{-e}/P$ obtained from the opening mode (Mode I) is less than zero is a situation that occurs due to the tensile forces acting on the system and in this case the crack is closed. However, within the scope of this study, because of pressure forces acting on the system, ${k}_{1}\sqrt{-e}/P$ values were higher than zero in the results and the opening mode occurred. The fact that the stress intensity factor ${k}_{2}\sqrt{-e}/P$ obtained from the sliding mode (Mode II) is greater than zero or less indicates that there is a difference between the vertical displacements in the slip plane in the crack.

Appendix

$$K_{11} (t,y) = K_{22} (t,y) = - \frac{1}{t + y} + \frac{6y}{{t + y}} - \frac{{4y^{2} }}{{(t + y)^{3} }}$$

(34a)

$$K_{13} (t,y) = K_{14} (t,y) = - \frac{2yt}{{(y + t)^{2} }}$$

(34b)

$$K_{23} (t,y) = K_{24} (t,y) = - \frac{{2y^{2} t}}{{(y^{2} + t^{2} )^{2} }}$$

(34c)

$$K_{31} (t,x) = K_{41} (t,x) = - \frac{{4xt^{2} }}{{(x^{2} + t^{2} )^{2} }}$$

(34d)

$$K_{32} (t,x) = K_{42} (t,x) = \frac{{4x^{3} }}{{(x^{2} + t^{2} )^{2} }}$$

(34e)

$$M_{11} (r_{1} ,s_{1} ) = - \frac{1}{\pi }\frac{e}{2}K_{11} \left( { - \frac{e}{2}r_{1} + \frac{e}{2}, - \frac{e}{2}s_{1} + \frac{e}{2}} \right)$$

(35a)

$$M_{13} (r_{3} ,s_{1} ) = - \frac{1}{\pi }\frac{a - b}{2}K_{13} \left( {\frac{a - b}{2}r_{3} + \frac{b + a}{2}, - \frac{e}{2}s_{1} + \frac{e}{2}} \right)$$

(35b)

$$M_{14} (r_{4} ,s_{1} ) = \frac{1}{\pi }\frac{d - c}{2}K_{14} \left( {\frac{d - c}{2}r_{4} + \frac{d + c}{2}, - \frac{e}{2}s_{1} + \frac{e}{2}} \right)$$

(35c)

$$M_{22} (r_{2} ,s_{2} ) = - \frac{1}{\pi }\frac{e}{2}K_{22} \left( { - \frac{e}{2}r_{2} + \frac{e}{2}, - \frac{e}{2}s_{2} + \frac{e}{2}} \right)$$

(35d)

$$M_{23} (r_{3} ,s_{2} ) = - \frac{1}{\pi }\frac{a - b}{2}K_{23} \left( {\frac{a - b}{2}r_{3} + \frac{b + a}{2}, - \frac{e}{2}s_{2} + \frac{e}{2}} \right)$$

(35e)

$$M_{24} (r_{4} ,s_{2} ) = \frac{1}{\pi }\frac{d - c}{2}K_{24} \left( {\frac{d - c}{2}r_{4} + \frac{d + c}{2}, - \frac{e}{2}s_{2} + \frac{e}{2}} \right)$$

(35f)

$$M_{31} (r_{1} ,s_{3} ) = - \frac{1}{\pi }\frac{e}{2}K_{31} \left[ { - \frac{e}{2}r_{1} + \frac{e}{2},\frac{a - b}{2}s_{3} + \frac{b + a}{2}} \right]$$

(35g)

$$M_{32} (r_{2} ,s_{3} ) = - \frac{1}{\pi }\frac{e}{2}K_{32} \left[ { - \frac{e}{2}r_{2} + \frac{e}{2},\frac{a - b}{2}s_{3} + \frac{b + a}{2}} \right]$$

(35h)

$$M_{41} (r_{1} ,s_{4} ) = - \frac{1}{\pi }\frac{e}{2}K_{41} \left[ { - \frac{e}{2}r_{1} + \frac{e}{2},\frac{d - c}{2}s_{4} + \frac{d + c}{2}} \right]$$

(35i)

$$M_{42} (r_{2} ,s_{4} ) = - \frac{1}{\pi }\frac{e}{2}K_{42} \left[ { - \frac{e}{2}r_{2} + \frac{e}{2},\frac{d - c}{2}s_{4} + \frac{d + c}{2}} \right]$$

(35j)