Research on tunable characteristics of trapped thickness-twist waves in a magneto-elastic inhomogeneous plate

Abstract

Characteristics of trapped thickness-twist waves in an inhomogeneous plate consists of the piezomagnetic material and elastic material affected by the magnetic field and compressive stress are investigated theoretically in the article. Variations of the effective elastic, piezomagnetic and magnetic permeability constants in the piezomagnetic material with the magnetic field and compressive stress are analyzed. The active controls of trapping characteristics have been achieved. Bisection method is used to solve the frequency equation of trapped thickness-twist waves. It is found that the number of trapped modes increase as the central region length increase and the magnetic field can not only induce new trapped modes in the structure but also accelerate the energy trapping. The advantage of this method is that the trapping characteristics can be modulated easily and without physical contact.

1 Introduction

Acoustic wave devices such as resonators, sensors and transformers have received much attention with the rapid development of communication technology. In order to facilitate the integration of these devices with the performance not affected by mounting and wiring, acoustic wave devices with energy trapping features have been developed [1, 2], in which the vibration modes are confined to be near the specific region and there are no vibrations in the rest. Researchers have made a great effort on studying energy trapping behaviors in various device structures [3,4,5,6,7,8].

Cai et al. [9] investigated the acoustic radiation forces exerted on a cylindrical particle near the surface of a periodically structured brass plate and found trapping effect appears when resonance of the structured plate occurs. The energy trapping behaviors in a beam structure of generic boundary conditions with attached springs and/or finite masses have been discussed in detail [10]. Weber [11] investigated theoretically the trapped rotational interfacial waves by using a Lagrangian formulation of fluid motion in a rotating ocean. By symmetrically placing the rectangular cavities with specific aspect ratios on either side of a duct, new trapped modes were founded in the structure [12]. The effects of elastic bottom and barriers on characteristics of trapped modes were analyzed respectively [13, 14]. The existence of trapped modes in specific structures placed in the fluid had been proved [15,16,17].

Choura and Yigit [18, 19] found that the vibration confinement in flexible structures could be achieved by applying appropriate distributed feedback forces. The trapping phenomenon in acoustic devices was founded to be able to facilitate the energy harvesting and discussed in detail [20]. The existence of trapped modes in various elastic beams and plates were studied [21,22,23,24,25]. Polzikova et al. [26] investigated the energy trapping characteristics of Rayleigh waves in a composite resonator structure. Kokkonen et al. [27] developed a method to determine the energy trapping range of the resonator. Trapped thickness-twist waves were founded in an inhomogeneous piezoelectric plate, in which the frequency of the wave in central region is lower than that in outer regions [28]. The energy trapping effect had been achieved by placing an additional mass-loading layer in the gap region between the two working electrodes in lateral-field-excited acoustic wave devices [29].

In order to enhance the energy utilization, researchers devote themselves to seek various approaches to improve the energy trapping features of acoustic wave devices. Tiersten [30] analyzed the modulation of trapped thickness-shear modes in AT-cut quartz resonators. The effects of electrodes on trapped modes in acoustic wave resonators were analyzed comprehensively [31,32,33,34]. Yang and Kosinski [35] pointed out that the effects of piezoelectric coupling on energy trapping need to be considered in a partially electroded piezoelectric crystal plate with monoclinic symmetry. Besides, functionally graded materials were widely used in acoustic devices to improve the energy trapping features [36,37,38].

In order to maintain the stability of acoustic wave devices, the energy trapping features, which are susceptible to external disturbances, should be highly tunable to improve the device performance. Once the device structure is fixed, the energy trapping features are hardly affected by approaches proposed above [30,31,32,33,34,35,36,37,38]. In this paper, we investigate the effects of the magnetic field and compressive stress on energy trapping features of thickness-twist modes in an inhomogeneous plate, in which the central region is the piezomagnetic material and the rest is the elastic material. The advantage of this method is that the energy trapping features of acoustic wave devices are tuned easily without changing the device structure.

2 Theoretical model and solution procedure

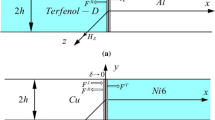
The inhomogeneous plate, in which the thickness-twist waves propagation, is shown in Fig. 1. The central region (|x|< a) of the plate with thickness 2 h is the piezomagnetic material Terfenol-D and the rest region is the elastic material Ag. The magnetic field and compressive stress applied in the central region are along z direction. The nonlinear constitutive relation of the piezomagnetic material is [39]:

$$\begin{aligned} & \varepsilon_{ij} = \frac{1}{E}\left[ {\left( {1 + \nu } \right)\sigma_{ij} - \nu \sigma_{kk} \delta_{ij} } \right] + \frac{{\lambda_{s} }}{{M_{s}^{2} }}\left[ {\frac{3}{2}M_{i} M_{j} - M_{k} M_{k} \left( {\frac{1}{2}\delta_{ij} + \frac{{{\tilde{\sigma }}_{ij} }}{{\sigma_{s} }}} \right)} \right], \\& H_{k} = \left\{ {\frac{1}{kM}f^{ - 1} \left( {\frac{M}{{M_{s} }}} \right)\delta_{kl} - \frac{{\lambda_{s} }}{{\mu_{0} M_{s}^{2} }}\left[ {\frac{{2{\tilde{\sigma }}_{kl} - \left( {{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } } \right)\delta_{kl} }}{{\sigma_{s} }}} \right]} \right\}M_{l} ,\end{aligned}$$

(1)

where ε_ij and σ_ij are the strain and the stress tensors, E and ν are Young’s modulus and Poisson’s ratio, λ_s, M_s and σ_s are the saturation magnetostriction, magnetization and stress, respectively. $k = {3\chi_{m} } / {M_{s}}$ is the relaxation factor, where χ_m is the susceptibility in the initial linear region. δ_ij is the Kronecker delta. $M = \sqrt {M_{k} M_{k} }$ denotes the magnitude of the magnetization vector M. ${\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } = {{2\tilde{\sigma }_{ij} \tilde{\sigma }_{ij} } {\left/ {\vphantom {{2\tilde{\sigma }_{ij} \tilde{\sigma }_{ij} } 3}} \right. \kern-\nulldelimiterspace} 3}$, where $\tilde{\sigma }_{ij} = {{3\sigma_{ij} } {\left/ {\vphantom {{3\sigma_{ij} } 2}} \right. \kern-\nulldelimiterspace} 2} - {{\sigma_{kk} \delta_{ij} } \mathord{\left/ {\vphantom {{\sigma_{kk} \delta_{ij} } 2}} \right. \kern-\nulldelimiterspace} 2}$ is 3/2 times as much as the deviatoric stress σ_ij. $f\left( x \right) = \coth \left( x \right) - {1 {\left/ {\vphantom {1 x}} \right. \kern-\nulldelimiterspace} x}$ is the Langevin function and $\mu_{0} = 4\pi \times 10^{ - 7}$ H/m is the vacuum permeability.

Fig. 1

Inhomogeneous plate with the piezomagnetic material in the central region and elastic material in outer regions

Using the engineering shear strain, the matrix forms of Eq. (1) shown in Appendix A can be expressed into the linear forms of the constitutive relations in the piezomagnetic material [40]:

$$\begin{gathered} \sigma_{ij} = c_{ijkl} \left( {{\varvec{H}},{\varvec{\sigma}}} \right)\varepsilon_{kl} - q_{mij} \left( {{\varvec{H}},{\varvec{\sigma}}} \right)H_{m} , \hfill \\ B_{n} = q_{nkl} \left( {{\varvec{H}},{\varvec{\sigma}}} \right)\varepsilon_{kl} + \mu_{nm} \left( {{\varvec{H}},{\varvec{\sigma}}} \right)H_{m} , \hfill \\ \end{gathered}$$

(2)

where σ_ij and B_n are the components of the stress and magnetic flux density, $c_{ijkl} \left( {{\varvec{H}},{\varvec{\sigma}}} \right)$, $q_{mij} \left( {{\varvec{H}},{\varvec{\sigma}}} \right)$ and $\mu_{nm} \left( {{\varvec{H}},{\varvec{\sigma}}} \right)$ are the effective elastic constants, piezomagnetic constants and magnetic permeability constants, respectively. H and σ are applied magnetic field vector and stress vector. The expressions of these material constants are shown in Appendix B for brevity.

2.1 Solutions for the central region

First, consider the central region (|x|< a) of the plate shown in Fig. 1. The upper and lower surfaces of the plate are unelectroded and traction-free. Thickness-twist waves are governed by:

$$\begin{gathered} u_{x} = u_{y} = 0,\quad \quad u_{z} = u\left( {x,y,t} \right), \hfill \\ \quad \quad \quad \varphi = \varphi \left( {x,y,t} \right), \hfill \\ \end{gathered}$$

(3)

where u_x, u_y and u_z are mechanical displacements along x, y and z directions, respectively. φ is the magnetic potential. Because the matrix forms of the effective material constants in the piezomagnetic material are the same as those in [40, 41], the governing equations of thickness-twist waves can be expressed as [41]:

$$\begin{gathered} c_{44} \nabla^{2} u + q_{15} \nabla^{2} \varphi = \rho \ddot{u}, \hfill \\ q_{15} \nabla^{2} u - \mu_{11} \nabla^{2} \varphi = 0, \hfill \\ \end{gathered}$$

(4)

where c₄₄, q₁₅ and μ₁₁ are the elastic, piezomagnetic and magnetic permeability constants, respectively. ρ is the mass density. $\nabla^{2} { = }{{\partial^{2} } \mathord{\left/ {\vphantom {{\partial^{2} } {\partial x^{2} }}} \right. \kern-\nulldelimiterspace} {\partial x^{2} }} + {{\partial^{2} } \mathord{\left/ {\vphantom {{\partial^{2} } {\partial y^{2} }}} \right. \kern-\nulldelimiterspace} {\partial y^{2} }}$ is the two-dimensional Laplacian operator and the dot refers to time differentiation. The solutions for trapped thickness-twist waves propagation in the x direction and symmetric in the y direction can be expressed as [28]:

$$\begin{gathered} u = \left( {A_{1} \cos \xi_{1} x + A_{2} \sin \xi_{1} x} \right)\cos \xi_{2} y\exp \left( {i\omega t} \right), \hfill \\ \varphi = \left[ {\left( {B_{1} \cosh \xi_{2} x + B_{2} \sinh \xi_{2} x} \right) + \frac{{q_{15} }}{{\mu_{11} }}\left( {A_{1} \cos \xi_{1} x + A_{2} \sin \xi_{1} x} \right)} \right]\cos \xi_{2} y\exp \left( {i\omega t} \right), \hfill \\ \end{gathered}$$

(5)

where

$$\begin{gathered} \xi_{1} = \sqrt {\frac{{\rho \omega^{2} }}{{\overline{c}_{44} }} - \xi_{2}^{2} } = {{\sqrt {\omega^{2} - \omega_{m}^{2} } } \mathord{\left/ {\vphantom {{\sqrt {\omega^{2} - \omega_{m}^{2} } } {v_{T} }}} \right. \kern-\nulldelimiterspace} {v_{T} }},\quad \overline{c}_{44} = c_{44} + \frac{{q_{15}^{2} }}{{\mu_{11} }},\quad v_{T} = \sqrt {\frac{{\overline{c}_{44} }}{\rho }} , \hfill \\ \xi_{2} = \frac{m\pi }{{2h}},\quad \omega_{m}^{2} = \left( {\frac{m\pi }{{2h}}} \right)^{2} \frac{{\overline{c}_{44} }}{\rho },\quad \left( {m = 0,2,4,...} \right), \hfill \\ \end{gathered}$$

A₁, A₂, B₁ and B₂ are undetermined constants, ω is the wave frequency, i² = −1 and t is the time, $\overline{c}_{44}$ is the effective elastic constant, v_T is the shear wave speed and ω_m is the cutoff frequency of thickness-twist waves in the piezomagnetic material. The nonzero stress τ_xz and magnetic flux density B_x can be obtained by substituting Eq. (5) into Eq. (2):

$$\begin{aligned} \tau_{xz} = & c_{44} \frac{\partial u}{{\partial x}} + q_{15} \frac{\partial \varphi }{{\partial x}} = \left[ {\overline{c}_{44} \xi_{1} \left( { - A_{1} \sin \xi_{1} x + A_{2} \cos \xi_{1} x} \right)} \right. \\ & + \left. {q_{15} \xi_{2} \left( {B_{1} \sinh \xi_{2} x + B_{2} \cosh \xi_{2} x} \right)} \right]\cos \xi_{2} y\exp \left( {i\omega t} \right), \\ \end{aligned}$$

(6a)

$$B_{x} = q_{15} \frac{\partial u}{{\partial x}} - \mu_{11} \frac{\partial \varphi }{{\partial x}} = - \mu_{11} \xi_{2} \left( {B_{1} \sinh \xi_{2} x + B_{2} \cosh \xi_{2} x} \right)\cos \xi_{2} y\exp \left( {i\omega t} \right).$$

(6b)

2.2 Solutions for outer regions

Next consider the outer regions of the plate (|x|> a). The governing equations of thickness-twist waves in the elastic material are [42]:

$$\begin{gathered} c^{\prime}_{44} \nabla^{2} u^{\prime} = \rho^{\prime}\ddot{u}^{\prime}, \hfill \\ \nabla^{2} \varphi^{\prime} = 0, \hfill \\ \end{gathered}$$

(7)

where $u^{\prime}$, $\varphi^{\prime}$, $c^{\prime}_{44}$ and $\rho^{\prime}$ are the mechanical displacement, magnetic potential, elastic constant and mass density, respectively. The solutions for trapped thickness-twist waves propagation in outer regions are expressed as [28]:

$$\begin{gathered} u^{\prime} = \left\{ \begin{gathered} A^{\prime}_{1} \exp \left[ { - \xi^{\prime}_{1} \left( {x - a} \right)} \right]\cos \xi_{2} y\exp \left( {i\omega t} \right),\;\;\;\,\,x > a, \hfill \\ A^{\prime}_{2} \exp \left[ {\xi^{\prime}_{1} \left( {x + a} \right)} \right]\cos \xi_{2} y\exp \left( {i\omega t} \right),\quad \;\;\;x < - a, \hfill \\ \end{gathered} \right. \hfill \\ \varphi^{\prime} = \left\{ \begin{gathered} B^{\prime}_{1} \exp \left[ { - \xi_{2} \left( {x - a} \right)} \right]\cos \xi_{2} y\exp \left( {i\omega t} \right),\quad x > a, \hfill \\ B^{\prime}_{2} \exp \left[ {\xi_{2} \left( {x + a} \right)} \right]\cos \xi_{2} y\exp \left( {i\omega t} \right),\quad \;\;x < - a, \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$

(8)

where

$$\begin{gathered} \xi ^{\prime}_{1} = \sqrt {\xi _{2}^{2} - \frac{{\rho ^{\prime}\omega ^{2} }}{{c^{\prime}_{{44}} }}} = {{\sqrt {{\omega ^{\prime}_{m}} ^{2} - {\omega} ^{2} } } \mathord{\left/ {\vphantom {{\sqrt {{\omega ^{\prime}_{m}} ^{2} - \omega ^{2} } } {v^{\prime}_{T} }}} \right. \kern-\nulldelimiterspace} {v^{\prime}_{T} }}, \hfill \\ v^{\prime}_{T} = \sqrt {\frac{{c^{\prime}_{{44}} }}{{\rho ^{\prime}}}} ,\;\;{\omega ^{\prime}_{m}} ^{2} = \left( {\frac{{m\pi }}{{2h}}} \right)^{2} \frac{{c^{\prime}_{{44}} }}{{\rho ^{\prime}}},\;\;\left( {m = 0,2,4,...} \right), \hfill \\ \end{gathered}$$

$A^{\prime}_{1}$, $A^{\prime}_{2}$, $B^{\prime}_{1}$ and $B^{\prime}_{2}$ are undetermined constants. $v^{\prime}_{T}$ is the shear wave speed and $\omega^{\prime}_{m}$ is the cutoff frequency of thickness-twist waves in the elastic material. The nonzero stress $\tau^{\prime}_{xz}$ and magnetic flux density $B^{\prime}_{x}$ can be obtained:

$$\tau^{\prime}_{xz} = \left\{ {\begin{array}{*{20}c} {c^{\prime}_{44} \frac{{\partial u^{\prime}}}{\partial x} = - c^{\prime}_{44} \xi^{\prime}_{1} A^{\prime}_{1} \exp \left[ { - \xi^{\prime}_{1} \left( {x - a} \right)} \right]\cos \xi_{2} y\exp \left( {i\omega t} \right),} & {x > a,} \\ {c^{\prime}_{44} \frac{{\partial u^{\prime}}}{\partial x} = c^{\prime}_{44} \xi^{\prime}_{1} A^{\prime}_{2} \exp \left[ {\xi^{\prime}_{1} \left( {x + a} \right)} \right]\cos \xi_{2} y\exp \left( {i\omega t} \right),} & {x < - a,} \\ \end{array} } \right.$$

(9a)

$$B^{\prime}_{x} = \left\{ {\begin{array}{*{20}c} { - \mu^{\prime}_{11} \frac{{\partial \varphi^{\prime}}}{\partial x} = \mu^{\prime}_{11} \xi_{2} B^{\prime}_{1} \exp \left[ { - \xi_{2} \left( {x - a} \right)} \right]\cos \xi_{2} y\exp \left( {i\omega t} \right),} & {x > a,} \\ { - \mu^{\prime}_{11} \frac{{\partial \varphi^{\prime}}}{\partial x} = - \mu^{\prime}_{11} \xi_{2} B^{\prime}_{2} \exp \left[ {\xi_{2} \left( {x + a} \right)} \right]\cos \xi_{2} y\exp \left( {i\omega t} \right),} & {x < - a,} \\ \end{array} } \right.$$

(9b)

where $\mu^{\prime}_{11}$ is the magnetic permeability constant in the elastic material.

2.3 Frequency equation

When the trapped thickness-twist waves propagate in the inhomogeneous plate mentioned above, the following boundary conditions, continuity conditions, and attenuation conditions must be satisfied:

• (1) The mechanical and magnetic conditions at $y = \pm h$

  $$\tau_{yz} = \tau^{\prime}_{yz} = 0,\quad B_{y} = B^{\prime}_{y} = 0.$$

  (10)

• (2) The continuity conditions at $x = \pm a$ can be expressed as

  $$\begin{gathered} u\left( {a,y} \right) = u^{\prime}\left( {a,y} \right),\quad \tau_{xz} \left( {a,y} \right) = \tau^{\prime}_{xz} \left( {a,y} \right), \hfill \\ \varphi \left( {a,y} \right) = \varphi^{\prime}\left( {a,y} \right),\quad B_{x} \left( {a,y} \right) = B^{\prime}_{x} \left( {a,y} \right), \hfill \\ u\left( { - a,y} \right) = u^{\prime}\left( { - a,y} \right),\quad \tau_{xz} \left( { - a,y} \right) = \tau^{\prime}_{xz} \left( { - a,y} \right), \hfill \\ \varphi \left( { - a,y} \right) = \varphi^{\prime}\left( { - a,y} \right),\quad B_{x} \left( { - a,y} \right) = B^{\prime}_{x} \left( { - a,y} \right). \hfill \\ \end{gathered}$$

  (11)

• (3) The attenuation conditions at $x \to \pm \infty$

  $$\begin{gathered} u^{\prime}\left( { - \infty ,y} \right) \to 0,\quad \varphi^{\prime}\left( { - \infty ,y} \right) \to 0, \hfill \\ u^{\prime}\left( {\infty ,y} \right) \to 0,\quad \varphi^{\prime}\left( {\infty ,y} \right) \to 0. \hfill \\ \end{gathered}$$

  (12)

Equation (10) and Eq. (12) are satisfied automatically by the mechanical displacement and magnetic potential forms in Eq. (5) and Eq. (8). Equation (5), Eq. (6), Eq. (8) and Eq. (9) are substituted into Eq. (11) yields eight linear homogeneous algebraic equations for coefficients $A_{1}$, $A_{2}$, $B_{1}$, $B_{2}$, $A^{\prime}_{1}$, $A^{\prime}_{2}$, $B^{\prime}_{1}$ and $B^{\prime}_{2}$:

$$\begin{gathered} A_{1} \cos \xi_{1} a + A_{2} \sin \xi_{1} a = A^{\prime}_{1} , \hfill \\ \overline{c}_{44} \left( { - A_{1} \xi_{1} \sin \xi_{1} a + A_{2} \xi_{1} \cos \xi_{1} a} \right) + q_{15} \left( {B_{1} \xi_{2} \sinh \xi_{2} a + B_{2} \xi_{2} \cosh \xi_{2} a} \right) \hfill \\ = - c^{\prime}_{44} \xi^{\prime}_{1} A^{\prime}_{1} , \hfill \\ B_{1} \cosh \xi_{2} a + B_{2} \sinh \xi_{2} a + \frac{{q_{15} }}{{\mu_{11} }}\left( {A_{1} \cos \xi_{1} a + A_{2} \sin \xi_{1} a} \right) = B^{\prime}_{1} , \hfill \\ \mu_{11} \left( {B_{1} \xi_{2} \sinh \xi_{2} a + B_{2} \xi_{2} \cosh \xi_{2} a} \right) = - \mu^{\prime}_{11} \xi_{2} B^{\prime}_{1} , \hfill \\ A_{1} \cos \xi_{1} a - A_{2} \sin \xi_{1} a = A^{\prime}_{2} , \hfill \\ \overline{c}_{44} \left( {A_{1} \xi_{1} \sin \xi_{1} a + A_{2} \xi_{1} \cos \xi_{1} a} \right) + q_{15} \left( { - B_{1} \xi_{2} \sinh \xi_{2} a + B_{2} \xi_{2} \cosh \xi_{2} a} \right) \hfill \\ = c^{\prime}_{44} \xi^{\prime}_{1} A^{\prime}_{2} , \hfill \\ B_{1} \cosh \xi_{2} a - B_{2} \sinh \xi_{2} a + \frac{{q_{15} }}{{\mu_{11} }}\left( {A_{1} \cos \xi_{1} a - A_{2} \sin \xi_{1} a} \right) = B^{\prime}_{2} , \hfill \\ \mu_{11} \left( { - B_{1} \xi_{2} \sinh \xi_{2} a + B_{2} \xi_{2} \cosh \xi_{2} a} \right) = \mu^{\prime}_{11} \xi_{2} B^{\prime}_{2} . \hfill \\ \end{gathered}$$

(13)

To obtain the non-trivial solutions, the determinant of the coefficient matrix in Eq. (13) is equal to zero, which yields the frequency equation of thickness-twist waves propagation in the inhomogeneous magneto-elastic plate.

3 Numerical results and discussion

In the numerical calculation, the material constants of Terfenol-D [43] and polycrystalline Ag [44] are summarized in Table 1. The half thickness of the plate h = 1 mm and m = 2. Bisection method is applied to solve the frequency equation of the trapped thickness-twist waves propagation in the inhomogeneous plate.

Table 1 Material constants of Terfenol-D and Ag

Kindly check and confirm the layout of Tables 1 and 2 is correct.The layout of Tables 1 and 2 is correct.

3.1 Effective material constants for Terfenol-D

Figure 2 illustrates the variation of the effective elastic constant $\overline{c}_{44}$ of Terfenol-D affected by the magnetic field and compressive stress. As seen in Fig. 2, $\overline{c}_{44}$ decreases as the magnetic field increases under different compressive stresses. When the magnetic field is no more than 2.8 kOe, the curve shifts to the right as the compressive stress increases, because a larger magnetic field, which overcomes the resistance from the compressive stress, is needed to maintain the same magnetization. As the magnetic field is larger than 2.8 kOe, the effects of the magnetic field and compressive stress on $\overline{c}_{44}$ are complicated.

Fig. 2

Variations of the effective elastic constant $\overline{c}_{44}$ for Terfenol-D affected by the magnetic field and compressive stress

3.2 Verification of the numerical calculation method

In order to verify the accuracy of the numerical calculation method, the piezoelectric materials PZT-5 and PZT-6B are chosen for the central and outer regions, respectively. The dispersion relation of thickness-twist waves propagation in the inhomogeneous piezoelectric plate is shown in Fig. 3. The first trapped mode appears at a/h = 0.3 × 10^–3, which is a fairly small value and not marked in following figures for brevity. The frequencies of the first and third modes, which are the first two modes symmetric in x, at a/h = 10 are ω₁ = 7,122,352.227 rad/s and ω₃ = 7,177,872.527 rad/s, respectively. These values are the same as which given in [28] that ω₁ = 7,122,352 rad/s and ω₃ = 7,177,873 rad/s, the accuracy of the numerical calculation method proposed in the article is verified to some extent.

Fig. 3

Dispersion relation of trapped thickness-twist waves propagation in the inhomogeneous piezoelectric plate with PZT-5 for central region and PZT-6B for outer regions [28]

3.3 Effects of the magnetic field and compressive stress on characteristics of trapped thickness-twist waves

Figure 4 shows the effect of the magnetic field on the dispersion relation of thickness-twist waves propagation in the inhomogeneous plate with piezomagnetic material Terfenol-D for the central region and elastic material Ag for outer regions when the compressive stress σ_z/σ_s = 0. As can be seen from Fig. 4a that there are four trapped modes in the structure when Terfenol-D is not magnetization, i.e. H_z = 0. The numbers of the trapped mode increase as the central region length a/h increase while the frequencies decrease with a/h. As the magnetic field H_z increases to 1kOe, seven new trapped modes appear shown in Fig. 4b. When H_z increases to 2kOe and 6 kOe, more modes are trapped in the structure depicted in Fig. 4c and Fig. 4d. As seen in Fig. 4, the capture speed of the modes for the case that H_z increases from 0 to 1kOe is faster than that increases from 1 to 6kOe. This is due to the fact that the natural frequency ω_m decreases rapidly when H_z increases from 0 to 1kOe while this tendency is alleviated as H_z increases continually.

Fig. 4

The effect of the magnetic field on the dispersion relation of trapped thickness-twist waves propagation in the inhomogeneous plate with piezomagnetic material Terfenol-D for the central region and elastic material Ag for outer regions when the compressive stress σ_z/σ_s = 0: a H_z = 0 kOe; b H_z = 1 kOe; c H_z = 2 kOe; d H_z = 6 kOe

The effect of the compressive stress on the dispersion relation of trapped thickness-twist waves at H_z = 1kOe is shown in Fig. 5. As can be seen from Figs. 4b and 5, the numbers of trapped modes decrease as the compressive stress increases because the initial compressive stress makes the magnetic domain rotate to the hard magnetization direction, i.e., the magnetic field strength is weakened by the compressive stress.

Fig. 5

The effect of the compressive stress on the dispersion relation of trapped thickness-twist waves propagation in the inhomogeneous plate at H_z = 1kOe: a σ_z/σ_s =  − 0.2; b σ_z/σ_s =  − 0.3

Figure 6 shows the frequencies of trapped thickness-twist waves versus H_z under no compressive stress at a/h = 5. When H_z = 0, there are two trapped modes, which is also can be seen in Fig. 4a. As H_z increases from 0 to 1kOe, four new trapped modes appear quickly and one more trapped mode appears when H_z increases from 1 to 6kOe. This is desirable for tuning characteristics of trapped thickness-twist waves with the small external stimulation. As described in Fig. 6, the frequencies of all trapped modes decrease with H_z. This is because the cutoff frequency ω_m of thickness-twist waves in the piezomagnetic material decreases as the H_z increases.

Fig. 6

The frequencies of trapped thickness-twist waves versus H_z under no compressive stress at a/h = 5

The acoustic attenuation of the modes and its frequency dependence on the piezomagnetic material are shown in Table 2. The displacement components are normalized by dividing the maximum absolute value. As can be seen, the attenuation of each mode is accelerated as ω_m (ω) decreases, which is caused by the increase of the magnetic field. The attenuation of the lower-order mode is faster than that of the higher-order mode.

Table 2 The acoustic attenuation of different modes

The relative displacement components u* (u* = u/|u|_max) of new trapped modes induced by the magnetic field at y = 0 (in the case that a/h = 5 and H_z = 6kOe) are shown in Fig. 7. It can be seen that the relative displacement components of these new trapped modes are mainly confined to be near the central region |a/h|< 10, which explains the energy trapping phenomenon.

Fig. 7

Relative displacement components of new trapped modes induced by the magnetic field along the x direction at y = 0 in the case that H_z = 6kOe and a/h = 5: a third mode (ω = 4.449887 × 10⁶ rad/s), b fourth mode (ω = 4.554294 × 10⁶ rad/s), c fifth mode (ω = 4.682147 × 10⁶ rad/s), d sixth mode (ω = 4.828871 × 10⁶ rad/s), e seventh mode (ω = 4.985215 × 10.⁶ rad/s)

Figure 8 shows the relative displacement component u*of the first trapped mode affected by the magnetic field when a/h = 5 and σ_z/σ_s = 0. It can be seen that the confined region of the displacement decreases as the magnetic field increases, which means that more energies are trapped to be near the central region. The speed of the energy trapping is faster for the case that H_z increases from 0 to 0.5kOe than that increases from 0.5kOe to 6kOe.

Fig. 8

The relative displacement component of the first mode affected by the magnetic field when a/h = 5 and σ_z/σ_s = 0

4 Conclusion

The effects of the magnetic field and compressive stress on characteristics of the trapped thickness-twist waves propagating in an inhomogeneous plate have been investigated. The effective material constants of the piezomagnetic material affected by the magnetic field and compressive stress are analyzed. The numerical results show that the magnetic field can not only induce new trapped thickness-twist modes but also accelerate the energy trapping. The advantages of the approach for tuning characteristics of trapped thickness-twist waves proposed in the article are that the operation is easy and the device structure is not changed. The results are of great significance for designing high-performance magneto-elastic acoustic devices.

Appendices

Appendix A: The matrix forms of Eq. (1)

The matrix forms of Eq. (1) are described as follows (using the engineering shear strain, i.e., γ_xy = 2ε_xy; $G = \frac{E}{{2\left( {1 + \nu } \right)}}$):

$$\begin{aligned} \left\{ \begin{gathered} \varepsilon _{x} \hfill \\ \varepsilon _{y} \hfill \\ \varepsilon _{z} \hfill \\ \gamma _{{yz}} \hfill \\ \gamma _{{zx}} \hfill \\ \gamma _{{xy}} \hfill \\ \end{gathered} \right\} = & \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 E}} \right. \kern-\nulldelimiterspace} E}} & {{{ - \nu } \mathord{\left/ {\vphantom {{ - \nu } E}} \right. \kern-\nulldelimiterspace} E}} & {{{ - \nu } \mathord{\left/ {\vphantom {{ - \nu } E}} \right. \kern-\nulldelimiterspace} E}} & 0 & 0 & 0 \\ {{{ - \nu } \mathord{\left/ {\vphantom {{ - \nu } E}} \right. \kern-\nulldelimiterspace} E}} & {{1 \mathord{\left/ {\vphantom {1 E}} \right. \kern-\nulldelimiterspace} E}} & {{{ - \nu } \mathord{\left/ {\vphantom {{ - \nu } E}} \right. \kern-\nulldelimiterspace} E}} & 0 & 0 & 0 \\ {{{ - \nu } \mathord{\left/ {\vphantom {{ - \nu } E}} \right. \kern-\nulldelimiterspace} E}} & {{{ - \nu } \mathord{\left/ {\vphantom {{ - \nu } E}} \right. \kern-\nulldelimiterspace} E}} & {{1 \mathord{\left/ {\vphantom {1 E}} \right. \kern-\nulldelimiterspace} E}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 G}} \right. \kern-\nulldelimiterspace} G}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 G}} \right. \kern-\nulldelimiterspace} G}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 G}} \right. \kern-\nulldelimiterspace} G}} \\ \end{array} } \right]\left\{ \begin{gathered} \sigma _{x} \hfill \\ \sigma _{y} \hfill \\ \sigma _{z} \hfill \\ \tau _{{yz}} \hfill \\ \tau _{{zx}} \hfill \\ \tau _{{xy}} \hfill \\ \end{gathered} \right\} \\ & + \frac{{\lambda _{s} }}{{M_{s}^{2} }}\left[ {\begin{array}{*{20}c} {1 - {{\tilde{\sigma }_{x} } \mathord{\left/ {\vphantom {{\tilde{\sigma }_{x} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & { - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} - {{\tilde{\sigma }_{x} } \mathord{\left/ {\vphantom {{\tilde{\sigma }_{x} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & { - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} - {{\tilde{\sigma }_{x} } \mathord{\left/ {\vphantom {{\tilde{\sigma }_{x} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & 0 & 0 & 0 \\ { - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} - {{\tilde{\sigma }_{y} } \mathord{\left/ {\vphantom {{\tilde{\sigma }_{y} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & {1 - {{\tilde{\sigma }_{y} } \mathord{\left/ {\vphantom {{\tilde{\sigma }_{y} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & { - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} - {{\tilde{\sigma }_{y} } \mathord{\left/ {\vphantom {{\tilde{\sigma }_{y} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & 0 & 0 & 0 \\ { - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} - {{\tilde{\sigma }_{z} } \mathord{\left/ {\vphantom {{\tilde{\sigma }_{z} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & { - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} - {{\tilde{\sigma }_{z} } \mathord{\left/ {\vphantom {{\tilde{\sigma }_{z} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & {1 - {{\tilde{\sigma }_{z} } \mathord{\left/ {\vphantom {{\tilde{\sigma }_{z} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & 0 & 0 & 0 \\ { - {{2\tilde{\tau }_{{yz}} } \mathord{\left/ {\vphantom {{2\tilde{\tau }_{{yz}} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & { - {{2\tilde{\tau }_{{yz}} } \mathord{\left/ {\vphantom {{2\tilde{\tau }_{{yz}} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & { - {{2\tilde{\tau }_{{yz}} } \mathord{\left/ {\vphantom {{2\tilde{\tau }_{{yz}} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & 3 & 0 & 0 \\ { - {{2\tilde{\tau }_{{zx}} } \mathord{\left/ {\vphantom {{2\tilde{\tau }_{{zx}} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & { - {{2\tilde{\tau }_{{zx}} } \mathord{\left/ {\vphantom {{2\tilde{\tau }_{{zx}} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & { - {{2\tilde{\tau }_{{zx}} } \mathord{\left/ {\vphantom {{2\tilde{\tau }_{{zx}} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & 0 & 3 & 0 \\ { - {{2\tilde{\tau }_{{xy}} } \mathord{\left/ {\vphantom {{2\tilde{\tau }_{{xy}} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & { - {{2\tilde{\tau }_{{xy}} } \mathord{\left/ {\vphantom {{2\tilde{\tau }_{{xy}} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & { - {{2\tilde{\tau }_{{xy}} } \mathord{\left/ {\vphantom {{2\tilde{\tau }_{{xy}} } {\sigma _{s} }}} \right. \kern-\nulldelimiterspace} {\sigma _{s} }}} & 0 & 0 & 3 \\ \end{array} } \right]\left\{ \begin{gathered} M_{x}^{2} \hfill \\ M_{y}^{2} \hfill \\ M_{z}^{2} \hfill \\ M_{y} M_{z} \hfill \\ M_{z} M_{x} \hfill \\ M_{x} M_{y} \hfill \\ \end{gathered} \right\}, \\ \end{aligned}$$

(A1)

$$\begin{aligned} \left\{ \begin{gathered} H_{x} \hfill \\ H_{y} \hfill \\ H_{z} \hfill \\ \end{gathered} \right\} = & \frac{1}{kM}f^{ - 1} \left( {\frac{M}{{M_{s} }}} \right)\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left\{ \begin{gathered} M_{x} \hfill \\ M_{y} \hfill \\ M_{z} \hfill \\ \end{gathered} \right\} \\ & - \frac{{\lambda_{s} }}{{\mu_{0} M_{s}^{2} }}\left[ {\begin{array}{*{20}c} {2\tilde{\sigma }_{x} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} & {2\tilde{\tau }_{xy} } & {2\tilde{\tau }_{zx} } \\ {2\tilde{\tau }_{xy} } & {2\tilde{\sigma }_{y} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} & {2\tilde{\tau }_{yz} } \\ {2\tilde{\tau }_{zx} } & {2\tilde{\tau }_{yz} } & {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \\ \end{array} } \right]\left\{ \begin{gathered} M_{x} \hfill \\ M_{y} \hfill \\ M_{z} \hfill \\ \end{gathered} \right\}. \\ \end{aligned}$$

(A2)

Appendix B: The effective material constants

The effective material constants of the piezomagnetic material can be expressed as follows:

$$\begin{gathered} c_{ijkl} \left( {{\varvec{H}},{\varvec{\sigma}}} \right) = S_{{_{ijkl} }}^{ - 1} \left( {{\varvec{H}},{\varvec{\sigma}}} \right), \hfill \\ q_{mij} \left( {{\varvec{H}},{\varvec{\sigma}}} \right) = c_{ijkl} \left( {{\varvec{H}},{\varvec{\sigma}}} \right)\overline{q}_{mkl} \left( {{\varvec{H}},{\varvec{\sigma}}} \right), \hfill \\ \mu_{nm} \left( {{\varvec{H}},{\varvec{\sigma}}} \right) = \overline{\mu }_{nm} \left( {{\varvec{H}},{\varvec{\sigma}}} \right) - q_{nkl} \left( {{\varvec{H}},{\varvec{\sigma}}} \right)S_{ijkl} \left( {{\varvec{H}},{\varvec{\sigma}}} \right)q_{mij} \left( {{\varvec{H}},{\varvec{\sigma}}} \right), \hfill \\ \end{gathered}$$

(B1)

where

$$S_{11} = \frac{1}{E} - \frac{{\lambda_{s} M_{z}^{2} }}{{\sigma_{s} M_{s}^{2} }} + \frac{{k\lambda_{s}^{2} \frac{{M_{z}^{2} }}{{M_{s}^{2} }}\left( {1 + \frac{{2\tilde{\sigma }_{x} }}{{\sigma_{s} }}} \right)^{2} }}{{\frac{{\mu_{0} M_{s} }}{{\frac{1}{{M_{3}^{2} }} - \csc {\text{h}}^{2} \left( {M_{3} } \right)}} - k\lambda_{s} \left( {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B2)

$$S_{12} = - \frac{v}{E} + \frac{{\lambda_{s} M_{z}^{2} }}{{2\sigma_{s} M_{s}^{2} }} + \frac{{k\lambda_{s}^{2} \frac{{M_{z}^{2} }}{{M_{s}^{2} }}\left( {1 + \frac{{2\tilde{\sigma }_{x} }}{{\sigma_{s} }}} \right)\left( {1 + \frac{{2\tilde{\sigma }_{y} }}{{\sigma_{s} }}} \right)}}{{\frac{{\mu_{0} M_{s} }}{{\frac{1}{{M_{3}^{2} }} - \csc {\text{h}}^{2} \left( {M_{3} } \right)}} - k\lambda_{s} \left( {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B3)

$$S_{13} = - \frac{v}{E} + \frac{{\lambda_{s} M_{z}^{2} }}{{2\sigma_{s} M_{s}^{2} }} - \frac{{2k\lambda_{s}^{2} \frac{{M_{z}^{2} }}{{M_{s}^{2} }}\left( {1 + \frac{{2\tilde{\sigma }_{x} }}{{\sigma_{s} }}} \right)\left( {1 - \frac{{\tilde{\sigma }_{z} }}{{\sigma_{s} }}} \right)}}{{\frac{{\mu_{0} M_{s} }}{{\frac{1}{{M_{3}^{2} }} - \csc {\text{h}}^{2} \left( {M_{3} } \right)}} - k\lambda_{s} \left( {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B4)

$$S_{22} = \frac{1}{E} - \frac{{\lambda_{s} M_{z}^{2} }}{{\sigma_{s} M_{s}^{2} }} + \frac{{k\lambda_{s}^{2} \frac{{M_{z}^{2} }}{{M_{s}^{2} }}\left( {1 + \frac{{2\tilde{\sigma }_{y} }}{{\sigma_{s} }}} \right)^{2} }}{{\frac{{\mu_{0} M_{s} }}{{\frac{1}{{M_{3}^{2} }} - \csc {\text{h}}^{2} \left( {M_{3} } \right)}} - k\lambda_{s} \left( {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B5)

$$S_{23} = - \frac{v}{E} + \frac{{\lambda_{s} M_{z}^{2} }}{{2\sigma_{s} M_{s}^{2} }} - \frac{{2k\lambda_{s}^{2} \frac{{M_{z}^{2} }}{{M_{s}^{2} }}\left( {1 + \frac{{2\tilde{\sigma }_{y} }}{{\sigma_{s} }}} \right)\left( {1 - \frac{{\tilde{\sigma }_{z} }}{{\sigma_{s} }}} \right)}}{{\frac{{\mu_{0} M_{s} }}{{\frac{1}{{M_{3}^{2} }} - \csc {\text{h}}^{2} \left( {M_{3} } \right)}} - k\lambda_{s} \left( {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B6)

$$S_{33} = \frac{1}{E} - \frac{{\lambda_{s} M_{z}^{2} }}{{\sigma_{s} M_{s}^{2} }} + \frac{{4k\lambda_{s}^{2} \frac{{M_{z}^{2} }}{{M_{s}^{2} }}\left( {1 - \frac{{\tilde{\sigma }_{z} }}{{\sigma_{s} }}} \right)^{2} }}{{\frac{{\mu_{0} M_{s} }}{{\frac{1}{{M_{3}^{2} }} - \csc {\text{h}}^{2} \left( {M_{3} } \right)}} - k\lambda_{s} \left( {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B7)

$$S_{44} = \frac{1}{G} - \frac{{3\lambda_{s} M_{z}^{2} }}{{\sigma_{s} M_{s}^{2} }} + \frac{{9k\lambda_{s}^{2} \frac{{M_{z}^{2} }}{{M_{s}^{2} }}}}{{3\mu_{0} M_{s} - k\lambda_{s} \left( {2\tilde{\sigma }_{y} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B8)

$$S_{55} = \frac{1}{G} - \frac{{3\lambda_{s} M_{z}^{2} }}{{\sigma_{s} M_{s}^{2} }} + \frac{{9k\lambda_{s}^{2} \frac{{M_{z}^{2} }}{{M_{s}^{2} }}}}{{3\mu_{0} M_{s} - k\lambda_{s} \left( {2\tilde{\sigma }_{x} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B9)

$$S_{66} = \frac{1}{G} - \frac{{3\lambda_{s} M_{z}^{2} }}{{\sigma_{s} M_{s}^{2} }},$$

(B10)

$$\overline{q}_{31} = - \frac{{k\mu_{0} \lambda_{s} M_{z} \left( {1 + \frac{{2\tilde{\sigma }_{x} }}{{\sigma_{s} }}} \right)}}{{\frac{{\mu_{0} M_{s} }}{{\frac{1}{{M_{3}^{2} }} - \csc {\text{h}}^{2} \left( {M_{3} } \right)}} - k\lambda_{s} \left( {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B11)

$$\overline{q}_{32} = - \frac{{k\mu_{0} \lambda_{s} M_{z} \left( {1 + \frac{{2\tilde{\sigma }_{y} }}{{\sigma_{s} }}} \right)}}{{\frac{{\mu_{0} M_{s} }}{{\frac{1}{{M_{3}^{2} }} - \csc {\text{h}}^{2} \left( {M_{3} } \right)}} - k\lambda_{s} \left( {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B12)

$$\overline{q}_{33} = \frac{{2k\mu_{0} \lambda_{s} M_{z} \left( {1 - \frac{{\tilde{\sigma }_{z} }}{{\sigma_{s} }}} \right)}}{{\frac{{\mu_{0} M_{s} }}{{\frac{1}{{M_{3}^{2} }} - \csc {\text{h}}^{2} \left( {M_{3} } \right)}} - k\lambda_{s} \left( {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B13)

$$\overline{q}_{24} = \frac{{3k\mu_{0} \lambda_{s} M_{z} }}{{3\mu_{0} M_{s} - k\lambda_{s} \left( {2\tilde{\sigma }_{y} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B14)

$$\overline{q}_{15} = \frac{{3k\mu_{0} \lambda_{s} M_{z} }}{{3\mu_{0} M_{s} - k\lambda_{s} \left( {2\tilde{\sigma }_{x} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B15)

$$\overline{\mu }_{11} = \mu_{0} + \frac{{k\mu_{0}^{2} M_{s}^{2} }}{{3\mu_{0} M_{s} - k\lambda_{s} \left( {2\tilde{\sigma }_{x} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B16)

$$\overline{\mu }_{22} = \mu_{0} + \frac{{k\mu_{0}^{2} M_{s}^{2} }}{{3\mu_{0} M_{s} - k\lambda_{s} \left( {2\tilde{\sigma }_{y} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B17)

$$\overline{\mu }_{33} = \mu_{0} + \frac{{k\mu_{0}^{2} M_{s}^{2} }}{{\frac{{\mu_{0} M_{s} }}{{\frac{1}{{M_{3}^{2} }} - \csc {\text{h}}^{2} \left( {M_{3} } \right)}} - k\lambda_{s} \left( {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)}},$$

(B18)

with $M_{z} = M_{s} \left( {\coth M_{3} - \frac{1}{{M_{3} }}} \right)$ and $M_{3} = kH_{z} + \frac{{k\lambda_{s} M_{z} }}{{\mu_{0} M_{s}^{2} }}\left( {2\tilde{\sigma }_{z} - \frac{{{\text{I}}_{\sigma }^{2} - 3{\text{II}}_{\sigma } }}{{\sigma_{s} }}} \right)$.