Micromechanical modeling of the biaxial behavior of strain-induced crystallizable polyethylene terephthalate-clay nanocomposites

Abstract

The present work addresses the question of the quantitative prediction of the biaxial response of polymer–clay nanocomposites experiencing strain-induced crystallization. Polyethylene terephthalate is taken as material model to represent the continuous amorphous phase of nanocomposites. A continuum-based micromechanical model is developed to predict the combined effect of strain-induced phase transformation and nanocomposite structural characteristics on the overall elastic-viscoplastic response. Comparisons with available experimental data are presented to illustrate the capabilities of the model in relation to various loading parameters in terms of loading path, loading rate and loading temperature. The model is used to provide a better understanding of the relationship between nanocomposite structural characteristics, phase transformation, intrinsic properties and loading parameters.

1 Introduction

The adding of clay in a polymer has become a traditional way for producing lightweight nanocomposites. In the latter, the homogeneous dispersion of individual nano-sized clay layers into the matrix material (so-called exfoliated state) constitutes the most favorable situation to optimize the macroscopic properties [1,2,3]. Compared to their counterpart microcomposites, they present superior chemical/thermal resistance, gas barrier properties and thermo-mechanical properties. Among them, clay-polyethylene terephthalate (PET) nanocomposite systems have several engineering application domains such as food/beverage packaging, gas/liquid containers and flame-retardant systems. The structure–property relationship in PET-clay nanocomposites was investigated in several studies [4,5,6,7,8,9,10,11,12]. It is now admitted that the continuum-based modeling is helpful for the establishment of the relationship between (nano)structure and mechanical properties of polymer/clay nanocomposites. The reliability of model predictions depends on the utilized method, along with the underlying assumptions, allowing to capture the desired property or the set of properties (i.e., elastic constants, yield and post-yield features). Numerical simulations on 3D/2D material elements were realized in some studies to examine the elastic constants of polymer–clay nanocomposites in connection to the intercalated morphology [13,14,15,16,17,18,19]. Analytical models were also proposed to constitutively relate nanocomposite morphology and macroscopic properties [20,21,22,23,24,25,26,27,28,29,30,31,32,33]. In micromechanical constitutive models based on the Eshelby inclusion theory, the constitutive representation consists in discrete spheroids (the clay stacks being represented by an equivalent effective inclusions) randomly dispersed in a continuous polymer matrix. In the latter models, the polymer matrix is assumed to be a rate-independent elastic medium and, at the best, may present plasticity. Nonetheless, a physical consistent constitutive representation should take into account the crystallization process that PET experiences during the mechanical loading. This phase transformation affects the overall mechanical properties and is strongly dependent on the loading parameters in terms of loading level, multiaxial loading, loading rate and loading temperature [34, 35]. The consequence of the clay incorporation on the phase transformation was revealed in very few experimental reports available in the literature [7], but the separate and synergistic effects of structural and loading parameters are difficult to assess experimentally. In order to ensure a reliable design of PET-clay systems, the constitutive model can provide help but should integrate the connection between actual (nano)structure features, loading parameters (temperature, strain rate and loading mode) and phase transformation.

The main purpose of this paper is to develop a modeling for PET-clay nanocomposites based upon the continuum-based micromechanical framework to predict the effect of strain-induced phase transformation and clay nanoparticle characteristics (content, aspect ratio and exfoliated/intercalated state) on the overall elastic-viscoplastic response in relation to the external loading parameters in terms of loading path, loading rate and loading temperature. The model predictability is verified under biaxial loading paths for different temperatures and strain rates.

The outline of this contribution is as follows. Section 2 presents the micromechanics-based constitutive equations. In Sect. 3, the theoretical predictions are compared with available experimental data to verify the capabilities of the present model. Concluding remarks are given in Sect. 4.

2 Micromechanics-based model

2.1 Constitutive equations

The initial two-phase composite becomes a three-phase composite from the onset of phase transformation. The material system is treated as an Eshelby-type inclusion problem in which the representative volume element consists in randomly oriented discrete elastic isotropic spheroids (i.e., the clay particles and the crystals to which we confer the subscripts clay and cry) randomly dispersed in a continuous elasto-viscoplastic isotropic medium (i.e., the amorphous phase to which we confer the subscript am). The three phases are assumed to be perfectly bonded at interfaces.

Fig. 1

Stiffness of neat PET and PET-clay systems a as a function of temperature and b as a function of crystallinity

The Hooke’s law constitutively relates the macroscopic stress tensor ${\overline{\varvec{\sigma }}}$ to the elastic macroscopic strain tensor ${\overline{\varvec{\varepsilon }}}^{e}$ as follows¹:

$${\overline{\varvec{\sigma }}} = {\overline{\mathbf{C}}}:{\overline{\varvec{\varepsilon }}}^{e}$$

(1)

The macroscopic elastic stiffness tensor ${\overline{\mathbf{C}}}$ of the multiphase composite is given by [36]:

$${\overline{\mathbf{C}}} = {\mathbf{C}}_{{\rm am}} .\left\{ {{\mathbf{I}} - \left( {{\mathbf{Y}}_{{\rm clay}} + {\mathbf{Y}}_{{\rm cry}} } \right).\left[ {\left( {{\mathbf{S}}_{{\rm clay}} .{\mathbf{Y}}_{{\rm clay}} + {\mathbf{S}}_{{\rm cry}}. {\mathbf{Y}}_{{\rm cry}} } \right) + {\mathbf{I}}} \right]^{ - 1} } \right\}$$

(2)

where I is the identity tensor, S_clay and S_cry are the Eshelby tensors and, Y_clay and Y_cry are two fourth-order tensors expressed as:

$${\mathbf{Y}}_{{{\text{clay}}}} = - \phi_{{{\text{clay}}}} \left[ {{\mathbf{S}}_{{{\text{clay}}}} + \left( {{\mathbf{C}}_{{{\text{clay}}}} - {\mathbf{C}}_{{{\text{am}}}} } \right)^{ - 1} . {\mathbf{C}}_{{{\text{am}}}} } \right]^{ - 1} \quad {\text{and}}\quad {\mathbf{Y}}_{{{\text{cry}}}} = - \phi_{{{\text{cry}}}} \left[ {{\mathbf{S}}_{{{\text{cry}}}} + \left( {{\mathbf{C}}_{{{\text{cry}}}} - {\mathbf{C}}_{{{\text{am}}}} } \right)^{ - 1} . {\mathbf{C}}_{{{\text{am}}}} } \right]^{ - 1}$$

(3)

where $\phi_{{\rm clay}}$ is the volume fraction of clay and $\phi_{{\rm cry}}$ is the volume fraction of the newly-formed crystals.

The fourth-order isotropic elastic stiffness tensors, C_am, C_clay and C_cry, are expressed, in Cartesian components, as follows:

$$\left( {{\mathbf{C}}_{{\rm am}} } \right)_{ijkl} = \frac{{E_{{\rm am}} }}{{2\left( {1 + \nu_{{\rm am}} } \right)}}\left[ {\left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} } \right) + \frac{{2\nu_{{\rm am}} }}{{1 - 2\nu_{{\rm am}} }}\delta_{ij} \delta_{kl} } \right]$$

(4)

$$\left( {{\mathbf{C}}_{{\rm clay}} } \right)_{ijkl} = \frac{{E_{{\rm clay}} }}{{2\left( {1 + \nu_{{\rm clay}} } \right)}}\left[ {\left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} } \right) + \frac{{2\nu_{{\rm clay}} }}{{1 - 2\nu_{{\rm clay}} }}\delta_{ij} \delta_{kl} } \right]$$

(5)

$$\left( {{\mathbf{C}}_{{\rm cry}} } \right)_{ijkl} = \frac{{E_{{\rm cry}} }}{{2\left( {1 + \nu_{{\rm cry}} } \right)}}\left[ {\left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} } \right) + \frac{{2\nu_{{\rm cry}} }}{{1 - 2\nu_{{\rm cry}} }}\delta_{ij} \delta_{kl} } \right]$$

(6)

in which E_am, E_clay and E_cry are the Young’s moduli and, $\nu_{{\rm am}}$, $\nu_{{{\text{clay}}}}$ and $\nu_{{{\text{cry}}}}$ are the Poisson’s ratios. The term $\delta_{ij}$ denotes the Kronecker-delta symbol. Note that individual clay platelets exhibit isotropy but intercalated clay stacks present transversal isotropy. The intercalated cluster of clay is replaced by an equivalent particle modeled by an effective (homogeneous) elastic anisotropic spheroid as described in “Appendix A”. By this way, the clay structural parameters are integrated, i.e., number of clay layers N, interlayer spacing d₀₀₁ and clay layer dimensions (thickness d_S and length L_S).

The temperature dependence of the amorphous phase is taken into account according to the following function [37]:

$$E_{{\rm am}} \left( \theta \right) = \frac{1}{2}\left( {E_{g} + E_{r} } \right) - \frac{1}{2}\left( {E_{g} - E_{r} } \right)\tanh \left( {\frac{5}{\Delta \theta }\left( {\theta - \theta_{g} } \right)} \right) + X_{g} \left( {\theta - \theta_{g} } \right)$$

(7)

where E_g is the amorphous modulus in the glassy region, E_r is the amorphous modulus in the rubbery region, $\Delta \theta$ is the interval of the temperature range across which the glass transition occurs and X_g is the slope outside the glass transition region. The variation with temperature $\theta$ of the amorphous Poisson’s ratio $\nu_{{\rm am}}$ around $\theta_{g}$ is given by the following function:

$$\nu_{{\rm am}} \left( \theta \right) = \nu_{g} + \left( {\nu_{r} - \nu_{g} } \right)\exp \left( {\frac{{\theta - \left( {2\left( {\theta_{g} + \Delta \theta - \theta } \right)} \right)^{2} }}{{\theta_{g} + \Delta \theta }}} \right)\;{\text{for}}\;\theta < \theta_{g}$$

(8)

$$\nu_{{\rm am}} \left( \theta \right) = \nu_{r} \;{\text{for}}\;\theta \ge \theta_{g}$$

(9)

where $\nu_{g}$ is the amorphous Poisson’s ratio in the glassy region and $\nu_{r}$ is the amorphous Poisson’s ratio in the rubbery region.

The macroscopic plastic yielding of the nanocomposite is developed from the continuum plasticity theory. The macroscopic yield surface $\overline{F}$ is expressed as a function of the macroscopic stress ${\overline{\varvec{\sigma }}}$ and the macroscopic equivalent plastic strain $\overline{e}^{p}$ as follows [36]:

$$\overline{F} = \left( {1 - \phi_{{\rm clay}} - \phi_{{\rm cry}} } \right)^{2} {\overline{\varvec{\sigma }}}:\left( {{\mathbf{P}}^{{\text{T}}}. {\mathbf{B}}.{\mathbf{P}}} \right):{\overline{\varvec{\sigma }}} - \frac{2}{3}\left[ {\sigma_{y} + h\left( {\overline{e}^{p} } \right)^{q} } \right]^{2} \le 0$$

(10)

in which the von Mises yield criterion with isotropic plastic hardening governs the amorphous plastic yielding where $\sigma_{y}$ is the initial yield strength of the amorphous phase and, h and q are the hardening parameters of the amorphous phase. The terms P and B are two fourth-order tensors, respectively, written as follows:

$${\mathbf{P}} = \left[ {{\mathbf{I}} + \left( {{\mathbf{S}}_{{\rm clay}} - {\mathbf{I}}} \right).\left( {{\mathbf{Y}}_{{\rm clay}} + {\mathbf{Y}}_{{\rm cry}} } \right)} \right]^{ - 1} \;{\text{and}}\;B_{ijkl} = B_{IK}^{\left( 1 \right)} \delta_{ij} \delta_{kl} + B_{IJ}^{\left( 2 \right)} \left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} } \right)$$

(11)

where $B_{IK}^{\left( 1 \right)}$ and $B_{IJ}^{\left( 2 \right)}$ are given in “Appendix B”. In Eq. (10), P^T is the transpose of P.

Regarding the associative plastic flow rule, the macroscopic plastic strain rate ${{\dot{\overline{\varvec{\varepsilon }}}}}^{p}$ is obtained from the differentiation of the macroscopic yield function $\overline{F}$ with respect to the macroscopic stress ${\overline{\varvec{\sigma }}}$:

$${\dot{\overline{\varvec{\varepsilon }}}}^{p} = \dot{\lambda }\frac{{\partial \overline{F}}}{{\partial {\overline{\varvec{\sigma }}}}} = 2\left( {1 - \phi_{{\rm clay}} - \phi_{{\rm cry}} } \right)^{2} \dot{\lambda }\left( {{\mathbf{P}}^{{\text{T}}}. {\mathbf{B}}.{\mathbf{P}}} \right):{\overline{\varvec{\sigma }}}$$

(12)

where $\dot{\lambda }$ is the plastic multiplier computed from the plastic consistency condition: $\dot{\lambda }\left\langle {\dot{\overline{F}}} \right\rangle = 0$, the yield condition being formulated in a Kuhn-Tucker form by: $\dot{\lambda } \ge 0$, $\left\langle {\overline{F}} \right\rangle \le 0$, $\dot{\lambda }\left\langle {\overline{F}} \right\rangle = 0$.

The macroscopic equivalent plastic strain rate $\dot{\overline{e}}^{p}$ is given by:

$$\dot{\overline{e}}^{p} = \sqrt {\frac{2}{3}{\dot{\overline{\varvec{\varepsilon }}}}^{p} :\left( {{\mathbf{P}}^{{\text{T}}}. {\mathbf{B}}.{\mathbf{P}}} \right)^{ - 1} :{\dot{\overline{\varvec{\varepsilon }}}}^{p} } = 2\left( {1 - \phi_{{\rm clay}} - \phi_{{\rm cry}} } \right)^{2} \dot{\lambda }\sqrt {\frac{2}{3}{\overline{\varvec{\sigma }}}:\left( {{\mathbf{P}}^{{\text{T}}}. {\mathbf{B}}.{\mathbf{P}}} \right):{\overline{\varvec{\sigma }}}}$$

(13)

2.2 Phase transformation

The clay-polymer interactions may provoke the perturbation of the crystallinity. In addition to the nanocomposite structural characteristics, the micromechanical model includes the progressive phase transformation under applied macroscopic deformation. The progressive evolution of crystallization is expressed by an Avrami-type relationship [38, 39]:

$$\phi_{{\rm cry}} = \phi_{\infty \_cry} \kappa \;{\text{and}}\;\dot{\kappa } = \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{ref} }}\alpha_{av} K_{av} \left( { - \ln \left( {1 - \kappa } \right)} \right)^{{\frac{{\alpha_{av} - 1}}{{\alpha_{av} }}}} \left( {1 - \kappa } \right)$$

(14)

in which $\phi_{\infty \_cry}$ is the maximum crystal degree, $\kappa$ is the total degree of transformation, $\dot{\varepsilon }$ is the applied strain rate, $\dot{\varepsilon }_{ref}$ is the reference strain rate, $\alpha_{av}$ is the Avrami exponent and K_av is the phase transformation rate function defined as follows:

$$K_{av} = 1.47 \times 10^{ - 3} \left( {\frac{4\pi Nu}{{3\phi_{\infty \_cry} }}} \right)^{1/3} \exp \left( { - \left( {\frac{\theta - 141}{{47.33}}} \right)^{2} } \right)$$

(15)

in which Nu is the number density of nuclei in the amorphous phase.

The intrinsic viscosity of the amorphous phase is introduced by means of the Duvaut-Lions viscoplastic approach (see “Appendix C”). By this way, the rate-dependency of both the crystallization and the amorphous plastic flow may affect the macroscopic stress.

2.3 Biaxiality effect on intercalation-exfoliation states

Biaxial loading was used in the literature to enhance the exfoliation extent in clay nanocomposites [5, 7]. In our modeling approach, the progressive exfoliation from the original aggregated clay to the completely delaminated one is considered with the following equation:

$$N = \delta N_{0} + 1$$

(16)

in which N₀ is the average number of silicate layers per clay stack before mechanical loading and $\delta$ is an exfoliation degree parameter expressed as a two-parameter Weibull statistical distribution:

$$\delta = 1 - \exp \left( { - \left( {\frac{{\left\| {{\overline{\varvec{\sigma }}}} \right\|}}{\beta }} \right)^{\alpha } } \right)$$

(17)

in which $\alpha$ and $\beta$ are two material parameters and $\left\| {{\overline{\varvec{\sigma }}}} \right\|$ is the equivalent value of the macroscopic stress tensor ${\overline{\varvec{\sigma }}}$ for which the components are given under a general biaxial stretching by:

$$\overline{\sigma }_{11} > 0,\overline{\sigma }_{22} = R\overline{\sigma }_{11} \;{\text{and}}\;\overline{\sigma }_{ij} = 0\;{\text{for}}\;{\text{all}}\;{\text{other}}\;{\text{components}}$$

(18)

where $R = {{\overline{\sigma }_{22} } \mathord{\left/ {\vphantom {{\overline{\sigma }_{22} } {\overline{\sigma }_{11} }}} \right. \kern-\nulldelimiterspace} {\overline{\sigma }_{11} }}$ is the stress biaxial ratio.

3 Results

The model parameters are provided in Table 1. The amorphous elastic constants both in the glassy and rubbery states were taken from available data of the literature [40,41,42]. The crystal elastic constants were taken from the work of Matsuo and Sawatari [43] while the crystal shape factor was obtained from an experimental stiffening curve taken from the work of Cosson et al. [44] on previously crystallized neat PET. Unless otherwise explicitly indicated the clay nanoplatelets were regarded as completely exfoliated with dimensions and elastic constants taken from the molecular dynamics results of Manevitch and Rutledge [45].

Table 1 Model constants

3.1 Clay and crystallization reinforcing effect

The model is first used to point out the separate and synergistic effects of clay particles and crystals on the nanocomposite stiffening. Figure 1 presents the impact of the clay loading on the structure-stiffness relationship with temperature variation in amorphous PET (Fig. 1a) or with increase in amount of newly-formed crystals (Fig. 1b). A global view at these plots shows that the increase in clay concentration has a homothetic effect on the modulus variation with temperature in the case of the amorphous PET. Interestingly, the increase in clay concentration amplifies the reinforcing effect in a crystallized PET.

3.2 Comparison with experiments

In what follows, the capabilities of the micromechanics-based model to capture the overall mechanical behavior of PET-based nanocomposites are examined by comparing model simulations to available experimental data [7, 46]. Note that the crystallization in the course of straining was not measured in the work of Shen et al. [7], only the maximum amount was provided. The maximum crystal degree taken from Shen et al. [7] being temperature and rate-dependent, the reduced strain rate $a_{\theta } \dot{\varepsilon }$ is here introduced to plot master curves. Figure 2a shows that when the maximum crystal degree is plotted as a function of the reduced strain rate $a_{\theta } \dot{\varepsilon }$, a straight line fit perfectly describes the experimental data of both neat PET and its nanocomposite.

Fig. 2

Maximum crystal degree as a function of a reduced strain rate $a_{\theta } \dot{\varepsilon }$ (1: neat PET and 2: PET-clay system at 6% wt. clay), b average tactoid thickness (1: 95 °C and 1/s, 2: 102 °C and 1/s); Solid lines: model; Symbols: experimental data of Shen et al. [7]

3.2.1 Neat PET

The material constants for the neat PET were the outcome of a standard optimization procedure that provides the best fit of the uniaxial crystallization data of Salem [41] and the equal biaxial stress–strain data of Shen et al. [7]. Figure 3 presents the model results in comparison with Shen et al. [7] data for different strain rates and temperatures. The different features of the stress–strain response are satisfactory captured by the model, including the initial linear elasticity, the yield strength and the post-yield behavior. As expected, the maximum crystal amount is perfectly caught by the model.

Fig. 3

Model results for neat PET under EB loading at different loading conditions (1: 95 °C and 1/s, 2: 102 °C and 2/s, 3: 102 °C and 1/s): a stress–strain response, b strain-induced crystallization; Solid lines: model; Symbols: experimental data of Shen et al. [7]

3.2.2 PET-clay nanocomposite

Figure 4 presents the equal biaxial (EB) response of a PET-based nanocomposite system for different strain rates and temperatures. The model reproduces adequately the important effect of the loading parameters on the mechanical response. Especially, the delay in the onset of strain stiffening due to the temperature increase or the strain rate decrease. Again, the maximum crystal amount is satisfactory reproduced by the model. The PET-clay system having a lower crystallinity than the neat PET, the model is then found able to capture the crystallization reduction due to a confinement effect related to the restriction in mobility of the polymer chains trapped between the clay layers. The model is therefore able to connect both the clay structural characteristics and the phase transformation with the macroscopic behavior.

Fig. 4

Model results for a PET-clay system (6% wt. clay) under EB loading at different loading conditions (1: 95 °C and 1/s, 2: 102 °C and 2/s, 3: 102 °C and 1/s): a stress–strain response, b strain-induced crystallization; Solid lines: model; Symbols: experimental data of Shen et al. [7]

Figure 5 presents model predictions under constant width (CW) condition in comparison of experimental data of Figiel et al. [46] for neat PET and two of its nanocomposites.

Fig. 5

Model results for neat PET and PET-clay systems (1: 2.5% wt. clay, 2: 1% wt. clay, 3: neat PET) under CW loading at 100 °C and 1/s: a stress–strain response, b strain-induced crystallization; Solid lines: model; Symbols: experimental data of Figiel et al. [46]

The clay content effect on the plastic flow response is adequately reproduced by the model, especially the reinforcing effect on the strain hardening ability. It can be also observed that the incubation strain, below which no phase transformation is detected, decreases when the clay loading increases. The model can be used to predict the stress-crystallinity evolution in response to a temperature change. Illustrative examples of the EB material response are presented in Figs. 6 and 7 for the neat PET and its nanocomposite, respectively, for two successive temperatures: 102 °C and 95 °C. The simulation consists to an isothermal straining at 102 °C up to a pre-determined strain level, then a progressive cooling is performed at a constant rate until a temperature of 95 °C. The isothermal stress response and phase transformation at 102 °C and 95 °C are also presented in the figure.

Fig. 6

Model results for neat PET considering two temperature levels under EB loading at 1/s (1: 102 °C, 2: 95 °C, 3: 102 °C and then 95 °C)

Fig. 7

Model results for a PET-clay system (6% wt. clay) considering two temperature levels under EB loading at 1/s (1: 102 °C, 2: 95 °C, 3: 102 °C and then 95 °C)

As a final point of discussion, the model ability to relate structural state, overall response and loading parameters is shown. Figure 8 shows the model prediction under EB stretching at two stretching temperatures considering intercalated morphology, exfoliated morphology and strain-induced intercalated-exfoliated morphology transformation.

Fig. 8

Model results for a PET-clay system (6% wt. clay) under EB loading considering different morphology states (1: intercalated morphology, 2: exfoliated morphology, 3: strain-induced intercalated-exfoliated morphology transformation): a 95 °C and 1/s, b 102 °C and 1/s

As expected intercalated and exfoliated states lead to lower and upper bound model predictions, respectively, between which the experimental data of Shen et al. [7] fall. The degree of exfoliation may be increased by the biaxial stretching caused by the delamination of the intercalated layers [5, 7]. The model results may be then better favorably compared to the experimental data when an evolution from intercalation to exfoliation states caused by the EB loading is introduced. The EB stretching improves the exfoliation as the average tactoid thickness diminishes in the course of the loading. The split of the large tactoids into thinner and smaller tactoids is significantly influenced by the stretching temperature as illustrated in Fig. 9a, the better delamination of tactoids at the lowest stretching temperature leading to the hardening ability enhancement due to the new exfoliated state. The correlation between crystallinity rate and exfoliated clay is observed in Fig. 2b. The decrease in the tactoid thickness with the EB stretching produces an increase in crystal degree due to the decrease in confinement effect on the crystallization of the polymer chains. The combined effect of strain-induced nanocomposite structural evolution and strain-induced phase transformation leads to the enhanced stiffening as illustrated in Fig. 9b.

Fig. 9

Model results for a PET-clay system (6% wt. clay) on the EB loading effect on a the average thickness of the intercalated clay stack (1: 95 °C and 1/s, 2: 102 °C and 1/s), b the stiffening considering different morphology states (1: intercalated morphology, 2: exfoliated morphology, 3: strain-induced intercalated-exfoliated morphology transformation)

4 Concluding remarks

In this paper, the strain-induced crystallization was incorporated into an elastic-viscoplastic micromechanical constitutive representation of the PET-clay nanocomposite. The model-experiments comparisons demonstrated the capability of the model to describe the biaxial elastic-viscoplastic response of neat PET and its nanocomposites under different loading conditions in terms of strain rate and temperature. The model provides a useful tool to tailor and optimize the microstructure-property relationship of strain-induced crystallizable PET-clay nanocomposites. Separate and synergistic effects of nanocomposite structural characteristics, phase transformation and loading parameters on the overall response were highlighted thanks to the model.

Appendices

Appendix A

The intercalated cluster of clay is replaced by an equivalent homogeneous nanoparticle having transversely isotropic properties. Each intercalated clay stack is seen as a laminated composite sub-structure, consisting of several clay platelets separated by polymer, for which the elastic tensor is estimated using the laminate theory [30]. The elastic stiffness tensor C_clay is given from the six elastic constants written as:

$$\begin{aligned} E_{11} & = E_{33} = \phi {}_{S/P}E_{S} + \left( {1 - \phi_{S/P} } \right)E_{{\text{G}}} \\ E_{22} & = \frac{{E_{{\text{S}}} E_{{\text{G}}} }}{{\phi_{S/P} E_{{\text{G}}} + \left( {1 - \phi_{S/P} } \right)E_{{\text{S}}} - \phi_{S/P} \left( {1 - \phi_{S/P} } \right)\eta_{1} E_{{\text{G}}} E_{{\text{S}}} }} \\ \nu_{12} & = \nu_{23} = \phi_{S/P} \nu_{{\text{S}}} + \left( {1 - \phi_{S/P} } \right)\nu_{{\text{G}}} \\ \nu_{13} & = \frac{{\nu_{{\text{S}}} \phi_{S/P} E_{{\text{S}}} \left( {1 - \nu_{{\text{G}}}^{{2}} } \right) + \nu_{{\text{G}}} \left( {1 - \phi_{S/P} } \right)E_{{\text{G}}} \left( {1 - \nu_{{\text{S}}}^{{2}} } \right)}}{{\phi_{S/P} E_{{\text{S}}} \left( {1 - \nu_{{\text{G}}}^{{2}} } \right) + \nu_{{\text{G}}} \left( {1 - \phi_{S/P} } \right)E_{{\text{G}}} \left( {1 - \nu_{{\text{S}}}^{{2}} } \right)}} \\ G_{12} & = G_{23} = \frac{{G_{{\text{S}}} G_{{\text{G}}} }}{{\phi_{S/P} G_{{\text{G}}} + \left( {1 - \phi_{S/P} } \right)G_{{\text{S}}} - \phi_{S/P} \left( {1 - \phi_{S/P} } \right)\eta_{2} G_{{\text{G}}} G_{{\text{S}}} }} \\ G_{13} & = \frac{{E_{11} }}{{2\left( {1 + \nu_{13} } \right)}} \\ \end{aligned}$$

(A1)

The two parameters $\eta_{1}$ and $\eta_{2}$ are given by:

$$\begin{aligned} \eta_{1} & = \frac{{\nu_{{\text{S}}}^{2} {{E_{{\text{G}}} } \mathord{\left/ {\vphantom {{E_{{\text{G}}} } {E_{{\text{S}}} }}} \right. \kern-\nulldelimiterspace} {E_{{\text{S}}} }} + \nu_{{\text{G}}}^{2} {{E_{{\text{S}}} } \mathord{\left/ {\vphantom {{E_{{\text{S}}} } {E_{{\text{G}}} }}} \right. \kern-\nulldelimiterspace} {E_{{\text{G}}} }} - 2\nu_{{\text{S}}} \nu_{{\text{G}}} }}{{\phi_{S/P} E_{{\text{S}}} + \left( {1 - \phi_{S/P} } \right)E_{{\text{G}}} }} \\ \eta_{2} & = \frac{{\nu_{{\text{S}}}^{2} {{G_{{\text{G}}} } \mathord{\left/ {\vphantom {{G_{{\text{G}}} } {G_{{\text{S}}} }}} \right. \kern-\nulldelimiterspace} {G_{{\text{S}}} }} + \nu_{{\text{G}}}^{2} {{G_{{\text{S}}} } \mathord{\left/ {\vphantom {{G_{{\text{S}}} } {G_{{\text{G}}} }}} \right. \kern-\nulldelimiterspace} {G_{{\text{G}}} }} - 2\nu_{{\text{S}}} \nu_{{\text{G}}} }}{{\phi_{S/P} G_{{\text{S}}} + \left( {1 - \phi_{S/P} } \right)G_{{\text{G}}} }} \\ \end{aligned}$$

(A2)

where E is the Young’s modulus, G is the shear modulus and $\nu$ is the Poisson’s ratio. The subscripts S and G refer to the silicate and the gallery (confined polymer matrix in the intersilicate layers whose elastic constants are taken equal to those of the amorphous PET), respectively. The term $\phi_{S/P}$ is the volume fraction of silicate in the intercalated clay stack:

$$\phi_{S/P} = \frac{{Nd_{S} }}{t}$$

(A3)

where t is the thickness of the intercalated clay stack:

$$t = \left( {N - 1} \right)d_{001} + d_{S}$$

(A4)

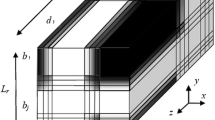
The quantities N, d₀₀₁ and d_S are the clay structural parameters schematically defined in Fig. 

Fig. 10

Intercalated clay stack

10. They denote, respectively, the average number of silicate layers per clay stack, the average silicate interlayer spacing and the thickness of the silicate layer, respectively. When the intercalated morphology is invoked in the main body of the paper, the employed average structural parameters are N = 8, L_S = 200 nm, d_S = 1 nm and d₀₀₁ = 2 nm.

The volume fraction of intercalated clay stacks can be expressed as:

$$\phi_{{\rm clay}} = \frac{{\rho_{m} }}{{\rho_{S} \phi_{S/P} }}W_{S}$$

(A5)

where W_S is the silicate weight fraction, $\rho_{S}$ is the silicate density and $\rho_{m}$ is the density of the polymer matrix:

$$\rho_{m} = \phi_{{\rm am}} \rho_{{\rm am}} + \phi_{{\rm cry}} \rho_{{\rm cry}}$$

(A6)

The PET, crystal and clay densities were taken equal to 1.335 g/cm³, 1.445 g/cm³ and 2.3 g/cm³, respectively.

The aspect ratio of the intercalated clay stack $\alpha_{{\rm clay}}$ is given by:

$$\alpha_{{\rm clay}} = \frac{{\left( {N - 1} \right)d_{001} + d_{S} }}{{L_{S} }}$$

(A7)

where L_S is the clay layer length.

The crystal volume fraction $\phi_{{\rm cry}}$ is calculated from the crystal weight fraction W_cry as follows:

$$\phi_{{\rm cry}} = \frac{{W_{{\rm cry}} }}{{W_{{\rm cry}} + \left( {\frac{{\rho_{{\rm cry}} }}{{\phi_{{\rm am}} \rho_{{\rm am}} + \phi_{{\rm clay}} \rho_{{\rm clay}} }}} \right)\left( {1 - W_{{\rm cry}} } \right)}}$$

(A8)

Appendix B

The parameters $B_{IK}^{\left( 1 \right)}$ and $B_{IJ}^{\left( 2 \right)}$ are given by:

$$B_{IK}^{\left( 1 \right)} = - \frac{1}{3} + \frac{2}{{4725\left( {1 - \nu_{{\rm am}} } \right)^{2} }}\left\{ {\begin{array}{*{20}c} {\left[ \begin{gathered} 3\left( {35\nu_{{\rm am}}^{2} - 70\nu_{{\rm am}} + 36} \right)\Delta_{IK} \hfill \\ + 7\left( {50\nu_{{\rm am}}^{2} - 59\nu_{{\rm am}} + 8} \right)\left( {\Delta_{I} + \Delta_{K} } \right) \hfill \\ - 2\left( {175\nu_{{\rm am}}^{2} - 343\nu_{{\rm am}} + 103} \right) \hfill \\ \end{gathered} \right]\left( {\frac{{\phi_{{\rm clay}} }}{{D_{II} D_{KK} }} + \frac{{\phi_{{\rm cry}} }}{{E_{II} E_{KK} }}} \right)} \\ { + 21\left( {25\nu_{{\rm am}} - 2} \right)\left( {1 - 2\nu_{{\rm am}} } \right)\left( \begin{gathered} \phi_{{\rm clay}} \frac{{\left( {G_{II} + G_{KK} } \right)}}{{D_{II} D_{KK} }} \hfill \\ + \phi_{{\rm cry}} \frac{{\left( {H_{II} + H_{KK} } \right)}}{{E_{II} E_{KK} }} \hfill \\ \end{gathered} \right)} \\ { + 21\left( {25\nu_{{\rm am}} - 23} \right)\left( {1 - 2\nu_{{\rm am}} } \right)\left( \begin{gathered} \phi_{{\rm clay}} \frac{{\left( {G_{II} \Delta_{K} + G_{KK} \Delta_{I} } \right)}}{{D_{II} D_{KK} }} \hfill \\ + \phi_{{\rm cry}} \frac{{\left( {H_{II} \Delta_{K} + H_{KK} \Delta_{I} } \right)}}{{E_{II} E_{KK} }} \hfill \\ \end{gathered} \right)} \\ { + 1575\left( {1 - 2\nu_{{\rm am}} } \right)^{2} \left( {\phi_{{\rm clay}} \frac{{G_{II} G_{KK} }}{{D_{II} D_{KK} }} + \phi_{{\rm cry}} \frac{{H_{II} H_{KK} }}{{E_{II} E_{KK} }}} \right)} \\ \end{array} } \right\}$$

(B1)

$$B_{IJ}^{\left( 2 \right)} = \frac{1}{2} + \frac{1}{{1575\left( {1 - \nu_{{\rm am}} } \right)^{2} }}\left( {\frac{{\phi_{{\rm clay}} }}{{D_{IJ} D_{IJ} }} + \frac{{\phi_{{\rm cry}} }}{{E_{IJ} E_{IJ} }}} \right)\left[ \begin{gathered} \left( {70\nu_{{\rm am}}^{2} - 140\nu_{{\rm am}} + 72} \right)\Delta_{IJ} \hfill \\ - \left( {175\nu_{{\rm am}}^{2} - 266\nu_{{\rm am}} + 75} \right)\frac{{\left( {\Delta_{I} + \Delta_{J} } \right)}}{2} \hfill \\ + \left( {350\nu_{{\rm am}}^{2} - 476\nu_{{\rm am}} + 164} \right) \hfill \\ \end{gathered} \right]$$

where $\Delta_{I}$, $\Delta_{IJ}$, $D_{IJ}$, $E_{IJ}$, $G_{IJ}$ and $H_{IJ}$ are defined by:

$$\begin{aligned} \Delta_{1} & = \frac{{3\left[ {1 - \alpha^{4} g\left( {\alpha^{2} } \right)} \right]}}{{1 - \alpha^{4} }}, \\ \Delta_{2} & = \Delta_{3} = \frac{1}{2}\left( {3 - \Delta_{1} } \right), \\ \Delta_{11} & = \frac{{5\left[ {2 + \alpha^{4} - 3\alpha^{4} g\left( {\alpha^{2} } \right)} \right]}}{{2\left( {1 - \alpha^{4} } \right)^{2} }}, \\ \Delta_{12} & = \Delta_{21} = \Delta_{13} = \Delta_{31} = \frac{{15\alpha^{4} \left[ { - 3 + \left( {1 + 2\alpha^{4} } \right)g\left( {\alpha^{2} } \right)} \right]}}{{4\left( {1 - \alpha^{4} } \right)^{2} }}, \\ \Delta_{22} & = \Delta_{23} = \Delta_{32} = \Delta_{33} = \frac{1}{8}\left( {15 - 3\Delta_{11} - 4\Delta_{12} } \right) \\ \end{aligned}$$

(B2)

with

$$g\left( \alpha \right) = \left\{ \begin{gathered} \frac{{\cosh^{ - 1} \alpha }}{{\alpha \sqrt {\alpha^{2} - 1} }}\quad {\text{if}}\;\alpha > 1 \hfill \\ \frac{{\cos^{ - 1} \alpha }}{{\alpha \sqrt {1 - \alpha^{2} } }}\quad {\text{if}}\;\alpha < 1 \hfill \\ \end{gathered} \right.$$

(B3)

$$\begin{aligned} D_{IJ} & = 2\left( {V_{IJ} + NP_{IJ} } \right) \\ E_{IJ} & = 2\left( {V_{IJ} + NI_{IJ} } \right) \\ \end{aligned}$$

(B4)

and

$$\begin{gathered} \left\{ {\left. {\begin{array}{*{20}c} {G_{I1}^{{}} } \\ {G_{I2}^{{}} } \\ {G_{I3}^{{}} } \\ \end{array} } \right\}} \right. = \left[ {\begin{array}{*{20}c} {U_{11} + 2V_{11} + WP_{11}^{{}} } & {U_{21} + MP_{21}^{{}} } & {U_{31} + MP_{31}^{{}} } \\ {U_{12} + MP_{12}^{{}} } & {U_{22} + 2V_{22} + WP_{22}^{{}} } & {U_{32} + MP_{32}^{{}} } \\ {U_{13} + MP_{13}^{{}} } & {U_{23} + MP_{23}^{{}} } & {U_{33} + 2V_{33} + WP_{33}^{{}} } \\ \end{array} } \right]^{ - 1} \left\{ {\left. {\begin{array}{*{20}c} {U_{I1} + MP_{I1}^{{}} } \\ {U_{I2} + MP_{I2}^{{}} } \\ {U_{I3} + MP_{I3}^{{}} } \\ \end{array} } \right\}} \right. \hfill \\ \left\{ {\left. {\begin{array}{*{20}c} {H_{I1}^{{}} } \\ {H_{I2}^{{}} } \\ {H_{I3}^{{}} } \\ \end{array} } \right\}} \right. = \left[ {\begin{array}{*{20}c} {U_{11} + 2V_{11} + WI_{11}^{{}} } & {U_{21} + MI_{21}^{{}} } & {U_{31} + MI_{31}^{{}} } \\ {U_{12} + MI_{12}^{{}} } & {U_{22} + 2V_{22} + WI_{22}^{{}} } & {U_{32} + MI_{32}^{{}} } \\ {U_{13} + MI_{13}^{{}} } & {U_{23} + MI_{23}^{{}} } & {U_{33} + 2V_{33} + WI_{33}^{{}} } \\ \end{array} } \right]^{ - 1} \left\{ {\left. {\begin{array}{*{20}c} {U_{I1} + MI_{I1}^{{}} } \\ {U_{I2} + MI_{I2}^{{}} } \\ {U_{I3} + MI_{I3}^{{}} } \\ \end{array} } \right\}} \right. \hfill \\ \end{gathered}$$

(B5)

with

$$\begin{aligned} U_{11} & = \left( {4\nu_{{\rm am}} + \frac{2}{{\alpha^{2} - 1}}} \right)f\left( \alpha \right) + 4\nu_{{\rm am}} + \frac{4}{{3\left( {\alpha^{2} - 1} \right)}}, \\ U_{12} & = U_{13} = \left( {4\nu_{{\rm am}} - \frac{{2\alpha^{2} + 1}}{{\alpha^{2} - 1}}} \right)f\left( \alpha \right) + 4\nu_{{\rm am}} - \frac{{2\alpha^{2} }}{{\alpha^{2} - 1}}, \\ U_{21} & = U_{31} = \left( { - 2\nu_{{\rm am}} - \frac{{2\alpha^{2} + 1}}{{\alpha^{2} - 1}}} \right)f\left( \alpha \right) - \frac{{2\alpha^{2} }}{{\alpha^{2} - 1}}, \\ U_{22} & = U_{23} = U_{32} = U_{33} = \left( { - 2\nu_{{\rm am}} + \frac{{4\alpha^{2} - 1}}{{4\left( {\alpha^{2} - 1} \right)}}} \right)f\left( \alpha \right) + \frac{{\alpha^{2} }}{{2\left( {\alpha^{2} - 1} \right)}}, \\ \end{aligned}$$

(B6)

$$\begin{aligned} V_{11} & = \left( { - 4\nu_{{\rm am}} + \frac{{4\alpha^{2} - 2}}{{\alpha^{2} - 1}}} \right)f\left( \alpha \right) - 4\nu_{{\rm am}} + \frac{{12\alpha^{2} - 8}}{{3\left( {\alpha^{2} - 1} \right)}}, \\ V_{12} & = V_{21} = V_{13} = V_{31} = \left( { - \nu_{{\rm am}} - \frac{{\alpha^{2} + 2}}{{\alpha^{2} - 1}}} \right)f\left( \alpha \right) - 2\nu_{{\rm am}} - \frac{2}{{\alpha^{2} - 1}}, \\ V_{22} & = V_{23} = V_{32} = V_{33} = \left( {2\nu_{{\rm am}} - \frac{{4\alpha^{2} - 7}}{{4\left( {\alpha^{2} - 1} \right)}}} \right)f\left( \alpha \right) + \frac{{\alpha^{2} }}{{2\left( {\alpha^{2} - 1} \right)}}, \\ \end{aligned}$$

(B7)

$$\begin{aligned} MP_{IJ} & = \frac{{\lambda_{{\rm am}} \mu_{{\rm clay}} - \lambda_{{\rm clay}} \mu_{{\rm am}} }}{{\left( {\mu_{{\rm clay}} - \mu_{{\rm am}} } \right)\left[ {2\left( {\mu_{{\rm clay}} - \mu_{{\rm am}} } \right) + 3\left( {\lambda_{{\rm clay}} - \lambda_{{\rm am}} } \right)} \right]}}, \\ NP_{IJ} & = \frac{{\mu_{{\rm am}} }}{{2\left( {\mu_{{\rm clay}} - \mu_{{\rm am}} } \right)}}, \\ MI_{IJ} & = \frac{{\lambda_{{\rm am}} \left( {1 - \Omega_{IK}^{\left( i \right)} \delta_{kk} } \right) - 2\mu_{{\rm am}} \Omega_{IJ}^{\left( i \right)} }}{{2\left( {\mu_{{\rm cry}} - \mu_{{\rm am}} } \right)}}, \\ NI_{IJ} & = \frac{{\mu_{{\rm am}} }}{{2\left( {\mu_{{\rm cry}} - \mu_{{\rm am}} } \right)}}, \\ WP_{II} & = MP_{II}^{{}} + 2NP_{II} , \\ WI_{II} & = MI_{II}^{{}} + 2NI_{II}. \\ \end{aligned}$$

(B8)

in which $\lambda$ and $\mu$ are the Lame’s constants and

$$\left\{ {\left. {\begin{array}{*{20}c} {\Omega_{I1}^{{}} } \\ {\Omega_{I2}^{{}} } \\ {\Omega_{I3}^{{}} } \\ \end{array} } \right\}} \right. = \left[ {\begin{array}{*{20}c} \gamma & {\lambda_{{\rm cry}} - \lambda_{{\rm am}} } & {\lambda_{{\rm cry}} - \lambda_{{\rm am}} } \\ {\lambda_{{\rm cry}} - \lambda_{{\rm am}} } & \gamma & {\lambda_{{\rm cry}} - \lambda_{{\rm am}} } \\ {\lambda_{{\rm cry}} - \lambda_{{\rm am}} } & {\lambda_{{\rm cry}} - \lambda_{{\rm am}} } & \gamma \\ \end{array} } \right]^{ - 1} \left\{ {\left. {\begin{array}{*{20}c} {\lambda_{{\rm cry}} - \lambda_{{\rm am}} } \\ {\lambda_{{\rm cry}} - \lambda_{{\rm am}} } \\ {\lambda_{{\rm cry}} - \lambda_{{\rm am}} } \\ \end{array} } \right\}} \right.$$

(B9)

with $\gamma = \lambda_{{\rm cry}} - \lambda_{{\rm am}} + 2\left( {\mu_{{\rm cry}} - \mu_{{\rm am}} } \right)$.

Appendix C

The Duvaut-Lions approach was employed to transform plasticity to viscoplasticity [47, 48]:

$${\dot{\varvec{\varepsilon }}}^{vp} = \frac{1}{\eta }{\mathbf{C}}_{{\rm am}}^{ - 1} :\left( {{\overline{\varvec{\sigma }}} - {\overline{\overline{\varvec{\sigma }}}}} \right)$$

(C1)

$${\dot{\mathbf{e}}}^{vp} = \frac{1}{\eta }\left( {{\overline{\mathbf{e}}}^{vp} - {\overline{\overline{\varvec{e}}}}^{p} } \right)$$

(C2)

where $\eta$ is a viscosity parameter, ${\overline{\varvec{\sigma }}}$ and ${\overline{\overline{\varvec{\sigma }}}}$ are the total average viscoplastic stress tensor and the overall inviscid plastic stress tensor, respectively, and, ${\overline{\mathbf{e}}}^{vp}$ and ${\overline{\overline{\varvec{e}}}}^{p}$ are the viscoplastic strain tensor and the inviscid plastic strain tensor, respectively. The inviscid solution, in terms of the actual stress tensor ${\overline{\overline{\varvec{\sigma }}}}_{n + 1}$ and the internal variable ${\overline{\overline{\varvec{e}}}}_{n + 1}^{p}$, is updated at each increment allowing the calculation of the new stress ${\overline{\varvec{\sigma }}}_{n + 1}$ and the viscoplastic strain ${\overline{\mathbf{e}}}^{vp}_{n + 1}$ by integrating the two previous equations using a backward Euler algorithm:

$${\overline{\varvec{\sigma }}}_{n + 1} = \frac{{\left( {{\overline{\varvec{\sigma }}}_{n} + {\mathbf{C}}_{{\rm am}} :\Delta {\overline{\varvec{\varepsilon }}}_{n + 1} } \right) + \frac{{\Delta t_{n + 1} }}{\eta }{\overline{\overline{\varvec{\sigma }}}}_{n + 1} }}{{1 + \frac{{\Delta t_{n + 1} }}{\eta }}}$$

(C3)

$${\overline{\mathbf{e}}}^{vp}_{n + 1} = \frac{{{\overline{\mathbf{e}}}^{vp}_{n} + \frac{{\Delta t_{n + 1} }}{\eta }{\overline{\overline{\varvec{e}}}}^{p}_{n + 1} }}{{1 + \frac{{\Delta t_{n + 1} }}{\eta }}}$$

(C4)

where $\Delta t_{n + 1}$ is the time step. When ${{\Delta t_{n + 1} } \mathord{\left/ {\vphantom {{\Delta t_{n + 1} } \eta }} \right. \kern-\nulldelimiterspace} \eta } \to \infty$ the inviscid solution is recovered and when ${{\Delta t_{n + 1} } \mathord{\left/ {\vphantom {{\Delta t_{n + 1} } \eta }} \right. \kern-\nulldelimiterspace} \eta } \to 0$ the elastic solution is achieved.