Scattering of anti-plane waves by scalene triangular boundary with embedded cavity in anisotropic medium based on mapping space

Abstract

Both surface boundary motion and cavity stress concentration have always been concerned in anisotropic medium. In this paper, the mapping function from anisotropic medium to homogeneous medium was established, and the relationship between the free boundary of anisotropic medium and the mapping of homogeneous medium boundary was proved. In the space of homogeneous medium mapping, the wave displacement function was obtained by solving the equation of motion that meets the zero-stress boundary conditions by the variable separation method and the symmetric method. Based on the complex function, the multi-polar coordinate method and the region-matching technique, the algebraic equations were established at auxiliary boundaries and free boundary conditions in the complex domain. Then, according to the sample statistics, instead of the Fourier expansion method, the least square method was used to solve the undetermined coefficient of the algebraic equations by discrete boundary. Finally, the process of the wave propagation was shown in the time domain by inverse Fourier transform.

1 Introduction

The dynamic response of nonlinear boundary has always been an important research topic in the field of wave motion. It is helpful to research on inverse problems of the elastic wave, and the site survey and prospecting, seismic research, underwater detection and target identification, large-scale wall vibration analysis, nondestructive testing, flaw detection, etc. At present, a variety of theoretical methods and numerical methods on convex-concave boundaries have been used to obtain fruitful results in isotropic medium. For example, the wave function expansion method [1], Hermite function and mapping function [2], the Graf’s addition theorem [3], weighted residual method [4], and other methods [5,6,7,8,9,10] were used to study concave boundary; the semi-circular auxiliary boundary [11,12,13,14], the complex displacement fields and complex coordinates [15,16,17,18], and other methods [19, 20] were used to study convex boundary. However, there are relatively few studies on nonlinear boundaries in anisotropic media. The pioneering work in this area started in the early 1990s, in which the complex wave function method was used to study SH wave scattered by circular cavities, depressions, and cylindrical semicircular sedimentary valleys in anisotropic media [21,22,23,24,25,26]. Subsequently, the propagation of gradient material and multilayer piezoelectric material were studied [27,28,29,30,31,32,33,34], and the boundary element method was used to study the scattering of SH waves by cavities and inclusions in an anisotropic body and an anisotropic elastic layer [35,36,37]. But there is almost no research report on the convex boundary.

Based on the existing research results, the SH wave scattering problem of scalene triangles with shallow circular cavity in anisotropic medium is studied in this paper. A more flexible non-semicircle region division method was used to solve the shallow cavity problem, and the auxiliary circle was applied to solve the singularity of the reflex angle at the triangle corner which singularity was proposed by Achenbach [38]. The mapping function from anisotropic medium to homogeneous medium was derived and revised the transformation function of Liu et al. [21, 22]. The relationship between the free boundary of anisotropic medium and the boundary of mapped homogeneous medium was proved, and the wave displacement function was obtained by solving the wave equation that meets the scalene triangle zero-stress boundary conditions by the variable separation method in the mapped homogeneous medium space. The wave functions that satisfy the boundary conditions of the half space were derived by using symmetry method and complex coordinates in the mapping space of the uniform medium. The defect of directly constructing the half-space scattering wave function in the literature which did not consider anisotropic material asymmetry was corrected. Especially for the difference in the range of wave function series and multiple auxiliary boundary continuous conditions, a more effective least square method which only needs discrete boundaries was proposed. And the boundary equation amplitudes were adjusted to coordinate Euclidean distance weight. After a numerical simulation, the high accuracy of the auxiliary boundary continuity, the zero-stress boundary condition, the comparison with finite element method, proved the correctness of the region-matching technique, the wave function equation and the least square method. Finally, the effects of different angles of incidence, the frequency content of the excitation, parameters of material medium, and positions of cavity were discussed in the frequency domain; the process of the wave propagation and the scattering around the triangle and the shallow circle were shown in the time domain. For many years, the mapping function from anisotropic medium to homogeneous medium and the function of constructing the half-space scattering wave were given.

2 Methodology

2.1 Model

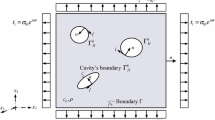
The typical project structure is shown in Fig. 1, which consists of a scalene triangle on half space and a cavity under free surface, where O stands for the triangular peak, C₁ and C₂ symbolize the hypotenuse with the gradients of 1:n₁ and 1:n₂, and O₂ is circle center with rounded edge D₂, and S represents free flat surface of half space. Anti-plane wave propagates in the anisotropic half space with modulus C₄₄, C₄₅, C₅₅, and density ρ at the incident angle α.

Fig. 1

The model of the scalene triangle with a hole and regions divided

2.2 Equation of motion and mapping function

In order to solve the singularity of the reflex angle at the triangle corner and obtain the global displacement function which satisfies Helmholtz equation and complicated boundary conditions, with the help of the region-matching technique and auxiliary circle, the space can be divided into region ①, ②, ③, ④ and ⑤ by the auxiliary boundary D₁ with circle center O₁, auxiliary boundary D₃ with circle center O₃ and so on. P, P₁ and P₂ are the projection of O, O₁ and O₂ on the flat surface in region ③. O₃ is the intersection of the extension lines of C₁ and the mid-perpendicular of the X₄X₅, where X₄ and X₅ are the intersection points of the trapezoidal edge and the circles D₄ and D₅, respectively. The coordinate systems are established as shown in the figure, where auxiliary circles D₄ and D₅ to solve singularity of reflex angle. Each angle is presented in Appendix A.

From the stress–strain relationship in anisotropic medium, the SH wave equation is

$$C_{55} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2C_{45} \frac{{\partial^{2} w}}{\partial x\partial y} + C_{44} \frac{{\partial^{2} w}}{{\partial y^{2} }} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }}.$$

(1)

Introducing complex variables $z = x + yi$ and $\overline{z} = x - yi$, in the complex plane ($z$_, $\overline{z}$), Eq. (1) can be rewritten as:

$$\left( {C_{55} - C_{44} + 2C_{45} i} \right)\frac{{\partial^{2} w}}{{\partial z^{2} }} + 2\left( {C_{44} + C_{55} } \right)\frac{{\partial^{2} w}}{{\partial z\partial \overline{z}}} + \left( {C_{55} - C_{44} - 2C_{45} i} \right)\frac{{\partial^{2} w}}{{\partial \overline{z}^{2} }} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }}.$$

(2)

Correspondingly, radial stress and hoop stress have the forms of

$$\begin{gathered} \tau_{rz} = \frac{1}{2}\left\{ {\left[ {\left( {C_{55} + C_{44} } \right)\frac{\partial w}{{\partial z}} + \left( {C_{55} - C_{44} - 2C_{45} i} \right)\frac{\partial w}{{\partial \overline{z}}}} \right]{\text{e}}^{\theta i} + \left[ {\left( {C_{55} - C_{44} + 2C_{45} i} \right)\frac{\partial w}{{\partial z}} + \left( {C_{55} + C_{44} } \right)\frac{\partial w}{{\partial \overline{z}}}} \right]{\text{e}}^{ - \theta i} } \right\} \hfill \\ \tau_{\theta z} = \frac{1}{2}\left\{ {\left[ {\left( {C_{55} i + C_{44} i} \right)\frac{\partial w}{{\partial z}} + \left( {C_{55} i - C_{44} i + 2C_{45} } \right)\frac{\partial w}{{\partial \overline{z}}}} \right]{\text{e}}^{\theta i} + \left[ {\left( { - C_{55} i + C_{44} i + 2C_{45} } \right)\frac{\partial w}{{\partial z}} + \left( { - C_{55} i - C_{44} i} \right)\frac{\partial w}{{\partial \overline{z}}}} \right]{\text{e}}^{ - \theta i} } \right\}. \hfill \\ \end{gathered}$$

(3)

In order to convert the left side of formula (2) into a form ${{\partial^{2} w} \mathord{\left/ {\vphantom {{\partial^{2} w} {\partial \chi \partial \overline{\chi }}}} \right. \kern-\nulldelimiterspace} {\partial \chi \partial \overline{\chi }}}$, the following conversion is performed

$$\frac{{\partial^{2} w}}{{\partial \chi \partial \overline{\chi }}} = \left( {\frac{\partial z}{{\partial \chi }}\frac{\partial z}{{\partial \overline{\chi }}}} \right)\frac{{\partial^{2} w}}{{\partial z^{2} }} + \left( {\frac{{\partial \overline{z}}}{\partial \chi }\frac{\partial z}{{\partial \overline{\chi }}} + \frac{\partial z}{{\partial \chi }}\frac{{\partial \overline{z}}}{{\partial \overline{\chi }}}} \right)\frac{{\partial^{2} w}}{{\partial z\partial \overline{z}}} + \left( {\frac{{\partial \overline{z}}}{\partial \chi }\frac{{\partial \overline{z}}}{{\partial \overline{\chi }}}} \right)\frac{{\partial^{2} w}}{{\partial \overline{z}^{2} }} + \frac{\partial w}{{\partial z}}\left( {\frac{{\partial^{2} z}}{{\partial \overline{\chi }\partial \chi }}} \right) + \frac{\partial w}{{\partial \overline{z}}}\left( {\frac{{\partial^{2} \overline{z}}}{{\partial \overline{\chi }\partial \chi }}} \right).$$

(4)

Comparing formula (2) and formula (4), we get:

$$\left\{ {\begin{array}{*{20}l} {\frac{\partial z}{{\partial \chi }}\frac{\partial z}{{\partial \overline{\chi }}} = C_{55} - C_{44} + 2C_{45} i} \hfill & {\left( {\text{a}} \right)} \hfill \\ {\frac{{\partial \overline{z}}}{\partial \chi }\frac{\partial z}{{\partial \overline{\chi }}} + \frac{\partial z}{{\partial \chi }}\frac{{\partial \overline{z}}}{{\partial \overline{\chi }}} = 2\left( {C_{44} + C_{55} } \right)} \hfill & {\left( {\text{b}} \right)} \hfill \\ {\frac{{\partial \overline{z}}}{\partial \chi }\frac{{\partial \overline{z}}}{{\partial \overline{\chi }}} = C_{55} - C_{44} - 2C_{45} i} \hfill & {\left( {\text{c}} \right)} \hfill \\ {\frac{{\partial^{2} z}}{{\partial \overline{\chi }\partial \chi }} = \frac{{\partial^{2} \overline{z}}}{{\partial \overline{\chi }\partial \chi }} = 0} \hfill & {\left( {\text{d}} \right)} \hfill \\ \end{array} } \right..$$

(5)

From item (d), the solution form of z is:

$$z = a\chi + b\overline{\chi } + c.$$

(6)

Set the special solution $c = 0$; from (a), (b) and (c), know that there are three unknown real numbers in z. Let $a = \hat{x} + \hat{y}i,b = \hat{x} + \hat{z}i$ or $a = \hat{x} + \hat{z}i,b = \hat{y} + \hat{z}i$; substitute z into items (a), (b) and (c); get

$$\left\{ {\begin{array}{*{20}l} {a = \frac{{C_{45} + \left( {C_{44} \pm \sqrt {C_{44} C_{55} - C_{45}^{2} } } \right)i}}{{\sqrt {C_{44} } }}} \hfill \\ {b = \frac{{C_{45} + \left( {C_{44} \mp \sqrt {C_{44} C_{55} - C_{45}^{2} } } \right)i}}{{\sqrt {C_{44} } }}} \hfill \\ \end{array} } \right.\;{\text{or}}\;\left\{ {\begin{array}{*{20}l} {a = \frac{{C_{55} \pm \sqrt {C_{44} C_{55} - C_{45}^{2} } + C_{45} i}}{{\sqrt {C_{55} } }}} \hfill \\ {b = \frac{{C_{55} \mp \sqrt {C_{44} C_{55} - C_{45}^{2} } + C_{45} i}}{{\sqrt {C_{55} } }}} \hfill \\ \end{array} } \right..$$

$\chi$ and $\overline{\chi }$ are expressed as

$$\left\{ {\begin{array}{*{20}c} {\chi = \frac{{b\overline{z} - \overline{a}z}}{{b\overline{b} - a\overline{a}}}} \\ {\overline{\chi } = \frac{{\overline{b}z - a\overline{z}}}{{b\overline{b} - a\overline{a}}}} \\ \end{array} } \right..$$

(7)

Comparing the above four results, it is known that when the second solution (a) term takes a positive sign in a homogeneous medium, $\chi = z$,$\overline{\chi } = \overline{z}$. Therefore, this solution is taken for convenience, of course other solutions are also correct.

In order to convert into complex forms of Helmholtz equation that is easy to solve [17], $4u\frac{{\partial^{2} w}}{{\partial \xi \partial \overline{\xi }}} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }}$, a and b are expressed by dimensionless $\gamma_{1} ,\gamma_{2}$ and equivalent elastic modulus $\mu$

$$\left\{ {\begin{array}{*{20}c} {\xi = \frac{1}{2}\left( {\overline{\gamma }_{1} z - \gamma_{2} \overline{z}} \right)} \\ {\overline{\xi } = \frac{1}{2}\left( {\gamma_{1} \overline{z} - \overline{\gamma }_{2} z} \right)} \\ \end{array} } \right.,$$

(8)

where $\left\{ {\begin{array}{*{20}c} {\gamma_{1} = \frac{{C_{55} + \sqrt {C_{44} C_{55} - C_{45}^{2} } + C_{45} i}}{{C_{55} }}} \\ {\gamma_{2} = \frac{{C_{55} - \sqrt {C_{44} C_{55} - C_{45}^{2} } + C_{45} i}}{{C_{55} }}} \\ \end{array} } \right.$, and $\mu = {{\left( {C_{44} C_{55} - C_{45}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {C_{44} C_{55} - C_{45}^{2} } \right)} {C_{55} }}} \right. \kern-\nulldelimiterspace} {C_{55} }}$.

For the convenience of expression, define a mapping function $\xi = \user2{\not\xi }\left( z \right)$ to represent complex conversion. The above formula (1) is transformed into

$$4\frac{{\partial^{2} w}}{{\partial \xi \partial \overline{\xi }}} = \frac{1}{{c_{T}^{2} }}\frac{{\partial^{2} w}}{{\partial t^{2} }},$$

(9)

where $c_{T}^{2} = \frac{\mu }{\rho }$. After separating the time variables, the above formula becomes

$$\frac{{\partial^{2} w}}{{\partial \xi \partial \overline{\xi }}} = \left( \frac{ik}{2} \right)^{2} w,$$

(10)

where $k = {\omega \mathord{\left/ {\vphantom {\omega {c_{T} }}} \right. \kern-\nulldelimiterspace} {c_{T} }}$.

For hole in infinite space, the solution of the above formula (10) is

$$w\left( {\xi ,\overline{\xi }} \right) = \sum\limits_{n = - \infty }^{ + \infty } {A_{n} H_{n}^{1} \left( {k\left| \xi \right|} \right)\left( {\frac{\xi }{\left| \xi \right|}} \right)^{n} } ,$$

(11)

where $H_{n}^{1}(\,)$ is Hankel function of first kind with nth order.

Combining Eqs. (3) and (8), the radial stress and the hoop stress can be expressed as:

$$\begin{gathered} \tau_{rz} = \left( {f_{1}^{r} \frac{\partial w}{{\partial \xi }} + f_{2}^{r} \frac{\partial w}{{\partial \overline{\xi }}}} \right){\text{e}}^{\theta i} + \left( {f_{3}^{r} \frac{\partial w}{{\partial \xi }} + f_{4}^{r} \frac{\partial w}{{\partial \overline{\xi }}}} \right){\text{e}}^{ - \theta i} \hfill \\ \tau_{\theta z} = \left( {f_{1}^{\theta } \frac{\partial w}{{\partial \xi }} + f_{2}^{\theta } \frac{\partial w}{{\partial \overline{\xi }}}} \right){\text{e}}^{\theta i} + \left( {f_{3}^{\theta } \frac{\partial w}{{\partial \xi }} + f_{4}^{\theta } \frac{\partial w}{{\partial \overline{\xi }}}} \right){\text{e}}^{ - \theta i} , \hfill \\ \end{gathered}$$

(12)

where $f_{1}^{r}$$f_{2}^{r}$$f_{3}^{r}$$f_{4}^{r}$$f_{1}^{\theta }$$f_{2}^{\theta }$$f_{3}^{\theta }$$f_{4}^{\theta }$ are presented in Appendix.

Establish a Cartesian coordinate system (x',y'), which is defined as $\xi = x^{\prime} + y^{\prime}i,\overline{\xi } = x^{\prime} - y^{\prime}i$. According to the literature [2], this coordinate system (x',y') is a homogeneous medium mapping coordinate system correspond to an anisotropic medium coordinate system (x,y). It is known from Eq. (8) that the complex modulus |ξ| is related to the complex z phase angle θ and modulus |z|, and the complex ξ phase angle θ' is only related to the z phase angle θ. Suppose the functional relationship is $\theta^{\prime} = f\left( \theta \right) = angle\left( {\user2{\not\xi }\left( z \right)} \right)$.

2.3 Wave function in region ①, ④, ⑤

There is only standing wave W^D() in the closed region ①, ④ or ⑤, which needs to satisfy governing Eq. (2) and free hypotenuse condition.

In the coordinate system (x,y), the zero-stress condition of the free surface hypotenuse C₁ and C₂. can be expressed as:

$$\tau_{{\theta_{0} {\text{z}}}}^{{\text{C}}} = \left\{ {\begin{array}{*{20}c} 0 & {\theta_{0} = \alpha_{1} } \\ 0 & {\theta_{0} = \alpha_{2} } \\ \end{array} } \right..$$

(13)

In the Cartesian coordinate system(x₀,y₀) and ($x^{\prime}_{0}$,$y^{\prime}_{0}$), the boundary stress is expressed as

$$\left\{ {\begin{array}{*{20}l} {\tau_{{\theta_{0} z}} = \left( {f_{1}^{\theta } {\text{e}}^{\theta i} + f_{3}^{\theta } {\text{e}}^{ - \theta i} } \right)\frac{\partial w}{{\partial \xi }} + \left( {f_{2}^{\theta } {\text{e}}^{\theta i} + f_{4}^{\theta } {\text{e}}^{ - \theta i} } \right)\frac{\partial w}{{\partial \overline{\xi }}}} \hfill & {({\text{a}})} \hfill \\ {\tau_{{\theta^{\prime}_{0} z}} = \frac{{2i\mu^{\prime}}}{{r^{\prime}}}\left( {\zeta \frac{\partial w}{{\partial \zeta }} - \overline{\zeta }\frac{\partial w}{{\partial \overline{\zeta }}}} \right) = \frac{{ir\mu^{\prime}}}{{r^{\prime}}}\left( {\left( {\overline{\gamma }_{1} {\text{e}}^{\theta i} - \gamma_{2} {\text{e}}^{ - \theta i} } \right)\frac{\partial w}{{\partial \zeta }} - \left( {\gamma_{1} {\text{e}}^{ - \theta i} - \overline{\gamma }_{2} {\text{e}}^{\theta i} } \right)\frac{\partial w}{{\partial \overline{\zeta }}}} \right)} \hfill & {({\text{b}})} \hfill \\ \end{array} } \right..$$

(14)

Substituting the boundary condition (13) into item (a) of the above formula (14), get

$$\frac{{{{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial \xi }}} \right. \kern-\nulldelimiterspace} {\partial \xi }}}}{{{{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial \overline{\xi }}}} \right. \kern-\nulldelimiterspace} {\partial \overline{\xi }}}}} = - \frac{{\left( {f_{2}^{\theta } {\text{e}}^{\theta i} + f_{4}^{\theta } {\text{e}}^{ - \theta i} } \right)}}{{\left( {f_{1}^{\theta } {\text{e}}^{\theta i} + f_{3}^{\theta } {\text{e}}^{ - \theta i} } \right)}}.$$

(15)

Substituting the above formula (15) into the term (b), the boundary stress in the coordinate system ($x^{\prime}_{0}$,$y^{\prime}_{0}$) is obtained

$$\tau_{{\theta^{\prime}_{0} {\text{z}}}}^{{\text{C}}} = \left\{ {\begin{array}{*{20}c} 0 & {\theta^{\prime}_{0} = f\left( {\alpha_{1} } \right)} \\ 0 & {\theta^{\prime}_{0} = f\left( {\alpha_{2} } \right)} \\ \end{array} } \right..$$

(16)

In order to easily obtain equations that meet the boundary conditions, the coordinate system ($x^{\prime}_{e}$,$y^{\prime}_{e}$) is established, in which the $x^{\prime}_{e}$-axis bisects the angle of the triangle corner in mapping space. The governing equation in the polar coordinate system ($r^{\prime}_{e}$,$\theta^{\prime}_{e}$) corresponding to the coordinates ($x^{\prime}_{e}$,$y^{\prime}_{e}$) is

$$\frac{1}{{r^{\prime}_{e} }}\frac{\partial }{\partial r}\left( {r^{\prime}_{e} \frac{\partial w}{{\partial r^{\prime}_{e} }}} \right) + \frac{1}{{r^{2^{\prime}}_{e}}}\frac{{\partial^{2} w}}{{\partial \theta^{{2^{\prime}}}_{e}}} + k^{2} w = 0.$$

(17)

The wave equation that satisfies the boundary conditions is:

$$w = \sum {A_{{\lambda_{1} }} J_{{\lambda_{1} }} (kr^{\prime}_{e} )\cos (\lambda_{1} \theta^{\prime}_{e} ) + B_{{\lambda_{2} }} J_{{\lambda_{2} }} (kr^{\prime}_{e} )\sin (\lambda_{2} \theta^{\prime}_{e} )} ,$$

(18)

where $\lambda_{1} = \frac{2m\pi }{{f\left( {\alpha_{1} } \right) - f\left( {\alpha_{2} } \right)}}$ and $\lambda_{2} = \frac{(2m + 1)\pi }{{f\left( {\alpha_{1} } \right) - f\left( {\alpha_{2} } \right)}}$, $m = 0,1,2 \cdots$.

In the complex plane $(\xi_{e} ,\overline{\xi }_{e} )$ corresponding to the coordinate system ($x^{\prime}_{e}$,$y^{\prime}_{e}$), the standing wave function of the above formula (18) is written as

$$W^{D3(1)} \left( {\xi_{e} ,\overline{\xi }_{e} } \right) = W_{0} \sum\limits_{m = 0}^{ + \infty } {\left\{ {C_{m}^{{}} J_{{mp_{0} }} \left( {K_{\rm I} \left| {\xi_{e} } \right|} \right)\left[ {\left( {\frac{{\xi_{e} }}{{\left| {\xi_{e} } \right|}}} \right)^{{mp_{0} }} + \left( { - 1} \right)^{m} \left( {\frac{{\xi_{e} }}{{\left| {\xi_{e} } \right|}}} \right)^{{ - mp_{0} }} } \right]} \right\}} ,$$

(19)

where W₀ is the displacement amplitude, and it is supposed to a unity in this paper; C_m is a coefficient to be determined; J_mp0() is Bessel function with mp₀ th order; p₀ = π/(f(α₁)-f(α₂)). In W^D3(1), the superscripts (1) mean region ①; the superscripts D3 represent auxiliary boundary D₃; K₁ is the shear wave number of region ①. The following symbols are marked in the similar way.

According to the moving coordinates from ($x^{\prime}_{e}$,$y^{\prime}_{e}$) to ($x^{\prime}_{0}$,$y^{\prime}_{0}$), ξ₀ can be expressed as

$$\xi_{e} = \xi_{0} {\text{e}}^{{q_{0} i}} ,$$

(20)

where q₀ = -(f(α₁) + f(α₂))/2.

Substituting (20) into Eq. (19) and returning to the coordinate system (x₀,y₀), in the complex plane $(Z_{j} ,\overline{Z}_{j} )$, Eq. (19) can be expressed as

$$W^{D3(1)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = W_{0} \sum\limits_{m = 0}^{ + \infty } {\left\{ {C_{m}^{{}} J_{{mp_{0} }} \left( {K_{1} \left| {\user2{\not\xi }\left( {Z_{0j} } \right){\text{e}}^{{q_{0} i}} } \right|} \right)\left[ {\left( {\frac{{\user2{\not\xi }\left( {Z_{0j} } \right){\text{e}}^{{q_{0} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{0j} } \right){\text{e}}^{{q_{0} i}} } \right|}}} \right)^{{mp_{0} }} + \left( { - 1} \right)^{m} \left( {\frac{{\user2{\not\xi }\left( {Z_{0j} } \right){\text{e}}^{{q_{0} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{0j} } \right){\text{e}}^{{q_{0} i}} } \right|}}} \right)^{{ - mp_{0} }} } \right]} \right\}} ,$$

(21)

where $\begin{array}{*{20}c} {Z_{0j} = Z_{3} + b_{03} } & {j = 3} \\ \end{array}$; $b_{03} = H - H_{3} + \left( {H\tan (\alpha_{1} ) - H_{3} \tan (\alpha_{4} )} \right)i$, which is the complex coordinates of O₃ with the origin at O.

The corresponding shear stresses are:

$$\begin{gathered} \tau_{{^{{r_{j} z}} }}^{D3(1)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = 0}^{ + \infty } {C_{m}^{{}} \tilde{P}_{{mp_{0} }}^{J} \left( {Z_{0j} } \right)} \hfill \\ \tau_{{^{{\theta_{j} z}} }}^{D3(1)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = 0}^{ + \infty } {C_{m}^{{}} \tilde{Q}_{{mp_{0} }}^{J} \left( {Z_{0j} } \right)} , \hfill \\ \end{gathered}$$

(22)

where $\tilde{P}_{mp}^{J}$ and $\tilde{Q}_{mp}^{J}$ are presented in Appendix, and H_j = 0; J represents Bessel functions in Appendix equation, and if J is replaced by H, it means Hankel function.

Similarly, in the ④ and ⑤ region, the scattered wave can be rewritten as

$$W^{D4(4)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = W_{0} \sum\limits_{m = 0}^{ + \infty } {\left\{ {F_{m}^{{}} J_{{mp_{4} }} \left( {K_{4} \left| {\user2{\not\xi }\left( {Z_{4j} } \right){\text{e}}^{{q_{4} i}} } \right|} \right)\left[ {\left( {\frac{{\user2{\not\xi }\left( {Z_{4j} } \right){\text{e}}^{{q_{4} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{4j} } \right){\text{e}}^{{q_{4} i}} } \right|}}} \right)^{{mp_{4} }} + \left( { - 1} \right)^{m} \left( {\frac{{\user2{\not\xi }\left( {Z_{4j} } \right){\text{e}}^{{q_{4} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{4j} } \right){\text{e}}^{{q_{4} i}} } \right|}}} \right)^{{ - mp_{4} }} } \right]} \right\}} ,$$

(23)

$$W^{D5(5)} \left( {Z_{5} ,\overline{Z}_{5} } \right) = W_{0} \sum\limits_{m = 0}^{ + \infty } {\left\{ {G_{m}^{{}} J_{{mp_{5} }} \left( {K_{5} \left| {\user2{\not\xi }\left( {Z_{5j} } \right){\text{e}}^{{q_{5} i}} } \right|} \right)\left[ {\left( {\frac{{\user2{\not\xi }\left( {Z_{5j} } \right){\text{e}}^{{q_{5} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{5j} } \right){\text{e}}^{{q_{5} i}} } \right|}}} \right)^{{mp_{5} }} + \left( { - 1} \right)^{m} \left( {\frac{{\user2{\not\xi }\left( {Z_{5j} } \right){\text{e}}^{{q_{5} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{5j} } \right){\text{e}}^{{q_{5} i}} } \right|}}} \right)^{{ - mp_{5} }} } \right]} \right\},}$$

(24)

where $\begin{array}{*{20}c} {Z_{4j} = Z_{4} + b_{44} } & {j = 4} \\ \end{array}$, $\begin{array}{*{20}c} {Z_{5j} = Z_{5} + b_{55} } & {j = 5} \\ \end{array}$ and $q_{4} = - \left( {f\left( {\alpha_{6} } \right) + f\left( {{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \right)/2$, $q_{5} = - \left( {f\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}} \right) + f\left( {\alpha_{7} } \right)} \right)/2$, $p_{4} = {\pi \mathord{\left/ {\vphantom {\pi {\left( {f\left( {\alpha_{6} } \right) - f\left( {{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {f\left( {\alpha_{6} } \right) - f\left( {{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \right)}}$, $p_{5} = {\pi \mathord{\left/ {\vphantom {\pi {\left( {f\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}} \right) - f\left( {\alpha_{7} } \right)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {f\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}} \right) - f\left( {\alpha_{7} } \right)} \right)}}$, $b_{44} = b_{55} = 0$.

The corresponding shear stresses are:

$$\begin{gathered} \tau_{{^{{r_{j} z}} }}^{D4(4)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = 0}^{ + \infty } {\left\{ {F_{m}^{{}} \tilde{P}_{{mp_{4} }}^{J} \left( {Z_{4j} } \right)} \right\}} \hfill \\ \tau_{{^{{\theta_{j} z}} }}^{D4(4)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = 0}^{ + \infty } {\left\{ {F_{m}^{{}} \tilde{Q}_{{mp_{4} }}^{J} \left( {Z_{4j} } \right)} \right\}} , \hfill \\ \end{gathered}$$

(25)

$$\begin{gathered} \tau_{{^{{r_{j} z}} }}^{D5(5)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = 0}^{ + \infty } {\left\{ {G_{m}^{{}} \tilde{P}_{{mp_{5} }}^{J} \left( {Z_{5j} } \right)} \right\}} \hfill \\ \tau_{{^{{\theta_{j} z}} }}^{D5(5)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = 0}^{ + \infty } {\left\{ {G_{m}^{{}} \tilde{Q}_{{mp_{5} }}^{J} \left( {Z_{5j} } \right)} \right\}} . \hfill \\ \end{gathered}$$

(26)

2.4 Wave function in region ②

In the region ②, the total waves consist of the incident wave W⁽ⁱ⁾, the reflected wave W^(r) from the horizontal free surface S, and the scattered waves W^D1 and W^D2 by the auxiliary boundary D₁ and the cavity edge D₂.

Due to the anisotropy of the material, a semi-infinite space scattering field cannot be directly constructed by the symmetric method, so it needs to be constructed with the help of the material homogeneity field of the mapping space. The surface stress is $\tau_{{\theta^{\prime}_{0} {\text{z}}}}^{{\text{S}}} = 0$ from Eq. (14), and material is isotropic in mapping space (x',y'). Based on the complex coordinates and the symmetric method, a semi-infinite space scattering field that satisfies boundary conditions is constructed, as shown in Fig. 2. The scattering wave equation with two symmetrical cavities is

$$w = \sum\limits_{m = - \infty }^{ + \infty } {A_{{m^{\prime}}} H_{{m^{\prime}}}^{1} (k\left| {\user2{\not\xi }_{2} \left( z \right)} \right|)\left( {\frac{{\user2{\not\xi }_{2} \left( z \right)}}{{\left| {\user2{\not\xi }_{2} \left( z \right)} \right|}}} \right)^{{m^{\prime}}} + A_{{m^{\prime}}} H_{{m^{\prime}}}^{1} (k\left| {\user2{\not\xi }_{{\overline{2}}} \left( z \right)} \right|)\left( {\frac{{\user2{\not\xi }_{{\overline{2}}} \left( z \right)}}{{\left| {\user2{\not\xi }_{{\overline{2}}} \left( z \right)} \right|}}} \right)^{{m^{\prime}}} } .$$

(27)

Fig. 2

Circle symmetry in mapping space

By taking the relationship of ${\varvec{\xi}}_{2} = {\varvec{\xi}}_{{\underline {2} }} - 2h_{2}$,${\varvec{\xi}}_{{\underline {2} }} = - \overline{{{\varvec{\xi}}_{{\overline{2}}} }}$,${\varvec{\xi}}_{2} = {\varvec{\xi}}_{{4{\text{p}}}} - h_{2}$,${\varvec{\xi}}_{4} = {\varvec{\xi}}_{{4{\text{p}}}} - l_{2}$ ($h_{2} = real\left( {\user2{\not\xi }\left( {H_{2} } \right)} \right)$,$l_{2} = imag\left( {\user2{\not\xi }\left( {H_{2} } \right)} \right) \times i$) into Eq. (27), it is expressed as

$$\begin{gathered} w = \sum\limits_{m = - \infty }^{ + \infty } {A_{{m^{\prime}}} H_{{m^{\prime}}}^{1} (k\left| {{\varvec{\xi}}_{2} } \right|)\left( {\frac{{{\varvec{\xi}}_{2} }}{{\left| {{\varvec{\xi}}_{2} } \right|}}} \right)^{{m^{\prime}}} + A_{{m^{\prime}}} H_{{m^{\prime}}}^{1} (k\left| { - \overline{{{\varvec{\xi}}_{2} }} - 2h_{2} } \right|)\left( {\frac{{ - \overline{{{\varvec{\xi}}_{2} }} - 2h_{2} }}{{\left| { - \overline{{{\varvec{\xi}}_{2} }} - 2h_{2} } \right|}}} \right)^{{m^{\prime}}} } \hfill \\ = \sum\limits_{m = - \infty }^{ + \infty } {A_{{m^{\prime}}} H_{{m^{\prime}}}^{1} (k\left| {{\varvec{\xi}}_{4} - \user2{\not\xi }\left( {H_{2} } \right)} \right|)\left( {\frac{{{\varvec{\xi}}_{4} - \user2{\not\xi }\left( {H_{2} } \right)}}{{\left| {{\varvec{\xi}}_{4} - \user2{\not\xi }\left( {H_{2} } \right)} \right|}}} \right)^{{m^{\prime}}} + \left( { - 1} \right)^{m} A_{{m^{\prime}}} H_{{m^{\prime}}}^{1} (k\left| {{\varvec{\xi}}_{4} + \overline{\user2{\not\xi }}\left( {H_{2} } \right)} \right|)\left( {\frac{{{\varvec{\xi}}_{4} + \overline{\user2{\not\xi }}\left( {H_{2} } \right)}}{{\left| {{\varvec{\xi}}_{4} + \overline{\user2{\not\xi }}\left( {H_{2} } \right)} \right|}}} \right)^{{ - m^{\prime}}} } . \hfill \\ \end{gathered}$$

(28)

According to Eq. (28), the equation of the scattered wave W^D2(2) generated by the boundary D₂, which satisfies the governing Eq. (2) and the free boundary condition S in the complex plane ($z_{j}$,$\overline{z}_{j}$), can be written as

$$W^{D2(2)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = W_{0} \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {E_{m}^{{}} \left[ \begin{gathered} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{7j} } \right) - \user2{\not\xi }\left( {H_{2} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{7j} } \right) - \user2{\not\xi }\left( {H_{2} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{7j} } \right) - \user2{\not\xi }\left( {H_{2} } \right)} \right|}}} \right)^{m} + \hfill \\ \left( { - 1} \right)^{m} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{7j} } \right) + \overline{\user2{\not\xi }}\left( {H_{2} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{7j} } \right) + \overline{\user2{\not\xi }}\left( {H_{2} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{7j} } \right) + \overline{\user2{\not\xi }}\left( {H_{2} } \right)} \right|}}} \right)^{ - m} \hfill \\ \end{gathered} \right]} \right\}} .$$

(29)

where $Z_{7j} = \left\{ {\begin{array}{*{20}c} {Z_{1} + b_{71} } & {j = 1} \\ {Z_{2} + b_{72} } & {j = 2} \\ \end{array} } \right.$ and $b_{71} = H_{1} - L_{2} i$, $b_{72} = H_{2}$.

Similarly, in the complex plane ($z_{j}$,$\overline{z}_{j}$), the equation of the scattered wave W^D1(2) generated by the boundary D₁, can be written as

$$W^{D1(2)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = W_{0} \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {D_{m}^{{}} \left[ \begin{gathered} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{6j} } \right) - \user2{\not\xi }\left( {H_{1} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{6j} } \right) - \user2{\not\xi }\left( {H_{1} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{6j} } \right) - \user2{\not\xi }\left( {H_{1} } \right)} \right|}}} \right)^{m} + \hfill \\ \left( { - 1} \right)^{m} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{6j} } \right) + \overline{\user2{\not\xi }}\left( {H_{1} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{6j} } \right) + \overline{\user2{\not\xi }}\left( {H_{1} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{6j} } \right) + \overline{\user2{\not\xi }}\left( {H_{1} } \right)} \right|}}} \right)^{ - m} \hfill \\ \end{gathered} \right]} \right\}} .$$

(30)

where $Z_{6j} = \left\{ {\begin{array}{*{20}c} {Z_{1} + b_{61} } & {j = 1} \\ {Z_{2} + b_{62} } & {j = 2} \\ \end{array} } \right.$ and $b_{61} = H_{1}$, $b_{62} = H_{2} + L_{2} i$.

In the above formula, W₀ is the displacement amplitude; D_m and E_m are coefficients to be determined; ${\varvec{H}}_{m}^{1} ( \cdot )$ is Hankel function of first kind with mth order.

The corresponding shear stresses are:

$$\begin{gathered} \tau_{{^{{r_{j} z}} }}^{D1(2)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {D_{m}^{{}} \tilde{P}_{m}^{{H^{1} }} \left( {Z_{6j} } \right)} \hfill \\ \tau_{{^{{\theta_{j} z}} }}^{D1(2)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {D_{m}^{{}} \tilde{Q}_{m}^{{H^{1} }} \left( {Z_{6j} } \right)} . \hfill \\ \end{gathered}$$

(31)

$$\begin{gathered} \tau_{{^{{r_{j} z}} }}^{D1(2)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {D_{m}^{{}} \tilde{P}_{m}^{{H^{1} }} \left( {Z_{6j} } \right)} \hfill \\ \tau_{{^{{\theta_{j} z}} }}^{D1(2)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {D_{m}^{{}} \tilde{Q}_{m}^{{H^{1} }} \left( {Z_{6j} } \right)} . \hfill \\ \end{gathered}$$

(32)

In the above stress formula, q = 0, and see Appendix in detail.

In the Cartesian coordinate system o₆x₆y₆, the incident wave with incidence angle α [21], can be written as

$$W^{(i)} = W_{i} {\text{e}}^{{iK_{2}^{i} (y_{6} \sin \alpha_{i} - x_{6} \cos \alpha_{i} )}} = W_{i} {\text{e}}^{{\frac{{ - iK_{2}^{i} }}{2}({\text{z}}_{6} {\text{e}}^{{\alpha_{i} i}} + {\overline{\text{z}}}_{6} {\text{e}}^{{ - \alpha_{i} i}} )}} ,$$

(33)

where $W_{i} = W_{0}$.

Substituting above formula into the wave Eq. (1), the wave velocity is:

$$c_{si} = \left\{ {{{\left[ {\left( {\cos a_{i} } \right)^{2} C_{55} - \left( {2\sin a_{i} \cos a_{i} } \right)C_{45} + \left( {\sin a_{i} } \right)^{2} C_{44} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {\cos a_{i} } \right)^{2} C_{55} - \left( {2\sin a_{i} \cos a_{i} } \right)C_{45} + \left( {\sin a_{i} } \right)^{2} C_{44} } \right]} \rho }} \right. \kern-\nulldelimiterspace} \rho }} \right\}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} .$$

Reflected wave can be written as

$$W^{(r)} = W_{r} {\text{e}}^{{iK_{2}^{r} (y_{6} \sin \alpha_{r} + x_{6} \cos \alpha_{r} )}} = W_{r} {\text{e}}^{{\frac{{iK_{2}^{r} }}{2}({\text{z}}_{6} {\text{e}}^{{ - \alpha_{r} i}} + {\overline{\text{z}}}_{6} {\text{e}}^{{\alpha_{r} i}} )}} .$$

(34)

Substituting above formula into the wave Eq. (1), the wave velocity is:

$$c_{sr} = \left\{ {{{\left[ {\left( {\cos a_{r} } \right)^{2} C_{55} + \left( {2\sin a_{r} \cos a_{r} } \right)C_{45} + \left( {\sin a_{r} } \right)^{2} C_{44} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {\cos a_{r} } \right)^{2} C_{55} + \left( {2\sin a_{r} \cos a_{r} } \right)C_{45} + \left( {\sin a_{r} } \right)^{2} C_{44} } \right]} \rho }} \right. \kern-\nulldelimiterspace} \rho }} \right\}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} .$$

Substituting the total wave $W = W^{(i)} + W^{(r)}$ into the zero stress condition $\left. {\tau_{{x_{3} z_{3} }}^{S} } \right|_{{x_{3} = 0}} = 0$ at the free boundary, obtain

$$\left\{ {\begin{array}{*{20}l} {\cot a_{r} = \cot a_{i} - {{2C_{45} } \mathord{\left/ {\vphantom {{2C_{45} } {C_{55} }}} \right. \kern-\nulldelimiterspace} {C_{55} }}} \hfill \\ {W_{r} = W_{i} } \hfill \\ {K_{2}^{r} = {{K_{2}^{i} \sin \alpha_{i} } \mathord{\left/ {\vphantom {{K_{2}^{i} \sin \alpha_{i} } {\sin \alpha_{r} }}} \right. \kern-\nulldelimiterspace} {\sin \alpha_{r} }}} \hfill \\ \end{array} \quad a_{i} \ne 0} \right.\;{\text{or}}\;\left\{ {\begin{array}{*{20}l} {a_{r} = a_{i} } \hfill \\ {W_{r} = W_{i} } \hfill \\ {K_{2}^{r} = K_{2}^{i} } \hfill \\ \end{array} \quad a_{i} = 0} \right..$$

When cotα_r1 = cotα_i − 2C₄₅/C₅₅ ≥ 0, the reflected wave is in the first quadrant; while cotα_r1 = cotα_i − 2C₄₅/C₅₅ < 0, the reflected wave does not exist because the anisotropic medium changes the direction of wave propagation. It means that the incident angle α_i only be less than acot(2C₄₅/C₅₅) near the surface. Its total expression is

$$W^{{\left( {i + r} \right)}} \left( {Z_{j} ,\overline{Z}_{j} } \right) = W_{0} {\text{e}}^{{\frac{{ - iK_{2}^{i} }}{2}({\text{z}}_{6j} {\text{e}}^{{\alpha_{i} i}} + {\overline{\text{z}}}_{6j} {\text{e}}^{{ - \alpha_{i} i}} )}} + W_{0} {\text{e}}^{{\frac{{iK_{2}^{r} }}{2}({\text{z}}_{6j} {\text{e}}^{{ - \alpha_{r} i}} + {\overline{\text{z}}}_{6j} {\text{e}}^{{\alpha_{r} i}} )}} .$$

(35)

Substituting it into Eq. (3), get the stress expression

$$\begin{gathered} \tau_{{r_{j} z}}^{{\left( {i + r} \right)}} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \frac{1}{2}\left\{ \begin{gathered} \left[ {\left( {C_{55} + C_{44} } \right)U\left( {{\text{z}}_{6j} } \right) + \left( {C_{55} - C_{44} - 2C_{45} i} \right)V\left( {{\text{z}}_{6j} } \right)} \right]{\text{e}}^{\theta i} + \hfill \\ \left[ {\left( {C_{55} - C_{44} + 2C_{45} i} \right)U\left( {{\text{z}}_{6j} } \right) + \left( {C_{55} + C_{44} } \right)V\left( {{\text{z}}_{6j} } \right)} \right]{\text{e}}^{ - \theta i} \hfill \\ \end{gathered} \right\} \hfill \\ \tau_{{\theta_{j} z}}^{{\left( {i + r} \right)}} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \frac{1}{2}\left\{ \begin{gathered} \left[ {\left( {C_{55} i + C_{44} i} \right)U\left( {{\text{z}}_{6j} } \right) + \left( {C_{55} i - C_{44} i + 2C_{45} } \right)V\left( {{\text{z}}_{6j} } \right)} \right]{\text{e}}^{\theta i} + \hfill \\ \left[ {\left( { - C_{55} i + C_{44} i + 2C_{45} } \right)U\left( {{\text{z}}_{6j} } \right) + \left( { - C_{55} i - C_{44} i} \right)V\left( {{\text{z}}_{6j} } \right)} \right]{\text{e}}^{ - \theta i} \hfill \\ \end{gathered} \right\}. \hfill \\ \end{gathered}$$

(36)

See Appendix in detail.

2.5 Wave function in region ③

In the enclosed region ③, the total waves are composed of W^D1 W^D3 W^D4 and W^D5 generated by the auxiliary boundaries D₁, D₃, D₄ and D₅, respectively. In the complex plane ($z_{j}$,$\overline{z}_{j}$), they can be written as

$$W^{D1(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = W_{0} \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {I_{m} J_{m} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{1j} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1j} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1j} } \right)} \right|}}} \right)^{m} } \right\}} ,$$

(37)

$$W^{D3(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = W_{0} \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {K_{m}^{{}} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{3j} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{3j} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{3j} } \right)} \right|}}} \right)^{m} } \right\}} ,$$

(38)

$$W^{D4(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = W_{0} \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {M_{m}^{{}} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{4j} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{4j} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{4j} } \right)} \right|}}} \right)^{m} } \right\}} ,$$

(39)

$$W^{D5(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = W_{0} \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {N_{m}^{{}} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{5j} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{5j} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{5j} } \right)} \right|}}} \right)^{m} } \right\}} ,$$

(40)

where $Z_{1j} = \left\{ {\begin{array}{*{20}l} {Z_{3} + b_{13} } \hfill & {j = 3} \hfill \\ {Z_{4} + b_{14} } \hfill & {j = 4} \hfill \\ {Z_{5} + b_{15} } \hfill & {j = 5} \hfill \\ \end{array} } \right.$ $Z_{3j} = \left\{ {\begin{array}{*{20}l} {Z_{1} + b_{31} } \hfill & {j = 1} \hfill \\ {Z_{4} + b_{34} } \hfill & {j = 4} \hfill \\ {Z_{5} + b_{35} } \hfill & {j = 5} \hfill \\ \end{array} } \right.$ $Z_{4j} = \left\{ {\begin{array}{*{20}l} {Z_{3} + b_{43} } \hfill & {j = 3} \hfill \\ {Z_{1} + b_{41} } \hfill & {j = 1} \hfill \\ {Z_{5} + b_{45} } \hfill & {j = 5} \hfill \\ \end{array} } \right.$ $Z_{5j} = \left\{ {\begin{array}{*{20}l} {Z_{3} + b_{53} } \hfill & {j = 3} \hfill \\ {Z_{1} + b_{51} } \hfill & {j = 1} \hfill \\ {Z_{4} + b_{54} } \hfill & {j = 4} \hfill \\ \end{array} } \right.$ and $b_{31} = H_{1} + H_{3} + \left( {{{ - L} \mathord{\left/ {\vphantom {{ - L} 2}} \right. \kern-\nulldelimiterspace} 2} + H_{3} \tan (\alpha_{4} )} \right)i$, $b_{34} = H_{3} + \left( { - L + H_{3} \tan (\alpha_{4} )} \right)i$, $b_{35} = H_{3} + \left( {H_{3} \tan (\alpha_{4} )} \right)i$, $b_{13} = - b_{31}$, $b_{14} = - H_{1} - {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-\nulldelimiterspace} 2}i$, $b_{15} = - H_{1} + {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-\nulldelimiterspace} 2}i$, $b_{43} = - b_{34}$, $b_{41} = - b_{14}$, $b_{45} = Li$, $b_{53} = - b_{35}$, $b_{51} = - b_{15}$, $b_{54} = - b_{45}$.

The corresponding shear stresses are:

$$\begin{gathered} \tau_{{^{{r_{j} z}} }}^{D1(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {I_{m}^{{}} \tilde{P}_{m}^{{J^{{}} }} \left( {Z_{3j} } \right)} \right\}} ,\delta = 0 \hfill \\ \tau_{{^{{\theta_{j} z}} }}^{D1(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {I_{m}^{{}} \tilde{Q}_{m}^{{J^{{}} }} \left( {Z_{3j} } \right)} \right\}} ,\delta = 0 \hfill \\ \end{gathered}$$

(41)

$$\begin{gathered} \tau_{{^{{r_{j} z}} }}^{D3(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {K_{m}^{{}} \tilde{P}_{m}^{{H^{1} }} \left( {Z_{1j} } \right)} \right\}} ,\delta = 0 \hfill \\ \tau_{{^{{\theta_{j} z}} }}^{D3(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {K_{m}^{{}} \tilde{Q}_{m}^{{H^{1} }} \left( {Z_{1j} } \right)} \right\}} ,\delta = 0 \hfill \\ \end{gathered}$$

(42)

$$\begin{gathered} \tau_{{^{{r_{j} z}} }}^{D4(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {M_{m}^{{}} \tilde{P}_{m}^{{H^{1} }} \left( {Z_{4j} } \right)} \right\}} ,\delta = 0 \hfill \\ \tau_{{^{{\theta_{j} z}} }}^{D4(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {M_{m}^{{}} \tilde{Q}_{m}^{{H^{1} }} \left( {Z_{4j} } \right)} \right\}} ,\delta = 0 \hfill \\ \end{gathered}$$

(43)

$$\begin{gathered} \tau_{{^{{r_{j} z}} }}^{D5(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {N_{m}^{{}} \tilde{P}_{m}^{{H^{1} }} \left( {Z_{5j} } \right)} \right\}} ,\delta = 0 \hfill \\ \tau_{{^{{\theta_{j} z}} }}^{D5(3)} \left( {Z_{j} ,\overline{Z}_{j} } \right) = \sum\limits_{m = - \infty }^{ + \infty } {\left\{ {N_{m}^{{}} \tilde{Q}_{m}^{{H^{1} }} \left( {Z_{5j} } \right)} \right\}} ,\delta = 0 \hfill \\ \end{gathered}$$

(44)

where δ is the variable in the formula. See Appendix in detail.

2.6 Boundary conditions and solving method

Based on the continuity conditions of displacement and stress at the auxiliary boundary D₁, D₃, D₄, D₅, and the radial zero-stress at the cavity edge D₂, a system of equations is established for solving the unknown complex coefficients.

$$\left\{ {\begin{array}{*{20}l} {W^{D3(1)} \left( {Z_{3} ,\overline{Z}_{3} } \right) = W^{D1(3)} \left( {Z_{3} ,\overline{Z}_{3} } \right) + W^{D3(3)} \left( {Z_{3} ,\overline{Z}_{3} } \right) + W^{D4(3)} \left( {Z_{3} ,\overline{Z}_{3} } \right) + W^{D5(3)} \left( {Z_{3} ,\overline{Z}_{3} } \right)} \hfill & {Z_{3} \in D_{3} } \hfill \\ {\tau_{{r_{3} z}}^{D3(1)} \left( {Z_{3} ,\overline{Z}_{3} } \right) = \tau_{{r_{3} z}}^{D1(3)} \left( {Z_{3} ,\overline{Z}_{3} } \right) + \tau_{{r_{3} z}}^{D3(3)} \left( {Z_{3} ,\overline{Z}_{3} } \right) + \tau_{{r_{3} z}}^{D4(3)} \left( {Z_{3} ,\overline{Z}_{3} } \right) + \tau_{{r_{3} z}}^{D5(3)} \left( {Z_{3} ,\overline{Z}_{3} } \right)} \hfill & {Z_{3} \in D_{3} } \hfill \\ {W^{D4(4)} \left( {Z_{4} ,\overline{Z}_{4} } \right) = W^{D1(3)} \left( {Z_{4} ,\overline{Z}_{4} } \right) + W^{D3(3)} \left( {Z_{4} ,\overline{Z}_{4} } \right) + W^{D4(3)} \left( {Z_{4} ,\overline{Z}_{4} } \right) + W^{D5(3)} \left( {Z_{4} ,\overline{Z}_{4} } \right)} \hfill & {Z_{4} \in D_{4} } \hfill \\ {\tau_{{r_{4} z}}^{D4(4)} \left( {Z_{4} ,\overline{Z}_{4} } \right) = \tau_{{r_{4} z}}^{D1(3)} \left( {Z_{4} ,\overline{Z}_{4} } \right) + \tau_{{r_{4} z}}^{D3(3)} \left( {Z_{4} ,\overline{Z}_{4} } \right) + \tau_{{r_{4} z}}^{D4(3)} \left( {Z_{4} ,\overline{Z}_{4} } \right) + \tau_{{r_{4} z}}^{D5(3)} \left( {Z_{4} ,\overline{Z}_{4} } \right)} \hfill & {Z_{4} \in D_{4} } \hfill \\ {W^{D5(5)} \left( {Z_{5} ,\overline{Z}_{5} } \right) = W^{D1(3)} \left( {Z_{5} ,\overline{Z}_{5} } \right) + W^{D3(3)} \left( {Z_{5} ,\overline{Z}_{5} } \right) + W^{D4(3)} \left( {Z_{5} ,\overline{Z}_{5} } \right) + W^{D5(3)} \left( {Z_{5} ,\overline{Z}_{5} } \right)} \hfill & {Z_{5} \in D_{5} } \hfill \\ {\tau_{{r_{5} z}}^{D5(5)} \left( {Z_{5} ,\overline{Z}_{5} } \right) = \tau_{{r_{5} z}}^{D1(3)} \left( {Z_{5} ,\overline{Z}_{5} } \right) + \tau_{{r_{5} z}}^{D3(3)} \left( {Z_{5} ,\overline{Z}_{5} } \right) + \tau_{{r_{5} z}}^{D4(3)} \left( {Z_{5} ,\overline{Z}_{5} } \right) + \tau_{{r_{5} z}}^{D5(3)} \left( {Z_{5} ,\overline{Z}_{5} } \right)} \hfill & {Z_{5} \in D_{5} } \hfill \\ W^{D1(2)} \left( {Z_{1} ,\overline{Z}_{1} } \right) + W^{D2(2)} \left( {Z_{1} ,\overline{Z}_{1} } \right) + W^{{\left( {i + r} \right)}} \left( {Z_{1} ,\overline{Z}_{1} } \right) = W^{D1(3)} \left( {Z_{1} ,\overline{Z}_{1} } \right) + W^{D3(3)} \left( {Z_{1} ,\overline{Z}_{1} } \right) \\ + W^{D4(3)} \left( {Z_{1} ,\overline{Z}_{1} } \right) + W^{D5(3)} \left( {Z_{1} ,\overline{Z}_{1} } \right) \hfill & {Z_{1} \in D_{1} } \hfill \\ \tau_{{r_{1} z}}^{D1(2)} \left( {Z_{1} ,\overline{Z}_{1} } \right) + \tau_{{r_{1} z}}^{D2(2)} \left( {Z_{1} ,\overline{Z}_{1} } \right) + \tau_{{r_{1} z}}^{{\left( {i + r} \right)}} \left( {Z_{1} ,\overline{Z}_{1} } \right) = \tau_{{r_{1} z}}^{D1(3)} \left( {Z_{1} ,\overline{Z}_{1} } \right) + \tau_{{r_{1} z}}^{D3(3)} \left( {Z_{1} ,\overline{Z}_{1} } \right) \\ + \tau_{{r_{1} z}}^{D4(3)} \left( {Z_{1} ,\overline{Z}_{1} } \right) + \tau_{{r_{1} z}}^{D5(3)} \left( {Z_{1} ,\overline{Z}_{1} } \right) \hfill & {Z_{1} \in D_{1} } \hfill \\ {\tau_{{r_{2} z}}^{D1(2)} \left( {Z_{2} ,\overline{Z}_{2} } \right) + \tau_{{r_{2} z}}^{D2(2)} \left( {Z_{2} ,\overline{Z}_{2} } \right) + \tau_{{r_{2} z}}^{{\left( {i + r} \right)}} \left( {Z_{2} ,\overline{Z}_{2} } \right) = 0} \hfill & {Z_{2} \in D_{2} } \hfill \\ \end{array} } \right.$$

(45)

Currently, the Fourier expansion method is commonly used to solve the undetermined coefficients of algebraic equations, and it is an average approximation of the entire boundary conditions. Due to the wave field high gradient of the triangle edge and the auxiliary boundary corner point, The Fourier expansion method whose convergence speed is slow is difficult to solve the problem of the scalene triangle. Therefore, this paper proposes the least square method with the direct discrete boundary conditions. According to the set distance on the boundary, the discrete points are taken and the displacement and stress on the two sides of the discrete points are equal, as shown in Fig. 3. An infinite number of points n can be taken on the boundary to form an infinite number of equations to solve the undetermined coefficients C_m, D_m, E_m…. In order to minimize the error of the undetermined coefficient of the finite term, a large number of sample points n (n ≫ m) are approximated to the true solution by the least square method. This paper uses equidistant discrete points and stress terms divided by μk (not reflected in the formula) to coordinate the weights of Euclidean distance. The matrix is expressed as

$$\overline{M}^{T} MX = \overline{M}^{T} N,$$

(46)

where

$$M = \left[ {\begin{array}{*{20}c} { - \tilde{c}_{nm}^{3} } & 0 & 0 & 0 & 0 & {\tilde{i}_{nm}^{3} } & {\tilde{k}_{nm}^{3} } & {\tilde{m}_{nm}^{3} } & {\tilde{n}_{nm}^{3} } \\ { - \tilde{c}_{nm}^{3\tau } } & 0 & 0 & 0 & 0 & {\tilde{i}_{nm}^{3\tau } } & {\tilde{k}_{nm}^{3\tau } } & {\tilde{m}_{nm}^{3\tau } } & {\tilde{n}_{nm}^{3\tau } } \\ 0 & 0 & 0 & { - \tilde{f}_{nm}^{4} } & 0 & {\tilde{i}_{nm}^{4} } & {\tilde{k}_{nm}^{4} } & {\tilde{m}_{nm}^{4} } & {\tilde{n}_{nm}^{4} } \\ 0 & 0 & 0 & { - \tilde{f}_{nm}^{4\tau } } & 0 & {\tilde{i}_{nm}^{4\tau } } & {\tilde{k}_{nm}^{4\tau } } & {\tilde{m}_{nm}^{4\tau } } & {\tilde{n}_{nm}^{4\tau } } \\ 0 & 0 & 0 & 0 & {\tilde{g}_{nm}^{5} } & {\tilde{i}_{nm}^{5} } & {\tilde{k}_{nm}^{5} } & {\tilde{m}_{nm}^{5} } & {\tilde{n}_{nm}^{5} } \\ 0 & 0 & 0 & 0 & {\tilde{g}_{nm}^{5\tau } } & {\tilde{i}_{nm}^{5\tau } } & {\tilde{k}_{nm}^{5\tau } } & {\tilde{m}_{nm}^{5\tau } } & {\tilde{n}_{nm}^{5\tau } } \\ 0 & { - \tilde{d}_{nm}^{1} } & { - \tilde{e}_{nm}^{1} } & 0 & 0 & {\tilde{i}_{nm}^{1} } & {\tilde{k}_{nm}^{1} } & {\tilde{m}_{nm}^{1} } & {\tilde{n}_{nm}^{1} } \\ 0 & { - \tilde{d}_{nm}^{1\tau } } & { - \tilde{e}_{nm}^{1\tau } } & 0 & 0 & {\tilde{i}_{nm}^{1\tau } } & {\tilde{k}_{nm}^{1\tau } } & {\tilde{m}_{nm}^{1\tau } } & {\tilde{n}_{nm}^{1\tau } } \\ 0 & { - \tilde{d}_{nm}^{2\tau } } & { - \tilde{e}_{nm}^{2\tau } } & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \quad X = \left[ {\begin{array}{*{20}c} {C_{m} } \\ {D_{m} } \\ {E_{m} } \\ {F_{m} } \\ {G_{m} } \\ {I_{m} } \\ {K_{m} } \\ {M_{m} } \\ {N_{m} } \\ \end{array} } \right] \quad N = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ {\zeta_{n}^{1} } \\ {\zeta_{n}^{1\tau } } \\ {\zeta_{n}^{2\tau } } \\ \end{array} } \right]$$

The above formulas are presented in Appendix for more details.

Fig. 3

Discrete points of auxiliary circle and hole edge

2.7 Surface displacement amplitude and cavity stress

In region ①, ②, ③, ④ and ⑤ the wave field W_j are

$$W_{j} = \left\{ {\begin{array}{*{20}l} {W^{D3(1)} } \hfill & \textcircled{1} \hfill \\ {W^{D1(2)} + W^{D2(2)} + W^{(i + r)} } \hfill & \textcircled{2} \hfill \\ {W^{D1(3)} + W^{D3(3)} + W^{D4(3)} + W^{D5(3)} } \hfill & \textcircled{3} \hfill \\ {W^{D4(4)} } \hfill & \textcircled{4} \hfill \\ {W^{D5(5)} } \hfill & \textcircled{5} \hfill \\ \end{array} } \right..$$

(47)

Equation (47) can also be expressed as

$$W_{j} = \left| {W_{j} } \right|{\text{e}}^{{(\omega t - \phi_{j} )i}} \quad j = 1,2, \ldots .$$

(48)

where |W_j| is the displacement amplitude, and ϕ_j is the phase angle of W_j

$$\phi_{j} = \arctan \left( {{{{\text{Im}} (W_{j} )} \mathord{\left/ {\vphantom {{{\text{Im}} (W_{j} )} {{\text{Re}} (W_{j} )}}} \right. \kern-\nulldelimiterspace} {{\text{Re}} (W_{j} )}}} \right)$$

(49)

The dimensionless frequency of the incident waves can be expressed as

$$\eta = \frac{{2r_{2} }}{\lambda } = \frac{{kr_{2} }}{\pi }$$

(50)

where K₁ = K₂ = K₃ = K₄ = K₅ = k, and k is given by Eq. (10). λ is the wavelength of the incident waves. It is well known that the effect of elastic waves on the surface displacement and the cavity stress highly relies on the wavelength. As can be seen from Eq. (50), the dimensionless frequency η is introduced to represent the ratio of the radius (r₂) of the cavity to the wavelength and indirectly represents the magnitude of the wave number.

In region ②, the cavity hoop stress can be expressed as

$$\tau_{\theta z} = \tau_{{\theta_{2} z}}^{D1(2)} + \tau_{{\theta_{2} z}}^{D2(2)} + \tau_{{\theta_{2} z}}^{(i + r)} .$$

(51)

The dimensionless hoop stress is

$$\begin{array}{*{20}c} {\tau_{\theta z}^{*} = \left| {{{\tau_{\theta z}^{{}} } \mathord{\left/ {\vphantom {{\tau_{\theta z}^{{}} } {\tau_{0}^{{}} }}} \right. \kern-\nulldelimiterspace} {\tau_{0}^{{}} }}} \right|,} & {\left| {Z_{2} } \right| = r_{2} } \\ \end{array} .$$

(52)

where $\tau_{0}^{{}} = \mu kW_{0}$.

3 Numerical examples and discussions

3.1 Precision and convergence discussion

A number of precision discussion are carried out to determine the truncation values of n, m, and the optimal value of r₄, r₅. For convenience, set r₄ = r₅ = r, H₁ = 0; the tolerance for the continuity of the auxiliary boundary and the zero-stress condition of the cavity edge, is used as a precision metric. The precision of tolerance with n, m, r is discussed by a typical example (Table 1), where the incident angle α = 0° or 60° (the max incident angle α_max = acot(2C₄₅/C₅₅) = 68°), the triangular edge slope n₁ = 0.5 and n₂ = 1.5, and the material parameters κ = 0.8 and ν = 0.2(κ = C₄₄/C₅₅, ν = C₄₅/C₅₅). Generally, more terms of n and m are required for higher dimensionless frequency of incident waves. For the number of truncation terms of m and n, 70 (η = 1.0) and 360 are enough to get the high precision results of the examples in this paper, respectively; for the value of r, 1.0 is the best precision results (Figs. 4, 5, and 6).

Fig. 4

The precision of tolerance vs the circle radius of r

Fig. 5

The precision of tolerance vs the terms number of n

Fig. 6

The precision of tolerance vs the terms number of m

The convergence of displacement amplitudes with increasing M at three selected positions, the numerical results of the auxiliary boundary, the cavity edge and the free surface are given in Figs. 7 and 8, which the frequency of the incident η = 2.0. As shown in figure, the amplitude of the displacement is stable as M increases to 25, the displacement W and stress τ_rz continuity of the auxiliary boundary D are good, and the stress τ_θz of the free surface and τ_rz of the circular cavity boundary D₂ are close to 0, which indicate that the wave function and the least square method are effective.

Fig. 7

The continuity of the auxiliary boundary and free edge zero-stress at α = 0°

Fig. 8

The continuity of the auxiliary boundary and free edge zero-stress at α = 60°

Table 1 Parameters of scalene triangle and cavity

3.2 Correctness verification

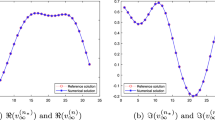
An important method to verify the theory is to compare the solution results of the isosceles triangular boundary in isotropic medium [39], as shown in Fig. 9. For comparison, the circular cavity is assumed to be deep enough (H₂ = 100,000), so that its impact on the free surface will become very weak, and the model with deep cavity will be close to a triangular boundary without cavity; the material parameters (κ = 1.0 ν = 0.0) are degenerated into isotropic material. It is seen that a sound agreement of the free surface motions can be observed not only for low but also high-frequency waves.

Fig. 9

Comparisons of the proposed solution results with those of Song et al. [39]

Another important method to verify the theory is to compare with the solution results of the finite element method (FEM), as shown in Fig. 10, which display the free surface displacement amplitudes |W/W₀|, the cavity edge stress $\tau_{\theta z}^{*}$ and the displacement cloud at a certain time. The FEM results are obtained by the commercial software Ls-Dyna with explicit dynamics method and user-defined material models, whose constitutive relation is built according to Eq. (53). The geometric model is meshed by shell element whose edge length 0.1 and grid only with out-of-plane translational degree of freedom, the mesh area is large enough to eliminate the effects of boundary reflections. And sine excitation is applied to the bottom or right edge of the analysis area, corresponding to incident angle 0° or − 90°. The calculation time is long enough to ensure that it is in a steady state, and less than the time that reflected wave reaches the area of cavity. The surface displacement magnitude is measured from the displacement of the surface element nodes; the stress of cavity edge comes from the nearest element of the cavity edge. It means that the cavity stress is the average of cavity edge area rather than the cavity edge, so the FEM stress results may be a bit inaccurate. For incident angle α =  − 90°, it is difficult to obtain a sufficient reflected wave near the surface area due to limitation of computational grid domain and computer computing power. Therefore, the finite element analysis results may be some deviations. But the results from the proposed method are agree with those from the finite element method on the overall trend, which is a very effective support for the paper theory.

$$\left\{ {\begin{array}{*{20}c} {\tau_{xz} = C_{55} \frac{\partial w}{{\partial x}} + C_{45} \frac{\partial w}{{\partial y}}} \\ {\tau_{yz} = C_{45} \frac{\partial w}{{\partial x}} + C_{44} \frac{\partial w}{{\partial y}}} \\ \end{array} } \right.$$

(53)

Fig. 10

Comparisons of the proposed solution results with FEM results at η = 0.5 n₁ = 0.5

3.3 The characteristics of mapping function

It can be known from the anisotropic material coordinate system (x,y) and the isotropic material coordinate system (x',y') that the shape of the triangle and the cavity changes with κ or ν. In the isotropic material space κ only changes the mapping coordinate x expansion ratio; ν affects the scaling of the mapping coordinates x and y (Figs. 11 and 12).

Fig. 11

The shape of triangle and cavity vs κ

Fig. 12

The shape of triangle and cavity vs ν

3.4 Parameters study in the frequency domain

Each position of free surface can be expressed by dimensionless y/(L/2) in the Cartesian coordinate system o₆x₆y₆, where − 1 represents the left triangle foot point, (n₂-n₁)/(n₂ + n₁) is triangle vertex, and 1 represents the right triangle foot point.

• (1) The comparison of cavity

  It can be seen from the below figure that the cavity has a large impact on the surface at low or high frequencies, while it has a smaller impact at incident angle 30° (Fig. 13).

• (2) The influence of incident waves frequency

  In order to reveal the influence of dimensionless frequencies on the free surface displacement and the cavity stress, the first row pictures in Fig. 14 give the displacement amplitudes as a function of 2y/L and η at various angles of the incidence (α = 0°, 30°, 60°) and the slope n₁ = 0.5, and the second-row pictures give the cavity stress as a function of θ and η. It shows that the number of the wave peaks in the triangular region increases as the wave dimensionless frequencies increases, and the peak and oscillation frequency increases on one side of the incident wave, while they decrease on the another side; the peak and the oscillation frequency of the area near the larger triangle slope significantly increase, but the increase will move to the side of wave incoming direction when the angle of incidence changes large. The cavity concentrated stress is distributed over both sides of the wave propagation direction, and the shear stress near the free boundary is greater than that on the infinite space, which is due to the superposition of the incident wave and the free boundary reflection wave. The displacement amplitude of the triangular surface is of a peak shape, and the displacement amplitude of the free flat surface is mountain-shaped whose ridges show fluctuations.

• (3) The influence of κ

  In order to reveal the influence of material parameters on the free surface displacement and the cavity stress, the first-row pictures in Fig. 15 give the displacement amplitudes as a function of 2y/L and κ at various angles of the incidence (α = 0°, 30°, 60°) and the slope n₁ = 1.0, and the second-row pictures give the cavity stress as a function of θ and κ. It shows that the surface displacement and the cavity stress have an increasing trend as the κ decreases, but the trend gradually weakens as the incident angle increases; the number of free surface displacement peaks decreases as κ increases, while the number of cavity stress peaks increases.

• (4) The influence of ν

Fig. 13

The free surface displacement amplitudes |W_j| of the triangle without cavity and with cavity

Fig. 14

3D plots of surface displacement amplitudes |W_j| and cavity edge stress $\tau_{{\theta_{z} }}^{*}$ vs η at n₁ = 0.5 κ = 0.8

Fig. 15

3D plots of surface displacement amplitudes |W_j| and cavity edge stress $\tau_{{\theta_{z} }}^{*}$ vs κ at η = 1.0 n₁ = 1.0 ν = 0.0

The first-row pictures in Fig. 16 give the displacement amplitudes as a function of 2y/L and ν at various angles of the incidence (α = 0°, 30°, 60°) and the slope n₁ = 1.0, and the second-row pictures give the cavity stress as a function of θ and ν. There is no obvious regular change in surface displacement and cavity stress as ν changes, and the overall level is at the same.

Fig. 16

3D plots of surface displacement amplitudes |W_j| and cavity edge stress $\tau_{{\theta_{z} }}^{*}$ vs ν at η = 1.0 n₁ = 1.0 κ = 1.0

3.5 Time domain response

The transient response is obtained from the frequency domain results through the inverse Fourier transform (IFT) algorithm. The incident time signal is a Ricker wavelet

$$Ri(t) = \left( {1 - 2\pi^{2} f_{c}^{2} t^{2} } \right){\text{e}}^{{ - \pi^{2} f_{c}^{2} t^{2} }}$$

(54)

with the characteristic frequency f_c = 0.5 Hz.

The calculated frequencies range from 0.0 to 2.0 Hz with 1/33 Hz intervals. The transfer function for every position is deduced in the previous chapter for a particular frequency ω (or the wave number k). Then, the time domain results can be synthesized by using the inverse FFT, and the shear wave propagates with the velocity $c_{T} = 3$. In Fig. 17, the reference point is set to be (x,y) = (8, − 16) for t = 0 s; in Figs. 18 and 19, the reference point is set to be (x,y) = (20,-15) for t = 0 s. The reference coordinate system (x,y) is o₆x₆y₆.

Fig. 17

3D plots of surface displacement amplitudes |W_j| vs time at n₁ = 0.5

Fig. 18

Snapshots for α = 0° at 9 specified times

Fig. 19

Snapshots for α = 60° at 9 specified times

In Fig. 17, the synthetic displacement contour, with y range from − 12 to 12, contains 800 discrete positions located along the surface of the triangle. When the reference point is (8, − 16), the vertical Ricker wave reaches the flat surface (x = 0) at t = 2.3 s ($c_{si} = 3.44$); after the vertical wave leave away from the flat surface several scattered waves appear one after another whose amplitudes are obviously different. The incident angle 60° Ricker wave reaches the flat surface (y =  − 12) at t = 2.6 s ($c_{si} = 2.83$); when the wave reaches the triangle, several scattered waves appear one after another whose amplitudes are also obviously different.

Figures 18 and 19 show the displacement of nodes with equally distance 0.03 at the incident angle 0° and 60°, respectively. These snapshots show the wave fields at 9 specified time points to illustrate the process of the wave propagation and scattering around the triangular shape and the shallow circle. In Fig. 18, when the incident wave passes through the hole, the scattered wave is produced by the hole, which propagates in the opposite direction (t = 5 s); when the incident wave reaches the free surface, a reflected wave is produced, and a circular scattered wave is also produced in the triangular area (t = 8–10 s). This appearance of displacement also corresponds to Fig. 17. In Fig. 19, when the incident wave passes through the hole, the scattered wave is produced, which propagates in the opposite direction (t = 9 s); when the wave reaches the triangular area, a less obvious circular scattered wave is produced (t = 11–13 s). The amplitude and the range of influence on the left side of the triangle are significantly higher than those on the right side, which also corresponds to Fig. 17. Besides, the shape of wave scattered by circular cavity is non-circular, which is the biggest difference from a homogeneous medium. Besides, through the time domain results of various time points, it can be used for the transient response analysis of underground structures or surface structures to provide support for strength design.

4 Conclusions

This paper derives the mapping function, which transforms from anisotropic space to isotropic space. By using the mapping space and adopting the symmetric method, the zero-stress boundary condition of the semi-infinite cavity is solved. Finally, through the complex variable function coordinate transformation, the region-matching method and the least square method, the solution of the wave to the typical oblique triangle boundary is obtained in the frequency domain. From the formula derivation and numerical simulation, the following conclusions can be drawn:

• (1) It can be seen from the formula derivation that there are four mapping functions, that is, there are four mapping spaces, and each mapping function can solve the problem. Therefore, we can further research on cracks, special-shaped cavities and free-surface boundary in the mapping space, just as do with homogeneous medium.

• (2) From the simulation results, κ determines the x scaling, and ν determines the x y scaling in the mapping space.

• (3) Because the anisotropic medium changes the direction of wave propagation, the incident angle α_i only be less than acot(2C₄₅/C₅₅) near the free surface, which can be used for shock absorption design.

• (4) It can be seen that the triangle and the cavity have a significant amplification effect on the elastic wave, which can even be amplified by more than 4 times; the concentrated stress of the cavity is significantly increased and even can be amplified by more than 5 times.

• (5) The snapshots show the process of the wave propagation and scattering around the triangle and shallow cavity in the time domain. Besides, the time domain results of various points can be used for the transient response analysis of the underground structures or the surface structures to provide support for structural strength designs.

Appendices

Appendix A

Expressions of each angle in Fig. 1 model

$$\alpha_{1} = \arctan (n_{1}),\; \alpha_{2} = \arctan (n_{2}),\; \alpha_{3} = \pi - \arctan \left( {\frac{{L + r_{4} + r_{5} }}{{2H_{1}}}} \right),\; \alpha_{4} = \alpha_{1},\; \alpha_{5} = \pi - 2 \angle O_{3} X_{5} X_{4} - \alpha_{1} ,\;\alpha_{6} = \pi - \alpha_{2} ,\;\alpha_{7} = \pi - \alpha_{1} ,$$

where $\angle O_{3} X_{5} X_{4} = \arccos \left( {\frac{{L_{{X_{5} X_{4} }}^{2} + L_{{X_{5} O}}^{2} - L_{{OX_{4} }}^{2} }}{{2L_{{X_{5} X_{4} }}^{{}} L_{{X_{5} O}}^{{}} }}} \right)$_,

$L_{{X_{5} X_{4} }}^{{}} = \sqrt {\left[ {r_{5} \cos \left( {\alpha_{1} } \right) - r_{4} \cos \left( {\alpha_{2} } \right)} \right]^{2} + \left[ {L - r_{5} \sin \left( {\alpha_{1} } \right) - r_{4} \sin \left( {\alpha_{2} } \right)} \right]^{2} }$_, $L_{{OX_{4} }}^{{}} = {H \mathord{\left/ {\vphantom {H {\cos \left( {\alpha_{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\cos \left( {\alpha_{2} } \right)}} - r_{4}$_, $L_{{OX_{5} }}^{{}} = {H \mathord{\left/ {\vphantom {H {\cos \left( {\alpha_{1} } \right)}}} \right. \kern-\nulldelimiterspace} {\cos \left( {\alpha_{1} } \right)}} - r_{5}$_, $r_{3} = {{L_{{X_{5} X_{4} }}^{{}} } \mathord{\left/ {\vphantom {{L_{{X_{5} X_{4} }}^{{}} } {\left( {2{\text{sin((}}\alpha_{{4}} { + }\alpha_{{5}} {)/2)}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2{\text{sin((}}\alpha_{{4}} { + }\alpha_{{5}} {)/2)}} \right)}}$_, $H_{3} = \left( {r_{3} + r_{5} } \right)\cos (\alpha_{4} )$.

Appendix B

Expressions of functions

$$\tilde{c}_{nm}^{3} = W_{0} \left. {J_{{mp_{0} }} \left( {K_{1} \left| {\user2{\not\xi }\left( {Z_{3} + b_{03} } \right){\text{e}}^{{q_{0} i}} } \right|} \right)\left[ {\left( {\frac{{\user2{\not\xi }\left( {Z_{3} + b_{03} } \right){\text{e}}^{{q_{0} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{3} + b_{03} } \right){\text{e}}^{{q_{0} i}} } \right|}}} \right)^{{mp_{0} }} + \left( { - 1} \right)^{m} \left( {\frac{{\user2{\not\xi }\left( {Z_{3} + b_{03} } \right){\text{e}}^{{q_{0} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{3} + b_{03} } \right){\text{e}}^{{q_{0} i}} } \right|}}} \right)^{{ - mp_{0} }} } \right]} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$

$$\tilde{i}_{nm}^{3} = \left. {W_{0} J_{m}^{{}} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{3} + b_{13} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{3} + b_{13} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{3} + b_{13} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$

$$\tilde{k}_{nm}^{3} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{3} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{3} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{3} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$

$$\tilde{m}_{nm}^{3} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{3} + b_{43} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{3} + b_{43} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{3} + b_{43} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$

$$\tilde{n}_{nm}^{3} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{3} + b_{53} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{3} + b_{53} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{3} + b_{53} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$

$$\tilde{c}_{nm}^{3\tau } = \left. {\tilde{P}_{{mp_{0} }}^{J} \left( {\user2{\not\xi }\left( {Z_{3} + b_{03} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$

$$\tilde{i}_{nm}^{3\tau } = \left. {\tilde{P}_{m}^{J} \left( {\user2{\not\xi }\left( {Z_{3} + b_{13} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} ,\delta = 0}}$$

$$\tilde{k}_{nm}^{3\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{3} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} ,\delta = 0}}$$

$$\tilde{m}_{nm}^{3\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{3} + b_{43} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} ,\delta = 0}}$$

$$\tilde{n}_{nm}^{3\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{3} + b_{53} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} ,\delta = 0}}$$

$$\tilde{f}_{nm}^{4} = W_{0} \left. {J_{{mp_{4} }} \left( {K_{4} \left| {\user2{\not\xi }\left( {Z_{4} } \right){\text{e}}^{{q_{4} i}} } \right|} \right)\left[ {\left( {\frac{{\user2{\not\xi }\left( {Z_{4} } \right){\text{e}}^{{q_{4} i}} }}{{\user2{\not\xi }\left( {Z_{4} } \right){\text{e}}^{{q_{4} i}} }}} \right)^{{mp_{4} }} + \left( { - 1} \right)^{m} \left( {\frac{{\user2{\not\xi }\left( {Z_{4} } \right){\text{e}}^{{q_{4} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{4} } \right){\text{e}}^{{q_{4} i}} } \right|}}} \right)^{{ - mp_{4} }} } \right]} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$

$$\tilde{i}_{nm}^{4} = \left. {W_{0} J_{m}^{{}} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{4} + b_{14} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{4} + b_{14} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{4} + b_{14} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$

$$\tilde{k}_{nm}^{4} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{4} + b_{34} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{4} + b_{34} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{4} + b_{34} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$

$$\tilde{m}_{nm}^{4} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{4} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{4} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{4} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$

$$\tilde{n}_{nm}^{4} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{4} + b_{54} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{4} + b_{54} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{4} + b_{54} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$

$$\tilde{f}_{nm}^{4\tau } = \left. {\tilde{P}_{{mp_{0} }}^{J} \left( {\user2{\not\xi }\left( {Z_{4} + b_{04} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$

$$\tilde{i}_{nm}^{4\tau } = \left. {\tilde{P}_{m}^{J} \left( {\user2{\not\xi }\left( {Z_{4} + b_{14} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} ,\delta = 0}}$$

$$\tilde{k}_{nm}^{4\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{4} + b_{34} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} ,\delta = 0}}$$

$$\tilde{m}_{nm}^{4\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{4} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} ,\delta = 0}}$$

$$\tilde{n}_{nm}^{4\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{4} + b_{54} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} ,\delta = 0}}$$

$$\tilde{g}_{nm}^{5} = W_{0} \left. {J_{{mp_{5} }} \left( {K_{5} \left| {\user2{\not\xi }\left( {Z_{5} } \right){\text{e}}^{{q_{5} i}} } \right|} \right)\left[ {\left( {\frac{{\user2{\not\xi }\left( {Z_{5} } \right){\text{e}}^{{q_{5} i}} }}{{\user2{\not\xi }\left( {Z_{5} } \right){\text{e}}^{{q_{5} i}} }}} \right)^{{mp_{5} }} + \left( { - 1} \right)^{m} \left( {\frac{{\user2{\not\xi }\left( {Z_{5} } \right){\text{e}}^{{q_{5} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{5} } \right){\text{e}}^{{q_{5} i}} } \right|}}} \right)^{{ - mp_{5} }} } \right]} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$

$$\tilde{i}_{nm}^{5} = \left. {W_{0} J_{m}^{{}} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{5} + b_{15} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{5} + b_{15} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{5} + b_{15} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$

$$\tilde{k}_{nm}^{5} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{5} + b_{35} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{5} + b_{35} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{5} + b_{35} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$

$$\tilde{m}_{nm}^{5} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{5} + b_{45} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{5} + b_{45} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{5} + b_{45} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$

$$\tilde{n}_{nm}^{5} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{5} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{5} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{5} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$

$$\tilde{g}_{nm}^{5\tau } = \left. {\tilde{P}_{{mp_{0} }}^{J} \left( {\user2{\not\xi }\left( {Z_{5} + b_{05} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$

$$\tilde{i}_{nm}^{5\tau } = \left. {\tilde{P}_{m}^{J} \left( {\user2{\not\xi }\left( {Z_{5} + b_{15} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} ,\delta = 0}}$$

$$\tilde{k}_{nm}^{5\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{5} + b_{35} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} ,\delta = 0}}$$

$$\tilde{m}_{nm}^{5\tau } = \left. {P_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{5} + b_{45} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} ,\delta = 0}}$$

$$\tilde{n}_{nm}^{5\tau } = \left. {\frac{{\mu_{3} K_{3} W_{0} }}{2}P_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{5} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} ,\delta = 0}}$$

$$\tilde{d}_{nm}^{1} = W_{0} \left. {\left[ \begin{gathered} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) - \user2{\not\xi }\left( {H_{1} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) - \user2{\not\xi }\left( {H_{1} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) - \user2{\not\xi }\left( {H_{1} } \right)} \right|}}} \right)^{m} + \hfill \\ \left( { - 1} \right)^{m} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) + \user2{\not\xi }\left( {H_{1} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) + \user2{\not\xi }\left( {H_{1} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) + \user2{\not\xi }\left( {H_{1} } \right)} \right|}}} \right)^{ - m} \hfill \\ \end{gathered} \right]} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$

$$\tilde{e}_{nm}^{1} = \left. {W_{0} \left[ \begin{gathered} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) - \user2{\not\xi }\left( {H_{2} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) - \user2{\not\xi }\left( {H_{2} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) - \user2{\not\xi }\left( {H_{2} } \right)} \right|}}} \right)^{m} + \hfill \\ \left( { - 1} \right)^{m} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) + \user2{\not\xi }\left( {H_{2} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) + \user2{\not\xi }\left( {H_{2} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) + \user2{\not\xi }\left( {H_{2} } \right)} \right|}}} \right)^{ - m} \hfill \\ \end{gathered} \right]} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$

$$\tilde{i}_{nm}^{1} = \left. {W_{0} J_{m}^{{}} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{1} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$

$$\tilde{k}_{nm}^{1} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{1} + b_{31} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{31} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{31} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$

$$\tilde{m}_{nm}^{1} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{1} + b_{41} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{41} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{41} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$

$$\tilde{n}_{nm}^{1} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{1} + b_{51} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{51} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{51} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$

$$\tilde{d}_{nm}^{1\tau } = \left. {\tilde{P}_{{mp_{0} }}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{1} + b_{61} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$

$$\tilde{e}_{nm}^{1\tau } = \left. {\tilde{P}_{{mp_{0} }}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{1} + b_{71} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$

$$\tilde{i}_{nm}^{1\tau } = \left. {\tilde{P}_{m}^{J} \left( {Z_{1} } \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} ,\delta = 0}}$$

$$\tilde{k}_{nm}^{1\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {Z_{1} + b_{31} } \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} ,\delta = 0}}$$

$$\tilde{m}_{nm}^{1\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {Z_{1} + b_{41} } \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} ,\delta = 0}}$$

$$\tilde{n}_{nm}^{1\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {Z_{1} + b_{51} } \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} ,\delta = 0}}$$

$$\zeta_{nm}^{1} = \left. {W_{0} {\text{e}}^{{\frac{{ - iK_{2}^{i} }}{2}(\left( {Z_{1} + b_{31} } \right){\text{e}}^{{\alpha_{i} i}} + \overline{{\left( {Z_{1} + b_{31} } \right)}} {\text{e}}^{{ - \alpha_{i} i}} )}} + W_{0} {\text{e}}^{{\frac{{iK_{2}^{r} }}{2}(\left( {Z_{1} + b_{31} } \right){\text{e}}^{{ - \alpha_{r} i}} + \overline{{\left( {Z_{1} + b_{31} } \right)}} {\text{e}}^{{\alpha_{r} i}} )}} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \phi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$

$$\zeta_{nm}^{1\tau } = \left. {\frac{1}{2}\left\{ \begin{gathered} \left[ {\left( {C_{55} + C_{44} } \right)U\left( {Z_{1} + b_{31} } \right) + \left( {C_{55} - C_{44} - 2C_{45} i} \right)V\left( {Z_{1} + b_{31} } \right)} \right]{\text{e}}^{{\theta_{1} i}} + \hfill \\ \left[ {\left( {C_{55} - C_{44} + 2C_{45} i} \right)U\left( {Z_{1} + b_{31} } \right) + \left( {C_{55} + C_{44} } \right)V\left( {Z_{1} + b_{31} } \right)} \right]{\text{e}}^{{ - \theta_{1} i}} \hfill \\ \end{gathered} \right\}} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \phi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$

$$\tilde{d}_{nm}^{2\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{2} + b_{62} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{2} } \right| = r_{2} } \\ { - \pi \le \varphi_{n} (Z_{2} ) \le \pi } \\ \end{array} }}$$

$$\tilde{f}_{nm}^{2\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{2} + b_{72} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{2} } \right| = r_{2} } \\ { - \pi \le \varphi_{n} (Z_{2} ) \le \pi } \\ \end{array} }}$$

$$\zeta_{n}^{2\tau } = \left. {\frac{1}{2}\left\{ \begin{gathered} \left[ {\left( {C_{55} + C_{44} } \right)U\left( {Z_{2} + b_{32} } \right) + \left( {C_{55} - C_{44} - 2C_{45} i} \right)V\left( {Z_{2} + b_{32} } \right)} \right]{\text{e}}^{{\theta_{2} i}} + \hfill \\ \left[ {\left( {C_{55} - C_{44} + 2C_{45} i} \right)U\left( {Z_{2} + b_{32} } \right) + \left( {C_{55} + C_{44} } \right)V\left( {Z_{2} + b_{32} } \right)} \right]{\text{e}}^{{ - \theta_{2} i}} \hfill \\ \end{gathered} \right\}} \right|_{{\begin{array}{*{20}c} {\left| {Z_{2} } \right| = r_{2} } \\ { - \pi \le \phi_{n} (Z_{2} ) \le \pi } \\ \end{array} }}$$

where $\left| {Z_{j} } \right|$, $\varphi_{n} (Z_{j} )$ represents the modulus and phase angle of complex numbers, respectively.

$$\begin{array}{*{20}l} {f_{1}^{r} = \frac{1}{4}\left[ {\left( {C_{55} + C_{44} } \right)\left( {\overline{\gamma }_{1} } \right) + \left( {C_{55} - C_{44} - 2C_{45} i} \right)\left( { - \gamma_{2} } \right)} \right]} \hfill & {f_{1}^{\theta } = \frac{1}{4}\left[ {\left( {C_{55} i + C_{44} i} \right)\left( {\overline{\gamma }_{1} } \right) + \left( {C_{55} i - C_{44} i + 2C_{45} } \right)\left( { - \gamma_{2} } \right)} \right]} \hfill \\ {f_{2}^{r} = \frac{1}{4}\left[ {\left( {C_{55} + C_{44} } \right)\left( { - \overline{\gamma }_{2} } \right) + \left( {C_{55} - C_{44} - 2C_{45} i} \right)\left( {\gamma_{1} } \right)} \right]} \hfill & {f_{2}^{\theta } = \frac{1}{4}\left[ {\left( {C_{55} i + C_{44} i} \right)\left( { - \overline{\gamma }_{2} } \right) + \left( {C_{55} i - C_{44} i + 2C_{45} } \right)\left( {\gamma_{1} } \right)} \right]} \hfill \\ {f_{3}^{r} = \frac{1}{4}\left[ {\left( {C_{55} - C_{44} + 2C_{45} i} \right)\left( {\overline{\gamma }_{1} } \right) + \left( {C_{55} + C_{44} } \right)\left( { - \gamma_{2} } \right)} \right]} \hfill & {f_{3}^{\theta } = \frac{1}{4}\left[ {\left( { - C_{55} i + C_{44} i + 2C_{45} } \right)\left( {\overline{\gamma }_{1} } \right) + \left( { - C_{55} i - C_{44} i} \right)\left( { - \gamma_{2} } \right)} \right]} \hfill \\ {f_{4}^{r} = \frac{1}{4}\left[ {\left( {C_{55} - C_{44} + 2C_{45} i} \right)\left( { - \overline{\gamma }_{2} } \right) + \left( {C_{55} + C_{44} } \right)\left( {\gamma_{1} } \right)} \right]} \hfill & {f_{4}^{\theta } = \frac{1}{4}\left[ {\left( { - C_{55} i + C_{44} i + 2C_{45} } \right)\left( { - \overline{\gamma }_{2} } \right) + \left( { - C_{55} i - C_{44} i} \right)\left( {\gamma_{1} } \right)} \right]} \hfill \\ \end{array}$$

$$\begin{gathered} P_{t}^{H} (s) = \frac{{W_{0} k}}{2}\left\{ {H_{{_{t - 1} }}^{{}} (k\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} } \right|)\left[ {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} } \right|}}} \right]^{t - 1} - \left( { - 1} \right)^{m} \kappa H_{{_{t + 1} }}^{{}} (k\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right|)\left[ {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right|}}} \right]^{ - t - 1} } \right\}{\text{e}}^{qi} \hfill \\ Q_{t}^{H} (s) = \frac{{W_{0} k}}{2}\left\{ { - H_{{_{t + 1} }}^{{}} (k\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} } \right|)\left[ {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} } \right|}}} \right]^{t + 1} + \left( { - 1} \right)^{m} \kappa H_{{_{t - 1} }}^{{}} (k\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right|)\left[ {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right|}}} \right]^{ - t + 1} } \right\}{\text{e}}^{ - qi} \hfill \\ \end{gathered}$$

$$\begin{gathered} \tilde{P}_{t}^{H} (s) = \left( {f_{1}^{r} P_{t}^{H} (s) + f_{2}^{r} Q_{t}^{H} (s)} \right){\text{e}}^{\theta i} + \left( {f_{3}^{r} P_{t}^{H} (s) + f_{4}^{r} Q_{t}^{H} (s)} \right){\text{e}}^{ - \theta i} \hfill \\ \tilde{Q}_{t}^{H} (s) = \left( {f_{1}^{\theta } P_{t}^{H} (s) + f_{2}^{\theta } Q_{t}^{H} (s)} \right){\text{e}}^{\theta i} + \left( {f_{3}^{\theta } P_{t}^{H} (s) + f_{4}^{\theta } Q_{t}^{H} (s)} \right){\text{e}}^{ - \theta i} \hfill \\ \end{gathered}$$

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} = \left[ {\user2{\not\xi }\left( s \right) - \user2{\not\xi }\left( {H_{j} } \right)} \right]{\text{e}}^{qi}$,$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} = \left[ {\user2{\not\xi }\left( s \right) + \overline{\user2{\not\xi }}\left( {H_{j} } \right)} \right]{\text{e}}^{qi}$, $H_{j}$ is the depth of the corresponding circle center from the surface and takes a negative value if it is above the horizontal plane. H is Bessel functions or Hankel function. $P_{t}^{H} (s)$, $Q_{t}^{H} (s)$ represent $\frac{\partial w}{{\partial \xi }}$,$\frac{\partial w}{{\partial \overline{\xi }}}$. $\delta = \left\{ {\begin{array}{*{20}c} 0 & {given} \\ 1 & {else} \\ \end{array} } \right.$

$$\begin{gathered} U\left( {{\text{z}}_{3j} } \right) = \left( {\frac{{ - iK_{2}^{i} }}{2}{\text{e}}^{{\alpha_{i} i}} } \right)W_{0} {\text{e}}^{{\frac{{ - iK_{2}^{i} }}{2}({\text{z}}_{3j} {\text{e}}^{{\alpha_{i} i}} + {\overline{\text{z}}}_{3j} {\text{e}}^{{ - \alpha_{i} i}} )}} + \left( {\frac{{iK_{2}^{r} }}{2}{\text{e}}^{{ - \alpha_{r} i}} } \right)W_{0} {\text{e}}^{{\frac{{iK_{2}^{r} }}{2}({\text{z}}_{3j} {\text{e}}^{{ - \alpha_{r} i}} + {\overline{\text{z}}}_{3j} {\text{e}}^{{\alpha_{r} i}} )}} \hfill \\ V\left( {{\text{z}}_{3j} } \right) = \left( {\frac{{ - iK_{2}^{i} }}{2}{\text{e}}^{{ - \alpha_{i} i}} } \right)W_{0} {\text{e}}^{{\frac{{ - iK_{2}^{i} }}{2}({\text{z}}_{3j} {\text{e}}^{{\alpha_{i} i}} + {\overline{\text{z}}}_{3j} {\text{e}}^{{ - \alpha_{i} i}} )}} + \left( {\frac{{iK_{2}^{r} }}{2}{\text{e}}^{{\alpha_{r} i}} } \right)W_{0} {\text{e}}^{{\frac{{iK_{2}^{r} }}{2}({\text{z}}_{3j} {\text{e}}^{{ - \alpha_{r} i}} + {\overline{\text{z}}}_{3j} {\text{e}}^{{\alpha_{r} i}} )}} \hfill \\ \end{gathered}$$

where $U\left( {{\text{z}}_{3j} } \right)$, $V\left( {{\text{z}}_{3j} } \right)$ represent $\frac{\partial w}{{\partial z}}$, $\frac{\partial w}{{\partial \overline{z}}}$.