Crack identification in laminated composites based on modal responses using metaheuristics, artificial neural networks and response surface method: a comparative study

Abstract

Structures that are difficult to maintain and access need to have an efficient and robust process for continuous monitoring. Such monitoring through damage detection and identification studies is present in several engineering applications as it allows that corrective measures be applied in order to guarantee the structural safety of a given structure, machine or equipment. In particular, laminated composite materials, often used in aeronautical structures, have a complex failure mechanism where delamination or cracks in these materials are often not visible on the surface. Thus, the use of optimization methods for the characterization of damages in these materials becomes relevant. In this study, both the metaheuristic sunflower optimization, the artificial neural networks and the response surface method were used to solve an inverse crack identification problem. The crack was modeled as a thin elliptical hole in a rectangular laminated plate numerically modeled using the finite element method. As a result of the methods used, different approaches to the problem were obtained that present reliable shape, size and position identification of a crack sized between 3 and 30 mm. The results showed substantial and promising results in the uses of both metaheuristic techniques and artificial neural networks. However, neural networks have a certain competitive advantage over optimization techniques as long as the data that feeds the model present a certain level of quantity and quality. Results obtained were able to identify all damage parameters (location, extension and orientation), with errors less than 1%.

1 Introduction

Structures in general subject to cyclic loading are subject to the appearance of structural cracks, which can propagate and eventually lead to sudden failure of the structural component or equipment. Methods of detecting these cracks in an "embryonic" stage, in order to avoid sudden failure, have been the focus of several studies [11]. This process of damage detection and identification is known as structural health monitoring (SHM).

In particular, structures made of composite materials or simply laminated structures have a complex failure mechanism [15], and these are often difficult to visualize on the surface. Therefore, for these structures, the application of the SHM is more relevant. These materials are increasingly present in the industry stand out for having exceptional strength and rigidity, low relative density, low maintenance cost and flexibility to adjust mechanical properties in the preliminary stages of complex structure design [15].

Equally important, methods for property identification based on vibration response assume that modal responses, such as natural frequencies, mode shapes and modal damping, are a function of the physical properties of the structure: mass, stiffness and damping [5]. Therefore, it is possible to identify characteristics that alter such physical properties through modal response. Vibration-based damage identification is a diverse theme and has shown consistent results. Hassiotis et al. [12] proposed a solution to identify reduction in stiffness of beam structures based on natural frequencies. Owolabi et al. [22] proposed a similar analysis using natural frequencies and amplitude of frequency response function.

Regarding laminated composite structures, some studies could be highlighted. The studies of Hu et al. [14], which proposed a solution for detecting damage in a plate of laminated composite material based on the strain energy calculated through modal displacements, and Gomes et al. [11], which proposed a method of identifying the parameters of a circular damage in a plate of laminated composite material based on natural frequencies, through an inverse method of optimization.

According to Gomes et al. [9] the development of an efficient structural monitoring technologies aims to provide safety and cost savings. However, the number of practical applications of these technologies is still finite. This is mainly due to the complexity of possible damage scenarios and the high-performance requirements of the identification methods employed.

In general, damage identification problems can be solved through inverse problems and computational intelligence. The methods most discussed in the literature in relation to inverse methods in general are (1) methods based on optimization, (2) methods based on artificial intelligence and (3) metamodeling methodology.

Optimization-based methods generally employ modeling in two or more steps. A direct model, usually numerically modeled in FEM or BEM, is used considering the parameterization of the induced damage. In a later step some specific optimization algorithm (usually metaheuristic) is used in order to minimize an objective function that can be composed of different structural responses.

Regarding the optimization-based damage identification, an approach based on an improved particle swarm optimization (PSO) algorithm is proposed by Wei et al. [32] for structural damage detection in this study. The authors verified both the feasibility and the robustness of a modified PSO considering three different test structures (beam, truss and plate). The results show that the method is efficient and effective for structural damage identification when measurement noise is considered.

In the same research field, Khatir et al. [17] proposed an eXtended isogeometric analysis (X-IGA) combined with PSO for crack identification in two-dimensional linear elastic problems based on inverse problem. The objective function minimized the error between the calculated and measured structural displacements. Convergence studies at various positions of crack on the plate are calculated, and the results show that the proposed technique can detect damage with minimum accuracy 95%. Correspondingly, Pereira et al. [24] developed a numerical identification and characterization of crack propagation through the use of a new optimization metaheuristics called Lichtenberg optimization (LA). The authors showed substantial results on crack identification in plates-like structures using the (LA) based only in strain fields. In the same way,

Recently, Fathi et al. [6] presented a new geometry-based crack detection approach for plate structures based on the integration of a dynamic extended finite element method (xFEM) and a physics-based optimization algorithm called enhanced vibrating particles system (EVPS). The study indicates the efficiency of the proposed XFEM-EVPS method in detecting crack location.

Optimization-based methods are known as robust methods since an algorithm will minimize the error between model and experiment. This error tends to zero and so the damage is accurately detected or identified. The efficiency of this strategy basically occurs by the correct modeling of the damage, the sensitivity of the structural response (stress, deformation, vibration, etc.) and also by the capacity of the optimization algorithm to deal with the multimodal function. Furthermore, despite the accuracy of these methods, the disadvantage is due to the computational cost or simulation time due to the use of metaheuristic techniques.

One of the alternatives for these inconveniences is the use of artificial intelligence or, more specifically, artificial neural networks. The strategy in using ANN is based on feeding the model with a database with information regarding the damage in question. From this point on, the algorithm will perform training in order to learn from the data and then generate a complex model that may or may not present significant accuracy.

An inverse analysis based on the ANN technique is introduced for effective identification of crack damage in aluminum plates by Lu et al. [19]. The authors discussed the capability of the inverse approach considering by two crack cases from experiments. Results show substantial accuracy regarding the damage parameter prediction (central position, size, and orientation). Furthermore, Saeed et al. [26], presented an ANN for crack identification based on modal response considering damaged beams. The authors located the damage with satisfactory accuracy, even if the input data are corrupted with various level of noise. In like manner, Oliver et al. [21] presented an ANN for damage identification in laminated composite structures considering the natural frequency shifts. The obtained results from numerical examples indicate that the proposed approach can detect true damage locations and estimate damage magnitudes with satisfactory accuracy for this particular geometry, even under high measurement noise.

ANN have the advantage of reduced computational time to identify or detect damage compared to optimization-based techniques. On the other hand, accuracy can only be achieved if a database with a significant sampling is available. Fine-tuning the ANN parameters also significantly contributes to the quality of the results. In order to get around the problem of number of points, sampling and experiments, metamodeling techniques are considered.

To the best of the authors' knowledge, there are no (or very few) studies in the literature investigating the performance of both the optimization, ANN and metamodeling strategies for crack identification in plate-like structures. The objective of this work is to propose a solution for the identification of cracks in a plate of laminated composite through these three different methods. The major contribution in this is study could be listed as (1) the use of a response surface methodology (RSM) for direct problem modeling and model evaluation, (2) the use of the Sunflower Optimization (SFO) optimization algorithm to obtain the crack parameters from the modal response obtained through the direct problem, iii) an artificial neural network (ANN) to identify the parameters of the crack from the modal response obtained through the direct problem and then (4) conduct a comparative study between the proposed methods.

2 Backgrounds

2.1 Cracks in laminated composites structures

Cracks in composite laminates subjected to mechanical loads can be classified as interlaminar cracks aligned to the fibers in the layers, interlaminar cracks generated by the separation of the layers and rupture of the fibers [28] apud [30].

Due to the complex fault mechanism, special precautions should be taken into account to avoid failures in structures manufactured from composite laminates. These are subject to the appearance of barely visible damage (BVD), such damage can be internal cracks due to low-speed impacts suffered by the structure during its operation or manufacture or even due to moisture trapped inside the material that expands and contracts due to variations in temperature.

In particular, the aerospace industry, which benefits from the good mechanical properties that is obtained combined with the specific low density, is especially sensitive to such problems since the structures used in this sector are subject to severe conditions of cyclic mechanical stress and high temperature variations.

The crack can be characterized as a reduction in the stiffness of the structure in the place where it is located. Several studies address different ways of defining this reduction of stiffness. A frequently used form is to modify the geometry by inserting a through hole into the desired format for crack representation.

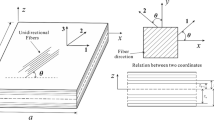
For the direct problem solved by finite element analysis (FEA), it is necessary to choose a method for modeling a crack in the structure, several studies address different ways of doing so. Gomes et al. [10] and Waisman & Berger-Vergiat [31] adopted the method of modeling the limits of the crack as a circumference in a two-dimensional structure, where the position of the center of the circumference on the x and y axes, as well as the radius of this are the parameters of the crack. The study of Chatzi et al. [4] and Liang et al. [18] proposed a more sophisticated modeling in the form of an ellipse, parameterized by the position of its center in x and y, the smaller and larger rays and the angle of inclination of the larger radius in relation to the horizontal. Agathos et al. [1] used a similar approach, but in three-dimensional space. Figure 1 illustrates a simple crack damage modeled as an ellipse.

Fig. 1

Plate with: a an arbitrary void and b a crack modeled as ellipse

2.2 Damage identification based on modal analysis

The main advantage in the use of the vibration/modal analysis for the damage identification process is that it does not require the sensors to be positioned close to the damage for it to be identified [3], which allows the application of the method in large or difficult-to-access structures.

The evaluation of the existence of damage in any structure consists simply in the comparison of the structural responses obtained through a vibration test in this with the structural response of an equal structure not damaged (obtained experimentally or numerically through modal analysis). Once the existence of damage is discovered, the knowledge of the number of existing damages, the spatial disposition of these in the structure and its characteristics become relevant (in a crack, for example, its size and orientation).

The detection of damage parameters is based on the generation of structural damage responses with different parameters and the comparison of its structural response in vibration with the structural response obtained in the original structure. At this stage, experimental analysis is, in most cases, unfeasible and modal analysis becomes the best alternative.

Modal analysis consists of a technique used to obtain the natural frequencies and mode shapes of a structure through Eq. 1.

$$\left[ {K - \omega \cdot M} \right]\phi = 0$$

(1)

The eigenvector $\phi$ is evaluated only for n natural frequencies in the m nodes of interest, thus obtaining an n dimension vectors (1 × m), these must be normalized in the nodes of interest according to Eq. 2 so that a single response can be obtained that can be compared with other modal analyses and with experimental results.

$$\hat{\phi }_{{\left( j \right)}} = \frac{{\phi _{{\left( j \right)}} }}{||{\phi _{{\left( j \right)}} }||}$$

(2)

being $\hat{\phi }_{{\left( j \right)}}$ is the normalized autovector evaluated in the nodes of interest and in the jth mode. To simplify the notation, $\phi _{{\left( j \right)}}$ will be used for the normalized autovector instead of $\hat{\phi }_{{\left( j \right)}}$. Natural frequencies are calculated by Eq. 3, in Hertz units.

$$f_{{\left( j \right)}} = \frac{{\omega _{{\left( j \right)}} }}{{2\pi }}$$

(3)

2.3 Response surface methodology

The response surface method (RSM) consists of a set of statistical techniques for constructing an empirical model that can associate an output variable with a series of input variables [27].

$$y = F\left( {x_{1} ,x_{2} , \ldots ,x_{k} } \right) + \varepsilon ~$$

(4)

where y is the response, x_i the variables and ε the error.

For the adjustment function F, it is common to use first- or second-order polynomials, according to Eqs. 5 and 6, respectively, obtained in Mukhopadhyay et al. [20]. The parameter β in both equations is calculated in such a way as to better adjust a set of points.

$$y = \beta _{{\text{o}}} + \mathop \sum \limits_{{i = 1}}^{k} \beta _{i} x_{i} + \mathop \sum \limits_{{i = 1}}^{k} \mathop \sum \limits_{{j > i}}^{k} \beta _{{ij}} x_{i} x_{j} + \varepsilon$$

(5)

$$y = \beta _{{\text{o}}} + \mathop \sum \limits_{{i = 1}}^{k} \beta _{i} x_{i} + \mathop \sum \limits_{{i = 1}}^{k} \mathop \sum \limits_{{j > i}}^{k} \beta _{{ij}} x_{i} x_{j} + \mathop \sum \limits_{{i = 1}}^{k} \beta _{{ii}} x_{i}^{2} + \varepsilon$$

(6)

2.3.1 Composite central design

One of the methods of obtaining points through Design of Experiments (DoE) is the use of the composite central design, which consists of a set of points arranged as in Fig. 2.

Fig. 2

Composite central design representation for 2 and 3 input variables

It α determined so that the model obtained presents certain characteristics [20]. The schema represented in Fig. 2 can be extrapolated to the specified number of input variables. The total number of points in this configuration will be given by Eq. 7.

$$n_{{\text{s}}} = 2^{k} + 2k + n_{{\text{o}}}$$

(7)

being n_s the total number of experiments, not the number of experiments at the center point, k the number of input variables.

2.3.2 Model quality check

The quality of the model should be verified for future predictions according to the R² criterion according to Eqs. 8, 9 and 10.

$$R^{2} = \frac{{{\text{SS}}_{{\text{R}}} }}{{{\text{SS}}_{{\text{T}}} }} = 1 - \frac{{{\text{SS}}_{{\text{E}}} }}{{{\text{SS}}_{{\text{T}}} }}~~~~\left( {0 \le R^{2} \le 1} \right)$$

(8)

$$R_{{{\text{adj}}}}^{2} = 1 - \frac{{{\raise0.7ex\hbox{${{\text{SS}}_{{\text{E}}} }$} \!\mathord{\left/ {\vphantom {{{\text{SS}}_{{\text{E}}} } {\left( {n_{{\text{s}}} - p} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {n_{{\text{s}}} - p} \right)}$}}}}{{{\raise0.7ex\hbox{${{\text{SS}}_{{\text{T}}} }$} \!\mathord{\left/ {\vphantom {{{\text{SS}}_{{\text{T}}} } {\left( {n_{{\text{s}}} - 1} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {n_{{\text{s}}} - 1} \right)}$}}}} = 1 - \frac{{n_{{\text{s}}} - 1}}{{n_{{\text{s}}} - p}}\left( {1 - R^{2} } \right)~~~~\left( {0 \le R_{{{\text{adj}}}}^{2} \le 1} \right)$$

(9)

$$R_{{{\text{pred}}}}^{2} = 1 - \frac{{{\text{PRESS}}}}{{{\text{SS}}_{{\text{T}}} }}~~~~\left( {0 \le R_{{{\text{pred}}}}^{2} \le 1} \right)$$

(10)

where SS_T, SS_E, SS_R and PRESS are the total sum of squares, due to the model, residual error and predicted residual error, respectively, and p = k + 1.

It is desired to have R² close to 1, however, in order to use the model for future predictions must meet the criterion of difference between R_adj² and R_pred² less than or equal to 0.2, according to Mukhopadhyay et al. [20].

2.4 Sunflower optimization method

The Sunflower Optimization (SFO) method, proposed by Gomes et al. [9] is a metaheuristic optimization method that is based on the flower pollination process proposed by Yang [33] with the addition of a movement of plants toward the sun, which increases the convergence speed of the method, in relation to its predecessor.

A population of N_pop plants containing parameters between a specified lower and upper limit is randomly created. The sun is assumed to be the best plant among those generated. At the beginning of each iteration m (%) of the plants will die and give way to new plants generated randomly, p (%) of the plants will pollinate each other and give rise to the new plants according to Eq. 11. In addition, Fig. 3 shows the pseudocode of the SFO algorithm [7, 8].

$$\vec{X}_{{\left( {i,j + 1} \right)}} = \vec{X}_{{\left( {i + 1,j} \right)}} + {\text{rand}}\left( {\vec{X}_{{\left( {i,j} \right)}} - \vec{X}_{{\left( {i + 1,j} \right)}} } \right)$$

(11)

Fig. 3

SFO pseudocode

The random function multiplies the vector, term-to-term by a random value between 0 and 1 generated evenly.

The rest of the plants will take steps toward the sun. The direction of plants in the sun will be the second displayed in Eq. 12.

$$\vec{s}_{i} = \frac{{X^{*} - X_{i} }}{{\left\| {X^{*} - X_{i} } \right\|}},~\quad ~i = 1,2, \ldots ,~N_{{{\text{pop}}}}$$

(12)

The step of each plant will be calculated according to Eq. 13 and the maximum step is calculated in Eq. 14.

$$d_{i} = \lambda \times P_{i} \left( {\left\| {X_{i} + X_{{i - 1}} } \right\|} \right) \times \left\| {X_{i} + X_{{i - 1}} } \right\|$$

(13)

$$d_{{\max }} = \frac{{\left\| {X_{{\max }} - X_{{\min }} } \right\|}}{{2 \times N_{{{\text{pop}}}} }}$$

(14)

Finally, the new plantation will be calculated by Eq. 15.

$$\vec{X}_{{\left( {i,j + 1} \right)}} = \vec{X}_{{\left( {i,j} \right)}} + d_{i} \times \vec{s}_{i}$$

(15)

2.5 Artificial neural networks

Artificial neural networks (ANN) are based on the mechanism of functioning of neurons. Just as organic neural networks learn from their environment and control the behavior of the organism according to the stimuli they receive, ANNs receive data sets and, from these, learn to predict the response of future inputs they may receive [2, 13]. The equations that define the output of a k neuron from n inputs are given in Eqs. 16 and 17.

$$v_{k} = \mathop \sum \limits_{{j = 1}}^{n} w_{{kj}} \cdot x_{j}$$

(16)

$$y_{k} = \varphi \cdot \left( {v_{k} + b_{k} } \right)$$

(17)

where x_j is the input signals, w_kj the weights of the synapses between j and k, v_k is the linear combination factor of neuron k, b_k is the tendency of neuron k, ϕ is the activation function and y_k is the output of neuron k.

An ANN consists of the arrangement of neurons described in layers, neurons of the first layer, called input, receives the input signals x_n and send signals to the first hidden layer, in which neurons of a layer receive signals from neurons of the previous layer and send signals to neurons of the next layer, neurons of the last layer, called output, produce the y_k-output signals.

The ANN described must go through a training process consisting of optimizing w_ki weights from an optimization function, also called a training function, associated with an error function to evaluate network performance after each iteration of the training.

The error function used was mean squared normalized error (MSE) according to Eq. 10 was used to evaluate the performance of ANN. In cases where there were few samples, the mean squared normalized error regularized (MSEREG) function was used to improve the generalization capacity of the network according to Eq. 20.

$${\text{MSE}} = \frac{1}{N}\mathop \sum \limits_{{i = 1}}^{N} \left( {Y_{i} - \hat{Y}_{i} } \right)^{2}$$

(18)

$${\text{MSW}} = \frac{1}{n}\mathop \sum \limits_{{j = 1}}^{n} \left( {w_{j} } \right)^{2}$$

(19)

$${\text{MSEREG}} = \gamma \cdot {\text{MSW}} + \left( {1 - \gamma } \right) \cdot {\text{MSE}}$$

(20)

where Y_i are the output signals of the network, $\hat{Y}_{i}$ are the output signals provided to the network for training, and γ is the regularization factor.

3 Methodology

The methodology considered in this study consists in the development of the direct problem to obtain the modal response to a plate with a crack and later on the development of the inverse problem that is based on the structural modal response of the laminated and the use of the responses obtained by the direct problem. The inverse problem is divided into three fronts: (1) using optimization algorithm SFO, (2) using ANN and (3) using RSM.

3.1 Direct problem and damage modeling

The structure chosen for analysis was a plate of dimensions 30 × 30 cm² of symmetrical laminate [0/90]_3S. Each layer has a thickness of 0.18 mm with properties according to Table 1, the plate is free of boundary conditions, therefore, free to move and rotate in space in all directions, causing in 6 free body modes that will be discarded for analysis, the natural frequencies will therefore be numbered from the first frequency that is not associated with a free body mode.

Table 1 Material properties

The natural frequencies of interest will be 1, 2, 3 and 6, according to the Analysis of the RSM performed presented later, the nodes of interest are the nodes located in the sensors shown in Fig. 4 the mesh created for the calculation of the structural response by the finite element method is shown in Fig. 5. The generic problem of identifying damage is to deduce the existence of damage to a structure through measurements made on sensors distributed in specific locations. It is known that the quality of these measurements, that is, the quality of structural monitoring, is largely dependent on where the sensors are located in the structure [10]. In this study, no specific study on the sensor placement optimization (SPO) problem has been carried out. However, for operational practice it was decided to use 8 sensors. These sensors were placed symmetrically at the ends of the laminated plate in question (Fig. 4). The choice of sensors at the edges of the plates is justified by the type of damage addressed (crack). Thus, the position of sensors on voids is avoided (if the crack position coincides with the sensor position).

Fig. 4

Plate geometry and sensor positioning, dimensions in mm (legend: blue circle sensors)

Fig. 5

Undamaged plate mesh considering shell elements

The mode shapes of the undamaged structure are shown in Table 2 considering an induced damage in an arbitrary position. It is observed that natural frequencies 4 and 5 have very close values and practice shows that these vary considerably in different tests, therefore, the mode shape 4 could be confused with 5 and vice versa, which would cause a problem of discontinuity in the structural response that would be harmful to the methods of identification of applied damages.

Table 2 Damage influence on modal response (mode shape and natural frequency)

If it is a roughly two-dimensional structure, the representation of the crack as an elliptical through hole is adequate. The vector of parameters required to define the damage will be defined as X as shown in Eq. 21.

$$\varvec{X} = \left[ {x_{o} ,y_{o} ,a,\theta ,b/a} \right]$$

(21)

The parametric definition of the ellipse perimeter is made according to Eq. 22 and its graphic representation is Fig. 6.

$$\left\{ {\begin{array}{*{20}l} {x = x_{o} + a \cdot \cos \left( t \right) \cdot \cos \left( \theta \right) - b \cdot \sin \left( t \right) \cdot \sin \left( \theta \right)} \\ {y = y_{o} + a \cdot \cos \left( t \right) \cdot \sin \left( \theta \right) + b \cdot \sin \left( t \right) \cdot \cos \left( \theta \right)} \\ \end{array} } \right.~;\quad ~t = \left( {0,~2\pi } \right)$$

(22)

Fig. 6

Graphic representation of the parametric equation of the ellipse

Simply perform the Boolean operation of subtracting the inner area to the ellipse over the original geometry to obtain the geometry of the damaged structure. In order to obtain higher mesh quality, a rectangular casing was created around the three of dimensions that conforms Eqs. 23 and 24, within which a more refined mesh was generated (Fig. 7). The final mesh obtained is represented in Fig. 8.

$$x_{{\text{e}}} = 0.006*{\text{ceil}}\left( {\frac{{\max \left[ {\begin{array}{*{20}c} {0.024} \\ {2 \cdot a \cdot \cos \left( \theta \right)} \\ {2 \cdot b \cdot \sin \left( \theta \right)} \\ \end{array} } \right]}}{{0.006}}} \right)$$

(23)

$$y_{{\text{e}}} = 0.006*{\text{ceil}}\left( {\frac{{\max \left[ {\begin{array}{*{20}c} {0.024} \\ {2 \cdot b \cdot \cos \left( \theta \right)} \\ {2 \cdot a \cdot \sin \left( \theta \right)} \\ \end{array} } \right]}}{{0.006}}} \right)$$

(24)

Fig. 7

Parameterization of the elliptical crack and casing

Fig. 8

Plate mesh with elliptical crack

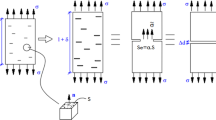
The process adopted to solve the direct problem can be described in four main steps. These steps are described as follows:

Step 1: Using modal analysis and FEM, the normalized mode shapes of the chosen plate for analysis in the nodes and natural frequencies of interest ϕ_h and the natural frequencies of interest f_h are stored.

Step 2: The normalized mode shapes of the damaged plate ϕ_d, natural frequencies and nodes of interest and the natural frequencies of interest f_d.

Step 3: A reference direction is adopted for each vibrate mode obtained. The reference direction was assumed from a reference node chosen arbitrarily and performing the operation given in Eq. 25.

$$\phi _{{\left( j \right)}} = {\text{sign}}(\phi _{{\left( {r,j} \right)}} )\Delta \phi _{{\left( j \right)}}$$

(25)

$${\text{sign}}\left( x \right) = \left\{ {\begin{array}{*{20}l} { - 1,} \hfill & {{\text{if}}\;x < 0} \hfill \\ {0,} \hfill & {{\text{if}}\;x = 0} \hfill \\ {1,} \hfill & {{\text{if}}\;x > 1} \hfill \\ \end{array} } \right.$$

(26)

The reference nodes chosen must be the same in all analyses made so that the answers can be compared between them.

Step 4: The structural responses of the damaged plate Δf and Δϕ are calculated by:

$$\Delta f_{{\left( j \right)}} = f_{{d\left( j \right)}} - f_{{h\left( j \right)}}$$

(27)

$$\Delta \phi _{{\left( {ij} \right)}} = \phi _{{d\left( {ij} \right)}} - \phi _{{h\left( {ij} \right)}}$$

(28)

The described process results in a structural response (Δf, Δϕ) unique for each set of crack parameters, and ideally for an undamaged plate, it assumes a value (Δf, Δϕ) = (0, 0).

3.1.1 Direct problem modeling as a response surface

The modeling of the direct problem as a response surface was initially developed with the objective of producing a precise numerical model that eliminates the need to use the FEM at each direct problem evaluation, but it was found that this objective was not achieved with the model created. However, the results were used to obtain a better understanding of the characteristics of the problem in order to identify the structural parameters most relevant to the method.

Therefore, we want to obtain a response surface capable of estimating structural responses from the damage parameters, so the input and output variables will be given, respectively, by Eqs. 29 and 30.

$$X = \left[ {x_{o} ,y_{o} ,a,\theta ,b/a} \right]$$

(29)

$$Y = \left[ {\Delta f,\;\Delta \phi } \right]$$

(30)

where Δf = [Δf₍₁₎, Δf₍₂₎,…, Δf₍₆₎] the natural frequencies from 1 to 6 and Δϕ the vibration amplitudes normalized in each of the 8 nodes of interest and in the 6 natural frequencies.

The data needed to generate the response surface is obtained using the central DoE method composed with α = 1. The points are translated into the damage parameters through Eq. 31.

$$\left\{ {\begin{array}{*{20}l} {x_{{\text{o}}} = 150 + 104~x_{1} ~\left[ {{\text{mm}}} \right]} \hfill \\ {y_{{\text{o}}} = 150 + 104~x_{2} ~\left[ {{\text{mm}}} \right]} \hfill \\ {a = 16.5 + 13.5~x_{3} ~\left[ {{\text{mm}}} \right]} \hfill \\ {\theta = 90~x_{4} ~\left[ ^\circ \right]} \hfill \\ {b/a = 0.2 + 0.1~x_{5} ~\left[ - \right]} \hfill \\ \end{array} } \right.$$

(31)

The data are adjusted by a second-order polynomial. A total of 54 quadratic surfaces are generated, which model the output values.

3.2 Inverse problem modeling

The inverse problem simply consists in identifying the crack using the answers obtained through the direct process. The methods applied will be RSM, SFO and ANN.

3.2.1 Modeling of sunflower optimization

The parameters used to solve the inverse problem by the SFO method are shown in Table 3. The choice of SFO control parameters is based on the best configuration that results in a perfect balance of exploration–exploitation [7]. For all evaluated cases, the stopping criterion was defined as the maximum number of generations. The lateral boundaries in the identification problem define a minimum and maximum size that the problem can handle. It is known that very small damages are not able to significantly alter the modal response [9]. Therefore, a minimum acceptable damage of 3 mm in length was defined, which can already be considered a small damage in a large-scale structure.

Table 3 Parameters used in the SFO

The objective function chosen was the one that seeks to penalize the difference between the vibration amplitudes of a plate with the damage induced to the plate with any damage, in which the function is evaluated. Such amplitudes are evaluated in only frequencies and nodes of interest. Equation 32 represents the objective function J described.

$$J = \sum\limits_{{i = 1,2,3,6}} {\left( {\sum\limits_{{j = 1}}^{8} {\left| {\Delta \hat{\phi }_{{\left( {i,j} \right)}} - \Delta \phi _{{\left( {i,j} \right)}} } \right|} } \right)}$$

(32)

3.2.2 Modeling of the artificial neural network

The artificial neural network proposed to solve the inverse problem has as input the modes of vibration of interest and as a result the parameters of damage, according to Eqs. 33 and 34.

$$X = ({{\Delta }}\phi _{{\left( {1,1} \right)}} ,{{\Delta }}\phi _{{\left( {2,1} \right)}} , \ldots ,{{\Delta }}\phi _{{\left( {8,1} \right)}} ,{{\Delta }}\phi _{{\left( {1,2} \right)}} ,{{\Delta }}\phi _{{\left( {2,2} \right)}} , \ldots ,$$

$${{\Delta }}\phi _{{\left( {8,2} \right)}} ,{{\Delta }}\phi _{{\left( {1,3} \right)}} ,{{\Delta }}\phi _{{\left( {2,3} \right)}} , \ldots ,{{\Delta }}\phi _{{\left( {8,3} \right)}} ,{{\Delta }}\phi _{{\left( {1,6} \right)}} ,{{\Delta }}\phi _{{\left( {2,6} \right)}} , \ldots ,{Tt{\Delta }}\phi _{{\left( {8,6} \right)}} )$$

(33)

$$Y = \left( {x_{o} ,y_{o} ,a,\theta ,b/a} \right)$$

(34)

Input and output values are mapped between − 1 and 1 before being inserted into the network so that equal weight is given to variations of the different signals.

The architecture represented in Fig. 9 called Feed Forward, which was proposed for this problem contains 32 input neurons, 32 neurons in the first hidden layer, 16 in the two subsequent hidden layers, and 5 in the output. The choice of the type of architecture and the number of neurons was based on trial and error until an ANN was obtained that could well represent the problem. The parameters used in the network are shown in Table 4.

Fig. 9

ANN architecture

Table 4 Parameters used in ANN

4 Numerical results and discussion

4.1 RSM results

The models generated by The RSM were evaluated according to the criterion of the difference between R_adj² and R_pred² less than or equal to 0.20. Table 5 presents this analysis and highlight in italic the modal answers in which the criterion is reached and in bold in which it is not reached.

Table 5 R² of the models for the first six modes

It is noted that the worst results are obtained in natural frequencies 4 and 5, which shows that they present a more complex behavior than the other ones, thus justifying the elimination of these responses in the proposals to solve the inverse problem developed in this work.

4.2 SFO results

Gomes et al. [11] and Gomes and Almeida [7] described a new metaheuristic algorithm based on the biological process of orientation of the sunflowers toward the sun and by pollination and generation of new flowers (individuals in a population). The cycle of these plants is unique and always the same: every day, they wake up and follow the sun like the hands of a clock, resembling a radar tracking the target. At night, they travel in the opposite direction to wait again for their departure the next morning.

Considering the damage identification strategy through the inverse optimization method, several optimization algorithms are available in the literature. Metaheuristic techniques are known to have superior performance and are recommended to deal with the complexity of this problem. Most traditional metaheuristic algorithms are used such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO). Other metaheuristic techniques have also been developed and have shown substantial performance compared to more traditional techniques, such as: Colliding bodies optimization (CBO) [16], Gravitational Search Algorithm (GSA) [25], Lichtenberg Algorithm [23] and many others.

Table 6 shows the result of damage identification (of the crack parameters) considering 12 different runs of the SFO algorithm. It is noteworthy that this study does not aim to compare or discuss the efficiency of the SFO metaheuristic in relation to other metaheuristics. The SFO algorithm was chosen as the optimizer due to its superior and significant performance when applied to identification and damage problems [7, 9]. There is no metaheuristic technique superior to another (No Free Lunch Theorem), but techniques that have superior performance to solve a certain type of problem.

Table 6 Inverse crack identification using SFO algorithm considering multiple runs

Damage was induced with parameters X = {0.1054; 0.1878; 0.0186; − 62.1377; 0.1232}. Table 6 shows that the damage was identified with excellent accuracy. In general, the results for the different runs show small variability and this variability is due to the stochastic nature of the metaheuristic. In general, for crack identification problems, the θ parameter is considered as one of the most difficult to identify parameters. Furthermore, the result shows that the a/b ratio also presented a certain level of error in relation to the goal of 0.1232.

The results obtained are presented in Figs. 10 and 11 for one specific run. Figure 10 shows the evolution of the crack found by the SFO method in each generation shown and Fig. 11 presents the evolution of parameters over generations. In Fig. 10, the global best is the induced damage with known parameters (X). The current best is the best individual of each generation. In addition, the entire population of diaries is displayed in the physical space of the laminated CFRP plate.

Fig. 10

Cracks identified, induced and population throughout the iterations of the SFO (legend: blue line current best, red line global best and gray line individuals). (Color figure online)

Fig. 11

Graph of the evolution of the parameters of the crack and the objective function (legend: yellow line target and blue line calculated). (Color figure online)

4.3 ANN results

The second damage identification strategy concerns the use of ANN. The previous section addressed the use of metaheuristics for damage identification and excellent results were obtained regarding the accuracy of crack identification. However, the optimization methodology can be slow, as each identification process requires a relatively high number of objective function evaluations. In order to get around this inconvenience, ANN models are considered. Once the ANN is well trained, the model can predict the position and extent of damage (crack) instantly.

The ANN architecture and parameters were discussed in the previous sections. Table 7 shows the overall model error results in relation to the damage variables. Figure 12 shows an example of the model result obtained by ANN after the training phase. Random and unknown damages of the model were chosen (they were not part of the training phase). Substantial identification results can be observed. In all examples, the predicted damage was close to the induced damage as well as its extent (crack size). It is also noteworthy that the θ variable (more difficult to interpret in the identification process) was accurately identified by the ANN model.

Table 7 Summary of the results obtained by ANN

Fig. 12

ANN results for 6 different cracks (legend: red line induced and blue line predicted damages). (Color figure online)

4.4 Comparison of results

Finally, the last results section discusses the comparison of the studied methods for crack identification in laminated plates. As discussed previously, the quadratic model using RSM was not able to model the problem due to its complexity. On the other hand, both models using SFO and ANN were able to identify the induced damage with substantial accuracy.

The strategy of gradually increasing the number of problem evaluations (population × generations) until obtaining a substantial result was considered. Figures 13 through 16 show the graphical damage identification results for values of 100, 1000, 2000 and 5000 objective function ratings, respectively. It is observed that even for a small number of assessments, ANN is able to predict the damage position relatively well. Results using SFO have the advantage of being able to better accurately identify the orientation variables (θ). However, with the addition of the number of samples (database for ANN), the result is similar to the result obtained by the SFO. In addition, Tables 8 and 9 show the errors associated with each method.

Fig. 13

Comparison between ANN and SFO with 100 direct problem evaluations (legend: blue line calculated, red line induced damage and gray line individuals). (Color figure online)

Fig. 14

Comparison between ANN and SFO with 1000 direct problem ratings (legend: blue line calculated, red line induced damage and gray line individuals). (Color figure online)

Fig. 15

Comparison between ANN and SFO with 2000 direct problem ratings (legend: blue line calculated, red line induced damage and gray line individuals). (Color figure online)

Fig. 16

Comparison between ANN and SFO with 5000 direct problem ratings (legend: blue line calculated, red line induced damage and gray line individuals)

Table 8 SFO results with different parameters

Table 9 ANN results with different sample numbers

5 Conclusions

The results of the SFO and ANN methods created showed that both methods are reliable for obtaining the crack parameters, within a continuous set, and can be used to estimate the location, size and orientation of a crack in laminated composite plates. Numerical analysis, shows that, given a sufficient number of evaluations of the direct problem, the associated errors can be reduced according to the need of the desired application.

The SFO method differs from ANN in terms of the field of application, since the SFO requires little time for implementation, but a longer time to generate a substantial reliable result, since it requires the evaluation of the problem direct to each new individual evaluated. ANN, on the other hand, requires a longer time for its generation, taking into account the time to obtain a consistent set of samples, but presents a short, almost instantaneous time to present the results.

The results presented indicate that the RSM model, although inadequate to adjust the structural responses, proved useful for the verification of the best structural responses for use in the inverse problem and allowed the generation of the objective function and the creation of the artificial neural network in order to obtain substantial results.