Abstract
This paper deals with the dynamics and control of underactuated nonholonomic mechanical systems. It is shown in this investigation that the same analytical methods can be used for effectively solving both the forward and the inverse dynamic problems relative to underactuated mechanical systems subjected to a general set of holonomic and/or nonholonomic algebraic constraint equations. The approach developed in this work is based on the combination of two fundamental methods of analytical dynamics, namely the Udwadia–Kalaba equations and the Underactuation Equivalence Principle. While the Udwadia–Kalaba equations represent a fundamental mathematical tool of classical mechanics, the Underactuation Equivalence Principle is a new method recently discovered in the field of analytical dynamics and is associated with nonholonomic mechanical systems. In the paper, these two important analytical methods are discussed in detail. Furthermore, numerical experiments are performed in this investigation in order to demonstrate the effectiveness of the proposed approach considering as an illustrative example of a dynamic model a mobile robot.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper deals with the development of a unified method for solving the forward and inverse dynamic problems of underactuated mechanical systems constrained by a general set of holonomic and/or nonholonomic constraints. In particular, the Udwadia–Kalaba equations and the Underactuation Equivalence Principle are the principal analytical methods of interest for this investigation. The analytical method developed in this work is applied to an unicycle-like mobile robot that is employed as a demonstrative example. In this section, background materials containing a concise literature survey, the formulation of the problem of interest for this study, the scope, the motivation, and the contributions of this investigation, and the organization of the manuscript are provided.
1.1 Background and significance of this research work
In several areas of industrial engineering, the study of the mechanical behavior of dynamical systems characterized by a nonlinear structure represents an important issue. This problem is particularly relevant in different engineering applications in which the design of a machine or a mechanism represents almost always an approximated solution affected by a certain degree of uncertainty [1, 2]. As thoroughly discussed in the literature, appropriate analytical methods and computational procedures are required for the development of effective control laws for influencing the dynamic evolution of a nonlinear dynamical model of a complex mechanical system in order to obtain the desired performance [3]. In the development of effective control strategies for a given mechanical system, the first step is to devise a reliable mathematical model of the dynamical system capable of correctly capturing its intrinsic nonlinear physics [4]. Subsequently, the control design for the nonlinear mechanical system under study can be performed using several analytical approaches and computational methodologies that belong to the field of mechanical engineering [5, 6]. In the development of a new control system, it is important to note that the classical control methods based on the linearization of the equations of motion of the mechanical system are not suitable for solving the control problem associated with a nonlinear mechanical system [7, 8]. Such methods involve a loss of information on the complex dynamic behavior that a nonlinear system can experience and, therefore, these methods work properly only when the time response of the mechanical system takes place around a fixed point of the state space or in the neighborhood of a prescribed space trajectory. However, this is not the case for several machines and mechanisms used in mechanical engineering applications in which a fully nonlinear dynamic behavior is found [9, 10]. Therefore, in this general case, more complex control strategies are necessary for solving the nonlinear control problem. A possible approach for obtaining the solution of this problem is based on the use of nonlinear optimization techniques based on the adjoint method. The nonlinear optimization techniques which rely on the adjoint approach, however, are complex to analytically formulate and numerically implement even in the case of simple nonlinear mechanical systems. On the other hand, as discussed in the paper, an effective strategy for solving this challenging problem is based on the inverse dynamic approach.
In recent years, the research on autonomous robots has gained a great attention because of its large potential for solving practical problems in different areas of mechanical engineering such as, for example, transportation and logistics, space investigation, ocean observation, military defense, monitoring of large civil infrastructures, and unmanned exploration of hazardous and remote environments. Therefore, several control approaches were developed in order to obtain the stabilization and the trajectory tracking control of mobile robots. In mechanical engineering, mobile robots are typically modeled as nonholonomic mechanical systems. These systems are subjected to a certain degree of complexity in the analytical model and to a given degree of uncertainty in the parameters that define the dynamical model. Typically, the unknown parameters of the dynamical model of a mobile robot need to be identified by using system identification algorithms based on experimental data. In order to address and solve the nonlinear control problem of mobile robots, several effective control approaches have been presented in the literature. For example, the methods based on the state-dependent Riccati equation, the feedback linearization method, the sliding mode control approach, and nonlinear control methods based on the control Lyapunov function represent effective control approaches suitable for solving the nonlinear control problem associated with a mechanical system subjected to a given set of holonomic constraints [11,12,13,14]. Furthermore, additional examples of nonlinear control strategies successfully applied to the stabilization and tracking control of mobile robots are based on the fuzzy control, adaptive control, neural network, and robust control approaches [15,16,17,18,19]. However, all the methods mentioned before are based on nonstandard approaches that cannot be equally applied in a straightforward manner to both holonomic and nonholonomic mechanical systems. Also, these analytical and computational methods do not entirely take into account the complex nonlinear effects of the underactuated mechanical models that describe the dynamics of mobile robots. In this paper, on the other hand, an effective control method based on an inverse dynamic approach suitable for underactuated mechanical systems constrained by holonomic and/or nonholonomic algebraic equations is presented.
1.2 Formulation and motivation of the problem of interest for this investigation
The fundamental motivation behind the development of this paper is to devise a unique method by which the forward and inverse dynamic problems of underactuated mechanical systems constrained by holonomic and/or nonholonomic constraints can be formulated and solved. In general, the mechanical systems encountered in industrial applications are dynamical systems which undergo large displacements and large reference rotations [20, 21]. In addition, a mechanical system can be unconstrained or constrained by holonomic and/or nonholonomic constraints. For example, multibody mechanical systems are dynamical systems composed of rigid and/or deformable bodies that are interconnected by intermediate mechanical components called kinematic joints [22,23,24,25]. While the methods of classical mechanics can be effectively used for modeling rigid multibody mechanical systems, the mathematical description of rigid-flexible multibody systems needs the use of more advanced analytical techniques that combines the finite element method with the general principles of classical mechanics such as, for instance, the D’Alembert–Lagrange principle of virtual work. The analysis of the dynamic behavior of a flexible multibody system allows for finding the stability characteristics of the dynamical system and can be employed for assessing the quality of the strain and stress fields of the mechanical components that play a fundamental role for the system structural integrity [26, 27]. Multibody mechanical systems can be mathematically described considering the differential-algebraic equations of motion of constrained mechanical systems, namely a set of differential equations that describe the dynamic evolution in time coupled with a set of algebraic equations that mathematically represent the holonomic and/or nonholonomic constraints. In the field of analytical dynamics, one of the main goals is to correctly derive the nonlinear equations of motion which effectively describe the dynamic behavior of constrained mechanical systems [28,29,30]. In particular, the equations of motion of a multibody mechanical system are typically represented with a set of differential-algebraic equations (DAEs) because of the presence of the kinematic constraints which interconnect the bodies of the dynamical system. Since the generalized constraint forces represent additional unknown of the constrained dynamic problem that enters in the formulation of the equations of motion, there are several effective methods for solving the forward dynamic problem of a mechanical system in conjunction with the determination of the constraint reaction forces and moments. On the other hand, the dual problem is represented by the inverse dynamic problem in which one needs to determine the control actions to impose to a mechanical system in order to obtain the desired dynamic behavior as well as an acceptable dynamic performance. In many engineering applications, the mathematical model that describes the mechanical system to control is nonlinear, underactuated, and nonholonomic. Thus, the equations of motion form a nonlinear set of DAEs in which the constraint equations are nonholonomic and the control actions are not applied to each degree of freedom of the dynamical system because of practical limitations. The inverse dynamic problem for nonlinear underactuated mechanical systems is, therefore, a challenging issue that is not fully solved yet.
The first challenge associated with the control problem of mechanical systems is the nonlinearity of the equations of motion. While for linear mechanical systems there are numerous mathematical techniques available in the literature for obtaining effective control laws, in the case of nonlinear systems there are only special analytical methods which are suitable only for specific applications. More importantly, in general, the analytical methods of the linear control do not work properly when applied to the linearization of the equations of motion since the linearized equations fail to completely capture the essence of the dynamic problem. The second important challenge is related to the underactuation property of the models of several mechanical systems. Underactuated mechanical systems are mechanical systems in which the number of the control actions is less than the number of the system degrees of freedom and, therefore, this class of dynamical systems is particularly difficult to influence and control. The third challenge of interest for this investigation is the presence of nonholonomic constraint equations, namely the nonlinear algebraic equations that involve the system generalized coordinates, velocities, and accelerations which cannot be reconducted or integrated into simple algebraic equations defined only in terms of the position coordinates. Thus, nonholonomic mechanical systems are dynamical systems whose current configuration depends on the entire trajectory followed to reach a given point of the configuration space, namely mechanical systems subjected to nonintegrable constraints on generalized coordinates, velocities, accelerations [31]. In conclusion, nonlinearity, underactuation, and nonholonomy represent crucial aspects which make the control problem of mechanical systems difficult to solve [32]. These challenges are addressed in this investigation employing a simple inverse dynamic analytical approach.
1.3 Scope and contribution of this study
In this paper, a general and effective method for solving the forward and inverse dynamic problems of mechanical systems having an underactuated structure and subjected to holonomic and/or nonholonomic constraints is proposed. The method developed in this work is based on the combinations of two analytical methods recently developed in the field of classical mechanics, namely the central equations of constrained motion devised by Udwadia and Kalaba as well as the Underactuation Equivalence Principle formulated for the first time by the authors [33, 34]. While the analytical approach to the dynamics of constrained mechanical systems developed by Udwadia and Kalaba allows for solving forward and inverse dynamic problems in the same mathematical framework, the Underactuation Equivalence Principle is used for extending the scope of application of the central equations of constrained motion from fully actuated mechanical systems to underactuated mechanical systems. Therefore, the Underactuation Equivalence Principle allows for mathematically formalizing the underactuation property of a mechanical system considering a particular set of nonholonomic constraints defined at the acceleration level which produce a generalized constraint force vector identically equal to zero. By using the Underactuation Equivalence Principle, one can demonstrate that the generalized acceleration vector of an unconstrained mechanical system having an underactuated structure is equal to the generalized acceleration vector of a mechanical system constrained by a set of nonholonomic constraints that mathematically represent the underactuation property of the dynamical system. By doing so, the inverse dynamic problem of an underactuated mechanical system can be analytically formalized and numerically solved in the same framework used for addressing the forward dynamic problems employing the Udwadia–Kalaba equations that originate from the Gauss principle of least constraint [35]. As shown in the paper, the proposed method can be used for analytically solving in an explicit manner the forward and inverse dynamic problems of a broad family of nonlinear mechanical systems constrained by holonomic and/or nonholonomic constraints having an underactuated structure. However, for some nonholonomic underactuated mechanical systems, it turns out that an arbitrary set of generalized accelerations cannot be obtained by applying any vector of control actions even considering the inverse dynamic approach developed in this research work. This important issue will be addressed in detail in future investigations.
The Udwadia–Kalaba equations can be used for obtaining in a closed form the generalized force vector relative to a general set of holonomic and/or nonholonomic constraints leading to the solution of both the forward and the inverse dynamic problems associated with fully actuated mechanical systems. The Underactuation Equivalence Principle, on the other hand, allows for extending the Udwadia–Kalaba approach to underactuated mechanical systems by mathematically formulating the underactuation property of a dynamical system as a set of nonholonomic constraints. The effectiveness of the inverse dynamic method developed in this study is demonstrated by means of numerical experiments and is applied to the tracking control problem of mobile robots. In the numerical example considered in this work, both holonomic and nonholonomic constraints are used in order to demonstrate the effectiveness of the method developed in this investigation. The proposed method is applied to the forward and inverse dynamic problems of a simple nonlinear dynamical system representing a benchmark problem in the field of nonlinear control for underactuated nonholonomic mechanical systems. In particular, the unicycle-like mobile robot is used as a case study. In order to obtain an effective control action based on the inverse dynamic approach, the unicycle-like mobile robot is subjected to a set of holonomic constraint equations that allow for imposing the path and the time law of the mechanical system. The pure rolling condition of the mobile robot, on the other hand, is modeled considering a set of nonholonomic constraints at the velocity level. Furthermore, the underactuated structure of this mechanical system is mathematically represented by using a set of nonholonomic constraints at the acceleration level. The generalized constraint force vector representing the pure rolling constraint for the mobile robot is explicitly calculated and an arbitrary trajectory for the robot center of mass compatible with the pure rolling constraint is designed and implemented. First, the control laws which correspond to the designed trajectory are analytically calculated. Subsequently, the control actions are validated by means of numerical experiments. The numerical results obtained by means of dynamical simulations show that the nonlinear control laws designed using the proposed approach are effectively capable of controlling the unicycle-like mobile robot, thereby demonstrating the practical feasibility of the control approach developed in this work.
1.4 Organization of the paper
The remaining part of this manuscript is organized as follows. In Sect. 2, the analytical methods necessary for the symbolic derivation and the computer implementation of the differential-algebraic equations of motion of a general mechanical system constrained by holonomic and/or nonholonomic constraints are recalled and the nonlinear control method developed in the paper is illustrated. In Sect. 3, an unicycle-like mobile robot is employed as a simple case study for demonstrating the effectiveness of the inverse dynamic control approach developed in the paper. In Sect. 4, the summary of the paper, the conclusions formulated in this investigation, and the possible directions for future research work are reported.
2 Background materials and analytical methods
In this section, the mathematical background necessary for the analytical derivation and the computer implementation of the differential-algebraic equations of motion of a general mechanical system constrained by holonomic and/or nonholonomic constraints is recalled. Subsequently, the nonlinear control method developed in the paper is illustrated. To this end, the analytical formulation of the central equations of constrained dynamics is presented and the Udwadia–Kalaba approach to the solution of the forward and inverse dynamic problems for fully actuated mechanical systems is described in detail. Finally, the use of the Underactuation Equivalence Principle for extending the Udwadia–Kalaba nonlinear control method from fully actuated dynamical systems to underactuated mechanical systems is shown and the key steps of the null space method for obtaining the underactuation nonholonomic constraints are discussed.
2.1 Method of Lagrange multipliers for holonomic and nonholonomic systems
In this section, the use of a general method based on the Lagrange multiplier technique for handling holonomic as well as nonholonomic systems is described [36,37,38]. Considering a general nonlinear mechanical system, the matrix form of the equations of motion obtained starting from the basic principles of classical mechanics employing an analytical approach based on a redundant set of generalized coordinates can be written as follows:
where t is time, \(\mathbf{q} \equiv \mathbf{q}(t)\) denotes the vector that contains the system generalized coordinates, \(\mathbf{M} \equiv \mathbf{M}(\mathbf{q},t)\) represents the system mass matrix, \({\mathbf{Q }_b} \equiv {\mathbf{Q }_b}(\mathbf{q },{\dot{\mathbf{q}}},t)\) identifies the total generalized force vector of the body forces, and \({\mathbf{Q }_c} \equiv {\mathbf{Q }_c}(\mathbf{q},{\dot{\mathbf{q}}},t)\) stands for the total generalized force vector associated with the algebraic constraints that limit the motion of the mechanical system. In general dynamic problems relative to constrained mechanical systems, the generalized force vector associated with the algebraic constraints \({\mathbf{Q }_c}\) is formed by a set of additional unknowns which depend on the specific nature of the algebraic constraint equations imposed on the mechanical system. In analytical mechanics, the algebraic equations that model the nonlinear constraints applied to a mechanical system can be distinguished into two categories, namely holonomic constraints and nonholonomic constraints [39,40,41]. While holonomic constraints are represented by a set of algebraic equations defined at the position level, nonholonomic constraints can be defined at the velocity level as well as at the acceleration level. Therefore, in general, the constraint equations are given by a set of algebraic equations written in terms of the generalized coordinate vector \(\mathbf{q}\) and its first and second time derivatives \({\dot{\mathbf{q}}}\) and \({\ddot{\mathbf{q}}}\). Although there is not a common agreement between the researchers within the applied mechanics community on this definition [42,43,44], in classical mechanics the holonomic constraint equations are traditionally referred to as integrable constraints since the corresponding algebraic equations can be integrated or simply rewritten only in terms of the generalized coordinate vector \(\mathbf{q}\). By doing so, one can reduce the algebraic equations that model holonomic constraints to the following simple form:
where \(\mathbf{f} \equiv \mathbf{f}(\mathbf{q},t)\) represents a nonlinear constraint vector function of dimensions \({n_f}\) defined only in terms of the system generalized coordinate vector \(\mathbf{q}\). In engineering applications, typical examples of holonomic constraints are the algebraic equations that model the geometric coupling between the kinematic pairs of the mechanical joints of a multibody mechanical system. On the other hand, one can classify the nonholonomic constraints as velocity nonholonomic constraints and acceleration nonholonomic constraints. The velocity nonholonomic constraints are represented by algebraic equations defined in terms of the generalized coordinate vector \(\mathbf{q}\) and its first time derivative \({\dot{\mathbf{q}}}\). Thus, the algebraic equations that model the velocity nonholonomic constraints assume the following general form:
where \(\mathbf{g} \equiv \mathbf{g}(\mathbf{q},{\dot{\mathbf{q}}},t)\) denotes a nonlinear constraint vector function of dimension \({n_g}\) defined only in terms of the system generalized coordinate vector \(\mathbf{q}\) and its first time derivative \({\dot{\mathbf{q}}}\). It is assumed that the vector function \(\mathbf{g}\) cannot be integrated or rewritten in terms of an equivalent vector function \(\mathbf{f}_g\) defined only in terms of the generalized coordinate vector \(\mathbf{q}\). In applied mechanics, a common example of a nonholonomic constraint defined at the velocity level is the pure rolling condition. Furthermore, the acceleration nonholonomic constraints represent the most general form of constraint equations. As mentioned before, the acceleration nonholonomic constraints are represented by algebraic equations defined in terms of the generalized coordinate vector \(\mathbf{q}\) and its first and second time derivatives \({\dot{\mathbf{q}}}\) and \({\ddot{\mathbf{q}}}\). The algebraic equations that model the acceleration nonholonomic constraints are given by:
where \(\mathbf{h} \equiv \mathbf{h}(\mathbf{q},{\dot{\mathbf{q}}},{\ddot{\mathbf{q}}},t)\) identifies a nonlinear constraint vector function of dimension \({n_h}\) defined in terms of the vectors \(\mathbf{q}\), \({\dot{\mathbf{q}}}\), and \({\ddot{\mathbf{q}}}\). Even in this case, it is assumed that the vector function \(\mathbf{h}\) cannot be integrated or rewritten in terms of an equivalent vector function \(\mathbf{g}_h\) defined only in terms of the vectors \(\mathbf{q}\) and \({\dot{\mathbf{q}}}\) as well as an equivalent vector function \(\mathbf{f}_h\) defined only in terms of the generalized coordinate \(\mathbf{q}\). As discussed in this section, an important example of an acceleration nonholonomic constraint is the underactuation property of a mechanical system subjected to external control inputs. In general, a mechanical system can be subjected to holonomic constraints as well as nonholonomic constraints defined at both the velocity and acceleration levels. In this general case in which one has at the same time the algebraic equations (2), (3), and (4), the total number of constraint equations \({n_c}\) is given by:
Each set of constraint equations generates a generalized constraint force vector that represents an additional vector of unknown external forces. Therefore, the total generalized vector associated with the algebraic constraints \({\mathbf{Q }_c}\) can be obtained by summing the holonomic constraint generalized force vector, the velocity nonholonomic constraints generalized force vector, and the acceleration constraint generalized force vector as follows:
where \({\mathbf{Q }_{c,f}} \equiv {\mathbf{Q }_{c,f}}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is the generalized constraint force vector associated with the set of holonomic constraints defined by Eq. (2), \({\mathbf{Q }_{c,g}} \equiv {\mathbf{Q }_{c,g}}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is the generalized constraint force vector relative to the set of velocity nonholonomic constraints defined by Eq. (3), and \({\mathbf{Q }_{c,h}} \equiv {\mathbf{Q }_{c,h}}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is the generalized constraint force vector corresponding to the set of acceleration nonholonomic constraints defined by Eq. (4). One can demonstrate that a simple analytical approach based on the Lagrange multiplier technique can be used for writing the generalized force vector associated with the holonomic constraint equations as well as the nonholonomic constraint equations [45]. To this end, one can write:
where \({{\varvec{\lambda }}_f} \equiv {{\varvec{\lambda }}_f}(t)\) is the vector of Lagrange multipliers associated with the holonomic constraints equations, \({{\varvec{\lambda }}_g} \equiv {{\varvec{\lambda }}_g}(t)\) is the vector of Lagrange multipliers relative to the velocity nonholonomic constraint equations, and \({{\varvec{\lambda }}_h} \equiv {{\varvec{\lambda }}_h}(t)\) is the vector of Lagrange multipliers corresponding to the acceleration nonholonomic constraint equations, whereas \({\mathbf{f}_\mathbf{q}} = \frac{{\partial \mathbf{f}}}{{\partial \mathbf{q}}}\) represents the Jacobian matrix of the holonomic constraint vector \(\mathbf{f}\) computed with respect to the generalized coordinate vector \(\mathbf{q}\), \({\mathbf{g}_{{\dot{\mathbf{q}}}}} = \frac{{\partial \mathbf{g}}}{{\partial {\dot{\mathbf{q}}}}}\) represents the Jacobian matrix of the velocity nonholonomic constraint vector \(\mathbf{g}\) computed with respect to the generalized velocity vector \({{\dot{\mathbf{q}}}}\), and \({\mathbf{h}_{{\ddot{\mathbf{q}}}}} = \frac{{\partial \mathbf{h}}}{{\partial {\ddot{\mathbf{q}}}}}\) represents the Jacobian matrix of the acceleration nonholonomic constraint vector \(\mathbf{h}\) computed with respect to the generalized acceleration vector \({{\ddot{\mathbf{q}}}}\). The total generalized constraint force vector \({\mathbf{Q }_c}\) can be expressed by using the Lagrange multiplier technique as follows:
Consequently, the system equations of motion given by Eq. (1) can be rewritten by using the explicit formulation of the total constraint generalized force vector as:
The equations of motion of a mechanical system constrained by a general set of algebraic equations and modeled using the redundant coordinate approach form a set of n ordinary differential equations that involve \(n + n_c\) unknown quantities represented by the generalized coordinate vector \(\mathbf{q}\) as well as the vectors of Lagrange multipliers \(\varvec{{\lambda }} _f\), \(\varvec{{\lambda }} _g\), and \(\varvec{{\lambda }} _h\). Therefore, it is apparent that the \(n_c\) algebraic equations that model the holonomic and nonholonomic constraints given by Eqs. (2), (3), and (4) are necessary for closing this mathematical problem. Considering the coupling between the differential equations of motion and the algebraic constraint equations, one can write the following system of DAEs which describe the dynamic behavior of a mechanical system constrained by a general set of algebraic constraints:
where the following general set of the initial conditions is assumed:
The set of DAEs that form the dynamic equations (10) together with the corresponding set of the initial conditions (11) constitute the general form of the fundamental problem of constrained motion [46].
2.2 Central equations of constrained motion
In this subsection, the principal aspects of the analytical formulation of the central equations of constrained motion are presented. The central equations of constrained dynamics allow for obtaining an analytical solution to the fundamental problem of constrained motion (10). These equations are also called Udwadia–Kalaba equations since Udwadia and Kalaba originally solved the fundamental problem of constrained motion employing the Gauss principle of least constraint in conjunction with advanced linear algebra techniques [47]. According to the Gauss principle of least constraint, the motion of a mechanical system constrained by algebraic equations occurs at each instant of time following a trajectory that corresponds to the minimum deviation between the generalized acceleration vector of the constrained system and the generalized acceleration vector of the unconstrained system [48]. In the case of both unconstrained and constrained mechanical systems, it can be proved that the Gauss principle of least constraint is one of the basic principles of classical mechanics that is fully equivalent to the well-known D’Alembert–Lagrange principle of virtual work combined with the Lagrange multiplier techniques [49]. As shown in this section, the Udwadia–Kalaba equations are obtained starting from the Gauss principle of least constraint and make use of the mathematical concept borrowed from the numerical linear algebra called the Moore–Penrose pseudoinverse matrix [50]. In particular, the solution of the fundamental problem of constrained dynamics based on the Uwdadia–Kalaba equations leads to the central equations of constrained dynamics and allows for explicitly calculating in a closed form the generalized acceleration vector \({\ddot{\mathbf{q}}}\) and the vector of Lagrange multipliers \(\varvec{\lambda }\) of a mechanical system constrained by a general set of holonomic and/or nonholonomic constraints [51]. Without loss of generality, this method is based on the assumption that the acceleration nonholonomic constraints are nonlinear functions of the generalized coordinate and velocity vectors \(\mathbf{q}\) and \({\dot{\mathbf{q}}}\) but, at the same time, linear functions of the generalized acceleration vector \({\ddot{\mathbf{q}}}\). Considering this fundamental hypothesis, one can rewrite the general form of the acceleration nonholonomic constraint equations \(\mathbf{h}\) as follows:
where \({\mathbf{A}_h} \equiv {\mathbf{A}_h}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a \({n_h} \times n\) constraint Jacobian matrix and \({\mathbf{b}_h} \equiv {\mathbf{b}_h}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a constraint quadratic velocity vector of dimension \({n_h}\) both associated with the acceleration nonholonomic constraint equations. On the other hand, in order to be able to write the general form of the central equations of constrained dynamics, one needs to express the holonomic constraint defined at the position level given by Eq. (2) and the nonholonomic constraints defined at the velocity level given by Eq. (3) in a standard form expressed at the acceleration level that corresponds to the index-one form of the differential-algebraic equations of motion of the mechanical system. To this end, the computation of the second time derivative of the holonomic constraint equations (2) leads to:
where \({\mathbf{A}_f} \equiv {\mathbf{A}_f}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a \({n_f} \times n\) constraint Jacobian matrix and \({\mathbf{b}_f} \equiv {\mathbf{b}_f}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a constraint quadratic velocity vector of dimension \({n_f}\) both associated with the holonomic constraint equations that are, respectively, given by:
where the partial derivatives that appear in the previous equation are, respectively, defined as \({\left( {{\mathbf{f}_\mathbf{q}}{\dot{\mathbf{q}}}} \right) _\mathbf{q}} = \frac{{\partial \left( {{\mathbf{f}_\mathbf{q}}{\dot{\mathbf{q}}}} \right) }}{{\partial \mathbf{q}}}\), \({\mathbf{f}_{\mathbf{q}t}} = \frac{{{\partial ^2}{} \mathbf{f}}}{{\partial \mathbf{q}\partial t}}\), and \({\mathbf{f}_{tt}} = \frac{{{\partial ^2}{} \mathbf{f}}}{{\partial {t^2}}}\). Following an analogous mathematical procedure, the computation of the first time derivative of the velocity nonholonomic constraint equations (3) leads to:
where \({\mathbf{A}_g} \equiv {\mathbf{A}_g}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a \({n_g} \times n\) constraint Jacobian matrix and \({\mathbf{b}_g} \equiv {\mathbf{b}_g}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a constraint quadratic velocity vector of dimension \({n_g}\) both associated with the velocity nonholonomic constraint equations that are, respectively, defined as:
where the partial derivatives that appear in the previous equations are, respectively, given by \({\mathbf{g}_{{\dot{\mathbf{q}}}}} = \frac{{\partial \mathbf{g}}}{{\partial {\dot{\mathbf{q}}}}}\), \({\mathbf{g}_\mathbf{q}} = \frac{{\partial \mathbf{g}}}{{\partial \mathbf{q}}}\), and \({\mathbf{g}_t} = \frac{{\partial \mathbf{g}}}{{\partial t}}\). Considering the standard index-one form of the constraint equations, one obtains a set of holonomic and nonholonomic algebraic constraints that is nonlinear in terms of the generalized coordinate and velocity vectors \(\mathbf{q}\) and \({\dot{\mathbf{q}}}\) as well as linear in terms of the generalized acceleration vector \({\ddot{\mathbf{q}}}\). Therefore, one can assemble the holonomic and nonholonomic constraint equations in a compact matrix form given by:
where \(\mathbf{A} \equiv \mathbf{A}(\mathbf{q},\mathbf{q},t)\) is a \({n_c} \times n\) constraint Jacobian matrix and \(\mathbf{b} \equiv \mathbf{b}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a constraint quadratic velocity vector of dimension \({n_c}\) both associated with the holonomic and nonholonomic constraint equations that are, respectively, defined considering the following assembly of constraint matrices and vectors:
Considering the standard form of the holonomic and nonholonomic constraint equations (17), one can express the fundamental problem of constrained motion (10) in the following index-one form:
where \(\varvec{\lambda } \equiv \varvec{\lambda } (t)\) is the total vector of Lagrange multipliers associated with the holonomic and nonholonomic constraint equations that can be assembled to yield:
By doing so, one can write the total vector of constraint equations \({\mathbf{Q }_c}\) in terms of the total vector of Lagrange multipliers \({\varvec{\lambda }}\) employing the Jacobian matrix of the constraint equations \(\mathbf{A}\) as follows:
One can demonstrate that the Udwadia–Kalaba equations represent the analytical solution of the fundamental problem of constrained motion written in the standard index-one form (19). The analytical solution of the mathematical problem given by Eq. (19) is also referred to as the central equations of constrained dynamics [52]. The Udwadia–Kalaba equations lead to the following closed-form solution for the generalized acceleration vector \({{\ddot{\mathbf{q}}}}\) and for the vector of the Lagrange multipliers \({\varvec{\lambda }}\) associated with a mechanical system constrained by a general set of holonomic and nonholonomic constraints:
where \({\mathbf{a}_b} \equiv {\mathbf{a}_b}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a vector of dimension n that represents the generalized acceleration of the mechanical system in the absence of constraint equations, \({\mathbf{a}_c} \equiv {\mathbf{a}_c}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a vector of dimension n that represents the generalized acceleration of the mechanical system induced by the presence of holonomic and/or nonholonomic constraint equations, \(\mathbf{F} \equiv \mathbf{F}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a \({n_c} \times {n_c}\) matrix referred to as the constraint feedback matrix which models the effect of the holonomic and/or nonholonomic constraints as a nonlinear feedback force field, and \(\mathbf{e} \equiv \mathbf{e}(\mathbf{q},{\dot{\mathbf{q}}},t)\) is an acceleration error vector of dimension \(n_c\) which quantifies the violation of the constraint equations at the acceleration level obtained considering the generalized acceleration vector in the absence of constraint equations. The physical interpretation of these matrix and vector quantities can be described as follows. The generalized acceleration vector \({\mathbf{a}_b}\) is referred to as the unconstrained generalized acceleration vector since it represents the generalized acceleration vector obtained in the absence of algebraic constraints. Without loss of generality, one can assume that the system mass matrix has a full rank \(\mathrm{{rank}}(\mathbf{M}) = n\) [53]. Therefore, the unconstrained generalized acceleration vector \({\mathbf{a}_b}\) can be easily calculated as follows:
The acceleration error vector \(\mathbf{e}\), on the other hand, can be simply obtained by introducing the unconstrained generalized acceleration vector \({\mathbf{a}_b}\) into the constraint equations defined at the acceleration level as follows:
Thus, the acceleration error vector \(\mathbf{e}\) analytically quantifies the deviation between the ideal unconstrained generalized acceleration vector \({\mathbf{a}_b}\) and the actual constrained generalized acceleration vector \({{\ddot{\mathbf{q}}}}\). As mentioned before, the constraint feedback matrix \(\mathbf{F}\) is a nonlinear matrix function that allows for writing the vector of Lagrange multipliers \({\varvec{\lambda }}\) as the matrix product of the constraint feedback matrix \(\mathbf{F}\) and the acceleration error vector \(\mathbf{e}\). It can be demonstrated that the constraint feedback matrix \(\mathbf{F}\) can be explicitly computed in the following manner:
where \(\mathbf{K } \equiv \mathbf{K }(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a \({n_c} \times {n_c}\) matrix which defines the structure of mechanical system constrained by the holonomic and/or nonholonomic algebraic constraints and \({\mathbf{K }^ + }\) indicates the Moore–Penrose pseudoinverse matrix of the matrix \(\mathbf{K }\) [54]. In particular, the matrix \(\mathbf{K }\) is referred to as the kinetic matrix corresponding to the constrained mechanical system. In fact, one can simply observe that the essence of the dynamic behavior of the constrained mechanical system under consideration is embedded in the kinetic matrix \(\mathbf{K }\). On the other hand, in the computation of the constraint feedback matrix \(\mathbf{F}\), it is important to note that the Moore–Penrose pseudoinverse matrix coincides with the regular inverse when there are no kinetic singularities as well as no redundant constraints equations. Therefore, in this case the rank of the kinetic matrix is full and is given by \(\mathrm{{rank}}(\mathbf{K }) = {n_c}\). This is the case when both the mass matrix and the Jacobian matrix have full rank, namely \(\mathrm{{rank}}(\mathbf{M}) = n\) and \(\mathrm{{rank}}(\mathbf{A}) = {n_c}\). Moreover, the constraint feedback matrix \(\mathbf{F}\) allows for expressing the constraint generalized force vector \({\mathbf{Q }_c}\) in the following analytical form:
Consequently, the generalized acceleration vector induced by the presence of the algebraic constraints \({\mathbf{a}_c}\) can be readily obtained as:
The explicit calculation of the generalized constraint forces \({\mathbf{Q }_c}\) and the generalized acceleration vector relative to the algebraic constraints \({\mathbf{a}_c}\) represents the most important analytical results obtained considering the central equations of constrained dynamics (22) associated with the fundamental problem of constrained motion (19).
2.3 Udwadia–Kalaba equations for solving forward and inverse dynamic problems
In this subsection, the use of the Udwadia–Kalaba approach to the solution of the forward and inverse dynamic problems for fully actuated mechanical systems is described. As discussed in this section, the central equations of constrained dynamics are an effective method for calculating the generalized acceleration vector of a mechanical system constrained by a general set of holonomic and/or nonholonomic algebraic equations and, at the same time, the corresponding constraint generalized force vector. To this end, Eqs. (22) and (26) can be used. In particular, one can define the following block matrix:
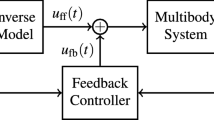
where \(\mathbf{C } \equiv \mathbf{C }(\mathbf{q},{\dot{\mathbf{q}}},t)\) is a \((n + {n_c}) \times n\) matrix that is referred to as constraint control matrix. One can demonstrate that a necessary and sufficient condition for obtaining in a closed form the analytical solution provided by the Udwadia–Kalaba equations is that the constraint control matrix \(\mathbf{C}\) must have a full rank [55]. For a mechanical system, the forward dynamic problem consists in calculating the motion of the components that form the mechanical system starting from the initial conditions of the system state and assuming the external forces as known data [56]. However, in forward dynamic problems, the constraint forces are additional unknowns. By using the central equations of constrained dynamics (22), one can obtain in a closed form the system generalized acceleration vector and the generalized force vector associated with the algebraic constraints. By doing so, one can transform the equations of motion of a constrained mechanical system associated with the forward dynamic problem from a set of DAEs into a set of ODEs. On the other hand, the inverse dynamic problem associated with a mechanical system consists in determining the additional external forces and moments that serve as control actions in order to force the mechanical system to follow an assigned trajectory starting from a known set of initial conditions and considering as known physical quantities also the external forces applied to the dynamical system [57]. For this purpose, the Udwadia–Kalaba equations can still be employed by devising a virtual set of holonomic constraints as shown in the paper. Considering the central equations of constrained dynamics, one can also determine the generalized control forces that constrain the system to follow a prescribed path with an assigned time law. In particular, in the Udwadia–Kalaba approach to the inverse dynamic problems, the constrained equations do not correspond to mechanical joints acting on the dynamical system and can be assumed to be virtual constraints that must be satisfied by the dynamical evolution of the mechanical system. Therefore, the vector of generalized constrained forces can be interpreted as a vector of generalized control actions which can be effectively used in order to force the system to follow a preassigned path with a given time law. At the end of the implementation of this analytical process, one can always recover the control forces and moments that serve as the actual control inputs starting from the generalized constraint control force vector obtained employing the Udwadia–Kalaba inverse dynamic method. The implementation of this important analytical method is discussed in detail in the paper.
2.4 Underactuation nonholonomic constraints
In this subsection, a general and effective method for explicitly determining the set of nonholonomic constraint equations defined at the acceleration level and associated with the underactuation property of a general mechanical system is presented. In particular, the use of the Underactuation Equivalence Principle for extending the Udwadia–Kalaba nonlinear control method from fully actuated dynamical systems to underactuated mechanical system is described in detail in this subsection. By doing so, the application of the Udwadia–Kalaba approach to the solution of the inverse dynamic problems for underactuated mechanical systems is illustrated. As discussed in this subsection, the Udwadia–Kalaba equations can be effectively used for solving both forward and inverse dynamic problems associated with nonlinear mechanical systems constrained by holonomic and/or nonholonomic constraints. For this purpose, consider the following analytic form of the equations of motion:
where \({\mathbf{B }_u} \equiv {\mathbf{B }_u}(\mathbf{q},t)\) is a \(n \times {n_u}\) influence matrix associated with the control inputs and \(\mathbf{u} \equiv \mathbf{u}(t)\) is the vector of control actions having dimension \(n_u\). In particular, the transpose of the input influence matrix \({\mathbf{B }_u}\) has dimensions \({n_u} \times n\) and is denoted with \(\mathbf{B }_u^\mathrm{T}\). In order to obtain the nonholonomic constraint equations at the acceleration level that mathematically describe the underactuation property of the mechanical system of interest, the null space of the matrix \(\mathbf{B }_u^\mathrm{T}\) can be employed for eliminating from the equations of motion the terms associated with the generalized force vector of control actions \({\mathbf{Q }_u} = {\mathbf{B }_u}{} \mathbf{u}\). For this purpose, one can write:
where \({\mathbf{N }_u} \equiv {\mathbf{N }_u}(\mathbf{q},t)\) is a \(n \times {m_u}\) matrix that defines the kernel of the matrix \(\mathbf{B }_u^\mathrm{T}\) and the scalar quantity \({m_u} = n - {n_u}\) identifies the degree of underactuation of the mechanical system under examination. Since the columns of the matrix \({\mathbf{N }_u}\) span the null space of the matrix \(\mathbf{B }_u^\mathrm{T}\), one can write:
where \({\mathbf{O}_{\left[ {{n_u} \times {m_u}} \right] }}\) and \({\mathbf{O}_{\left[ {{m_u} \times {n_u}} \right] }}\) represent zero matrices having dimensions \({n_u} \times {m_u}\) and \({m_u} \times {n_u}\), respectively. It follows that:
where \({\mathbf{0 }_{\left[ {{m_u}} \right] }}\) denotes a zero vector of dimension \({m_u}\). Consequently, the general form of the nonholonomic constraint equations defined at the acceleration level and associated with the underactuated structure of the dynamical system at hand can be readily obtained by multiplying the system equations of motion by the transpose of the kernel matrix \({\mathbf{N }_u}\). Thus, one can write:
which leads to:
where \({\mathbf{A}_h} \equiv {\mathbf{A}_h}(\mathbf{q},{\dot{\mathbf{q}}},t)\) and \({\mathbf{b}_h} \equiv {\mathbf{b}_h}(\mathbf{q},{\dot{\mathbf{q}}},t)\) are matrix and vector quantities, respectively, of dimensions \({m_u} \times n\) and \({m_u}\) that define the structure of the nonholonomic constraint vector \(\mathbf{h}\) representing the underactuation property of the mechanical system. These matrix and vector quantities are, respectively, given by:
Considering the definition of the underactuation nonholonomic constraints based on the null space approach, one obtains:
and
where:
and
It is, therefore, apparent that the underactuation nonholonomic constraint equations lead to an constraint generalized force vector that is identically equal to the zero vector, which is consistent with the Underactuation Equivalence Principle [58,59,60,61]. By using the analytical approach developed in this subsection, one can systematically formulate the acceleration-level nonholonomic constraint equations associated with an underactuated mechanical system mathematically described by a nonlinear set of ordinary differential equations.
3 Numerical results and discussion
In this section, a simple case study is analyzed in order to demonstrate the effectiveness of the control method based on the inverse dynamic approach developed in the paper. The case study considered herein as the demonstrative example is an unicycle-like mobile robot. First, a description of the demonstrative example is provided in this section. Then, the equations of motion and the generalized constraint forces associated with the nonholonomic constraints of the unicycle-like mobile robot are symbolically derived by using the analytical methods of classical mechanics and the fundamental equations of constrained motion. Subsequently, a general parametric form of the path of the unicycle-like mobile robot is designed and the tracking problem associated with the desired time law is solved employing the Udwadia–Kalaba method. Finally, a set of dynamical simulations is performed in the MATLAB computational environment for verifying the effectiveness of the tracking controller designed by using the methodological approach developed in the paper. To this end, the numerical results obtained by means of numerical experiments are discussed.
3.1 Description of the demonstrative example
In this subsection, a description of the case study considered as a demonstrative example is reported. The system under study is a wheeled mobile robot shown in Fig. 1. Assuming that the wheeled robot is a rigid body, this planar mechanical system can be modeled as a unicycle-like mobile robot having \(n = 3\) degrees of freedom subjected only to \(n_{c,r} = 1\) nonholonomic constraint equation. The nonholonomic constraint considered for the mobile robot is the pure rolling condition which does not restrict the configuration space of the mechanical system. In particular, one can assume as the translational generalized coordinates of the mobile robot the abscissa and the ordinate of the robot center of mass G, which are, respectively, denoted with \(x \equiv x(t)\) and \(y \equiv y(t)\) and are measured with respect to an inertial frame of reference, whereas the orientation angle relative to the robot sagittal plane denoted with \(\theta \equiv \theta (t)\) and measured with respect to the horizontal axis of the global reference frame can be used as the rotational generalized coordinate of the mobile robot. As shown in Fig. 1, the radius of the wheels the robot is denoted with R, while L and H denote, respectively, half the length of the axle track and half the width of the robot chassis. The mass of the robot is denoted with m and its moment of inertia relative to the axis passing through its center of mass G and orthogonal to the plane of the chassis is denoted with \({I_{zz}}\). Furthermore, in order to take into account the dissipative phenomena which occur during the motion of the wheeled robot, a linear dissipative force field characterized by a viscous damping coefficient \(\sigma \) is considered in the dynamical model of the mechanical system. Additionally, in order to consistently perform the dynamic analysis, the time evolution of the mobile robot is calculated starting from a set of initial conditions, respectively, given by:
where \({x_0}\) is the initial horizontal displacement, \({y_0}\) is the initial vertical displacement, \({\theta _0}\) is the initial angular displacement, \({u_0}\) is the initial horizontal velocity, \({v_0}\) is the initial vertical velocity, and \({\omega _0}\) is the initial angular velocity. The numerical data used for the parameters that describe the mechanical model of the unicycle-like mobile robot are reported in Table 1.
3.2 Derivation of the equations of motion
In this subsection, the equations of motion of the unicycle-like mobile robot are analytically derived by using the methods of classical mechanics. As mentioned before, the geometric configuration of this mechanical system is completely described by a set of \(n = 3\) independent parameters. To this end, the generalized coordinates of the mobile robot can be grouped into a configuration vector denoted with \(\mathbf{q} \equiv \mathbf{q}(t)\) and given by:
By using the methods of analytical mechanics such as, for example, the D’Alembert–Lagrange principle of virtual work [62], one can readily obtain the equations of motion of the mobile robot written in a compact matrix form as follows:
where \(\mathbf{M} \equiv \mathbf{M}(\mathbf{q},t)\) represents the system mass matrix and \({\mathbf{Q }_\sigma } \equiv {\mathbf{Q }_\sigma }({\dot{\mathbf{q}}},t)\) denotes the generalized force vector associated with the dissipative terms acting on the mechanical system. For the unicycle-like mobile robot used as a demonstrative example, these vector and matrix quantities can be, respectively, expressed as follows:
The system equations of motion given by Eq. (42) represent a set of \(n = 3\) ordinary differential equations which requires a set of \(2n = 6\) initial conditions which are, respectively, denoted in a matrix form as \(\mathbf{q}(0) = {\mathbf{q}_0}\) and \({\dot{\mathbf{q}}}(0) = {\mathbf{p}_0}\). The set of initial conditions for the unicycle-like mobile robot can be explicitly written as:
For the forward and inverse dynamic problem under study, the initial conditions (44) are assumed as a set of input data. However, it is important to note that, when a tracking controller is applied on the dynamic model of the unicycle-like mobile robot, the initial conditions must be consistent with the path and the time law imposed on the mechanical system.
3.3 Enforcement of the pure rolling constraint
In this subsection, the generalized force vector that describes the action of the pure rolling nonholonomic constraint on the unicycle-like mobile robot is analytically derived employing the Udwadia–Kalaba approach. To this end, one can assume that the dynamic model of the unicycle-like mobile robot is subjected to the pure rolling constraint which can be mathematically modeled considering a single nonholonomic algebraic constraint equation. In particular, when the pure rolling constraint is imposed on the mechanical system, an additional vector of generalized forces appears in the formulation of the equations of motion. This generalized force vector is denoted with \({\mathbf{Q }_r} \equiv {\mathbf{Q }_r}(\mathbf{q},{\dot{\mathbf{q}}},t)\) and is necessary for forcing the mobile robot to satisfy the nonholonomic constraint equation. Considering the effect of the nonholonomic constraint equation that describes the pure rolling condition, the system equations of motion assume the following mathematical form:
where the generalized constraint force vector \({\mathbf{Q }_r}\) associated with the pure rolling constraint can be explicitly calculated by using the central equations of constrained dynamics and considering the nonholonomic constraint equation which represents the pure rolling condition of the wheeled robot. The pure rolling constraint is a nonholonomic constraint equation defined at the velocity level which is identified by the scalar function \({g_r} \equiv {g_r}(\mathbf{q},{\dot{\mathbf{q}}},t)\). The scalar function \({g_r}\) is used in order to mathematically represent the physical property that the velocity vector \({\mathbf{v }_G}\) relative to the center of mass G of the mobile robot must be parallel to the sagittal plane of the mechanical system. Consequently, the pure rolling constraint condition can be represented using the following algebraic equation:
where the constraint function \({g_r}\) is explicitly defined as:
where \({\mathbf{v }_G}\) is the absolute velocity of the robot center of mass and \(\mathbf{j}\) is the unit vector associated with the vertical axis of the body-fixed reference frame expressed with respect to the global reference system that are, respectively, given by:
In order to be able to use the fundamental equations of constrained motion given by Eq. (22), the nonholonomic constraint equation relative to the pure rolling condition (46) must be represented in the standard form described by Eq. (17). In order to achieve this goal, one can readily compute the time derivative of the pure rolling constraint to yield:
where \({\mathbf{A}_r} \equiv {\mathbf{A}_r}(\mathbf{q},t)\) and \({\mathbf{b}_r} \equiv {\mathbf{b}_r}(\mathbf{q},{\dot{\mathbf{q}}},t)\), respectively, represent the constraint matrix and the constraint vector corresponding to the pure rolling condition which can be readily obtained by computing the time derivative of the constraint Eq. (46). These matrix and vector quantities are defined as:
Since system mass matrix has a full rank \(\mathrm{{rank}}(\mathbf{M}) = 3\) and the rank of the constraint matrix \(\mathrm{{rank}}({\mathbf{A}_r}) = 1\) is equal to the number of the constraint equations representing the pure rolling \({n_{c,r}} = 1\), the generalized constraint force vector \({\mathbf{Q }_r}\) which satisfies the pure rolling condition can be explicitly computed by using Eq. (26) to yield:
The generalized force vector \({\mathbf{Q }_r}\) is a vector of generalized constraint forces which identifies the force fields generated by the nonholonomic constraint equation of the pure rolling condition given by Eq. (46). Since in this process the constraint force vector \({\mathbf{Q }_r}\) has been explicitly determined employing the central equations of constrained dynamics and, on the other hand, it is well-known that the drift of the algebraic equations at the velocity level is of minor entity, the system equations of motion associated with the unicycle-like mobile robot can be directly solved by using an explicit numerical integration method without considering the algebraic constraint equation corresponding to the pure rolling condition [63, 64]. Therefore, the method based on the Udwadia–Kalaba equations allows for transforming the equations of motion of a mechanical system subjected to a set of nonholonomic constraints from a nonlinear set of DAEs to a nonlinear system of ODEs.
3.4 Motion planning
In this subsection, a general trajectory for the configuration vector of the unicycle-like mobile robot is designed in a parametric form by solving a simple motion planning problem. In general, the motion planning represents an important problem associated with the nonlinear control problem of mechanical systems. In the case of mobile robots, the problem of motion planning is also referred to as the navigation problem and is represented by the process of generating the desired motion subdividing the autonomous navigation problem into simple separate tasks, thereby obtaining the desired state trajectory by also avoiding the contact between the mobile robot and the obstacles found in the external environment. To this end, the motion planning problem for the unicycle-like mobile robot consists of designing a trajectory which satisfies the pure rolling constraint and, if necessary, a set of boundary conditions. Employing a parametric approach, this challenging problem can be subdivided into two independent subproblems: (a) the design of an appropriate path \(\mathbf{r} \equiv \mathbf{r}(s)\) and (b) the design of an adequate time law \(s \equiv s(t)\) associated with the desired path. In particular, the time law s can be analytically derived by calculating the arc length parameter along the path \(\mathbf{r}\). However, since it is well-known that only in few cases the calculation of the arc length parameter s provides a closed-form formula for the solution of the line integral, the path \(\mathbf{r}\) can be more conveniently redefined using another parametric representation \(\mathbf{r} \equiv \mathbf{r}(\gamma )\) based on the curve parameter \(\gamma \equiv \gamma (t)\) which represents a general dimensionless parameter. Furthermore, the parameter \(\gamma \) can be assumed to be an arbitrary function of time t in order to identify the time evolution of a generic point P on the parametric curve \(\mathbf{r}\) and, therefore, it serves for defining the desired time law. On the other hand, one can always recover the arc length parameter s from the analytical representation of the parametric curve \(\mathbf{r}\) defined in terms of the dimensionless parameter \(\gamma \). For this purpose, in a two-dimensional space, the arc length parameter s can be computed using the parametric representation of the curve considered as follows:
where \(\xi \equiv \xi (\gamma )\) and \(\eta \equiv \eta (\gamma )\), respectively, denote the abscissa and the ordinate of a generic point on the parametric path \(\mathbf{r}\) identified by the parameter \(\gamma \) and the prime symbol stands for the derivative of the scalar terms computed with respect to the parameter \(\gamma \), respectively, given by \(\xi ' = {{d\xi } / {d\gamma }}\) and \(\eta ' = {{d\eta } / {d\gamma }}\). Thus, one can explicitly write:
It is important to note that, while the desired path \(\mathbf{r}\) must satisfy the constraint equations imposed on the mechanical system, including the pure rolling nonholonomic constraint (46) and, if needed, some boundary conditions that serve to better define the geometric shape of the path, the curve parameter \(\gamma \) associated with the time law can be designed as an arbitrary function of time which requires to satisfy only the given initial conditions (44). For the problem at hand, an effective method suitable for the design of the path \(\mathbf{r}\) in a general parametric form can be employed considering the following analytical steps. First, a continuous path \(\mathbf{r}\) composed of the parametric functions \(\xi \) and \(\eta \) is selected for the center of mass G of the mobile robot. By doing so, the first and the second time derivatives of the parametric path (53) can be readily calculated considering a general expression of the curve parameter \(\gamma \) associated with the time law to yield:
where the second derivatives with respect to the curve parameter are, respectively, defined as \(\xi '' = {{{d^2}\xi } / {d{\gamma ^2}}}\) and \(\eta '' = {{{d^2}\eta } / {d{\gamma ^2}}}\). Subsequently, when the pure rolling nonholonomic constraint (46) is applied on the mechanical system, the imposition of the designed path \(\mathbf{r}\) automatically forces the orientation angle of the mobile robot to follow a prescribed law defined as \(\varphi \equiv \varphi (\gamma )\). The definition of the prescribed law \(\varphi \) for the orientation angle keeps the consistency between the pure rolling nonholonomic constraint and the desired path designed in the process of the motion planning. Therefore, the prescribed parametric representation of the orientation angle \(\varphi \) of the mobile robot can be indirectly derived from the pure rolling nonholonomic constraint equation (46) to yield:
where \(\mathbf{t} \equiv \mathbf{t}(\gamma )\) is a unit vector that is tangent to the curve vector \(\mathbf{r}\). Using this analytical approach, the prescribed representation of the path (53) and of the orientation angle (55) both designed in a parametric form are consistent with the pure rolling nonholonomic constraint (46). Furthermore, one can easily compute the first and the second time derivatives of the prescribed orientation parameter \(\varphi \) for the mobile robot as follows:
and
It is worth to note that the second time derivatives (54) and (57) of the prescribed path \({{\ddot{\mathbf{r}}}}\) and orientation parameter \({\ddot{\varphi }}\) are necessary for calculating the control actions which force the mobile robot to follow the designed path \(\mathbf{r}\) in conjunction with the scalar function \(\gamma \) that serves as a time law without violating the nonholonomic constraint equation associated with the pure rolling condition (46).
3.5 Tracking controller design
In this subsection, a nonlinear controller capable of tracking the path and the time law devised in the design phase for the motion planning is developed. To this end, the underactuated structure of the unicycle-like mobile robot is considered. The unicycle-like mobile robot is controlled using two motors which provide the control torques \({u_1} \equiv {u_1}(t)\) and \({u_2} \equiv {u_2}(t)\) applied, respectively, on the right and left wheels. In the equations of motion, the introduction of the control inputs \({u_1}\) and \({u_2}\) produces a generalized force vector denoted with \({\mathbf{Q }_u} \equiv {\mathbf{Q }_u}(\mathbf{q},t)\) corresponding to the external control actions. Therefore, the matrix form of the system equations of motion becomes:
where the generalized force vector \({\mathbf{Q }_u}\) relative to the external control actions can be readily obtained employing the D’Alembert–Lagrange principle of virtual work and considering the underactuated structure of the wheeled robot as follows:
where \({\mathbf{B }_{u}} \equiv {\mathbf{B }_{u}}(\mathbf{q},t)\) is an input influence matrix of dimensions \({n \times {n_u}}\) and \(\mathbf{u} \equiv \mathbf{u}(t)\) is a control input vector of dimension \({n_u}=2\) which are, respectively, defined as:
It is apparent that the system under study is an underactuated mechanical system because the rank of the input influence matrix \(\mathrm{{rank}}({\mathbf{B }_{u}}) = 2\) is lower than the number of system degrees of freedom \(n = 3\). In order to obtain a more convenient representation of the generalized force vector \({\mathbf{Q }_u}\) associated with the external control actions \(\mathbf{u}\), the following linear transformation of variables can be applied:
where \({v_1} \equiv {v_1}(t)\) and \({v_2} \equiv {v_2}(t)\) are two new control inputs which, respectively, represent a generalized force acting on the robot center of mass G collocated along its sagittal plane and a generalized moment applied at the robot center of mass G and acting orthogonally to the robot axles, while \(\mathbf{v } \equiv \mathbf{v }(t)\) is a new input vector and \({\mathbf{B }_{v,u}}\) is a constant transformation matrix which are, respectively, given by:
By using the transformation of the control variables, the generalized vector relative to the control actions \({\mathbf{Q }_u}\) can be easily rewritten as follows:
Furthermore, considering the definition of the new vector of control inputs \(\mathbf{v }\), the generalized vector associated with the external control actions \({\mathbf{Q }_u}\) can be expressed as a linear function of the vector of control inputs \(\mathbf{v }\) as follows:
where \({\mathbf{B }_{v}} \equiv {\mathbf{B }_{v}}(\mathbf{q},t)\) is a new input influence matrix of dimensions \({n \times {n_u}}\). On the other hand, one can readily write the inverse relationship between the old input vector \(\mathbf{u}\) and the new input vector \(\mathbf{v }\) as:
where \({\mathbf{B }_{u,v}}\) is a constant transformation matrix given by:
The alternative representation of the generalized force vector associated with the control actions \({\mathbf{Q }_u}\) in terms of the new vector of control inputs \(\mathbf{v }\) allows for obtaining a straightforward formulation of the underactuation requirement as a nonholonomic constraint equation at the acceleration level considering the Underactuation Equivalence Principle. To this end, the nonholonomic constraint equation associated with the underactuated structure of the mobile robot can be written in terms of system generalized coordinates as follows:
where the scalar function \({h_t} \equiv {h_t}(\mathbf{q},{\dot{\mathbf{q}}},{\ddot{\mathbf{q}}},t)\) represents a constraint function formulated at the acceleration level which can be analytically obtained considering the structure of the equations of motion of the unicycle-like mobile robot as follows:
where \({\mathbf{Q }_b} \equiv {\mathbf{Q }_b}(\mathbf{q},{\dot{\mathbf{q}}},t)\) denotes the total generalized force vector applied on the mobile robot defined as:
Equation (68) yields the following nonholonomic constraint equation formulated at the acceleration level:
This algebraic equation is a nonholonomic constraint equation which is linear in the generalized accelerations, involves all the system generalized coordinates, and reproduces the underactuation requirement expressed in a dynamic form.
An alternative procedure for obtaining the nonholonomic constraint equation defined at the acceleration level that represents the underactuation property of the unicycle-like mobile robot given by Eq. (70) is based on the use of the null space method. In this case, one can readily compute the degree of underactuation of the mobile robot as \({m_u} = n - {n_u} = 3 - 2 = 1\). Furthermore, in order to use this alternative approach, one can write the transpose of the actuator influence matrix \({\mathbf{B }_u}\) as follows:
It can be easily proved that:
where \({\mathbf{n}_u} \equiv {\mathbf{n}_u}(\mathbf{q},t)\) is a vector of dimension n associated with the kernel of the matrix \(\mathbf{B }_u^\mathrm{T}\). In fact, one can readily verify that:
or
By using the analytical method based on the null space approach, the following equivalent form of the nonholonomic constraint equation relative to the underactuation requirement of the unicycle-like mobile robot can be obtained:
where it is apparent that Eq. (75) is equivalent to Eq. (70).
In order to design a tracking controller consistent with the underactuation nonholonomic constraint by using the fundamental equations of constrained dynamics, the desired trajectory for the mobile robot must be imposed on the mechanical system as a set of holonomic constraint equations given by:
where the vector function associated with the holonomic constraints denoted with \({\mathbf{f}_t} \equiv {\mathbf{f}_t}(\mathbf{q},t)\) is defined as:
where \(\xi \) and \(\varphi \) represent the prescribed laws, respectively, defined for the abscissa of the center of mass G and for the orientation angle of the mobile robot which were designed in the phase of the motion planning considering Eqs. (53) and (55). In order to use the analytical results arising from the central equations of constrained motion given by Eqs. (22) and (26) for deriving the tracking controller, the nonholonomic constraint equation for the underactuation requirement (67) and the holonomic constraint equations associated with the prescribed trajectory (76) must be represented in the standard matrix form as follows:
where \({\mathbf{A}_t} \equiv {\mathbf{A}_t}(\mathbf{q},t)\) and \({\mathbf{b}_t} \equiv {\mathbf{b}_t}(\mathbf{q},{\dot{\mathbf{q}}},t)\), respectively, represent the constraint matrix and the constraint vector corresponding to the underactuation constraint combined with the desired trajectory which can be readily obtained by calculating the second time derivative of the holonomic constraint equations defined by Eq. (76). By doing so, one obtains:
and
Since system mass matrix has full rank \(\mathrm{{rank}}(\mathbf{M}) = 3\) and the rank of the constraint matrix \(\mathrm{{rank}}({\mathbf{A}_t}) = 3\) is equal to the number of constraint equations representing the underactuation constraint as well as the prescribed trajectory \({n_{c,t}} = 3\), the generalized force vector associated with the control action \({\mathbf{Q }_t}\) which satisfies the imposed holonomic and nonholonomic constraints can be explicitly computed by using Eq. (26) to yield:
or equivalently:
where, as expected, \({a_{1,t}} \equiv {a_{1,t}}(\mathbf{q},{\dot{\mathbf{q}}},t)\) and \({a_{2,t}} \equiv {a_{2,t}}(\mathbf{q},{\dot{\mathbf{q}}},t)\) represent the two effective control actions applied to the unicycle-like mobile robot that results from the imposition of the prescribed trajectory constraints combined with the underactuation nonholonomic constraint. The tracking control actions \(a_{1,t}\) and \(a_{2,t}\) are, respectively, given by:
It is noteworthy to emphasize the point that the structure of the underactuation constraint equation given by Eq. (67) prevents to impose directly as the trajectory constraints the abscissa \(\xi \) and, at the same time, the ordinate \(\eta \) of the system center of mass G otherwise the constraint matrix given by Eq. (79) would not have a full rank. On the other hand, an arbitrary trajectory can still be imposed indirectly to the mobile robot by setting a prescribed abscissa \(\xi \), or a prescribed ordinate \(\eta \), and a prescribed orientation angle \(\varphi \) as the holonomic constraint equations associated with the prescribed trajectory. In order to obtain the control inputs associated with the nonlinear tracking controller given by Eq. (81), one can write:
where \({\mathbf{v }_t} \equiv {\mathbf{v }_t}(\mathbf{q},{\dot{\mathbf{q}}},t)\) represents the vector of control inputs associated with the tracking controller. By doing so, the generalized control inputs \({v_{1,t}} \equiv {v_{1,t}}(\mathbf{q},{\dot{\mathbf{q}}},t)\) and \({v_{2,t}} \equiv {v_{2,t}}(\mathbf{q},{\dot{\mathbf{q}}},t)\) that form the control vector \({\mathbf{v }_t}\) corresponding to the nonlinear tracking controller defined by Eq. (81) can be readily obtained as follows:
or equivalently:
As mentioned before, the actual control torques \({u_{1,t}} \equiv {u_{1,t}}(\mathbf{q},{\dot{\mathbf{q}}},t)\) and \({u_{2,t}} \equiv {u_{2,t}}(\mathbf{q},{\dot{\mathbf{q}}},t)\), which serve to practically implement the nonlinear tracking controller on the unicycle-like mobile robot, can be derived by using the following inverse change of variables:
or equivalently:
The analytical expressions of the control torques represent the nonlinear force fields associated with the tracking control inputs which force the mechanical system to follow an arbitrary path \(\mathbf{r}\) according to a general time law \(\gamma \) as discussed in the previous subsection.
3.6 Dynamical simulations
In this subsection, the numerical results of a set of dynamical simulations are reported in order to demonstrate the feasibility of the nonlinear control approach developed for the unicycle-like mobile robot. To this end, the effectiveness of the tracking controller given by Eq. (88) proposed in the previous subsection is verified by means of numerical experiments performed by using a MATLAB computer code developed by the authors. In particular, two different trajectories are considered in this subsection, namely an elliptical path having a linear time law and an eight-shaped path having a parabolic time law. Since the generalized force vector associated with the holonomic and nonholonomic constraints and the generalized force vector associated with the nonlinear control action can be analytically calculated as demonstrated by Eqs. (51) and (59), one can use an explicit numerical integration method in order to march forward the numerical solution of the equations of motion on the discrete time grid. For this purpose, the computational algorithm used for performing the numerical simulations is the well-known fourth-order explicit Runge–Kutta method. In the numerical integration scheme based on the Runge–Kutta algorithm, a constant time step equal to \(\varDelta t = 5 \times {10^{ - 3}}\;(\mathrm{{s}})\) is used and a time interval equal to \(T = 5\;(\mathrm{{s}})\) is considered.
In order to clarify the computer implementation of the Runge–Kutta numerical algorithm applied to the dynamic problem at hand, consider the following general structure of the equations of motion:
where \(\mathbf{M} \equiv \mathbf{M}(\mathbf{q},t)\) represents the dynamical system mass matrix and \(\mathbf{Q } \equiv \mathbf{Q }(\mathbf{q},{\dot{\mathbf{q}}},t)\) denotes the total vector of generalized forces acting on the mechanical system. If the dynamic problem is properly formulated, namely if the mass matrix \(\mathbf{M}\) has a full rank, one can readily obtain the system generalized acceleration vector \({\ddot{\mathbf{q}}}\) by solving a system of linear equations as follows:
On the other hand, one can assume the following general definition of the system state vector associated with the system state-space representation:
where \(\mathbf{z } \equiv \mathbf{z }(t)\) indicates the state vector of the mechanical system having dimension 2n. By doing so, one can transform the original system of n second-order differential equations into the following system of 2n first-order differential equations:
where \(\mathbf{N } \equiv \mathbf{N }(\mathbf{z },t)\) is a vector having dimension 2n which represents the system state function. When the classical fourth-order Runge–Kutta method with a constant step size is used for obtaining a numerical solution of the equations of motion, the time axis is discretized from the initial time \(t = 0\) to the final time \(t = T\) considering an equally spaced sequence of time instants given by:
where \(\varDelta t\) represents the constant time step used in the numerical algorithm, i is an integer number associated to the current time instant, and \(N = {T / {\varDelta t}}\) is an integer number. Similarly, the numerical solution associated with the current time instant \({t^i}\) is denoted with \({\mathbf{z }^i} \approx \mathbf{z }({t^i})\). This numerical solution can be obtained at each time step by performing a time marching starting from the given set of initial conditions \(\mathbf{z }({t^0}) = {\mathbf{z }_0}\). One can prove that the fundamental formula of the explicit fourth-order Runge–Kutta scheme can be concisely written as follows:
where \({\mathbf{z }^i}\) is the numerical solution at the current time step, \({\mathbf{z }^{i + 1}}\) denotes the numerical solution at the next time step, whereas \(\mathbf{z }_1^i\), \(\mathbf{z }_2^i\), \(\mathbf{z }_3^i\), and \(\mathbf{z }_4^i\) represent the four partial stage solutions of the Runge–Kutta method which are, respectively, defined as:
From the previous equations, it is apparent that the classical Runge–Kutta scheme requires four function calls for the computation of the numerical solution at each time step of the time grid.
The first trajectory considered in this subsection is an elliptical path having a linear time law. For simplicity, the first state trajectory is labeled with the number 1. Therefore, the path \({\mathbf{r}_1} \equiv {\mathbf{r}_1}(t)\) is an elliptical curve having an abscissa \({\xi _1} \equiv {\xi _1}({\gamma _1})\) and an ordinate \({\eta _1} \equiv {\eta _1}({\gamma _1})\) characterized by a linear time law \({\gamma _1} \equiv {\gamma _1}(t)\). The elliptical path of the first trajectory can be analytically described employing the following parametric form:
where the constant parameters that appear in Eq. (96) are, respectively, given by \({C_1} = 0\;(\mathrm{{m}})\), \({D_1} = 0\;(\mathrm{{m}})\), \({a_1} = \mathrm{{1}}\mathrm{{.5}}\;(\mathrm{{m}})\), and \({b_1} = 0.\mathrm{{5}}\;(\mathrm{{m}})\). The linear time law of the first trajectory is defined as:
where the constant parameters that appear in Eq. (97) are, respectively, given by \({\beta _1} = 2\;({\mathrm{{1}} / \mathrm{{s}}})\) and \({\delta _1} = 0\;(\mathrm{{ - }})\). The time law described by Eq. (97) is represented in Fig. 2. Furthermore, the set of initial conditions used for the first state trajectory is reported in Table 2. In Fig. 3a, the longitudinal control force associated with the first state trajectory \(v_1^1\) is shown, while the angular control moment relative to the same trajectory \(v_2^1\) is represented in Fig. 3b. Figure 3c, d, respectively, represent the right and left control actions \(u_{1}^{1}\) and \(u_{2}^{1}\) relative to the first state trajectory associated with the elliptical path and the linear time law. Figure 4a, b, respectively, represent the horizontal displacement \(x_1\) and the vertical displacement \(y_1\) of the center of mass G of the unicycle-like mobile robot resulting from the implementation of the nonlinear tracking controller associated with the first trajectory, while Fig. 4c represents the corresponding angular displacement \({\theta _1}\). Figure 4d represents the actual elliptical path followed by the mobile robot.
The second trajectory considered in this subsection is an eight-shaped path having a quadratic time law. For simplicity, the second-state trajectory is labeled with the number 2. Therefore, the path \({\mathbf{r}_2} \equiv {\mathbf{r}_2}(t)\) is an eight-shaped curve having an abscissa \({\xi _2} \equiv {\xi _2}({\gamma _2})\) and an ordinate \({\eta _2} \equiv {\eta _2}({\gamma _2})\) characterized by a quadratic time law \({\gamma _2} \equiv {\gamma _2}(t)\). The eight-shaped path of the second trajectory can be analytically described employing the following parametric form:
where the constant parameters that appear in Eq. (98) are, respectively, given by \({C_2} = 0\;(\mathrm{{m}})\), \({D_2} = 0\;(\mathrm{{m}})\), \({a_2} = 2\;(\mathrm{{m}})\), and \({b_2} = 1\;(\mathrm{{m}})\). The quadratic time law of the second trajectory is defined as:
where the constant parameters that appear in Eq. (99) are, respectively, given by \({\alpha _2} = - 0.15\;({{\mathrm{{1}} / \mathrm{{s}}}^2})\), \({\beta _2} = - 0.01\;({\mathrm{{1}} / \mathrm{{s}}})\), and \({\delta _2} = 0\;(\mathrm{{ - }})\). The time law described by Eq. (99) is represented in Fig. 5. Furthermore, the set of initial conditions used for the second-state trajectory is reported in Table 3. In Fig. 6a, the longitudinal control force associated with the second-state trajectory \(v_1^2\) is shown, while the angular control moment relative to the same trajectory \(v_2^2\) is represented in Fig. 6b. Figure 6c, d, respectively, represent the right and left control actions \(u_{1_{\phantom {\sum }}}^2\) and \(u_2^2\) relative to the second-state trajectory associated with the eight-shaped path and the quadratic time law. Figure 7a, b, respectively, represent the horizontal displacement \(x_2\) and the vertical displacement \(y_2\) of the center of mass G of the unicycle-like mobile robot resulting from the implementation of the nonlinear tracking controller associated with the second trajectory, while Fig. 7c represents the corresponding angular displacement \({\theta _2}\). Figure 7d represents the actual eight-shaped path followed by the mobile robot.
3.7 Discussion of the numerical results
In this subsection, a brief discussion on the set of numerical results found by means of numerical experiments is provided. As shown in the previous subsection, for both the state trajectories considered, the computer implementation of the proposed control laws resulting from the combination of the designed paths with the designed time laws leads to a consistent set of numerical results for the dynamic behavior of the unicycle-like mobile robot. However, because of the numerical approximations, the actual state trajectories are always affected by a small numerical error and, therefore, deviate from the desired state trajectories. In order to quantify the numerical errors that appear in the actual state trajectories when compared to the desired state trajectories, one can use the root-mean-square (RMS) deviations between these two trajectories. To this end, one can write:
where \({x_\mathrm{RMS}}\) and \({y_\mathrm{RMS}}\), respectively, denote the RMS deviation of the horizontal and vertical displacements, \({{t^n}}\) is the discrete time, x and y, respectively, identify the horizontal and vertical displacements of the robot center of mass that result from the dynamic analysis, while \(\xi \) and \(\eta \), respectively, represent the horizontal and vertical displacements of the robot center of mass that are considered in the reference trajectory. Table 4 shows the RMS deviations of the numerical solution obtained for the elliptical path combined with the linear time law, whereas Table 5 shows the RMS deviations of the numerical solution obtained for the eight-shaped path combined with the quadratic time law. The numerical data reported in Tables 4 and 5 demonstrate that only a small numerical error affects the actual state trajectories and, therefore, the numerical results found in this section are geometrically correct.
4 Summary, conclusions, and future directions of research
The focus of the research of the authors is on the development of analytical, computational, and experimental methods for the analysis and the synthesis of machines, mechanisms, and structures. For this purpose, the main research objective of the authors is to successfully carry out the dynamic analysis of multibody systems, to effectively devise control algorithms suitable for controlling nonlinear dynamical systems, and to efficiently perform the experimental identification of the structural parameters of mechanical systems [65,66,67,68,69,70]. In order to accomplish these challenging goals, the mathematical methods of three interrelated scientific disciplines are employed, namely multibody dynamics, nonlinear control, and system identification. In this paper, on the other hand, the forward and inverse dynamic problems associated with underactuated nonholonomic mechanical systems are addressed and solved in the same computational framework and employing a seamless dynamical approach. To this end, the fundamental equations of constrained motion, also known as Udwadia–Kalaba equations, are effectively used in conjunction with a new method of classical mechanics called Underactuation Equivalence Principle. As shown in this investigation, the method developed in the paper can be effectively applied to a wide category of underactuated mechanical systems that are constrained by holonomic and/or nonholonomic algebraic equations.
In analytical dynamics, a mechanical system is called nonholonomic when it is subjected to nonholonomic constraints. A set of algebraic equations involving the system generalized coordinates and their time derivatives is referred to as nonholonomic constraints when it is formulated at the velocity and/or at the acceleration levels and it is not integrable or amenable to be rewritten at the position level. Furthermore, in the field of nonlinear control, a mechanical system is said to be underactuated when the number of the effective control inputs, namely the control forces and the control moments, is lower than the number of the system degrees of freedom, which is given by the number of generalized coordinates minus the number of independent holonomic constraint equations. In general, underactuated nonholonomic mechanical systems represent a class of dynamical systems that is challenging to mathematically describe and to precisely control. The Udwadia–Kalaba equations, on the other hand, represent an effective analytical method recently discovered in the field of classical mechanics. This method is capable of deriving in a closed form the generalized accelerations of mechanical systems constrained by holonomic and/or nonholonomic constraints together with the corresponding analytical form of the generalized constraint forces. The Udwadia–Kalaba equations are also referred to as fundamental equations of constrained motion, or central equations of constrained dynamics, since they provide important mathematical results in this field. Thus, the fundamental equations of constrained dynamics represent an effective mathematical tool capable of solving the forward dynamic problem of holonomic and/or nonholonomic mechanical systems. The Udwadia–Kalaba approach can be used to predict the motion of a mechanical system governed by ordinary differential equations coupled with algebraic equations formulated at the position, velocity, and acceleration levels. As thoroughly discussed in the paper, the Udwadia–Kalaba equations can also be employed for effectively solving inverse dynamics problems, namely to find the generalized control forces and control moments that correspond to a prescribed trajectory for a given mechanical system. Following the Uwdadia–Kalaba approach to the solution of inverse dynamic problems, the constraint equations can be considered as the mathematical representation of the desired behavior of the mechanical system under study and the central equations of constrained motion can be interpreted as the closed-form solution of the inverse dynamic problem for fully actuated mechanical systems. As shown in this investigation, by introducing an additional mathematical method called Underactuation Equivalence Principle, the effectiveness of the Udwadia–Kalaba equations can be extended from fully actuated mechanical systems to underactuated mechanical systems.
While the nonlinear control problem of fully actuated multibody mechanical systems represents a relatively less complex task, the problem of the trajectory tracking for underactuated multibody mechanical systems is much more challenging and represents still an open issue. Underactuated dynamical systems are mechanical systems characterized by a set of control actions that cannot span all the system degrees of freedom. Therefore, the main idea behind the development of this paper is the application of the Underactuation Equivalence Principle to the fundamental equations of constrained motion. The Underactuation Equivalence Principle allows for mathematically representing the underactuation property of a given mechanical system as a particular set of nonholonomic constraint equations. By doing so, one can readily find a set of nonlinear control actions for an underactuated mechanical system subjected to a general system of algebraic constraints. The analytical method developed in this paper is validated by means of numerical experiments. To this end, a demonstrative example of an underactuated nonholonomic mechanical system that serves as a benchmark problem in the field of nonlinear control is employed. For this purpose, the nonlinear tracking problem corresponding to a given path and time law of a unicycle-like mobile robot is considered. The unicycle-like mobile robot is a nonlinear nonholonomic mechanical system that serves as a simple benchmark problem for testing the effectiveness of new nonlinear control algorithms. The numerical results analyzed in the paper demonstrated that the proposed method can effectively solve the forward and inverse dynamic problems for a large class of underactuated nonholonomic mechanical systems. However, for certain nonholonomic mechanical systems, there is a particular set of generalized accelerations that cannot be altered by the implementation of any vector of control inputs even employing the inverse dynamic approach developed in this paper, as will be demonstrated in future investigations.
The main contributions of this investigation can be summarized as follows. First, the general form of the equations of motion of a mechanical system subjected to an arbitrary set of constraint equations is obtained. For this purpose, holonomic as well as nonholonomic constraint equations are taken into account. The structure of the nonholonomic constraint equations considered in this work is quite general and can be expressed at both the velocity and the acceleration levels. Considering the general form of the equations of motion mentioned before, the generalized force vector associated with the algebraic constraints is explicitly obtained in the paper by using the Uwdadia–Kalaba equations, a fundamental analytical tool of classical mechanics. In particular, an alternative form of the Uwdadia–Kalaba equations suitable for modeling rigid multibody mechanical systems is employed in this investigation. Subsequently, an analytical method based on the use of the Uwdadia–Kalaba equations is employed for solving the forward and the inverse dynamic problems of nonlinear mechanical systems in the same computational framework. This method is extended from fully actuated mechanical systems to underactuated mechanical systems by introducing an analytical method called Underactuation Equivalence Principle. The basic idea behind this new method of analytical mechanics is discussed in detail in the paper. Furthermore, a computational approach based on the use of null space of the actuator influence matrix is introduced in this paper in order to obtain in a general and systematic manner the nonholonomic constraint equations associated with the Underactuation Equivalence Principle. The analytical developments presented in this investigation are verified by means of numerical experiments. In particular, the numerical example considered in the paper is a simple benchmark problem used in robotics for the developments of new nonlinear control algorithms. The benchmark problem considered in this work is the tracking control of an unicycle-like mobile robot. The unicycle-like mobile robot is a simple example of a nonlinear mechanical system subjected to a nonholonomic constraint equation represented by the pure rolling condition. Therefore, this example can effectively serve for illustrating the use of the Udwadia–Kalaba equations for solving both forward and inverse dynamic problems. The equations of motion of the unicycle-like mobile robot are analytically derived in the paper and a computational approach based on the classical explicit fourth-order Runge–Kutta method with a constant step size is developed in this investigation in order to be able to simulate the dynamic behavior of the mechanical system at hand. Finally, a general analytical approach is developed for constructing two examples of state trajectories of the unicycle-like mobile robot in which both the path and the time law of the mobile robot are specified by the user in accordance with the system initial conditions and the system nonlinear constraint equations. The numerical experiments performed in this work show that the state trajectories designed using the proposed approach are effectively imposed on the mobile robot by using the inverse dynamic method developed in the paper, thereby verifying the consistency and the effectiveness of the analytical developments carried out in this research study.
There are several viable directions of research that will be explored in future investigations. First, the effectiveness of the combined use of the Udwadia–Kalaba method with the Underactuation Equivalence Principle could be tested in the case of more complex dynamical systems such as, for example, multibody mechanical systems. Furthermore, one could try to verify the effectiveness of the proposed approach in the case of incomplete information on the system state and when the dynamical system is affected by an external source of an uncontrollable noise. For this purpose, an extended Kalman filter could be designed and used as a state observer. For a nonlinear dynamical system, the use of a state observer serves to construct an estimation of the system state necessary for the implementation of the nonlinear control law calculated by combining the Udwadia–Kalaba equations with the Underactuation Equivalence Principle. Another promising direction for future research works could be the use of the proposed method for computing a set of feedforward control actions in conjunction with a standard feedback controller designed employing, for instance, the pole placement technique or the optimal control method. To this end, the design of a feedback control action based on a linear dynamic model developed considering small perturbations of the equations of motion could improve the robustness of the solution of the inverse dynamic problem devised employing the nonlinear control method developed in the paper. Also, future research work will be devoted to the investigation of the methods mentioned before in order to improve the performance and the range of applicability of the inverse dynamic approach developed in this investigation.
References
Villecco, F., Pellegrino, A.: Evaluation of uncertainties in the design process of complex mechanical systems. Entropy 19(9), 475 (2017)
Villecco, F., Pellegrino, A.: Entropic measure of epistemic uncertainties in multibody system models by axiomatic design. Entropy 19(7), 291 (2017)
Gawronski, W.K.: Advanced Structural Dynamics and Active Control of Structures. Springer, New York (2004)
Slotine, J.J.E., Li, W.: Applied Nonlinear Control. Prentice-Hall, Englewood Cliffs, NJ (1991)
Sinha, N.K., Ananthkrishnan, N.: Elementary Flight Dynamics with an Introduction to Bifurcation and Continuation Methods. CRC Press, Boca Raton (2013)
Sinha, N.K., Ananthkrishnan, N.: Advanced Flight Dynamics with Elements of Flight Control, CRC Press, Boca Raton (2017)
Concilio, A., De Simone, M.C., Rivera, Z.B., Guida, D.: A new semi-active suspension system for racing vehicles. FME Trans. 45(4), 578–584 (2017)
Quatrano, A., De Simone, M.C., Rivera, Z.B., Guida, D.: Development and implementation of a control system for a retrofitted CNC machine by using arduino. FME Trans. 45(4), 578–584 (2017)
Sharifzadeh, M., Akbari, A., Timpone, F., Daryani, R.: Vehicle tyre/road interaction modeling and identification of its parameters using real-time trust-region methods. IFAC-PapersOnLine 49(3), 111–116 (2016)
Sharifzadeh, M., Timpone, F., Farnam, A., Senatore, A., Akbari, A.: Tyre-Road Adherence Conditions Estimation for Intelligent Vehicle Safety Applications. Advances in Italian Mechanism Science, pp. 389–398. Springer, Cham (2017)
Khalil, H.K.: Nonlinear Control. Prentice Hall, Englewood Cliffs, NJ (2014)
Sands, T.: Nonlinear-adaptive mathematical system identification. Computation 5(4), 47 (2017)
Strano, S., Terzo, M.: A SDRE-based tracking control for a hydraulic actuation system. Mech. Syst. Signal Process. 60, 715–726 (2015)
Strano, S., Terzo, M.: Accurate state estimation for a hydraulic actuator via a SDRE nonlinear filter. Mech. Syst. Signal Process. 75, 576–588 (2016)
Xu, J.X., Guo, Z.Q., Lee, T.H.: Design and implementation of a Takagi-Sugeno-type fuzzy logic controller on a two-wheeled mobile robot. IEEE Trans. Ind. Electron. 60(12), 5717–5728 (2013)
Chwa, D.: Fuzzy adaptive tracking control of wheeled mobile robots with state-dependent kinematic and dynamic disturbances. IEEE Trans. Fuzzy Syst. 20(3), 587–593 (2012)
Mohareri, O., Dhaouadi, R., Rad, A.B.: Indirect adaptive tracking control of a nonholonomic mobile robot via neural networks. Neurocomputing 88, 54–66 (2012)
Su, K.H., Chen, Y.Y., Su, S.F.: Design of neural-fuzzy-based controller for two autonomously driven wheeled robot. Neurocomputing 73(13–15), 2478–2488 (2010)
Park, B.S., Yoo, S.J., Park, J.B., Choi, Y.H.: Adaptive neural sliding mode control of nonholonomic wheeled mobile robots with model uncertainty. IEEE Trans. Control Syst. Technol. 17(1), 207–214 (2009)
Shabana, A.A.: Dynamics of Multibody Systems, 4th edn. Cambridge University Press, Cambridge (2013)
De Jalon, J.G., Bayo, E.: Kinematic and Dynamic Simulation of Multibody Systems: The Real-Time Challenge. Springer Science and Business Media, Berlin (2012)
Patel, M., Orzechowski, G., Tian, Q., Shabana, A.A.: A new multibody system approach for tire modeling using ANCF finite elements. Proc. Inst. Mech. Eng. K J. Multi-body Dyn. 230(1), 69–84 (2016)
Poetsch, G., Evans, J., Meisinger, R., Kortum, W., Baldauf, W., Veitl, A., Wallaschek, J.: Pantograph/catenary dynamics and control. J. Veh. Syst. Dyn. 28(2–3), 159–195 (1997)
Seo, J.H., Kim, S.W., Jung, I.H., Park, T.W., Mok, J.Y., Kim, Y.G., Chai, J.B.: Dynamic analysis of a pantograph/catenary system using absolute nodal coordinates. J. Veh. Syst. Dyn. 44(8), 615–630 (2006)
Seo, J.H., Sugiyama, H., Shabana, A.A.: Three-dimensional large deformation analysis of the multibody pantograph/catenary systems. J. Nonlinear Dyn. 42(2), 199–215 (2005)
Sun, J., Tian, Q., Hu, H.: Structural optimization of flexible components in a flexible multibody system modeled via ANCF. Mech. Mach. Theory 104, 59–80 (2016)
Tian, Q., Liu, C., Machado, M., Flores, P.: A new model for dry and lubricated cylindrical joints with clearance in spatial flexible multibody systems. Nonlinear Dyn. 64(1–2), 25–47 (2011)
Barbagallo, R., Sequenzia, G., Oliveri, S.M., Cammarata, A.: Dynamics of a high-performance motorcycle by an advanced multibody/control co-simulation. Proc. Inst. Mech. Eng. K J. Multi-body Dyn. 230(2), 207–221 (2016)
Cammarata, A., Angeles, J., Sinatra, R.: Kinetostatic and inertial conditioning of the McGill Schonflies-motion generator. Adv. Mech. Eng. 2, 186203 (2010)
Cammarata, A.: Optimized design of a large-workspace 2-DOF parallel robot for solar tracking systems. Mech. Mach. Theory 83, 175–186 (2015)
Goldstein, H., Poole, C.P., Safko, J.L.: Classical Mechanics. Pearson New International Edition, Essex (2014)
Siciliano, B., Sciavicco, L., Villani, L., Oriolo, G.: Robotics: Modelling, Planning, and Control. Springer Advanced Textbooks in Control and Signal Processing Series. Springer, London (2009)
Udwadia, F.E., Schutte, A.D.: Equations of motion for general constrained systems in Lagrangian mechanics. Acta Mech. 213(1–2), 111–129 (2010)
Guida, D., Pappalardo, C.M.: Forward and inverse dynamics of nonholonomic mechanical systems. Meccanica 49(7), 1547–1559 (2014)
Pappalardo, C.M.: A natural absolute coordinate formulation for the kinematic and dynamic analysis of rigid multibody systems. Nonlinear Dyn. 81(4), 1841–1869 (2015)
Meirovitch, L.: Methods of Analytical Dynamics. Courier Corporation, Chelmsford (2010)
Udwadia, F.E., Kalaba, R.E.: Analytical Dynamics: A New Approach. Cambridge University Press, Cambridge (2007)
Lanczos, C.: The Variational Principles of Mechanics. Courier Corporation, Chelmsford (2012)
Shabana, A.A.: Computational Continuum Mechanics, 3rd edn. Wiley, London (2018)
Shabana, A.A.: Computational Dynamics, 2nd edn. Wiley, London (2009)
Meirovitch, L.: Fundamentals of Vibrations. Waveland Press, Long Grove (2010)
Flannery, M.R.: The enigma of nonholonomic constraints. Am. J. Phys. 73(3), 265–272 (2005)
Landau, L.D., Lifshitz, E.M.: Mechanics. Butterworth-Heinemann, London (1976)
Flannery, M.R.: The elusive D’Alembert–Lagrange dynamics of nonholonomic systems. Am. J. Phys. 79(9), 932–944 (2011)
Flannery, M.R.: D’Alembert–Lagrange analytical dynamics for nonholonomic systems. J. Math. Phys. 52(3), 032705 (2011)
Greiner, W.: Classical Mechanics: Systems of Particles and Hamiltonian Dynamics. Springer Science and Business Media, Berlin (2009)
Udwadia, F.E., Kalaba, R.E.: A new perspective on constrained motion. Proc. Math. Phys. Sci. 439(1906), 407–410 (1992)
Hertz, H.: The Principles of Mechanics Presented in a New Form. Courier Corporation, Chelmsford (2003)
Ramm, E.: Principles of least action and of least constraint. GAMMMitteilungen 34(2), 164–182 (2011)
Pennestrí, E., Valentini, P.P., De Falco, D.: An application of the Udwadia–Kalaba dynamic formulation to flexible multibody systems. J. Frankl. Inst. 347(1), 173–194 (2010)
Udwadia, F.E., Kalaba, R.E.: On motion. J. Frankl. Inst. 330(3), 571–577 (1993)
Udwadia, F.E., Kalaba, R.E.: On the foundations of analytical dynamics. Int. J. Non-linear Mech. 37(6), 1079–1090 (2002)
Udwadia, F.E., Wanichanon, T.: On general nonlinear constrained mechanical systems. Numer. Algebra Control Optim. 3(3), 425–443 (2013)
De Falco, D., Pennestrí, E., Vita, L.: Investigation of the influence of pseudoinverse matrix calculations on multibody dynamics simulations by means of the Udwadia–Kalaba formulation. J. Aerosp. Eng. 22(4), 365–372 (2009)
Udwadia, F.E., Phohomsiri, P.: Explicit equations of motion for constrained mechanical systems with singular mass matrices and applications to multi-body dynamics. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 462(2071), 2097–2117 (2006)
Udwadia, F.E., Wanichanon, T.: Hamel’s paradox and the foundations of analytical dynamics. Appl. Math. Comput. 217(3), 1253–1265 (2010)
Udwadia, F.E.: Equations of motion for constrained multibody systems and their control. J. Optim. Theory Appl. 127(3), 627–638 (2005)
Udwadia, F.E.: Optimal tracking control of nonlinear dynamical systems. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 464(2097), 2341–2363 (2008)
Fantoni, I., Lozano, R.: Non-Linear Control for Underactuated Mechanical Systems. Springer Science and Business Media, Berlin (2002)
Golub, G.H., Van Loan, C.F.: Matrix Computations. JHU Press, Baltimore (2012)
Strang, G.: Introduction to Linear Algebra. Wellesley-Cambridge Press, Wellesley (1993)
Kane, T.R., Levinson, D.A.: Dynamics Theory and Applications. McGraw Hill, New York (1985)
Wehage, R.A., Haug, E.: Generalized coordinate partitioning for dimension reduction in analysis of constrained dynamic systems. J. Mech. Des. 104(1), 247–255 (1982)
Wehage, K.T., Wehage, R.A., Ravani, B.: Generalized coordinate partitioning for complex mechanisms based on kinematic substructuring. Mech. Mach. Theory 92, 464–483 (2015)
De Simone, M.C., Russo, S., Rivera, Z.B., Guida, D.: Multibody model of a UAV in presence of wind fields. In: International Conference on Control, Artificial Intelligence, Robotics, and Optimization (ICCAIRO) IEEE, Prague, Czech Republic, 20–22 May 2017, pp. 83–88 (2017)
De Simone, M.C., Guida, D.: On the development of a low cost device for retrofitting tracked vehicles for autonomous navigation. In: Programme and Proceedings of the XXIII Conference of the Italian Association of Theoretical and Applied Mechanics (AIMETA 2017), 4–7/09/2017, Salerno, Italy, 2017, pp. 71–82 (2017)
De Simone, M.C., Guida, D.: Modal coupling in presence of dry friction. Machines 6(1), 8 (2018)
De Simone, M.C., Rivera, Z.B., Guida, D.: Obstacle avoidance system for unmanned ground vehicles by using ultrasonic sensors. Machines 6(2), 18 (2018)
De Simone, M.C., Guida, D.: Identification and Control of an Unmanned Ground Vehicle by using Arduino. UPB Scientific Bulletin, Series D: Mechanical Engineering 80(1), 141–154 (2018)
De Simone, M.C., Rivera, Z.B., Guida, D.: Finite element analysis on squeal-noise in railway applications. FME Trans. 46(1), 93–100 (2018)
Acknowledgements
This research paper was principally developed by the first author (Carmine M. Pappalardo). The detailed review carried out by the second author (Domenico Guida) considerably improved the quality of the work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Pappalardo, C.M., Guida, D. On the dynamics and control of underactuated nonholonomic mechanical systems and applications to mobile robots. Arch Appl Mech 89, 669–698 (2019). https://doi.org/10.1007/s00419-018-1491-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00419-018-1491-6