Modal characterization with nonlinear behaviors of a two-link flexible manipulator

Abstract

This present work has made a noteworthy attempt to demonstrate brief modeling of N-link manipulator and subsequent modal characterization along with the determination of static deflection of a two-link flexible manipulator with a payload. In addition, investigation of nonlinear phenomena of dynamic responses under 3:1 internal resonance has also been accomplished considering geometric nonlinearities. An appropriate and realistic dynamic modeling of the two-link manipulator taking into account of inertia coupling and geometry compatibility between equations of motion and boundary conditions has been derived using the extended Hamilton’s principle. The effect of parametric variation on system eigenfrequencies is well tabulated, and the corresponding eigenspectrums are illustrated graphically. Further, the nonlinear phenomena of dynamic solutions have been demonstrated by using MMS of second order for its statutory effect onto the system instability for the existence of S-N bifurcations. The effect of nonlinearities and various design parameters on the dynamic responses and subsequent bifurcations for 3:1 internal resonance has also been demonstrated. The outcome of the present work enables new understanding into the design criterion and performance limitation of multi-link flexible robots.

1 Introduction

Since the last three decades, research in the field of robot kinematics has gained great interest among the numerous researchers worldwide that is mainly due to the increase in the use of robotic manipulators in various challenging fields of engineering and science like mining, aerospace, manufacturing by carrying out the functions like assembling, space exploration, painting, spraying, grinding. Traditionally, the robot manipulators have been designed by considering all members as rigid bodies and hence the dynamic equations for rigid body model have been thoroughly derived to demonstrate its performance by many researchers. But for the last decade, the researchers have focused their attention toward the flexible manipulator due to its practical relevance. Low weight and flexibility of the links have been the major concern for the researchers which has resulted in faster movement of the manipulators, which, in turn, has reduced the operating costs of the system, better transportability and safer operation significantly. A number of researchers [1,2,3,4,5] have studied and tried to solve the vibration problem of the single-link manipulator by improving their dynamic models and considering different loading conditions. A brief description about the development of flexible manipulators has been depicted here.

Low [1] analytically formulated the equations of motion of mechanical manipulators with the elastic links using Hamilton principle. Coleman [2] analyzed the vibration eigenfrequency of a flexible slewing beam with a payload attached at one end using wave propagation method (WPM). The results showed that the large frequencies are asymptotically identical to those for the clamped-free beam independent of the payload. Hwang [3] numerically solved the system of loosely coupled dynamic equations expressed in terms of the absolute, joint and elastic coordinates. Flexible 2-DOF double-pendulum and spatial manipulator systems have been used as examples to demonstrate and verify the application of the computational procedures. Yuan [4] derived the equations of motion for a hub-beam system using the Newton’s second law for the sake of retaining the simple physical structure of the problem. A simple linear feedback law has also been obtained via Lyapunov- type method. Poppelwell and Chang [5] determined the natural frequencies of a single-link flexible manipulator when the center of gravity of the payload does not coincide with manipulator end. Low and Vidyasagar [6] derived the equations of motion for rigid and flexible links robot manipulators using Hamilton’s principle resulting in nonlinear integro-differential equations. Also, performance of two-link manipulator considering one rigid and other flexible link has been studied. Ower and Van De Vegte [7] used the Lagrangian dynamics approach to model the planar motion of a manipulator consisting of two flexible links and two rotary joints. The equations have been linearized and represented by a transfer matrix. Benati and Morro [8] derived the boundary conditions along with the partial differential equations of motion for chain of flexible links by considering each link as a continuous body. Matsuno et al. [9] studied the two-link flexible manipulators in contact with constraint surface and developed dynamic equations of joint angles, vibrations of flexible links and contact force. Zhang et al. [10] derived a partial differential equation (PDE) model of flexible two-link manipulator and transformed to a form appropriate for the development of stable control designs. Oakley and Cannon [11] developed the dynamic equations for a general two-link manipulator including geometric offsets and concentrated inertias using assumed mode method. Chiou and Shahinpoor [12] analyzed the stability limitations for force-controlled two-link flexible manipulator and compared it with the model considering rigid body dynamics. The effect of link flexibility, nonlinear effect due to discontinuous contact with environment and force sensor stiffness on the stability has been explored. The assumed mode method has been used to study the dynamics of multi-link flexible manipulator. Fung and Chang [13] derived equations of motions and corresponding boundary conditions of nonlinearly constrained flexible manipulator with a tip mass for four flexible dynamic models, geometric offsets and concentrated inertias beam theories. Zhang and Liu [14] developed a PDE model for a flexible two-link manipulator with a changeable payload at the free end. An adaptive boundary control scheme has been proposed for the model for vibration suppression and simultaneous position regulation in the presence of uncertain payload. Ahmed et al. [15] derived the dynamic modeling of a planar two-link flexible manipulator based on closed-form equations of motion using Euler–Lagrange’s method along with assumed mode method. The model considered structural damping, hub inertia and payload. Sato et al. [16] derived the equations of motion of two-link manipulator in consideration of characteristics of driving source and examined the measurement method for force of collision between link and object. The study concluded that it is possible to absorb the impact force by active motion and the results have been compared with those obtained experimentally. Sato et al. [17] derived the equation of motion and also analyzed theoretically and experimentally investigated the dynamic characteristics of two-link system controller based on the trajectory for saving energy. Ata et al. [18] investigated the effect of different sets of initial and boundary conditions on the joint torques of two-link flexible manipulator. The elastic deflection for each link has been computed using the assumed mode method for four modes of vibration. Simulation results have been presented to analyze the effect of boundary conditions on the required hub torque for both the links. Abe and Hashimobo [19] proposed a feedforward control technique for two flexible links attached to one motor to suppress residual vibrations in a point-to-point motion. In this proposed method, an attempt was made to express the trajectory of the joint angle using a combination of cycloidal and polynomial functions, which enables the easy generation of a smooth motion. Lochan et al. [20] presented a survey on two-link manipulator based on the existing works till 2016. The classification of manipulators has been done based on dynamic analyses, complexities involved and control strategies used. It also mentions whether the work conducted is solely based on simulation or it has been validated by experiments. Yang et al. [21] considered trajectory tracking control of a two-link flexible manipulator model in space. Method of backstepping control has been used to design the controller of nonlinear system. Tip trajectory synchronization of two identical two-link flexible manipulator has been presented by Lochan et al. [22]. A second-order PID terminal SMC control technique has been used to evaluate the robustness of the controller in the presence of payload variation. Assumed mode method has been used to model the two-link flexible manipulator. Lochan et al. [23] designed a controller for two-link flexible manipulator to track the chaotic signal in the presence of bounded disturbances and to regulate the tip deflection to its desired value close to zero. It has been shown that the manipulator dynamics follow the desired trajectory with good tracking performance in the presence of bounded disturbances. Lyapunov stability criterion has been used to achieve the stability of the sliding surface and convergence of error dynamics. Pedro and Tshabalala [24] modeled a two-link flexible manipulator using Lagrangian formulation, and then, actuator dynamics have been included to improve its simulation of real-time control. It has been illustrated that the PID controllers are able to adequately control tracking of the FRMs, though the vibration suppression and tracking performance has not been good as that of the hybrid NNMPC/PID controller. Ding and Shen [25] demonstrated that assumed mode method has a good accuracy to predict the displacement of the endpoint of the manipulator by comparing the results obtained by assumed mode method and absolute nodal coordinate formulation. It has been concluded that the AMM is not efficient for analyzing the strength of robotic manipulator. Pratiher and Dwivedy [26] used method of multiple scales to solve the temporal equation after discretization by Galerkin’s method. Pratiher [27] used method of multiple scales as one of the perturbation techniques to derive a set of first-order ordinary differential equations that govern the time variation of the amplitude and phase of the responses of a magneto-elastic beam having prismatic harmonic joint.

From the existing literature, it is evident that till date, most of the existing works emphasize on the evaluation of dynamic performances and system design focusing on single-link flexible manipulator under different loading and application conditions. However, for a two-link manipulator, most of the researchers have laid their attention only on the derivation of dynamic modeling. There has been an almost trivial study to apprehend the modal characterization of a flexible two-link manipulator system which is very essential for vibration point of view.

On this foundation, the present paper goes few steps ahead to demonstrate the modal characterization and derivation of static deflection along with the investigation of nonlinear response of a two-link flexible robot manipulator with a payload. The present model is more accurate in the sense that it takes into account the geometric compatibility arising in the equations of motion and the boundary conditions along with the geometric nonlinearities due to axial stretching of the links. The primary contribution of this paper is to investigate the effect of parametric variation on the system eigenfrequencies and eigenspectrums of the system which has yet not been explored. Further, the influence of various design parameters on the nonlinear characteristics and system instability with bifurcations of two-link manipulator is investigated for the case of 3:1 internal resonance arising due to inertial coupling between the links.

To the best of author’s knowledge, no study has yet been carried out to explore the similar outcomes those are presented here. Further, this work furnishes a better image of structural design based on vibration phenomenon: a prerequisite for designing a flexible manipulator, and hence, offers a noteworthy contribution toward the development and design of flexible two-link manipulator.

2 Mathematical model and solution procedures

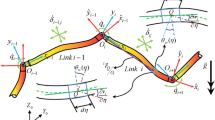
A schematic diagram of a flexible two-link manipulator incorporating payload is shown in Fig. 1. A brief procedure to model N-link manipulator is presented considering the stretching effect and gravitational forces acting on the beam and masses in addition to bending deformation of the system. Here, first link is fixed at one end and attached to the motor on the other end, while second link is attached to the first motor from one end and carrying the second motor on the other, thus forming a chain of N links with a payload mass the end of the Nth link. The motor and the payload mass at the end of the link are considered as concentrated mass. Let (X, Y) represent the global coordinate system with $\left( {\widehat{{X}},\widehat{{Y}}} \right)$ as the unit vectors. Here, $\left( {\hat{{{x}}}_{{N}} ,\hat{{y}}_{{N}} } \right)$ are the orthogonal unit vectors of the moving coordinate system attached with Nth link. The links are modeled based on Euler–Bernoulli beam element neglecting the effect of rotary inertia and shear deformation. The elastic deformation ${w}_{{N}} ({x},{t})$ is assumed to be small as compared to the length of the links. The relations between the unit vectors of inertial and moving coordinate system for the both the links are given as.

$$\begin{aligned} \left[ {{\begin{array}{l} {\hat{{{x}}}_1 } \\ {\hat{{{y}}}_1 } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {{\hbox {c}}\theta _1 }&{} {{\hbox {s}}\theta _1 } \\ {{-\hbox {s}}\theta _1 }&{} {{\hbox {c}}\theta _1 } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\widehat{{X}}} \\ {\widehat{{Y}}} \\ \end{array} }} \right] , \left[ {{\begin{array}{l} {\hat{{{x}}}_2 } \\ {\hat{{{y}}}_2 } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {{\hbox {c}}\left( {\theta _1 +{{w}}_{1\mathrm{L}}^{'} +\theta _2 } \right) }&{} {{\hbox {s}}\left( {\theta _1 +{{w}}_{1\mathrm{L}}^{'} +\theta _2 } \right) } \\ {{-\hbox {s}}\left( {\theta _1 +{{w}}_{1\mathrm{L}}^{'} +\theta _2 } \right) }&{} {{\hbox {c}}\left( {\theta _1 +{{w}}_{1\mathrm{L}}^{'} +\theta _2 } \right) } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\hat{{{X}}}} \\ {\hat{{{Y}}}} \\ \end{array} }} \right] ,\\ \left[ {{\begin{array}{l} {\hat{{{x}}}_{{N}} } \\ {\hat{{{y}}}_{{N}} } \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ll} {{\hbox {c}}\left( {\sum \limits _{{ i}=1}^{{N}} {\left( {\theta _{{i}} +{{w}}^\prime _{(i -1)\mathrm{L}} } \right) } } \right) }&{} {{\hbox {s}}\left( {\sum \limits _{{ i}=1}^{{N}} {\left( {\theta _{{i}} +{{w}}_{(i -1)\mathrm{L}}^{'} } \right) } } \right) } \\ {{-\hbox {s}}\left( {\sum \limits _1^{{N}} {\left( {\theta _{{i}} +{{w}}_{(i-1)\mathrm{L}}^{'} } \right) } } \right) }&{} {{\hbox {c}}\left( {\sum \limits _{{ i}=1}^{{N}} {\left( {\theta _{{i}} +{{w}}_{(i-1)\mathrm{L}}^{'} } \right) } } \right) } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\hat{{{X}}}} \\ {\hat{{{Y}}}} \\ \end{array} }} \right] \end{aligned}$$

Here, s and c stand for sine and cosine, respectively. The end point (R) and the general point (s) on the flexible links are given, respectively, as:

$$\begin{aligned} {R}_1= & {} {L}_1 \hat{{{x}}}_1 +{w}_{1\mathrm{L}} \hat{{{y}}}_1 , \quad {R}_2 ={R}_1 +{L}_2 \hat{{{x}}}_2 +{w}_{2\mathrm{L}} \hat{{{y}}}_2 ,\quad \ldots , \quad {R}_{{N}} ={R}_{{N}{-}1} +{L}_{{N}} \hat{{{x}}}_{{N}} +{w}_{{N\mathrm{L}}} \hat{{{y}}}_{{N}} \end{aligned}$$

(1)

$$\begin{aligned} {s}_1= & {} \left( {x} \right) \hat{{{x}}}_1 +\left( {{y}+{w}_1 } \right) \hat{{{y}}}_1 , \,\,{s}_2 ={R}_1 +\left( {x} \right) \hat{{{x}}}_2 +\left( {{y}+{w}_2 } \right) \hat{{{y}}}_2 ,\ldots , \,\, {s}_{{N}} ={R}_{(N-1)} +\left( {x} \right) \hat{{{x}}}_{{N}} +\left( {{y}+{w}_{{N}} } \right) \hat{{{y}}}_{{N}}\nonumber \\ \end{aligned}$$

(2)

Here, $\left( {{x},{y}} \right)$ denotes the undeformed position of an arbitrary point on the link.

Fig. 1

A schematic diagram of planar two-link flexible robotic manipulator in deflected configuration

Total kinetic energy T of the system is given by:

$$\begin{aligned} {T}=\sum \limits _{{ i}=1}^{{N}} {\left( {\left( {1/2} \right) {m}_{{i}} \dot{{R}}_{{i}}^{{T}} \dot{{R}}_{{i}} +\left( {1/2} \right) \int \limits _0^{{L}_{{i}} } {\rho _{{i}} \dot{{s}}_{{i}}^{{T}} \dot{{s}}_{{i}} {\mathrm{d}x}} } \right) } \end{aligned}$$

(3)

Total potential energy U of the system is given by:

$$\begin{aligned} {U}= & {} {U}_1 +{U}_2 +{U}_3 +{U}_4\nonumber \\ {U}_1= & {} \sum \limits _{{ i}=1}^{{N}} {\left( {1/2} \right) \int \limits _0^{{L}_{{i}} } {{E}_{{i}} {I}_{{i}} \left( {{{w}}_{{i}}^{''} } \right) ^{2}{\mathrm{d}x}} } , \,\,{U}_2 =\sum \limits _{{ i}=1}^{{N}} {\left( {1/2} \right) \int \limits _0^{{L}_{{i}} } {{E}_{{i}} {A}_{{i}} \left( {\left( {1/2} \right) {{w}}_{{i}}^{'2}} \right) ^{2}{\mathrm{d}x}}}\nonumber \\ {U}_3= & {} \sum \limits _{{ i}=1}^{{N}} {\int \limits _0^{{L}_\mathrm{i} } {\rho _{{i}} {g} \left( \begin{array}{l} {w}_{(i-1)\mathrm{L}} +{x\cos }\left( {\sum \limits _{j=1}^{{i}} {\left( {\theta _{{j}} +{{w}}_{(j-1)\mathrm{L}}^{'} } \right) } }\right) +\\ \left( {{y}+{w}_{{i}} } \right) {\sin }\left( {\sum \limits _{j=1}^{i} {\left( {\theta _{{j}}+{{w}}_{(j-1)\mathrm{L}}^{'} } \right) } } \right) \end{array}\right) {\mathrm{d}x}} } ,\nonumber \\ {U}_4= & {} {m}_{{i}} {g}\left( {{w}_{(i-1)\mathrm{L}} +{L}_{{i}} {\cos }\left( {\sum \limits _{{ i}=1}^{{N}} {\left( {\theta _{{i}} +{{w}}_{(i-1)\mathrm{L}}^{'} } \right) } } \right) +{w}_{{i\mathrm{L}}} {\sin }\left( {\sum \limits _{{ i}=1}^{{N}} {\left( {\theta _{{i}} +{{w}}_{(i-1)\mathrm{L}}^{'} } \right) } } \right) } \right) \end{aligned}$$

(4)

Here, ${U}_{1}$, ${U}_{2}$, ${U}_{3}$ and ${U}_{4}$ represent the elastic strain energy, energy due to axial stretching, potential energy of the link and potential energy of masses at the end of the link, respectively.

3 Dynamic modeling

The equations of motion and associated boundary conditions for the two-link flexible manipulator are modeled in this section from Eqs. (3–4) by exploiting extended Hamilton’s principle between two time stages which can be expressed mathematically as:

$$\begin{aligned} \sum \limits _1^2 {\int \limits _{\mathrm{t}_1 }^{\mathrm{t}_2 } {\delta \left( {{T}_{{N}} {-U}_{{N}} } \right) {\mathrm{d}t}=0} } , \quad \quad \delta (t_1 )=\delta (t_2 )=0. \end{aligned}$$

(5)

Substituting Eqs. (1–4) in Eq. (5), and carrying out mathematical procedures as explained in [13], the following governing equations of motion and the boundary conditions of the system can be obtained for both the links.

$$\begin{aligned}&\rho _1 {A}_1 \left( {\ddot{{w}}_1 +{x}\ddot{\theta }_1 {{-w}}_1 \dot{\theta }_1 ^{2}+{g}} \right) +{E}_1 {I}_1 {w}_1^{{''}\,{''}} {-E}_1 {A}_1 \left( {\left( {3/2} \right) {{w}}_1 ^{'2}{{w}}_1^{''} } \right) =0 \end{aligned}$$

(6)

$$\begin{aligned}&{w}_1 (0,{t})=0, \quad {{w}}_1^{'} (0,{t})=0\nonumber \\&\quad \int \limits _0^{{L}_2 } {\rho _2 {A}_2 \left( {\begin{array}{l} {x}\ddot{{w}}_2 +{x}^{2}{\ddot{{w}}}_{1\mathrm{L}}^{'} +{x}^{2}\ddot{\theta }_1 +{x}^{2}\ddot{\theta }_2 \\ +{g}\left( {{x\sin }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) +{w}_2 {\cos }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) } \right) \\ +2{w}_2 \dot{{w}}_2 \dot{\theta }_1 +2{w}_2 \dot{{w}}_2 \dot{\theta }_2 +2{w}_2 \dot{{w}}_2 {\dot{{w}}}_{1\mathrm{L}}^{'} \\ {{-w}}_2\, {}^{2}\ddot{\theta }_1 +{w}_2\, {}^{2}\ddot{\theta }_2 +{w}_2\, {}^{2}{\ddot{{w}}}_{1\mathrm{L}}^{'} \\ \end{array}} \right) {\mathrm{d}x}} +{E}_1 {I}_1 {{w}}_{1\mathrm{L}}^{''} \nonumber \\&\quad +{m}_2 \left( {\begin{array}{l} {L}_2 \ddot{{w}}_{2\mathrm{L}} +{L}_2\, {}^{2}{\ddot{{w}}}'_{1\mathrm{L}} +{L}_2\, {}^{2}\ddot{\theta }_2 +{L}_2\, {}^{2}\ddot{\theta }_1 \\ +{g}\left( {\begin{array}{l} {L}_2 {\sin }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) \\ {{-w}}_{2\mathrm{L}} {\cos }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) \\ \end{array}} \right) {-}2{w}_{2\mathrm{L}} \dot{{w}}_{2\mathrm{L}} \\ \end{array}} \right) =0\nonumber \\&\quad \left( {{m}_1 +{m}_2 } \right) \left( {\ddot{{w}}_{1\mathrm{L}} +{L}_1 \ddot{\theta }_1 +{g}{{-w}}_{1\mathrm{L}} \dot{\theta }_1^{2}} \right) +\int \limits _0^{{L}_2 } {\rho _2 {A}_2 \left( {\ddot{{w}}_{1\mathrm{L}} +{L}_1 \ddot{\theta }_1 +{g}{{-w}}_{1\mathrm{L}} \dot{\theta }_1^{2}} \right) } {\mathrm{d}x}{-E}_1 {I}_1{{w}}_{1\mathrm{L}}^{'''}\nonumber \\&\qquad +{E}_2 {I}_2 {{w}}_2^{'''} \left( {0,{t}} \right) +{E}_1 {A}_1 \left( {\left( {1/2} \right) {{w}}_{1\mathrm{L}}^{'3}} \right) =0 \end{aligned}$$

(7)

$$\begin{aligned}&\rho _2 {A}_2 \left( {\begin{array}{l} \ddot{{w}}_1 +{x}{\ddot{{w}}}_{1\mathrm{L}}^{'} +{x}\ddot{\theta }_1 +{x}\ddot{\theta }_2 +{g\sin }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) {{-w}}_2 \dot{\theta }_1 ^{2} \\ {{-w}}_2 \dot{\theta }_2 ^{2}{{-w}}_2 {\dot{{w}}}_{1\mathrm{L}} ^{'2}{-}2\dot{\theta }_1 \dot{\theta }_2 {v}_2 {-}2\dot{\theta }_2 {w}_2 {\dot{{w}}}_{2\mathrm{L}}^{'} +2\dot{\theta }_1 {w}_2 {\dot{{w}}}_{2\mathrm{L}}^{'} \\ \end{array}} \right) +{E}_2 {I}_2 {{{w}}_2^{{''}{''}}} {-E}_2 {A}_2 \left( {\left( {3/2} \right) {{w}}_2 ^{'2}{{w}}_2^{''} } \right) =0\nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned}&{w}_2 \left( {0,{t}} \right) =0, \quad {{w}}_2^{'} \left( {0,{t}} \right) =0, \quad {E}_2 {I}_2 {{w}}_2^{''} \left( {{L}_2 ,{t}} \right) =0\nonumber \\&{m}_2 \left( {\begin{array}{l} \ddot{{w}}_{2\mathrm{L}} +{L}_2 {\ddot{{w}}}_{1\mathrm{L}}^{'} +{L}_2 \ddot{\theta }_1 +{L}_2 \ddot{\theta }_2 {-}2{w}_{2\mathrm{L}} \dot{\theta }_2 {\dot{{w}}}_{1\mathrm{L}}^{'} {{-w}}_{2\mathrm{L}} {\dot{{w}}}_{1\mathrm{L}} ^{'2}{{-w}}_{2\mathrm{L}} \dot{\theta }_1 ^{2} \\ {{-w}}_{2\mathrm{L}} \dot{\theta }_2 ^{2}{-2w}_{2\mathrm{L}} \dot{\theta }_1 \dot{\theta }_2 {-}{g\sin }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) {-2w}_{2\mathrm{L}} \dot{\theta }_1 {\dot{{w}}}_{1\mathrm{L}}^{'} \\ \end{array}} \right) {-E}_2 {I}_2{{w}}_{2\mathrm{L}}^{'''} \nonumber \\&\quad +{E}_2 {A}_2 \left( {\left( {1/2} \right) {{w}}_{2\mathrm{L}}^{'}} ^{3} \right) =0 \end{aligned}$$

(9)

Equations (7–9) have been obtained by comparing the coefficients of $\delta \left( {{w}_1 } \right)$, $\delta \left( {{{w}}_{1\mathrm{L}}^{'} } \right)$, $\delta \left( {{w}_{1\mathrm{L}} } \right)$, $\delta \left( {{w}_2 } \right)$, $\delta \left( {{{w}}'_{2\mathrm{L}} } \right)$ and $\delta \left( {{w}_{2\mathrm{L}} } \right)$, respectively, on both sides of Eq. (5).

3.1 Free vibration analysis

Variable separation method has been used to discretize the deflection functions which are the explicit function of space and time and expressed as ${w}^{1}\left( {{x},{t}} \right) =\sum \nolimits _{{i=1}}^{{n}} {{W}^{1}_{{i}} \left( {x} \right) {\cos }\left( {\varOmega _{{i}} {t}} \right) }$ and ${w}^{2}\left( {{x},{t}} \right) =\sum \nolimits _{{i=1}}^{{n}} {{W}^{2}_{{i}} \left( {x} \right) {\cos }\left( {\varOmega _{{i}} {t}} \right) }$. Here, ${W}_{{i}}^1 \left( {x} \right)$, ${W}_{{i}}^2 \left( {x} \right)$ are the corresponding ith mode of eigenfunction for links 1 and 2, respectively, and ${\cos }\left( {\varOmega _{{i}} {t}} \right)$ is the time modulation for a unknown ith mode of eigenfrequency $\varOmega _{{i}}$ of the whole system. Substitution in Eqs. (6–9) results in the equations governing the mode shape of the system along with the corresponding boundary conditions. The solution of the equations of motion gives the eigenfunction for both the links in the following form:

$$\begin{aligned} {W}_1 ^{{n}}({x})= & {} {B}^{{n}}_1 {\sin }\left( {\beta ^{{n}}{x}} \right) +{B}_2 {\cos }\left( {\beta ^{{n}}{x}} \right) +{B}^{{n}}_3 {\sinh }\left( {\beta ^{{n}}{x}} \right) +{B}^{{n}}_4 {\cosh }\left( {\beta ^{{n}}{x}} \right) \end{aligned}$$

(10)

$$\begin{aligned} {W}_2^{{n}} \left( {x} \right)= & {} {C}^{{n}}_1 {\sin }\left( {\mu \beta ^{{n}}{x}} \right) +{C}^{{n}}_2 {\cos }\left( {\mu \beta ^{{n}}{x}} \right) +{C}^{{n}}_3 {\sinh }\left( {\mu \beta ^{{n}}{x}} \right) +{C}^{{n}}_4 {\cosh }\left( {\mu \beta ^{{n}}{x}} \right) {-W}_1^{{n} ^{\prime }}\left( {{L}_1 } \right) {x} \end{aligned}$$

(11)

Here, unknown $({B}^{{n}}_1 \cdots {B}^{{n}}_4 ,{C}^{{n}}_1 \cdots {C}^{{n}}_4 ,)$ are the integration constants for nth mode of vibration and can be obtained by substituting Eqs. (10) and (11) into the boundary conditions that result a set of five algebraic equations in five unknown in terms of characteristics exponent $(\bar{{\beta }})$ and the following nondimensional parameters.

$$\begin{aligned}&\beta ^{4}={\rho _1 {A}_1 \varOmega ^{2}}/{{E}_1 {I}_1 }, \chi ={{E}_2 {I}_2 }/{{E}_1 {I}_1 }, \alpha _{\mathrm{M}} ={\rho _2 {A}_2 }/{\rho _1 {A}_1 }, \mu ^{4}={\alpha _{\mathrm{M}} }/\chi , \quad \bar{{\beta }}=\beta {L}_1 , \nonumber \\&\quad \alpha _{\mathrm{L}} ={{L}_2 }/{{L}_1 }, \alpha _{\mathrm{m}_1 } ={{m}_1 }/{\rho _1 {A}_1 {L}_1 }, \alpha _{\mathrm{m}_2 } ={\mathrm{m}_2 }/{\rho _1 {A}_1 {L}_1 },\;{\hbox {and}}\;\delta =\mu \alpha _{\mathrm{L}} . \end{aligned}$$

(12)

$$\begin{aligned}&\quad \left[ {{K}\left( {\beta ^{{n}}} \right) } \right] =\left[ {{\begin{array}{lllll} 0&{} 0&{} {{K}^{{n}}_{13} }&{} {{K}^{{n}}_{14} }&{} {{K}^{{n}}_{15} } \\ \\ 0&{} 0&{} {{K}^{{n}}_{23} }&{} {{K}^{{n}}_{24} }&{} {{K}^{{n}}_{25} } \\ \\ {{K}^{{n}}_{11} }&{} {{K}^{{n}}_{12} }&{} {{K}^{{n}}_{33} }&{} 0&{} {{K}^{{n}}_{35} } \\ \\ {{K}^{{n}}_{41} }&{} {{K}^{{n}}_{42} }&{} {{K}^{{n}}_{43} }&{} 0&{} {{K}^{{n}}_{45} } \\ \\ {{K}^{{n}}_{51} }&{} {{K}^{{n}}_{52} }&{} {{K}^{{n}}_{53} }&{} {{K}^{{n}}_{54} }&{} {{K}^{{n}}_{55} } \\ \\ \end{array} }} \right] \left[ {{\begin{array}{l} {{B}^{{n}}_1 } \\ {{B}^{{n}}_2 } \\ {{C}^{{n}}_1 } \\ {{C}^{{n}}_2 } \\ {{C}^{{n}}_3 } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(13)

The elements of the above matrix are expressed below:

$$\begin{aligned} {K}^{{n}}_{13}= & {} \alpha _{\mathrm{m}_2 } \bar{{\beta }}^{{n}}{\sin }\left( {\delta \bar{{\beta }}^{{n}}} \right) {-}\chi \mu ^{3}{\cos }\left( {\delta \bar{{\beta }}^{{n}}} \right) , \quad {K}^{{n}}_{14} =\alpha _{\mathrm{m}_2 } \bar{{\beta }}^{{n}}\left( {{\cos }\left( {\delta \bar{{\beta }}^{{n}}} \right) {-}{\cosh }\left( {\delta \bar{{\beta }}^{{n}}} \right) } \right) \nonumber \\&+\chi \mu ^{3}\left( {{\sin }\left( {\delta \bar{{\beta }}^{{n}}} \right) {-}{\sinh }\left( {\delta \bar{{\beta }}^{{n}}} \right) } \right) ,\nonumber \\ {K}^{{n}}_{15}= & {} \alpha _{\mathrm{m}_2 } \bar{{\beta }}^{{n}}{\sinh }\left( {\delta \bar{{\beta }}^{{n}}} \right) +\chi \mu ^{3}{\cosh }\left( {\delta \bar{{\beta }}^{{n}}} \right) , {K}^{{n}}_{23} ={\sin }\left( {\delta \bar{{\beta }}^{{n}}} \right) , \quad {K}^{{n}}_{24} ={\cos }\left( {\delta \bar{{\beta }}^{{n}}} \right) \nonumber \\&+{\cosh }\left( {\delta \bar{{\beta }}^{{n}}} \right) , \quad {K}^{{n}}_{25} ={-}{\sinh }\left( {\delta \bar{{\beta }}^{{n}}} \right) ,\nonumber \\ {K}^{{n}}_{31}= & {} \left( {\alpha _{\mathrm{m}_1 } +\alpha _{\mathrm{m}2} +\alpha _{\mathrm{M}} \alpha _{\mathrm{L}} } \right) \bar{{\beta }}^{{n}}\left( {{\sin }\left( {\bar{{\beta }}^{{n}}} \right) {-}{\sinh }\left( {\bar{{\beta }}^{{n}}} \right) } \right) {-}\left( {{\cos }\left( {\bar{{\beta }}^{{n}}} \right) +{\cosh }\left( {\bar{{\beta }}^{{n}}} \right) } \right) ,\nonumber \\ {K}^{{n}}_{32}= & {} \left( {\alpha _{\mathrm{m}_1 } +\alpha _{\mathrm{m}2} +\alpha _{\mathrm{M}} \alpha _{\mathrm{L}} } \right) \bar{{\beta }}^{{n}}\left( {{\cos }\left( {\bar{{\beta }}^{{n}}} \right) {-}{\cosh }\left( {\bar{{\beta }}^{{n}}} \right) } \right) +\left( {\sin }\left( {\bar{{\beta }}^{{n}}} \right) \right. \nonumber \\&\left. {-\sinh }\left( {\bar{{\beta }}^{{n}}} \right) \right) , \,\, {K}^{{n}}_{33} ={\alpha _{\mathrm{M}} }/\mu , \,\, {K}^{{n}}_{35} ={-}{\alpha _{\mathrm{M}} }/\mu ,\nonumber \\ {K}^{{n}}_{41}= & {} {-}{\cos }\left( {\bar{{\beta }}^{{n}}} \right) +{\cosh }\left( {\bar{{\beta }}^{{n}}} \right) , \quad {K}^{{n}}_{42} ={\sin }\left( {\bar{{\beta }}^{{n}}} \right) +{\sinh }\left( {\bar{{\beta }}^{{n}}} \right) , \quad {K}^{{n}}_{43} =\mu , \quad {K}^{{n}}_{44} =0, \quad {K}^{{n}}_{45} =\mu ,\nonumber \\ {K}^{{n}}_{51}= & {} \left( {1/{\alpha _{\mathrm{m}} \left( {\bar{{\beta }}^{{n}}} \right) ^{2}}} \right) \left( {{\sin }\left( {\bar{{\beta }}^{{n}}} \right) +{\sinh }\left( {\bar{{\beta }}^{{n}}} \right) } \right) , \quad {K}^{{n}}_{52} =\left( {1/{\alpha _{\mathrm{m}} \left( {\bar{{\beta }}^{{n}}} \right) ^{2}}} \right) \left( {{\cos }\left( {\bar{{\beta }}^{{n}}} \right) +{\cosh }\left( {\bar{{\beta }}^{{n}}} \right) } \right) ,\nonumber \\ {K}^{{n}}_{54}= & {} \left[ {\begin{array}{l} \left( {\left( {{\alpha _{\mathrm{m}_2 } \alpha _{\mathrm{L}} }/{\alpha _{\mathrm{M}} }} \right) +\left( {1/{\mu ^{2}\left( {\bar{{\beta }}^{{n}}} \right) ^{2}}} \right) } \right) {\cos }\left( {\delta \bar{{\beta }}^{{n}}} \right) {-}\left( {\left( {{\alpha _{\mathrm{m}_2 } \alpha _{\mathrm{L}} }/{\alpha _{\mathrm{M}} }} \right) {-}\left( {1/{\mu ^{2}\left( {\bar{{\beta }}^{{n}}} \right) ^{2}}} \right) } \right) {\cosh }\left( {\delta \bar{{\beta }}^{{n}}} \right) + \\ \left( {{\alpha _{\mathrm{L}} }/{\mu \bar{{\beta }}^{{n}}}} \right) \left( {{\sin }\left( {\delta \bar{{\beta }}^{{n}}} \right) {-}{\sinh }\left( {\delta \bar{{\beta }}^{{n}}} \right) } \right) {-}\left( {2/{\mu ^{2}\left( {\bar{{\beta }}^{{n}}} \right) ^{2}}} \right) \\ \end{array}} \right] \nonumber \\ {K}^{{n}}_{55}= & {} \left( {\left( {{\alpha _{\mathrm{m}_2 } \alpha _{\mathrm{L}} }/{\alpha _{\mathrm{M}} }} \right) {-}\left( {1/{\mu ^{2}\left( {\bar{{\beta }}^{{n}}} \right) ^{2}}} \right) } \right) {\sinh }\left( {\delta \bar{{\beta }}^{{n}}} \right) +\left( {{\alpha _{\mathrm{L}} }/{\mu \bar{{\beta }}^{{n}}}} \right) {\cosh }\left( {\delta \bar{{\beta }}^{{n}}} \right) \end{aligned}$$

(14)

The eigenfrequency equation for the system is obtained for the existence of nontrivial solution for Eq. (14), i.e., $\hbox {det}\left| {{K}\left( {\beta ^{{n}}} \right) } \right| =0$; here ${K}\left( {\bar{{\beta }}^{{n}}} \right)$ denotes the coefficient matrix. The expressions for the integration constants $({B}^{{n}}_2 ,{C}^{{n}}_1 \cdots {C}^{{n}}_3 )$ emerging in eigenfunctions in terms of ${B}_1$ which has assumed to have unit magnitude are obtained by some mathematical manipulations and given as:

$$\begin{aligned} {B}^{{n}}_2= & {} {-}{\left( {{K}^{{n}}_{13} {C}^{{n}}_1 +{K}^{{n}}_{15} {C}^{{n}}_3 +{K}^{{n}}_{11} } \right) }/{{K}^{{n}}_{12} }, {C}^{{n}}_1 =\left( {{\left( {{K}^{{n}}_{35} {K}^{{n}}_{24} {-}{K}^{{n}}_{25} {K}^{{n}}_{34} } \right) }/{\left( {{K}^{{n}}_{23} {K}^{{n}}_{34} {-}{K}^{{n}}_{33} {K}^{{n}}_{24} } \right) }} \right) {C}^{{n}}_3 , \nonumber \\ {C}^{{n}}_2= & {} {-}{\left( {{K}^{{n}}_{23} {C}^{{n}}_1 +{K}^{{n}}_{25} {C}^{{n}}_3 } \right) }/{{K}^{{n}}_{24} }, \quad {C}^{{n}}_3 =\left[ {{\left( {{K}^{{n}}_{11} {K}^{{n}}_{42} {-}{K}^{{n}}_{41} {K}^{{n}}_{12} } \right) \left( {{K}^{{n}}_{23} {K}^{{n}}_{34} {-}{K}^{{n}}_{33} {K}^{{n}}_{24} } \right) }/{d}} \right] ,\nonumber \\ {d}= & {} \left( {{K}^{{n}}_{35} {K}^{{n}}_{24} {-}{K}^{{n}}_{25} {K}^{{n}}_{34} } \right) \left( {{K}^{{n}}_{43} {K}^{{n}}_{12} {-}{K}^{{n}}_{13} {K}^{{n}}_{42} } \right) +\left( {{K}^{{n}}_{23} {K}^{{n}}_{34} {-}{K}^{{n}}_{33} {K}^{{n}}_{24} } \right) \left( {{K}^{{n}}_{45} {K}^{{n}}_{12} {-}{K}^{{n}}_{15} {K}^{{n}}_{42} } \right) \end{aligned}$$

(15)

Fig. 2

Two-link manipulator model for static analysis

3.2 Static analysis

For the static analysis, only the effects of steady loading conditions are considered which in this case includes the gravitational forces acting on links and masses of motors attached to them in addition to the bending load. Here, the two-link manipulator shown in Fig. 2 is initially considered in vertical plane. The equation of motions and associated boundary conditions can be obtained from Eqs. (1–9) by eliminating the temporal terms. The similar result shall be obtained by applying minimum potential energy theorem where the temporal terms in potential energy function can be neglected.

$$\begin{aligned}&\rho _1 {A}_1 {g}+ {E}_1 {I}_1 {{w}}_1^{{''}\,{''}} =0 \end{aligned}$$

(16)

$$\begin{aligned}&{w}_1 (0,{t})=0,{{w}}'_1 (0,{t})=0, {E}_1 {I}_1 {{w}}_{1\mathrm{L}}^{'''} +{E}_2 {I}_2 {{w}}_2^{'''} \left( {0,{t}} \right) +\int \limits _0^{{L}_2 } {\rho _2 {A}_2 {g\hbox {d}x}{-}\left( {{m}_1 +{m}_2 } \right) {g}} =0,\nonumber \\&{E}_1 {I}_1 {{w}}_{1\mathrm{L}}^{''} +{m}_2 {g}\left( {{L}_2 {\sin }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) {{-w}}_{2\mathrm{L}} {\cos }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) } \right) \nonumber \\&\quad +\int \limits _0^{{L}_2 } {\rho _2 {A}_2 {g}\left( {{x\sin }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) +{w}_2 {\cos }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) } \right) {\mathrm{d}x}} =0 \end{aligned}$$

(17)

$$\begin{aligned}&{E}_2 {I}_2 {w}_2^{{''}\,{''}} +\rho _2 {A}_2 {\sin }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) =0. \end{aligned}$$

(18)

$$\begin{aligned}&{w}_2 \left( {0,{t}} \right) =0, {{w}}_2^{'} \left( {0,{t}} \right) =0, {E}_2 {I}_2 {{w}}_{2\mathrm{L}}^{'''} -{m}_2 {g\sin }\left( {\theta _2 +{{w}}_{1\mathrm{L}}^{'} } \right) =0\; \hbox {and}\;{E}_2 {I}_2 {{w}}_2^{''} \left( {{L}_2 ,{t}} \right) =0 \end{aligned}$$

(19)

However, it is initially assumed that the links are being held in horizontal position before the deflection. We obtain the resulting equations of motion as:

$$\begin{aligned}&\rho _1 {A}_1 {g}+ {E}_1 {I}_1 {{w}}_1^{{''}\,{''}} =0 \end{aligned}$$

(20)

$$\begin{aligned}&{w}_1 (0,{t})=0, \quad {{w}}_1^{'} (0,{t})=0, \quad {E}_1 {I}_1 {{w}}_{1\mathrm{L}}^{''} +{\rho _2 {A}_2 {gL}_2^2 }/2+{m}_2 {gL}_2 =0,\nonumber \\&\quad {E}_1 {I}_1 {{w}}_{1\mathrm{L}}^{'''} +{E}_2 {I}_2 {{w}}_2^{'''} \left( 0 \right) +\rho _2 {A}_2 {gL}_2 {-}\left( {{m}_1 +{m}_2 } \right) {g}=0 \end{aligned}$$

(21)

$$\begin{aligned}&{E}_2 {I}_2 {{w}}_2^{{''}\,{''}} +\rho _2 {A}_2 {g}=0, \end{aligned}$$

(22)

$$\begin{aligned}&{w}_2 \left( {0,{t}} \right) =0, \quad {{w}}_2^{'} \left( {0,{t}} \right) =0, \quad {E}_2 {I}_2 {{w}}_2^{''} \left( {{L}_2 ,{t}} \right) =0{ and }{E}_2 {I}_2 {{w}}_{2\mathrm{L}}^{'''} {-m}_2 {g}=0 \end{aligned}$$

(23)

Using boundary conditions Eqs. (21) and (23), one may obtain the expressions for static for links 1 and 2 as:

$$\begin{aligned} {w}_1 \left( {x} \right)= & {} \left( {{-}{\rho _1 {A}_1 {g}}/{24{E}_1 {A}_1 }} \right) {x}^{4}+\left( {\begin{array}{l} {m}_1 +2{m}_2 +\rho _1 {A}_1 {L}_1 + \\ 2\rho _2 {A}_2 {L}_2 \\ \end{array}} \right) \left( {{g}/{6{E}_1 {I}_1 }} \right) {x}^{3}\nonumber \\&-\left( {\begin{array}{l} ({m}_1 +2{m}_2 ){L}_1 +{m}_2 {L}_2 + \\ \rho _1 {A}_1 {L}_1 ^{2}+\rho _2 {A}_2 \left( {{L}_1 {-}{{L}_2 }/2} \right) \\ \end{array}} \right) \left( {{g}/{2{E}_2 {I}_2 }} \right) {x}^{2}\nonumber \\ {w}_2 \left( {x} \right)= & {} \left( {{-}{\rho _2 {A}_2 {g}}/{24{E}_2 {A}_2 }} \right) {x}^{4}+\left( {{m}_2 +\rho _2 {A}_2 {L}_2 } \right) \left( {{g}/{6{E}_2 {I}_2 }} \right) {x}^{3}{-}\left( {{m}_2 +{\rho _2 {A}_2 {L}_2 }/2} \right) \left( {{{L}_2 {g}}/{2{E}_2 {I}_2 }} \right) {x}^{2}\nonumber \\ \end{aligned}$$

(24)

3.3 3:1 Internal resonance

The nonlinear characteristics and stability of two-link flexible manipulator have been studied for the case of 3:1 internal resonance. The geometric nonlinearities arising due to stretching effect and the inertial coupling in equations of motion of both the links expressed as Eqs. (6) and (8) are retained, and also representative damping is included. The rotational motions of the motors and gravitational terms are neglected for the present study.

Nonlinear equations of motion for links 1 and 2 are expressed as

$$\begin{aligned} \left( {\rho _1 {A}_1 \ddot{{w}}_1 +{E}_1 {I}_1 {w}_1 ^{{\prime \prime }\, {\prime \prime } }} \right) {-}\frac{3{E}_1 {A}_1 }{2}\left( {{{w}}_1 ^{'2}{{w}}_1^{''} } \right) +{c}_1 \dot{{w}}_1 =0 \end{aligned}$$

(25)

$$\begin{aligned} \left( {\rho _2 {A}_2 \left( {\ddot{{w}}_1 +{x}{\ddot{{w}}}_{1\mathrm{L}}^{'} } \right) +{E}_2 {I}_2 {w}_2 ^{{\prime \prime }\,{\prime \prime } }} \right) {-}\frac{3{E}_2 {A}_2 }{2}\left( {{{w}}_2 ^{'2}{{w}}_2^{''} } \right) +{c}_2 \dot{{w}}_2 =0 \end{aligned}$$

(26)

For nondimensional terms, $\bar{{{w}}}_1 ={{w}_1 }/{{L}_1 }$; $\bar{{{w}}}_2 ={{w}_2 }/{{L}_2 }$; $\bar{{{x}}}={x}/{{L}_1}$, $\tau ={t}\sqrt{{{E}_1 {I}_1 }/{\rho _1 {A}_1 {L}_1 ^{4}}}$, $\bar{{{c}}}={{cL}^{2}}/{\sqrt{\rho {AEI}}}$, Eqs. (25–26) are expressed after dropping bar for simplicity as

$$\begin{aligned}&\ddot{{w}}_1 +{w}_1 ^{{\prime \prime }\,{\prime \prime } }{-}\left( {{3{A}_1 {L}_1 ^{2}}/{2{I}_1 }} \right) \left( {{{w}}_1 ^{'2}{{w}}_1^{''} } \right) +{c}_1 \dot{{w}}_1 =0 \end{aligned}$$

(27)

$$\begin{aligned}&\left( {\ddot{{w}}_2+ \bar{x}\ddot{{w}}_{1\mathrm{L}}' +\left( {{{{{\chi }}}}/{\alpha _{\mathrm{M}} }} \right) { {{w}}}_2^{\prime \prime \, \prime \prime } } \right) - \frac{3A_2L_2^2}{I_2} \left( {\chi /{\alpha _{\mathrm{M}} \alpha _{\mathrm{L}}^2}} \right) \left( {{{w}}_2 ^{'2}{{w}}_2^{\prime \prime } } \right) +{c}_2 \dot{{w}}_2 =0 \end{aligned}$$

(28)

Henceforth, ()’and $(\cdot )$ represent the differentiation with respect to space parameter ${\bar{{x}}}$ and time ${\tau }$, respectively. When the system is excited by a broadband signal, most of the input excitation energy is injected into the first mode. Governing equation of motion Eqs. (27) and (28) are discretized by using assumed mode expressions, ${w}_1 (\bar{{{x}}},\tau )={r}\psi _1 \left( {\bar{{{x}}}} \right) {u}_1 \left( \tau \right)$; here, ${u}_1 \left( \tau \right)$ and ${u}_2 \left( \tau \right)$ are the time modulation for the first and second links, respectively, r is the scaling factor, and $\psi _1 \left( {\bar{{{x}}}} \right)$ and $\psi _2 \left( {\bar{{{x}}}} \right)$ are the eigenfunction of the first and second links, respectively, given in Eqs. (10–11) and expressed as :

$$\begin{aligned} \psi _1 \left( {\bar{{{x}}}} \right)= & {} {\sin }\left( {\bar{{\beta }}\bar{{{x}}}} \right) {-}{\sinh }\left( {\bar{{\beta }}\bar{{{x}}}} \right) +{B}_2 \left( {{\cos }\left( {\bar{{\beta }}\bar{{{x}}}} \right) {-}{\cosh }\left( {\bar{{\beta }}\bar{{{x}}}} \right) } \right) \end{aligned}$$

(29)

$$\begin{aligned} \psi _2 \left( {\bar{{{x}}}} \right)= & {} {C}_1 {\sin }\left( {\delta \bar{{\beta }}\bar{{{x}}}} \right) +{C}_2 {\cos }\left( {\delta \bar{{\beta }}\bar{{{x}}}} \right) +{C}_3 {\sinh }\left( {\delta \bar{{\beta }}\bar{{{x}}}} \right) +{C}_4 {\cosh }\left( {\delta \bar{{\beta }}\bar{{{x}}}} \right) \nonumber \\&{-} \bar{{{x}}}\alpha _{\mathrm{L}} \bar{{\beta }}\left( {{\cos }\left( {\bar{{\beta }}} \right) -{\cosh }\left( {\bar{{\beta }}} \right) -{B}_2 ({\sin }\left( {\bar{{\beta }}} \right) +{\sinh }\left( {\bar{{\beta }}} \right) } \right) \end{aligned}$$

(30)

Here, $\bar{{\beta }}$ is the first-mode eigenfrequency for the two-link manipulator system for the defined nondimensional parameters given in Eq. (12) and ${B}_2$, ${C}_1$, ${C}_2$ and ${C}_3$ can be calculated as explained in previous section. Now ordering the damping terms in Eqs. (27) and (28) in terms of $\varepsilon$, a small dimensionless parameter and utilizing the orthogonal property of the mode shapes, following nonlinear nondimensional ordinary differential equations are obtained:

$$\begin{aligned}&\ddot{{u}}_1 (\tau )+\varOmega _1 ^{2}{u}_1 (\tau ){-}\alpha _1 {u}_1 ^{3}(\tau )+2\varepsilon ^{2}\mu _1 \dot{{u}}=0 \end{aligned}$$

(31)

$$\begin{aligned}&\ddot{{u}}_2 (\tau )+\alpha _2 \ddot{{u}}_1 +\varOmega _2 ^{2}{u}_2 (\tau ){-}\alpha _3 {u}_2 ^{3}(\tau )+2\varepsilon ^{2}\mu _2 \dot{{u}}=0 \end{aligned}$$

(32)

Here, $\varOmega _1 ^{2}=\left( {{\int \limits _0^1 {\psi _1 ^{{\prime \prime }\,{\prime \prime }}\left( {\bar{{{x}}}} \right) \psi _1 \left( {\bar{{{x}}}} \right) {\hbox {d}}\bar{{{x}}}} }/{\int \limits _0^1 {\psi _1 ^{2}\left( {\bar{{{x}}}} \right) {\hbox {d}}\bar{{{x}}}} }} \right)$, $\varOmega _2 ^{2}=\left( {\chi /{\alpha _{\mathrm{M}} }} \right) \left( {{\int \limits _0^1 {\psi _2 ^{{\prime \prime }\,{\prime \prime }}\left( {\bar{{{x}}}} \right) \psi _2 \left( {\bar{{{x}}}} \right) {\hbox {d}}\bar{{{x}}}} }/{\int \limits _0^1 {\psi _2 ^{2}\left( {\bar{{{x}}}} \right) {\hbox {d}}\bar{{{x}}}} }} \right)$,

$$\begin{aligned}&\alpha _1 =\left( {{3{r}^{2}{A}_1 {L}_1 ^{2}}/{{I}_1 }} \right) \left( {{\int \limits _0^1 {{\psi }_1 ^{'2}\left( {\bar{{{x}}}} \right) {\psi }_1^{''} \left( {\bar{{{x}}}} \right) \psi _1 \left( {\bar{{{x}}}} \right) {\hbox {d}}\bar{{{x}}}} }/{\int \limits _0^1 {\psi _1 ^{2}\left( {\bar{{{x}}}} \right) {\hbox {d}}\bar{{{x}}}} }} \right) , \quad {c}_1 =2\varepsilon ^{2}\mu _1 , \nonumber \\&\quad \alpha _2 ={\psi }_1^{'} \left( 1 \right) \left( {{\int \limits _0^1 {\bar{{{x}}}\psi _2 \left( {\bar{{{x}}}} \right) d\bar{{{x}}}} }/{\int \limits _0^1 {\psi _2 ^{2}\left( {\bar{{{x}}}} \right) {\hbox {d}}\bar{{{x}}}} }} \right) \nonumber \\&\quad \alpha _3 =\left( {{3{A}_2 {L}_2 ^{2}{r}^{2}}/{{I}_2 }} \right) \left( {\chi /{\alpha _{\mathrm{M}} }} \right) \left( {{\int \limits _0^1 {{\psi }_2 ^{'2}\left( {\bar{{{x}}}} \right) {\psi }''_2 \left( {\bar{{{x}}}} \right) \psi _2 \left( {\bar{{{x}}}} \right) {\hbox {d}}\bar{{{x}}}} }/{\int \limits _0^1 {\psi _2 ^{2}\left( {\bar{{{x}}}} \right) {\hbox {d}}\bar{{{x}}}} }} \right) , \quad {c}_2 =2\varepsilon ^{2}\mu _2 \end{aligned}$$

(33)

Now, method of multiple scales is exploited to obtain the analytical and closed-form solution of ${u}_1$ and ${u}_2$ which have been expressed in terms of fast and slow timescales.

$$\begin{aligned} {u}_1= & {} \varepsilon {u}_{11} \left( {{T}_0 ,{T}_1 ,{T}_2 } \right) +\varepsilon ^{2}{u}_{12} \left( {{T}_0 ,{T}_1 ,{T}_2 } \right) +\varepsilon ^{3}{u}_{13} \left( {{T}_0 ,{T}_1 ,{T}_2 } \right) \end{aligned}$$

(34)

$$\begin{aligned} {u}_{2}= & {} \varepsilon {u}_{{21}} \left( {{T}_{0} {,T}_{1} {,T}_{2} } \right) {+\varepsilon }^{{2}}{u}_{{22}} \left( {{T}_{0} {,T}_{1} {,T}_{2} } \right) {+\varepsilon }^{{3}}{u}_{{23}} \left( {{T}_{0} {,T}_{1} {,T}_{2} } \right) \end{aligned}$$

(35)

Here, ${T}_0 =\tau$ is the fast timescale and ${T}_1 =\varepsilon \tau$ and ${T}_2 =\varepsilon ^{2}\tau$ are slow timescales. Using chain rule, time derivatives in terms of ${T}_0$, ${T}_1$ and ${T}_2$ become

$$\begin{aligned} {\mathrm{d}}/{{\mathrm{d}t}}= & {} \partial /{\partial {T}_0 }+\varepsilon \partial /{\partial {T}_1 }+\varepsilon ^{2}\partial /{\partial {T}_2 }, \quad {{\hbox {d}}^{2}}/{{\mathrm{d}t}^{2}}={\partial ^{2}}/{\partial {T}_0 ^{2}}+2\varepsilon \left( {{\partial ^{2}}/{\partial {T}_0 \partial {T}_1 }} \right) \nonumber \\&+\varepsilon ^{2}\left( {2\left( {{\partial ^{2}}/{\partial {T}_0 \partial {T}_2 }} \right) +{\partial ^{2}}/{\partial {T}_1 ^{2}}} \right) \end{aligned}$$

(36)

Substituting Eqs. (34–36) into Eq. (31) and after equating the coefficients of the same powers of ${\varepsilon }$, the following equations are obtained:

$$\begin{aligned}&{O}\left( {\varepsilon ^{1}} \right) : {\partial ^{2}{u}_{11} }/{\partial {T}_0 ^{2}}+\varOmega _1 ^{2}{u}_{11} =0 \end{aligned}$$

(37)

$$\begin{aligned}&{O}\left( {\varepsilon ^{2}} \right) : \left[ {{\partial ^{2}{u}_{12} }/{\partial {T}_0 ^{2}}+2\left( {{\partial ^{2}{u}_{11} }/{\partial {T}_0 \partial {T}_1 }} \right) +\varOmega _1 ^{2}{u}_{12} } \right] =0 \end{aligned}$$

(38)

$$\begin{aligned}&{O}\left( {\varepsilon ^{3}} \right) : {\partial ^{2}{u}_{13} }/{\partial {T}_0 ^{2}}+2\left( {{\partial ^{2}{u}_{12} }/{\partial {T}_0 \partial {T}_1 }} \right) +{\partial ^{2}{u}_{11} }/{\partial {T}_1 ^{2}}+2\left( {{\partial ^{2}{u}_{11} }/{\partial {T}_0 \partial {T}_2 }} \right) \nonumber \\&\quad +\varOmega _1 ^{2}{u}_{13} {-}\alpha _1 {u}_{11} ^{3}+2\mu _1 \left( {{\partial {u}_{11} }/{\partial {T}_0 }} \right) =0 \end{aligned}$$

(39)

The general solution of Eq.(37) can be expressed as:

$$\begin{aligned} {u}_{11} ={P}\left( {{T}_1 ,{T}_2 } \right) {e}^{{i}\varOmega _1 {\mathrm{T}}_0 }+\bar{{{P}}}\left( {{T}_1 ,{T}_2 } \right) {e}^{{-}i\varOmega _1 {\mathrm{T}}_0 } \end{aligned}$$

(40)

Here, $\bar{{{P}}}\left( {{T}_1 ,{T}_2 } \right)$ is the complex conjugate of ${P}\left( {{T}_1 ,{T}_2 } \right)$. Now, substituting Eq. (40) into Eq. (38) gives:

$$\begin{aligned} {\partial ^{{2}}{u}_{{12}} }/{\partial {T}_{0} ^{{2}}}{+\varOmega }_{1} ^{{2}}{u}_{{12}} ={-2i}\left( {{\partial {P}}/{\partial {T}_{1} }} \right) {e}^{{{i}\varOmega }_{1} {{T}}_{0} }+{2i}\left( {{\partial {\bar{{P}}}}/{\partial {T}_{1} }} \right) {e}^{{{-}{i}\varOmega }_{1} {{T}}_{0} } \end{aligned}$$

(41)

The elimination of secular terms in Eq. (41) yields the particular solution as:

$$\begin{aligned} {u}_{{12}} {=0} \end{aligned}$$

(42)

Similarly, the following expression is obtained for the response of ${u}_{13}$:

$$\begin{aligned} {\partial ^{{2}}{u}_{{13}} }/{\partial {T}_{0} ^{{2}}}{+\varOmega }_{1} ^{{2}}{u}_{{13}} =\left( {{{-}2{i}\varOmega }_{1} \left( {{\partial {P}}/{\partial {T}_2}} \right) {+3\alpha }_{1} {P}^{{2}}{\bar{{P}}{-}2{i}\varOmega }_1 \mu _1 {P}} \right) {e}^{{{i}\varOmega }_{1} {{T}}_{0} }{+\alpha }_{1} {P}^{{3}}{e}^{{3\mathrm{i}\varOmega }_{1} {{T}}_{0} }+{\hbox {CC}} \end{aligned}$$

(43)

Here, CC stands for the complex conjugate. Expression of ${P}\left( {{T}_{2} } \right)$ is written in the polar form as $P\left( {T_{2} } \right) = \left( {1/2} \right) a\left( {T_{2} } \right) e^{{i\phi \left( {T_{2} } \right) }}$. Now, eliminating the secular terms from Eq. (43) and separating real and imaginary parts, the following governing equations are obtained for the amplitude ${a}\left( {{T}_{2} } \right)$ and phase $\phi \left( {{T}_{2} } \right)$:

$$\begin{aligned} {\partial {a}}/{\partial {T}_{2} }{-}\mu _1 {a=0}, \quad {a}\varOmega _1 {\partial \phi }/{\partial {T}_{2} }+\left( {3/8} \right) {\alpha }_{1} {a}^{{3}}=0 \end{aligned}$$

(44)

For steady-state condition, the solution of Eq. (44) for a and $\phi$ is as follows:

$$\begin{aligned} {a=a}_{0} \exp ({-}\mu _1 {T}_2 ), \quad \phi {=-}{{3\alpha }_{1} {a}_{0} ^{{2}}{T}_{2} }/{{8\varOmega }_{1} }+\phi _{0} \end{aligned}$$

(45)

Here, ${a}_{0}$ and $\phi _{0}$ are arbitrary constants determined by initial conditions. The particular solution of Eq. (43) is:

$$\begin{aligned} {u}_{{13}} {=-}\left( {{{\alpha }_{1} {P}^{{3}}}/{{8\varOmega }_{1} ^{{2}}}} \right) {e}^{{3{i}\varOmega }_{1} {{T}}_{0} } \end{aligned}$$

(46)

Substituting Eqs. (40, 42, 46) into Eq. (34), and replacing the timescales by original variable $\tau$, one may obtain the following expression for the response for link 1.

$$\begin{aligned} {u}_{1} {=\varepsilon }\left( {{a}/{2}} \right) {\cos }\left( {{\omega \tau +}\phi } \right) {{-}\varepsilon }^{{3}}\left( {{{\alpha }_{1} {a}^{{3}}{\cos }\left( {{3\omega \tau +3}\phi } \right) }/{{64\varOmega }_{1} ^{{2}}}} \right) \end{aligned}$$

(47)

Here, ${\omega =\varOmega }_{1} {-}\left( {{3}/{{8}\varOmega _1 }} \right) {\varepsilon }^{{2}}{\alpha }_{1} {a}_{0} ^{{2}}$; a and $\phi$ are given by Eq. (45).

A similar procedure is adopted as in the case of link 2 to obtain the equations of motion corresponding to each timescale given as:

$$\begin{aligned}&{O}\left( {{\varepsilon }^{{1}}} \right) : \quad {\partial ^{{2}}{u}_{{21}} }/{\partial {T}_{0} ^{{2}}}{+\varOmega }_{2} ^{{2}}{u}_{{21}} {+\alpha }_{2} \left( {{\partial ^{{2}}{u}_{{11}} }/{\partial {T}_{0} ^{{2}}}} \right) {=0} \end{aligned}$$

(48)

$$\begin{aligned}&{O}\left( {{\varepsilon }^{{2}}} \right) :{\partial ^{{2}}{u}_{{22}} }/{\partial {T}_{0} ^{{2}}}{+\varOmega }_{2} ^{{2}}{u}_{{22}} {+2}\left( {{\partial ^{{2}}{u}_{{21}} }/{\partial {T}_{0} \partial {T}_{1} }} \right) {+\alpha }_{2} \left( {{\partial ^{{2}}{u}_{{12}} }/{\partial {T}_{0} ^{{2}}}} \right) {+2\alpha }_{2} \left( {{\partial ^{{2}}{u}_{{11}} }/{\partial {T}_{0} \partial {T}_{1} }} \right) {=0} \end{aligned}$$

(49)

$$\begin{aligned}&{O}\left( {{\varepsilon }^{{3}}} \right) : \left[ {\begin{array}{l} {\partial ^{{2}}{u}_{{23}} }/{\partial {T}_{0} ^{{2}}}{+\varOmega }_{2} ^{{2}}{u}_{{23}} {+2}\left( {{\partial ^{{2}}{u}_{{22}} }/{\partial {T}_{0} \partial {T}_1 }} \right) {+}{\partial ^{{2}}{u}_{{21}} }/{\partial {T}_{1} ^{{2}}}{+2}\left( {{\partial ^{{2}}{u}_{{21}} }/{\partial {T}_{0} \partial {T}_{2} }} \right) {+\alpha }_{2} \left( {{\partial ^{{2}}{u}_{{13}} }/{\partial {T}_{0} ^{{2}}}} \right) \\ {+2\alpha }_{2} \left( {{\partial ^{{2}}{u}_{{12}} }/{\partial {T}_{0} \partial {T}_{1} }} \right) {+\alpha }_{2} \left( {{\partial ^{{2}}{u}_{{11}} }/{\partial {T}_{1} ^{{2}}}} \right) {+2\alpha }_{2} \left( {{\partial ^{{2}}{u}_{{11}} }/{\partial {T}_{0} \partial {T}_{2} }} \right) {{-}\alpha }_{3} {u}_{{21}} ^{{3}}+2\mu _2 \left( {{\partial {u}_{21} }/{\partial {T}_0 }} \right) \\ \end{array}} \right] {=0}\nonumber \\ \end{aligned}$$

(50)

General solution of Eq. (48) can be expressed as:

$$\begin{aligned} {u}_{{21}} {=}\left[ {{Q}\left( {{T}_{1} {,T}_{2} } \right) {e}^{{{i}\varOmega }_{2} {{T}}_{0} }{+}{{\varOmega }_{1} ^{{2}}{\alpha }_{2} {P}\left( {{T}_2 } \right) {e}^{{{i}\varOmega }_{1} {{T}}_{0} }}/{\left( {{\varOmega }_{2} ^{{2}}{{-}\varOmega }_{1} ^{{2}}} \right) }{+\hbox {CC}}} \right] \end{aligned}$$

(51)

Substituting Eqs. (40) and (51) into Eq. (49), one may obtain the following equation as:

$$\begin{aligned} {\partial ^{{2}}{u}_{{22}} }/{\partial {T}_{0} ^{{2}}}{+\varOmega }_{2} ^{{2}}{u}_{{22}} {={-}2\varOmega }_{2} \left( {{\partial {Q}\left( {{T}_{1} {,T}_{2} } \right) }/{\partial {T}_{1} }} \right) {e}^{{{i}\varOmega }_{2} {{T}}_{0} }{+\hbox {CC}} \end{aligned}$$

(52)

Eliminating the secular term proportional to ${e}^{{{i}\varOmega }_{1} {{T}}_{0} }$, hence its coefficient should be zero, i.e., ${\partial {Q}\left( {{T}_{1} {,T}_{2} } \right) }/$${\partial {T}_{1} }{=0}$, which results ${Q=Q}\left( {{T}_{2} } \right)$. The particular solution of Eq. (52) is

$$\begin{aligned} {u}_{{22}} {=0} \end{aligned}$$

(53)

Similarly, one may obtain the following expression for response ${u}_{{23}}$:

$$\begin{aligned} {\partial ^{{2}}{u}_{{23}} }/{\partial {T}_{0} ^{{2}}}{+\varOmega }_{2} ^{{2}}{u}_{{23}} {=}\left[ {\begin{array}{l} {{-}2{i}\varOmega }_{2} \left( {{\partial {Q}\left( {{T}_{2} } \right) }/{\partial {T}_{2} +\mu _2 {Q}}} \right) {e}^{{{i}\varOmega }_{2} {{T}}_{0} }{+}\left( {{{9\alpha }_{1} {\alpha }_{2} {P}^{{3}}}/{8}} \right) {e}^{{3{i}\varOmega }_{1} {{T}}_{0} }-{2i}\alpha _2 \varOmega _1 \left( {{\partial {P}}/{\partial {T}_2 }} \right) {e}^{{{i}\varOmega }_1 {{T}}_{0} }{+} \\ {\alpha }_{3} \left( {\left( {{\varOmega _1 ^{2}\alpha _2 {P}}/{2\left( {\varOmega _2 ^{2}{-}\varOmega _1 ^{2}} \right) }} \right) {e}^{{i}\varOmega _1 {T}_0 }{+Q}\left( {{T}_{2} } \right) {e}^{{{i}\varOmega }_{2} {{T}}_{0} }{+\hbox {CC}}} \right) ^{{3}} \\ \end{array}} \right] \end{aligned}$$

(54)

The particular solution of Eq. (54) can be expressed by the following form:

$$\begin{aligned}&{u}_{{23}} {=}\left[ {{u}_{{231}} {+u}_{{232}} {+u}_{{233}} {+u}_{{234}} {+u}_{{235}} {+u}_{{236}} {+u}_{{237}} {+u}_{{238}} } \right] .\nonumber \\&{u}_{{231}} {=K}_1 {\exp }\left( {{\varOmega }_2 {T}_0 } \right) , \quad {u}_{{232}} {=K}_2 {\exp }\left( {{3\varOmega }_{1} {T}_0 } \right) , \quad {u}_{{233}} {=K}_3 {\exp }\left( {{\varOmega }_{1} {T}_0 } \right) , \nonumber \\&\quad {u}_{{234}} {=K}_4 {\exp }\left( {{\varOmega }_{2} {T}_0 } \right) , {u}_{{235}} {=}K_5 {\exp }\left( {{2\varOmega }_{2} {+\varOmega }_{1} } \right) {T}_0 ,\nonumber \\&{u}_{{236}} {=K}_6 {\cos }\left( {{2\varOmega }_{2} {{-}\varOmega }_{1} } \right) {T}_0 , {u}_{{237}} {=K}_7 \exp \left( {{\varOmega }_{2} {{-}2\varOmega }_{1} } \right) {T}_0 , {u}_{{238}} {=K}_8 {\exp }\left( {{3\varOmega }_{2} {T}_0 } \right) \end{aligned}$$

(55)

It was observed that due to the inertial coupling existing in the second link, the nondimensional frequency, $\varOmega _2$ of second link, is nearly three times the nondimensional frequency $\varOmega _1$ of first link for the first mode for identical masses and link properties, which represent a condition of internal resonance. Hence, ${u}_{231}$ and ${u}_{232}$ in Eq. (66) result in small divisor terms in the present case of internal resonance of 3:1 between two links. The nearness of $\varOmega _1$ to $\left( {1/3} \right) \varOmega _2$ can be expressed as $3\varOmega _1 =\varOmega _2 +\varepsilon ^{2}\sigma$, here $\sigma$ represents the detuning parameter on substitution in Eq. (54), and further elimination of secular terms results in equations:

$$\begin{aligned} {-}2{i}\varOmega _2 \left( {{\partial {Q}}/{\partial {T}_2 }} \right) +\alpha _3 \left( {3{Q}^{2}\bar{{{Q}}}+6{Q}{k}^{2}{P}\bar{{{P}}}} \right) {-}2{i}\varOmega _2 \mu _2 {Q}+\left( {\alpha _3 {k}^{3}{P}^{3}{-}{9\alpha _1 \alpha _2 {P}^{3}}/8} \right) {\exp }\left( {{i}\sigma {T}_2 } \right) =0 \end{aligned}$$

(56)

Here, ${k=}\left( {{{\varOmega }_{1} ^{{2}}{\alpha }_{2} }/{\left( {{\varOmega }_{2} ^{{2}}{{-}\varOmega }_{1} ^{{2}}} \right) }} \right)$. Express ${Q}\left( {{T}_{2} } \right)$ in polar form as ${Q}\left( {{T}_{2} } \right) {=}\left( {{1}/{2}} \right) {b}\left( {{T}_{2} } \right) {e}^{{{i}\gamma }\left( {{{T}}_{2} } \right) }$ and substitute in Eq. (56). Now separating real and imaginary parts from the resulting equation and transformed into an autonomous system by letting $\varphi :\varphi =\sigma {T}_2 +3\phi -\gamma$ we obtain:

$$\begin{aligned}&\varOmega _2 \left( {{\partial {b}}/{\partial {T}_2 }} \right) ={-}\varOmega _2 \mu _2 {b}+\left( {\alpha _3 {k}^{3}{-}{9\alpha _1 \alpha _2 }/8} \right) \left( {{{a}^{3}}/8} \right) {\sin }\left( \varphi \right) \end{aligned}$$

(57)

$$\begin{aligned}&{b}\varOmega _2 \left( {{\partial \varphi }/{\partial {T}_2 }} \right) ={b}\varOmega _2 \sigma +{3\alpha _3 {k}^{2}{a}^{2}{b}}/4{-}{9\alpha _1 {a}^{2}{b}\varOmega _2 }/{8\varOmega _1 }+{3\alpha _3 {b}^{3}}/8+\left( {\alpha _3 {k}^{3}{-}{9\alpha _1 \alpha _2 }/8} \right) \left( {{{a}^{3}}/8} \right) {\cos }\left( \varphi \right) \nonumber \\ \end{aligned}$$

(58)

Equations (57) and (59) are the governing equation for modulation of the amplitude and the phase of the free oscillation term. The first-order solution for the time response of link 2 in terms of original time variable is given by:

$$\begin{aligned} {u}_2 =\left( {1/2} \right) {b\cos }\left( {3\varOmega _1 \tau +3\phi +\varphi } \right) +\left( {{\alpha _2 {a}}/{16}} \right) {\cos }\left( {\varOmega _1 \tau +\phi } \right) \end{aligned}$$

(59)

Here, b and $\varphi$ are given by the autonomous set of Eqs. (57) and (58). For steady-state response the amplitude and phase become constant with respect to time in Eqs. (57) and (58) after which the elimination of phase from both the equations results in the frequency response equation of the system. The stability of the response of second link depends on the stability of the steady-state solution for the amplitude b and phase $\varphi$ given by Eqs. (57–58). If the steady-state solutions are ${b}_{0}$ and $\varphi _0$, their stability is studied by introducing small variations ${b}_1$ and $\varphi _1$ given as ${b}={b}_0 +{b}_1$, $\varphi =\varphi _0 +\varphi _1$ which on substitution in Eqs. (57–58) and linearizing the resulting equations, the following Jacobian matrix is obtained.

$$\begin{aligned} \left\{ {\dot{{X}}} \right\} =\left[ {{\begin{array}{ll} {\varOmega _2 \mu _2 }&{} {\left( {\alpha _3 {k}^{3}{-}{9\alpha _1 \alpha _2 }/8} \right) \left( {{{a}_0 ^{3}}/8} \right) \cos \left( {\varphi _0 } \right) } \\ {{\sigma _1 }/{{b}_0 +}{3\alpha _3 {k}^{2}{a}_0 ^{2}}/{4{b}_0 \varOmega _2 }{-}{9\alpha _1 {a}_0 ^{2}}/{8{b}_0 \varOmega _1 }+{3\alpha _3 {b}_0 }/{8\varOmega _2 }}&{} {-\left( {\alpha _3 {k}^{3}{-}{9\alpha _1 \alpha _2 }/8} \right) \left( {{{a}_0 ^{3}}/8{b}_0 \varOmega _2 } \right) \sin \left( {\varphi _0 } \right) } \\ \end{array} }} \right] \left\{ {X} \right\} \end{aligned}$$

(60)

Here,

$$\begin{aligned} \left\{ {X} \right\} ^{{T}}=\left[ {{b}_1 ,\varphi _1 } \right] \end{aligned}$$

(61)

Stability of the steady-state solution is now decided by the nature of eigenvalues of Jacobian matrix $\left[ {A} \right]$. If all the eigenvalues have negative or zero real parts, the steady-state solutions are stable, otherwise unstable.

Fig. 3

Static deflection of two-link manipulator

Fig. 4

First four mode of vibration of flexible two-link manipulator with tip mass

4 Results and discussion

4.1 Static analysis

Static analysis is very important to understand the displacement profile which may further guide the designer to easily interpret the stress and strain distributions in the system before the process of its design takes place. For the deflection of the tip end, it is assumed that the payload moves vertically downward instead of moving in a circular arc. It is valid if it is assumed to have a low flexure beam. However, industrial manipulators may not satisfy this condition; hence, appropriate modification shall be necessary. Figure 3 shows the static deflection of planar two-link manipulator. To get an idea about the variation of static defection with the flexural rigidity, the three different cases considered here are ${E}_{1} {I}_{1} {>E}_{2} {I}_{2}$, ${E}_{1} {I}_{1} {=E}_{2} {I}_{2}$ and ${E}_{1} {I}_{1} {<E}_{2} {I}_{2}$. The beam characteristics considered are ${L}_1 {, L}_2 {=0.35\,\hbox {m}}$, ${b}_1 {, b}_2 {=0.03\,\hbox {m}}$, ${h}_1 {, h}_2 {=0.003\,\hbox {m}}$, ${\rho }_1 ,\,\rho _2 {=7800\,\hbox {kg}/\hbox {m}}^{3}$. For first case ${E}_1 {=200\,\hbox {GPa}}$ and ${E}_2 {=100\,\hbox {GPa}}$, for second case ${E}_1 {=200\,\hbox {GPa}}$ and ${E}_2 {=200\,\hbox {GPa}}$ and for third case ${E}_1 {=100\,\hbox {GPa}}$ and ${E}_2 {=200\,\hbox {GPa}}$ are considered.

4.2 Eigenfrequencies and spectrums

In Table 1, for a wide range of $\alpha _{\mathrm{m}2}$ (defined in Eq. 15), the corresponding first six eigenfrequency parameters, $\bar{{\beta }}$, are listed, which are the roots of the eigenfrequency equation that has been solved numerically using Newton–Raphson method. The two links are considered to be identical, which renders the values of $\alpha _{\mathrm{L}}$, $\alpha _{\mathrm{M}}$, $\chi$ and $\mu$ as unity, and also the mass parameter $\alpha _{\mathrm{m}1}$ is taken as 1. For the simplicity, we have considered ${E}_1 {I}_1 ={E}_2 {I}_2 ={EI}$, $\rho _1 {A}_1 =\rho _2 {A}_2 =\rho {A}$ and ${L}_1 ={L}_2 ={L}$. From Table 1, it can be observed that the $\bar{{\beta }}$ decreases as $\alpha _{\mathrm{m}2}$ increases, which is obvious from the fact that the natural frequency of a system decreases as the mass of the system increases. Variation of nondimensional eigenfrequency parameter with respect to system mass parameters ($\alpha _{\mathrm{m}1}$ and $\alpha _{\mathrm{m}2}$) is shown in Table 2. It can be noticed that as the system mass parameters increase, the nondimensional eigenfrequency parameter decreases.

Table 1 Variation of nondimensional eigenfrequency parameter with tip mass parameter ($\alpha _{\mathrm{m}2} )$

Table 2 Variation of nondimensional eigenfrequency parameter with system mass parameter ($\alpha _{\mathrm{m}2}$ and $\alpha _{\mathrm{m}2}$)

The effect of flexural rigidity ratio $\left( {\chi ={{E}_2 {I}_2 }/{{E}_1 {I}_1 }} \right)$ on the nondimensional eigenfrequency parameter is shown in Table 3. First six eigenfrequency parameters have been tabulated for a wide range of flexural rigidity ratio which shall cover all the practical values, while other parameters are taken as unity. It is evident from the table that the eigenfrequencies tend to increase with the increasing flexural rigidity ratio. Also, from Tables 4 and 5 it is noticeable that the eigenfrequencies show a decreasing trend with the increase in nondimensional beam mass density and length parameters.

In further text, the effect of variation of essential system parameters over the first four mode shapes of the system is studied. The first four mode shapes of the two-link flexible manipulator system considering $\alpha _{\mathrm{m}1}$, $\alpha _{\mathrm{m2}}\, \alpha _L$, $\alpha _{\mathrm{M}}$, $\chi$ and $\mu$ as unity are shown in Fig. 4. The effect of variation of system mass parameters on the mode shapes is depicted in Fig. 5. A significant decrease in amplitude of the payload with increase in system mass parameter can be noticed for the lower mode shapes; however, higher mode shapes tend to clutter together along the length of manipulator.

Fig. 5

Effect of mass () on eigenspectrums of two-link manipulator

Fig. 6

Effect of flexural rigidity on first four eigenspectrums of flexible two-link manipulator

The flexural rigidity ratio has a noticeable effect on lower as well as higher mode shapes of the manipulator which is shown in Fig. 6. The mode shapes tend to spread out along the length of manipulator and the amplitude of the payload tends to decrease as the flexural rigidity ratio increases. This effect can be very much useful while designing the arms of a robot manipulator made of different materials, as the changes in the flexibility may cause the variation in the amplitude of payload.

The effect of variation of beam mass density ratio parameter on the mode shapes can be observed in Fig. 7. Here also, the effect of mass density parameter is pronounced over the mode shapes for both lower and higher order of vibration. So it can be concluded that the variation of materials in two different arms of the two-link manipulator can cause the significant changes in the amplitude of payload.

Fig. 7

Effect of mass density () on first four mode shapes of flexible two-link manipulator

Fig. 8

A typical frequency response characteristics for link 2

Table 3 Variation of nondimensional eigenfrequency parameter with flexural rigidity ratio $\left( \chi \right)$

Table 4 Variation of nondimensional eigenfrequency parameter with nondimensional mass density parameter $\left( {\alpha _{\mathrm{M}} } \right)$

Table 5 Variation of nondimensional eigenfrequency parameter with nondimensional length parameter $\left( {\alpha _{\mathrm{L}} } \right)$

4.3 Internal resonance: nonlinear phenomena and bifurcations

Internal resonance arising due to the inertial coupling between the two links has been investigated in the present section. The beam characteristics considered here are the same as those in static analysis. The dimensionless parameter, scaling factor and nondimensional representative damping coefficient are considered as 0.1. The initial conditions for link 1 and link 2 are ${u}_{10} =0.1$, $\dot{{u}}_{10} =0$, ${u}_{20} =0$ and $\dot{{u}}_{20} =0$.

For the steady-state response the system exhibits spring softening behavior as shown in Fig. 8 in which the bending represents the presence of nonlinearity in the system. Jump-up and jump-down phenomenon, represented by dotted arrow, is observed at the critical points, B and E, respectively, during starting and stopping of the system. This jump phenomenon observed for the existence of saddle-node bifurcation may cause catastrophic failure of the manipulator. The solid lines represent the stable steady-state solution; dotted line symbolizes the unstable solutions.

Fig. 9

Effect of nondimensional payload mass on frequency response curve of second link

Fig. 10

Effect of nondimensional mass density on frequency response curve of second link

The demonstration of variation of payload mass parameter and beam mass density parameter on the frequency response curve is shown in Figs. 9 and 10, respectively. The maximum amplitude of the steady-state response decreases as the mass parameter of the payload is increased. However, the maximum amplitude tends to increase with the beam mass density parameter. The increase in flexural rigidity ratio tends to increase the amplitude of the system, and the jump-up phenomena start at higher frequencies, which is depicted in Fig. 11.

The coefficients corresponding to cubic nonlinear terms arising due to the axial stretching in both the links can be varied by their respective geometric properties as given in Eq. (33). The effect of nonlinearity variation associated with link 1 and link 2 on the frequency characteristics is elucidated in Figs. 12 and 13, respectively. A sharp increase in amplitude of system response along with the shifting of response curve is observed with the increase in nonlinear coefficient associated with link 1. However, the response curve witnesses substantial decrease in jump length with the increase in cubic nonlinear coefficient associated with link 2.

Fig. 11

Effect of flexural ratio on frequency response curve of second link

Fig. 12

Effect of geometric nonlinearity due to axial stretching $(\alpha _{{1}} )$ of second ink on frequency response characteristics

The effect of nondimensional damping parameter on the frequency response curve is shown in Fig. 14, and it can be observed that the slight increase in damping parameter results in large reduction of peak amplitude of the system. The amplitude of the link 1 or in other words the initial excitation given to link 1 has a pronounced effect of the amplitude of link 2 which is depicted in Fig. 15. A large variation in amplitude of second link is observed for a slight increase in excitation. Also, the jump phenomenon starts at the higher frequency for larger amplitude of first link.

Fig. 13

Effect of geometric nonlinearity due to axial stretching $\alpha _3$ of second link on frequency response characteristics

Fig. 14

Effect of damping on frequency response curve of second link.

Fig. 15

Effect of amplitude of link 1 on frequency response curve of second link

5 Conclusions

The objective of this present work is to describe a brief modeling of N-link flexible manipulator and subsequent generation of eigenfrequencies from the free vibration analysis essential for the design of a two-link flexible manipulator. The modeling is based on the classical Euler–Bernoulli beam model, and eigenfrequency equation has been solved numerically to obtain the eigenspectrums of the system analytically. Static analysis has been carried out to obtain expressions for the defection of manipulator links under gravitational forces. Finally, nonlinear analysis has been accomplished to demonstrate the effect of parametric variation on the stability of the system. The results obtained in this article are summarized as follows:

• 1. The system eigenfrequencies tend to decrease with increase in payload mass, beam mass density and length parameters; however, it increases with flexural rigidity ratio. It is noticed while the system mass parameters tend to affect the lower modes vibration, pronounced effect of beam mass density parameter and flexural rigidity ratio has been observed on higher modes of vibration also.

• 2. Method of multiple scales of second order has been used to interpret the nonlinear behavior of the two link of manipulator for the case of 3:1 internal resonance arising due to inertial coupling. The frequency characteristic curves demonstrate typical nonlinear phenomena such as jump, multivalued amplitudes and S-N bifurcation. These phenomena are highly valuable explicit design variables which often control the stability and safety issues which further restrict the working flexibility of the manipulator.

• 3. The variation of the frequency characteristics with system parameters is inspected thoroughly. The payload mass parameter and nonlinearity coefficient associated with second link tend to decrease the peak amplitude of steady-state response of the system. The system experiences jump phenomenon at higher frequencies for larger values of flexural rigidity ratio and nonlinearity coefficient associated with first link.

• 4. The present model can be used for a greater accuracy as the mode shapes thus obtained included the inertial coupling present in the equations of motion and boundary conditions. Also, for nonlinear analysis the mode shapes thus obtained shall give more accurate results which has been absent in previous models where the mode shapes of the beams with predefined boundary conditions have been used. This improvement in dynamic model shall result in better control strategy to attenuate the vibration of two-link manipulator, especially in space robots.