The effect of longitudinal cracks on buckling loads of columns

Abstract

This paper focuses on development of a new mathematical model and its analytical solution for the buckling analysis of elastic longitudinally cracked columns with finite axial adhesion between the cracked sections. Consequently, the analytical solution for buckling loads is derived for the first time. The critical buckling loads are calculated for different crack lengths and various degrees of the contact adhesion. It is shown that the critical buckling loads can be greatly affected by the crack length and degree of the connection between the cracked sections. Finally, the presented results can be used as a benchmark solution.

1 Introduction

Columns are compression members that are extensively used in structural, mechanical, aerospace, aeronautic, offshore and ocean engineering. In construction, columns are supporting elements for beams, floors, and roofs. They are typical examples of structural elements of building frames, trusses, bridges, multi-storey buildings, and superstructures with new technology, and construction materials. Columns are generally constructed from materials with good compressive strength, such as concrete, timber, steel, and so on.

Nevertheless, stability of compressed columns is one of the main design issues. In other words, long columns in compression are generally prone to buckling. Thus, the stability of slender columns must be controlled to ensure their safety or safety of the entire structure against collapse.

In practice, perfect columns do not exist. They always contain imperfections and unavoidable defects, such as cracks, which are due to mechanical vibrations, cyclic and impact loads, material processing, component manufacturing, structural poor working environment, and others. The presence of cracks reduces the flexural rigidity of a column, its compressive strength, and load-bearing capacity. Consequently, the influence of cracks should be certainly taken into consideration in the stability analysis of cracked columns under compression.

The buckling of cracked columns has received considerable attention, and there exist many interesting investigations in the literature. For example, analytical solutions have been developed for studying the buckling behavior of elastic columns with transverse cracks [1,2,3,4,5,6,7,8], and several numerical models as well [9,10,11,12,13]. However, all those studies have been studying the buckling behavior of columns with transverse cracks. Nevertheless, columns may also have internal longitudinal cracks which can have a crucial impact on their stability and load carrying capacity. Only a few analytical [14,15,16] and numerical [17,18,19,20,21] investigations have been proposed for analyzing the stability of longitudinally cracked columns. Furthermore, it should be noted that some researches have included in their analysis relaxed kinematics such as different joint models at the crack or delamination tips which, see e.g., [15, 16, 22,23,24,25]. However, it should be noted that all of these studies developed so far have dealt with perfectly open longitudinal cracks. In reality, almost all cracks are not fully open and generally crack bridging or some finite adhesion between the cracked sections exists.

However, as the authors’ knowledge is concerned it seems that there exists no analytical solution in the open literature for the buckling analysis of longitudinally cracked columns with finite longitudinal interface adhesion between the cracked segments. Hence, the aim of this paper is to derive a novel mathematical model and its analytical solution for studying the buckling behavior of longitudinally cracked columns with finite longitudinal interface adhesion between the cracked segments. Therefore, this novel analytical formulation proposed in this paper will definitely contribute importantly to the knowledge about the buckling behavior of longitudinally cracked columns with incomplete interaction between adjacent cracked segments.

Finally, an illustrative example is given to present the analytical solution of a timber column with a longitudinal crack and finite longitudinal adhesion between the cracked sections.

2 Theoretical formulation and governing equations

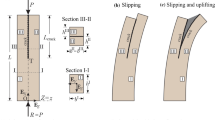
Consider an initially straight, planar, column of undeformed length L and an arbitrary but symmetric cross section, see Fig. 1. The column is cracked in longitudinal direction. A longitudinal crack divides the column into three segments I, II, and III. The crack is located at the tip of the column. The crack length $L_{\mathrm{crack}}$ is arbitrary. Besides, the crack width extends across the entire width of the column. Hence, a relative crack length is defined as $\bar{L}_{\mathrm{crack}}=L_{\mathrm{crack}}/L$. The column is placed in the (X, Z) plane of a spatial/global Cartesian coordinate system with coordinates (X, Y, Z) and unit base vectors $\mathbf {E}_X, \mathbf {E}_Y$ and $\mathbf {E}_Z$. The undeformed reference axis of the longitudinally cracked column is common to all segments. It is defined as an intersection of the (X, Z)-plane and their crack plane. It is parameterized by the undeformed arc-length x. Local coordinate system (x, y, z) is assumed to coincide initially with global coordinates. The column is loaded with a concentric conservative compressive load P.

2.1 Assumptions

The formulation of the governing equations for buckling analysis of longitudinally cracked columns is also based on the following basic assumptions:

• 1. The column and its segments are planar, prismatic, homogeneous, isotropic, and linear elastic;

• 2. Each segment is modeled with a linearized Reissner planar beam theory [26];

• 3. The crack is longitudinal and exists before the column is subjected to compressive loading;

• 4. The segments II and III are continuously connected with an adhesive bonding layer of negligible thickness and finite stiffness;

• 5. The segments II and III can slip relative to each other;

• 6. The interlayer slips are small;

• 7. The segments’ cross sections are not changing in shape and size during deformation;

• 8. Only global type of instability occurs;

• 9. Thermal, rheological, and inertia effects are ignored.

2.2 Governing equations

2.2.1 Algebraic-differential equations of the segments

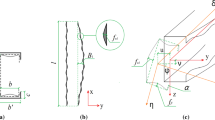
The governing algebraic-differential equations of a column with preexisted longitudinal crack are the kinematic, equilibrium, and constitutive equations along with boundary conditions. Further, there are also constraining equations which define the relations by which individual segment is composed into a complete structure. A compact comma notation $(\bullet )^{i}$ will be used throughout the paper, where superscript i $=$ (I, II, III) indicates to which segment the quantity $(\bullet )$ belongs to. In the same manner, $(\bullet )^{\prime }=\mathrm{d}(\bullet )/\mathrm{d}x$ shall be used for the first derivative of the quantity $(\bullet )$ with respect to the material coordinate x. Thus, the governing differential-algebraic equations of a longitudinally cracked column are as follows:

$$\begin{aligned}&1+u^{i\prime }-(1+\varepsilon ^i)\cos {\varphi ^i}=0, \end{aligned}$$

(1)

$$\begin{aligned}&w^{i\prime }+(1+\varepsilon ^i)\sin {\varphi ^i}=0, \end{aligned}$$

(2)

$$\begin{aligned}&\varphi ^{i\prime }-\kappa ^{i}=0, \end{aligned}$$

(3)

$$\begin{aligned}&R_{X}^{i\prime }+p_{X}^{i}=0, \end{aligned}$$

(4)

$$\begin{aligned}&R_{Z}^{i\prime }+p_{Z}^{i}=0, \end{aligned}$$

(5)

$$\begin{aligned}&M_{Y}^{i\prime }-(1+\varepsilon ^i)(R_{X}^{i}\sin \varphi ^i+R_{Z}^{i}\cos \varphi ^i)=0, \end{aligned}$$

(6)

$$\begin{aligned}&R_{X}^{i}\cos \varphi ^i-R_{Z}^{i}\sin \varphi ^i-C_{11}^i\,\varepsilon ^i-C_{12}^i\,\kappa ^i=0, \end{aligned}$$

(7)

$$\begin{aligned}&\mathcal{M}_Y^i-C_{21}^i\,\varepsilon ^i-C_{22}^i\,\kappa ^i=0, \end{aligned}$$

(8)

where $u^i$ and $w^i$ are the axial and transverse displacements, $\varphi ^i$ is the rotation, $\varepsilon ^i$ is the extensional strain, and $\kappa ^{i}$ is the pseudocurvature of the segment’s reference axis, $R_{X}^{i}, R_{X}^{i}$, and $M_{Y}^{i}$ are the generalized equilibrium internal forces of ith segment, $p_{X}^{i}$ and $p_{Z}^{i}$ are the contact tractions, $C_{11}^i=E^iA^i$, $C_{12}^i=C_{21}^i=E^iS^i$, and $C_{22}^i=E^iJ^i$ are the material and geometric constants; where $A^i$ is the segment i cross-sectional area, $E^i$ is the Young’s modulus, $S^i$ is the static moment, and $J^i$ is the segment i second moment with respect to the reference axis. The corresponding boundary conditions to Eqs. (1)–(8) are: $x^i=0$:

$$\begin{aligned}&S_1^i + R_{X}^i(0)=0 \qquad \mathrm{or} \qquad u^i(0)-u_1^i=0, \end{aligned}$$

(9)

$$\begin{aligned}&S_2^i + R_{Z}^i(0)=0 \qquad \mathrm{or} \qquad w^i(0)-u_2^i=0, \end{aligned}$$

(10)

$$\begin{aligned}&S_3^i + M_{Y}^i(0)=0 \qquad \mathrm{or} \qquad \varphi ^i(0)-u_3^i=0, \end{aligned}$$

(11)

$x^i=L^i$:

$$\begin{aligned}&S_4^i - R_{X}^i(L^i)=0 \qquad \mathrm{or} \qquad u^i(L^i)-u_4^i=0, \end{aligned}$$

(12)

$$\begin{aligned}&S_5^i - R_{Z}^i(L^i)=0 \qquad \mathrm{or} \qquad w^i(L^i)-u_5^i=0, \end{aligned}$$

(13)

$$\begin{aligned}&S_6^i - M_{Y}^i(L^i)=0 \qquad \mathrm{or} \qquad \varphi ^i(L^i)-u_6^i=0, \end{aligned}$$

(14)

where $u_k^i$ and $S_k^i$$(k=1,2, \ldots ,6)$ are given values of generalized boundary displacements and their complementary forces at the segments’ edges, i.e., $x^i=0$ and $x^i=L^i$; $L^i$ is the length of the ith segment.

2.2.2 Constraining equations of segments II and III

Note from Fig. 1 that the longitudinal crack divides the column into three segments, I–III. Generally, this longitudinal crack is not perfect, which means that there still exists some adhesion or connection between the segments II and III. Therefore, the deformations of these segments are not independent, but are constrained to each other. As a result, during deformation of the segment II, a deformation of the segment III is constrained to follow the deformation of the segment II, and vise versa. In the present paper, Sects. 2 and 3 can only slip over each other, while relative deformation in transverse direction is neglected. In this case, contact tractions evolve between the segments II and III. A detailed derivation of the contact model is here omitted, but the interested reader is referred to [27,28,29,30,31,32]. Thus, a slip and the corresponding contact tractions in axial direction develop between the segments II and III

$$\begin{aligned}&\varDelta _X=u^{\mathrm{II}}-u^{\mathrm{III}}, \end{aligned}$$

(15)

$$\begin{aligned}&\varDelta _Z=w^{\mathrm{II}}-w^{\mathrm{III}}=0, \end{aligned}$$

(16)

$$\begin{aligned}&p_X^{\mathrm{II}}=-p_X^{\mathrm{III}}=\mathcal{F}_X(\varDelta _X), \end{aligned}$$

(17)

where $\varDelta _X$ and $\varDelta _Z$ are the slip and uplift between the segments II and III, respectively, $p_X^{\mathrm{II}}$ and $p_X^{\mathrm{III}}$ are the contact tractions in axial direction, and $\mathcal{F}_X$ is the nonlinear constitutive function determined experimentally for the actual type of the contact. It will be shown next that by considering the relations (15)–(17) in Eqs. (1)–(8), the governing algebraic-differential equations, Eqs. (1)–(8), and boundary conditions, Eqs. (11)–(14), of the segments II and III, can be considerably simplified.

2.3 Linearized buckling equations of longitudinally cracked column

Linearized governing equations of the new mathematical model for the analytical investigation of the effect of longitudinal cracks on buckling loads of cracked columns are derived using the first variation of the nonlinear system of governing equations, Eqs. (1)–(17), see e.g., [33]

$$\begin{aligned} \delta {\varvec{\varPi }}({\varvec{x}},\delta {\varvec{x}})=\mathrm{\lim _{\beta \rightarrow 0}}\frac{{\varvec{\varPi }}({\varvec{x}}+\beta \delta {\varvec{x}})- {\varvec{\varPi }}({\varvec{x}})}{\beta }= \frac{\mathrm{d}}{\mathrm{d}\beta }{\varvec{\varPi }}({\varvec{x}}+\beta \delta {\varvec{x}})\bigg \arrowvert _{\beta =0}, \end{aligned}$$

(18)

where ${\varvec{\varPi }}$ is the functional, ${\varvec{x}}$ and $\delta {\varvec{x}}$ are the generalized displacements and their increments, respectively, and $\beta$ is the scalar parameter. The linearized buckling equations of the longitudinally cracked column can be derived, if the linearized governing equations are evaluated at the primary configuration of the cracked column. Hence, the primary configuration is any deformed but straight configuration of the longitudinally cracked column or its segments, and is given as follows:

Section 1:

$$\begin{aligned} \begin{array}{ccccc} \varepsilon ^\mathrm{I}=\displaystyle -\frac{P}{C_{11}^\mathrm{I}}, &{} \kappa ^\mathrm{I}=0 &{} u^\mathrm{I}=u^\mathrm{I}(0)-\displaystyle \frac{xP}{C_{11}^\mathrm{I}}, &{} w^\mathrm{I}=0, &{} R_{X}^\mathrm{I}=-P, \\ R_{Z}^\mathrm{I}=0, &{} M_{Y}^\mathrm{I}=0. &{} &{} &{} \end{array} \end{aligned}$$

(19)

Fig. 1

Longitudinally cracked column subjected to compressive load: a undeformed configuration, b deformed (buckled) configuration with slipping between II and III

Sections 2 and 3 in case of slipping, ($i=\mathrm{II,III}$):

$$\begin{aligned} \begin{array}{ccccc} \varepsilon ^i=\displaystyle -\frac{P}{\sum _i C_{11}^i}, &{} \kappa ^i=0 &{} u^{i}=u^{i}(0)-\displaystyle \frac{xP}{\sum _i C_{11}^i}, &{} w^i=0, &{} R_{X}^i=-\displaystyle \frac{C_{11}^iP}{\sum _i C_{11}^i}, \\ R_{Z}^i=0, &{} M_{Y}^i=0, &{} \varDelta _X=0 &{} p_X^i=0. &{} \end{array} \end{aligned}$$

(20)

Thus, the linearized equations and boundary conditions of each segment of the longitudinally cracked column, when written at the primary configuration, Eqs. (19)–(20), are:

Section 1:

$$\begin{aligned}&\delta u^{\mathrm{I}\prime }-\delta \varepsilon ^\mathrm{I}=0, \end{aligned}$$

(21)

$$\begin{aligned}&\delta w^{\mathrm{I}\prime }+\left( 1-\displaystyle \frac{P}{C_{11}^\mathrm{I}}\right) \delta \varphi ^\mathrm{I}=0, \end{aligned}$$

(22)

$$\begin{aligned}&\delta \varphi ^{\mathrm{I}\prime }-\delta \kappa ^\mathrm{I}=0, \end{aligned}$$

(23)

$$\begin{aligned}&\delta R_{X}^{\mathrm{I}\prime }=0, \end{aligned}$$

(24)

$$\begin{aligned}&\delta R_{Z}^{\mathrm{I}\prime }=0, \end{aligned}$$

(25)

$$\begin{aligned}&\delta M_{Y}^{\mathrm{I}\prime }-\left( 1-\displaystyle \frac{P}{C_{11}^\mathrm{I}}\right) \left( \delta R_{Z}^\mathrm{I}-P \delta \varphi ^\mathrm{I}\right) =0, \end{aligned}$$

(26)

$$\begin{aligned}&\delta R_{X}^\mathrm{I}-C_{11}^\mathrm{I}\delta \varepsilon ^\mathrm{I}-C_{12}^\mathrm{I}\delta \kappa ^\mathrm{I}=0, \end{aligned}$$

(27)

$$\begin{aligned}&\delta M_Y^\mathrm{I}-C_{21}^\mathrm{I}\delta \varepsilon ^\mathrm{I}-C_{22}^\mathrm{I}\delta \kappa ^\mathrm{I}=0, \end{aligned}$$

(28)

$$\begin{aligned}&S_1^\mathrm{I} + \delta R_{X}^\mathrm{I}(0)=0 \qquad \mathrm{or} \qquad \delta u^\mathrm{I}(0)-u_1^\mathrm{I}=0, \end{aligned}$$

(29)

$$\begin{aligned}&S_2^\mathrm{I} + \delta R_{Z}^\mathrm{I}(0)=0 \qquad \mathrm{or} \qquad \delta w^\mathrm{I}(0)-u_2^\mathrm{I}=0, \end{aligned}$$

(30)

$$\begin{aligned}&S_3^\mathrm{I} + \delta M_{Y}^\mathrm{I}(0)=0 \qquad \mathrm{or} \qquad \delta \varphi ^\mathrm{I}(0)-u_3^\mathrm{I}=0, \end{aligned}$$

(31)

$$\begin{aligned}&S_4^\mathrm{I} - \delta R_{X}^\mathrm{I}(L^\mathrm{I})=0 \qquad \mathrm{or} \qquad \delta u^\mathrm{I}(L^i)-u_4^\mathrm{I}=0, \end{aligned}$$

(32)

$$\begin{aligned}&S_5^\mathrm{I} - \delta R_{Z}^\mathrm{I}(L^\mathrm{I})=0 \qquad \mathrm{or} \qquad \delta w^\mathrm{I}(L^i)-u_5^\mathrm{I}=0, \end{aligned}$$

(33)

$$\begin{aligned}&S_6^\mathrm{I} - \delta M_{Y}^\mathrm{I}(L^\mathrm{I})=0 \qquad \mathrm{or} \qquad \delta \varphi ^\mathrm{I}(L^\mathrm{I})-u_6^\mathrm{I}=0, \end{aligned}$$

(34)

Equations (21)–(28) constitute a system of 2 algebraic and 8 differential equations for 8 unknown functions $\delta u^{\mathrm{I}}, \delta w^{\mathrm{I}}, \delta \varphi ^{\mathrm{I}}, \delta R_{X}^{\mathrm{I}}, \delta R_{Z}^{\mathrm{I}}, \delta M_{Y}^{\mathrm{I}}, \varepsilon ^\mathrm{I}$, and $\kappa ^\mathrm{I}$. Moreover, Eqs. (29)–(34) represent 6 boundary conditions, either kinematic or static.

Sections 2 and 3 in case of slipping, ($i=\mathrm{II,III}$):

$$\begin{aligned}&\delta u^{i\prime }-\delta \varepsilon ^i=0, \end{aligned}$$

(35)

$$\begin{aligned}&\delta w^{\mathrm{II}\prime }+\left( 1-\displaystyle \frac{P}{\sum _i C_{11}^i}\right) \delta \varphi ^{\mathrm{II}}=0 \quad \mathrm{and} \quad \delta w^{\mathrm{III}}=\delta w^{\mathrm{II}}, \end{aligned}$$

(36)

$$\begin{aligned}&\delta \varphi ^{\mathrm{II}\prime }-\delta \kappa ^{\mathrm{II}}=0 \quad \mathrm{and} \quad \delta \varphi ^{\mathrm{III}}=\delta \varphi ^{\mathrm{II}} \quad \mathrm{and} \quad \delta \kappa ^{\mathrm{III}}=\delta \kappa ^{\mathrm{II}}, \end{aligned}$$

(37)

$$\begin{aligned}&\delta R_{X}^{\mathrm{II}\prime }-\delta p_{X}^{\mathrm{II}}=0 \quad \mathrm{and} \quad \delta R_{X}^{\mathrm{III}\prime }-\delta p_{X}^{\mathrm{III}}=0 \end{aligned}$$

(38)

$$\begin{aligned}&\delta R_{Z}^\prime =0, \end{aligned}$$

(39)

$$\begin{aligned}&\delta M_{Y}^{\prime }-\left( 1-\displaystyle \frac{P}{\sum _i C_{11}^i}\right) (\delta R_{Z}-P \delta \varphi ^{\mathrm{II}})=0 \quad \mathrm{and} \quad \delta M_{Y}=\sum _i \delta M_{Y}^i \end{aligned}$$

(40)

$$\begin{aligned}&\delta R_{X}^{i}-C_{11}^i\delta \varepsilon ^i-C_{12}^i\delta \kappa ^i=0, \end{aligned}$$

(41)

$$\begin{aligned}&\delta M_Y^i-C_{21}^i\delta \varepsilon ^i-C_{22}^i\delta \kappa ^i=0 \end{aligned}$$

(42)

$$\begin{aligned}&\delta \varDelta _X-\delta u^{\mathrm{II}}+\delta u^{\mathrm{III}}=0 \end{aligned}$$

(43)

$$\begin{aligned}&\delta p_{X}^{\mathrm{II}}-K\delta \varDelta _X=0 \end{aligned}$$

(44)

$$\begin{aligned}&\delta p_{X}^{\mathrm{II}}+\delta p_{X}^{\mathrm{III}}=0 \end{aligned}$$

(45)

$$\begin{aligned}&S_1^i + \delta R_{X}^i(0)=0 \quad \quad \mathrm{or} \quad \quad \delta u^i(0)-u_1^i=0, \end{aligned}$$

(46)

$$\begin{aligned}&\sum _i S_2^i + \delta R_{Z}(0)=0 \quad \quad \mathrm{or} \quad \quad \delta w^{\mathrm{II}}(0)-u_2^{\mathrm{II}}=0, \end{aligned}$$

(47)

$$\begin{aligned}&\sum _i S_3^i + \delta M_{Y}(0)=0 \quad \quad \mathrm{or} \quad \quad \delta \varphi ^{\mathrm{II}}(0)-u_3^{\mathrm{II}}=0, \end{aligned}$$

(48)

$$\begin{aligned}&S_4^i - \delta R_{X}^i(L^i)=0 \quad \quad \mathrm{or} \quad \quad \delta u^i(L^i)-u_4^i=0, \end{aligned}$$

(49)

$$\begin{aligned}&\sum _i S_5^i - \delta R_{Z}(L^{\mathrm{II}})=0 \quad \quad \mathrm{or} \quad \quad \delta w^{\mathrm{II}}(L^{\mathrm{II}})-u_5^{\mathrm{II}}=0, \end{aligned}$$

(50)

$$\begin{aligned}&\sum _i S_6^i - \delta M_{Y}(L^{\mathrm{II}})=0 \quad \quad \mathrm{or} \quad \quad \delta \varphi ^{\mathrm{II}}(L^{\mathrm{II}})-u_6^{\mathrm{II}}=0, \end{aligned}$$

(51)

Equations (35)–(45) constitute a system of 11 algebraic and 8 differential equations for 19 unknown functions $\delta u^{\mathrm{II}}, \delta u^{\mathrm{III}}, \delta w^{\mathrm{II}}, \delta w^{\mathrm{III}}, \delta \varphi ^{\mathrm{II}}, \delta \varphi ^{\mathrm{III}}, \delta R_{X}^{\mathrm{II}}, \delta R_{X}^{\mathrm{III}},\delta R_{Z}, \delta M_{Y}, \delta M_{Y}^{\mathrm{II}}$, $\delta M_{Y}^{\mathrm{III}}, \varepsilon ^{\mathrm{II}}$, $\varepsilon ^{\mathrm{III}}$, $\kappa ^{\mathrm{II}}$, $\kappa ^{\mathrm{III}}$, $\delta \varDelta _X, \delta p_{X}^{\mathrm{II}}$, and $\delta p_{X}^{\mathrm{III}}$. Moreover, Eqs. (46)–(51) represent 8 boundary conditions, either kinematic or static.

2.4 Continuity conditions

At the junction of the segments I–III, namely at point T, see Fig. 1, the kinematic continuity conditions and continuity in equilibrium forces and moments have to be assured. These conditions are expressed as follows, ($i=\mathrm{II, III}$):

$$\begin{aligned}&\delta u^\mathrm{I}(L^\mathrm{I})-\delta u^{\mathrm{II}}(0)=0, \end{aligned}$$

(52)

$$\begin{aligned}&\delta u^\mathrm{I}(L^\mathrm{I})-\delta u^{\mathrm{III}}(0)=0, \end{aligned}$$

(53)

$$\begin{aligned}&\delta w^\mathrm{I}(L^\mathrm{I})-\delta u^{\mathrm{II}}(0)=0, \end{aligned}$$

(54)

$$\begin{aligned}&\delta \varphi ^\mathrm{I}(L^\mathrm{I})-\delta \varphi ^{\mathrm{II}}(0)=0, \end{aligned}$$

(55)

$$\begin{aligned}&\delta R_X^\mathrm{I}(L^\mathrm{I})-\sum _i \delta R_X^i(0)=0, \end{aligned}$$

(56)

$$\begin{aligned}&\delta R_Z^\mathrm{I}(L^\mathrm{I})-\delta R_Z^{\mathrm{II}}(0)=0, \end{aligned}$$

(57)

$$\begin{aligned}&\delta M_Y^\mathrm{I}(L^\mathrm{I})-\delta M_Y^{\mathrm{II}}(0)=0. \end{aligned}$$

(58)

Fig. 2

Geometric and material properties of a column with preexisted longitudinal tip crack

Fig. 3

Normalized buckling load, $\bar{P}_{\mathrm{cr}}$, of a longitudinally cracked C–F column versus normalized crack length, $\bar{L}_{\mathrm{crack}}$, for different Ks, where K (kN/cm$^2$)

Fig. 4

Normalized buckling load, $\bar{P}_{\mathrm{cr}}$, of a longitudinally cracked P–P column versus normalized crack length, $\bar{L}_{\mathrm{crack}}$, for different Ks, where K (kN/cm$^2$)

Fig. 5

Normalized buckling load, $\bar{P}_{\mathrm{cr}}$, of a longitudinally cracked C–P column versus normalized crack length, $\bar{L}_{\mathrm{crack}}$, for different Ks, where K (kN/cm$^2$)

2.5 Analytical solution

An analytical solution of the buckling equations of a longitudinally cracked column can be found if the system of the derived linearized buckling equations (21)–(28), (35)–(44), and the corresponding boundary conditions (29)–(34), (46)–(51), and continuity conditions (52)–(58) are written as a homogeneous system of first order linear differential equations as

$$\begin{aligned} {\varvec{Y}}^{\prime }(x)={\varvec{A}}{\varvec{Y}}(x), \end{aligned}$$

(59)

and

$$\begin{aligned} {\varvec{Y}}(0)={\varvec{Y}}_0, \end{aligned}$$

(60)

where ${\varvec{Y}}(x)$ is the vector of 14 unknown basic functions of the problem, i.e., ${\varvec{Y}}=(\delta u^{\mathrm{I}}, \delta u^{\mathrm{II}}, \delta u^{\mathrm{III}}, \delta w^{\mathrm{I}}, \delta w^{\mathrm{II}}, \delta \varphi ^{\mathrm{I}}$, $\delta \varphi ^{\mathrm{II}}, \delta R_{X}^{\mathrm{I}}, \delta R_{X}^{\mathrm{II}}, \delta R_{X}^{\mathrm{III}},\delta R_{Z}^{\mathrm{I}}, \delta R_{Z}, \delta M_{Y}^{\mathrm{I}}, \delta M_{Y})^T$, ${\varvec{Y}}(0)$ is the vector of unknown integration constants, and ${\varvec{A}}$ is the constant real $14 \times 14$ matrix. An analytical solution of the problem (59)–(60) is simply obtained with Mathematica [34] and given in compact form as, see e.g., [35]:

$$\begin{aligned} {\varvec{Y}}(x)={e}^{{\varvec{A}}\displaystyle x}{\varvec{Y}}_0. \end{aligned}$$

(61)

Using the appropriate boundary and continuity conditions yields a system of 14 linear, homogeneous algebraic equations for the 14 unknown integration constants which are the initial values of the kinematic quantities and equilibrium moments and forces

$$\begin{aligned} {\varvec{K}}{\varvec{Y}}_0={\varvec{0}}, \end{aligned}$$

(62)

where ${\varvec{K}}$ denotes the tangent $14 \times 14$ stiffness matrix. For a non-trivial solution of (62) to exist, the determinant of the matrix ${\varvec{K}}$ must vanish. The characteristic equation is given by

$$\begin{aligned} \big \arrowvert {\varvec{K}}\big \arrowvert =0. \end{aligned}$$

(63)

and the lowest eigenvalue is a measure of the critical buckling load $P_{\mathrm{cr}}$. The analytical expressions for critical buckling loads are generally too cumbersome to be presented as closed-form expressions. As a result, in the next section, the results for buckling loads are presented in tabular and graphical form.

3 Illustrative example

In what follows, an illustrative example of analytical investigation is given to analyze the variation of the critical buckling loads with a crack length and a degree of adhesion between the cracked segments. To this end, the buckling loads of four different columns with classical boundary conditions are calculated using the present analytical model. The analyzed columns are clamped-free (C–F), pinned-pinned (P–P), clamped-pinned (C–P), and clamped-clapped (C–C). The geometric and material properties of the longitudinally cracked column under consideration are given in Fig. 2. Note that the normalized buckling load is defined as $\bar{P}_{\mathrm{cr}}=P_{\mathrm{cr}}/P_\mathrm{E}$, where $P_{\mathrm{cr}}$ is the critical buckling load of the cracked column and $P_\mathrm{E}$ is the Euler buckling load for the uncracked column. Besides, the normalized crack length is defined as $\bar{L}_{\mathrm{crack}}=L^{\mathrm{II}}/L$, where $L^{\mathrm{II}}=L^{\mathrm{III}}$ is the crack length and L is the undeformed length of the column. The results are shown by Figs. 3, 4, 5, 6, 7 and 8 and Tables 1, 2, 3 and 4.

Fig. 6

Normalized buckling load, $\bar{P}_{\mathrm{cr}}$, of a longitudinally cracked C–C column versus normalized crack length, $\bar{L}_{\mathrm{crack}}$, for different Ks, where K (kN/cm$^2$)

Fig. 7

Normalized buckling load, $\bar{P}_{\mathrm{cr}}$, of a longitudinally cracked C–F column as a function of crack length $\bar{L}_{\mathrm{crack}}$, and contact stiffness Ks, where K (kN/cm$^2$)

Fig. 8

Contours of the normalized critical buckling load, $\bar{P}_{\mathrm{cr}}$, of longitudinally cracked columns for various $\bar{L}_{\mathrm{crack}}$ and Ks: a C–F case, b P–P case, c C–P case, and d C–C case

The results of a longitudinally cracked C–F column are given in Fig. 3 and Table 1, respectively. It can be seen from Fig. 3 and Table 1 that the normalized buckling load of the C–F column, $\bar{P}_{\mathrm{cr}}$, can decrease significantly as the crack length $L_{\mathrm{crack}}$ increases and/or the longitudinal stiffness K of the contact decreases. The effect of the crack length is obviously dependent on K, and vice versa. It is interestingly to note that in the limiting case, when the column is fully cracked, i.e., $\bar{L}_{\mathrm{crack}}=1$ and $K=0$ kN/cm$^2$, the critical buckling load is only 43.75% of the Euler buckling load for the uncracked column. On the other hand, when there is perfectly stiff connection between the segments I and III, or there is no longitudinal crack at all, the critical buckling load is the Euler buckling load for the uncracked column. In all other cases, the critical buckling load is affected appreciably by the presence of a longitudinal crack, except for $\bar{L}_{\mathrm{crack}}\lesssim 0.2$ or $K\gtrsim 10$ kN/cm$^2$, as can clearly be seen from Fig. 3 and Table 1. It is also interesting to note that the relation between $\bar{P}_{\mathrm{cr}}$ and $\bar{L}_{\mathrm{crack}}$ is clearly nonlinear.

Table 1 Normalized buckling load, $\bar{P}_{\mathrm{cr}}$, of a longitudinally cracked C–F column for different normalized crack lengths, $\bar{L}_{\mathrm{crack}}$, and Ks, where K (kN/cm$^2$)

Table 2 Normalized buckling load, $\bar{P}_{\mathrm{cr}}$, of a longitudinally cracked P–P column for different normalized crack lengths, $\bar{L}_{\mathrm{crack}}$, and Ks, where K (kN/cm$^2$)

Table 3 Normalized buckling load, $\bar{P}_{\mathrm{cr}}$, of a longitudinally cracked C–P column for different normalized crack lengths, $\bar{L}_{\mathrm{crack}}$, and Ks, where K (kN/cm$^2$)

Table 4 Normalized buckling load, $\bar{P}_{\mathrm{cr}}$, of a longitudinally cracked C–C column for different normalized crack lengths, $\bar{L}_{\mathrm{crack}}$, and Ks, where K (kN/cm$^2$)

The results of a longitudinally cracked P–P column are given in Fig. 4 and Table 2, respectively. As would be expected, the normalized buckling loads of the P–P column, $\bar{P}_{\mathrm{cr}}$, decrease significantly as the crack length $L_{\mathrm{crack}}$ increases and/or the longitudinal stiffness K of the contact decreases, as well. Again, the effect of the crack length is obviously dependent on K, and vice versa. In the limiting case, namely when the column is fully cracked, i.e., $\bar{L}_{\mathrm{crack}}=1$ and $K=0$ kN/cm$^2$, the critical buckling load is again only 43.75% of the Euler buckling load of the uncracked column. Similarly, for a perfectly stiff connection between the segments I and III, or there is no longitudinal crack at all, the critical buckling load is the Euler buckling load for the uncracked column. In all other cases, the critical buckling load is affected appreciably by the presence of a longitudinal crack, except for $\bar{L}_{\mathrm{crack}}\lesssim 0.24$ or $K\gtrsim 8$ kN/cm$^2$, as can clearly be seen from Fig. 3 and Table 1. It is also interesting to note that the relation between $\bar{P}_{\mathrm{cr}}$ and $\bar{L}_{\mathrm{crack}}$ is clearly nonlinear.

The results of a longitudinally cracked C–P column are given in Fig. 5 and Table 3, respectively. For the case of longitudinally cracked C–P column, the results reveal similar trends as in the previous two examples. The critical buckling load is considerably affected by the presence of a longitudinal crack. Further, the critical buckling load is also significantly affected by the contact stiffness K. Thus, for finite contact stiffness, the normalized critical buckling load is in the range $0.4375 \le \bar{P}_{\mathrm{cr}} < 1.0$, while for $\bar{L}_{\mathrm{crack}}=0$ and/or $K=\infty$ the $\bar{P}_{\mathrm{cr}}=1.0$. The effect of longitudinal crack on $\bar{P}_{\mathrm{cr}}$ can be neglected for $\bar{L}_{\mathrm{crack}}\lesssim 0.18$ or $K\gtrsim 32$ kN/cm$^2$, as can clearly be seen from Fig. 5 and Table 3.

The results of a longitudinally cracked C–C column are given in Fig. 6 and Table 4, respectively. Again, for the case of longitudinally cracked C–P column the results reveal similar trends as in the previous three examples. Nevertheless, it can be seen that $\bar{P}_{\mathrm{cr}}$ is decreased notably for $\bar{L}_{\mathrm{crack}}>0$ independently on K, except for very stiff connections $K>10^3$ kN/cm$^2$.

The effect of a longitudinal crack and contact stiffness can be shown also by three-dimensional plot. For example, Fig. 7 shows a normalized buckling load $\bar{P}_{\mathrm{cr}}$ of a longitudinally cracked C–F column as a function of $\bar{L}_{\mathrm{crack}}$ and K. This way, it is clearly seen again that in the case of a longitudinally cracked C–F column the effect of a longitudinal crack on buckling load can be neglected for $\bar{L}_{\mathrm{crack}}\lesssim 0.37$ or $K\gtrsim 6$ kN/cm$^2$.

Finally, the results for all four types of boundary conditions are compared to each other. Thus, the different contours for $\bar{P}_{\mathrm{cr}}$ are shown in Fig. 8.

It can be observed in Fig. 8 that increasing $\bar{L}_{\mathrm{crack}}$ decreases the critical buckling load, $P_{cr}$ in all cases of supporting conditions. This effect is the largest for C–F case, while for C–C case is the smallest. Furthermore, the effect of the crack length on the critical buckling load can be neglected, namely, is less than 10% in C–F case for $\bar{L}_{\mathrm{crack}}\lesssim 0.27$ and/or $K\gtrsim 6$ kN/cm$^2$, in P–P case for $\bar{L}_{\mathrm{crack}}\lesssim 0.24$ and/or $K\gtrsim 8$ kN/cm$^2$, in C–F case for $\bar{L}_{\mathrm{crack}}\lesssim 0.18$ and/or $K\gtrsim 32$ kN/cm$^2$, and in C–C case $\bar{L}_{\mathrm{crack}}\lesssim 0.04$ and/or $K\gtrsim 1000$ kN/cm$^2$.

4 Conclusions

The paper presented a new mathematical model and its analytical solution for the buckling analysis of longitudinally cracked columns and finite adhesion between the cracked sections. The critical buckling loads were calculated for different types of boundary conditions. The parametric study was performed by which the effects of crack length and degree of adhesion were analyzed in detail. Based on the result obtained, the following conclusions can be drawn:

• 1. The analytical solution of the buckling behavior of elastic longitudinally cracked columns with finite axial adhesion between the cracked sections was derived for the first time.

• 2. The critical buckling load decreases with the increasing of the crack length. Furthermore, the critical buckling load also decreases with decreasing the contact stiffness in longitudinal direction.

• 3. The effect of the crack length on the critical buckling load can be neglected, namely, is less than 10%, in C–F case for $\bar{L}_{\mathrm{crack}}\lesssim 0.37$ and/or $K\gtrsim 6$ kN/cm$^2$, in P–P case for $\bar{L}_{\mathrm{crack}}\lesssim 0.24$ and/or $K\gtrsim 8$ kN/cm$^2$, in C–P case for $\bar{L}_{\mathrm{crack}}\lesssim 0.18$ and/or $K\gtrsim 32$ kN/cm$^2$, and in C–C case $\bar{L}_{\mathrm{crack}}\lesssim 0.04$ and/or $K\gtrsim 1000$ kN/cm$^2$.

• 4. The present mathematical model is general and relatively easy to comprehend.

• 5. The analytical results can be used as a benchmark solution.

• 6. Due to the length and complexity of the obtained analytical solution, the closed-form expressions cannot be shown in the paper.