Dynamic response of a circular inclusion embedded in inhomogeneous half-space

Abstract

Dynamic response of a shallow circular inclusion under incident SH wave in radially inhomogeneous half-space is researched by applying complex function theory and multipolar coordinate system. Considering that the mass density of the half-space varies along with the radius direction, the governing equation is expressed as a Helmholtz equation with a variable coefficient. Based on the conformal mapping method, the Helmholtz equation with a variable coefficient is transformed into its normalized form. Then, the expressions of incident wave, reflected wave and scattering wave are obtained, and the standing wave function is deduced by considering the circular inclusion subsequently. According to displacement and stress continuous condition of the inclusion, the undetermined coefficients in scattering wave and standing wave are solved. Finally, dynamic stress concentration factor around the inclusion is calculated and discussed. Numerical results demonstrate the validity of the method and influential factors of dynamic stress concentration factor.

1 Introduction

The problem of elastic wave propagation in continuous medium is an important issue in elastodynamics. Research about wave propagation can provide help for many fields in practical engineering, such as geological exploration, structure seismology and damage identification. As defects, including cavities, inclusions and cracks, always exist in continuous medium, scattering of elastic waves and dynamic stress concentration around defects are often discussed in wave motion researches. Early in 1973, Pao and Mow [1] researched the problems of dynamic stress concentration around several kinds of defects. Then, lots of numerical examples were given. Similar problems were also discussed based on complex function theory by Liu et al. [2] in 1982. Moreover, because most materials and media in nature are inhomogeneous, researches of wave propagation in inhomogeneous medium have become increasingly popular in wave motion field in recent years. However, analytical solutions of governing equations with variable coefficients are tough to obtain because mass density or modulus is no longer constant in inhomogeneous medium, so solving problems of wave propagation in inhomogeneous medium confronts new challenges.

Wave propagation problems have still widely been discussed in the past few years. Ultrasonic waves scattering by closed cracks subject to contact acoustic nonlinearity (CAN) was researched by Blanloeuil et al. [3]. The scattering was nonlinear, and 2D finite element coupled with analytical approach was applied to solve the problem. Then, directivity patterns were analyzed and the characteristics of the nonlinear scattering from a closed crack were identified. The time-harmonic response of a laterally loaded fixed-head pile group embedded in a transversely isotropic multilayered half-space was studied by Ai, Li and Wang [4] by using finite element and indirect boundary element coupling method. Then the validity of the method in this work was verified and the influences of the soil’s anisotropy and layering on the dynamic response of pile groups were investigated. Liu et al. [5] studied the theoretical solutions of SH waves propagating in periodically layered piezomagnetic structure. When the piezomagnetism was ignored or the magnetic circuit was closed and open, the dispersion equation and transmission coefficients were derived in order to reveal the wave behavior. Same features were observed for the band gaps of the magnetically closed and open cases except the zero-order mode. Barnwell et al. [6] discussed the effect of nonlinear elastic pre-stress on antiplane elastic wave propagation in a two-dimensional periodic structure. Based on the plane-wave-expansion method, the permissable eigenfrequencies were determined. Numerical results showed that pre-stress significantly affects the band gap structure for Mooney–Rivlin-type and Fung-type materials. It also leads to the possibility of phononic cloaks for a specific class of materials. Free vibration analysis of nonuniform rectangular membranes was researched by Bahrami and Teimourian [7] based on wave propagation approach. The obtained hints are useful for the analysis of energy transmission in micro-/nano-devices. Shi et al. [8] investigated the wave propagation characteristics of double-layer grapheme sheets (DLGSs). By using nonlocal Mindlin–Reissner plate theory, cutoff frequency and escape frequency were analyzed in the study. The study provides a better representation of wave propagation in DLGSs. It also has implications in their application as electromechanical oscillators. Eskandari et al. [9] paid their attention on the elastodynamics response of a surface-stiffened transversely isotropic half-space subjected to a buried time-harmonic normal load. The half-space was reinforced by a Kirchhoff thin plate on its surface. Some plots of practical importance were depicted based on the proposed numerical scheme. Sheikhhassani and Dravinski [10] discussed the dynamic stress concentration factor around the multiple multilayered inclusions which were embedded in an elastic half-space. The BEM results were contrasted with the analytical results, and the other cases of scattering were considered as well. The dispersive behavior of finite-amplitude time-harmonic Love waves propagating in a pre-stressed compressible elastic half-space was investigated by Kayestha et al. [11]. The half-space was overlaid with two compressible elastic surface layers of finite thickness, and the layers were different composed of the half-space. Then, numerical results demonstrated the variation of the Love wave speed with the pre-stress and the propagation angle. Khurana and Tomar [12] studied the propagation of Rayleigh-type surface waves in nonlocal micropolar elastic solid half-space. Frequency equations of two modes of Rayleigh-type waves and their conditions of existence were derived. Phase speeds of these waves were computed, and their variation against wavenumber is presented subsequently. An improved analytical approach of scattering of Lamb waves was researched by Poddar and Giurgiutiu [13]. The method is efficient and accurate to calculate the scattering of straight-crested Lamb waves from geometric discontinuities. A perfectly matched layer formulation for the GFDM was obtained by Salete et al. [14]. The stability of perfectly matched layer regions was also guaranteed to solve the problem of wave propagation.

In the past decade, more and more problems on wave propagation in inhomogeneous medium were researched by many scholars. Achenbach and Balogun [15] discussed the problem of antiplane surface waves on a half-space. The half-space was inhomogeneous, and the mass density and the shear modulus were depth dependent. The dependence function was arbitrary, and then the restrictions for the existence of surface waves were discussed. Anisotropic and dispersive wave propagation within linear strain-gradient elasticity was investigated by Rosi and Auffray [16]. The problem is derived theoretically, and then numerical results on hexagonal chiral and achiral lattices were discussed. Hei et al. [17, 18] researched the dynamic response of elastic waves by cavity or inclusion in exponentially inhomogeneous medium. By applying the complex function theory and conformal mapping technique, the dynamic behavior of the inhomogeneous medium was investigated. Then, dynamic stress concentration factor around the cavity and the inclusion was calculated. Doc et al. [19] studied the multimodal sound propagation in a waveguide with varying cross section based on the Bremmer series method. The accuracy and convergence of the solution were inspected, and a comparison was made. The solution showed that the first-order Bremmer series was a relevant alternative to classical WKB or one-way approximations. The problem of localization of random acoustic sources in an inhomogeneous medium was considered by Khazaie et al. [20] via different source localization methods. The sound source position was described by a random variable. The sound propagation medium was assumed to have spatially varying parameters with known values. The results indicated that the source identification methods have different robustness in the presence of uncertainties. Leiderman et al. [21] presented an analytic numerical method to simulate the interaction of ultrasonic guided waves with nonuniform interfacial imperfections in elastic multilayered structures. The method could suit the condition of anisotropic and isotropic layers, and the upper and lower substrates may be solid, fluid or vacuum.

This paper aims to research scattering of SH wave by a circular inclusion in radially inhomogeneous half-space. The mass density of the background medium is no longer constant, and the Helmholtz equation becomes a partial differential equation with a variable coefficient. Based on the conformal mapping method, the Helmholtz with a variable coefficient is converted into its normalized form. Then incident wave, reflected wave, scattering wave and standing wave are obtained. Considering different parameters, dynamic stress concentration around the circular inclusion is calculated and discussed. The validity of the method is confirmed, and the influential factors of dynamic stress concentration factor are determined.

2 Statement of inhomogeneity

Fig. 1

Scattering model of a circular inclusion in inhomogeneous half-space

Fig. 2

Verification of DSCF by the degeneration procedure ($\beta =1.0$, ${{\mu }_{2}}=0$, $\alpha =0$, ${d}/{a}=50$)

Fig. 3

Distribution of DSCF around the circular inclusion ($\beta =1.0$, $\alpha =0$, ${d}/{a}=50$)

Fig. 4

Distribution of DSCF with different $\beta a$ (${{k}^{*}}=0.5$, ${{\mu }^{*}}=0.25$, ${d}/{a}=2$)

Fig. 5

Distribution of DSCF with different $\beta a$ (${{k}^{*}}=2.0$, ${{\mu }^{*}}=4.0$, ${d}/{a}=2$)

Fig. 6

Distribution of DSCF with $\beta a=0.8$ (${{k}^{*}}=0.5$, ${{\mu }^{*}}=0.25$, ${d}/{a}=2$)

Fig. 7

Distribution of DSCF with $\beta a=0.9$ (${{k}^{*}}=0.5$, ${{\mu }^{*}}=0.25$, ${d}/{a}=2$)

Fig. 8

Distribution of DSCF with $\beta a=1.0$ (${{k}^{*}}=0.5$, ${{\mu }^{*}}=0.25$, ${d}/{a}=2$)

Fig. 9

Distribution of DSCF with $\beta a=1.1$ (${{k}^{*}}=0.5$, ${{\mu }^{*}}=0.25$, ${d}/{a}=2$)

Fig. 10

Distribution of DSCF with $\beta a=1.2$ (${{k}^{*}}=0.5$, ${{\mu }^{*}}=0.25$, ${d}/{a}=2$)

Fig. 11

Distribution of DSCF with ${{k}_{1}}a=0.1$ (${{k}^{*}}=0.5$, ${{\mu }^{*}}=0.25$, $\beta a=1.2$)

Fig. 12

Distribution of DSCF with ${{k}_{1}}a=0.5$ (${{k}^{*}}=0.5$, ${{\mu }^{*}}=0.25$, $\beta a=1.2$)

Fig. 13

Distribution of DSCF with ${{k}_{1}}a=1.0$ (${{k}^{*}}=0.5$, ${{\mu }^{*}}=0.25$, $\beta a=1.2$)

Fig. 14

Distribution of DSCF with ${{k}_{1}}a=2.0$ (${{k}^{*}}=0.5$, ${{\mu }^{*}}=0.25$, $\beta a=1.2$)

Fig. 15

Variation of DSCFs with $\beta a$ (${{k}^{*}}=2.0$, ${{\mu }^{*}}=4.0$, ${d}/{a}=2$)

Fig. 16

Variation of DSCFs with $\beta a$ (${{k}_{1}}a=1.0$, ${d}/{a}=2$)

Fig. 17

Variation of DSCFs with d / a (${{k}^{*}}=2.0$, ${{\mu }^{*}}=4.0$, $\beta a=0.8$)

Fig. 18

Variation of DSCFs with d / a (${{k}_{1}}a=1.0$, $\beta a=0.8$)

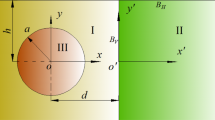
The model of the radially inhomogeneous half-space with a circular inclusion under SH wave with arbitrary incident angle $\alpha$ is shown in Fig. 1. The horizontal surface is at ${{y}_{1}}=0$, and the origin of the coordinate xoy is supposed to be located at the center of the inclusion. The radius of the inclusion is a, and the burial depth is d. Hence, xoy coordinate system has the following connection with ${{x}_{1}}{{o}_{1}}{{y}_{1}}$ coordinate

$$\begin{aligned} \left\{ \begin{array}{lr} {{x}_{1}}=x&{}\\ {{y}_{1}}=y+d.&{} \\ \end{array} \right. \end{aligned}$$

(1)

The inhomogeneous background medium of the half-space (medium I) is different with the shallow inclusion (medium II). The circular inclusion is homogeneous. ${{\rho }_{1}}$ and ${{\mu }_{1}}$ are the mass density and shear modulus of medium I, while ${{\rho }_{2}}$ and ${{\mu }_{2}}$ are mass density and shear modulus of medium II. The wave number ratio ${{k}^{*}}$ is ${{k}^{*}}={{{k}_{2}}}/{{{k}_{1}}}$, and shear modulus ratio ${{\mu }^{*}}$ is ${{\mu }^{*}}={{{\mu }_{1}}}/{{{\mu }_{2}}}$. In polar coordinate, the density of medium I is a function which can be expressed as

$$\begin{aligned} {{\rho }_{1}}\left( r \right) ={{\rho }_{1}}{{\beta }^{2}}{{r}^{2\left( \beta -1 \right) ,}} \end{aligned}$$

(2)

where ${{\rho }_{1}}$ is a constant, $\beta$ is the inhomogeneity parameter of medium I, and $\beta >0$.

Based on the property of the inhomogeneous half-space, the wave velocity in medium I is given by

$$\begin{aligned} {{c}_{1}}\left( r \right) =\dfrac{{{c}_{1}}}{\beta }{{r}^{1-\beta }}, \end{aligned}$$

(3)

where ${{c}_{1}}=\sqrt{{{{\mu }_{1}}}/{{{\rho }_{1}}}}$ is the reference wave velocity in medium I.

3 Governing equations

Considering the radial inhomogeneity of the half-space and the harmonic and steady excitation, then supposing that the body force equals to zero, the wave equation in polar coordinate can be written as

$$\begin{aligned} \dfrac{{{\partial }^{2}}w}{\partial {{r}^{2}}}+\dfrac{1}{r}\dfrac{\partial w}{\partial r}+\dfrac{1}{{{r}^{2}}}\dfrac{{{\partial }^{2}}w}{\partial {{\theta }^{2}}}+k_{1}^{2}{{\beta }^{2}}{{r}^{2\left( \beta -1 \right) }}w=0, \end{aligned}$$

(4)

where $w=w(x,y)$ is the displacement function and ${{k}_{1}}=\omega /{{c}_{1}}$ is the reference wave number.

Introducing the complex variable system $z=r{{\text {e}}^{\text {i}\theta }}$, Eq. (4) becomes

$$\begin{aligned} \frac{{{\partial }^{2}}w}{\partial z\partial \bar{z}}+\frac{1}{4}{{\beta }^{2}}{{\left( z\bar{z} \right) }^{\beta -1}}k_{1}^{2}w=0. \end{aligned}$$

(5)

Based on the transformation method applied in [18], a conformal transformation is introduced

$$\begin{aligned} \chi ={{z}^{\beta }},~\bar{\chi }={{\bar{z}}^{\beta }}. \end{aligned}$$

(6)

Substituting Eq. (6) into Eq. (5) yields the normalized Helmholtz equation

$$\begin{aligned} \frac{{{\partial }^{2}}w}{\partial \chi \partial \bar{\chi }}+\frac{1}{4}k_{1}^{2}w=0. \end{aligned}$$

(7)

4 Displacement fields and stress components

Based on the derivation in the section above, the incident wave which propagates with $\alpha$ in medium I can be expressed as

$$\begin{aligned} {{w}^{\left( i \right) }}={{w}_{0}}\exp \left[ \frac{\text {i}{{k}_{1}}}{2}\left( {{\chi }_{1}}{{\text {e}}^{-\text {i}\alpha }}+{{{\bar{\chi }}}_{1}}{{\text {e}}^{\text {i}\alpha }} \right) \right] , \end{aligned}$$

(8)

where ${{\chi }_{1}}={{\left( z+d\text {i} \right) }^{\beta }}$ and ${{\bar{\chi }}_{1}}={{\left( \bar{z}-d\text {i} \right) }^{\beta }}$. ${{w}_{0}}$ is the displacement amplitude of incident wave, and ${{k}_{1}}$ is the reference wave number of the background medium. Correspondingly, the reflected wave in medium I is

$$\begin{aligned} {{w}^{\left( r \right) }}={{w}_{0}}\exp \left[ \frac{\text {i}{{k}_{1}}}{2}\left( {{\chi }_{1}}{{\text {e}}^{\text {i}\alpha }}+{{{\bar{\chi }}}_{1}}{{\text {e}}^{-\text {i}\alpha }} \right) \right] . \end{aligned}$$

(9)

Moreover, in medium I, the scattering wave excited by the homogeneous inclusion obeys

$$\begin{aligned} {{w}^{\left( s \right) }}\left( \chi ,\bar{\chi } \right) =\sum \limits _{n=-\infty }^{\infty }{{{A}_{n}}\left\{ H_{n}^{\left( 1 \right) }\left( {{k}_{1}}\left| \chi \right| \right) {{\left\{ \frac{\chi }{\left| \chi \right| } \right\} }^{n}}+H_{n}^{\left( 1 \right) }\left( {{k}_{1}}\left| {{\chi }_{2}} \right| \right) {{\left\{ \frac{{{\chi }_{2}}}{\left| {{\chi }_{2}} \right| } \right\} }^{-n}} \right\} }, \end{aligned}$$

(10)

where ${{A}_{n}}$ are undetermined coefficients and $H_{n}^{\left( 1 \right) }\left( \cdot \right)$ is the first kind Hankel function of nth order. ${{\chi }_{2}}={{(z+2d\text {i})}^{\beta }}$, and the scattering wave can satisfy the zero-stress boundary condition at ${{y}_{1}}=0$ and the Sommerfeld radiation condition at infinity automatically.

Because the inclusion is homogeneous, the standing wave in medium II can be expressed as

$$\begin{aligned} {{w}^{\left( t \right) }}=\sum \limits _{n=-\infty }^{\infty }{{{B}_{n}}}{{J}_{n}}\left( {{k}_{2}}\left| z \right| \right) {{\left\{ \frac{z }{\left| z \right| } \right\} }^{n}}, \end{aligned}$$

(11)

where ${{k}_{2}}$ is the wave number corresponding to medium II. ${{J}_{n}}$ is the Bessel function of the nth order, and ${{B}_{n}}$ are undetermined coefficients.

With the aids of a derivative method for compound function utilized in [18], then aiming at the radially inhomogeneous half-space, the stress components have the form of

$$\begin{aligned} {{\tau }_{rz}}= & {} \mu \left( \frac{\partial w}{\partial \chi }\frac{{\mathrm{d}}\chi }{{\mathrm{d}}z}{{\text {e}}^{\text {i}\theta }}+\frac{\partial w}{\partial \bar{\chi }}\frac{{\mathrm{d}}\bar{\chi }}{{\mathrm{d}}\bar{z}}{{\text {e}}^{-\text {i}\theta }} \right) \end{aligned}$$

(12)

$$\begin{aligned} {{\tau }_{\theta z}}= & {} i\mu \left( \frac{\partial w}{\partial \chi }\frac{{\mathrm{d}}\chi }{{\mathrm{d}}z}{{\text {e}}^{\text {i}\theta }}-\frac{\partial w}{\partial \bar{\chi }}\frac{{\mathrm{d}}\bar{\chi }}{{\mathrm{d}}\bar{z}}{{\text {e}}^{-\text {i}\theta }} \right) . \end{aligned}$$

(13)

Substituting different displacement fields into Eqs. (12) and (13), respectively, the detailed stress components can be obtained.

5 Boundary conditions and dynamic stress concentration factor

Considering the connection between the background medium and the circular inclusion, the boundary condition is the continuity condition of displacement and stress at $r=a$, respectively,

$$\begin{aligned} \left\{ \begin{array}{ll} {w}_\mathrm{I}={w}_\mathrm{II}&{}\\ {\tau }_{rz,\mathrm{I}}= {\tau }_{rz,\mathrm{II}},&{} \\ \end{array} \right. \end{aligned}$$

(14)

where ${{w}_{\mathrm{I}}}={{w}^{\left( i \right) }}+{{w}^{\left( r \right) }}+{{w}^{\left( s \right) }}$, ${{w}_{\mathrm{II}}}={{w}^{\left( t \right) }}$, ${{\tau }_{rz,{\mathrm{I}}}}=\tau _{rz}^{\left( i \right) }+\tau _{rz}^{\left( r \right) }+\tau _{rz}^{\left( s \right) }$, ${{\tau }_{rz,{\mathrm{II}} }}=\tau _{rz}^{\left( t \right) }$. Hence, the boundary condition can be expressed as

$$\begin{aligned} \left\{ \begin{array}{lr} \sum \limits _{n=-\infty }^{\infty }{\left( {{A}_{n}}{{\varepsilon }_{n}}+{{B}_{n}}{{\delta }_{n}} \right) =\varepsilon }&{}\\ \sum \limits _{n=-\infty }^{\infty }{\left( {{A}_{n}}{{\xi }_{n}}+{{B}_{n}}{{\zeta }_{n}} \right) =\xi },&{} \\ \end{array} \right. \end{aligned}$$

(15)

where

$$\begin{aligned} {{\varepsilon }_{n}}= & {} -\left( H_{n}^{\left( 1 \right) }\left( {{k}_{1}}\left| \chi \right| \right) {{\left\{ \frac{\chi }{\left| \chi \right| } \right\} }^{n}}+H_{n}^{\left( 1 \right) }\left( {{k}_{1}}\left| {{\chi }_{2}} \right| \right) {{\left\{ \frac{{{\chi }_{2}}}{\left| {{\chi }_{2}} \right| } \right\} }^{-n}} \right) \end{aligned}$$

(16)

$$\begin{aligned} {{\delta }_{n}}= & {} {{J}_{n}}\left( {{k}_{2}}\left| z \right| \right) {{\left\{ \frac{z }{\left| z \right| } \right\} }^{n}} \end{aligned}$$

(17)

$$\begin{aligned} \varepsilon= & {} {{w}_{0}}\left( \exp \left[ \frac{\text {i}{{k}_{1}}}{2}\left( {{\chi }_{1}}{{\text {e}}^{-\text {i}\alpha }}+{{{\bar{\chi }}}_{1}}{{\text {e}}^{\text {i}\alpha }} \right) \right] +\exp \left[ \frac{\text {i}{{k}_{1}}}{2}\left( {{\chi }_{1}}{{\text {e}}^{\text {i}\alpha }}+{{{\bar{\chi }}}_{1}}{{\text {e}}^{-\text {i}\alpha }} \right) \right] \right) \end{aligned}$$

(18)

$$\begin{aligned} {{\xi }_{n}}= & {} -\dfrac{{{\mu }_{1}}{{k}_{1}}}{2}\left\{ \left[ H_{n-1}^{\left( 1 \right) }\left( {{k}_{1}}\left| \chi \right| \right) {{\left( \dfrac{\chi }{\left| \chi \right| } \right) }^{n-1}}\cdot \dfrac{{\mathrm{d}}\chi }{{\mathrm{d}}z} \right. \right. \nonumber \\&\left. +H_{n-1}^{\left( 1 \right) }\left( {{k}_{1}}\left| {{\chi }_{2}} \right| \right) {{\left( \dfrac{{{\chi }_{2}}}{\left| {{\chi }_{2}} \right| } \right) }^{-n+1}}\cdot \dfrac{\mathrm{d}{{\chi }_{2}}}{{\mathrm{d}}z} \right] {{\text {e}}^{\text {i}\theta }}\nonumber \\&-\left[ H_{n+1}^{\left( 1 \right) }\left( {{k}_{1}}\left| \chi \right| \right) {{\left( \dfrac{\chi }{\left| \chi \right| } \right) }^{n+1}}\cdot \dfrac{{\mathrm{d}}\bar{\chi }}{{\mathrm{d}}\bar{z}} \right. \nonumber \\&\left. \left. +\,H_{n+1}^{\left( 1 \right) }\left( {{k}_{1}}\left| {{\chi }_{2}} \right| \right) {{\left( \dfrac{{{\chi }_{2}}}{\left| {{\chi }_{2}} \right| } \right) }^{-n-1}}\cdot \dfrac{\mathrm{d}{{{\bar{\chi }}}_{2}}}{{\mathrm{d}}\bar{z}} \right] {{\text {e}}^{-\text {i}\theta }} \right\} \end{aligned}$$

(19)

$$\begin{aligned} {{\zeta }_{n}}= & {} \frac{{{\mu }_{2}}{{k}_{2}}}{2}\left\{ {{J}_{n-1}}\left( {{k}_{2}}\left| z \right| \right) {{\left( \frac{z }{\left| z \right| } \right) }^{n-1}}\cdot {{\text {e}}^{\text {i}\theta }} \right. \nonumber \\&\left. -{{J}_{n+1}}\left( {{k}_{2}}\left| z \right| \right) {{\left( \frac{z }{\left| z \right| } \right) }^{n+1}}\cdot {{\text {e}}^{-\text {i}\theta }} \right\} \end{aligned}$$

(20)

$$\begin{aligned} \xi= & {} \frac{\text {i}}{2}{{\mu }_{1}}{{k}_{1}}{{w}_{0}}\left\{ \left[ \frac{\mathrm{d}{{\chi }_{1}}}{{\mathrm{d}}z}{{\text {e}}^{\text {i}\left( \theta -\alpha \right) }}+\frac{\mathrm{d}{{{\bar{\chi }}}_{1}}}{{\mathrm{d}}\bar{z}}{{\text {e}}^{\text {i}\left( \alpha -\theta \right) }} \right] \cdot \exp \left[ \frac{\text {i}{{k}_{1}}}{2}\left( {{\chi }_{1}}{{\text {e}}^{-\text {i}\alpha }}+{{{\bar{\chi }}}_{1}}{{\text {e}}^{\text {i}\alpha }} \right) \right] \right. \nonumber \\&\left. +\left[ \frac{\mathrm{d}{{\chi }_{1}}}{{\mathrm{d}}z}{{\text {e}}^{\text {i}\left( \theta +\alpha \right) }}+\frac{\mathrm{d}{{{\bar{\chi }}}_{1}}}{{\mathrm{d}}\bar{z}}{{\text {e}}^{-\text {i}\left( \theta +\alpha \right) }} \right] \cdot \exp \left[ \frac{\text {i}{{k}_{1}}}{2}\left( {{\chi }_{1}}{{\text {e}}^{\text {i}\alpha }}+{{{\bar{\chi }}}_{1}}{{\text {e}}^{-\text {i}\alpha }} \right) \right] \right\} . \end{aligned}$$

(21)

Multiplying ${{\text {e}}^{-\text {i}m\theta }}$ with both sides of Eq. (15) and integrating on the interval $\left( -\pi ,\pi \right)$ yields

$$\begin{aligned} \sum \limits _{n=-\infty }^{\infty }{\left[ \begin{matrix} {{\varepsilon }_{mn}} &{}\quad {{\delta }_{mn}} \\ {{\xi }_{mn}} &{}\quad {{\zeta }_{mn}} \\ \end{matrix} \right] }\left[ \begin{matrix} {{A}_{n}} \\ {{B}_{n}} \\ \end{matrix} \right] =\left[ \begin{matrix} {{\varepsilon }_{m}} \\ {{\xi }_{m}} \\ \end{matrix} \right] \begin{matrix} {} &{} {} \\ \end{matrix}\quad m=n=0,\pm 1,\pm 2\ldots \end{aligned}$$

(22)

Hence, the undefined coefficients ${{A}_{n}}$ and ${{B}_{n}}$ can be solved.

Based on the definition of dynamic stress concentration factor (DSCF), the expression of DSCF is

$$\begin{aligned} \tau _{\theta z}^{*}=\left| {\tau _{\theta z}^{\left( \cdot \right) }}/{{{\tau }_{0}}} \right| , \end{aligned}$$

(23)

where $\tau _{\theta z}^{\left( \cdot \right) }=\tau _{\theta z}^{\left( i \right) }+\tau _{\theta z}^{\left( r \right) }+\tau _{\theta z}^{\left( s \right) }$ and ${{\tau }_{0}}=\frac{1}{2}{{\mu }_{1}}{{k}_{1}}{{w}_{0}}$ is the stress amplitude of incident wave.

6 Numerical results and discussion

In order to verify the validity of the method presented in this paper, some degenerated results are considered to compare with published results. In Fig. 2, we set $\beta =1.0$, ${{\mu }_{2}}=0$, ${d}/{a}=50$ to simulate the condition of plane SH wave propagating in homogeneous infinite medium with a circular cavity. The numerical results coincide with the results in [1] by Pao and Mow perfectly.

Figure 3 demonstrates the distribution of DSCF around the circular inclusion in homogeneous infinite medium by setting $\beta =1.0$, ${{k}_{1}}=1$, ${d}/{a}=50$. The degenerated results are the same as the results in [18].

Figures 4 and 5 show the distribution of DSCF at different ${{k}^{*}}$ and ${{\mu }^{*}}$ when inhomogeneity parameter $\beta a$ equals 0.6, 0.8, 1.0 and 1.2. In the examples, the incident angle is supposed to be zero in order to simplify the solving of the problem. The dimensionless wave number in the background medium is ${{k}_{1}}a=1.0$. When the background medium is softer than the inclusion (Fig. 4), the DSCF is small, but when the background medium is harder than the inclusion (Fig. 5), the DSCF turns bigger. In half-space, the distribution of DSCF no longer has the property of symmetry because of the influence of the surface. The distribution of DSCF becomes complex when the inhomogeneity parameter augments. This phenomenon which appears in both the background medium is softer or harder than the circular inclusion.

The distribution of DSCF at different inhomogeneity parameter $\beta a$ is presented in Figs. 6, 7, 8, 9 and 10 when ${{k}_{1}}a$ is 0.1, 0.5, 1.0 and 1.5. The DSCF increases as the wave number augments, but the distribution of DSCF changes little when the wave number turns bigger. When $\beta a=0.8$, the maximum of DSCF appears at $\theta ={\pi }/{2}$ and $\theta =3{\pi }/{2}$ except the case of ${{k}_{1}}a=1.0$. When $\beta a=0.9$ and 1.0, the maximum of DSCF is at $\theta ={\pi }/{2}$ and $\theta =3{\pi }/{2}$ as well. Moreover, when $\beta a=1.0$, the problem degenerates to the case of homogeneous problem. When $\beta a>1.0$, the distribution of DSCF becomes complicated. The maximum of DSCF has the tendency to appear at $\theta =\pi$. It can be inferred that the maximum of DSCF will move from $\theta ={\pi }/{2}$ and $\theta =3{\pi }/{2}$ to $\theta =\pi$ when the inhomogeneous parameter increases.

Because the surface has an effect on the propagation of SH wave, the depth of the inclusion will influence the distribution of DSCF. Figures 11, 12, 13 and 14 demonstrate the distribution of DSCF with different ${{k}_{1}}a$ when the depth of the inclusion d / a equals 2.0, 5.0, 10.0 and 15.0. The influence of the burial depth is little when ${{k}_{1}}a=0.1$. That is because ${{k}_{1}}a=0.1$ approaches the problem of steady case. When the wave number augments, the effect of burial depth appears. In the condition of ${{k}_{1}}a=1.0$ and ${{k}_{1}}a=1.5$, the distribution of DSCF changes obviously with the depth of the inclusion increasing. Furthermore, the distribution of DSCF has the tendency to be symmetric with the x-axis which approaches the full-space condition. The influence of the depth on the DSCF indicates that deep inclusion embedded can be safer because of the lower dynamic stress around it.

Figures 15 and 16 plot the variation of DSCFs at $\theta ={\pi }/{2}$ with changing inhomogeneity parameter $\beta a$. The dynamic stress concentration factors are almost the same when $\beta a<0.3$ because the mass density of the background medium is small. When $\beta a>0.3$, the DSCFs under different ${{k}_{1}}a$ are different from each other. In Fig. 15, the DSCFs increase when $\beta a<1.3$ and decrease when $\beta a>1.3$ except the condition of ${{k}_{1}}a=1.5$. The dynamic stress concentration factor at high density is much bigger than the one at low density, but when $\beta a>1.3$, the phenomenon is opposite. That is because the maximum of DSCF moves to $\theta =\pi$ when $\beta a>1.0$ gradually. In the case of ${{k}_{1}}a=1.5$, the distribution of DSCF around the inclusion is complicated, so the variation of DSCF with $\beta a$ is complicated as well. Similarly in Fig. 16, the DSCFs increase when $\beta a<1.3$ and decrease when $\beta a>1.3$. Moreover, when $\beta a>1.3$, the DSCFs no longer decrease monotonically under the condition of ${{k}^{*}}=0.5$ (${{\mu }^{*}}=0.25$) and ${{k}^{*}}=4.0$ (${{\mu }^{*}}=16.0$). The DSCFs fluctuate with the inhomogeneity parameter changing.

The variation of DSCFs with changing depth of the inclusion d / a is given in Figs. 17 and 18. With the depth varying, the DSCFs fluctuate regularly. When d / a is small, the value of DSCF is big due to the influence of the surface. However, the value of DSCF becomes smaller and nearly stable when ${d}/{a}>20$. That presents the case of full-space problem. As the wave number ${{k}_{1}}a=0.1$, the DSCFs varies little with the increasing burial depth because it approaches the problem of steady case. This conclusion is identical to the conclusion in Figs. 11, 12, 13 and 14. When ${{k}_{1}}a$ becomes larger, the variation of DSCFs is significant.

7 Conclusions

Dynamic response of a circular inclusion in inhomogeneous half-space is researched in the present paper based on the complex function theory and multipolar coordinates system. Considering the property of the background medium, the Helmholtz equation with a variable coefficient is transformed into its normalized form. The general expressions of displacement fields and stress components are obtained, and dynamic stress distribution induced by circular inclusion is calculated and discussed. According to the numerical results, some inclusions are obtained:

• (1) The high rigidity of the inclusion decreases the DSCF around it, while the soft inclusion enhances the stress around it.

• (2) The changing of inhomogeneity parameter influences the distribution of DSCF evidently, and it influences the maximum of DSCF as well.

• (3) The depth of the inclusion is a significant parameter to affect DSCF around the inclusion, especially under high-frequency incident wave.

Generally, the inhomogeneity of the underground medium is nonnegligible in practical engineering, and the rigid, deep-embedded inclusion is much safer than the soft, shallow-embedded one.