1 Introduction

The specific advantages for composite laminates such as high strength-to-weight ratio, stiffness-to-weight ratio and easy tailorability to any shape make them suitable for use in aircraft, spacecraft, space structures, marines, automobiles and medical applications. It leads to high-performance lightweight structures with much high reliability and durability in their service life. However, there remains the risk of interfacial delamination due to induced transverse shear stresses at interfaces [1]. The stresses must be accurately calculated at every point in the laminate and suitable failure theory be used to ensure that the structure maintains the required factor of safety before actual testing is conducted. The displacements and stresses are evaluated through analytical modeling and numerical modeling using classical laminate theory (CLT), first-order shear deformation theory (FSDT), third-order theory (TOT), higher-order theory (HOT), layerwise theory (LWT), zigzag theory (ZIGT) and global–local theory (GLT), or more accurately by using three-dimensional (3D) elasticity solution. Obtaining 3D solutions for general loading and general boundary conditions is very difficult or in some cases not possible. Displacement-based 2D theories, which employ different degrees of approximations in the displacement field, are more simple to formulate and use.

The CLT [2,3,4] assumes that the straight lines normal to the mid-surface before deformation remain straight and normal to the mid-surface after deformation; in other words, the deformation of the plate is due to bending and inplane stretching. It results in under-prediction of deflections. The FSDT [5,6,7,8,9,10] allows constant rotation of the transverse normals. Arbitrary shear correction factors, which are dependent on lamination, geometric parameters, loading and boundary conditions, are taken into account to provide a better evaluation of the transverse shear deformability on a strain energy basis. Thus, its accuracy is greatly dependent on the choice of the shear correction factors. The CLT and FSDT are based on the state of plane stress and use the reduced form of constitutive equation. The TOT [11,12,13] utilizes quadratic variation of the transverse shear strains in its displacement field approximation and satisfies vanishing transverse shear stress conditions on the bottom and top surfaces. Thus, there is no need of shear corrections factors and the accuracy of the results is improved than the FSDT although the computational effort is increased. The HOT [14,15,16,17,18] introduces additional unknowns to the displacement field. The CLT, FSDT, TOT and HOT are categorized as equivalent single-layer theories (ESLTs), since they make suitable assumptions for the kinematics of deformation through the entire thickness of the laminate. The ESLTs are often found to yield sufficiently accurate global response for thin to moderately thick laminates. However, their accuracy deteriorates when the laminate becomes thicker. And also they are incapable of predicting state of stress at the layer interfaces which are responsible for failure or success of the laminates during their service life. The reviews [19,20,21] provide further details on these ESL theories. The inability of these non-layerwise ESLTs to accurately predict the transverse shear stresses directly from the constitutive equations has remained a great concern [22].

To improve the predictions of displacements and stresses in thick laminates, layerwise theory [23, 54, 55] is employed. This theory introduces discrete-layer transverse shear effects by allowing the inplane displacements to vary in layerwise manner through the laminate and can very well capture the zigzag distribution of inplane displacements particularly for thick laminates which have been observed from the exact 3D solutions [25,26,27]. The computational expense is huge for the LWT, since the number of unknowns increases proportionately with the increase in number of layers. The ZIGT [28,29,30,31,32, 45,46,47,48,49,50] is an efficient counterpart of LWT. Murakami’s zigzag theory [31] is based on the geometric zigzag functions which do not satisfy continuity of transverse shear stresses across laminate thickness, rather it satisfies displacement continuity. This theory was extended by Toledano and Murakami [32] by choosing inplane and transverse displacements to be a superposition of Murakami zigzag functions with cubic polynomials. This resulted in yielding continuous and piecewise fourth-order transverse shear stresses and a continuous fifth-order transverse normal stress. The effect of choosing and not choosing Murakami zigzag function in any equivalent single-layer model was thoroughly researched by Carrera et al. [33, 35, 37, 38, 58, 60], Demasi [56], Ali et al. [40], Ganapathi and Mackecha [41], Umasree and Bhaskar [42], D’Ottavio et al. [43] and Vidal and Polit [44]. It is established that inclusion of Murakami zigzag functions to the displacement field has selective advantage in obtaining accuracy, not universal advantage.

Apart from considering same approximation for displacements as done by LWT, the zigzag theory includes additional quadratic and cubic variation or trigonometric variation globally for inplane displacement field. The zigzag pattern variation in inplane displacement is taken a priori in each layer of the multilayered laminate. The computational expensiveness is eleminated/reduced drastically by enforcing continuity of displacements and stresses at all interfaces. The efficiency is restored back to the same as that of an equivalent single-layer theory. This theory presents a better representation of the actual deformation in anisotropic laminated composite structures. A historical review of various approaches used for zigzag theories is given by Carrera [52]. As a general classification, a zigzag theory can be a Lekhnitskii-type multilayered theory extended from beams to plates by Ren [53]. The second category is called Ambartsumian-type multilayered theory, which is extended to anisotropic as well as non-symmetric plates by Whitney [54], Chou and Carleone [55] and by Di Sciuva [30, 45] for anisotropic multilayered plates and shells. This approach was furthered by Cho and Parmerter [48] for general laminate configurations. The third category of zigzag theory can be called as Reissner multilayer theory which considers transverse stresses and displacements as primary unknowns [28, 29] and uses the popularly known Reissner’s mixed variational theorem. Murakami [31] employed a kinematic-based zigzag function in the inplane displacement field, and this approach was championed by Carrera [51], Demasi [56, 81], Brischetto et al. [58, 59] and Rodrigues et al. [60]. Many zigzag theories suffer from the drawback while implementing in finite elements for plates and shells [61] that C\(^1\)-continuity is required in transverse displacement but is not desirable. It has also been noticed that transverse shear stresses vanish along clamped boundaries when calculated from constitutive equations, which should not be the case. This led to a refined zigzag theory by Tessler et al. [62]. In this refined theory, layerwise zigzag functions were added to the FSDT approximations of inplane displacement field. Such zigzag functions did not require imposition of transverse shear stress continuity condition, yet yielded accurate results. Since this refined theory possessed first derivatives in the strain field, it led to successful development of C\(^0\)-continuous finite elements for beams and plates [63, 64], and a correct description of non-vanishing transverse shear forces at clamped boundaries. The refined zigzag theory originally developed for laminated beams has been extended by Tessler et al. [65] to laminated composite and sandwich plates. This variationally consistent refined zigzag theory is seen to accurately reflect effect of transverse shear flexibility in its through-the-thickness prediction of displacement and stress entities. Unlike similar first- order zigzag theories, this refined zigzag theory accurately models clamped boundary conditions in laminated beams and plates. Gherlone [67] made a critical comparative assessment on Murakami-type zigzag function and the refined zigzag function [62]. It revealed that the two functions lead to identical results for any two-layer laminate, three-layer symmetric laminate, periodic laminates ([0/90/0/90/...]). But if the periodic laminate contains a weak interface, then the refined zigzag function is observed to yield more accurate results. The superiority of refined zigzag function over Murakami zigzag function has also been observed in case of non-symmetric laminates, which Murakami [66] has attributed to the fact that the periodicity in the laminate breaks down, and hence, the very basis of his zigzag function approximation suffers casualty.

The more realistic kinematics- and material property-based zigzag theory of Di Sciuva [30] was refined by Tessler and coresearchers [65, 68] by adding a set of piecewise linear functions and was found to yield good accuracy for bending, free vibration and buckling of laminated composite plates. Based on the approach of deriving assumed transverse shear stresses [69], Iurlaro et al. [70] developed a mixed refined zigzag theory using Reissner’s mixed variational theorem. It is felt that linear piecewise functions alone are not sufficient to yield correct descriptions of inplane displacements in thick plates, which are rather observed to be nonlinear across thickness. In order to satisfy this observation, Di Sciuyva [71] and Cho and Parmerter [47, 48] enhanced the zigzag theory by adding quadratic and cubic terms in the inplane displacement field approximation for laminated plates by a priori satisfying the interlaminar transverse shear stress continuity condition. Transverse normal deformation was added in Toledano and Murakami’s zigzag theory [32]. Relaxing this conditions, Nemeth [72] developed another cubic zigzag theory. Since Nemeth’s theory does not satisfy continuity of transverse shear stresses, it yields piecewise quadratic distribution for these stresses. The thickness deformation being more pronounced in thick laminated plates, Barut et al. [73] employed piecewise quadratic functions in inplane displacement field and a global quadratic function in the transverse displacement component. The key idea behind these zigzag formulations is of adding piecewise linear zigzag-shaped C\(^0\)-continuous functions to the linearly or quadratically varying global thickness functions to inplane displacements and of determining their coefficients in such a way that equilibrium of transverse shear stresses is satisfied in the laminate thickness.

The transverse stresses are primarily responsible for causing interlaminar delamination in the laminate, thus resulting in its damage. In order to provide improved prediction of these stresses, Icardi [74,75,76,77] has presented several 3D zigzag theories and their sublaminate counterparts for elastic laminated beams, plates and sandwich plates. The zigzag theory in Ref. [74] has considered zero transverse shear at top and bottom surfaces, and interfacial continuity of transverse shear stresses and transverse normal stress, whereas this theory has been further refined in Refs. [75,76,77] by adding continuity conditions on the transverse normal stress gradient. Higher-order energy contribution has been incorporated in a parent FSDT-based C\(^0\) finite element through strain energy updating, and this has resulted in overcoming the C\(^2\)-continuity requirement in interpolation functions based on this zigzag theory. In another study using refined zigzag theory, Icardi and Sola [78] have demonstrated that inserting a reinforcing thread for stitching or tufting significantly reduces transverse displacement as well as transverse shear stress. More recently, a discrete-layer model and a sublaminate model have been developed by the same researchers [79] from five-variable equivalent single-layer zigzag theory for laminated beam and plate structures by increasing the number of computational layers and variables.

A unified formulation approach proposed by Carrera [80] has been extensively used by Demasi [81,82,83,84,85,86,87] for obtaining various layerwise models and equivalent single-layer models in a single formulation. The layerwise models are basically needed for sandwich laminates involving very high inhomogeneity in the adjacent face and core layers and are an alternative to computationally highly expensive solid finite elements.

Global–local theory (GLT) has been developed to accurately calculate the transverse shear stresses from the constitutive equations. In the GLT of Li and Liu [88], local layerwise terms up to third order are superimposed with a global third-order variation of inplane displacements. Williams [89] has made a general framework of this theory for the analysis of delaminated elastic composite plates. However, the number of primary displacement variables has been very large (44 for a five-layer laminate). Zhen and Wanji [90] further extended the GLT for mth-order polynomial of the global thickness coordinate. However, it has been pointed out by Kapuria and Nath [91] that the GLT yields erroneous results for multi-material inhomogeneous composite laminate or sandwich laminates with more than three layers.

It has been found that the zigzag theory [92] accurately calculates all displacements and stresses for elastic as well as piezoelectric laminates. The accurate calculation of the transverse stresses is, however, obtained by integrating the 3D equilibrium equations, not from the direct use of constitutive equations. The proposed approach considers layerwise linear variation of inplane displacement field components along with a global third-order variation. The global variation is intended to incorporate the accuracy of the third-order theory (TOT), and the local layerwise linear variations are intended to predict slope discontinuity in inplane displacements. The approach works well to yield accurate responses for displacements and stresses. The existing model, of which the present model is an extension, is capable of predicting accurate transverse shear stresses from equilibrium equations for simply supported and non-simply supported boundary conditions [93]. However, its accuracy is poor when transverse stresses are calculated from constitutive equations. The present work proposes to modify the above-mentioned zigzag theory by incorporating layerwise cubic representation of the deflection of each layer in the laminated plate. The present model is a displacement model, and it uses the variational principle to derive equilibrium plate equations and variationally consistent boundary conditions. This variationally consistent model can be solved analytically or using any numerical methods for any set of boundary conditions. The classical Navier solution meant for simply supported plates is easy to apply analytically than the more complex Levy solution meant to simulate clamped as well as other boundary solutions. In this work, simply supported rectangular plates are used to assess accuracy of the proposed theory. Its applicability to other types of boundary conditions is not explored in this work.

2 Formulation

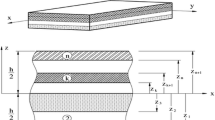
Consider a cross-ply laminated elastic rectangular plate (Fig. 1) of dimensions a along x-axis, b along y-axis and thickness h along z-axis consisting of L perfectly bonded orthotropic layers with the midplane chosen as the reference x-y plane. The z-coordinate of the bottom surface of the kth layer is denoted as \(z_{k-1}\). The layer in which the reference plane lies or is at the bottom of is denoted as the \(k_0\)th layer. Mechanical loads of intensity \(p_{z_1}\) and \(p_{z_2}\) are applied on bottom and top surfaces of the laminate.

Fig. 1
figure 1

Geometry of laminated composite plate

Full size image

The idealized 3D linear constitutive equations with principal material axes \(x_1, x_2, x_3\) are given by

$$\begin{aligned} {\begin{array}{ll} \varepsilon =S\,\sigma , \quad \sigma =C\varepsilon \\ \end{array}} \end{aligned}$$
(1)

where the components of stress \(\sigma \) and engineering strain \(\varepsilon \) are given with respect to the principal material axes by

$$\begin{aligned} \begin{array}{ll} \sigma =\left[ \begin{matrix} \sigma _1&{} \sigma _2&{} \sigma _3&{}\tau _{23}&{} \tau _{31}&{} \tau _{12}\\ \end{matrix} \right] ^{{\mathrm{T}}} \\ \varepsilon =\left[ \begin{matrix} \varepsilon _1&{} \varepsilon _2&{} \varepsilon _3&{} \gamma _{23}&{} \gamma _{31}&{} \gamma _{12}\\ \end{matrix}\right] ^{{\mathrm{T}}}\\ \end{array} \end{aligned}$$
(2)

S and C are matrices of elastic compliance and elastic stiffness with \(C=S^{-1}\) and

$$\begin{aligned} {\begin{array}{ll} s_{11}=1/E_1,\\ s_{22}=1/E_2,\\ s_{33}=1/E_3, \end{array}} {\begin{array}{ll} \quad s_{44}=1/G_{23},\\ \quad s_{55}=1/G_{31},\\ \quad s_{66}=1/G_{12}, \end{array}} {\begin{array}{ll} \quad s_{12}=-\,\nu _{21}/E_2=-\,\nu _{12}/E_1\\ \quad s_{13}=-\,\nu _{31}/E_3=-\,\nu _{13}/E_1\\ \quad s_{23}=-\,\nu _{32}/E_3=-\,\nu _{23}/E_2 \end{array}} \end{aligned}$$

\(E_i,\,G_{ij},\, \nu _{ij}\) are Young’s moduli, shear moduli and Poisson’s ratios, respectively.

Consider the reference axes x, y, z such that \(z=x_3\) and the material principal axes \(x_1,x_2\) are oriented at 0\(^{\circ }\) or 90\(^{\circ }\) with respect to the inplane reference axes x, y. Using transformation relations among stresses and strains from the material coordinate system (\(x_1,x_2,x_3\)) to the global reference coordinate system (x, y, z), the 3D constitutive equations for each layer of the laminate are obtained as

$$\begin{aligned} \left[ \begin{matrix}\sigma _x\\ \sigma _y\\ \sigma _z\\ \tau _{yz}\\ \tau _{zx}\\ \tau _{xy}\end{matrix}\right]= & {} \left[ \begin{matrix}{\bar{c}}_{11}&{}\quad {\bar{c}}_{12}&{}\quad {\bar{c}}_{13}&{}\quad 0&{}\quad 0&{}\quad 0\\ \bar{c}_{12}&{}\quad {\bar{c}}_{22}&{}\quad {\bar{c}}_{23}&{}\quad 0&{}\quad 0&{}\quad 0\\ {\bar{c}}_{13}&{}\quad {\bar{c}}_{23}&{}\quad \bar{c}_{33}&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad {\bar{c}}_{44}&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {\bar{c}}_{55}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {\bar{c}}_{66} \end{matrix}\right] \left[ \begin{matrix} \varepsilon _x\\ \varepsilon _y\\ \varepsilon _z\\ \gamma _{yz}\\ \gamma _{zx}\\ \gamma _{xy}\end{matrix}\right] \end{aligned}$$
(3)

The elements \({\bar{c}}_{ij}\) of matrix \({\bar{C}}\) are given in Ref. [94]. In the compact form, Eq. (3) can be written as

$$\begin{aligned} \sigma= & {} {\bar{Q}}\varepsilon +{\bar{Q}}_3^{{\mathrm{T}}}\varepsilon _z,\quad \tau ={\hat{Q}}\gamma \nonumber \\ \sigma _z= & {} {\bar{c}}_{13}\varepsilon _x+{\bar{c}}_{23}\varepsilon _y+{\bar{c}}_{33}\varepsilon _z \end{aligned}$$
(4)

where inplane stress \(\sigma \), inplane strain \(\varepsilon \), transverse shear stress \(\tau \), transverse shear strain \(\gamma \) and the elastic stiffnesses \({\bar{c}}_{ij}\) are given by

$$\begin{aligned} \begin{array}{rclrclrclrclrclrcl} \sigma &{}=&{}\left[ \begin{matrix}\sigma _x\\ \sigma _y\\ \tau _{xy}\\ \end{matrix} \right] ,&{} \varepsilon &{}=&{}\left[ \begin{matrix}\varepsilon _x\\ \varepsilon _y\\ \gamma _{xy}\\ \end{matrix} \right] ,&{} {\bar{Q}}&{}=&{} \left[ \begin{matrix} {\bar{c}}_{11}&{} {\bar{c}}_{12}&{} 0\\ {\bar{c}}_{12}&{} {\bar{c}}_{22}&{} 0\\ 0&{} 0&{} \bar{c}_{66}\\ \end{matrix} \right] \\ \tau &{}=&{}\left[ \begin{matrix}\tau _{zx}\\ \tau _{yz}\\ \end{matrix} \right] , &{} \gamma &{}=&{}\left[ \begin{matrix}\gamma _{zx}\\ \gamma _{yz}\\ \end{matrix} \right] ,&{} {\hat{Q}}&{}=&{}\left[ \begin{matrix} {\bar{c}}_{55}&{} 0\\ 0&{} {\bar{c}}_{44}\\ \end{matrix} \right] , &{} {\bar{Q}}_3&{}=&{}\left[ \begin{matrix}{\bar{c}}_{13}&{} {\bar{c}}_{23}&{}0\\ \end{matrix} \right] \end{array} \end{aligned}$$
(5)

Let \(u_x,\, u_y\) and w be the inplane and transverse displacements. Small strain conditions are assumed in the present work. By using the subscript comma for differentiation, the strain–displacement relations are given as

$$\begin{aligned} {\begin{array}{rl} \varepsilon _x&{}=u_{x,x}\\ \gamma _{yz}&{}=u_{y,z}+w_{,y}\\ \end{array}}\quad {\begin{array}{rl} \varepsilon _y&{}=u_{y,y}\\ \gamma _{zx}&{}=u_{x,z}+w_{,x}\\ \end{array}}\quad {\begin{array}{rl} \varepsilon _z&{}=w_{,z}\\ \gamma _{xy}&{}=u_{x,y}+u_{y,x}\\ \end{array}} \end{aligned}$$
(6)

A layerwise approximation is assumed for the transverse displacement:

$$\begin{aligned} \ w(x,y,z)=w_0(x,y)+zw_1^k(x,y)+z^2w_2^k(x,y)+z^3w_3^k(x,y) \end{aligned}$$
(7)

where the layerwise terms \(w_1^k\), \(w_2^k\) and \(w_3^k\) are taken so as to satisfy continuity of transverse displacement, transverse normal stress and gradient of transverse normal stress at the interfaces. The inplane displacement components \(u_x\) and \(u_y\) are written in the matrix form u as \(u=\left[ \begin{matrix}u_x &{} u_y\\ \end{matrix} \right] ^{{\mathrm{T}}}\), which are approximated layerwise [92] as

$$\begin{aligned} u(x,y,z)= & {} u_k(x,y) + z \psi _k^*(x,y) +z^2\xi (x,y) +z^3\eta (x,y) \end{aligned}$$
(8)

where

$$\begin{aligned} \begin{array}{rclrclrclrclrclrcl} u_k&{}=&{}\left[ \begin{matrix}u_{k_{\scriptstyle x}}\\ u_{k_{\scriptstyle y}}\\ \end{matrix} \right] ,\quad &{} \psi ^*_k&{}=&{}\left[ \begin{matrix}\psi ^*_{k_{\scriptstyle x}}\\ \psi ^*_{k_{\scriptstyle y}}\\ \end{matrix} \right] ,\quad \xi &{}=&{}\left[ \begin{matrix}\xi _x\\ \xi _y\\ \end{matrix} \right] ,\quad &{} \eta &{}=&{}\left[ \begin{matrix}\eta _x\\ \eta _y\\ \end{matrix} \right] \end{array} \end{aligned}$$
(9)

\(u_k\) and \(\psi _k^*\) represent the layerwise translation and shear rotation components. The expression for transverse shear strain is obtained by substituting u from Eq. (8) and w from Eq. (7):

$$\begin{aligned} \gamma= & {} \psi _k^*+2 z\xi +3 z^2\eta +{w_{0_{\scriptstyle d}}}+z{w^k_{1_{\scriptstyle d}}}+ z^2{w^k_{2_{\scriptstyle d}}}+ z^3{w^k_{3_{\scriptstyle d}}} \end{aligned}$$
(10)

where

$$\begin{aligned} \begin{array}{rclrclrclrclrclrcl} {w_{0_{\scriptstyle d}}}&{}=&{}\left[ \begin{matrix}w_{0,x}\\ w_{0,y}\\ \end{matrix} \right] ,&{}\ {w^k_{1_{\scriptstyle d}}}&{}=&{}\left[ \begin{matrix}w^k_{1,x}\\ w^k_{1,y}\\ \end{matrix} \right] ,&{}\ {w^k_{2_{\scriptstyle d}}}&{}=&{}\left[ \begin{matrix}w^k_{2,x}\\ w^k_{2,y}\\ \end{matrix} \right] ,&{}\ {w^k_{3_{\scriptstyle d}}}&{}=&{}\left[ \begin{matrix}w^k_{3,x}\\ w^k_{3,y}\\ \end{matrix} \right] \end{array} \end{aligned}$$
(11)

In order to reduce the computational complexity in calculating transverse shear stresses, the derivatives of the layerwise terms \(w^k_{1}\), \(w^k_{2}\) and \(w^k_{3}\) are neglected [95]. Let us assume \(\psi _{k}(x,y)=\psi _{k}^{*}(x,y)+{w_{0_{\scriptstyle d}}}(x,y)\) for simplicity and write Eqs. (10) and (8) as

$$\begin{aligned} \gamma= & {} \psi _{k}+2 z\xi +3 z^2\eta \end{aligned}$$
(12)
$$\begin{aligned} {u}= & {} {u_k} -z{w_{0_{\scriptstyle d}}}+ z \psi {_k} +z^2\xi +z^3\eta \end{aligned}$$
(13)

Using the expression of \(\gamma \) from Eq. (12) and using Eq. (4)\(_2\), the transverse shear stress is obtained as

$$\begin{aligned} \begin{array}{rclrclrclrclrclrcl} \tau= & {} {\hat{Q}^k}[\psi _{k}+ 2z\xi +3z^2\eta ]\qquad \end{array} \end{aligned}$$
(14)

It is known firstly that the transverse shear stresses \(\tau \) on top and bottom surfaces are zero and secondly that \(\tau \) and u are continuous at layer interfaces. Using these conditions in Eqs. (13) and (14), we get

$$\begin{aligned} \tau (z_0)=0&\quad \Rightarrow \quad&\psi _{1}+2z_0\xi +3 z_0^2\eta = 0 \end{aligned}$$
(15)
$$\begin{aligned} \tau (z_i^{-})=\tau (z_i^+)&\quad \Rightarrow \quad&{{\hat{Q}}^{i+1}}\psi _{{i+1}}-{\hat{Q}^i}\psi _{i}+2z_i{{\hat{Q}}^i_1}\xi +3z_i^2 {\hat{Q}_1^i}\eta =0 \end{aligned}$$
(16)
$$\begin{aligned} \tau (z_L)=0&\quad \Rightarrow \quad&\psi _{L}+2z_L\xi +3 z_L^2\eta =0 \end{aligned}$$
(17)
$$\begin{aligned} {u}(z_i^-)={u}(z_i^+)&\quad \Rightarrow \quad&{u_{i+1}}+z_i\psi _{{i+1}}-{u_i}-z_i\psi _{i}=0 \end{aligned}$$
(18)

where \(i=1,\ldots ,L-1\). \({{\hat{Q}}^i_1}\) is given as \({{\hat{Q}}_1^i}= {{\hat{Q}}^{i+1}}-{{\hat{Q}}^i}\). Equations (15)–(18) constitute 4L equations involving \(4L+4\) unknowns \({u_k},\,\psi _k\), \(\xi \) and \(\eta \), which is written as

$$\begin{aligned} {A{\bar{x}}}=0 \end{aligned}$$
(19)

where A is a \(4L\times (4L+4)\) matrix and \({\bar{x}}\) is a column vector of (\(4L+4\)) displacement variables given by

$$\begin{aligned} {\bar{x}}=\left[ \begin{matrix}{u_1^{{\mathrm{T}}}}&\psi {_1^{{\mathrm{T}}}}&{u_2^{{\mathrm{T}}}}&\psi {_2^{{\mathrm{T}}}}&\ldots \ \ {u_L^{{\mathrm{T}}}}&\psi {_L^{{\mathrm{T}}}}&\xi ^{{\mathrm{T}}}&\eta ^{{\mathrm{T}}}\end{matrix}\right] ^{{\mathrm{T}}} \end{aligned}$$
(20)

The matrix A is partitioned into \(2\times 2\) sub-matrices A(p, q) and have the following nonzero sub-matrices:

$$\begin{aligned} \begin{array}{ll} {A}(1,2)={I_2}, &{}\quad {A}(2i+1,2i-1)=-{I_2}\\ {A}(1,2L+1)=2z_0{I_2},&{} \quad {A}(2i+1,2i)=-z_i{I_2}\\ {A}(1,2L+2)=3z_0^2{I_2},&{}\quad {A}(2i+1,2i+1)={I_2}\\ {A}(2i,2i)=-{{\hat{Q}}^i},&{}\quad {A}(2i+1,2i+2)=z_i{I_2}\\ {A}(2i,2i+2)= {{\hat{Q}}^{i+1}},&{}\quad {A}(2L,2L)={I_2}\\ {A}(2i,2L+1)=2z_i{{\hat{Q}}^i_1}, &{}\quad {A}(2L,2L+1)=2z_L{I_2}\\ {A}(2i,2L+2)=3z_i^2{{\hat{Q}}^i_1},&{}\quad {A}(2L,2L+2)=3z_L^2{I_2} \end{array} \end{aligned}$$
(21)

for \(i=1,2\ldots ,L-1\). The vector \({{\bar{x}}}\) is partitioned into vectors \({{\bar{x}}_2}=[\begin{matrix}{u_0^{{\mathrm{T}}}}&\psi {_0^{{\mathrm{T}}}}\end{matrix}]^{{\mathrm{T}}}\) containing four primary reference variables of \(k_0\)th layer and \({{\bar{x}}_1}\) containing the remaining variables. Accordingly, matrix A is partitioned into sub-matrices \({A_1}(4L\times 4L)\) and \({A_2}(4L\times 4)\) as \({A}=[\begin{matrix} {A_1}&{A_2}\end{matrix}]\) with following \(2\times 2\) sub-matrices

$$\begin{aligned}&\begin{array}{rclrclrclrclrclrcl} A_1(j,2k-1)&{}=&{}A(j,2k-1),&{}\quad A_1(j,2k)&{}=&{}A(j,2k),\ \hbox {for}\quad k<k_0\\ A_1(j,2k-1)&{}=&{}A(j,2k+1),&{}\quad A_1(j,2k)&{}=&{}A(j,2k+2),\ \hbox {for}\quad k\ge k_0\end{array} \end{aligned}$$
(22)
$$\begin{aligned}&A_2(j,1)=A(j,2k_0-1),\quad A_2(j,2)=A(j,2k_0) \end{aligned}$$
(23)

where \(j=1, 2, \ldots ,2L\), \(k=1, 2, \ldots , (L+1)\). Thus, we have

$$\begin{aligned}&\left[ \begin{matrix}{A_1}&{} {A_2}\\ \end{matrix} \right] \left[ \begin{matrix}{{\bar{x}}_1}\\ {{\bar{x}}_2}\\ \end{matrix} \right] =0\end{aligned}$$
(24)
$$\begin{aligned} \Rightarrow {\bar{x}_1}= & {} -{A_1^{-1}}{A_2}{{\bar{x}}_2}={{\bar{A}}_2^1u_0}+{{\bar{A}}_2^2}\psi _{0} \end{aligned}$$
(25)

Using Eq. (25), the variables \({u_k},\,\psi _{k},\,\xi \) and \(\eta \) can be expressed explicitly as

$$\begin{aligned} \begin{array}{rclrclrclrclrclrcl} {u_k}&{}=&{} {u_0}+{{\bar{A}}_2^2}(2k'-1)\psi _{0},\qquad \psi _{k}={{\bar{A}}_2^2}(2k')\psi _{0}\\ \xi &{}=&{}{{\bar{A}}_2^2}(2L-1)\psi _{0},\qquad \qquad \quad \eta ={{\bar{A}}_2^2}(2L)\psi _{0}\end{array} \end{aligned}$$
(26)

with \(k'=k\) for \(k<k_0\) and \(k'=k-1\) for \(k>k_0\). Substituting these expressions of \({u_k},\, \psi _{k},\, \xi \), and \(\eta \) into Eq. (13) yields

$$\begin{aligned}&{u}(x,y,z)={u_0}-z{w_{0_{\scriptstyle d}}}+ {R^k}(z) \psi _{0} \end{aligned}$$
(27)

where \({R^k}(z)\) is \(2\times 2\) matrix of function of z. For \(k\ne k_0\)

$$\begin{aligned} \begin{array}{rclrclrclrclrclrcl} {R^k}(z)= & {} {\bar{A}_2^2}(2k'-1)+z{{\bar{A}}_2^2}(2k')+z^2{{\bar{A}}_2^2}(2L-1) +z^3{\bar{A}_2^2}(2L) \end{array} \end{aligned}$$
(28)

and for \(k=k_0\)

$$\begin{aligned} \begin{array}{rclrclrclrclrclrcl} { R^k}(z)= & {} z {I_2}+z^2{{\bar{A}}_2^2}(2L-1) +z^3{\bar{A}_2^2}(2L)\end{array} \end{aligned}$$
(29)

Let us neglect the contribution of \(\varepsilon \) to normal stress and obtain the transverse normal stress \(\sigma _z\) using Eq. (4)\(_3\) as:

$$\begin{aligned} \sigma _z= & {} {\bar{c}}_{33}\varepsilon _z={\bar{c}}_{33}[ w_1^k+ 2zw_2^k+ 3z^2w_3^k ] \end{aligned}$$
(30)

The gradient of the transverse normal stress becomes

$$\begin{aligned} \sigma _{z,z}={\bar{c}}_{33}[ 2w_2^k+6zw_3^k] \end{aligned}$$
(31)

The continuity of w is now imposed to yield \((w(z_i^+)=w(z_i^-))\)

$$\begin{aligned}&z_i(w_1^{i+1}-w_1^i)+z_i^2(w_2^{i+1}-w_2^i)+z_i^3(w_3^{i+1}-w_3^i)=0 \end{aligned}$$
(32)

The continuity of \(\sigma _z\) and its gradient are imposed to yield

$$\begin{aligned} {\bar{c}}_{33}^{i+1}[w_1^{i+1}+2z_iw_2^{i+1}+3z_i^2w_3^{i+1}]-{\bar{c}}_{33}^{i}[ w_1^{i}+2z_i w_2^{i}+3z_i^2 w_3^{i}]= & {} 0 \end{aligned}$$
(33)
$$\begin{aligned} {\bar{c}}_{33}^{i+1}[2 w_2^{i+1}+6z_iw_3^{i+1}] -{\bar{c}}_{33}^{i}[2 w_2^{i}+6z_iw_3^{i}]= & {} 0 \end{aligned}$$
(34)

where \(i=1,\ldots ,L-1\). Mechanical loads of intensity \(p_{z_1}\) and \(p_{z_2}\) are applied on bottom and top surfaces of the plate. Using these conditions, we get

$$\begin{aligned} {\bar{c}}_{33}^{1}[w_1^{1}+2z_0w_2^{1}+3z_0^2w_3^{1}]= & {} p_{z_1} \end{aligned}$$
(35)
$$\begin{aligned} {\bar{c}}_{33}^{L}[w_1^{L}+2z_Lw_2^{L}+3z_L^2w_3^{L}]= & {} p_{z_2} \end{aligned}$$
(36)

The \(3L-1\) equations given by Eqs. (32)–(36) along with the expression \(w_1^{k_{\scriptstyle 0}}=w_{1_{\scriptstyle 0}}\) constitute 3L equations involving 3L unknowns \(w_1^k\), \(w_2^k\) and \(w_3^k\), which can be written in the compact form

$$\begin{aligned} {D{\bar{y}}}={D_m}+{D_r}w_{1_{\scriptstyle 0}} \end{aligned}$$
(37)

where D, \({D_m}\) and \({D_r}\) are of sizes \((3L\times 3L)\), \((3L\times 1)\) and \((3L\times 1)\) respectively and \({{\bar{y}}}\) is a column vector of all 3L variables

$$\begin{aligned} {{\bar{y}}}=\left[ \begin{matrix}w_1^1&w_2^1&w_3^1&w_1^2&w_2^2&w_3^2&\ldots&w_1^{L}&w_2^{L}&w_3^{L}\end{matrix}\right] ^{{\mathrm{T}}} \end{aligned}$$
(38)

D, \({D_m}\) and \({D_r}\) have following nonzero elements for \(i=1,2\ldots ,L-1\).

$$\begin{aligned} {D}(3i-2,3i+1)= & {} z_i,\qquad \qquad {D}(3i,3i-1)=-2{\bar{c}}_{33}^{i}\nonumber \\ {D}(3i-2,3i-2)= & {} -z_i,\qquad \quad \ {D}(3i,3i+3)=6{\bar{c}}_{33}^{i+1}z_i\nonumber \\ {D}(3i-2,3i+2)= & {} z_i^2,\qquad \qquad {D}(3i,3i)=-6{\bar{c}}_{33}^{i}z_i\nonumber \\ {D}(3i-2,3i-1)= & {} -z_i^2,\qquad \quad \ {D}(3L-2,1)={\bar{c}}_{33}^{1}\nonumber \\ {D}(3i-2,3i+3)= & {} z_i^3,\qquad \qquad \, {D}(3L-2,2)=2z_0{\bar{c}}_{33}^{1}\nonumber \\ {D}(3i-2,3i)= & {} -z_i^3,\qquad \quad \ \, {D}(3L-2,3)=3z_0^2{\bar{c}}_{33}^{1}\nonumber \\ {D}(3i-1,3i+1)= & {} {\bar{c}}_{33}^{i+1},\qquad \quad \ \ {D}(3L-1,1)={\bar{c}}_{33}^{L}\nonumber \\ {D}(3i-1,3i-2)= & {} -{\bar{c}}_{33}^{i},\qquad \quad \ {D}(3L-1,2)=2z_L{\bar{c}}_{33}^{L}\nonumber \\ {D}(3i-1,3i+2)= & {} 2{\bar{c}}_{33}^{i+1}z_i,\qquad \ \, {D}(3L-1,3)=3z_L^2{\bar{c}}_{33}^{L}\nonumber \\ {D}(3i-1,3i-1)= & {} -2{\bar{c}}_{33}^{i}z_i,\qquad \, {D}(3L,3k_0-2)=1\nonumber \\ {D}(3i-1,3i+3)= & {} 3{\bar{c}}_{33}^{i+1}z_i^2,\qquad \ {D_m}(3L-2,1)=p_{z_1}\nonumber \\ {D}(3i-1,3i)= & {} -3{\bar{c}}_{33}^{i}z_i^2,\qquad {D_m}(3L-1,1)=p_{z_2}\nonumber \\ {D}(3i,3i+2)= & {} 2{\bar{c}}_{33}^{i+1},\qquad \quad \ {D_r}(3L,1)=1 \end{aligned}$$
(39)

Now \({{\bar{y}}}\) can be obtained by solving Eq. (37) as

$$\begin{aligned} {\bar{y}}= & {} {{\bar{D}}_m}+{{\bar{D}}_r}w_{1_{\scriptstyle 0}} \end{aligned}$$
(40)

with \({\bar{D}_m}={D^{-1}}{D_m}\) and \( {\bar{D}_r}={D^{-1}}{D_r}\). The explicit expressions for \(w_1^k\), \(w_2^k\) and \(w_3^k\) can be written using Eq. (40) as

$$\begin{aligned} w_1^k= & {} {{\bar{D}}_m}(3k-2)+{{\bar{D}}_r}(3k-2)w_{1_{\scriptstyle 0}}\nonumber \\ w_2^k= & {} {{\bar{D}}_m}(3k-1)+{{\bar{D}}_r}(3k-1)w_{1_{\scriptstyle 0}}\nonumber \\ w_3^k= & {} {{\bar{D}}_m}(3k)+{{\bar{D}}_r}(3k)w_{1_{\scriptstyle 0}} \end{aligned}$$
(41)

These expressions are substituted into Eq. (7) which yields

$$\begin{aligned} w(x,y,z)= & {} w_0(x,y)+ R^{1k}(z)+R^{2k}(z)w_{1_{\scriptstyle 0}}(x,y) \end{aligned}$$
(42)

where \(R^{1k}(z)\) and \(R^{2k}(z)\) are layerwise functions of z, given by

$$\begin{aligned} R^{1k}(z)= & {} z{\bar{D}}_m(3k-2)+z^2{\bar{D}}_m(3k-1)+z^3{\bar{D}}_m(3k)\nonumber \\ R^{2k}(z)= & {} z{\bar{D}}_r(3k-2)+z^2{\bar{D}}_r(3k-1)+z^3{\bar{D}}_r(3k) \end{aligned}$$
(43)

Thus, the final displacement field defined by the inplane components u and transverse component w is expressed in terms of only six mechanical variables \(u_{0_{\scriptstyle x}}\), \(u_{0_{\scriptstyle y}}\), \(\psi _{0_{\scriptstyle x}}\), \(\psi _{0_{\scriptstyle y}}\), \(w_0\) and \(w_{1_{\scriptstyle 0}}\). In order to develop a compact formulation for the present theory, a generalized strain–displacement relation is obtained for the rectangular laminated elastic composite plate. This is done by expressing the assumed displacement field given by Eqs. (27) and (42) as

$$\begin{aligned} {u}= & {} {f_1}(z){\bar{u}_1},\qquad w=R^{1k}(z)+{f_2}(z){\bar{u}_2} \end{aligned}$$
(44)

where

$$\begin{aligned} \begin{array}{rclrclrclrclrclrcl} {{\bar{u}}_1}&{}=&{} \left[ \begin{matrix}{u_0^{{\mathrm{T}}}}&{} -{w_{0_{\scriptstyle d}}^{{\mathrm{T}}}}&{} \psi {_0^{{\mathrm{T}}}}\\ \end{matrix} \right] ^{{\mathrm{T}}},\qquad {{\bar{u}}_2}&{}=&{}\left[ \begin{matrix}w_0&{} w_{1_{\scriptstyle 0}}\\ \end{matrix} \right] ^{{\mathrm{T}}}\\ {f_1}(z)&{}=&{}\left[ \begin{matrix}{I_2}&{} z{I_2}&{} {R^k}(z)\\ \end{matrix} \right] ,\qquad {f_2}(z)&{}=&{}\left[ \begin{matrix}1&{} R^{2k}(z)\\ \end{matrix} \right] \end{array}\end{aligned}$$
(45)

Thus, the original strain–displacement relations given in Eq. (6) can be reformulated as

$$\begin{aligned} \varepsilon= & {} \varepsilon _{0}+z{K}+\varPhi ^k(z)\psi {_{0_{\scriptstyle d}}} \end{aligned}$$
(46)
$$\begin{aligned} \gamma= & {} {R^k_{,z}}(z)\psi _{0}+R^{2k}(z){I_2}w_{1_{\scriptstyle 0d}} \end{aligned}$$
(47)
$$\begin{aligned} \varepsilon _z= & {} R^{1k}_{,z}(z)+R^{2k}_{,z}(z)w_{1_{\scriptstyle 0}} \end{aligned}$$
(48)

where

$$\begin{aligned} \varepsilon _{0}= & {} \left[ \begin{matrix}u_{0_{\scriptstyle x},x}&{} u_{0_{\scriptstyle y},y}&{} u_{0_{\scriptstyle x},y}+u_{0_{\scriptstyle y},x}\\ \end{matrix} \right] ^{{\mathrm{T}}}\nonumber \\ {K}= & {} \left[ \begin{matrix}-w_{0,xx}&{} -w_{0,yy}&{} -2w_{0,xy}\\ \end{matrix} \right] ^{{\mathrm{T}}}\nonumber \\ \psi {_{0_{\scriptstyle d}}}= & {} \left[ \begin{matrix}\psi _{0_{\scriptstyle x},x}&{} \psi _{0_{\scriptstyle x},y}&{} \psi _{0_{\scriptstyle y},x}&{} \psi _{0_{\scriptstyle y},y}\\ \end{matrix} \right] ^{{\mathrm{T}}} \nonumber \\ \varPhi ^{k}(z)= & {} \left[ \begin{matrix} R^k_{11}(z)&{} 0&{} 0&{} 0\\ 0&{} 0&{} 0&{}R^k_{22}(z)\\ 0&{} R^k_{11}(z)&{} R^k_{22}(z)&{} 0\\ \end{matrix} \right] \end{aligned}$$
(49)

The above expressions for strains given in Eqs. (46)–(48) can be rewritten in the compact form

$$\begin{aligned} \begin{array}{rclrclrclrclrclrcl} \varepsilon= & {} {f_3}(z){\bar{\varepsilon }}_{1},\qquad \gamma = {f_4}(z){\bar{\varepsilon }}_{2},\qquad \varepsilon _z= R^{1k}_{,z}(z)+R^{2k}_{,z}(z)w_{1_{\scriptstyle 0}} \end{array} \end{aligned}$$
(50)

by writing generalized strains \({\bar{\varepsilon }}_1\) and \({\bar{\varepsilon }}_2\), and their coefficients \({f_3}(z)\) and \({f_4}(z)\) as

$$\begin{aligned} {\bar{\varepsilon }}_{1}= & {} \left[ \begin{matrix}\varepsilon _{0}\\ {K}\\ \psi {_{0_{\scriptstyle d}}}\\ \end{matrix} \right] ,\quad {\bar{\varepsilon }}_{2}=\left[ \begin{matrix} \psi _{\mathbf {0}}\\ w_{1_{\scriptstyle 0d}} \\ \end{matrix} \right] \end{aligned}$$
(51)
$$\begin{aligned} {f_3}(z)= & {} \left[ \begin{matrix}{I_3}&{} z{I_3}&{} \varPhi ^{k}(z)\\ \end{matrix} \right] ,\quad {f_4}(z)=\left[ \begin{matrix} {R^k_{,z}}(z)&{} R^{2k}(z)I_2\\ \end{matrix} \right] \end{aligned}$$
(52)

The variational principle is now applied to obtain the equilibrium equations and variationally consistent boundary conditions, \(\int _V\sigma _{ij}\delta \varepsilon _{ij}\,\mathrm{d}V =0\), for all virtual generalized displacements. V denotes the volume of the plate. The components \(T^n_i\) of the traction vector on the surface \(\varGamma \) with outward normal \(\underline{n}=n_i \underline{\hbox {e}}_{i}\) are given by \( T^n_i=\sigma _{ji}n_j\). Using the notation \(\langle \ldots \rangle =\sum _{k=1}^L\int _{z_{k-1}^+}^{z_k^-}(\ldots )\,{ d}z\) for integration across the laminate thickness, it results in the following variational equation:

$$\begin{aligned}&\int _A[\langle \delta \varepsilon ^{\scriptstyle T}\sigma +\delta \gamma ^{\scriptstyle T}\tau +\delta \varepsilon _z\sigma _z \rangle -p^1_z\delta w(x,y,z_0)-p^2_z\delta w(x,y,z_L,t)]\,\mathrm{d}A\nonumber \\&\ \ -\int _{\varGamma _L}\langle \sigma _{n}\delta u_n+\tau _{ns}\delta u_s+ \tau _{nz}\delta w\rangle \,\mathrm{d}s=0 \end{aligned}$$
(53)

for all \(\delta {u_0}\), \(\delta w_0\), \(\delta w_{1_{\scriptstyle 0}}\) and \(\delta \psi _{0}\). The stress resultants and load terms are derived from this expression as follows.

Using Eqs. (50), the strain energy terms in Eq. (53) can be expressed as

$$\begin{aligned} \langle \delta \varepsilon ^{\scriptstyle T}\sigma +\delta \gamma ^{\scriptstyle T}\tau +\delta \varepsilon _z\sigma _z\rangle =\delta {\bar{\varepsilon }}_{1}^{{\mathrm{T}}}{F_1}+ \delta {\bar{\varepsilon }}_{2}^{{\mathrm{T}}}{F_2} + \delta w_{1_{\scriptstyle 0}}{\bar{M}} \end{aligned}$$
(54)

The stress resultants \({F_1}\) of \(\sigma \), \({F_2}\) of \(\tau \) and \({\bar{M}}\) of \(\sigma _z\) are defined as

$$\begin{aligned} {F_1}= & {} \left[ \begin{matrix}{N}\\ {M}\\ {P}\\ \end{matrix}\right] =\langle {f_3^{{\mathrm{T}}}}(z)\sigma \rangle =\left[ \begin{matrix}\langle \sigma \rangle \\ \langle z\sigma \rangle \\ \langle {\varPhi ^{k}(z)}^{{\mathrm{T}}}\sigma \rangle \\ \end{matrix}\right] \end{aligned}$$
(55)
$$\begin{aligned} {F_2}= & {} \left[ \begin{matrix}{Q}\\ {{\bar{Q}}}\\ \end{matrix}\right] =\langle {f_4^{{\mathrm{T}}}}(z)\tau \rangle = \left[ \begin{matrix}\langle {{R^k_{,z}}}^{{\mathrm{T}}}(z)\tau \rangle \\ R^{2k}(z){I_2}\tau \rangle \\ \end{matrix} \right] \end{aligned}$$
(56)
$$\begin{aligned} {\bar{M}}= & {} \langle R^{2k}_{,z}(z)\sigma _z\rangle \end{aligned}$$
(57)

with

$$\begin{aligned} {N}= & {} \left[ \begin{matrix}N_x&{} N_y&{} N_{xy}\\ \end{matrix} \right] ^{{\mathrm{T}}},\quad {M}=\left[ \begin{matrix}M_x&{} M_y&{} M_{xy}\\ \end{matrix} \right] ^{{\mathrm{T}}}\nonumber \\ {P}= & {} \left[ \begin{matrix}P_x&P_{yx}&P_{xy}&P_y\end{matrix}\right] ^{{\mathrm{T}}},\quad {Q}=\left[ \begin{matrix}Q_x&{} Q_y\\ \end{matrix} \right] ^{{\mathrm{T}}},\quad {{\bar{Q}}}=\left[ \begin{matrix}{\bar{Q}}_x&{} {\bar{Q}}_y\\ \end{matrix} \right] ^{{\mathrm{T}}} \end{aligned}$$
(58)

Let us define resultant of transverse shear stresses as

$$\begin{aligned} \begin{array}{rclrclrclrclrclrcl} V_x&{}=&{}\langle \tau _{xz}\rangle ,\quad &{} V_y&{}=&{}\langle \tau _{yz}\rangle ,\quad &{} V_n&{}=&{}\langle \tau _{nz}\rangle ,\quad &{} V_s&{}=&{}\langle \tau _{sz}\rangle \\ V_{2x}&{}=&{}\langle R^{2k}\tau _{xz}\rangle ,\quad &{} V_{2y}&{}=&{}\langle R^{2k}\tau _{yz}\rangle , \quad &{} V_{2n}&{}=&{}\langle R^{2k}\tau _{nz}\rangle , \quad &{} V_{2s}&{}=&{}\langle R^{2k}\tau _{sz}\rangle \end{array} \end{aligned}$$
(59)

The mechanical load terms in Eq. (53) on the bottom and top surfaces can be expressed as

$$\begin{aligned}&-p_z^1[\delta w_0+ R^{2k}(z_0)\delta w_{1_{\scriptstyle 0}}] -p_z^2 [\delta w_0+ R^{2k}(z_L)\delta w_{1_{\scriptstyle 0}}] =-F_3\delta w_0-F_4\delta w_{1_{\scriptstyle 0}}\qquad \end{aligned}$$
(60)

by defining \(F_3=p^1_z+p^2_z, F_4=p^1_zR^{2k}(z_0)+p^2_zR^{2k}(z_L)\). The terms in Eq. (53) due to mechanical loads at the lateral surface of the plate can be expressed in terms of stress resultants defined in Eqs. (55) and (56) as

$$\begin{aligned} \langle \sigma _n\delta u_n+\tau _{ns}\delta u_s+\tau _{nz}\delta w\rangle= & {} \langle \sigma _n\delta u_n+\tau _{ns}\delta u_s\rangle +V_n\delta w_0 +V_{2n}\delta w_{1_{\scriptstyle 0}} \end{aligned}$$
(61)
$$\begin{aligned} \int _{\varGamma _L} \langle \sigma _n\delta u_n +\tau _{ns}\delta u_s\rangle \,\mathrm{d}s= & {} \int _{\varGamma _L} [N_n\delta u_{0_{\scriptstyle n}}+N_{ns}\delta u_{0_{\scriptstyle s}} -M_n\delta w_{0,n} \nonumber \\&+\,M_{ns,s}\delta w_0 +P_n\delta \psi _{0_{\scriptstyle n}} +P_{ns}\delta \psi _{0_{\scriptstyle s}}]\,\mathrm{d}s+\sum _i\varDelta M_{ns}(s_i)\delta w_0(s_i) \end{aligned}$$
(62)

where the lateral surface has corners at \(s=s_i\). Now using Eqs. (61) and (62), the lateral surface loads in Eq. (53) contribute

$$\begin{aligned}&-\int _{\varGamma _L} [ N_n\delta u_{0_{\scriptstyle n}}+N_{ns}\delta u_{0_{\scriptstyle s}} -M_n\delta w_{0,n}+(V_n+M_{ns,s})\delta w_0 +V_{2n}\delta w_{1_{\scriptstyle 0}} \nonumber \\&\quad +\,P_n\delta \psi _{0_{\scriptstyle n}} +P_{ns}\delta \psi _{0_{\scriptstyle s}} ]\,\mathrm{d}s - \sum _i\varDelta M_{ns}(s_i)\delta w_0(s_i) \end{aligned}$$
(63)

Thus, variational equation (53) reduces to the following form in terms of the plate variables only:

$$\begin{aligned}&\int _A[ \delta {\bar{\varepsilon }}_{1}^{{\mathrm{T}}}{F_1}+ \delta {\bar{\varepsilon }}_{2}^{{\mathrm{T}}}{F_2}+ \delta w_{1_{\scriptstyle 0}}{\bar{M}} -F_3\delta w_0-F_4\delta w_{1_{\scriptstyle 0}} ]\,\mathrm{d}A\nonumber \\&\qquad -\int _{\varGamma _L} {}^*[ N_n\delta u_{0_{\scriptstyle n}}+N_{ns}\delta u_{0_{\scriptstyle s}} -M_n\delta w_{0,n}+(V_n+M_{ns,s})\delta w_0+V_{2n}\delta w_{1_{\scriptstyle 0}} \nonumber \\&\qquad +\,P_n\delta \psi _{0_{\scriptstyle n}} +P_{ns}\delta \psi _{0_{\scriptstyle s}}]\,\mathrm{d}s- {}^* \sum _i\varDelta M_{ns}(s_i)\delta w_0(s_i) =0 \end{aligned}$$
(64)

The terms inside the symbol \(^*[\ ]\) are the contributions of loads acting at lateral surface of the plate. The area integral in Eq. (64) is expressed in terms of generalized virtual displacements \(\delta u_{0_{\scriptstyle x}}\), \(\delta u_{0_{\scriptstyle y}}\), \(\delta w_0\), \(\delta w_{1_0}\), \(\delta \psi _{0_{\scriptstyle x}}\) and \(\delta \psi _{0_{\scriptstyle y}}\) by using Eqs. (45) and (51) and by employing Green’s theorem wherever required. This yields

$$\begin{aligned}&\int _A[ -\delta u_{0_{\scriptstyle x}}(N_{x,x}+N_{xy,y}) -\delta u_{0_{\scriptstyle y}}(N_{xy,x}+N_{y,y})\nonumber \\&\qquad -\,\delta w_0(M_{x,xx}+2M_{xy,xy}+M_{y,yy})-\delta \psi _{0_{\scriptstyle x}}(P_{x,x}+P_{yx,y}) \nonumber \\&\qquad -\,\delta \psi _{0_{\scriptstyle y}}(P_{xy,x}+P_{y,y}) +\delta \psi _{0_{\scriptstyle x}}Q_x +\delta \psi _{0_{\scriptstyle y}}Q_y \nonumber \\&\qquad -\,\delta w_{1_{\scriptstyle 0}}({\bar{Q}}_{x,x}+{\bar{Q}}_{y,y}) + \delta w_{1_{\scriptstyle 0}} {\bar{M}} -F_3\delta w_0 -F_4\delta w_{1_{\scriptstyle 0}}]\,\mathrm{d}A\nonumber \\&+\int _{\varGamma _L}[\delta u_{0_{\scriptstyle x}}(N_xn_x+N_{xy}n_y)+\delta u_{0_{\scriptstyle y}}(N_{xy}n_x+N_yn_y) \nonumber \\&\qquad -\,\delta w_{0,x}(M_xn_x+M_{xy}n_y) -\delta w_{0,y}(M_{xy}n_x+M_yn_y) \nonumber \\&\qquad +\,\delta w_0\{(M_{x,x}+M_{xy,y})n_x+(M_{xy,x}+M_{y,y})n_y\} \nonumber \\&\qquad +\,\delta \psi _{0_{\scriptstyle x}}(P_xn_x+P_{yx}n_y)+\delta \psi _{0_{\scriptstyle y}}(P_{xy}n_x +P_yn_y) \nonumber \\&\qquad +\,\delta w_{1_{\scriptstyle 0}}({\bar{Q}}_{x}n_x +{\bar{Q}}_yn_y) - {}^*\{N_n\delta u_{0_{\scriptstyle n}}+N_{ns}\delta u_{0_{\scriptstyle s}} \nonumber \\&\qquad -\,M_n\delta w_{0,n} +(V_n+M_{ns,s})\delta w_0 + V_{2n}\delta w_{1_{\scriptstyle 0}}\nonumber \\&\qquad +\,P_n\delta \psi _{0_{\scriptstyle n}} +P_{ns}\delta \psi _{0_{\scriptstyle s}} \}]\,\mathrm{d}s - {}^*\sum _i\varDelta M_{ns}(s_i)\delta w_0(s_i)=0 \end{aligned}$$
(65)

The terms involving \(\delta u_{0_{\scriptstyle x}}\), \(\delta u_{0_{\scriptstyle y}}\), \( \delta \psi _{0_{\scriptstyle x}}\), \( \delta \psi _{0_{\scriptstyle y}}\), \(\delta w_{0,x}\) and \(\delta w_{0,y}\) in the integrand of \(\varGamma _L\) are expressed in terms of components \(n,\,s\) as follows:

$$\begin{aligned}&\int _{\varGamma _L}[ \delta u_{0_{\scriptstyle x}}(N_xn_x+N_{xy}n_y)+\delta u_{0_{\scriptstyle y}}(N_{xy}n_x+N_yn_y) -\delta w_{0,x}(M_xn_x+M_{xy}n_y) \nonumber \\&\qquad -\,\delta w_{0,y}(M_{xy}n_x+M_yn_y) +\delta \psi _{0_{\scriptstyle x}}(P_xn_x+P_{yx}n_y) +\delta \psi _{0_{\scriptstyle y}}(P_{xy}n_x +P_yn_y) \nonumber \\&= \int _{\varGamma _L}[N_n\delta u_{0_{\scriptstyle n}}+N_{ns}\delta u_{0_{\scriptstyle s}} -M_n\delta w_{0,n}+M_{ns,s}\delta w_0 +P_n\delta \psi _{0_{\scriptstyle n}}+P_{ns}\delta \psi _{0_{\scriptstyle s}}]\,\mathrm{d}s\nonumber \\&\qquad +\,\sum _i\varDelta M_{ns}(s_i)\delta w_0(s_i) \end{aligned}$$
(66)

Each of the coefficients of the generalized virtual displacements appearing in the area integral of Eq. (65) have been equated to zero to yield following equations for the elastic laminated plate:

$$\begin{aligned}&N_{x,x}+N_{xy,y}=0 \end{aligned}$$
(67)
$$\begin{aligned}&N_{xy,x}+N_{y,y}=0 \end{aligned}$$
(68)
$$\begin{aligned}&M_{x,xx}+2M_{xy,xy}+M_{y,yy}+ F_3=0 \end{aligned}$$
(69)
$$\begin{aligned}&{\bar{Q}}_{x,x}+{\bar{Q}}_{y,y}-{\bar{M}}+ F_4=0 \end{aligned}$$
(70)
$$\begin{aligned}&P_{x,x}+P_{yx,y}-Q_x=0 \end{aligned}$$
(71)
$$\begin{aligned}&P_{xy,x}+P_{y,y}-Q_y=0 \end{aligned}$$
(72)

The following boundary conditions are obtained from the boundary integral in Eq. (65):

$$\begin{aligned}&u_{0_{\scriptstyle n}}= u^*_{0_{\scriptstyle n}} \quad \hbox {or}\quad N_n= N_n^*\nonumber \\&u_{0_{\scriptstyle s}}= u^*_{0_{\scriptstyle s}}\quad \, \hbox {or}\quad N_{ns} =N_{ns}^*\nonumber \\&w_0=w_0^*\quad \hbox {or}\quad V_n+ M_{ns,s}=V^*_n+M^*_{ns,s}\nonumber \\&w_{0,n}=w^*_{0,n}\quad \hbox {or}\quad M_n= M_n^* \nonumber \\&w_1^0=w_1^{0*}\quad \hbox {or}\quad V_{2n}=V_{2n}^*\nonumber \\&\psi _{0_{\scriptstyle n}}= \psi ^*_{0_{\scriptstyle n}}\quad \ \hbox {or}\quad P_n =P_n^*\nonumber \\&\psi _{0_{\scriptstyle s}}=\psi ^*_{0_{\scriptstyle s}}\quad \, \hbox { or}\quad P_{ns} =P^*_{ns} \end{aligned}$$
(73)

The superscript \(^*\) denotes a prescribed value. The first set of boundary conditions are the essential boundary conditions, and the second set are the natural boundary conditions.

The plate constitutive equations give the relations between plate stress resultants \({F_1}\), \({F_2}\) and \({\bar{M}}\) with generalized plate mechanical strains \({\bar{\varepsilon }}_1\), \({\bar{\varepsilon }}_2\) and \(w_{1_{\scriptstyle 0}}\). In order to develop them, the stresses \(\sigma \), \(\tau \) and \(\sigma _z\) given in Eq. (4) are expressed in terms of the generalized strains given in Eq. (50) and are substituted into Eqs. (55), (56) and (57) which yield

$$\begin{aligned} {F_1}= & {} {A}{\bar{\varepsilon }}_{1}+{{\tilde{A}}}+{{\hat{A}}}w_{1_{\scriptstyle 0}} \nonumber \\ {F_2}= & {} {{\bar{A}}}{\bar{\varepsilon }}_{2} \nonumber \\ {\bar{M}}= & {} {{\hat{A}}^{{\mathrm{T}}}}{\bar{\varepsilon }}_{1}+B+{\hat{B}} w_{1_{\scriptstyle 0}} \end{aligned}$$
(74)

The coefficient matrices are given by

$$\begin{aligned} {A}= & {} \langle {f_3^{{\mathrm{T}}}}(z){{\bar{Q}}}{f_3}(z)\rangle ,\quad {{\hat{A}}}=\langle {f_3^{{\mathrm{T}}}}(z){{\bar{Q}}_3}^{{\mathrm{T}}}R^{2k}_{,z}(z)\rangle \nonumber \\ {{\bar{A}}}= & {} \langle {f_4^{{\mathrm{T}}}}(z){{\hat{Q}}}{f_4}(z)\rangle ,\quad \ B=\langle R^{2k}_{,z}(z){\bar{c}}_{33}R^{1k}_{,z}(z) \rangle \nonumber \\ {{\tilde{A}}}= & {} \langle {f_3^{{\mathrm{T}}}}(z){{\bar{Q}}_3}^{{\mathrm{T}}}R^{1k}_{,z}(z)\rangle ,\quad {\hat{B}}=\langle {\bar{c}}_{33}(R^{2k}_{,z}(z))^2 \rangle \end{aligned}$$
(75)

The explicit expressions for their elements are given below.

$$\begin{aligned} {A}= & {} \left[ \begin{matrix}\langle {\bar{Q}}\rangle &{}\quad \langle z{\bar{Q}}\rangle &{}\quad \langle {{\bar{Q}}}\varPhi ^{k}\rangle \\ &{}\quad \langle z^2{\bar{Q}}\rangle &{}\quad \langle z{{\bar{Q}}}\varPhi ^{k}\rangle \\ &{}\quad \hbox {symm.}&{}\quad \langle \varPhi ^{{k}^{{\mathrm{T}}}}{\bar{Q}}\varPhi ^{k}\rangle \\ \end{matrix}\right] ,\ {{\tilde{A}}}=\left[ \begin{matrix}\langle {{\bar{Q}}_{3}^{{\mathrm{T}}}}R^{1k}_{,z}\rangle \\ \langle z\mathbf {{\bar{Q}}_{3}^{{\mathrm{T}}}}R^{1k}_{,z}\rangle \\ \langle \varPhi ^{{k}^{{\mathrm{T}}}}{{\bar{Q}}_{3}^{{\mathrm{T}}}}R^{1k}_{,z}\rangle \\ \end{matrix}\right] \nonumber \\ {{\hat{A}}}= & {} \left[ \begin{matrix}\langle {{\bar{Q}}_{3}^{{\mathrm{T}}}}R^{2k}_{,z}\rangle \\ \langle z{{\bar{Q}}_{3}^{{\mathrm{T}}}}R^{2k}_{,z}\rangle \\ \langle \varPhi ^{{k}^{{\mathrm{T}}}}{{\bar{Q}}_{3}^{{\mathrm{T}}}}R^{2k}_{,z}\rangle \\ \end{matrix}\right] ,\ {{\bar{A}}}=\left[ \begin{matrix} \langle {R^{k^{{\mathrm{T}}}}_{,z}} {{\hat{Q}} R^k_{,z}}\rangle &{}\quad \langle {R^{k^{{\mathrm{T}}}}_{,z}} {{\hat{Q}}} R^{2k}\rangle \\ \hbox {symm.} &{}\quad \langle {{\hat{Q}}} (R^{2k})^2\rangle \\ \end{matrix} \right] \end{aligned}$$
(76)

The plate constitutive equations as given in Eq. (74) are now substituted into the governing equations in Eqs. (67)–(72) to obtain equations in terms of the plate primary variables:

$$\begin{aligned} {L{\bar{U}} }=\left[ \begin{matrix}0&{} 0&{} -F_3&{} -F_4+B&{} 0&{} 0\\ \end{matrix} \right] ^{{\mathrm{T}}} \end{aligned}$$
(77)

where

$$\begin{aligned}&{{\bar{U}}}=\left[ \begin{matrix}u_{0_{\scriptstyle x}} &{} u_{0_{\scriptstyle y}} &{} w_0 &{} w_{1_{\scriptstyle 0}} &{}\psi _{0_{\scriptstyle x}} &{} \psi _{0_{\scriptstyle y}} \\ \end{matrix} \right] ^{{\mathrm{T}}} \end{aligned}$$
(78)

L is symmetric matrix of linear differential operators in x and y. The elements of L are

$$\begin{aligned}&L_{11}=-\,A_{11}(\ )_{,xx} -A_{33}(\ )_{,yy}\nonumber \\&L_{12}= -\,(A_{12}+A_{33})(\ )_{,xy} \nonumber \\&L_{13}= A_{14}(\ )_{,xxx}+(A_{15}+2A_{36})(\ )_{,xyy} \nonumber \\&L_{14}= -\,{\hat{A}}_{1}(\ )_{,x}\nonumber \\&L_{15}=-\,A_{17}(\ )_{,xx} -A_{38}(\ )_{,yy}\nonumber \\&L_{16}=-\,(A_{1,10}+A_{39})(\ )_{,xy}\nonumber \\&L_{22}= -\,A_{33}(\ )_{,xx}-A_{22}(\ )_{,yy}\nonumber \\&L_{23}=( A_{24}+2A_{36})(\ )_{,xxy} +A_{25}(\ )_{,yyy}\nonumber \\&L_{24}= -\,{\hat{A}}_{2}(\ )_{,y}\nonumber \\&L_{25}= -\,(A_{27}+A_{38})(\ )_{,xy} \nonumber \\&L_{26}=-\,A_{39}(\ )_{,xx}-A_{2,10}(\ )_{,yy}\nonumber \\&L_{33}=-\,A_{44}(\ )_{,xxxx}-(A_{45}+A_{54}+4A_{66})(\ )_{,xxyy}-A_{55}(\ )_{,yyyy}\nonumber \\&L_{34}={\hat{A}}_{4}(\ )_{,xx}+{\hat{A}}_{5}(\ )_{,yy}\nonumber \\&L_{35}=A_{47}(\ )_{,xxx}+(A_{57}+2A_{68})(\ )_{,xyy} \nonumber \\&L_{36}=(A_{4,10}+2A_{69})(\ )_{,xxy}+A_{5,10}(\ )_{,yyy}\nonumber \\&L_{44}=-\,{\hat{B}}+{\bar{A}}_{33}(\ )_{,xx}+{\bar{A}}_{44}(\ )_{,yy}\nonumber \\&L_{45}=({\bar{A}}_{31}-{\hat{A}}_7)(\ )_{,x}\nonumber \\&L_{46}=({\bar{A}}_{42} -{\hat{A}}_{10})(\ )_{,y}\nonumber \\&L_{55}={\bar{A}}_{11}-A_{77}(\ )_{,xx}-A_{88}(\ )_{,yy}\nonumber \\&L_{56}=-\,(A_{7,10}+A_{89})(\ )_{,xy} \nonumber \\&L_{66}={\bar{A}}_{22}-A_{99}(\ )_{,xx}-A_{10,10}(\ )_{,yy} \end{aligned}$$
(79)

Equation (77) represents a system of partial differential equations (PDEs), which can be solved by using various analytical methods. Navier solutions have been obtained in the present work.

3 Navier solution for laminated rectangular plate

Analytical Navier solution is obtained for simply supported rectangular plate of sides a and b along the axes x and y for the boundary conditions at \(x=0,\,a\)

$$\begin{aligned}&\ N_x =0,\quad u_{0_{\scriptstyle y}}=0,\quad w_0 =0,\quad M_x =0\nonumber \\&w_{1_{\scriptstyle 0}} =0,\quad {\bar{M}} =0, \quad P_x = 0,\quad \psi _{0_{\scriptstyle y}}=0\quad \end{aligned}$$
(80)

and at \(y=0,\,b\)

$$\begin{aligned}&\ N_y =0,\quad u_{0_{\scriptstyle x}}=0,\quad w_0 =0,\quad M_y =0\nonumber \\&w_{1_{\scriptstyle 0}}=0,\quad {\bar{M}} =0,\quad P_y = 0,\quad \psi _{0_{\scriptstyle x}}=0 \end{aligned}$$
(81)

The solution and loading terms are expanded in a double Fourier series, satisfying the boundary conditions identically, as

$$\begin{aligned} (w_0, w_{1_{\scriptstyle 0}})= & {} \sum _{m=1}^\infty \sum _{n=1}^\infty (w_0, w_{1_{\scriptstyle 0}}) _{mn} \sin {\bar{m}} x\sin {\bar{n}} y\nonumber \\ (u_{0_{\scriptstyle x}}, \psi _{0_{\scriptstyle x}})= & {} \sum _{m=1}^\infty \sum _{n=1}^\infty (u_{0_{\scriptstyle x}}, \psi _{0_{\scriptstyle x}})_{mn} \cos {\bar{m}} x\sin {\bar{n}} y\nonumber \\ (u_{0_{\scriptstyle y}}, \psi _{0_{\scriptstyle y}})= & {} \sum _{m=1}^\infty \sum _{n=1}^\infty (u_{0_{\scriptstyle y}}, \psi _{0_{\scriptstyle y}})_{mn} \sin {\bar{m}} x\cos {\bar{n}} y \end{aligned}$$
(82)

with \({\bar{m}}=m\pi /a\) and \({\bar{n}}=n\pi /b\). Substituting these expressions in Eq. (77) yields a system of equations for the (m, n)th Fourier component:

$$\begin{aligned} {K{\bar{U}}^{mn}}=\left[ \begin{matrix}0&{} 0&{} -F_3&{} -F_4+B&{} 0&{} 0\\ \end{matrix} \right] ^{{\mathrm{T}}}_{mn} \end{aligned}$$
(83)

K is symmetric stiffness matrix having elements

$$\begin{aligned}&K_{11}={\bar{m}}^2A_{11}+{\bar{n}}^2A_{33}\nonumber \\&K_{12}= {\bar{m}}{\bar{n}}(A_{12}+A_{33})\nonumber \\&K_{13}=-\,{\bar{m}}^3 A_{14}-{\bar{m}}{\bar{n}}^2(A_{15}+2A_{36})\nonumber \\&K_{14}= -\,{\bar{m}}{\hat{A}}_{1}\nonumber \\&K_{15}={\bar{m}}^2A_{17}+{\bar{n}}^2A_{38}\nonumber \\&K_{16}= {\bar{m}}{\bar{n}}(A_{1,10}+A_{39})\nonumber \\&K_{22}={\bar{n}}^2A_{22}+{\bar{m}}^2A_{33}\nonumber \\&K_{23}=-\,{\bar{m}}^2{\bar{n}}( A_{24}+2A_{36})-{\bar{n}}^3A_{25}\nonumber \\&K_{24}=-\,{\bar{n}}{\hat{A}}_{2}\nonumber \\&K_{25}= {\bar{m}}{\bar{n}}(A_{27}+A_{38}) \nonumber \\&K_{26}={\bar{m}}^2A_{39}+{\bar{n}}^2A_{2,10}\nonumber \\&K_{33}={\bar{m}}^4A_{44} +{\bar{m}}^2{\bar{n}}^2(A_{45}+A_{54}+4A_{66}) +{\bar{n}}^4A_{55}\nonumber \\&K_{34}={\bar{m}}^2 {\hat{A}}_{4}+{\bar{n}}^2 {\hat{A}}_{5}\nonumber \\&K_{35}=-\,{\bar{m}}^3A_{47} -{\bar{m}}{\bar{n}}^2(A_{57}+2A_{68}) \nonumber \\&K_{36}=-\,{\bar{m}}^2{\bar{n}}(A_{4,10}+2A_{69}) -{\bar{n}}^3A_{5,10}\nonumber \\&K_{44}={\hat{B}}+{\bar{m}}^2{\bar{A}}_{33}+{\bar{n}}^2{\bar{A}}_{444}\nonumber \\&K_{45}={\bar{m}}({\bar{A}}_{31}-{\hat{A}}_{7})\nonumber \\&K_{46}={\bar{n}}({\bar{A}}_{42}-{\hat{A}}_{10})\nonumber \\&K_{55}={\bar{A}}_{11}+{\bar{m}}^2A_{77}+{\bar{n}}^2A_{88}\nonumber \\&K_{56}={\bar{m}}{\bar{n}}(A_{7,10}+A_{89})\nonumber \\&K_{66}={\bar{A}}_{22}+{\bar{m}}^2A_{99}+{\bar{n}}^2 A_{10,10} \end{aligned}$$
(84)

After obtaining the displacements, the strains are calculated using strain–displacement equations and the transverse shear stress components are calculated using constitutive Eq. (4).

4 Results and discussion

The effect of addition of new layerwise terms in the approximation of the transverse displacement is investigated by comparing the results of the present theory with exact 3D elasticity solution which is obtained from piezothermoelasticity solutions [96] and the conventional zigzag theory (ZIGT) which is a special case of Kapuria’s zigzag theory for piezoelectric hybrid cross-ply plates [92]. The 3D and ZIGT results are computed using the computer programs of these theories, which are available with the present authors. Three laminated composite plates, namely two-layer plate (a), three-layer plate (b) and four-layer plate (c), are considered whose configurations are given in Fig. 2. The material 1 is a typical unidirectional graphite–epoxy material which is used extensively in Pagano’s works [25] as well as by several other researchers. The graphite–epoxy material 2 is taken from works of Rower at al. [97]. Two-layer cross-ply composite plate (a) has laminas at [\(0^\circ /90^\circ \)] with thicknesses 0.5h and 0.5h, and three- layer cross-ply composite plate (b) has laminas at [\(0^\circ /90^\circ /0^\circ \)] with thicknesses h / 3, h / 3, h / 3. These plates are made of graphite–epoxy material 1. The four-layer cross-ply composite plate (c) has laminas at [\(0^\circ /90^\circ /0^\circ /90^\circ \)] with thicknesses 0.25h, 0.25h, 0.25h, 0.25h and is made of graphite–epoxy material 2. The mechanical properties of composite materials 1 and 2 are given in Table 1.

Fig. 2
figure 2

Configurations of composite plates

Full size image
Table 1 Material properties
Full size table

Two load cases are considered.

  • Load case 1. Uniform load \(p_{z_2}=-\,p_0\) applied on the top surface.

  • Load case 2. Sinusoidal load \(p_{z_2}=-\,p_0\sin (\pi x/a)\sin (\pi y/b)\) applied on the top surface.

The displacement and stress entities are non-dimensionalized with \(S=a/h\) and \(E_0=6.9\) GPa for plates (a), (b) and \(E_0=10\) GPa for plate (c): \(({\bar{u}}, {\bar{v}}, {\bar{w}})=100(u, v, w/S)E_0/hS^3p_0,\quad ({\bar{\sigma }}_x, {\bar{\tau }}_{yz}, {\bar{\tau }}_{zx})=(\sigma _x, S \tau _{yz}, S \tau _{zx})/S^2p_0\), \({\bar{\sigma }}_z=\sigma _z/p_0\).

4.1 Convergence study for uniformly applied load

A convergence study is conducted to determine the number of terms for m and n in the double Fourier series expansion under uniformly distributed load and is given in Table 2 for exact 3D, ZIGT and HZIGT theories for three-layer square symmetric plate (b) at \(S=10\). The 3D exact solution yields converged results for displacements and stresses at \(m=n=91\). In case of ZIGT, the convergence of transverse shear stress (calculated from equilibrium equations) is found to be slow than that of inplane displacements and inplane stresses. The result reported for ZIGT in all subsequent analysis is obtained with \(m=n=201\). The present HZIGT is seen to produce convergence at \(m=n=121\) for all entities except \({\bar{\sigma }}_y\), which is seen to oscillate between m and \(m+10\) terms. Henceforth, we report average value of \({\bar{\sigma }}_y\) obtained by taking \(m=n=121\) and \(m=n=131\), whereas \(m=n=121\) is taken for all other entities.

Table 2 Convergence study for number of terms \(m=n\) for composite square plate (b)under uniformly distributed load at top \((S=10)\)
Full size table
Table 3 Exact 3D results and percentage errors in 2D theories for square composite plates (a) and (b) under uniformly distributed mechanical load on top
Full size table

4.2 Response to uniform load on top of plate

Table 3 shows responses for square laminated plates (a) and (b) under this uniform load for three aspect ratios \(S=5, 10\) and 20. The results are obtained for 3D solution by taking \(m=n=91\), for ZIGT with \(m=n=201\) and for present HZIGT with \(m=n=121\). Percentage errors are listed in the table for the HZIGT and the ZIGT for direct assessment. It is observed from the table that the inplane displacements are accurately calculated by the present theory HZIGT than the existing ZIGT. For thick plate (a) with \(S=5\), both these displacements are consistently improved, whereas these are comparable or slightly improved for other aspect ratios.

The midsurface deflections are of comparable magnitude in these thickness cases. Similar relative accuracy is seen in three-layer composite plate (b). Moreover, the symmetric plate (b) is seen to have better predictions for displacements than the two-layer antisymmetric plate (a). Due to the inclusion of layerwise terms in transverse deflection, the resulting transverse normal strain is of non-negligible magnitude especially in thick laminates and its influence decreases with increase in plate aspect ratio. For example, the error in w has reduced from 16.3 to 2.11% as S has changed from 5 to 10. The inplane normal stress and constitutively calculated transverse shear stress are seen to be more accurate for symmetric plate (b) too.

The present model has yielded interlaminar transverse shear stress, using constitutive relations, with error less that 2% in symmetric laminate, but not in the antisymmetric plate (a). The through-the-thickness distributions for \({\bar{\tau }}_{zx}\) in plate (b) are plotted in Fig. 3 using the present model that are calculated using both equilibrium equations (marked short and long dash) and the constitutive equations (marked small dash and indicated HZIGT-C). A significant deviation is observed in the two outer layers and are due to the mathematical simplicity imposed on \(\gamma \) in Eq. (12) to reduce the computational complexity. It is hoped that inclusion of these terms in \(\gamma \) will improve transverse stresses in outer layers.

Fig. 3
figure 3

Through-the-thickness distributions of \({\bar{u}}\), \({\bar{w}}\) and \({\bar{\tau }}_{zx}\) for three-layer square composite plate (b) under uniformly distributed mechanical load on top

Full size image

The response of the four-layer antisymmetric plate (c) to the uniform pressure load on top surface of the laminate is shown in Table 4. It shows a mixed prediction of improved displacement u and worsened displacement v. This can only be attributed to the cubic term in w which grows much rapidly than the quadratic term with increase of distance from mid-surface. The present formulation (HZIGT) has predicted significant deviations from the original ZIGT for all aspect ratios, though the transverse shear stress calculation has been a significant improvement.

Table 4 Exact 3D results and percentage errors in 2D theories for composite square plate (c) under uniformly distributed mechanical load on top
Full size table
Table 5 Exact 3D results and percentage errors in 2D theories for rectangular composite plate (c) under sinusoidal mechanical load on top (\(b/a=3\))
Full size table
Fig. 4
figure 4

Through-the-thickness distributions of \({\bar{u}}\), \({\bar{w}}\), and \({\bar{\tau }}_{zx}\) for four-layer rectangular (\(b/a=3\)) composite plate (c) under sinusoidal mechanical load on top

Full size image

4.3 Response to sinusoidal load on top of plate

Static response of the four-layer composite rectangular plate (c) having length-to-breadth ratio \(b/a=3\) under sinusoidally applied pressure load on top surface of the plate is obtained for displacements and stresses and is given in Table 5 for \(S=5, 10\) and 20. The displacements predicted by the present HZIGT are found not to be as accurate as that yielded by the ZIGT. The accuracy, however, improved for the inplane stress and the transverse shear stress calculated using constitutive equations has fair accuracy with a maximum error below 10%. The transverse shear stress calculated from the use of equilibrium equations is matching very well with the 3D exact solution, which is shown in Fig. 4. As it is observed for uniform loading in square plate (a), the proposed nonlinear approximation of transverse displacement is not capable of providing correct estimate of the transverse shear stress from constitutive equations when antisymmetric configurations are analyzed. Also, it is anticipated that there needs to be further refinement in the inplane displacement field approximation by the way of using double-superposition hypothesis as researched by Zhen and Wanji [90], and Kapuria and Nath [91].

5 Conclusions

By proposing a layerwise approximation for the transverse displacement, a variationally consistent analytical formulation is presented for laminated composite plates with a view to obtain transverse stresses by using constitutive equations. Owing to layerwise representation of the displacement field, the displacement variables increase proportionately with the number of layers in the laminate. An equivalent single-layer expression is obtained by utilizing the continuity conditions on displacements, transverse stresses and the transverse normal stress gradient. Layerwise qubic functions are used for deflection in order to obtain quadratically varying transverse stresses directly from constitutive equations. Static analysis is done using two-layer, three-layer and four-layer composite plates which are applied with both uniform and sinusoidally varying pressure load on their top surfaces. A mixed result is obtained in that the present theory provides comparatively better results in symmetric laminates than in antisymmetric laminates. It is inferred that refinement of the existing ZIGT is not alone sufficient by modifying the transverse displacement. The inplane displacement field has equal significance in providing correct transverse stress values, since both these displacement fields are related to the transverse stresses through their strain–displacement relations and constitutive equations.