Damage identification in multi-step waveguides using Lamb waves and scattering coefficients

Abstract

Damage detection in uniform structures has been studied in numerous previous researches. However, damage detection in non-uniform structures is less studied. In this paper, a damage detection algorithm for identifying rectangular notch parameters in a stepped waveguide using Lamb waves is presented. The proposed algorithm is based on mode conversion and scattering phenomena because of interaction of Lamb wave modes with defects. The analysis is divided into two steps: notch localization and notch geometry detection. The main advantage of this method is its ability to detect all of the notch parameters in a waveguide with arbitrary number of step discontinuities. The method is applied to a numerical example and the results show that it can successfully identify the notch location, depth, and width in a multi-step plate.

1 Introduction

Structural health monitoring (SHM) using Lamb waves has received significant attention because of their numerous advantages. One of their advantages is that they can be easily generated into a structure using small pieces of piezoelectric ceramics. Furthermore, Lamb waves are advantageous for global inspection. Someone can inspect the health of a large area of a structure using a limited number of sensors and actuators without moving them along the structure. Therefore, an in situ inspection would be possible [1, 2]. The purpose of SHM projects is not only detection of large defects and structural failures, but also identification of damages in their early stage of growth before they could reach a dangerous level for the structure [3, 4].

Employing Lamb waves for SHM in simple geometry structures is feasible. Beams and plates with a constant thickness are examples of such structures. In most of the previous damage detection studies, damage detection problem is considered in simple uniform waveguides [5,6,7,8,9,10].

Although there are also studies on damage detection in non-uniform waveguides [11,12,13], no algorithm has been presented for detection of all damage parameters (location and geometry) in such structures. As most of the structures in real applications are non-uniform, it is necessary to develop methods capable of detecting damages in more complex waveguides.

In this article, we propose a method for identifying notch parameters as damage in a stepped plate with an arbitrary number of symmetrical thickness variations using Lamb wave propagation. The proposed algorithm is an extension of damage detection algorithm presented by the authors for damage detection in uniform plates [14]. In the authors’ previous paper [14], a damage detection approach based on scattering coefficients in simple uniform waveguides was presented. In non-uniform waveguides, however, damage identification is more challenging. First, Lamb waves interact with discontinuities in the waveguide. This interaction causes several reflections and transmissions in the waveguide. Moreover, mode conversion occurs as a result of interaction of Lamb waves with discontinuities and defects in the waveguide [15]. This is the main challenge in developing a method for health monitoring of such structures since the interpretation of signals received by the sensors is not feasible, especially when there exist several damages and discontinuities in the waveguide. Therefore, choosing proper sensor location and damage detection scheme is necessary to reduce this complexity. Another challenge is to relate sensor measurements to damage parameters considering the effect of discontinuities and damages on the incident wave. In non-uniform waveguides with thickness variation, one may not identify damage intensity simply comparing the wave amplitudes at different locations. Hence, the advantage of employing the scattering coefficients for damage detection is more significant. Furthermore, the effect of thickness variations on the wave speed must be considered for both damage localization and quantification.

To address the challenges, a damage detection method based on Lamb wave mode power and scattering coefficients is developed. In this method, a Lamb wave mode is generated into the structure and the power loss due to damage is computed from the measurements collected by sensors, considering the effect of damage, mode conversions, discontinuities and wave attenuation on the power of Lamb wave. The proposed algorithm predicts location and dimensions of the existing notch (damage) in the structure.

To relate the computed power loss of Lamb waves to damage parameters, we use the method and results presented by Kim and Roh [16, 17]. They have introduced scattering coefficients for a rectangular notch, which identifies reflection and transmission coefficients of Lamb waves in interaction with notch considering mode conversion phenomenon. More details about damage detection method and scattering coefficients are discussed in the following sections.

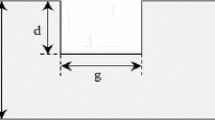
Figure 1 shows the schematic of the problem considered in this study. The proposed method allows a user to identify not only the notch location, but also its geometry (depth and width) as shown in Fig. 1. The fundamentals of this approach can be developed for health monitoring of other types of non-uniform structures and also other types of damages.

Fig. 1

Schematic of considered damage detection problem and rectangular notch geometry in a waveguide

2 Lamb waves

Lamb wave particle displacement in structures is superposition of guided longitudinal and transverse shear waves. They can propagate in symmetric, antisymmetric or a combination of symmetric and antisymmetric modes. To study the Lamb wave modes, the Rayleigh–Lamb equation is used [18]. Various numerical techniques are introduced to obtain dispersion curves of different waveguides [1, 19]. In this paper, an aluminum waveguide is considered. The phase velocity dispersion curve of an aluminum plate is shown in Fig. 2a. According to this figure, several modes can propagate in the waveguide at high frequencies. Moreover, complicated mode conversion occurs between these modes due to interaction with defects and discontinuities (Sect. 3). The multiple-mode characteristic of Lamb waves results in complex signal and makes the signal interpretation complicated for damage detection purposes [20, 21]. To overcome this challenge, a lot of researchers use lower frequency excitations for damage identification (e.g., [6,7,8, 21,22,23,24]). At low frequency excitations, only the fundamental modes ($S_0$ and $A_0$) can propagate in the waveguide. Although the fundamental modes are long wave modes and may have not enough sensitivity to small defects, signal interpretation would be easier when only fundamental modes exist in the waveguide. The symmetric $S_0$ mode is faster and has much lower attenuation than the antisymmetric $A_0$ mode. $A_0$ mode is considered more sensitive to damage; however, there are cases when the $S_0$ mode has advantages over the $A_0$ mode in detecting the damage [25,26,27]. In this paper, we select the central frequency below the cutoff frequency of the $A_1$ mode so that only the fundamental modes are propagated in the structure.

In the practical excitation of Lamb waves into the structure, a group of frequencies exist in the generated wave. In this case, one should consider the group velocity of Lamb waves. The group velocity is the velocity that is used for damage localization purposes, and its dispersion curve for an aluminum plate is shown in Fig. 2b.

Fig. 2

a Phase velocity and b group velocity dispersion curve of aluminum plate with Young’s modulus $E = 71$ GPa, density $\rho = 2.7\,\hbox {g cm}^{-3}$, Poisson’s ratio $\upsilon = 0.33$

According to Fig. 2 and in a stepped waveguide, the velocity is different at each section of the waveguide due to the thickness variations. This change in propagation velocity is important in damage localization procedure. Furthermore, the thickness variation is considered in computing the wave power, which is the basis of the proposed damage detection algorithm.

3 Interaction of Lamb waves with defects and discontinuities

In order to study the damage detection problem in non-uniform structures, one should consider the interaction of generated wave with defects and discontinuities in the waveguide. Interaction of ultrasonic-guided waves with defects and discontinuities has been vastly studied by researchers (Cho [15], Puthillath et al [28], Alleyne and Cawley [29, 30], Lowe et al. [31], Gunavan and Hirose [32], Kim and Roh [16, 17], to name a few), and more important theory and concepts can be found in the books by Achenbach [18], Auld [33] and Graff [34]. The results of these studies provide valuable information which can be used for developing damage detection algorithms.

Wave scattering and mode conversion are two main consequences of the wave interaction with defects and discontinuities. In the following subsections, we describe the concepts of mode conversion and scattering coefficients which form the basis of our damage detection algorithm.

3.1 Mode conversion and scattering coefficients

Mode conversion phenomenon of Lamb waves is defined as energy transformation from one Lamb wave mode to another [2]. In the study of mode conversion in a waveguide, two issues are important to be considered: the geometry of waveguide and the existing damages in the structures. Both of these factors can cause mode conversion in the structure. If the waveguide geometry is symmetric, the mode conversion is only possible in the same mode group and it could not occur between symmetric and antisymmetric Lamb wave modes. However, if the waveguide is asymmetric, the mode conversion would also occur between mode families.

On the other hand, defects in a waveguide could cause mode conversions [35]. The defects in structures occur without any control and they usually make the geometry of the waveguide asymmetric. A good example is a transverse crack in a structure. The presence of cracks and notches causes mode conversion in the structure both in the mode families and between them. According to the above explanations, it can be inferred that if in a symmetric waveguide, the mode conversion between symmetric and antisymmetric modes occurs, a defect should be present in the structure. This point can be used in damage detection for simple structures, like uniform beams and plates. For example, the mode conversion phenomenon is shown in Fig. 3, which is due to the presence of a crack in the waveguide. In this figure, the incident wave is $S_0$ and it is assumed that the excitation frequency is selected such that only the fundamental modes ($S_0$ and $A_0 )$ can be propagated in the waveguide. Although the incident wave is $S_0$, the reflected and transmitted waves contain both $S_0$ and $A_0$ modes. According to the principle of conservation of energy, the sum of reflected and transmitted wave powers is equal to the power of incident wave.

Fig. 3

Scattering of Lamb wave modes by interaction with a crack

It is worth mentioning that it is assumed the mode conversion takes place only between fundamental modes, although according to the works presented by Achenbach et al [36,37,38], appearing of non-monochromatic waves is also possible.

Consider a multi-step plate as shown in Fig. 1. As the geometry of the structure is symmetric, no mode conversion occurs because of interaction of Lamb modes with discontinuities. Therefore, if we generate $S_0$ or $A_0$ mode into the structure at low frequencies and mode conversion is observed from the signals collected by sensors, we can expect a defect in the structure. This fact is used as the basis of our proposed damage detection approach in this paper.

3.2 Scattering coefficients

The reflected and transmitted coefficients of Lamb waves can be defined as the ratio of scattered amplitudes of reflected and transmitted modes to the amplitude of incident mode. If the power of Lamb modes be used instead of their amplitude, the scattering coefficients would be independent of the measurement direction of mode amplitudes. Therefore, more general coefficients could be obtained. Several studies have been done on computing the scattering coefficients [16, 17, 30,31,32].

In this paper, the method presented by Kim and Roh [17] is used to compute the scattering coefficients. The reflected/ transmitted coefficients are defined as the square root of the ratio of reflected/ transmitted mode power to the incident mode power. Using the method presented in [17], the scattering coefficients of Lamb waves, caused by a rectangular notch, are computed (see Appendix for more details). Note that since in the proposed damage detection method only the transmission coefficients are needed, we do not discuss the reflection coefficients in the following sections to avoid complexity.

For example, the scattering coefficient diagrams obtained for a 5 mm aluminum plate are shown in Fig. 4 for the excitation frequency of 100 kHz. The notch depth is considered from 0 to 50% of the plate thickness, percentage of d / H, and the notch width (g) is considered to be 0–10 mm. As long as in this paper we use transmission coefficients, only the scattering diagrams for the transmission coefficients are presented here. The diagrams are computed for both $A_0$ and $S_0$ incident modes. In the scattering coefficients, the first character, i.e., T, shows the transmission coefficient. The second character represents the incident mode to the notch. “S” represents $S_0$ and “A” represents $A_0$ mode. Finally, the third character represents the scattered mode under consideration. For example, TSA means the transmission coefficient of $A_0$ mode when the incident mode to the notch is $S_0$. These scattering diagrams form the basis for notch geometry identification algorithm and will be used in the related section.

Note that the scattering coefficients depend on the thickness of the structure. As it will be discussed in proposed damage detection method, it is necessary to compute these scattering diagrams for all of the thicknesses we have in our multi-step structure. However, since the general shape of the diagrams are the same and are slightly different for the thicknesses which are used in the numerical examples, the scattering diagrams for the other thicknesses are not shown here.

Fig. 4

Scattering coefficient diagrams for an 5 mm aluminum plate at 100 kHz excitation frequency, a TSS, b TSA, c TAS, d TAA

4 Damage detection approach

In this section, we propose a general damage detection approach for a plate with arbitrary number of step discontinuities. There are two main challenges in developing this SHM algorithm for this problem where the previous common methods cannot be employed. These challenges are as follows:

• Since there are several discontinuities in the waveguide, the wave modes will be reflected at the discontinuities and the sensors receive a lot of wave packets because of these successive reflections and transmissions. This makes the signal interpretation difficult.

• The algorithm should be able to predict not only the location of the notch, but also its intensity, i.e., its depth and width (Fig. 1).

To overcome these challenges, we propose a method which is based on mode conversion and Lamb waves power. First, we need to choose an appropriate sensor placement to solve the main difficulties which are related to signal interpretation. There are two common methods for damage detection: pulse-echo and pitch-catch [2]. The pulse-echo method cannot be used in this case since the effect of damage cannot be separated from the reflections. Moreover, the power of reflected wave from damage is much less than that of transmitted wave and makes the signal interpretation difficult, specially for small defects.

In this study, the pitch-catch sensor placement is employed. Two sensors are placed on the structure at the beginning and the end of the inspection area as shown in Fig. 1. The first sensor is used only to measure the power of generated incident Lamb wave mode (as the reference value) at the beginning of the inspection zone, and the second sensor measures the power of transmitted wave going away from the inspection area. Optimal selection of sensor location plays an important role in feasibility of signal interpretation and damage detection procedure. For example, one should minimize the effect of multiple reflections from the plate boundaries on the measurements. Furthermore, analyzing the regions where non-propagating and trapped modes exist is also of great importance in sensor placement. When a Lamb wave is scattered by a discontinuity/defect, both propagating and non-propagating modes are generated into the structure. The number of generated propagating modes is finite and depends on the value of wave frequency relative to the cutoff frequency (Fig. 2) [39]. However, the number of generated non-propagating modes is infinite [39]. In this study, the sensor locations are selected 200 mm away from the edges and discontinuities where the effect of non-propagating modes on the measurements can be neglected. The optimal sensor locations can be identified more accurately using dynamic Saint Venant’s principle (DSVP) [40, 41], which determines the distance beyond which edge effects could be ignored [42]. Numerous theoretical and experimental studies have been devoted to examination of dynamic Saint Venant’s principle, and have confirmed application of such phenomenon in various engineering situations including elastic wave propagation in structures (see [43] for a review). For instance, He et al. [42] studied the end effect in cylindrical waveguides using dynamic Saint-Venant’s principle where the end effects zone is approximated 2.2 times of the waveguide radius. Diligent et al. [44] measured the excitation of evanescent waves generated at a free end of a plate upon reflection of the first symmetrical mode, and concluded that evanescent modes can be neglected beyond distance of five times the plate’s width. This approach is advantageous in identification of optimal sensor locations for structural health monitoring purposes considering the effect of edges and discontinuities in structures.

In order to detect the notch geometry in the structure, we use the idea introduced in our previous study [15] and extend that for the multi-step plate. The idea is based on mode conversion phenomenon, scattering coefficients and power loss in Lamb wave modes.

The damage detection approach is divided into two parts: damage localization and damage geometry identification. The proposed approaches for each of these problems are introduced in the following sections.

4.1 Notch localization procedure

Detection of damage location is the first step in a damage detection plan. As it will be discussed later, damage location also affects the accuracy of the notch geometry detection. Therefore, it is important to localize the damage with high accuracy. In this article, a damage localization algorithm based on mode conversion phenomenon is proposed.

Consider a plate with $n-1$ symmetric discontinuity as shown in Fig. 1. Also suppose that there is a notch at the $i{\mathrm{th}}$ part of this plate. When an incident mode ($A_0 /S_0$) is excited into the plate, the interaction of incident mode with the notch causes mode conversion. Therefore, both $A_0$ and $S_0$ modes will be observed by the sensors. Since the geometry of the considered structure is symmetric, mode conversion can be considered as a sign of existence of damage in the structure. Using the difference between time arrivals of $S_0$ and $A_0$ modes, someone can compute the anticipated time difference of collected $S_0$ and $A_0$ modes from the sensor as follows:

$$\begin{aligned} \Delta t=t_{A} -t_S =d_i \left( \frac{1}{V_{A(i)} }-\frac{1}{V_{S(i)} }\right) + L_{i+1} \left( \frac{1}{V_{A(i+1)} }-\frac{1}{V_{S(i+1)} }\right) +\cdots +L_n \left( \frac{1}{V_{A(n)} }-\frac{1}{V_{S(n)} }\right) \end{aligned}$$

(1)

where $d_i$ is the distance of notch to the ith discontinuity, $L_i$ is the length of ith step, and $V_{m(i)}$ represents the group velocity of mode m in the ith step and can be obtained from Fig. 2b for each thickness. Using this equation, one can compute the notch localization diagram theoretically. This diagram shows the distance of notch (damage) from the sensor based on time difference of arrived $S_0$ and $A_0$ modes to the sensor.

For example, consider the plate shown in Fig. 5. This aluminum plate has three steps with the thicknesses of 6, 5 and 4 mm. Using Eq. (1), the damage localization diagram for this plate is computed as shown in Fig. 6. Note that this plot consists of three lines (one for each step) and the slopes of these lines are different from each other. Using this plot, one can detect the distance of existing damage from sensor and detect the location of damage in the waveguide. The detail of this procedure is discussed in the numerical examples.

It is worth mentioning that in practice, the signals can be gathered using piezoelectric patches or a laser vibrometer. There are several techniques to separate $A_0$ and $S_0$ modes in a signal [35, 45,46,47]. Moreover, note that the sensor may receive $A_0$ and $S_0$ modes several times because of reflections happening in the waveguide; however, in the presented approach, we need to use the first arrived $A_0$ and $S_0$ modes to the sensor for the damage detection purpose. This is because only the first arrived modes are related to the mode conversion phenomenon and the modes that will arrive later are results of multiple reflections in the waveguide and cannot be interpreted easily.

Fig. 5

Schematic of considered example for damage localization diagram

Fig. 6

Damage localization diagram for the plate shown in Fig. 7

4.2 Detection of notch geometry

In SHM plans, it is important to identify the severity of damages in order to determine the remaining life of the structure. In this section, an algorithm is presented to extract the notch dimensions in a multi-step plate. The method is based on mode conversion phenomenon and scattering coefficients. This method is developed in a way that only two sensors are needed for damage detection of whole structure having arbitrary number of discontinuities.

The basic idea of this method is damage detection based on power of Lamb wave modes and scattering coefficients. As it was described before, interaction of Lamb wave modes with damage causes mode conversion phenomenon. The power of each of the reflected and transmitted modes from the defect is related to its geometry (Fig. 4). Therefore, the basic idea is to use two sensors before and after the damage and determine the power of incident, reflected and transmitted modes and scattering coefficients. Hence, these coefficients can be related to the notch geometry. Now consider the damage detection problem as shown in Fig. 1. Two sensors are used at the beginning and the end of inspection zone. The power of Lamb wave modes can be computed from the signals collected by the sensors. However, these powers cannot be used directly for computing scattering coefficients since there are other issues which cause power loss in the structure. These issues are wave attenuation in the waveguide and power loss due to discontinuities in the structure. If someone neglects these effects, the power reduction in Lamb modes would be considered only as the effect of damage. This assumption would cause erratic results in the computation of scattering coefficients, as well as in the geometry identification of the notch. Hence, someone should omit the effect of wave attenuation and discontinuities from the measurements. In the following sections, we first discuss the power loss due to discontinuities and wave attenuation. Next, we introduce the formulation and approach of notch geometry identification based on scattering coefficients.

4.2.1 Transmission coefficients at discontinuities

When an incident wave interacts with the step discontinuity, part of the wave reflects to the first step and part of that transmits to the next step of the structure. In this case, it is necessary to compute power loss of the wave because of this change of thickness. We can apply the same procedure described in Sect. 3.1 (Ref. [17]) to obtain transmission coefficients. For example, these coefficients are computed for a step-down discontinuity with the thicknesses of 6 and 5 mm as shown in Fig. 7. In this case, no mode conversion occurs since the geometry of the structure is symmetric. Therefore, the reflected and transmitted modes are the same as the incident mode. Similar graphs can be computed for all of the step discontinuities which exist in the waveguide.

In the damage detection procedure, the transmission coefficient of step discontinuity is shown by $D_s^m$ where m can be either $A_0$ or $S_0$ mode.

Fig. 7

Transmission coefficient from step discontinuity for $d_{1}= 6\,\hbox {mm}$ and a $S_0$ mode and b $A_0$ mode

4.2.2 Lamb wave attenuation

The wave attenuation phenomena would decrease the amplitude and power of the wave in a waveguide. Wave attenuation is the result of the distance a wave would propagate. It is necessary to consider the attenuation effect in the formulations in order to increase the prediction accuracy. The attenuation of Lamb wave amplitude can be estimated, as follows [48];

$$\begin{aligned} A_2 =A_1 \mathrm{e}^{(-k_i \Delta x)} \end{aligned}$$

(2)

where $A_1$ and $A_2$ are the wave amplitudes at the locations $x_1$ and $x_2$, respectively. $\Delta x$ is the propagation distance from point $x_1$ to $x_2$. In Eq. (2), $k_i$ represents the attenuation coefficient and can be computed using the following [48];

$$\begin{aligned} k_i =\frac{\omega \zeta }{c_\mathrm{g} }, \end{aligned}$$

(3)

where $\omega$ is the excitation frequency, $\xi$ is the damping of the structure and $c_\mathrm{g}$ is the group velocity of the wave. As the group velocity of Lamb wave modes are usually different for a single excitation frequency, their attenuation coefficients would be different, according to Eq. (3). Moreover, for a stepped plate the group velocity is different in each section of the plate and one should consider this difference in the formulations.

A power decay coefficient is defined for attenuation. According to Eq. (2), we define the power attenuation coefficient, $D_\zeta$, as;

$$\begin{aligned} D_{\zeta }^{2} =\frac{P_2 }{P_1 }=\left( \frac{A_2 }{A_1 }\right) ^{2}=\mathrm{e}^{(-2k_i \Delta x)}, \end{aligned}$$

(4)

where $P_i$ is the power of wave at the location $x_i$. This coefficient will be used later to eliminate the effect of attenuation from the scattering coefficients.

4.2.3 Computation of scattering coefficients using sensors

In order to extract the notch geometry, it is necessary to determine the transmission coefficients of the wave from the notch. In this section, a formulation is introduced in order to compute the transmission coefficients of Lamb wave modes and eliminate the effect of step discontinuities and wave attenuation from these coefficients.

Consider a multi-step plate having a notch at ith step as shown in Fig. 1. Furthermore, consider that the mode $\alpha$, which can be either $S_0$ or $A_0$, is excited as incident wave. The power of incident mode computed from sensor1 is shown as $P_{\mathrm{incident}}^\alpha$. The scattered transmitted modes are collected by sensor2. The power of received mode $\beta$ by sensor2 is introduced as $P_{{ transmitted}}^\beta$. According to the type of scattering coefficient, which is computed, the received mode $\beta$ can be either $S_0$ or $A_0$.

According to Sect. 3.1, the scattering coefficients are defined as the square root of the ratio of reflected/transmitted mode power to that of incident mode. If $D_{sj}^m$ is the transmission coefficient of mode m from the jth discontinuity and $D_\xi$ is the power attenuation coefficient of mode m at ith step of the plate, the power of scattered modes arrived at the sensor2 are computed as follows:

$$\begin{aligned} \sqrt{P_{\mathrm{received}}^\beta }=D_{\xi 1}^\alpha D_{s1}^\alpha D_{\xi 2}^\alpha D_{s2}^\alpha \cdots D_{s(i-1)} D_{\xi i(bc)}^\alpha . T\alpha \beta . D_{\xi i(ac)}^\beta D_{si}^\beta \ldots . D_{s(n-1)}^\beta D_{\xi n}^\beta \sqrt{P_{\mathrm{incident}}^\alpha } \end{aligned}$$

(5)

In this equation, $T\alpha \beta$ is the transmission coefficient of mode $\beta$ from the notch when the incident mode is $\alpha$. Moreover, $D_{\xi i(bc)}^m$ and $D_{\xi i(ac)}^m$ are the power attenuation coefficients of mode m at ith step because of traveled distance before and after the notch, respectively.

One can reformulate Eq. (5) in order to compute the scattering coefficients, as follows;

$$\begin{aligned} T\alpha \beta =\frac{\sqrt{P_{\mathrm{received}}^\beta }}{D_{\xi 1}^\alpha D_{s1}^\alpha D_{\xi 2}^\alpha D_{s2}^\alpha \cdots D_{s(i-1)} D_{\xi i(bc)}^\alpha .D_{\xi i(ac)}^\beta D_{si}^\beta \ldots . D_{s(n-1)}^\beta D_{\xi n}^\beta \sqrt{P_{\mathrm{incident}}^\alpha }} \end{aligned}$$

(6)

Therefore, using the known coefficients of D and the wave powers computed from sensors 1 and 2, the transmission coefficients can be computed. These coefficients are used in the geometry identification as is described in the next section.

As it can be seen from Eq. (6), for computing the coefficients precisely, it is necessary to know the location of notch as precise as possible. This indicates the importance of the notch localization step, as is presented in Sect. 4.1.

Fig. 8

Schematic of the presented example

4.2.4 Notch geometry identification algorithm

When we generate $S_0$ mode into the structure, both $S_0$ and $A_0$ mode are received by sensor 2 because of mode conversion phenomenon. The same phenomenon will happen in the case of generating $A_0$ into the structure as incident wave. Therefore, one can obtain four transmission coefficients, i.e., TSS, TSA, TAS, TAA. However, according to the reciprocating theorem, the coefficients TSA and TAS are the same. Therefore, only three of these four coefficients are distinct. In this algorithm, we need all of these three coefficients to complete the identification procedure for notch geometry. The reason is that using two coefficients could lead to non-unique solutions as it will be shown in the examples.

The algorithm can be classified into these four steps:

• 1. Generating $S_0$ mode into the plate and extracting the TSS and TSA coefficients.

• 2. Generating $A_0$ mode into the plate and extracting the TAA coefficient.

• 3. Comparing the computed scattering coefficients with their corresponding diagrams as shown in Fig. 4. Therefore, a set of solution would be obtained for the coefficients as “solution curves”. Three solution curves could be obtained, containing the solution for the problem, i.e., the notch depth ratio, % d/H, and width, g, for the corresponding coefficient.

• 4. Plotting the obtained three solution curves in a single diagram. As long as the solution for the problem could satisfy each curve, the intersection of these curves would be the unique solution for the problem. Our experience with this algorithm shows the possibility of intersection in more than one point for every two curves. That is why three coefficients are used in our method.

5 Example

A notched aluminum plate with two symmetric thickness variations is considered as shown in Fig. 8. This plate has three steps and the notch is considered to be in the second step of the plate. The thickness of each part of the plate is considered to be 6, 5 and 4 mm for the first, second and third step of the plate, respectively.

For this example, the discontinuity transmission coefficients ($D_{si}$) and the attenuation coefficients (k) are computed using the discussed methods and are presented in Tables 1 and 2, respectively. In Table 1, $D_{s1}$ means the transmission coefficient for the first discontinuity (6–5 mm) and $D_{s2}$ is the transmission coefficient of the second discontinuity (5–4 mm). In Table 2, $k_i^m$ means the attenuation coefficient of mode m in the ith step of the plate.

Table 1 Transmission coefficients from step discontinuities in Fig. 10

Table 2 Attenuation coefficients for the example shown in Fig. 10

In order to investigate the effect of wave attenuation, a damping of 0.001 is assumed for this plate. The inspection length of the plate is set to be 600 mm and the parameters of existing notch are presented in Table 3.

Table 3 Notch parameters of presented example

To generate desired wave mode into the structure, a 5-cycle Hanning-windowed sinusoidal tone burst with a central frequency 100 kHz is used. The problem is simulated in $\hbox {ABAQUS}^{\circledR }$ [49] software. It should be mentioned that at the sensor locations, the axial displacements of a point at the top surface of the plate are considered as the output signals. In practice, these signals can be gathered using piezoelectric patches. Moreover, using a laser vibrometer, these signals can be easily obtained and the Lamb wave modes can be differentiated.

As the first step of damage detection, the location of the notch is determined. For this purpose, $S_0$ mode is generated into the structure as described above. The resulting signals from sensor2 are shown in Fig. 9. The signals are normalized using the maximum amplitude of incident wave. In this signal, the occurrence of mode conversion phenomenon is obvious and $S_0$ and $A_0$ modes can be observed and differentiated from each other. The time difference between these two modes should be computed to identify the distance between the notch and sensor 2 using Fig. 9. To compute the time difference, the scale-average wavelet power (SAP) is defined and used [1], as follows;

$$\begin{aligned} \hbox {SAP}^{2}(n)=\frac{1}{M}\sum \limits _{i=1}^M {\left| {\hbox {CWT}(a_i ,n)} \right| ^{2}} . \end{aligned}$$

(7)

In Eq. (7), CWT is the continuous wavelet transform of the signal, a is the scale, M is the largest scale during CWT, and n represents the number of sampling point. This energy spectrum for Fig. 9a is shown in Fig. 9b. The 9th complex Gaussian function is used as the mother wavelet function in Eq. (7). Using this spectrum, the time difference is obtained as $\Delta t =4.96 \hbox {e}-5$. Using this $\Delta t$ in the diagram of Fig. 6, the notch location is predicted in the second step of the plate and 305.3 mm far from sensor2. This result is shown in Fig. 10 and the notch location is predicted successfully.

Fig. 9

a Signals received by sensor 2 in $S_0$ mode excitation case, b energy spectrum of the signal

Fig. 10

Notch localization using time difference between $S_0$ and $A_0$ modes

Fig. 11

Signals received by sensor 2 in $A_0$ mode excitation case

Now, using the predicted location of the notch we can predict the notch dimensions. As it was described in the notch geometry identification algorithm, we need to generate both $S_0$ and $A_0$ into the structure separately. The $S_0$ mode was used for damage localization and we only need to excite $A_0$ mode in the plate. The measured signal by sensor 2 is shown in Fig. 11. Using the received signals from the sensor2 in both $S_0$ and $A_0$ mode excitations, the wave mode powers are computed. The procedure of computation of Lamb mode power from sensors can be found in Ref. [50] in more details. The calculated mode powers are as;

$$\begin{aligned} \begin{array}{ll} P_{\mathrm{incident}}^{S0} =1,\quad P_{\mathrm{received}}^{S0} =0.743,\quad P_{\mathrm{received}}^{A0} =0.036 &{}\quad (S_0~ \hbox {excitation})\\ P_{\mathrm{incident}}^{A0} =1,\quad P_{\mathrm{received}}^{A0} =0.684 &{}\quad (A_0 ~\hbox {excitation}) \end{array} \end{aligned}$$

(8)

where $P_\alpha ^\beta$ means the power of received $\alpha$ mode when the incident mode is $\beta$. Note that these powers are normalized with respect to the power of incident mode obtained from sensor 1.

Using these powers and the formulation presented at Sect. 4.2.3, the transmission coefficients TSS, TSA and TAA can be computed. Knowing the received mode powers, the attenuation coefficients, step discontinuity transmission coefficients, as well as notch location, we can obtain the scattering coefficients using the following equations:

$$\begin{aligned} \hbox {TSS}= & {} \frac{\sqrt{P_{\mathrm{received}}^{S0} }}{D_{S1}^{S0} D_{S2}^{S0} D_{\zeta 1}^{S0} D_{\zeta 2}^{S0} D_{\zeta 3}^{S0} \sqrt{P_{\mathrm{incident}}^{S0} }}=0.928 \end{aligned}$$

(9)

$$\begin{aligned} \hbox {TSA}= & {} \frac{\sqrt{P_{\mathrm{received}}^{A0} }}{D_{S1}^{A0} D_{S2}^{A0} D_{\zeta 1(bc)}^{S0} D_{\zeta 1(ac)}^{A0} D_{\zeta 2}^{A0} D_{\zeta 3}^{A0} \sqrt{P_{\mathrm{incident}}^{S0} }}=0.210 \end{aligned}$$

(10)

$$\begin{aligned} \hbox {TAA}= & {} \frac{\sqrt{P_{\mathrm{received}}^{A0} }}{D_{s1}^{A0} D_{s2}^{A0} D_{\zeta 1}^{A0} D_{\zeta 2}^{A0} D_{\zeta 3}^{A0} \sqrt{P_{\mathrm{incident}}^{A0} }}=0.936 \end{aligned}$$

(11)

In order to clarify the extraction of above coefficients, the schematic of extraction of TSA coefficient is shown in Fig. 12. This figure indicates the locations/regions that the coefficients affect the power of Lamb wave. The accuracy of proposed method depends on the accuracy of calculate Lamb wave mode powers. Hence, it is important to use accurate measurement techniques and noise filtering processes to accurately predict damage parameters in experimental studies.

Fig. 12

Schematic of extraction of TSA coefficient

Intersecting the plane of coefficients TSS, TSA and TAA by the diagrams shown in Fig. 4a, b, d, respectively, we obtain the solution curves, as shown in Fig. 13. Note that since the notch was predicted in the part of the plate which has 5 mm thickness, we can use the diagrams shown in Fig. 4. If the notch is detected to be in other thicknesses of the plate, one should compute and use the corresponding diagrams for that as described in Sect. 3.1.

Using Fig. 13, the notch geometry can be identified. It is noticed that these three curves may not intersect precisely at a single point, because of computational, simulation, or experimental errors. Therefore, we take the centroid of the triangle formed by the intersection of the three curves, as the intersection point. As it can be seen, the notch depth ratio and its width are identified as 30.6% and 2.06 mm, respectively. Therefore, all of the notch parameters are identified with acceptable accuracy using the present algorithm. The results are tabulated in Table 4. Note that according to Fig. 13, if we use only two of the scattering coefficients for notch geometry detection, the result may not be unique since the TSS and TSA coefficients intersect at two different points.

Fig. 13

Intersection of result curves to predict the notch geometry

Table 4 Final results of damage detection in presented example

As it is observed in this example, all of the damage parameters are predicted successfully. One of the challenges that the proposed algorithm might have in practice is its ability to detect small size damages. Looking at the scattering diagrams (Fig. 4), one can observe that for small size damages ($<10\%$), the change in scattering coefficients is small. Therefore, one needs high accuracy in identifying the wave powers received by sensors, and also accurate consideration for the power loss in the waveguide. Small error in identification of scattering coefficients may cause considerable error in damage detection results.

6 Conclusions

In this paper, a novel method for identification of notch parameters in multi-step plates was proposed. This algorithm could successfully detect the notch location, width and depth in a plate having arbitrary number of symmetric step discontinuities. The method was based on mode conversion phenomenon of Lamb waves and the scattering coefficients. Damage detection was done using only two sensors in the structure in a pitch-catch configuration. The results show that the method can predict all of the notch parameters with acceptable accuracy.

Since the geometry of most of the structures in the industry is not uniform and is more complex than the usual previous studied cases, it is important to develop new techniques for more real applications. The proposed algorithm introduced several techniques which can be extended for damage detection in more complex cases. Using an effective sensor placement, scattering coefficients and mode conversion phenomenon for damage detection are the most important introduced techniques which can be extended for other structural health monitoring problems such as other types of structures and damages. As an important example, future studies are needed to develop similar damage detection approaches for waveguides with asymmetric step discontinuities, where more complicated mode conversion and scattering occur.

Appendix

In this section, the concepts and mathematical formulation of computing scattering coefficients are briefly discussed. The formulations and procedure are introduced by Kim and Roh [17], and more details of the formulations and procedure can be found in Refs. [16, 17].

The displacement and stress components of nth mode Lamb wave $w_n$ can be written as

$$\begin{aligned} w^{n}=W_n \left( {k_n ,y} \right) \mathrm{e}^{i\left( {k_n x-\omega t} \right) }, \end{aligned}$$

(A.1)

where $w_n =\left[ {u_n ,v_n ,\sigma _n ,\tau _n } \right] ^{\mathrm{T}}$ and $W_n =\left[ {U_n \left( {k_n ,y} \right) ,V_n \left( {k_n ,y} \right) ,S_n \left( {k_n ,y} \right) ,T_n \left( {k_n ,y} \right) } \right] ^{\mathrm{T}}$. Here, $u^{n}$ and $v^{n}$ denote longitudinal and transverse displacements, respectively, while $\sigma ^{n}$ and $\tau ^{n}$ denote normal and shear stresses, respectively. $U_n$, $V_n$, $S_n$, and $T_n$ are modal functions for each corresponding component. The equation form of each modal function is different for the symmetric and antisymmetric modes.

Considering the power of nth mode Lamb wave, $C_n^2$, Lamb wave modal functions are normalized by $C_n$ for direct comparison of reflection and transmission coefficients, and the normalized wave form is expressed as follows

$$\begin{aligned} {\overline{w}}^{n}={\overline{W}}_n \left( {k_n ,y} \right) \mathrm{e}^{i\left( {k_n x-\omega t} \right) }, \end{aligned}$$

(A.2)

where ${\overline{W}}_n =W_n /C_n$. The nth mode Lamb wave after reflection or transmission can be expressed with the normalized modal functions as [16]

$$\begin{aligned} {\overline{w}}^{n}=D_n {\overline{W}}_n \left( {k_n ,y} \right) \mathrm{e}^{i\left( {k_n x-\omega t} \right) }, \end{aligned}$$

(A.3)

where $D_n$ is the reflection/transmission coefficient of nth mode Lamb wave after interaction with a discontinuity provided that the incident wave has a unit power.

When an incident wave interacts with notch, the scattering mechanism can be divided into three main processes. The incident wave strikes the B1 boundary and some portion of its energy is reflected in Region 1 and the remaining portion is transmitted to Region 2. The transmitted wave strikes the boundary B2 and wave is reflected and transmitted to regions 2 and 3, respectively. The reflected wave strikes the boundary B1, and some portion is transmitted to Region 1 while the other portion is reflected to Region 2. This procedure is repeated again and again until final reflected and transmitted waves are generated (Fig. 14) [17].

Fig. 14

Scattering of Lamb wave by a rectangular notch

To solve for the scattering coefficients at each process, the displacement and stress components induced by the scattered propagating and non-propagating modes must be the same as those of the incident wave at the points on the boundaries. To find reflected and transmitted waves at each process, one can apply the boundary conditions and continuity conditions for displacements and stresses at the boundaries. For instance, in process 1 one may write (Fig. 14):

$$\begin{aligned}&\left\{ {{\begin{array}{l} {\left( \sigma \right) _{W_{i1} } +\left( \sigma \right) _{W_{r1} } =0} \\ {\left( \tau \right) _{W_{i1} } +\left( \tau \right) _{W_{r1} } =0} \\ \end{array} }} \right. ,\quad \left( {x,y} \right) \in \gamma _1\nonumber \\&\left\{ {{\begin{array}{l} {\left( u \right) _{W_{i1} } +\left( u \right) _{W_{r1} } =\left( u \right) _{W_{t1} } } \\ {\left( v \right) _{W_{i1} } +\left( v \right) _{W_{r1} } =\left( v \right) _{W_{t1} } } \\ {\left( \sigma \right) _{W_{i1} } +\left( \sigma \right) _{W_{r1} } =\left( \sigma \right) _{W_{t1} } } \\ {\left( \tau \right) _{W_{i1} } +\left( \tau \right) _{W_{r1} } =\left( \tau \right) _{W_{t1} } } \\ \end{array} }} \right. ,\quad \left( {x,y} \right) \in \gamma _2 \end{aligned}$$

(A.4)

where $w_{i1}$, $w_{r1}$ and $w_{t1}$ represent incident, reflected and transmitted Lamb wave at the left notch boundary. Normalizing Eq. (A.4) using the power, one may solve for the reflected and transmitted coefficients of each mode, i.e., $D_n$.

Note that each of the wave components $\sigma ,\tau ,u$ and v consist of several propagating and non-propagating modes. For example, $u=\sum _{i=0}^\infty u_{S,i} +\sum _{i=0}^\infty u_{A,i}$, where i is the number of considered propagating and non-propagating modes, and A and S represent symmetric and antisymmetric modes, respectively. when the product of frequency and plate thickness is low, one should only consider fundamental modes ($A_0~ \hbox {and}~S_0 )$ since higher order modes do not propagate in this range. However, sufficient number of non-propagating modes needs to be considered for acceptable accuracy. It is shown in Ref. [17] that for notch depths up to 85% of the plate thickness, considering 300 non-propagating modes, results in acceptable results.

For each scattering process, the scattering graphs are constructed in Ref. [17], and transmission and reflection coefficients of propagating modes are pre-calculated at various types of notch boundaries. All field information for non-propagating modes is included in the scattering graphs. For a Lamb wave of the same kind and a notch of the same depth, the transmission and reflection coefficients in the graphs can be referred to whenever the scattering process occurs.

The described three scattering processes occur again and again until no energy is left in Region 2. Therefore, so many iterations are needed to calculate the final transmission and reflection coefficients. To compute the final reflection and transmission coefficients, a straightforward matrix transformation method is presented by Kim and Roh [17] considering infinite repetitions of the scattering processes. This method can be used to compute the final scattering coefficients for various notch intensities (see [17] for more details). The computed scattering coefficients required for this study are shown in Fig. 4.

To verify the extracted scattering coefficients, results are compared with those obtained from finite element simulation. The results are demonstrated in Fig. 15 for selected cases which show the computed scattering coefficients from theory and simulation are in match.

Fig. 15

Comparison of transmission coefficients computed from theoretical formulations ($\circ$) and FEM simulation ($\Box$) for an 5 mm aluminum plate at 100 kHz excitation frequency. a TSA, b TSS, c TAS, and d TAA