1 Introduction

Chemical reactions during the formation of concrete lead to volume deformation of the internal gel material and the formation of a large number of pores. Based on their size and shape, these pores can be classified as capillary pores and gel pores. Most of the pores have irregular shapes [1]. These pores have a significant impact on the mechanical properties of concrete structures and result in several complex concrete properties. In seepage problems, the matrix bulk modulus and the effective bulk modulus are important factors that affect the Biot effective stress coefficient and permeability calculations [2]. Therefore, calculating the formula for the bulk modulus of a concrete structure is important for calculating the seepage and mechanical properties of concrete structures and certain multi-pore rock materials.

In recent years, many researchers have studied the relationship between the effective mechanical parameters and mechanical parameters of the matrix material of porous materials. These investigations have primarily focused on empirical formulae and experimental studies of porous materials, such as ceramics [3,4,5]. In 1968, Wachtman Jr [3] proposed bulk modulus and shear modulus versus porosity relationships for single-crystalline materials and similar brittle and porous materials. In 1987, Phani [4] proposed a formula for the effective elastic modulus of polycrystalline rare earth oxide. In 1996, ARNS [6] experimentally studied the effective mechanical parameters of sandstone and granite and compared and analyzed the errors of the empirical formula and numerical calculations versus the theoretical formula and their causes. The results showed that each type of solid porous material has a key porosity; when the porosity exceeds the key porosity, the matrix cannot bear the external load. In 2013, Yang et al. [7] studied the mechanical properties of a sandy soil material using numerical calculations and experiments; however, there was no further analysis of the mechanical parameters of the porous medium.

Research on pore shapes has primarily focused on theories for circular pores [8,9,10,11,12,13]. In 1999, based on an effective mechanical parameter formula proposed by previous researchers, Luo [14] studied the relationship between the pore shape and the effective mechanical parameters of circular pores; the results showed that the pore shape had a significant impact on the mechanical parameters. In 2001, Charles [15] calculated the elastic moduli of porous materials using numerical simulations and suggested that in a material with circular pores, such as ceramics, the difference between the pore shape in the numerical simulation and the actual pore shape was the main source of error. In 2000, Roberts and Garboczi [16] used FEM to study the influence of porosity and pore shape on the elastic properties of porous ceramics. In 2002, Ymaman [1] studied the characteristics of the pore structure of concrete and the corresponding relationship between the water–cement ratio and the porosity using experiments; the results showed that the presence of other media in the pores had a significant impact on the mechanical properties of the concrete. In 2006, Shao and sun [17] investigated the constitutive relations of porous media and discovered that nonlinearity between stress and deformation is an intrinsic property of a porous medium; however, further verification was needed to confirm the relationship. In 2007, Li [18] derived a relationship between the porosity and bulk modulus of circular pores based on elasticity. In 2010, Zhang et al. [19] developed a tensor evolution model for the effective coefficient and obtained a relationship between the effective stress coefficient and deformation in porous media. In 2012, Xiuli [20] investigated the effective mechanical properties of brittle materials, such as concrete; however, only concretes with porosities up to 0.10 were tested.

In contrast to ceramics, rock materials, such as concrete, do not contain regular circular pores. Therefore, when theories for circular pores are applied to analyze the effective mechanical parameters of rock materials, such as concrete, it is difficult to obtain accurate results. This paper derives a theoretical formula for calculating the effective bulk modulus and the matrix bulk modulus of a medium with square pores based on a formula for square opening problems [21] and the method of Li et al. [18]. The results from the theoretical formula are compared with the results of numerical calculations as well as test results and data from previous studies. Finally, the critical porosity was identified based on the comparison of the results, and the applicability of the theoretical formula for different ranges of porosity was analyzed.

2 Elasticity theory for a square pore

2.1 Curvilinear formula for a square

A rectangular sheet has a square opening with a side length of a located far from the boundary (Fig. 1). Uniformly distributed loads are applied to both sides, and the concentration is q (Fig. 2). The coordinate origin is at the center of the square opening, and the coordinate axes are parallel to the boundaries [21]. Therefore, the infinite domain with the square opening in the Z plane is transformed to a central unit circle in the \(\zeta \) plane via an approximation transformation formula in a complex variable function as shown in formula (1) [23]:

$$\begin{aligned} z=\omega (\zeta )=R\left( \frac{1}{\zeta }-\frac{1}{6}\zeta ^{3}+\frac{1}{56}\zeta ^{7}-\cdots \right) \end{aligned}$$
(1)

where R is a real number that represents the size of the square. The first two terms in the formula are used for the approximation:

$$\begin{aligned} z=\omega (\zeta )=R\left( \frac{1}{\zeta }-\frac{1}{6}\zeta ^{3}\right) \end{aligned}$$
(2)

Let \(\rho =1\) and \(\zeta =\sigma =e^{i\theta }\). The curve of the opening shown in Fig. 1 is a square. Based on the calculation, the side length of the square is \(a={5R}/3\).

Fig. 1
figure 1

A square pore

Full size image

The solution for the elastic deformation of a square opening is based on the approach proposed by Zhilun [22] (Fig. 2). The uniformly distributed external load is decomposed into uniformly distributed forces along the x-axis and y-axis of an infinite board with a square opening, and no surface force is applied to the opening.

Fig. 2
figure 2

Stress on a square pore

Full size image

The displacement solution for the square pore is based on the transformation formula proposed in formula (1). Formula (3) is obtained using the complex variable function method for the displacement solution in elasticity mechanics. For the detailed process, please refer to reference [22]:

$$\begin{aligned} u+i\upsilon =\frac{1+u}{E}\left[ {\frac{3-u}{1+u}\varphi (\zeta )-\frac{\omega (\zeta )}{\overline{{\omega }'(\zeta )} }\overline{{\varphi }'(\zeta )} -\overline{\psi (\zeta )} } \right] \end{aligned}$$
(3)

where u, \(\upsilon \), E and \(\mu \) represent the displacements of the pore in the x and y directions and the matrix’s elastic modulus and Poisson’s ratio. The analytical functions \(\phi (\zeta )\) and \(\psi (\zeta )\)are defined as follows:

$$\begin{aligned} \varphi (\zeta )= & {} qR\left[ {\frac{1}{4\zeta }+\left( \frac{3}{7}\cos 2\phi +i\frac{3}{5}\sin 2\phi \right) \zeta +\frac{1}{24}\zeta ^{3}} \right] \end{aligned}$$
(4)
$$\begin{aligned} \psi (\zeta )= & {} -qR\left[ {\frac{e^{-2i\varphi }}{2\zeta }+\frac{13\zeta -26\left( \frac{3}{7}\cos 2\phi +i\frac{3}{5}\sin 2\phi \right) \zeta ^{3}}{12(2+\zeta ^{4})}} \right] \end{aligned}$$
(5)
$$\begin{aligned} \omega (\zeta )= & {} R\left( \frac{1}{\zeta }-\frac{1}{6}\zeta ^{3}\right) \end{aligned}$$
(6)

where \(\phi \) is the angle between the orientation of the stress on the sheet and the x-axis.

2.2 Pore elasticity assumption

When deriving a theoretical formula for a porous medium such as concrete, three basic assumptions must be made. The first is that the matrix is isotropic, and the deformation of the pore is small compared to the size of the pore; therefore, each point on the pore boundary has an identical displacement in the same direction. The second assumption is that the stress concentrations at the four corners of the square are ignored. The third assumption is that the structure’s matrix material has the same elastic properties as non-porous structure [18, 22].

The purpose of calculating the relationship for the bulk modulus is to obtain the Biot coefficient. The value of the Biot coefficient is crucial for calculating the stress and deformation in concrete dams because the value determines the influence that the pressure of infiltrated water has on the stress field of the porous medium. Because the pore hydro-pressure results in linear deformation of the pore structure, the most important assumption for the derivation of the theoretical formula in this paper is that the strain of the pore in response to the effective force is linearly related to the pore pressure [2]:

$$\begin{aligned} K= & {} \frac{\mathrm{d}p}{\mathrm{d}\varepsilon _v } = \frac{V\mathrm{d}p}{\mathrm{d}V} \end{aligned}$$
(7)
$$\begin{aligned} \eta= & {} \frac{V_\mathrm{c}}{V} = \frac{V_\mathrm{c}^\mathrm{i}}{V^\mathrm{i}} \end{aligned}$$
(8)

where i is the pore identifier, \(\eta \) is the porosity, K is the bulk modulus, p is the external load, \(\varepsilon _v \) is the volume strain, V is the concrete volume, and \(V_\mathrm{c} \) is the pore volume.

2.3 Walsh functions based on the reciprocal work theorem

Reference [18] provides the derivation procedure of Walsh functions, which are applicable to porous material. In this paper, the derivation of the effective bulk modulus is based on Walsh functions assuming that the concrete volume is V. In the formula, \(V_\mathrm{c} \) is the pore volume, q is the external load, and a group of static pressures p are applied to the interior surface in the pore and the exterior surface of structure. Formula (9) is obtained via the reciprocal work theorem. Based on formulae (7) and (9), the Walsh functions for concrete are derived as shown in formula (10):

$$\begin{aligned} \frac{\varDelta V}{Vq}= & {} \frac{\varDelta {V}'}{Vp}+\frac{\varDelta V_\mathrm{c}}{Vq} \end{aligned}$$
(9)
$$\begin{aligned} \beta _{\mathrm{eff}}= & {} \beta _\mathrm{m}+\frac{\varDelta V_\mathrm{c}}{Vq} \end{aligned}$$
(10)

where\(\beta =1/{K={3(1-2\mu )}/E}\)is the compression coefficient, \(\beta _{\hbox {eff}} \)is the effective compression coefficient of the concrete, \(\beta _\mathrm{m}\)is the matrix compression coefficient of the concrete, \(\varDelta V_\mathrm{c}\)is the change in pore volume, and \(\varDelta {V}'\)is the change in solid volume.

3 Theoretical formula for the effective bulk modulus of a medium with square pores based on 2D model

Based on the theory developed in Sect. 2, the bulk modulus relationship of concrete with square pores is analyzed. The main idea is to calculate the pore displacements under elastic deformation based on the stress characteristics. Using the elastic deformation of the pore structure, the volume deformation is calculated. The volume deformation is then substituted into the Walsh functions to derive the bulk modulus relationship for concrete structures.

3.1 Deformation displacement of square pores

When the porosity is relatively low, the space between the pores is relatively large. Therefore, interactions between pores are ignored. In the calculation, the deformation of a square pore is treated as a problem with a square opening in an infinite board. When calculating the deformation of a square pore based on the stress state shown in Fig. 2, a board with a square opening is subject to forces in the x and y directions; i.e., the values of \(\phi \) are \(0^{\circ }\) and \(90^{\circ }\), respectively. The elastic displacements for \(\phi \) at \(0^{\circ }\) and \(90^{\circ }\) are added to obtain formula (11), where \(E_\mathrm{m} \) and \(\mu _\mathrm{m} \) are the matrix material’s elastic modulus and Poisson’s ratio, respectively [22]:

$$\begin{aligned} u+i\upsilon =\frac{1+\mu _\mathrm{m}}{E_\mathrm{m}}qR\left[ \!\right. ( F(\mu _\mathrm{m} ,\theta )+H(\mu _\mathrm{m} ,\theta )\left. i \right] \end{aligned}$$
(11)

where

$$\begin{aligned} F(\mu _\mathrm{m} ,\theta )= & {} \frac{1}{qR}\hbox {Re}\left. {\left[ {\frac{3-\mu _\mathrm{m}}{1+\mu _\mathrm{m}}\varphi (\zeta )-\frac{\omega (\zeta )}{\overline{{\omega }'(\zeta )} }\overline{{\varphi }'(\zeta )} -\overline{\psi (\zeta )} } \right] } \right| _{\phi =0^{\circ }} \nonumber \\&+\frac{1}{qR}\hbox {Re}\left. {\left[ {\frac{3-\mu _\mathrm{m} }{1+\mu _\mathrm{m} }\varphi (\zeta )-\frac{\omega (\zeta )}{\overline{{\omega }'(\zeta )} }\overline{{\varphi }'(\zeta )} -\overline{\psi (\zeta )} } \right] } \right| _{\phi =90^{\circ }} \end{aligned}$$
(12)
$$\begin{aligned} H(\mu _\mathrm{m} ,\theta )= & {} \frac{1}{qR}\hbox {Im}\left. {\left[ {\frac{3-\mu _\mathrm{m} }{1+\mu _\mathrm{m} }\varphi (\zeta )-\frac{\omega (\zeta )}{\overline{{\omega }'(\zeta )} }\overline{{\varphi }'(\zeta )} -\overline{\psi (\zeta )} } \right] } \right| _{\phi =0^{\circ }} \nonumber \\&+\frac{1}{qR}\hbox {Im}\left. {\left[ {\frac{3-\mu _\mathrm{m} }{1+\mu _\mathrm{m} }\varphi (\zeta )-\frac{\omega (\zeta )}{\overline{{\omega }'(\zeta )} }\overline{{\varphi }'(\zeta )} -\overline{\psi (\zeta )} } \right] } \right| _{\phi =90^{\circ }} \end{aligned}$$
(13)
$$\begin{aligned} \left. {\overline{\psi (\zeta )} } \right| _{\phi =0^{\circ }}= & {} -qR\left[ {\frac{1}{2}\zeta +\frac{13}{6(4\cos 4\theta +5)\zeta }+\frac{13\zeta ^{3}}{12(4\cos 4\theta +5)}} \right. \nonumber \\&-\left. {\frac{156}{112(4\cos 4\theta +5)\zeta ^{3}}-\frac{78}{112(4\cos 4\theta +5)}\zeta } \right] \end{aligned}$$
(14)
$$\begin{aligned} \left. {\overline{\psi (\zeta )} } \right| _{\phi =90^{\circ }}= & {} -qR\left[ {-\frac{1}{2}\zeta +\frac{13}{6(4\cos 4\theta +5)\zeta }+\frac{13\zeta ^{3}}{12(4\cos 4\theta +5)}} \right. \nonumber \\&+\left. {\frac{156}{112(4\cos 4\theta +5)\zeta ^{3}}\hbox {+}\frac{78}{112(4\cos 4\theta +5)}\zeta } \right] \end{aligned}$$
(15)
$$\begin{aligned} \left. {{\varphi }'(\zeta )} \right| _{\phi = 0^{\circ }}= & {} qR\left[ {-\frac{1}{4\zeta ^{2}}+\frac{3}{7}+\frac{1}{8}\zeta ^{2}} \right] \end{aligned}$$
(16)
$$\begin{aligned} \left. {{\varphi }'(\zeta )} \right| _{\phi =90^{\circ }}= & {} qR\left[ {-\frac{1}{4\zeta ^{2}}-\frac{3}{7}+\frac{1}{8}\zeta ^{2}} \right] \end{aligned}$$
(17)
$$\begin{aligned} \left. {\overline{{\varphi }'(\zeta )} } \right| _{\phi =0^{\circ }}= & {} qR\left[ {-\frac{1}{4}\zeta ^{2}+\frac{3}{7}+\frac{1}{8\zeta ^{2}}} \right] \end{aligned}$$
(18)
$$\begin{aligned} \overline{\left. {{\varphi }'(\zeta )} \right| } _{\phi =90^{\circ }}= & {} qR\left[ {-\frac{1}{4}\zeta ^{2}-\frac{3}{7}+\frac{1}{8\zeta ^{2}}} \right] \end{aligned}$$
(19)
$$\begin{aligned} \frac{\omega (\zeta )}{\overline{{\omega }'(\zeta )} }= & {} \frac{\zeta }{6}-\frac{13\zeta }{6(2\zeta ^{4}+1)} \end{aligned}$$
(20)

3.2 Derivation of the theoretical formula for the bulk modulus relation

The change in the pore area is calculated based on the area formula. The original area is subtracted from the area after the elastic deformation (based on the assumption that the displacements in the same direction are uniform at each point on the pore boundary) as shown in formula (21):

$$\begin{aligned} \varDelta V_\mathrm{c}^\mathrm{i}= & {} (a+2u)(a+2v)-a^{2} \nonumber \\= & {} 2(u+v)a+4uv \nonumber \\\approx & {} 2(u+v)a \end{aligned}$$
(21)

According to reference [22], a is the length of the side of a square; i.e., \(a={5R}/3\).

The parameters uandv, which were calculated in formula (11), are substituted into formula (21):

$$\begin{aligned} \varDelta V_\mathrm{c}^\mathrm{i}= & {} \frac{10}{3}\frac{1+\mu _\mathrm{m} }{E_\mathrm{m} }qR^{2}[F(\mu _\mathrm{m} ,\theta )+H(\mu _\mathrm{m} ,\theta )] \end{aligned}$$
(22)
$$\begin{aligned} V_\mathrm{c}^\mathrm{i}= & {} a^{2}=\frac{25}{9}R^{2} \end{aligned}$$
(23)

Formulae (22) and (23) give:

$$\begin{aligned} \frac{\varDelta V_\mathrm{c}^\mathrm{i}}{V_\mathrm{c}^\mathrm{i} }=\frac{6}{5}\frac{1+\mu _\mathrm{m} }{E_\mathrm{m} }q[F(\mu _\mathrm{m} ,\theta )+H(\mu _\mathrm{m} ,\theta )] \end{aligned}$$
(24)

Formula (24) and \(1/{K_\mathrm{m} }={3(1-2\mu _\mathrm{m} )}/E_\mathrm{m} \) are substituted into formula (10):

$$\begin{aligned} \beta _{\mathrm{eff}}= & {} \beta _\mathrm{m} +\frac{V_\mathrm{c} }{V}\frac{\varDelta V_\mathrm{c} }{V_\mathrm{c} q}\nonumber \\= & {} \beta _\mathrm{m} +\eta \frac{\varDelta V_\mathrm{c} ^\mathrm{i}}{V_\mathrm{c} ^\mathrm{i}q}\nonumber \\= & {} \beta _\mathrm{m} +\eta \frac{2}{5}\frac{1+\mu _\mathrm{m} }{1-2\mu _\mathrm{m} }\beta _\mathrm{m} \left[ \!\right. F(\mu _\mathrm{m} ,\theta )+H(\mu _\mathrm{m} ,\theta )\left. \! \right] \end{aligned}$$
(25)
$$\begin{aligned} \frac{1}{K}= & {} \frac{1}{K_\mathrm{m} }+\eta \frac{1}{K_\mathrm{m} }\frac{2}{5}\frac{1+\mu _\mathrm{m} }{1-2\mu _\mathrm{m} }\left[ \!\right. F(\mu _\mathrm{m} ,\theta )+H(\mu _\mathrm{m} ,\theta )\left. \! \right] \end{aligned}$$
(26)
$$\begin{aligned} K= & {} \frac{1}{1+\alpha \eta }K_\mathrm{m} \end{aligned}$$
(27)

Finally, the formula for \(\alpha \) is obtained as follows:

$$\begin{aligned} \alpha =\frac{2}{5}\frac{1+\mu _\mathrm{m} }{1-2\mu _\mathrm{m} }\left[ \!\right. F(\mu _\mathrm{m} ,\theta )+H(\mu _\mathrm{m} ,\theta )\left. \! \right] \end{aligned}$$
(28)

Formula (27) is the theoretical formula for a structure with square pores, and formula (28) is the expression for \(\alpha \) in formula (27).

Formula (27) primarily describes the relationship between the effective bulk modulus and the matrix bulk modulus for a single pore. When the porosity is very low and the pores are evenly distributed, the spacing is quite large, so the interaction between pores can be ignored. However, when the porosity increases, the spacing between the pores decreases; therefore, the interaction between pores should be considered. In this paper, the interaction between pores is included by transforming formula (26) into formula (29)[18]:

$$\begin{aligned} \frac{1}{K}=\frac{1}{K_\mathrm{m} }+\frac{\eta }{1-\eta }\frac{1}{K_\mathrm{m} }\frac{2}{5}\frac{1+\mu _\mathrm{m} }{1-2\mu _\mathrm{m} }\left[ \!\right. F(\mu _\mathrm{m} ,\theta )+H(\mu _\mathrm{m} ,\theta )\left. \! \right] \end{aligned}$$
(29)

Formula (28) are substituted into formula (29), and formula (30) is obtained by recombining:

$$\begin{aligned} K=\frac{1-\eta }{1-(1-\alpha )\eta }K_\mathrm{m} \end{aligned}$$
(30)

Formula (30) is the theoretical formula for a multi-pore structure that considers the interactions between the pores, where \(\alpha \) is given by formula (28). This formula shows that the bulk modulus is primarily related to Poisson’s ratio and the porosity of the matrix. When \(\theta \) are \(0^{\circ }\) and \(90^{\circ }\), the displacements in the x and y directions are calculated.

Li [18] derived a formula for the relationship between the effective bulk modulus and the matrix bulk modulus for a porous medium based on the circular pore model:

$$\begin{aligned} K=\frac{1-\eta }{1+\alpha \eta }K_\mathrm{m} \end{aligned}$$
(31)

where \(\alpha =\frac{1+\mu _\mathrm{m} }{2(1-2\mu _\mathrm{m} )}\).

4 The comparison between formula results and numerical results

To investigate the relationship for the effective bulk modulus for porous concrete structures, this paper derived a formula for the relationship between the effective bulk modulus and the matrix material’s bulk modulus based on a theoretical formula for an opening from elasticity and geometrical theory. The formula is verified via numerical calculations using the concrete simulation analysis software SAPTIS, which was developed by Zhang [24]. The numerical calculation procedure is as follows: create a model with different porosities; define the mechanical parameters of the matrix material of the model; apply uniform load on six surfaces (numerical simulation of elastic deformation); extract \(\varepsilon _x ,\varepsilon _y ,\varepsilon _z \) from the results and then calculate the effective bulk modulus of the model via physical equations from elasticity theory [22]. In the paper, the shape function used in the numerical simulation is a linear shape function.

Errors in the numerical calculation results of the effective bulk modulus will occur because the grid is normally square, and excessively large grid dimensions lead to different pore characteristics from that of a circular pore. When small grids are used in numerical calculations of irregular openings, the errors in the results are significantly lower. Therefore, in numerical simulations, the grid density should be sufficiently high so that in a random pore model, the errors induced by the grid’s geometrical characteristics are minimized. The simulation in this paper is based on a \(10\times 10\times 10\) cm cube, which contains one million grid cells (the minimum pore is a grid cell). Figure 3b shows a randomly generated porous medium. A comparison with an actual CT scan of concrete pores [14] (Fig. 3a) shows that the shapes of the numerous irregular connected pores in the numerical model are similar to those in concrete.

Reference [6] presented sandstone test data from a previous study, statistically analyzed the bulk modulus K for different porosities, and suggested that the matrix bulk modulus was 37 GPa and that the Poisson’s ratio was 0.20. The numerical calculations in this paper are based on the test parameters in reference [6]. In the theoretical calculations, the displacements in the x and y directions (i.e., \(\theta \) of \(0^{\circ }\) and \(90^{\circ }\)) and a Poisson’s ratio of 0.20 are substituted into formulae (12) and (13) as follows:

$$\begin{aligned} \left[ \!\right. F(\mu _\mathrm{m} ,\theta )+H(\mu _\mathrm{m} ,\theta )\left. \! \right] =3.5602 \end{aligned}$$

Yaman [1] analyzed the relationship between the water–cement ratio and the porosity after the formation of a concrete structure using experiments. The results showed that ordinary concrete had a maximum porosity of 0.18. In addition, reference [20] found that brittle engineering materials normally had relatively low porosities. In this paper, to verify the validity and applicability of the theoretical formula for calculating the effective bulk modulus of concrete, the maximum porosity is limited to 0.30.

Fig. 3
figure 3

An actual pore structure versus a numerically simulated pore structure. a CT scan image [14]. b Randomly generated pore model (porosity of 0.12)

Full size image

Formula (30) shows that when the porosity approaches 1, the effective bulk modulus approaches zero. However, this result is different from real situations. As the porosity continues to increase, the calculated results of the effective bulk modulus begin to deviate from the test results. Every brittle lithological engineering material analyzed in the previous study [6] had a key porosity; the key porosity for sandstone was 0.47. The mechanical properties are different below and above the key porosity; that is, when the porosity is less than the key porosity, the matrix bears the external load, whereas when the porosity exceeds the key porosity, the porous medium nearly fails to bear the external load. Therefore, regardless of which theoretical formula is used, when the porosity exceeds 0.45, the numerical results deviate significantly from the theoretical calculations (Fig. 4). In addition, in the numerical calculations, structures with high porosities have distinct anisotropic mechanical properties. The 2D isotropic elastic constant bulk modulus K that relate stresses and strains in the 2D problems (used in this paper) are expressed in terms of 3D bulk modulus \(\tilde{K}\) (plane stress in this paper):\(K={9\tilde{K}\tilde{G}}/{(3\tilde{K}+4\tilde{G})}\)(3D shear modulus \(\tilde{G})\). With this interrelations, the results of 3D numerical simulation is amended and then compared to the results of theoretical formula, as shown in Fig. 4 [25, 26].

Fig. 4
figure 4

Theoretical results versus numerical results

Full size image

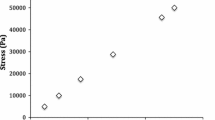
In this paper, the test data from reference [6] are used as the mechanical parameters for the numerical simulation. To verify the validity and applicability of the theoretical formula for rock materials with square pores, several results are presented in Fig. 5, including numerical results for different porosities, results from the theoretical formula for a single square pore and the theoretical formula for multiple pores from this paper(the theoretical formula results based on plane stress), test data [6] and Garboczi numerical simulation data from reference [16], and results from the theoretical formula for circular pores (31) in reference [18].

Fig. 5
figure 5

Porosity versus bulk modulus

Full size image

A comparison of the results in Fig. 5 shows that the numerical results from this study match the results of the Garboczi’s numerical calculations and that the test results basically match the numerical results. As the porosity increases, the results from the theoretical formula for a circular pore gradually begin to deviate from the numerical and test results. When the theoretical formula for a square pore is used and the porosity is less than 0.09, the results from the single-pore theoretical formula match the numerical calculation results, whereas when the porosity exceeds 0.09, the results from the theoretical formula for multiple square pores match the numerical results. In this paper, the critical porosity \(\eta _l \) was found to be 0.09. Reference [18] also suggested that when the porosity is relatively low, the single-pore formula is a better representation of the relationship between the effective bulk modulus and the matrix bulk modulus.

5 Analysis

When the effective mechanical properties of a rock material, such as concrete, are investigated using a square pore model, the theoretical geometrical formula for square pores primarily converts the square pore to a central circle in another plane via a complex variable function. The first two terms in formula (1) are used to approximate the square. Figure 1 shows that when the stress concentration induced by the square’s four corners are ignored (i.e., the effective mechanics solution in this paper is primarily based on elasticity), the four edges of the square guarantee the validity of the calculated results. Therefore, the elasticity formula for a square opening is the foundation for solving for the effective coefficient. Besides, different number of the first few items in the formula would lead to different square shape. The difference is mainly reflected in the radius of curvature of the square pore. The more the first few items are, the smaller the radius of curvature is. However, the side length of the square pore does not change. The displacements in the x and y directions is mainly used in the theoretical calculation. Therefore, the influence of curvature at the corner on the calculation results is very small.

The relationship between the effective bulk modulus and the matrix modulus for porous continuous medium with square pores was derived. However, there must be some error when the numerical simulation result of the 3D model (Fig. 3) is compared with the theoretical formula result. To analyze the influence of the error, a two-dimensional model and a three-dimensional model with same pore distribution and porosity have been established (as shown in Fig. 6). The effective bulk modulus were obtained by the two models being applied the loads respectively, the results are \(K_{s}=2.3923\,\mathrm{GPa}\) and \(K_{c}=2.4264\,\mathrm{GPa}\). Then the porosity and other corresponding parameters of the two models are substituted into the theoretical square pore formula and circular pore formula respectively, and the results are obtained: \(K_{\mathrm{squar,F}}=2.4324\,\mathrm{GPa}\) and \(K_{\mathrm{circle,F}}=2.7348\,\mathrm{GPa}\). As a result, although there is a certain difference between the results obtained from the 2D model and the 3D model, the formula derived in the paper is still more accurate to obtain the effective bulk modulus for the porous continuous medium with square pores. The shape of the pore is an important factor affecting the calculation result of effective bulk modulus.

Fig. 6
figure 6

The simulation model

Full size image

Reference [13] suggested that the primary source of errors in numerical simulations of pores is the differences in the pore shape. The theoretical formula derived from a square pore matches the results of tests and numerical simulations well. The calculated results show that when the grid has a sufficiently high density, the shapes of random pores are similar to those in real materials. Therefore, refining the model grids is an effective way to reduce the errors in numerical simulations. Figure 6 shows that when the porosity is relatively high, single pores connect to each other to form new pore shapes. A comparison with Fig. 3 shows that the shapes of these new pores are very similar to those in real materials; thus, the calculated effective coefficients of rock materials such as concrete from numerical calculations match the effective coefficients of actual concrete structures. Therefore, this paper compared the results of numerical calculations with those from the theoretical formula to verify the validity of the theoretical formula.

Because numerically simulated pores are not circular, the errors in the numerical simulation are larger than the results using square pores. In addition, because the shapes of the pores in a concrete structure are primarily controlled by self-induced deformation, the pores in both low porosity and high porosity concretes are primarily polygonal [1]. Therefore, when analyzing the effective coefficients of rock materials such as concrete, the results of the theoretical formula for circular pores will have relatively large differences from the actual coefficients.

Fig. 7
figure 7

Blocks with identical dimensions and different porosities (0.048 and 0.18, respectively)

Full size image

In the theoretical formula for a square pore, when the porosity is less than the critical value, the theoretical formula for a single pore should be applied, and when the critical porosity is exceeded, the theoretical formula for multiple pores should be used. The results from the theoretical formula and numerical calculations deviate from test results in different porosity ranges. This macroscale phenomenon is caused by two main factors. The first is that in the elasticity calculation [22], the pore boundary stress concentration affects the material within a certain range, beyond which pore boundary stress concentration characteristics will disappear. In a low-porosity medium, the space between the pores is greater than the extent of the stress concentrations at the pore boundaries, so there is no interaction between the pores. However, as the porosity increases, the pore spacing decreases, and the interaction between the pores increases. The second factor is that when the porosity is low, the numerically calculated pore shape and structure are very similar to those of the theoretical model, and when the porosity is relatively high, some pores will connect. Figure 7 shows two diagrams of the pore distributions of materials with different porosities. The structure with the porosity of 0.048 has relatively large spacing between pores, and most of the pores are not connected. In contrast, the structure with the porosity of 0.18 has less spacing between the pores, and most of the pores are connected; the resulting pore shapes are highly random, and the pore shapes are similar to those in actual materials (as shown in Fig. 3).

The critical porosity \(\eta _l \) of many porous rock materials is generally approximately 0.10. As suggested in reference [15], when the porosity exceeds 0.10, different calculation methods result in different deviations from test results. Similar results were also reported in reference [18]. Therefore, different formulae for the bulk modulus are appropriate for different macroscale scenarios. The porosity of concrete is usually low; the maximum porosity obtained via tests in reference [1] was 0.18, and the pores had irregular polygonal shapes and were connected. Therefore, the effective bulk modulus of pores continues structure can be calculated using formula (32).

$$\begin{aligned} K=\left\{ \begin{array}{ll} \frac{1}{1+\alpha \eta }K_\mathrm{m} &{}\quad \eta \le \eta _l \\ \frac{1-\eta }{1-(1-\alpha )\eta }K_\mathrm{m} &{}\quad \eta \ge \eta _l \\ \end{array}\right. \end{aligned}$$
(32)

6 Discussion

The relationship between the effective bulk modulus and the matrix modulus of porous continuous medium with square pores is derived. However, when the pores are filled with other mediums or the pores become deformed, the macroscopic mechanical parameters of porous continuous medium would be influenced. It is a problem for further study, which contains the analysis of the macromechanical parameters of pores continuum medium due to the deformation of the pores and the filler or from microperspective. Limited by time, conditions, and other reasons, the above study is hard to complete now. The formula will be improved in the further study.

7 Conclusions

This paper derived the relationship between the effective bulk modulus and the effective matrix modulus for media with square pores. Based on previous studies on brittle materials, such as ceramics and sandstone, as well as a comparison with test data and the results of numerical calculations, the applications of the theoretical formula for the effective bulk modulus was analyzed. The following conclusions are drawn:

  1. (1)

    When the porosity is less than the key porosity, the results of the theoretical formula for a square pore are consistent with the results of the numerical calculations. The theoretical formula provides accurate results for the relationship with the bulk modulus. The results of the theoretical formula for a square pore also match the numerical results and the results of tests on sandstone from previous studies. The theoretical formula is valid for the pore structures of rock materials such as concrete.

  2. (2)

    The porosity of concrete is usually low; however, because of the interaction between pores, there is a critical porosity in the theoretical formula. When the critical porosity is not exceeded, the solution for the effective bulk modulus should be based on the theoretical formula for a single square pore. When the critical porosity is exceeded, the effective bulk modulus should be calculated using the theoretical formula for multiple square pores.

  3. (3)

    Understanding the relationship between the effective bulk modulus and the matrix bulk modulus of a porous structure provides a solid theoretical basis for analyzing the Biot effective stress coefficient. Therefore, the theoretical solution for a square pore is important for research on how the pore-scale hydro-pressure affects concrete structures in seepage calculation.

  4. (4)

    The pore shape is an important factor affecting the calculation results with the formula in the paper. The previous literatures, such as [18], mainly focused on the circular pores, while the engineering structures are usually with irregular pores, such as concrete, sandstone. This theoretical formula will decrease the error caused by the pore shape and help to obtain a more accurate result of effective bulk modulus for porous continuous medium with square pores.

This paper derived a theoretical formula for the effective bulk modulus for a square pore and investigated its applicability. However, the theoretical formula is not valid for relatively high porosities. The results from the theoretical formula were compared with the results of tests of sandstone and numerical calculations. Therefore, future research will focus on the results of tests of concrete structures and investigations of the key porosity for concrete.