1 Introduction

The static and dynamic behaviours of railway tracks are of importance for several tasks and topics in railway engineering. In track design [1], loads and displacements, the force distribution, and the deformation of the track have to be determined with the help of a suitable track model. An optimum track displacement under the static load must be achieved by certain track elements. The stress in each track element must be known to avoid damage. In vehicle–track interaction [2, 3], the dynamic loading of the track is determined and resilience is put to the track (e.g. rail pads) or to the vehicle (wheelset). The vehicle–track–soil interaction [4, 5] aims at the static and dynamic forces that are acting on the ground and excite the ground vibration [6]. Finally, mitigation measures [7] are developed to reduce the ground vibration for example by elastic track elements [8,9,10].

These track engineering problems are often solved with the classical track model of the “Zimmermann beam” [11]. This model is based on the Winkler hypothesis [12] that the track–soil interaction can be easily described by a bedding modulus locally relating the displacement and the force at the track–soil interface. This model has an explicit (static) solution and is therefore widely used by practitioners, track designers, consultants and railway managers. In research work, however, the importance of a more realistic soil behaviour has been observed [2, 13, 14] and the soil is now always included as a continuous homogeneous or layered soil. Therefore in this contribution, a track model is proposed that retains the simple representation of the track characteristics of the “Zimmermann track” and combines it with a correct representation of the soil. The solutions for the track and the continuous soil are found and coupled in the frequency–wavenumber domain. The solution in space domain is then calculated by a wavenumber integral.

The present method of the integration in the wavenumber domain has already been used by the author for infinitely extended plates on the soil [15] and for infinite beams on the soil [16] to realize intense parametric studies on soil–structure interaction. The wavenumber domain method has been applied on railway tracks by Jones [17] and others [18, 19]. Slab tracks have a simpler geometry and therefore are even better suited for this wavenumber domain method [5, 20, 21]. More complicated track models and methods have been proposed. The 2.5D method combines a wavenumber approach along the track with a FEM or FEBEM model across the track [22,23,24]. The track–soil modelling can be more detailed by a three-dimensional finite-element boundary-element method (FEBEM) [25], or a time-domain FEBEM [26]. Other research models use large three-dimensional finite-element models of the soil to represent the infinite half-space [27,28,29].

The present method (given with all necessary formulae) is a compromise for practitioners to correctly include the track–soil interaction with a minimum of discretization effort and computation time. It is well suited to investigate the track behaviour around resonances where wider distributions of amplitudes can be observed along the track. Therefore, the focus of this contribution has been put on track–soil resonances due to soil layering and on vehicle–track resonances due to elastic track elements. Frequency-dependent transfer function as well as deformations for relevant track systems and frequencies have been analysed.

The contribution consists of the following sections. Section 2 gives the dynamic soil stiffness in wavenumber domain, whereas Sect. 3 presents the same for the multi-beam track model. Section 4 describes the track–soil coupling and the solution by wavenumber integrals, and Sect. 5 the vehicle–track interaction. At the end of the method sections, Sect. 6 offers some numerical details. The following results sections start with the vehicle, track and soil parameters in Sect. 7. In Sect. 8, frequency-dependent compliance and force transfer functions are presented where the stiffness of the ballast, the stiffness and layering of the soil, and an under-ballast plate will be analysed. The last subsection is devoted to the mitigation effects of elastic track elements. Section 9 considers the force and displacement distribution along the track where strong differences can be observed between different frequencies and track–soil systems. Finally, passages of complete trains are calculated and compared with measurements in Sect. 10. This leads to clear conclusions about the correct track–soil model in Sect. 11.

2 Dynamic stiffness of a layered soil in wavenumber–frequency domain

The soil consists of a number of horizontal layers with thicknesses \(h_{i}\). Each layer is an elastic continuum, which is described by the field equation for the displacement \(\mathbf{u}_{S}\)

$$\begin{aligned} G\left( {{\hbox {div}}\, {\hbox {grad}} \mathbf{u}_S +\frac{1}{1-2\nu }grad\, div \mathbf{u}_S } \right) =\rho {\ddot{\mathbf{u}}}_S \end{aligned}$$
(1)

and by the material constants G shear modulus, \(\nu \) Poisson’s ratio, \(\rho \) mass density, D hysteretic damping (\(G=G_{\textit{0}}(1+\mathrm{i}2D)\)). For the time- and space-harmonic function

$$\begin{aligned} \mathbf{u}_S (\mathbf{x},t)\hbox {=}{} \mathbf{a} \,\hbox {exp}(\hbox {i} {\varvec{\upxi }} \cdot \mathbf{x}+\hbox {i}\omega t) \end{aligned}$$
(2)

with the angular frequency \(\omega = 2\pi f\) and the wavenumber vector \(\varvec{\upxi }\), equation (1) reads as

$$\begin{aligned} G\left( {{\varvec{\upxi }}\cdot {\varvec{\upxi }} \mathbf{a}+\frac{1}{1-2\nu }\mathbf{a}\cdot {\varvec{\upxi }} {\varvec{\upxi }}} \right) =\rho \omega ^{2}{} \mathbf{a}. \end{aligned}$$
(3)

The solutions of this equation are defined by

$$\begin{aligned} \begin{array}{lll} \mathbf{a}\cdot {\varvec{\upxi }}=0&{}\quad \hbox {and}\quad &{}\frac{\omega }{\xi _S }=\sqrt{\frac{G}{\rho }}=v_S \\ \mathbf{a} \left\| { {\varvec{\upxi }}} \right. &{}\quad \hbox {and}\quad &{}\frac{\omega }{\xi _P }=\frac{2-2\nu }{1-2\nu }\sqrt{\frac{G}{\rho }}=v_P \\ \end{array} \end{aligned}$$
(4)

as a shear and a compressional wave.

The stiffness of the soil for a plane stress wave on the surface is obtained by combining a shear and a compressional wave for each layer. For the homogeneous half-space, the boundary conditions yield the explicit solution

$$\begin{aligned} H_S (\xi ,\omega )=\frac{u_S }{F^{{\prime }{\prime }}}=\frac{\xi _S ^{2}\sqrt{\xi _{\mathrm{P}} ^{2}-\xi ^{2}}}{\hbox {i}G\left[ {(\xi _S ^{2}-2\xi ^{2})^{2}+4\xi ^{2}\sqrt{\xi _S ^{2}-\xi ^{2}}\sqrt{\xi _{\mathrm{P}}^{2}-\xi ^{2}}} \right] } \end{aligned}$$
(5)

for the vertical compliance. The corresponding compliance of a layered soil is given in Appendix 1.

For the track–soil interaction, the displacements across the track–soil interface (x-direction)

$$\begin{aligned} u_S (x,\xi _y ,\omega )=\frac{1}{2\pi }\mathop {\int }\limits _{-\infty }^{+\infty } {H_S (\xi _x ,\xi _y ,\omega )p_1 (\xi _x )} \exp (\hbox {i}\xi _x x)\hbox {d}\xi _x \end{aligned}$$
(6)

due to a harmonic strip load along the track (y-direction) are calculated where the wavenumber transform

$$\begin{aligned} p_1 (\xi _x )=\frac{\sin \xi _x b/2}{\xi _x b/2}\quad \quad \quad \quad \quad \quad \end{aligned}$$
(7)

of the uniform load distribution across the track width b has been used. Moreover, the average displacement

$$\begin{aligned} {\overline{u_S}} (\xi _y ,\omega )=\frac{1}{b}\mathop {\int }\limits _{-b/2}^{+b/2} {u_{S}} (x,\xi _y ,\omega )\exp (\hbox {i}\xi _x x)\hbox {d}x \end{aligned}$$
(8)

across the track is calculated. Finally, the soil compliance for a strip load

$$\begin{aligned} H_{SS} (\xi _y ,\omega )= & {} \frac{1}{2\pi b}\mathop {\int }\limits _{-b/2}^{+b/2} {\mathop {\int }\limits _{-\infty }^{+\infty } {H_S (\xi _x ,\xi _y ,\omega )p_1 (\xi _x )} \exp (\hbox {i}\xi _x x)\hbox {d}\xi _x \hbox {d}x} \nonumber \\= & {} \frac{1}{2\pi }\mathop {\int }\limits _{-\infty }^{+\infty } {H(\xi _x ,\xi _y ,\omega )p_1 ^{2}(\xi _x )} \hbox {d}\xi _x \end{aligned}$$
(9)

is established, see [16] for further details.

The inverse

$$\begin{aligned} {{K}_{S}}^{\prime }(\xi _y ,\omega )=\frac{1}{H_{SS} (\xi _y ,\omega )} \end{aligned}$$
(10)

will be used for coupling the soil with the track.

3 The multi-beam model of the track

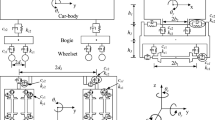
The ballasted track is modelled as a multiple beam system. The first beam represents the two rails, the second beam represents the sleepers and the third beam is used as the base of the track system (Fig. 1). Each beam is described by

  • \({{ EI}}_{j}\)—the bending stiffness and

  • \({m_{j}}^\prime \)—the mass per length,

which are assembled in a diagonal stiffness matrix EI and a diagonal mass matrix \({ {\mathbf{m}}^\prime }\).

Fig. 1
figure 1

Track model consisting of rail, rail pad, sleeper, sleeper pad, ballast, ballast mat, ballast plate and continuous soil

Full size image

The multi-beam system fulfils the set of differential equations

$$\begin{aligned} {\mathbf{EIu}_{T}}^{\prime \prime \prime \prime }+\mathbf{m}^{\prime }\ddot{\mathbf{u}}_T +\mathbf{K^{\prime }u}_T =F^{\prime }_T \mathbf{e}_1 \end{aligned}$$
(11)

for the track displacements \(\mathbf{u}_{T}\) under the track load \(F_{T}^\prime \). In the frequency–wavenumber domain, this reads as

$$\begin{aligned} (\xi _y ^{4}{} \mathbf{EI}-\omega ^{2}{} \mathbf{m}^{{\prime }}+{\mathbf{K}_T}^ {{\prime }})\mathbf{u}_T =F_T \mathbf{e}_\mathbf{1 } \end{aligned}$$
(12)

where \(\xi _{y}\) is the wavenumber along the track axis. Note that the wavenumber transform of the vertical point load \({F_{T}}^\prime (y)=F_{T}~\delta (y)\) is the constant force \(F_{T}\).

The track beams are connected by elastic track elements, the rail pads between rail and sleeper, the sleeper pads between sleeper and ballast, the ballast, and the ballast mat under the ballast (Fig. 1). The elastic elements are characterized by complex stiffnesses which are assembled in the global stiffness matrix

$$\begin{aligned} {\mathbf{K}_T}^{{\prime }}=\left[ {-{\begin{array}{l@{\quad }l@{\quad }l} {{k_R}^{\prime }}&{} {{-k_R}^{\prime }}&{} 0 \\ {{k_R}^{\prime }}&{} {{k_R}^{\prime }+{k_{11}}^{\prime }}&{} {{-k_{12}}^{\prime }} \\ 0&{} {{-k_{21}}^{\prime }}&{} {{k_{22}}^{\prime }} \\ \end{array} }} \right] \end{aligned}$$
(13)

where \({k_{R}}^\prime \) is the rail pad stiffness per length and the \({k_{ij}}^\prime \) represent the dynamic stiffness matrix \({\mathbf{K}_{B}}^\prime \) of the ballast

$$\begin{aligned} {\mathbf{K}_B}^{\prime }=\frac{{k_B}^{\prime }\xi _B h_B }{\sin (\xi _B h_B )}\left[ {{\begin{array}{cc} {\cos (\xi _B h_B )}&{} {-1} \\ {-1}&{} {\cos (\xi _B h_B )} \\ \end{array} }} \right] \end{aligned}$$
(14)

The ballast is described by the static stiffness \({k_{B}}^\prime \), the height \(h_{B}\), and the wavenumber \(\xi _{B}=\omega /v_{B}\) of the longitudinal wave velocity \(v_{B}\). For low frequencies, the ballast stiffness approaches the static stiffness \({k_{B}}^\prime \)

$$\begin{aligned} {\mathbf{K}_B}^{\prime }=\left[ {{\begin{array}{cc} {k_B}^{\prime }&{} {-k_B}^{\prime } \\ {-k_B}^{\prime }&{} {k_B}^{\prime } \\ \end{array} }} \right] , \end{aligned}$$
(15)

but in general, it includes the mass effects of a continuous ballast at higher frequencies. If the ballast is between other elastic elements (sleeper pads or ballast mat), transfer matrices are used to derive the dynamic stiffness matrix of the pad–ballast–mat support section, see Appendix 2.

4 Track–soil coupling and the solution as wavenumber integrals

In order to couple the track and the soil, the dynamic soil stiffness (10) is added to the dynamic track stiffness (12) at the last diagonal element \(K_{33}\) and the dynamic stiffness matrix of the track–soil system is established

$$\begin{aligned} {\mathbf{K}_{TS}}^{\prime }(\xi _y ,\omega )={\mathbf{K}_T}^{\prime }(\xi _y ,\omega )+{\mathbf{K}_S}^{\prime }(\xi _y ,\omega ) \end{aligned}$$
(16)

The displacements in the frequency–wavenumber domain are calculated by the inversion of this matrix

$$\begin{aligned} \mathbf{u}_T (\xi _y ,\omega )={\mathbf{K}_{TS}}^{{\prime }^{-1}}(\xi _y ,\omega )\mathbf{F}^{\prime }(\omega )={\mathbf{K}_{TS}}^{{\prime }^{-1}}(\xi _y ,\omega )F_T (\omega )\mathbf{e}_\mathbf{1 } \end{aligned}$$
(17)

The displacements in space domain (along the track) can be calculated by the inverse Fourier transformation as

$$\begin{aligned} \mathbf{u}_T (y,\omega )=\frac{F_T (\omega )}{2\pi }\mathop {\int }\limits _{-\infty }^{+\infty } {{\mathbf{K}_{TS}}^{{\prime }^{-1}}(\xi _y ,\omega )\mathbf{e}_1 \exp (i\xi _y y)} {\hbox {d}}\xi _y \end{aligned}$$
(18)

The force distribution on the track–soil interface can then be calculated by a similar Fourier integral

$$\begin{aligned} {F_S}^{\prime }(y,\omega )= & {} \frac{1}{2\pi }\mathop {\int }\limits _{-\infty }^{+\infty } {{K_S}^{\prime }(\xi _y ,\omega )u_S (\xi _y ,\omega )\exp (i\xi _y y)} {\hbox {d}}\xi _y \nonumber \\= & {} \frac{F_T (\omega )}{2\pi }\mathop {\int }\limits _{-\infty }^{+\infty } {{K_S}^{\prime }(\xi _y ,\omega )\mathbf{e}_3 {\mathbf{K}_{TS}}^ {{\prime }^{-1}}(\xi _y ,\omega )\mathbf{e}_1 \exp (i\xi _y y)} {\hbox {d}}\xi _y \end{aligned}$$
(19)

using the displacements of the track–soil interface \(u_{S}(\xi _{y}, \omega )=u_{3}(\xi _{y}, \omega )\) and the soil stiffness (10). Finally, the total force that acts on the track–soil interface is calculated as the integral over the infinite track length

$$\begin{aligned} F_S (\omega )= & {} \mathop {\int }\limits _{-\infty }^{+\infty } {{F_S}^{\prime }(y,\omega )} {\hbox {d}}y={F_S}^{\prime }(\xi _y =0,\omega ) \nonumber \\= & {} F_T (\omega ){K_S}^{\prime }(\xi _y =0,\omega )\mathbf{e}_3 {\mathbf{K}_{TS}}^{{\prime }^{-1}}(\xi _y =0,\omega )\mathbf{e}_1 \end{aligned}$$
(20)

This soil force can easily be obtained as the transformed integrand at \(\xi _{y}=0\) without any integration.

5 Vehicle–track interaction

The track–soil model yields the dynamic stiffness of the track at the excitation point

$$\begin{aligned} K_T (\omega )=\frac{F_T (\omega )}{u_1 (y=0,\omega )} \end{aligned}$$
(21)

from Eq. (18) and the track–soil force transfer function

$$\begin{aligned} H_{TS} (\omega )=\frac{F_S (\omega )}{F_T (\omega )} \end{aligned}$$
(22)

from Eq. (20).

The track model is combined with a vehicle model. A single rigid wheel mass \(m_{W}\) is used throughout this paper. The dynamic stiffness \(K_{V}( \omega )=-m_{W} \omega ^{2}\) of the vehicle is introduced into the vehicle–track interaction analysis. A force \(F_{V}\) acting on the vehicle yields a force \(F_{T}\) acting on the track according to

$$\begin{aligned} H_{VT} (\omega )=\frac{F_T }{F_V }(\omega )=\frac{K_T (\omega )}{K_T (\omega )+K_V (\omega )} \end{aligned}$$
(23)

and a force \(F_{S}\) on the soil [2, 4]

$$\begin{aligned} H_{VS} (\omega )=\frac{F_S }{F_V }(\omega )=\frac{F_T }{F_V }(\omega )\frac{F_S }{F_T }(\omega )=\frac{K_T (\omega )}{K_T (\omega )+K_V (\omega )}\frac{F_S }{F_T }(\omega )=H_{VT} (\omega )H_{TS} (\omega ). \end{aligned}$$
(24)

6 Numerical integration

The wavenumber integrals (18, 19) are evaluated numerically. The soil has a hysteretic material damping so that the integrands have no infinite poles. The numerical integration is done by the rectangle rule with a constant step which is chosen so that the slowest shear wave (Rayleigh wave) and the fastest compression wave of the soil layers are well represented. The infinite integral is truncated at a sufficiently large wavenumber. Typical values for the integration are

  • \(n(k_{x})=300\), \(n(k_{y})=1000\) integration steps, and up to \(n(k_{y})=3000\) for the solution along the track,

  • integration up to the tenfold of the shear wave number, (or for the static case, up to 10/\(h_{1}\) or 10/m),

  • another criterion reflects the oscillations of the complex exponential function; at least five integration steps must be calculated for each oscillation.

The integrals (9) of the strip wave compliances of the soil are calculated once and stored for the repeated use, thus reducing the computer time. If the stored soil compliances are used, the method is almost as fast as the Winkler soil calculation.

7 Standard track parameter and their variation

The unisolated and isolated ballast tracks (Fig. 1) have the following parameters (standard parameters are underlined):

Mass of the wheelset

\(m_{W}\) = 1500 kg

Bending stiffness of the UIC60 rails

\({EI}_{R} = 2 \times 2.1\, 10^{11} \times 3.0 \,10^{-5}\text {Nm}^{2} = 12.6 \,10^{6} \text {Nm}^{2}\)

Mass per length of the rails

\({m}_{R}^\prime = 2 \times 60\) kg/m

Stiffness of the rail pads

\(k_{R} = 300\, 10^{6}\) N/m

Hysteretic damping of the rail pads

\(D_{R} = 10\)%

Mass of the sleeper

\(m_{S} = 340\) kg

Length of the sleepers

\(b = 2.6\) m

Distance of the sleepers

\(d = 0.6\) m

Stiffness of the sleeper pads

\(k_{S} = 25\), 50, 100, 200 \(10^{6}\) N/m

Height of the ballast

\(h_{B} = 0.3\) m

Stiffness of the ballast

\(k_{B} = 300\), 650, 1300, 2600 \(10^{6}\) N/m

Longitudinal wave velocity of the ballast

\(v_{B} = 200\), 300, 400, 600 m/s

Young’s modulus of concrete

\(E_{P} = 3 10^{10}\) N/\(\text {m}^{2}\)

Mass density of concrete

\(\rho _{P} = 2.5 10^{3}\) kg/\(\text {m}^{3}\)

Thickness of the ballast plate

\(t = \underline{0}\), 0.5, 0.7, 1.0, 1.5 m

Shear modulus of the soil (layer)

\(G = 2\), 4.5, 8, 18 \(10^{7}\) N/\(\text {m}^{2}\)

Shear wave velocity of the soil (layer)

\(v_{S} = 100\), 150, 200, and 300 m/s

Mass density of the soil

\(\rho = 2 10^{3}\) kg/\(\text {m}^{3}\)

Poisson’s ratio of the soil

\(\nu = 0.33\)

Hysteretic damping of the soil

\(D = 2.5\)%

Height of the soil layer

\(h_{L} = 1\) m

Velocity contrast half-space to layer

\(v_{S\textit{2}}\)/\(v_{S\textit{1}} = \underline{1}\), 1.25, 1.5, 2, 4

8 Compliance and force transfer functions of ballast tracks

This section presents the frequency-dependent compliances of the track–soil systems under the dynamic axle load (inverse of 21) and the frequency-dependent force transfer functions of the complete vehicle–track–soil system (24).

8.1 Stiffness of the ballast

Figure 2a shows the frequency-dependent compliances of the track for different stiffnesses of the ballast. A clear influence of the softest ballast can be found. The stiffer ballast materials have only an influence on the high-frequency compliance. The compliances of the ballast tracks without any isolation measure are almost constant, only weakly decreasing with frequency. The force transfer functions of the complete vehicle–track system presented in Fig. 2b start at zero frequency with the value 1 and show a weak maximum at higher frequencies with a value of \(F_{S}/F_{V}=2\)–3. The vehicle–track resonant frequency clearly depends on the stiffness of the ballast. It is at 60 Hz for the softest and at 110 Hz for the stiffest ballast.

The stiffness of the ballast can be understood as the stiffness of a ballast layer or as the stiffness of a ballast block under the rail seats. A soft ballast can be a ballast layer of a soft ballast material or a ballast block of a stiffer material. By that, the local stiffness of ballast tracks due to tamping could be considered in the ballast model.

Fig. 2
figure 2

Amplitude (top) and phase (bottom) of the compliance (left) and the vehicle–track–soil force transfer (right) functions of tracks with different ballast materials, \(v_{B}= square~200\), circle 300, triangle 400, plus 600 m/s

Full size image

8.2 Stiffness and layering of the soil

The compliances and force transfer functions for homogeneous soils are given in Fig. 3. The soil has a strong influence on the static and low-frequency track compliances which is in the range of \(u_{R}/F_{T}=2 \,\text {to}\, 9\times 10^{-9}\) m/N. At higher frequencies, the compliances of the different soils are close together and that means that the soft soils have a strong decrease in the compliances while the stiff soils have almost constant compliances. At low frequencies, the phase of the compliance has an almost linear decrease where the softest soil has the strongest decrease. This is caused by the radiation damping of the soil which is linearly increasing with frequency. At mid-frequencies, the damping of the soil is higher than the stiffness, and the soil becomes dynamically stiff. Other track components such as the ballast or the rail pads get a stronger influence on the dynamic compliance of the track. The force transfer functions (Fig. 3b) show little variation and almost no resonance maximum. Only the stiffest soil shows a weak maximum at 110 Hz. The softer soils have a stronger damping due to the radiation of the soil, and the force transfer functions are close to the value \(F_{S}/F_{V}=1\). In general, the soil has a strong influence on the low-frequency behaviour, whereas the ballast is more important at higher frequencies.

Fig. 3
figure 3

Amplitude (top) and phase (bottom) of the compliance (left) and the vehicle–track–soil force transfer (right) functions of tracks on different homogeneous soils, \(v_{S}=square~100\), circle 150, triangle 200, plus 300 m/s

Full size image

The characteristics of both, the compliances and the force transfer functions, are stronger if a layered soil is considered. At first, a layer of the wave velocity \(v_{S\textit{1}}=100\), 150, 200, and 300 m/s is analysed which lies on a stiffer half-space of \(v_{S\textit{2}}=2~v_{S\textit{1}}\). A layered soil has less radiation damping than the homogeneous half-space. Therefore, resonances of the track compliances become visible for the layered soil. This track–soil resonance can be very low at 25 Hz for the softest layer. The resonant frequency increases with the layer stiffness up to 80 Hz. The theoretical layer resonances are higher between \(f_{L}=v_{S\textit{1}}\)/2\(h_{L}=50\) and 150 Hz what clearly demonstrates the strong influence of the track mass. The complete vehicle–track–soil system has similar resonances between 25 and 75 Hz (Fig. 4b). The resonance amplification of the force transfer are stronger and increase with frequency up to \(F_{S}/F_{V}=3\), whereas the maximum amplitudes of the compliances in Fig. 4a decrease with increasing frequency and stiffness. The force transfer functions display a second minor resonance above 100 Hz which can be attributed to the vehicle–track interaction.

Fig. 4
figure 4

Amplitude (top) and phase (bottom) of the compliance (left) and the vehicle–track–soil force transfer (right) functions of tracks on different layered soils, \(h_{L} = 1\) m, \(v_{S2}=2v_{S1}\), \(v_{S1}= square~100\), circle 150, triangle 200, plus 300 m/s

Full size image

In Fig. 5, the influence of the stiffness or velocity contrast between the layer and the underlying half-space is demonstrated. The wave velocity of the layer is kept constant at \(v_{S\textit{1}}=100\) m/s and the half-space is varied as \(v_{S\textit{2}}=4\), 2, 1.5, 1.2, 1.0 \(v_{S\textit{1}}\). That means that the changes from a strong contrast to a weak contrast and to a homogeneous soil can be studied. The track–soil resonance at 65 Hz is shifted to less than 40 Hz, and at the same time, the resonance amplitude reduces from \(u_{R}/F_{T}=5 \,\text {to} \,3 \times 10^{-9}\) m/N and even vanishes for the velocity contrast of \(v_{S\textit{2}}/v_{S\textit{1}}=1.2\) and 1.0. The phase curves vary strongly for the high stiffness contrast, whereas it smoothly changes from \(0^\circ \) to \(45^\circ \) for the homogeneous soil. Similar track–soil resonances between 40 and 60 Hz are found for the force transfer functions (Fig. 5b). Small vehicle track resonances exist above 100 Hz, but are only visible for the strong layering with reduced radiation damping.

Fig. 5
figure 5

Amplitude (top) and phase (bottom) of the compliance (left) and the vehicle–track–soil force transfer (right) functions of tracks on different layered soils, \(h_{L} = 1\) m, \(v_{S1}=200\) m/s, velocity contrast \(v_{S2}/v_{S1}= square~4\), circle 2, triangle 1.5, plus  1.25, times 1.0 (homogeneous soil)

Full size image

All these results can be understood in the way that the ballast track has a resonance in the lower frequency range which is hidden by the strong radiation damping of the homogeneous soil and which is visible for the reduced damping of a layered situation.

8.3 Under-ballast plates of different heights

If a concrete plate lies between the ballast and the soil, the mass and the bending stiffness of the track are increased. The effects on the compliance and force transfer functions are shown in Fig. 6. The additional bending stiffness of the under-ballast plate distributes the load on a longer track section and yields a reduced track compliance of \(2 \times 10^{-9}\) m/N for the thickest plate. At 100 Hz, the differences in stiffness have been equalized and the vehicle–track resonant frequency is uniform at 115 Hz (Fig. 6b). The effect of the additional track mass is stronger. It yields a low-frequency track–soil resonance at 15–25 Hz depending on the height of the plate. After the small resonance amplification, a reduction in the force amplitudes can be observed which reaches a value of \(F_{S}/F_{V}=0.5\) for the thickest plate. The under-ballast plate reduces the damping of the ballast track considerably, and the amplifications at the vehicle–track resonances are higher. The behaviour of a track with under-ballast plate shows some similarities with a track on a layered soil, namely the two resonances at low and high frequencies.

Fig. 6
figure 6

Amplitude (top) and phase (bottom) of the compliance (left) and the vehicle–track–soil force transfer (right) functions of ballast tracks on concrete plates of different thicknesses \(t= square~1.5\), circle 1.0, triangle 0.7, plus 0.5 m, times no plate, homogeneous soil with \(v_{S}=200\) m/s

Full size image

8.4 Mitigation effects of elastic track elements

As mitigation measures for railway induced ground vibrations, the following elastic track elements are used, elastic rail pads between rail and sleeper, elastic sleeper pads between sleeper and ballast, elastic ballast mats under the ballast, and springs under an additional under-ballast plate. Figure 7 shows the results of four different sleeper pads as an example. In case of elastic track elements, clear resonances of the track system exist (Fig. 7a). The resonant frequencies with sleeper pads are in the wide range of 40–105 Hz, the lowest for the softest sleeper pads. The maximum amplitudes at this track resonance are clearly increasing for the softer sleeper pads. The force transfer functions in Fig. 7b show also clear resonances at somewhat lower frequencies between 30 and 60 Hz where the corresponding resonance amplitudes are between \(F_{S}\)/\(F_{V}=4.5\) and 3. For frequencies above the resonant frequency, the force amplitudes are clearly decreasing. They are between \(F_{S}\)/\(F_{V} = 0.08\) and 1.0 at 100 Hz and between \(F_{S}\)/\(F_{V} = 0.04\) and 0.3 at 150 Hz. It is worth to mention that the soft sleeper pads reduce the influence of the soil and its radiation damping and therefore cause the higher resonance amplitudes, but on the other end, yield also a stronger reduction at high frequencies.

Fig. 7
figure 7

Amplitude (top) and phase (bottom) of the compliance (left) and the vehicle–track–soil force transfer (right) functions of tracks with sleeper pads of stiffness \(k_{S}=square~ 25\), circle 50, triangle 100, plus 200 kN/mm, times no sleeper pads

Full size image

Similar calculations have been performed for rail pads and ballast mats. The results have been evaluated in Table 1 for stiffness values which are comparable for all three types of elastic elements. For a similar stiffness per sleeper, many results are close together for rail pads, sleeper pads and ballast mats. The static compliance, the maximum compliance and the resonance amplification of the track and the vehicle–track system are very similar. Even the final vehicle–track resonant frequency does not vary considerably between 40–90 Hz (rail pads), 30–60 Hz (sleeper pads) and 20–50 Hz (ballast mats). The strongest differences can be found for the track resonant frequencies (without wheelset mass). They are almost outside the frequency range of 150 Hz for the rail pads, and on the other hand they are much lower at 25–60 Hz for the ballast mats. This is due to the high mass on the ballast mats (the whole track) and the low rail mass on the rail pads. The unsprung vehicle mass yields considerably lower vehicle–track resonant frequencies in case of the elastic rail pads, whereas the effect of the vehicle is small for the under-ballast mats.

According to the differences in the vehicle–track resonant frequencies, the force reduction is stronger for the mitigation systems with higher isolated track mass. The maximum reduction is obtained by the ballast mats which is \(F_{S}\)/\(F_{V} = 0.05\) to 0.5 at 100 Hz and \(F_{S}\)/\(F_{V} = 0.02\) to 0.18 at 150 Hz. Sleeper pads yield also acceptable reductions down to \(F_{S}\)/\(F_{V} = 0.08\) and 0.04 at 100 and 150 Hz, respectively. Rail pads are consequentially less effective; only soft rail pads can yield a reduction below 100 Hz. The prediction of the mitigation effect follows these simple rules as far as only a single resonant frequency is included. If the vehicle–track resonant frequency for an elastic element coincides with the track–soil resonance of a layered soil, amplifications of the force can occur at frequencies where a reduction would be expected for a simple mitigation system, see also [10] for the problematic combination of rail and sleeper pads.

The static compliances are rather high, at about \(u_{R}/F_{T}=10 \times 10^{-9}\) m/N for the softest material of each elastic element. Softer elements with higher static compliances are not used as mitigation measures because of safety reasons.

9 Static and dynamic deformations of the track and force distribution

The deformation u(y) of the track is presented as amplitude and phase for four different track situations and for five frequencies. At first, a standard ballast track on a stiff soil (\(v_{S} = 300\) m/s) yields quite regular results (Fig. 8 left). The force on the soil is distributed along a length of \(y=\pm 1\) m, and the force outside this region is almost zero. The displacements of the rail are also concentrated around the exciting force (\(y=0\)), but they attenuate much weaker than the forces. No zero is observed, and the amplitudes at \(y=\pm 8\) m are still 10% of the maximum at the excitation point. The amplitudes are very similar for all frequencies of \(f = 0\), 25, 50, 75 and 100 Hz. The phase functions \(\varphi \) (y) are nearly linear and regularly decreasing. The slope of the phase function represents a wave velocity \(v = \omega \)/\({\vert }\) d \(\varphi \)/d\(y{\vert }\) which in this standard situation equals the Rayleigh wave of the soil \(v_{R} = 270\) m/s.

Table 1 Characteristics of isolated tracks, stiffness of elastic track elements, static compliance, track resonant and vehicle–track resonant frequency, maximum compliance and amplification, total force transfer at resonance, at 100 and 150 Hz
Full size table
Fig. 8
figure 8

Amplitudes of the soil force densities (top) and rail displacements (middle), phase of the soil displacements (bottom) along the track on a homogeneous soil of \(v_{S}=300\) m/s (left) and \(v_{S}=150\) m/s (right), for different frequencies \(f=square~0\), circle 25, triangle 50, plus  75, times 100 Hz

Full size image

The soft soil of \(v_{S}=150\) m/s (Fig. 8 right) yields results similar to those of the stiff soil for frequencies up to 50 Hz. According to the lower stiffness and wave velocity, the amplitudes are higher and the phase delay is stronger. A soft soil also yields a wider distribution of forces and displacements. The forces are distributed up to \(y=\pm 1.5~\) m, and the displacements have considerable amplitudes at \(y=\pm 8\) m. This low-frequency behaviour changes remarkably at higher frequencies. The displacements are much lower and, in addition, are restricted to the track length \(y=\pm 1.5~\) m around the excitation. The phase functions do not continue their regular decrease. They are irregular due to the low amplitudes and indicate higher wave velocities. The characteristic change could be attributed to the coincidence of the dispersive bending wave of the track and the constant Rayleigh wave of the soil [20], but according to [15], a static stiffness ratio or elastic length should be essential for this characteristic frequency where the wave velocity deviates from the Rayleigh wave and a strong attenuation occurs.

The layered soil in Fig. 9 left has a small resonance at about 50 Hz (triangle), visible in the force and the deformation amplitude. The slope of the phase functions is considerably higher for 75 and 100 Hz indicating a change of the wave velocity from the Rayleigh wave velocity \(v_{R}=360\) m/s of the half-space to \(v_{R}=180\) m/s for the softer layer. In addition, higher displacement and force amplitudes can be found for 75 Hz which attenuate very weakly with distance. On the contrary, the displacements for 0, 25, and 100 Hz attenuate very rapidly and are almost zero at distances further than \(y=\pm 2\) m. In that case, the displacement amplitudes are similar to the force distribution.

Fig. 9
figure 9

Amplitudes of the soil force densities (top) and rail displacements (middle), phase of the soil displacements (bottom) along the track on a layered soil of \(v_{S1,2}=200\),400 m/s, \(h_{L}=1\) m (left) and along the track on sleeper pads of \(k_{S}=50~\)kN/mm (right), for different frequencies \(f=square\, 0\), circle25, triangle50, + 75, times100 Hz

Full size image

The last example is a track with under-sleeper pads (Fig. 9 right). The distribution of the forces and the displacements look very similar. They are somewhat wider than the force distribution of the other cases. The maximum force and displacement amplitudes, which can be found at the resonant frequency of 50 Hz, are much higher than for the other tracks, \(u_{R}/F_{T}=18\) compared to 4.5 \(10^{-9}\) m/N. The force and displacements at lower frequencies attenuate rapidly and are almost zero at \(y=\pm 2\) m. The forces and displacements at higher frequencies attenuate weakly and still have considerable amplitudes at \(\hbox {y} = \pm 8\) m.

To conclude, the distributions of the soil forces and especially of the track displacements change considerably with the frequency and are different for different track systems. In particular, at resonant frequencies due to soil layering or elastic track elements, the attenuation with distance can be modified remarkably.

Fig. 10
figure 10

Sleeper displacement (top) and velocity (bottom) time histories for the passage of an eight-unit ICE3 train, track on stiff soil (\(v_{S} = 300\) m/s) (a), track on soft soil (\(v_{S} = 150\) m/s) (b), track on soft Winkler soil (c) and measurements on a soft soil (d)

Full size image

10 Track response to train passages, calculation and measurement

The track deformation for a single axle load can be used to establish the time history of a complete train passage. Typical patterns of track displacement and track particle velocities can be found. Figure 10 shows the result for an eight-carriage ICE3 train with the axle loads defined by \(F_{i} = 160\) kN, axle distance \(l_{A} = 2.5\) m, bogie distance \(l_{B}=17.375\) m and carriage length \(l_{C} = 24.775\) m.

The ballast track on a stiff soil (\(v_{S} = 300\) m/s, Fig. 10a) has small displacements of 0.2 mm and particle velocities of 10 mm/s. The soft soil (\(v_{S} = 150\) m/s, Fig. 10b) yields much deeper displacements of 0.7 mm and particle velocities of 28 mm/s. The patterns of the displacement and velocity time histories are somewhat different for both soil conditions. The soft soil yields stronger displacements between the two axle loads of a bogie (0.5 mm, 70% of the maximum) and between the two bogies of two neighboured carriages (0.27 mm, 38% of the maximum). The velocity histories consist of a minimum and maximum for each axle load, which are almost the same for all axles in case of the stiff soil and are clearly different in case of the soft soil where the second maximum of a bogie is stronger than the first maximum. The displacement and velocity time histories come almost back to zero between the two bogies of a carriage.

Figure 10c shows the results of a soft Winkler soil which has almost the same maximum displacements of 0.67 mm as the soft continuous soil. It can be clearly seen that the displacements between two axles (0.3 mm, 45% of the maximum) and between two bogies (0 mm) are much smaller than for the continuous soil. Moreover, for the Winkler soil, a small upward displacement can be observed between the two bogies of a carriage.

Finally, experimental results from [30] are presented in Fig. 10d which compare well with the continuous soft soil, but are quite different from the Winkler soil results. The experimental results represent well the deep displacements between the axles and the smooth behaviour between the bogies, as well as the different maxima for the axles in the velocity time history. These are the characteristics found for the continuous soil (Fig. 10b) and not present in the Winkler results (Fig. 10c). Moreover, the results for the stiff continuous soil (Fig. 10a) agree well with the measurements in [31] so that it can be concluded that the track displacements under train loads are strongly influenced by the underlying continuous soil which is well represented by the proposed method.

11 Conclusion

The calculation in wavenumber domain provides a fast dynamic calculation of railway tracks on a continuous soil. The frequency-dependent transfer functions of the track compliance and the vehicle–track force transfer have been shown for some ballasted tracks. The effect of the ballast on the high-frequency behaviour and the soil material on the low-frequency behaviour has been discussed. Layered soils display track–soil resonances because of their reduced radiation damping, whereas the same resonances are hidden by the damping in homogeneous soils. Track–soil resonances become also visible in case of a higher track mass, for example due to an under-ballast plate. Elastic track elements show clear vehicle–track resonances and considerably reduced amplitudes at higher frequencies. For a typical elastic sleeper pad (\(k_{S} = 50~\) kN/mm), the vehicle–track resonant frequency is at about 35 Hz and the reduction at 100 Hz is at about 0.1. The resonances due to the elastic elements as well as the soil layering cause strong changes from the quasi-static to the dynamic track deformation which may include a weaker or stronger attenuation along the track and changes in the soil–track wave velocity. A specific advantage of the wavenumber method is the possible modelling of infinite tracks so that the track deformation (or displacement time history) under a complete train could be calculated for different continuous and Winkler soils. The measurements of an ICE3 train clearly demonstrate big differences for the Winkler soil model and a good agreement for the continuous soil method which has been proposed here.