Abstract
We show that Dedekind, in his proof of the principle of definition by mathematical recursion, used implicitly both the concept of an inductive cone from an inductive system of sets and that of the inductive limit of an inductive system of sets. Moreover, we show that in Dedekind’s work on the foundations of mathematics one can also find specific occurrences of various profound mathematical ideas in the fields of universal algebra, category theory, the theory of primitive recursive mappings, and set theory, which undoubtedly point towards the mathematics of twentieth and twenty-first centuries.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Es steht alles schon bei Dedekind. [Everything is already in Dedekind.]
Emmy Noether (van der Waerden 1975, p. 31)
Permítaseme opinar aquí que la verdadera originalidad en todo saber es siempre paradójicamente la “luz nueva” que engendra la asimilación cada vez más profunda de los fundamentos, y no un amontonamiento (que empieza a sobrarnos) de datos a la luz de lo ya conocido. [Let me here give my opinion that the real originality in all knowledge is always paradoxically the “new light” engendered by the increasingly profound assimilation of the foundations, and not an accumulation (which begins to be more than enough) of data in the light of what is already known.]
Juan B. Sancho Guimerá (Sancho Guimerá 1959, pp. 18–19)
Mathematical ideas do not live fully till they are presented clearly, and we never quite achieve that ultimate clarity. Just as each generation of historians must analyse the past again, so in the exact sciences we must in each period take up the renewed struggle to present as clearly as we can the underlying ideas of mathematics.
S. MacLane (MacLane 1970, p. 570)
1 Introduction
The present article aims to show that Dedekind (1888, §9) in his proof of the principle of definition by mathematical recursion, used in an implicit way both the notion of an inductive cone from an inductive system of sets and that of the inductive limit of an inductive system of sets. As a consequence of this, the dictum of Noether: “Everything is already in Dedekind” (van der Waerden 1975, p. 31), when praising him in connection with her own innovations, would be partially confirmed once more.
In addition to the result just specified—which identifies the essential mathematical constructs underlying the aforementioned proof—this article will also show that in Dedekind (1888) there are also anticipations of some modern and profound mathematical ideas in the fields of universal algebra, category theory, the theory of primitive recursive mappings, and set theory.
Having described in broad terms the objectives to be attained in this article (see below for further details), perhaps it is pertinent at this point to notice what Gray (2000) remarks about the work done by Dedekind in his professional career and to make a few comments connected with it.
Specifically, Gray (2000, pp. 107–108) wrote the following:
Dedekind contributed much more to mathematics than his constructive definition of the real numbers (“Dedekind’s cuts”, discovered in 1858 but only published in Stetigkeit und irrationale Zahlen [1872]). The modern esteem in which this work is held is entirely justified, but Dedekind’s other achievements are generally known only to specialists, not just because of their difficulty but, I fear, from an exaggerated attention paid by historians and popularizers to the foundations of mathematics. Dedekind did much more for mathematics than just arithmetizing elementary analysis. He was a profound unifier of mathematics and one of the creators of modern algebraic number theory; the concepts of ring, module, ideal, field, and vector space are as much his contributions as anyone else’s.
Certainly, Dedekind did much more for mathematics than just arithmetizing elementary analysis by providing a set-theoretic definition of the complete ordered field of the real numbers (in terms of the notion of “cut”, which is, ultimately, an order-theoretical concept) which surely were, moreover, considered by Dedekind as free creations of the human mind. Nevertheless, focusing on the program of arithmetization of analysis, it should be mentioned that Dedekind, as well as other illustrious proponents of the this program, by struggling against the domination of geometrical intuition, placed the focus mainly on rigour, with regard to both the definition of the basic mathematical concepts and the soundness of the mathematical proofs, but without explicitly proposing any logical system. (Of course, this was not understood as a harmonious relationship between two components: a proof-theoretical one, having to do with the syntactical consequence relation, and a model-theoretical one, having to do with the semantical consequence relation).
Actually, Dedekind was, together with Leopold Kronecker (and Ernst Kummer), one of the builders of algebraic number theory; Dedekind used “ideals”, which have a set-theoretic nature—and generalize the ideal numbers of Kummer—while Kronecker used “divisors”, which have a computational character. Along with his other mathematical contributions (to name just a few, to Galois theory, characters of finite Abelian groups, group determinant—essential in Georg Frobenius’s construction of the theory of characters of nonabelian groups—lattice theory, and, in collaboration with Heinrich Weber, to the theory of algebraic functions of a single variable), he also provided a foundation for the natural numbers. This foundation was based, as we would say in contemporary terminology, on the concept of Dedekind–Peano algebra, or, equivalently, after the work of Lawvere (1964), on the principle of definition by mathematical recursion.Footnote 1 To this we add that, as also noted, e.g., by Gray (2000, p. 108), Dedekind put a great deal of effort into editing Dirichlet’s lectures on the theory of numbers (adding eleven substantial supplements), that he collaborated with Weber in the edition of the works of Bernhard Riemann, and that he also edited some of Gauss’s manuscripts on number theory for the edition of Gauss’s Werke.
Besides that, rephrasing what MacLane (1970, p. 570) wrote, inasmuch as a mathematical idea is really profound, e.g., that of an inductive cone from an inductive system of sets and that of the inductive limit of an inductive system of sets, it takes longer to reach maturity and it does not live fully until it is presented clearly, and we never quite achieve that ultimate clarity. Therefore, in mathematics in each epoch we must take up the renewed struggle to present as clearly as we can the brilliant ideas of the great mathematicians.
Moreover, Dedekind certainly was a profound unifier of mathematics since, paraphrasing in this case what Sancho (1959, p. 18–19) wrote, the real originality of Dedekind in the world of mathematics was always the “new light” engendered by his increasingly profound assimilation of the foundations of mathematics; under the influence of Dirichlet, his underlying philosophy of mathematics and his mathematical trademark were the principles of “overcoming problems with a minimum of blind calculation and a maximum of perceptive thought”, which were exactly the words spoken by Minkowski (1905, p. 162–163) in a memorial lecture devoted to Dirichlet when talking about “the other Dirichlet Principle”.
So that, although we fully agree with Gray (2000, pp. 107–108) concerning the imbalance in favour of the research works devoted to Dedekind’s works on the foundations of mathematics to the detriment of those devoted to Dedekind’s other achievements, however we think that by paying some attention to Dedekind’s writing on the foundations of arithmetic one can still, eventually, highlight some mathematical things that have hitherto gone unnoticed.
Before proceeding to describe the contents of the ensuing sections of this article, we recall that for Dedekind, as stated in the Preface to the First Edition of Dedekind (1888), anyone possessing what is usually called good common sense has the mental faculty to carry out “the long series of simple inferences corresponding to our step-by-step understanding (Treppenverstandes)”. Moreover, Dedekind (1888) also considers, in addition to the mental faculty just mentioned, the following mental faculties as basic. (1) That “It very frequently happens that different things, a, b, c, ...for some reason can be considered from a common point of view, can be associated in the mind, and we say that they form a system S ...”, i.e., the power of the mind to create from given things a new thing, their system, that is necessarily different from each of these things. And (2) “...the ability of the mind to relate things to things, to let a thing correspond to a thing, or to represent a thing by a thing, an ability without which no thinking is possible. Upon this unique and therefore absolutely indispensable foundation, ...must, in my judgment, the whole science of numbers be established”. Thus, for Dedekind, the notion of mapping between sets (\(\equiv \) systems) is the foundation upon which number theory is built.
This last basic mental faculty, we suggest, may be pointing—in a movement from the local to the global—to the fact that mappings (between sets) will, ultimately, become morphisms (between mathematical objects), which are the essential constituents of the different mathematical universes (\(\equiv \) categories) associated with the diverse mathematical objects, and on which, until they be replaced by something else more fundamental yet to be conceived, the whole science of mathematics must be established.
We now proceed to explain the contents of the subsequent sections of this article.
In Sect. 2, we recall some historical facts regarding both the concept of projective system and that of projective limit of a projective system, which are the dual of the concepts of inductive system and of inductive limit of an inductive system, respectively, and which, in addition, chronologically precede them. In this section, we just want, in addition to recalling the aforementioned historical facts, to highlight and prove—following the footsteps of Weil when he pointed out in Weil (1975) that Cantor’s set is homeomorphic to a projective limit of finite discrete spaces, i.e., to a pro-object—that a classical theorem of Cantor has a proof by means of the concept of projective limit. And that Dedekind (1888), in the proof of one of his theorems, obtains, at a crucial step, using the principle of definition by mathematical recursion, a countably infinite family of injective mappings that belongs to the projective limit of a suitable projective system of sets. (This will be stated in Sect. 3.)
In Sect. 3, we shall show that to some extent one can find in Dedekind’s work specific occurrences of some modern mathematical ideas in the fields of universal algebra, category theory, the theory of primitive recursive mappings, and set theory which point towards the mathematics of twentieth and twenty-first centuries.
With regard to universal algebra the facts on which we rely are, essentially, the following.
(1) The introduction by Dedekind of the mono-unary algebras, i.e., of the pairs \(\mathbf {S} = (S,\varphi )\) where S is a set and \(\varphi \) a mapping from S to S, and his investigation of such a type of mathematical objects, e.g., his study of \(\mathrm {Sg}_{\mathbf {S}}\), the subalgebra generating operator on S (which Dedekind denotes by \((\cdot )_{0}\) or \(\varphi _{0}(\cdot )\)), and of the principle of proof by algebraic induction for mono-unary algebras.
(2) His axiomatic definition of the simply infinite systems—nowadays usually called Dedekind–Peano algebras—which are ordered triples \(\mathbf {S} = (S,\varphi ,e)\) where S is a set, \(\varphi \) a mapping from S to S, and e an element of S satisfying the following conditions:
-
1.
\(\forall \, x,y\in S\), if \(x\ne y\), then \(\varphi (x)\ne \varphi (y)\), i.e., the mapping \(\varphi \) is injective.
-
2.
\(\forall \, x\in S\), \(e\ne \varphi (x)\), i.e., e is not in the image of \(\varphi \).
-
3.
\(\mathrm {Sg}_{(S,\varphi )}(\{e\}) = S\), where \(\mathrm {Sg}_{(S,\varphi )}\) is the subalgebra generating operator on the reduct \((S,\varphi )\) of \((S,\varphi ,e)\).
And (3), his investigation of such a type of mathematical objects. For instance, Dedekind, after stating the fundamental principle of definition by mathematical recursion, shows, on the one hand, that all simply infinite systems are isomorphic to the simply infinite system \((N,\mathrm {sc},1)\) of strictly positive natural numbers and that, therefore, any two simply infinite systems are isomorphic; on the other hand, that every system isomorphic to the set N is equipped, in a natural way, with a structure of Dedekind–Peano algebra.
On the basis of the two preceding theorems, he remarks that all simply infinite systems form a class by putting into it all and only those algebras \(\mathbf {S} = (S,\varphi ,e)\) that are isomorphic to a determinate simply infinite system \((N,\mathrm {sc},1)\), called the representative of the class, and that the class is not changed by taking as representative any other simply infinite system belonging to it. In this connection, notice that Dedekind (1888, art. 34), after defining when two systems are isomorphic (\(\equiv \) similar) and taking into account several preceding theorems, makes, referred to the systems, the following definition: “We can therefore separate all systems into classes by putting into a determinate class all and only those systems Q, R, S, ...that are similar to a determinate system R, called the representative of the class; according to 33 the class is not changed by taking as representative any other system belonging to it”.
These results show the extreme modernity of Dedekind’s mathematical thought, i.e., his category-theoretic thinking. Actually, for Dedekind it is not necessary to choose a specific option from among a multiplicity of possible choices. Besides, for him, one essentially knows a mathematical object exactly when one knows its relations, by means of suitable transformations, to all other mathematical objects of the same nature, and this is, in essence, the contents of the just-mentioned way of thinking. This, of course, does not mean, in particular, that Dedekind absolutely forbids one to make choices. However, for Dedekind, choices should not be made when it is not necessary.
Furthermore, as shown by his correspondence with Lipschitz (1986), he disliked basing anything in mathematics on arbitrary representations or expressions. He said, in this regard, that in the exposition of ideal theory that he published in the Bulletin des Sciences Mathématiques, that in the interest of brevity, he had marred (ich verunziere) the theory by using explicit representations of fields in the form \(\mathbb {Q}(\alpha )\), where \(\alpha \) satisfies an algebraic relation over \(\mathbb {Q}\). One can say that for Dedekind what matters about a fundamental mathematical object—as is the case, e.g., with the complete ordered field of real numbers or the Dedekind–Peano algebra of natural numbers—is not the way under which it is concretely represented, but its characterization by means of a suitable universal (or couniversal) property or, in other words, for having the property of being the solution of a definite universal (or couniversal) problem. In this regard, it would seem appropriate to recall what Manes (1976, p. 84) wrote about products (this is the familiar classical result, but one which is, obviously, extensible to the remaining limits and colimits):
Because of 1.6 [Any two products of \((A_{i})_{i\in I}\) are isomorphic, we append], we can think in terms of the product of \((A_{i})_{i\in I}\) and write it as \(\prod _{i\in I}A_{i}\). In practice, “\(\prod _{i\in I}A_{i}\)” is either any convenient choice of—or the isomorphism class of all—I-tuples
with the universal property; for most categorical purposes, these distinctions do not matter.
Besides, two of the pillars underpinning the monumental edifice Was sind und was sollen die Zahlen? constructed by Dedekind are the concepts of set and mapping (together with the identity mapping associated to every set, the composition of mappings, and their properties), which, when replaced by those of object and morphism, respectively, are the building blocks of the notion of category. We note that Dedekind, in contrast to what happens in contemporary set theory, does not reduce the concept of mapping to that of set, exactly as in category theory, which is an essentially two-sorted theory (with a sort for objects and another for morphisms), where the notion of morphism is not reduced to that of object.
Moreover, Dedekind clearly anticipated the theory of primitive recursive mappings because from the principle of definition by mathematical recursion—which was proved, for the first time in the history of mathematics, in Dedekind (1888)—the parameterized operation of primitive recursion immediately follows, which, together with the generalized composition of number-theoretic mappings, is, from a structural standpoint, at the basis of such a theory.
Furthermore, in Sect. 3 we elucidate the exact relationship between Dedekind’s chains and Zermelo’s chains and show that when Dedekind (1888) is carefully studied, it becomes evident that Dedekind, besides using the relations of inclusion and strict inclusion, and the operations of union and intersection, also employed the power set operator, the difference of two sets (hence, in an implicit way, the axiom schema of separation), the Cartesian product, functional sets, and even natural isomorphisms between functional sets. Moreover, he used, in an implicit way, the axiom schema of replacement, proved, constructively, that a certain projective limit is nonempty, and defined the underlying set of the free abelian monoid on a set.
In Sect. 4, after recalling the notions of inductive system of sets, of an inductive cone from an inductive system of sets, and of the inductive limit of an inductive system of sets, we show that Dedekind (1888) used these concepts in an implicit way.
In Sect. 5 we consider, on the one hand, the degree to which Garrett Birkhoff was aware of the structural approach to algebra as conducted by Noether (herself inspired by Dedekind), by Noether’s algebraic school in Göttingen, and by Emil Artin in Hamburg in the 1930s, and, on the other hand, if Dedekind (1888) had any direct influence on Birkhoff in his work on universal algebra.
In Appendix A we provide, in agreement with the algebraic standpoint of Dedekind, a new model, based on many-sorted universal algebra, of the theory of primitive recursive mappings which will allow us to diagrammatically prove that the three basic mathematical operations, addition, multiplication, and exponentiation, defined by Dedekind in \(\S \S \) 11–13 of Dedekind (1888), are primitive recursive.
The following notational conventions will be used throughout the article. We will denote, as in Dedekind (1888), by N the set \(\{1,2,3,\ldots \}\) of all strictly positive natural numbers, while \(\mathbb {N}\) will be reserved for the set \(\{0,1,2,\ldots \}\) of all (von Neumann) natural numbers, and, also as in Dedekind (1888), by \(Z_{n}\) the set \(\{1, \ldots , n\}\), while n will be reserved for the set \(\{0,\ldots , n-1\}\). Instead of using, as in Dedekind (1888), \(\prec \), for the binary relation of inclusion between sets, \(\varvec{\mathfrak {M}}\), for the (unary) operation of union, \(\varvec{\mathfrak {G}}\), for the (unary) operation of intersection, and \(A_{0}\) or \(\varphi _{0}(A)\), for the chain relative to \(\varphi \) of a subset A of the underlying set S of a mono-unary algebra \(\mathbf {S} = (S,\varphi )\), we will use, unless otherwise specified, \(\subseteq \), \(\bigcup \), \(\bigcap \), and \(\mathrm {Sg}_{\mathbf {S}}(A)\), respectively. Besides, for a mapping  and a subset X of A, instead of using, as in Dedekind (1888), f(X) or \(X'\), for the direct image of X under f, we will use f[X]. Moreover, \(\mathrm {Im}(f)\), the image of f, will stand for f[A], and \(f[\cdot ]\) will denote the mapping from \(\mathrm {Sub}(A)\) to \(\mathrm {Sub}(B)\), the sets of subsets of A and B, respectively, which sends \(X\subseteq A\) to \(f[X]\subseteq B\).
and a subset X of A, instead of using, as in Dedekind (1888), f(X) or \(X'\), for the direct image of X under f, we will use f[X]. Moreover, \(\mathrm {Im}(f)\), the image of f, will stand for f[A], and \(f[\cdot ]\) will denote the mapping from \(\mathrm {Sub}(A)\) to \(\mathrm {Sub}(B)\), the sets of subsets of A and B, respectively, which sends \(X\subseteq A\) to \(f[X]\subseteq B\).
More specific notational conventions will be included and explained in the following sections.
2 Some historical facts and set-theoretic examples regarding the concepts of projective system and of projective limit
It will be convenient to recall next—before stating the definition of the concepts of inductive system of sets, of an inductive cone from an inductive system of sets, and of the inductive limit of an inductive system of sets in Sect. 4—some historical facts and set-theoretic examples concerning both the notion of projective system of sets and that of projective limit of a projective system of sets. This is for the following reasons. (1) These notions chronologically precede both the concept of inductive system of sets and that of inductive limit of an inductive system of sets. And (2) these notions are the dual of the concepts of inductive system of sets and of the inductive limit of an inductive system of sets, respectively. In this regard, our historical source is Weil (1975).
In what follows we have not attempted to give an exhaustive treatment of this subject; we have just sought to highlight, at this stage, in addition to the aforementioned historical facts, that (1) a theorem of Cantor (see below) has a proof by means of the concept of projective limit and that (2) this last concept was also used, implicitly, by Dedekind at a crucial step in the proof of one of his theorems (see below).
For additional examples regarding the concepts of projective and inductive limits, see, e.g., Dieudonné (1989) and Krömer (2010).
The concept of a projective limit—which is a generalization of the sequential limit of Hans Freudenthal and Lev Pontrjagin, see the quotation below—was introduced by Weil (1975, p. 23–28) to discuss the structure of locally compact groups and to prove that every compact group is the projective limit of a family of compact Lie groups. In fact, Weil (1975, pp. 28–29) makes the following remarks on the development of the concept of projective limit:
La notion de limite projective d’une suite de groupes finis paraît avoir été introduite pour la première fois par J. Herbrand (dans Herbrand 1933). Auparavant, P. Alexandroff avait introduit en topologie la notion de spectre projective (dans Alexandroff 1928), cas particulier de la notion topologique de limite projective, analogue à celle qui est étudiée ici. Les limites projectives de suites de groupes abéliens finis étaient aussi apparues implicitement dans un travail de L. Pontrjagin (dans Pontrjagin 1931). L. Pontrjagin paraît avoir considéré le premier des limites de suites de groupes compacts (dans Pontrjagin 1934). La notion de limite projective d’une suite de groupes (et la notion analogue pour les espaces topologiques) a été introduite dans toute généralité par Freudenthal (dans Freudenthal 1937), dont la terminologie diffère quelque peu de celle qui est proposée ici; il introduit aussi une autre espèce de limite, sur laquelle nous reviendrons dans les notes du \(\S \, 28\). Quant à la définition d’une limite projective au moyen d’un ensemble filtrant quelconque, elle m’a été communiquée il y a quelques années, dans le cas des groupes compacts, par C. Chevalley; l’extension correspondante de la notion de spectre projective est due à Kurosh (dans Kurosh 1935); pour le cas particulier des limites projectives de groupes abéliens finis, une définition équivalente a été donnée récemment par R. Baer (dans Baer 1937), qui cependant évite en apparence d’introduir une topologie dans les groupes qu’il définit, et pour cette raison est amené à introduir deux conditions superflues (les conditions \(1.\, \mathrm {G}\) et \(1.\, \mathrm {H}\), \(\mathrm {p}.\, 872\) de son mémoire, sont conséquences des autres).
Before proceeding any further, recall—because we will immediately afterwards make use of both the concept of a projective system of sets and that of the projective limit of a projective system of sets—that a projective system of sets is an ordered pair \((\mathbf {I},\mathcal {A})\) where \(\mathbf {I} = (I,\preccurlyeq )\) is a preordered set, i.e., a set I equipped with a preorder \(\preccurlyeq \) on I (i.e., a reflexive and transitive relation \(\preccurlyeq \) on I), and \(\mathcal {A} = ((A_{i})_{i\in I},(f_{i',i})_{(i,i')\in \preccurlyeq })\) such that:
-
1.
\(\forall \,i\in I\), \(A_{i}\) is a set.
-
2.
\(\forall \,(i,i')\in \preccurlyeq \),
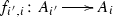 .
. -
3.
\(\forall \,i\in I\), \(f_{i,i} = \mathrm {id}_{A_{i}}\).
-
4.
\(\forall \,i,i',i''\in I\), if \((i,i')\in \preccurlyeq \) and \((i',i'')\in \preccurlyeq \), then \(f_{i'',i} = f_{i',i}\circ f_{i'',i'}\).
The mappings  are called the transition mappings of the projective system of sets \((\mathbf {I},\mathcal {A})\). Notice that \(\mathcal {A}\) is a contravariant functor from \(\mathbf {C}(\mathbf {I})\), the category canonically associated with \(\mathbf {I}\), to \(\mathbf {Set}\), the category of sets (in a fixed Grothendieck universe \(\varvec{\mathcal {U}}\)) and mappings.
are called the transition mappings of the projective system of sets \((\mathbf {I},\mathcal {A})\). Notice that \(\mathcal {A}\) is a contravariant functor from \(\mathbf {C}(\mathbf {I})\), the category canonically associated with \(\mathbf {I}\), to \(\mathbf {Set}\), the category of sets (in a fixed Grothendieck universe \(\varvec{\mathcal {U}}\)) and mappings.
On the other hand, if \((\mathbf {I},\mathcal {A})\) is a projective system of sets, then a projective limit of \((\mathbf {I},\mathcal {A})\) is an ordered pair \((\varprojlim (\mathbf {I},\mathcal {A}),(f_{i})_{i\in I})\) where \(\varprojlim (\mathbf {I},\mathcal {A})\) is a set and, for every \(i\in I\), \(f_{i}\) is a mapping from \(\varprojlim (\mathbf {I},\mathcal {A})\) to \(A_{i}\), such that, for every \((i,i')\in \preccurlyeq \), \(f_{i} = f_{i',i}\circ f_{i'}\) and, for every ordered pair \((L,(g_{i})_{i\in I})\) where L is a set and, for every \(i\in I\),  , if, for every \((i,i')\in \preccurlyeq \), \(g_{i} = f_{i',i}\circ g_{i'}\), then there exists a unique mapping
, if, for every \((i,i')\in \preccurlyeq \), \(g_{i} = f_{i',i}\circ g_{i'}\), then there exists a unique mapping  such that, for every \(i\in I\), \(g_{i} = f_{i}\circ u\).
such that, for every \(i\in I\), \(g_{i} = f_{i}\circ u\).
Remark 1
The set \(\varprojlim (\mathbf {I},\mathcal {A})\) is the subset of \(\prod _{i\in I}A_{i}\), the Cartesian product of the family of sets \((A_{i})_{i\in I}\), defined as follows:
where, for every \(i\in I\), \(\mathrm {pr}_{i}\) is the canonical projection from \(\prod _{i\in I}A_{i}\) to \(A_{i}\). And, for every \(i\in I\), \(f_{i}\) is the restriction of \(\mathrm {pr}_{i}\) to \(\varprojlim (\mathbf {I},\mathcal {A})\).
If \((\mathbf {I},\varvec{\mathcal {A}})\) is a projective system of structured sets (and transition morphisms) of some species, then, under appropriate conditions, \(\varprojlim (\mathbf {I},\mathcal {A})\) can be equipped with a structure of the same species in such a way that the canonical mappings are actually morphisms.
We next try to illuminate, as much as we can, this last technical concept. The projective limit \(\varprojlim (\mathbf {I},\mathcal {A})\)—along with the mappings \(f_{i}\) from \(\varprojlim (\mathbf {I},\mathcal {A})\) to \(A_{i}\)—of a projective system \((\mathbf {I},\mathcal {A})\) can be interpreted as the optimal way of obtaining the equalizer of an equation (represented by a parallel pair of mappings between two adequate Cartesian products) obtained from the transition mappings  of the projective system \((\mathbf {I},\mathcal {A})\).
of the projective system \((\mathbf {I},\mathcal {A})\).
Although of a topological, but not set-theoretic, nature, we notice that Weil (1975, Chapter V, pp. 92–93) announced without proof (he literally wrote, on \(\mathrm {p}.\, 93\), that: “l’on montre facilement”) that Cantor’s set (\(\equiv \) Cantor’s nowhere dense perfect set)—which was independently constructed by Smith (1875, p. 147)—is homeomorphic to a projective limit of finite discrete spaces. For a proof of it, see, e.g., Hocking and Young (1988, pp. 97–100).
Following this, we append as a further example of projective limit one related to the following theorem: “Every transfinite aggregate T has parts with the cardinal number \(\aleph _{0}\)”, which was stated and proved—without employing the notion just mentioned—by Cantor (1955, p. 105). And we do this for the following reasons.
(1) The theorem of Cantor was set out in the same historical period that another theorem of Dedekind (1888, art. 159) which reads as follows: “\({\varSigma }\) is an infinite set if, and only if, every initial segment of N has an embedding into \({\varSigma }\)”. But, while Cantor’s proof of his theorem is not trivial, Dedekind’s proof of the conditional: “If \({\varSigma }\) is infinite, then every initial segment of N has an embedding into \({\varSigma }\)” makes use, as an intermediate step, of the fact that if \({\varSigma }\) is infinite, then there exists a part T of \({\varSigma }\) which is simply infinite and consequently similar to the number-sequence N, which has, in his conceptual framework, a straightforward proof, because it is founded on his definition of infinite system, of chain generated by an element, of simply infinite system, and on the theorem that asserts that all simply infinite are similar to the number-sequence N.
(2) Both theorems were proved by using, implicitly, the countable axiom of choice, something which is well known.
(3) Dedekind, in the proof of his theorem, obtained, at a crucial step, by using the principle of definition by mathematical recursion, a countably infinite family of injective mappings that belongs to the projective limit of a suitable projective system of sets (for details, see Sect. 3 when considering \(\mathrm {art}.\, 159\) of \(\S \, 14\)). And
(4), the theorem of Cantor has, as we will state below, an alternative proof by means of the concept of projective limit.
With regard to the last of the previous points, it is worthwhile to quote a part of Michael Atiyah’s answer in Raussen and Skau (2004, p. 24) to the question, formulated by these interviewers, about the underlying motives for providing different proofs with different strategies for the Atiyah-Singer Index Theorem: “Any good theorem should have several proofs, the more the better. For two reasons: usually, different proofs have different strengths and weaknesses, and they generalize in different directions—they are not just repetitions of each other. ...the more perspectives, the better!”
However, before doing that, because it will throw some light on the aforementioned alternative proof, we show—by using the axiom of dependent choices of Paul Bernays, which is weaker than the axiom of choice, but stronger than the countable axiom of choice—that the above theorem of Cantor can be proved in a simpler way. Recall that the axiom of dependent choices says the following: If A is a nonempty set and \({\varPhi }\) a binary relation on A such that for every \(x\in A\) there exists a \(y\in A\) such that \((x,y)\in {\varPhi }\), then there exists a sequence \((x_{n})_{n\in \mathbb {N}}\) in A such that, for every \(n\in \mathbb {N}\), \((x_{n},x_{n+1})\in {\varPhi }\). Then, the proof of Cantor’s theorem runs as follows: If the set T is infinite, then for every \(k\in \mathbb {N}\), the set \(\mathcal {M}(k+1,T)\) of the injective mappings from \(k+1\) to T is nonempty, and hence, \(\bigcup _{k\in \mathbb {N}}\mathcal {M}(k+1,T)\ne \varnothing \). Then on \(\bigcup _{k\in \mathbb {N}}\mathcal {M}(k+1,T)\) we define the binary relation \({\varPhi }\) as follows: \(((x_{i})_{i\in m},(y_{j})_{j\in n})\in {\varPhi }\) if, and only if, \(n = m+1\) and, for every \(i\in m\), \(x_{i} = y_{i}\), where m and \(n\ge 1\). Thus, by the axiom of dependent choices, there exists a family \(((x_{i})_{i\in n+1})_{n\in \mathbb {N}}\), in the set \(\bigcup _{k\in \mathbb {N}}\mathcal {M}(k+1,T)\), such that, for every \(n\in \mathbb {N}\), \(((x_{i})_{i\in n+1},(x_{i})_{i\in n+2})\in {\varPhi }\). Therefore, the union of the images of the families \((x_{i})_{i\in n+1}\), comprising the family \(((x_{i})_{i\in n+1})_{n\in \mathbb {N}}\), is the countably infinite set which we wanted to obtain.
We now turn to the proof of Cantor’s theorem through the use of the projective limits. Consider, on the one hand, the family of sets \((\mathcal {M}(n+1,T))_{n\in \mathbb {N}}\) and, on the other hand, the family of transition mappings \((f_{n+1,n})_{n\in \mathbb {N}-1}\), where, for every \(n\in \mathbb {N}-1\), \(f_{n+1,n}\) is the mapping from \(\mathcal {M}(n+1,T)\) to \(\mathcal {M}(n,T)\) obtained from the canonical embedding \(\mathrm {in}_{n,n+1}\) of n into \(n+1\). Thus \(f_{n+1,n}\) assigns to every injective mapping \(\varphi \) from \(n+1\) to T the injective mapping \(\varphi \circ \mathrm {in}_{n,n+1}\), i.e., the restriction of \(\varphi \) to n. In this way, we obtain a projective system of sets, denoted by \(\mathcal {M}(T)\). It happens that, for every \(n\in \mathbb {N}-1\), \(f_{n+1,n}\) is surjective and that, for every \(n\in \mathbb {N}\), the sets \(\mathcal {M}(n+1,T)\) are nonempty. Then, by the countable axiom of choice, we choose a family \((g_{n,n+1})_{n\in \mathbb {N}-1}\) such that, for every \(n\in \mathbb {N}-1\), \(g_{n,n+1}\) is a mapping from \(\mathcal {M}(n,T)\) to \(\mathcal {M}(n+1,T)\) and \(f_{n+1,n}\circ g_{n,n+1}\) is the identity mapping at \(\mathcal {M}(n,T)\). Then we have that, for every \(n\in \mathbb {N}-1\), the structural mapping \(f_{n}\) from \(\varprojlim \mathcal {M}(T)\) to \(\mathcal {M}(n,T)\) is surjective. Moreover, since, for every \(n\in \mathbb {N}\), we have that \(\mathcal {M}(n+1,T)\) is nonempty, it follows that \(\varprojlim \mathcal {M}(T)\) is nonempty, and hence, the infinite set T has subsets with the cardinal number \(\aleph _{0}\).
With regard to the dual concept of projective limit, Weil (1975, p. 109) makes the following remark, based on the fact that the character groups of the groups of an inverse sequence form themselves a direct sequence:
On est ainsi conduit à définir, chaque fois que l’on s’est donné un ensemble ordonné filtrant d’indices \(\alpha \), des groupes \(H_{\alpha }\), et, chaque fois que \(\alpha \prec \beta \), un isomorphisme de \(H_{\alpha }\) dans \(H_{\beta }\), un groupe H, réunion de groupes isomorphes aux \(H_{\alpha }\), qu’on pourra appeler la limite inductive des \(H_{\alpha }\) par rapport aux isomorphismes donnés; il n’est pas difficile de formuler pour cette notion un système d’axiomes convenable, par analogie avec les axiomes de la limite projective. ...La notion de limite inductive, pour les suites de groupes et d’espaces topologiques, a été introduite (avec une terminologie et des axiomes quelque peu différents de ceux qui sont suggérés ici) par Freudenthal (dans Freudenthal 1937).
In connection with Weil’s previous historical notes, it seems pertinent to suggest reading what Dieudonné (1989, pp. 72–73) wrote concerning Pontrjagin’s amazing missed opportunity, in 1931, of defining the concept of projective limit.
3 Universal algebra, category theory, primitive recursive mappings, and the axiom schema of replacement in Was sind und was sollen die Zahlen?
In this section, our main aim is to point out some facts contained in Was sind und was sollen die Zahlen?—one of the masterpieces by Dedekind—which are usually passed over in silence, or are not sufficiently emphasized. However, it will occasionally be impossible to avoid repeating some well-known remarks on Dedekind (1888), mostly due to Zermelo, for discursive coherence and because they are partially connected to the above. We hope that, after having done that, it will be clear that Dedekind’s work is, in particular, a precursor of universal algebra, category theory, the theory of primitive recursive mappings, as well as of a form of the axiom schema of replacement. The task to be addressed is a difficult one taking into account the amount of effort deployed, for the past 129 years, in discussing, almost exclusively from a nonmathematical point of view, the works of Dedekind on the foundations of mathematics in general, and, above all, his masterpiece What are numbers and what are they good for? in particular.
Dedekind in \(\S \, 1\), after elucidating (but not formally defining) in \(\text {art.}\, 1\) the notion of thing, defined the identity of two things—by means of Leibniz’s (second order) Principle of the Identity of Indiscernibles—and established its fundamental properties. Next, in \(\text {art.}\, 2\), he stated the comprehension principle and the notion of a system, which for him is an object. Actually, he said: “It very frequently happens that different things a, b, c, ...for some reason can be considered from a common point of view, can be associated in the mind, and we say that they form a system S”. Then he considered the membership relation and established the principle of extensionality for systems, indicating that: “[a system] S is completely determined when, for every thing, it is determined whether it is an element of S or not”, and emphasizing that: “How this determination is brought about, and whether we know a way of deciding upon it, is a matter of indifference for all what follows; ...”, thus membership is only a determined question but not a necessarily decidable one. This makes manifest his radical divergence from Kronecker’s decidability requirements about the definition of concepts (only the definitions for which there is a proof of decidability are acceptable), which from Dedekind’s standpoint: “impose limitations on the free formation of concepts in mathematics which I do not believe to be justified”. Following this, in \(\text {art.}\, 3\) he defined the set-theoretic relation of inclusion between systems and proved its fundamental properties. Then in \(\text {art.}\, 6\), he defined the set-theoretic relation of proper inclusion between systems, in \(\text {art.}\, 8\), the set-theoretical operation of union and its basic properties, and in \(\text {art.}\, 17\), the set-theoretic operation of intersection and its basic properties.
Afterwards, in \(\S \, 2\), \(\text {art.}\, 21\), Dedekind defined the concept of a mapping (he used the term transformation), for every system S, the identity mapping at S, which we denote by \(\mathrm {id}_{S}\), and the (direct) image of a subset of the domain of a mapping, and stated the fundamental relations between the formation of direct images and the inclusion relation, as well as those between the formation of direct images and the operations of union and intersection, respectively. In \(\text {art.}\, 25\) he defined the composition of mappings, which for  and
and  we denote by \(g\circ f\), and stated its essential property: associativity.
we denote by \(g\circ f\), and stated its essential property: associativity.
Next, in \(\S \, 3\), \(\text {art.}\, 26\), Dedekind defined both the concept of an injective mapping and that of a bijective mapping; in \(\text {art.}\, 32\), he defined the binary relation of isomorphism between sets, which he stated has the properties of an equivalence relation.
In \(\S \, 4\), Dedekind discussed, using modern terminology, the mono-unary algebras, i.e., those pairs \(\mathbf {S} = (S,\varphi )\), where S is a set and \(\varphi \) a mapping from S into itself. And, in particular, for a fixed, but arbitrary, mono-unary algebra \(\mathbf {S}\), \(\text {art.}\, 37\), he defined when a part of S is a chain relative to \(\varphi \), i.e., he defined what nowadays is called a subalgebra of \(\mathbf {S}\).
At this point, and before going on with our discussion of Dedekind (1888), we would like to notice that Dedekind’s chain theory—which being as it is a fundamental mathematical idea necessarily occurs in a natural way in several different mathematical fields—was employed by Zermelo (1967, pp. 184–185) in an essential way—together with the axiom of choice—in his second proof of Cantor’s well-ordering principle. Specifically, given a set M and a choice mapping \(\varphi \) for M, i.e., a mapping \(\varphi :\mathrm {Sub}(M)-\{\varnothing \}\longrightarrow M\), where \(\mathrm {Sub}(M)\), we recall, is the set of all subsets of M, such that, for every nonempty subset X of M, \(\varphi (X)\in X\), we call, in agreement with the definition given in Zermelo (1967, p. 184), a subset \(\mathcal {K}\) of \(\mathrm {Sub}(M)\) a Zermelo-chain relative to the choice mapping \(\varphi \) for M or, simply, a \(\mathrm {Z}\)-chain, if it possesses the following properties:
-
1.
\(M\in \mathcal {K}\).
-
2.
For every \(\mathcal {L} \subseteq \mathcal {K}\), if \(\mathcal {L}\ne \varnothing \), then \(\bigcap _{L\in \mathcal {L}}L\in \mathcal {K}\).
-
3.
\(\{K-\{\varphi (K)\}\mid K\in \mathcal {K}\}\subseteq \mathcal {K}\).
We now explain the relationship between Dedekind’s chains and Zermelo’s chains. From the given choice mapping \(\varphi :\mathrm {Sub}(M)-\{\varnothing \}\longrightarrow M\) for M one obtains the endomapping \(\widehat{\varphi }\) of \(\mathrm {Sub}(M)\) defined as follows: \(\widehat{\varphi }(\varnothing ) = \varnothing \), and, for every nonempty subset X of M, \(\widehat{\varphi }(X) = X-\{\varphi (X)\}\). Thus, for the ordered pair \((\mathrm {Sub}(M),\widehat{\varphi })\), which is an example of a mono-unary algebra, one can consider the concept of chain relative to \(\widehat{\varphi }\). So that a part \(\mathcal {K}\) of \(\mathrm {Sub}(M)\) is a chain relative to \(\widehat{\varphi }\) if, and only if, \(\widehat{\varphi }[\mathcal {K}]\subseteq \mathcal {K}\). Therefore, a subset \(\mathcal {K}\) of \(\mathrm {Sub}(M)\) is a \(\mathrm {Z}\)-chain exactly if it is a chain relative to \(\widehat{\varphi }\) and \(\mathcal {K}\) is a closure system on M, i.e., \(\mathcal {K}\) satisfies the first two conditions previously enumerated. Therefore, Zermelo’s chains are a specialization of Dedekind’s chains. Moreover, if we denote by \(\mathbf {Set}_{\mathrm {ch,m}}\) the category whose objects are the ordered pairs \((M,\varphi )\), where M is a set and \(\varphi \) a choice mapping for M, and whose morphisms from \((M,\varphi )\) to \((M',\varphi ')\) are the injective mappings f from M to \(M'\) such that \(f\circ \varphi = \varphi '\circ f[\cdot ]\), i.e., for every \(X\in \mathrm {Sub}(M)-\{\varnothing \}\), \(f(\varphi (X)) = \varphi '(f[X])\), and by \(\mathbf {Alg}_{\mathrm {m-u}}\) the category of mono-unary algebras and morphisms of mono-unary algebras, then there exists a functor from \(\mathbf {Set}_{\mathrm {ch,m}}\) to \(\mathbf {Alg}_{\mathrm {m-u}}\) whose object mapping assigns to \((M,\varphi )\) precisely \((\mathrm {Sub}(M),\widehat{\varphi })\), and whose morphism mapping assigns to  in \(\mathbf {Set}_{\mathrm {ch,m}}\) the morphism
in \(\mathbf {Set}_{\mathrm {ch,m}}\) the morphism  in \(\mathbf {Alg}_{\mathrm {m-u}}\). Besides, from the functor from \(\mathbf {Set}_{\mathrm {ch,m}}\) to \(\mathbf {Alg}_{\mathrm {m-u}}\) which sends \((M,\varphi )\) to \((M,\mathrm {id}_{M})\) to the above functor there exists a pointwise monomorphic natural transformation.
in \(\mathbf {Alg}_{\mathrm {m-u}}\). Besides, from the functor from \(\mathbf {Set}_{\mathrm {ch,m}}\) to \(\mathbf {Alg}_{\mathrm {m-u}}\) which sends \((M,\varphi )\) to \((M,\mathrm {id}_{M})\) to the above functor there exists a pointwise monomorphic natural transformation.
We point out that the mono-unary algebras are very important in the field of universal algebra—because, in particular, many important features of an algebra are determined from its unary algebraic operations—just as are the derived notions of discrete flows, i.e., ordered pairs \((\mathbf {X},f)\) with \(\mathbf {X}\) a topological Hausdorff space and  a homeomorphism, in the area of topological dynamics (de Vries 1993), and of multiunary algebras, i.e., ordered pairs \(\mathbf {S} = (S,(\varphi _{i})_{i\in I})\), where S is a set and, for every \(i\in I\), \(\varphi _{i}\) is an endomapping of S, in the domain of algebraic automata theory (Büchi 1989).
a homeomorphism, in the area of topological dynamics (de Vries 1993), and of multiunary algebras, i.e., ordered pairs \(\mathbf {S} = (S,(\varphi _{i})_{i\in I})\), where S is a set and, for every \(i\in I\), \(\varphi _{i}\) is an endomapping of S, in the domain of algebraic automata theory (Büchi 1989).
Afterwards, in \(\text {art.}\, 44\), Dedekind defined, in an impredicative way (since at this stage the set of all natural numbers is not yet available for use), an operator \(\mathrm {Sg}_{\mathbf {S}}\) which sends a (nonempty) subset A of S to \(\mathrm {Sg}_{\mathbf {S}}(A)\), the subalgebra generated by A. We must point out that he spoke of the chain of the system A (relative to \(\varphi \)), not of the subalgebra generated by A, and that he denoted it by \(A_{0}\) or \(\varphi _{0}(A)\) not by \(\mathrm {Sg}_{\mathbf {S}}(A)\). And he stated (we once more use contemporary terminology) that the operator \(\mathrm {Sg}_{\mathbf {S}}\) is a closure operator on S which, in addition, is completely additive. Therefore \(\mathrm {Sg}_{\mathbf {S}}\) is, in particular, an algebraic closure operator on S. Specifically, Dedekind stated the following facts:
-
1.
In \(\text {art.}\, 48\), he remarked that the subalgebra generated by A is characterized as the smallest subalgebra of \((S,\varphi )\) that contains A.
-
2.
In \(\text {art.}\, 45\), he proved that the operator \(\mathrm {Sg}_{\mathbf {S}}\) is extensive or inflationary.
-
3.
From what Dedekind stated in \(\text {art.}\, 51\), one obtains, as an evident corollary, that the operator \(\mathrm {Sg}_{\mathbf {S}}\) is idempotent.
-
4.
In \(\text {art.}\, 54\), he proved that the operator \(\mathrm {Sg}_{\mathbf {S}}\) is isotone.
-
5.
In \(\text {art.}\, 57\), he proved that the mapping \(\varphi [\cdot ]\) from \(\mathrm {Sub}(S)\) to \(\mathrm {Sub}(S)\) commutes with the operator \(\mathrm {Sg}_{\mathbf {S}}\), i.e., that \(\varphi [\cdot ]\circ \mathrm {Sg}_{\mathbf {S}} = \mathrm {Sg}_{\mathbf {S}}\circ \varphi [\cdot ]\) or, equivalently, that for every \(A\subseteq S\), \(\varphi [\mathrm {Sg}_{\mathbf {S}}(A)] = \mathrm {Sg}_{\mathbf {S}}(\varphi [A])\).
-
6.
In \(\text {art.}\, 61\), he proved that the operator \(\mathrm {Sg}_{\mathbf {S}}\) commutes with the unions of arbitrary nonempty families of parts of S, i.e., that, for every nonempty family \((A_{i})_{i\in I}\) of subsets of S, \(\mathrm {Sg}_{\mathbf {S}}(\bigcup _{i\in I}A_{i}) = \bigcup _{i\in I}\mathrm {Sg}_{\mathbf {S}}(A_{i})\). Thus \(\mathrm {Sg}_{\mathbf {S}}\) is a completely additive operator. This result is characteristic of the mono-unary algebras \((S,\varphi )\), since, for arbitrary signatures \(\varvec{{\varSigma }} = ({\varSigma },\mathrm {ar})\), where \({\varSigma }\) is a set of operation symbols and \(\mathrm {ar}\) a mapping from \({\varSigma }\) to \(\mathbb {N}\), and \(\varvec{{\varSigma }}\)-algebras \(\mathbf {A} = (A,(F_{\sigma })_{\sigma \in {\varSigma }})\), where A is a set and, for every \(\sigma \in {\varSigma }\), \(F_{\sigma }\) a mapping from \(A^{\mathrm {ar}(\sigma )}\) to A, what is true is that the operator \(\mathrm {Sg}_{\mathbf {A}}\) commutes with the unions of nonempty upward directed families of parts of A. Implied in the above theorem of Dedekind is the following. In order to be able to have families of parts of S one must have the set \(\mathrm {Sub}(\mathrm {Sub}(S))\) and to establish that \(\mathrm {Sg}_{\mathbf {S}}\) is completely additive one must have a mapping from \(\mathrm {Sub}(\mathrm {Sub}(S))\) to \(\mathrm {Sub}(\mathrm {Sub}(S))\) which sends a set \(\mathcal {A}\) in \(\mathrm {Sub}(\mathrm {Sub}(S))\) to the set \(\{\mathrm {Sg}_{\mathbf {S}}(A)\mid A\in \mathcal {A}\}\) in \(\mathrm {Sub}(\mathrm {Sub}(S))\). Thus we have here an implicit use of the axiom schema of replacement in order to obtain from \(\mathcal {A}\), by means of \(\mathrm {Sg}_{\mathbf {S}}\)—which is acting as a functional condition—precisely \(\{\mathrm {Sg}_{\mathbf {S}}(A)\mid A\in \mathcal {A}\}\).
Moreover, in \(\text {art.}\, 62\) Dedekind proved that, for every nonempty family \((A_{i})_{i\in I}\) of subsets of S, \(\mathrm {Sg}_{\mathbf {S}}(\bigcap _{i\in I}A_{i}) \subseteq \bigcap _{i\in I}\mathrm {Sg}_{\mathbf {S}}(A_{i})\). Hence Dedekind obviously knew that \(\mathrm {Sg}_{\mathbf {S}}\) was not necessarily a completely multiplicative operator.
Before proceeding further, notice that, for a mono-unary algebra \(\mathbf {S} = (S,\varphi )\), the structural operation \(\varphi \) is also an endomorphism of \(\mathbf {S}\).
We think it is extremely important to point out that a profound and clear reflection on the essential role played by the notion of chain in the definition by Dedekind of the system of natural numbers—which allowed him to reduce complexity to simplicity—can be found in the letter that Dedekind sent to Hans Keferstein on February 27, 1890 (van Heijenoort 1967, p. 101).
We notice that Dedekind, to define the operator \(\mathrm {Sg}_{\mathbf {S}}\), took for granted, implicitly, that there exists, strictly speaking, the set \(\mathrm {Sub}(S)-\{\varnothing \}\), since he considered the action of \(\mathrm {Sg}_{\mathbf {S}}\) only on nonempty subsets of S. And recall also that (in Dedekind 1888, art. 2) he wrote the following: “On the other hand, we intend here for certain reasons wholly to exclude the empty system which contains no element at all, ...”. However, Dedekind (1888, art. 2), just after the above quotation, also wrote that: “...although for other investigations it may be appropriate to imagine such a system”. Thus, judging by what Dedekind said in the last quotation, it does not seem unreasonable to think that he would have admitted \(\mathrm {Sub}(S)\) as a legitimate set (notice that in this case \(\mathrm {Sg}_{\mathbf {S}}(\varnothing ) = \varnothing \)). Furthermore, since Dedekind has defined, for every (nonempty) set S, \(\mathrm {id}_{S}\), the identity mapping at S, we have, for an arbitrary (nonempty) set S, the mono-unary algebra \((S,\mathrm {id}_{S})\), hence the set of all subalgebras of \((S,\mathrm {id}_{S})\), i.e., in this case, strictly speaking, the set of all nonempty subsets of S. But, as above, it does not seem unjustified to think that Dedekind would have admitted \(\mathrm {Sub}(S)\) as the set of all subalgebras of \((S,\mathrm {id}_{S})\). Moreover, since Dedekind also used functional sets (see below), we can conclude that, for every (nonempty) set S, the set \(\mathrm {Hom}(S,2)\), of all mappings from S to 2, which is isomorphic to \(\mathrm {Sub}(S)\), is available to him. Thus, without distorting the thought of Dedekind, we can infer that he allowed, in addition to the set-theoretical operations of union and intersection, the power set operation. Afterwards, Dedekind proved, in \(\mathrm {art.}\,59\), for mono-unary algebras, the principle of proof by algebraic induction which, as a matter of fact, is the basis, in \(\text {art.}\, 80\), for the classical principle of proof by (finite) mathematical induction. Notice that the condition \(\sigma \) in \(\mathrm {art.}\,59\), i.e., that \(\varphi [\mathrm {Sg}_{\mathbf {S}}(A)\cap {\varSigma }]\subseteq {\varSigma }\), is equivalent to: \(\mathrm {Sg}_{\mathbf {S}}(A)\cap {\varSigma }\) is a subalgebra of \(\mathbf {S}\), i.e., to \(\varphi [\mathrm {Sg}_{\mathbf {S}}(A)\cap {\varSigma }]\subseteq \mathrm {Sg}_{\mathbf {S}}(A)\cap {\varSigma }\). Moreover, Dedekind announced without proof in \(\text {art.}\, 63\) of \(\S \, 4\) a theorem from which follows a corollary that is the basis for the proof of the theorem of Cantor–Bernstein, also known as the theorem of Dedekind–Cantor–Bernstein–Schröder. But before stating and proving this theorem in \(\text {art.}\, 63\), as well as the corollary, we note that all sets involved in the theorem are subsets of the underlying set S of an arbitrary, but fixed, mono-unary algebra \(\mathbf {S} = (S,\varphi )\). Moreover, for simplicity of notation, for a subset A of S, throughout the proof we let \(A_{0}\) stand for \(\mathrm {Sg}_{\mathbf {S}}(A)\).
63. Theorem. If \(\varphi [K]\subseteq L\subseteq K\), and therefore K is a chain, L is also a chain. If it is a proper part of K, and U is the system of all those elements of K which are not contained in L, and if the chain \(U_{0}\) is a proper part of K, and if V is the system of all those elements of K which are not contained in \(U_{0}\), then \(K = U_{0}\cup V\) and \(L = \varphi [U_{0}]\cup V\). If finally \(L = \varphi [K]\), then \(V\subseteq \varphi [V]\).
Before proving this theorem notice that in it Dedekind twice used the difference between sets (obtained by applying the axiom schema of separation).
Proof
From \(L\subseteq K\), it follows that \(\varphi [L]\subseteq \varphi [K]\), but \(\varphi [K]\subseteq L\), thus \(\varphi [L]\subseteq L\), i.e., L is a \(\varphi \)-chain. \(\square \)
Now suppose that \(L\subset K\), that \(U_{0}\subset K\), where \(U = K-L\), and that \(V = K-U_{0}\). Then \(K = U_{0}\cup V\) and \(L = \varphi [U_{0}]\cup V\).
It is obvious that \(K = U_{0}\cup V\), since \(V = K-U_{0}\).
To prove that \(L = \varphi [U_{0}]\cup V\), we state, as a lemma, that \(U_{0} = U\cup \varphi [U_{0}]\). Since \(U\subseteq U_{0}\) and \(\varphi [U_{0}]\subseteq U_{0}\), we have that \(U\cup \varphi [U_{0}]\subseteq U_{0}\). To prove the converse inclusion, it suffices to show that \(\varphi [U\cup \varphi [U_{0}]] \subseteq U\cup \varphi [U_{0}]\). But, \(\varphi [U\cup \varphi [U_{0}]] = \varphi [U]\cup \varphi [\varphi [U_{0}]]\). On the other hand, from \(U\subseteq U_{0}\) it follows that \(\varphi [U]\subseteq \varphi [U_{0}]\); moreover, \(\varphi [U_{0}]\subseteq U_{0}\), hence \(\varphi [\varphi [U_{0}]]\subseteq \varphi [U_{0}]\), so \(\varphi [U]\cup \varphi [\varphi [U_{0}]]\subseteq \varphi [U_{0}]\), therefore \(\varphi [U]\cup \varphi [\varphi [U_{0}]]\subseteq U\cup \varphi [U_{0}]\). Hence \(U_{0}\subseteq U\cup \varphi [U_{0}]\). Consequently \(U_{0} = U\cup \varphi [U_{0}]\).
We next prove that \(L = \varphi [U_{0}]\cup V\). But, from \(U_{0}\subset K\), it follows that \(\varphi [U_{0}]\subseteq \varphi [K]\), yet \(\varphi [K]\subseteq L\), hence \(\varphi [U_{0}]\subseteq L\). On the other hand, from \(U\subseteq U_{0}\) it follows that \(V = K-U_{0}\subseteq K-U = K-(K-L) = L\), i.e., that \(V\subseteq L\). Hence \(\varphi [U_{0}]\cup V\subseteq L\). To prove the converse inclusion, taking into account that K can be represented as \(K = U\cup L\) and since \(K = U\cup (\varphi [U_{0}]\cup V)\), because \(K = U_{0}\cup V\) and \(U_{0} = U\cup \varphi [U_{0}]\), we infer that L cannot be included in U, because \(U = K-L\), so that \(L \subseteq \varphi [U_{0}]\cup V\). Consequently \(L = \varphi [U_{0}]\cup V\).
Now assume that \(L = \varphi [K]\). Then we can assert, by the above, that \(\varphi [K] = \varphi [U_{0}]\cup V\). But it happens that \(K = U_{0}\cup V\), so \(\varphi [K] = \varphi [U_{0}]\cup \varphi [V]\), hence \(\varphi [U_{0}]\cup \varphi [V] = \varphi [U_{0}]\cup V\). But \(V\subseteq \varphi [U_{0}]\cup V\), hence \(V\subseteq \varphi [U_{0}]\cup \varphi [V]\).
It only remains to prove that V cannot be included in \(\varphi [U_{0}]\). But \(\varphi [U_{0}]\subseteq U_{0}\) and \(V = K-U_{0}\). Hence V cannot be included in \(\varphi [U_{0}]\), since, if it could, then it would be included in \(U_{0}\), which would be absurd. Q.E.D.
From this theorem, we obtain the following corollary.
Corollary
If a set M is isomorphic to one of its subsets \(M'\), then it is also isomorphic to any other subset T of M such that \(T\supseteq M'\).
Proof
Let f be an arbitrary, but fixed, bijection from M to \(M'\), \(Q = T-M'\), and \(\mathcal {T}_{M',T}\) the subset of \(\mathrm {Sub}(M)\) defined as follows:
We have that \(M\in \mathcal {T}_{M',T}\), therefore \(\mathcal {T}_{M',T}\ne \varnothing \). Let \(\overline{A}\) be \(\bigcap _{A\in \mathcal {T}_{M',T}}A\). Then \(Q\subseteq \overline{A}\) and \(f[\overline{A}]\subseteq \overline{A}\), hence \(\overline{A}\in \mathcal {T}_{M',T}\) and it is, in fact, the smallest member of \(\mathcal {T}_{M',T}\). It happens that \(\overline{A} = Q\cup f[\overline{A}]\). In fact, by the above, it is clear that \(Q\cup f[\overline{A}]\subseteq \overline{A}\). To prove the converse inclusion, i.e., that \(\overline{A}\subseteq Q\cup f[\overline{A}]\), let r be an element of \(\overline{A}-Q\) and suppose that \(r\not \in f[\overline{A}]\). Then \(f[\overline{A}]\subseteq \overline{A}-\{r\}\). On the other hand, we have that \(f[\overline{A}-\{r\}]\subseteq f[\overline{A}]\), because \(\overline{A}-\{r\}\subseteq \overline{A}\) and \(f[\cdot ]\) is isotone. Therefore \(f[\overline{A}-\{r\}]\subseteq \overline{A}-\{r\}\). But \(Q\subseteq \overline{A}-\{r\}\), because \(Q\subseteq \overline{A}\) and \(r\not \in Q\). Thus \(\overline{A}-\{r\}\in \mathcal {T}_{M',T}\), but \(\overline{A}-\{r\}\subset \overline{A}\), which is a contradiction, because \(\overline{A}\) is the smallest member of \(\mathcal {T}_{M',T}\). Therefore \(\overline{A} = Q\cup f[\overline{A}]\). Thus \(T = \overline{A}\cup (M'-f[\overline{A}])\), since \(T = Q\cup M'\) and \(Q\cup M' = (Q\cup f[\overline{A}])\cup (M'-f[\overline{A}])\). But \(\overline{A}\) is isomorphic to \(f[\overline{A}]\), hence T is isomorphic to \(f[\overline{A}]\cup (M'-f[\overline{A}])\). However, \(f[\overline{A}]\cup (M'-f[\overline{A}]) = M'\) and \(M'\) is isomorphic to M; consequently, T is isomorphic to M. Q.E.D. \(\square \)
From the preceding corollary, as we have said above, the theorem of Cantor–Bernstein follows immediately. On this subject we refer the reader to the following work by Dedekind: Ähnliche (deutliche) Abbildung und ähnliche Systeme. 1887.7.11, which is included in Dedekind (1930–1932, Vol. III, pp. 447–448), and to Noether’s illuminating accompanying commentary.
In \(\S \, 5\), \(\text {art.}\, 64\), Dedekind defined the notions of infinite set and of finite set. He wrote: “A system S is said to be infinite when it is similar to a proper part of itself (32); otherwise S is said to be a finite system”. And in a footnote he wrote: “If one does not care to employ the notion of similar systems (32) one must say: S is said to be infinite, when there is a proper part of S (6) into which S can be distinctly (similarly) mapped (26), (36)”. This shows that Dedekind knew that in the image analysis of an injective mapping f from a set A to another B as the composition \(\mathrm {in}_{\mathrm {Im}(f)}\circ f^{\mathrm {e}}\), where \(f^{\mathrm {e}}\) is the epimorphic mapping from A to \(\mathrm {Im}(f)\) defined by \(f^{\mathrm {e}}(a) = f(a)\), for all a in A, and \(\mathrm {in}_{\mathrm {Im}(f)}\) the canonical embedding of \(\mathrm {Im}(f)\) into B, the epimorphic part \(f^{\mathrm {e}}\) is an isomorphism. Afterwards, in \(\text {art.}\, 66\), Dedekind stated the “proof” of the existence of an infinite set, which, as it is well known, is mathematically unacceptable because the faulty General Comprehension Principle is, ultimately, involved in it, by considering “the totality S of all things which can be objects of my [Dedekind’s] thought”, i.e., the “set” of all sets, which is not a set. Let us recall that the just-mentioned Principle asserts that there exists a “functional operator” \(\mathrm {Ext}\) that assigns to every property \(\varphi \) (an unsaturated entity, in Frege’s terminology) its extension, \(\mathrm {Ext}(\varphi )\) (a saturated entity, in Frege’s terminology), i.e., the object consisting of all x such that \(\varphi (x)\) (that fall under \(\varphi \)).
Actually, Dedekind was well aware of the difficulties raised by some of his principles, whether implicit or explicit, since, e.g., in the preface to the third edition of Was sind und was sollen die Zahlen?, he wrote:
...doubts had arisen about the reliability [Sicherheit] of important foundations of my conception. Even today I do not underestimate the importance, and to some extend the correctness, of these doubts. But my trust in the inner harmony of our logic is not thereby shattered; I believe that a rigorous investigation of the power [Schöpferkraft] of the mind to create from determinate elements a new determinate object, their system, that is necessarily different from each of these elements, will certainly lead to an unobjectionable formulation of the foundations of my work.
As a sample of those principles about which Dedekind doubted their reliability, and without trying to be exhaustive, we indicate the following ones:
(1) the aforementioned General Comprehension Principle, which, e.g., enabled him to obtain, in \(\text {art.}\, 66\), the “system” that has been indicated above and, in \(\text {art.}\, 134\), to gather together in a “class” all simply infinite systems,
(2) the principle, stated in \(\text {art.}\, 34\), that allows the formation of the quotient “system” of the “system” of all systems by the similarity (\(\equiv \) isomorphism) relation between systems (which for sets is legitimate because it is a particular case of the axiom schema of replacement), and
(3) the principle, also stated in \(\text {art.}\, 34\), that every equivalence relation on a system has a transversal (\(\equiv \) a system of representatives) (which for sets is valid since it is the following form of the axiom of choice: every surjective mapping is a retraction).
Following this, in \(\S \, 6\), \(\text {art.}\, 71\), Dedekind defined the simply infinite systems—nowadays called Dedekind–Peano algebras. These, let us recall, are ordered triples \(\mathbf {S} = (S,\varphi ,e)\) where S is a set, \(\varphi \) a mapping from S to S, and e an element of S, satisfying the following conditions: the mapping \(\varphi \) is injective, e is not in the image of \(\varphi \), and \(\mathrm {Sg}_{(S,\varphi )}(\{e\}) = S\), where \(\mathrm {Sg}_{(S,\varphi )}\) is the subalgebra generating operator on the reduct \((S,\varphi )\) of \((S,\varphi ,e)\). Then, in \(\text {art.}\, 72\), he provided a proof sketch of the following theorem: from every infinite set one can obtain, by using the difference between sets (thus by applying the axiom schema of separation), a Dedekind–Peano algebra, which, up to isomorphism, is the Dedekind–Peano algebra of the natural numbers (see below the commentary on \(\S \, 10\)).
The proof runs as follows. Let S be an infinite set. Then let \(\varphi \) be a fixed injective mapping from S into itself such that \(\varphi [S]\) is a proper part of S and let e be a fixed element of \(S-\varphi [S]\). Since \(\mathrm {Sg}_{(S,\varphi )}(\{e\})\) is a chain (relative to \(\varphi \)) and \(e\in \mathrm {Sg}_{(S,\varphi )}(\{e\})\), it follows that \(\varphi (e)\in \mathrm {Sg}_{(S,\varphi )}(\{e\})\). Moreover, \(\varphi [\mathrm {Sg}_{(S,\varphi )}(\{e\})] = \mathrm {Sg}_{(S,\varphi )}(\{\varphi (e)\})\) and \(\mathrm {Sg}_{(S,\varphi )}(\{\varphi (e)\})\) is the smallest chain (relative to \(\varphi \)) which contains \(\{\varphi (e)\}\). Therefore \(\varphi [\mathrm {Sg}_{(S,\varphi )}(\{e\})]\) is included in \(\mathrm {Sg}_{(S,\varphi )}(\{e\})\). Hence there exists a unique mapping \(\varphi _{e}\) from \(\mathrm {Sg}_{(S,\varphi )}(\{e\})\) into itself such that \(\varphi \circ \mathrm {in}_{\mathrm {Sg}_{(S,\varphi )}(\{e\})} = \mathrm {in}_{\mathrm {Sg}_{(S,\varphi )}(\{e\})}\circ \varphi _{e}\) and, as \(\varphi \circ \mathrm {in}_{\mathrm {Sg}_{(S,\varphi )}(\{e\})}\) is injective, \(\varphi _{e}\) is injective. Moreover, \(e\not \in \varphi _{e}[\mathrm {Sg}_{(S,\varphi )}(\{e\})] = \mathrm {Sg}_{(S,\varphi )}(\{\varphi _{e}(e)\})\) because, from \(\mathrm {Sg}_{(S,\varphi )}(\{e\})\subseteq S\) it follows that \(\mathrm {Sg}_{(S,\varphi )}(\{\varphi _{e}(e)\})\subseteq \varphi [S]\), and, by hypothesis, \(e\not \in \varphi [S]\)—observe that \(\varphi _{e}[\mathrm {Sg}_{(S,\varphi )}(\{e\})] = \varphi [\mathrm {Sg}_{(S,\varphi )}(\{e\})]\) and \(\varphi _{e}(e) = \varphi (e)\). Thus \((\mathrm {Sg}_{(S,\varphi )}(\{e\}),\varphi _{e},e)\) is a simply infinite system. Moreover, for a simply infinite system \(\mathbf {S} = (S,\varphi ,e)\), from \(\text {art.}\, 79\) it follows, obviously, that, for every \(X\subseteq S\), if \(e\in X\) and \(\varphi [X]\subseteq X\), then \(X = S\). De facto we have: if \(\mathbf {S} = (S,\varphi ,e)\) is such that  and \(e\in S\), then, \(\mathrm {Sg}_{(S,\varphi )}(\{e\}) = S\) if, and only if, for every \(X\subseteq S\), if \(e\in X\) and \(\varphi [X]\subseteq X\), then \(X = S\).
and \(e\in S\), then, \(\mathrm {Sg}_{(S,\varphi )}(\{e\}) = S\) if, and only if, for every \(X\subseteq S\), if \(e\in X\) and \(\varphi [X]\subseteq X\), then \(X = S\).
In \(\S \, 7\) Dedekind defined and investigated, the relation “<” between pairs of natural numbers, using the fact that he had, in an implicit way, a free algebra, and stating, ultimately, that the set of natural numbers is well-ordered. (In \(\text {art.}\, 96\), he proved that every nonempty subset of N has a minimum element, which is the characteristic property of the concept of well-ordering on a set, together with the transitivity and the irreflexivity.)
We point out that, in \(\text {art.}\, 84\), Dedekind proved, for a simply infinite system \(\mathbf {S} = (S,\varphi ,e)\), that the restriction of the operator \(\mathrm {Sg}_{(S,\varphi )}\) to S is injective, i.e., that, for every x, \(y\in S\), if \(\mathrm {Sg}_{(S,\varphi )}(\{x\}) = \mathrm {Sg}_{(S,\varphi )}(\{y\})\), then \(x = y\). Furthermore, in \(\text {art.}\, 87\), he proved, by using the difference between sets, that every number-chain is monogenic or principal, i.e., that, for every subset K of S, if \(\varphi [K]\subseteq K\), then there exists at least one (and, by \(\text {art.}\, 84\), at most one) \(x\in K\) such that the subalgebra of \((S,\varphi )\) generated by \(\{x\}\) is K. Besides, in \(\text {art.}\, 98\), Dedekind defined the initial segment determined by a natural number n, i.e., defines the set \(\{1,\ldots , n\}\), and introduces the useful notation \(Z_{n}\) for it. Observe that Dedekind wrote, in this respect, the following:
If n is any number, then we shall denote by \(Z_{n}\) the system of all numbers that are not greater than n, and hence not contained in \(n'_{0}\) ...
Therefore, in doing so, Dedekind was defining \(Z_{n}\) as \(N- n'_{0}\), i.e., by using, once more, the difference between sets. Concerning the relation “<” we recall that, given an algebraic signature \(\varvec{{\varSigma }}\) and a \(\varvec{{\varSigma }}\)-algebra \(\mathbf {A} = (A,(F_{\sigma })_{\sigma \in {\varSigma }})\), we obtain a binary relation \(\mathrm {S}_{\mathbf {A}}\) on A, the algebraic successor relation on A, defined as follows:
If \(a \mathrm {S}_{\mathbf {A}} b\), then we say that b is an algebraic successor of a, or that a is an algebraic predecessor of b. Then, using \(\mathrm {S}_{\mathbf {A}}\), we define the binary relation \(<_{\mathbf {A}}\) on A as \(\mathrm {S}^{\mathrm {t}}_{\mathbf {A}} = \bigcup _{n\in \mathbb {N}-1}\mathrm {S}^{n}_{\mathbf {A}}\), the transitive closure of \(\mathrm {S}_{\mathbf {A}}\). For the Dedekind–Peano algebras the relation \(<_{\mathbf {A}}\) is an strict order, i.e., an irreflexive and transitive relation on A, and satisfies the minimal condition, and in this case \(<_{\mathbf {A}}\) is called the natural ordering on \(\mathbf {A}\). One can, informally, say that a Dedekind–Peano algebra \(\mathbf {A} = (A,(F_{\sigma })_{\sigma \in {\varSigma }})\) is “ordered” by the family \((F_{\sigma })_{\sigma \in {\varSigma }}\) of its structural operations. Moreover, it happens that the Dedekind–Peano algebra of the natural numbers is linearly ordered by its natural ordering. This may explain why Dedekind (1888, art. 71) changed his terminology, concerning the structural mapping \(\varphi \), by writing the following: “...and say the simply infinite system N is ordered by this mapping \(\varphi \).”
Dedekind devoted \(\S \, 8\) to investigating the finite and infinite parts of the set of all natural numbers. In particular, he characterized the finite and infinite parts of N in terms of the well-ordering < on N as: a part T of N is finite if, and only if, T has a greatest element, or, what is equivalent, a part T of N is infinite if, and only if, there does not exist a greatest element in T.
In \(\S \, 9\) Dedekind proved, for the first time in the history of mathematics, the principle of definition by mathematical recursion. This principle, in category-theoretic terms and using \(\mathbb {N}\), states that the following diagram

where \(\kappa _{0}\) is the mapping from 1 to \(\mathbb {N}\) that sends 0 to 0 and \(\mathrm {sc}\) the successor mapping, is an initial object in the category \(\mathbf {Srd}\), of simple recursion data (see Manes and Arbib 1986, p. 53–54). It has been proposed by Lawvere (1964, p. 1507) as one of the axioms for a category-theoretic approach to the foundations of mathematics. We will show, in Sect. 4, that in his proof of this principle Dedekind used, in an implicit way, the concept of an inductive cone from an inductive system of sets and that of the inductive limit of an inductive system of sets. With regard to the principle under consideration Lawvere (1964, p. 1508) announced without proof the following theorem: “All of Peano’s Postulates hold for \(\mathbb {N}\)”. This provides an example of the fact that the axioms used to specify a certain type of mathematical object are not necessarily unique, and in addition, it shows that the principle of definition by mathematical recursion is strictly stronger than the principle of proof by mathematical induction. Actually, we have the following theorem.
Theorem
An ordered triple \(\mathbf {A} = (A,f,e)\), where A is a set, f an endomorphism of the set A, and e an element of A, is a Dedekind–Peano algebra if, and only if, \(\mathbf {A}\) satisfies the principle of definition by mathematical recursion, i.e., for every ordered triple \(\mathbf {A}' = (A',f',e')\), where \(A'\) is a set,  , and \(e'\in A'\), there exists a unique mapping
, and \(e'\in A'\), there exists a unique mapping  such that \(\kappa _{e'} = h\circ \kappa _{e}\) and \(h\circ f = f'\circ h\), where \(\kappa _{e}\) is the mapping from 1 to A that sends 0 to e, and \(\kappa _{e'}\) the mapping from 1 to \(A'\) that sends 0 to \(e'\).
such that \(\kappa _{e'} = h\circ \kappa _{e}\) and \(h\circ f = f'\circ h\), where \(\kappa _{e}\) is the mapping from 1 to A that sends 0 to e, and \(\kappa _{e'}\) the mapping from 1 to \(A'\) that sends 0 to \(e'\).
That \(\mathbf {A}\) satisfies the principle of definition by mathematical recursion if \(\mathbf {A}\) is a Dedekind–Peano algebra is the content of Dedekind’s \(\S \, 9\).
In \(\S \, 10\), Dedekind investigated the class of simply infinite systems. Specifically, he stated, in \(\text {art.}\, 132\), that any two simply infinite systems are isomorphic (this theorem follows from the principle of definition by mathematical recursion)—from the viewpoint of mathematical logic this theorem asserts the categoricity of the concept of simply infinite system. Then in \(\text {art.}\, 133\), he stated that every system isomorphic to the underlying system of a simply infinite system is also equipped with a structure of simply infinite system, which is certainly an example of the principle of transport of structure or, what is equivalent, of the principle that structure is abstract. Thus we can see in these theorems of Dedekind’s—which together state that simply infinite systems are unique up to a unique isomorphism—his interest in the subject of what the right morphisms are between structured sets and an instance of those properties which are characteristic of the category-theoretic universal constructions.
In \(\S \S \) 11–13, Dedekind defined the arithmetical operations of addition, multiplication, and exponentiation and proved their essential properties (in particular, the compatibility of the order relation with the addition). We notice that, e.g., addition is obtained by Dedekind from a countably infinite family  , where each of the mappings
, where each of the mappings  is given by applying the principle of definition by mathematical recursion. Thus, \(+_{1}\) is \(\mathrm {id}_{N}\), the identity mapping at N, and, for \(m\in N-\{1\}\), \(+_{m}\) is such that \(+_{m}(1) = \mathrm {sc}(m)\) and, for \(n\in N\), \(+_{m}(\mathrm {sc}(n)) = \mathrm {sc}(+_{m}(n))\).
is given by applying the principle of definition by mathematical recursion. Thus, \(+_{1}\) is \(\mathrm {id}_{N}\), the identity mapping at N, and, for \(m\in N-\{1\}\), \(+_{m}\) is such that \(+_{m}(1) = \mathrm {sc}(m)\) and, for \(n\in N\), \(+_{m}(\mathrm {sc}(n)) = \mathrm {sc}(+_{m}(n))\).
At this stage, in order to support our claim about Dedekind’s anticipation of Gödel’s notion of a primitive recursive mapping, we begin by recalling Gödel’s definition of the above-mentioned set of number-theoretic mappings.
Gödel (1931, pp. 179–180) defined a subset \(\mathrm {PRM}\), the set of all “recursive” mappings (currently known as the set of all primitive recursive mappings) of \(\bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\), the set of all number-theoretic mappings—a “parenthetic consideration” for him—as follows:
Eine zahlentheoretische Funktion \(\phi \) heißt rekursiv, wenn es eine endliche Reihe von zahlentheoretischen Funktionen \(\phi _{1},\phi _{2},\ldots , \phi _{n}\) gibt, whelche mit \(\phi \) endet und die Eigenschaft hat, daß jede Funktion \(\phi _{k}\) der Reihe entweder aus zwei der vorhergehenden rekursiv definiert ist oder aus irgend welchen der vorhergehenden durch Einsetzung entsteht oder schließlich eine Konstante oder die Nachfolgerfunktion \(x+1\) ist. [A number-theoretic function \(\phi \) is said to be recursive if there is a finite sequence of number-theoretic functions \(\phi _{1},\phi _{2},\ldots , \phi _{n}\) that ends with \(\phi \) and has the property that every function \(\phi _{k}\) of the sequence is recursively defined in terms of two of the preceding functions or results from any of the preceding functions by substitution, [here Gödel adds a footnote explaining more precisely the meaning of the expression “by substitution” (durch Einsetzung), we add] or, finally, is a constant or the successor function \(x+1\).]
Let us notice the formal identity of the above definition of the notion of primitive recursive mapping and the definition of the concept of proof of a sentence \(\varphi \). Moreover, from such a definition one concludes that a number-theoretic mapping is primitive recursive if, and only if, it belongs to the union of the underlying many-sorted set of a suitable subalgebra of a convenient many-sorted algebra with \((\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))_{n\in \mathbb {N}}\) as underlying many-sorted set and equipped with a family of constants, the successor mapping, families of operators of primitive recursion, and families of operators of substitutions.
Remark 2
The reader will find in Appendix A a many-sorted algebraic model of the theory of primitive recursive mappings.
We suggest that Dedekind clearly anticipated Gödel’s theory of primitive recursive mappings, since from the principle of definition by mathematical recursion the parameterized operation of primitive recursion (\(\equiv \) recursion \(\equiv \) primitive recursion) immediately follows. This operation, together with the generalized composition (\(\equiv \) substitution) of number-theoretic mappings—itself an obvious generalization of the composition of mappings, which, as we have already seen, was clearly defined by Dedekind—is, from a structural standpoint, at the basis of such a theory. Thus, although recursion theory, like other theories, did not reach a mature form with Dedekind, it had at least a substantial beginning with him.
Remark 3
The reader will also find in Appendix A a diagrammatic proof of the fact that the three basic mathematical operations, addition, multiplication, and exponentiation, defined by Dedekind in §§11–13 of Dedekind (1888), are primitive recursive.
In §14 art. 159, Dedekind proved the following theorem: “If \({\varSigma }\) is an infinite system, then every one of the number-systems \(Z_{n}\) defined in 98 is similarly representable into \({\varSigma }\) (i.e., similar to a part of \({\varSigma }\)), and conversely”.
Note that in his proof of this theorem, specifically of the converse part, Dedekind considered, for a set \({\varSigma }\) and every n, the set \(\mathcal {M}(Z_{n},{\varSigma })\) of all injective mappings from \(Z_{n}\) to \({\varSigma }\) and an element \((\alpha _{n})_{n\in N}\) of \(\prod _{n\in N}\mathcal {M}(Z_{n},{\varSigma })\), as arbitrarily given, or as he said: “regarded as given, but respecting which nothing further is assumed”. Thus we have, in this case, as Zermelo pointed out, an implicit use of the countable axiom of choice by Dedekind. From here, with the aid of the principle of definition by mathematical recursion, he proved the existence of a new family of such mappings \((\psi _{n})_{n\in N}\) possessing the special property that whenever \(Z_{m}\subseteq Z_{n}\), the mapping \(\psi _{m}\) of the part \(Z_{m}\) is contained in the mapping \(\psi _{n}\) of \(Z_{n}\), i.e., the mappings \(\psi _{m}\) and \(\psi _{n}\) completely coincide with each other for all numbers contained in \(Z_{m}\) (i.e., \(\psi _{n}\!\upharpoonright \!_{Z_{m}}\), the restriction of \(\psi _{n}\) to \(Z_{m}\), is \(\psi _{m}\)), so that always \(\psi _{m}(m) = \psi _{n}(m)\).
To this end, he defined an appropriate triple \(({\varOmega },\theta ,\omega )\) consisting of a set \({\varOmega }\), a mapping \(\theta \) from \({\varOmega }\) to \({\varOmega }\), and an \(\omega \in {\varOmega }\). Actually, in \(\text {art.}\, 159\), he wrote: “we understand by \({\varOmega }\) that system whose elements are all possible similar representations of all systems \(Z_{n}\) into \({\varSigma }\).” Hence \({\varOmega }= \bigcup _{n\in N}\mathcal {M}(Z_{n},{\varSigma })\), and, here, Dedekind, in addition to considering functional sets and the union of a countably infinite family of sets, made use, implicitly, of the axiom schema of replacement to obtain the set \(\{\mathcal {M}(Z_{n},{\varSigma })\mid n\in N\}\) from the functional condition consisting in associating to each \(n\in N\) the set \(\mathcal {M}(Z_{n},{\varSigma })\).
Moreover, Dedekind explicitly defined the mapping \(\theta \) from \({\varOmega }\) to \({\varOmega }\) as follows. Since \({\varOmega }= \bigcup _{n\in N}\mathcal {M}(Z_{n},{\varSigma })\) and \((\mathcal {M}(Z_{n},{\varSigma }))_{n\in N}\) is a family of pairwise disjoint sets, to give a mapping \(\theta \) from \({\varOmega }\) to \({\varOmega }\) is equivalent, by the universal property of the coproduct—in this case of the disjoint union—to give a family \((\theta _{n})_{n\in N}\) where, for every \(n\in N\), \(\theta _{n}\) is a mapping from \(\mathcal {M}(Z_{n},{\varSigma })\) to \({\varOmega }\), i.e., a family \((\theta _{n})_{n\in N}\) should be chosen in \(\prod _{n\in N}\mathrm {Hom}(\mathcal {M}(Z_{n},{\varSigma }),{\varOmega })\). But it happens that, for every \(n\in N\) and \(\beta \in \mathcal {M}(Z_{n},{\varSigma })\),  is exactly the mapping \(\gamma \) defined by Dedekind in his proof. So here the axiom of choice is not used, because the components of the family \((\theta _{n})_{n\in N}\) are explicitly defined and, in addition, in a uniform or natural way. (The axiom of choice is not always necessary when making a simultaneous and independent choice of elements.) We summarize his definition of the mapping \(\theta \) as follows:
is exactly the mapping \(\gamma \) defined by Dedekind in his proof. So here the axiom of choice is not used, because the components of the family \((\theta _{n})_{n\in N}\) are explicitly defined and, in addition, in a uniform or natural way. (The axiom of choice is not always necessary when making a simultaneous and independent choice of elements.) We summarize his definition of the mapping \(\theta \) as follows:

where \(\text {in}_{n}\) is the canonical inclusion from \(\mathcal {M}(Z_{n},{\varSigma })\) to \({\varOmega }\), \(\theta _{n}\) is defined as follows:

with \(k = \mathrm {min}\{\,p\in Z_{n'}\mid \alpha _{n'}(p)\not \in \beta [Z_{n}]\,\}\), and \(\theta = \left[ \theta _{n}\right] _{n\in N}\) is the unique mapping from \({\varOmega }\) to \({\varOmega }\) such that, for every n, \(\left[ \theta _{n}\right] _{n\in N}\circ \mathrm {in}_{n} = \theta _{n}\). Moreover, he took for \(\omega \) precisely \(\alpha _{1}\).
Then Dedekind obtained, by means of the principle of definition by mathematical recursion, from \(\alpha _{1}\in {\varOmega }\) and \(\theta \), the family \((\psi _{n})_{n\in N}\) in \(\prod _{n\in N}\mathcal {M}(Z_{n},{\varSigma })\) possessing the special property that whenever \(Z_{m}\subseteq Z_{n}\), \(\psi _{n}\!\upharpoonright \!_{Z_{m}} = \psi _{m}\). Therefore, if, similarly to what we did in Sect. 2 with regard to a theorem of Cantor, we consider the family of sets \((\mathcal {M}(Z_{n},{\varSigma }))_{n\in N}\) and, on the other hand, the family of transition mappings \((f_{n',n})_{n\in N}\), where, for every \(n\in N\), \(f_{n',n}\) is the mapping from \(\mathcal {M}(Z_{n'},{\varSigma })\) to \(\mathcal {M}(Z_{n},{\varSigma })\) obtained from the canonical embedding of \(Z_{n}\) into \(Z_{n'}\), then we obtain a projective system of sets, denoted by \(\mathcal {M}({\varSigma })\) and it happens that \((\psi _{n})_{n\in N}\in \varprojlim \mathcal {M}({\varSigma })\), the projective limit of \(\mathcal {M}({\varSigma })\). Thus Dedekind had, constructively, proved that \(\varprojlim \mathcal {M}({\varSigma })\ne \varnothing \) and, consequently, that the canonical embedding of \(\varprojlim \mathcal {M}({\varSigma })\) into \(\prod _{n\in N}\mathcal {M}(Z_{n},{\varSigma })\) is a section.
To the above we add that in the last step of the proof of the theorem at issue—to prove that there exists an injective mapping \(\chi \) from N to \({\varSigma }\)—Dedekind explicitly defined \(\chi \) by making use of the family \((\psi _{n})_{n\in N}\). Actually, \(\chi = \left[ \psi _{n}\circ \mathrm {in}_{\{n\},Z_{n}}\right] _{n\in N}\) is the unique mapping from N to \({\varSigma }\) such that, for every \(n\in N\), the following diagram

commutes, where \(\text {in}_{\{n\},Z_{n}}\) is the canonical embedding of \(\{n\}\) into \(Z_{n}\) and \(\text {in}_{\{n\},N}\) the canonical embedding of \(\{n\}\) into N.
There is no doubt for us, grounding our conviction on his actual work, that Dedekind was well aware of how to define mappings from the union \(\bigcup _{i\in I}A_{i}\) of a family \((A_{i})_{i\in I}\) of pairwise disjoint sets to another set B, when, for every \(i\in I\) a mappings \(f_{i}\) from \(A_{i}\) to B is available—which is an instance of a universal property. This procedure, as shown above, is twice implicit in the proof of the above theorem and once, as we will see, in the theorem stated in \(\text {art.}\, 160\).
In \(\text {art.}\, 160\), Dedekind proved the following theorem: “A system \({\varSigma }\) is finite or infinite, according as there does or does not exist a system \(Z_{n}\) similar to it”. In this connection, Zermelo (2010, p. 259) once again highlighted Dedekind’s implicit use of the axiom of choice in his proof. We notice that Dedekind inferred, from the hypothesis that a set \({\varSigma }\) is finite and the theorem stated in \(\text {art.}\, 159\), that there exists a \(Z_{n}\) such that the set \(\mathcal {M}(Z_{n},{\varSigma }) = \varnothing \). But since for every (nonempty) set S, there exists an injective mapping from \(Z_{1}\) to S, he concluded that \(\mathrm {min}\{n\in N\mid \mathcal {M}(Z_{n},{\varSigma }) = \varnothing \}\) must be of the form \(n'\), i.e., of the form \(\mathrm {sc}(n)\), for a (unique) \(n\in N\). Therefore, because \(n<n'\), there exists an injective mapping \(\psi \) from \(Z_{n}\) to \({\varSigma }\). Then, to prove that \(\psi [Z_{n}] = {\varSigma }\), Dedekind proceeded by reductio ad absurdum. Thus, he supposed that \(\psi [Z_{n}]\subset {\varSigma }\) and selected an element \(\alpha \) from the set \({\varSigma }-\psi [Z_{n}]\). From here, since \(Z_{n}\cap \{n'\} = \varnothing \), Dedekind obtained a new injective mapping \(\varphi \) from \(Z_{n'}\), which is \(Z_{n}\cup \{n'\}\), to \({\varSigma }\) by using the injective mapping \(\psi \) from \(Z_{n}\) to \({\varSigma }\) and the mapping from \(\{n'\}\) to \({\varSigma }\) which sends \(n'\) to \(\alpha \). But, by hypothesis, \(\mathcal {M}(Z_{n'},{\varSigma }) = \varnothing \). Hence \(\psi [Z_{n}] = {\varSigma }\) and \(Z_{n}\) is isomorphic to \({\varSigma }\).
Moreover, from \(\text {art.}\, 161\) to \(\text {art.}\, 171\), Dedekind defined, among other things, the concept of cardinal number of a finite set and stated some of its fundamental properties. We notice that Dedekind, in \(\text {art.}\, 166\), considered, for a nonempty finite set B, the set \(B\cup \{\gamma \}\) under the hypothesis that \(\gamma \not \in B\) (\(\equiv \) \(B\cap \{\gamma \} = \varnothing \)) and that, in \(\text {art.}\, 168\), for two finite sets A and B, he says: “...and if A and B have no common element, then \(A\cup B\), ...”, thus allowing the empty set—recall that in \(\text {art.}\, 2\), Dedekind had written: “...we intend here for certain reasons wholly to exclude the empty system which contains no element at all ...” Moreover, in the proof of the theorem stated in \(\text {art.}\, 171\), Dedekind used, for the set \(\{\psi ^{-1}[\{\alpha '\}]{\mid } \alpha '\in \psi [{\varSigma }]\}\) of all nonempty fibres of a noninjective mapping \(\psi \) from a nonempty finite set \({\varSigma }\)—set obtained from \(\mathrm {Sub}({\varSigma })\) by applying the axiom schema of separation—the finite version of what is today called Zermelo’s principle: If \(\mathcal {P}\) is a partition of a set A, then there exists a \(T\subseteq A\) such that, for every \(P\in \mathcal {P}\), \(T\cap P\) has exactly one element.
Finally, in \(\text {art.}\, 172\), Dedekind wrote:
In this way we reach the notion, very useful in many cases [e.g., in classical algebra, algebraic geometry, and complex function theory, we add], of systems in which every element is endowed with a certain frequency-number which indicates how often it is to be reckoned as an element of the system.
Here Dedekind foresaw, for a set S, what is currently known as the concept of multiset over S, i.e., the set \(\mathbb {N}^{(S)}\) of all mappings x from S to \(\mathbb {N}\) such that \(\mathrm {card}(\mathrm {supp}(x))<\aleph _{0}\), where \(\mathrm {supp}(x)\), the support of x, is \(\{s\in S\mid x(s)\ne 0\}\), which is the underlying set of the free abelian monoid on S. Once more, another solution to a universal problem. And also pointing to the fact that multisets, unlike sets, do not satisfy the principle of extensionality.
After having surveyed the contents of Dedekind (1888), trying to understand their true originality, we would now like to highlight certain issues which have already been raised in the above survey.
Dedekind, in addition to having used, as it is obvious, the relations of inclusion and of strict inclusion, as well as the union and intersection of sets, used the difference of two sets (obtained by, implicitly, applying the axiom schema of separation), as we have seen, e.g., in the theorems stated in \(\text {art.}\, 63\), and in \(\text {art.}\, 87\), as well as in the definition established in \(\text {art.}\, 98\), and also employed—as an attentive reading shows—Cartesian products, functional sets (\(\equiv \) mapping sets), and even natural isomorphisms between functional sets. Thus, e.g., in \(\text {art.}\, 131\), Dedekind stated, for a set \({\varOmega }\), a (natural) isomorphism between the set of all binary operations on \({\varOmega }\), i.e., the set of all mappings from \({\varOmega }\times {\varOmega }\) to \({\varOmega }\), and the set of all mappings from \({\varOmega }\) to \(\mathrm {End}({\varOmega })\), the set of all endomorphisms of the set \({\varOmega }\), which is a precursor of the theorem of Curry–Schönfinkel—according to which, for every set A, the functor \((\cdot )^{A}\) from \(\mathbf {Set}\), the category of sets and mappings, to \(\mathbf {Set}\) is right adjoint to the functor \(A\times (\cdot )\) between the same categories. Dedekind also stated in \(\text {art.}\, 131\), as a theorem, that given a mono-unary algebra \((S,\omega )\) and a subset A of S, the subalgebra of \((S,\omega )\) generated by A, \(A_{0}\), is precisely \(A\cup \bigcup _{n\in N}\omega ^{n}[A]\), and he says: “We advise the reader to return to the earlier theorems 57 and 58 with this conception of a chain.”
Dedekind possibly made such a recommendation in order that we might become aware, now that the natural numbers are available to us, of the following facts:
(1) there is an alternative proof of the theorem stated in \(\text {art.}\, 57\) and (2) the subalgebra generated by a subset A of S has another, constructive, description as the union of an ascending chain of subsets of S, obtained by applying the principle of definition by mathematical recursion—something that he could not do in \(\text {art.}\, 58\) because up until then the set of all natural numbers was not formally available to him. From here it follows that Dedekind has proved the coincidence between an impredicative, top-down, definition of \(\mathrm {Sg}_{(S,\omega )}\) and a constructive, bottom-up, definition of \(\mathrm {Sg}_{(S,\omega )}\).
We close this section by reiterating that Dedekind can be regarded, in particular and by restricting our attention to Dedekind (1888)—after having linked every factual statement to supporting evidence—as one of the precursors of universal algebra, category theory, the theory of primitive recursive mappings, and of some axioms of set theory. As for category theory, we highlight his instrumental use of both the concept of set and that of mapping, together with the identity mappings, the partial operation of composition of mappings, and their fundamental properties: identities act as identities with respect to composition, and composition is associative. For Frege, incidentally, these were not logical notions (any more than the membership relation was logical for him). Moreover, contrary to what Frege and Dedekind thought, nowadays we know that a logic (understood, as we have said in Sect. 1, as a suitable combination of two components: a proof-theoretical and a model-theoretical one) cannot prove the existence of anything, let alone of infinite sets. Furthermore, we remark that the views of Frege and Dedekind about the essence of natural numbers are radically different. In fact, for Frege the natural numbers are defined by means of another idea—the extension of a concept—they are the sequence determined by a certain procedure, and they do not admit of any kind of polymorphism, i.e., are absolutely unique, while for Dedekind they are defined globally, i.e., up to isomorphism (Dedekind 1888, art. 73 and §10), as a construct (i.e., a set equipped with extra structure) characterized by a (categorical and finitely axiomatizable) system of axioms. We have here a concrete example of the extreme modernity of the mathematical thought of Dedekind, which allows us to conclude that Dedekind had broken loose from old habits of mathematical thinking and had left the narrow classical mathematical world completely. In this respect, it is most enlightening to compare what we have just stated about Dedekind with what Grothendieck (1971, p. 194) says about “raisonner directement sur des catégories fibrées sans utiliser des clivages explicites,” by omitting the cleavage as a part of the structure of the concept of fibred category:
Il est d’ailleurs probable que, contrairement à l’usage encore prépondérant maintenant, lié à d’anciennes habitudes de pensée, il finira par s’avérer plus commode dans les problémes universels, de ne pas mettre l’accent sur une solution supposée choisie une fois pour toutes, mais de mettre toutes les solutions sur un pied d’égalité.
4 Dedekind’s principle of definition by mathematical recursion
In this section, we shall show that Dedekind (1888, §9) used, in an implicit way, both the notion of an inductive cone from an inductive system of sets and that of the inductive limit of an inductive system of sets in his proof of the principle of definition by mathematical recursion. But before doing that we first explain, in a succinct way, how other mathematicians proceeded at the time with regard to this principle and, on the basis of Hilbert’s first-hand report, we show that, unfortunately, the impact of Dedekind’s algebraic approach to the foundation of the system of natural numbers appears to have had no influence on his fellow mathematicians. Yet right now, and linked to this last point, we notice that it was not until many years later that this aspect of Dedekind’s approach had any influence. Concretely, this happened when universal algebra and category theory, after reaching the appropriate degree of maturity, were able to grasp and show the essence of some profound mathematical ideas clearly. Thus, for example, the principles of proof by mathematical induction and of definition by mathematical recursion were generalized, by the working universal algebraist, to the principles of proof by algebraic induction and of definition by algebraic recursion, respectively (see the remark at the end of this section), and the principle of definition by mathematical recursion was proved to be equivalent, by working categoricians, to the axioms of Dedekind–Peano. To this we add that, among other things, what makes Dedekind’s principle of definition by mathematical recursion remarkable is—in addition to the just-mentioned facts and its use to prove, e.g., that a certain projective limit is nonempty, as we have seen in Sect. 3—that from this principle the parameterized operation of primitive recursion immediately follows, which, together with the generalized composition of number-theoretic mappings and some basic number-theoretic mappings, is at the basis of the theory of primitive recursive mappings. Indeed, the set formed by gathering together the mappings involved in this theory is, within the hierarchy of the constructive number-theoretic mappings, one of the most fundamental types.
Although it is true that, e.g., Grassmann (1861), Peirce (1881), and Peano (1889), apparently recursively defined the basic arithmetical operations—sum, product, and exponentiation—their definitions were not in any way mathematically justified because these authors lacked a principle of definition by mathematical recursion and also, what is certainly more important, its corresponding proof. Even Dedekind in Gedanken über die Zahlen (Dugac 1976, p. 300), composed between 1872 and 1878, was fully aware of the fact that he did not yet have a correct proof of the principle of definition by mathematical recursion—in contrast to his conviction of the correctness of his proof of the principle of proof by mathematical induction—because he wrote:
Der Beweis der Richtigkeit der Beweismethode von n auf \(n+1\) ist richtig; dagegen ist der Beweis (Vollständigkeit) der Begriffserklärung durch die Methode von n auf \(n+1\) an dieser Stelle noch nich genügend; die Existenz (widerspruchsfrei) des Begriffs bleibt zweifelhaft. Dies wird erst möglich durch die Deutlichkeit durch die Betrachtung des Systems [n]!!!!!! Fundament. [The proof of the correctness of the method of proof from n to \(n+1\) is correct; in contrast, the proof (completeness) of the definition of concepts by the method from n to \(n+1\) is not yet sufficient at this point; the existence (free of contradictions) of the concept remains in doubt. This will become possible only by the distinctness, by the consideration of the system [n]!!!!!! Foundation.]
From this it follows that, for Dedekind, a recursive definition is definitely only admissible if it has been proved that such a definition unequivocally characterizes that which is intended to be defined with it. And by taking account of this fact cleanly and explicitly in the formulation and proof of his principle of definition by mathematical recursion, Dedekind (1888) made a substantial and invaluable contribution to the rigorous development of arithmetic as a science in its own right.
It is worth noting that Bertrand Russell in his discussion of Dedekind’s pamphlet in Chapter \(\mathrm {XXX}\)—entitled “Dedekind’s theory of number”—of Russell (1903), surprisingly, among other remarkable omissions, mentions neither Dedekind’s principle of definition by mathematical recursion nor its explicit use by Dedekind to obtain the basic arithmetic operations. Actually, Russell (1903, p. 245) wrote the following:
The fundamental ideas of the pamphlet in question are these: (1) the representation (Abbildung) of a system (21); (2) the notion of a chain (37); (3) the chain of an element [sic] (44); (4) the generalized form of mathematical induction (59); (5) the definition of a singly infinite system (71). From these five notions Dedekind deduces numbers and ordinary Arithmetic.
And, after explaining these notions and then mentioning that Dedekind proceeded to deduce the various properties of simply infinite systems, in particular, the principle of proof by mathematical induction, art. 80, to define the order relation between numbers, art. 89, and to state some of its properties, arts. 88, 90, Russell (1903, p. 247), somewhat rashly—taking into account what has been stated until now in this article—wrote: “From this point everything proceeds simply”, and “The only further point that seems important for our present purpose is the definition of cardinals”.
Before continuing with our exposition, we notice that Heck (2012) has been able to detect—concealed among the convoluted ideograms used by Frege (1966), which, by the way, is by no means a lesser merit—that Frege formally proved, in addition to (a generalized form of) the principle of proof by mathematical induction, the principle of definition by mathematical recursion. In this respect, it is interesting to recall that Frege (1879), after defining
(1) a procedure (Verfahren) as a binary relation,
(2) for a procedure f, when a property F is f-hereditary,
(3) the binary relation \(<_{f}\) of f-precedence (\(\equiv \) proper ancestral), and
(4) the binary relation \(\le _{f}\) as the reflexive closure of the relation \(<_{f}\) (\(\equiv \) ancestral), proves, among other theorems about the general theory of sequences (allgemeine Reihenlehre), that, given a procedure f and a property F, if F is f-hereditary, x has the property F and \(x<_{f}y\), then y also has the property F. And this theorem—interpreting x as 0 and f as the successor mapping—is the foundation of the (generalized) principle of proof by mathematical induction (generalized because f is a relation and not necessarily a mapping).
Moreover, to partially understand the reduced or almost nil impact of What are numbers and what are they good for? on the Dedekind’s contemporaries, we have to recall the qualified testimony of Hilbert (1931, p. 487) on the mathematicians’ opinion about the mentioned work:
Auf meiner ersten Station, in Berlin, hörte ich in allen mathematischen Kreisen bei jung und alt von der damals eben erschienenen Arbeit Dedekinds ,, Was sind und was sollen die Zahlen?“ sprechen — meist in gegnerischem Sinne. [On my first stop, in Berlin, I heard in all mathematical circles that everyone, young and old, talked about Dedekind’s essay “What are numbers and what are they good for?”, which had just then appeared—but mostly in an hostile sense.]
And, in this regard, we must point out that such hostility towards Dedekind’s essay came from the prevailing mathematical community at that time: that of the algorithmic mathematicians. On this matter, one has to take into account that when speaking about nineteenth-century mathematicians, they can be classified, in a broad sense, into two classes (not necessarily mutually exclusive): the one of the computational mathematicians and the one of the conceptual mathematicians. The first class, represented, inter alia, by Kronecker—a dominant figure in the mathematical panorama of the last third of the late nineteenth century—is essentially typified by upholding, to a greater or lesser degree, the following principles. Natural numbers are given, they are not in need of any foundation, and everything else must be constructed. This is substantiated, e.g., in the following dictum uttered by Kronecker in a talk at the 1886 meeting of the Berliner Naturforscher-Versammlung and quoted by Weber (1891, p. 19) in his obituary of Kronecker (who died in 1891):
Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk. [The good Lord made the integers, but all else is the work of man.]
For these people, only potentially infinite sets, decidable definitions, and constructive proofs of existence are admissible in mathematics. The second class, which includes, among others, to Dedekind, is characterized by the acceptance of actually infinite sets—completed infinite sets—by establishing natural and canonical definitions—not subject to any decidability constraints—by stating concise and accurate theorems—without necessarily requiring proofs of constructive character for those of existential type—and by setting up general theories—having models not necessarily pairwise isomorphic. And also by the strengthening of demonstrative exactitude, by a strong turn towards abstraction, and by the elimination of any appeal to intuition.
Before showing the implicit use made by Dedekind, in his proof of the principle of definition by mathematical recursion, of the concepts of an inductive cone from an inductive system of sets and of the inductive limit of an inductive system of sets—which until now, to the best of our knowledge, nobody has noticed—for completeness of exposition, we next recall these concepts.
An inductive system of sets is an ordered pair \((\mathbf {I},\mathcal {A})\) where \(\mathbf {I} = (I,\preccurlyeq )\) is an upward directed preordered set, and \(\mathcal {A} = ((A_{i})_{i\in I},(f_{i,i'})_{(i,i')\in \preccurlyeq })\) such that:
-
1.
\(\forall \,i\in I\), \(A_{i}\) is a set.
-
2.
\(\forall \,(i,i')\in \preccurlyeq \),
 .
. -
3.
\(\forall \,i\in I\), \(f_{i,i} = \mathrm {id}_{A_{i}}\).
-
4.
\(\forall \,i,i',i''\in I\), if \((i,i')\in \preccurlyeq \) and \((i',i'')\in \preccurlyeq \), then \(f_{i,i''} = f_{i',i''}\circ f_{i,i'}\).
The mappings  are called the transition mappings of the inductive system of sets \((\mathbf {I},\mathcal {A})\). We notice that \(\mathcal {A}\) is a covariant functor from \(\mathbf {C}(\mathbf {I})\), the category canonically associated with \(\mathbf {I}\), to \(\mathbf {Set}\), the category of sets (in a fixed Grothendieck universe \(\varvec{\mathcal {U}}\)) and mappings.
are called the transition mappings of the inductive system of sets \((\mathbf {I},\mathcal {A})\). We notice that \(\mathcal {A}\) is a covariant functor from \(\mathbf {C}(\mathbf {I})\), the category canonically associated with \(\mathbf {I}\), to \(\mathbf {Set}\), the category of sets (in a fixed Grothendieck universe \(\varvec{\mathcal {U}}\)) and mappings.
Let \((\mathbf {I},\mathcal {A})\) be an inductive system of sets. An inductive cone from \((\mathbf {I},\mathcal {A})\) is an ordered pair \((L,(f_{i})_{i\in I})\) where L is a set and, for every \(i\in I\),  , such that, for every \((i,i')\in \preccurlyeq \), \(f_{i} = f_{i'}\circ f_{i,i'}\). On the other hand, a morphism from \((L,(f_{i})_{i\in I})\) to another inductive cone \((L',(f'_{i})_{i\in I})\) from \((\mathbf {I},\mathcal {A})\) is a mapping h from L to \(L'\) such that, for every \(I\in I\), \(f'_{i} = h\circ f_{i}\). Then an inductive limit of \((\mathbf {I},\mathcal {A})\) is an initial inductive cone from \((\mathbf {I},\mathcal {A})\), i.e., an inductive cone \((L,(f_{i})_{i\in I})\) from \((\mathbf {I},\mathcal {A})\) such that, for every inductive cone \((L',(f'_{i})_{i\in I})\) from \((\mathbf {I},\mathcal {A})\), there exists a unique morphism from \((L,(f_{i})_{i\in I})\) to \((L',(f'_{i})_{i\in I})\). If \((L,(f_{i})_{i\in I})\) is an inductive limit of \((\mathbf {I},\mathcal {A})\), which is unique up to isomorphism, then \(\varinjlim (\mathbf {I},\mathcal {A})\) stands for L.
, such that, for every \((i,i')\in \preccurlyeq \), \(f_{i} = f_{i'}\circ f_{i,i'}\). On the other hand, a morphism from \((L,(f_{i})_{i\in I})\) to another inductive cone \((L',(f'_{i})_{i\in I})\) from \((\mathbf {I},\mathcal {A})\) is a mapping h from L to \(L'\) such that, for every \(I\in I\), \(f'_{i} = h\circ f_{i}\). Then an inductive limit of \((\mathbf {I},\mathcal {A})\) is an initial inductive cone from \((\mathbf {I},\mathcal {A})\), i.e., an inductive cone \((L,(f_{i})_{i\in I})\) from \((\mathbf {I},\mathcal {A})\) such that, for every inductive cone \((L',(f'_{i})_{i\in I})\) from \((\mathbf {I},\mathcal {A})\), there exists a unique morphism from \((L,(f_{i})_{i\in I})\) to \((L',(f'_{i})_{i\in I})\). If \((L,(f_{i})_{i\in I})\) is an inductive limit of \((\mathbf {I},\mathcal {A})\), which is unique up to isomorphism, then \(\varinjlim (\mathbf {I},\mathcal {A})\) stands for L.
Remark 4
The set \(\varinjlim (\mathbf {I},\mathcal {A})\) is the quotient set \(\coprod _{i\in I}A_{i}/R_{(\mathbf {I},\mathcal {A})}\) where \(R_{(\mathbf {I},\mathcal {A})}\) is the smallest equivalence relation on \(\coprod _{i\in I}A_{i} (= \bigcup _{i\in I}(A_{i}\times \{i\}))\), the coproduct of the family of sets \((A_{i})_{i\in I}\), that contains all ordered pairs in \(\coprod _{i\in I}A_{i}\) of the form \(((x,i),(f_{i,i'}(x),i')), \text { where }x\in A_{i} \text { and } (i,i')\in \preccurlyeq \). And, for every \(i\in I\), \(f_{i}\) is the composition of \(\mathrm {in}_{i}\), the canonical embedding of \(A_{i}\) into \(\coprod _{i\in I}A_{i}\), and \(\mathrm {pr}_{R_{(\mathbf {I},\mathcal {A})}}\), the canonical projection from \(\coprod _{i\in I}A_{i}\) to \(\coprod _{i\in I}A_{i}/R_{(\mathbf {I},\mathcal {A})}\).
We now try to illuminate, as far as we can, this last technical concept. The inductive limit \(\varinjlim (\mathbf {I},\mathcal {A})\)—along with the mappings \(f_{i}\) from \(A_{i}\) to \(\varinjlim (\mathbf {I},\mathcal {A})\)—of an inductive system \((\mathbf {I},\mathcal {A})\) is the optimal way of classifying the sets \(A_{i}\) (after putting them together but not mixing them) that occur in the net of interactions between them given by the transition mappings  of the inductive system \((\mathbf {I},\mathcal {A})\). As Aristotle (1984, Z 17, 1041b11–1042a2) wrote:
of the inductive system \((\mathbf {I},\mathcal {A})\). As Aristotle (1984, Z 17, 1041b11–1042a2) wrote:
As regards that which is compounded out of something so that the whole is one—not like a heap, however, but like a syllable,—the syllable is not its elements, ba is not the same as b and a, nor is flesh fire and earth; for when they are dissolved the wholes, i.e. the flesh and the syllable, no longer exist, but the elements of the syllable exist, and so do fire and earth. The syllable, then, is something—not only its elements (the vowel and the consonant) but also something else; and the flesh is not only fire and earth or the hot and the cold, but also something else.
We next recall the statements, but not the proofs, of Dedekind’s theorems contained in arts. 125, and 126 (written in slanted typeface) of \(\S \, 9\) of Dedekind (1888)—as translated into English by Ewald (1996, pp. 816–818)—to make our paper as self-contained as possible. And working directly on them we will attempt to show that the concepts of an inductive cone from an inductive system of sets and of the inductive limit of an inductive system of sets are implicit in his proof of the principle of definition by mathematical recursion.
But before doing that we make the following, obvious, observation. We consider, on the one hand, the well-ordered set \(\mathbf {N} = (\mathbb {N},\le )\) and, on the other hand, the ordered pair
where, for every \(n\in \mathbb {N}-1\), n is \(\{0,\ldots ,n-1\}\) and \(\mathrm {in}_{n,\mathrm {sc}(n)}\) the canonical embedding of n into \(\mathrm {sc}(n) = n\cup \{n\}\). Then the pair \((\mathbf {N},\mathcal {N})\), where \(\mathcal {N}\) is the ordered pair \(\left( (n)_{n\in \mathbb {N}-1},(\mathrm {in}_{m,n})_{\begin{array}{c} m, n\in \mathbb {N}-1\\ m\le n \end{array}}\right) \) in which, for every \(m,n\in \mathbb {N}-1\) with \(m\le n\), we let \(\mathrm {in}_{m,n}\) stand for:
is an inductive system of sets.
Dedekind’s art. 125 says the following.
125. Theorem. Given an arbitrary (similar or dissimilar) mapping \(\theta \) of a system \({\varOmega }\) into itself, and given a determinate element \(\omega \) in \({\varOmega }\), then to every number n there corresponds one and only one mapping \(\psi _{n}\) of the associated number-system \(Z_{n}\) explained in (98), which satisfies the conditionsFootnote 2
\(\mathrm {I}\). \(\psi _{n}(Z_{n}) \prec {\varOmega }\),
\(\,\,\mathrm {II}.\) \(\psi _{n}(1) = \omega \),
\(\mathrm {III}\). \(\psi _{n}(t') = \theta \psi _{n}(t)\), if \(t<n\), where the symbol \(\theta \psi _{n}\) has the meaning given in (25).
In the sequel, \(\mathbb {N} = \{0, 1, \ldots \}\) and \(n = \{0, \ldots , n-1\}\) stand for \(N = \{1, 2, \ldots \}\) and \(Z_{n} = \{1, \ldots , n\}\), respectively. And, in consequence, all involved mappings are redefined taking care of such a convention. This is an inessential variation with regard to Dedekind’s notation, but it is in accordance with current standards in set theory.
In \(\text {art.}\, 125\), Dedekind, from a triple \(({\varOmega },\theta ,\omega )\), showed, by means of the principle of proof by mathematical induction, that there exists a family of mappings \((\psi _{n})_{n\in \mathbb {N}-1}\) in \(\prod _{n\in \mathbb {N}-1}\mathrm {Hom}(n,{\varOmega })\) such that, for every \(n\in \mathbb {N}-1\), the mapping \(\psi _{n}\) from n to \({\varOmega }\) satisfies the following conditions:
-
1.
\(\psi _{n}(0) = \omega \), and
-
2.
for every \(i\in \{0,\ldots ,n-2\}\), \(\psi _{n}(\mathrm {sc}(i)) = \theta (\psi _{n}(i)) = \theta ^{\mathrm {sc}(i)}(\omega )\).
Consequently, for every \(i\in \{0,\ldots ,n-2\}\), we have that:
From this it immediately follows that, for every \(n\in \mathbb {N}-1\) and every \(i\in n\), we have that \(\psi _{n}(i) = \psi _{\mathrm {sc}(n)}(i)\), i.e., that \(\psi _{\mathrm {sc}(n)}\!\!\upharpoonright _{n}\), the restriction of the mapping  to n, is equal to the mapping \(\psi _{n}\) from n to \({\varOmega }\).
to n, is equal to the mapping \(\psi _{n}\) from n to \({\varOmega }\).
We notice that Dedekind did not restrict himself here to simply proving that \(\prod _{n\in \mathbb {N}-1}\mathrm {Hom}(n,{\varOmega })\) is not empty (which is obvious, since, e.g., the family of mappings \((\kappa _{n})_{n\in \mathbb {N}-1}\), where, for every \(n\in \mathbb {N}-1\), \(\kappa _{n}\) is the mapping from n to \({\varOmega }\) that, to every \(i\in n\), assigns \(\omega \), belongs to it). What he did was to obtain, explicitly—in this case by means of the principle of proof by mathematical induction—a family of mappings \((\psi _{n})_{n\in \mathbb {N}-1}\) in \(\prod _{n\in \mathbb {N}-1}\mathrm {Hom}(n,{\varOmega })\), by constructing each of its components, \(\psi _{n}\), and all in such a way that each of them satisfies some specific conditions and, moreover, are such that, for every \(n\in \mathbb {N}-1\), \(\psi _{\mathrm {sc}(n)}\!\!\upharpoonright _{n} = \psi _{n}\).
As we will see below, the above \(\text {art.}\, 125\) can be interpreted as saying that in it Dedekind has defined an inductive cone from the inductive system of sets \((\mathbf {N},\mathcal {N})\) defined above.
Dedekind’s art. 126 says the following.
126. Theorem of definition by induction. Given an arbitrary mapping \(\theta \) (similar or dissimilar) of a system \({\varOmega }\) into itself, and given a determinate element \(\omega \) in \({\varOmega }\), then there exists one and only one mapping \(\psi \) of the number-series N which satisfies the conditions
\(\mathrm {I}\). \(\psi (N) \prec {\varOmega }\),
\(\,\,\mathrm {II}.\) \(\psi (1)=\omega \),
\(\mathrm {III}\). \(\psi (n')=\theta \psi (n)\), where n represents every number.
In \(\text {art.}\, 126\), Dedekind, from a triple \(({\varOmega },\theta ,\omega )\) and the family of mappings \((\psi _{n})_{n\in \mathbb {N}-1}\) in \(\prod _{n\in \mathbb {N}-1}\mathrm {Hom}(n,{\varOmega })\) obtained in \(\text {art.}\, 125\), showed that there exists a unique mapping \(\psi \) from \(\mathbb {N}\) to \({\varOmega }\) defined, for every \(i\in \mathbb {N}\), as \(\psi (i) = \psi _{\mathrm {sc}(i)}(i)\), and that it fulfils the following conditions:
-
1.
\(\psi (0) = \omega \), and
-
2.
for every \(n\in \mathbb {N}\), \(\psi (\mathrm {sc}(n)) = \theta (\psi (n))\).
In fact, \(\psi (0) = \omega \) because \(\psi (0) = \psi _{\mathrm {sc}(0)}(0) = \omega \), by the definition of \(\psi \) and of \(\psi _{\mathrm {sc}(0)}\). Moreover, for every \(n\in \mathbb {N}\), \(\psi (\mathrm {sc}(n)) = \theta (\psi (n))\), because
by the definition of \(\psi \) and of \(\psi _{\mathrm {sc}({\mathrm {sc}(n)})}\).
On the other hand, from the fact that, for every \(i\in \mathbb {N}\), we have that \(\psi (i) = \psi _{\mathrm {sc}(i)}(i)\), it follows that: \(\psi (0) = \psi _{1}(0)\) (from which we get that \(\psi \circ \mathrm {in}_{1,\mathbb {N}} = \psi _{1}\), where \(\mathrm {in}_{1,\mathbb {N}}\) is the canonical embedding of 1 into \(\mathbb {N}\)); \(\psi (1) = \psi _{2}(1)\) (from which we get, since also \(\psi _{2}\!\!\upharpoonright _{1} = \psi _{1}\), that \(\psi \circ \mathrm {in}_{2,\mathbb {N}} = \psi _{2}\), where \(\mathrm {in}_{2,\mathbb {N}}\) is the canonical embedding of 2 into \(\mathbb {N}\)), etc. So, by the principle of proof by mathematical induction, for every \(n\in \mathbb {N}-1\), we have that \(\psi \circ \mathrm {in}_{n,\mathbb {N}} = \psi _{n}\), where, for every \(n\in \mathbb {N}-1\), \(\mathrm {in}_{n,\mathbb {N}}\) is the canonical embedding of n into \(\mathbb {N}\). Conversely, for each  , if, for every \(n\in \mathbb {N}-1\), we have that \(\psi '\circ \mathrm {in}_{n,\mathbb {N}} = \psi _{n}\), then \(\psi '\), necessarily, must be such that, for every \(i\in \mathbb {N}\), \(\psi '(i) = \psi _{\mathrm {sc}(i)}(i)\).
, if, for every \(n\in \mathbb {N}-1\), we have that \(\psi '\circ \mathrm {in}_{n,\mathbb {N}} = \psi _{n}\), then \(\psi '\), necessarily, must be such that, for every \(i\in \mathbb {N}\), \(\psi '(i) = \psi _{\mathrm {sc}(i)}(i)\).
We finally set out what is implicit in Dedekind’s proof of the principle of definition by mathematical recursion.
For the family of mappings \((\psi _{n})_{n\in \mathbb {N}-1}\) in \(\text {art.}\, 125\), it happens that, for every \(n\in \mathbb {N}-1\), \(\psi _{n} = \psi _{\mathrm {sc}(n)}\circ \mathrm {in}_{n,\mathrm {sc}(n)}\), i.e., that, for every \(n\in \mathbb {N}-1\), \(\psi _{\mathrm {sc}(n)}\!\!\upharpoonright _{n} = \psi _{n}\). Hence, for the family of mappings \((\psi _{n})_{n\in \mathbb {N}-1}\), it holds, by the principle of proof by mathematical induction, that, for every \(m,n\in \mathbb {N}-1\) with \(m\le n\), \(\psi _{m} = \psi _{n}\circ \mathrm {in}_{m,n}\), i.e., that, for every \(m,n\in \mathbb {N}-1\) with \(m\le n\), \(\psi _{n}\!\!\upharpoonright _{m} = \psi _{m}\). In other words, that \(({\varOmega },(\psi _{n})_{n\in \mathbb {N}-1})\) is an inductive cone from the inductive system \((\mathbf {N},\mathcal {N})\).
Afterwards, in \(\text {art.}\, 126\), Dedekind, starting from a triple \(({\varOmega },\theta ,\omega )\) and the family of mappings \((\psi _{n})_{n\in \mathbb {N}-1}\) in \(\prod _{n\in \mathbb {N}-1}\mathrm {Hom}(n,{\varOmega })\), proved, as we have seen above, that there exists a unique mapping \(\psi \) from \(\mathbb {N}\) to \({\varOmega }\) such that, for every \(n\in \mathbb {N}-1\), \(\psi _{n} = \psi \circ \mathrm {in}_{n,\mathbb {N}}\), i.e., that there exists a unique morphism from the inductive cone \((\mathbb {N},(\mathrm {in}_{n,\mathbb {N}})_{n\in \mathbb {N}-1})\) to the inductive cone \(({\varOmega },(\psi _{n})_{n\in \mathbb {N}-1})\). In other words, that the inductive cone \((\mathbb {N},(\mathrm {in}_{n,\mathbb {N}})_{n\in \mathbb {N}-1})\) from \((\mathbf {N},\mathcal {N})\) is a solution of a universal problem.
Remark 5
As it is well known, Dedekind’s principle of definition by mathematical recursion is a particular instance, in the field of universal algebra, of the principle of definition by algebraic recursion. Recall that, for an algebraic signature \(\varvec{{\varSigma }}\) and the category \(\mathbf {Alg}(\varvec{{\varSigma }})\), of \(\varvec{{\varSigma }}\)-algebras and homomorphisms between \(\varvec{{\varSigma }}\)-algebras, the last mentioned principle states that, for a set X (of variables), a \(\varvec{{\varSigma }}\)-algebra \(\mathbf {A}\), and a mapping f from X to A, the underlying set of \(\mathbf {A}\), there exists a unique homomorphism \(f^{\sharp }\) from \(\mathbf {T}_{\varvec{{\varSigma }}}(X)\), the free \(\varvec{{\varSigma }}\)-algebra on X, to \(\mathbf {A}\) such that \(f = f^{\sharp }\circ \eta _{X}\), where \(\eta _{X}\) is the canonical mapping from X to \(\mathrm {T}_{\varvec{{\varSigma }}}(X)\), the underlying set of \(\mathbf {T}_{\varvec{{\varSigma }}}(X)\), i.e., the value at X of the unit of the adjunction from \(\mathbf {Set}\) to \(\mathbf {Alg}(\varvec{{\varSigma }})\). Also the principle of proof by mathematical induction, stated by Dedekind for mono-unary algebras, is a particular case of the principle of proof by algebraic induction. Therefore, we can say that Dedekind was a precursor of both principles in the field of universal algebra.
5 Dedekind and Birkhoff’s works in the 1930s on universal algebra and lattice theory
In this section, we consider, on the one hand, to what degree Garrett Birkhoff was aware of the structural approach to algebra—to a large extent resulting from the algebraic work of Dedekind—as carried out by Noether (herself inspired by Dedekind), by Noether’s algebraic school (Götingen), and by Emil Artin (Hamburg) in the 1930s, and, therefore, if he had an indirect influence of Dedekind, and, on the other hand, if the above-mentioned booklet by Dedekind, because of its highly algebraic contents, had any direct influence on Birkhoff in his work on universal algebra.
It is apparent that classical universal algebra, as a mathematical discipline and as we know it today, was not founded by Dedekind; it was founded by Birkhoff and it came into being in Birkhoff (1935). We notice, in passing, that, in \(\S \, 2\) of the article just mentioned, Birkhoff defined an abstract algebra as a pair \((\mathfrak {C},F)\), where \(\mathfrak {C}\) is a set and F a set of operations, such that each operation \(f_{i}\in F\) is a mapping from a set \(\mathfrak {D}_{i}\) of sequences of elements of \(\mathfrak {C}\), to be called the “proper domain” of \(f_{i}\), to \(\mathfrak {C}\). Therefore each \(f_{i}\) is a mapping from a subset \(\mathfrak {D}_{i}\) of \(\bigcup _{\alpha \in \mathcal {O}_{i}}\mathfrak {C}^{\alpha }\), where \(\mathcal {O}_{i}\) is a set of, not necessarily finite, ordinal numbers, to \(\mathfrak {C}\). Hence the operations \(f_{i}\) are, in Birkhoff’s terminology, not “uniform”, i.e., its arguments do not have a fixed length, a generalization currently abandoned (even by Birkhoff himself, who, from \(\S \, 8\) onwards of the above-mentioned article, considered exclusively “uniform” operations, i.e., operations \(f_{i}\) such that the proper domain of \(f_{i}\) is \(\mathfrak {C}^{k_{i}}\), for some, possibly transfinite, ordinal \(k_{i}\)).
In order to carry out the foregoing it seems fitting to begin by recalling what Birkhoff said in Albers and Alexanderson (2008, p. 2) about his work on lattice theory (Birkhoff 1933) and his unawareness of Dedekind’s work on the same subject:
My ideas about lattices developed gradually. Philip Hall [though officially supervised by R. H. Fowler, Birkhoff, who spent 1932–33 in Cambridge, UK, was Hall’s first research student, we add] did not know of the important work of Dedekind on “Dualgruppen,” although he did call my attention to Fritz Klein’s related papers on “Verbände.” It was my father who, when he told Ore at Yale about what I was doing some time in 1933, found out from Ore that my lattices coincided with Dedekind’s Dualgruppen. Ore had edited Dedekind’s collected works [together with Robert Fricke and Emmy Noether in 1930–32, we add]. I was lucky to have gone beyond Dedekind before I discovered his work. It would have been quite discouraging if I had discovered all my results anticipated by Dedekind.
Besides, we also have to suggest an attentive reading of Birkhoff (1934), which was written after Ore called it to his attention to the close relation between his aforementioned article and two earlier articles of Dedekind on “Dualgruppen”: Über Zerlegungen von Zahlen durch ihre größten gemeinsamen Teiler (1897) and Über die von drei Moduln erzeugte Dualgruppe (1900), reprinted as articles \(\mathrm {XXVIII}\) (pp. 103–147) and \(\mathrm {XXX}\) (pp. 236–271), respectively, in the second volume of Dedekind’s Gessammelte mathematische Werke (published in 1931).
From the above quotation by Birkhoff it plainly follows that after having published his ideas about lattices, he knew, at least since 1933, the articles by Dedekind just cited. Therefore, in principle, it is reasonable to think that he might have been also acquainted with Dedekind’s masterpiece Was sind und was sollen die Zahlen?, whose sixth edition (1930) was reprinted in 1932 (Dedekind, 1930-1932, Vol. III, art. LI, pp. 335–390). However, as we shall see below, at least one sentence included in Birkhoff (1935) certainly points to the fact that Was sind und was sollen die Zahlen? was not known by him at that time, concretely from 1933 until 1935.
Birkhoff actually went far beyond the mono-unary algebras and the simply infinite systems of Dedekind in his seminal paper: On the structure of abstract algebras (Birkhoff 1935). Certainly, the principal results contained in the above-mentioned paper—for instance, as highlighted by the author himself (Birkhoff 1987, p. 112): “...a general construction of ‘free’ algebras having any number of ‘generators’, given any set of ‘operations’ and ‘identities.’ Deepest and most original was the so called \(\mathrm {HSP}\)-Theorem”—were not anticipated by Dedekind. Furthermore, Birkhoff was, as he said of himself (Birkhoff 1987, p. V), “a self-taught algebraist”, on the basis of his in-depth knowledge of the algebraic works, of among others, Noether and the members of her school, set forth in detail in van der Waerden’s two-volume textbook on abstract algebra Moderne Algebra (first ed., 1930–1931). We can also point out that in July 1933 Birkhoff visited Munich and met Constantin Carathéodory, who advised him to read Andreas Speiser’s Gruppentheorie and van der Waerden’s Moderne Algebra. Therefore, Birkhoff was aware of the abstract structural approach to algebra through van der Waerden’s treatise, and so one can say that he was indirectly influenced of Dedekind.
The sentence alluded to above (Birkhoff 1935, p. 434) reads as follows: “Only recently the object of special research has been what I consider to be a dual notion, that of the ‘lattice’ of the subalgebras of an algebra”. We consider this enough evidence to justify the conclusion that Dedekind (1888) was not known by Birkhoff from 1933 until 1935. To this we add, for sure, that Birkhoff never cites Dedekind (1888) in his papers on universal algebra and history of algebra. And exactly the same can be said of MacLane and Birkhoff (1988) since, on p. 15 of such an excellent textbook, they wrote: “Formally, we shall describe \(\mathbf {N}\) by axioms essentially due to G. Peano ...Peano Postulates ...”, and such postulates, up to definitional equivalence, are—as has already been stated in the comments on \(\S \, 6\) contained in Sect. 3—the conditions set out in \(\text {art.}\, 71\) of Dedekind (1888). Therefore Dedekind (1888) did not have any direct influence on Birkhoff in his work on universal algebra. Although, with regard to the first quotation contained in this paragraph, in Dedekind (1888) one can find, as pointed out in Sect. 3, an investigation of the subalgebras of a mono-unary algebra.
We finish this section by saying that some of the seeds planted by Dedekind in the last quarter of the nineteenth century began, finally, to germinate and fructify in a wonderful way with Birkhoff in the 1930s.
Change history
07 February 2018
The original version of this article unfortunately contained a mistake: The equation on page 34 was incorrect. The corrected equation is given below.
Notes
We refer the reader to Sect. 3 for the equivalence between the Dedekind–Peano algebra axioms and Lawvere’s Axiom 3 (Lawvere 1964, p. 1507). In this respect, it seems pertinent to point that the aforementioned principle laid the groundwork, through the derived principle of primitive recursion with parameters and the generalized composition of mappings, for Kurt Gödel to obtain, at the beginning of the 1930s, the set of all primitive recursive mappings in his work on the incompleteness of certain mathematical theories (Gödel 1931).
For clearness here and in the following theorem (126) I have especially mentioned condition \(\mathrm {I}\), although properly it is a consequence of \(\mathrm {II}\) and \(\mathrm {III}\).
References
Albers, D.J., and G.L. Alexanderson (eds.). 2008. Mathematical people, 2nd ed. Wellesley, MA: A. K. Peters Ltd.
Alexandroff, P. 1928. Untersuchungen über Gestalt und Lage abgeschlossneser Mengen. Annals of Mathmatics 2 (30): 101–187.
Aristotle, 1984. The complete works of Aristotle. (The Revised Oxford Translation), vol. 2, ed. J. Barnes. Princeton, NJ: Princeton University Press.
Baer, R. 1937. Abelian fields and duality of Abelian groups. American Journal of Mathematics 59: 869–888.
Birkhoff, G. 1933. On the combination of subalgebras. Proceedings of the Cambridge Philosophical Society 29: 441–464.
Birkhoff, G. 1934. Note on the paper “On the combination of subalgebras.”. Proceedings of the Cambridge Philosophical Society 30: 200.
Birkhoff, G. 1935. On the structure of abstract algebras. Proceedings of the Cambridge Philosophical Society 31: 433–454.
Birkhoff, G. 1987. Selected papers on algebra and topology. Boston: Birkhäuser Boston Inc.
Büchi, J.R. 1989. Finite automata, their algebras and grammars. Towards a theory of formal expressions. Edited and with a preface by Dirk Siefkes. New York: Springer-Verlag.
Cantor, G. 1955. Contributions to the founding of the theory of transfinite numbers. Translated, and provided with an introduction and notes, by Philip E. B. Jourdain. New York: Dover Publications, Inc.
Dedekind, R. 1888. Was sind und was sollen die Zahlen? Braunschweig: Friedr. Vieweg & Sohn. (English trans: R. Dedekind). Essays on the theory of numbers. I: Continuity and irrational numbers. II: The nature and meaning of numbers. (Authorized trans: Wooster Woodruff Beman), Dover, New York, 1963. Beman’s translation has been extensively revised by William Ewald in (Ewald, 1996, pp. 787–833).
Dedekind, R. 1930–1932. Gessammelte mathematische Werke. Herausgegeben von Robert Fricke, Emmy Noether, Øystein Ore. Vols. I–III. Braunschweig: Friedr. Vieweg & Sohn.
de Vries, J. 1993. Elements of topological dynamics. Mathematics and its applications, vol. 257. Dordrecht: Kluwer Academic Publishers Group.
Dieudonné, J. 1989. A History of algebraic and differential topology 1900–1960. Boston, Basel: Birkhäuser.
Dugac, P. 1976. Richard Dedekind et les fondements des mathématiques (avec de nombreux textes inédites). Préface de Jean Dieudonné. Collection des Travaux de l’Académie Internationale d’Histoire des Sciences No. 24. L’Histoire des Sciences, Textes et Études. Paris: Librairie Philosophique J. Vrin.
Ewald, W. 1996. From Kant to Hilbert: A source book in the foundations of mathematics. Vol. II. Ed. William Ewald. Oxford Science Publications. New York: The Clarendon Press, Oxford University Press.
Frege, G. 1879. Begriffsschrift, Eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle: Verlag von L. Nebert.
Frege, G. 1966. Grundgesetze der Arithmetik. Band I, II. Hildesheim: Georg Olms Verlagsbuchhandlung.
Freudenthal, H. 1937. Entwicklungen von Räumen und ihren Gruppen. Compositio Mathematica 4: 145–234.
Gödel, K. 1931. Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I. Monatshefte für Mathematik und Physik 38: 173–198.
Gray, J. 2000. Linear differential equations and group theory from Riemann to Poincaré, 2nd ed. Boston: Birkhäuser Boston Inc.
Grassmann, H. 1861. Lehrbuch der Arithmetik für höhere Lehranstalten. Berlin: Verlag von T. C. F. Enslin (Adolph Enslin).
Grothendieck, A. 1971. Revêtements étales et groupe fondamental (SGA1), éd. par A. Grothendieck, Lecture notes in mathematics, No. 224. Berlin, New York: Springer.
Heck Jr., R.G. 2012. Reading Frege’s Grundgesetze. Oxford: The Clarendon Press, Oxford University Press.
Herbrand, J. 1933. Théorie arithmétique des corps de nombres de degré infini II. Mathematische Annalen 108: 699–717.
Hilbert, D. 1931. Die Grundlegun der elementaren Zahlenlehre. Mathematische Annalen 104: 485–494.
Hocking, J.G., and G.S. Young. 1988. Topology, 2nd ed. New York: Dover Publications Inc.
Krömer, R. 2010. From Cantor to Sheaves: The development of the concepts of direct and inverse limits—A case study on shifts in mathematical methodology in the prehistory of category theory. In Symposium on the philosophy of the logic of sheaves, October 19–21. 2010. Universidad del Valle, Cali, Colombia.
Kurosh, A.G. 1935. Kombinatorischer Aufbau der bikompakten topologischen Räume. Compositio Mathematica 2: 471–476.
Lawvere, F.W. 1964. An elementary theory of the category of sets. Proceedings of National Academy of Sciences USA 52: 1506–1511.
Lipschitz, R. 1986. Briefwechsel mit Cantor, Dedekind, Helmholtz, Kronecker, Weierstrass und anderen. Ed. Winfried Scharlau. Dokumente zur Geschichte der Mathematik, 2. Freiburg: Friedr. Vieweg & Sohn, Braunschweig; Deutsche Mathematiker Vereinigung.
MacLane, S. 1970. Hamiltonian mechanics and geometry. American Mathematical Monthly 77: 570–586.
MacLane, S., and G. Birkhoff. 1988. Algebra, 3rd ed. New York: Chelsea Publishing Co.
Manes, E.G. 1976. Algebraic theories, vol. 26., Graduate texts in mathematics New York, Heidelberg: Springer.
Manes, E.G., and M.A. Arbib. 1986. Algebraic approaches to program semantics., Texts and monographs in computer science, AKM series in theoretical computer science New York: Springer.
Minkowski, H. 1905. Peter Gustav Lejeune Dirichlet und seine Bedeutung für die heutige Mathematik. Jahresber. Deutsch. Math.-Verein. 14: 149–163.
Peano, I. 1889. Arithmetices principia, nova methodo exposita. Turin: Fratres Bocca. (English trans: G. Peano). The principles of arithmetic, presented by a new method. (Trans: Jean van Heijenoort in van Heijenoort) (1967, pp. 83–97).
Peirce, C.S. 1881. On the logic of number. American Journal of Mathematics 4: 85–95.
Pontrjagin, L. 1931. Über den algebraischen Inhalt topologischer Dualitätssätze. Mathematische Annalen 105: 165–205.
Pontrjagin, L. 1934. Sur les groupes topologiques compacts et le cinquième problème de Hilbert. Comptes rendus de l’Académie des Sciences Paris 198: 238–240.
Raussen, M., and Chr Skau. 2004. Interview with Michael Atiyah and Isadore Singer. Newsletter of the European Mathematical Society 53: 24–30.
Russell, B. 1903. The principles of mathematics, vol. 1. Cambridge: Cambridge University Press.
Sancho Guimerá, J.B. 1959. Teoría de cuerpos algebraicos con ley de composición conmutativa. Revista Matemática Hispano-Americana, \(4.^{a}\) Serie 19: 18–39.
Smith, H.J.S. 1875. On the integration of discontinuous functions. Proceedings of the London Mathematical Society 6: 140–153.
van der Waerden, B.L. 1975. On the sources of my book Moderne Algebra. Historia Mathematica 2: 31–40.
van Heijenoort, J. (ed.). 1967. From Frege to Gödel. A source book in mathematical logic, 1879–1931. Cambridge, MA: Harvard University Press.
Weber, H. 1891/92. Leopold Kronecker. Jahresber. Deutsch. Math.-Verein 2: 5–31.
Weil, A. 1975. L’intégration dans les groupes topologiques et ses applications. Hermann: Deuxième édition.
Zermelo, E. 1967. A new proof of the possibility of a well-ordering. In From Frege to Gödel. A source book in mathematical logic, 1879–1931, ed. J. van Heijenoort, 183–198. Cambridge, MA: Harvard University Press.
Zermelo, E. 2010. Ernst Zermelo: Collected Works/Gesammelte Werke. Vol. I/Band I. Set Theory, Miscellanea/Mengenlehre, Varia. Ed. Heinz-Dieter Ebbinghaus, Craig G. Fraser and Akihiro Kanamori. Schriften der Mathematisch-Naturwissenschaftlichen Klasse der Heidelberger Akademie der Wissenschaften [Publications of the Mathematics and Natural Sciences Section of Heidelberg Academy of Sciences], 21. Berlin: Springer.
Acknowledgements
We would like to thank all who helped us by reading parts of the manuscript and suggesting mathematical improvements: Enric Cosme, Emily Riehl, Roberto Rubio, Sergiu Rudeanu, and Rafael Sivera. Our thanks are further due to our dear friend José García Roca—example of intelligence, goodness, and integrity—for correcting the English and suggesting improvements. And also for his tireless encouragement and invaluable continued moral support. Moreover, we are greatly indebted to the reviewer for his helpful comments and important stylistic suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jeremy Gray.
The original version of this article was revised: The equation on page 34 was incorrect. The equation was corrected in the article.
Appendix A: A many-sorted algebraic model of the theory of primitive recursive mappings
Appendix A: A many-sorted algebraic model of the theory of primitive recursive mappings
We next provide—in the algebraic spirit of Dedekind—a new model, based on many-sorted universal algebra, of the theory of primitive recursive mappings which will allow us to diagrammatically prove that the three basic mathematical operations, addition, multiplication, and exponentiation, defined by Dedekind in \(\S \S \) 11–13 of Dedekind (1888), are primitive recursive. We remark that the just-mentioned many-sorted algebraic model, appropriately modified, can be used to supply many-sorted algebraic models of the theories of general recursive mappings and of recursive partial mappings. Moreover, the subalgebra generating operators associated with these models make the notion of relative recursiveness, in each case, natural.
Since the set of all primitive recursive mappings will be the union of the underlying many-sorted set of the smallest many-sorted subalgebra of a convenient many-sorted algebra, we begin by defining the many-sorted signature of the many-sorted algebra at issue. Note that in what follows \(\mathbb {N}^{\star }\) stands for the underlying set of the free monoid on \(\mathbb {N}\), that \(\curlywedge \) is the binary operation of concatenation on \(\mathbb {N}^{\star }\), and that \(\lambda \) denotes the empty word on \(\mathbb {N}\). Moreover, given sets A, B, and C, and mappings  and
and  , we denote by \(\left<f,g\right>\) the unique mapping from C to \(A\times B\) such that \(\mathrm {pr}_{A}\circ \left<f,g\right> = f\) and \(\mathrm {pr}_{B}\circ \left<f,g\right> = g\), where \(\mathrm {pr}_{A}\) is the canonical projection from \(A\times B\) to A and \(\mathrm {pr}_{B}\) the canonical projection from \(A\times B\) to B.
, we denote by \(\left<f,g\right>\) the unique mapping from C to \(A\times B\) such that \(\mathrm {pr}_{A}\circ \left<f,g\right> = f\) and \(\mathrm {pr}_{B}\circ \left<f,g\right> = g\), where \(\mathrm {pr}_{A}\) is the canonical projection from \(A\times B\) to A and \(\mathrm {pr}_{B}\) the canonical projection from \(A\times B\) to B.
Definition
We denote by \(\varvec{{\varSigma }}^{\mathrm {pr}}\) the \(\mathbb {N}\)-sorted signature, for the primitive recursive mappings, whose (w, n)-th coordinate, where \((w,n)\in \mathbb {N}^{\star }\times \mathbb {N}\), is defined as follows:
Definition
We denote by  the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra whose underlying \(\mathbb {N}\)-sorted set,
the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra whose underlying \(\mathbb {N}\)-sorted set,  , is \((\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))_{n\in \mathbb {N}}\), so its n-th coordinate is the set of all mappings from \(\mathbb {N}^{n}\) to \(\mathbb {N}\), and where the structural operations are the following:
, is \((\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))_{n\in \mathbb {N}}\), so its n-th coordinate is the set of all mappings from \(\mathbb {N}^{n}\) to \(\mathbb {N}\), and where the structural operations are the following:
-
1.
\(\kappa _{0,0}\), the 0-ary constant mapping determined by 0, which is the mapping from \(\mathbb {N}^{0}\) to \(\mathbb {N}\) that sends the unique element of \(\mathbb {N}^{0}\) to 0.
-
2.
\(\mathrm {sc}\), the successor mapping.
-
3.
\(\mathrm {pr}_{1,0}\), the identity mapping at \(\mathbb {N}\).
-
4.
For every \(n\ge 2\) and every \(i\in n\), \(\mathrm {pr}_{n,i}\), the i-th canonical projection from \(\mathbb {N}^{n}\) to \(\mathbb {N}\).
-
5.
For every \(m\in \mathbb {N}-1\) and every \(n\in \mathbb {N}\), \({\varOmega }_{\mathrm {C}}^{m,n}\), the operator of (generalized) composition of arity \((m)\curlywedge (n\mid i\in m)\) and co-arity n, which is the mapping from \(\mathrm {Hom}(\mathbb {N}^{m},\mathbb {N})\times (\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))^{m}\) to \(\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) that sends a pair \((f,(g_{i})_{i\in m})\) in \(\mathrm {Hom}(\mathbb {N}^{m},\mathbb {N})\times (\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))^{m}\) to the mapping \({\varOmega }_{\mathrm {C}}^{m,n}(f,(g_{i})_{i\in m})\) from \(\mathbb {N}^{n}\) to \(\mathbb {N}\) obtained by composing \(\left<g_{i}\right>_{i\in m}\) and f, where \(\left<g_{i}\right>_{i\in m}\) is the unique mapping from \(\mathbb {N}^{n}\) to \(\mathbb {N}^{m}\) such that, for every \(i\in m\), \(g_{i} = \mathrm {pr}_{m,i}\circ \left<g_{i}\right>_{i\in m}\).
-
6.
For every \(m\in \mathbb {N}\), \({\varOmega }_{\mathrm {R}}^{m}\), the operator of primitive recursion (also known as the parameterized operation of primitive recursion) of arity \((m)\curlywedge (m+2)\) and co-arity \(m+1\), which is the mapping from \(\mathrm {Hom}(\mathbb {N}^{m},\mathbb {N})\times \mathrm {Hom}(\mathbb {N}^{m+2},\mathbb {N})\) to \(\mathrm {Hom}(\mathbb {N}^{m+1},\mathbb {N})\) that sends a pair (f, g) in \(\mathrm {Hom}(\mathbb {N}^{m},\mathbb {N})\times \mathrm {Hom}(\mathbb {N}^{m+2},\mathbb {N})\) to the mapping \({\varOmega }_{\mathrm {R}}^{m}(f,g)\) from \(\mathbb {N}^{m+1}\) to \(\mathbb {N}\) obtained from f and g by primitive recursion. Let us recall that, for every \(m\in \mathbb {N}\), if
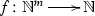 and
and 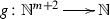 , then, from the principle of definition by mathematical recursion, it follows immediately that there exists a unique mapping
, then, from the principle of definition by mathematical recursion, it follows immediately that there exists a unique mapping 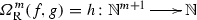 such that the following diagram:
such that the following diagram: 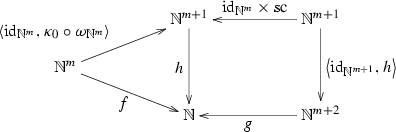
commutes (where \(\omega _{\mathbb {N}^{m}}\) is the unique mapping from \(\mathbb {N}^{m}\) to \(1 = \{0\}\) and \(\kappa _{0}\) the mapping from 1 to \(\mathbb {N}\) that sends 0 to 0), i.e., such that:
-
(a)
\(\forall a\in \mathbb {N}^{m}\,(h(a,0) = f(a)).\)
-
(b)
\(\forall a\in \mathbb {N}^{m}\,\,\forall n\in \mathbb {N}\,(h(a,\mathrm {sc}(n)) = g(a,n,h(a,n))).\)
-
(a)
In the above definition, we have identified the set \(\mathrm {Hom}(\mathbb {N}^{1},\mathbb {N})\) with the set \(\mathrm {End}(\mathbb {N})\), of all endomorphisms of the set \(\mathbb {N}\). Moreover, to simplify the notation, no distinction has been made between the symbols of operation and their realizations on the \(\mathbb {N}\)-sorted set \((\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))_{n\in \mathbb {N}}\).
Since it will be used below to define the set of all primitive recursive mappings, we will next recall under what conditions an \(\mathbb {N}\)-sorted subset of the underlying \(\mathbb {N}\)-sorted set  of
of  is a subalgebra of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra
is a subalgebra of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra  .
.
Definition
An \(\mathbb {N}\)-sorted subset \(\mathcal {F}=(\mathcal {F}_{n})_{n\in \mathbb {N}}\) of the underlying \(\mathbb {N}\)-sorted set  of
of  is a subalgebra of
is a subalgebra of  exactly if it satisfies the following conditions:
exactly if it satisfies the following conditions:
-
1.
\(\kappa _{0,0}\in \mathcal {F}_{0}\).
-
2.
\(\mathrm {sc}\in \mathcal {F}_{1}\).
-
3.
\(\mathrm {pr}_{1,0}\in \mathcal {F}_{1}\).
-
4.
For every \(n\ge 2\) and every \(i\in n\), \(\mathrm {pr}_{n,i}\in \mathcal {F}_{n}\).
-
5.
For every \(m\in \mathbb {N}-1\), every \(n\in \mathbb {N}\), every \(f\in \mathcal {F}_{m}\), and every \((g_{i})_{i\in m}\in (\mathcal {F}_{n})^{m}\), \({\varOmega }_{\mathrm {C}}^{m,n}(f,(g_{i})_{i\in m})\in \mathcal {F}_{n}\).
-
6.
For every \(m\in \mathbb {N}\), every \(f\in \mathcal {F}_{m}\), and every \(g\in \mathcal {F}_{m+2}\), \({\varOmega }_{\mathrm {R}}^{m}(f,g)\in \mathcal {F}_{m+1}\).
We denote by  the set of all subalgebras of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra
the set of all subalgebras of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra  .
.
We next state the fundamental properties of the set of all subalgebras of  .
.
Proposition
The set  , of all subalgebra of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra
, of all subalgebra of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra  , is an algebraic closure system on
, is an algebraic closure system on  , i.e.,
, i.e.,  satisfies the following conditions:
satisfies the following conditions:
-
1.
\((\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))_{n\in \mathbb {N}}\) is a subalgebra de
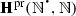 .
. -
2.
If \((\mathcal {F}^{i})_{i\in I}\) is a nonempty family of subalgebras of
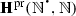 , then \(\bigcap _{i\in I}\mathcal {F}^{i}\) is a subalgebra of
, then \(\bigcap _{i\in I}\mathcal {F}^{i}\) is a subalgebra of 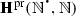 .
. -
3.
If \((\mathcal {F}^{i})_{i\in I}\) is a nonempty family of subalgebras of
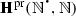 , and if, for every \(i,j\in I\), there exist \(k\in I\) such that \(\mathcal {F}^{i}\cup \mathcal {F}^{j}\subseteq \mathcal {F}^{k}\), then \(\bigcup _{i\in I}\mathcal {F}^{i}\) is a subalgebra of
, and if, for every \(i,j\in I\), there exist \(k\in I\) such that \(\mathcal {F}^{i}\cup \mathcal {F}^{j}\subseteq \mathcal {F}^{k}\), then \(\bigcup _{i\in I}\mathcal {F}^{i}\) is a subalgebra of 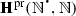 .
.
From the algebraic closure system  on
on  we obtain the algebraic closure operator \(\mathrm {Sg}_{\mathrm {pr}}\) on
we obtain the algebraic closure operator \(\mathrm {Sg}_{\mathrm {pr}}\) on  induced by it, as stated in the following corollary.
induced by it, as stated in the following corollary.
Corollary
For the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra  , the endomorphism \(\mathrm {Sg}_{\mathrm {pr}}\) of the set
, the endomorphism \(\mathrm {Sg}_{\mathrm {pr}}\) of the set  , of all \(\mathbb {N}\)-sorted subsets of
, of all \(\mathbb {N}\)-sorted subsets of  , defined as:
, defined as:

has the following properties:
-
1.
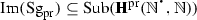 , i.e., for every
, i.e., for every 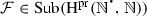 , \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is a subalgebra of
, \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is a subalgebra of 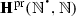 .
. -
2.
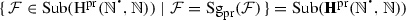 , i.e., the fixed points of \(\mathrm {Sg}_{\mathrm {pr}}\) are exactly the subalgebras of
, i.e., the fixed points of \(\mathrm {Sg}_{\mathrm {pr}}\) are exactly the subalgebras of 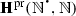 .
. -
3.
\(\mathrm {Sg}_{\mathrm {pr}}\) is extensive, i.e., for every
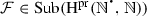 , it happens that \(\mathcal {F}\subseteq \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\).
, it happens that \(\mathcal {F}\subseteq \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\). -
4.
\(\mathrm {Sg}_{\mathrm {pr}}\) is isotone, i.e., for every
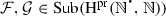 , if \(\mathcal {F}\subseteq \mathcal {G}\), then \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\subseteq \mathrm {Sg}_{\mathrm {pr}}(\mathcal {G})\).
, if \(\mathcal {F}\subseteq \mathcal {G}\), then \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\subseteq \mathrm {Sg}_{\mathrm {pr}}(\mathcal {G})\). -
5.
\(\mathrm {Sg}_{\mathrm {pr}}\) is idempotent, i.e., for every
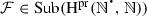 , it happens that \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}) = \mathrm {Sg}_{\mathrm {pr}}(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}))\).
, it happens that \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}) = \mathrm {Sg}_{\mathrm {pr}}(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}))\). -
6.
\(\mathrm {Sg}_{\mathrm {pr}}\) is algebraic, i.e., for every nonempty family \((\mathcal {F}^{i})_{i\in I}\) in
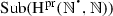 , if, for every \(i,j\in I\), there exists a \(k\in I\) such that \(\mathcal {F}^{i}\cup \mathcal {F}^{j}\subseteq \mathcal {F}^{k}\), then \(\mathrm {Sg}_{\mathrm {pr}}(\bigcup _{i\in I}\mathcal {F}^{i}) = \bigcup _{i\in I}\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}^{i})\).
, if, for every \(i,j\in I\), there exists a \(k\in I\) such that \(\mathcal {F}^{i}\cup \mathcal {F}^{j}\subseteq \mathcal {F}^{k}\), then \(\mathrm {Sg}_{\mathrm {pr}}(\bigcup _{i\in I}\mathcal {F}^{i}) = \bigcup _{i\in I}\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}^{i})\).
Thus, for any  , \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is the smallest subalgebra of
, \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is the smallest subalgebra of  that includes \(\mathcal {F}\). \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is called the subalgebra of
that includes \(\mathcal {F}\). \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is called the subalgebra of  generated by \(\mathcal {F}\) and \(\mathrm {Sg}_{\mathrm {pr}}\) the subalgebra generating operator on
generated by \(\mathcal {F}\) and \(\mathrm {Sg}_{\mathrm {pr}}\) the subalgebra generating operator on  .
.
Definition
Let \(\mathcal {F} = (\mathcal {F}_{n})_{n\in \mathbb {N}}\) be a countable \(\mathbb {N}\)-sorted subset of  , i.e., an \(\mathbb {N}\)-sorted subset of
, i.e., an \(\mathbb {N}\)-sorted subset of  such that \(\mathrm {card}(\coprod \mathcal {F})\le \aleph _{0}\). Then we call the mappings in \(\bigcup \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\), the union of the subalgebra of
such that \(\mathrm {card}(\coprod \mathcal {F})\le \aleph _{0}\). Then we call the mappings in \(\bigcup \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\), the union of the subalgebra of  generated by \(\mathcal {F}\), the \(\mathcal {F}\)-primitive recursive mappings or the primitive recursive mappings relative to \(\mathcal {F}\), and, to shorten the notation, we will write \(\mathrm {PRM}(\mathcal {F})\) instead of \(\bigcup \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\). In particular, the set of all primitive recursive mappings, denoted by \(\mathrm {PRM}\), is \(\bigcup \mathrm {Sg}_{\mathrm {pr}}((\varnothing )_{n\in \mathbb {N}})\), the union of the subalgebra of
generated by \(\mathcal {F}\), the \(\mathcal {F}\)-primitive recursive mappings or the primitive recursive mappings relative to \(\mathcal {F}\), and, to shorten the notation, we will write \(\mathrm {PRM}(\mathcal {F})\) instead of \(\bigcup \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\). In particular, the set of all primitive recursive mappings, denoted by \(\mathrm {PRM}\), is \(\bigcup \mathrm {Sg}_{\mathrm {pr}}((\varnothing )_{n\in \mathbb {N}})\), the union of the subalgebra of  generated by the \(\mathbb {N}\)-sorted set \((\varnothing )_{n\in \mathbb {N}}\) (which is constantly empty).
generated by the \(\mathbb {N}\)-sorted set \((\varnothing )_{n\in \mathbb {N}}\) (which is constantly empty).
We next provide, for a countable \(\mathbb {N}\)-sorted subset \(\mathcal {F}\) of  , a constructive characterization of \(\mathrm {PRM}(\mathcal {F})\) (which is also valid when \(\mathcal {F}\) is arbitrary).
, a constructive characterization of \(\mathrm {PRM}(\mathcal {F})\) (which is also valid when \(\mathcal {F}\) is arbitrary).
Proposition
Let \(\mathcal {F} = (\mathcal {F}_{n})_{n\in \mathbb {N}}\) be an \(\mathbb {N}\)-sorted subset of  such that \(\mathrm {card}(\coprod \mathcal {F})\le \aleph _{0}\) and \(f\in \bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\). Then \(f\in \mathrm {PRM}(\mathcal {F})\) if, and only if, there exists a formative construction for f relative to \(\varvec{{\varSigma }}^{\mathrm {pr}}\) and \(\mathcal {F}\), i.e., if, and only if, there exists a \(p\in \mathbb {N}-1\) and a family \((f_{i})_{i\in p}\) in \(\bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) such that \(f = f_{p-1}\) and, for every \(i\in p\), it happens that:
such that \(\mathrm {card}(\coprod \mathcal {F})\le \aleph _{0}\) and \(f\in \bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\). Then \(f\in \mathrm {PRM}(\mathcal {F})\) if, and only if, there exists a formative construction for f relative to \(\varvec{{\varSigma }}^{\mathrm {pr}}\) and \(\mathcal {F}\), i.e., if, and only if, there exists a \(p\in \mathbb {N}-1\) and a family \((f_{i})_{i\in p}\) in \(\bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) such that \(f = f_{p-1}\) and, for every \(i\in p\), it happens that:
-
1.
\(f_{i}\in \mathcal {F}_{n}\), for some \(n\in \mathbb {N}\), or
-
2.
\(f_{i} = \kappa _{0,0}\), or
-
3.
\(f_{i} = \mathrm {sc}\), or
-
4.
\(f_{i} = \mathrm {pr}_{1,0}\), or
-
5.
\(f_{i} = \mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), or
-
6.
\(f_{i}\) is \(m+1\)-ary and \(f_{i} = {\varOmega }_{\mathrm {R}}^{m}(f_{j},f_{k})\), for a j and a \(k\in i\) such that \(f_{j}\) is m-ary and \(f_{k}\) is \(m+2\)-ary, or
-
7.
\(f_{i}\) is n-ary and \(f_{i} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\), for an \(m\in \mathbb {N}-1\), a \(j\in i\) and a family \((k_{\alpha })_{\alpha \in m}\in i^{m}\) such that \(f_{j}\) is m-ary and, for every \(\alpha \in m\), \(f_{k_{\alpha }}\) is n-ary.
Proof
Let \(\mathcal {L}\) denote the \(\mathbb {N}\)-sorted subset of  whose n-th coordinate, \(\mathcal {L}_{n}\), for \(n\in \mathbb {N}\), has as elements all mappings \(f\in \mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) for which there exists a formative construction for f relative to \(\varvec{{\varSigma }}^{\mathrm {pr}}\) and \(\mathcal {F}\). Since \(\mathrm {PRM}(\mathcal {F})\) is the union of the underlying \(\mathbb {N}\)-sorted set of the least subalgebra of
whose n-th coordinate, \(\mathcal {L}_{n}\), for \(n\in \mathbb {N}\), has as elements all mappings \(f\in \mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) for which there exists a formative construction for f relative to \(\varvec{{\varSigma }}^{\mathrm {pr}}\) and \(\mathcal {F}\). Since \(\mathrm {PRM}(\mathcal {F})\) is the union of the underlying \(\mathbb {N}\)-sorted set of the least subalgebra of  that contains \(\mathcal {F}\), to show that \(\mathrm {PRM}(\mathcal {F})\subseteq \bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\) it suffices to verify that \(\mathcal {L}\) contains \(\mathcal {F}\) and that \(\mathcal {L}\) is a subalgebra of
that contains \(\mathcal {F}\), to show that \(\mathrm {PRM}(\mathcal {F})\subseteq \bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\) it suffices to verify that \(\mathcal {L}\) contains \(\mathcal {F}\) and that \(\mathcal {L}\) is a subalgebra of  . \(\square \)
. \(\square \)
We have that \(\mathcal {F}\subseteq \mathcal {L}\), since, for \(n\in \mathbb {N}\) and \(f\in \mathcal {F}_{n}\), the family \((f_{i})_{i\in 1}\) with \(f_{0} = f\), is a formative construction for f. It is obvious that \(\kappa _{0,0}\in \mathcal {L}_{0}\), that \(\mathrm {sc}\) and \(\mathrm {pr}_{1,0}\in \mathcal {L}_{1}\) and that, for every \(n\ge 2\) and every \(j\in n\), \(\mathrm {pr}_{n,j}\in \mathcal {L}_{n}\). Moreover, given an \(m\in \mathbb {N}-1\), an \(n\in \mathbb {N}\), an \(f\in \mathcal {L}_{m}\), and an m-indexed family \((g_{j})_{j\in m}\) in \(\mathcal {L}_{n}\), then, by virtue of the definition of \(\mathcal {L}\), there exists a formative construction \((f_{i})_{i\in n_{f}}\) for f and, for every \(j\in m\), there exists a formative construction \((f_{j,i})_{i\in n_{j}}\) for \(g_{j}\). Since it may be helpful for the sake of understanding, let us represent the situation just described by the following figure:
Then, for \(n = n_{f}+\left( \sum _{j\in m}n_{j}\right) +1\) and taking as \((h_{i})_{i\in n}\) the family of mappings whose last term is \({\varOmega }_{\mathrm {C}}^{m,n}(f,(g_{j})_{j\in m})\) and being the other terms those formed by the terms of the previous figure, going from left to right and from top to bottom, we have that \((h_{i})_{i\in n}\) is a formative construction for \({\varOmega }_{\mathrm {C}}^{m,n}(f,(g_{j})_{j\in m})\). Hence \({\varOmega }_{\mathrm {C}}^{m,n}(f,(g_{j})_{j\in m})\in \mathcal {L}_{n}\). In the same way one proves that \(\mathcal {L}\) is closed under \({\varOmega }_{\mathrm {R}}^{m}\). Therefore \(\mathcal {L}\) is a subalgebra of  . From all this we conclude that \(\mathrm {PRM}(\mathcal {F}) \subseteq \bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\).
. From all this we conclude that \(\mathrm {PRM}(\mathcal {F}) \subseteq \bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\).
We next show, by induction limited to an initial segment of \(\mathbb {N}\), that \(\bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\) is a subset of \(\mathrm {PRM}(\mathcal {F})\).
Let \(n\in \mathbb {N}\) and \(f\in \mathcal {L}_{n}\). Then, by definition, there exists a \(p\in \mathbb {N}-1\) and a family \((f_{i})_{i\in p}\) in \(\bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) such that \(f = f_{p-1}\) and, for every \(i\in p\), we have that \(f_{i}\in \mathcal {F}_{n}\), for some \(n\in \mathbb {N}\), or \(f_{i} = \kappa _{0,0}\), or \(f_{i} = \mathrm {sc}\), or \(f_{i} = \mathrm {pr}_{1,0}\), or \(f_{i} = \mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), or \(f_{i}\) is \(m+1\)-ary and \(f_{i} = {\varOmega }_{\mathrm {R}}^{m}(f_{j},f_{k})\), for a j and a \(k\in i\) such that \(f_{j}\) is m-ary and \(f_{k}\) is \(m+2\)-ary, or \(f_{i}\) is n-ary and \(f_{i} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\), for an \(m\in \mathbb {N}-1\), a \(j\in i\) and a family \((k_{\alpha })_{\alpha \in m}\in i^{m}\) such that \(f_{j}\) is m-ary and, for every \(\alpha \in m\), \(f_{k_{\alpha }}\) is n-ary.
Now we will prove, by induction on \(i\in p\), that \(f = f_{p-1}\in \mathrm {PRM}(\mathcal {F})\). For \(i = 0\), \(f_{0}\in \mathrm {PRM}(\mathcal {F})\), because, in this case, \(f_{0}\) either belongs to \(\mathcal {F}_{n}\), for some \(n\in \mathbb {N}\), or is of the form \(\kappa _{0,0}\), or \(\mathrm {sc}\), or \(\mathrm {pr}_{1,0}\), or \(\mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), and then \(f_{0}\in \mathrm {PRM}(\mathcal {F})\), because \(\mathrm {PRM}(\mathcal {F})\) is the union of the underlying \(\mathbb {N}\)-sorted set of the least subalgebra of  that contains \(\mathcal {F}\). Let \(k\in p\) and let us suppose that, for every \(i\in k\), \(f_{i}\in \mathrm {PRM}(\mathcal {F})\). Then, by definition, \(f_{k}\in \mathcal {F}_{n}\), for some \(n\in \mathbb {N}\), or \(f_{k} = \kappa _{0,0}\), or \(f_{k} = \mathrm {sc}\), or \(f_{k} = \mathrm {pr}_{1,0}\), or \(f_{k} = \mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), or \(f_{k}\) is \(m+1\)-ary and \(f_{k} = {\varOmega }_{\mathrm {R}}^{m}(f_{u},f_{v})\), for a u and a \(v\in k\) such that \(f_{u}\) is m-ary and \(f_{v}\) is \(m+2\)-ary, or \(f_{k}\) is n-ary and \(f_{k} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\), for an \(m\in \mathbb {N}-1\), a \(j\in k\) and a family \((k_{\alpha } )_{\alpha \in m}\in k^{m}\) such that \(f_{j}\) is m-ary and, for every \(\alpha \in m\), \(f_{k_{\alpha }}\) is n-ary. It is evident that in the first five cases \(f_{k}\in \mathrm {PRM}(\mathcal {F})\). In the last two cases too \(f_{k}\in \mathrm {PRM}(\mathcal {F})\), because being, by hypothesis, \(f_{0},\dots ,f_{k-1}\in \mathrm {PRM}(\mathcal {F})\), also \(f_{u}\), \(f_{v}\) and \(f_{k_{0}},\dots ,f_{k_{m-1}}\in \mathrm {PRM}(\mathcal {F})\), hence, since \(\mathrm {PRM}(\mathcal {F})\) is the union of the underlying \(\mathbb {N}\)-sorted set of the least subalgebra of
that contains \(\mathcal {F}\). Let \(k\in p\) and let us suppose that, for every \(i\in k\), \(f_{i}\in \mathrm {PRM}(\mathcal {F})\). Then, by definition, \(f_{k}\in \mathcal {F}_{n}\), for some \(n\in \mathbb {N}\), or \(f_{k} = \kappa _{0,0}\), or \(f_{k} = \mathrm {sc}\), or \(f_{k} = \mathrm {pr}_{1,0}\), or \(f_{k} = \mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), or \(f_{k}\) is \(m+1\)-ary and \(f_{k} = {\varOmega }_{\mathrm {R}}^{m}(f_{u},f_{v})\), for a u and a \(v\in k\) such that \(f_{u}\) is m-ary and \(f_{v}\) is \(m+2\)-ary, or \(f_{k}\) is n-ary and \(f_{k} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\), for an \(m\in \mathbb {N}-1\), a \(j\in k\) and a family \((k_{\alpha } )_{\alpha \in m}\in k^{m}\) such that \(f_{j}\) is m-ary and, for every \(\alpha \in m\), \(f_{k_{\alpha }}\) is n-ary. It is evident that in the first five cases \(f_{k}\in \mathrm {PRM}(\mathcal {F})\). In the last two cases too \(f_{k}\in \mathrm {PRM}(\mathcal {F})\), because being, by hypothesis, \(f_{0},\dots ,f_{k-1}\in \mathrm {PRM}(\mathcal {F})\), also \(f_{u}\), \(f_{v}\) and \(f_{k_{0}},\dots ,f_{k_{m-1}}\in \mathrm {PRM}(\mathcal {F})\), hence, since \(\mathrm {PRM}(\mathcal {F})\) is the union of the underlying \(\mathbb {N}\)-sorted set of the least subalgebra of  that contains \(\mathcal {F}\), \(f_{k} = {\varOmega }_{\mathrm {R}}^{m}(f_{u},f_{v})\in \mathrm {PRM}(\mathcal {F})\) and \(f_{k} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\in \mathrm {PRM}(\mathcal {F})\). Therefore, for every \(k\in p\), \(f_{k}\in \mathrm {PRM}(\mathcal {F})\). Hence, for \(k = p-1\), \(f = f_{p-1}\in \mathrm {PRM}(\mathcal {F})\). From this it follows that \(\bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\subseteq \mathrm {PRM}(\mathcal {F})\). Hereby completing our proof.
that contains \(\mathcal {F}\), \(f_{k} = {\varOmega }_{\mathrm {R}}^{m}(f_{u},f_{v})\in \mathrm {PRM}(\mathcal {F})\) and \(f_{k} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\in \mathrm {PRM}(\mathcal {F})\). Therefore, for every \(k\in p\), \(f_{k}\in \mathrm {PRM}(\mathcal {F})\). Hence, for \(k = p-1\), \(f = f_{p-1}\in \mathrm {PRM}(\mathcal {F})\). From this it follows that \(\bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\subseteq \mathrm {PRM}(\mathcal {F})\). Hereby completing our proof.
From the above proposition, for \(\mathcal {F} = (\varnothing )_{n\in \mathbb {N}}\) one obtains, immediately, a constructive characterization of the set \(\mathrm {PRM}\).
Corollary
Let f be an element of \(\bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\). Then \(f\in \mathrm {PRM}\) if, and only if, there exists a \(p\in \mathbb {N}-1\) and a family \((f_{i})_{i\in p}\) in \(\bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) such that \(f = f_{p-1}\) and, for every \(i\in p\), it happens that:
-
1.
\(f_{i} = \kappa _{0,0}\), or
-
2.
\(f_{i} = \mathrm {sc}\), or
-
3.
\(f_{i} = \mathrm {pr}_{1,0}\), or
-
4.
\(f_{i} = \mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), or
-
5.
\(f_{i}\) is \(m+1\)-ary and \(f_{i} = {\varOmega }_{\mathrm {R}}^{m}(f_{j},f_{k})\), for a j and a \(k\in i\) such that \(f_{j}\) is m-ary and \(f_{k}\) is \(m+2\)-ary, or
-
6.
\(f_{i}\) is n-ary and \(f_{i} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\), for an \(m\in \mathbb {N}-1\), a \(j\in i\) and a family \((k_{\alpha })_{\alpha \in m}\in i^{m}\) such that \(f_{j}\) is m-ary and, for every \(\alpha \in p\), \(f_{k_{\alpha }}\) is n-ary.
Since it will be used afterwards, to prove that the multiplication and exponentiation are primitive recursive mappings, we notice that, for every \(n\in \mathbb {N}\) and every \(k\in \mathbb {N}\), the constant mapping  , which sends every element of \(\mathbb {N}^{n}\) to k, is a primitive recursive mapping.
, which sends every element of \(\mathbb {N}^{n}\) to k, is a primitive recursive mapping.
Proposition
The addition  , defined as:
, defined as:
is a primitive recursive mapping.
Proof
This is so because \(+ = {\varOmega }_{\mathrm {R}}^{1}(\mathrm {pr}_{1,0},{\varOmega }_{\mathrm {C}}^{1,3}(\mathrm {sc},(\mathrm {pr}_{3,2})))\), or in a diagrammatic manner:

where \({\varOmega }_{\mathrm {C}}^{1,3}(\mathrm {sc},(\mathrm {pr}_{3,2}))\) is the mapping from \(\mathbb {N}^{3}\) to \(\mathbb {N}\) obtained as:

\(\square \)
Proposition
The multiplication  , defined as:
, defined as:
is a primitive recursive mapping.
Proof
This is so because \(\cdot = {\varOmega }_{\mathrm {R}}^{1}(\kappa _{1,0}, {\varOmega }_{\mathrm {C}}^{2,3}(+,(\mathrm {pr}_{3,2},\mathrm {pr}_{3,0})))\), or in a diagrammatic manner:

where \({\varOmega }_{\mathrm {C}}^{2,3}(+,(\mathrm {pr}_{3,2},\mathrm {pr}_{3,0}))\) is the mapping from \(\mathbb {N}^{3}\) to \(\mathbb {N}\) obtained as:

\(\square \)
Proposition
The exponentiation  , defined as:
, defined as:
is a primitive recursive mapping.
Proof
This is so because \(\mathrm {exp} = {\varOmega }_{\mathrm {R}}^{1}(\kappa _{1,1}, {\varOmega }_{\mathrm {C}}^{2,3}(\cdot ,(\mathrm {pr}_{3,2},\mathrm {pr}_{3,0})))\), or in a diagrammatic manner:

where \({\varOmega }_{\mathrm {C}}^{2,3}(\cdot ,(\mathrm {pr}_{3,2},\mathrm {pr}_{3,0}))\) is the mapping from \(\mathbb {N}^{3}\) to \(\mathbb {N}\) obtained as:

\(\square \)
Rights and permissions
About this article
Cite this article
Climent Vidal, J., Soliveres Tur, J. The modernity of Dedekind’s anticipations contained in What are numbers and what are they good for?. Arch. Hist. Exact Sci. 72, 99–141 (2018). https://doi.org/10.1007/s00407-018-0202-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-018-0202-6





 with the universal property; for most categorical purposes, these distinctions do not matter.
with the universal property; for most categorical purposes, these distinctions do not matter.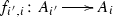 .
. .
.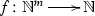 and
and 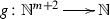 , then, from the principle of definition by mathematical recursion, it follows immediately that there exists a unique mapping
, then, from the principle of definition by mathematical recursion, it follows immediately that there exists a unique mapping  such that the following diagram:
such that the following diagram: 
 .
.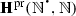 , then
, then 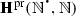 .
.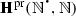 , and if, for every
, and if, for every 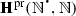 .
.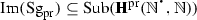 , i.e., for every
, i.e., for every 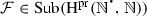 ,
, 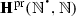 .
.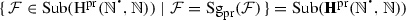 , i.e., the fixed points of
, i.e., the fixed points of 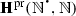 .
.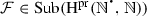 , it happens that
, it happens that  , if
, if 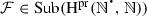 , it happens that
, it happens that 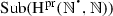 , if, for every
, if, for every