1 Introduction

Extreme cold events bring serious socioeconomic consequences and can disrupt ecological systems and energy supplies (Zhou et al. 2009; Barlow et al. 2015; Zhang et al. 2022). Such events have occurred with increasing frequency over recent decades (Johnson et al. 2018; Cohen et al. 2020; Vihma et al. 2020), and this frequency is not expected to decrease under the long-term global warming trend because of the increase in climatic variability (Kodra et al. 2011; Gao et al. 2015). In the Northern Hemisphere, Europe and Asia have experienced frequent cold extremes. During the winters of 2009 and 2010, northern and western Europe experienced several intense cold extremes (Cattiaux et al. 2010), and these successive cold outbreaks led to record snow cover. The severe cold spell “Alexa” hit the eastern Mediterranean in December 2013, leading to widespread snowfall and losses of approximately 100 million US dollars (Hochman et al. 2020). East Asia (EA), including South Korea, Japan, and China, was struck by an extreme cold surge in January 2016, which caused nearly 100 deaths and great economic losses (Yamaguchi et al. 2019; Dai and Mu 2020). The most recent cold extremes affecting EA occurred in December 2020 and January 2021 owing to three cold air outbreaks. Many cities in China set new records for low temperatures (Zheng et al. 2021). Beijing station observed minimum temperatures of − 19.6 ℃ on 7 January, 2021, which was the third coldest day on record since 1951 (Zhou et al. 2022). In addition, North America experienced cold extremes in February 2021, resulting in power outages and 151 deaths in Texas (Zhang et al. 2022).

It is widely recognized that a negative North Atlantic Oscillation (NAO) is closely associated with the occurrence of cold extremes in the Northern Hemisphere. Cattiaux et al. (2010) pointed out that the persistent negative phase of the NAO was responsible for the occurrence of several cold spells during winter 2010 over northern and Western Europe. Kautz et al. (2020) studied the extended-range predictability of 2018 Eurasian cold spells and found the amplitude of the cold spells was increased by a regime shift of the NAO to the negative phase. Li et al. (2021) investigated the impact of the winter NAO on the multidecadal variability of the surface air temperature (SAT) of EA and demonstrated that more cold winters would occur when the NAO is in the negative phase over multidecadal timescales. In addition, Zheng et al. (2021) pointed out that the negative NAO, Siberian High, and Ural High are direct reasons to the outbreaks of EA cold surges during 2020/2021. Furthermore, the synergistic effects of the warm Arctic and cold tropical Pacific cannot be ignored. Zhang et al. (2022) also investigated extreme cold events (ECEs) across EA and North America during the winter of 2020/21. They pointed out that the concurrence of anomalous thermal conditions in the Arctic, North Atlantic, and Pacific oceans and the interactive Arctic–lower-latitude atmospheric circulation process resulted in these ECEs. Many researchers have investigated other factors that are conducive to the occurrence of cold extremes, such as winter Arctic sea ice, Eurasian snow cover, and the East Asian winter monsoon (Ding and Sikka 2006; Wu et al. 2011; Yu et al. 2018).

The ability to accurately forecast extreme cold spells would bring many benefits, but serious challenges remain. On the one hand, the predictability of cold extremes is limited by the chaotic nature of the atmosphere (Lorenz 1963; Mu et al. 2003; He et al. 2006; Feng and He 2007; Duan and Mu 2009). On the other hand, the small sample size limits our knowledge of the physical mechanisms that generate them. Despite these challenges, much progress has been achieved in recent years. For example, the THORPEX Interactive Grand Global Ensemble (TIGGE) has been developed (Bougeault et al. 2010; Swinbank et al. 2016) to increase the forecast skill associated with high-impact weather events. There are 13 centers that can provide ensemble forecast data for scientific research. The TIGGE program was set up to study the predictability of high-impact weather events and improve their accuracy over periods of one day to two weeks. To study the predictability of high-impact weather events over longer timescales, the subseasonal-to-seasonal (S2S) program has also been established (Vitart et al. 2017). Both the TIGGE and S2S programs have accelerated our understanding of the predictability of high-impact weather events. Apart from the model advances, many theoretical research methods have emerged (e.g., Mu et al. 2003; Mohamad and Sapsis 2018). The Lyapunov exponent (LE) is a classic method used to study the error growth associated with the predictability of dynamical systems (Wolf et al. 1985; Fraedrich 1986). However, the LE measures the global error growth, whereas the predictability reflects the local properties of dynamical systems, thereby limiting its applications. Although the Local LE (LLE) approach addresses local predictability, it characterizes the dynamics of error growth in only the linear regime and fails to capture the dynamics of nonlinear error growth (Nese 1989; Yoden and Nomura 1993). To overcome the above-mentioned limitations, Ding and Li (2007) proposed the nonlinear LLE (NLLE) method (Ding and Li 2007). To study the predictability of extreme events, Li et al. (2019) proposed the backward NLLE method (BNLLE). Both the NLLE and BNLLE methods are effective means of studying atmospheric predictability (Li et al. 2020; He et al. 2021, Li et al. 2022). However, Li et al. (2017) highlighted that they might be susceptible to uncertainties within the forecast models. In addition, limited sizes of initial errors have larger fluctuations growing with forecast time, thereby influencing the saturation time of forecast errors associated with the predictability. Li et al. (2017) introduced the attractor radius (AR) and global AR (GAR) to depict the geometric characteristics and average behavior of chaotic systems. From the geometric characteristics and average behavior of error growth, the predictability limits of chaotic systems can be quantified. In addition, the predictabilities quantified using the AR and GAR correspond to practical and potential predictabilities, respectively, and the AR is the GAR × \(\sqrt 2\). By applying the AR and GAR to the Lorenz-63 model and operational forecast data, the AR and GAR can be verified as effective and feasible approaches to predictability analysis. Feng et al. (2019) used these two statistics to study the relationship between deterministic and ensemble mean forecast errors in the Lorenz-96 model. Ma et al. (2021) investigated atmospheric predictability using multiple reanalysis datasets from different centers and the AR and GAR. Zhao et al. (2021) analyzed differences in the predictability limits associated with atmospheric models and coupled ocean–atmosphere systems using the AR and GAR, and they found that coupled systems have higher practical predictability in the lower troposphere, whereas uncoupled systems have higher practical predictability in the middle and upper atmosphere.

These studies have demonstrated that the AR and GAR are effective means of investigating the predictability of both theoretical models and operational forecast models. However, previous studies have failed to apply the AR and GAR to the predictability of extreme weather or climate events, which attract considerable public attention. Quantifying the predictability limits of extreme events is challenging but worthwhile. Because of the effectiveness of the AR and GAR in the analysis of predictability, a new method, based on the AR and GAR, is presented in this study. This new method will be applied to quantitatively investigate the local predictability of the 2020/21 cold extremes over EA.

The remainder of this paper is organized as follows. In Sect. 2, we describe the AR and GAR methodology, the new method, and the data used in this study. The local predictability of the cold extremes is studied in Sect. 3. Finally, a discussion and our conclusions are presented in Sect. 4.

2 Methodology and data

2.1 Attractor radius (AR) and global attractor radius (GAR)

The AR and GAR are two invariant statistics of an attractor. For a specific state \({\varvec{x}}_{i}\) on the compact attractor \({\mathcal{A}}\), the distance between the specific state \({\varvec{x}}_{i}\) and all other states on the compact attractor \({\mathcal{A}}\) can be expressed as follows:

$$R_{L} \left( {x_{i} } \right) = \sqrt {E\left( {\parallel x_{i} - x\parallel^{2} } \right)} ,{\mkern 1mu} {\mkern 1mu} x_{i} {\mkern 1mu} \,{\text{and}}\,{\mkern 1mu} {\mkern 1mu} x \in {\mathcal{A}},$$
(1)

where E represents the expectation, and \(\parallel { }\parallel\) denotes the \(L_{2}\) norm of the vector. As \({\varvec{R}}_{L}\) measures the distance between the specific state \({\varvec{x}}_{i}\) and all other states on the compact attractor \({\mathcal{A}}\), the distance \({\varvec{R}}_{L}\) is referred to as the local AR (LAR).

In particular, if \({\varvec{x}}_{i}\) is the mean state of \({\mathcal{A}}\), that is \({\varvec{x}}_{E} = E\left( {\varvec{x}} \right)\), the distance between the specific state \({\varvec{x}}_{E}\) and all other states on the compact attractor \({\mathcal{A}}\) can be expressed as follows:

$${\varvec{R}}_{E} = \sqrt {E\left( {\parallel {\varvec{x}}_{E} - {\varvec{x}}\parallel^{2} } \right)} ,{\mkern 1mu} {\mkern 1mu} {\text{and}}{\mkern 1mu} {\mkern 1mu} {\varvec{x}} \in {\mathcal{A}},$$
(2)

where \({\varvec{R}}_{E}\) is the AR. Although \({\varvec{x}}_{E}\) represents the mean state of the attractor \({\mathcal{A}}\), \({\varvec{x}}_{E}\) does not necessarily fall on the attractor. Actually, the AR has the same form as the standard deviation in statistics, which represents the variability of a variable (Li et al. 2017).

The GAR of the compact attractor \({\mathcal{A}}\) is defined as the average of all LARs of the states \({\varvec{x}}\) on the compact attractor \({\mathcal{A}}\). The GAR can be expressed as

$${\varvec{R}}_{G} = \sqrt {E\left( {{\varvec{R}}_{L}^{2} } \right)} = \sqrt {E\left( {\parallel {\varvec{x}} - {\varvec{y}}\parallel^{2} } \right)} ,{\mkern 1mu} {\mkern 1mu} {\varvec{x}}{\mkern 1mu} {\mkern 1mu} {\text{and}}{\mkern 1mu} {\mkern 1mu} {\varvec{y}} \in {\mathcal{A}}.$$
(3)

Note that, from the form of Eq. (3), \({\varvec{R}}_{G}\) represents the average distance between any two states on the compact attractor \({\mathcal{A}}\).

Li et al. (2017) proved a constant relationship between the AR and GAR. The relationship is

$${\varvec{R}}_{G} = \sqrt 2 {\varvec{R}}_{E} .$$
(4)

Considering this simple relationship, the computing cost of \({\varvec{R}}_{G}\) can be reduced significantly.

2.2 Quantifying the global and local predictability

As the AR and GAR are two invariant statistics of the attractor confined in the chaotic system, they can be used to estimate the global and local predictability limits of both theoretical systems and real atmospheric systems (Li et al. 2017; Feng et al. 2019; Ma et al. 2021; Zhao et al. 2021).

For an n-dimensional dynamical system, a perturbed state \(\hat{\user2{x}}_{0}\) can be obtained by superimposing the initial error \({\varvec{\delta}}_{0}\) on the initial state \({\varvec{x}}_{0}\). That is

$$\hat{\user2{x}}_{0} = {\varvec{x}}_{0} + {\varvec{\delta}}_{0} .$$
(5)

From the two local states \({\varvec{x}}_{0}\) and \(\hat{\user2{x}}_{0}\), the dynamical trajectories of them varying time are denoted by \({\varvec{x}}\left( t \right)\) and \(\hat{\user2{x}}\left( t \right)\). Then, the evolution of the root-mean-square error (RMSE) as it also varies with time can be expressed by

$$e\left( {{\varvec{x}}_{0} ,{\varvec{\delta}}_{0} , t} \right) = \parallel \hat{\user2{x}}\left( t \right) - {\varvec{x}}\left( t \right)\parallel .$$
(6)

The global ensemble average of the RMSEs over the samples can be denoted by.

$$\overline{e}\left( {{\varvec{\delta}}_{0} , t} \right) = \sqrt {\left\langle {e^{2} \left( {{\varvec{x}}_{0} ,{\varvec{\delta}}_{0} , t} \right)} \right\rangle_{N} } ,{\varvec{x}}_{0} \in {\mathcal{A}},$$
(7)

where \(\left\langle . \right\rangle_{N}\) denotes the ensemble mean of N samples. Li et al. (2017) pointed out that when \(\overline{e}\left( {{\varvec{\delta}}_{0} , t} \right)\) exceeds the AR (GAR), further forecasts lose their accuracy. The global practical (potential) predictability limit \(T_{gpl}^{{pr\left( {po} \right)}}\) can be expressed by.

$$T_{gpl}^{{pr\left( {po} \right)}} = t_{{ar\left( {gar} \right)}} - t_{0} .$$
(8)

Here, \(t_{0}\) represents the initial time, and \(t_{{ar\left( {gar} \right)}}\) is the time when \(\overline{e}\left( {{\varvec{\delta}}_{0} , t} \right)\) reaches the AR (GAR).

For the local predictability, if a large number of initial errors are superimposed on the initial state \({\varvec{x}}_{0}\), then the local ensemble average of the RMSEs is defined as:

$$\overline{e}\left( {{\varvec{x}}_{0} ,{\varvec{\delta}}_{0} , t} \right) = \sqrt {\left\langle {e^{2} \left( {{\varvec{x}}_{0} ,{\varvec{\delta}}_{0} , t} \right)} \right\rangle_{N} } ,{\varvec{x}}_{0} \in {\mathcal{A}},$$
(9)

where N is the number of initial errors, and \(\left\langle . \right\rangle_{N}\) denotes the ensemble mean of N samples. When \(\overline{e}\left( {{\varvec{x}}_{0} ,{\varvec{\delta}}_{0} , t} \right)\) exceeds the AR (GAR), the local practical (potential) predictability of the state \({\varvec{x}}_{0}\) is lost (Li et al. 2017). The local practical (potential) predictability limit \(T_{{lpl, x_{0} }}^{{pr\left( {po} \right)}}\) of the state \({\varvec{x}}_{0}\) can be expressed as

$$T_{{lpl, x_{0} }}^{{pr\left( {po} \right)}} = t_{{ar\left( {gar} \right)}} - t_{0} ,$$
(10)

and \(t_{{ar\left( {gar} \right)}}\) is the time when \(\overline{e}\left( {{\varvec{x}}_{0} ,{\varvec{\delta}}_{0} , t} \right)\) reaches the AR (GAR). Therefore, based on Eq. (10), the practical (potential) accurate forecast time starts from the state \({\varvec{x}}_{0}\), can be obtained.

2.3 Backward searching for the initial condition (BaSIC) method

As extreme events have more impact on society than normal events, it is worth investigating how best to estimate the local predictability limits. Next, we will introduce a new method to quantify the local predictability limits of extreme events.

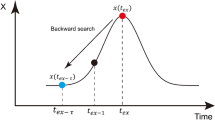
In a phase space, an arbitrary condition \({\varvec{x}}_{0}\) on a dynamical trajectory has a local predictability limit. That is, the accurate forecast period from the condition \({\varvec{x}}_{0}\) has an upper limit. If the condition \({\varvec{x}}_{1}\) is where the condition \({\varvec{x}}_{0}\) loses its predictability, the timespan between the two conditions is the local predictability limit of the condition \({\varvec{x}}_{0}\). Conversely, a given condition \({\varvec{x}}_{1}\) has a corresponding initial condition (IC) \({\varvec{x}}_{0}\) that can predict the given condition \({\varvec{x}}_{1}\). In addition, two points should be noted. First, any condition on the trajectory between the two conditions \({\varvec{x}}_{0}\) and \({\varvec{x}}_{1}\) can predict the condition \({\varvec{x}}_{1}\). Second, any condition preceding the IC \({\varvec{x}}_{0}\) cannot predict the condition \({\varvec{x}}_{1}\). Therefore, the maximum prediction lead time (MPLT) of the condition \({\varvec{x}}_{1}\) is the timespan between the two conditions. Based on this rationale, a given extreme condition has a corresponding IC, and the MPLT of the given extreme condition is the time period between the extreme condition and the corresponding IC. Thus, to obtain the MPLT of the extreme condition, a corresponding IC must first be determined.

Let \({\varvec{x}}_{ex}\) be the extreme condition in a time series ([\({\varvec{x}}_{1}\), \({\varvec{x}}_{2}\), …, \({\varvec{x}}_{ex}\), …]). The IC precedes the extreme condition \({\varvec{x}}_{ex}\), and so we must backward search for the IC. From Eq. (10), for a given condition \({\varvec{x}}_{0}\), the local practical predictability of the condition \({\varvec{x}}_{0}\) is lost when the \(\overline{e}\left( {{\varvec{x}}_{0} ,{\varvec{\delta}}_{0} , t} \right)\) exceeds the AR. Therefore, to determine the IC, we need to find a condition \({\varvec{x}}_{0}^{*}\) whose \(\overline{e}\left( {{\varvec{x}}_{0}^{*} ,{\varvec{\delta}}_{0} , t} \right)\) exceeds the AR at the extreme condition \({\varvec{x}}_{ex}\). The condition \({\varvec{x}}_{0}^{*}\) is the corresponding IC. Therefore,

$$J\left( {{\varvec{x}}_{0}^{*} } \right) = { }0{ ,}$$
(11)

where

$$J\left( {\varvec{x}} \right) = \parallel \overline{e}\left( {{\varvec{x}},{\varvec{\delta}}, t} \right) - {\text{ AR }}\parallel ,$$
(12)

the condition \({\varvec{x}}\) precedes the extreme condition \({\varvec{x}}_{ex}\), and \({\varvec{\delta}}\) is the error perturbed on the condition \({\varvec{x}}\). By solving Eqs. (11) and (12), the IC \({\varvec{x}}_{0}^{*}\) of the extreme condition can be obtained, and the MPLT of the extreme condition \({\varvec{x}}_{ex}\) is the time period between the IC \({\varvec{x}}_{0}^{*}\) and the extreme condition \({\varvec{x}}_{ex}\). As the AR is the threshold in Eq. (12), the MPLT represents the local practical predictability of the extreme condition \({\varvec{x}}_{ex}\). To obtain the potential MPLT of the extreme condition \({\varvec{x}}_{ex}\), we replace AR with GAR in Eq. (12). Therefore, based on the above procedure, the practical and potential MPLTs of the extreme condition \({\varvec{x}}_{ex}\) can be determined. In addition, it should be noted that the practical or potential MPLT is the upper limit of the local practical or potential predictability of extreme events. As the core of our new method is the procedure: Backward Searching for the Initial Condition, we have named it the BaSIC method.

2.4 Data

The TIGGE project comprises 13 Numerical Weather Prediction (NWP) centers, which can provide the ensemble forecast data for scientific research, such as ensemble forecasting or predictability (Bougeault et al. 2010; Swinbank et al. 2016). In this study, we used the SAT in the ensemble forecast daily data from the European Centre for Medium-Range Weather Forecasts (ECMWF), because of its higher forecast skills in ensemble forecast. The SAT ensemble forecasts are initialized at 00Z and 1200Z every day, and the forecast range is up to 15 days. We selected the ensemble forecasts starting at 00Z December 1 2020 to January 31 2021 when the cold extremes occurred. There is 1 control member and 50 perturbed members, giving a total of 51 members. The observed SAT data were from the fifth generation European Center for Medium Range Forecasting Reanalysis (ERA5, Hersbach et al. 2020), and this also runs from December 1 2020 to January 31 2021. Both the ensemble data and the verified observed data have a resolution of 0.5°. The AR and GAR were calculated from the ERA-interim (ERAI) reanalysis dataset (Dee et al. 2011) with a 0.5° grid from 1 January 1979 to 31 December 2018 every 6 h.

3 Results

Figure 1 shows the spatial distribution of the AR calculated from the ERA-interim dataset. We also used the ERA5 and NCEP datasets to calculate the AR. Both the amplitudes and spatial distributions of the AR calculated using these two datasets were similar to that from the ERA-interim dataset, indicating that the dataset used has little influence on the AR (figures not shown). Therefore, we will use the AR calculated from the ERA-interim dataset for analysis in this study. Figure 1 shows that the AR has a distinct spatial distribution, with the regions south of 40°N having a smaller AR, whereas regions north of 40°N have a larger AR. The AR values on the Tibetan Plateau and across northwest China are smaller than those from other regions of China. A small area in southern China has a larger AR than the surrounding areas. In addition, the AR over the land has a larger amplitude than that over the oceans at the same latitude. Zhao et al. (2021) pointed out that different dynamical instabilities are responsible for the distinct spatial patterns of the AR. At low latitudes, barotropic and convective instabilities are dominant, whereas baroclinic instability plays the leading role in the middle latitudes. Therefore, the higher variability in the middle latitudes leads to a larger AR, and the lower variability in the low latitudes results in a smaller AR.

Fig. 1
figure 1

Spatial distribution of the AR of the SAT

Full size image

Three ECEs affected EA (20°–50°N, 100°–120°E; denoted by the black box in Fig. 2b–d) over the winter of 2020/21, and Fig. 2a shows the daily averaged SAT time series for EA. From Fig. 2a, we see that the first two ECEs occurred on 20,201,214 and 20,201,230, and the third ECE occurred on 20,210,107. For these three cold extremes, most regions of EA show large significantly negative SAT anomalies (Fig. 2b–d), and the third extreme cold event was stronger than the other two. In addition, the spatial distributions (Fig. 2b–d) show that the SAT on the Tibetan Plateau was always higher than normal, acting as the heat source for the EA region.

Fig. 2
figure 2

a Average time series of SAT and b–d SAT anomalies (relative to 1991–2020, units: °C) for the three extreme cold events that occurred in December 2020 and January 2021. Gray shading in a shows the periods of the three extreme cold events. Black boxes (b–d) denote the East Asia study region. Black dots in (b–d) denote that anomalies are significant at the 90% confidence level (two-tailed Student’s t test)

Full size image

Before quantifying the local predictability of the three ECEs, we will first consider the global predictabilities of SATs in December 2020 (hereafter 202,012) and January 2021 (hereafter 202,101). The ensemble forecasts from the ECMWF center are run at 00Z and 12Z every day, with outputs every 6 h, and the total output time is 360 h (15 days). We used the ensemble forecasts initialized at 00Z every day. Therefore, the average SAT forecasts with a lead time of 15 days could be obtained for the two months during which the extreme cold events occurred. To quantify the global predictability of the SAT for these two months, we first calculated the RMSE. Figure 3 shows the average daily RMSE for 202,012, with a lead time of 15 days, calculated using the ensemble forecast data and ERA5 reanalysis, and we see that the larger RMSEs are located mainly across northern EA during the first 5 days. In addition, a small part of western EA also has larger RMSE values, while other regions maintain smaller RMSEs. This indicates that the forecast skill for northern and western EA is lower than that for the other regions. From the 6th to the 10th day, the RMSE over the whole EA region shows an obvious increase compared with the first 5 days, and the larger RMSE extends to southern EA. The RMSE in some parts of northern EA increased to 5 °C. For the next few days, the RMSE across northern EA remained large, and the RMSE in southern EA increased further, matching the values in some areas of northern EA.

Fig. 3
figure 3

Spatial distributions of RMSE (shading: ℃) as a function of lead time (days) in December 2020

Full size image

Figure 4 shows the mean daily RMSE in 202,101 with a lead time of 15 days. Similar to 202,012, the RMSE in most regions was relatively small during the first 5 days. However, for northern EA, the RMSE values in 202,101 are generally less than those from 202,012. Between the 6th and the 10th days, the RMSE increased quickly, and from the 7th to the 10th day, the RMSEs in northern EA are larger than those in 202,012, especially on the 9th and 10th days (Fig. 4i and j). In addition, the RMSE extends further to the south. For the last 5 days, most EA regions have a larger RMSE, reaching or exceeding 5 °C.

Fig. 4
figure 4

As Fig. 3, but for January 2021

Full size image

The AR and GAR averaged over the EA regions were 3.17 and 4.48, respectively. From the AR and GAR methodology, the global practical and potential predictability limits are determined when the RMSE reaches the AR and GAR, respectively. Figure 5 shows that the average RMSEs of the two months vary with lead time. During the early period (the first 5 days), the RMSE in 202,012 is slightly larger than that in 202,101, which is consistent with the spatial distributions shown in Figs. 3 and 4. This is caused mainly by the larger RMSE in northern EA during 202,012. After the first 5 days, the RMSE in 202,101 exceeds that in 202,012. This is mainly because the RMSEs in 202,101 show a sharper increase than those in 202,012, especially in northern EA. The RMSE in 202,101 reached the AR on the 8th day, whereas that in 202,012 reached the AR on the 10th day. Therefore, the global practical predictability limits (PrPLs) of SAT across EA for 202,012 and 202,101 were 10 and 8 days, respectively. For 202,012, the RMSE continued to increase after exceeding the AR, but it did not reach the GAR within 15 days. For 202,101, the RMSE also did not reach the GAR within 15 days. Therefore, the global potential predictability limits (PoPLs) of SAT for these two months were both greater than 15 days. Lorenz (1969) pointed out that the upper limit of atmospheric predictability was less than two weeks. However, some studies have found that the upper limit of atmospheric predictability exceeds two weeks because of external forcing signals, such as the sea ice component and sea surface temperature (Kautz et al. 2020; Xiang et al. 2020). In the TIGGE project, the ECMWF center couples the ocean and atmosphere. Therefore, the ensemble forecast data contain the external forcing signals, which help to extend to the upper limit of atmospheric predictability. Moreover, from Fig. 5, owing to the gap between the practical and potential predictability limits, the NWP model still has much room for improvement.

Fig. 5
figure 5

RMSE averaged over East Asia as a function of lead time (days) for the two months. Blue and red solid lines represent December 2020 and January 2021, respectively. Lower and upper dotted lines denote AR and GAR values, respectively

Full size image

Although the average PrPLs for the whole EA region over 202,012 and 202,101 were 10 and 8 days, respectively, some regions had PrPLs that exceeded 15 days. The PrPLs in these regions were not calculated because of the limited timespan of the ensemble forecast data. For the sake of analysis, the PrPLs in these regions were set to 15 days. Figure 6 shows the spatial distributions of the global PrPLs of the SAT for the two months. For 202,012, the northeastern and middle regions of EA had higher PrPLs, exceeding 12 days, and even 15 days for some of these regions. Some northern and northwestern regions had lower PrPLs of less than 4 days. Other than these regions, the remaining regions had PrPLs of approximately 8–12 days. The spatial distribution of the PrPLs appears to contradict the spatial distribution of the RMSE (Fig. 3) because the larger RMSEs are located mainly in the northern EA in these forecasts. However, the PrPLs are determined by both the RMSE and AR. Although the larger RMSE values are located mainly in the northern EA, the ARs in these regions also have larger values. As a result, the PrPLs are high in these regions. Similarly, the northwest regions have relatively smaller RMSEs in the forecasts. However, the ARs in these regions are also smaller, leading to lower PrPLs. Figure 6b shows the spatial PrPLs for 202,101. Like 202,012, the northern and northwestern regions have lower PrPLs than the other regions. Overall, the EA regions have lower PrPLs than 202,012. In 202,101, except in some coastal zones where the PrPLs reached 15 days, most regions had PrPLs of approximately 8–10 days. Therefore, the two months have different PrPLs, and the PrPLs for 202,012 were larger than those for 202,101.

Fig. 6
figure 6

Spatial distributions of global practical predictability limits for the two months, (shading indicates number of days)

Full size image

Having analyzed the global PrPLs for the two months, we will now consider the local PrPLs associated with the three periods of extreme cold. The three cold extremes occurred on 20,201,214, 20,201,230, and 20,210,107, and we will first consider the evolution of the forecast errors. Forecast errors from 3 days prior to each event are given. Figure 7a–c shows the evolution of the daily forecast errors for the first ECE from 20,201,212 to 20,201,214. The forecast SAT is greater than the observed SAT in the northern EA, but less than the observations in the southern EA. In addition, the difference between the ensemble forecast and the observed SAT increases as the day of the ECE approaches. Overall, the ensemble forecasts overestimated the SAT when compared with the observations, and the forecast errors in northern EA contribute a lot. For the second and third ECEs, as with the first ECE, the northern EA had SATs in the ensemble forecasts that exceeded the observed SAT, whereas the forecast SATs for southern EA were less than the observed values.

Fig. 7
figure 7

Spatial distributions of forecast errors (shading: °C) for the three extreme cold events with a 3-day lead time before each event. Left, middle, and right panels are the first, second, and third events, respectively

Full size image

To quantify the local PrPLs of the three ECEs, we must first determine the three ICs of the extreme SATs on 20,201,214, 20,201,230, and 20,210,107. After determining the three ICs, we can then obtain their local PrPLs. Figure 8 shows that the RMSE averaged over the EA region varies with the lead time starting from different dates. For the three ECEs, the RMSE grows as the lead time increases, and it takes less time for the RMSE to reach a larger value if the start date is closer to the extreme SAT days (20,201,204; 20,201,230; and 20,210,107). Moreover, for the third ECE, it takes less time for the RMSEs to reach a larger value when compared with the other two events. This is mainly because the third ECE is stronger than the other two.

Fig. 8
figure 8

RMSE averaged over the EA region as a function of lead time (days) starting from different dates before the extreme cold days (shading, ℃) for the three extreme cold events

Full size image

We used Eqs. (11) and (12) to calculate the ICs of the three extreme cold events, and the dates of the three ICs were 20,201,208; 20,201,222; and 20,210,101. Figure 9 shows the variations of the RMSEs starting from the three corresponding ICs for the three ECEs. For the first ECE, the RMSE first decreases, but from 20,201,209 it then increases monotonically with time. On the extreme cold day of 20,201,214, the RMSE is still smaller than the AR and GAR, demonstrating that the local predictability is not lost. That is, when the forecast runs from 20,201,208, the first ECE can be predicted. We also calculated the variations of the RMSE from 20,201,207. The RMSE exceeds the AR before the extreme cold day on 20,201,214, indicating a loss of local predictability for the ECE. Therefore, this further verifies that the SAT on 20,201,208 is the IC of the first ECE, and the MPLT of the first ECE was determined to be 6 days (20,201,214–20,201,208). Moreover, the RMSE exceeds the AR on approximately 20,201,217. Thus, the local PrPL of the IC on 20,201,208 was 9 days. As the RMSE does not exceed the GAR during the 15-day forecast period, the local PoPL of the IC on 20,201,208 is more than 15 days. Figure 9b shows the variations in the RMSE starting from 20,201,222 for the second ECE. The growth of the RMSE tends to increase with time. The RMSE reaches the AR on the extreme cold day of 20,201,230. For the other ICs preceding 20,201,222, the RMSE reaches the AR before the extreme cold day of 20,201,230. Hence, the MPLT of the second ECE was 8 days (20,201,230–20,201,222), and the local PrPL for 20,201,222 was also 8 days. In contrast to the first IC, the RMSE for the second IC reaches the GAR on 20,210,103; i.e., within 15 days. Consequently, the PrPL for 20,201,222 was 12 days. Figure 9c shows the variations in RMSE starting from 20,210,101 for the third ECE. The RMSE from 20,210,101 reaches the AR before the extreme cold day of 20,210,107. For the other ICs preceding 20,210,101, the RMSE reaches the AR after the extreme cold day of 20,210,107. Therefore, the MPLT of the third ECE was 6 days (20,210,107–20,210,101), and the local PrPL and PoPL for 20,210,101 were approximately 9 and 10 days, respectively. Therefore, based on the AR method, the MPLTs were 6, 8, and 6 days for the three extreme cold days of 20,201,214, 20,201,230, and 20,210,107, respectively. To calculate the local PoPL of these three cold days, we simply replace the AR with the GAR in Eq. (12). The PoPLs of these three extreme cold events were longer but are not shown in the study.

Fig. 9
figure 9

RMSE averaged over EA as a function of lead time (days) starting from the corresponding initial conditions of the three extreme cold events. Lower and upper dotted lines denote AR and GAR, respectively

Full size image

Based on our analysis of the RMSE growth averaged over the EA region, the local PrPLs of the three cold days can be quantified. However, the average RMSE growth was obtained by calculating the spatial average and filtering out the regional dynamical information related to RMSE growth. In practice, the regional dynamical characteristics are also important to the local predictability. Therefore, we will now further investigate the regional dynamical information associated with the RMSE growth.

Figure 10 shows the spatial variations in the RMSE associated with the first ECE from its corresponding IC day. On the initial day (20,201,208), larger RMSEs are located mainly in the northern-central and some western regions. During the next 2 days, the RMSEs over most regions, especially the two regions mentioned above, tended to decrease, which is also seen in Fig. 9a. For the next 3 days, the RMSEs in the northern regions show an obvious increase. In addition, the areas with a large RMSE also extend compared with previous days. On the extreme SAT day (20,201,214), the RMSEs continue to increase, and some southern regions have larger RMSEs. For the next 2 days, most regions have larger RMSEs, and the local practical predictability of 20,201,208 is almost lost completely because the average RMSE tends to exceed the AR. During the forecast, the northern regions always maintain larger RMSEs, which serve as a source of error to limit the upper extent of the predictability.

Fig. 10
figure 10

Spatial distributions of RMSE (shading: °C) as a function of lead time (days) starting from the corresponding initial conditions of the first extreme cold event

Full size image

Figure 11 shows the spatial variations of RMSEs for the second ECE. On the initial day (20,201,222), like the first ECE, the larger RMSEs are located mainly in the northern-central and some western regions. During the following days, the rate of growth in the forecast errors differs among the regions. The forecast errors for the southeastern regions are obviously larger than those from the middle regions. On the extreme SAT day (20,201,230), except for some northeastern regions, most regions had larger RMSEs and the RMSE reaches the AR, indicating the loss of the local predictability. From the growth tendency of the spatial forecast errors, the second ECE differs from the first with a forecast error growth tendency extending gradually from the north to the south. Therefore, the dynamical characteristics of the second ECE are also different from the first. Different regions, especially the northern, western, and southeastern regions, serve as sources of errors to limit the upper extent of predictability.

Fig. 11
figure 11

As Fig. 10, but for the second extreme cold event

Full size image

The spatial pattern of RMSE growth for the third ECE is shown in Fig. 12. During the first 3 days, the spatial forecast errors have similar distributions to those from the first ECE. That is, some western and northern regions have larger forecast errors. In contrast to the first ECE, during the next few days, the forecast errors did not extend from the north to the south, and most regions showed simultaneous growth. On the extreme SAT day (20,210,107), the forecast errors in most regions are larger than previous days. However, the local predictability was not lost, because the AR was not reached (see Fig. 9c). For the next 2 days, the forecast errors increased and the regions also extended. And the RMSE reaches the AR, indicating the loss of the local predictability. Therefore, from the growth of the spatial forecast errors, most regions (especially the northern regions) contributed to the loss of the local predictability. Our analysis demonstrates that the forecast errors for these three extreme cold days showed different spatial growth patterns, which reflect the differing dynamical characteristics associated with the three cold days. In addition, the northern regions of EA contribute significantly to the loss of local predictability for the three extreme cold days.

Fig. 12
figure 12

As Fig. 10, but for the third extreme cold event

Full size image

4 Discussion and conclusions

Extreme cold events have major impacts on society, and accurate forecasts of such events are important to policy makers and the public. However, the accurate forecasting of extreme events poses great challenges. Since the pioneering work of Lorenz (1963), many researchers have been dedicated to the field of atmospheric predictability, and many theoretical methods have emerged (He et al. 2016; Li et al. 2019). The recently developed AR and GAR methods depict the dynamical characteristics of chaotic systems and can quantitatively estimate the atmospheric predictability effectively (Li et al. 2017). However, the AR and GAR cannot quantify the predictability of extreme events. Given that the AR and GAR can characterize the dynamics of chaotic systems well, this study presents a new method, BaSIC, that can be used to quantitatively study the predictability of extreme events and is based on the AR and GAR. It should be noted that the AR and GAR were developed in the Lorenz model which contained the stationary and nonstationary dynamics. In addition, the AR and GAR have also studied the predictability of the real atmosphere, which also contains the stationary and nonstationary dynamics (Li et al. 2017; Ma et al. 2021; Zhao et al. 2021). It demonstrates that the BaSIC method can be used to study the predictability of extreme events which are more related to the nonstationary dynamics. The BaSIC method takes the extreme condition and AR (GAR) as a target condition and the threshold, respectively. In practice, the extreme condition is on the nonstationary evolutionary trajectory. By backward searching for an IC on the nonstationary evolutionary trajectory, on which perturbed initial errors will grow to reach the threshold (AR or GAR) at the time of the extreme condition, the local predictability of the extreme condition can be determined.

To verify the feasibility of the BaSIC method, we applied it to the 2020/21 extreme cold events that occurred in EA. Two ECEs occurred in 202,012 and one in 202,101. Before studying the local predictability of the three events, we first quantitatively investigated the global predictability of the SATs in 202,012 and 202,101 using the AR and GAR method. The SAT RMSE calculated from the ensemble forecasts and the observed data in 202,012 reached the average AR of the EA regions within 10 days. Therefore, the global PrPL of SAT for 202,012 was 10 days. For 202,101, the global PrPL was 8 days. The difference in the global PrPLs between the two months was mainly the result of the different spatial growth patterns of the forecast errors. For the northern EA regions, the RMSE in 202,101 increased faster than that in 202,012 after the early period. The RMSEs in 202,012 and 202,101 continued to increase after reaching the AR but failed to reach the GAR during the whole forecasts. This indicates that their global PoPLs were both longer than 15 days. Although Lorenz (1969) pointed out that the upper limit of atmospheric predictability is no more than two weeks, some studies have found that the upper limit of atmospheric predictability is longer than two weeks because of external forcing signals, such as the sea ice component and sea surface temperature. We used ensemble forecasts and observed data from the ECMWF model, which takes account of the external forcing signals and so leads to a potential predictability that exceeds two weeks. Apart from the average global predictability of the EA regions, we also studied the regional global predictability. Figure 6 shows that the global PrPLs of the SAT are distributed heterogeneously across the EA regions. For 202,012, higher global PrPLs are found mainly across the northeastern and middle regions of EA, and they exceed 12 or even 15 days in places. Lower global PrPLs of less than 4 days occur mainly in some northern and southwestern regions of EA. Like 202,012, some northern and southwestern regions also had lower PrPLs than other regions of EA. However, on the whole, the global PrPLs in 202,101 were lower than those in 202,012. From Fig. 6, we see that the spatial distribution of PrPLs does not correspond to that of RMSE. That is, higher (lower) global PrPLs coincide with smaller (larger) RMSEs. This is because the global PrPLs are determined by both the RMSE and the AR. The RMSE is not the only factor to influence the global PrPLs. For the regions with larger RMSEs, such as northern EA, the ARs also have large values. This demonstrates that the RMSE will need more time to reach the large AR, thereby leading to high predictability in these regions.

After studying the global predictability of SATs in 202,012 and 202,101, we turned to the local predictability of the three extreme cold days that occurred over the two months. The ensemble forecasts have larger forecast errors for these three cold events and overall, northern EA had forecast SATs that were higher than the observed SATs, whereas southern EA had forecast SATs that were lower than the observed SATs. In addition, the RMSE tended to reach a larger size in less time if the start date is closer to the extreme SAT day. Using the BaSIC method, the corresponding IC date of the first ECE was 20,201,208. The RMSE increased from 20,201,208 but did not reach the AR on the extreme day (20,201,214), indicating that the local predictability was still not lost. For other dates preceding 20,201,208, the RMSEs grew to exceed the AR before the extreme day (figure not shown). Hence, the local practical predictability of the first ECE was 6 days (20,201,214–20,201,208). For the second and third ECEs, the local practical predictabilities were calculated to be 8 and 6 days, respectively, using the BaSIC method.

As the predictability is associated with the error growth, we further analyzed the growth of the forecast errors from the corresponding ICs for ECEs. For the first ECE, the larger forecast errors are distributed mainly across the northern-central and some western regions of EA, and the forecast errors extend to the southern regions as the forecast time increases. During the forecast, the northern regions always maintain larger RMSEs, which serve as a source of error to restrict the upper limit of the predictability. For the second ECE, the spatial forecast errors differ from those of the first ECE. During the early period, larger forecast errors are distributed over different EA regions; i.e., they are not confined only to the northern regions, but also cover the western and southeastern regions. During the later period, the forecast errors have increased across most parts of EA, and grown to a larger size. The growth tendency of the spatial forecast errors associated with the second ECE differs from the first, with the RMSE growth tendency extending from the north to the south. Therefore, different regions, especially the northern, western, and southeastern regions, serve as sources of error to restrict the upper limit of the predictability. For the third ECE, during the early period, some western and northern regions had larger forecast error distributions, similar to those of the first ECE. However, during the next few days, most regions showed simultaneous growth, which differs from the first event. Hence, from the growth of the spatial forecast errors, most regions (especially the northern regions) contributed to the loss of the local predictability for the third ECE.

Therefore, the three extreme cold events showed different spatial growth patterns in the forecast errors, even though they all occurred over a relatively short period of time. This demonstrates that these three events had different dynamical characteristics. In addition, our analysis shows that northern EA had larger forecast errors for the three cold events, which indicates that these northern regions are favorable for the growth of forecast errors and make a significant contribution to the loss of local predictability for these cold events. Adding more observation sites and reducing the initial errors in these northern regions may improve the forecast skill for extreme cold events like those studied here.

This paper demonstrates that our new BaSIC method was able to quantitatively analyze the local predictability of the three extreme cold events that occurred over the winter of 2020/21. In addition, the calculation of local predictability using the BaSIC method requires fewer computational resources than other approaches. Therefore, it is expected that the BaSIC method will be an effective approach for future atmospheric predictability studies, especially with respect to extreme weather and climatic events.