Improving statistical prediction and revealing nonlinearity of ENSO using observations of ocean heat content in the tropical Pacific

Abstract

It is well-known that the upper ocean heat content (OHC) variability in the tropical Pacific contains valuable information about dynamics of El Niño–Southern Oscillation (ENSO). Here we combine sea surface temperature (SST) and OHC indices derived from the gridded datasets to construct a phase space for data-driven ENSO models. Using a Bayesian optimization method, we construct linear as well as nonlinear models for these indices. We find that the joint SST-OHC optimal models yield significant benefits in predicting both the SST and OHC as compared with the separate SST or OHC models. It is shown that these models substantially reduce seasonal predictability barriers in each variable—the spring barrier in the SST index and the winter barrier in the OHC index. We also reveal the significant nonlinear relationships between the ENSO variables manifesting on interannual scales, which opens prospects for improving yearly ENSO forecasting.

1 Introduction

El Niño–Southern Oscillation (ENSO) is the dominant mode of interannual climate variability which originates in the tropical Pacific, but impacts climate conditions over the world (Trenberth 2019; Alexander et al. 2002; Wang and Picaut 2004). Historically, two conceptual elements are considered as key ingredients underlying ENSO. The first one is a Bjerknes mechanism (Bjerknes 1969) based on positive ocean-atmosphere feedback: weakening of the trade winds in response to increasing sea surface temperature (SST) results in even warmer SST in the equatorial eastern and central Pacific. The second was realized by Wyrtki (1975, 1985), who supposed that accumulation of warm water in the equatorial Pacific is a necessary precondition for the initiation of a warm ENSO event (El Niño). Strong trade winds contribute to accumulating warm water in the western part of the basin, thus building up of the east-west slope of sea level. Eventually, excessive amount of warm water provides favorable conditions for triggering the Bjerknes feedback yielding the weakening of the trade winds due to increasing of SST that contributes to eastward transport of accumulated warm water. Further studies developed the Bjerkens–Wyrtki hypothesis to explain the distinctive cyclic nature of ENSO. In the so-called recharging oscillator theory of ENSO, charge-discharge of the warm water, and hence, the heat content in the tropical Pacific is regarded as a key process underlying the observed oscillations (Cane and Zebiak 1985; Jin 1997). This theory involves the meridional subsurface water transport driven by the wind stress curl (also known as Sverdrup transport) as the main source of the heat content alteration. The anomalous heat content stored in the tropics due to the equatorward mass transport during the cold (La Niña) and neutral phases of ENSO eventually enables an El Niño event onset, which, in turn, changes the wind stress curl outside the equator, and, as a result, discharges warm water. After that the charging stage of the oscillation starts again. Alternative theory of ENSO is based on the delayed oscillator models (Suarez and Schopf 1988; Galanti and Tziperman 2000) highlighting the role of oceanic equatorial waves as carriers of thermocline depth anomalies along the equator. Such anomalies impact the SST and therefore can lead to initiating the Bjerknes feedback. Different directions and propagating times inherent for different equatorial wave modes provide complex quasiperiodical ENSO-like oscillations in such models. All the key physical processes that theories account for are shown to take place in the coupled shallow-water ocean-atmosphere models (Zebiak and Cane 1987; Anderson and McCreary 1985; Jin and Neelin 1993). The role of stochastic forcing in ENSO dynamics is also important, as was noticed (e.g., in Philander and Fedorov 2003; Fedorov et al. 2003; Chen et al. 2016; Hu and Fedorov 2019; Martinez-Villalobos et al. 2019), since it is responsible for ENSO irregularity. Typically, it is associated with an atmospheric noise producing short-scale zonal wind anomalies (e.g., westerly wind bursts (Levine and Jin 2017; Hu and Fedorov 2019)). Among the drivers of such anomalies are indicated, for example, the Madden–Julian oscillation (Zhang and Gottschalck 2002; Chiodi et al. 2014; Puy et al. 2016), or large-scale subtropical atmospheric patterns (Vimont et al. 2003; Sullivan et al. 2021).

Growing amount of high-resolution measurements of different geophysical fields in recent decades offers great opportunities of verifying existing concepts of ENSO as well as for constructing data-driven prognostic models. The data-driven, or statistical, ENSO models became an efficient tool for interseasonal ENSO forecasting; they can compete with dynamical, i.e. constructed from the “first principles”, models in this regard (Barnston et al. 2012). The common problem for both statistical and dynamical ENSO models is the spring predictability barrier (SPB) (Jin et al. 2008; Barnston et al. 2012) which substantially limits the tropical SST forecasts that start from the winter and spring seasons. Many statistical ENSO models (Penland and Sardeshmukh 1995; Kondrashov et al. 2005; Gavrilov et al. 2019) are based on purely SST anomalies in the tropical Pacific which accurate forecast is the main goal in ENSO predictive modeling (Barnston et al. 2012). In such models, the SPB is caused by the observed growing loss of autocorrelations in tropical SST trough May-June. Relying on theoretical understanding of ENSO, many studies are focused on finding additional atmospheric and oceanic predictors which can help to lower the SPB. Various predictors based on ocean heat content (OHC) (Clarke and Van Gorder 2003), warm water volume (Meinen and McPhaden 2000; Chen et al. 2020), as well as atmospheric fields (Clarke and Van Gorder 2003; Byshev et al. 2016; Chen et al. 2020; Mukhin et al. 2021) has been suggested. Nevertheless, there is still no conventional way to derive statistically justified predictors from data and to include them into prognostic models. Often (Chen et al. 2020; Mukhin et al. 2021) such predictors are determined by finding significant lagged correlations between time series of SST-based ENSO index which needs to be predicted and corresponding time series of another ENSO-related climate variables. Typically, the obtained predictors are passed to the model as a fixed forcing (e.g. as components of regression (Clarke and Van Gorder 2003; Chen et al. 2020)), but not as dynamical variables, which makes it difficult to use such models for “no look ahead” forecast requiring extrapolation of the predictors to the future.

In this study we introduce an efficient predictor of ENSO-related SST variability constructed from OHC anomalies in the tropical Pacific. The proposed signal is obtained simply using the standard empirical orthogonal function (EOF) decomposition. We construct an optimal data-driven ENSO model which uses this predictor along with the SST-based predictor as equitable dynamical variables. Being phase-shifted, these SST- and OHC-based variables complement each other providing proper phase space capturing the ENSO dynamics. We demonstrate that the model obtained surpasses the purely SST-based model in predicting SST variability and allows to substantially lower the SPB. Also, we show that joint analysis of the SST- and OHC-based variables uncovers the long-term nonlinear relationships between the ENSO variables, thus revealing ENSO nonlinerity on interannual time scales.

The paper is organized as follows. In Sect. 2 we present a general form of the proposed data-driven model of ENSO, outline its phase space, parameterizations and the learning procedure. In Sect. 3, we describe the analyzed data and the EOF analysis used for obtaining the variables capturing the meaningful processes contributing to ENSO dynamics. The different data-driven stochastic models (linear and nonlinear) based on obtained variables are compared. Then we analyze prediction skills and qualitative properties of the models. In Sect. 4 we discuss the obtained results and conclude.

2 Data-driven ENSO model

2.1 Phase space of the model

In constructing our ENSO model we use the concept of data-driven stochastic model developed in Molkov et al. (2012), Mukhin et al. (2015b), and Gavrilov et al. (2017) and adapted for high-dimensional and spatially distributed data in Mukhin et al. (2015a) and Gavrilov et al. (2019)). Let the time series ${\mathbf {X}}=({\mathbf {x}}_1,\ldots ,{\mathbf {x}}_N$), ${\mathbf {x}}_n \in \mathbb {R}^D$ represents observations of some ENSO-related climate variable obtained in D nodes of a spatial grid at equidistant time moments $t_1,\ldots ,t_N$. Without loss of generality, we suppose that the time series is monthly sampled and has zero mean, i.e. $\frac{1}{N}\sum \nolimits _{n=1}^{N}{\mathbf {x}}_n = {\mathbf {0}}$. We use the conventional Empirical orthogonal function (EOF) analysis (Hannachi et al. 2007; Hannachi 2021) to construct the phase space of the ENSO model from observed data ${\mathbf {X}}$. The corresponding state variables are obtained as d leading principal components (PCs) ${\mathbf {p}}_n={\mathbf {V}}^T{\mathbf {x}}_n,~{\mathbf {p}}_n \in \mathbb {R}^d$, i.e. the projections of data vectors ${\mathbf {x}}_n$ at time $t_n$ to d EOFs (columns of the $D \times d$ matrix ${\mathbf {V}}$), that explain a substantial part of data variance: $\sum \nolimits _{k=1}^d\left<p_{k,n}^2\right>_n$. The transformation from PCs space back into physical space is a linear map:

$$\begin{aligned} {\mathbf {x}}_n={\mathbf {V}}{\mathbf {p}}_n+{\mathbf {V}}'{\mathbf {p}}'_n, \end{aligned}$$

(1)

where ${\mathbf {V}}'$ is a $D \times D-d$ matrix, which columns are the residual EOFs and ${\mathbf {p}}'_n \in \mathbb {R}^{D-d}$ are the corresponding PCs.

Although the leading EOFs characterize the most meaningful processes contributing to the observed dynamics, the residual EOFs keep the useful information about short autocorrelations in the observed dynamics, which could improve the short-term prediction of a state trajectory. In this work we construct the evolution model for the leading and residual PCs separately. The particular functional form of the corresponding models in the context of ENSO modeling is described in the next section.

2.2 Functional form of the model

2.2.1 Leading PCs

The general form of the model we use for describing evolution of leading PCs is a stochastic model with memory (Molkov et al. 2012; Mukhin et al. 2015a; Gavrilov et al. 2017):

$$\begin{aligned} {\mathbf {p}}_{n}={\mathbf {f}}\big ({\mathbf {p}}_{n-1},\ldots ,{\mathbf {p}}_{n-l}\big )+\widehat{{\mathbf {g}}}\cdot \varvec{\xi }_n. \end{aligned}$$

(2)

Here the first term ${\mathbf {f}}$ is a deterministic function depending on l successive states of the system. The second term in (2) is a random component aimed at modeling poorly resolved processes (e.g., the processes which time scales are close to the sampling time). This component is expressed as the product of a low-triangular deterministic $d \times d$ matrix $\widehat{{\mathbf {g}}}$ and a random vector $\varvec{\xi }_n \in \mathbb {R}^d$ which is assumed taken from Gaussian uncorrelated (in space and time) processes with zero means and unit variances. Resulting noise in the model has the covariance matrix $\widehat{{\mathbf {g}}}\widehat{{\mathbf {g}}}^T$. Note that neither parameters of the function ${\mathbf {f}}$ nor the matrix $\widehat{{\mathbf {g}}}$ are know a priori; they need to be estimated through model learning.

In this work we use two different parameterizations of deterministic part ${\mathbf {f}}$ of the model (2) which account phase locking of the ENSO dynamics to the annual cycle (Chen and Jin 2020). The first one is a linear parameterization, suggested by Mukhin et al. (2021):

$$\begin{aligned} {\mathbf {f}}\big ({\mathbf {z}}_n\big )={\mathbf {A}}_n{\mathbf {z}}_n. \end{aligned}$$

(3)

Here ${\mathbf {z}}_n \in \mathbb {R}^{ld}$ contains the components of the vectors ${\mathbf {p}}_{n-1},\ldots ,{\mathbf {p}}_{n-l}$, ${\mathbf {A}}_n$ is a $d \times ld$ matrix of coefficients. To model the seasonal forcing needed for accounting possible annual cycles in data, the coefficients are defined to be periodic with the period $T=12$ month. They are decomposed into the discrete Fourier series:

$$\begin{aligned} {\mathbf {A}}_n={\mathbf {A}}^0+\sum _{k=1}^{q}\left[ {{\mathbf {A}}^k_c \cos {\frac{2\pi k }{T}n}+{\mathbf {A}}^k_s \sin {\frac{2\pi k }{T}n}}\right] , \end{aligned}$$

(4)

where the parameter q taking values from 0 to 6 (${\mathbf {A}}^6_s={\mathbf {0}}$ by definition; the case $q=0$ corresponds to a simple linear model with constant ${\mathbf {A}}_n={\mathbf {A}}^0$) regulates possible dependence of the model on different harmonics of the annual cycle.

The second parameterization we consider is nonlinear. In this case the deterministic part ${\mathbf {f}}$ of the model is represented by a single layer perceptron with the hyperbolic tangent activation function:

$$\begin{aligned} {\mathbf {f}}\big ({\mathbf {z}}_n\big )=\sum \limits _{i=1}^m\varvec{\alpha }_{i} \tanh (\varvec{\omega }_{i}^T{\mathbf {z}}_n+\varvec{\delta }_{i}^T{\mathbf {c}}_n+\gamma _{i}). \end{aligned}$$

(5)

Here ${\mathbf {c}}_n=\left( \cos \frac{2\pi }{T}n,\sin \frac{2\pi }{T}n\right)$ is a two-dimensional harmonic signal which is passed to the model input together with the sate vector ${\mathbf {z}}_n$ in order to model the seasonal forcing, $T=12$ month, $\varvec{\alpha }_i\in \mathbb {R}^{d}$, $\varvec{\omega }_i\in \mathbb {R}^{ld}$, $\varvec{\delta }_i\in \mathbb {R}^{2}$, $\gamma _i\in \mathbb {R}$ are the unknown coefficients. The function in the form (5) is able to approximate an arbitrary nonlinear dependence just by increasing the number of neurons m (Cybenko 1989). The efficiency of such a parameterization in different ENSO-related examples was demonstrated in Mukhin et al. (2015a, b), and Gavrilov et al. (2019).

Given some fixed value of the leading d PCs, the complexity of the model deterministic part ${\mathbf {f}}$ is defined by its structural parameters (or hyperparametrs) l, q in the case of linear parameterization (3)–(4) and l, m in the case of nonlinear parameterization (5). To avoid overfitting of the model, the choice of the hyperparameters should be statistically justified, or optimal. According to Gavrilov et al. (2017, 2019), and Mukhin et al. (2021), we use the Bayesian optimality criterion for estimating them, which relies on assessing the probability density function of data given the particular model; see details in Appendix A.

2.2.2 Residual PCs

When mapping the phase variables of the model (2) to the physical space (e.g. SST field defined on geographical grid), the forecast produced by the model can be slightly improved by taking into account dynamics of the residual PCs of the field of interest, which are not included in the phase space of the model. For this purpose, we construct a simple additional model for the residual PCs in the same way as described by Gavrilov et al. (2019). According to this work, the evolution law of each k-th residual PC $\{p_{k,n}'\}$ ($k= 1,\ldots ,D-d$) is approximated by the first-order autoregressive model separately:

$$\begin{aligned} p'_{k,n}=b_k p'_{k,n-1}+\sigma _k\cdot \eta _{k,n}. \end{aligned}$$

(6)

Here $\{\eta _{k,n}\}$ is a sample of the uncorrelated Gaussian noise with the variance equal to 1 and zero mean, $b_k$ and $\sigma _k$ are the parameters estimated by the least square method. In doing so, we represent the residual PCs as independent red noise processes. Including such a model in the forecasting scheme is aimed at improving the prediction skills at lead times of order of autocorrelation times of the processes captured by the residual PCs.

3 Results

3.1 Data and preprocessing

We construct the data-driven model from two datasets reflecting ENSO-related variability. The first one is the monthly sea surface temperature (SST) taken from extended reconstructed SST (ERSST) data set (version 5) with $2^{\circ }\times 2^{\circ }$ spatial resolution (Huang et al. 2017). The second dataset is the monthly time series of ocean heat content (OHC) in 0–300 m depth layer defined on a $1^0\times 1^0$ grid provided by the Institute of Atmospheric Physics (Cheng et al. 2017). From both datasets we took data in the tropical Pacific region (10 S–10 N, 120 E–80 W) covering the time interval from Jan 1960 to Dec 2020; the total duration of the time series is $N=732$ months. The anomalies were prepared from this data by subtracting the monthly climatology within the 1960–2020 interval followed by removing the linear regression on the CO$_2$ trend. Note that such a simple subtraction of the monthly climatology does not remove the annual cycle completely, because its contribution to ENSO dynamics is generally non-additive. The data-driven model with periodic dependence described in Sect. 2.2 allows to reflect a non-additive response of ENSO to the annual cycle, i.e. ENSO phase locking which is discussed in Sect. 3.3.2.

3.2 EOF analysis

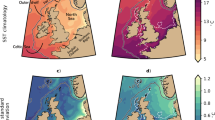
Figure 1 shows the spatial patterns corresponding to the two leading EOFs of the sea surface temperature anomalies (SSTA) and ocean heat content anomalies (OHCA) fields obtained as described in Sect. 3.1. For both data sets they explain more than 70% of data variance. It is often noted (Martinez-Villalobos et al. 2019; Deser et al. 2009; Bamston et al. 1997) that the first EOF of SSTA in the tropical Pacific is associated with ENSO and the corresponding PC strongly correlates with the Niño 3.4 index. The second EOF together with the first EOF allow to describe the diversity of ENSO, i.e. variety of SSTA patterns arising during different El Niño events (e.g., “canonical” or “Modoki” El Niño (Takahashi et al. 2011)).

Fig. 1

Spatial patterns corresponding to the two leading EOFs of SSTA (top panel, color scale in $^{\circ }$C) and OHCA (bottom panel, color scale in $10^9$ J/m$^2$) fields. Fractions of explained variance in percentage are shown for each EOF in the titles of the panels

Fig. 2

Phase trajectories reflecting the relationships between the leading PCs of SSTA and OHCA in different planes. The color markers correspond to December of the year of a very strong El Niño event (as classified by https://ggweather.com/enso/oni.htm). All quantities are normalized by their standard deviations. The absolute values of the Pearson correlation coefficient between the PCs are shown in the titles of the panels

In order to interpret the OHCA EOFs we consider the planes of different combinations of the two leading SSTA and OHCA PCs (Fig. 2). It is clearly seen from this figure that the first OHCA and SSTA PCs strongly correlate (Fig. 2b). Note that the corresponding EOF patterns shown in Fig. 1a, c are also similar. What we can learn from the Fig. 2c, d is a cyclic nature of trajectories in both SSTA PC1-OHCA PC2 and OHCA PC1-PC2 planes indicating an apparent phase shift between these variables. We obtain that the peak absolute value of correlation between the SSTA PC1 and OHCA PC2 is achieved with a lag of about 5–9 months, as Fig. 3b demonstrates. We note that the similar results about the relationships between SST and OHC in the tropical Pacific have been obtained by Meinen and McPhaden (2000) and Clarke et al. (2007) using warm water volume observations. The EOF pattern corresponding to the second OHCA PC (Fig. 1d) dominates mainly in the central and western tropical Pacific and can be associated with the OHC accumulation and discharge before and during the El Niño events (Zebiak 1989; Clarke et al. 2007; Cheng et al. 2019).

Fig. 3

Comparison of the SSTA PC1 and the OHCA PC2. Top panel: time series of the SSTA PC1 (blue) and the OHCA PC2 (red), divided by their standard deviations. Bottom panel: lagged cross correlations between these time series (see the legend)

Fig. 4

Spatial distributions of the SSTA forecast RMSE (normalized by the standard deviation of the CO$_2$ detrended SSTA time series at each grid point) given by three different models for different lead time. The contours in the central and right panels bound the areas of significant improvements for the forecast RMSE of joint L-SST + OHC and NL-SST + OHC models over the separate L-SST model

3.3 ENSO modeling

In this section we analyze prediction skills and qualitative properties of the different data-driven ENSO models, built in accordance with the scheme described in the Sect. 2. As it follows from the analysis performed in the previous section, the first SSTA (OHCA) and second OHCA PCs contain most useful information about ENSO dynamics. We can state that they reflect the ENSO recharge oscillator and are therefore the correct choice of phase variables for the stochastic model (2). Although the first OHCA and SSTA PCs are very close (see Fig. 2b), here we use the last one, since it can be mapped directly to the SSTA field or, in particular, to the widely used Niño 3.4 index. Here we construct and compare the stochastic models of the following types:

• 1. Separate linear models (3)–(4), the first learnt from the SSTA PC1 (L-SST model) and the second—from the OHCA PC2 (L-OHC model);

• 2. Joint linear model (3)–(4), i. e. the model learnt from both these PCs (L-SST+OHC model);

• 3. Joint nonlinear model (5) (NL-SST+OHC model).

We train each model using the Bayesian optimization procedure described in Appendix A. The estimated optimal values of the hyperparameters are $l=2$ and $q=1$ for the L-SST and L-SST+OHC models, $l=3$ and $q=1$ for the L-OHC model and $l=2$ and $m=5$ for the NL-SST+OHC model. Note that the the obtained $q=1$ implies the coefficients of a model are the sine functions with the period $T=12$ month, see Eq. (4). The future states of the system can be predicted by iterating these models starting from the current states. Then the predicted values of PCs can be transformed to the physical space (e.g. the Niño 3.4 index) using Eq. (1), where the residual PCs are all SSTA PCs except for the SSTA PC1. Since the described models are stochastic (see Eqs. (2) and (6)), the forecasts they produce are random sequences of states, which means that different model runs yield different forecasts. According with (Gavrilov et al. 2019; Mukhin et al. 2021), the future value of a quantity x is assessed from a model forecast as the ensemble median $\overline{x}$ over a large number of the model runs.

3.3.1 Prediction skill analysis

To analyze and compare prediction skills of the data-driven models, we use two conventional metrics. The first one is the root mean square forecast error (RMSE), defined through the differences between the true and predicted values of a variable of interest x, for the time instances inside the learning set:

$$\begin{aligned} e_j=\sqrt{\frac{\sum \nolimits _{n=l}^{N-j}(x_{n+j}-\overline{x}_{n,j})^2}{N-j-l+1}}. \end{aligned}$$

(7)

Here the index j denotes the forecast lead time in months, $x_{n+j}$ is a true value of the predicted variable at time $t_{n+j}$, $\overline{x}_{n,j}$ is the value predicted by the model starting at time $t_n$.

Fig. 5

Seasonal dependence of the prediction skills of different models calculated for the Niño 3.4 index. The forecast RMSE 7 normalized by the standard deviation of the CO$_2$ detrended Niño 3.4 index (upper panels) and the correlations 8 (bottom panels) are shown for different target months and lead times ranging from 1 to 12 months. The contours in the central and right panels bound the areas of significant improvements of the joint L-SST + OHC and NL-SST + OHC model prediction skills relative to the separate L-SST model. The left-tailed statistical test is used for the RMSE metric, and the right-tailed test is used for the correlation metric (see the text)

Fig. 6

The same as in Fig. 5 but for the OHCA PC2 (see the text). The RMSE is normalized to the standard deviation of the OHCA PC2

Fig. 7

Leading temporal EOF in ENSO dynamics. Top panel: variance explained by the leading temporal (12-month) EOF of the SSTA PC1 (a) and the OHCA PC2 (b) is shown as a function of the first month of the EOF. The black boxes correspond to the data-based PCs and the color curves correspond to the PCs produced by the L-SST + OHC (blue) and NL-SST + OHC (red) models. Bottom panel: the leading temporal EOF of the SSTA PC1 (c) and the OHCA PC2 (d). The black curves correspond to the data-based temporal EOFs and the color curves correspond to the temporal EOFs in the behavior of the L-SST + OHC (blue) and NL-SST + OHC (red) models. The 90% confidence intervals are evaluated using the ensemble of 1000 model runs (see the text)

The second metric is the Pearson correlation between the variable and its forecast:

$$\begin{aligned} r_j=\frac{\sum \nolimits _{n=l}^{N-j}\varDelta x_{n+j}\cdot \varDelta \overline{x}_{n,j}}{\sqrt{ \sum \nolimits _{n=l}^{N-j}(\varDelta x_{n+j})^2 \cdot \sum \nolimits _{n=l}^{N-j}(\varDelta \overline{x}_{n,j})^2 }}, \end{aligned}$$

(8)

where $\varDelta x_{n+j}$ and $\varDelta \overline{x}_{n,j}$ are the deviations of $x_{n+j}$ and $\overline{x}_{n,j}$ from their means. The metrics (7)–(8) complement each other: while the RMSE measures a distance between the real and predicted values, the correlation metric reflects their relative similarity (in terms of linear relationships).

Hindcast skill of SST field

In practice, the correct prediction of SST variability in the tropical Pacific is the main goal of both statistical and dynamical ENSO models (Barnston et al. 2012). Figure 4 shows the spatial distributions of RMSE for all components ${\mathbf {x}}_n$ of the SST field obtained using the three considered models described above. As we can see from Fig. 4, all models provide the best forecasts in the central tropical Pacific, for lead times up to 5 months. At the same time, both the L-SST + OHC and NL-SST + OHC models yield significantly lower the RMSE than the L-SST model for lead times up to 11 months.

To find the areas where these SST + OHC models demonstrate statistically significant improvements of the prediction skills, we use a surrogates test similar to the test suggested by Mukhin et al. (2021). First, we produce 1000 surrogates of the first SSTA PC using the optimal L-SST model and 1000 surrogates of the second OHCA PC using the optimal L-OHC model. Each surrogate is a stochastic time series produced by the corresponding model starting from random initial point. The length of each surrogate $N=732$ months is equal to the length of the original dataset. Then we train the SST+OHC models with optimal values of their hyperparametes on each pair of surrogates and calculate the metric (7) in the physical space. Using the obtained ensemble of the RMSE values we can find the areas where the RMSE of the SST + OHC models constructed from data lies on the tail of distribution. Thus the null hypothesis to be rejected supposes that the model that includes the information about both SST and OHC variability delivers the same prediction skills as the separate SST and OHC models. The areas where the null hypothesis is rejected at significance levels of 0.1 and 0.35 are marked by contours in Fig. 4. We observe that the the most significant improvements of the 11-month prediction skills using the SST+OHC models appears in the central tropical Pacific around the Niño 3.4 region (5 S–5 N, 160 E–150 W) (Bamston et al. 1997).

Seasonal dependence of model prediction skills

Figure 5 shows the month-to-month distribution of the prediction skill of different models for the Niño 3.4 index. The top panel corresponds to the RMSE metric (7) and the low panel—to the correlation metric (8). For all models we observe drop of the skills in the Niño 3.4 forecasts in the late spring and summer months. In other words, the Niño 3.4 index is less-predictable in the months when ENSO events normally start to develop. It is a manifestation of the so-called ”spring predictability barrier” which is a common problem for statistical and dynamical ENSO models (Bamston et al. 1997). From Fig. 5 one can see that the joint SST+OHC models have significantly better prediction skills as compared with the separate linear SST model, for all months including ones associated with the spring barrier. The 0.1 and 0.35 significance levels are evaluated for both metrics using the statistical test described above with 1000 surrogates. Figure 6 displays the month-to-month dependence of the prediction skills for second OHCA PC, which plays the role of an index characterizing OHC accumulation in the tropical Pacific. For this variable, we also see the predictability barrier, but now the drop of the prediction skills falls in the winter months.Thus we obtain that predictability barriers of first SSTA PC and second OHCA PC are shifted to each other by 5–7 months. It is consistent with Fig. 3 which demonstrates the equivalent phase shifting between these PCs. Again, the SST + OHC models outperform the separate OHC-based model.

In this section we found that both the L-SST + OHC and NL-SST + OHC models yield significant benefits in the forecast as compared with separate models. At the same time, they deliver almost the same prediction skills, with no significant differences. This means that the nonlinearity does not matter for intra-annual multi-month forecasts in the tropical Pacific region. In the next section, we show that, nevertheless, the NL-SST + OHC model captures significant nonlinear laws that manifest themselves in the observed dynamics on inter-annual scales.

3.3.2 Simulation of ENSO phase locking

The spring predictability barrier is closely connected with ENSO phase locking to the annual cycle (Liu et al. 2019). Tippett and L’Heureux (2020) demonstrated that approximately 90% of observed seasonal evolution of the Niño 3.4 index can be explained by deterministic year-long signal defined on the June–May interval, which reaches a maximum in December and has the lowest absolute values at the boundaries of the interval—in June and May. This signal, multiplied by different amplitudes in different June–May windows, “isolates the intrinsic seasonal cycle of ENSO evolution and its phase-locking to the annual cycle” (Tippett and L’Heureux 2020).

Technically, we can retrieve the seasonal cycle of this type from a monthly ENSO index by means of the EOF decomposition applied to the set of non-overlapping successive 12-month segments of the index time series. The leading EOF of the obtained yearly 12-channel time series (hereinafter, the temporal EOF) determines the required 12-month cycle, whereas the corresponding PC is a yearly time series of the cycle amplitudes. Obviously, this leading EOF depends on the dividing the time series into the segments, or, equivalently, selecting the start month of the segment. Since we naturally interest in obtaining the cycle that explains a substantial part of variability, we select the start month providing that the leading temporal EOF captures the largest variance of the original index.

Fig. 8

Relationships between state variables. Left column: the planes of the amplitudes of the leading temporal EOF of the SSTA PC1 (May is the first month) and the OHCA PC2 (January is the first month). Black points correspond to data and colored points—to the approximations of data via linear (blue) and quadratic regression models (red). Central and right columns: PDs in the same planes, estimated from 1000 runs of the L-SST + OHC and NL-SST + OHC models, respectively

We have checked if strong seasonal cycles underlie the first SSTA PC and second OHCA PC time series. The black boxes in Fig. 7 indicate the fraction of variance explained by the leading temporal EOFs depending on the segment start months. This figure shows a strong cycle in the SSTA PC that starts in May–June and captures about 86% of variance, which is in agreement with the results obtained by Tippett and L’Heureux (2020) for the Niño 3.4 index. For the second OHCA PC, 88% of variance is explained by the cycle starting from December–January. This tells us that we would be facing a winter (not spring) barrier, if we constructed a model based on this OHC time series alone. In Fig. 7c, d the temporal EOFs determining the shapes of the above cycles are plotted. Although, as expected, the SST cycle peaks in December, the OHC accumulation cycle culminates in August–September.

Now let us look how our data-driven models reproduce these cycles. We repeated the cycle analysis described above for the time series generated by both the L-SST + OHC and NL-SST + OHC models; the results are shown in Fig. 7 by blue and red, respectively. We performed 1000 model runs per model, calculated the leading temporal EOFs for each time series from this ensemble, and then evaluated the confidence intervals for the EOFs and variances in each month. Overall, we can say that both models reproduce well the temporal EOF patterns and therefore capture the seasonal cycles in the two key variables of ENSO.

Fig. 9

Testing the significance of the quadratic term. PDs of the coefficient C of the quadratic model fitted to each of 1000 surrogate time series produced by the linear model. Each plot from left to right corresponds to a particular plane from Fig. 8a–d. Blue lines denote the values of coefficient C of the quadratic model fitted on data. Red lines mark the 10th and 90th percentiles

Figure 8a–d shows several planes of lead-lag and synchronous dependencies between the temporal EOF (cycle) amplitudes in the SSTA PC1 and the OHCA PC2 time series. It can be observed from the planes (c) and (d) that the dependencies of the OHC cycle amplitude on the previous OHC and SST cycle amplitudes look nonlinear. To verify the nonlinearities observed, we fit the linear $Y=B\cdot X+A+\varepsilon$ as well as quadratic $Y=C\cdot X^2+B\cdot X+A+\varepsilon$ functions to the observed dependencies and analyze the significance of the quadratic terms. The traditional least square method was used for estimating the coefficients A, B and C as well as the variance of an approximation error $\varepsilon$ represented as Gaussian noise without point-to-point correlations. The resulting fits are shown by blue and red in Fig. 8a–d. We can notice that the curves of the linear and quadratic models are most distinct in the planes (c)–(d). Testing the significance of the quadratic approximation can be performed via rejecting the null-hypothesis that the obtained value of the coefficient C in the quadratic term could be obtained from a similar sample but with a linear dependence between variables. For each plane, using the linear function fitted to the original sample, we generated an ensemble of 1000 random surrogate samples. Then we fitted the quadratic model to each surrogate and used the resulting values of C as the ensemble corresponding to the null-hypothesis. Such ensembles relating to the planes from Fig. 8 are shown in Fig. 9. It is seen from this figure that the quadratic approximation is significant by level 0.1 for the planes (c) and (d) from Fig. 8 indicating an apparent nonlinear dependence of the current OHC cycle on the previous OHC and SST cycles.

Next, we can use our optimal data-driven models for verifying the detected nonlinear relationships. To this end, we took an ensemble of 1000 monthly time series of SSTA PC1 and OHCA PC2 generated by the NL-SST + OHC model, and, for comparison, the same ensemble but generated by the L-SST + OHC model. Then we calculated the OHC and SST cycles amplitudes from these time series and plotted resulting probability densities (PDs) in the planes shown in Fig. 8. Naturally, no nonlinearity can be captured by a linear model, therefore, the L-SST + OHC model yields Gaussian PD in all the planes considered. However, the optimal nonlinear (NL-SST + OHC) model produces apparently non-Gaussian PDs thus confirming pronounce nonlinear laws underlying the inter-cycle dynamics. We can also conclude that although this nonlinear model does not provide additional benefits in short-term forecasting over the linear model, it nevertheless more adequately reflects the dynamical properties of ENSO on interannual scales.

4 Discussion

In this study we have utilized gridded datasets of the tropical Pacific SST and OHC anomalies in the 0–300 m depth layer to reveal the dynamical variables containing meaningful information about ENSO as well as to construct the data-driven model based on these variables. The EOF analysis applied to both data sets clearly demonstrates phase relationships between the first SSTA and second OHCA PCs yielding the largest absolute cross-correlations when the corresponding time series are shifted by about 5–9 months. While the first SSTA EOF is known to be associated with SST variability in the highly ENSO-related region, the second OHCA EOF, in accordance with Clarke et al. (2007), likely reflects the OHC accumulation and discharge before and during the El Niño events, respectively.

We constructed and compared different (linear and nonlinear) data-driven stochastic models based on the SSTA PC1 and OHCA PC2 variables taken separately and together. It is shown that the data-driven models combining these two variables yield significant benefits in predicting both the SST and OHC variability and allow to substantially lower the seasonal predictability barriers as compared with the separate models. Thus the second OHCA EOF can be used as an effective additional ENSO predictor in statistical models.

We then obtained that the seasonal cycles (dominating 12-month patterns) in SST and OCH variability are different: while the SST cycle peaks in early winter and drops in late spring, the OHC accumulation cycle is shifted forward by approximately 8 months. Generally speaking, a strong seasonal cycle in a single variable, defined as the leading temporal EOF, unavoidably leads to the existence of a predictability barrier when we use a statistical model derived from the time series of this variable. The reason is that the variable values at months inside the cycle interval are highly correlated, but the inter-cycle connections are more stochastic. A possible way to overcome such a barrier is to invoke an additional variable that is connected with the original one, but has no barrier in the same months. As it is seen from Figs. 5, 6 and 7, there is a pronounce winter (Dec–Jan) predictability barrier in the OHC accumulation variability, in contrast to the well-known spring barrier in the SST variability. Note that if the similar seasonal patterns in the SST-based Niño-family indices are mentioned in other studies (Kondrashov et al. 2005; Tippett and L’Heureux 2020; Chen and Jin 2020, 2021), the corresponding OHC seasonal evolution has not been in focus yet. Since it is found that the joint SST+OHC models outperform the separate SST and OHC models in prediction skill, we conclude that the detected SST and OHC accumulation cycles strongly interact, and hence, the use of the combined SST-OHC phase space helps to lower the seasonal barriers in the ENSO variables.

We also derived from data that the inter-annual interaction of the cycles is substantially nonlinear, and the optimal data-driven model with the nonlinear parameterization confirms this. It is important that ENSO manifests its nonlinear dynamical properties on long, interannual scales, while nonlinearity on several-month intervals is not resolved. This finding opens prospects for developing nonlinear statistical models for yearly ENSO variability, which could expand the horizon of ENSO forecasts.

Appendix: Bayesian approach to ENSO model learning and optimization

Here we outline the Bayesian approach we use for learning and optimization of the stochastic model (2). The optimal model relied on observed data is supposed to be a right balance between the “too simple” model poorly describing data and “too complex” model which contains too many parameters and tends to be ovefitted to the available sample rather than to capture the laws underlying the dynamics. Let the ${\mathbf {H}}=\left\{ H_1,H_2,\ldots ,H_i,\ldots \right\}$ is the set of possible hypotheses about the model complexity. In the case of a stochastic model (2) each hypothesis $H_i$ is determined by the particular combination of the hyperparametrs l, q in the case of the linear parameterization (3)–(4) of deterministic part ${\mathbf {f}}$ and l, m in the case of the nonlinear parameterization (5). According to the Bayes rule the probability $P(H_{i}|{\mathbf {Y}})$ that the model $H_i$ produces the observed time series ${\mathbf {Y}}=({\mathbf {p}}_1,\ldots ,{\mathbf {p}}_n)$ is equal to:

$$\begin{aligned} P(H_{i}|{\mathbf {Y}})=\frac{P({\mathbf {Y}}|H_{i} )P(H_{i} )}{\sum _{i}P({\mathbf {Y}}|H_{i})P(H_{i})}. \end{aligned}$$

(9)

Here probability density function (PDF) $P({\mathbf {Y}}|H_{i} )$ is the evidence (marginal likelihood) of the model $H_i$ characterizing the probability of the observed data ${\mathbf {Y}}$ to belong to the whole possible ensemble of time series which can be produced by the model $H_i$; $P(H_{i} )$ is a prior probability of the model $H_i$. The denominator in (9) is a normalization term which does not depend on $H_i$. Assuming all the models from ${\mathbf {H}}$ equiprobable a priori, the expression (9) can be rewritten as $P(H_{i}|{\mathbf {Y}})=\alpha P({\mathbf {Y}}|H_{i} )$ where $\alpha$ is independent of $H_i$. Let us define the Bayesian criterion of the model optimality

$$\begin{aligned} L=-\log {P({\mathbf {Y}}|H_{i} )}, \end{aligned}$$

(10)

minimization of which leads to maximization of the PDF $P({\mathbf {Y}}|H_{i} )$. The optimality criterion (10) has a clear interpretation. If the model $H_i$ is too simple, than the observed data likely lie on a tail of the PDF $P({\mathbf {Y}}|H_{i} )$. Therefore, the probability that the observed data ${\mathbf {Y}}$ could be produced by such a model is small. In contrast, the overfitted model, due to a large number of parameters, produces a widely distributed population of different datasets, which lowers again the PDF of the observed ${\mathbf {Y}}$. Therefore, the optimality (10) helps to select the optimal model that is neither too simple nor overfitted model.

The evidence $P({\mathbf {Y}}|H_{i} )$ is expressed via integration of the product of the corresponding likelihood function $P({\mathbf {Y}}|\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}},H_{i} )$ and the prior distribution $P(\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}}|H_{i} )$ over the model parameter space:

$$\begin{aligned} \begin{array}{c} P({\mathbf {Y}} |H_i) = \int P({\mathbf {Y}}|\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}},H_{i} ) \cdot P(\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}}|H_{i} ) d\varvec{\mu }_{{\mathbf {f}}}\varvec{\mu }_{\widehat{{\mathbf {g}}}}. \end{array} \end{aligned}$$

(11)

Here the vectors $\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}}$ contain parameters of the deterministic part ${\mathbf {f}}$ and the stochastic part of the model (2), respectively. The likelihood function $P({\mathbf {Y}}|\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}},H_{i} )$ corresponds to the assumption that the stochastic part of the model is the delta-correlated in time Gaussian process with the amplitude $\widehat{{\mathbf {g}}}$ (see Sect. 2.2.1):

$$\begin{aligned}P({\mathbf {Y}}|\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}},H_{i} ) = \nonumber \\ \prod \limits _{n=1}^{l}P_\mathcal {N}({\mathbf {p}}_n,\widehat{I}) \times \prod \limits _{n=l+1}^{N} P_\mathcal {N}({\mathbf {p}}_n-{\mathbf {f}}\big ({\mathbf {p}}_{n-1},\ldots ,{\mathbf {p}}_{n-l}\big ),\widehat{{\mathbf {g}}}\widehat{{\mathbf {g}}}^T). \end{aligned}$$

(12)

Here $\hat{I}$ is the $d \times d$ identity matrix, $P_\mathcal {N}({\mathbf {u}},\widehat{\Sigma }):=\frac{1}{\sqrt{(2\pi )^{d} |\widehat{\Sigma }|}}\exp {\left( -\frac{1}{2} {\mathbf {u}}^{T}\widehat{\Sigma }^{-1}{\mathbf {u}} \right) }$, ${\mathbf {u}} \in \mathbb {R}^d$, $\prod \limits _{n=1}^{l}P_\mathcal {N}({\mathbf {p}}_n,\widehat{I})$ is a term describing PDF of the initial state of the model (see Gavrilov et al. 2017 for more details). The prior PDF $P(\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}}|H_{i} )$ is the product of Gaussian PDFs for each parameter of the model. The proper choice of dispersions of the corresponding PDFs for linear (3)–(4) and nonlinear (5) parametrizations is discussed in detail in Mukhin et al. (2021), and Seleznev et al. (2019).

The evidence (11) is estimated using the Laplace’s method based on approximate integrating in the neighborhood of maximum of integrand. Let us denote the minus logarithm of the integrand in (11) as $\varPsi _{H_i}(\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}})$. Then the integrand can be rewritten as:

$$\begin{aligned} \begin{array}{l} P({\mathbf {Y}}|\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}},H_{i} ) \cdot P(\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}}|H_{i} ) = \exp (-\varPsi _{H_i}(\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}})). \end{array} \end{aligned}$$

(13)

The integration of (11) using Laplace method by decomposing the function $\varPsi _{H_i}(\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}})$ in the neighborhood of its minimum into a second-order Taylor series leads to the following expression for the optimality criterion (10):

$$\begin{aligned} L= & {} -\log {P({\mathbf {Y}}|H_{i} )}\nonumber \\= & {} \varPsi _{H_i}(\overline{\varvec{\mu }_{{\mathbf {f}}}},\overline{\varvec{\mu }_{\widehat{{\mathbf {g}}}}})+ \frac{1}{2} \ln \left[ \frac{1}{(2\pi )^M}\left| \nabla \nabla ^T\varPsi _{H_i}(\overline{\varvec{\mu }_{{\mathbf {f}}}},\overline{\varvec{\mu }_{\widehat{{\mathbf {g}}}}}) \right| \right] . \end{aligned}$$

(14)

Here $\varPsi _{H_i}(\overline{\varvec{\mu }_{{\mathbf {f}}}},\overline{\varvec{\mu }_{\widehat{{\mathbf {g}}}}})$ is the function value at its minimum, M is full number of model parameters collected in vectors $\varvec{\mu }_{{\mathbf {f}}},\varvec{\mu }_{\widehat{{\mathbf {g}}}}$, $\nabla \nabla ^T \varPsi _{H_i}(\overline{\varvec{\mu }_{{\mathbf {f}}}},\overline{\varvec{\mu }_{\widehat{{\mathbf {g}}}}})$ is the $M \times M$ matrix of the second derivatives (hessian matrix) at the minimum. The first term in (14) reflects the accuracy of data approximation by the model. It decreases with expanding the model complexity, i.e. with growing of number of parameters, and therefore prevents too simple models. In contrast, the second term in (14) increases with growing of the number of model parameters and penalizes the overfitted models. The particular algorithm we use for numerical calculation of (14) can be found in Seleznev et al. (2019).

In practice, to select the optimal hyperparameters, we iterate over the integers q (or m) and l in a wide predefined range and select those that provide the smallest L. In this work we define the range $[ 0,1, \ldots , 6 ]$ for q, $[1,2,\ldots ,10]$ for m, and $[1,2,\ldots ,10]$ for l.