Understanding the links between climate feedbacks, variability and change using a two-layer energy balance model

Abstract

A simple, two-layer energy balance model (EBM) is used to investigate climate variability in Coupled Model Intercomparison Project Phase 5 (CMIP5) models and examine possible links between variability and climate sensitivity, and the roles of stochastic variability, radiative feedbacks and ocean mixing. The EBM represents global variability that, while somewhat stronger than the CMIP5 models, simulates reasonable ratios between shorter and longer timescales. Variability in the EBM to the range of parameters from the Global Climate Models is found to be particularly sensitive to stochastic variability, especially on interannual time-scales. Radiative feedbacks and ocean mixing parameters are also important, particularly for decadal timescales. A modest amount of the model-to-model spread in the variance of global temperature in the CMIP5 models is explained by the EBM. The EBM exhibits a stronger link between equilibrium climate sensitivity and the magnitude of the variability than it does for transient climate response, especially on decadal and longer timescales. The EBM results suggests that spread in stochastic forcing across the CMIP5 models is the single greatest factor degrading the correlation between variability and climate sensitivity, although model to model differences in radiative forcing and mixing into the deep ocean are also important. The findings suggest that from a theoretical point of view investigating constraints from variability may be a fruitful exercise. However, they also suggest that normalizing variability in general circulation models by stochastic forcing, uptake into the deep ocean and radiative forcing are all important first steps to reduce factors that will otherwise confound the correlations.

1 Introduction

Modelling suggests that further climate change this century is inevitable (Collins et al. 2013; Peters et al. 2013), but global and regional climate change projections retain large uncertainties for a given emissions scenario (Meehl et al. 2007; Collins et al. 2013; Boucher et al. 2013). Much of this uncertainty results from the range in ‘climate sensitivity’ in climate models (Flato et al. 2013; Grose et al. 2018), and constraining this range would bring profound benefits in reducing costs of mitigating and adapting to climate change (Hope 2015). The range of model sensitivity has long been known to result largely from differences in the strength of radiative feedbacks—particularly those of clouds (Bony et al. 2006; Zelinka et al. 2013).

At the same time, the climate system is characterized by large natural global scale variability on timescales from years to decades (e.g. Kirtman et al. 2013; Power et al. 2006; Hawkins and Sutton 2009; Deser et al. 2012). As is the case with climate sensitivity, the range of this variability manifest in climate models is extremely large. In particular, the decadal standard deviation of hemispheric or global scale temperatures in Coupled Model Intercomparison Project phase 5 (CMIP5, Taylor et al. 2012) models vary by a factor of more than four (Power et al. 2017; Colman and Power 2018). In contrast to climate sensitivity, however, the reasons for this range are not clear. Models do represent some features of e.g. the Interdecadal Pacific Oscillation (IPO, Power et al. 1999, 2006; Folland et al. 1999) but the structure of decadal variability differs widely (Meehl et al. 2012; Kosaka and Xie 2013; Dai et al. 2015). Furthermore, although representation of coupled ocean/atmosphere features such as the IPO are important for regional decadal variability (Chen and Tung 2014), their roles in global scale variability are less clear (Liu 2012). It is found that models with only mixed-layer physics can show global variability at longer timescales (decadal and beyond) only marginally weaker than that of fully coupled models (Middlemas and Clement 2016). This suggests that long term global variability may not be sensitively dependent on the details of ocean/atmosphere dynamic coupling but may be closer to a ‘Hasselmann’ style response (Hasselmann 1976) to shorter timescale stochastic forcing (Liu 2012; Roe 2009). This study will investigate climate variability under the Hasselmann framework, considering the contributions from feedbacks, stochastic forcing, and heat capacity.

Theory suggests that radiative feedbacks should play a role in the magnitude of climate variability at a range of timescales (Von Storch and Zwiers 2001; Roe 2009; Mahadevan and Deutch 2009). Interannual variability is known to have strong radiative feedbacks not only on regional scales (e.g. Sun et al. 2003; Bellenger et al. 2014; Li et al. 2015; Rädel et al. 2016; Myers et al. 2018), but also global scales (Colman and Power 2010). Individual feedback processes which have been found to operate on interannual timescales include water vapour, snow and cloud feedbacks (Minschwaner and Dessler 2004; Hall and Qu 2006; Qu and Hall 2014; Dessler 2010, 2013). Consistent with this, suppressing radiative feedbacks from water vapour or surface albedo in Global Climate Models (GCMs) reduces interannual variability (Hall and Manabe 1999, 2000; Schneider et al. 1999; Hall 2004), just as it does in forced climate change (Lahellec and Dufresne 2013). At decadal timescales, again both observations (Brown et al. 2014; Andrews et al. 2015; Zhou et al. 2016; Gregory and Andrews 2016; Ying and Huang 2016) and models (Brown et al. 2014, 2015; Colman and Hanson 2017; Colman and Power 2018) suggest an important role for radiative feedbacks in the magnitude and phase of variability.

Since feedbacks are established as important in both climate sensitivity and climate variability, there are grounds for expecting links between the magnitude of climate variability and climate sensitivity. Bolstering this expectation, relationships have been found across models for the strength of individual climate change feedbacks from decadal or interannual timescale changes with those from climate change (Dessler 2010, 2013; Dessler and Wong 2009; Zhou et al. 2015; Colman and Hanson 2013, 2017). However, a number of factors may confound a direct correlation between the magnitude of climate variability and change. For a start, radiative feedbacks are clearly not the only factor of importance. Theoretical considerations indicate that effective oceanic depth is important for setting the timescale and magnitude of the variability (Roe 2009; Farneti and Vallis 2011), but the relative importance of stochastic forcing, radiative feedbacks, and ocean effective depth/uptake on variability, and whether these are similar to the uptake response to climate forcing in transient climate change are less clear (Baker and Roe 2009; Soldatenko and Colman 2019).

The ultimate motivation behind the present paper remains the question of possible links—specifically correlations across different models—between variability and climate change in GCMs. If such correlations exist, they may permit observations of the former to constrain the latter. There are tantalizing hints of a relationship across CMIP5 models between equilibrium climate sensitivity (ECS) and the magnitude of decadal variability in the tropics (Colman and Power 2018), and between climate sensitivity and the spread in decadal length trends in global temperatures under unforced variability (Nijsse et al. 2019). Further, theoretical arguments from single layer stochastic/feedback models suggest such links are anticipated (Roe 2009; Williamson et al. 2018). A recent study by Cox et al. (2018a) attempted to establish such constraints from observations. In this particular case concerns have been subsequently raised on the effectiveness of removing the forced signal from the historical climate change temperature signal (Brown et al. 2018; Rypdal et al. 2018), but the overall approach remains one of considerable interest.

Links such as found by Colman and Power (2018) and Cox et al. (2018a, b) are only convincing if they are based on sound theoretical arguments, otherwise they are open to the possibility that they are simply statistical flukes. Indeed, in response to studies of this nature, Williamson et al. (2018) urge that ‘the search for emergent constraints (needs to) becomes more theory-led than it has been to date’. Williamson et al. (2018) lead the way with analysis of simple 1, 2 and multi-layer models asking what theory suggests for the relationships between short term-variability and climate change, and what differences it implies between pre-industrial and historical runs for CMIP5 models. This is a promising direction, but they do not examine what physical processes these simple models suggest are the causes of the wide spread in variability—i.e. what factors are the main ‘spoilers’ of the correlations between sensitivity and variability across the CMIP5 models, and how the relationships vary as a function of timescale of variability. The present study, then, uses the ‘theory-led’ approach to ask what simple models suggest about these factors, and how they relate to the CMIP5 models.

The approach taken is to develop and utilize a two-layer energy balance/feedback model (EBM) for the climate system, to explore and understand its variability on a range of timescales and to relate these to variability and climate change sensitivity found in the CMIP5 GCMs. The advantage of such a model is that it is simple to understand and easy to set up (with only 2 or 3 independent parameters); yet similar models have been shown to capture enough of the essentials of the climate system to be capable of quantitatively describing the transient response of GCMs to very different time dependent forcing with the same set of parameters (Held et al. 2010; Geoffroy et al. 2013a, b; Caldeira and Myhrvold 2013; Gregory et al. 2015). Of course, there are caveats in using such a simple model. Clearly, ocean/atmosphere dynamics and feedbacks play a critical role in the mechanisms driving patterns of variability such as El Nino-Southern Oscillation (ENSO), and ENSO related indices can explain around 30% of global interannual temperature variance in the observed record (Trenberth et al. 2002; Ayers 2017). Nevertheless, there is substantial evidence, as described above, of the important role of radiative feedbacks on global scales, and the utility of the ‘Hasselmann’ type approach for understanding variability.

In summary then, we will use the EBM approach to explore four questions:

• 1. How well can important aspects of global scale variability on timescales from interannual to multi-decades in CMIP5 models be understood and quantitatively described using a simple two-layer EBM?

• 2. What relative role do radiative feedbacks play in determining the magnitude of global variability, especially on longer timescales?

• 3. What parameters control potential relationships between the magnitude of variability and transient climate response (TCR) (Collins et al. 2013) and/or ECS.

• 4. What do differences across GCMs in their magnitude of stochastic forcing, the strength of radiative feedbacks and in other parameters therefore imply for the potential for constraining ECS or TCR through observations of variability.

The layout of this paper is as follows: Sect. 2 will describe the EBM. Section 3 will explore the sensitivity of variability in the EBM to model parameters. Section 4 will consider the relationships between variability and climate sensitivity in CMIP5 GCMs as represented by the EBM, and their sensitivity to different processes. Finally, summary and conclusions will be presented in Sect. 5.

2 Model description and analysis methodology

2.1 The energy balance model

The model used here is a two-layer EBM (Gregory 2000; Held et al. 2010; Rypdal 2012; Caldeira and Myhrvold 2013) that is comprised of two sub-systems: (a) atmosphere/land surface and the ocean mixed layer and (b) the deep ocean. Evolution of the model is described by the temperature perturbations T and T_D with respect to their reference (equilibrium) values T₀ and T_D,0 viz:

$$C\frac{dT}{dt} = - \lambda T - \gamma (T - T_{D} ) + F,$$

(1)

$$C_{D} \frac{{dT_{D} }}{dt} = \gamma (T - T_{D} ),$$

(2)

where $\lambda$ is a climate feedback parameter (in W m⁻² K⁻¹), $\gamma$ represents the coupling strength between the two subsystems (in W m⁻² K⁻¹) and characterizes the deep ocean heat uptake, and $F$ is a radiative forcing (in W m⁻²). The specific effective heat capacities $C$ and $C_{D}$ of the fast and slow subsystems are such that $C \ll C_{D}$. Temperature variation of the fast system $T$ is identified with the global mean surface temperature change.

Deterministic formulations of such 2-layer models have been considered and analyzed in a number of papers. Geoffroy et al. (2013a) (hereafter G13) explored the analytical solutions of the two-layer model for hypothetical climate forcing scenarios, and suggested the approach of calibrating the model parameters to imitate the dynamics of coupled ocean–atmosphere general circulation models from CMIP5. Gregory et al. (2015) analyzed the two-layer model and its upper-, zero- and deep-layer approximations, and discussed the TCR, the global mean surface air temperature change T under two scenarios, one with a step forcing (the abrupt 4 × CO₂ experiment) and one with the 1pctCO₂ scenario (atmospheric CO₂ increasing at 1% per year). Importantly, they found that despite the simplicity of the model, it was able to capture the evolution of average global surface temperature over time under both types of idealized forcing.

To explore model variability, we add stochastic radiative forcing $F_{s}$ (Hasselmann 1976) into the right-hand side of Eq. 1, approximated by a Gaussian delta-correlated random process with zero mean and variance $\sigma_{s}^{2}$.

The parameter $\sigma_{s}$, the standard deviation of stochastic forcing, requires some discussion which will be provided below. Here we only highlight that our objective is to study the climate variability on annual, decadal and multi-decadal (30 years) timescales. Therefore, stochastic forcing should reflect at least monthly timescale fluctuations of radiative forcing, which in this context can be viewed as ‘noise’.

The inverse of the climate feedback parameter $\alpha = 1/\lambda$ (in W m⁻² K⁻¹) is referred to here as the ‘sensitivity parameter’ (e.g., Eslami 1994; Rozenvasser and Yusupov 2000; Cacuci 2003). Note that this sensitivity is different to that of the Intergovernmental Panel on Climate Change (IPCC) terminology, ‘climate sensitivity’ which refers here to ECS or TCR. From the viewpoint of dynamical systems theory, we can interpret the ECS as the climate system’s sensitivity with respect to parameters around its attractor. For a system without radiative feedbacks (i.e. with only the ‘Planck’ response), we can define a ‘reference climate sensitivity parameter’ $\alpha_{0}$ (Bony et al. 2006; Roe 2009):

$$\alpha_{0} = \frac{1}{{4\varepsilon \sigma T_{0}^{3} }} \approx 0.30 \;{\text{W}}\;{\text{m}}^{ - 2} \;{\text{K}}^{ - 1} ,$$

(3)

where $\varepsilon = 0.62$ is the Earth’s emissivity (Karper and Engler 2013), $\sigma = 5.67 \times 10^{ - 8}$ is the Stephan-Boltzmann constant (in kg s⁻³ K⁻⁴), $T_{0} = 288$ K is the ‘reference’ global mean surface temperature. Note that an alternative formulation would set T₀ as the temperature at the effective radiating height in the atmosphere (around 255 K), and ε = 1.0. A slightly smaller α₀ (~ 0.27 W m⁻² K⁻¹) is calculated for this. In the present paper, we will adopt the usage in Eq. 3, as the EBM is formulated with respect to the surface temperature.

If we eliminate all radiative feedbacks, we obtain $\alpha_{0} \approx 0.30$ (Colman 2003; Roe 2009), and the corresponding climate feedback parameter $\lambda_{0} = 1/\alpha_{0} \approx 3.13\; ({\text{W }}\;{\text{m}}^{ - 2} \;{\text{K}}^{ - 1} )^{ - 1}$. For convenience, instead of $\lambda$, we can use the dimensionless feedback factor f such that $\lambda = (1 - f)/\alpha_{0}$ (e.g., Roe 2009). Introducing the deterministic radiative forcing caused by atmospheric greenhouse gases $F_{d}$, we can rewrite the equations of two-layer model as follows:

$$C\frac{dT}{dt} = - \frac{1 - f}{{\alpha_{0} }}T - \gamma (T - T_{D} ) + F_{d} + F_{s} ,$$

(4)

$$C_{D} \frac{{dT_{D} }}{dt} = \gamma (T - T_{D} ).$$

(5)

In practice, of course, in GCMs the net feedback factor is the result of contributions from water vapour/lapse rate, surface albedo and clouds (Colman 2003; Bony et al. 2006), but here the total f (or $\lambda$) only will be considered.

Deterministic radiative forcings to derive ECS and TCR for this model are:

• 1. Step function

$$F_{d} (t) = \left\{ {\begin{array}{*{20}l} 0 \\ {F_{{2 \times {\text{CO}}_{2} }} } \\ \end{array} } \right. \begin{array}{*{20}c} {\text{if}} \\ {\text{if}} \\ \end{array} \begin{array}{*{20}c} {t < 0} \\ {t \ge 0} \\ \end{array} ,$$

(6)

• 2. Linear function of time assuming a logarithmic relationship between $F_{d}$ and the concentration of carbon dioxide (CO₂) in the atmosphere:

$$F_{d} (t) = \left\{ {\begin{array}{*{20}l} 0 \\ {\kappa t} \\ {\kappa t_{st} } \\ \end{array} \, \begin{array}{*{20}c} {\text{if}} \\ {\text{if}} \\ {\text{if}} \\ \end{array} } \right. \, \begin{array}{*{20}c} {t < 0} \\ {0 \le t < t_{st} } \\ {t \ge t{}_{st}} \\ \end{array} ,$$

(7)

where $\kappa = F_{{2 \times {\text{CO}}_{2} }} /t_{{2 \times {\text{CO}}_{2} }}$ with $t_{{2 \times {\text{CO}}{}_{2}}} \approx 70$ years. Function (7) provides the 1% growth in CO₂ concentration until $\kappa t_{st}$, where $t_{st}$ is a stabilization time.

Key characteristics of the model, including analytic solutions and sensitivity of those solutions to changes in parameters $C,\; C_{D} , \;f,\; \gamma$ and $\sigma_{s}$ are provided in Soldatenko and Colman (2019). The base values of $C, \;C_{D} ,\; \lambda$ and $\gamma$ used here are rounded values of the multi-model means of the CMIP5 fitted values under climate change from G13: viz $C = 7.34 \;{\text{W}}\;{\text{year}}\; {\text{m}}^{ - 2} \;{\text{K}}^{ - 1}$, $C_{D} = 105.5 \;{\text{W}}\; {\text{year}}\; {\text{m}}^{ - 2} \;{\text{K}}^{ - 1}$, $\lambda = 1.13\;{\text{W}}\;{\text{m}}^{ - 2} \;{\text{K}}^{ - 1}$. and $\gamma = 0.73 \;{\text{W}}\;{\text{m}}^{ - 2} \;{\text{K}}^{ - 1}$. Using the relationship between the dimensionless feedback factor f and the feedback parameter $\lambda$, we obtain $f \approx 0. 6 4$.

A Monte Carlo approach is used for the solution of the equations of the two-layer model and to thereby obtain estimates of the variance of the surface temperature perturbations T used, Ten thousand integrations are performed for each set of model parameters, this being large enough a sample for accurate estimates of both variance and its sensitivity to the individual parameters (Soldatenko and Colman 2019). Each realization is obtained by numerical integration of the model equations using a Euler–Maruyama scheme. All ensemble members are run for 1000 years with a time step of approximately 6 days. Annual means are calculated from 12-monthly averages of temperature, and interannual variance then derived. To retrieve decadal and multi-decadal (30-year) variances, a moving average approach is employed (e.g. Colman and Power 2018).

2.2 GCM data

The results from the EBM are compared below with GCM results taken from the CMIP5 archive. GCM temperature variances and stochastic forcing are derived from the pre-industrial (PI) runs of the models, where available up to 300 years in length. Where multiple realizations are available, the first archived experiment is used. ECS, TCR and effective 2 × CO₂ radiative forcing are taken from Table 9.5 of Flato et al. (2013). GCMs chosen were restricted to those with ESM parameters available from G13, and are the same group as considered by Williamson et al. (2018). The models used, their sensitivities and 2 × CO₂ forcings are listed in Table 1.

Table 1 The GCMs used in this study, listing: their calculated values of monthly stochastic forcing; climate change feedback parameter, ECS and TCR from Flato et al. (2013); $F_{{2 \times CO_{2} }}$ from Geoffroy et al. (2013a); interannual and decadal feedback parameters calculated using the methodology in Colman and Hanson (2017)

The advantage of the use of PI results rather than the historical is that by construction it removes the possibility of volcanic or secular (e.g. CO₂ or aerosol) forcing affecting the diagnosed variability of the GCM results and thereby ‘contaminating’ possible correlations with climate sensitivity (Cox et al. 2018a; Brown et al. 2018; Rypdal et al. 2018). This approach is also consistent with that used by Colman and Power (2018). Results comparing historical and PI correlations with ECS in Williamson et al. (2018), however, suggest that similar qualitative results to those below would be found using historical GCM output.

It is important to note that stochastic forcing comes not from imposed ‘external’ influences (such as from increases in CO₂) but from ‘internally generated’ month-timescale top of atmosphere radiative imbalances, caused primarily by cloud fluctuations (see below). It can be considered a ‘forcing’ because it is a top of atmosphere energy imbalance. Pains are taken to diagnose the radiative imbalance in the GCMs is genuinely a ‘forcing’, and not a response of the climate system, by removing the component of top of atmosphere radiative fluctuations correlated with surface temperature fluctuations (see below).

The SST fluctuations, therefore, are not themselves considered ‘forcing’. They occur in GCMs from internal variability (however generated), with that variability in turn amplified/damped by radiative feedbacks. In this paradigm, the ‘feedback’ is considered the ‘instantaneous’ top of atmospheric radiative response to surface temperature changes, irrespective of how those temperature changes arise. This forcing/feedback framework is a common one in the literature (e.g. Roe 2009; Colman and Power 2018; Williamson et al. 2018; Nijsse et al. 2019).

Estimates of temperature variance and stochastic forcing from the CMIP5 models were calculated by first detrending annual mean temperatures and TOA radiation (to remove any residual drift), then removing the annual cycle by subtracting off mean January, mean February etc. For temperature, annual, monthly, decadal and 30-year variances we calculated after first averaging the monthly temperature fluctuations into annual means, then passing 10 year and 30 year running means through these timeseries prior to the calculation of variances.

For the stochastic forcing, a slightly different last step was taken. Before calculating the monthly TOA radiation variances, global temperature-related variations in radiation were removed, by calculation of the regression between the two, then removal of the temperature-related component. As discussed above, we wish to calculate the variation in the TOA that represents the ‘forcing’ alone. The assumption here is that radiative responses which are correlated with temperature changes on very short (e.g. monthly) timescales are radiative ‘feedbacks’ (i.e. responses to the temperature variation) rather than forcing. In the event, the fraction of the total TOA radiation variance correlated with surface temperature fluctuations at monthly timescales was typically small, at around only 5% of the full standard deviation in radiation.

The remaining variation, taken to represent the stochastic forcing in the models, was found to be dominated by shortwave variations (not shown), which were dominated in turn by the ‘all sky’ (i.e. clouds) rather than clear sky variations. This confirms our expectations that synoptic timescale variations of clouds provide the primary radiative ‘noise’ (Trenberth et al. 2014).

Monthly stochastic forcing standard deviations are listed in Table 1. The multi model mean value is ~ 0.61 W m⁻². Observational estimates based on CERES (Clouds and the Earth’s Radiant Energy System) satellite data indicate that global scale total TOA variability has a standard deviation of around 0.62 W m⁻² on monthly timescales (Trenberth et al. 2014), a value comparable to the multi model mean (although, as with the models, some of the observed value will likely represent the response, i.e. feedback, from surface temperature changes).

A second set of global temperature fluctuations was also derived, where temperature variation associated with ENSO was removed. The purpose of this is to explore the sensitivity of the results to the absence of the largest known dynamical driver of interannual variability (McPhaden et al. 2006). The presence of ENSO related variability has also been found to affect the ability of Hasselmann type models to fit the power spectra of CMIP5 models (Lutsko and Takahashi 2018). To remove ENSO variability, monthly global temperatures were modified by regressing them against NINO3.4 sea surface temperatures, then removing NINO3.4 related variations. Removing ENSO resulted in standard deviations of temperature variability reducing by around 19%, 15% and 18% on interannual, decadal and 30-year timescales respectively. In the event, there were no significant differences between the results obtained (e.g. the correlations found between variability and climate sensitivities) between using temperature variances with and without ENSO removed, so the results are shown only for one case only (with ENSO removed). Since our results are insensitive to the removal of ENSO, we do not further investigate the effect of removing other dynamical modes of variability (e.g. such as the North Atlantic Oscillation).

Since a primary focus is to explore the climate variability on a broad range of timescales, the assumption is made that the monthly timescale stochastic forcing is considered as Gaussian white noise. Although the implied lack of correlation is unlikely to be strictly correct (e.g. serial correlation may be expected following from phases of the Madden–Julian Oscillation or from modulation of forcing by longer term variability, such as from ENSO) it does not significantly affect the results from the two-layer model.

2.3 Sensitivity analysis method

Prior to application of the two- layer model to study variability in individual GCMs, we explore the dependence of the model dynamics (variability) on its parameters. Since the model considered is stochastic rather than deterministic, conventional so-called ‘sensitivity analysis’ techniques used in studies of deterministic dynamical systems cannot be employed. This is because output results vary between numerical experiments even when identical initial conditions and parameters are set. A number of approaches have been suggested and previously explored for solving non-deterministic equations of this sort, e.g. in specific problems in biochemistry (Damiani et al. 2013; Tsourtis et al. 2015; Hoffmann et al. 2017). These methods can be divided into two groups: those connected with Monte Carlo experiments, and those based on sensitivity of probability density functions, using the equivalents of the conventional sensitivity coefficient and the Fisher Information Matrix. Since we focus on the local sensitivity analysis of annual, decadal and inter-decadal climate variability, Monte Carlo experiments were chosen as the best approach for solving this problem.

Some previous studies (e.g., Lea et al. 2000; Eyink et al. 2004; Thuburn 2005; Wang 2013; Wang et al. 2014; Soldatenko et al. 2015; Soldatenko and Chichkine 2016) have shown that in sensitivity analysis of dynamical systems that produce chaotic behavior it is expedient to explore sensitivities averaged over a long (theoretically infinite) time interval $t \in [0,\;\tau ]$, where $\tau \to \infty$. Let us introduce the response function as (e.g. Cacuci 2003).

$$R = \int\limits_{0}^{\tau } {\varphi\, (t;\;{\mathbf{x}}(t),\,{\varvec{\upalpha}})} \, dt,$$

(8)

where $\varphi$ is a (nonlinear) function of the model state x evolving over time depending on the parameter vector α. The averaged value of (8) is defined as

$$\left\langle R \right\rangle = \mathop {\lim }\limits_{\tau \to \infty } \frac{1}{\tau }\int\limits_{0}^{\tau } {\varphi (t;\;{\mathbf{x}}(t),{\varvec{\upalpha}})}\;dt.$$

(9)

Then the sensitivity of interest with respect to variations in the parameter α_j is computed by (Wang 2013)

$$\frac{d}{{d\alpha_{j} }}\left\langle R \right\rangle = \mathop {\lim }\limits_{{\delta \alpha_{j \to 0} }} \frac{\delta \left\langle R \right\rangle }{{\delta \alpha_{j} }} = \mathop {\lim }\limits_{{\delta \alpha_{j} \to 0}} \mathop {\lim }\limits_{\tau \to \infty } \frac{1}{\tau }\int\limits_{0}^{\tau } {\frac{\delta \varphi }{{\delta \alpha_{j} }}dt} ,$$

(10)

where $\delta \varphi = \varphi \left( {x^{0} + \delta x^{0} ,\alpha_{1}^{0} , \ldots ,\alpha_{j}^{0} + \delta \alpha_{j} , \ldots ,\alpha_{m}^{0} } \right) - \varphi ({\mathbf{x}}^{0} ,\;{\varvec{\upalpha}}^{0} )$ is a difference in function $\varphi$ at any instant of time between the perturbed parameter simulation and the unperturbed control model run that generates the reference trajectory. In our calculations, the variance of surface temperature anomaly is considered as a key metric of climate system variability, consequently we define $\varphi = Var(T(t))$.

3 Sensitivity of variability in the EBM

In this Section, we conduct ‘sensitivity analyses’ as described above of annual, decadal and inter-decadal (30-year) variability for the EBM with respect to f, γ, C, C_D and $\sigma_{s}$. The purpose of this is to understand how changes in these parameters affect temperature variability on different timescales before then considering how these parameters affect correlation between variability and sensitivity.

First, however, we need to establish the accuracy of the numerical algorithm used in this study bearing in mind that the order of the Euler–Maruyama method for stochastic differential equations is $\left( {\Delta t} \right)^{1/2}$. Since the two-layer model in deterministic formulation (no stochastic forcing is applied) admits an explicit analytical solution for the step and linearly growing forcing (G13), we can analyze the accuracy of the applied numerical algorithm by comparing the exact (analytical) and numerical results. Figure 1 shows the ensemble global mean surface temperature response T for both step forcing with $F_{0} = F_{{4 \times {\text{CO}}_{2} }}$ and 1pctCO₂ forcing obtained by numerical integration of the two-layer model equations with the ‘standard’ (i.e. multi-model mean) values of model parameters (see Table 2). It was found, that on the time interval $t \in \left[ {0, \;1000} \right] \;{\text{year}}$ the differences of numerical and analytical solutions do not exceed 0.01 K in absolute values.

Fig. 1

Ensemble global mean surface temperature response obtained for a step forcing with $F_{0} = F_{{4 \times {\text{CO}}_{2} }}$ (black line); and 1pctCO₂ forcing (blue line). The red line is a schematic of the CO₂ forcing timeseries; a and c show the full timeseries, b and d represent a ‘zoom in’ to the first 200 years

Table 2 Maximum, minimum and multi-model mean values of radiative feedback parameter $\lambda$, climate system inertia parameters C, C_D and $\gamma$ derived from analysis of the CMIP5 models (G13); the corresponding values for dimensionless feedback factor f and standard deviation of stochastic forcing $\sigma_{S}$ from this study

To analyze the model variance sensitivity with respect to $C, \;C_{D} , \;f, \;\gamma$ and $\sigma_{s}$, we need to set a range of reasonable values for each of these parameters and then, first, calculate the climate variability within the range of each parameter and, second, compute an ‘average’ of sensitivity coefficients $\bar{S}_{\alpha }$, where $\alpha = (C, \;C_{D} , \;f,\; \gamma , \;\sigma_{s} )^{\text{T}}$. In our calculations, ranges of climate system inertia parameters C and C_D, radiative feedback parameter $\lambda$, and coupling parameter $\gamma$ are those that have been derived in G13 from the analysis of the CMIP5 models under simplified (instantaneous CO₂ quadrupling) forcing (see Table 2). The range of dimensionless feedback factor f that is used instead of $\lambda$, and the range of stochastic forcing standard deviation $\sigma_{s}$ are also included in Table 2. Both for reference purposes, and also acknowledging that credible values in the climate system may lie outside the values found in G13, the ranges of all two-layer model parameters were slightly expanded keeping the base values unchanged.

It is important to collate the climate variability computed numerically via the two-layer model with those represented in GCMs. The detailed analysis of this comparison will be provided in the next section. The inter-annual, decadal and multi-decadal EBM variances for with standard settings of all parameters are about one-and-a-half times the (ENSO removed) average values obtained via the CMIP5 models analysis (see Table 3). This over-estimation is reduced if ENSO variability in included in the GCMs, as this increases GCM variability by around 15–20% (see above). Despite the variances being somewhat too great for the EBM, Table 3 shows that the EBM simulates quite well the ratio between interannual variance $Var(T_{A} )$ and the decadal one $Var(T_{Dec} )$, and between decadal $Var(T_{Dec} )$ and multi-decadal $Var(T_{ID} )$, variances. From CMIP5 models we have $Var(T_{A} ) /Var(T_{Dec} ) \approx 3.31$ and $Var(T_{Dec} ) /Var(T_{ID} ) \approx 3.02$, while from EBM $Var(T_{A} ) /Var(T_{Dec} ) \approx 3.76$ and $Var(T_{Dec} ) /Var(T_{ID} ) \approx 2.78$. This gives us some confidence that the simple two-layer EBM both qualitatively and quantitatively reproduces overall features of variability from interannual to multi-decades in comparison with CMIP5 models. Also bolstering the use of the EBM is that Williamson et al. (2018) found that the expectation of a linear relationship between ECS and short-term variability holds for this relatively simple 2-layer model, in a similar way as for more complex vertical gradient diffusion models. A future study will investigate the current results with more complex models.

Table 3 Global mean surface temperature variances (× 0.01 K²) calculated via the two-layer model with base parameter values and those derived in this study from the CMIP5 model analysis

G13 demonstrated that ‘fitted’ model parameters can achieve a very good match of the two-layer deterministic forced model results with those obtained via CMIP5 models. Since here we are interested in correlations between variability and climate sensitivity, it is highly desirable to understand which of the parameters provide the most significant influence on the variance of surface temperature perturbation $\left\langle {\delta T^{2} } \right\rangle = \left\langle {T^{2} } \right\rangle - \left\langle T \right\rangle^{2}$ produced by the two-layer model.

Figure 2 shows how changes in model parameters affect the variance $\left\langle {\delta T^{2} } \right\rangle$ at annual, decadal and multi-decadal timescales. In calculations, we applied the monothetic OFAT (one-factor-at-a-time) analysis, varying each parameter over its range and holding others at their base (i.e. CMIP5 model average) values. It is obvious that within this approach we cannot explore how interactions among the parameters affect $\delta T^{2}$. However, our model is a simple one; hence the use of monothetic method can be considered as a good starting point. As shown in Fig. 2, the variance $\left\langle {\delta T^{2} } \right\rangle$ calculated within the OFAT method, as expected, is dependent on the climate ‘timescale’ considered. The variance is much more ‘sensitive’ to mixed layer depth for interannual variability than for decadal or 30-year (Fig. 2a). Increasing parameters $f$ and $\sigma_{s}$ cause accelerating growth of the variance $\left\langle {\delta T^{2} } \right\rangle$ for all timescales, strongest at shorter. Note that considering the sensitivity in relative terms across the timescales (i.e. the sensitivity normalised by the mean value of the variance at that timescale) tells a somewhat different story. When considered this way, sensitivities of variances to given changes in $\sigma_{s}$ are virtually the same across all timescales. In other words, the fractional change to $\left\langle {\delta T^{2} } \right\rangle$ for a given increase in stochastic forcing is roughly the same irrespective of timescale (not shown). Furthermore, the fractional change in variance for given changes in f now increases with timescale, i.e. is greatest for 30-year variability and least for interannual.

Fig. 2

Annual (blue), decadal (red) and 30-year (green) variance of the surface temperature in the EBM as a function of a upper layer effective heat capacity C, b stochastic variability σ_s, c parameter γ, d lower layer effective heat capacity C_D, and e feedback parameter f. In each frame the parameters that are not being varied take their values from the CMIP5 multi-model mean from Table 2. The vertical dashed lines and black bars on the x-axis show the CMIP5 model range (also shown in Table 2)

By contrast to the above, decreases in $\left\langle {\delta T^{2} } \right\rangle$ are found when parameters $C$ and $\gamma$ increase, with increases in $\gamma$ effectively increasing the mixed layer depth of the model. The change in the parameter $C_{D}$ has little effect on the annual, decadal and multi-decadal climate variability except perhaps at very small values of C_D, beyond the lower range of the CMIP5 models.

Absolute sensitivity of coefficients with respect to the model parameters calculated around their base values for different climate timescales are given in Table 4. Positive/negative coefficients $S_{\alpha }$ imply that the infinitesimal perturbations in the parameters α causes increases/decreases in the variance $\left\langle {\delta T^{2} } \right\rangle$, and correspond with the sign of the gradients in Fig. 2. Using sensitivity coefficients, we can, if it is required, estimate how the uncertainty in the parameter α affects the model output

$$\Delta \left\langle {\delta T^{2} \left( \alpha \right)} \right\rangle \approx \left\langle {\delta T^{2} \left( {\alpha^{ * } + \delta \alpha } \right)} \right\rangle - \left\langle {\delta T^{2} \left( {\alpha^{ * } } \right)} \right\rangle \approx \delta \alpha \left. {S_{\alpha } } \right|_{{\alpha = \alpha^{ * } }} ,$$

(11)

where $\delta \alpha$ is an infinitesimal variation in the parameter $\alpha$.

Table 4 Sensitivity coefficients for annual, decadal and 30-year variability estimated around the base parameter values

In practice, absolute changes to different parameters are hard to compare because of their differing units. To rank the relative importance of the parameters for their influence on $\left\langle {\delta T^{2} } \right\rangle$, we also calculate the relative sensitivity coefficients by normalising the absolute sensitivity by the mean values of the parameter, viz $S_{\alpha }^{R} = \left( {\alpha /\left\langle {\delta T^{2} } \right\rangle } \right)S_{\alpha }$. The relative sensitivity coefficients calculated for different climate timescales around the base parameter values are shown in Table 5.

Table 5 Relative sensitivity coefficients for annual, decadal and 30-year variability estimated around the base parameter values

From Table 5 we conclude that the standard deviation of stochastic forcing $\sigma_{S}$ has the largest rank for all timescales; for decadal and 30-year timescales feedback parameter $f$ and heat exchange coefficient $\gamma$ rank second and third, respectively, followed by heat capacity of the upper layer $C$ and lower layer effective heat capacity $C_{D}$. For annual variability heat capacity of the upper layer $C$ and feedback parameter $f$ rank second and third, respectively, followed by heat exchange coefficient $\gamma$ and lower layer effective heat capacity $C_{D}$.

A closely related question is how much the variance actually changes across the GCM ranges for each of the parameters. This can be estimated from the absolute differences that we find in the variances shown in Fig. 2 (i.e. varying one parameter across the GCM range, but holding all others at their mean values). These results are shown in Table 6 and indicate that the order of impact on the variance is the same as calculated for the relative sensitivity coefficients above (i.e. in Table 5). The greatest absolute range in variance is induced by differences in GCM values of σ_s at all timescales, followed by f and γ at decadal and 30-year timescales. For interannual variability, again the range in C is second most important after σ_s, although f has almost as much impact.

Table 6 Range of variance (× 10⁻² K²) for the full range of GCM values for each parameter, keeping all other parameters at their model mean values. Shown are annual, decadal and 30-year variances

Thus, considering the second hypothesis mentioned in the introduction we can conclude: radiative feedback factor plays a very important role in the magnitude of global variability on all time scales in the EBM. The longer the timescale the greater the importance of feedbacks. Differences in mixed layer depth are most important at shorter timescales, and the magnitude of stochastic forcing is very important at all timescales.

In the following section we evaluate how the EBM and CMIP5 variances range across the ensemble of models, and what the EBM implies for the relationship between climate variability across different timescales and climate sensitivity.

4 Analysis of climate variability and change of CMIP5 models

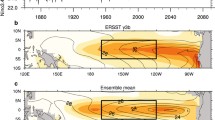
We saw above that the mean value of the temperature standard deviation (SD) implied by the EBM shows fair agreement with the average SD of the CMIP5 models, and good ratios of SDs between timescales. How well are individual model SDs predicted? Figure 3 shows the SD (with ENSO removed) for individual CMIP5 GCMs against the EBM with the corresponding G13 parameters. Taking all timescales together, the EBM shows reasonable correlation, albeit with substantial scatter and consistently higher SDs than for the GCMs (as noted above). For the individual timescales there is considerable scatter, with the EBM explaining fair levels of inter-model variance (~ 25%) for interannual and decadal timescales, but less for 30-year (13%). Although the explained variances are only fair, it nevertheless demonstrates that a significant amount of the variability in GCMs is explainable from simple model fits to climate change response. This itself means that some features of longer timescale variability are captured by the processes captured by the EBM, despite their extreme simplicity, and by climate change values of parameters, i.e. despite differences in the values of feedbacks, effective mixed layer depths, dynamical processes etc., expected between climate variability and the climate change fitted values. So, on reflection, explained variances across models of up to 25% could be considered surprisingly large. It therefore remains useful to explore what potential physical insights we might obtain using the EBM by exploring the question: what parameters are the most important in establishing any relationship between variability and climate sensitivity for either ECS or TCR, and what can be expected to ‘spoil’ it?

Fig. 3

A comparison between the SD of CMIP5 GCMs at interannual, interdecadal and 30-year timescales, compared with the SDs predicted by the EBM using the G13 values. Lines of best fit and explained variances are shown for the three timescales separately and the 1:1 line is shown in dashed blue

Before we investigate this question in detail, we ask whether the difference in feedbacks operating for interannual and decadal variability compared with those under climate change reduce the strength of the correlation shown in Fig. 3: i.e. what if we used the actual feedbacks at these timescales derived from the CMIP5 models themselves? The EBM calculations were therefore repeated using interannual and decadal feedback parameters calculated from PI experiments using the methodology of Colman and Hanson (2017), along with other values taken from G13 as before. These variability-derived feedback parameters are listed in Table 1. The resulting temperature SD correlations at interannual and decadal timescales between CMIP5 models and the corresponding EBM simulations are shown in Fig. 4. This reveals that the correlation at decadal timescales is indeed a little higher (with explained variance of 36%), although the regression slope now differs substantially from 1:1. However, at interannual timescales, the correlation is now weaker (15%). The reason for this decreased correlation at interannual timescales is unclear and warrants further investigation. However, the increased correlation at decadal timescales is consistent with the high relative importance of feedbacks for variability at longer timescales, as shown in Table 5, and indicates that allowing for differences in feedback strengths between variability and climate change may modestly increase correlations for some timescales.

Fig. 4

A comparison between the SD of CMIP5 GCMs at interannual and decadal timescales, compared with the SDs predicted by the EBM using the monthly stochastic forcing, σ_s in Table 1, the G13 values of C, C_D, and γ, and using values of feedback parameter, λ (listed in Table 1) derived from interannual and interdecadal variability from 300 years of the pre-industrial (PI) experiments following Colman and Hanson (2017). Lines of best fit and explained variances are shown for the two timescales separately and the 1:1 line is shown in dashed blue

We return to the question of what the EBM indicates might be expected to degrade/strengthen the correlation between climate sensitivity measures and the magnitude of temperature variability. To investigate this question, the EBM was run as before with corresponding variables taken from G13 and the stochastic forcings from Flato et al. (2013), but this time predicting ECS and TCR. A third sensitivity measure (hereafter called T140) also calculated is the 1% compounded CO₂ forced transient response for a quadrupling of CO₂ (i.e. the quadrupling equivalent of TCR). The reason for the latter is that it has proved to be a parameter useful for understanding the spread in temperature response under representative concentration pathways, RCPs (Gregory et al. 2015; Grose et al. 2018). In the event the results are not significantly different for T140 than for TCR, so only the TCR results will be shown.

The correlations found by the EBM for the G13/Flato et al. (2013) parameters, between sensitivity and variability are shown in Fig. 5 for ECS and Fig. 6 for TCR. The EBM predicts a high degree of correlation (i.e. high explained variance across the models) between variability and ECS with an R² of 0.58 at interannual timescales, and up to 0.68 for 30-year. The correlations for TCR are consistently somewhat smaller ranging from an R² of 0.25 for interannual up to 0.36 for 30-year. In short, the correlations predicted are stronger for longer timescales and for ECS but are statistically significant in all cases. Interestingly the higher correlation between variability and ECS mirrors the higher degree of correlation across models of ECS versus TCR for RCP projected warming over the twenty-first century (Gregory et al. 2015; Grose et al. 2018). The reasons for the latter possibly relate to differences in the heat uptake between climate change and variability timescales. These will be the subject of a future study with the EBM.

Fig. 5

ECS versus standard deviation of temperature for the EBM driven with the CMIP5 derived parameters for G13 and Flato et al. (2013), for the timescales interannual, decadal and 30-year. Lines of best fit and explained variance are also shown

Fig. 6

As for Fig. 5, but for TCR

The correlations in Figs. 5 and 6, although high, are not perfect, however. What factors increase/decrease this correlation? To determine this, the EBM was next run in two ways. In the first, it was run with all parameters corresponding to the differing CMIP5 values from G13 and Flato et al. (2013), then with parameters one-by-one replaced by their multi-model means, to determine the impact of removing cross-model variation in that parameter. The results are shown in Fig. 7. In the second, it was run with λ varying across models, but all other values set at their multi-model means, then one-by-one the parameters were allowed to vary across the GCM values (Fig. 8).

Fig. 7

Explained variance in correlations between SD of temperature, and a ECS and b TCR for the EBM driven by the CMIP5 model parameters for C, C_D, γ from G13, and λ, σ_s and $F_{{2 \times CO_{2} }}$ (‘F’) from Table 1 (left cluster of 3 coloured bars labelled ‘All vary’) then with the individual CMIP5 GCM parameter values replaced one-by-one with the multi-model mean of the parameter for (left to right) λ, C, C_D, γ, σ_s and $F_{{2 \times CO_{2} }}$ (‘F’). Shown left to right for each parameter in blue, orange and grey are the results for Annual (I/A), Decadal (Dec) and 30-year timeframes (30 yr)

Fig. 8

Explained variance in correlations between SD of temperature, and a ECS and b TCR for a range of parameter settings. In the left-most cluster of three columns, to the left of the vertical blue line, the EBM is driven by CMIP5 GCM specific λ values from Table 1, with all other parameters specified as the average of the multi-model values (given in Table 2). The EBM is then driven with the multi-model parameter means replaced one-by-one by the individual CMIP5 GCM parameter values (i.e. for C, C_D, γ, σ_s and F) with all other parameters (except λ) kept at their multi-model means. Shown left to right for each parameter in blue, orange and grey are the results for Annual (I/A), Decadal (Dec) and 30-year timeframes (30 yr)

Considering Fig. 7, it is immediately apparent that eliminating the range of the feedback essentially destroys the correlations for both ECS and TCR with variability. (As an interesting aside, it does not destroy the correlation between TCR and ECS, as F still varies across the models, so will drive a range in ECS and TCR, even without feedbacks—not shown). The ranges in ECS and TCR are both reduced by around 1 K; ECS from a range of 2.48 to 1.5 K, TCR from 1.59 to 0.42 K, so there is less spread. This illustrates the key importance of feedbacks in establishing this correlation in the EBM. It can be easily understood in the case of the ECS/variability correlation: the only factor producing spread in the ECS remains F, which plays no role in variability in the EBM. Any remaining non-zero correlation must relate to the correlations arising from the parameters derived in G13.

For the TCR, the loss of correlation with λ fixed is even more marked (it is now zero at interannual timescales), and is harder to understand. Variables such as gamma, C and C_D play a role in setting the transient warming time as well as the variability so may be expected to provide some correlation. However, the EBM predicts that without corresponding feedbacks operating these variables do not produce any significant correlation.

For TCR the correlation is insensitive to eliminating the ranges of C, C_D, γ or F at all timescales (Fig. 7b). This indicates that if all other parameter values vary, then the fact that these parameters differ across models play insignificant roles in decreasing the correlation. That is, they are of secondary importance in determining the closeness of the correlation between TCR and variability. This is reflected in Fig. 8b, which shows that allowing these parameters to be the only ones to differ across models has minimal effect on the correlations (except for C at the shortest timescales).

Notably, replacing $\sigma_{s}$ by the mean value increases correlation of TCR and interannual variability to nearly 0.8, and TCR and decadal and 30-year variability to nearly 1 (Fig. 7b). This means that, irrespective of the other variables, $\sigma_{s}$ is the key variable which, were it to be similar across models, would restore high long-timescale correlations with TCR.

Figure 8 backs this up. Figure 8 shows the ‘converse’ of Fig. 7. This means instead of allowing all parameters to vary, then replacing them one-by-one with the multi-model mean (Fig. 7), Fig. 8 starts with all parameters (except for λ) as the multi-model mean, and replaces them one-by-one with the individual model values. Figure 8 confirms that allowing $\sigma_{s}$ to vary reduces the correlations, particularly at shorter timescales. This is consistent with the results of Sect. 3, above, as differences in the stochastic forcing, which would be expected to have, at most, only a minor influence on TCR,¹ have a relatively large impact on the variability of the model, particularly at shorter timescales.

In short, the EBM results for correlations with TCR and variability therefore predict that the spread in the $\sigma_{s}$ is the key parameter marring the correlation between TCR and variability, but that even with the range present in CMIP5 models, correlations should be reasonably high. The EBM gives close to perfect correlations between TCR and variability except when $\sigma_{s}$ has the CMIP5 range.

For ECS, the situation is slightly different. Correlations between variability and ECS are again relatively insensitive to the spread in C and C_D (Fig. 7a). Correlations again increase when $\sigma_{s}$ does not vary, but in this case, they do not go to 1 for the longer timescales as they did for TCR. This is clearly because other variables F and γ also affect the correlation. Removing the spread in F increases correlation at all timescales. Removing the spread in γ, however, has the counter intuitive effect of decreasing the correlation between variability and ECS. The impact of F is easily understood: it causes spread in ECS but does not affect variability, so reducing its spread produces greater correlation. However, it is less important for TCR correlation, presumably since it is only one factor causing the spread in TCR between models, but a dominant factor for ECS. The puzzle is why eliminating the spread in γ reduces the correlation between ECS and variability. It turns out that γ is weakly negatively correlated with C and positively correlated with λ across models (not shown). C plays little role in determining correlations (Fig. 7a) but the correlation with λ means that it reinforces the variability spread correlated with λ and therefore in the presence of other varying parameters removing it reduces the correlations.

Figure 8a confirms the results from for ECS shown in Fig. 7a. The inter-model ranges in γ, $\sigma_{s}$ and F acting alone all to some extent spoil the correlation between variability and ECS, with $\sigma_{s}$ having the strongest effect. The spoiling effect of σ_s is strongest on short timescales; γ, and F are largely timescale independent. The weak correlation of γ and λ noted above is not so important here—any spread in γ which is not fully correlated with λ will act to mar the perfect correlation of λ varying alone. Again, these results are consistent with the ‘parameter sensitivity’ results of Sect. 3, and the results of Soldatenko and Colman (2019): it is no surprise that the spread in σ_s is a key driver of the lack of correlation as it the strongest relative driver of spread in variability.

5 Summary and conclusions

There is a critical ongoing need for deeper understanding of the reason for the large spread in both temperature climate variability and climate change. There is a critical need too for understanding what links may lie between them, and whether we can exploit those links to provide possible constraints on the magnitude of future global warming. Here we use a simple 2-layer energy balance model (EBM) to ask what factors might contribute to the spread in variability, and which factors might provide (or indeed limit) the degree of correlation between the magnitude of unforced variability and climate sensitivity (both ECS and TCR) across timescales from interannual to multi-decadal. Following Williamson et al. (2018), it is hoped that this ‘theory-led’ approach can provide hints as to directions we might explore in ultimately establishing climate change constraints based on links between GCM variability and change, coupled with observations of unforced variability.

We examined the EBM theoretically to determine for which parameters variability showed most sensitivity across different timescales. Results showed the most important factor, considering the range of the CMIP5 model parameters, to be stochastic forcing, particularly at the shorter timescale (i.e. interannual). However radiative feedbacks also strongly affect variability in the EBM, with greater sensitivity at longer timescales. This is consistent with the strong positive feedbacks found in GCMs across interannual and decadal timescales (e.g. Dessler 2010; Dessler and Wong 2009; Zhou et al. 2015; Colman and Hanson 2013, 2017; Colman and Power 2018), and their role found in unforced variability from GCM experiments (e.g. Hall and Manabe 1999, 2000; Hall 2004).

The EBM was then run with climate change fitted parameters for CMIP5 model derived by G13, along with stochastic forcing calculated from the CMIP5 models. Variability was diagnosed for interannual, decadal and 30-year timescales for both the CMIP5 models and the EBM. For average CMIP5 parameters the ratios of interannual to decadal and decadal to 30-year SDs are in reasonable agreement between CMIP5 models and the EBM, although overall the EBM simulates somewhat larger variability than found in the models. The correlation across CMIP5 models between the GCM variances and those simulated by the EBM are modest, with around 25% variability explained for longer timescale (decadal and 30-year). On reflection it is perhaps striking that it is as large as this given the simplicity of the model, and the stipulation of parameters derived purely from centennial timescale forcing and response. Presumably it reflects that there are physical processes, particularly feedbacks operating to an extent in analogue between variability and climate change (Zhou et al. 2015; Colman and Power 2018), e.g. in that correlations exist between climate change feedbacks and feedbacks under decadal variability (Colman and Hanson 2017).

The EBM is then used to ask what correlations we might expect to be fruitful to pursue (under the assumptions of the EBM) and why we might or might not expect these to provide constraints on climate change. The EBM predicts that the correlations between sensitivity and variability should be higher at longer timescales in the GCMs. It also predicts that $\sigma_{s}$ variation is most responsible for degrading that correlation, although differences in γ and F are also important. This is consistent with the findings that the stochastic forcing was also the single greatest cause of the spread in the first place (see also Soldatenko and Colman 2019). Furthermore, the stochastic forcing spread is the one factor that is irrelevant for ECS and likely to play a small role, only, in TCR. Normalising variability by the SD of the stochastic forcing might therefore prove a more fruitful line of investigation than comparing variability alone when seeking to provide constraints from the real world (e.g. Cox et al. 2018a).

The EBM predicts lower correlations between variability and TCR than with ECS, consistent with there ocean heat uptake factors affecting TCR, whereas ECS is dependent on forcing and feedback alone.

The overall implications of the current work are that variability may indeed provide a fruitful direction for constraining sensitivity, particularly if stochastic forcing differences in CMIP5 models can be reduced or removed in the analysis, and stochastic forcing errors and biases reduced in future generations of GCMs. Understanding the differences in the heat uptake (and specifically γ) and normalising for difference in F may further improve correlations. Clearly, deeper understating of the differences in feedbacks across timescales and from climate change is also critical, given the central importance of λ.

There are some important caveats to the current study, particularly given the simplicity of the EBM.

• 1. Firstly, the EBM does not include ‘internal’ coupled processes, so dynamically driven or amplified variations in temperature in GCMs due to processes such as to ENSO or the IPO will not be captured. This might intuitively lead us to expect smaller overall fluctuations in the EBM than in the models. For example, around 20% and 15% of GCM interannual and decadal SD respectively is correlated with NINO3.4. In fact, the EBM was found to overestimate interannual and decadal variances compared with the GCMs—by around 10–15% on average. This increases to around 50% when ENSO related variability is explicitly removed from the GCMs (Table 3). Of course, the EBM also lacks internal dissipative processes which may act to bolster its variability relative to the GCMs and therefore contribute to some of this overestimation of variance.

The above discussion relates to multi-model means. Not including internal processes also means that dynamical aspects of differences between GCM variances will not be captured. Again, we might intuitively expect a smaller range across the EBM than the GCMs. Interestingly however (and encouragingly) the EBM/GCM SD fit (Fig. 3) is close to 1:1, particularly at decadal and interannual timescales. The absolute range of the spread, however, is greater in the EBM than in the GCMs for interannual and decadal variability but around the same for 30-year variations.

• 2. Secondly and related to the first point above, global averaging in the EBM precludes regional contributions to variability and change. The EBM does not represent land surface areas, or SST pattern changes. The latter, in particular, are known to be important for many aspects of climate variability and change. For example, the time evolution of spatial feedbacks over the Southern Ocean affects ‘effective’ climate sensitivity (Senior and Mitchell 2000; Armour et al. 2013). Notably these limitations do not preclude the EBM from representing century-timescale global secular trends in response to different types of greenhouse gas forcing (Geoffroy et al. 2013a, b). Despite the skill of the EBM in producing these trends, however, we may expect the lack of regional process and pattern representation to degrade both its representation of climate variability and correlations between climate variability and climate sensitivity.

Arising from this, we might intuitively expect higher correlations between climate sensitivity and variability as variability timescales increase—i.e. as patterns of variability become more ‘similar’ to expected patterns of climate change on decadal and longer timescales (e.g. Brown et al. 2014; Dai et al. 2015; Colman and Power 2018). That is, we might expect long term EBM variability driven by climate change derived parameters from GCMs to be more closely related to corresponding climate change derived from those same parameters. The EBM does indeed predict closer correlations between variability and both ECS and TCR on longer timescales than short (Figs. 5, 7).

These results must be treated with caution however, as inter-GCM feedback correlations between climate change and climate variability are known to be sensitive to the different SST patterns under different timescale variability (Zhou et al. 2015; Colman and Hanson 2017, 2018). In particular, there are stronger long term (decadal) water vapour and lapse rate feedback correlations with secular climate change feedbacks, but stronger short-term (interannual) correlations for clouds and surface albedo (Zhou et al. 2016; Colman and Hanson 2017, 2018). The reasons for these differences are not clear, and need further research.

Aside from the ‘pattern’ effects, it could be hypothesised that the improvement in the correlations at longer timescales seen in Figs. 5 and 7 are mostly to do with reduction in the importance of the mixed layer depth as a source of inter-model variations as timescales increase (Fig. 2a). This appears less likely however, as if this were the case then removal of variations across models in C would have more impact at shorter timescales that longer—which is not evident in Fig. 7.

• 3. A third important factor to be borne in mind in interpreting the current results is that the EBM is specified from climate change derived parameters. This was, of course, part of the ‘design’ of the study, and the subject of some of its key hypotheses. However, it is likely to decrease correlations that might otherwise be higher. The mixed layer depths C and mixing factors γ are important, particularly on shorter timescales (Fig. 2). These might well be different from those under climate change, as effective heat uptake may differ under variability versus secular forcing (Hegerl and Bindoff 2005). This would be expected to mar the EBM versus GCM correlations in Figs. 3 and 4, and between variability and sensitivity (Figs. 5, 6). A fruitful future investigation could consider the effective mixed layer/ocean heat uptake implied by interannual and decadal variation (e.g. AchutaRao et al. 2006), estimating it from unforced variability in GCMs and observations and adjust the EBM accordingly. We speculate that this could improve correlations, particularly between variability and TCR, given the importance of ocean heat uptake for both. Note that although the cross model spread in TCR is less predictive than that of ECS for cross model spread in twenty-first century warming (Grose et al. 2018), the value of TCR is more relevant to the absolute magnitude of expected warming, and improving correlation in the EBM between TCR and variability across models would be a very useful development.

The one exception to the use of climate change derived parameters in the EBM just discussed is of interannual/decadal feedbacks (derived from the same GCMs), shown in Fig. 4. The improvement in decadal correlation between Figs. 3 and 4 (to over a third of explained variance) is encouraging, implying that if we can derive decadal feedbacks from observations or process understanding this might provide a fruitful path to strengthening constraints on ECS/TCR. Two issues cloud this, however. Firstly, there is a change in the decadal correlation gradient, which now differs markedly from 1:1 (Fig. 4), which demands further investigation. Secondly, the fact that correlations are worse at interannual timescales when using interannually derived feedbacks is surprising and also needs further investigation.

• 4. A fourth issue of caution involves assumptions made regarding stochastic forcing. The role of stochastic forcing in the current results is striking, as the EBM suggests that it could be a key ‘spoiler’ of cross GCM climate change/variability correlations. In interpreting this, however, we need to bear in mind that only monthly stochastic forcing is applied in the EBM. Clearly, we might expect a range of forcing on shorter and longer timescales in both the real world and in GCMs (e.g. Trenberth et al. 2014), for example including known radiative impacts from variations such as the Madden–Julian Oscillation (e.g. Wheeler and Hendon 2004). ENSO itself may be conceptually considered radiative or dynamic ‘forcing’ that effects broad regions and longer timescales (Power et al. 1999; Folland et al. 1999; Chiang and Sobel 2002), but this is obviously missing in the monthly forcing applied to the EBM. The implication is that correlations found between GCM variability and ECS (Colman and Power 2018; Nijsse et al. 2019) will be ‘seeing’ stochastically forced variability not seen by the EBM, which may be important for the strength of that correlation.

Despite these limitations of the EBM, it does highlight an expected critical role of stochastic forcing on the variability spread. Understanding the range in the stochastic forcing is therefore an important area of further research in understanding variability/sensitivity correlations. In particular, given that the primary source of the forcing is shown here to be from SW cloud ‘noise’ (80% by SW and 80% of that from clouds) further investigation is needed to understand this basic process in GCMs, and why it varies across models by a factor of more than three.

• 5. Finally, stochastic surface forcing in GCMs, such as from changes in latent and sensible heat could also be important in forcing variability. Although they do not affect TOA radiances directly, processes linking them to internal dynamics (e.g. feedbacks on ENSO—Gebbie et al. 2007) may indirectly cause extra TOA forcing. Surface processes which impact TOA radiation in this way on monthly timescales in GCMs will to that extent be ‘picked up’ by the EBM. A fundamental assumption of the EBM is that since the top ‘layer’ of the model represents both atmosphere and upper layer of the ocean, only TOA radiance changes (i.e. at the ‘boundary’ of the model) affect the energy of the system—and therefore the surface temperature. However, a further development of the EBM could usefully separate these components and explicitly consider the role of surface forcing in variability.

Considering the limitations discussed here of the EBM, it is again noteworthy that it can explain between a quarter and a third of cross model spread in temperature variance. Future work, such as the development of more sophisticated (e.g. better vertically resolved, multi-sector or zonally averaged) models—could improve on this.

With the emerging availability of CMIP6 GCMs, and a revealed broader range of ECS, further work needs to investigate the range of unforced variability, whether correlations found for CMIP5 are similar to those found in CMIP6, and to understand those correlations. The current study should provide an important benchmark against which that can be compared.