1 Introduction

We use [4] for terminology and notation not defined here and only consider simple undirected graphs. An edge-colored graph is a graph in which each edge is assigned a color. Given an edge-colored graph G, we call it a properly edge-colored graph if its any two adjacent edges have different colors. Thus, in a properly edge-colored graph, the edges with same color form a matching. If for each color \(\alpha\), the set of edges with color \(\alpha\) forms an induced matching in G, then we say that G is strongly edge-colored. Therefore, a strongly edge-colored graph is always properly edge-colored, and every path of length 3 in strongly edge-colored graphs has 3 colors. Furthermore, a matching M is rainbow if the edges in M have distinct colors.

Given an edge-colored graph \(G=(V,E)\), we use \(\delta (G)\) and d(G) to denote the minimum degree and the average degree of G respectively. For a vertex \(v\in V\), the color degree, \({\hat{d}}_G(v)\) of v is the number of distinct colors on edges incident to v. When it is clear from the context what G is, we would omit the subscript. We use \({\hat{\delta }}(G)\), \({\hat{\Delta }}(G)\) and \({\hat{d}}(G)\) to denote the minimum color degree, the maximum color degree and the average color degree of G respectively, i.e., \({\hat{\delta }}(G)=\min \{{\hat{d}}(v): v\in V\}\), \({\hat{\Delta }}(G)=\max \{{\hat{d}}(v): v\in V\}\) and \({\hat{d}}(G)=\sum _{v\in V}{{\hat{d}}(v)}/n\). Clearly, for an edge-colored graph G, we have \(d(v)\ge {\hat{d}}(v)\) for each \(v\in V\).

Rainbow matchings in edge-colored graphs were originally studied in connection to the famous conjecture of Ryser [13], which equivalently states that every properly edge-colored complete bipartite graph \(K_{n, n}\) with n colors contains a rainbow matching of size n, where n is odd. Unlike uncolored matchings for which the maximum matching problem is solvable in polynomial time, the maximum rainbow matching problem is NP-Complete, even for bipartite graphs, mentioned in Garey and Johnson [5] as the multiple choice matching problem. Therefore, the existence of rainbow matchings has also been studied in its own right.

During the last decades, many researchers have studied the sufficient conditions to ensure that a properly edge-colored graph G has a rainbow matching of size \(\delta (G)\). In [14], Wang asked does there exist a function \(f(\delta (G))\), such that every properly edge-colored graph G with \(|V(G)|\ge f( \delta (G))\) contains a rainbow matching of size \(\delta (G)\). Diemunsch et al. [3] proved that such function does exist and \(f( \delta (G))\le \frac{98}{23}\delta (G)\). Gyárfás and Sárközy [6] improved the result to \(f( \delta (G))\le 4\delta (G)-3\). Later, this problem was generalized to find the function \(f({{\hat{\delta }}}(G))\) for any edge-colored graph G. Lo and Tan [12] showed that \(f({{\hat{\delta }}}(G))\le 4{{\hat{\delta }}}(G)-4\) is sufficient for \({{\hat{\delta }}}(G)\ge 4\). As far as we know, the best result so far is \(f({{\hat{\delta }}}(G))\le \frac{7}{2}{{\hat{\delta }}}(G)+2\) in [11]. In addition, the lower bound for the size r(G) of the maximum rainbow matchings in edge-colored graph G has also been studied independently, in terms of the minimum color degree of G. In [15], Li and Wang showed that \(r(G)\ge \lceil \frac{5{{\hat{\delta }}}(G)-13}{12}\rceil\) for every edge-colored graph G, and they conjectured that \(r(G)\ge \lceil {{\hat{\delta }}}(G)/2\rceil\) for \({{\hat{\delta }}}(G)\ge 4\). Consider a properly edge-colored \(K_4\), whose edges of the same color form a matching of size 2. For convenience, it is denoted as \(\widetilde{K_4}\). It is easy to verify that \(\widetilde{K_4}\) has no a rainbow matching of size 2, which motivates the restriction \({{\hat{\delta }}}(G)\ge 4\). In particular, the bound of this conjecture is sharp for properly edge-colored complete graphs. This conjecture was partially confirmed in [10] and fully confirmed in [8]. In particular, Kostochka and Yancey [8] proved that if G is not \(\widetilde{K_4}\), then \(r(G)\ge \lceil \delta (G)/2\rceil\).

Since the maximum rainbow matchings problem in edge-colored graphs in terms of the minimum color degree is well studied, it is natural to study this problem under the average color degree condition. Michael Ferrara raised [9] the following related question during the Rocky Mountain and Great Plains Graduate Research Workshop in Combinatorics in 2017.

Question 1

If G is an edge-colored graph with \({\hat{d}}(G)\ge 2k\), does G contain a rainbow matching of size k?

Since the average color degree condition is weaker than the minimum color degree, it is more difficult to study the maximum rainbow matchings problem under the average color degree condition. Therefore, there are few known results under the average color degree condition. Recently, Kritschgau [9] studied Question 1, and proved some sufficient conditions to bound from below r(G) in G with a prescribed average color degree. We denote by \(C_t\) the cycle with t vertices.

Theorem 1

(Kritschgau [9]) Each condition below guarantees that \(r(G)\ge k\) for each edge-colored graph G with \({\hat{d}}(G)\ge 2k\).

\({\mathrm{(i)}}\):

\(|V(G)|\ge 12k^{2}+4k\).

\({\mathrm{(ii)}}\):

G is properly edge-colored and \(|V(G)|\ge 8k\).

\({\mathrm{(iii)}}\):

G is \(C_4\)-free.

\({\mathrm{(iv)}}\):

G is \(C_3\)-free.

Moreover, if G is \(C_3\)-free, then we only need to assume \({\hat{d}}(G)> 2(k-1)\) to get \(r(G)\ge k\).

Though Kritschgau [9] did not resolve Question 1 for all graphs, he believe the answer is affirmative. Recall that Kostochka and Yancey showed that \(r(G)\ge k\) for all edge-colored graph G with \({{\hat{\delta }}}(G)\ge 2k-1\) and \(G\ne \widetilde{K_4}\). Inspired by the result for \(C_3\)-free edge-colored graphs in [9], we want to study the consistency of the maximum rainbow matching between the minimum color degree condition and the average color degree condition. It would be interesting to ask the following question.

Question 2

If G is not \(\widetilde{K_4}\) and \({\hat{d}}(G)\ge 2k-1\), does G contain a rainbow matching of size k?

If the answer of Question 2 is affirmative, then it would be best possible, since the properly edge-colored complete graph \(K_{t+1}\) satisfies \({\hat{d}}(K_{t+1})\ge t\) for each \(t\in {\mathbb {N}}\), but \(r(K_{t+1})\le \lceil t/2\rceil\). In this paper, we partially resolve Question 2 and obtain the following result.

Theorem 2

For all positive integers k, let G is an edge-colored graph with \({\hat{d}}(G) \ge 2k-1\) and \(G\ne \widetilde{K_4}\). If \(|V(G)|\ge 4k-4\), then \(r(G)\ge k\).

Remark 1

Theorem 2 implies that, for any k, only finitely many edge-colored graphs with average color degree at least \(2k-1\) can fail to have a rainbow matching of size k. Furthermore, it is easy to verify that these graphs G that may fail satisfy \(|E(G)|\ge |V(G)|^2/4+3|V(G)|/4\). By the Tuŕan number of \(C_3\) and \(C_4\), these graphs all contain \(C_3\) and \(C_4\). Therefore, Theorem 2 can deduce Theorem 1.

In addition, the topic of rainbow matchings in strongly edge-colored graphs in terms of the minimum color degree has been also well studied. Note that for strongly edge-colored graph G, we have \(d(v)={\hat{d}}(v)\) for each \(v\in V(G)\). In 2015 Babu-Chandran-Vaidyanathan [1] showed that \(r(G)\ge \lfloor 3\delta (G)/4\rfloor\) for any strongly edge-colored graph G with \(|V(G)|\ge 2\lfloor 3\delta (G)/4\rfloor\). They also proposed an interesting question: Is there a constant c greater than 3/4 such that every strongly edge-colored graph G has \(r(G)\ge \lfloor c\delta (G)\rfloor\) if \(|V(G)|\ge 2\lfloor c \delta (G)\rfloor\)? Clearly, \(c\le 1\). The best result so far on this question is from Cheng-Tan-Wang [2], and they proved the following result.

Theorem 3

(Cheng-Tan-Wang [2]) If G is a strongly edge-colored graph with \(|V(G)|\ge 2\delta (G)+1\), then \(r(G)\ge \delta (G)\).

Rather than considering host graphs with a prescribed minimum color degree, we consider host graphs with a prescribed average color degree, and obtain the following a sharp result.

Theorem 4

For all positive integers k, if G is a strongly edge-colored graph with \(d(G) \ge 2k-1\), then \(r(G)\ge k\).

Next, we will prove Theorems 2 and 4 in Sects. 2 and 3 respectively. Finally, we close the paper with some remarks and conjectures in Sect. 4.

2 Proof of Theorem 2

In this section, we will prove Theorem 2 by induction on k. For \(k = 1\), Theorem 2 clearly holds. In the following, we assume Theorem 2 holds for all \(k'<k\). To the contrary, suppose that G with edge coloring \(\varphi\) is a counterexample to Theorem 2 with the fewest edges. That is, for each edge-colored graph \(G'\) with \(|E(G')|<|E(G)|\), if \(G'\) satisfies the conditions of Theorem 2, then \(r(G')\ge k\).

In the following, set \(V:=V(G)\) and \(|V|=n\). For \(v\in V\), we use N(v) to denote the neighborhood of v, i.e., \(N(v)=\{u\in V : uv\in E(G)\}\). For \(U\subseteq V\), let G[U] denote the induced subgraph of G on vertex set U. The color used on G[U] will be denoted \(\varphi (G[U])\), i.e., \(\varphi (G[U])=\{\varphi (e): e\in E(G[U])\}\). If \(U=V\), then we write that \(\varphi (G)\) simply.

2.1 Preliminary Results

By induction hypothesis, we have \(r(G)=k-1\). Choose a rainbow matching M of size \(k-1\) in G, which maximizes \(|\varphi (G[V\setminus V(M)])|\). Set \(H:=G[V\setminus V(M)]\). Clearly, \(0\le |\varphi (H)|\le k-1\). We say that a color appearing in G is free if it does not appear on an edge of M, otherwise it is unfree. Therefore, we can divide \(\varphi (G)\) into two disjoint subset \(\varphi _f\) and \(\varphi _{uf}\), where \(\varphi _{uf}=\{\varphi (e): e\in E(M)\}\) and \(\varphi _f=\varphi (G)\setminus \varphi _{uf}\). In addition, a free edge in G is an edge colored with a free color. For every vertex \(v\in V\), let \({\hat{d}}^{f}(v)\) and \({\hat{d}}^{uf}(v)\) denote the free color degree and the unfree color degree of v in G respectively. Clearly, we have \({\hat{d}}(v)={\hat{d}}^{f}(v)+{\hat{d}}^{uf}(v)\). Without loss of generality, let \(E(M)=\{u_iv_i: 1\le i\le k-1\}\) and \(\varphi (u_iv_i)=i\) for every edge \(u_iv_i\in E(M)\).

Claim 1

\({{\hat{\Delta }}}(G)\le |\varphi (H)|+2(k-1)\).

Proof

Suppose that there is a vertex \(v\in V\) such that \({\hat{d}}(v)\ge |\varphi (H)|+2k-1\). Let \(G^{*}=G-v\), which is obtained from G by deleting the vertex v and all edges incident with v. Since \({\hat{d}}(v)\le n-1\) and \({\hat{d}}(G)\ge 2k-1\), we have

$$\begin{aligned} {\hat{d}}(G^*)\ge \frac{(2k-1)n-2(n-1)}{n-1}> 2(k-1)-1. \end{aligned}$$

By induction hypothesis, \(G^{*}\) contains a rainbow matching \(M^*\) of size \(k-1\). Let \(H^*=G[V\setminus V(M^*)]\). Then we have \(|\varphi (H^*)|\le |\varphi (H)|\). Since \({\hat{d}}(v) \ge |\varphi (H)|+2k-1>|\varphi (H^*)|+2(k-1)\), there is at least one vertex \(u\in N(v)\) such that \(u \notin V(M^*)\) and \(\varphi (uv) \notin \varphi (M^*)\). Let \(M'=M^* \cup \{uv\}\), which yields a rainbow matching of size k in G. \(\square\)

Furthermore, recalling the result of Kostochka and Yancey, it follows that \({{\hat{\delta }}}(G)<2k-1\), otherwise G contains a rainbow matching of size k. Therefore, we have \(2k-1\le {\hat{d}}(G)< {{\hat{\Delta }}}(G)\le |\varphi (H)|+2(k-1)\), i.e., \(|\varphi (H)|\ge 2\). In addition, since \(|\varphi (H)|\le k-1\), we have \(k\ge 3\) in the the following proofs.

By the minimality of G, it is easy to prove the following property.

Lemma 1

([8]) The edges of each color class of \(\varphi\) form a forest of stars.

Now, let us consider the relationship between the rainbow matching M and the induced subgraph H. Given a color \(\alpha \in \varphi (H)\), let \(H^\alpha\) denote the subgraph of H with the edges in color class \(\alpha\), and \(s_H(\alpha )\) denote the number of stars in \(H^\alpha\). Since \(\varphi (H)\subseteq \varphi _{uf}\), we partition M into \(X_1,X_2,X_3\) as following:

\({\mathrm{(1)}}\):

For every \(e\in X_{1}\), \(s_H(\varphi (e))\ge 2\);

\({\mathrm{(2)}}\):

For every \(e\in X_{2}\), \(s_H(\varphi (e))=1\);

\({\mathrm{(3)}}\):

For every \(e\in X_{3}\), \(s_H(\varphi (e))=0\).

For \(v\in V(M)\), let \(E_H^{f}(v)=\{uv\in E(G): \varphi (uv)\in \varphi _{f}\}\). In order to get a more detailed estimate, we partition \(X_3\) into \(Y_1,Y_2,Y_3\) as following:

\({\mathrm{(i)}}\):

For every \(e\in Y_{1}\), every endpoint v of edge e with \(|\varphi (E_H^{f}(v))|\ge 1\);

\({\mathrm{(ii)}}\):

For every \(e\in Y_{2}\), there is only one endpoint v of edge e with \(|\varphi (E_H^{f}(v))|\ge 1\);

\({\mathrm{(iii)}}\):

For every \(e\in Y_{3}\), every endpoint v of edge e with \(|\varphi (E_H^{f}(v))|=0\).

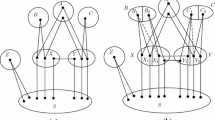
For convenience, let \(x_{j}=|X_{j}|\) and \(y_{j}=|Y_{j}|\) for \(1\le j\le 3\). Next, we will analyze the partitions above. In Fig. 1, we list three configurations (1.1), (1.2) and (1.3), which can not appear in G, otherwise, they would yield a rainbow matching of size k in G. In particular, by Configuration (1.1), we can directly obtain the following claim.

Claim 2

For every edge \(u_iv_i\in X_{1}\), we have \(|E^f_H(u_i)|+|E^f_H(v_i)|=0\).

Proof

Suppose that there is an edge \(e\in E^f_H(u_i)\cup E^f_H(v_i)\) such that \(\varphi (e)\in \varphi _f\). Since \(s_H(\varphi (u_iv_i))\ge 2\), we can choose an edge \(e'\in E(H^i)\) such that \(e'\cap e=\emptyset\). Therefore, we can take e and \(e'\) instead of \(u_iv_i\) to yield a rainbow matching of size k. \(\square\)

Fig. 1
figure 1

Some configurations that can not appear in G, where \(\{\alpha , \beta \}\subseteq \varphi _f\)

Full size image

Claim 3

For every edge \(u_iv_i\in X_{2}\), if \(|E(H^i)|=1\), then we have \(|E^f_H(u_i)|+|E^f_H(v_i)|\le 4\); if \(|E(H^i)|\ge 2\), then we have \(|E^f_H(u_i)|+|E^f_H(v_i)|\le 2\).

We omit the proof of Claim 3 as the proof is similar to that of Claim 2. In Fig. 2 we list the extremal configurations for \(|E(H^i)|=1\) (see Configuration (2.1)), and \(|E(H^i)|\ge 2\) (see Configuration (2.2)). In addition, for Configuration (2.1), we have the following claim. For simplify, let \(G_{3}:=G[V\setminus V(X_3)]\).

Fig. 2
figure 2

Two extremal configurations of Claim 3, where \(\{\alpha , \beta \}\subseteq \varphi _f\)

Full size image

Claim 4

For every edge \(u_iv_i\in X_{2}\), if \(|E^f_H(u_i)|+|E^f_H(v_i)|= 4\), then \({\hat{d}}^f_{G_3}(u_i)+{\hat{d}}^f_{G_3}(v_i)= 4\).

Proof

Fix \(u_iv_i\in X_{2}\). Since \(|E^f_H(u_i)|+|E^f_H(v_i)|= 4\), Configurations (2.1) appears in G. Let \(\varphi (E_H^{f}(u_i))=\varphi (E_H^{f}(v_i))=\{\alpha ,\beta \}\). If \(X_1\cup X_2=\{u_iv_i\}\), then \({\hat{d}}^f_{G_3}(u_i)+{\hat{d}}^f_{G_3}(v_i)= d^f_{H}(u_i)+{\hat{d}}^f_{H}(v_i)=4\). Next, we consider each edge \(u_jv_j\in X_1\cup X_2\) with \(u_jv_j\ne u_iv_i\). Since \(E(H^i)\ne \emptyset\) and \(E(H^j)\ne \emptyset\), there is \(e_1\in E(H^i)\) and \(e_2\in E(H^j)\) such that \(e_1\) and \(e_2\) either adjacent or disjoint. If \(e_1\cap e_2=\emptyset\), then \(\varphi (E_{u_jv_j}^{f}(u_i))=\varphi (E_{u_jv_j}^{f}(v_i))=\emptyset\), since Configurations (1.2) in Fig. 1 can not appear in G. If \(e_1\cap e_2\ne \emptyset\), then \(\varphi (E_{u_jv_j}^{f}(u_i)), \varphi (E_{u_jv_j}^{f}(v_i))\subseteq \{\alpha ,\beta \}\), since Configurations (1.3) in Fig. 1 can not appear in G. Therefore, \(u_i\) and \(v_i\) can only connect \(\alpha\) color edges or \(\beta\) color edges in \(G_3\), i.e., \({\hat{d}}^f_{G_3}(u_i)+{\hat{d}}^f_{G_3}(v_i)= 4\). \(\square\)

Claim 5

For every edge \(u_iv_i\in Y_1\), we have \({\hat{d}}(u_i)+{\hat{d}}(v_i)+|E^f_H(u_i)|+|E^f_H(v_i)|\le 2|\varphi (H)|+n+2k-2\).

Proof

For every edge \(u_iv_i\in Y_1\), we have \(|\varphi (E_H^{f}(u_i))|\ge 1\) and \(|\varphi (E_H^{f}(v_i))|\ge 1\). First, we claim that \(|\varphi (E_H^{f}(u_i))|\le 2\) and \(|\varphi (E_H^{f}(v_i))|\le 2\). Otherwise, without loss of generality, suppose that there are three distinct vertices \(w_1,w_2,w_3\in N(u_i)\cap V(H)\) such that \(\varphi (u_iw_1)\ne \varphi (u_iw_2)\ne \varphi (u_iw_3)\) and \(\{\varphi (u_iw_1),\varphi (u_iw_2), \varphi (u_iw_3)\}\subseteq \varphi _f\). Since \(|\varphi (E_H^{f}(v_i))|\ge 1\), there is one vertex \(w_4\in N(v_i)\cap V(H)\) such that \(\varphi (v_iw_4) \in \varphi _f\). Note that \(w_4\) may belong to \(\{w_1, w_2, w_3\}\). In this case, we can always find two vertex disjoint free edges \(v_iw_4\) and \(u_iw_t\) with \(t\in \{1,2,3\}\) to replace \(u_iv_i\) to yield a rainbow matching of size k in G.

Next, we will discuss all the possible cases. Set \(f(i):={\hat{d}}(u_i)+{\hat{d}}(v_i)+|E^f_H(u_i)|+|E^f_H(v_i)|\).

Case 1: \(|\varphi (E_H^{f}(u_i))|=|\varphi (E_H^{f}(v_i))|=2\). In this case, \(E_H^{f}(u_i)\cup E_H^{f}(v_i)\) can only form a properly edge-colored \(C_4\). Otherwise, we can always find two vertex disjoint free edges \(u_iw\) and \(v_iw'\) with \(w, w'\in V(H)\) to replace \(u_iv_i\) to yield a rainbow matching of size k in G. Thus, \(|E^f_H(u_i)|+|E^f_H(v_i)|=4\). By Claim 1, we have \(f(i)\le 2{{\hat{\Delta }}}(G)+4\le 2|\varphi (H)|+4k\).

Case 2: \(|\varphi (E_H^{f}(u_i))|=2\) and \(|\varphi (E_H^{f}(v_i))=1\). Under the circumstances, there are two distinct vertices \(w_1,w_2\in N(u_i)\cap V(H)\) such that \(\varphi (u_iw_1)\ne \varphi (u_iw_2)\) and \(\{\varphi (u_iw_1),\varphi (u_iw_2)\}\subseteq \varphi _f\). Similarly, there is also one vertex \(w_3\in N(v_i)\cap V(H)\) such that \(\varphi (v_iw_3)\in \varphi _f\). In order to avoid a rainbow matching of size k in G, either \(w_3=w_1\) and \(\varphi (v_iw_3)=\varphi (u_iw_2)\) or \(w_3=w_2\) and \(\varphi (v_iw_3)=\varphi (u_iw_1)\), which implies that \(|E_H^{f}(v_i)|=1\). For \(w\in V(H)\backslash \{w_1,w_2\}\), if there exists \(u_iw\in E(G)\), then either \(\varphi (u_iw)=\varphi (u_iw_3)\) or \(\varphi (u_iw)\in \varphi _{uf}\). Hence, \(|E_H^{f}(u_i)|+|E_H^{f}(v_i)|\le |V(H)|-|E_H^{uf}(u_i)|+1\). Note that \({\hat{d}}(u_i)= {\hat{d}}_M(u_i)+{\hat{d}}^{f}_H(u_i)+{\hat{d}}^{uf}_H(u_i)\), \({\hat{d}}^{f}_H(u_i)=2\) and \({\hat{d}}^{uf}_H(u_i)\le |E_H^{uf}(u_i)|\). Therefore, we have

$$\begin{aligned} \begin{aligned} f(i) \le&2k-3+2+{\hat{d}}^{uf}_H(u_i)+{\hat{d}}(v_i)+|V(H)|-|E_H^{uf}(u_i)|+1\\ \le&2k-1+{\hat{d}}(v_i)+n-2(k-1)+1\le n+2k+|\varphi (H)|. \end{aligned} \end{aligned}$$

Case 3: \(|\varphi (E_H^{f}(u_i))|=1\) and \(|\varphi (E_H^{f}(v_i))=2\). The case is symmetric to the Case 2.

Case 4: \(\varphi (E_H^{f}(u_i))=\{\alpha _1\}\), \(\varphi (E_H^{f}(v_i))=\{\alpha _2\}\) and \(\alpha _1\ne \alpha _2\). It is easy to check \(|E_H^{f}(u_i)|=|E_H^{f}(v_i)|=1\), otherwise, we can obtain a rainbow matching of size k in G. Therefore, \(f(i)\le 2{{\hat{\Delta }}}(G)+2\le 2|\varphi (H)|+4k-2\).

Case 5: \(\varphi (E_H^{f}(u_i))=\varphi (E_H^{f}(v_i))=\{\alpha \}\). In this case, we have \(f(i)\le 2{{\hat{\Delta }}}(G)+|V(H)|\le 2|\varphi (H)|+n+2k-2\).

In conclusion, since \(|\varphi (H)|\ge 2\) and \(n\ge 4k-4\), we have \(f(i)\le 2|\varphi (H)|+n+2k-2\). \(\square\)

Finally, by the definition of \(Y_2\), it is easy to get the following claim.

Claim 6

For every edge \(u_iv_i\in Y_2\), we have \(|E^f_H(u_i)|+|E^f_H(v_i)|\le |V(H)|=n-2k+2\).

2.2 Estimating the Total Color Degree of G

In this section, using above claims, we will estimate the total color degree of G. For convenience, let \(f(i):={\hat{d}}(u_i)+{\hat{d}}(v_i)+|E^f_H(u_i)|+|E^f_H(v_i)|\) for every \(u_iv_i\in E(M)\). Then we have

$$\begin{aligned} \begin{aligned} \sum _{v\in V}{{\hat{d}}(v)} =&\sum _{v\in V(M)}{{\hat{d}}(v)}+\sum _{w\in V(H)}{{\hat{d}}(w)}\\ \le&\sum _{u_iv_i\in E(M)}\left( {\hat{d}}(u_i)+{\hat{d}}(v_i)\right) +\sum _{w\in V(H)}{{\hat{d}}^{f}(w)}+\sum _{w\in V(H)}{{\hat{d}}^{uf}(w)}\\ \le&\sum _{u_iv_i\in E(M)}f(i)+|V(H)|(k-1), \end{aligned} \end{aligned}$$
(1)

since \({\hat{d}}^{uf}(v)\le |\varphi _{uf}|=k-1\) for all \(v\in V\). Next, we break the proof step into two cases.

Case 1: \(|\varphi (H)|=k-1\).

Note that \(|\varphi (H)| = k-1\), which means that \(M = X_1\cup X_2\) and \({{\hat{\Delta }}}(G)\le 3(k-1)\). Recalling Claim 2, we have \(f(i)\le 2{{\hat{\Delta }}}(G)\le 6(k-1)\) for any \(u_iv_i\in X_1\). By Claim 3 and 4, we have

$$\begin{aligned} f(i)\le \max \{{\hat{d}}^{uf}(u_i)+{\hat{d}}^{uf}(v_i)+4+4,2{{\hat{\Delta }}}(G)+3\}\le 6(k-1)+3 \end{aligned}$$

for any \(u_iv_i\in X_2\), where the last inequality follows from \(k\ge 3\). Therefore, for any \(u_iv_i\in E(M)\),

$$\begin{aligned} f(i)\le 6(k-1)+3. \end{aligned}$$

According to Inequality (1), \({\hat{d}}(G)\ge 2k-1\) and \(n\ge 4k-4\), we have

$$\begin{aligned} \begin{aligned} (2k-1)n\le \sum _{v\in V}{{\hat{d}}(v)} \le&(k-1)(6(k-1)+3)+(n-2k+2)(k-1)\\ =&n(k-1)+4(k-1)(k-1)+3(k-1)<(2k-1)n, \\ \end{aligned} \end{aligned}$$

which is contradictory.

Case 2: \(|\varphi (H)|<k-1\).

According to Inequality (1), Claim 1–6, \(|\varphi (H)|=x_1+x_2\), and \(n\ge 4k-4\), we have

$$\begin{aligned} \begin{aligned} \sum _{v\in V}{{\hat{d}}(v)} \le&\sum _{u_iv_i\in E(M)\setminus Y_1} f(i)+ \sum _{u_iv_i\in Y_1} f(i)+|V(H)|(k-1)\\ \le&2{{\hat{\Delta }}}(G)\cdot (k-1-y_1)+\sum _{u_iv_i\in E(M)\setminus Y_1} \left( |E^f_H(u_i)|+|E^f_H(v_i)|\right) \\ +&\sum _{u_iv_i\in Y_1} f(i)+|V(H)|(k-1)\\ \le&2{{\hat{\Delta }}}(G)\cdot (k-1-y_1)+0\cdot (x_1+y_3) +4x_2+y_2(n-2k+2)\\ +&y_1\cdot \max _{u_iv_i\in Y_1} f(i)+|V(H)|(k-1)\\ \le&2{{\hat{\Delta }}}(G)\cdot (k-1-y_1)+4x_2+y_2(n-2k+2)\\ +&y_1(2|\varphi (H)|+n+2k-2)+(n-2k+2)(k-1)\\ \le&2(|\varphi (H)|+2k-2)(k-1)+4x_2+(y_1+y_2)(n-2k+2)\\ +&(n-2k+2)(k-1)\\ =&2(k-1)n+4x_2-(n-4k+4)|\varphi (H)|-(n-2k+2)y_3\\ <&(2k-1)n, \\ \end{aligned} \end{aligned}$$

which is also contradictory.

3 Proof of Theorem 4

In this section, we will prove Theorem 4 by induction on k. The base case \(k = 1\) is trivial. Suppose \(k\ge 2\), and let G with strongly edge coloring \(\varphi\) be a counterexample to Theorem 4 with the fewest edges. Let \(n:=|V(G)|\). By the result of Kostochka and Yancey [8] and Theorem 3, we may assume that \(n\ge 2k+1\) and \(\delta (G)\le k-1\).

For the sake of contradiction, we still consider the total degree of G in the following proofs. Since \(\delta (G)\le k-1\), there is a vertex \(v\in V(G)\) such that \(d(v)\le k-1\). By the minimality of G, we have \(d(v)\ge 1\). Let \(u\in N(v)\), \(\varphi (uv)=\alpha\), and \(G^\alpha\) denote the subgraph of G with the edges in color class \(\alpha\). Since G is strongly edge-colored, \(G^\alpha\) is an induced matching in G. Hence, \(d(u)\le n-2|E(G^\alpha )|+1\). Let \(G^{*}\) be obtained from G by deleting the vertex v, u and all edges in \(G^\alpha\), then \(r(G^{*})< k-1\). By induction hypothesis, \(d(G^{*})< 2k-3\). Therefore, we have

$$\begin{aligned} \begin{aligned} (2k-1)n\le&\sum _{v\in V}{ d(v)} =2\left( d(u)+d(v)\right) +2(|E(G^\alpha )|-1)+(n-2)d(G^{*})\\<&2(k-1+n-2|E(G^\alpha )|+1)+2(|E(G^\alpha )|-1)+(n-2)(2k-3)\\ =&(2k-1)n+4-2(|E(G^\alpha )|+k)\\ <&(2k-1)n, \\ \end{aligned} \end{aligned}$$

which is contradictory.

4 Concluding Remarks

Though we were not able to resolve Question 2 for all graphs, we believe the answer is affirmative:

Conjecture 1

All but \(\widetilde{K_4}\) edge-colored graphs G with \({\hat{d}}(G)\ge 2k-1\) contain a rainbow matching of size at least k.

We remark that using the ideas introduced in the proof of Theorem 2, for properly edge-colored graph G, it is conceivable that the lower bound for |V(G)| in Theorem 2 may be further improved. However, it would be very interesting (and seems to be difficult) to prove conjecture 1 for all properly edge-colored graphs. If conjecture 1 for all properly edge-colored graphs is true, then it would yield a good upper bound on the rainbow Turán number of matchings. Given a graph H, the rainbow Turán number of H is defined as the maximum number of edges in a properly edge-colored graph on n vertices with no rainbow copy of H. The systematic study of rainbow Turán number was initiated in 2007 by Keevash-Mubayi-Sudakov-Verstraëte [7]. They asymptotically determined the rainbow Turán number for any non-bipartite graph, but for the rainbow Turán number of matchings, there are still no good results so far.