Odd Induced Subgraphs in Planar Graphs with Large Girth

Abstract

A long-standing conjecture asserts that there is a positive constant c such that every n-vertex graph without isolated vertices contains an induced subgraph with all degrees odd on at least cn vertices. Recently, Ferber and Krivelevich confirmed the conjecture with $c\ge 10^{-4}$. However, this is far from optimal for special family of graphs. Scott proved that $c\ge (2\chi )^{-1}$ for graphs with chromatic number $\chi \ge 2$ and conjectured that $c\ge \chi ^{-1}$. Partial tight bounds of c are also established by various authors for graphs such as trees, graphs with maximum degree 3 or $K_4$-minor-free graphs. In this paper, we further prove that $c\ge 2/5$ for planar graphs with girth at least 7, and the bound is tight. We also show that $c\le 1/3$ for general planar graphs and $c\ge 1/3$ for planar graphs with girth at least 6.

1 Introduction

All graphs considered here are finite, simple and undirected, unless otherwise specified. Gallai proved that every graph has a vertex partition into two sets, each of which induces a subgraph with all degrees even (see [12], Exercise 5.19). This implies that every graph contains an induced subgraph with all degrees even on at least half of its number of vertices. However, the situation is less clear for induced subgraph with all degrees odd. Call a graph with all degrees odd an odd graph. The following long-standing conjecture was cited by Caro [4] as “part of the graph theory folklore".

Conjecture 1.1

(Caro [4]) There exists a positive constant c such that every n-vertex graph without isolated vertices contains an odd induced subgraph with at least cn vertices.

Caro [4] pointed out that if this conjecture were true, then c would be at most 2/7, which could be seen by considering the graph with vertex set $Z_{7}$ and edges between i and $i\pm 1$, $i\pm 2\,\,(\text {mod}\,\,7)$ for $i\in \{0,\ldots ,6\}$. Clearly, it is natural to restrict our attention to graphs without isolated vertices as no odd graph can have an isolated vertex. Caro [4] initially proved that every n-vertex graph without isolated vertices contains an odd induced subgraph with at least $\Omega (\sqrt{n})$ vertices, answering a question of Alon. This was further improved to $\Omega (n/\log n)$ by Scott [15]. Very recently, Ferber and Krivelevich [6] confirmed Conjecture 1.1 with $c=10^{-4}$.

For special family of graphs, some tight bounds of Conjecture 1.1 were established by various authors. The best possible bound $2\lfloor (n+1)/3\rfloor$ for n-vertex trees has been proved by Radcliffe and Scott [14], while Berman et al. [3] proved an optimal bound 2n/5 for n-vertex graphs with maximum degree 3 and without isolated vertices. Recently, Hou et al. [8] obtained the tight bound 2n/5 for $K_4$-minor-free graphs with n vertices and without isolated vertices.

There is another conjecture related to odd induced subgraphs. In 1991, Scott [15] proved that every n-vertex graph with chromatic number $\chi$ and without isolated vertices contains an odd induced subgraph with at least $n/(2\chi )$ vertices. This implies Conjecture 1.1 for graphs with bounded chromatic number. Moreover, Scott suggested the following conjecture.

Conjecture 1.2

(Scott [15]) Every n-vertex graph with chromatic number $\chi$ and without isolated vertices contains an odd induced subgraph with at least $n/\chi$ vertices.

It was shown in [15] that it would be enough to prove Conjecture 1.2 for bipartite graphs. If holds, then the bound $n/\chi$ is best possible for $\chi =2,3$ as stated by Scott [15]. For more results and problems related to special graphs, we refer the reader to [1, 2, 5, 9,10, – 11, 13, 16].

In this paper, we consider odd induced subgraphs in planar graphs with large girth. A planar graph is a graph that can be embedded into the plane so that its edges meet only at their ends. A plane graph is a particular planar embedding of a planar graph. The girth of a graph is the length of its shortest cycle. The following is the main result of the paper.

Theorem 1.3

For $g\in \{6,7\}$, every n-vertex planar graph with girth at least g and without isolated vertices has an odd induced subgraph with at least $c_gn$ vertices, where $c_6=1/3$ and $c_7=2/5$.

Note that every planar graph with girth at least 6 has chromatic number at most 3 by Grötzsch’s Theorem [7]. This means that the result $c_6=1/3$ in Theorem 1.3 confirms a special case of Conjecture 1.2 for $\chi =3$. For general planar graphs, we also claim that $c\le 1/3$ by considering several classes of graphs (see Proposition 1.4). Since an odd graph must have even number of vertices, we further assert that every n-vertex planar graph with girth at least $g\in \{6,7\}$ and without isolated vertices has an odd induced subgraph with at least $2\lceil c_gn/2\rceil$ vertices by Theorem 1.3. This is actually tight as implied by the following proposition.

Proposition 1.4

$(\mathrm {i})$ For any $n\equiv 0\,\,(\text {mod}\,\,6)$, there exist n-vertex planar graphs without isolated vertices containing an odd induced subgraph with at most n/3 vertices.

$(\mathrm {ii})$ For some values of n, there exist n-vertex planar graphs with girth at least $g\in \{6,7\}$ and without isolated vertices containing an odd induced subgraph with at most $2\lceil c_gn/2\rceil$ vertices.

This paper is organized as follows. In the remainder of this section, we describe notation and terminology used in our proof. In Sect. 2, we give some reducible configurations of the minimal counterexample. Using the discharging method, we prove Theorem 1.3 in Sect. 3. The final section contains some conclusion remarks. Let G be a graph. For any $v\in V(G)$, denote $N_{G}(v)$ the set of neighbors of v in G and $d_G(v)$ the degree of v in G. A k-vertex, $k^{+}$-vertex, or $k^{-}$-vertex is a vertex with degree equal to k, at least k, or at most k, respectively. For any $S\subseteq V(G)$, let G[S] denote the induced subgraph of G on S and $G-S=G[V(G)\setminus S]$. For a set ${\mathscr {H}}$ of graphs, a graph is ${\mathscr {H}}$-free if it contains no member of ${\mathscr {H}}$ as a subgraph. If ${\mathscr {H}}=\{H\}$, we simply write H-free instead of ${\mathscr {H}}$-free. Usually, we denote $C_k$ a cycle of length k and write $[k]:=\{1,\ldots ,k\}$.

2 Reducible Configurations

In this section, we outline the main ideas in our proof of Theorem 1.3, and give some useful properties of minimal counterexamples.

We prove Theorem 1.3 by contradiction. Let G be a counterexample of Theorem 1.3 such that |V(G)| is minimal. For any $S\subseteq V(G)$, we call S c-good if G[S] is an odd induced subgraph in G such that $|S|\ge c\,|V(G)|$ for some constant $c>0$. The main ideas of our proof are as follows. We first pick some set $V_0\subseteq V(G)$ such that $G'=G-V_0$ has no isolated vertices. It follows that $G'$ has a $c_g$-good set $S'$ by the minimality of G. We aim to find a subset $S_0\subseteq V_0$ with $|S_0|\ge c_g|V_0|$ such that $S'\cup S_0$ induces an odd induced subgraph of G, which means that $S'\cup S_0$ is a $c_g$-good set of G by noting that

$$\begin{aligned} |S'\cup S_0|=|S'|+|S_0|\ge c_g(|V(G)|-|V_0|)+c_g|V_0|=c_g|V(G)|. \end{aligned}$$

This leads to a contradiction.

Suppose that G is a minimal n-vertex planar graph with girth at least 6 and without isolated vertices such that every odd induced subgraph in G has less than cn vertices for $c\in \{2/5, 1/3\}$. Clearly, G is connected by the minimality of |V(G)|. Recall that every tree with n vertices contains an odd induced subgraph with at least $2\lfloor (n+1)/3\rfloor$ vertices, implying that G is not a tree as $2\lfloor (n+1)/3\rfloor \ge 2n/5$ for $n\ge 2$. To simplify the presentation, let $V_1=\{v:v\in V(G)\,\,\text {and}\,\,d_G(v)=1\}$ and $G_1=G-V_1$. Write $V_2=\cup _{v\in V_1}N_G(v)$. For each $v\in V(G)$, let $N^{1}_{G}(v)=N_{G}(v)\cap V_1$ and $N^{1}_{G}[v]=N^{1}_{G}(v)\cup \{v\}$. In view of $N^{1}_{G}(v)$, we define two subsets $\pi (v)$ and L(v) by letting

$$\begin{aligned} \pi (v)= \left\{ \begin{array}{ll} \{v'\}, &{} \hbox {if there exists some} \,v'\in N^1_G(v);\\ \{v\}, &{} \hbox {if} \,N^1_G(v)=\emptyset ; \\ \end{array} \right. \end{aligned}$$

and

$$ L(v) = \left\{ {\begin{array}{*{20}{l}} {L,}&{{\text{if there exists some 2 - subset}}{\mkern 1mu} L\;{\text{of}}\;N_G^1(v);} \\ {N_G^1[v],}&{{\text{if}}{\mkern 1mu} |N_G^1(v)| \leq 1.} \end{array}} \right.$$

Note that a 2-subset L of $N^1_G(v)$ is a vertex subset of $N^1_G(v)$ with $|L|=2$. Clearly, $|L(v)|\le 2$. For each $i\in \{0,1\}$, denote $T^i_v$ the maximum subset of $N^{1}_{G}[v]$ such that $v\in T^i_v$ and $|T^i_v\setminus \{v\}|\equiv i\,\,(\text {mod}\,\,2)$, implying that

$$\begin{aligned} |T^i_v|= \left\{ \begin{array}{ll} |N^{1}_{G}(v)|+i, &{} \hbox {if} |N^{1}_{G}(v)| \hbox {is odd;} \\ |N^{1}_{G}(v)|+1-i, &{} \hbox {if} |N^{1}_{G}(v)| \hbox {is even.} \end{array} \right. \end{aligned}$$

(1)

In what follows, we present series of lemmas with respect to $G_1$ by finding good subsets in the minimal counterexample G.

2.1 Finding 2/5-Good Subsets in G

We may assume that G is a minimal n-vertex planar graph with girth at least 6 such that every odd induced subgraph in G has less than 2n/5 vertices, and call a subset $S\subseteq V(G)$ good instead of 2/5-good for short throughout this subsection.

Lemma 2.1

For each $u\in V_2$, we have $d_{G_{1}}(u)\ge 3$.

Proof

Suppose that there exists a vertex $u\in V_2$ such that $d_{G_{1}}(u)\le 2$. Clearly, we have $|N_{G}^{1}(u)|\ge 1$. This together with (1) implies that

$$\begin{aligned} \frac{|T^i_u|+1-i}{|N_{G}^{1}(u)|+2}>\frac{|T^i_u|+1-i}{|N_{G}^{1}(u)|+3}\ge \frac{2}{5} \end{aligned}$$

(2)

for each $i\in \{0,1\}$, where the equality holds if and only if $i=1$ and $|N_{G}^{1}(u)|=2$. Since G is connected but not a tree, we know that $d_{G_{1}}(u)>0$. This means that $d_{G_{1}}(u)\in [2]$.

Suppose that $d_{G_{1}}(u)=1$, say $N_{G_1}(u)=\{u_1\}$. Let $G'=G-(N_{G}^{1}[u]\cup \pi (u_1))$. Clearly, $d_{G_1}(u_1)\ge 2$ as G is not a tree, then $G'$ contains no isolated vertices. This implies that $G'$ has a good set $S'$ by the minimality of G. It follows from (2) that $S'\cup T^0_u\cup \pi (u_1)$ is good in G if $u_1\in S'$ (implying that $N_{G}^{1}(u_1)\ne \emptyset$), and $S'\cup T^1_u$ is good in G if $u_1\notin S'$, a contradiction.

Suppose that $d_{G_{1}}(u)=2$, say $N_{G_1}(u)=\{u_1,u_2\}$. Clearly, if $N_{G}^{1}(u_i)\ne \emptyset$ for some $i\in [2]$, then $d_{G_{1}}(u_i)\ge 2$ by the argument above. It follows that $G'=G-(N_{G}^{1}[u]\cup \pi (u_1)\cup \pi (u_2))$ contains no isolated vertices as G is $\{C_3,C_4\}$-free, implying a good set $S'$ in $G'$. If $u_1,u_2\notin S'$, then $S'\cup T^1_u$ is good in G by (2). If $u_i\in S'$ for some $i\in [2]$, then it follows from (2) that either $S'\cup T^1_u\cup \pi (u_1)\cup \pi (u_2)$ (if $u_{3-i}\in S'$) or $S'\cup T^0_u\cup \pi (u_i)$ (if $u_{3-i}\notin S'$) is good in G, a contradiction. This completes the proof of Lemma 2.1. $\square$

By Lemma 2.1, we have $d_{G_1}(v)\ge 2$ for each $v\in V(G_1)$. Moreover, every 2-vertex in $G_1$ is also a 2-vertex in G.

Lemma 2.2

There is no adjacent 2-vertices in $G_1$.

Proof

Suppose that $G_1$ has two adjacent 2-vertices u and v. Let $N_{G_1}(v)=\{u,v_1\}$ and $N_{G_1}(u)=\{v,u_1\}$. Clearly, $d_{G_1}(u_1)\ge 2$ and $d_{G_1}(v_1)\ge 2$. Moreover, if $N_{G}^{1}(x)\ne \emptyset$ for some $x\in \{u_1,v_1\}$, then $d_{G_{1}}(x)\ge 3$ by Lemma 2.1. It follows that $G'=G-(\{u, v\}\cup \pi (u_1)\cup \pi (v_1))$ contains no isolated vertices as G is $\{C_4,C_5\}$-free. Thus, $G'$ has a good set $S'$. If $u_1,v_1\notin S'$, then $S'\cup \{u,v\}$ is good in G. Otherwise, either $S'\cup \pi (u_1)\cup \{u\}$ (if $u_1\in S'$) or $S'\cup \pi (v_1)\cup \{v\}$ (if $v_1\in S'$) is good in G. This leads to a contradiction and completes the proof of Lemma 2.2. $\square$

Lemma 2.3

There is no 2-vertex adjacent to a 3-vertex in $G_1$.

Proof

Suppose that there is a 2-vertex v adjacent to a 3-vertex u in $G_1$. Let $N_{G_1}(v)\setminus \{u\}=\{v_1\}$ and $N_{G_1}(u)\setminus \{v\}=\{u_1,u_2\}$. Note that $u_1$, $u_2$ and $v_1$ are distinct vertices as G is triangle-free. By Lemmas 2.1 and 2.2 , we know that $N^1_G(v)=\emptyset$ and $d_{G}(v_1)\ge d_{G_1}(v_1)\ge 3$. It is easy to check that for each $i\in \{0,1\}$

$$\begin{aligned} \frac{|T^i_u|+1-i}{|N_{G}^{1}(u)|+4}\ge \frac{2}{5} \end{aligned}$$

(3)

providing $|N^1_{G}(u)|\notin \{0,2\}$, where the equality holds if and only if $|N_{G}^{1}(u)|=1$.

First, suppose that $|N^1_{G}(u)|\notin \{0,2\}$. Let

$$\begin{aligned} G'=G-(N^1_G[u]\cup \pi (u_1)\cup \pi (u_2)\cup \{v\}). \end{aligned}$$

Note that $d_{G_{1}}(u_i)\ge 3$ if $N^1_G(u_i)\ne \emptyset$ for any $i\in [2]$ by Lemma 2.1. This implies that $G'$ contains no isolated vertices as $d_{G}(v_1)\ge 3$ and G is $\{C_3,C_4\}$-free. It follows that $G'$ has a good set $S'$ by the minimality of G. If $u_1,u_2\notin S'$, then $S'\cup T^1_u$ is good in G by (3). If $u_i\in S'$ for some $i\in [2]$, then it follows from (3) that either $S'\cup T^1_u\cup \pi (u_1)\cup \pi (u_2)$ (if $u_{3-i}\in S'$) or $S'\cup T^0_u\cup \pi (u_i)$ (if $u_{3-i}\notin S'$) is good in G, a contradiction.

Next, it suffices to check the cases for $|N^1_{G}(u)|\in \{0,2\}$. Suppose that $|N^1_G(u)|=0$. Let

$$\begin{aligned} G'=G-(\{u,v\}\cup \pi (u_1)\cup \pi (u_2)\cup \pi (v_1)). \end{aligned}$$

It is easy to check that $G'$ contains no isolated vertices as G is $\{C_3,C_4,C_5\}$-free, implying that $G'$ has a good set $S'$. Clearly, $S=S'\cup \pi (v_1)\cup \{v\}$ is good in G if $v_1\in S'$ and $S=S'\cup \{u, v\}$ is good in G if $v_1,u_1,u_2\notin S'$. Now, we further consider the case for $v_1\notin S'$ and $u_i\in S'$ for some $i\in [2]$, then either $S'\cup \pi (u_i)\cup \{u\}$ (if $u_{3-i}\notin S'$) or $S'\cup \pi (u_1)\cup \pi (u_2)\cup \{u,v\}$ (if $u_{3-i}\in S'$) is good in G, a contradiction.

Suppose that $|N^1_G(u)|=2$. Let

$$\begin{aligned} V_0=N^{1}_{G}[u]\cup \pi (u_1)\cup \pi (u_2)\cup L(v_1)\cup \{v\} \;\;\text {and}\;\; G'=G-V_0. \end{aligned}$$

Note that $|T^1_u|=2$, $|L(v_1)|\le 2$ and $|V_0|\le 8$. Clearly, $G'$ contains no isolated vertices as G is $\{C_4,C_5\}$-free and $d_{G_1}(v_1)\ge 3$, yielding that $G'$ has a good set $S'$. If $u_i\in S'$ for some $i\in [2]$, then either $S'\cup T^1_u\cup \pi (u_1)\cup \pi (u_2)$ (if $u_{3-i}\in S'$) or $S'\cup N_G^1[u]\cup \pi (u_i)$ (if $u_{3-i}\notin S'$) is good in G. Suppose that $u_1,u_2\notin S'$. If $v_1\notin S'$, then $S'\cup N^1_G[u]\cup \{v\}$ is good in G. If $v_1\in S'$ (implying that $|N^1_G(v_1)|\ge 2$), then $S'\cup L(v_1)\cup T^1_u$ is good in G as $|L(v_1)|=|T^1_u|=2$. This completes the proof of Lemma 2.3. $\square$

We mention that these three lemmas are enough to prove Theorem 1.3 for planar graphs with girth at least 7.

2.2 Finding 1/3-Good Subsets in G

We may assume that G is a minimal n-vertex planar graph with girth at least 6 such that every odd induced subgraph in G has less than n/3 vertices, and call a subset $S\subseteq V(G)$ good instead of 1/3-good for short throughout this subsection. Note that a set S is 2/5-good implies that S is also 1/3-good. It follows that Lemmas 2.1, 2.2 and 2.3 are still valid for G considered in this subsection. To prove Theorem 1.3 for $g=6$, we need more auxiliary lemmas.

Lemma 2.4

There is no 2-vertex adjacent to a 4-vertex in $G_1$.

Proof

Suppose that there is a 4-vertex u in $G_1$ with $N_{G_1}(u)=\{v, u_1, u_2, u_3\}$ and $N_{G_1}(v)=\{u, v_1\}$. Note that $v_1$ and $u_i$ are distinct vertices as G is triangle-free for $i\in [3]$. Clearly, $d_G(v)=d_{G_{1}}(v)=2$ and $d_G(v_1)\ge d_{G_1}(v_1)\ge 4$ by Lemmas 2.1 and 2.3 . It is easy to check that for each $i\in \{0,1\}$

$$\begin{aligned} \frac{|T^i_u|+1-i}{|N_{G}^{1}(u)|+5}\ge \frac{1}{3} \end{aligned}$$

(4)

providing $|N^1_{G}(u)|\notin \{0,2\}$, where the equality holds if and only if $|N_{G}^{1}(u)|=1$.

First, suppose that $|N^1_{G}(u)|\notin \{0,2\}$. Let

$$\begin{aligned} G'=G-(N_G^1[u]\cup \pi (u_1)\cup \pi (u_2)\cup \pi (u_3)\cup \{v\}). \end{aligned}$$

Note that $d_{G_{1}}(u_i)\ge 3$ if $N^1_G(u_i)\ne \emptyset$ for any $i\in [3]$ by Lemma 2.1. This implies that $G'$ contains no isolated vertices as G is $\{C_3,C_4\}$-free and $d_{G_1}(v_1)\ge 4$. It follows that $G'$ has a good set $S'$. Let $I=\{i\in [3]:u_i\in S'\}$ and

$$ S = \left\{ {\begin{array}{*{20}{l}} {S^{\prime} \cup T_u^0 \cup ({ \cup _{i \in I}}\pi ({u_i})),}&{{\text{if}}\;{\mkern 1mu} |I|{\text{ }}{\mkern 1mu} is\;odd;} \\ {S^{\prime} \cup T_u^1 \cup ({ \cup _{i \in I}}\pi ({u_i})),}&{{\text{if}}\;{\mkern 1mu} |I|{\text{ }}{\mkern 1mu} is\; even.} \end{array}} \right.$$

Clearly, S is good in G by (4), a contradiction.

Next, we check the cases for $|N^1_{G}(u)|\in \{0,2\}$. Suppose that $|N_G^1(u)|=0$. Let

$$\begin{aligned} G'=G-(\{u, v\}\cup \pi (u_1)\cup \pi (u_2)\cup \pi (u_3)\cup \pi (v_1)). \end{aligned}$$

Clearly, $G'$ contains no isolated vertices as G is $\{C_3,C_4,C_5\}$-free and $d_{G_1}(v_1)\ge 4$, implying a good set $S'$ in $G'$. If $v_1\in S'$, then $S'\cup \pi (v_1)\cup \{v\}$ is good in G. Suppose that $v_1\notin S'$ and let

$$ S = \left\{ {\begin{array}{*{20}{l}} {S^{\prime} \cup \{ u\} \cup ({ \cup _{i \in I}}\pi ({u_i})),}& {{\text{if}}\;\left| I \right|\; is\;odd;} \\ {S^{\prime} \cup \{ u,v\} \cup ({ \cup _{i \in I}}\pi ({u_i})),}& {{\text{if}}\; \left| I \right| is\;even,} \end{array}} \right. $$

where I is defined as before. It is easy to check that S is good in G, a contradiction.

Suppose that $|N_G^1(u)|=2$. Let

$$\begin{aligned} V_0=N_G^1[u]\cup \pi (u_1)\cup \pi (u_2)\cup \pi (u_3)\cup L(v_1)\cup \{v\} \;\;\text {and}\;\; G'=G-V_0. \end{aligned}$$

Note that $|L(v_1)|\le 2$ and then $|V_0|\le 9$. Clearly, $G'$ contains no isolated vertices as G is $\{C_3,C_4,C_5\}$-free and $d_{G_1}(v_1)\ge 4$, implying a good set $S'$ in $G'$. If $v_1\in S'$ (implying that $|N^1_G(v_1)|\ge 2$), then $S'\cup L(v_1)\cup \{v\}$ is good in G as $|L(v_1)|=2$. Suppose that $v_1\notin S'$ and let

$$ S = \left\{ {\begin{array}{*{20}{l}} {S^{\prime} \cup N_G^1[u] \cup ({ \cup _{i \in I}}\pi ({u_i})),}&{{\text{if}}\;\left| I \right|\; is\;odd;} \\ {S^{\prime} \cup N_G^1[u] \cup \{ v\} \cup ({ \cup _{i \in I}}\pi ({u_i})),}&{{\text{if}}\; \left| I \right|\; is\;even,} \end{array}} \right. $$

where I is defined similarly. Clearly, S is good in G, a contradiction. This completes the proof of Lemma 2.4. $\square$

For any two vertices $x,y\in V(G)$, let $N^2_G(x,y)=\{z\in N_G(x)\cap N_G(y):d_G(z)=2\}$. Note that $|N^2_G(x,y)|\le 1$ as G is $C_4$-free.

Lemma 2.5

A 5-vertex is adjacent to at most three 2-vertices in $G_1$.

Proof

Suppose that there is a 5-vertex u in $G_1$ with $N_{G_1}(u)=\{v,u_1,u_2,u_3,u_4\}$ and $N_{G_1}(u_i)=\{u,v_i\}$ for each $i\in [4]$. Note that $u_i$, $v_i$ and v are distinct vertices for $i\in [4]$ since G is $\{C_3, C_4\}$-free. Clearly, $d_G(u_i)=2$ and $d_{G}(v_i)\ge 5$ for each $i\in [4]$ by Lemmas 2.1 and 2.4 . Let $U=\{u_1, u_2, u_3, u_4\}$ and $G'=G-(N^{1}_{G}[u]\cup U\cup \pi (v))$. Recall that $d_{G_{1}}(v)\ge 3$ if $N^1_G(v)\ne \emptyset$. This implies that $G'$ contains no isolated vertices as G is $C_4$-free and $d_G(u_i)=2$ for each $i\in [4]$. It follows that $G'$ has a good set $S'$. Let $S=S'\cup T^1_u$ if $v\notin S'$ and $S=S'\cup T^0_u\cup \pi (v)$ if $v\in S'$. For each $j\in \{0,1\}$, it is easy to check that

$$\begin{aligned} \frac{|T^j_u|+1-j}{|N^{1}_{G}(u)|+6}\ge \frac{1}{3} \end{aligned}$$

providing $|N^1_G(u)|\ge 3$, implying that S is good in G unless $|N^1_G(u)|\in \{0,1,2\}$.

Case 1. $|N^1_G(u)|=2$.

Let $V_0=N^{1}_{G}[u]\cup U\cup L(v_1)\cup \pi (v)$ and $G'=G-V_0$. Recall that $d_{G}(v_1)\ge 5$ and $d_{G_{1}}(v)\ge 3$ if $N^1_G(v)\ne \emptyset$. It follows that $G'$ contains no isolated vertices as G is $\{C_4,C_5\}$-free. Thus, $G'$ has a good set $S'$. If $v\in S'$, then $S'\cup N^{1}_{G}[u]\cup \pi (v)$ is good in G in view of $|V_0|\le 10$ and $|N^{1}_{G}[u]|=3$. If $v\notin S'$ and $v_1\notin S'$, then $S'\cup N^{1}_{G}[u]\cup \{u_1\}$ is also good in G. Thus, we have $v\notin S'$ and $v_1\in S'$, implying that $L(v_1)\subseteq N^1_G(v_1)$ and $|L(v_1)|=2$. It follows that $S'\cup T^1_u\cup L(v_1)$ is good in G as $|T^1_u|=2$.

Case 2. $|N^1_G(u)|=1$. For each $j\in \{0,1\}$, let

$$\begin{aligned} I_j=\{i\in [4]:|N^1_G(v_i)|=j\} \;\;\text {and}\;\; I_2=\{i\in [4]:|N^1_G(v_i)|\ge 2\}. \end{aligned}$$

Clearly, $|I_0|+|I_1|+|I_2|=4$. In what follows, we get a contradiction by showing that $|I_j|\le 1$ for each $j\in \{0,1,2\}$. Otherwise, we may assume that $[2]\subseteq I_j$ for some $j\in \{0,1,2\}$. Now, we define a set $V^*$ according to $I_j$ as follows: if $j=2$, then let $V^*\subseteq N^1_G(v_1)\cup N^1_G(v_2)$ with $|V^*\cap N^1_G(v_i)|=2$ for each $i\in [2]$; otherwise, $V^*=N^1_G[v_1]\cup N^1_G[v_2]\cup N^2_G(v_1,v_2)$. Let $V_0=N^{1}_{G}[u]\cup U\cup V^*\cup \pi (v)$ and $G'=G-V_0$. Note that $|V_0|\le 12$ as $|N^2_G(v_1,v_2)|\le 1$. Clearly, $G'$ contains no isolated vertices as G is $\{C_4,C_5\}$-free and $d_G(v_i)\ge 5$ for each $i\in [4]$. Thus, $G'$ has a good set $S'$. If $v_1,v_2\notin S'$, then either $S'\cup \{u_1,u_2,u\}\cup N^1_G(u)$ (if $v\notin S'$) or $S'\cup \{u_1,u_2,u\}\cup \pi (v)$ (if $v\in S'$) is good in G as $|V_0|\le 12$. If $v_i\in S'$ for some $i\in [2]$, then either $S'\cup (V^*\cap N^1_G(v_i))\cup N^1_G[u]$ (if $v\notin S'$) or $S'\cup (V^*\cap N^1_G(v_i))\cup \{u\}\cup \pi (v)$ (if $v\in S'$) is good in G as $|V_0|\le 12$ and $|V^*\cap N^1_G(v_i)|=2$.

Case 3. $|N^1_G(u)|=0$. Let

$$\begin{aligned} I_0=\{i\in [4]:|N^1_G(v_i)|=0\} \;\;\text {and}\;\; I_1=\{i\in [4]:|N^1_G(v_i)|\ge 1\}. \end{aligned}$$

We first claim that $|I_0|\le 2$. Otherwise, we may assume that $[3]\subseteq I_0$. Let

$$\begin{aligned} V_0=U\cup \{u,v_1,v_2,v_3\}\cup \pi (v)\cup (\cup _{1\le k<\ell \le 3}N^2_G(v_k,v_\ell )) \;\;\text {and}\;\; G'=G-V_0. \end{aligned}$$

Clearly, $|V_0|\le 12$ and $G'$ contains no isolated vertices as G is $\{C_4,C_5\}$-free and $d_G(v_i)\ge 5$ for each $i\in [4]$. Thus, $G'$ has a good set $S'$. It follows that either $S'\cup \{u,u_1,u_2,u_3\}$ (if $v\notin S'$) or $S'\cup \{u,u_1,u_2\}\cup \pi (v)$ (if $v\in S'$) is good in G. Thus, we have $|I_0|\le 2$. Let $\pi (v_i)=\{\pi _i\}$ for each $i\in [4]$ and

$$\begin{aligned} V'_0=U\cup \pi (v)\cup \{u\}\cup (\cup _{i\in [4]}\pi (v_i))\cup (\cup _{1\le k<\ell \le 4}N^2_G(\pi _k,\pi _\ell )). \end{aligned}$$

Note that $|\cup _{1\le k<\ell \le 4}N^2_G(\pi _k,\pi _\ell )|\le 1$ as $|I_0|\le 2$. Thus, $|V_0|\le 11$. Clearly, $G''=G-V'_0$ contains no isolated vertices as G is $\{C_4,C_5\}$-free and $d_G(v_i)\ge 5$ for each $i\in [4]$. Thus, $G''$ has a good set $S''$. Let $I=\{i\in [4]:v_i\in S''\}$. If $|I|\ge 2$ (say $[2]\in I$), then $S''\cup \{u_1,u_2\}\cup \pi (v_1)\cup \pi (v_2)$ is good in G. This implies that $| [4]\setminus I|\ge 3$. Suppose that $[3]\subseteq [4]\setminus I$, i.e., $v_i\notin S''$ for $i\in [3]$. It follows that either $S''\cup \{u,u_1,u_2,u_3\}$ (if $v\notin S''$) or $S''\cup \{u,u_1,u_2\}\cup \pi (v)$ (if $v\in S''$) is good in G. This completes the proof of Lemma 2.5. $\square$

We mention that these lemmas comprise the heart of the proof of Theorem 1.3 for planar graphs with girth at least 6.

3 Proof of Theorem 1.3

In this section, we prove Theorem 1.3 by way of the discharging method. Let G be a plane graph and denote by F(G) the set of faces of G. For each face $f\in F(G)$, the degree $d_G(f)$ of f is the number of edges in its boundary. A k-face or $k^{+}$-face is a face with degree equal to k or at least k, respectively. Note that all the Lemmas are proved in Section 2 for graphs with girth at least 6. The condition that G is $C_6$-free for $g=7$ is only used in the discharging process.

Proof of Theorem 1.3

Let G be a minimal n-vertex plane graph with girth at least g and without isolated vertices such that every odd induced subgraph in G has less than $c_gn$ vertices for $g\in \{6,7\}$, where $c_6=1/3$ and $c_7=2/5$. Recall that $G_1$ is the graph obtained from G by deleting all its vertices with degree exactly one. In Section 2, we present series of local structures of $G_1$, which finally show that such graph doesn’t exist by way of the discharging method as proved later. It follows that G doesn’t exist or is a single edge (as G is connected). This leads to a contradiction in either case. In what follows, we prove that $G_1$ doesn’t exist.

We first define the initial charge function $\mu _{G_1}(x)$ on $G_1$ such that $\mu _{G_1}(v)=d_{G_1}(v)-4$ for each v $\in$ $V(G_1)$ and $\mu _{G_1}(f)=d_{G_1}(f)-4$ for each $f\in F(G_1)$. By Euler’s formula, we have

$$\begin{aligned} \sum _{v\in V(G_1)}(d_{G_1}(v)-4)+\sum _{f\in F(G_1)}(d_{G_1}(f)-4)=-8. \end{aligned}$$

Next, by defining suitable discharging rules, we aim to change $\mu _{G_1}(x)$ to the final charge function $\mu '_{G_1}(x)$ such that $\mu '_{G_1}(x)\ge 0$ for all $x\in V(G_1)\cup F(G_1)$. The discharging rules on $G_1$ are as follows:

• (R1) Each 2-vertex gets $\frac{g-4}{3}$ from each incident $g^{+}$-face;

• (R2) Each 3-vertex gets $\frac{1}{3}$ from each incident $g^{+}$-face;

• (R3) Each $5^+$-vertex gives $\frac{1}{3}$ to each adjacent 2-vertex (specially for $g=6$).

Claim 3.1

For every face $f\in F(G_1)$, we have $\mu _{G_1}'(f)$ $\ge 0$.

Proof

For each $\ell \in \{2,3\}$, let $t_{\ell }(f)$ be the number of $\ell$-vertices on the face $f\in F(G_1)$. Clearly, the number of $4^+$-vertices on f is $d_{G_1}(f)-t_2(f)-t_3(f)$. Note that there is at most one 2-vertex between any two consecutive $4^+$-vertices on f by Lemmas 2.2 and 2.3 . It follows that $t_2(f)\le d_{G_1}(f)-t_2(f)-t_3(f)$, i.e.,

$$\begin{aligned} 2t_2(f)+t_3(f)\le d_{G_1}(f). \end{aligned}$$

In particular, we have $2t_2(f)\le d_{G_1}(f)$. Thus, for each $f\in F(G_1)$, we conclude by (R1) and (R2) that

$$\begin{aligned} \mu _{G_1}'(f)&\ge \mu _{G_1}(f)-\frac{g-4}{3}\times t_2(f)-\frac{1}{3}\times t_3(f)\nonumber \\&=d_{G_1}(f)-4-\frac{g-6}{6}\times 2t_2(f)-\frac{1}{3}\times (2t_2(f)+t_3(f))\nonumber \\&\ge \frac{10-g}{6}\times d_{G_1}(f)-4. \end{aligned}$$

(5)

This together with the fact $d_{G_1}(f)\ge g\in \{6,7\}$ implies that $\mu _{G_1}'(f)\ge 0$ if (i) $g=6$, or (ii) $g=7$ and $d_{G_1}(f)\ge 8$. It remains to consider the case for $g=d_{G_1}(f)=7$. Clearly, we have $2t_2(f)\le 6$ in this situation. Thus, the desired result also holds in view of (5) providing that $2t_2(f)+t_3(f)\le d_{G_1}(f)-1=6$. Suppose that $g=d_{G_1}(f)=2t_2(f)+t_3(f)=7$. By (5), we have $\mu _{G_1}'(f)\ge (2-t_2(f))/3$, implying that $\mu _{G_1}'(f)\ge 0$ unless $t_2(f)=3$. Note that it is impossible to warrant $t_2(f)=3$ and $t_3(f)=1$ in any 7-face f by Lemmas 2.2 and 2.3 . Hence, we have $\mu _{G_1}'(f)\ge 0$ for each $f\in F(G_1)$. This completes the proof of Claim 3.1. $\square$

Claim 3.2

For every vertex $v\in V(G_1)$, we have $\mu _{G_1}'(v)\ge 0$.

Proof

Recall that $G_1$ has minimum degree at least two by Lemma 2.1. We first prove this for $g=7$. By (R1) and (R2), we have $\mu _{G_1}'(v)=d_{G_1}(v)-4+2\times 1=0$ for each 2-vertex v and $\mu _{G_1}'(v)=d_{G_1}(v)-4+3\times 1/3=0$ for each 3-vertex v. Since any $4^+$-vertex doesn’t involve in the discharging procedure, its charge remains nonnegative. This means that $\mu _{G_1}'(v)$ $\ge 0$ for all $v\in V(G_1)$. Now, we show that the claim holds for $g=6$. Clearly, the charge of any 4-vertex remains nonnegative. Recall that there is no 2-vertex adjacent to a $4^-$-vertex in $G_1$ by Lemmas 2.2, 2.3 and 2.4 . It follows from (R1) and (R3) that $\mu _{G_1}'(v)=d_{G_1}(v)-4+2\times 2/3+2\times 1/3=0$ for each 2-vertex v. It is also easy to see that $\mu _{G_1}'(v)=d_{G_1}(v)-4+3\times 1/3=0$ for each 3-vertex v by (R2). Note that there are at most three 2-vertices get charges from the same 5-vertex by Lemma 2.5. This implies that $\mu _{G_1}'(v)=d_{G_1}(v)-4-3\times 1/3=0$ for each 5-vertex v by (R3). At last, we have $\mu _{G_1}'(v)=d_{G_1}(v)-4-d_{G_1}(v)\times 1/3\ge 0$ for each $6^+$-vertex v. Thus, we complete the proof of Claim 3.2. $\square$

By Claims 3.1 and 3.2 , we have $\mu '_{G_1}(x)\ge 0$ for all $x\in V(G_1)\cup F(G_1)$. This leads to a contradiction, completing the proof of Theorem 1.3. $\square$

4 Concluding Remarks

We have shown that every n-vertex planar graph with girth at least g and without isolated vertices has an odd induced subgraph with at least $c_gn$ vertices for $g\in \{6,7\}$, where $c_6=1/3$ and $c_7=2/5$. For some small graphs, we claim that both bounds are tight as shown by Proposition 1.4. We also find several classes of planar graphs with $c=1/3$, all of which contain small cycles. It is interesting to see whether every n-vertex planar graph without isolated vertices has an odd induced subgraph with at least n/3 vertices. In the end, we give a proof of Proposition 1.4.

Fig. 1

Planar graphs with $c=1/3$

Proof of Proposition 1.4

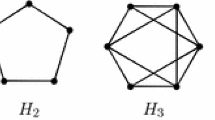
$(\mathrm {i})$ Note that any graph in Fig. 1 contains an odd induced subgraph with at most 2 vertices. It follows that Proposition 1.4$(\mathrm {i})$ holds for these graphs and their disjoint union.

$(\mathrm {ii})$ Note that any cycle of length $3k+i$ for $i\in \{0,1,2\}$ has an odd induced subgraph with at most 2k vertices. As a consequence, if $g=7$, then Proposition 1.4$(\mathrm {ii})$ holds for any cycle of length 7, 8, 11, and the disjoint union of two cycles of length 8; if $g=6$, then it is valid for any cycle of length 7, 8, and any cycle of length 6 with a pendent edge at some vertex of the cycle. $\square$