Sub-Ramsey Numbers for Matchings

Abstract

Given a graph G and a positive integer k, the sub-Ramsey number sr(G, k) is defined to be the minimum number m such that every $K_{m}$ whose edges are colored using every color at most k times contains a subgraph isomorphic to G all of whose edges have distinct colors. In this paper, we will concentrate on $sr(nK_{2},k)$ with $nK_{2}$ denoting a matching of size n. We first give upper and lower bounds for $sr(nK_{2},k)$ and exact values of $sr(nK_{2},k)$ for some n and k. Afterwards, we show that $sr(nK_{2},k)=2n$ when n is sufficiently large and $k<\frac{n}{8}$ by applying the Local Lemma.

1 Introduction

All graphs considered in this paper are simple and finite. For terminology and notation not defined here, we refer the reader to [5].

Let G be a graph and k a positive integer. An edge-coloring of G is a mapping $C: E(G)\rightarrow {\mathbb {N}}$, where ${\mathbb {N}}$ is the set of natural numbers. We call C k-bounded if each color appears at most k times. If $k=1$, i.e., all edges of G have distinct colors, then we say that G is rainbow. The sub-$Ramsey\,number$ sr(G, k) is defined to be the minimum number m such that every k-bounded edge-coloring of $K_{m}$ contains a rainbow subgraph isomorphic to G.

The study of sub-Ramsey theory dates back to 1975 when Fred Galvin posed the Advanced Problem 6034 in the American Mathematical Monthly [12]. The problem description is as follows:

Suppose that the edges of the complete graph on n vertices are colored so that no color appears more than k times. (1) If $n\ge k+2$, show that there is a rainbow triangle. (2) Show that this is not necessarily so if $n=k+1$.

Galvin [12] gave a solution to this problem. After that, some related generalizations began to emerge. In Ref. [3] the authors gave the definition of the sub-Ramsey number and proved that $sr(G,k)\le r(G,k)$ (the definition of r(G, k) will be given later), and hence each sr(G, k) is guaranteed to be finite. So far the sub-Ramsey number has been considered for several special graph classes-complete graphs, paths, cycles and stars. Denote by $K_{n}$, $P_{n}$ and $C_{n}$ the complete graph, path and cycle of n vertices respectively, and $K_{1,n}$ the star with $n+1$ vertices. For complete graphs, Alspach et al. [3] proved that

$$\begin{aligned} k(n-1)+1\le sr(K_{n},k)\le \frac{n(n-1)(n-2)(k-1)+3}{4}, \end{aligned}$$

where $n\ge 4$ and $k\ge 2$. After that Hell et al. [16] showed that

$$\begin{aligned} cn^{3/2}\le sr(K_{n}, k)\le (2n-3)(n-2)(k-1)+3 \end{aligned}$$

for some constant c, which improved the results of Alspach et al. For paths and cycles, Hahn and Thomassen proved that $sr(P_{n},k)=sr(C_{n},k)=n$ when $n\ge ck^{3}$ in Ref. [15]. Albert et al. [1] later showed that if n is sufficiently large and $k\le cn$ for $c< \frac{1}{32}$, then $sr(C_{n},k)=n$. The sub-Ramsey numbers of stars have not been completely solved so far. The authors of Refs. [9, 13, 14] gave upper and lower bounds for $sr(K_{1,n},k)$ and some exact values of $sr(K_{1,n},k)$ when n or k is fixed. In addition to this, sub-Ramsey numbers for arithmetic progressions are also studied [2, 4]. In this paper, we will concentrate on the sub-Ramsey number of $nK_{2}$ which is a matching of n independent edges.

First, according to the definition of $sr(nK_{2},k)$, we can get the following simple results:

• 1. $sr(nK_{2},k)\ge 2n$.

  Note that $K_{m}$ contains no $nK_{2}$ for $m<2n$.

• 2. $sr(nK_{2},k)\ge \left\lfloor \frac{3+\sqrt{1+8k(n-1)}}{2}\right\rfloor$.

  Since $K_{m}$ can be colored with at most $n-1$ colors when $\left( {\begin{array}{c}m\\ 2\end{array}}\right) \le k(n-1)$, we have

  $$\begin{aligned} sr(nK_{2},k)\ge \left\lfloor \frac{1+\sqrt{1+8k(n-1)}}{2}\right\rfloor +1\ge \left\lfloor \frac{3+\sqrt{1+8k(n-1)}}{2}\right\rfloor . \end{aligned}$$

• 3. $sr(nK_{2},1)=2n$.

When $m=2n$ and $k=1$, $K_{m}$ must contain a rainbow $nK_{2}$, and hence $sr(nK_{2},1)\le 2n$. Since $sr(nK_{2},1)\ge 2n$, we can get $sr(nK_{2},1)=2n$. Therefore, we assume $k\ge 2$ in the rest of the paper.

Let r(G, k) denote the Ramsey number for graph G, that is, r(G, k) is the minimum number m such that if the edges of $K_{m}$ are partitioned into at most k classes then some class contains a subgraph isomorphic to G. The following proposition shows the relationship between sr(G, k) and r(G, k).

Proposition 1

(Alspach et al. [3]) Let G be a given graph and k a positive integer. Then $sr(G,k)\le r(G,k)$.

So knowing what is the value of $r(nK_{2},k)$ is necessary to solve for $sr(nK_{2},k)$. In 1975, the Ramsey numbers for matchings are given by Cockayne and Lorimer [7].

Theorem 1

(Cockayne and Lorimer [7]) If $n_{1},n_{2},\ldots ,n_{c}$ are positive integers and $n_{1}=max(n_{1},n_{2},\ldots , n_{c})$, then $r(n_{1}K_{2},n_{2}K_{2},\ldots ,n_{c}K_{2})=n_{1}+1+\sum \nolimits _{i=1}^c(n_{i}-1)$.

From this theorem we can know that if $c=k$ and $n_{1}=n_{2}=\cdots =n_{k}=n$ then $r(nK_{2},k)=n(k+1)+1-k$, so $sr(nK_{2},k)\le r(nK_{2},k)=n(k+1)+1-k$. Our following result improves the upper bound of $sr(nK_{2},k)$ from O(nk) to $O(nk^{\frac{1}{2}})$.

Theorem 2

Let $n\ge 3$ and $k\ge 5$ be two integers. Then

$$\begin{aligned} sr(nK_{2},k)\le \left\lfloor \frac{5+\sqrt{1+4n(n-1)(k-1)}}{2}\right\rfloor . \end{aligned}$$

It is easy to verify that the upper bound of Theorem 2 is also true for $sr(3K_{2},3)$ and $sr(nK_{2},4)$ with $n\in \{3, 4, 5, 6\}$. Our next theorems give some exact values of $sr(nK_{2},k)$ when n or k is fixed. It is clear that $sr(K_{2},k)=2$ so that $n\ge 2$ is assumed.

Theorem 3

$sr(2K_{2},k)=\max \left\{ 5,\left\lfloor \frac{3+\sqrt{1+8k}}{2}\right\rfloor \right\}$.

Theorem 4

• (1) $sr(nK_{2},2)=2n$ for all $n\ge 3$;

• (2) $sr(nK_{2},3)=2n$ for all $n\ge 3$;

• (3) $sr(nK_{2},4)=2n$ for all $n\ge 3$;

• (4) $2n\le sr(nK_{2},5)\le 2n+1$.

Theorem 4 shows that $sr(nK_{2},2)=sr(nK_{2},3)=sr(nK_{2},4)=2n$ attains the lower bound 2n and the upper bound of Theorem 2 for some n. A case is now considered which shows that $sr(3K_{2},5)=7$. It is probably the case that the upper bound of Theorem 2 is closer to the truth than the lower bound 2n for some k.

Proposition 2

$sr(3K_{2},5)=7$.

It became clear that $sr(nK_{2},k)\le sr(nK_{2},k+1)$. Judging from these results, the gap between the lower bound 2n and the upper bound of Theorem 2 is not large. A question mentioned in Erdős et al. [8] is that of how fast can we allow k to grow and guarantee that there exists a rainbow Hamilton cycle in a k-bounded edge-colored $K_{n}$. After that, this question was considered by many researchers. Albert et al. [1] proved the following theorem, which showed that the growth rate of k can be linear.

Theorem 5

(Albert et al. [1]) If n is sufficiently large and k is at most $\lceil cn\rceil$, where $c<\frac{1}{32}$, then any k-bounded coloring of $K_{n}$ contains a rainbow Hamilton cycle.

For other results related to the above question, we recommend papers [10, 11, 15]. From Theorem 5 we can easily conclude that if n is sufficiently large and k is at most $\lceil cn\rceil$, where $c<\frac{1}{16}$, then any k-bounded coloring of $K_{2n}$ contains a rainbow $nK_{2}$. Here, we show that $c<\frac{1}{8}$ is enough by giving the following theorem.

Theorem 6

If n is sufficiently large and $k<\frac{n}{8}$, then $sr(nK_{2},k)=2n$.

We give the proofs of our results in the rest of this paper. Before that, we need to introduce a definition. An (H, k)-colored graph G is a k-bounded edge-colored G so that no $H\subseteq G$ is rainbow. We use C(G) to denote the set of colors appearing on the edges of G.

2 Proof of Theorem 2

Let $K_{m}$ be $(nK_{2},k)$-colored and let the colors used be $c_{1},c_{2},\ldots ,c_{p}$. Denote by $m_{i}$ the number of edges colored $c_{i}$, where $i=1, 2, \ldots , p$, then $m_{i}\le k$ and

$$\begin{aligned} \sum _{i=1}^{p}m_{i}=\left( {\begin{array}{c}m\\ 2\end{array}}\right) =\frac{m(m-1)}{2}. \end{aligned}$$

Let W denote the number of unordered pairs of disjoint edges of $K_{m}$ colored by the same color. Clearly,

$$\begin{aligned} W\le \sum ^p_{i=1}\left( {\begin{array}{c}m_{i}\\ 2\end{array}}\right) =\sum ^p_{i=1}m_{i}\frac{m_{i}-1}{2} \le \sum ^p_{i=1}m_{i}\frac{k-1}{2}=\left( {\begin{array}{c}m\\ 2\end{array}}\right) \frac{k-1}{2}. \end{aligned}$$

(1)

Let ${\mathscr {G}}$ denote the set of all subgraphs of $K_{m}$ isomorphic to $nK_{2}$. Each unordered pairs of disjoint edges colored by the same color appears in

$$\begin{aligned} \frac{\left( {\begin{array}{c}m-4\\ 2\end{array}}\right) \left( {\begin{array}{c}m-6\\ 2\end{array}}\right) \ldots \left( {\begin{array}{c}m-(2n-2)\\ 2\end{array}}\right) }{(n-2)!} \end{aligned}$$

graphs in ${\mathscr {G}}$. But $K_{m}$ contains

$$\begin{aligned} \frac{\left( {\begin{array}{c}m\\ 2\end{array}}\right) \left( {\begin{array}{c}m-2\\ 2\end{array}}\right) \left( {\begin{array}{c}m-4\\ 2\end{array}}\right) \ldots \left( {\begin{array}{c}m-(2n-2)\\ 2\end{array}}\right) }{n!} \end{aligned}$$

$nK_{2}$’s each of which must contain a pair of edges of the same color by $K_{m}$ be $(nK_{2},k)$-colored. Thus,

$$\begin{aligned} W\frac{\left( {\begin{array}{c}m-4\\ 2\end{array}}\right) \left( {\begin{array}{c}m-6\\ 2\end{array}}\right) \ldots \left( {\begin{array}{c}m-(2n-2)\\ 2\end{array}}\right) }{(n-2)!} \ge \frac{\left( {\begin{array}{c}m\\ 2\end{array}}\right) \left( {\begin{array}{c}m-2\\ 2\end{array}}\right) \left( {\begin{array}{c}m-4\\ 2\end{array}}\right) \ldots \left( {\begin{array}{c}m-(2n-2)\\ 2\end{array}}\right) }{n!}. \end{aligned}$$

By inequality (1), we have

$$\begin{aligned} \left( {\begin{array}{c}m\\ 2\end{array}}\right) \frac{k-1}{2}\frac{\left( {\begin{array}{c}m-4\\ 2\end{array}}\right) \left( {\begin{array}{c}m-6\\ 2\end{array}}\right) \ldots \left( {\begin{array}{c}m-(2n-2)\\ 2\end{array}}\right) }{(n-2)!} \ge \frac{\left( {\begin{array}{c}m\\ 2\end{array}}\right) \left( {\begin{array}{c}m-2\\ 2\end{array}}\right) \left( {\begin{array}{c}m-4\\ 2\end{array}}\right) \ldots \left( {\begin{array}{c}m-(2n-2)\\ 2\end{array}}\right) }{n(n-1)(n-2)!}. \end{aligned}$$

Finally,

$$\begin{aligned} \frac{k-1}{2} \ge \frac{\left( {\begin{array}{c}m-2\\ 2\end{array}}\right) }{n(n-1)}. \end{aligned}$$

This yields

$$\begin{aligned} m\le \left\lfloor \frac{5+\sqrt{1+4n(n-1)(k-1)}}{2}\right\rfloor . \end{aligned}$$

Since the upper bound must be greater than or equal to the lower bound, we assume that $k\ge 5$. Then we have

$$\begin{aligned} \begin{aligned} \left\lfloor \frac{5+\sqrt{1+4n(n-1)(k-1)}}{2}\right\rfloor&\ge \left\lfloor \frac{5+\sqrt{1+16n(n-1)}}{2}\right\rfloor \\&\ge \left\lfloor \frac{5+\sqrt{16(n-1)(n-1)}}{2}\right\rfloor \\&=\left\lfloor 2n+\frac{1}{2}\right\rfloor \\&=2n. \end{aligned} \end{aligned}$$

Hence the theorem holds.

3 Proof of Theorem 3

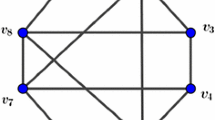
Consider the complete graph $K_{4}$ on the vertex set $\{v_{1},v_{2},v_{3},v_{4}\}$. Clearly, $K_{4}$ contains

$$\begin{aligned} \frac{\left( {\begin{array}{c}4\\ 2\end{array}}\right) \left( {\begin{array}{c}2\\ 2\end{array}}\right) }{2}=3 \end{aligned}$$

matchings of size 2. Color each of the three matchings with one color (see Fig. 1).

Fig. 1

2-bounded edge-coloring of $K_{4}$ contains no rainbow $2K_{2}$

If $K_{4}$ is edge-colored with 3 colors such that $C(v_{1}v_{2})=C(v_{3}v_{4})=1$, $C(v_{1}v_{3})=C(v_{2}v_{4})=2$ and $C(v_{1}v_{4})=C(v_{2}v_{3})=3$, then it contains no rainbow $2K_{2}$. So, $sr(2K_{2},k)\ge 5$. Note that we already showed that $sr(2K_{2},k)\ge \left\lfloor \frac{3+\sqrt{1+8k}}{2}\right\rfloor$. Now, we proceed by proving the following lemma which also appears in Ref. [6].

Lemma 1

Any edge-coloring of $K_{m}$ $(m\ge 5)$ with at least 2 colors contains a rainbow subgraph isomorphic to $2K_{2}$.

Proof

For $m\ge 5$, let the edges of $K_{m}$ be colored with at least 2 colors. Suppose that $K_{m}$ contains no rainbow $2K_{2}$. Let $e_{1}=v_{1}v_{2}$ be an arbitrary edge of $K_{m}$. Assume that $C(e_{1})=1$ and $U=V(K_{m})-\{v_{1},v_{2}\}$. Then $C(e)=1$ for all edges $e\in E(K_{m}[U])$. Moreover, $C(e)=1$ for all edges $e\in [\{v_{1},v_{2}\},U]$, since$|U|\ge 3$, where $[\{v_{1},v_{2}\},U]$ is the set of edges between $\{v_{1},v_{2}\}$ and U. Then $K_{m}$ is monochromatic, a contradiction. $\square$

If $\left( {\begin{array}{c}m\\ 2\end{array}}\right) >k$, which yields $m\ge \left\lfloor \frac{3+\sqrt{1+8k}}{2}\right\rfloor$, then, clearly, $K_{m}$ is colored such that at least two colors are used. By Lemma 1, $K_{m}$ contains a rainbow $2K_{2}$. Therefore, $sr(2K_{2},k)\le \left\lfloor \frac{3+\sqrt{1+8k}}{2}\right\rfloor$. In conclusion, we have this theorem.

4 Proof of Theorem 4

The lower bounds are obvious. For the upper bounds of (1)–(3) of Theorem 4, we prove them by contradiction. Before giving the proofs, we first make some assumptions. Suppose that $m=2n$ and $K_{m}$ is $(nK_{2},k)$-colored where $k\in \{2, 3, 4\}$. Let $C(E(K_{m}))=\{c_{1},c_{2},\ldots ,c_{p}\}$ and denote by $e_{i}$ the number of edges colored $c_{i}$. Then $e_{i}\le k$ and

$$\begin{aligned} \sum _{i=1}^{p}e_{i}=\left( {\begin{array}{c}2n\\ 2\end{array}}\right) =\frac{2n(2n-1)}{2}=2n^{2}-n\le kp. \end{aligned}$$

Let ${\mathscr {G}}$ denote the set of all subgraphs of $K_{m}$ isomorphic to $nK_{2}$, s denote the number of unordered pairs of disjoint edges of $K_{m}$ colored by the same color. Clearly,

$$\begin{aligned} s\le \sum ^p_{i=1}\left( {\begin{array}{c}e_{i}\\ 2\end{array}}\right) =\sum ^p_{i=1}e_{i}\frac{e_{i}-1}{2} \le \sum ^p_{i=1}e_{i}\frac{k-1}{2}=\frac{(2n^{2}-n)(k-1)}{2}, \end{aligned}$$

(2)

and each pair of edges of the same color appears in

$$\begin{aligned} \frac{\left( {\begin{array}{c}2n-4\\ 2\end{array}}\right) \left( {\begin{array}{c}2n-6\\ 2\end{array}}\right) \ldots \left( {\begin{array}{c}2\\ 2\end{array}}\right) }{(n-2)!} \end{aligned}$$

graphs in ${\mathscr {G}}$ if the edges are vertex-disjoint. Note that $K_{m}$ contains

$$\begin{aligned} \frac{\left( {\begin{array}{c}2n\\ 2\end{array}}\right) \left( {\begin{array}{c}2n-2\\ 2\end{array}}\right) \left( {\begin{array}{c}2n-4\\ 2\end{array}}\right) \ldots \left( {\begin{array}{c}2\\ 2\end{array}}\right) }{n!} \end{aligned}$$

subgraphs isomorphic to $nK_{2}$ each of which must contain a pair of edges of the same color. Thus,

$$\begin{aligned} s\frac{\left( {\begin{array}{c}2n-4\\ 2\end{array}}\right) \left( {\begin{array}{c}2n-6\\ 2\end{array}}\right) \ldots \left( {\begin{array}{c}2\\ 2\end{array}}\right) }{(n-2)!}\ge \frac{\left( {\begin{array}{c}2n\\ 2\end{array}}\right) \left( {\begin{array}{c}2n-2\\ 2\end{array}}\right) \left( {\begin{array}{c}2n-4\\ 2\end{array}}\right) \ldots \left( {\begin{array}{c}2\\ 2\end{array}}\right) }{n!}. \end{aligned}$$

(3)

Then we have

• (1) When $k=2$, it follows that $s\le \frac{2n^{2}-n}{2}$ from inequality (2), and hence

  $$\begin{aligned} \frac{2n^{2}-n}{2}\ge \frac{\left( {\begin{array}{c}2n\\ 2\end{array}}\right) \left( {\begin{array}{c}2n-2\\ 2\end{array}}\right) }{n(n-1)} \end{aligned}$$

  by inequality (3). This yields $\frac{1}{2}\le n\le 2$. But $n\ge 3$, a contradiction.

• (2) When $k=3$, $s\le 2n^{2}-n$ can be obtained from inequality (2). Hence, we have

  $$\begin{aligned} 2n^{2}-n\ge \frac{\left( {\begin{array}{c}2n\\ 2\end{array}}\right) \left( {\begin{array}{c}2n-2\\ 2\end{array}}\right) }{n(n-1)} \end{aligned}$$

  by inequality (3). This yields $\frac{1}{2}\le n\le 3$. Recall that $n\ge 3$. We have $n=3$. Then, by Theorem 2,

  $$\begin{aligned} sr(3K_{2},3)\le \left\lfloor \frac{5+\sqrt{1+4\times 3\times 2\times 2}}{2}\right\rfloor =6. \end{aligned}$$

• (3) Similarly, we know that $s\le \frac{3(2n^{2}-n)}{2}$ when $k=4$ by inequality (2). Then, we have

  $$\begin{aligned} \frac{3(2n^{2}-n)}{2}\ge \frac{\left( {\begin{array}{c}2n\\ 2\end{array}}\right) \left( {\begin{array}{c}2n-2\\ 2\end{array}}\right) }{n(n-1)} \end{aligned}$$

  by inequality (3). This yields $\frac{1}{2}\le n\le 6$. Recall that $n\ge 3$. We have $n\in \{3, 4, 5, 6\}$. Then, by Theorem 2,

  $$\begin{aligned} sr(nK_{2},4)\le \left\lfloor \frac{5+\sqrt{1+4\times n\times (n-1)\times 3}}{2}\right\rfloor \le 2n. \end{aligned}$$

• (4) By Theorem 2,

  $$\begin{aligned} sr(nK_{2},5)< \frac{5+\sqrt{1+4n(n-1)(5-1)}}{2}< 2n+2. \end{aligned}$$

  So $2n\le sr(nK_{2},5)\le 2n+1$.

5 Proof of Proposition 2

By Theorem 4 (4), we have $sr(3K_{2},5)\le 7$. Now, consider $K_{6}$ on the vertex set $\{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6}\}$. Color the edges $\{v_{2}v_{4}, v_{2}v_{6}, v_{3}v_{4}, v_{3}v_{6}, v_{5}v_{6}\}$ with red color and the edges $\{v_{1}v_{2}, v_{1}v_{3}, v_{1}v_{5}, v_{4}v_{5}, v_{4}v_{6}\}$ with blue color and the edges $\{v_{1}v_{4}, v_{1}v_{6}, v_{2}v_{3}, v_{2}v_{5}, v_{3}v_{5}\}$ with green color. It is routine to verify that any completion of this coloring to a 5-bounded edge-coloring will result in a $(3K_{2},5)$-colored graph. Thus, $sr(3K_{2},5)\ge 7$ (see Fig. 2). This proposition holds.

Fig. 2

5-bounded edge-coloring of $K_{6}$ contains no rainbow $3K_{2}$

6 Proof of Theorem 6

It is clear that $sr(nK_{2},k)\ge 2n$. To prove that $sr(nK_{2},k)\le 2n$, we just have to show that if n is sufficiently large and $k<\frac{n}{8}$, then any k-bounded edge-coloring of $K_{2n}$ contains a rainbow perfect matching. This proof technique follows the lines of modification of the Local Lemma listed by Albert et al. in Ref. [1].

Lemma 2

(Albert et al. [1]) Let $A_{1}, A_{2}, \ldots , A_{N}$ denote events in some probability space. Suppose that for each i there is a partition of $[N]\backslash \{i\}$ into $X_{i}$ and $Y_{i}$. Let $m=\max \{|Y_{i}|: i\in [N]\}$ and $\beta =\max \{Pr(A_{i}| \bigcap _{j\in X}\overline{A_{j}}): i\in [N],\,X\subseteq X_{i}\}$. If there exists $0\le \alpha <1$ such that $\alpha (1-m\alpha )\ge \beta$ then $Pr(\bigcap _{i=1}^{N}\overline{A_{i}})>0$.

Let $K=K_{2n}$ be a k-bounded edge-colored complete graph satisfying n is sufficiently large and $k<\frac{n}{8}$. Now, construct a graph G whose vertex set is the edge set of K and two edges $e,\,f$ of K correspond to the two end-vertices of an edge of G if and only if $C(e)=C(f)$. Thus a set of vertices of G is independent if and only if it corresponds to a rainbow set of edges of K. Then we only need to prove that K contains a perfect matching whose edge set is an independent vertex set in G.

Let H be a perfect matching chosen randomly and independently from the set of $\frac{(2n)!}{2^{n}n!}$ perfect matchings of K. Let $\{e_{i}f_{i}: 1\le i\le N\}$ be the edge set of G and

$$\begin{aligned} A_{i}=\{H: e_{i}, f_{i}\in E(H)\}. \end{aligned}$$

We will show that $Pr(\bigcap _{i=1}^{N}\overline{A_{i}})>0$ to prove the conclusion we want. For $1\le i\le N$, let

$$\begin{aligned} Y_{i}=\{j\ne i: one\,of\,e_{j}, f_{j}\,shares\,a\,vertex\,with\,one\,of\,e_{i}, f_{i}\} \end{aligned}$$

and $X_{i}=[N]\backslash (Y_{i}\cup \{i\})$. Obviously, $Y_{i}\le 8nk$, so $m\le 8nk$. Let $X\subseteq X_{i}$, then no edge in X shares an end-vertex with either $e_{i}$ or $f_{i}$. Let $e_{i}=u_{1}u_{2}$, $f_{i}=v_{1}v_{2}$ and M be a perfect matching containing both $e_{i}$ and $f_{i}$ but no edges of X. Consider two edges $a=a_{1}a_{2}$ and $b=b_{1}b_{2}$ of M. There are at least $(n-2)(n-3)\cdot 4$ choices for a, b. For each such M, we construct $M_{a,b}$ by removing the edges $e_{i}, f_{i}, a, b$ from M and adding 4 edges $u_{1}a_{1}$, $u_{2}a_{2}$, $v_{1}b_{1}$, $v_{2}b_{2}$ which does not contain an edge of X. Then, taking $F(M)=\{M_{a,b}: a, b\,as\,above\}$, we have $|F(M)|\ge 4(n-2)(n-3)$ and $F(M)\cap F(M')=\emptyset$ for $M\ne M'$. Let ${\mathscr {M}}$ denote the set of perfect matchings containing $e_{i}$ and $f_{i}$. Then, we have

$$\begin{aligned} \begin{aligned} Pr\left( A_{i}| \bigcap _{j\in X}\overline{A_{j}}\right)&=\sum \limits _{M\in {\mathscr {M}}}Pr\left( H=M| \bigcap _{j\in X}\overline{A_{j}}\right) \\&\le \frac{1}{4n^{2}-20n+25}\sum \limits _{M\in {\mathscr {M}}}Pr\left( H\in \{M\}\cup F(M)| \bigcap _{j\in X}\overline{A_{j}}\right) \\&\le \frac{1}{4n^{2}-20n+25}. \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} \beta \le \frac{1}{4n^{2}-20n+25}. \end{aligned}$$

We choose

$$\begin{aligned} \alpha =\frac{1-\sqrt{1-(8+\epsilon )k/n}}{16nk}, \end{aligned}$$

then

$$\begin{aligned} \alpha (1-m\alpha )\ge \frac{8+\epsilon }{32n^{2}}=\frac{1+\epsilon /8}{4n^{2}}. \end{aligned}$$

Thus $\alpha (1-m\alpha )\ge \beta$ when $\epsilon >0$ is sufficiently small and n is sufficiently large which means $Pr(\bigcap _{i=1}^{N}\overline{A_{i}})>0$ by Lemma 2. Therefore, we can find a rainbow perfect matching in K. This completes the proof of Theorem 6.