Several Extreme Coefficients of the Tutte Polynomial of Graphs

Abstract

Let $t_{i,j}$ be the coefficient of $x^iy^j$ in the Tutte polynomial T(G; x, y) of a connected bridgeless and loopless graph G with order v and size e. It is trivial that $t_{0,e-v+1}=1$ and $t_{v-1,0}=1$. In this paper, we obtain expressions for another six extreme coefficients $t_{i,j}$’s with $(i,j)=(0,e-v)$,$(0,e-v-1)$,$(v-2,0)$,$(v-3,0)$,$(1,e-v)$ and $(v-2,1)$ in terms of small substructures of G. We also discuss their duality properties and their specializations to extreme coefficients of the Jones polynomial.

1 Introduction

Let $G = (V, E)$ be a graph with vertex set V and edge set E. The order, the size and the number of connected components of G are denoted by $v=v(G)$, $e=e(G)$ and $c=c(G)$, respectively. For $A \subseteq E$, we denote by G / A the graph obtained from G by contracting all edges in A, $G-A$ the graph obtained from G by deleting edges in A and $G|_A$ the restriction of G to A, namely $G|_A = G-(E\backslash A)$.

The Tutte polynomial T(G; x, y) of a graph $G = (V,E)$, introduced in [10], is a two-variable polynomial which can be recursively defined as:

$$\begin{aligned} T(G;x,y)= {\left\{ \begin{array}{ll} 1&{} \text {if }E = \emptyset ,\\ xT(G/f; x,y) &{} \text {if }f\text { is a bridge},\\ yT(G-f; x,y) &{} \text {if }f\text { is a loop},\\ T(G/f;x,y) + T(G-f;x,y) &{} \text {if }f\text { is neither a loop nor a bridge}. \end{array}\right. } \end{aligned}$$

It is independent of the order of edges selected for deletion and contraction in the reduction process to the empty graph. One way of seeing this is through the rank-nullity expansion of the Tutte polynomial. Let $A\subseteq E$. We identify A with the spanning subgraph (V, A) of G, i.e. $G|_A$, temporarily for the sake of simplicity. Let r(A) denote the rank $v-c(A)$ and n(A) denote the nullity $|A|-v+c(A)$. Then

$$\begin{aligned} T (G; x, y) = \sum _{A \subseteq E}(x- 1)^{r(E)-r(A)}(y-1)^{n(A)}. \end{aligned}$$

Moreover, the Tutte polynomial has a spanning forest expansion [10], i.e.

$$\begin{aligned} T (G; x, y) = \sum _{i,j}t_{ij}x^iy^j, \end{aligned}$$

where $t_{ij}$ is the number of spanning forests of G with internal activity i and external activity j.

Without loss of generality we always assume that $G=(V,E)$ is a connected bridgeless and loopless graph. It is trivial that $t_{00} = 0$ if $e>0$, $t_{0,e-v+1}=1$ and $t_{v-1,0}=1$. It is basic in graph theory to establish relations between the coefficients of graph polynomials and subgraph structures in the graph. See, for example, [1] for similar results on the characteristic polynomial and the chromatic polynomial. The purpose of this paper is to establish a relation between several extreme coefficients of the Tutte polynomial and subgraph structures of the graph. To state our results, we need some additional definitions and notation.

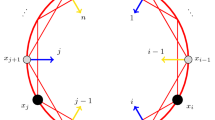
Let G be a connected bridgeless and loopless graph. A parallel class of G is a maximal subset of E sharing the same endvertices. Let $C\subseteq E$. Then C is said to be a series class if $c(G-C)=|C|$ and $G-C$ is bridgeless. A series class is shown in Fig. 1. A parallel (resp. series) class is called trivial if it contains only one edge. In case that G is disconnected, its parallel (resp. series) classes will be defined to be the union of parallel (resp. series) classes of connected components of G. It is obvious that parallel classes partition the edge set E. Series classes also partition the edge set E, i.e. each edge of G is contained in a unique series class of G. See [3] for details. Let $p=p(G)$ (resp. $s=s(G)$) and $p'=p'(G)$ (resp. $s'=s'(G)$) be the number of parallel (resp. series) classes and non-trivial parallel (resp. series) classes of G, respectively.

Fig. 1

A series class $C=\{e_1,e_2,\ldots ,e_k\}$: each $G_i$ is connected and bridgeless for $i=1,2,\ldots ,k$

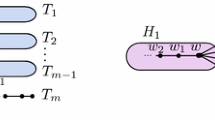
Let $\Delta =\Delta (G)$ be the number of triangles of ${\tilde{G}}$, the graph obtained from G by replacing each parallel class by a single edge. If $C\subseteq E$ satisfies: (1) $C=C_1\cup C_2\cup C_3$, where $C_{i}\subseteq E$ is a series class and $|C_i|=k_i$ for $i=1,2,3$, (2) G has the structure as shown in Fig. 2, where $G-C= G_1\cup G_2\cup \cdots \cup G_{k_1+k_2+k_3-1}$ and each $G_i$ is connected and bridgeless for $i=1,2,\ldots ,k_1+k_2+k_3-1$, then we say C is a $\Theta$ class of G. The total number of $\Theta$ classes of G is denoted by $\Theta =\Theta (G)$.

Fig. 2

A $\Theta$ class $C=\{e_1,e_2,\ldots ,e_{k_1+k_2+k_3}\}$: each $G_i$ is connected and bridgeless for $i=1,2,\ldots ,k_1+k_2+k_3-1$

Theorem 1

Let $G = (V, E)$ be a loopless and bridgeless connected graph. Then

• (1) $t_{0,e-v} = s - (e-v+1)$,

• (2) $t_{0,e-v-1} ={e-v+1 \atopwithdelims ()2} - (e-v)s + {s \atopwithdelims ()2} - \Theta$,

• (3) $t_{v-2,0} = p - (v-1)$,

• (4) $t_{v-3,0} ={v-1 \atopwithdelims ()2} - (v-2)p + {p \atopwithdelims ()2}-\Delta$.

Theorem 2

Let $G = (V, E)$ be a loopless and bridgeless connected graph. Then

• (1) $t_{1,e-v} = s'$,

• (2) $t_{v-2,1} = p'$.

In fact, four extreme coefficients in Theorem 1 can be obtained from extreme coefficients of the chromatic polynomial and flow polynomials, which will be seen from the proof of Theorem 1 in Sect. 3, but we have not found them in the literature. Theorem 2 is completely new as far as we know. In Sect. 5, we discuss the duality in Theorems 1 and  2. In the final section several consequences on extreme coefficients of chromatic, flow and Jones polynomials are derived.

2 Möbius Function, The Chromatic and Flow Polynomials

To prove Theorem 1, we need two results that express the chromatic and flow polynomials of graphs as characteristic polynomials of two lattices related to graphs, which was proven by Rota in the 1960s [9].

Let P be a poset. The unique minimum element and unique maximum element in P, if they exist, are denoted by ${\widehat{0}}={\widehat{0}}_P, {\widehat{1}}={\widehat{1}}_P$, respectively. A segment [x, y], for $x,y\in P$, is the set of all elements z between x and y, i.e. $\{z | x\le z\le y\}$. Note that the segment [x, y] endowed with the induced order structure is a poset in its own right and ${\widehat{0}}_{[x,y]} = x, {\widehat{1}}_{[x,y]} = y$. An element ycovers an element x when the segment [x, y] contains two elements. A poset is locally finite if every segment is finite.

Let P be a locally finite poset. Then the Möbius function of P is an integer-valued function defined on the Cartesian set $P\times P$ such that

$$\begin{aligned} \mu (x,y)&=1 \; \text{ if }\ x = y,\\ \mu (x,y)&=0 \;\text{ if }\ x \nleq y,\\ \sum _{x\le z\le y} \mu (x,z)&=0 \; \text{ if }\ x <y. \end{aligned}$$

If P has the minimum element, then

$$\begin{aligned} \mu ({\widehat{0}},x) = -\sum _{y<x} \mu ({\widehat{0}},y)\ \text{ if }\ x >{\widehat{0}}. \end{aligned}$$

A finite poset P is ranked (or graded) if for every $x\in P$ every maximal chain with x as top element has the same length, denoted rk(x). Here the length of a chain with k elements is $k - 1$. If P is ranked, the function rk called the rank function, is zero for minimal elements of P and $rk(y) = rk(x) + 1$ if $x, y\in P$ and y covers x.

Let P be a ranked poset with maximum and minimum elements and t be a variable. Then the characteristic polynomial of P is defined by

$$\begin{aligned} q(P;t) = \sum _{x\in P}\mu ({\widehat{0}},x)t^{rk({\widehat{1}})-rk(x)}. \end{aligned}$$

Let G be a graph. We denote by $P(G; \lambda )$ and $F(G; \lambda )$ the chromatic and flow polynomials of G, respectively.

Let $G = (V, E)$ be a loopless graph. A flat of G is a spanning subgraph $H \subseteq G$ such that each connected component of H is a vertex-induced subgraph of G. Then the set L(G) consisting of all flats of G forms a graded lattice ordered by the refinement relation on the set of partitions of V, that is, $K \in L(G) \le H\in L(G)$ means that $\{V(K_1), \ldots , V(K_s)\}$ is finer than $\{V(H_1), \ldots , V(H_t)\}$, where $K_1, \ldots , K_s$ are connected components of K and $H_1, \ldots , H_t$ are connected components of H. Note that the minimum element in L(G) is the empty graph $E_v$ with $v=v(G)$ vertices. Moreover, $rk(H) = r(H)$ for $H\in L(G)$ and $P(G; \lambda ) = \lambda ^{c(G)}q(L(G); \lambda )$.

Theorem 3

([9]) LetGbe a loopless graph. Then

$$\begin{aligned} P(G; \lambda )= \sum _{H\in L(G)}\mu (E_v,H)\lambda ^{c(H)}. \end{aligned}$$

Note that when G contains parallel edges, Theorem 3 is still valid if we take ${\tilde{G}}$ in place of G in L(G).

Let $G = (V,E)$ be a bridgeless graph. The set $L'(G)$ consisting of all spanning subgraphs of G without bridges also forms a graded lattice with the partial order defined by $H_1 \le H_2$ if $E(H_1) \supseteq E(H_2)$. Note that the minimum element in $L'(G)$ is graph G itself. Moreover, $rk(H) = n(G) - n(H)$ for $H\in L'(G)$.

Theorem 4

Let G be a bridgeless graph. Then

$$\begin{aligned} F(G; \lambda ) = \sum _{H\in L'(G)}\mu (G,H)\lambda ^{n(H)}. \end{aligned}$$

Proof

Let $H \in L'(G)$ and AG be an abelian group of order $\lambda$. Suppose $N_{=}(H)$ is the function counting AG-flows of $\overrightarrow{G}$ such that ${\mathbf {0}}$ is assigned to an edge e if and only if $e\in E\backslash E(H)$, and $N_{\ge }(H) =\sum _{H'\ge H}N_=(H')$ is the function counting AG-flows of $\overrightarrow{G}$ such that ${\mathbf {0}}$ is assigned to each edge e of $E\backslash E(H)$. Note that $N_=(G) = F(G; \lambda )$. By the Möbius Inversion Theorem,

$$\begin{aligned} N_{=}(G) = \sum _{H\in L'(G)}\mu (G,H)N_{\ge }(H). \end{aligned}$$

It is not difficult to see that $N_{\ge }(H) = \lambda ^{n(H)}$, which completes the proof. $\square$

3 Proof of Theorem 1

It is well known that the Tutte polynomial contains as special cases the chromatic polynomial P(G; x) and the flow polynomial F(G; y). More precisely,

$$\begin{aligned}&P(G; x)=(-1)^{r(G)}x^{c(G)}T(G; 1 - x, 0), \end{aligned}$$

(1)

$$\begin{aligned}&F(G; y)=(-1)^{n(G)}T(G; 0, 1-y). \end{aligned}$$

(2)

In [6], Kook et al. obtained the following convolution formula for the Tutte polynomial.

$$\begin{aligned} T(G;x,y) = \sum _{A\subseteq E}T(G/A; x,0)T(G|_A;0,y). \end{aligned}$$

(3)

We write $X_1 = 1-x$ and $Y_1 = 1-y$. Recall that G is a connected loopless and bridgeless graph. By inserting Eqs. (1) and (2) into Eq. (3), we obtain

$$\begin{aligned} T(G;x,y)=\sum _{A\subseteq E}(-1)^{r(G/A)+n(G|_A)}X_1^{-c(G/A)}P(G/A;X_1)F(G|_A;Y_1). \end{aligned}$$

(4)

Note that $P(G; x)=0$ if G contains loops and $F(G; y)=0$ if G contains bridges. Hence, we only consider all sets A such that G / A is loopless and $G|_A$ is bridgeless in the summation of Eq. (4).

Case 1.$A = E$. In this case, $G/A=K_1$, an isolated vertex and $G|_A=G$. By Theorem 4, the corresponding contribution of A to the summation of Eq. (4) is

$$\begin{aligned} (-1)^{n(G)}\left[ Y_1^{n(G)} + \sum _{{\mathop {rk(H)=1}\limits ^{H\in L'(G)}}}\mu (G,H)Y_1^{n(G)-1}+\sum _{{\mathop { rk(H)=2}\limits ^{H\in L'(G)}}}\mu (G,H)Y_1^{n(G)-2}+\cdots \right] . \end{aligned}$$

Case 2.$A \ne E$. In this case, if G / A does not contain loops, then $v(G/A)\ge 2$ and hence each term of the corresponding contribution of A to the summation of Eq. (4) will contain x.

Thus, we have

$$\begin{aligned} T(G; x, y)&=y^{n(G)} + (-1)[n(G) + \sum _{{\mathop {rk(H)=1}\limits ^{H\in L'(G)}}}\mu (G,H)]y^{n(G)-1} \\&\quad + \left[ {n(G) \atopwithdelims ()2} + (n(G)-1)\sum _{{\mathop {rk(H)=1}\limits ^{H\in L'(G)}}}\mu (G,H) \right. \\&\quad \left. + \sum _{{\mathop {rk(H)=2}\limits ^{H\in L'(G)}}}\mu (G,H)\right] y^{n(G)-2}\\&\quad + \cdots . \end{aligned}$$

Let $H=G-A \in L'(G)$. Then $rk(H) =1$$\Longleftrightarrow$$n(H)=n(G)-1$$\Longleftrightarrow$$|A| = c(G -A)$. Hence,

$$\begin{aligned} \sum _{{\mathop {rk(H)=1}\limits ^{H\in L'(G)}}} \mu (G, H)=\sum _{{\mathop {G - A\ \text {is bridgeless}}\limits ^{A\subseteq E, |A| = c(G-A)}}} (-1)= \sum _{A\ \text {is a series class}} (-1)=-s(G). \end{aligned}$$

If $C\subseteq E$ satisfies: (1) $C=C_1\cup C_2$, where $C_{i}\subseteq E$ is a series class and $|C_i|=k_i$ for $i=1,2$, (2) G has the structure as shown in Fig. 3, where $G-C= G_1\cup G_2\cup \cdots \cup G_{k_1+k_2-1}$ and each $G_i$ is connected and bridgeless for $i=1,2,\ldots ,k_1+k_2-1$, then we say C is an $\infty$ class of G. The total number of $\infty$ classes of G is denoted by $\infty (G)$.

Fig. 3

An $\infty$ class $C=\{e_1,e_2,\ldots ,e_{k_1+k_2}\}$: each $G_i$ is connected and bridgeless for $i=1,2,\ldots ,k_1+k_2-1$

Let $H'=G-A' \in L'(G)$. Then $rk(H') =2$$\Longleftrightarrow$$|A'| = c(G -A') +1$$\Longleftrightarrow$$A'$ is either a $\Theta$ class or an $\infty$ class. If $A'$ is a $\Theta$ class, then $\mu (G,H')=2$ and if $A'$ is an $\infty$ class, then $\mu (G,H')=1$. Note that $\infty (G)=\left( {\begin{array}{c}s(G)\\ 2\end{array}}\right) -3\Theta (G)$. Thus

$$\begin{aligned} \sum \limits _{\begin{array}{c} \scriptstyle H\in L'(G) \\ \scriptstyle rk(H)=2 \end{array}}\mu (G,H)=1\times \left[ \left( {\begin{array}{c}s(G)\\ 2\end{array}}\right) -3\Theta (G)\right] +2\times \Theta (G)=\left( {\begin{array}{c}s(G)\\ 2\end{array}}\right) -\Theta (G). \end{aligned}$$

Theorem 1 (1) and (2) are thus established. Now we prove 1 (3) and (4) similarly.

Case 1.$A = \emptyset$. In this case, $G/A =G$ and $G|_A =E_v$, the empty graph with v vertices. By Theorem 3, the contribution of A to the summation of Eq. (4) is

$$\begin{aligned} (-1)^{r(G)}\left[ X_1^{r(G)} + \sum _{{\mathop {rk(H)=1}\limits ^{H\in L(G)}}}\mu (E_v,H)X_1^{r(G)-1}+\sum _{{\mathop { rk(H)=2}\limits ^{H\in L(G)}}}\mu (E_v,H)X_1^{r(G)-2}+\cdots \right] . \end{aligned}$$

Case 2.$A \ne \emptyset$. In this case, if $G|_A$ does not contain bridges, then $n(G|_A)\ge 1$ and hence each term of the corresponding contribution of A to the summation of Eq. (4) will contain y.

Hence,

$$\begin{aligned} T(G; x, y)&=x^{r(G)} + (-1)[r(G) + \sum _{{\mathop {rk(H)=1}\limits ^{H\in L(G)}}}\mu (E_v,H)]x^{r(G)-1} \\&\quad + \left[ {r(G) \atopwithdelims ()2} + (r(G)-1)\sum _{{\mathop {rk(H)=1}\limits ^{H\in L(G)}}}\mu (E_v,H) \right. \\&\quad \left. + \sum _{{\mathop {rk(H)=2}\limits ^{H\in L(G)}}}\mu (E_v,H)\right] x^{r(G)-2} \\&\quad + \cdots . \end{aligned}$$

Clearly,

$$\begin{aligned} \sum _{{\mathop {rk(H)=1}\limits ^{H\in L(G)}}} \mu (E_v, H)=-p(G). \end{aligned}$$

Let ${\tilde{G}}$ be the graph obtained from G by replacing each parallel class by a single edge. Note that $rk(H)=2$$\Longleftrightarrow$$c(H)=v-2$$\Longleftrightarrow$$H=P_3\cup E_{v-3}$ (but ${\tilde{G}}[V(P_3)]\ne C_3$), $P_2\cup P_2\cup E_{v-4}$ or $C_3\cup E_{v-3}$, where $P_2$ (resp. $P_3$) is a path with 2 (resp. 3) vertices and $C_3$ (i.e. triangle) is a cycle with 3 vertices. The former two have the Möbius function value 1 and the third one has the Möbius function value 2. Then

$$\begin{aligned} \sum _{{\mathop {rk(H)=2}\limits ^{H\in L(G)}}} \mu (E_v, H)=1\times \left[ {p(G) \atopwithdelims ()2}-3\Delta (G)\right] +2\times \Delta (G)={p(G) \atopwithdelims ()2}-\Delta (G). \end{aligned}$$

This completes the proof of Theorem 1. $\square$

4 Proof of Theorem 2

We shall prove by induction on the number of edges of G. The base case is the double edge, whose Tutte polynomials is $x+y$, Theorem 2 (1) and (2) are both satisfied. Now we assume that Theorem 2 holds for connected loopless and bridgeless graphs H with $e(H)<k$. Let G be a connected loopless and bridgeless graph with $e(G)=k$. Take an edge f of G, then G / f and $G-f$ are both connected, G / f is bridgeless but may have loops and $G-f$ is loopless but may have bridges.

(1) Note that $t_{1,e-v}(G)=t_{1,e-v}(G/f)+t_{1,e-v}(G-f)$. Let $\nu (f)$ be the number of edges of the series class that f belongs to.

Case 1.$\nu (f)=1$. In this case, $G-f$ has no bridges. Thus $G-f$ is a loopless and bridgeless connected graph and hence $t_{1,e-v}(G-f)=t_{1,(e-1)-v+1}(G-f)=0$. Thus, $t_{1,e-v}(G)=t_{1,e-v}(G/f)$.

Subcase 1.1.G / f is loopless. In this subcase, $s'(G/f)=s'(G)$. By induction hypothesis, $t_{1,e-v}(G/f)=s'(G/f)$. Hence $t_{1,e-v}(G)=s'(G)$.

Subcase 1.2.G / f has loops. Suppose that $\{e_1,e_2,\ldots ,e_k\}$ are all loops of G / f. Then $G/f-e_1-e_2-\cdots -e_k$ is connected, loopless and bridgeless, and

$$\begin{aligned} T(G/f;x,y)=y^kT(G/f-e_1-e_2-\cdots -e_k;x,y). \end{aligned}$$

Thus, $t_{1,e-v}(G/f)=s'(G/f-e_1-e_2-\cdots -e_k)=s'(G)$. Hence $t_{1,e-v}(G)=s'(G)$.

Case 2.$\nu (f)=2$. In this case, $G-f$ has exactly one single bridge $f'$ and $\{f,f'\}$ consists of a series class of G. $T(G-f; x,y)=xT(G-f/f'; x,y)$ and hence $t_{1,e-v}(G-f)=1$.

Subcase 2.1.G / f is loopless. In this subcase, $s'(G/f)=s'(G)-1$. By induction hypothesis, $t_{1,e-v}(G/f)=s'(G/f)$. Hence $t_{1,e-v}(G)=t_{1,e-v}(G-f)+t_{1,e-v}(G/f)=1+(s'(G)-1)=s'(G)$.

Subcase 2.2.G / f has loops. In this subcase, the loop is exactly the edge $f'$ which is both parallel and series to f. Then

$$\begin{aligned} T(G/f;x,y)=yT(G/f-f';x,y). \end{aligned}$$

Thus $t_{1,e-v}(G/f)=s'(G/f-f')=s'(G)-1$. Hence $t_{1,e-v}(G)=t_{1,e-v}(G-f)+t_{1,e-v}(G/f)=1+(s'(G)-1)=s'(G)$.

Case 3.$\nu (f)\ge 3$. In this case, $G-f$ has has more than 2 bridges and hence $t_{1,e-v}(G-f)=0$. Thus $t_{1,e-v}(G)=t_{1,e-v}(G/f)$. Note that G / f is loopless. By induction hypothesis, $t_{1,e-v}(G/f)=s'(G/f)$. Note that $s'(G/f)=s'(G)$ and hence $t_{1,e-v}(G)=s'(G)$. This completes the proof of Theorem 2 (1).

(2) Note that $t_{v-2,1}(G)=t_{v-2,1}(G/f)+t_{v-2,1}(G-f)$. Let $\mu (f)$ be the number of edges of the parallel class that f belongs to.

Case 1.$\mu (f)=1$. In this case, G / f has no loops. Thus G / f is a loopless and bridgeless connected graph and hence $t_{v-2,1}(G/f)=0$. Thus $t_{v-2,1}(G)=t_{v-2,1}(G-f)$.

Subcase 1.1.$G-f$ is bridgeless. In this subcase, $p'(G-f)=p'(G)$. By induction hypothesis, $t_{v-2,1}(G-f)=p'(G-f)$. Hence $t_{v-2,1}(G)=p'(G)$.

Subcase 1.2.$G-f$ has bridges. Suppose that $\{e_1,e_2,\ldots ,e_k\}$ are all bridges of $G-f$. Then $G-f/e_1/e_2/\cdots /e_k$ is connected, loopless and bridgeless, and

$$\begin{aligned} T(G-e;x,y)=x^kT(G-f/e_1/e_2/\cdots /e_k;x,y). \end{aligned}$$

Thus $t_{v-2,1}(G-f)=p'(G-f/e_1/e_2/\cdots /e_k)=p'(G)$. Hence $t_{v-2,1}(G)=p'(G)$.

Case 2.$\mu (f)=2$. In this case, G / e has exactly a single loop $f'$ which is parallel to f in G. $T(G/f; x,y)=yT(G/f-f'; x,y)$ and hence $t_{v-2,1}(G/f)=1$.

Subcase 2.1.$G-f$ is bridgeless. In this subcase, $p'(G-f)=p'(G)-1$. By induction hypothesis, $t_{v-2,1}(G-f)=p'(G-f)$. Hence $t_{v-2,1}(G)=t_{v-2,1}(G/f)+t_{v-2,1}(G-f)=1+(p'(G)-1)=p'(G)$.

Subcase 2.2.$G-f$ has bridges. In this subcase, the bridge is exactly the edge $f'$ parallel to f. Then

$$\begin{aligned} T(G-f;x,y)=xT(G-f/f';x,y). \end{aligned}$$

Thus $t_{v-2,1}(G-f)=p'(G-f/f')=p'(G)-1$. Hence $t_{v-2,1}(G)=t_{v-2,1}(G/f)+t_{v-2,1}(G-f)=1+(p'(G)-1)=p'(G)$.

Case 3.$\mu (f)\ge 3$. In this case, G / f has has more than 2 loops and hence $t_{v-2,1}(G/f)=0$. Thus $t_{v-2,1}(G)=t_{v-2,1}(G-f)$. Note that $G-f$ is bridgeless. By induction hypothesis, $t_{v-2,1}(G-f)=p'(G-f)$. Note that $p'(G-f)=p'(G)$ and hence $t_{v-2,1}(G)=p'(G)$. This completes the proof of Theorem 2 (2). $\square$

5 Duality

The readers have seen the duality in both theorems and their proofs. In this section, we clarify it in the case of connected bridgeless and loopless plane graphs.

It is well known that if G is a plane graph and $G^*$ is the dual graph of G, then

$$\begin{aligned} T(G^*;x,y)=T(G;y,x). \end{aligned}$$

Let $t^*_{i,j}$ be the coefficient of $x^iy^j$ in the Tutte polynomial $T(G^*;x,y)$, and we have $t^*_{i,j}=t_{j,i}$. Loops and bridges, deletion and contraction will interchange by taking dual of a plane graph. The dual of a bridgeless and loopless connected plane graph is still a bridgeless and loopless connected plane graph. Let G be a bridgeless and loopless connected plane graph and $G^*$ be the dual of G. Let $v^*$ and $e^*$ be the order and size of $G^*$, respectively. Then

$$\begin{aligned} e^*= & {} e,\\ v^*= & {} e-v+2,\\ s(G^*)= & {} p(G),\\ p(G^*)= & {} s(G),\\ s'(G^*)= & {} p'(G),\\ p'(G^*)= & {} s'(G),\\ \Theta (G^*)= & {} \Delta (G),\\ \Delta (G^*)= & {} \Theta (G). \end{aligned}$$

Coefficients in Theorems 1 and 2 are dual in the case that G is a bridgeless and loopless connected plane graph. Note that

$$\begin{aligned} t^*_{0,v-1}=t^*_{0,e^*-v^*+1}=1=t_{v-1,0}, \end{aligned}$$

and

• (1)
  $$\begin{aligned} t^*_{0,v-2}= & {} t^*_{0,e^*-v^*}\\= & {} v^*+s(G^*)-e^*-1\\= & {} (e-v+2)+p(G)-e-1\\= & {} p(G)-v+1\\= & {} t_{v-2,0}. \end{aligned}$$
• (2)
  $$\begin{aligned} t^*_{0,v-3}= & {} t^*_{0,e^*-v^*-1}\\= & {} {e^*-v^*+1 \atopwithdelims ()2} - (e^*-v^*)s(G^*) + {s(G^*) \atopwithdelims ()2} - \Theta (G^*)\\= & {} {v-1 \atopwithdelims ()2} - (v-2)p(G) + {p(G) \atopwithdelims ()2} - \Delta (G)\\= & {} t_{v-3,0}. \end{aligned}$$
• (3)
  $$\begin{aligned} t^*_{1,v-2}= & {} t^*_{1,e^*-v^*}\\= & {} s'(G^*)\\= & {} p'(G)\\= & {} t_{v-2,1}. \end{aligned}$$

6 Several Consequences

In this section, we deduce the results on extreme coefficients of the Jones polynomials of graphs [3] and extreme coefficients of the chromatic and flow polynomials. In [3], Dong and Jin introduced the Jones polynomial of graphs. In the case of plane graphs, it (up to a simple pre-factor) reduces to the Jones polynomial of the alternating link constructed from the plane graph via the medial construction. We denote by $J_G(t)$ the Jones polynomial of G. Then

$$\begin{aligned} J_G(t)=(-1)^{v-1}t^{e-v+1}T(-t,-t^{-1}). \end{aligned}$$

Theorem 5

([2, 3]) Let$G=(V,E)$be a connected bridgeless and loopless graph with ordervand size e. Then

$$\begin{aligned} J_G(t)=b_0+b_1t+b_2t^2+\cdots +b_{e-2}t^{e-2}+b_{e-1}t^{e-1}+b_{e}t^{e}, \end{aligned}$$

where$(-1)^{e-i}b_i$is a non-negative integer for$i=0,1,2,\ldots ,e$and in particular,

$$\begin{aligned} b_0= & {} (-1)^{e},\\ b_1= & {} (-1)^{e}[e-v+1-s(G)],\\ b_{e-2}= & {} \left( {\begin{array}{c}p(G)-v+2\\ 2\end{array}}\right) +p'(G)-\Delta (G),\\ b_{e-1}= & {} v-1-p(G),\\ b_{e}= & {} 1. \end{aligned}$$

We can deduce Theorem 5 by using Theorems 1 and 2 and taking $x=-t,y=-t^{-1}$, and further obtain:

Corollary 6

$$\begin{aligned} b_2=(-1)^{e}\left[ \left( {\begin{array}{c}s(G)-e+v\\ 2\end{array}}\right) +s'(G)-\Theta (G)\right] . \end{aligned}$$

Proof

$$\begin{aligned} b_2= & {} (-1)^{e}[t_{0,e-v-1}+t_{1,e-v}]\\= & {} (-1)^{e}\left[ {e-v+1 \atopwithdelims ()2} - (e-v)s(G) + {s(G) \atopwithdelims ()2} - \Theta (G)+s'(G)\right] \\= & {} (-1)^{e}\left[ \left( {\begin{array}{c}s(G)-e+v\\ 2\end{array}}\right) +s'(G)- \Theta (G)\right] . \end{aligned}$$

$\square$

We can also deduce extreme coefficients of chromatic and flow polynomials. We list them as follows and omit the proofs.

Theorem 7

([7, 8]) LetGbe a loopless and bridgeless connected graph of orderv. Let$P(G;\lambda )=a_0\lambda ^v+a_1\lambda ^{v-1}+\cdots +a_{v-1}\lambda$. Then

$$\begin{aligned} a_0= & {} 1,\\ a_1= & {} -p(G),\\ a_2= & {} \left( {\begin{array}{c}p(G)\\ 2\end{array}}\right) -\Delta (G). \end{aligned}$$

Theorem 8

LetGbe a loopless and bridgeless connected graph of ordervand sizee. Let$F(G;\lambda )=c_0\lambda ^{e-v+1}+c_1\lambda ^{e-v}+\cdots +c_{e-v+1}$. Then

$$\begin{aligned} c_0= & {} 1,\\ c_1= & {} -s(G),\\ c_2= & {} \left( {\begin{array}{c}s(G)\\ 2\end{array}}\right) -\Theta (G). \end{aligned}$$

Theorem 8 may be known but we have not found it in the literature. In [5], Kauffman generalized the Tutte polynomials from graphs to signed graphs, which includes the Jones polynomial [4] of both alternating and non-alternating links. It is worth studying extreme coefficients of the signed Tutte polynomial.