Alternating Sign Matrices: Extensions, König-Properties, and Primary Sum-Sequences

Abstract

This paper is concerned with properties of permutation matrices and alternating sign matrices (ASMs). An ASM is a square $(0,\pm 1)$-matrix such that, ignoring 0’s, the 1’s and $-1$’s in each row and column alternate, beginning and ending with a 1. We study extensions of permutation matrices into ASMs by changing some zeros to $+1$ or $-1$. Furthermore, several properties concerning the term rank and line covering of ASMs are shown. An ASM A is determined by a sum-matrix $\varSigma (A)$ whose entries are the sums of the entries of its leading submatrices (so determined by the entries of A). We show that those sums corresponding to the nonzero entries of a permutation matrix determine all the entries of the sum-matrix and investigate some of the properties of the resulting sequence of numbers. Finally, we investigate the lattice-properties of the set of ASMs (of order n), where the partial order comes from the Bruhat order for permutation matrices.

1 Introduction

An alternating sign matrix, abbreviated to ASM, is an $n\times n$$(0,\pm 1)$-matrix such that, ignoring 0’s, the 1’s and $-1$’s in each row and column alternate, beginning and ending with a 1. An $n\times n$ ASM A can be regarded as the adjacency matrix of a signed bipartite graph B whose vertices in each set of its bipartition have a specified order (to account for the alternating sign property). Thus, B has a vertex for each row and column of the matrix $A=[a_{ij}]$, and an edge between a row vertex i and a column vertex j when the corresponding entry $a_{ij}$ is nonzero, and associated to that edge is the sign of the entry $a_{ij}$. The set of $n\times n$ ASMs is denoted by $\mathcal {A}_n$. Permutation matrices are the ASMs without any $-1$’s. We denote by $\mathcal {P}_n$ the set of $n\times n$ permutation matrices corresponding to the set $\mathcal {S}_n$ of permutations of $\{1,2,\ldots ,n\}$. Thus $\mathcal {P}_n\subseteq \mathcal {A}_n$. If $\pi =(\pi _1, \pi _2, \ldots , \pi _n) \in \mathcal {S}_n$, the corresponding permutation matrix has its ones in positions $(i,\pi _i)$ ($i \le n$). We will also use the shorter notation $\pi =(\pi _1\pi _2 \dots \pi _n)$. Some recent developments concerning ASMs, related objects and generalizations may be found in [4,5,6].

There is a partial order defined on the set $\mathcal {S}_n$ (and so on $\mathcal { P}_n$) called the Bruhat order and denoted by $\preceq _B$. If $\sigma ,\tau \in \mathcal {S}_n$, then $\sigma \preceq _B \tau$ (read as, $\sigma$precedes$\tau$in the Bruhat order) provided $\sigma$ can be obtained from $\tau$ by a sequence of transpositions (k, l) (interchanging k and l in a permutation) each of which decreases the number of inversions. The cover relation in this partial order results when one transposition is applied and it decreases the number of inversions by exactly one. The unique minimal permutation in the partially ordered set $(\mathcal {S}_n,\preceq _B)$ is the identity permutation, denoted as $\iota _n=(1,2,\ldots ,n)$, and the unique maximal permutation is the so-called anti-identity permutation, denoted as $\zeta _n=(n,n-1,\ldots ,1)$. If $\sigma \preceq _B \tau$, and $\sigma$ and $\tau$ have corresponding permutation matrices P and Q, then we also write $P\preceq _B Q$. The minimal permutation matrix and maximal permutation matrix are, respectively, the $n\times n$ identity matrix $I_n$ and $n\times n$ anti-identity matrix (with 1’s on the anti-diagonal) $L_n$. For more on the Bruhat order, and the so-called Bruhat shadow of a permutation matrix, see [3].

There is an equivalent, and computationally efficient, way to determine whether or not two permutations are related in the Bruhat order, best described in terms of their corresponding permutation matrices. It requires only the comparison of $(n-1)^2$ pairs of integers, after having computed certain sum-matrices, as defined next. For any $m\times n$ matrix $A=[a_{ij}]$, define the sum-matrix of A, denoted $\varSigma (A)=[\sigma _{ij}]$ to be the $m\times n$ matrix where

$$\begin{aligned} \sigma _{ij}=\sigma _{ij}(A)=\sum _{k\le i}\sum _{l\le j}a_{kl} \quad (1\le i\le m, \;1\le j\le n), \end{aligned}$$

the sum of the entries in the leading $i\times j$ submatrix of A. If P is an $n\times n$ permutation matrix, then the entries in the last row and last column of $\varSigma (A)$ are $1,2,\ldots ,n$ in that order. Note that if P is a permutation matrix, then $P^{-1}=P^T$, so $\varSigma (P^{-1})=\varSigma (P^T)=\varSigma (P)^T$. Let the entrywise ordering of two matrices A and B be written as $A \le B$. Let $\varSigma (\mathcal {P}_n):=\{\varSigma (P): P\in \mathcal {P}_n\}$. The characterization of Bruhat order in terms of sum-matrices is stated next (see [1] for a proof).

Lemma 1

Let $P,Q\in \mathcal {P}_n$. Then $P\preceq _B Q$ if and only if

$$\begin{aligned} \varSigma (P)\ge \varSigma (Q), \end{aligned}$$

that is, $\varSigma (P)$ dominates $\varSigma (Q)$ entrywise.

The Bruhat order on $\mathcal {P}_n$ can be extended to a Bruhat order on alternating sign matrices using sum-matrices: For $A_1,A_2\in \mathcal {A}_n$, then $A_1\preceq _B A_2$ provided $\varSigma (A_1)\ge \varSigma (A_2)$. In the next theorem we summarize some of the results of Lascoux and Schützenberger [12] which, in particular, contain a characterization of ASMs in terms of their sum-matrices. Let $\varSigma (\mathcal {A}_n):=\{\varSigma (A): A\in \mathcal {A}_n\}$.

Theorem 1

The partially ordered set $(\mathcal {A}_n,\preceq _B)$ is a lattice and is the smallest lattice extending the partially ordered set $(\mathcal {P}_n,\preceq _B)$, the MacNeille completion of $(\mathcal {P}_n,\preceq _B)$. The set $\varSigma (\mathcal {A}_n)$ consists of the set $\varSigma _n$ of all $n\times n$ nonnegative integral matrices $X=[x_{ij}]$ satisfying the following properties for each $i=1,2,\ldots ,n:$

• (LS-a) The integers in row i and in column i are taken from the set $\{0,1,\ldots , i\}$, beginning with a 0 or 1, and ending with i.

• (LS-b) The integers in row i and in column i are nondecreasing.

• (LS-c) Two consecutive entries in row i and in column i are equal or differ by 1.

There is a generalization of a permutation interchange that applies to $n\times n$ ASMs, namely, adding an interchange-matrix$T_n^{i,j}$ which is all zeros except for its $2\times 2$ matrix determined by rows i and $i+1$ and columns j and $j+1$ which equals

$$\begin{aligned} \left[ \begin{array}{rr} +1&{}-1\\ -1&{}+1\end{array}\right] \quad (1\le i,j\le n-1). \end{aligned}$$

Then it follows from [12] (see also Lemma 2 in [8]) that if $A_1,A_2\in \mathcal {A}_n$, then $A_1\preceq _B A_2$ if and only if $A_1$ can be obtained from $A_2$ by sequentially adding matrices of the form $T_n^{i,j}$ where the result of each addition is also an ASM.

A matrix is uniquely determined by its sum-matrix since we can recover $A=[a_{ij}]$ from $\varSigma (A)=[\sigma _{ij}]$ as follows:

$$\begin{aligned} a_{ij}=\sigma _{ij}-\sigma _{i-1,j} -\sigma _{i,j-1}+\sigma _{i-1,j-1} \end{aligned}$$

where $\sigma _{0,j}=\sigma _{i,0}$ for all i and j. Thus the mapping ${\varvec{\Sigma }}: \mathcal {A}_n\rightarrow \varSigma _n$ given by $A\rightarrow \varSigma (A)$ is a bijection. The sum-matrices of the minimal and maximal $n\times n$ ASMs have the special forms shown for $n=6$:

$$\begin{aligned} \varSigma (I_6)= \left[ \begin{array}{cccccc} 1&{}1&{}1&{}1&{}1&{}1\\ 1&{}2&{}2&{}2&{}2&{}2\\ 1&{}2&{}3&{}3&{}3&{}3\\ 1&{}2&{}3&{}4&{}4&{}4\\ 1&{}2&{}3&{}4&{}5&{}5\\ 1&{}2&{}3&{}4&{}5&{}6\end{array}\right] \quad \text{ and } \quad \varSigma (L_6)= \left[ \begin{array}{cccccc} 0&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}0&{}0&{}1&{}2\\ 0&{}0&{}0&{}1&{}2&{}3\\ 0&{}0&{}1&{}2&{}3&{}4\\ 0&{}1&{}2&{}3&{}4&{}5\\ 1&{}2&{}3&{}4&{}5&{}6\end{array}\right] . \end{aligned}$$

Thus the sum-matrix of every $n\times n$ ASM lies entrywise between $\varSigma (L_n)$ and $\varSigma (I_n)$, that is, each entry of $\varSigma (I_n)$, respectively, $\varSigma (L_n)$, is at least as large (at most as large) as the corresponding entry of the sum-matrix of every $A\in \mathcal {A}_n$.

Let $\widehat{\varSigma (\mathcal {A}_n})$ be the convex hull of $\varSigma (\mathcal {A}_n)$. From a proof in connection with the notion of sum-majorization in [4] we get the following characterization of the polytope $\widehat{\varSigma (\mathcal {A}_n)}$.

Theorem 2

The polytope $\widehat{\varSigma (\mathcal {A}_n)}$ equals the set of $n \times n$ real matrices $S=[\sigma _{ij}]$ satisfying

$$\begin{aligned} \begin{array}{ll} 0 \le \sigma _{ij}-\sigma _{i-1,j} \le 1 &{} (1\le i,j\le n) \\ 0 \le \sigma _{ij}-\sigma _{i,j-1} \le 1 &{} (1\le i,j\le n) \\ \sigma _{i,n}=i &{} (1\le i\le n) \\ \sigma _{n,j}=j &{} (1\le j\le n) \\ \end{array} \end{aligned}$$

(1)

where we define $\sigma _{0,j}=\sigma _{i,0}=0$ for all i and j. The set of extreme points of $\widehat{\varSigma (\mathcal {A}_n)}$ equals the set $\varSigma (\mathcal {A}_n)$ of sum-matrices of the $n\times n$ ASMs.

This paper is organized as follows. In Sect. 2 we study extensions of permutation matrices to ASMs obtained by changing some zeros (possibly none) into $+1$ or $-1$. König properties of ASMs are studied in Sect. 3 where, by this, we mean the term rank and the structure of minimum line coverings of such matrices. In Sect. 4, we investigate in more detail sum-matrices and show that in the case of $n\times n$ permutation matrices, at most n entries of the sum-matrix are needed to recover the permutation matrix from its sum-matrix. In Sect. 5 we investigate certain lattice properties of the Bruhat order.

2 ASM-Extensions

Let P be an $n\times n$ permutation matrix. Let $\alpha _n(P)$ denote the number of ASM-extensions of P, defined to be $n\times n$ ASMs obtained from P by replacing some 0’s (possibly none) by $+1$ or $-1$. In such an ASM-extension of P, the number of new $+1$’s equals the number of new $-1$’s. It is natural to ask for

$$\begin{aligned} \alpha _n^*:=\max \{\alpha _n(P): P\in \mathcal {P}_n\} \end{aligned}$$

and those $n\times n$ permutation matrices P that satisfy $\alpha _n(P)=\alpha _n^*$.

If $n=3$, there is only one non-permutation ASM and it does not contain 1’s in a permutation set of places. So $\alpha _3^*=1$. The $4\times 4$ permutation matrices

$$\begin{aligned} \left[ \begin{array}{c|c|c|c} &{}1&{}&{}\\ \hline 1&{}&{}&{}\\ \hline &{}&{}&{}1\\ \hline &{}&{}1&{}\end{array}\right] \quad \text{ and } \quad \left[ \begin{array}{c|c|c|c} &{}&{}1&{}\\ \hline &{}&{}&{}1\\ \hline 1&{}&{}&{}\\ \hline &{}1&{}&{}\end{array}\right] \end{aligned}$$

have ASM-extensions with two $-1$’s:

$$\begin{aligned} \left[ \begin{array}{r|r|r|r} &{}1&{}&{}\\ \hline 1&{}-1&{}1&{}\\ \hline &{}1&{}-1&{}1\\ \hline &{}&{}1&{}\end{array}\right] \quad \text{ and } \quad \left[ \begin{array}{r|r|r|r} &{}&{}1&{}\\ \hline &{}1&{}-1&{}1\\ \hline 1&{}-1&{}1&{}\\ \hline &{}1&{}&{}\end{array}\right] . \end{aligned}$$

(As usual, empty positions are assumed to contain a 0.) It is straightforward to verify that $\alpha _4^*=2$ and that the above two $4\times 4$ permutation matrices are the only ones achieving equality.

Consider the special $n\times n$ permutation matrix

$$\begin{aligned} Q_n^*=Q_{\lceil \frac{n}{2}\rceil }\oplus Q_{\lfloor \frac{n}{2}\rfloor }, \end{aligned}$$

where $Q_m$ is the $m\times m$ permutation matrix with 1’s on its anti-diagonal running from the lower left to the upper right. For instance, for $n=5$ and 6 we have

$$\begin{aligned} Q_5^*=\left[ \begin{array}{c|c|c|c|c} &{}&{}1&{}&{}\\ \hline &{}1&{}&{}&{}\\ \hline 1&{}&{}&{}&{}\\ \hline &{}&{}&{}&{}1\\ \hline &{}&{}&{}1&{}\end{array}\right] \quad \text{ and } \quad Q_6^*=\left[ \begin{array}{c|c|c|c|c|c} &{}&{}1&{}&{}&{}\\ \hline &{}1&{}&{}&{}&{}\\ \hline 1&{}&{}&{}&{}&{}\\ \hline &{}&{}&{}&{}&{}1\\ \hline &{}&{}&{}&{}1&{}\\ \hline &{}&{}&{}1&{}&{}\end{array}\right] . \end{aligned}$$

There is a ‘canonical’ symmetric ASM-extension $A_n^*$ of $Q_n^*$ as illustrated below for $n=7$ and $n=8$:

where the 0’s that are explicitly displayed are required in any extension of $Q_n^*$ to an ASM. In these canonical extensions, the $-1$’s are in the positions of the 1’s of a $Q_{n-2}^*$. In addition, the middle $(n-2)\times (n-2)$ principal submatrix contains all 1’s on its anti-diagonal. The sum-matrices of $A_7^*$ and $A_8^*$ are given by

(2)

Let $\mathcal {A}_n(Q_{2m}^*)$ denote the set of $n\times n$ ASM-extensions of $Q_{2m}^*$, that is, ASMs containing 1’s in those positions that are 1 in $Q_{2m}^*$. Then a matrix in $\mathcal {A}_n(Q_{2m}^*)$ has the form

$$\begin{aligned} A=\left[ \begin{array}{cc} Q_m'&{}X_m\\ Y_m&{}Q_m''\end{array}\right] , \end{aligned}$$

where $Q_m'$ and $Q_m''$ have 1’s wherever $Q_m$ has 1’s. It is straightforward to check that $Q_m'$ must have all zeros above its anti-diagonal and $Q_m''$ must have all zeros below its anti-diagonal. We conjecture that $\alpha _n^*=\alpha _n(Q_n^*)$. We remark that in [6] completions of certain $(0,-1)$-matrices to ASMs are considered where the matrices $Q_n^*$ also occur, and there is a related conjecture.

Let $F_{2m}$ be the so-called $2m\times 2m$ diamond ASM, the ASM with the largest number of nonzeros [7]. Then $F_{2m}\in \mathcal {A}_n(Q_{2m}^*)$. For instance, with $m=4$,

$$\begin{aligned} F_8=\left[ \begin{array}{r|r|r|r|r|r|r|r} &{}&{}&{}1&{}&{}&{}&{}\\ \hline &{}&{}1&{}-1&{}1&{}&{}&{}\\ \hline &{}1&{}-1&{}1&{}-1&{}1&{}&{}\\ \hline 1&{}-1&{}1&{}-1&{}1&{}-1&{}1&{}\\ \hline &{}1&{}-1&{}1&{}-1&{}1&{}-1&{}1\\ \hline &{}&{}1&{}-1&{}1&{}-1&{}1&{}\\ \hline &{}&{}&{}1&{}-1&{}1&{}&{}\\ \hline &{}&{}&{}&{}1&{}&{}&{}\end{array}\right] . \end{aligned}$$

Let $F_{2m}^{(1)}$ be the (0, 1)-matrix with $m(m-1)$ 1’s, obtained from $F_{2m}$ by replacing all its $-1$’s with 0’s. Then $Q_{2m}^*\le F_{2m}^{(1)}$ and it is straightforward to check that no other permutation matrix P satisfies $P\le F_{2m}^{(1)}$. Indeed, it is easily seen that, after permutations of rows and columns,

$$\begin{aligned} F_{2m}^{(1)}=\left[ \begin{array}{cc} T_m&{}O_m\\ O_m&{} T_m\end{array}\right] \end{aligned}$$

where $T_m$ is the $m\times m$ matrix with 1’s on and below its main diagonal and 0’s elsewhere; the 1’s on the main diagonal of $T_m$ are those corresponding to the 1’s of $Q_{2m}^*$. In particular, the permutation matrix $Q_{2m}^*$ is the only permutation matrix of which $F_{2m}$ is an ASM-extension. Since the matrix $F_{2m}$ has the maximum number of nonzeros among all matrices in $\mathcal {A}_{2m}$, $F_{2m}$ is the unique ASM-extension of $Q_{2m}^*$ with the maximum number of nonzeros.

The matrix $\varSigma (F_{2m})$ has a special form which is illustrated for $\varSigma (F_8)$ below with $\varSigma (A_8^*) -\varSigma (F_8^*)$ also given:

Thus $\varSigma (Q_8^*)\ge \varSigma (F_8^*)$, and hence $F_8\preceq _B Q_8^*$. (We remark that the odd case is different, since we have $\varSigma (A_7^*)\not \le \varSigma (F_7)$ and $\varSigma (F_7)\not \le \varSigma (A_7^*)$: see (2) for $\varSigma (A_7^*)$.)

Example 1

We calculate that

Using our calculation of $\varSigma (A_8^*)$, we get

In general, we have

where $C_1$ is a $m\times m$ matrix with 0’s above the anti-diagonal, 1’s on the anti-diagonal, and 2’s, 3’s, $\ldots$ on the diagonals below it, $C_2$ is an $m\times m$ matrix whose row i contains all i’s ($1\le i\le m$), and $J_m$ is the $m \times m$ all-ones matrix. $\square$

Lemma 2

Let A be an $n\times n$ ASM with $n=2m$. Then $A\in \mathcal {A}_{2m}(Q_{2m}^*)$ if and only if

$$\begin{aligned} Q_{2m}^*\preceq _B A\preceq _B A_{2m} ^*, \end{aligned}$$

that is, if and only if

$$\begin{aligned} \varSigma (A_{2m}^*) \le \varSigma (A)\le \varSigma (Q_{2m}^*), \end{aligned}$$

a certain interval in the Bruhat order on the permutations in $S_{2m}$.

Proof

We first show that if $A\in \mathcal {A}_{2m}(Q_{2m})$, then $\varSigma (A)\le \varSigma (Q_{2m}^*)$. But this is clear from the form of $\varSigma (Q_{2m}^*)$ given in Example 1. The reason is that any ASM-completion of $Q_{2m}^*$ has only 0’s above the anti-diagonal in its leading $m\times m$ submatrix and the other entries in the upper $m\times 2m$ submatrix are as large as they can be in any such ASM. A similar conclusion holds for the lower $m\times 2m$ submatrix.

We next verify that if $A\in \mathcal {A}_{2m}(Q_{2m}^*)$, then $\varSigma (A_{2m}^*)\le \varSigma (A)$. Partition $A_{2m}^*$ into $m\times m$ matrices as

$$\begin{aligned} A_{2m}^*=\left[ \begin{array}{cc} A_1^*&{}A_2^*\\ A_3^*&{}A_4^*\end{array}\right] . \end{aligned}$$

The matrix $A_1^*$ has all 0’s above the anti-diagonal, all 1’s on the anti-diagonal, and all $-1$’s on the diagonal immediately below the anti-diagonal. These $-1$’s occur as early as possible in rows $2,3,\ldots ,m$ of $A_{2m}^*$. The matrix $A_2^*$ has 1’s on its anti-diagonal except for a 0 in its upper right corner. These 1’s occur as late as possible in rows $2,3,\ldots ,m$ of $A_{2m}^*$. It follows from this that $\sigma _{ij}(A_{2m^*})\le \sigma _{ij}(A)$ for $1\le i\le m$ and $1\le j\le 2m$ and, similarly, for $1\le i\le 2m$ and $1\le j\le m$. Since an ASM remains an ASM under a 180$^{\circ }$ rotation (that is, reading an ASM from the lower right corner from leftwards and upwards also gives an ASM), the theorem now follows. $\square$

Corollary 1

Let $n=2m$. Then the cardinality of $\mathcal {A}(Q_{2m}^*)$ equals the number of $n\times n$ nonnegative integral matrices X with $\varSigma (A_{2m}^*)\le X\le \varSigma (Q_{2m}^*)$ (entrywise) satisfying (LS-a), (LS-b), and (LS-c). $\square$

We now consider $n\times n$ permutation matrices P satisfying $\alpha _n(P)=1$, that is, permutation matrices having no ASM-completions other than itself. We call such permutation matrices isolated. For instance, the following permutation matrix P is isolated:

$$\begin{aligned} P=\left[ \begin{array}{c|c|c|c|c} &{}&{}1&{}&{}\\ \hline &{}&{}&{}&{}1\\ \hline &{}1&{}&{}&{}\\ \hline 1&{}&{}&{}&{}\\ \hline &{}&{}&{}1&{}\end{array} \right] . \end{aligned}$$

(3)

Let $P=[p_{ij}]$ be a permutation matrix. Assume that $i_1<i_2<i_3<i_4$ and $j_1<j_2<j_3<j_4$ be such that either

• (i) P has 1’s in each of the positions $(i_1,j_3)$, $(i_2,j_4)$, $(i_3,j_1)$, $(i_4,j_2)$,

  or

• (ii) P has 1’s in each of the positions $(i_1,j_2)$, $(i_2,j_1)$, $(i_3,j_4)$, $(i_4,j_3)$.

If (i) or (ii) holds, we say that P has an open square.

Lemma 3

Let P be a permutation matrix. Assume that P has an open square. Then $\alpha _n(P)>1$.

Proof

Assume that case (i) above holds. Let the matrix A be obtained from P by changing the two entries in positions $(i_2,j_3)$ and $(i_3,j_2)$ (from 0) into $-1$, and also changing the two entries in positions $(i_2,j_2)$ and $(i_3,j_3)$ (from 0) into 1. Then A is an ASM, and it is an ASM completion of P. Thus, P has at least two ASM completions, so $\alpha _n(P)>1$. The proof in case (ii) is similar. $\square$

Note that having an open square is equivalent to saying that either (i) the permutation $\sigma$ of $\{1,2,\ldots ,n\}$ corresponding to the permutation matrix P contains the pattern 3, 4, 1, 2 (corresponding to $j_3,j_4,j_1,j_2$) or (ii) the permutation $\sigma$ of $\{1,2,\ldots ,n\}$ corresponding to the permutation matrix P contains the pattern 2, 1, 4, 3 (corresponding to $j_2,j_1,j_4,j_3$). Thus, P not having an open square is equivalent to the corresponding permutation in $S_n$ being a 3412-avoiding and 2143-avoiding permutation. Note that 2143 and 3412 are reverses of one another, and so the number of 3412-avoiding permutations equals the number of 2143-avoiding permutations. It follows from results on pattern-avoidance permutations (see e.g. page 154 of [2]) that the number of 2143-avoiding (resp. 3412-avoiding) permutations of $\{1,2,\ldots ,n\}$ is the same as the number of 1234-avoiding permutations, that is, that do not contain an increasing subsequence of length 4. By a theorem of Gessel (see page 176 of [2]), this number equals

$$\begin{aligned} \frac{1}{(n+1)^2(n+2)} \sum _{k=0}^n {{2k}\atopwithdelims ()k}{{n+1}\atopwithdelims (){k+1}}{{n+2}\atopwithdelims (){k+1}}. \end{aligned}$$

(4)

Example 2

The following permutation matrix P, corresponding to the permutation (3, 5, 1, 2, 4), contains an open square, shown with the corresponding ASM extension A. With 3, 5, 1, 2, it is not 3412-avoiding.

$$\begin{aligned} P=\left[ \begin{array}{c|c|c|c|c} &{}&{}1&{}&{}\\ \hline &{}*&{}*&{}&{}1\\ \hline 1&{}*&{}*&{}&{}\\ \hline &{}1&{}&{}&{}\\ \hline &{}&{}&{}1&{}\end{array} \right] , \;\;\;\; A=\left[ \begin{array}{r|r|r|r|r} &{}&{}1&{}&{}\\ \hline &{}1&{}-1&{}&{}1\\ \hline 1&{}-1&{}1&{}&{}\\ \hline &{}1&{}&{}&{}\\ \hline &{}&{}&{}1&{}\end{array} \right] . \end{aligned}$$

Note that the matrix P is obtained from the matrix in (3) by a transposition. $\square$

Theorem 3

Let P be an $n\times n$ permutation matrix corresponding to a permutation $\sigma \in S_n$. Then $\alpha _n(P)=1$, that is, P is an isolated permutation matrix, if and only if P does not have an open square, that is, if and only if $\sigma$ is both a 3412-avoiding and 2143-avoiding permutation.

Proof

This follows directly from Lemma 3 and Corollary 6.2 of [7]. $\square$

Since a permutation can be both 3412-avoiding and 2143-avoiding, we can only say that the number of $n\times n$ permutation matrices P that have only one ASM-completion is bounded above by twice the number in (4).

Consider again the $n\times n$ permutation matrix $Q_n^*=Q_{\lceil \frac{n}{2}\rceil }\oplus Q_{\lfloor \frac{n}{2}\rfloor }$. Then $Q_n^*$ contains ${{\lceil \frac{n}{2}\rceil }\atopwithdelims ()2} {{\lfloor \frac{n}{2}\rfloor }\atopwithdelims ()2}$ open squares. If e.g. $n=2m$ is even, then $Q_n^*$ corresponds to the permutation

$$\begin{aligned} \sigma _{2m}=(m,m-1,\ldots ,2,1, 2m,2m-1,\ldots ,m+2,m+1). \end{aligned}$$

We believe that $\sigma _{2m}$ contains the largest number of patterns 2143, namely ${m\atopwithdelims ()2}^2$and thus has the largest number of completions to an ASM with two $-1$’s, but this does not yet mean that $\alpha _n(Q_{n}^*)$ is maximum, although we expect it is.

3 König Properties of a Class of ASMs

Consider again the question of extensions of a permutation matrix P to ASMs A where A has 1’s where P has 1’s. A “dual” viewpoint is to ask, for a given ASM A, if there exists a permutation matrix P such that P has all its 1’s where A has a 1. This leads to a related question concerning term ranks. The term rank of ASMs was studied in [7]. We now consider the term rank of the nonnegative part of ASMs. For a real matrix A, let $A^+$ denote the matrix $\max \{A,O\}$ in which all negative entries are replaced with 0’s; we call $A^+$ the nonnegative part of A. Let $\rho (B)$ denote the term rank of a matrix B, i.e., the largest number of nonzeros in B with no two of these in the same row or column.

The maximum of $\rho (A^+)$ among all ASMs of order n is clearly n, and it is attained for permutation matrices.

The next result determines the minimum of $\rho (A^+)$ among all ASMs of order n.

Theorem 4

The minimum of $\rho (A^+)$ among ASMs of order n is $\lceil 2\sqrt{n+1} -2 \rceil$.

Proof

Let A be an ASM of order n and let $t = \rho (A^+)$. By König’s theorem there are t lines that cover (contain) all 1s in A, say e rows and f columns, where $e+f=t$. Permute rows such that these e rows become first, and permute columns such that these f columns become first. Note that this affects the ASM property of the $\pm 1$’s alternating. Then the permuted A has the form

$$\begin{aligned} A=\left[ \begin{array}{rr} A_1&{}A_2\\ A_3 &{} A_4 \end{array} \right] \end{aligned}$$

(5)

where $A_1$ has size $e \times f$. The matrix $A_4$ contains only $-1$’s and 0’s. Let $p_i$ and $n_i$ (resp.) be the number of 1’s and $-1$’s in the submatrix $A_i$ ($i \le 4$). So, $p_4=0$. Then, as line sums are not changed by the permutations,

$$\begin{aligned} \begin{array}{lll} (p_1-n_1)+(p_2-n_2)=e, \quad &{}&{} (p_1-n_1)+(p_3-n_3)=f.\\ p_3-n_3-n_4=n-e , \quad &{}&{} p_2-n_2-n_4=n-f. \end{array} \end{aligned}$$

Thus

$$\begin{aligned} n_1-p_1=(p_2-n_2)-e=n_4+n-f-e=n_4+n-t. \end{aligned}$$

But $n_1-p_1$ is at most the number of nonzeros in $A_1$, so $n_1-p_1\le ef \le (t/2)^2$ as $e+f=t$. Therefore,

$$\begin{aligned} n-t \le n_4+n-t =n_1-p_1\le t^2/4 \end{aligned}$$

so that $t^2+4t\ge 4n$ and $(t+2)^2\ge 4n+4$. This implies that

$$\begin{aligned} t \ge \lceil 2\sqrt{n+1} -2 \rceil . \end{aligned}$$

It follows that

$$\begin{aligned} \min \{\rho (A^+): A \in \mathcal {A}_n\} \ge \lceil 2\sqrt{n+1} -2 \rceil . \end{aligned}$$

On the other hand, Corollary 4.2 in [7] shows that

$$\begin{aligned} \min \{\rho (A): A \in \mathcal {A}_n\} =\lceil 2\sqrt{n+1} -2 \rceil \end{aligned}$$

where $\rho (A)$ denotes the term rank of A. Clearly $\rho (A) \ge \rho (A^+)$ for any matrix A, so it follows that $\min \{\rho (A^+): A \in \mathcal {A}_n\} = \lceil 2\sqrt{n+1} -2 \rceil$. $\square$

The previous theorem and its proof show the surprising fact that the minimum term rank among $n\times n$ ASMs is the same as the minimum term rank of the matrices obtained by replacing all negative entries with zeros. In [7], for each n, an ASM A is given which attains the minimum term rank in $\mathcal {A}_n$, and therefore also the minimum rank of $A^+$ in that class.

We now study the term rank and line covers of certain ASMs. In a matrix A a line cover is a set of lines (rows and columns) that contain all nonzeros of A. The minimum number of lines in a line cover of A is called the line cover number and it is denoted by $\tau (A)$. A classical theorem of König says that $\tau (A)=\rho (A)$, i.e., that the line cover number equals the term rank of A.

Let $D_3$ denote the unique ASM of order 3 with a single $-1$, so

$$\begin{aligned} D_3= \left[ \begin{array}{r|r|r} &{} 1 &{} \\ \hline 1&{}-1&{}1 \\ \hline &{} 1&{} \end{array} \right] . \end{aligned}$$

Consider an ASM A of order n. Let B be a matrix obtained from A by identifying a single $+1$ of A, say in position (i, j), with a single $+1$ of $D_3$ and inserting two new rows and two new columns such that $D_3$ is embedded in the resulting matrix. These new rows, and the new columns, may not be consecutive, but they must retain the same relative order as in $D_3$ and maintain the alternating sign property. We call the mentioned position (i, j) the insertion position. Such a matrix is an ASM and will be denoted by $A*D_3$ and called an $D_3$-extension of A. A row of a matrix with a unique nonzero (which must be 1) will be called a unit row, otherwise it is called a non-unit row. We define a unit column and a non-unit column similarly.

We now consider two specific types of such $D_3$-extensions B where, as above, the insertion position is (i, j):

• ($*\hbox {a}$) Row i is a non-unit row of A. Moreover, the $-1$ of the inserted $D_3$ is in the corresponding row of B. A similar type is obtained when column j is a non-unit row and the inserted $-1$ is in the corresponding column.

• ($*\hbox {b}$) Row i is a unit row with its nonzero (a $+1$) in column j. Moreover, the $-1$ of the inserted $D_3$ is in row i. A similar type is obtained by interchanging the roles of rows and columns in the previous sentence.

For instance, $D_3$ itself is a $D_3$-extension of $J_1=[1]$ of type ($*$b). Let $\mathcal {A}^{*}$ denote the class of ASMs that may be obtained from $J_1$ using a finite number of $D_3$-extensions of type ($*$a) or ($*$b). Observe that every matrix except $J_1$ in $\mathcal {A}^{*}$ has the property that every $+1$ is in a non-unit row or column. This is seen from the structure of the extension.

Example 3

The matrix $B_1$ below is obtained by a $D_3$-extension of type ($*$a) of $D_3$, using column 2 and insertion position (3, 2). $B_2$ is a $D_3$-extension of type ($*$b) of $D_3$, using column 3 and insertion position (2, 3).

$$\begin{aligned} D_3=\left[ \begin{array}{r|r|r} &{}+&{}\\ \hline +&{}-&{}+\\ \hline &{}+&{}\ \end{array} \right] , \quad B_1=\left[ \begin{array}{r|r|r|r|r} &{}&{}+&{}&{}\\ \hline &{}+&{}-&{}+&{}\\ \hline &{}&{}+&{}&{}\\ \hline +&{}&{}-&{}&{}+\\ \hline &{}&{}+&{}&{} \end{array} \right] , \quad B_2=\left[ \begin{array}{r|r|r|r|r} &{}&{}+&{}&{}\\ \hline &{}+&{}-&{}+&{}\\ \hline &{}&{}+&{}&{}\\ \hline +&{}&{}&{}-&{}+\\ \hline &{}&{}&{}+&{} \end{array} \right] . \end{aligned}$$

$\square$

For an ASM A let $n^-_r(A)$ (resp. $n^-_c(A)$) denote the number of rows (resp. columns) of A that contain at least one negative entry, i.e., the number of non-unit rows (resp. columns).

Lemma 4

Let A be an ASM which is not the direct sum of a permutation matrix and a smaller ASM. Then

$$\begin{aligned} \rho (A) \le n^-_r(A) + n^-_c(A). \end{aligned}$$

Proof

Let L be the set of lines in A that contain at least one $-1$. So, $|L|=n^-_r(A) + n^-_c(A)$. Moreover, by assumption, there is no 1 in A that lies both in a unit row and a unit column (because then A would be the direct sum of [1] and a smaller ASM). Therefore L covers all the ones in A, and clearly all the $-1$’s. So, L is a line cover, and

$$\begin{aligned} \rho (A) = \tau (A) \le |L|=n^-_r(A) + n^-_c(A). \end{aligned}$$

$\square$

The next result gives a simple expression for the term rank of each matrix in $\mathcal {A}^*$, namely that it is equal to the upper bound established in Lemma 4.

Theorem 5

Let A be an ASM in $\mathcal {A}^{*}$ of order $n \ge 3$. Then

$$\begin{aligned} \rho (A) = \rho (A^+)=n^-_r(A) + n^-_c(A). \end{aligned}$$

(6)

Moreover, a minimum line cover of A consists of all rows and columns that contain at least one entry equal to $-1$, and the corresponding set of lines in $A^+$ is a minimum line cover of $A^+$.

Proof

We prove the result by induction on the number k of $D_3$-extensions. If $k=1$, then $A=D_3$, and the result trivially holds. Assume that the theorem holds for up to k$D_3$-extensions, for some k. Let A be obtained from $J_1$ by $k+1$ successive $D_3$-extensions, and let $A'$ be the matrix obtained by the first k of these $D_3$-extensions. Then

$$\begin{aligned} \tau (A')=\rho (A') = \rho ((A')^+)=n^-_r(A') + n^-_c(A'). \end{aligned}$$

So, A is obtained by a $D_3$-extension of $A'$. Moreover,

$$\begin{aligned} \tau (A')+1 \le \tau (A^+) \le \tau (A') +2 \end{aligned}$$

(7)

as the added nonzeros (in A) can be covered by at most two lines, and at least one line is needed. There are two possible cases. Let the insertion position be (i, j).

Case 1 :  The extension is of type$(*a)$. Assume the extension is as described in the first part of $(*a)$; the other case is similar. Then

$$\begin{aligned} n^-_r(A)=n^-_r(A'), \quad \text{ and } \quad n^-_c(A)=n^-_c(A')+1. \end{aligned}$$

Consider the minimum line cover of $A'$ consisting of all rows and columns of $A'$ that contain a $-1$. The corresponding lines in $A^+$ cover all 1’s of $A^+$ except two $+1$ entries in the same column (that were added in producing A). Therefore, by adding this column, one gets a line cover of $A^+$ with $\tau (A')+1$ lines, and, by (7), that must be a minimum line cover of $A^+$. The corresponding lines in A also cover all the negative entries, so it is a minimum line cover of A. Thus,

$$\begin{aligned} \rho (A^+)=\tau (A^+)=\tau (A)=\tau (A')+1=(n^-_r(A') + n^-_c(A'))+1=n^-_r(A) + n^-_c(A). \end{aligned}$$

as desired.

Case 2 :  The extension is of type$(*b)$. Assume the extension is as described in the first sentence of $(*b)$; the other situation is treated similarly. (See the matrix $A_2$ in Example 3 where $(i,j)=(2,3)$.) Then

$$\begin{aligned} n^-_r(A)=n^-_r(A')+1, \quad \text{ and } \quad n^-_c(A)=n^-_c(A')+1. \end{aligned}$$

Let $p=\tau (A^+)$, so there is a set S of p positions of 1’s in $A'$ such that no pair of these positions in S are in the same line. Then S corresponds to a matching in the bipartite graph G corresponding to $A^+$.

Assume first that $(i,j) \not \in S$. Then S together with two of the $+1$’s that were added in the construction of A is a matching of size $p+2$ in G. Otherwise, S contains (i, j). Then $A^+$ contains another 1 in either row i or column j, but not both, such that this 1 is in a unit row or column. Let $S'$ be obtained from S by adding the position of such a 1 and removing position (i, j). Thus, $S'$ is also a matching in G and $|S'|=|S|$. Then we can proceed as just described and add two positions and obtain a matching of size $p+2$ in G. Therefore

$$\begin{aligned} \rho (A^+)=\tau (A')+2=(n^-_r(A') + n^-_c(A'))+2=n^-_r(A) + n^-_c(A) \end{aligned}$$

as desired. Moreover, we obtain a line cover of size equal to $\rho (A^+)$ by taking the line cover of $A'$ and add the two lines containing the added $-1$ of A. By induction, this line cover consists of all rows and columns that contain a $-1$ in A. The theorem now follows. $\square$

In Example 3, a minimum line cover for $B_1$ consists of rows 2 and 4, and column 3. A minimum line cover for $B_2$ consists of rows 2 and 4, and columns 3 and 4. Matchings of corresponding sizes are easy to find.

We remark that the result above also holds for some more general $D_3$-extensions than those specified in $(*b)$.

The ASM class $\mathcal {A}^*$ studied above has the special property that

$$\begin{aligned} \rho (A) = \rho (A^+) \end{aligned}$$

for every $A \in \mathcal {A}^*$. In other words, covering the negative entries as well does not require any more lines than just covering the positive entries. We now give an example which shows that this property does not hold for all ASMs.

Example 4

Let k be a positive integer, and consider the matrix $B^{(k)}$ given by

$$\begin{aligned} B^{(k)}= \left[ \begin{array}{r|r|r|r|r} &{}v_1&{}&{}\\ \hline &{}&{}+&{}&{}v_2 \\ \hline &{}+&{}-&{}+\\ \hline v_4&{}&{}+&{}\\ \hline &{}&{}&{}v_3 \\ \end{array} \right] , \end{aligned}$$

where each $v_i$ is a vector with $p=2k$ components; here $v_2$ and $v_4$ are row vectors while $v_1$ and $v_3$ are column vectors. The components of each $v_i$ alternate between $+1$ and $-1$ such that (i) the rows in $B^{(k)}$ corresponding to $v_2$ and $v_4$ are alternating, starting and ending with $+1$, and (ii) the columns in $B^{(k)}$ corresponding to $v_1$ and $v_3$ are alternating, starting and ending with $+1$. Now we extend $B^{(k)}$ into an ASM $A^{(k)}$ by adding rows and columns containing a single nonzero, a $+1$, in suitable positions. For instance, for every $-1$ in $v_2$ we introduce two new rows, one on top and one at the bottom of the present matrix, and containing a $+1$ in the same column as the mentioned $-1$.

Let C denote the column of $A^{(k)}$ containing $v_1$. Moreover, let S be the set of positions of the nonzeros in C as well as the $+1$’s in the rows of the $-1$’s in column C. Let L be a line cover of $A^{(k)}$. In particular, L covers S and there are two possibilities:

Case 1: LcontainsC. Then the set S may be covered by column C and one row for each $-1$ in $v_1$, so $k+1$ lines all together, and this is the minimum number of lines to cover S.

Case 2: Ldoes not containC. Then the set S can not be covered by less than $2k+1$ lines, and this minimum is attained when we use the $2k+1$ rows that contain the nonzeros of column C.

It follows that any minimum line cover L of $A^{(k)}$must contain the column C. Similarly, one shows that L must contain the column corresponding to $v_3$ and each of the rows corresponding to $v_1$ and $v_2$. It follows from this that

$$\begin{aligned} |L|=4(k+1)+1=4k+5. \end{aligned}$$

Here the additional 1 is due to the fact that we must cover the $-1$ in the center of $B^{(k)}$. Thus, $\rho (A^{(k)})=4k+5$. It also follows from this discussion that there is a line cover of $(A^{(k)})^+$ of cardinality $4k+4$, because we do not need to cover the $-1$ in the center of $B^{(k)}$. In fact,

$$\begin{aligned} \rho ((A^{(k)})^+)=4k+4<4k+5=\rho (A^{(k)}). \end{aligned}$$

Thus we have a class of ASMs A for which $\rho (A^+) < \rho (A)$. $\square$

4 Sum-matrices and primary sum-sequences of permutations

Let P be an $n\times n$ permutation matrix. Then clearly each row of $\varSigma (P)$ contains exactly one increase in a column that did not contain an increase in a previous row, and this increase determines where the 1 in a row occurs (in P). For example, consider the permutation (5, 2, 7, 4, 1, 6, 3) with corresponding $7\times 7$ permutation matrix P given below:

(8)

where we have shaded the cells where an increase first occurs and then those above it. As we see from (8), the set of shaded columns form a nested sequence of subsets of $\{1,2,3,4,5,6,7\}$, from the top row down to the corresponding positions of the 1’s of P:

$$\begin{aligned} \emptyset= & {} X_0\subset X_1\subset X_2\subset \cdots \subset X_7 \text{ where } |X_k|=k \text{ for } k=1,2,\ldots ,7:\\ X_1= & {} \{5\},X_2=\{2,5\},X_3=\{2,5,7\}, X_4=\{2,4,5,7\}, X_5=\{1,2,4,5,7\},\\ X_6= & {} \{1,2,4,5,6,7\}, X_7=\{1,2,3,4,5,6,7\}. \end{aligned}$$

This nested property holds in general. So the matrix $\varSigma (P)$ can be said to represent the usual way in which a permutation of $\{1,2,\ldots ,n\}$ is identified as a saturated chain from $\emptyset$ to $\{1,2,\ldots ,n\}$ in the lattice of subsets of $\{1,2,\ldots ,n\}$ ordered by set-inclusion. We define the nest$\mathcal {N}(P)$ of the permutation matrix P to be this nested sequence $X_0\subset X_1\subset X_2\subset \cdots \subset X_n=\{1,2,\ldots ,n\}$ where $|X_k|=k$ for $k=0,1,\ldots ,n$. By the above discussion the $k\times k$ submatrix of P given by $P[\{1,2,\ldots ,k\},X_k]$ is a permutation matrix.

Let $\pi =(\pi _1,\pi _2,\ldots ,\pi _n)$ be a permutation of $\{1,2,\ldots ,n\}$ with corresponding $n\times n$ permutation matrix P. We define the primary sum-sequence$\chi (P)=\chi (\pi )$ of P and $\pi$ to be the sequence $(c_1,c_2,\ldots ,c_n)$ where $c_k$ equals the $(k,\pi _k)$ entry of the sum-matrix $\varSigma (P)$ for $k=1,2,\ldots ,n$. Thus $c_k$ equals the number of 1’s of P in its leading $k\times \pi _k$ submatrix (which therefore contains a 1 in its lower right corner), equivalently, the rank of this submatrix. In terms of the permutation $\pi$,

$$\begin{aligned} c_k=|\{i\le k: \pi _i\le \pi _k\}|. \end{aligned}$$

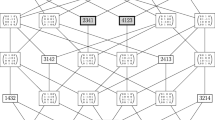
Thus we have a mapping $\chi _n:\mathcal {P}_n\rightarrow \mathcal {C}_n$ where $\mathcal {C}_n$ is the set of all sequences of length n with entries in $\{1,2,\ldots ,n\}$. We have $\chi (\iota _n)=\chi (I_n)=(1,2,\ldots ,n)$ and $\chi (\zeta _n)=\chi (L_n)=(1,1,\ldots ,1)$ where $\iota _n=(1,2,\ldots ,n)$ and $\zeta _n=(n,n-1,\ldots ,1)$ with corresponding permutation matrix $L_n$. In Fig. 1 we give the Hasse diagram of $(\mathcal {S}_3,\preceq _B)$ with the primary sum-sequences given in brackets.

Fig. 1

Hasse diagram of $(\mathcal {S}_3,\preceq _B)$ with primary sum-sequences in brackets

Example 5

Let $n=9$ and let $\pi =(3,7,2,4,9,1,8,5,6)$. Then computation shows that the primary sum-sequence of $\pi$ is $\chi (\pi )=(1,2,1,3,5,1,6,5,6)$. $\square$

Theorem 6

Let n be a positive integer. The mapping $\chi _n:\mathcal {P}_n\rightarrow \mathcal {C}_n$ is injective, that is, a permutation (matrix) is determined by its primary sum-sequence.

Proof

Let P be an $n\times n$ permutation matrix and let $\chi (P)=(c_1,c_2,\ldots ,c_n)$. The following recursive algorithm shows how to reconstruct P from $\chi (P)$.

• Begin with an $n\times n$ array X in which every position is empty.

• Consider $c_n$. This is computed from the 1 in the last row of P. Thus $c_n$ determines which column the 1 in row n of P is located, namely column $c_n$. Put a 1 in position $(n,c_n)$ of X and a 0 in all other positions of row n.

• Now consider $c_{n-1}$. Ignoring column $c_n$ and using the fact that the $(n-1)$ remaining columns of P contain a 1 in rows $1,2,\ldots ,n-1$, $c_{n-1}$ determines which column t the 1 in row $(n-1)$ is. Put a 1 in row $n-1$ of X in this column t and a 0 in all other positions of X in row $n-1$.

• Continue like this to construct a unique (0, 1)-matrix, and this matrix is P.

$\square$

The proof above implies that when $\chi (\pi )=(c_1,c_2,\ldots ,c_n)$, then $\pi =(\pi _1, \pi _2, \ldots , \pi _n)$ may be expressed in terms of $(c_1,c_2,\ldots ,c_n)$ as follows

$$\begin{aligned} \pi _k = \min \{s: s \ge c_k+|\{l>k: c_l \le c_k\}|, \;\; s \not = \pi _l \;(l >k)\} \;\;\;\;(k \le n). \end{aligned}$$

(9)

Theorem 6 also follows from the facts: (i) there is a bijection between the set of $n\times n$ permutation matrices and the set ${\varvec{\Sigma }}(\mathcal {P}_n)$ of their corresponding sum-matrices, and (ii) these sum-matrices are uniquely determined by their increases in rows that are not increases in previous rows. Thus the primary sum-sequence determines the permutation matrix.

Example 6

Let $c=(1,2,1,4,2)$. Then using the procedure in Theorem 6, or the expression (9), we get

$$\begin{aligned}&\left[ \begin{array}{c|c|c|c|c} &{}&{}&{}&{}\\ \hline &{}&{}&{}&{}\\ \hline &{}&{}&{}&{}\\ \hline &{}&{}&{}&{}\\ \hline &{}1&{} &{} &{} \end{array}\right] \rightarrow \left[ \begin{array}{c|c|c|c|c} &{}&{}&{}&{}\\ \hline &{}&{}&{}&{}\\ \hline &{}&{}&{}&{}\\ \hline &{}&{}&{}&{}1\\ \hline &{}1&{} &{} &{} \end{array}\right] \rightarrow \left[ \begin{array}{c|c|c|c|c} &{}&{}&{}&{}\\ \hline &{}&{}&{}&{}\\ \hline 1&{}&{}&{}&{}\\ \hline &{}&{}&{}&{}1\\ \hline &{}1&{} &{} &{} \end{array}\right] \rightarrow \\&\quad \left[ \begin{array}{c|c|c|c|c} &{}&{}&{}&{}\\ \hline &{}&{}&{}1&{}\\ \hline 1&{}&{}&{}&{}\\ \hline &{}&{}&{}&{}1\\ \hline &{}1&{} &{} &{} \end{array}\right] \rightarrow \left[ \begin{array}{c|c|c|c|c} &{}&{}1&{}&{}\\ \hline &{}&{}&{}1&{}\\ \hline 1&{}&{}&{}&{}\\ \hline &{}&{}&{}&{}1\\ \hline &{}1&{}&{}&{}\end{array}\right] . \end{aligned}$$

Thus $c=(1,2,1,4,2)$ is the primary sum-sequence of a permutation matrix. $\square$

It follows from Theorem 6 that if P is an $n\times n$ permutation matrix corresponding to a permutation $\pi =(\pi _1,\pi _2,\ldots ,\pi _n)$, then the sum-matrix $\varSigma (P)=[\sigma _{ij}]$ is determined by its values at the positions corresponding to the positions of the 1’s of P, that is, by the sequence $(\sigma _{i,\pi _i}:1\le i\le n)$. Now consider two $n\times n$ permutation matrices P and Q corresponding to permutations $\pi$ and $\tau$ with primary sum-sequences $\chi (P)$ and $\chi (Q)$, respectively.

Example 7

Let $n=4$ and consider the two permutations $\pi _1=(2,4,1,3)$ and $\pi _2=(2,4,3,1)$ where $\pi _1\preceq _B \pi _2$. Then $\chi (\pi _1)=(1,2,1,3)$ and $\chi (\pi _2)=(1,2,2,1)$. $\square$

Lemma 5

Let $P_1$ and $P_2$ be two $n\times n$ permutation matrices such that $P_1$ covers $P_2$ in the Bruhat order. Then there exists k and l with $1\le k<l\le n$ and a nonnegative integer r such that $\chi (P_2)=(b_1,b_2,\ldots ,b_n)$ is obtained from $\chi (P_1)=(a_1,a_2,\ldots ,a_n)$ by decreasing $b_k$ by r and increasing $b_l$ by $r+1$.

Proof

Let $\pi _1=(i_1,i_2,\ldots ,i_n)$ and $\pi _2=(j_1,j_2,\ldots ,j_n)$ be the permutations corresponding to $P_1$ and $P_2$, respectively. Then $\pi _1$ covers $\pi _2$ in the Bruhat order so that $\pi _1$ has exactly one more inversion than $\pi _2$. Hence there exists k and l with $k<l$ such that $i_k>i_l$ where for each t with $k<t<l$, $i_t>i_l$ or $i_t<i_k$ and $\pi _2$ is obtained from $\pi _1$ by switching $j_k$ and $j_l$. It is easy to check that $\chi (P_2)$ is obtained from $\chi (P_1)$ by decreasing $a_l$ by some nonnegative integer r and increasing $a_k$ by $r+1$. $\square$

If $a=(a_1,a_2,\ldots ,a_n)$ and $b=(b_1,b_2,\ldots ,b_n)$ are two arbitrary sequences of nonnegative integers, then b is obtained from a by a pseudoswitch, denoted as $a\vdash b$, provided that there exists integers $k<l$ and a nonnegative integer r such that b is obtained from a by decreasing $a_k$ by r and increasing $a_l$ by $r+1$. Denote the sum of the entries of a vector x by $\sigma (x)$. If $a\vdash b$, $\sigma (b)=\sigma (a)+1$. The level of a permutation (matrix) in the Bruhat order is its number of inversions.

Theorem 7

Let $P_1$ and $P_2$ be two $n\times n$ permutation matrices where $P_1$ is at level k and $P_2$ is a level l in the poset $(\mathcal {P}_n,\preceq _B)$ where $0\le k<l\le {n\atopwithdelims ()2}$. Then $P_1\preceq _B P_2$ if and only if $\chi (P_1)$ can be obtained from $\chi (P_2)$ by a sequence of $(l-k)$ pseudoswitches.

Proof

This theorem is an immediate consequence of Lemma 5 and the fact that if $\pi _1$ and $\pi _2$ are two permutations of $\{1,2,\ldots ,n\}$ such that $\pi _2\preceq _B \pi _1$, then $\pi _2$ can be obtained from $\pi _1$ by a sequence of $\sigma (\chi (P))-\sigma (\chi (P_2))$ transforms each of which increases the number of inversions by 1, that is, increases the level by 1 in $(\mathcal {P}_n,\preceq _B)$. $\square$

Example 8

In the poset $(\mathcal {S}_4,\preceq _B)$ we have the saturated chain of permutations (written compactly)

$$\begin{aligned} 1234,1324,3124,3142,3412,4312,4321, \end{aligned}$$

with corresponding primary sum-sequences (also written compactly)

$$\begin{aligned} 1234, 1133,1124, 1132, 1212,1112,1111. \end{aligned}$$

$\square$

The next result characterizes the primary sum-sequences of permutation matrices.

Theorem 8

The set $\chi (\mathcal {P}_n)$ of primary sum-sequences of $n\times n$ permutation matrices P is the set of integral vectors $c=(c_1, c_2, \ldots , c_n)$ satisfying

$$\begin{aligned} 1 \le c_i \le i \;\;\;\; (i \le n). \end{aligned}$$

(10)

Proof

Assume first that $(c_1, c_2, \ldots , c_n)=\chi (P)$ for some permutation matrix P with corresponding permutation $(j_1,j_2,\ldots ,j_n)$. By definition, for each $k\le n$ we have $c_k\ge 1$. Since the first k rows of P up to column $j_k$ contain at most k 1’s, we have that $c_k\le k$.

We prove the converse by induction on n. Assume the result holds for smaller values than n, and let $c=(c_1, c_2, \ldots , c_n)$ be an integral vector satisfying (10). Let $k=c_n$. So $1 \le k \le n$. By induction there exists an $(n-1)\times (n-1)$ permutation matrix $P'$ such that

$$\begin{aligned} \chi (P')=(c_1, c_2, \ldots , c_{n-1}). \end{aligned}$$

Let P be the matrix obtained from $P'$ by adding a row, as row n, and a column, as column k, and place a 1 in position (n, k) of P. Then, clearly, P is a permutation matrix of order n. Moreover, $(\chi (P))_i=(\chi (P'))_i=c_i$ for $i \le n-1$, and $(\chi (P))_n=k$ since the previous $k-1$ columns each have a 1 in one of the first $n-1$ rows. Thus, $\chi (P)=c$, as desired. $\square$

We remark that Theorem 6 is also a consequence of Theorem 8, as the set of integral vectors satisfying (10) has cardinality $1 \cdot 2 \cdot \cdots \cdot n=n!$. Thus the map $P \rightarrow \chi (P)$ is surjective between two sets of the same size, and it is therefore also injective.

Let P be an $n\times n$ permutation matrix with primary sum-sequence $\chi (P)=(c_1,c_2,\ldots ,c_n)$. The corresponding $n\times n$ (0, 1)-matrix C(P) with exactly n 1’s where these 1’s are in positions $(k,c_k)$ ($1\le k\le n$) is called the primary sum-matrix of P. Let $\mathcal {C}_n$ be the set of primary sum-matrices of $n\times n$ permutation matrices. By Theorem 8, $\mathcal {C}_n$ is the set of all $n\times n$ (0, 1)-matrices with exactly n 1’s where, for each $k=1,2,\ldots ,n$, the 1 in row k is in column $i\le k$. The primary sum-matrix of the identity $\iota _n$ is the identity matrix $I_n$; the primary sum-matrix matrix of the anti-identity permutation $\zeta _n$ is the matrix whose first column is the all ones vector, and all other columns are zero. It is easy to see that no other primary sum-matrix than the one associated with $\iota _n$ is a permutation matrix.

Example 9

Let P be the $5\times 5$ permutation matrix corresponding to the permutation (3, 5, 2, 1, 4). Then its primary sum-sequence equals (1, 2, 1, 1, 4) and its primary sum-matrix is

$$\begin{aligned} C(P)= \left[ \begin{array}{c|c|c|c|c} 1&{}&{}&{} &{} \\ \hline &{}1&{}&{}&{}\\ \hline 1&{}&{}&{}&{}\\ \hline 1&{}&{} &{}&{} \\ \hline &{}&{}&{}1&{}\end{array}\right] . \end{aligned}$$

$\square$

The column sum vector of a matrix A is denoted by $S_A$. Let S be a nonnegative integral vector of length n and define

$$\begin{aligned} \begin{array}{rl} \mathcal {C}_n(S) &{}= \{C \in \mathcal {C}_n: S_C=S\}, \\ \mathcal {P}_n(S) &{}= \{P \in \mathcal {P}_n: C(P) \in \mathcal {C}_n(S)\} \end{array} \end{aligned}$$

as the set of primary sum-matrices with column sum vector S and the corresponding set of permutation matrices, respectively.

Theorem 9

Let $S=(s_1, s_2, \ldots , s_n)$ be a nonnegative, integral vector. Then $S=S_C$ for some primary sum-matrix C if and only if

$$\begin{aligned} \begin{array}{cl} s_1 \ge 1, \\ s_i \ge 0, &{}(2 \le i \le n)\\ \sum _{j=n-k+1}^n s_j \le k, &{}(1 \le k < n)\\ \sum _{j=1}^n s_j =n. \end{array} \end{aligned}$$

(11)

Proof

Let $C=[c_{ij}] \in \mathcal {C}_n$. Then $S_C=(s_1, s_2, \ldots , s_n)$ is clearly nonnegative. Each row of C contains exactly one 1, so $c_{11}=1$ and $\sum _j s_j = n$. Moreover, C is lower triangular, so the last k columns cannot contain more than k 1’s (again, as each row has exactly one 1) which gives the final inequalities.

Conversely, assume that S satisfies (11). We shall construct a matrix $C \in \mathcal {C}_n(S)$. Initially, let C be the matrix whose first column is all ones, and all other entries are 0. Then, if $s_n =1$ shift the bottommost 1 in the first column of C to column n. Next, in the updated C, shift the $s_{n-1}$ bottommost 1’s in the first column to column $n-1$ (if $s_{n-1}=0$, nothing is done). As $s_{n-1}+s_n \le 2$, C will remain lower triangular. In the k’th step, for the present C, shift the $s_{n-k+1}$ bottommost 1’s in the first column to column $n-k+1$. As $\sum _{j=n-k+1}^n s_j \le k$, the new C will be lower triangular, and its column sum vector is clearly S, so $C \in \mathcal {C}(S)$. $\square$

Note that the condition of the theorem is a sort of majorization condition on S. We call the primary sum-matrix constructed in the proof of Theorem 9 the canonical primary sum-matrix with column sum S, and it will be denoted by $\hat{C}(S)$. The (unique) corresponding permutation matrix is denoted by $\hat{P}(S)$.

Example 10

Let $n=7$, and $S=(2,1,0,2,0,1,1)$. Then

$$\begin{aligned} \begin{array}{ll} \hat{C}(S)= \left[ \begin{array}{c|c|c|c|c|c|c} 1&{}&{}&{}&{}&{}&{}\\ \hline 1&{}&{}&{}&{}&{}&{}\\ \hline &{}1&{} &{}&{}&{}&{}\\ \hline &{}&{}&{}1&{}&{}&{}\\ \hline &{}&{}&{}1&{} &{}&{}\\ \hline &{}&{}&{}&{}&{}1&{}\\ \hline &{}&{}&{}&{}&{}&{}1\\ \end{array} \right] , &{} \hat{P}(S)= \left[ \begin{array}{c|c|c|c|c|c|c} &{}&{}1&{}&{}&{}&{}\\ \hline 1&{}&{}&{}&{}&{}&{}\\ \hline &{}1&{} &{}&{}&{}&{}\\ \hline &{}&{}&{}&{}1&{}&{}\\ \hline &{}&{}&{}1&{} &{}&{}\\ \hline &{}&{}&{}&{}&{}1&{}\\ \hline &{}&{}&{}&{}&{}&{}1\\ \end{array} \right] . \end{array} \end{aligned}$$

$\square$

Let $L_2$ denote the matrix backward identity matrix of order 2, so

$$\begin{aligned} L_2= \left[ \begin{array}{ll} 0 &{} 1 \\ 1 &{} 0 \end{array} \right] . \end{aligned}$$

We say that a (0, 1)-matrix has consecutive ones in columns if for every column its ones (if any) occur consecutively.

Theorem 10

Assume that S satisfies the conditions of Theorem 9. Then the following holds:

(i):

The canonical matrix $\hat{C}(S)$ has consecutive ones in columns, and it does not contain any submatrix equal to $L_2$.

(ii):

$\hat{C}(S) \preceq _B C$ for each matrix $C \in \mathcal {C}_n(S)$, i.e., $\hat{C}(S)$ is the least element in the poset $(\mathcal {C}(S), \preceq _B)$.

Proof

The construction of $\hat{C}(S)=[\hat{c}_{ij}]$ implies that the ones in this matrix are consecutive in each column, and that $\hat{C}(S)$ has a staircase pattern. Therefore, it has no submatrix equal to $L_2$.

Let $C =[c_{ij}]\in \mathcal {C}_n(S)$ and $C \not = \hat{C}(S)$. Let $\bar{C}$ be the (0, 1)-matrix whose first column is the all ones vector, and all other entries are 0. Then C may be obtained from $\bar{C}$ by suitable shifting of 1’s to the right in every row. If, for $i=n, n-1, \ldots , 1$, the 1 in row i is moved to the maximal column index j, then C would be equal to $\hat{C}(S)$, so this is not possible. Therefore, there is an i, and $j<k$, such that $c_{ij}=1$ and $\hat{c}_{ik}=1$, and we choose i largest possible with this property. Since column k of both $\hat{C}(S)$ and C have the same sum, there must exist $i'<i$, such that $c_{i'j}=1$ and $\hat{c}_{ik}=0$. This means that the submatrix of C consisting of rows i and $i'$ and columns j and k equals $L_2$.

Let $C'$ be the matrix obtained from C by replacing the mentioned submatrix $L_2$ by $I_2$. Then $C'\preceq _B C$. Now, if $C' = \hat{C}(S)$, we are done. Otherwise, we repeat the process above with C replaced by $C'$. It follows that $\hat{C}(S)$ is a least element in the poset $(\mathcal {C}(S), \preceq _B)$. $\square$

One may ask if part (ii) of Theorem 10 can be extended to a similar statement for the Bruhat order on the corresponding permutation matrices. This is not the case, as the next example shows.

Example10cont. Let again $n=7$ and $S=(2,1,0,2,0,1,1)$. Another matrix C in $\mathcal {C}(S)$ and the corresponding permutation matrix P are given by

$$\begin{aligned} \begin{array}{ll} C= \left[ \begin{array}{c|c|c|c|c|c|c} 1&{}&{}&{}&{}&{}&{}\\ \hline &{}1&{}&{}&{}&{}&{}\\ \hline 1&{}&{} &{}&{}&{}&{}\\ \hline &{}&{}&{}1&{}&{}&{}\\ \hline &{}&{}&{}1&{} &{}&{}\\ \hline &{}&{}&{}&{}&{}1&{}\\ \hline &{}&{}&{}&{}&{}&{}1\\ \end{array} \right] ,\quad &{} P= \left[ \begin{array}{c|c|c|c|c|c|c} &{}1&{}&{}&{}&{}&{}\\ \hline &{}&{}1&{}&{}&{}&{}\\ \hline 1&{}&{} &{}&{}&{}&{}\\ \hline &{}&{}&{}&{}1&{}&{}\\ \hline &{}&{}&{}1&{} &{}&{}\\ \hline &{}&{}&{}&{}&{}1&{}\\ \hline &{}&{}&{}&{}&{}&{}1\\ \end{array} \right] . \end{array} \end{aligned}$$

Then $(\varSigma (P))_{12}=1$, $(\varSigma (P))_{21}=0$ while $(\varSigma (\hat{P}(S)))_{12}=0$, $(\varSigma (\hat{P}(S)))_{21}=1$. So $\hat{P}(S) \not \preceq _B P$ and $P \not \preceq _B \hat{P}(S)$. $\square$

Remark 1

In [11] Fulton defined what he called the essential set of a $n\times n$ permutation matrix P corresponding to a permutation $\pi$ of $\{1,2,\ldots ,n\}$ as follows: Think of P as an $n\times n$ array of squares with one dot in each row and column and all other squares empty (corresponding to the 1’s and 0’s of P). For each dot in P shade all the squares from the dot and eastwards and from the dot and southwards leaving the diagram of unshaded squares of P. The essential set of P is the set of southeast corners of the connected components of the unshaded squares of the diagram. For example, we have

where the essential set consists of the squares with a $\star$ which are then replaced by the number of $\bullet$’s in the northwest submatrix they determine (equivalently, its rank).

Fulton shows that a permutation matrix is determined by these rank numbers and their locations, the ranked essential set and that, in general, none of these can be omitted. Notice that these rank numbers are entries of the sum-matrix of the permutation matrix P, corresponding to certain zeros of P. Thus these entries (with their locations) determine the permutation matrix P.

In [10] an algorithm is given that determines its ranked essential set. In [10] it is shown that a permutation matrix is determined by the rank function on a subset of its essential set called its core where the core has size at most n. In [9] it is proved that the average size of the essential set of an $n\times n$ permutation matrix is asymptotic to $\frac{n^2}{36}$. $\square$

We return to the notion of primary sum-sequence of a permutation matrix, and the algorithm given in the proof of Theorem 6. The following example implies that there may be no analogue of primary sum-sequence for ASMs.

Example 11

Consider the two $6\times 6$ ASMs

$$\begin{aligned} A_1=\left[ \begin{array}{r|r|r|r|r|r} &{}&{}&{}1&{}&{}\\ \hline &{}&{}1&{}&{}&{}\\ \hline &{}1&{}-1&{}&{}1&{}\\ \hline 1&{}&{}&{}-1&{}&{}1\\ \hline &{}&{}1&{}&{}&{}\\ \hline &{}&{}&{}1&{}&{}\end{array}\right] \quad \text{ and } \quad A_2=\left[ \begin{array}{r|r|r|r|r|r} &{}&{}&{}1&{}&{}\\ \hline &{}&{}1&{}&{}&{}\\ \hline &{}1&{}&{}-1&{}1&{}\\ \hline 1&{}&{}-1&{}&{}&{}1\\ \hline &{}&{}1&{}&{}&{}\\ \hline &{}&{}&{}1&{}&{}\end{array}\right] . \end{aligned}$$

Their sum-matrices are

Thus the sum-matrices $\varSigma (A_1)$ and $\varSigma (A_2)$ differ only in the the (3, 3)-entry shaded above. Hence if we try to mimic the algorithm given to determine a permutation matrix from its primary sum-sequence (in which a row is determined by the rows below it), it will fail when we transition from rows 6, 5, and 4 to row 3. $\square$

The notion of nests can be generalized to ASMs but, because of the presence of $-1$’s, the situation is more complicated.

Example 12

Consider the $8\times 8$ ASM

$$\begin{aligned} A=\left[ \begin{array}{r|r|r|r|r|r|r|r} &{}&{}1&{}&{}&{}&{}&{}\\ \hline &{}1&{}-1&{}&{}&{}1&{}&{}\\ \hline &{}&{}&{}1&{}&{}&{}&{}\\ \hline 1&{}-1&{}1&{}&{}&{}&{}&{}\\ \hline &{}1&{}-1&{}&{}1&{}&{}&{}\\ \hline &{}&{}1&{}-1&{}&{}&{}1&{}\\ \hline &{}&{}&{}&{}&{}&{}&{}1\\ \hline &{}&{}&{}1&{}&{}&{}&{}\end{array}\right] \end{aligned}$$

where

and the increases in each row (here we use rows rather than columns as we did for permutation matrices, and think of an initial column of all 0’s) are indicated again by shading the corresponding cells. For any ASM A, let $\varSigma (A)^*$ be the (0, 1)-matrix obtained from $\varSigma (A)$ by replacing each positive entry with a 1. Thus each row of $\varSigma (A)^*$ records the columns in which an increase occurs. For this example we have

$$\begin{aligned} \varSigma (A)^*=\left[ \begin{array}{c|c|c|c|c|c|c|c} &{}&{}1&{}&{}&{}&{}&{}\\ \hline &{}1&{}&{}&{}&{}1&{}&{}\\ \hline &{}1&{}&{}1&{}&{}1&{}&{}\\ \hline 1&{}&{}1&{}1&{}&{}1&{}&{}\\ \hline 1&{}1&{}&{}1&{}1&{}1&{}&{}\\ \hline 1&{}1&{}1&{}&{}1&{}1&{}1&{}\\ \hline 1&{}1&{}1&{}&{}1&{}1&{}1&{}1\\ \hline 1&{}1&{}1&{}1&{}1&{}1&{}1&{}1\end{array}\right] . \end{aligned}$$

Let $\alpha _1,\alpha _2,\ldots ,\alpha _8$ be the rows of $\varSigma (A)^*$ and define $\alpha _0=(0,0,0,0,0,0,0,0)$. So for $i=1,2,\ldots ,8$, $\alpha _i$ has its ones in the columns of each increase. Define $\alpha _0=(0,0,\ldots ,0)$. Then $\alpha _i-\alpha _{i-1}$ for $i=1,2,\ldots ,8$ are the rows of the ASM A. Moreover, $\alpha _1,\alpha _2,\ldots ,\alpha _8$ defines a saturated chain in the partially ordered set defined by Terwilliger [13] who shows that the saturated chains are in a one-to-one correspondence with the ASMs. This partially ordered set consists of all n-tuples of 0’s and 1’s with partial order defined by: $(a_1,a_2,\ldots ,a_n)\preceq (b_1,b_2,\ldots ,b_n)$ if and only if the difference sequence $(b_1-a_1,b_2-a_2,\ldots ,b_n-a_n)$ is a $(0,\pm 1)$-sequence. $\square$

Example 13

Consider the diamond ASM $D_7$:

$$\begin{aligned} D_7=\left[ \begin{array}{r|r|r|r|r|r|r} &{}&{}&{}1&{}&{}&{}\\ \hline &{}&{}1&{}-1&{}1&{}&{}\\ \hline &{}1&{}-1&{}1&{}-1&{}1&{}\\ \hline 1&{}-1&{}1&{}-1&{}1&{}-1&{}1\\ \hline &{}1&{}-1&{}1&{}-1&{}1&{}\\ \hline &{}&{}1&{}-1&{}1&{}&{}\\ \hline &{}&{}&{}1&{}&{}&{}\end{array}\right] \end{aligned}$$

where

Then $D_7$ corresponds to the saturated chain

$$\begin{aligned}&(0,0,0,1,0,0,0), (0,0,1,0,1,0,0), (0,1,0,1,0,1,0), (1,0,1,0,1,0,1),\\&(1,1,0,1,0,1,0), (1,1,1,0,1,1,1),(1,1,1,1,1,1,1). \end{aligned}$$

$\square$

5 Bruhat Lattice Properties of ASMs

If $A_1$ and $A_2$ are two $n\times n$ ASMs, then $\hbox {GLB}_{\mathcal {A}_n}\{A_1,A_2\}$ denotes the greatest lower bound of $A_1$ and $A_2$ in the lattice $(\mathcal {A}_n,\preceq _B)$. This greatest lower bound is the ASM whose sum matrix is the $n\times n$ matrix in which each entry equals the maximum of the corresponding entries of $A_1$ and $A_2$. The next example shows that $\hbox {GLB}_{\mathcal {A}_n}\{A_1,A_2\}$ may be a permutation matrix even though neither $A_1$ nor $A_2$ are permutation matrices.

Example 14

Let

$$\begin{aligned} A_1=\left[ \begin{array}{r|r|r|r} 1&{}&{}&{}\\ \hline &{}&{}1&{}\\ \hline &{}1&{}-1&{}1\\ \hline &{}&{}1&{}\end{array}\right] \quad \text{ and } \quad A_2=\left[ \begin{array}{r|r|r|r} &{}1&{}&{}\\ \hline 1&{}-1&{}1&{}\\ \hline &{}1&{}&{}\\ \hline &{}&{}&{}1\end{array}\right] . \end{aligned}$$

Then

$$\begin{aligned} \varSigma (A_1)=\left[ \begin{array}{r|r|r|r} 1&{}1&{}1&{}1\\ \hline 1&{}1&{}2&{}2\\ \hline 1&{}2&{}2&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] \quad \text{ and } \quad \varSigma (A_2)=\left[ \begin{array}{r|r|r|r} 0&{}1&{}1&{}1\\ \hline 1&{}1&{}2&{}2\\ \hline 1&{}2&{}3&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] . \end{aligned}$$

We have

$$\begin{aligned} \varSigma (\mathrm{GLB}_{\mathcal {A}_n}(A_1,A_2))= \left[ \begin{array}{c|c|c|c} 1&{}1&{}1&{}1\\ \hline 1&{}1&{}2&{}2\\ \hline 1&{}2&{}3&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] , \end{aligned}$$

and hence the increases correspond to a nested sequence and give the permutation matrix

$$\begin{aligned} \left[ \begin{array}{c|c|c|c} 1&{}&{}&{}\\ \hline &{}&{}1&{}\\ \hline &{}1&{}&{}\\ \hline &{}&{}&{}1\end{array}\right] . \end{aligned}$$

A permutation matrix and an ASM which is not a permutation matrix may have a greatest lower bound equal to a permutation matrix. For instance,

$$\begin{aligned} \left[ \begin{array}{c|c|c|c} &{}1&{}&{}\\ \hline 1&{}&{}&{}\\ \hline &{}&{}&{}1\\ \hline &{}&{}1&{}\end{array}\right] \quad \text{ and } \quad \left[ \begin{array}{r|r|r|r} 1&{}&{}&{}\\ \hline &{}&{}1&{}\\ \hline &{}-1&{}1&{}-1\\ \hline &{}&{}1&{}\end{array}\right] \end{aligned}$$

has $\hbox {GLB}_{\mathcal {A}_n}$ equal to

$$\begin{aligned} \left[ \begin{array}{c|c|c|c} 1&{}&{}&{}\\ \hline &{}1&{}&{}\\ \hline &{}&{}&{}1\\ \hline &{}&{}1&{}\end{array}\right] . \end{aligned}$$

$\square$

Example 15

Let $n=4$ and $\pi _1=(2431), \pi _2=(3241)$. Then the $\hbox {GLB}\{\pi _1,\pi _2\}=\tau =(2341)$. We have

$$\begin{aligned} \varSigma (\pi _1)= \left[ \begin{array}{l|l|l|l} 0&{} 1&{}1&{}1\\ \hline 0&{}1&{}1&{} 2\\ \hline 0&{}1&{} 2&{}3\\ \hline 1&{}2&{}3&{}4 \end{array} \right] , \; \varSigma (\pi _2)= \left[ \begin{array}{l|l|l|l} 0&{}0&{} 1&{}1\\ \hline 0&{}1&{}2&{}2\\ \hline 0&{}1&{}2&{}3\\ \hline 1&{}2&{}3&{}4 \end{array} \right] , \end{aligned}$$

and

$$\begin{aligned} \varSigma (\tau )= \left[ \begin{array}{l|l|l|l} 0&{}1&{}1&{}1\\ \hline 0&{}1&{}2&{}2\\ \hline 0&{}1&{}2&{}3\\ \hline 1&{}2&{}3&{}4 \end{array} \right] . \end{aligned}$$

In this case, both $\pi _1$ and $\pi _2$ cover $\tau$.

Another example is $\pi _1=(3421), \pi _2=(4312)$ where the $\hbox {GLB}\{\pi _1,\pi _2\} =\tau =(3412)$. We have

$$\begin{aligned} \varSigma (\pi _1)= \left[ \begin{array}{l|l|l|l} 0&{}0&{}1&{}1\\ \hline 0&{}0&{}1&{}2\\ \hline 0&{}1&{}2&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] , \; \varSigma (\pi _2)= \left[ \begin{array}{l|l|l|l} 0&{}0&{}0&{}1\\ \hline 0&{}0&{}1&{}2\\ \hline 1&{}1&{}2&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] \end{aligned}$$

and

$$\begin{aligned} \varSigma (\tau )= \left[ \begin{array}{l|l|l|l} 0&{}0&{}1&{}1\\ \hline 0&{}0&{}1&{}2\\ \hline 1&{}1&{}2&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] . \end{aligned}$$

In this case, both $\pi _1$ and $\pi _2$ also cover $\tau$. $\square$

So, if we take two permutations $\pi _1$ and $\pi _2$ of $\{1,2,\ldots ,n\}$, and form the entrywise maximum of the entries of $\varSigma (\pi _1)$ and $\varSigma (\pi _2)$ to get a matrix $M=\varSigma (\pi _1)\vee \varSigma (\pi _2)$, then M is the sum-matrix of the ASM $\hbox {GLB}_{\mathcal {A}_n}\{\pi _1,\pi _2\}$. Then $\hbox {GLB}_{\mathcal {A}_n}\{\pi _1,\pi _2\}$ is not a permutation matrix if and only if in some row of M, there are two or more increases that were not increases in the previous row, see further discussion below.

Now consider the two permutations $\pi _1=(3241)$ and $\pi _2=(4132)$ with $\hbox {GLB}_{\mathcal {A}_n}\{\pi _1,\pi _2\}=\tau =(3142)$. We have

$$\begin{aligned} \varSigma (\pi _1)=\left[ \begin{array}{c |c|c|c} 0&{}0&{} 1&{}1\\ \hline 0&{} 1&{}2&{}2\\ \hline 0&{}1&{}2&{} 3\\ \hline 1&{}2&{}3&{}4\end{array}\right] , \quad \varSigma (\pi _2)=\left[ \begin{array}{c|c|c|c} 0&{}0&{}0&{} 1\\ \hline 1&{}1&{}1&{}2\\ \hline 1&{}1&{} 2&{}3\\ \hline 1&{} 2&{}3&{}4\end{array}\right] , \end{aligned}$$

and

$$\begin{aligned} \varSigma (\tau )=\left[ \begin{array}{c|c|c|c} 0&{}0&{} 1&{}1\\ \hline 1&{}1&{}2&{}2\\ \hline 1&{}1&{}2&{} 3\\ \hline 1&{} 2&{}3&{}4\end{array}\right] . \end{aligned}$$

In this case, neither $\pi _1$ nor $\pi _2$ covers $\tau$. There is an ASM different from a permutation between $\pi _1$ and $\tau$ (namely, the ASM corresponding to 13 in the Hasse diagram of $(\mathcal {A}_4,\preceq _B))$, and another ASM different from a permutation between $\pi _2$ and $\tau$ (the ASM corresponding to 42 in the Hasse diagram of $(\mathcal {A}_4,\preceq _B)$). (Note that e.g., 42 in the diagram denotes a $4\times 4$ ASM with a 1 in position (4, 2) which is uniquely completable to an ASM by using the only $3\times 3$ ASM with a $-1$).

For small values of n we have enumerated all permutation matrices of order n, and computed the $\hbox {GLB}_{\mathcal {A}_n}$ of each pair of such matrices. The following table shows how many pairs that have a $\hbox {GLB}_{\mathcal {A}_n}$ which is a permutation matrix, and this number is denoted by $\#$P. The other pairs have a $\hbox {GLB}_{\mathcal {A}_n}$ which is an ASM different from a permutation matrix, and their number is denoted by $\#$ASM.

n	n!	$n!(n!-1)/2$	$\#$P	$\#$ASM
2	2	1	1	0
3	6	15	14	1
4	24	276	231	45
5	120	7140	5136	2004
6	720	258840	154385	104455

Next we characterize when the $\hbox {GLB}_{\mathcal {A}_n}$ of a set of permutation matrices is a permutation matrix. Let $P_1, P_2, \ldots , P_k$ be permutation matrices of order n, and let $A=[a_{ij}]= \mathrm{GLB}_{\mathcal {A}_n}\{P_1,P_2, \ldots , P_k\}$. Define $\varSigma (A)=[\hat{\sigma }_{ij}]$ and $\varSigma (P_t)=[\sigma ^{(t)}_{ij}]$ ($t \le k$). Thus, $\hat{\sigma }_{ij}=\max _t \sigma ^{(t)}_{ij}$ for each i, j. Also define for $1<i,j<n$

$$\begin{aligned} \begin{array}{rll} K_{ij}&{}=&{}\{t \le k: \sigma ^{(t)}_{ij}=\hat{\sigma }_{ij}\}, \\ I(i,j)&{}=&{}\{(i,1), \ldots , (i,j-1)\}, \\ J(i,j)&{}=&{}\{(1,j), \ldots , (i-1,j)\}. \end{array} \end{aligned}$$

With this notation, we have the following result.

Proposition 1

Let $P_1, P_2, \ldots , P_k$ be permutation matrices of order n, and let $A= \mathrm{GLB}_{\mathcal {A}_n}\{P_1,P_2, \ldots , P_k\}$.

Then A is a permutation matrix if and only if there is no position (i, j), with $1<i,j<n$, such that (a) for some $s\in K_{i-1,j-1}$ the matrix $P_s$ has a 1 in I(i, j), but no 1 in J(i, j), (b) for some $t\in K_{i-1,j-1}$ the matrix $P_t$ has a 1 in J(i, j), but no 1 in I(i, j), and (c) no $P_l$$(l \le k)$ has a 1 in position (i, j), or a 1 in both $I_1$ and in $I_2$.

Proof

The matrix $A=[a_{ij}]$ is a permutation matrix if and only if there is no position (i, j), with $1<i,j<n$, such that $a_{ij}=-1$. Using the properties of $\varSigma (A)=[\hat{\sigma }_{ij}]$, i.e., that $\varSigma (A)$ is nondecreasing in rows and columns, and the increase is at most 1, we see that $a_{ij}=-1$ if and only if, for some integer m,

$$\begin{aligned} \hat{\sigma }_{i-1,j-1}=m, \;\; \hat{\sigma }_{i-1,j}=\hat{\sigma }_{i,j-1}=\hat{\sigma }_{i,j}=m+1. \end{aligned}$$

But these equations correspond precisely to the statements (a)–(c) in the proposition. $\square$

Example 16

Let $n=4$ and let

$$\begin{aligned} P_1=\left[ \begin{array}{c|c|c|c} &{}1&{}&{}\\ \hline &{}&{}&{}1\\ \hline &{}&{}1&{}\\ \hline 1&{}&{}&{}\end{array}\right] \quad \text{ and } \quad P_2=\left[ \begin{array}{c|c|c|c} &{}&{}&{}1\\ \hline 1&{}&{}&{}\\ \hline &{}&{}1&{}\\ \hline &{}1&{}&{}\end{array}\right] . \end{aligned}$$

Then

$$\begin{aligned} \varSigma (P_1)=\left[ \begin{array}{r|r|r|r} 0&{}1&{}1&{}1\\ \hline 0&{}1&{}1&{}2\\ \hline 0&{}1&{}2&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] \quad \text{ and } \quad \varSigma (P_2)=\left[ \begin{array}{r|r|r|r} 0&{}0&{}0&{}1\\ \hline 1&{}1&{}1&{}2\\ \hline 1&{}1&{}2&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] . \end{aligned}$$

Then

$$\begin{aligned} \varSigma \left( \mathrm{GLB}_{\mathcal {A}_n}\{P_1,P_2\}\right) = \left[ \begin{array}{c|c|c|c} 0&{}1&{}1&{}1\\ \hline 1&{}1&{}1&{}2\\ \hline 1&{}1 &{}2&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] , \end{aligned}$$

whose corresponding ASM is

$$\begin{aligned} \left[ \begin{array}{r|r|r|r} 0&{}1&{}0&{}0\\ \hline 1&{}-1&{}0&{}1\\ \hline 0&{}0&{}1&{}0\\ \hline 0&{}1&{}0&{}0\end{array}\right] . \end{aligned}$$

In view of Proposition 1 consider $i=j=2$, and $k=2$. Then $K_{1,1}=\{1,2\}$ (as $\hat{\sigma }_{11}=0$) and $P_2$ satisfies condition (a) as it has a 1 in $I(2,2)=\{(2,1)\}$, and $P_1$ satisfies condition (b) due to the 1 in $I(2,2)=\{(1,2)\}$. Moreover, condition (c) holds, so the proposition also shows that $\mathrm{GLB}_{\mathcal {A}_n}\{P_1,P_2\}$ is not a permutation matrix. $\square$

The next result determines when the greatest lower bound of a set of permutation matrices is equal to the identity matrix $I_n$.

Theorem 11

Let $P_1, P_2, \ldots , P_k$ be permutation matrices of order n, and let $A= \mathrm{GLB}_{\mathcal {A}_n}\{P_1,P_2, \ldots , P_k\}$. Then $A=I_n$ if and only if for each $k=1, 2, \ldots , n-1$, there exists a $t \le k$ such that the leading $k \times k$ submatrix of $P_t$ is a permutation matrix.

Proof

Let $\varSigma (A)=[\hat{\sigma }_{ij}]$ and $\varSigma (P_t)=[\sigma ^{(t)}_{ij}]$ ($t \le k$). Assume $A=I_n$. Then $\varSigma (A)=\varSigma (I)$ is symmetric and

$$\begin{aligned} \hat{\sigma }_{ij}=i \;\;\;(i \le n, \;j=i, i+1, \ldots , n). \end{aligned}$$

(12)

Therefore

$$\begin{aligned} i=\hat{\sigma }_{ii}=\max _{t \le k} {\sigma }^{(t)}_{ii}={\sigma }^{(s)}_{ii} \end{aligned}$$

for some $s \le t$. So, the permutation matrix $P_s$ has i ones in its leading $i \times i$ submatrix, and therefore this submatrix must be a permutation matrix.

Conversely, assume that for each $k=1, 2, \ldots , n-1$ there exists a $t \le k$ such that the leading $k \times k$ submatrix of $P_t$ is a permutation matrix. This implies that

$$\begin{aligned} \hat{\sigma }_{ii}=\max _{t \le k} {\sigma }^{(t)}_{ii}=i \;\;\;(i \le n). \end{aligned}$$

Since rows and columns of $\varSigma (A)$ are nondecreasing and the last entry in row i, and in column i, is i, it follows that $\varSigma (A)$ satisfies (12). So, $A=I$, as desired. $\square$

Example 17

Let $n=4$ and let

$$\begin{aligned} P_1=\left[ \begin{array}{c|c|c|c} &{}1&{}&{}\\ \hline 1&{}&{}&{}\\ \hline &{}&{}1&{}\\ \hline &{}&{}&{}1\end{array}\right] \quad \text{ and } \quad P_2=\left[ \begin{array}{c|c|c|c} 1&{}&{}&{}\\ \hline &{}&{}1&{}\\ \hline &{}&{}&{}1\\ \hline &{}1&{}&{}\end{array}\right] . \end{aligned}$$

Then

$$\begin{aligned} \varSigma (P_1)=\left[ \begin{array}{r|r|r|r} 0&{}1&{}1&{}1\\ \hline 1&{}2&{}2&{}2\\ \hline 1&{}2&{}3&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] \quad \text{ and } \quad \varSigma (P_2)=\left[ \begin{array}{r|r|r|r} 1&{}1&{}1&{}1\\ \hline 1&{}1&{}2&{}2\\ \hline 1&{}1&{}2&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] . \end{aligned}$$

Then

$$\begin{aligned} \varSigma \left( \mathrm{GLB}_{\mathcal {A}_n}\{P_1,P_2\}\right) = \left[ \begin{array}{c|c|c|c} 1&{}1&{}1&{}1\\ \hline 1&{}2&{}2&{}2\\ \hline 1&{}2 &{}3&{}3\\ \hline 1&{}2&{}3&{}4\end{array}\right] , \end{aligned}$$

which gives $\mathrm{GLB}_{\mathcal {A}_n}\{P_1,P_2\}=I$. The leading $k \times k$ submatrix of $P_1$ is a permutation matrix for $k=2,3$ (and 4), while the leading $k \times k$ submatrix of $P_2$ is a permutation matrix for $k=1$ (and 4). $\square$

Another way to formulate Theorem 11 is:

Let$P_1, P_2, \ldots , P_k$be permutation matrices of ordern, and let

$$\begin{aligned} A= \mathrm{GLB}_{\mathcal {A}_n}\{P_1,P_2, \ldots , P_k\}. \end{aligned}$$

Then$A=I_n$if and only if for each$k=1, 2, \ldots , n-1$there exists a$t \le k$such that thekth term in$\chi (P_t)$equalsk, that is, thekth term in$\chi (I_n)$.