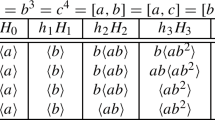Difference Sets Disjoint from a Subgroup

Abstract

We study finite groups G having a non-trivial, proper subgroup H and $D \subset G {\setminus } H, D \cap D^{-1}=\emptyset ,$ such that the multiset $\{ xy^{-1}:x,y \in D\}$ has every non-identity element occur the same number of times (such a D is called a difference set). We show that $|G|=|H|^2$, and that $|D \cap Hg|=|H|/2$ for all $g \notin H$. We show that H is contained in every normal subgroup of index 2, and other properties. We give a 2-parameter family of examples of such groups. We show that such groups have Schur rings with four principal sets, and that, further, these difference sets determine DRADs.

1 Introduction

For a group G we will identify a finite subset $X \subseteq G$ with the element $\sum _{x \in X} x \in {\mathbb {Q}} G$ of the group algebra. We also let $X^{-1}=\{x^{-1}:x \in X\}$. Also, write ${\mathcal {C}}_n$ for the cyclic group of order n. All groups considered herein will be assumed finite.

A $(v,k,\lambda )$difference set is a subset $D \subset G, |D|=k$, where G is a group such that every element $1 \ne g \in G$ occurs $\lambda$ times in the multiset $\{xy^{-1}:x,y \in D\}$. Further, $|G|=v$.

It is well-known that if $D \subset G$ is a difference set, then $gD=\{gd:d \in D\}$ and $\alpha (D)$ are also difference sets, for any $g \in G, \alpha \in \mathrm {Aut}(G)$. Thus in some sense, difference sets are spread out evenly over the group G. In this paper we seek to restrict the types of difference sets considered by imposing the following conditions:

We assume that $D \subset G$ is a $(v,k,\lambda )$ difference set where there is a subgroup $1\ne H \le G$ and $m \ge 0$ such that

• (1) $D \cap D^{-1}=Hg_1\cup \dots \cup Hg_m$;

• (2) $G {\setminus } (D \cup D^{-1})=H \cup Hg_1'\cup \dots \cup Hg_m'$.

Here $H, Hg_1,\dots , Hg_m, Hg_1',\dots , Hg_m'$ are distinct cosets of H. Let

$$\begin{aligned} h=|H|,\quad u=|G:H|. \end{aligned}$$

Then we have $h>1$. Following Webster [22], who considers the $m=0$ case, a group having a difference set of the above type will be called a $(v,k,\lambda )_m$DRAD difference set group (with difference set D and subgroup H). See also [5, 14, 15] for more on DRADs.

Recall that a group G has a skew Hadamard difference set if it has a difference set D where $G=D\cup D^{-1} \cup \{1\}$ and $D \cap D^{-1}=\emptyset$. Such groups have been studied in [2,3,4,5, 7,8,9,10, 12].

Theorem 1.1

Let G be a $(v,k,\lambda )_m$ DRAD difference set group with subgroup H and difference set D. Then

• (i) $m=0, h=u$ is even, $v=|G|=h^2$, and

  $$\begin{aligned} \lambda =\frac{1}{4} {h(h-2)},\,\,\, k=\frac{1}{2} h(h-1); \end{aligned}$$

• (ii) each non-trivial coset $Hg\ne H$ meets D in h / 2 points;

• (iii) H contains the normal subgroup generated by all the involutions in G.

Examples of such groups are given in $\S 8$. We conjecture that G is always a 2-group and that H is always a normal subgroup.

We note that Davis and Polhill [5] consider such difference sets, however, they are mostly concerned with the abelian case. They also note (ii) of Theorem 1.1.

Let $\Phi (G)$ be the Frattini subgroup of G, the intersection of all the maximal subgroups of G. We have the following result concerning maximal subgroups of G:

Theorem 1.2

Let G be a $(v,k,\lambda )_0$ DRAD difference set group with subgroup H and difference set D. Then

• (a) If $K \le G, |G:K|=2$, then $H \le K$ and $|K \cap D|=\lambda$.

• (b) Now assume that G is also a 2-group. Then $H \le \Phi (G)$. Further, D meets each maximal subgroup of G in exactly $\lambda$ points.

• (c) If $K \triangleleft G, |G:K|=p$, where p is an odd prime, then $H \le K$ and $|K \cap D|=\frac{1}{2} \frac{h(h-p)}{p}$.

Our original motivation for studying $(v,k,\lambda )_0$ DRAD difference set groups was to produce examples of Schur rings with a small number of principal sets.

A subring ${\mathfrak {S}}$ of the group algebra ${\mathbb {C}} G$ is called a Schur ring (or S-ring) [19, 20, 23, 24] if there is a partition $\mathcal {K}=\{C_i\}_{i=1}^r$ of G such that the following hold:

• 1. $\{1_G\}\in \mathcal {K}$;

• 2. for each $C\in \mathcal {K}$, $C^{-1}\in \mathcal {K}$;

• 3. ${C_i}\cdot {C_j}=\sum _k \lambda _{i,j,k} {C_k}$; for all $i,j \le r$.

The $C_i$ are called the principal sets of ${\mathfrak {S}}$. Then, as in [5, Theorem 3.3], we have:

Theorem 1.3

Let G be a $(v,k,\lambda )_0$ DRAD difference set group with difference set D and subgroup H. Then

$$\begin{aligned} \{1\}, \,\, H {\setminus } \{1\},\,\,D,\,\, D^{-1}, \end{aligned}$$

are the principal sets of a commutative Schur-ring over G.

Theorem 1.3 allows us to show

Theorem 1.4

Let G be a $(v,k,\lambda )_0$ DRAD difference set group with difference set D and subgroup H. Then the minimal polynomial for D is

$$\begin{aligned} \mu (D)=(x-k)\left( x+\frac{h}{2}\right) \left( x^2+\frac{h^2}{4}\right) . \end{aligned}$$

Further, the eigenvalues $k, -h/2,ih/2,-ih/2$ have multiplicities

$$\begin{aligned} 1,\,\,\,h-1,\,\,\, h(h-1)/2,\,\,, h(h-1)/2 \,\,\,\, \text {(respectively)}. \end{aligned}$$

We next give examples of families of non-abelian $(v,k,\lambda )_0$ DRAD difference set groups. Let $n \ge 2, 0 \le k<n-1$ and define the following bi-infinite family of groups:

$$\begin{aligned} {\mathfrak {G}}_{n,k}&=\langle a_1,\dots ,a_n,b_1,\dots ,b_n| a_i^2=b_{i+k}, 1\le i\le n, (\hbox { indices taken mod}\ n), \\ a_{2}^{a_1}&=a_{2}b_1, a_{3}^{a_1}=a_{3}b_2,\dots ,a_{k+1}^{a_1}=a_{k+1}b_k,\\ (a_1,a_{k+2})&=(a_1,a_{k+3})=\dots =(a_1,a_n)=1,\\ (a_i,a_j)&=1, \text { for } 1<i,j\le n, \text { and } b_1,\dots ,b_n \text{ are } \text{ central } \text{ involutions } \rangle . \end{aligned}$$

We will show:

Theorem 1.5

For $n \ge 2, 0 \le k<n-1,$ the group ${\mathfrak {G}}_{n,k}$ is a DRAD difference set group with $H=\langle b_1,\dots ,b_n\rangle$.

We note that in [5, Theorem 1.6] the authors show a similar result for abelian groups containing a ${\mathcal {C}}_2^n$ subgroup. The main point of [5] is to construct Doubly Regular Asymmetric Digraphs (DRADs), and they show that a difference set D determines a DRAD if $1_G \notin D$; and (ii) $D \cap D^{-1}=\emptyset$. Thus any DRAD difference set group will determine a DRAD. Thus Theorem 1.5 gives examples of DRADs that come from non-abelian groups.

Theorem 1.6

• (i) Any abelian group that is a DRAD difference set group is a 2-group.

• (ii) Let G be an abelian DRAD difference set group of order $h^2$. Then the exponent of G is at most h.

We note results of Kraemer, Jedwab, and Turyn [16, 18, 21] that say that a group of order $2^{2d+2}$ with a difference set must have exponent no more than $2^{d+2}$. Thus the above bound for DRAD difference set groups is smaller than their general bound.

We note that the difference sets that we study satisfy the parameter condition given by Kesava Menon in [17], and so (in this case, their complements) are examples of what are known as Menon difference sets. Thus the groups ${\mathfrak {G}}_{n,k}$ determine a 2-parameter family of non-abelian Menon difference sets.

2 Results Concerning the Parameters

In this section we prove Theorem 1.1 (i).

Let

$$\begin{aligned} A=Hg_1\cup \dots \cup Hg_m, \quad B=Hg_1'\cup \dots \cup Hg_m', \end{aligned}$$

and $D=A+D_1, D^{-1}=A+D_1^{-1},$ where $A \cap D_1=\emptyset$. Thus we have

$$\begin{aligned} |A|=|B|=hm,\quad |D|=k=hm+|D_1|. \end{aligned}$$

Then from (1) and (2) of $\S 1$ we obtain $G=H+B+D_1+A+D_1^{-1}.$ Thus we have

$$\begin{aligned} v=|G|=h+hm+|D_1|+hm+|D_1^{-1}|=h+2hm+2|D_1|=h+2k. \end{aligned}$$

Solving $v=hu, k(k-1)=\lambda (v-1), v=h+2k$ gives $\lambda =\frac{1}{4} \frac{(hu-h)(hu-h-2)}{hu-1}\in {\mathbb {N}}.$

Then $\frac{1}{4} \frac{(hu-h)(hu-h-2)}{hu-1}\in {\mathbb {N}}$ implies that $\frac{(hu-1-(u-1))(hu-1-(u+1)) }{hu-1 } \in {\mathbb {N}}$, which gives $x:=\frac{u^2-1}{hu-1} \in {\mathbb {N}}$. Thus $x(hu-1)=u^2-1$, which implies $x \equiv 1 \mod u$. But $1\le x= \frac{u^2-1}{hu-1} \le \frac{u}{h} +1<u+1$, and so $x \equiv 1 \mod u$ gives $x=1$, and so $h=u$. Then $\lambda =\frac{1}{4} \frac{(hu-h)(hu-h-2)}{hu-1}= \frac{1}{4} h(h-2)$, so that h is even.

It follows that there are $u-1=h-1$ non-trivial right cosets $Hg_1,Hg_2,\dots ,Hg_{h-1}.$ Let $d_i:=|D \cap Hg_i|,1\le i<h$. Then

$$\begin{aligned} \sum _{i=1}^{h-1} d_i=k=\frac{h(h-1)}{2} \,\,\, \mathrm{implies\,\,\, that }\,\,\, \frac{\sum _{i=1}^{h-1} d_i}{h-1}=\frac{h}{2}. \end{aligned}$$

Also

$$\begin{aligned} \sum _{i=1}^{h-1} d_i^2=\lambda (|H|-1)+k=(h-1)\frac{h^2}{4} \,\,\, \mathrm{implies\,\,\, that }\,\,\, \sqrt{ \frac{\sum _{i=1}^{h-1} d_i^2}{h-1}}=\frac{h}{2}. \end{aligned}$$

Then using well-known facts about quadratic and arithmetic means we conclude that $d_i=h/2,1\le i<h$. In particular, $D \cap D^{-1}$ cannot contain a coset of H; this gives $m=0$. This concludes the proof of Theorem 1.1 (i), (ii).

3 Basic Relations

Let D be the difference set where $G=D \cup D^{-1}\cup H, H \le G, D \cap H=D \cap D^{-1}=\emptyset$. Let $g_1=1,g_2,\dots ,g_h$ be coset representatives for G / H. Order the elements of G according to the cosets $Hg_1,Hg_2,\dots ,Hg_h$.

Then thinking of D, H and G as matrices via the regular representation (relative to the above order of G) we have

$$\begin{aligned} G=D+D^{-1}+H,\qquad D\cdot D^{-1}=\lambda G+(k-\lambda )\cdot 1. \end{aligned}$$

(3.1)

Note that the fact that $D^{-1}$ is also a difference set [11, p. 57], together with the last equation of (3.1), gives $DD^{-1}=D^{-1}D$.

Now solving for $D^{-1}$ from the first equation of (3.1), and using $DG=kG$, the second equation gives

$$\begin{aligned} (k-\lambda )(G-1)=D^2+DH. \end{aligned}$$

(3.2)

However (since $D^{-1}$ is also a difference set) we can interchange D and $D^{-1}$ so as to obtain

$$\begin{aligned} (k-\lambda )(G-1)=(D^{-1})^2+D^{-1}H. \end{aligned}$$

(3.3)

Now taking the inverse of Eq. (3.2) we have

$$\begin{aligned} (k-\lambda )(G-1)=(D^{-1})^2+HD^{-1}. \end{aligned}$$

(3.4)

Thus from Eqs. (3.3) and (3.4) we must have $D^{-1}H=HD^{-1}$; taking inverses gives $DH=HD.$

Thus from the above, $D,G,H,D^{-1}$ all commute, and $D^{-1}=D^T$ shows that $D, D^{-1}$ are normal matrices. Clearly H is a normal matrix. Thus we have

Lemma 3.1

The matrices D, H, G are commuting normal matrices and are simultaneously diagonalizable. $\square$

Now $|D \cap Hg|=\frac{h}{2}$ for all $g \notin H$, and so gives

$$\begin{aligned} DH=HD=\frac{h}{2} (G-H). \end{aligned}$$

(3.5)

For Theorem 1.1 (iii) we note that if $g \in G$ is an involution that is not in H, then $g \in D \cap D^{-1}$, a contradiction. This now concludes the proof of Theorem 1.1. $\square$

4 H and Subgroups of Index p

We prove Theorem 1.2 (a).

From Theorem 1.1 we know that $|G|=h^2, k=\frac{h(h-1)}{2},\lambda =\frac{h(h-2)}{4}$. Let $M\le G$ be a subgroup of index 2 and let $\pi :G \rightarrow G/M=\langle t:t^2=1\rangle$ be the quotient map. Let $|D \cap M|=d_1, |H \cap M|=h_1,$ so that

$$\begin{aligned} \pi (D)=d_1\cdot 1+(k-d_1)t,\quad \pi (H)=h_1\cdot 1 +(h-h_1) t. \end{aligned}$$

Let $d_2=k-d_1, h_2=h-h_1.$ Then we have the equations

$$\begin{aligned}&d_1+d_2=k,\quad h_1+h_2=h, \quad k=h(h-1)/2,\quad \lambda =h(h-2)/4. \end{aligned}$$

(4.1)

Now from Eqs. (3.2) and (3.5) we deduce that $D^2=\lambda G+\frac{h}{2}H-(k-\lambda )1.$ Taking the image of this under $\pi$, and using the fact that $\pi (D)=d_11+d_2t$, we obtain two equations (by looking at the coefficients of 1 and t):

$$\begin{aligned}&d_1^2+d_2^2=\lambda h^2/2+hh_1/2+\lambda -k; \quad 2d_1d_2=\lambda h^2/2+hh_2/2. \end{aligned}$$

(4.2)

Now $D+D^{-1}=G-H$ gives (by acting by $\pi$)

$$\begin{aligned}&2d_1+2d_2t=h^2/2(1+t)-(h_1+h_2t), \end{aligned}$$

which gives

$$\begin{aligned}&2d_1=h^2/2-h_1,\quad 2d_2=h^2/2-h_2. \end{aligned}$$

(4.3)

Solving Eqs. (4.1), (4.2), (4.3) we find that

$$\begin{aligned} h_1=h,\quad h_2=0,\quad d_1=\lambda ,\quad d_2=k-\lambda . \end{aligned}$$

Thus D meets M in $\lambda$ points, and all of H is in M.

If G is a 2-group then any maximal subgroup M has index 2, and we see that H is contained in M, and thus is in the Frattini subgroup. This gives Theorem 1.2 (b).

Let $N\triangleleft G$ be of index p, an odd prime. Let $\pi :G \rightarrow Q=G/N\equiv {\mathcal {C}}_p=\langle t\rangle$ be the quotient map. We let

$$\begin{aligned} \pi (D)=\sum _{i=0}^{p-1}x_it^i,\quad \pi (H)=\sum _{i=0}^{p-1}y_it^i, \end{aligned}$$

where $x_i,y_i \in {\mathbb {Z}}^{\ge 0}$ and $\sum _{i=0}^{p-1} x_i=k, \sum _{i=0}^{p-1}y_i=h.$

We may represent elements of Q as matrices where the generator t corresponds to the $p \times p$ matrix $U:=\begin{pmatrix} 0&{}1&{}0&{}0&{}\dots &{}0 \\ 0&{}0&{}1&{}0&{}\dots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\ddots &{}\dots &{}0 \\ 0&{}0&{}0&{}\dots &{}0&{}1 \\ 1&{}0&{}0&{}\dots &{}0&{}0 \end{pmatrix}.$ Then we can simultaneously diagonalize $\pi (D),\pi (D^{-1}),\pi (G),\pi (H)$ using the matrix $R=(\zeta ^{(i-1)(j-1)})$ (see [6]), where $\zeta =\exp {2\pi i/p}$:

$$\begin{aligned} R^{-1}\pi (G)R&= \mathrm{diag}(h^2,0,0,\dots ,0);\\ R^{-1}\pi (H)R&= \mathrm{diag} \left( \sum _{i=0}^{p-1}y_i, \sum _{i=0}^{p-1}y_i\zeta ^i, \sum _{i=0}^{p-1}y_i\zeta ^{2i}, \dots ,\right. \\&\left. \quad \sum _{i=0}^{p-1}y_i\zeta ^{(i(p-2)},\sum _{i=0}^{p-1}y_i\zeta ^{i(p-1)}\right) ;\\ R^{-1}\pi (D)R&= \mathrm{diag} \left( \sum _{i=0}^{p-1}x_i, \sum _{i=0}^{p-1}x_i\zeta ^i, \sum _{i=0}^{p-1}x_i\zeta ^{2i}, \dots ,\right. \\&\left. \quad \sum _{i=0}^{p-1}x_i\zeta ^{(i(p-2)},\sum _{i=0}^{p-1}x_i\zeta ^{i(p-1)}\right) ;\\ R^{-1}\pi (D^{-1})R&= \mathrm{diag} \left( \sum _{i=0}^{p-1}x_i, \sum _{i=0}^{p-1}x_i\zeta ^{-i}, \sum _{i=0}^{p-1}x_i\zeta ^{-2i}, \dots ,\right. \\&\left. \quad \sum _{i=0}^{p-1}x_i\zeta ^{(-i(p-2)},\sum _{i=0}^{p-1}x_i\zeta ^{-i(p-1)}\right) . \end{aligned}$$

From $H^2=hH$ we see that the minimal polynomial of H is $x(x-h)$, and so the minimal polynomial of $\pi (H)$ is a divisor of $x(x-h)$. In particular, the eigenvalues of $\pi (H)$ are either 0 or h. Now we know that $\sum _{i=0}^{p-1}y_i=h$, and for $1\le j\le p-1$ we must also have

$$\begin{aligned} \sum _{i=0}^{p-1}y_i\zeta ^{ij} \in \{0,h\}. \end{aligned}$$

(4.4)

We rewrite Eq. (4.4) as

$$\begin{aligned} \begin{pmatrix} 1&{}1&{}1&{}1&{}\dots &{}1\\ 1&{}\zeta &{}\zeta ^2&{}\zeta ^3&{}\dots &{}\zeta ^{p-1}\\ 1&{}\zeta ^{2}&{}\zeta ^{4}&{}\zeta ^6&{}\dots &{}\zeta ^{2(p-1)}\\ \vdots &{}\vdots &{}\vdots &{}\dots &{}\vdots \\ 1&{}\zeta ^{p-1}&{}\zeta ^{2(p-1)}&{}\zeta ^{3(p-1)}&{}\dots &{}\zeta ^{(p-1)^2} \end{pmatrix} \begin{pmatrix} y_0\\ y_1\\ y_2\\ y_3\\ \vdots \\ y_{p-1} \end{pmatrix} = \begin{pmatrix} h\\ 0 \text{ or } h\\ 0 \text{ or } h\\ 0 \text{ or } h\\ \vdots \\ 0 \text{ or } h \end{pmatrix}. \end{aligned}$$

(4.5)

Let T denote the matrix in (4.5). Now, since p is an odd prime, the minimal polynomial for $\zeta$ is $\sum _{i=0}^{p-1}x^i$ and $y_0,\dots ,y_{p-1} \in {\mathbb {Q}}$. Thus it follows from Eq. (4.5) that either (a) $y_0=y_1=y_2=\dots =y_{p-1}\ne 0$, or (b) $y_1=y_2=\dots =y_{p-1}=0$.

If we have (b), then $y_0=h,y_1=y_2=\dots =y_{p-1}=0$ and we are done. We now show that (a) is not possible. Assuming (a) we get $y_0=y_1=y_2=\dots =y_{p-1}=h/p.$ Thus $H=\frac{h}{p} J_p$, so that $\pi (H)=\mathrm{diag} (h,0,0,\dots ,0).$

Now from $\pi (D) \pi (D^{-1})=\lambda \pi (G) +(k-\lambda )$ we get

$$\begin{aligned}&\mathrm{diag} \left( \left( \sum _{i=0}^{p-1} x_i\right) ^2, \left( \sum _{i=0}^{p-1} x_i\zeta ^i\right) \left( \sum _{i=0}^{p-1} x_i\zeta ^{-i}\right) , \dots , \nonumber \right. \\&\left. \qquad \left( \sum _{i=0}^{p-1} x_i\zeta ^{i(p-1)}\right) \left( \sum _{i=0}^{p-1} x_i\zeta ^{-i(p-1)}\right) \right) \nonumber \\&\quad =\lambda \times \mathrm{diag}( h^2,0,0,\dots ,0)+ (k-\lambda ) \times \mathrm{diag}( 1,1,\dots ,1). \end{aligned}$$

(4.6)

The equation $\pi (D)+\pi (D^{-1})= \pi (G)-\pi (H)$ gives

$$\begin{aligned}&\mathrm{diag} \left( 2\sum _{i=0}^{p-1}x_i, \sum _{i=0}^{p-1}x_i(\zeta ^i+\zeta ^{-i}), \sum _{i=0}^{p-1}x_i(\zeta ^{2i}+\zeta ^{-2i}),\dots ,\right. \nonumber \\&\left. \qquad \sum _{i=0}^{p-1}x_i(\zeta ^{i(p-1)}+\zeta ^{-i(p-1})\right) \nonumber \\&\quad =\mathrm{diag} \left( h^2-h,0,0,\dots ,0\right) \end{aligned}$$

(4.7)

From the (2, 2) entry of (4.7) we get

$$\begin{aligned}&2x_0+(x_1+x_{p-1})(\zeta +\zeta ^{-1})+ (x_2+x_{p-2})(\zeta ^2+\zeta ^{-2})\nonumber \\&\quad +\dots + (x_{(p-1)/2}+x_{(p+1)/2})(\zeta ^{(p-1)/2}+\zeta ^{-(p-1)/2})=0. \end{aligned}$$

(4.8)

Again using the fact that the minimal polynomial for $\zeta$ is $\sum _{i=0}^{p-1}x^i$ we see that

$$\begin{aligned} 2x_0=x_1+x_{p-1}=x_2+x_{p-2}=\dots = x_{(p-1)/2}+x_{(p+1)/2}. \end{aligned}$$

Since $\sum _{i=0}^{p-1} x_i=k$ this gives

$$\begin{aligned} x_0=\frac{1}{p} k. \end{aligned}$$

Now by taking traces of the left and right hand sides of (4.6) we easily see that

$$\begin{aligned} \mathrm {Trace}(\pi (D) \pi (D^{-1}))=p\left( \sum _{i=0}^{p-1}x_i^2\right) =\lambda h^2+p(k-\lambda )= \frac{1}{4} \,{h}^{2} \left( {h}^{2}-2\,h+p \right) . \end{aligned}$$

(4.9)

Now the $x_i \in {\mathbb {Z}}$ and so from the (2, 2) entry of (4.6) we have (taking the real part)

$$\begin{aligned} \sum _{i=0}^{p-1}x_i^2=k-\lambda . \end{aligned}$$

(4.10)

Using (4.9) and (4.10) gives $\frac{1}{4} \,{h}^{2} \left( {h}^{2}-2\,h+p \right) =p(k-\lambda ),$ which simplifies to

$$\begin{aligned} \frac{1}{4} \,{h}^{3} \left( h-2 \right) =0, \end{aligned}$$

a contradiction. Thus (a) is not possible.

Now, assuming (b) again, the analogue of (4.8) is

$$\begin{aligned}&2x_0+(x_1+x_{p-1})(\zeta +\zeta ^{-1})+ (x_2+x_{p-2})(\zeta ^2+\zeta ^{-2})\\&\quad +\dots + (x_{(p-1)/2}+x_{(p+1)/2})(\zeta ^{(p-1)/2}+\zeta ^{-(p-1)/2})=-h. \end{aligned}$$

Thus

$$\begin{aligned} 2x_0+h=x_1+x_{p-1}=x_2+x_{p-2}=\dots = x_{(p-1)/2}+x_{(p+1)/2}. \end{aligned}$$

(4.11)

Since $\sum _{i=0}^{p-1} x_i=k$ Eq. (4.11) gives $px_0+\frac{h}{2} (p-1)=k.$ Solving we obtain $x_0=\frac{1}{2} \frac{h(h-p)}{p}.$ This completes the proof of Theorem 1.2. $\square$

5 The Schur Ring and Minimal Polynomials

We have $(G-H)^{-1}=G-H, (H-1)^{-1}=H-1,(D^{-1})^{-1}=D$, and so we just need to show that $D,D^{-1},H-1,1$ commute and span the ring that they generate. We have already seen in Lemma 3.1 that they commute. We have $H\cdot G=hG, D\cdot G=kG=D^{-1}\cdot G.$ Using Eqs. (3.2) and (3.5) we get

$$\begin{aligned} D^2=(k-\lambda )(G-1)-\frac{h}{2} (G-H). \end{aligned}$$

We collect together the rest of the products that we need:

$$\begin{aligned}&HD=DH=\frac{h}{2} (G-H);\quad H^2=hH,\\ {}&D^2=(k-\lambda )(G-1)-\frac{h}{2} (G-H) =(k-\lambda -\frac{h}{2} )(D+D^{-1})+(k-\lambda ) (H-1),\\ {}&D\cdot D^{-1}=D^{-1}\cdot D=\lambda G+(k-\lambda )1=\lambda D+\lambda D^{-1}+\lambda (H-1)+k1. \end{aligned}$$

Since $k=h(h-1)/2,\lambda =h(h-2)/4, k-\lambda =h^2/4\in {\mathbb {Z}},$ one can check that all the coefficients in the above sums are non-negative integers. This proves that $D,D^{-1},H-1,1$ commute and span the ring that they generate. Theorem 1.3 follows. $\square$

For a matrix or an element M of an algebra we let $\mu (M)$ denote the minimal polynomial of M. To help us find $\mu (D)$ we have the equations

$$\begin{aligned}&G=D+D^{-1}+H,\quad DD^{-1}=\lambda G+(k-\lambda ),\quad DH=\frac{h}{2} (G-H),\\&D^{-1}H=\frac{h}{2} (G-H),\quad D^2=(k-\lambda )(G-1)-\frac{h}{2} (G-H). \end{aligned}$$

Using these one can show that

$$\begin{aligned}&D^3=\frac{h^2}{4}D^{-1}+\left( \frac{1}{8} h^4-\frac{3}{8} h^3+\frac{1}{4} h^2\right) G;\\ {}&D^4=\left( \frac{1}{16}h^6-\frac{1}{4} h^5+\frac{3}{8} h^4-\frac{1}{4} h^3\right) G+\frac{1}{16} h^4. \end{aligned}$$

Using these relations one finds that D satisfies the polynomial $(x-k)\left( x+\frac{h}{2}\right) \left( x^2+\frac{h^2}{4}\right)$. Thus $\mu (D)$ divides this polynomial.

We note that $\frac{1}{k} D$ is a stochastic matrix, and since $D^2=(k-\lambda )(G-1)-\frac{h}{2} (G-H)$ it follows that

Lemma 5.1

The matrix $\frac{1}{k} D$ is an irreducible doubly stochastic matrix.$\square$

Further, we know that $\mu (D)$ factors as a product of distinct linear factors $(x-\kappa )$, where $\kappa$ is an eigenvalue (since D is diagonalizable by Lemma 3.1).

Next we note that k is an eigenvalue of D, since each row sum and column sum of D is k. Next we show that $-h/2$ is an eigenvalue of D: for $g \notin H$ we have $H-Hg \ne 0$ and

$$\begin{aligned} D\cdot ( H-Hg)&=DH(1-g)=\frac{h}{2} (G-H)(1-g)\\&=\frac{h}{2} (G-H-G+Hg)=-\frac{h}{2} (H-Hg). \end{aligned}$$

Thus $-\frac{h}{2}$ is an eigenvalue for D.

Since D is a matrix with real entries it follows that the eigenspaces for eigenvalues $\pm ih/2$ have the same dimension, and that either $\mu (D)=(x-k)(x+h/2)$ or $\mu (D)=(x-k)(x+h/2)(x^2+\frac{h^2}{4}).$ If $\mu (D)=(x-k)(x+h/2)$, then, since D is diagonalizable, Lemma 5.1 and the Perron Frobenius theorem show that D has eigenvalue k with multiplicity one, and $-h/2$ with multiplicity $h^2-1$. Now, since $D \cap H =\emptyset ,$ we see that D has trace zero. Thus we must have

$$\begin{aligned} k+(h^2-1)(-h/2)=0, \end{aligned}$$

but the lefthand side of this expression is $-h^2(h-1)$, which gives a contradiction. Thus $\mu (D)=(x-k)(x+h/2)(x^2+\frac{h^2}{4})$ and it easily follows from Trace$(D)=0$ that the eigenvalue $-h/2$ has multiplicity $h-1$. It then follows that $\pm ih/2$ have multiplicity k / 2 (since they have the same multiplicity). This proves Theorem 1.4.$\square$

6 Examples of DRAD Difference Set Groups

The groups ${\mathfrak {G}}_{n,k}$ have been defined in the introduction. We now show that they are DRAD difference set groups with $H=\langle b_1,b_2,\dots ,b_n\rangle .$ Now a transversal for H in G is the set of products $a_{i_1}a_{i_2}\cdots a_{i_u}$, where these are indexed by the sequences $i_1<i_2<\cdots <i_u$ of $1,2,\dots ,n$, or in other words, indexed by the subsets $X=\{i_1,i_2,\dots ,i_u\}$ of $\{1,2,\dots ,n\}$. We let $a_X=a_{i_1}a_{i_2}\cdots a_{i_u}$ denote the corresponding element of G. Here $a_\emptyset =1$. We may also employ a similar notation for the elements $b_X=b_{i_1}b_{i_2}\cdots b_{i_u}$.

We note that for any $g \in G$ we have $g^2 \in H$. We define the hypothesis

(H1): there is a set of distinct maximal subgroups $M_1,\dots ,M_{2^n-1}$ of H, and an ordering $S_1,\dots ,S_{2^n-1}$ of the non-empty subsets of $\{1,\dots ,n\}$ so that $a_{S_i}^2 \notin M_i$.

Proposition 6.1

The groups ${\mathfrak {G}}_{n,k}$ satisfy (H1).

Proof

We first show that the squares of the coset representatives $a_S, S \subseteq \{1,2,\dots ,n\}$, are distinct. We note that the subgroup $J=\langle a_2,a_3,\dots ,a_n\rangle$ is isomorphic to ${\mathcal {C}}_4^{n-1}$. We also have $J \triangleleft {\mathfrak {G}}_{n,k}$, so that ${\mathfrak {G}}_{n,k}=J\rtimes \langle a_1\rangle =J \rtimes {\mathcal {C}}_4$.

If $S \subseteq \{1,2,\dots ,n\}$ and $m \in {\mathbb {Z}}$ we let $S+m$ be the set $\{u+m:u \in S\}$, where we take numbers mod n so that $S+m \subseteq \{1,2,\dots ,n\}$.

Now for a coset representative $a_S, S=\{i_1,i_2,\dots ,i_u\} \subseteq \{2,\dots ,n\},$ we have $a_S \in J$ and so from the relations in ${\mathfrak {G}}_{n,k}$ we have

$$\begin{aligned} a_S^2=b_{i_1+k}b_{i_2+k}\dots b_{i_u+k}=b_{S+k}. \end{aligned}$$

We note that in this situation, since $1 \notin S$, we have $1+k \notin S+k$.

Now for a coset representative $a_S$ that is not in J we can write $S=\{1,i_1,i_2,\dots ,i_u\}$, where $a_{S {\setminus } \{1\}}\in J$. So if we let $K=S {\setminus } \{1\}$, then $a_S=a_1a_K$.

Now write $K=K_1\cup K_2$, where the elements $a_m,m \in K_2,$ commute with $a_1$, and those $a_m,m \in K_1,$ do not. Note that

$$\begin{aligned} K_1\subseteq \{2,\dots ,k+1\}, \,\,\,\, K_1 \cap K_2=\emptyset ,\,\,\,\, S=\{1\} \cup K_1 \cup K_2. \end{aligned}$$

Then from the relations in ${\mathfrak {G}}_{n,k}$ we have: $a_{K_2}^{a_1}=a_{K_2}, a_{K_1}^{a_1}=a_{K_1}b_{K_1-1}.$ Thus we have

$$\begin{aligned} a_S^2= (a_1a_{K_1}a_{K_2})^2&=a_1^2a_{K_1}^{a_1}a_{K_1}a_{K_2}^2 =b_{1+k}\cdot a_{K_1}b_{K_1-1}\cdot a_{K_1}\cdot a_{K_2}^2\nonumber \\&=b_{1+k}b_{K_1-1}b_{K_1+k}b_{K_2+k}=b_{K_1-1}b_{S+k}. \end{aligned}$$

(6.1)

We next show that $b_{1+k}$ has non-zero exponent in (6.1). But from the above we know that $K_1 \subseteq \{2,3,\dots ,k+1\},$ so that $1+k \notin K_1-1.$ If $1+k \in K_i+k, i=1,2,$ then $1 \in K_i,$ a contradiction. This shows that $b_{1+k}$ has non-zero exponent in (6.1).

Note that in the above we have also shown (i) of

Lemma 6.2

With the above definitions we have:

• (i) the element $b_{1+k}$ occurs with non-zero coefficient in $a_S^2$ if and only if $1 \in S$.

• (ii) The squares $a_S^2, S \subseteq \{1,2,\dots ,n\}$, where $1 \in S,$ are distinct.

Proof

(ii) We need to show that the map $S \mapsto b_{K_1-1}b_{S+k}$ is injective.

We represent S as a (column) vector $v_S \in V={\mathbb {F}}_2^n$, where the ith coordinate of $v_S$ is 1 if and only if $i \in S$. Then the action on V of replacing S by $S+1$ is determined by the $n \times n$ permutation matrix

$$\begin{aligned} P=\begin{pmatrix} 0&{}0&{}\dots &{}0&{}1\\ 1&{}0&{}\dots &{}0&{}0\\ 0&{}1&{}\dots &{}0&{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}\dots &{}1&{}0 \end{pmatrix}. \end{aligned}$$

Thus for any $i \in {\mathbb {Z}}$ we have

$$\begin{aligned} v_{S+i}=P^iv_S. \end{aligned}$$

Let $0_{k,m}$ denote the $k \times m$ zero matrix, and let $0_k=0_{k,k}$. If $k\le 0$ or $m \le 0$, then $0_{k,m}$ will be the empty matrix. Then, the map $S \mapsto K_1$, is determined by the $n \times n$ matrix

$$\begin{aligned} A=\mathrm {diag}(0_{1},I_k,0_{n-k-1}), \end{aligned}$$

so that $v_{K_1}= Av_S.$

Thus the map $S \mapsto b_{K_1-1}b_{S+k}$ is represented by the matrix $P^{-1}A+P^k,$ and we will be done if we can show that $P^{-1}A+P^k$ is a non-singular matrix in GL$(2,{\mathbb {F}}_2)$. But this is the same as showing that $B:=A+P^{k+1}$ is non-singular, where

$$\begin{aligned}&B= \begin{pmatrix} 0_1&{}0_{1,k}&{}0_{1,n-k-1}\\ 0_{k,1}&{}I_k&{}0_{k,n-k-1}\\ 0_{n-k-1,1}&{}0_{n-k-1,k}&{}0_{n-k-1} \end{pmatrix}+ \begin{pmatrix} 0_{1,n-k-1}&{}1&{}0_{1,k}\\ 0_{k,n-k-1}&{}0_{k,1}&{}I_k\\ I_{n-k-1}&{}0_{n-k-1,1}&{}0_{n-k-1,k} \end{pmatrix}. \end{aligned}$$

(6.2)

We note that since $k<n-1$ the second matrix is not a diagonal matrix, and that the submatrix $I_k$ in the second matrix of Eq. (6.2) occurs to the right of the diagonal. (This shows that $A+P^{k+1}$ is singular when $k=n-1$.) Thus the $I_k$ in the second matrix of Eq. (6.2) can be used to column-reduce the $I_k$ in the first matrix to zero. This shows that $A+P^{k+1}$ column-reduces to $P^{k+1}$, which is non-singular, and we are done.$\square$

Let $V^\times ={\mathbb {F}}_2^n {\setminus } \{0\}$. Then non-empty subsets of S correspond bijectively to elements of $V^\times$, as explained above. Further, maximal subgroups of H correspond to subspaces of V of dimension $n-1$, which, in turn, are determined by elements of $V^\times$: a vector $v \in V^\times$ determines the subspace $M_v=\{u \in V|u\cdot v=0\}$, where $\cdot$ is the usual dot-product on V taking values in ${\mathbb {F}}_2$. Since V is a vector space over ${\mathbb {F}}_2$ the correspondence $v \leftrightarrow M_v$ is bijective. Further, given a maximal subgroup (or subspace) M we let $v_M$ denote the corresponding vector.

Thus the correspondence of subsets with maximal subgroups that we require is $S \leftrightarrow M_S$ where $v_S \leftrightarrow v_{M_S}$, with $v_S \notin M_S$ i.e. $v_S \cdot v_{M_S}=1$. But this correspondence determines a function

$$\begin{aligned} \mu :V^\times \rightarrow V^\times , \text{ where } v_u\cdot v_{\mu (u)}=1 \text{ for } \text{ all } u \in V^\times . \end{aligned}$$

Conversely, such a function determines the correspondence that we want. We now show how to construct such a function:

Lemma 6.3

For all $n\in {\mathbb {N}}, V={\mathbb {F}}_2^n,$ there is a function $\mu :V^\times \rightarrow V^\times$ such that $u\cdot {\mu (u)}=1$ for all $u \in V^\times .$

Proof

We will show that there is a function $\mu$ that is an involution i.e. where we have $\mu (\mu (v))=v$ for all $v \in V^\times$. For $0 \le k\le n$ we let

$$\begin{aligned} ({\underline{1}}_k,0)=(1,1,1,\dots ,1,0,\dots ,0) \in V^\times , \end{aligned}$$

where there are k 1s (so for $k=0$ we have the zero vector of V).

Write $v \in V^\times$ as $v=(v_1,v_2,\dots ,v_n), v_i \in {\mathbb {F}}_2$. If $1\le k\le n$ where $v_k=1$ and $v_m=0$ for $k+1\le m\le n$, then we let

$$\begin{aligned} \mu (v)=({\underline{1}}_{k-1},0)-v, \end{aligned}$$

This satisfies $\mu (v)\cdot v=1$, as required. Further, since the same k works for $\mu (v)$, we have

$$\begin{aligned} \mu (\mu (v))= (1_{k-1},0)-((1_{k-1},0)-v)=v. \end{aligned}$$

This defines a function $\mu$ that is an involution.$\square$

Lemma 6.3 determines the pairing for hypothesis (H1) for the groups ${\mathfrak {G}}_{n,k}$, and concludes the proof of Proposition 6.1.$\square$

We will next show

Proposition 6.4

The groups ${\mathfrak {G}}_{n,k}$ are DRAD difference set groups.

Proof

We first note that since $b_1,\dots ,b_n$ are central involutions, all the maximal subgroups of H are normal subgroups of G.

As usual, subsets S of G will correspond to elements $\sum _{s \in S} s$, of the group algebra. We define D as follows:

$$\begin{aligned} D=\sum _{i=1}^{2^n-1} a_{S_i}M_i. \end{aligned}$$

Let $a_i=a_{S_i}$. We first show that $(a_iM_i)^{-1}=a_i(H-M_i).$ But this is true if and only if $a_i^{-1}M_i=a_i(H-M_i)$ if and only if $M_i=a_i^2(H-M_i)$ if and only if $M_i=H-a_i^2M_i$. But this latter equation is true since $a_i^2 \in H$ and $a_i^2 \notin M_i$.

Thus we have:

$$\begin{aligned} D^{-1}=\sum _{i=1}^{2^n-1}a_{S_i}(H-M_i). \end{aligned}$$

Let $1\le i\ne j\le 2^n-1$; then, since $M_i, M_j$ are distinct maximal subgroups of $H \cong {\mathcal {C}}_2^n$, we have $M_iM_j=2^{n-2}H,$ so that for $1\le i\ne j\le 2^n-1$ we have

$$\begin{aligned} M_i(H-M_j)=2^{n-1}H-2^{n-2}H=2^{n-2}H. \end{aligned}$$

We use this to obtain:

$$\begin{aligned} D\cdot D^{-1}&=\left( \sum _{i=1}^{2^n-1} a_{S_i}M_i\right) \left( \sum _{i=1}^{2^n-1}a_{S_i}(H-M_i)\right) \nonumber \\&=\sum _{1\le i \ne j\le n}^{2^n-1}a_{S_i}M_ia_{S_j}(H-M_j) + \sum _{1\le i \le n}^{2^n-1}a_{S_i}^2M_i(H-M_i) \nonumber \\&=2^{n-2}\sum _{1\le i \ne j\le n}^{2^n-1}a_{S_i}a_{S_j}H+ \sum _{1\le i \le n}^{2^n-1}a_{S_i}^2(2^{n-1}H-2^{n-1}M_i) \nonumber \\&=2^{n-2}\sum _{1\le i \ne j\le n}^{2^n-1}a_{S_i}a_{S_j}H+2^{n-1} \sum _{1\le i \le n}^{2^n-1}a_{S_i}^2(H-M_i) \end{aligned}$$

(6.3)

Since $|{\mathfrak {G}}_{n,k}|=2^{2n}, h=|H|=2^n$ we have $k=2^{n-1}(2^n-1),\, \lambda = 2^{n-1}(2^{n-1}-1).$

Returning to Eq. (6.3), in particular looking at the first sum of Eq. (6.3), we see that every non-trivial coset of H occurs $2^n-2$ times in Eq. (6.3). Thus from Eq. (6.3) we see that the coefficient in $DD^{-1}$ of each element of that coset is

$$\begin{aligned} 2^{n-2}(2^n-2)=2^{n-1}(2^{n-1}-1)=\lambda , \end{aligned}$$

as we desire.

The second sum of Eq. (6.3) gives the contributions to the trivial H-coset. We rewrite it as

$$\begin{aligned} 2^{n-1} \sum _{1\le i \le n}^{2^n-1}a_{S_i}^2(H-M_i)= 2^{n-1} \sum _{1\le i \le n}^{2^n-1}(H-a_{S_i}^2M_i). \end{aligned}$$

(6.4)

But we are assuming that $a_{S_i}^2\notin M_i$, so we must have $H-a_{S_i}^2M_i=M_i.$ Thus Eq. (6.4) is

$$\begin{aligned} 2^{n-1} \sum _{1\le i \le n}^{2^n-1}M_i. \end{aligned}$$

(6.5)

Now since the $M_i$ are distinct maximal subgroups, and there are $2^n-1$ of them, we see that every maximal subgroup of $H\cong {\mathcal {C}}_2^n$ is in the list $M_1,\dots , M_{2^n-1}$, and so one has

$$\begin{aligned} \sum _{1\le i \le 2^n-1}M_i=(2^n-1)\cdot 1 +(2^{n-1}-1)(H-1). \end{aligned}$$

Thus if $h' \in H, h' \ne 1,$ then the coefficient of $h'$ in Eq. (6.5) is

$$\begin{aligned} 2^{n-1}(2^{n-1}-1)=\lambda , \end{aligned}$$

as required. The coefficient of 1 in $D \cdot D^{-1}$ is then

$$\begin{aligned} k^2-\lambda (|{\mathfrak {G}}_{n,k}|-1)=2^{2n-2}(2^{n-1}-1)^2-2^{n-1}(2^{n-1}-1)(2^{2n}-1), \end{aligned}$$

which is equal to k, as required. Thus we have $D \cdot D^{-1}=\lambda (G-1)+k\cdot 1.$$\square$

7 Abelian Groups

Proof of Theorem 1.6 (i)

So suppose that G is abelian, that h is not a power of 2 and let p be an odd prime divisor of h. Let $g \in H$ be an element of order $p^u, u\ge 1$, where $\langle g\rangle \cong {\mathcal {C}}_{p^u},$ is a factor of the Sylow p-subgroup of H. Then $H={\mathcal {C}}_{p^u} \times U$, where U is some subgroup of H. Here $U \ne 1$ since 2|h.

Let $\psi$ be a character of H that does not kill g, but where $\chi (U)=1$. We then note that $\psi (H)=0$.

By [13, Corollary 5.5, p. 63] we can extend $\psi$ to an irreducible character $\chi$ of G that take values in some ${\mathbb {Q}}(\zeta _{p^v}), v \ge u$. Then we have $\chi (H)=\psi (H)=0$. Also $\chi (G)=0$. Now we have $G=D+D^{-1}+H$, so that

$$\begin{aligned} 0=\chi (G)=\chi (D)+\chi (D^{-1})+\chi (H)=\chi (D)+\chi (D^{-1}). \end{aligned}$$

Thus $\chi (D)=-\chi (D^{-1})$. We also have $\chi (D)\chi (D^{-1})=\lambda G+(k-\lambda )$, so that

$$\begin{aligned} -\chi (D)^2=k-\lambda =h^2/4. \end{aligned}$$

Thus $\chi (D)=\pm i h/2 \in {\mathbb {Q}}(i).$ But $\chi (D) \in {\mathbb {Q}}(\zeta _{p^v})$, and ${\mathbb {Q}}(\zeta _{p^v}) \cap {\mathbb {Q}}(i)={\mathbb {Q}},$ since p is an odd prime, so that $\pm ih/2 \in {\mathbb {Q}}$, a contradiction.$\square$

Proposition 7.1

• (i) If G is a semi-direct product of the form $G= N \rtimes {\mathcal {C}}_2, {\mathcal {C}}_2=\langle t\rangle$, then G is not a DRAD difference set group.

• (ii) Suppose that $G=K \rtimes {\mathcal {C}}_{2r}$ with subgroup H where ${\mathcal {C}}_{2r} \le H$. Then G is not a DRAD difference set group with subgroup H.

• (iii) Let p be an odd prime. Let G be a DRAD difference set group with subgroup H and difference set D. Then G is not a semi-direct product, $G= N \rtimes {\mathcal {C}}_p, {\mathcal {C}}_p=\langle t\rangle \le H.$

Proof

(i) Suppose it is, with subgroup H and difference set D. Let $\chi : G \rightarrow {\mathbb {C}}$ be the linear character where $\chi (t)=-1,\chi (N)=1$.

Since $t^2=1$ we see that $t \in H$, which then shows that $\chi (H)=0=\chi (G)$. Since $D+D^{-1}=G-H$ we get $\chi (D)+\chi (D^{-1})=0,$ so that $\chi (D^{-1})=-\chi (D)$. Thus $DD^{-1}=\lambda G+k-\lambda$ gives $\chi (D)\chi (D^{-1})=k-\lambda =h^2/4.$ Thus $\chi (D)=\pm ih/2.$ But $\chi (D) \in {\mathbb {Q}}$, since $D \in {\mathbb {Z}}{\mathbb {G}}$ and $\chi$ takes values in $\{\pm 1\}$. This contradiction concludes the proof of (i) and (ii), (iii) follow similarly.$\square$

Proof of Theorem 1.6 (ii)

Let the abelian DRAD difference set group G have difference set D and subgroup $H, |H|=h$. We know from Theorem 1.6 (i) that G has to be a 2-group. So assume that the exponent of G is $h2^u,$ where $u \ge 1$. Since G is abelian we may write $G={\mathcal {C}}_{h2^u} \times L$, where ${\mathcal {C}}_{h2^u}=\langle t\rangle$. Then we have $|L|=h/2^u \le h/2$.

If $|H\cap L|=h/2$, then we would have $L \le H$, and so a generator of one of the maximal cyclic subgroups of L would be in H. This would contradict Proposition 7.1 (ii). Thus we see that $|H \cap L| \le h/4.$

Let $K=\langle t^{h2^u/2}\rangle$, a subgroup of order 2. Then $K \le H$ and if $H \subset KL$, then $|H \cap L|=h/2$, which is a contradiction. Thus $H \not \subseteq KL$. Let $\alpha =t^sg_0 \in H {\setminus } KL$, where $g_0 \in L$. Then $t^s$ has order $2^v\ge 4$. Let $\alpha ':=\alpha ^{2^v/4}=t^{s2^v/4}g_0^{2^v/4}$, where $t^{s2^v/4}$ has order 4. Further, since $\alpha \in H$ we have $\alpha '=\alpha ^{2^v/4} \in H$, but since $t^{s2^v/4}$ has order 4 we also see that $\alpha ^{2^v/4} \not \in KL$. Thus we have $\alpha '=t^{s2^v/4}g_0'$ where $g_0' \in L$ and $t^{s2^v/4}$ has order 4. It follows that $s2^v/4=h2^u/4$ or $s2^v/4=3h2^u/4$. By replacing $\alpha '$ by its inverse, if necessary, we can assume that $\alpha '=t^{h2^u/4}g_0'.$

Define $\zeta =\exp \frac{2\pi i}{h2^u}$ and define the character $\chi$ by

$$\begin{aligned} \chi (t)=\zeta ,\qquad \chi (L)=1. \end{aligned}$$

Since $\alpha ' \in H$ and is not in the kernel of $\chi$ we see that $\chi (H)=0$. Since $G-H=D+D^{-1}$ it follows that $\chi (D)=-\chi (D^{-1})$, and so from $DD^{-1}=\lambda G+(k-\lambda )$ we obtain $\chi (D)^2=-h^2/4,$ so that $\chi (D)=\pm i h/2$. Replacing D with $D^{-1}$ as necessary we may assume $\chi (D)=ih/2.$

Now define

$$\begin{aligned} X_j=| t^jL \cap D|, \quad 0 \le j \le 2^{h2^u}-1. \end{aligned}$$

Then we clearly have $X_j \le |L|\le \frac{h}{2}.$ Also $\chi (D)=\sum _{j=0}^{h2^u-1} X_j\zeta ^j.$

Now from $\chi (D)=ih/2$ we have

$$\begin{aligned}&X_0+X_1\zeta ^1+X_2\zeta ^2+\dots + X_{h2^u/4-1}\zeta ^{h2^u/4-1}+X_{h2^u/4} i +X_{h2^u/4+1}\zeta ^{h2^u/4+1}\\ {}&\quad +\dots +X_{h2^u/2-1}\zeta ^{h2^u/2-1}-X_{h2^u/2}-X_{h2^u/2+1}\zeta ^{1}-X_{h2^u/2+2}\zeta ^{2}\\ {}&\quad -\dots -X_{3h2^u/4-1}\zeta ^{h2^u/4-1} -X_{3h2^u/4} i -X_{3h2^u/4+1}\zeta ^{h2^u/4+1}\\ {}&\quad -\dots -X_{h2^u-1}\zeta ^{h2^u/2-1}=ih/2. \end{aligned}$$

Using the fact that $1,\zeta ,\zeta ^2,\dots ,\zeta ^{h2^u/2-1}$ is a basis for ${\mathbb {Q}}(\zeta )/{\mathbb {Q}}$, and by looking at the coefficient of i in the above, we see that $X_{h2^u/4}-X_{3h2^u/4}=h/2.$ Thus

$$\begin{aligned} X_{h2^u/4}=X_{3h2^u/4}+h/2 \ge h/2. \end{aligned}$$

(7.1)

Recall that $X_{h2^u/4}=|t^{h2^u/4}L \cap D|.$ Here we note that $\alpha '=t^{h2^u/4}g_0' \in H,$ and since $H \cap D = \emptyset$ we thus have $\alpha ' \notin t^{h2^u/4}L \cap D$ and so does not contribute to the sum that gives $X_{h2^u/4}$. It follows that $X_{h2^u/4} <h/2$ contradicting Eq. (7.1). This contradiction gives the result.$\square$

Examples from [22, Theorem 9.3] show that the bound on the exponent given in Theorem 1.6 is strict.

8 Examples

Here we give a number of examples of non-abelian DRAD difference set groups that are not covered by the examples ${\mathfrak {G}}_{n,k}$. We use notation for groups of small order from Magma [1].

Example 8.1

$G=G_{64,3}, H \cong {\mathcal {C}}_2 \times {\mathcal {C}}_4, G/H \cong {\mathcal {C}}_2 \times {\mathcal {C}}_4.$ Here

$$\begin{aligned}&G=\langle a,b,c,d,e,f| a^2 = c, b^2 = d, c^2 = e, d^2 = f, e^2 = 1, f^2 = 1, b^a = b e,\\&\quad c^a = c, c^b = c, d^a = d, d^b = d, d^c = d, e^a = e, e^b = e, e^c = e, e^d = e,\\&\quad f^a = f, f^b = f, f^c = f, f^d = f, f^e = f\rangle , \quad H=\langle d,e\rangle ,\\&D=\{ a f, a b c d e f, a b c e, a d f, a e f, a d e f, a b c d, a b c f, b d f, b d e f, b d, b c e, b c d e f,\\&\quad b d e, b c d e, b c e f, c e, c e f, c d, c d f, a c e, a c d e f, a b d f, a c, a b, a c d f, a b d e, a b e f \}. \end{aligned}$$

Example 8.2

$G=G_{64,14}, H \cong {\mathcal {C}}_2 \times {\mathcal {C}}_4, G/H \cong D_8$. Here

$$\begin{aligned}&G=\langle a,b,c,d,e,f| a^2 = d, b^2 = f, c^2 = f, d^2 = e f, e^2 = 1, f^2 = 1, b^ a = b c,\\ {}&\quad c^ a = c e, c^ b = c f, d^ a = d, d^ b = d e f, d^c = d, e^ a = e, e^ b = e, e^c = e, e^d = e,\\ {}&\quad f^ a = f, f^ b = f, f^c = f, f^d = f, f^e = f \rangle ,\quad H=\langle cd,f\rangle ,\\ {}&D=\{ a b e f, a b f, b f, b e, b d, a e, a b c, a c e, b c d f, a c d f, a b c e f, a b c d e, b d e f, b c d e, d,\\ {}&\quad a d e, d e, a b c e, b c e, a b c d, a c e f, c e f, c f, a e f, a b c f, a d e f, b c f, a c d \}. \end{aligned}$$

Example 8.3

$G=G_{64,15}, H \cong {\mathcal {C}}_2 \times {\mathcal {C}}_4, G/H \cong D_8$.

Here

$$\begin{aligned}&G=\langle a,b,c,d,e,f| a^2 = d, b^2 = f, c^2 = f, d^2 = e f, e^2 = 1, f^2 = 1, b^a = b c,\\ {}&\quad c^a = c e, c^b = c f, d^a = d, d^b = d e f, d^c = d, e^a = e, e^b = e, e^c = e, e^d = e,\\ {}&\quad f^a = f, f^b = f, f^c = f, f^d = f, f^e = f \rangle , \quad H=\langle d,e\rangle \\ {}&D=\{ a b e f, b e f, b f, c d e, a e, b c, c d e f, a c e, a b d e, c e, b c d f, b d e f, a c, a d,\\ {}&\quad a b c d e f, b c d e f, a b c e, b c e, a b c d, a d f, a b, a c e f, c e f, a c f, a e f, a b c f, a b d f, b d f\}. \end{aligned}$$

Example 8.4

$G=G_{64,16}, H \cong {\mathcal {C}}_2 \times {\mathcal {C}}_4, G/H \cong D_8$. Here

$$\begin{aligned}&G=\langle a,b,c,d,e,f| a^2 = d, b^2 = c e, c^2 = e, d^2 = f, e^2 = 1, f^2 = 1, b^a = b c,\\ {}&\quad c^a = c e, c^b = c, d^a = d, d^b = d, d^c = d, e^a = e, e^b = e, e^c = e, e^d = e,\\ {}&\quad f^a = f, f^b = f, f^c = f, f^d = f, f^e = f \rangle ,\quad H=Z(G)=\langle d,e\rangle \\ {}&D=\{ b c, b c d f, b f, b c e, b d f, b e f, b d e f, b c d e f, a b c, a b f, a b e, a b c e f, c e, c d e f, \\ {}&\quad c d e, c e f, a d f, a c f, a c e, a d, a c, a c e f, a e, a e f, a b d f, a b c d, a b c d e f, a b d e\} \end{aligned}$$

Example 8.5

$G=G_{64,20}, H \cong {\mathcal {C}}_2 \times {\mathcal {C}}_2 \times {\mathcal {C}}_2, G/H \cong D_8$. Here

$$\begin{aligned}&G=\langle a,b,c,d,e,f| a^2 = d, b^2 = e, c^2 = f, d^2 = 1, e^2 = 1, f^2 = 1, b^a = b c,\\ {}&\quad c^a = c f, c^b = c, d^a = d, d^b = d, d^c = d, e^a = e f, e^b = e, e^c = e, e^d = e,\\ {}&\quad f^a = f, f^b = f, f^c = f, f^d = f, f^e = f \rangle , \quad H=Z(G)=\langle d,e,f\rangle \\ {}&D=\{ b d e f, a c d e, a b d e f, b c d e, b, a b c d e, a c d e f, b c d e f, a f, a b c d e f, b f, c f,\\ {}&a b c, b c f, a d, b d, a c d, a b d f, c d f, a c d f, a e, a b e, a b e f, c e f, a d e, b c e f, a b c e f, c d e \} \end{aligned}$$

We have also found over 400 DRAD groups of order 256.