On the Chromatic Edge Stability Number of Graphs

Abstract

The chromatic edge stability number $es _{\chi }(G)$ of a graph G is the minimum number of edges whose removal results in a graph $H \subseteq G$ with chromatic number $\chi (H) = \chi (G) - 1$. The chromatic bondage number $\rho (G)$ of G is the minimum number of edges between any two color classes in a $\chi (G)$-coloring of G, where the minimum is taken over all $\chi (G)$-colorings of G. In this paper, we characterize graphs for which these two parameters coincide. Moreover, we give general bounds and we determine these parameters for several classes of graphs.

1 Introduction

We consider in this paper finite simple graphs. If $G = (V(G),E(G))$ is a graph, a function $c : V(G) \rightarrow \{1,\dots ,k\}$ such that $c(u) \ne c(v)$ if $uv \in E(G)$ is called a proper coloring of G. If such a function exists, then G is called k-colorable, while elements in the image of c are called colors. Note that a proper coloring c can be uniquely described by the k partition sets of V(G) which we call color classes, written as ${\mathcal {C}} = (C_1,\ldots ,C_k)$. We call both the function c and the partition ${\mathcal {C}}$ a k-coloring of G.

The minimum k for which G is k-colorable is the chromatic number of G, which is denoted by $\chi (G)$. Then G is called k-chromatic. By a $\chi$-coloring of G we mean a coloring of G with $\chi (G)$ colors. The following parameters are introduced in [1, 3].

Definition 1.1

[1, 3] The chromatic edge stability number $es _{\chi }(G)$ of a nonempty graph G is defined to be the minimum number of edges of G whose removal results in a graph $H \subseteq G$ with $\chi (H) = \chi (G) - 1$. If G is empty (that is, $E(G) = \emptyset$), then we set $es _{\chi }(G) = 0$.

Definition 1.2

[1] The minimum number of edges between any two color classes in a $\chi$-coloring of a graph G, where the minimum is taken over all $\chi$-colorings of G, is called chromatic bondage number of G and is denoted by $\rho (G)$. If G is empty, then we set $\rho (G) = 0$.

Let us denote by t(G) the minimum number of vertices in a color class of the graph G where the minimum is taken over all $\chi$-colorings of G.

For example, for complete graphs $K_n$, $n \ge 2$, it holds that $es _{\chi }(K_n) = \rho (K_n) = t(K_n) = 1$. Since $\chi (K_n) = n$ and $\chi (K_n - e) = n-1$ for any edge $e \in E(K_n)$, it follows that $es _{\chi }(K_n) = 1$. On the other hand, any two vertices are colored distinctly in an n-coloring of $K_n$, hence $\rho (K_n) = t(K_n) = 1$.

Let G be an arbitrary nonempty bipartite graph. Then $es _{\chi }(G) = \rho (G) = \left| E(G) \right|$. The graph G and every nonempty subgraph are 2-chromatic which implies $es _{\chi }(G) = \left| E(G) \right|$. On the other hand, every edge of G connects vertices of different colors in any 2-coloring of G which implies $\rho (G) = \left| E(G) \right|$. We obtain t(G) by adding the cardinalities of the smaller partiton sets of each nonempty component of G. If G is a connected bipartite graph, then t(G) is the minimum of the cardinalities of the partition sets of G.

For graphs G with $\chi (G) = 3$ the chromatic edge stability number $es _{\chi }(G)$ is equal to the so-called bipartite edge frustration which was studied for example in [2, 4].

Staton [3] proved that if the maximum degree of a graph G is not large compared to its chromatic number, then the chromatic edge stability number is also not large.

Theorem 1.1

[3] If G is a graph with ${\varDelta }(G) < a(\chi (G) -1)$, then $es _{\chi }(G) \le (a-1)t(G)$.

Therefore, if ${\varDelta }(G) \le 2\chi (G) - 3$, then $es _{\chi }(G) \le t(G)$ and obviously $t(G) \le \left\lfloor n/\chi (G) \right\rfloor \le \alpha (G)$ for any graph G with n vertices and independence number $\alpha (G)$.

We will use the following observation (see [1]) which can be proved by considering a $\chi$-coloring of G with $\rho (G)$ edges between two color classes, removing these edges, and recoloring the vertices of one of the two color classes.

Proposition 1.1

[1] If G is nonempty, then $1 \le es _{\chi }(G) \le \rho (G)$.

In this paper we characterize some graphs G such that $es _{\chi }(G) = \rho (G)$. Moreover, we give general bounds and we determine these parameters exactly for specific classes of graphs such as joins of graphs, Cartesian products of graphs, complete multipartite graphs, and squares of paths (showing that the difference between $\rho (G)$ and $es _{\chi }(G)$ can be arbitrarily large).

2 General Results for $es _{\chi }(G)$ and $\rho (G)$

In [1] it was asked for which graphs the chromatic edge stability number and the chromatic bondage number coincide. In this section we give some partial results.

Proposition 2.1

If there exists a $\chi$-coloring of a graph G with at least two one-element color classes, then $es _{\chi }(G) = \rho (G) = 1$.

Proof

Assume that there exists a $\chi$-coloring c of G such that there are at least two vertices $v_{1},v_{2}\in V(G)$ that have unique colors, that is, there are two one-element color classes, say $C_{1} = \{v_1\}$ and $C_{2} = \{v_2\}$, in the partition ${\mathcal {C}}$. Each of the vertices $v_{1}$ and $v_{2}$ is connected to vertices of all other colors. Therefore, $v_{1}$ and $v_{2}$ are connected by an edge and $\rho (G) = 1$. This implies $es _{\chi }(G) = 1$ by Proposition 1.1 since G is nonempty. $\square$

For each graph G of order n with two vertices of degree $n-1$ it holds $es _{\chi }(G) = \rho (G) = 1$ by Proposition 2.1 since these vertices must have unique colors. Examples are complete graphs $K_n$ with $n \ge 2$ (see also Sect. 1) or more generally complete multipartite graphs $K_{1,1,n_3,\dots ,n_r}$, $r \ge 2$.

Theorem 2.1

Suppose that each $\chi$-coloring of $G \not \cong K_1$ contains a one-element color class. Then there is a $\chi$-coloring of G with a one-element color class connected to some other color class by exactly $\rho (G)$ edges.

Proof

By the assumptions, $\chi (G) \ge 2$. Consider a $\chi$-coloring of G that attains the chromatic bondage number $\rho (G)$, that is, there are two color classes $C_2$ and $C_3$connected by exactly $\rho (G)$ edges. If $C_2$ or $C_3$ is a singleton (a one-element set) then we are done, so suppose that $C_2$ and $C_3$ have at least two vertices each.

Let $S_2 \subseteq C_2$ and $S_3 \subseteq C_3$ be the sets of vertices incident to edges between $C_2$ and $C_3$. Each vertex in $S_2$ is adjacent to at least one vertex in $S_3$, and vice versa. We recolor all vertices of $C_2 \setminus S_2$ by the color of $C_3$ and obtain a new coloring ${\bar{c}}$ with color classes $\bar{C_2} = S_2$, $\bar{C_3} = C_3 \cup (C_2 \setminus S_2)$, and $\bar{C_i} = C_i$ for the other colors.

Consider now a one-element color class $\bar{C_1} \ne \bar{C_2}, \bar{C_3}$. $\bar{C_1}$ is connected to $\bar{C_2}$ by at most $\left| \bar{C_2} \right| = \left| S_2 \right|$ edges. Each vertex of $S_2$ is incident to at least one edge that connects $\bar{C_2}$ to $\bar{C_3}$ which implies $\left| S_2 \right| \le \rho (G)$. Therefore, $\bar{C_1}$ is connected to $\bar{C_2}$ by at most $\rho (G)$ edges and, by the minimality of $\rho (G)$, exactly $\rho (G)$ edges. $\square$

The assumption of Theorem 2.1 holds for each graph G of order n with ${\varDelta }(G) = n-1$.

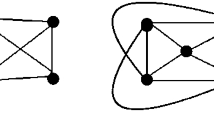
The conclusion of Theorem 2.1 cannot be generalized to all $\chi$-colorings of a graph G, as the counterexample in Fig. 1 shows. It holds that $\chi (G) = 3$ and in each3-coloring of G the vertex of degree 4 is in a one-element color class. By the figure, $\rho (G) = 1$, but on the other hand, the vertex of color 1 is adjacent to two vertices of color 2 and two of color 3.

Fig. 1

Graph G

Proposition 2.2

It holds that $\rho (G) = 1$ if and only if $es _{\chi }(G) = 1$.

Proof

If G is empty then $\rho (G) = es _{\chi }(G) = 0$, so assume that G is nonempty.

If $\rho (G) = 1$ then Proposition 1.1 implies $1 \le es _{\chi }(G) \le \rho (G) = 1$, that is, $es _{\chi }(G) = 1$.

On the other hand, assume $es _{\chi }(G) = 1$, that is, there is an edge $e = v_1v_2 \in E(G)$ such that $\chi (G-e) = \chi (G) - 1$. Consider a proper coloring c of $G-e$ with $\chi (G) - 1$ colors. Since the chromatic number of $G-e$ is smaller than $\chi (G)$, the end vertices of e must have the same color, $c(v_1) = c(v_2)$, and $v_1$ is not adjacent to any vertex of color $c(v_2)$ in $G-e$. Now we add the edge $e=v_1v_2$ and recolor $v_1$ by a new color $\chi (G)$ in order to obtain a proper coloring ${\bar{c}}$ of G with ${\bar{c}}(v_1) = \chi (G)$ and ${\bar{c}}(v) = c(v)$ for $v \ne v_1$. In this $\chi$-coloring, the single vertex $v_1$ of color $\chi (G)$ is adjacent to exactly one vertex, $v_2$, of color $c(v_2)$. This implies $\rho (G) = 1$. $\square$

Corollary 2.1

If $es _{\chi }(G) = 1$, then there exists a $\chi$-coloring of G that contains at least one one-element color class.

Proof

The coloring ${\bar{c}}$ constructed in the proof of Proposition 2.2 fulfills the condition. $\square$

Corollary 2.2

If $\rho (G) = 2$ for a graph G, then $es _{\chi }(G) = 2$.

Proof

If $\rho (G) = 2$, then $es _{\chi }(G) \ge 2$ by Proposition 2.2, and $es _{\chi }(G) \le \rho (G) = 2$ by Proposition 1.1 since G is nonempty. $\square$

Theorem 2.2

If a graph G has a vertex v incident to $es _{\chi }(G)$ edges $E'$ whose deletion results in a graph $H = G - E'$ with $\chi (H) = \chi (G) - 1$, then $es _{\chi }(G) = \rho (G)$.

Proof

Assume that G has a vertex v and an edge set $E'$ with the described property. Then $H = G - E'$ has chromatic number $\chi (H) = \chi (G) - 1$. Let c be a proper coloring of H with $\chi (G) - 1$ colors and assume that $c(v) = c_{1}$. This means that v is not adjacent to any vertex of color $c_{1}$ in H.

Consider now the graph G. The coloring ${\bar{c}}$ of G with ${\bar{c}}(v) = \chi (G)$ and ${\bar{c}}(w) = c(w)$ for $w \ne v$ is a proper coloring of G with $\chi (G)$ colors. The vertex v is in a one-element color class $C_{\chi (G)}$ and must be adjacent in G to some vertices of color $c_1$ (otherwise c would be a $(\chi (G)-1)$-coloring of G, a contradiction). Therefore, $\rho (G)$ is at most the number of edges between the color classes $C_{\chi (G)}$ and $C_{c_1}$ which is the number of neighbors of v of color $c_1$ which is at most $\left| E' \right| = es _{\chi }(G)$. Hence $\rho (G) \le es _{\chi }(G)$. Since $es _{\chi }(G) \le \rho (G)$ by Proposition 1.1, equality holds. $\square$

Corollary 2.3

If a graph G has a vertex v incident to $es _{\chi }(G)$ edges whose deletion results in a graph $G'$ with $\chi (G') = \chi (G) - 1$, then there is a $\chi$-coloring of G where v is in a one-element color class.

Proof

The proof of Theorem 2.2 implies this result. $\square$

Theorem 2.3

In a graph G, $es _{\chi }(G) = \rho (G)$ if and only if G is empty or if there exists a $\chi$-coloring of G such that the number of edges between some pair of color classes is equal to $es _{\chi }(G)$.

Proof

It holds that $\rho (G) = es _{\chi }(G) = 0$ if and only if G is empty, so assume that G is nonempty.

If $es _{\chi }(G) = \rho (G)$ then there exists a $\chi$-coloring of G such that the number of edges between a pair of color classes is equal to $\rho (G)$, that is, to $es _{\chi }(G)$.

On the other hand, if there exists a $\chi$-coloring of G such that the number of edges between some pair of color classes is equal to $es _{\chi }(G)$, then $\rho (G) \le es _{\chi }(G)$. Since $es _{\chi }(G) \le \rho (G)$ by Proposition 1.1, equality holds. $\square$

The following theorem provides a general lower bound for $es _{\chi }(G)$ which has many interesting implications. Some of them are formulated in the succeeding corollaries.

Theorem 2.4

Let G be a graph with $\chi (G) = k \ge 2$. If G contains s subgraphs $G_{1},\dots ,G_{s}$ with $\chi (G_{1}) = \dots = \chi (G_{s}) = k$ and if q is the maximum number of these subgraphs that share an edge, then $es _{\chi }(G) \ge \frac{1}{q}\sum _{i=1}^{s} es _{\chi }(G_i) \ge s/q$.

Proof

Let $E'$ be an edge set of G with $\left| E' \right| = es _{\chi }(G)$ and $\chi (G - E') = k - 1$. The set $E'$ must contain at least $es _{\chi }(G_i)$ edges of each graph $G_i$, $1 \le i \le s$. Therefore, $b = \sum _{i=1}^{s} \left| E' \cap E(G_i) \right| \ge \sum _{i=1}^{s} es _{\chi }(G_i) \ge s$. On the other hand, each edge of $E'$ is counted at most q times in b, so $\left| E' \right| q \ge b$ which implies $es _{\chi }(G) = \left| E' \right| \ge b/q \ge \frac{1}{q}\sum _{i=1}^{s} es _{\chi }(G_i) \ge s/q$. $\square$

Corollary 2.4

Let G be a graph with $\chi (G) = k \ge 2$. If G contains s subgraphs $G_{1},\dots ,G_{s}$ with $\chi (G_{1}) = \dots = \chi (G_{s}) = k$ and pairwise disjoint edge sets, then $es _{\chi }(G) \ge \sum _{i=1}^{s} es _{\chi }(G_i) \ge s$.

Proof

Each edge of G is contained in at most $q = 1$ of the given subgraphs since they are pairwise edge disjoint. The result follows from Theorem 2.4. $\square$

Corollary 2.5

If $H \subseteq G$ and $\chi (H) = \chi (G)$, then $es _{\chi }(H) \le es _{\chi }(G)$.

Proof

This is the case $s=1$ in Corollary 2.4. $\square$

Corollary 2.6

Let G be a graph with $\chi (G) = 3$. If G contains s odd cycles with pairwise disjoint edge sets, then $es _{\chi }(G) \ge s$.

Proof

The result follows by Corollary 2.4 since odd cycles are 3-chromatic. $\square$

Theorem 2.5

If G is nonempty, then $\rho (G) \ge t(G)$.

Proof

Let c be an arbitrary $\chi$-coloring of G with color classes ${\mathcal {C}} = (C_1,\dots , C_{\chi })$. By the definition of t(G), $\left| C_i \right| \ge t(G)$ for $i = 1,\dots ,\chi$. Moreover, there are $\chi$ sets $S_{1} \subseteq C_{1}$, ..., $S_{\chi } \subseteq C_{\chi }$, such that each vertex in $S_i$ is connected to each of the other color classes with at least one edge. It holds that $\left| S_{i} \right| \ge t(G)$ for $i = 1, \dots , \chi$, since otherwise the number of vertices in a color class can be reduced to less than t(G), a contradiction. This implies $\rho (G) \ge t(G)$. $\square$

Corollary 2.7

In a nonempty graph G, $\rho (G) = t(G)$ if and only if there exists a $\chi$-coloring of G with two color sets $C_1,C_2$ and two subsets $S_{1} \subseteq C_{1}$, $S_{2} \subseteq C_{2}$ such that $\left| S_{1} \right| = \left| S_{2} \right| = t(G)$ and each vertex in $S_{1}$ is connected to exactly one vertex in $S_{2}$ and vice versa.

Proof

Assume $\rho (G) = t(G)$ and that the smallest number of edges is between the two color classes $C_{1}$ and $C_{2}$. Let $S_{i}$ be the set of vertices of $C_{i}$ which are adjacent to vertices of $C_{3-i}$, $i = 1,2$. Then $\left| S_{i} \right| \le \rho (G)$ and, since $\rho (G) = t(G)$, $\left| S_{i} \right| \le t(G)$. Since $\left| S_{i} \right| \ge t(G)$ by the proof of Theorem 2.5, $\left| S_{1} \right| = \left| S_{2} \right| = t(G)$. This implies that each vertex in $S_1$ is adjacent to exactly one vertex in $S_2$, and vice versa.

Since $\rho (G) \ge t(G)$ by Theorem 2.5 and there are exactly t(G) edges between $C_1$ and $C_2$, the second implication follows. $\square$

Corollary 2.8

If $\rho (G) = t(G)$, then there exists a $\chi$-coloring of G with two color classes $C_{1}$ and $C_{2}$ with $\left| C_{1} \right| = t(G)$ and $\left| C_{2} \right| \ge t(G)$, such that each vertex of $C_{1}$ is connected to exactly one vertex in $C_{2}$ and each vertex of $C_{2}$ which is connected to $C_{1}$ has exactly one neighbor in $C_1$.

Proof

By Corollary 2.7, there are color classes $C_{1}$ and $C_{2}$ with subsets $S_{1} \subseteq C_{1}$ and $S_{2} \subseteq C_{2}$ such that $\left| S_{1} \right| = \left| S_{2} \right| = t(G)$ and each vertex in $S_{1}$ is connected to exactly one vertex in $S_{2}$ and vice versa. Recolor the vertices of $C_1 \setminus S_1$ by the color of the vertices of $C_2$ to obtain the required coloring. $\square$

Note that there is in general no correlation between t(G) and $es _{\chi }(G)$. Consider for example the graph $G_{r,s}$, $r,s \ge 1$, which consists of a cycle $C_{2r+1}$ with s attached paths of length 2 between any two adjacent vertices of the cycle. Then $\chi (G_{r,s}) = 3$: The vertices of the initial $C_{2r+1}$ must be colored by 3 colors, and the inner vertices of the paths attached between two vertices must be colored by the color not used at the attachment vertices. If exactly a vertices of the initial cycle are colored by a fixed color $i \in \{1,2,3\}$, then $1 \le a \le r$ and exactly $a + (2r+1 - 2a)s$ vertices of $G_{r,s}$ are colored by i, that is, $\left| C_i \right| = a(1 - 2s) + (2r+1)s$ which is minimal if $a = r$ is maximal. This is possible by coloring the vertices of the initial cycle by $1,2,\dots ,1,2,3$. Therefore, $t(G_{r,s}) = r(1 - 2s) + (2r+1)s = r + s$.

On the other hand, $G_{r,s}$ contains $2r+1$ pairwise edge disjoint $C_3$ which implies $es _{\chi }(G_{r,s}) \ge 2r+1$ by Corollary 2.6, and removing the $2r+1$ edges of the initial cycle gives a bipartite graph which implies $es _{\chi }(G_{r,s}) = 2r+1$. Therefore, $t(G_{r,s}) - es _{\chi }(G_{r,s}) = (r+s) - (2r+1) = s - r - 1$, which is unbounded.

3 Specific Graph Classes

In this section we determine the chromatic edge stability number and the chromatic bondage number for specific graph classes.

Definition 3.1

The union $G \cup H$ of two (not necessarily disjoint) graphs G and H is the graph with vertex set $V(G) \cup V(H)$ and edge set $E(G) \cup E(H)$.

If G and H are disjoint then the graphs G and H can be colored independently by $\chi (G)$ and $\chi (H)$ colors, respectively. If G and H have exactly one vertex u in common then again they can be colored independently with the restriction that vertex u obtains the same color in both colorings. This implies in both cases that $\chi (G \cup H) = \max \{\chi (G), \chi (H)\}$.

Theorem 3.1

If G and H are disjoint or if they have exactly one vertex in common, then $es _{\chi }(G \cup H) = es _{\chi }(G)$ if $\chi (G) > \chi (H)$, $es _{\chi }(G \cup H) = es _{\chi }(H)$ if $\chi (G) < \chi (H)$, and $es _{\chi }(G \cup H) = es _{\chi }(G) + es _{\chi }(H)$ if $\chi (G) = \chi (H)$.

Proof

If $\chi (G) \ne \chi (H)$, say without loss of generality $\chi (G) > \chi (H)$, then $es _{\chi }(G \cup H) \ge es _{\chi }(G)$ by Corollary 2.5 since $G \subseteq G \cup H$ and $\chi (G) = \chi (G \cup H)$. Equality holds by selecting an appropriate set $E'$ of edges of G with $\left| E' \right| = es _{\chi }(G)$ and $\chi (G - E') = \chi (G) - 1$.

If $\chi (G) = \chi (H)$ then either G and H and therefore also $G \cup H$ are empty, thus $es _{\chi }(G \cup H) = es _{\chi }(G) = es _{\chi }(H) = 0$, or $es _{\chi }(G \cup H) \ge es _{\chi }(G) + es _{\chi }(H)$ by Corollary 2.4 since G and H are edge disjoint. Equality holds by selecting an appropriate set of edges $E' = E'_G \cup E'_H$ with $E'_G \subseteq E(G)$, $\left| E'_G \right| = es _{\chi }(G)$, and $E'_H \subseteq E(H)$, $\left| E'_H \right| = es _{\chi }(H)$, such that $\chi (G - E'_G) = \chi (G) - 1$ and $\chi (H - E'_H) = \chi (H) - 1$. $\square$

In the determination of the chromatic edge stability number of a graph we can assume without loss of generality that the graph is 2-connected, since $es _{\chi }(G)$ of a not 2-connected graph G can be determined by Theorem 3.1 from the chromatic edge stability numbers of its blocks (maximal connected subgraphs without a cut-vertex).

Corollary 3.1

Let G be a graph with b blocks $B_1,\dots ,B_b$ such that $\chi (B_i) = \chi (G)$ for $1 \le i \le s$ and $\chi (B_i) < \chi (G)$ for $s < i \le b$. Then $es _{\chi }(G) = \sum _{i=1}^{s} es _{\chi }(B_i)$.

Theorem 3.2

If G and H are disjoint, or if they have exactly one vertex in common and $\chi (G) \ne \chi (H)$, then $\rho (G \cup H) = \rho (G)$ if $\chi (G) > \chi (H)$, $\rho (G \cup H) = \rho (H)$ if $\chi (G) < \chi (H)$, and $\rho (G \cup H) = \rho (G) + \rho (H)$ if $\chi (G) = \chi (H)$.

Proof

If $\chi (G) \ne \chi (H)$, say without loss of generality $\chi (G) > \chi (H)$, then each color class of a proper coloring of $G \cup H$ with $\chi (G \cup H) = \chi (G)$ colors contains vertices of G, which implies $\rho (G \cup H) \ge \rho (G)$. By using a $\chi$-coloring of $G \cup H$ composed by a $\chi$-coloring of H and a $\chi$-coloring of G with $\rho (G)$ edges between a color class that does not occur in H and another color class, equality follows.

If $\chi (G) = \chi (H)$, then by assumption G and H are disjoint, and either both graphs as well as $G \cup H$ are empty, hence $\rho (G \cup H) = \rho (G) = \rho (H) = 0$, or each color class of a $\chi$-coloring of $G \cup H$ contains vertices from G and from H. This implies that between any two color classes of a $\chi$-coloring of $G \cup H$ there are at least $\rho (G)$ edges in the subgraph G and $\rho (H)$ edges in the subgraph H, that is, $\rho (G \cup H) \ge \rho (G) + \rho (H)$. By choosing a $\chi$-coloring of G with $\rho (G)$ edges and a $\chi$-coloring of H with $\rho (H)$ edges between two fixed color classes (for example, by recoloring H, which is possible since G and H are vertex disjoint) we obtain a $\chi$-coloring of $G \cup H$ with exactly $\rho (G) + \rho (H)$ edges between the two fixed color classes, hence $\rho (G \cup H) = \rho (G) + \rho (H)$. $\square$

Note that the result of Theorem 3.2 does not necessarily hold if the graphs G and H have exactly one vertex in common and $\chi (G) = \chi (H)$. It holds that $\rho (G \cup H) \ge \rho (G) + \rho (H)$, but the last step in the proof may fail. Consider for example the graph G obtained by the union of two copies of $K_{1,1,2}$ with exactly one vertex of degree 5 in common (see Fig. 2). Then $\chi (G) = 3$ and G is uniquely 3-colorable (up to isomorphism). Therefore, $\rho (G) = 3 \ne 2 \rho (K_{1,1,2}) = 2$.

Fig. 2

Union G of two $K_{1,1,2}$ with one vertex of degree 5 in common

Theorem 3.2 implies that in the determination of the chromatic bondage number of a graph we can assume without loss of generality that the graph is connected, since $\rho (G)$ of a non-connected graph G can be determined applying this theorem iteratively on the components of G.

Corollary 3.2

Let G be a graph with b components $H_1,\dots ,H_b$ such that $\chi (H_i) = \chi (G)$ for $1 \le i \le s$ and $\chi (H_i) < \chi (G)$ for $s < i \le b$. Then $\rho (G) = \sum _{i=1}^{s} \rho (H_i)$.

A cactus graph is a graph with the property that each edge is contained in at most one cycle. Hence the blocks of a cactus graph are either trivial ($K_1$ or $K_2$) or cycles. Corollary 3.1 and the following proposition allow to determine $es _{\chi }(G)$ of a cactus graph G.

Proposition 3.1

[1] $es _{\chi }(C_n) = \rho (C_n) = 1$ if n is odd and $es _{\chi }(C_n) = \rho (C_n) = n$ if n is even.

Theorem 3.3

Let G be a cactus graph with s odd cycles. If $s > 0$, then $es _{\chi }(G) = \rho (G) = s$, otherwise $es _{\chi }(G) = \rho (G) = \left| E(G) \right|$.

Proof

If $s = 0$ then G is a $K_1$ or bipartite and $es _{\chi }(G) = \rho (G) = \left| E(G) \right|$ follows.

If G contains $s \ge 1$ odd cycles then these are edge disjoint and $\chi (G) = 3$. By Corollary 2.6, $es _{\chi }(G) \ge s$. To prove $\rho (G) \le s$ we color iteratively connected blocks by colors 1, 2, 3 as follows. Note that for each component each block except the first one has one previously colored cut vertex. Color isolated vertices by 1. If the block is a $K_2$, then use colors 1, 2 or 1, 3. If the block is an even cycle then color the vertices by 1, 2 or, if the cut vertex is colored by 3, by $1,3,1,2,\dots ,1,2$. If the block is an odd cycle then color the vertices by $1,2,\dots ,1,2,3$. Therefore, exactly s edges connect color classes $C_2$ and $C_3$ (one for each odd cycle), which implies $\rho (G) \le s$. Thus $es _{\chi }(G) = \rho (G) = s$ by Proposition 1.1. $\square$

Definition 3.2

The join $G \vee H$ of two disjoint graphs G and H is the graph composed by a copy of G and a copy of H in which each vertex of G is connected to each vertex of H.

The definition implies that in each proper coloring of $G \vee H$ each color class is contained either in V(G) or in V(H). By properly coloring the copy of G by $\chi (G)$ colors and the copy of H by $\chi (H)$ new colors it follows that $\chi (G \vee H) = \chi (G) + \chi (H)$. Note that each $\chi$-coloring of $G \vee H$ induces a $\chi$-coloring of G and a $\chi$-coloring of H with disjoint color sets, and vice versa.

Several graph classes can be described as the join of graphs, for example complete graphs $K_n = K_1 \vee K_1 \vee \dots \vee K_1$, complete multipartite graphs $K_{n_1,n_2,\dots ,n_r} = \overline{K_{n_1}} \vee \overline{K_{n_2}} \vee \dots \vee \overline{K_{n_r}}$, wheels $W_n = C_n \vee K_1$ ($n \ge 3$), or fans $F_n = P_n \vee K_1$.

Theorem 3.4

Let $\rho '(G) = \rho (G)$ if G is non-empty and $\rho '(G) = \infty$ if G is empty. Then

$$\begin{aligned} \rho (G \vee H) = \min \{\rho '(G), \rho '(H), t(G)t(H) \}. \end{aligned}$$

Proof

If G and H are nonempty then consider two arbitrary color classes of a $\chi$-coloring of $G \vee H$. Each color class is contained completely either in G or in H. If the color classes are both from G or both from H, then there are at least $\rho (G)$ or $\rho (H)$ edges between them, respectively; if one belongs to G and the other one to H, then there are at least t(G)t(H) edges between them. This implies $\rho (G \vee H) \ge \min \{\rho (G), \rho (H), t(G)t(H) \}$.

On the other hand, one can find $\chi$-colorings of $G \vee H$ with $\rho (G)$ edges between two color classes of G, or with $\rho (H)$ edges between two color classes of H, or with a color class of G with t(G) vertices and a color class of H with t(H) vertices, respectively. This implies $\rho (G \vee H) \le \min \{\rho (G), \rho (H), t(G)t(H) \}$, that is, equality holds if G and H are nonempty.

If one or both graphs G, H are empty then, by the definition of $\rho '$, one or both of the terms $\rho '(G), \rho '(H)$ can be removed from the assumption. By an analogous proof as above, equality holds for all graphs G and H. $\square$

For example, if G and H are empty then $G \vee H$ is a complete bipartite graph which implies $\rho (G \vee H) = \left| E(G \vee H) \right| = \left| V(G) \right| \,\left| V(H) \right| = t(G)t(H)$.

Similar arguments as in the proof of Theorem 3.4 yield the following upper bound for $es _{\chi }(G \vee H)$.

Theorem 3.5

Let $es _{\chi }'(G) = es _{\chi }(G)$ if G is non-empty and $es _{\chi }'(G) = \infty$ if G is empty. Then

$$\begin{aligned} es _{\chi }(G \vee H) \le \min \{ es _{\chi }'(G), es _{\chi }'(H), t(G)t(H) \}. \end{aligned}$$

Proof

If G is nonempty then there are $es _{\chi }(G)$ edges $E'$ in G such that $\chi (G-E') = \chi (G) - 1$. Hence, the graph $G' = (G \vee H) - E' \cong (G - E') \vee H$ fulfils $\chi (G') = \chi (G - E') + \chi (H) = \chi (G) + \chi (H) - 1 = \chi (G \vee H) - 1$ which implies $es _{\chi }(G \vee H) \le es _{\chi }(G)$. Analogously, if H is nonempty, then $es _{\chi }(G \vee H) \le es _{\chi }(H)$. By Proposition 1.1 and Theorem 3.4, $es _{\chi }(G \vee H) \le \rho (G \vee H) \le t(G)\,t(H)$. $\square$

If G and H are empty then $G \vee H$ is a complete bipartite graph and equality holds: $es _{\chi }(G \vee H) = \left| E(G \vee H) \right| = \left| V(G) \right| \,\left| V(H) \right| = t(G)t(H)$. We conjecture that in the statement of Theorem 3.5 equality always holds. In the following we prove equality for some classes of graphs.

Proposition 3.2

For wheels $W_n = C_n \vee K_1$ it holds $es _{\chi }(W_n) = \rho (W_n) = 1$ if n is odd and $es _{\chi }(W_n) = \rho (W_n) = n/2$ if n is even.

Proof

If n is odd then $\rho (W_n) = \min \{\rho (C_n), t(C_n)\} = \min \{1,1\} = 1$ by Proposition 3.1 and Theorem 3.4, hence $es _{\chi }(W_n) = 1$ by Proposition 2.2.

If n is even then $es _{\chi }(W_n) \le \rho (W_n) = \min \{\rho (C_n), t(C_n)\} = \min \{n, n/2\} = n/2$ by Propositions 1.1 and 3.1 and Theorem 3.4. On the other hand, $\chi (W_n) = 3$ and $W_n$ contains n / 2 edge disjoint cycles $C_3$, hence $es _{\chi }(W_n) \ge n/2$ by Corollary 2.6. $\square$

If n is odd then the result also follows from Proposition 2.1: $\chi (W_n) = 4$ and by coloring the vertices of the odd cycle successively with colors $1,2,\dots ,1,2,3$ and the central vertex with 4 we obtain a 4-coloring of $W_n$ with two uniquely colored vertices. By Proposition 2.1, $es _{\chi }(W_n) = \rho (W_n) = 1$.

Proposition 3.3

For fans $F_n = P_n \vee K_1$ it holds $es _{\chi }(F_1) = \rho (F_1) = 1$ and $es _{\chi }(F_n) = \rho (F_n) = \left\lfloor n/2 \right\rfloor$ if $n \ge 2$.

Proof

It holds that $es _{\chi }(F_1) = \rho (F_1) = 1$ since $F_1 \cong K_2$. Let $n \ge 2$. By Proposition 1.1 and Theorem 3.4, $es _{\chi }(F_n) \le \rho (F_n) = \min \{\rho (P_n), t(P_n)\} = \min \{n-1, \left\lfloor n/2 \right\rfloor \} = \left\lfloor n/2 \right\rfloor$. On the other hand, $\chi (F_n) = 3$ and $F_n$ contains $\left\lfloor n/2 \right\rfloor$ edge disjoint cycles $C_3$, hence $es _{\chi }(F_n) \ge \left\lfloor n/2 \right\rfloor$ by Corollary 2.6. $\square$

Consider in the following complete multipartite graphs $K_{n_1,n_2,\dots ,n_r}$, $r \ge 2$. By inductively using Theorem 3.4 as well as Proposition 1.1 we obtain:

Proposition 3.4

[1] If $r \ge 2$, then $es _{\chi }K_{n_1,\ldots ,n_r} \le K_{n_1,\ldots ,n_r} = \min _{1 \le i < j \le r} n_i\,n_j$.

Equality holds for example for complete graphs ($n_1 = \dots = n_r = 1$), complete bipartite graphs ($r = 2$), and balanced complete tripartite graphs: $es _{\chi }(K_{n_1,n_1,n_1}) = \rho (K_{n_1,n_1,n_1}) = n_1^2$ [1]. It is conjectured in [1] that equality always holds. The conjecture is a direct implication of the more general result of Theorem 2.4 and Proposition 3.4 (see Theorem 3.6). At first, we give a nice direct proof for arbitrary complete tripartite graphs.

Proposition 3.5

If $1 \le n_1 \le n_2 \le n_3$, then $es _{\chi }(K_{n_1,n_2,n_3}) = \rho (K_{n_1,n_2,n_3}) = n_1 n_2$.

Proof

By Proposition 3.4 we only need to prove $es _{\chi }(K_{n_1,n_2,n_3}) \ge n_1 n_2$. Consider an edge coloring of $K_{n_2,n_3} \subseteq K_{n_1,n_2,n_3}$ with $\chi '(K_{n_2,n_3}) = {\varDelta }(K_{n_2,n_3}) = n_3$ colors $1,\dots ,n_3$. Each of the $n_2$ vertices of the second partition set is incident with edges of each color $1,\dots ,n_3$. By connecting all $n_2$ edges of color i with the ith vertex of the first partition set ($1 \le i \le n_1$) we obtain $n_1 n_2$ edge disjoint cycles $C_3$ in $K_{n_1,n_2,n_3}$. Therefore, $es _{\chi }(K_{n_1,n_2,n_3}) \ge n_1 n_2$ by Corollary 2.6. $\square$

Theorem 3.6

If $1 \le n_1 \le n_2 \le \dots \le n_r$ and $r \ge 2$, then $es _{\chi }(K_{n_1,n_2,\dots ,n_r}) = \rho (K_{n_1,n_2,\dots ,n_r}) = n_1 n_2$.

Proof

Applying Proposition 3.4 we only need to prove $es _{\chi }(K_{n_1,n_2,\dots ,n_r}) \ge n_1 n_2$. Consider all $s = n_1 \cdot \dots \cdot n_r$ different complete subgraphs $K_r$ in $K_{n_1,\dots ,n_r}$. An edge between partition sets $V_i$ and $V_j$, $\left| V_i \right| = n_i$, $\left| V_j \right| = n_j$, is contained in exactly $s/(n_i n_j)$ subgraphs $K_r$, which is less than or equal to $q = s/(n_1 n_2)$. By Theorem 2.4, $es _{\chi }(K_{n_1,n_2,\dots ,n_r}) \ge \frac{1}{q} \sum _{i=1}^{s} es _{\chi }(K_r) = s/q = n_1 n_2$. $\square$

The results of this section and Proposition 2.2 allow the computation of $es _{\chi }(G)$ and $\rho (G)$ for at most all graphs G of order at most 5. By considering also the missing graph $C_5 + e$, for which $es _{\chi }(C_5 + e) = \rho (C_5 + e) = 1$ holds, we obtain the following result.

Theorem 3.7

Let G be a graph of order at most 5. Then $es _{\chi }(G) = \rho (G) = 0$ if G is empty, $es _{\chi }(G) = \rho (G) = \left| E(G) \right|$ if G is nonempty and bipartite, $es _{\chi }(G) = \rho (G) = 2$ if G is the wheel $W_4$, the fan $F_4$, or the hourglass graph $2 K_2 \vee K_1$, and $es _{\chi }(G) = \rho (G) = 1$ for all other graphs.

In [1] it was proved that for each $k \ge 3$ there are k-chromatic graphs G for which the difference between $\rho (G)$ and $es _{\chi }(G)$ can be arbitrarily large. It was shown for the square $P_6^2$ of a path of order 6 that $es _{\chi }(P_6^2) = 2 < \rho (P_6^2) = 3$. By Theorem 3.7, there is no graph of smaller order with $es _{\chi }(G) < \rho (G)$. In the following we consider the class $P_n^2$.

Theorem 3.8

If $n \in \{1,2\}$, then $es _{\chi }(P_n^2) = \rho (P_n^2) = n - 1$. If $n \ge 3$, then $es _{\chi }(P_n^2) = \left\lceil n/2 \right\rceil - 1$ and $\rho (P_n^2) = n - \left\lfloor (n + 2)/3 \right\rfloor - 1$.

Proof

If $n \in \{1,2\}$ then $P_n^2 \cong K_n$ and the result is obvious.

Let $n \ge 3$ and denote the vertices of $P_n$ by $(v_1,\dots ,v_n)$. The graph $P_n^2$ contains $\left\lceil n/2 \right\rceil - 1$ edge disjoint copies of $K_3$, namely induced by vertex sets $\{v_1,v_2,v_3\}$, $\{v_3,v_4,v_5\}$, $\{v_5,v_6,v_7\}$, ..., and $\chi (P_n^2) = 3$. Hence $es _{\chi }(P_n^2) \ge \left\lceil n/2 \right\rceil - 1$ by Corollary 2.6. On the other hand, by removing every second edge ($v_2v_3, v_4v_5, v_6v_7, \dots$) of the path $P_n$ we obtain a bipartite graph which implies $es _{\chi }(P_n^2) \le \left\lceil n/2 \right\rceil - 1$, and thus equality holds.

Consider now $\rho (P_n^2)$. Each 3-coloring of $P_n^2$ is forced by the distinct colors of the first three vertices, which implies that $P_n^2$ is uniquely colorable (up to permutation of colors), say with color classes $C_1 = \{v_1, v_4, v_7, \dots \}$, $C_2 = \{v_2, v_5, v_8, \dots \}$, and $C_3 = \{v_3, v_6, v_9, \dots \}$. The union of two color classes $\ne C_i$ induces a path of order $n - \left| C_i \right|$ with $n - \left| C_i \right| - 1$ edges. The minimum is attained if $\left| C_i \right|$ is maximal. Since $\left| C_1 \right| \ge \left| C_2 \right| \ge \left| C_3 \right|$ and $\left| C_1 \right| = \left\lfloor (n + 2)/3 \right\rfloor$, we obtain $\rho (P_n^2) = n - \left\lfloor (n + 2)/3 \right\rfloor - 1$. $\square$

This result implies that $P_n^2$ is another class of 3-chromatic graphs where the difference $\rho (P_n^2) - es _{\chi }(P_n^2) \approx n/6$ can be arbitrarily large.

The Cartesian product $G \Box H$ of two graphs G and H is the graph with vertex set $V(G) \times V(H)$ where two vertices $(u_1,v_1)$ and $(u_2,v_2)$ are adjacent if and only if $u_1 = u_2$ and $v_1v_2 \in E(H)$ or if $v_1 = v_2$ and $u_1u_2 \in E(G)$. This implies that the edge set of $G \Box H$ can be partitioned into $\left| V(G) \right|$ copies of E(H) (induced by vertices with the same first component) and $\left| V(H) \right|$ copies of E(G) (induced by vertices with the same second component). Note that $\chi (G \Box H) = \max \{\chi (G), \chi (H)\}$.

Theorem 3.9

$es _{\chi }(G \Box H) = \left| V(H) \right| es _{\chi }(G)$ if $\chi (G) > \chi (H)$, $es _{\chi }(G \Box H) = \left| V(G) \right| es _{\chi }(H)$ if $\chi (G) < \chi (H)$, $es _{\chi }(G \Box H) = \left| V(H) \right| es _{\chi }(G) + \left| V(G) \right| es _{\chi }(H)$ if $\chi (G) = \chi (H)$.

Proof

If $\chi (G) \ne \chi (H)$, say without loss of generality $\chi (G) > \chi (H)$, then $\chi (G \Box H) = \chi (G)$ and $G \Box H$ contains $\left| V(H) \right|$ vertex disjoint subgraphs isomorphic to G. By Corollary 2.4, $es _{\chi }(G \Box H) \ge \left| V(H) \right| es _{\chi }(G)$. Let $E_G$ be a set of edges of G with $\left| E_G \right| = es _{\chi }(G)$ and $\chi (G - E_G) = \chi (G) - 1$ and let $E'$ be the union of the edge sets corresponding to $E_G$ in the $\left| V(H) \right|$ copies of G in $G \Box H$. Then $G \Box H - E' \cong (G - E_G) \Box H$ and $\chi (G \Box H - E') = \max \{\chi (G - E_G), \chi (H)\} = \chi (G - E_G) = \chi (G) - 1$, that is, $es _{\chi }(G \Box H) \le \left| E' \right| = \left| V(H) \right| es _{\chi }(G)$.

If $\chi (G) = \chi (H) (= \chi (G \Box H))$ then either G and H and therefore also $G \Box H$ are empty, thus $es _{\chi }(G \Box H) = es _{\chi }(G) = es _{\chi }(H) = 0$, or $G \Box H$ contains $\left| V(H) \right|$ copies of G and $\left| V(G) \right|$ copies of H which are pairwise edge disjoint and have the same chromatic number as $G \Box H$. By Corollary 2.4, $es _{\chi }(G \Box H) \ge \left| V(H) \right| es _{\chi }(G) + \left| V(G) \right| es _{\chi }(H)$. Define an edge set $E_G$ of G as above, analogously an edge set $E_H$ of H, and $E'$ as the union of the edge sets corresponding to $E_G$ in the copies of G or corresponding to $E_H$ in the copies of H in $G \Box H$. Then $G \Box H - E' \cong (G - E_G) \Box (H - E_H)$ and $\chi (G \Box H - E') = \max \{\chi (G - E_G), \chi (H - E_H)\} = \chi (G - E_G) = \chi (G) - 1$ which implies $es _{\chi }(G \Box H) \le \left| E' \right| = \left| V(H) \right| es _{\chi }(G) + \left| V(G) \right| es _{\chi }(H)$. $\square$

Fig. 3

Graph $K_3 \Box K_2$

Theorem 3.10

$\rho (G \Box H) \ge \left| V(H) \right| \rho (G)$ if $\chi (G) > \chi (H)$, $\rho (G \Box H) \ge \left| V(G) \right| \rho (H)$ if $\chi (G) < \chi (H)$, and $\rho (G \Box H) \ge \left| V(H) \right| \rho (G) + \left| V(G) \right| \rho (H)$ if $\chi (G) = \chi (H)$.

Proof

If $\chi (G) \ne \chi (H)$, say without loss of generality $\chi (G) > \chi (H)$, then each color class of a $\chi$-coloring of $G \Box H$ contains vertices from each of the $\left| V(H) \right|$ vertex disjoint copies of G in $G \Box H$, which implies $\rho (G \Box H) \ge \left| V(H) \right| \rho (G)$.

If $\chi (G) = \chi (H)$, then either G and H and thus also $G \Box H$ are empty, which implies $\rho (G \Box H) = \rho (G) = \rho (H) = 0$, or each color class of a $\chi$-coloring of $G \Box H$ contains vertices from each of the $\left| V(H) \right|$ copies of G and from each of the $\left| V(G) \right|$ copies of H in $G \Box H$. This implies $\rho (G \Box H) \ge \left| V(H) \right| \rho (G) + \left| V(G) \right| \rho (H)$ since the edge sets of the copies of G and of H are pairwise disjoint. $\square$

Note that this lower bound is not always attained. Consider for example $K_3 \Box K_2$ (see Fig. 3). Theorem 3.10 states $\rho (K_3 \Box K_2) \ge 2 \rho (K_3) = 2$. On the other hand, $\chi (K_3 \Box K_2) = 3$ and a 3-coloring of the graph is unique up to isomorphism, which implies $\rho (K_3 \Box K_2) = 3$. By Theorem 3.9, $es _{\chi }(K_3 \Box K_2) = 2 es _{\chi }(K_3) = 2$, that is, this is another graph G of minimal order 6 (see Theorem 3.7) with $es _{\chi }(G) < \rho (G)$.