Independence Number and k-Trees of Graphs

Abstract

A tree T is called a k-tree if the maximum degree of T is at most k. In this paper, we give a sufficient condition for a graph to have a k-tree containing specified vertices as following: let G be a connected graph and let S be a subset of V(G). If $\alpha _G(S)\le (k-1)\kappa _G(S)+1$, then G has a k-tree containing S. Moreover, this condition is sharp.

1 Introduction

We consider simple graphs, which have neither loops nor multiple edges. For a graph G, let V(G) and E(G) denote the set of vertices and the set of edges of G, respectively. Let $\alpha (G)$ and $\kappa (G)$ denote the independence number of G and the connectivity of G, respectively. For a vertex v of G, we denote by $\deg _G(v)$ the degree of v in G. For a vertex set S of G, let $\langle S\rangle _G$ denote the subgraph induced by S in G. We define $\alpha _G(S)$ the maximum cardinality of the independent set of S in G, which is called the independence number of S in G. For two vertices x, y of G, the local connectivity $\kappa _G(x, y)$ is defined to be the maximum number of internally disjoint paths connecting x and y in G. We define $\kappa _G(S):=\min \{\kappa _G(x, y): x, y\in S, x\ne y\}$. Moreover, if $|S|=1$, $\kappa _G(S)$ is defined to be $+\infty$. For $X, Y\subset V(G)$, we denote the set of edges of G joining X to Y by $E_G(X, Y)$, and the number of edges in $E_G(X, Y)$ by $e_G(X, Y)$. For a tree T, a vertex of T with degree one is called a leaf of T and the set of leaves of T is denoted by Leaf(T).

In 1972, Chvátal and Erdös gave an independence number condition for a graph to have a Hamiltonian cycle (path) as following:

Theorem 1

(Chvátal and Erdös [1]) Let G be a connected graph.

• (1) If $\alpha (G)\le \kappa (G)$, then G has a Hamiltonian cycle unless $G\cong K_1$ or $K_2$.

• (2) If $\alpha (G)\le \kappa (G)+1$, then G has a Hamiltonian path.

A Hamiltonian cycle (path) is a cycle (path) which passes through all vertices of a graph. In this sense, we can consider a cycle (path) containing specified vertices as a generalization of a Hamiltonian cycle (path).

Theorem 2

(Fournier [2]) Let G be a 2-connected graph, and let $S\subset V(G)$. If $\alpha _G(S)\le \kappa (G)$, then G has a cycle covering S.

Theorem 3

(Ozeki and Yamashita [3]) Let G be a 2-connected graph and let $S\subset V(G)$. If $\alpha _G(S)\le \kappa _G(S)$, then G has a cycle covering S.

Let $k\ge 2$ be an integer. A tree T is called a k-tree if $\deg _T(x)\le k$ for all $x\in V(T)$, that is, the maximum degree of a k-tree is at most k. Since a Hamiltonian path is nothing but a spanning 2-tree, we can consider the existence of a spanning k-tree as an generalization of a Hamiltonian path. Similarly to considering a cycle passing through specified vertices, in [4], the authors focus on the existence of a k-tree containing specified vertices and obtained the following result:

Theorem 4

(Chiba et al. [4]) Let G be a graph and let k be an integer with $k\ge 3$. Let $S \subset V(G)$ with $\kappa _G(S)\ge m\ge 1$. If

$$\begin{aligned} \alpha _G(S)\le (k-1)m+1-\left\lfloor \frac{m-1}{k}\right\rfloor , \end{aligned}$$

then G has a k-tree containing S.

In [4], the authors said that they did not know whether the condition of above theorem was best possible condition or not. Here, we give the best condition as the following result:

Theorem 5

Let G be a connected graph and let k be an integer with $k\ge 2$. Let S be a vertex set of G. If

$$\begin{aligned} \alpha _G(S)\le (k-1)\kappa _G(S)+1, \end{aligned}$$

(1)

then G has a k-tree containing S.

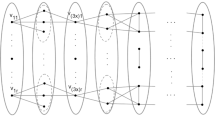
We show that the condition in Theorem 5 is sharp. Let $m\ge 1$ and $k\ge 2$ be integers. Let $K_m$ be a complete graph of order m and let $S=\{s_1, s_2,\ldots ,s_N\}$ where $N=(k-1)m+2$. Join $s_i(1\le i\le N)$ to all the vertices of $K_m$. Let G be the resulting graph. Then $\kappa _G(S)=m$ and $\alpha _G(S)=N=(k-1)\kappa _G(S)+2$. Let T ba a tree of G containing S and $V(T)=S\cup L$, where $L\subseteq V(K_m)$. Then $E(T)=E_T(S, L)\cup E_T(L, L)$, $|E(T)|=|V(T)|-1=|S|+|L|-1$ and $E_T(S, L)\cap E_T(L, L)=\emptyset$. We have $\sum _{v\in L}\deg _T(v)=e_T(S, L)+2e_T(L, L)=|S|+|L|-1+e_T(L, L)=(k-1)\kappa _G(S)+1+|L|+e_T(L, L)=|L|k+1+(k-1)(\kappa _G(S)-|L|)+e_T(L, L)\ge |L|k+1$, that is, there exists at least one vertex of L with degree at least $k+1$. So G has no k-tree containing S. Therefore the condition (1) is sharp.

In Theorem 5, given $S=V(G)$, by Menger’s theorem, we obtain the following result which is an extension of Theorem 1:

Theorem 6

(Neumann-Lara and Rivera-Campo [5]) Let k be an integer with $k\ge 2$ and let G be a connected graph. If $\alpha (G)\le (k-1)\kappa (G)+1$, then G has a spanning k-tree.

In [4], the authors gave not only an independence number condition but also a degree sum condition for the existence of a k-tree containing specified vertices. In this paper, we give a sharp independence number condition for the existence of a k-tree containing specified vertices. It is natural to ask the following problem.

Problem 1

Find a sharp degree sum condition for a graph to have a k-tree containing specified vertices.

In order to prove Theorem 5, we prove the following result which implies Theorem 5.

Theorem 7

Let G be a connected graph and let k be an integer with $k\ge 2$. Let S be a vertex set of G. Then either G has a k-tree covering S, or there exists a k-tree T in G such that

$$\begin{aligned} \alpha _G(S-V(T))\le \alpha _G(S)-(k-1)\kappa _G(S)-1. \end{aligned}$$

(2)

2 Proof of the Results

In order to prove Theorem 7, we need the following Lemmas.

Lemma 1

Let G be a connected graph. Let T be a tree of G with $|T|\ge 2$ and C be a cycle of G. Then there exists a tree $T^*$ of G such that $V(T)\cup V(C)\subseteq V(T^*)$ and $\varDelta (T^*)\le \varDelta (T)+1$.

Proof

We consider two cases: first, $V(T)\cap V(C)=\emptyset$. In this case, since G is a connected graph, there exists a path P connecting T and C. Let $V(P)\cap V(C)=\{u\}$ and $e=ux$ be an edge of C. Then $T^*=T+P+C-e$ is the desired tree of G.

Next we consider $V(T)\cap V(C)\ne \emptyset$. In this case, $T+C$ is a connected subgraph of G and $\varDelta (T+C)\le \varDelta (T)+2$. There exists l vertices $v_1, \ldots , v_l$ in C with $\deg _{T+ C}(v_i)=\deg _T(v_i)+2$($0\le i\le l$). We assign an orientation in C, and for every vertex $v_i$ its successor $v_i^+$ is well-defined. Let $T_1=T+C-\{v_iv_i^+:1\le i\le l\}$. Then $\varDelta (T_1)\le \varDelta (T)+1$ and $V(T_1)=V(T)\cup V(C)$. Therefore, $T_1$ contains a desired tree. $\square$

Lemma 2

Let G be a connected graph and $S\subset V(G)$ with $|S|\ge 2$ and $\kappa _G(S)\ge 2$. Then either the vertices of S can be covered by a cycle of G, or there exists a cycle C of G such that $\alpha _G(S-V(C))\le \alpha _G(S)-\kappa _G(S)$.

The connectivity conditions are only used to find a fan of certain width, which can be found even by the local connectivity condition. Therefore Lemma 2 can be shown by the same way as the proof of [6, Theorem 2].

By Lemma 2, we can obtain the following corollary.

Corollary 1

Let G be a connected graph and $S\subset V(G)$. Then either the vertices of S can be covered by one path of G, or there exists a path P of G such that $\alpha _G(S-V(P))\le \alpha _G(S)-(\kappa _G(S)+1)$.

Proof

Let w be a new vertex not contained in G, joining w to every vertex of G. Let $G^*$ be the resulting graph and $S\subset V(G^*)$. Obviously, $\alpha _{G^*}(S)=\alpha _G(S)$ and $\kappa _{G^*}(S)=\kappa _G(S)+1$. By Lemma 2, S is covered by a cycle D of $G^*$ or there exists a cycle C in $G^*$ such that $\alpha _{G^*}(S-V(C)) \le \alpha _{G^*}(S)-\kappa _{G^*}(S)$.

If the former holds and D passes through w, then S is covered by the path $D-w$ of G; otherwise, S is covered by a path obtained from D by removing an edge of D. If C passes through w, then the path $C-w$ of G satisfies the condition since $S-V(C-w)=S-V(C)$; otherwise, the path $C-e$ obtained from C by removing an edge e of C satisfies the condition since $S-V(C-e)=S-V(C)$. And $\alpha _G(S-V(C))=\alpha _{G^*}(S-V(C)) \le \alpha _{G^*}(S)-\kappa _{G^*}(S)=\alpha _G(S)-(\kappa _G(S)+1)$. Hence the corollary holds. $\square$

Proof of Theorem 7

If G has a k-tree covering S, then the theorem holds. Hence we assume that G has no k-tree containing all vertices of S.

First, we consider $\kappa _G(S)=1$. Choose a k-tree T of G so that

(T1) $|T\cap S|$ is as large as possible,

(T2) $Leaf(T)\subset S$ and Leaf(T) is an independent set of G subject to (T1).

We say T is the desired k-tree of G, that is

$$\begin{aligned} \alpha _G(S-V(T))\le \alpha _G(S)-(k-1)\kappa _G(S)-1=\alpha _G(S)-k. \end{aligned}$$

Otherwise, $\alpha _G(S-V(T))\ge \alpha _G(S)-k+1$. Let $S_0\subset S-V(T)$ be an independent set of G with $|S_0|=\alpha _G(S-V(T))$. By the choice of T, $|Leaf(T)|=l\ge k$. Suppose that $l\le k-1$. Then $\varDelta (T)\le |Leaf(T)|\le k-1$. By assumption, there exists a vertex $v\in S-V(T)$. Since G is a connected graph, there exists a path connecting v and T. We add this path to T and obtain a k-tree which contains more vertices of S than T, which contradicts the condition (T1). Therefore, the claim holds. We shall show that $X=Leaf(T)\cup S_0$ is an independent set of S in G. Let x and y are the vertices of X. By the choice of $S_0$ (or the condition (T2)), if $x, y\in S_0$ (or $x, y\in Leaf(T)$), then x and y are not adjacent in G. Hence we assume that $x\in Leaf(T)$ and $y\in S_0$. If x and y are adjacent in G, then $T+xy$ is a k-tree of G which contains more vertices of S than T, which contradicts the condition (T1). Therefore, X is an independent set of S in G and $|X|=|Leaf(T)|+|S_0|= l+\alpha _G(S-V(T))\ge \alpha _G(S)+1$, contradiction. Therefore, the theorem holds for $\kappa _G(S)=1$.

Next we consider $\kappa _G(S)\ge 2$. We prove this case by induction on k. For $k=2$, by Corollary 1, the theorem holds. Assume the theorem holds for some $k=t\ge 2$, that is, there exists a t-tree T in G such that

$$\begin{aligned} \alpha _G(S-V(T))\le \alpha _G(S)-(t-1)\kappa _G(S)-1. \end{aligned}$$

Let $S_1=S-V(T)$. By Lemma 2, there exists a cycle C such that $\alpha _G(S_1-V(C))\le \alpha _G(S_1)-\kappa _G(S_1)$ or C covers $S_1$. By Lemma  1, there exists a tree $T_1$ such that

$$\begin{aligned} V(T)\cup V(C)\subseteq V(T_1),\quad \text{ and }\quad \varDelta (T_1)\le \varDelta (T)+1\le t+1. \end{aligned}$$

If C covers $S_1$, then $T_1$ is a $(t+1)$-tree covering S, which contradicts the assumption. Hence, the cycle C satisfies $\alpha _G(S_1-V(C))\!\le \! \alpha _G(S_1)-\kappa _G(S_1)$. Obviously, $\alpha _G(S-V(T_1))\!\le \! \alpha _G(S-(V(T)\cup V(C)))=\alpha _G(S-V(T)-V(C))=\alpha _G(S_1-V(C))$. Hence

$$\begin{aligned} \alpha _G(S-V(T_1))&\le \alpha _G(S_1-V(C))\\&\le \alpha _G(S_1)-\kappa _G(S_1)\\&\le \alpha _G(S)-(t-1)\kappa _G(S)-1-\kappa _G(S_1)\\&\le \alpha _G(S)-t\cdot \kappa _G(S)-1. \end{aligned}$$

Hence, the theorem holds for $k=t+1$. Therefore, the theorem holds for all $k\ge 2$ by the principle of mathematical induction. $\square$