The Complexity of the Vertex 3-Colorability Problem for Some Hereditary Classes Defined By 5-Vertex Forbidden Induced Subgraphs

Abstract

We completely determine the complexity status of the vertex 3-colorability problem for the problem restricted to all hereditary classes defined by at most 3 forbidden induced subgraphs each on at most 5 vertices. We also present a complexity dichotomy for the problem and the family of all hereditary classes defined by forbidding an induced bull and any set of induced subgraphs each on at most 5 vertices.

1 Introduction

A coloring is an arbitrary mapping of colors to vertices (or edges) of some graph such that any adjacent vertices (or edges) receive distinct colors. In other words, a coloring of a graph G is an arbitrary mapping $c:V(G)\longrightarrow {\mathbb {N}}$ ($c:E(G)\longrightarrow {\mathbb {N}}$) such that $c(v_1)\ne c(v_2)$ for any adjacent vertices $v_1$ and $v_2$ ($c(e_1)\ne c(e_2)$ for any adjacent edges $e_1$ and $e_2$). A coloring is a k-coloring if the set ${{\mathbb {N}}}$ is replaced by $\overline{1,k}$. We will use this term only for the vertex case.

The edge k-colorability problem (abbreviated as the edge k-col problem) is to verify whether edges of a given graph can be colored in k colors. The vertex k-colorability problem (abbreviated as the k-col problem) is to verify whether vertices of a given graph can be colored in k colors. The chromatic number $\chi (G)$ of a graph G is the minimum number of colors in vertex colorings of G. The coloring problem (abbreviated as the col problem), for a given graph and a number k, is to determine whether its chromatic number is at most k or not. For any $k\ge 3$, the edge k-col and k-col problems are NP-complete. The col problem is also NP-complete.

A graph H is a subgraph of a graph G if H can be obtained from G by deletion of vertices and edges. A graph H is an induced subgraph of a graph G if H is obtained from G by deletion of vertices. A class is a set of simple graphs closed under isomorphism. A class of graphs is hereditary if it is closed under deletion of vertices. It is well known that any hereditary (and only hereditary) graph class ${{\mathcal {X}}}$ can be defined by a set of its forbidden induced subgraphs ${{\mathcal {Y}}}$. We write ${{\mathcal {X}}}=Free({{\mathcal {Y}}})$ in this case, and the graphs in ${{\mathcal {X}}}$ are said to be ${{\mathcal {Y}}}$-free. If ${{\mathcal {Y}}}=\{H\}$, then we will write “H-free” instead of “$\{H\}$-free”. We say that a graph H is $H_s$-free if it does not contain H as a subgraph.

The col problem for H-free graphs can be solved in polynomial time if H is an induced subgraph of a $P_4$ or a $P_3+K_1$, and it is NP-complete in all other cases [11]. A study of forbidden induced pairs was also initiated in [11]. However, when we forbid two induced subgraphs, the situation becomes more difficult. For example, now the computational complexity of the col problem is not known even for some hereditary classes defined by two forbidden induced subgraphs each on at most 4 vertices [13]. Some recent results about the complexity of the col problem restricted to several families of hereditary classes defined by small forbidden induced structures are presented in the papers [5, 7, 9, 15, 17].

The situation for the k-col problem is not clear even when only one induced subgraph is forbidden. The complexity of the 3-col problem is known for all classes of the form $Free(\{H\})$, where $|V(H)|\le 6$ [2]. A similar result for H-free graphs with $|V(H)|\le 5$ was recently obtained for the 4-col problem [6]. For each fixed k, the k-col problem can be solved in polynomial time for $P_5$-free graphs [8]. The 3-col problem can be solved in polynomial time for $P_7$-free graphs [1]. For every $k\ge 5$, the k-col problem is NP-complete in the class of $P_6$-free graphs [10]. Additionally, the 4-col problem is NP-complete for $P_7$-free graphs [10]. On the other hand, at the present time the complexity status of the k-col problem is open for $P_8$-free graphs and $k=3$, for $P_6$-free graphs and $k=4$.

So, there exist many gaps in understanding the complexity of the k-col and the col problems for hereditary classes. There are two ways to increase knowledge in the field. The first of them is to limit the number of forbidden induced subgraphs, the second one is to limit the size of forbidden structures. Bounding the number of forbidden induced structures or their size produces a family of hereditary classes. Possible progress in each of the research directions is to obtain a (partial) complete complexity dichotomy for larger values of the bound.

In this paper, we consider the 3-col problem and hereditary classes defined by forbidden induced subgraphs each on at most 5 vertices. There are complexity dichotomies for the problem and the families {$Free({{\mathcal {S}}})|$ each graph in ${{\mathcal {S}}}$ has at most 4 vertices}, $\{Free(\{H_1,H_2\})|~\max (|V(H_1)|,|V(H_2)|)\le 5\}$ [16]. Prior to our study, there was no a complexity dichotomy for the problem and the family {$Free({{\mathcal {S}}})|~{{\mathcal {S}}}$ has at most 3 graphs each on at most 5 vertices}. In this paper, we present a complexity dichotomy for the 3-col problem in the families: $\{Free(\{H_1,H_2,H_3\})|~\max \limits _{i\in \overline{1,3}}|V(H_i)|\le 5\}$ and {$Free({{\mathcal {S}}})|$  each graph in ${{\mathcal {S}}}$ has at most 5 vertices and $bull\in {{\mathcal {S}}}$}.

2 Notation and Formulation of the Main Result

For a vertex x of a graph, deg(x) means its degree, N(x) is its neighborhood, N[x] denotes its closed neighborhood. For a graph G, $\varDelta (G)$ is maximum degree of its vertices. The sum $G_1+G_2$ is the disjoint union of graphs $G_1$ and $G_2$ with non-intersected sets of vertices.

As usual, $P_n,C_n,K_n,O_n$, and $K_{p,q}$ stand, respectively, for a simple path with n vertices, a chordless cycle with n vertices, a complete graph with n vertices, an empty graph with n vertices, and a complete bipartite graph with p vertices in the first part and q vertices in the second. A k-fan $F_k$ is a graph obtained by connecting a vertex x to all vertices of a simple path $(x_1,\ldots ,x_k)$. A 3-fan is also called a diamond. A k-wheel $W_k$ is a graph obtained by connecting a vertex x to all vertices of a simple cycle $(x_1,\ldots ,x_k)$.

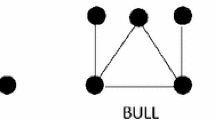
The graphs bull, cricket, butterfly, crown have a vertex set $\{x_{1},x_{2},x_{3},x_{4},x_{5}\}$. The edge set for a bull is $\{x_{1}x_{2},x_{1}x_{3},x_{2}x_{3},x_{1}x_{4},x_{2}x_{5}\}$, for a cricket  is $\{x_{1}x_{2},x_{1}x_{3},x_{2}x_{3},x_{1}x_{4},x_{1}x_{5}\}$, for a butterfly  is $\{x_{1}x_{2},x_{1}x_{3},x_{2}x_{3},x_{1}x_{4},x_{1}x_{5}, x_{4}x_{5}\}$, for a crown  is $\{x_{1}x_{2},x_{1}x_{3},x_{2}x_{3},x_{1}x_{4},x_{2}x_{4},x_{1}x_{5},x_{2}x_{5}\}$. A fish  is the graph obtained by identifying a vertex of a $K_3$ with a degree 2 vertex of a diamond. The graphs diamond, bull, cricket, butterfly, crown, fish are depicted in Figure 1.

Fig. 1

The graphs $diamond,bull,cricket,butterfly,crown,fish$

A spindle is the graph having vertices $x_{1},x_{2},x_{3},x_{4},x_{5},y,z$ and the edges $x_{1}x_{2},x_{2}x_{3},x_{3}x_{4},x_{4}x_{5},x_{5}x_{1}, yx_{1},yx_{2},yx_{3},zx_{4},zx_{5},zx_{1}$. A kite is the graph obtained by adding a new vertex to a diamond and an edge connecting the new vertex with a degree 2 vertex of the diamond. A dart is the graph obtained by adding a new vertex to a diamond and an edge connecting the new vertex with a degree 3 vertex of the diamond. A banner is the graph obtained by adding a new vertex to a $C_4$ and an edge connecting the new vertex with a vertex of the cycle. A house is the graph obtained by adding a new vertex to a $C_4$ and two edges connecting the new vertex with adjacent vertices of the cycle. The graphs spindle, kite, dart, banner, house are depicted in Fig. 2.

Fig. 2

The graphs $spindle, kite, dart, banner, house$

Let us define the following 6 classes of graphs:

• ${{{\mathcal {X}}}^*_1}$ is the set of all forests

• ${{{\mathcal {X}}}^*_2}$ is the set of line graphs of all forests of maximum degree at most 3

• ${{{\mathcal {X}}}^*_3}$ is the set of all graphs in which any 5 vertices induce a subgraph in ${{{\mathcal {X}}}^*_1}\cup {{{\mathcal {X}}}^*_2}\cup \{cricket,kite,diamond+K_1\}$.

• ${{{\mathcal {X}}}^*_4}$ is the set of all graphs in which any 5 vertices induce a subgraph in ${{{\mathcal {X}}}^*_1}\cup {{{\mathcal {X}}}^*_2}\cup \{kite,diamond+K_1,butterfly,crown\}$.

• ${{{\mathcal {X}}}^*_5}$ is the set of all graphs in which any 5 vertices induce a subgraph in ${{{\mathcal {X}}}^*_1}\cup {{{\mathcal {X}}}^*_2}\cup \{kite,diamond+K_1,house,C_4+K_1,F_4,W_4,bull,dart,crown\}$.

• ${{{\mathcal {X}}}^*_6}$ is the set of all graphs in which any 5 vertices induce a subgraph in ${{{\mathcal {X}}}^*_1}\cup {{{\mathcal {X}}}^*_2}\cup \{cricket,bull,house,banner,C_4+K_1,C_5\}$.

All these classes are hereditary. The main result of this paper can be formulated as follows. Let ${{\mathcal {S}}}$ be a set of graphs each on at most 5 vertices such that either ${{\mathcal {S}}}$ has at most 3 graphs or $bull \in {{\mathcal {S}}}$. Then the 3-col problem is polynomial for $Free({{\mathcal {S}}})$ whenever it does not include each of the mentioned 6 classes; otherwise, it is NP-complete.

3 Some New Results on NP-Completeness of the 3-col Problem

A badge is the graph drawn in Fig. 3.

Fig. 3

The graph badge

Lemma 1

The graph badge is 3-colorable. Moreover, in any 3-coloring of a badge, the vertices $x_1,x_2,x_3,x_4$ receive the same color.

Proof

Firstly, we show that a badge is 3-colorable. Assign 1 as the color of $x_1,x_2,x_3,x_4,y_2,y_3$, 2 as the color of $y_1,y_4,u_1,u_2,z_3$, 3 as the color of $z_1,z_2,z_4,u_3,u_4$. The resultant mapping is a 3-coloring. Let c be an arbitrary 3-coloring of a badge. Then, $c(x_1)=c(x_2),c(x_3)=c(x_4), c(u_1)=c(u_2),c(u_3)=c(u_4)$. Clearly, $c(x_1)\ne c(u_1), c(u_2)\ne c(u_3), c(x_2)\ne c(u_3)$. Hence, the vertices $x_1,u_2,u_3$ have pairwise distinct colors. Therefore, $c(x_1)=c(x_2)=c(x_3)=c(x_4)$. $\square$

A spider is the graph drawn in Fig. 4.

Fig. 4

The graph spider

A chevron is the graph drawn in Fig. 5.

Fig. 5

The graph chevron

The following lemma is easy to prove.

Lemma 2

The graph spider is 3-colorable. Additionally, $x,x_1,x_2,x_3,x_4$ have the same color in any 3-coloring of a spider. A chevron has the unique 3-coloring, where $\{x_1,x_2,x_3,x_4\}$, $\{y_1,y_2\}$, and $\{z_1,z_2\}$ are the color classes.

The graph castle is drawn in Fig. 6.

Fig. 6

The graph castle

Lemma 3

The graph castle is 3-colorable. Moreover, in any 3-coloring of a castle, the vertices $x_3$ and $y_3$ receive the same color.

Proof

Firstly, we show that a castle is 3-colorable. Assign 1 as the color of $x_1,z_3,y_1$, 2 as the color of $x_2,z_1,y_2$, 3 as the color of $x_3,z_2,y_3,v_1,v_2$. The resultant mapping is a 3-coloring.

Assume that there is a 3-coloring c of a castle such that $c(x_3)\ne c(y_3)$. We also assume that $c(x_1)=1$ and $c(x_2)=2$. There are the only four possible cases for the value of $(c(y_1),c(y_2))$, they are (1, 3), (3, 2), (2, 3), (3, 1). The first two cases are equivalent, the second two are also equivalent. In the first two cases, there are two vertices in $\{x_1,x_2,y_1,y_2\}$ with the same indices having the same color. In the second two cases, vertices in the set with the same color have different indices. Suppose that $c(y_1)=1$ and $c(y_2)=3$. Hence, $c(z_2)=1,c(v_1)=3,c(v_2)=2$. Therefore, $c(z_3)=1$. We have a contradiction, as $z_2$ and $z_3$ have the same color. Now, suppose that $c(y_1)=2$ and $c(y_2)=3$. Hence, $c(z_2)=1,c(z_1)=3$, and $c(z_3)=2$. The vertex $v_2$ must have the color 2, as $c(x_1)=1$ and $c(y_2)=3$. We have a contradiction, as $v_2$ and $z_3$ receive the same color. So, the initial assumption was false.$\square$

Let G be a graph, x be a vertex of G, whose neighborhood consists of 4 vertices $v_1,v_2,v_3,v_4$. Let H be an arbitrary graph in $\{badge,spider,chevron\}$. An H-implantation to x is to delete x from G, add H and the edges $x_1v_1,x_2v_2,x_3v_3,x_4v_4$. A castle-implantation to x is to delete x from G, add a castle and the edges $v_1x_3,v_2x_3,v_3y_3,v_4y_3$. By Lemmas 1–3, all the resultant graphs are 3-colorable whenever G is 3-colorable.

Lemma 4

The 3-col problem is NP-complete for each of the classes ${{\mathcal {X}}^*_3},{{\mathcal {X}}^*_4},{{\mathcal {X}}^*_5},{{\mathcal {X}}^*_6}$.

Proof

The 3-col problem is NP-complete for the class ${{\mathcal {Y}}}$ of all connected graphs having degrees of all vertices equal to 4 [4]. Let us consider a graph $G\in {{\mathcal {Y}}}$ and an arbitrary graph $H\in \{badge,spider,chevron\}$. We simultaneously apply an H-implantation to all vertices of G. The resultant graph $G'$ belongs to ${{\mathcal {X}}^*_3}$ or ${{\mathcal {X}}^*_4}$ or ${{\mathcal {X}}^*_5}$ if $H=badge$ or $H=spider$ or $H=chevron$, respectively. To justify this fact, let us consider an induced subgraph $G^*$ of $G'$ on at most 5 vertices. If $G^*$ is not connected, then $G^*\in {{\mathcal {X}}^*_1}\cup {{\mathcal {X}}^*_2}$, except the cases, when $G^*=diamond+K_1$ or $G^*=C_4+K_1,H=chevron$. If $G^*$ is connected, then it contains at most one edge in $E(G)\cap E(G')$ or it is isomorphic to a $P_5$. The graph $P_5$ belongs to ${{\mathcal {X}}^*_1}$. Clearly, $G^*$ belongs to one of the classes ${{\mathcal {X}}^*_3},{{\mathcal {X}}^*_4},{{\mathcal {X}}^*_5}$ (depending on the choice of H) whenever $|E(G^*)\cap E(G)|\le 1$. The graph $G'$ is 3-colorable if and only if G is 3-colorable, by Lemmas 1 and 2. Hence, the 3-col problem for ${{\mathcal {Y}}}$ can be polynomially reduced to the same problem for each of the classes ${{\mathcal {X}}^*_3},{{\mathcal {X}}^*_4},{{\mathcal {X}}^*_5}$. Therefore, it is NP-complete for each of them.

The 3-col problem is NP-complete for the class ${{\mathcal {Z}}}$ of all connected triangle-free graphs having degree of every vertex at most 4 [14]. Let $G\in {{\mathcal {Z}}}$. We will simultaneously apply a castle-implantation to all degree 4 vertices of G. Similar to the reasonings from the previous paragraph one can prove that the resultant graph $G''$ belongs to ${{\mathcal {X}}^*_6}$. By Lemma 3, $G''$ is 3-colorable if and only if G is 3-colorable. Thus, the 3-col problem for ${{\mathcal {Z}}}$ can be polynomially reduced to the same problem for ${{\mathcal {X}}^*_6}$. Therefore, it is NP-complete for ${{\mathcal {X}}^*_6}$.$\square$

4 Irreducible Graphs and their Properties

An odd wheel is an arbitrary graph in $\{W_3,W_5,W_7,\ldots \}$. A graph is said to be odd wheel-free if it does not contain an induced odd wheel. This property can be checked in polynomial-time. Since any odd wheel is not 3-colorable, a necessary condition for a graph to be 3-colorable is to be odd wheel-free. Note that a graph is odd wheel-free if and only if it is odd $wheel_s$-free, i.e. it does not contain an odd wheel as a subgraph. This property can be checked in polynomial time because it is equivalent to the property that every neighborhood induces a bipartite subgraph.

If a graph contains a spindle as a subgraph (not necessarily induced), then the graph is not 3-colorable. Hence, a necessary condition for a graph to be 3-colorable is to be $spindle_s$-free. This property can also be tested in polynomial time.

Two non-adjacent vertices of a graph are called twins if they have equal neighborhoods. Two vertices are said to be quasi-twins if the neighborhood of one of them is included in the neighborhood of the second one. If G is a graph, $x,y\in V(G)$, and $N(x)\subseteq N(y)$, then $\chi (G)=\chi (GP{\setminus }\{x\})$. Indeed, one can arrange a color of y from a 3-coloring of $G{\setminus }\{x\}$ to the vertex x to produce a 3-coloring of G.

A cut-vertex of a connected graph G is a vertex x, whose removal disconnects the graph. An x-block of G is any subgraph of G induced by all vertices of a connected component of $G{\setminus }\{x\}$ and x. Verifying that a given vertex is a cut-vertex of G and computing all the corresponding blocks can be done in linear time by the depth first search algorithm. If $G^x_1,\ldots ,G^x_s$ are all x-blocks of G, then $\chi (G)=\max \limits _{i\in \overline{1,s}}(\chi (G^x_i))$.

Clearly, if a vertex x of a graph G has degree at most 2, then G is 3-colorable if and only if $G{\setminus }\{x\}$ is 3-colorable. Moreover, by Brooks’ Theorem [3], a graph G is 3-colorable whenever $\varDelta (G)\le 3$ and G is not isomorphic to a $K_4$.

If $G_1,\ldots ,G_s$ are all connected components of a graph G, then $\chi (G)=\max \limits _{i\in \overline{1,s}}(\chi (G_i))$.

The properties, decompositions, and compressions above lead to consider irreducible graphs, i.e. connected odd wheel- and $spindle_s$-free graphs without pairs of quasi-twins, cut-vertices, vertices of degree at most 2 having maximum degree at least 4. The following lemma is clear.

Lemma 5

For any hereditary class ${{\mathcal {X}}}$, the 3-col problem for ${{\mathcal {X}}}$ can be polynomially reduced to the same problem for the set of all irreducible graphs in ${{\mathcal {X}}}$.

By R(p, q) we denote the corresponding Ramsey number, i.e. minimum number $\nu$ such that every graph with $\nu$ vertices contains an $O_p$ or a $K_q$ as an induced subgraph. As any irreducible graph must be $K_4$-free, the following lemma is true.

Lemma 6

For any irreducible $K_{1,p}$-free graph G, the inequality $\varDelta (G)\le R(p,3)-1$ holds.

As $R(4,3)=9$, for any irreducible $K_{1,4}$-free graph G, the inequality $4\le \varDelta (G)\le 8$ is true. Any vertex of maximum degree of any irreducible $K_{1,4}$-free graph must belong to some triangle of the graph. Indeed, the contrary would imply that in some irreducible $K_{1,4}$-free graph the neighbourhood of some vertex of maximum degree induce an empty graph and this empty graph has at most three vertices. Hence, the graph cannot be irreducible.

Lemma 7

There are no irreducible $\{K_{1,4},diamond,bull\}$-free graphs and $\{K_{1,4},diamond,cricket,butterfly\}$-free graphs.

Proof

Let G be an irreducible $\{K_{1,4},diamond\}$-free graph, x be a vertex of G of maximum degree. Then, there is a triangle (x, y, z), vertices $x'$ and $x''$ each adjacent to x and simultaneously non-adjacent to y and z. If $x'x''\in E(G)$, then G is not butterfly-free, otherwise G is not cricket-free. Hence, there are no irreducible graphs in $Free(\{K_{1,4},diamond,cricket,butterfly\})$. As G is irreducible, each of the degrees of y and z must be at least 3, simultaneously. Hence, there are vertices $y'$ and $z'$ such that $y'\in N(y){\setminus }(N(x)\cup N(z))$ and $z'\in N(z){\setminus }(N(x)\cup N(y))$. If G is bull-free, then $y'z', y'x', y'x'', z'x',z'x''$ are edges of G. Hence, the vertices $x',x'',y',z'$ induce a diamond or a $K_4$ in G. We have a contradiction. Thus, there are no irreducible $\{K_{1,4},diamond,bull\}$-free graphs.$\square$

Lemma 8

Every irreducible $\{kite,cricket,butterfly\}$-free graph is diamond-free. Every irreducible $\{K_{1,4},kite,bull\}$-free graph on at least 8 vertices is diamond-free.

Proof

Assume that there is an irreducible $\{kite,butterfly,cricket\}$-free graph G containing a diamond induced by vertices $x',x'',y,z$, where $x'x''\not \in E(G)$. As $x'$ and $x''$ are not quasi-twins, there are vertices $z'\in N(x'){\setminus }N(x'')$ and $y'\in N(x''){\setminus }N(x')$. Each of the vertices $y'$ and $z'$ belongs to $(N(y){\setminus }N(z))\cup (N(z){\setminus }N(y))$, as G is irreducible and kite-free. Without loss of generality, $z'y\in E(G)$. As G is $\{kite,butterfly\}$-free, $y'z\in E(G)$. Otherwise, $y'\in N(y){\setminus }N(z)$ and $y'z'\not \in E(G)$, as G is odd wheel-free and $y,x',z',y',x''$ induce a butterfly. As $z'$ and z are not quasi-twins, there is a vertex $y''\in N(z'){\setminus }N(z)$. Clearly, $y''$ and $x'$ are adjacent, otherwise $y''y\in E(G)$ and $y''x''\in E(G)$, as G is $\{kite,butterfly\}$-free and $x',z',y'',x'',z,y$ induce a $W_5$. Similarly, there is a vertex $z''\in (N(x'')\cap N(y')){\setminus }(N(y)\cup N(z))$. To avoid an induced kite, $x''y'',y'z',x'z''$ are edges of G. To avoid a cricket induced by $x'',y,z,y'',z''$, the vertices $y''$ and $z''$ must be adjacent. Then, $x',y,z,y'',z''$ induce a butterfly. We have a contradiction with the assumption.

Let G be an irreducible $\{K_{1,4},kite,bull\}$-free graph having at least 8 vertices. We show that G cannot contain an induced cycle $(x_1,x_2,x_3,x_4,x_5,x_6)$ and a vertex x adjacent to all vertices of the cycle. Assume that G contains such a cycle and such a vertex x. As G is connected and $|V(G)|\ge 8$, there is a vertex outside $V'$ having a neighbor in $V'$, where $V'\triangleq \{x,x_1,x_2,x_3,x_4,x_5,x_6\}$. As G is $K_{1,4}$-free, for every vertex outside $V'$ having a neighbor in $V'$, it has a neighbor in $V'{\setminus }\{x\}$. Let y be such a vertex. Let us show that y is adjacent to each of the vertices $x_1,x_2,x_3,x_4,x_5,x_6$. Suppose that $x_1$ and y are adjacent, but y and $x_2$ are not adjacent. If $yx\not \in E(G)$, then $yx_4$ and $yx_5$ are edges of G, to avoid an induced bull. Hence, $x,y,x_5,x_4,x_2$ induce a kite. If x and y are adjacent, then $yx_4\not \in E(G)$ and $yx_6 \not \in E(G)$, as G is odd wheel-free. Hence, $x,y,x_2,x_4,x_6$ induce a $K_{1,4}$. We have a contradiction in both cases. Clearly, $N(x)=\{x_1,x_2,x_3,x_4,x_5,x_6\}$, as a possible neighbor of x distinct from $x_1,x_2,x_3,x_4,x_5,x_6$ must be adjacent to each of the 6 vertices and to x, by the previous reasonings from this paragraph and the fact that G is $K_{1,4}$-free. Hence, G would not be odd wheel-free. Therefore, $N(x)\subseteq N(y)$, i.e. x and y are quasi-twins. We have a contradiction with the assumption about the existence of a 6-cycle and a vertex.

Assume that there is an irreducible $\{K_{1,4},kite,bull\}$-free graph G on at least 8 vertices containing an induced diamond. Let $x',x'',y,z,y',z'$ have the same meaning as in the first paragraph up to and including the hypothesis that $z'y\in E(G)$. We show in this paragraph that $yy'\not \in E(G)$, i.e. $y'z\in E(G)$. Suppose the opposite. Clearly, $z'y'\not \in E(G)$, otherwise $z',x',z,x'',y'$, and y induce a $W_5$. As z and $z'$ are not quasi-twins, there is a vertex $z_1\in N(z'){\setminus }N(z)$. Clearly, $z_1\ne y'$. The vertex $z_1$ cannot be adjacent to $x'$, otherwise $x',y,z,z_1,y'$ or $x',z',z_1,z,y'$ induce a bull. Hence, $z_1y\in E(G)$. As z and $y'$ are not quasi-twins, there is a vertex $z_2\in N(y'){\setminus }N(z)$. Clearly, $z_2\ne z'$, $x''z_2\not \in E(G)$, and $z_2y\in E(G)$. Clearly, $z_1\ne z_2$, otherwise $(z,x',z',z_1,y',x'')$ is an induced 6-cycle and y is adjacent to all its vertices. Since G is odd wheel-free, $z_1z_2\not \in E(G)$. Then, $y,z_1,z_2,x',x''$ induce a $K_{1,4}$.

So, $y'$ is adjacent to z and $x''$. As z and $z'$ are not quasi-twins, there is a vertex $y''\in N(z'){\setminus }N(z)$. We may assume that $y''$ is adjacent to $x'$ and $z'$, by a similar argument as above. As G is $spindle_s$-free, $y'y''\not \in E(G)$. Then, $x',y,z,y',y''$ induce a bull. We have a contradiction.$\square$

Lemma 9

Every irreducible $\{K_{1,4},bull,cricket\}$-free graph containing either a $F_4$ or a $W_4$ as an induced subgraph has at most 457 vertices.

Proof

Let G be an irreducible $\{K_{1,4},bull,cricket\}$-free graph. Assume that G contains an induced $F_4$. We use the same notation for vertices of the subgraph as in the definition. We will show that every vertex of G lies from x at distance at most 2. Assume that there is a vertex z of G lying from x at distance 3. Let $(x,x',y,z)$ be a length 3 induced path and $V'\triangleq \{x_1,x_2,x_3,x_4\}$. Clearly, $y\not \in N[x]$ and $N(z)\cap N[x]=\emptyset$. One may assume that $x'\in V'$. Suppose the opposite. Then, $x'\not \in V'$ and $N(y)\cap (\{x\}\cup V')=\emptyset$. Clearly, $x'x_1\not \in E(G)$ and $x'x_4\not \in E(G)$, otherwise both $x'x_1$ and $x'x_4$ are edges of G, to avoid an induced bull. It is impossible, as G is odd wheel-free. To avoid an induced cricket, $x'x_2$ and $x'x_3$ are edges of G. Hence, G is not odd wheel-free. We have a contradiction. So, $x'\in V'$. To avoid a bull induced by a subset of $V'\cup \{x,y,z\}$, either $N(y)\cap V'=V'$ or $N(y)\cap V'=\{x_1,x_4\}$ is true. The first case is impossible, as G is cricket-free. As G is irreducible, y is not a cut-vertex of G. Hence, there is an induced path connecting x and z of length at least 3. Its third vertex must be distinct from y and simultaneously adjacent to $x_1$ and $x_4$. It is impossible, as G is cricket-free and $spindle_s$-free. We have a contradiction with the assumption. As every vertex of G lies from x at distance at most 2 and $\varDelta (G)\le 8$, $|V(G)|\le 1+8+7\cdot 8=65$.

Assume that G has an induced $W_4$ and G is $F_4$-free. We also use the same notation for vertices of the subgraph $W_4$ as in the definition. As $x_1$ and $x_3$ are not quasi-twins, there is a vertex $y_1\in N(x_1){\setminus }N(x_3)$. As G is $\{K_4,F_4\}$-free, $y_1\in N(x_1){\setminus }(N(x_2)\cup N(x_3)\cup N(x_4)\cup N(x))$. Similarly, for any $i=\overline{2,4}$, there is a vertex $y_i\in N(x_i){\setminus }(\bigcup \limits _{j=1,j\ne i}^{4}N(x_j)\cup N(x))$. As G is bull-free, $y_1y_2, y_2y_3,y_3y_4,y_4y_1$ are edges of G. Similarly, $y_1y_3\not \in E(G)$ and $y_2y_4\not \in E(G)$. We will show that every vertex of G lies from x at distance at most 3. Assume that there is a vertex y lying at distance 4 from x. Consider an induced path $(x,a_1,a_2,a_3,y)$. We may consider that $a_1\in V'$. Otherwise, as G is $\{bull,K_4,F_4\}$-free, there are the only following cases: a) $N(a_1)\cap V'=\emptyset$, b) $N(a_1)\cap V'=\{x_1,x_3\}$, c) $N(a_1)\cap V'=\{x_2,x_4\}$. Moreover, $N(a_2)\cap V'=\emptyset$ and $N(a_3)\cap V''=\emptyset$, where $V''\triangleq \{y_1,y_2,y_3,y_4\}$. In case a, $a_1y_1,a_1y_2,a_1y_3,a_1y_4$ are edges of G, as G is bull-free. Since $G\in Free(\{bull,K_4,F_4\})$, $a_2y_1\not \in E(G),a_2y_2\not \in E(G),a_2y_3\not \in E(G),a_2y_4 \not \in E(G)$. Hence, $x,a_1,a_2,y_1,y_2$ induce a cricket. Let us consider case b, case c is similar. As G is $\{F_4,bull\}$-free, $a_1y_1\not \in E(G),a_1y_3\not \in E(G),a_2y_1 \in E(G), a_2y_3\in E(G)$. Hence, $y_1,y_3,a_1,a_2,a_3$ induce a $K_{1,4}$.

So, we assume that $a_1\in V'$. Suppose that $a_1=x_1$. We may also consider that $a_2=y_1$. Otherwise, $N(a_3)\cap V''=\emptyset$, $x,x_1,x_2,y_1,a_2$ induce a graph in $\{F_4, cricket\}$ or the graph bull is induced by one of the sets $\{x_1,x_2,y_1,a_2,a_3\}$ and $\{y_1,x_1,a_2,x,a_3\}$. As G is $\{K_{1,4},bull,cricket\}$-free, $a_3y_1,a_3y_2,a_3y_3,a_3y_4$ are edges of G. Hence, $y_1,y_2,a_1,a_3,a_4$ induce a bull. We have a contradiction with the assumption. So, distance between x and any vertex of G is at most 3. Hence, $|V(G)|\le 1+8+7\cdot 8+7\cdot 7\cdot 8=457$. $\square$

Lemma 10

The 3-col problem can be solved in polynomial time for each of the classes $Free(\{K_{1,4},bull,cricket,crown\})$ and $Free(\{K_{1,4},bull,cricket,butterfly\})$.

Proof

Let G be an irreducible $\{K_{1,4},bull,cricket\}$-free graph. By Lemma 9, we may assume that it is $\{F_4,W_4\}$-free. Let us show that $\varDelta (G)=4$. Let v be a vertex of G having neighbors $v_1,v_2,v_3,v_4,v_5$. As G is $\{K_{1,4},K_4,cricket\}$-free, there are three of them inducing a $P_3$ in G. Suppose that $(v_1,v_2,v_3)$ is the induced 3-path. As G is $\{K_4,F_4,W_4\}$-free, neither $v_4$ nor $v_5$ belongs to $N(v_1)\cup N(v_3)$. Hence, $v,v_1,v_3,v_4,v_5$ induce a cricket or a $K_{1,4}$. We have a contradiction.

Suppose that G contains an induced fish. Let $y_1$ and $y_2$ be the degree 3 vertices of the fish, $x_2$ be its degree 4 vertex, $(x_1,y_1,y_2)$ and $(x_2,z_1,z_2)$ are its triangles. We will show that $N(y_1){\setminus }\{y_2\}=N(y_2){\setminus }\{y_1\}$. Assume the opposite. Without loss of generality, one may assume that there is a vertex $y\not \in \{x_1,x_2,y_2\}$ adjacent to $y_1$ and non-adjacent to $y_2$. It cannot be adjacent to each of the vertices $x_1$ and $x_2$, as G is $\{F_4,W_4\}$-free. As G is bull-free, $yz_1$ and $yz_2$ are edges of G. As G is irreducible and $\{F_4,W_4\}$-free, there is a vertex $x\in N(x_1){\setminus }(N(x_2)\cup N(y_1)\cup N(y_2))$. To avoid an induced bull, $yx\in E(G)$. To avoid an induced cricket, x must be adjacent to at least one of the vertices $z_1$ and $z_2$. Hence, $x,y,x_2,z_1,z_2$ induce a $F_4$ or a $W_4$. Therefore, $N(y_1){\setminus }\{y_2\}=N(y_2){\setminus }\{y_1\}$ is true. Similarly, if there is a common neighbor of $z_1$ and $z_2$ distinct from $x_2$, then $N(z_1){\setminus }\{z_2\}=N(z_2){\setminus }\{z_1\}$. Such a neighbor must exist, otherwise, there are vertices $z'\in N(z_1){\setminus }N(z_2)$ and $z''\in N(z_2){\setminus }N(z_1)$, as G is irreducible. Recall that the degree of $x_2$ is 4. Hence, as G is bull-free, $z'z'',z'y_1,z'y_2,z''y_1,z''y_2$ are edges of G. We have a contradiction, as G is $K_4$-free. If $deg(y_1)=deg(y_2)=3$, then the graph $H^*$ formed by deleting $x_2,y_1,y_2$ and adding the edges $x_1z_1$ and $x_1z_2$ is 3-colorable if and only if it is so for G. It is not hard to see that $H^*$ is also $\{K_{1,4},bull,cricket\}$-free. So, for any induced fish, we may assume that a diamond included in it must be included in an induced crown.

Let $a_1,a_2,b_1,b_2$ be vertices of G inducing a diamond such that $a_1a_2\not \in E(G)$. Assume that this diamond is not included in an induced crown. Let $N_1\triangleq (N(a_1)\cup N(a_2)){\setminus }\{a_1,a_2,b_1,b_2\}$ and $N_2\triangleq (N(b_1)\cup N(b_2))\setminus \{a_1,a_2,b_1,b_2\}$. As G is $\{K_4,F_4,W_4\}$-free, none of the elements of $N_1$ is adjacent to an element of $\{b_1,b_2\}$, none of the elements of $N_2$ is adjacent to an element of $\{a_1,a_2\}$. As G is irreducible, then $\max (deg(a_1),deg(a_2))\ge 3$. As G is cricket-free, if $deg(a_1)=4$, then its two neighbors each distinct from $b_1$ and $b_2$ must be adjacent. Moreover, one of them is adjacent to $a_2$, otherwise there is a diamond included in an induced fish that is not included in an induced crown. As G is irreducible, $deg(a_2)=4$. Therefore, if $\max (deg(a_1),deg(a_2))=4$, then there are vertices $u_1\in N(a_1){\setminus }N(a_2), u_2\in N(a_2)\setminus N(a_1), u\in N(a_1)\cap N(a_2)$. As G is cricket-free, $uu_2$ is an edge of G. As G is bull-free, $u_1$ and $u_2$ are adjacent. Hence, G is not $spindle_s$-free. So, $deg(a_1)=deg(a_2)=3$.

Suppose that $N_2$ has two elements or one element simultaneously non-adjacent to $b_1$ and $b_2$ or $N_2=\emptyset$. Our aim is to show that G is 3-colorable if and only if $H^{**}\triangleq G{\setminus }\{a_1,a_2,b_1,b_2\}$ is 3-colorable. Since G is bull-free, if $N_2$ has two elements, then they must be adjacent. Assume that $H^{**}$ has a 3-coloring. There is a color (say, 1) distinct from the colors of the vertices in $N_1$. Assign 1 as the color of $a_1$ and $a_2$. If $|N_2|=2$, then its elements have the colors 1 and 2 or 1 and 3 or 2 and 3. In each of the three cases $b_1$ and $b_2$ can be colored in 2 and 3 such that the resultant coloring of G is a 3-coloring. Similarly, G has a 3-coloring whenever $|N_2|\le 1$.

By the previous reasonings and Lemmas 5 and 9, the 3-col problem for $Free(\{K_{1,4},bull,cricket,crown\})$ can be polynomially reduced to the 3-col problem for $Free(\{K_{1,4},bull,diamond,cricket,crown\})$. By Lemma 7, the problem is polynomial for $Free(\{K_{1,4},bull,cricket,crown\})$.

Assume that G is an irreducible $\{K_{1,4},bull,cricket,butterfly,F_4,W_4\}$-free graph. Let $a_1,a_2,b_1,b_2,b_3$ be vertices of G inducing a crown such that $(a_1,a_2,b_1)$, $(a_1,a_2,b_2)$, $(a_1,a_2,b_3)$ are the triangles of the subgraph. Let $N\triangleq \bigcup \limits _{i=1}^{3}N(b_i){\setminus }\{a_1,a_2\}$. We call the set N the neighborhood of the corresponding induced crown. It is easy to see that $deg(b_1)=deg(b_2)=deg(b_3)=3$, i.e. $|N|\le 3$. As G is bull-free, N does not induce a $K_3$. It is easy to verify that G is 3-colorable whenever N has at most 2 elements and $H'\triangleq G{\setminus }\{a_1,a_2,b_1,b_2,b_3\}$ has a 3-coloring. If N has 3 elements, then G is 3-colorable if and only if there is a 3-coloring of $H'$ in which the elements of N receive at most two distinct colors. The graph $G'$ is obtained from $H'$ by adding a new vertex adjacent to all elements of N. In other words, $G'$ can be obtained from G by contracting $\{a_1,a_2,b_1,b_2,b_3\}$ into a single vertex. Notice that the three edges between $\{b_1,b_2,b_3\}$ and N in G also exists in $G'$. Clearly, $G'$ is 3-colorable if and only if there is a 3-coloring of $H'$ in which the elements of N receive at most two distinct colors. In other words, G is 3-colorable if and only if $G'$ is 3-colorable.

By the reasonings above, we may assume that every induced diamond of G is contained in an induced subgraph crown of G, every induced subgraph crown of G has neighborhood with 3 elements. Any two induced copies of a crown have no common vertices. Let $G^*$ be the graph obtained by contracting vertices into a single vertex in every induced copy of a crown in the graph G. As G is 3-colorable if and only if $G'$ is 3-colorable, it is so for G and $G^*$. As G is $\{K_{1,4},cricket,butterfly,F_4,W_4\}$-free, every degree 4 vertex v of G is a degree 3 vertex of an induced diamond. In other words, v is a degree 4 vertex of an induced crown. Hence, $\varDelta (G^*)\le 3$, as $\varDelta (G)=4$. By Brooks’ Theorem, $G^*$ is 3-colorable. Hence, G is 3-colorable. Therefore, the 3-col problem for $Free(\{K_{1,4},bull,cricket,butterfly\})$ can be polynomially reduced to the 3-col problem for $Free(\{K_{1,4},bull,diamond,cricket,butterfly\})$. Hence, by Lemma 7, the lemma holds. $\square$

5 Main Result

Recall that ${{\mathcal {X}}^*_1}$ is the set of all forests, ${{\mathcal {X}}^*_2}$ is the set of all line graphs of forests of maximum degree at most 3. For any $i\in \overline{3,6}$, the class ${{\mathcal {X}}^*_i}$ is the set of all graphs in which any 5 vertices induce a subgraph in:

• ${{\mathcal {X}}^*_1}\cup {{\mathcal {X}}^*_2}\cup \{cricket,kite,diamond+K_1\}$ for $i=3$

• ${{\mathcal {X}}^*_1}\cup {{\mathcal {X}}^*_2}\cup \{kite,diamond+K_1,butterfly,crown\}$ for $i=4$

• ${{\mathcal {X}}^*_1}\cup {{\mathcal {X}}^*_2}\cup \{kite,diamond+K_1,house,C_4+K_1,F_4,W_4,bull,dart,crown\}$ for $i=5$

• ${{\mathcal {X}}^*_1}\cup {{\mathcal {X}}^*_2}\cup \{cricket,bull,house,banner,C_4+K_1,C_5\}$ for $i=6$

Theorem 1

Let ${{\mathcal {S}}}$ be a set of graphs each on at most 5 vertices such that either ${{\mathcal {S}}}$ has at most 3 graphs or $bull\in {{\mathcal {S}}}$. Then, the 3-col problem is NP-complete for ${{\mathcal {X}}=Free({{\mathcal {S}}})}$ if ${{\mathcal {X}}}$ includes at least one of the classes ${{\mathcal {X}}^*_1}$–${{\mathcal {X}}^*_6}$. It is polynomial-time solvable for each of the remaining cases.

Proof

It is known that the 3-col and the edge 3-col problems are NP-complete for $Free(\{C_3,C_4,\ldots ,C_k\})$ for every $k\ge 3$ [12]. Hence, for every $k\ge 3$, the 3-col problem is NP-complete for the class of line graphs of all $\{C_3,C_4,\ldots ,C_k\}$-free graphs of maximum degree at most 3. Therefore, the 3-col problem is NP-complete for ${{\mathcal {X}}}$ if ${{\mathcal {X}}^*_1}\cap {{\mathcal {S}}}=\emptyset$ or ${{\mathcal {X}}^*_2}\cap {{\mathcal {S}}}=\emptyset$. In other words, when ${\mathcal X}\supseteq {{\mathcal {X}}^*_1}$ or ${{\mathcal {X}}}\supseteq {{\mathcal {X}}^*_2}$. The 3-col problem is NP-complete for each of the classes ${{\mathcal {X}}^*_3},{{\mathcal {X}}^*_4},{{\mathcal {X}}^*_5},{{\mathcal {X}}^*_6}$, by Lemma 4. Hence, the problem is NP-complete for ${{\mathcal {X}}}$ if it includes at least one of the classes ${{\mathcal {X}}^*_1}$–${{\mathcal {X}}^*_6}$.

Assume that ${{\mathcal {X}}^*_1}\nsubseteq {{\mathcal {X}}},{{\mathcal {X}}^*_2}\nsubseteq {{\mathcal {X}}},{{\mathcal {X}}^*_3}\nsubseteq {{\mathcal {X}}},{{\mathcal {X}}^*_4}\nsubseteq {{\mathcal {X}}},{{\mathcal {X}}^*_5}\nsubseteq {{\mathcal {X}}},{{\mathcal {X}}^*_6}\nsubseteq {{\mathcal {X}}}$. If $G_1\in {{\mathcal {X}}^*_1}$ and $G_2\in {{\mathcal {X}}^*_2}$ are arbitrary graphs each having at most 5 vertices, $\{G_1,G_2\}\ne \{K_{1,4},bull\}$ and $\{G_1,G_2\}\ne \{K_{1,4},butterfly\}$, then the 3-col problem is polynomial-time solvable for $Free(\{G_1,G_2\})$ [16]. Hence, we may also assume that a $K_{1,4}$ is the unique forest in ${{\mathcal {S}}}$, a bull or a butterfly is an element of ${{\mathcal {S}}}$, $({{\mathcal {X}}^*_2}{\setminus }\{bull,butterfly\})\cap {{\mathcal {S}}}=\emptyset$. Suppose that $bull\in {{\mathcal {S}}}$. As ${{\mathcal {X}}^*_3}\nsubseteq {{\mathcal {X}}}$, ${{\mathcal {S}}}$ contains an element $G'$, which is an induced subgraph of a graph in $\{cricket,kite,diamond+K_1\}$. Hence, $G'\in \{cricket,kite,diamond+K_1,diamond\}$. Clearly, any $H+K_1$-free graph G is H-free or it contains at most $(\varDelta (G)+1)|V(H)|$ vertices. By this fact, Lemmas 7 and 8, the problem is polynomial for ${{\mathcal {X}}}$ if $G'\in \{kite,diamond+K_1,diamond\}$. If $cricket \in {{\mathcal {S}}}$, then $\{butterfly,crown\}\cap {{\mathcal {S}}}\ne \emptyset$, as ${{\mathcal {X}}^*_4}\nsubseteq {{\mathcal {X}}}$. By Lemma 10, the problem is polynomial for ${{\mathcal {X}}}$ in both possible cases. Suppose that $butterfly \in {{\mathcal {S}}}$ and $bull \not \in {{\mathcal {S}}}$. As ${{\mathcal {X}}^*_3}\nsubseteq {{\mathcal {X}}}$, ${{\mathcal {S}}}$ contains a graph $G''\in \{cricket,kite,diamond+K_1, diamond\}$. In other words, ${{\mathcal {S}}}=\{K_{1,4},butterfly,G''\}$. If $G''=cricket$, then ${{\mathcal {X}}}$ includes ${{\mathcal {X}}^*_5}$. If $G''\in \{kite,diamond+K_1,diamond\}$, then ${{\mathcal {X}}}$ includes ${{\mathcal {X}}^*_6}$. The last cases are impossible. $\square$

6 Concluding Remarks and Problems for Future Work

In this paper, we have presented a complexity dichotomy for the 3-col problem in the families: $\{Free(\{H_1,H_2,H_3\})|~\max \limits _{i\in \overline{1,3}}|V(H_i)|\le 5\}$ and $\{Free({{\mathcal {S}}})|$ each graph in ${{\mathcal {S}}}$ has at most 5 vertices and $bull\in {{\mathcal {S}}}\}$. More precisely, if ${{\mathcal {X}}}$ is a class in the families, then the 3-col problem is NP-complete for ${{\mathcal {X}}}$ if ${{\mathcal {X}}}\supseteq {{\mathcal {X}}^*_i}$ for some $i\in \overline{1,6}$, otherwise the problem can be solved in polynomial time for graphs ${{\mathcal {X}}}$. This result has a natural consequence for the col problem, as this problem becomes NP-complete for any class in the families that contains one of the 6 classes of graphs. However, we cannot claim polynomial-time solvability of the col problem for the remaining classes in the families, as some places in the proofs from Section 5 heavily use the assumption that the vertices may only be colored with at most 3 different colors. Clarification of the complexity of the col problem for at least some of these classes is an interesting research problem for future work. Concerning the 3-col problem, the next natural step pushing the research forward is to obtain a complexity dichotomy for all hereditary classes defined by four forbidden induced structures each on at most 5 vertices. Perhaps, such a dichotomy will already give a complete classification for all hereditary classes defined by forbidding induced subgraphs each on at most 5 vertices.