Spanning Tree Decompositions of Complete Graphs Orthogonal to Rotational 1-Factorizations

Abstract

In Krussel et al. (ARS Comb 57:77–82, 2000), Krussel, Marshall, and Verall proved that whenever $2n-1$ is a prime of the form $8m+7$, there exists a spanning tree decomposition of $K_{2n}$ orthogonal to the 1-factorization $GK_{2n}$. In this paper, we develop a technique for constructing spanning tree decompositions that are orthogonal to rotational 1-factorizations of $K_{2n}$. We apply our results to show that, for every $n>2$, there exists a spanning tree decomposition orthogonal to $GK_{2n}$. We include similar applications to other rotational families of 1-factorizations, and provide directions for further research.

1 Introduction

A graph $G=(V,E)$ consists of a finite set V of vertices and a set E of 2-element subsets of V called edges. A 1-factor in G is a set of edges that partition V,  and a 1-factorization is a partition of E into 1-factors. The 1-factorizations of the complete graph $K_{2n}$ are well-studied and we refer to [5, 6] for an introduction to the topic and a survey of many known results.

The number of non-isomorphic 1-factorizations of $K_{2n}$ grows very rapidly with n (see [2]), but one well-known family is denoted $GK_{2n}$, and can be easily described as follows (see Example 1.1 below). Place vertices $1, 2, \ldots , 2n-1$ in a circle around a central vertex labeled 2n. Add the edge $\{ 1, 2n \}$ and the edges $\{i+1, 2n-i \}$ for $0< i < n$ to form a 1-factor. Rotating this 1-factor around vertex 2n gives a partition of the edges of $K_{2n}$ into exactly $2n-1$ different 1-factors. This partition is the 1-factorization known as $GK_{2n}$.

Example 1

A 1-factor (left) of the complete graph $K_8$ (right) can be rotated to partition the edge set, giving the 1-factorization $GK_8$.

A 1-factorization of $K_{2n}$ is said to be rotational (also called 1-rotational) if it is stabilized by a permutation of the vertices that fixes one vertex and cyclically permutes the rest. The 1-factorization $GK_8$ illustrated above is an example, since the permutation $\rho =(1,2,3,\ldots ,7)$ fixes vertex 8 and cyclically permutes the other vertices. In doing so, $\rho$ also cyclically permutes the seven 1-factors of this 1-factorization, thereby stabilizing the set of them. So $GK_8$ is rotational, and analogously, we see that $GK_{2n}$ is rotational for any n. For rotational 1-factorizations (and the more general notions of pyramidal and k-pyramidal 1-factorizations), we refer the reader to [4, 5].

Given any 1-factorization ${\mathcal {F}}$ of $K_{2n}$, we say that a subgraph G is orthogonal to ${\mathcal {F}}$ if each 1-factor of ${\mathcal {F}}$ shares at most one edge with G. For example, the star graph, in which vertex 8 is adjacent to vertices 1 through 7, is a spanning tree for $K_8$ that is orthogonal to the 1-factorization $GK_8$ described above.

To avoid trivialities, let us assume that $n>2$. In [1], Brualdi and Hollingsworth conjectured that for any 1-factorization ${\mathcal {F}}$ of $K_{2n}$, there exists a partition of $K_{2n}$ into n disjoint spanning trees that are orthogonal to ${\mathcal {F}}$. In that same paper, they were able to prove that for any 1-factorization ${\mathcal {F}}$ of $K_{2n}$, there exist at least two disjoint spanning trees that are orthogonal to ${\mathcal {F}}$. In [3], Krussel et al. proved that there were at least three such trees. Regarding the 1-factorization $GK_{2n}$, however, they proved a much stronger result, stated as follows.

Theorem 1

[3, Thm. 3] If $2n-1$ is a prime number of the form $8m+7$ for some integer m, then there exists a full set of n disjoint spanning trees for $K_{2n}$ that are orthogonal to $GK_{2n}$.

In this paper, we develop a technique for finding spanning tree decompositions that are orthogonal to rotational 1-factorizations of $K_{2n}$. Applying our technique, we prove the following.

Theorem 2

For any integer $n>2$, there exists a full set of n disjoint spanning trees for $K_{2n}$ that are orthogonal to $GK_{2n}$.

Because our methods exploit the rotational nature of $GK_{2n}$, we believe that there are similar applications to other rotational families of 1-factorizations. In Sect. 7, we prove Theorem 2 and offer directions for further application of the results.

2 Terminology for Edges in Rotational Subgraphs of $K_{2n}$

We will be considering many different subgraphs of the complete graph $K_{2n}$. We draw such graphs in rotational form, meaning vertices 1 through $2n-1$ are spaced evenly around a circle in clockwise manner, and vertex 2n is placed at the center. An example of a subgraph drawn in rotational form appears in Example 1 above.

Definition 1

Suppose $K_{2n}$ is drawn in rotational form. For any edge $\{a, b\}$, if $2n \not \in \{a, b\}$, we define its length by

$$\begin{aligned} \mathrm{length}\{a, b\} = \mathrm{min}\{ |a-b|, 2n-1-|a-b| \}, \end{aligned}$$

and if $2n \in \{a, b\}$, we say the edge has length 0.

Definition 2

Suppose $K_{2n}$ is drawn in rotational form. For any edge $\{a, b\}$ of nonzero length, we define its center (denoted $\mathrm{center}\{a, b\}$) to be the unique vertex $x \not = 2n$ such that

$$\begin{aligned} \mathrm{length}\{a, x\} = \mathrm{length}\{x, b\}. \end{aligned}$$

For any edge $\{ a, 2n\}$ of length 0, we define the center to be a.

Example 2

A subgraph G of $K_8$ is drawn in rotational form. The length and center are given for each edge.

Note that, in rotational form, any edge of $K_{2n}$ is uniquely determined by its center and length.

3 Starter Graphs and Rotational Families

To obtain a rotational decomposition of $K_{2n}$, we begin with starter graphs, which are graphs drawn in rotational form that contain one edge of each length.

Definition 3

Fix any integer $n>0$ and any n-tuple of integers $(c_0,\ldots ,c_{n-1})$ satisfying $0< c_l <2n$ for each l $(0\le l < n)$. We define the starter graph, denoted $SG(c_0,\ldots ,c_{n-1})$, to be the subgraph of $K_{2n}$ with a single edge of length l and center $c_l$, for each l $(0\le l < n)$.

Example 3

The following are examples of starter graphs.

Definition 4

Suppose G is a subgraph of $K_{2n}$ with edge set E. Let $\rho$ denote the permutation of the vertex set that cyclically permutes $(1,2,3,\ldots ,2n-1)$ and fixes 2n. We define $\rho (G)$ to be the subgraph of $K_{2n}$ with edge set

$$\begin{aligned} \rho (E) = \{ \{ \rho (a), \rho (b) \} \, | \, \{a, b\} \in E \}. \end{aligned}$$

Equivalently, vertices a, b are adjacent in $\rho (G)$ if and only if the vertices $\rho ^{-1}(a)$, $\rho ^{-1}(b)$ are adjacent in G. Observe that, for any edge $\{a,b\}$ and integer i, the edge $\{ \rho ^i(a), \rho ^i(b) \}$ has the same length as $\{a,b\}$ and has center $c+i$, where c is the center of $\{a,b\}$.

Using the above, we can now introduce the notion of a rotational family of subgraphs.

Definition 5

Fix any integers $n,d>0$ and let G be any subgraph of $K_{2n}$. We define the rotational family ${\mathcal {F}}^{d}_G$ generated by G to be the set

$$\begin{aligned} {\mathcal {F}}^{d}_G := \{ G, \rho (G), \ldots , \rho ^{d-1}(G)\} \end{aligned}$$

where $\rho$ is the permutation given in Definition 4.

Proposition 1

Fix any integer $n>0$ and any n-tuple of integers $(c_0,\ldots ,c_{n-1})$ satisfying $0< c_l <2n$ for each l $(0 \le l < n)$. Let $G=SG(c_0,\ldots ,c_{n-1})$. Then the following hold.

• (i) The rotational family ${\mathcal {F}}^{2n-1}_G$ forms a decomposition of $K_{2n}$.

• (ii) If G is a 1-factor, then $\rho ^i(G)$ is a 1-factor for every integer i, and the rotational family ${\mathcal {F}}^{2n-1}_G$ forms a rotational 1-factorization of $K_{2n}$.

Proof

• (i). By way of contradiction, fix any l $(0 \le l < n)$ and suppose that for some i, j $(0 \le i<j<2n-1)$, the graphs $\rho ^i(G)$ and $\rho ^j(G)$ in ${\mathcal {F}}^{2n-1}_G$ share an edge of length l. Then $c_l + i \equiv c_l + j$ (mod $2n-1$), contradicting our choice of i, j. So the graphs in ${\mathcal {F}}^{2n-1}_G$ are pairwise edge-disjoint and partition the edges of $K_{2n}$.

• (ii). By Definition 4, the map $\rho$ is an isomorphism between G and $\rho (G)$. So every graph in ${\mathcal {F}}^{2n-1}_G$ is isomorphic to G, and the result follows. $\square$

4 Three Families of Rotational 1-Factorizations

We will illustrate our results using the following three families of rotational 1-factorizations, the first two of which are fairly common in the literature (see [5, 8]).

Definition 6

Fix any integer $n>0$. The 1-factorization $GK_{2n}$ of $K_{2n}$ is the rotational family ${\mathcal {F}}^{2n-1}_G$ generated by $G=SG(c_0,\ldots ,c_{n-1})$ where

$$\begin{aligned} c_l = 1 \; \text{ for } \text{ all } \; l \; (0 \le l <n). \end{aligned}$$

Definition 7

(Adapted from [8]) Fix any integer $n>0$. The 1-factorization $WK_{2n}$ of $K_{2n}$ is the rotational family ${\mathcal {F}}^{2n-1}_G$ generated by $G=SG(c_0,\ldots ,c_{n-1})$ where $c_l$ is given by the following table, depending on the form of n and l. (When appropriate, entries are to be read modulo $2n-1$.)

	$l< \lceil n/2 \rceil$			$l\ge \lceil n/2 \rceil$
	$l \equiv _4 0$	$l \equiv _4 2$	$l \equiv _4 1, 3$	$l = \lceil n/2 \rceil +2i$	$l = \lceil n/2 \rceil +2i+1$
$n=8k+0$	1	$12k+1$	1	$4k-3i$	$12k-2-3i$
$n=8k+1$	1	$12k+1$	1	$12k+1-3i$	$4k-1-3i$
$n=8k+2$	1	$12k+3$	2	$12k+4-3i$	$4k+1-3i$
$n=8k+3$	1	$12k+5$	1	$4k+1-3i$	$12k+2-3i$
$n=8k+4$	1	$12k+7$	2	$4k+3-3i$	$12k+5-3i$
$n=8k+5$	1	$12k+7$	$16k+9$	$12k+6-3i$	$4k-3i$
$n=8k+6$	1	$12k+9$	1	$12k+9-3i$	$4k+2-3i$
$n=8k+7$	1	$12k+11$	$16k+13$	$4k+2-3i$	$12k+7-3i$

Definition 8

Fix any integer $n>0$. The 1-factorization $HK_{2n}$ of $K_{2n}$ is the rotational family ${\mathcal {F}}^{2n-1}_G$ generated by the graph $G=SG(c_0,\ldots ,c_{n-1})$ where $c_l$ is given by the following table, depending on the form of n and l:

	$l< 2$		$2 \le l \le n-2$		$l > n-2$
	$l = 0$	$l =1$	$l \equiv _2 0$	$l \equiv _2 1$	$l = n- 1$
$n=2k+0$	1	k	$2k-1$	2k	$3k-1$
$n=2k+1$	1	k	2k	$2k+1$	k

5 Opposing Pair Graphs and Their Rotations

To construct spanning trees that are orthogonal to a given rotational 1-factorization, we use rotational families of graphs that are built using opposing pairs of edges. We begin this section by defining these terms.

Definition 9

Suppose $K_{2n}$ is drawn in rotational form and let $e_1$, $e_2$ be any pair of edges with centers $c_1$, $c_2$. We define the distance between them to be

$$\begin{aligned} \mathrm{dist}(e_1, e_2) = \mathrm{length}\{c_1, c_2 \}, \end{aligned}$$

and edges at distance $n-1$ are said to be opposing. Observe that, for any edge pair $\{e_1,e_2\}$ and integer i, we have $\mathrm{dist}(\rho ^i(e_1),\rho ^i(e_2)) = \mathrm{dist}(e_1,e_2).$

Definition 10

Suppose $K_{2n}$ is drawn in rotational form and let $e_1$, $e_2$ be any pair of edges with centers $c_1$, $c_2$. If $c_1 \not = c_2$, we define the direction of the pair $e_1$, $e_2$ to be the vertex

$$\begin{aligned} \mathrm{dir}(e_1, e_2) = \mathrm{center}\{c_1, c_2 \}. \end{aligned}$$

For the case $c_1=c_2$, we set $\mathrm{dir}(e_1, e_2) = c_1.$ Observe that, for any edge pair $\{e_1,e_2\}$ and integer i, we have $\mathrm{dir}(\rho ^i(e_1),\rho ^i(e_2)) = \mathrm{dir}(e_1,e_2)+i.$

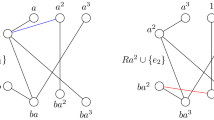
Example 4

A subgraph G of $K_8$ is drawn in rotational form below:

With this terminology in place, we can now define the graphs of interest.

Definition 11

Fix any integers $n > t \ge 0$ and any n-tuple of integers $(d_0,\ldots ,d_{n-1})$ satisfying $0< d_i <2n$ for each i $(0\le i < n)$. We define the opposing pair graph, denoted $OPG_t(d_0,\ldots ,d_{n-1})$, to be the subgraph of $K_{2n}$ with a single edge of length t and center $d_t$, and, for each $i \not = t$, an opposing pair of edges of length i and direction $d_i$. We refer to t as the exceptional length of the OPG.

Example 5

The following are examples of opposing pair graphs:

Let us next observe that any opposing pair graph can be expressed as a union of a pair of starter graphs.

Proposition 2

Fix any integers $n > t \ge 0$ and any n-tuple of integers $(d_0,\ldots ,d_{n-1})$ satisfying $0< d_i <2n$ for each i $(0\le i < n)$. Let $G=OPG_t(d_0,\ldots ,d_{n-1})$. Then

$$\begin{aligned} G = SG(a_0,\ldots ,a_{n-1}) \cup SG(b_0,\ldots ,b_{n-1}), \end{aligned}$$

where $a_i,b_i \equiv d_i \pm \lfloor n/2 \rfloor$ $\, (\text{ mod } 2n-1)$, respectively, for each $i \not =t$, and where $a_t = b_t = d_t$.

Proof

Let $X^-$, $X^+$ be the two starter graphs in the union above. For each $i \not = t$, the graph $X^-$ has a single edge of length i and center $a_i$, and $X^+$ has a single edge of length i and center $b_i$. These two edges form an opposing pair of length i and direction $d_i$, as desired. When $i=t$, both graphs $X^-$ and $X^+$ share a single edge of length t and center $d_t$. So $X^- \cup X^+$ gives the desired opposing pair graph G. $\square$

Notice that any opposing pair graph in $K_{2n}$ has exactly $2n-1$ edges, which is the same as the number of edges required for a spanning tree of $K_{2n}$. Indeed, the graph $OPG_4(1,2,9,3,6)$, which is the left-most graph depicted in Example 5, is a spanning tree for $K_{10}$. In general, however, an opposing pair graph need not be acyclic. By a standard result about spanning trees [7, p. 68], if S is any set of $2n-1$ edges in $K_{2n}$, then S will be a spanning tree for $K_{2n}$ iff S is acyclic and iff S forms a connected graph on the vertex set.

If we find an opposing pair graph that forms a spanning tree for $K_{2n}$, then it is useful to note that each of its rotations will be spanning trees as well. But unlike the starter graphs in Proposition 1, the rotations of an opposing pair graph do not form a decomposition of $K_{2n}$. If we stop rotating in time, however, we can come fairly close, as the following result indicates.

Proposition 3

Fix any integers $n > t \ge 0$ and any n-tuple of integers $(d_0,\ldots ,d_{n-1})$ satisfying $0< d_i <2n$ for each i $(0\le i < n)$. Let $G=OPG_t(d_0,\ldots ,d_{n-1})$. Then the following hold.

• (i) The graphs in the rotational family ${\mathcal {F}}^{n-1}_G$ are pairwise edge-disjoint.

• (ii) The set of edges in $K_{2n}$ that are not contained in any graph of ${\mathcal {F}}^{n-1}_G$ form a subgraph with exactly $2n-1$ edges.

• (iii) If G is a spanning tree for $K_{2n}$, then every rotation of G is a spanning tree for $K_{2n}$. In particular, every graph in the rotational family ${\mathcal {F}}^{n-1}_G$ is a spanning tree for $K_{2n}$.

Proof

• (i). By way of contradiction, suppose that for some $0 \le i<j<n-1$, the graphs $\rho ^i(G)$ and $\rho ^j(G)$ share an edge of length $x\not = t$. Then by Proposition 2,

  $$\begin{aligned} d_x \pm \lfloor n/2 \rfloor + i \equiv d_x \pm \lfloor n/2 \rfloor + j (\text{ mod } 2n-1). \end{aligned}$$

  But then $j-i \equiv 0, \pm (n-1)$, which is impossible for these values of i, j. Similarly, if $\rho ^i(G)$ and $\rho ^j(G)$ share an edge of length t, then $d_t +i \equiv d_t+j$ contradicting our choice of i, j.

• (ii). Each of the $n-1$ graphs in ${\mathcal {F}}^{n-1}_G$ has $2n-1$ edges, so by (i), their union has $(n-1)(2n-1)$ edges. Since $K_{2n}$ has $n(2n-1)$ edges, the result follows.

• (iii). By Definition 4, the map $\rho$ is an isomorphism between G and $\rho (G)$. So every graph in ${\mathcal {F}}^{n-1}_G$ is isomorphic to G, and the result follows. $\square$

The graph with $2n-1$ edges, mentioned in part (ii) of the above proposition, deserves special attention. We make the following definition.

Definition 12

Fix any integers $n > t \ge 0$ and any n-tuple of integers $(d_0,\ldots ,d_{n-1})$ satisfying $0< d_i <2n$ for each i $(0\le i < n)$. Let $G=OPG_t(d_0,\ldots ,d_{n-1})$. We define the graph $\widetilde{G}$ by

$$\begin{aligned} \widetilde{G} = K_{2n} {\setminus } \left( \bigcup \nolimits _{H \in {\mathcal {F}}^{n-1}_G} H \right) . \end{aligned}$$

In other words, $\widetilde{G}$ is the complementary graph in $K_{2n}$ of the union of the rotational family ${\mathcal {F}}^{n-1}_G$.

Example 6

The complementary graphs $\widetilde{G}$ for the graphs of Example 5:

Note that when $G=OPG_t(d_0,\ldots ,d_{n-1})$, the graph $\widetilde{G}$ has exactly n edges of length t and a single edge of each length $i \not = t$ (see Example 6). Occasionally it happens that both G and $\widetilde{G}$ are spanning trees for $K_{2n}$. When this occurs, G is of great use in constructing an orthogonal spanning tree decomposition.

6 Orthogonality and Opposing Pair Graphs

Theorem 3

Fix any integers $n>t \ge 0$ and fix any two n-tuples of integers $(c_0,\ldots ,c_{n-1})$ and $(d_0,\ldots ,d_{n-1})$ satisfying $0< c_i, d_i <2n$ for each i $(0 \le i <n)$. Let $S=SG(c_0,\ldots ,c_{n-1})$ and $G=OPG_t(d_0,\ldots ,d_{n-1})$. Suppose S is a 1-factor. Then the following hold.

• (i) If G is orthogonal to the 1-factorization ${\mathcal {F}}^{2n-1}_S$, then every rotation of G is orthogonal to ${\mathcal {F}}^{2n-1}_S$. In particular, every graph in the rotational family ${\mathcal {F}}^{n-1}_G$ is orthogonal to ${\mathcal {F}}^{2n-1}_S$.

• (ii) If G is orthogonal to the 1-factorization ${\mathcal {F}}^{2n-1}_S$, then the graph $\widetilde{G}$ is also orthogonal to ${\mathcal {F}}^{2n-1}_S$.

Proof

• (i) If $\rho (G)$ is not orthogonal to ${\mathcal {F}}^{2n-1}_S$, there exists an integer j such that $\rho ^j(S) \in {\mathcal {F}}^{2n-1}_S$ and where $\rho ^j(S)$ shares more than one edge with $\rho (G)$. But then by Definition 4, G shares more than one edge with $\rho ^{j-1}(S) \in {\mathcal {F}}^{2n-1}_S$, so that G is not orthogonal to ${\mathcal {F}}^{2n-1}_S$. By contrapositive, $\rho (G)$ is orthogonal whenever G is, so by repeated application of $\rho$, the result follows.

• (ii) By (i), each of the $n-1$ rotations of G in ${\mathcal {F}}^{n-1}_G$ shares one edge with each of the $2n-1$ rotations of S in the 1-factorization ${\mathcal {F}}^{2n-1}_S$. By Proposition 3(i), these rotations of G are edge-disjoint. This leaves exactly one edge from each 1-factor in ${\mathcal {F}}^{2n-1}_S$ as the set of edges of $\widetilde{G}$, as desired. $\square$

Our next goal is to characterize which opposing pair graphs $OPG_t(d_0,\ldots ,d_{n-1})$ are orthogonal to the 1-factorization generated by a given starter $SG(c_0,\ldots ,c_{n-1})$. To obtain the characterization, we begin with the following lemma, which concerns a partition of a set of integers.

Lemma 1

Fix any integer $n \ge 2$ and subsets $A, B \subseteq \{ 1, 2, \ldots , 2n-1 \}$ such that $|A|=|B|=n-1$ and where

$$\begin{aligned} B \equiv \{a+n \, | \, a \in A \} \quad (\mathrm{{mod}}\; 2n-1). \end{aligned}$$

Then the following are equivalent.

• (i) $A \cup B = \{ 1, 2, \ldots , 2n-2 \}$.

• (ii) $A = \{ n, n+1, \ldots , 2n-2 \} \,$ and $\, B = \{ 1,2, \ldots , n-1 \}$.

Proof

Since (ii) clearly implies (i), it remains to consider the converse. Suppose (i) holds. Then $0 \not \in A$ and it suffices to show that, for any i $(0\le i \le n-2)$, if $i \not \in A$, then $i+1 \not \in A$. To this end, suppose $i \not \in A$. Then $i+n \not \in B$, so $i+n \in A$, forcing $i+2n \in B$. But $i+2n \equiv i+1$, so $i+1 \not \in A$. $\square$

With the above lemma in place, we now characterize the opposing pair graphs that are orthogonal to a given rotational 1-factorization. Without loss of generality, we may restrict our attention to opposing pair graphs that satisfy $d_t=c_t$, in view of Theorem 3(i) above.

Theorem 4

Fix any integers $n>t \ge 0$ and fix any two n-tuples of integers $(c_0,\ldots ,c_{n-1})$ and $(d_0,\ldots ,d_{n-1})$ satisfying $0< c_i, d_i <2n$ for each i $(0 \le i <n)$. Let $S=SG(c_0,\ldots ,c_{n-1})$ and $G=OPG_t(d_0,\ldots ,d_{n-1})$. Suppose S is a 1-factor and suppose $d_t=c_t$. Then the graph G is orthogonal to the 1-factorization ${\mathcal {F}}^{2n-1}_S$ if and only if

$$\begin{aligned} \{ d_i -c_i + (-1)^n \lfloor n/2 \rfloor \}_{i\not = t} \equiv \{1, 2, \ldots , n-1 \} \quad (\mathrm{{mod}}\; 2n-1). \end{aligned}$$

Proof

First note that an edge of length x and center y is in $\rho ^i(S)$ if and only if

$$\begin{aligned} y-c_x \equiv i \quad (\mathrm{{mod}}\; 2n-1). \end{aligned}$$

(1)

The graph G has a single edge of length t with center $d_t=c_t$, and so it shares this edge with the starting 1-factor $S = \rho ^0(S)$. By Proposition 2, for each length $l \not = t$, G has a pair of edges of length l and centers $d_l \pm \lfloor n/2 \rfloor$. Now G is orthogonal to ${\mathcal {F}}^{2n-1}_S$ if and only if it shares exactly 1 edge with each of the other rotations $\rho ^i(S)$ $(1 \le i \le 2n-2)$ in ${\mathcal {F}}^{2n-1}_S$. By (1), this occurs if and only if

$$\begin{aligned} A \cup B = \{ 1, 2, \ldots , 2n-2 \} \end{aligned}$$

where A, B are subsets of $\{ 1, 2, \ldots , 2n-1 \}$ satisfying $A \equiv \{ d_i-c_i-\lfloor n/2 \rfloor \}_{i \not = t}$ and $B \equiv \{ d_i-c_i+\lfloor n/2 \rfloor \}_{i \not = t}$ $\, (\mathrm{{mod}}\; 2n-1).$

When n is even, $B \equiv \{a+n \, | \, a \in A \}$ $\, (\mathrm{{mod}}\; 2n-1).$ So by Lemma 1, G is orthogonal to ${\mathcal {F}}^{2n-1}_S$ if and only if $B = \{1, 2, \ldots , n-1 \}$ as desired. When n is odd, $A \equiv \{b+n \, | \, b \in B \}$ $\, (\mathrm{{mod}}\; 2n-1).$ So by swapping the roles of A and B in Lemma 1, G is orthogonal to ${\mathcal {F}}^{2n-1}_S$ if and only if $A = \{1, 2, \ldots , n-1 \}$ as desired. $\square$

Since there are exactly $(n-1)!$ ways to pair up the elements of the sets appearing on the two sides of the congruence in Theorem 4, we have the following corollary.

Corollary 1

Fix any integers $n>t \ge 0$ and fix any two n-tuples of integers $(c_0,\ldots ,c_{n-1})$ and $(d_0,\ldots ,d_{n-1})$ satisfying $0< c_i, d_i <2n$ for each i $(0 \le i <n)$. Let $S=SG(c_0,\ldots ,c_{n-1})$ and $G=OPG_t(d_0,\ldots ,d_{n-1})$. Suppose S is a 1-factor. Then there are exactly $(n-1)!$ different opposing pair graphs orthogonal to the 1-factorization ${\mathcal {F}}^{2n-1}_S$ that have a single edge of length t and center $d_t=c_t$.

7 Application to Rotational 1-Factorizations

Definition 13

Fix any integer $n>2$. We define $DGK_{2n}$ to be the spanning tree decomposition of $K_{2n}$ given by ${\mathcal {F}}^{n-1}_G \cup \{ \widetilde{G} \}$, where ${\mathcal {F}}^{n-1}_G$ is the rotational family generated by the graph $G=OPG_{n-1}(d_0,\ldots ,d_{n-1})$, and where $d_l$ is given by the following table, depending on the form of n and l. (When appropriate, entries are to be read modulo $2n-1$.)

	$l = 0$	$1 \le l \le n-2$	$l =n-1$
$n=2k+0$	k	$n-(-1)^l(n-\lceil l/2 \rceil )$	1
$n=2k+1$	n	$n-(-1)^l\lceil l/2 \rceil$	1

Proof of Theorem 2

Using the criteria given in Theorems 4 and 3, it is easily verified that the spanning tree decomposition $DGK_{2n}$ of Definition 13 is orthogonal to the 1-factorization $GK_{2n}$ given in Definition 6. We also observe that each graph in $DGK_{2n}$ has exactly $2n-1$ edges. So to prove that these graphs are trees, it suffices to check that they are connected, which is straightforward using Definition 13. $\square$

We suspect that similar families of spanning tree decompositions can be found that are orthogonal to other families of 1-factorizations, as the following result suggests.

Proposition 4

For every integer n $(2<n<11)$, there exist orthogonal spanning tree decompositions of $K_{2n}$ for the 1-factorizations $WK_{2n}$ and $HK_{2n}$.

Proof

For each value of n, the table below gives an opposing pair graph G that is a spanning tree $K_{2n}$ and that is orthogonal to $WK_{2n}$ (respectively $HK_{2n}$). For each of these, the complementary graph $\widetilde{G}$ is also a tree. Accordingly, there is a spanning tree decomposition of $K_{2n}$ given by ${\mathcal {F}}^{n-1}_G \cup \{ \widetilde{G} \}$, where ${\mathcal {F}}^{n-1}_G$ is the rotational family generated by the graph G, and where each tree in the decomposition is orthogonal to $WK_{2n}$ (respectively $HK_{2n}$), as desired. $\square$

n	Opposing pair graph for $WK_{2n}$	Opposing pair graph for $HK_{2n}$
3	$OPG_{2}(3,4,1)$	$OPG_{2}(3,4,1)$
4	$OPG_{3}(4,6,5,1)$	$OPG_{3}(4,6,5,1)$
5	$OPG_{4}(5,7,3,3,1)$	$OPG_{4}(5,4,7,1,1)$
6	$OPG_{5}(8,5,6,4,7,1)$	$OPG_{5}(3,9,10,9,9,1)$
7	$OPG_{6}(7,9,9,10,9,2,1)$	$OPG_{6}(3,10,12,10,10,12,1)$
8	$OPG_{7}(10,11,6,12,10,7,8,1)$	$OPG_{7}(3,12,14,11,13,13,11,1)$
9	$OPG_{8}(7,8,5,12,11,9,11,5,1)$	$OPG_{8}(3,13,16,16,11,13,13,15,1)$
10	$OPG_{9}(11,13,8,15,10,3,19,2,9,1)$	$OPG_{9}(3,15,18,18,13,16,16,15,12,1)$