Cubic Graphs with Large Ratio of Independent Domination Number to Domination Number

Abstract

A dominating set in a graph $G$ is a set $S$ of vertices such that every vertex outside $S$ has a neighbor in $S$; the domination number $\gamma (G)$ is the minimum size of such a set. The independent domination number, written $i(G)$, is the minimum size of a dominating set that also induces no edges. Henning and Southey conjectured $i(G)/\gamma (G) \le 6/5$ for every cubic (3-regular) graph $G$ with sufficiently many vertices. We provide an infinite family of counterexamples, giving for each positive integer $k$ a 2-connected cubic graph $H_k$ with $14k$ vertices such that $i(H_k)=5k$ and $\gamma (H_k)=4k$.

1 Introduction

A dominating set in a graph $G$ is a vertex subset $S$ such that every vertex outside $S$ has a neighbor in $S$. The domination number of $G$, written $\gamma (G)$, is the minimum size of such a set. An independent dominating set in $G$ is a dominating set of vertices that induces no edges. The independent domination number of $G$, written $i(G)$, is the minimum size of such a set. An independent set of vertices is also a dominating set if and only if it is a maximal independent set, so $i(G)$ is the minimum size of a maximal independent set in $G$.

Favaron [3] and Gimbel and Vestergaard [4] proved that if $G$ is an $n$-vertex graph with no isolated vertices, then $i(G) \le n+2-2\sqrt{n}$. However, this bound is not sharp for cubic (3-regular) graphs: Lam, Shiu, and Sun [8] proved that if $G$ is an $n$-vertex connected cubic graph, then $i(G)\le 2n/5$ except for $K_{3,3}$. Possibly the bound can be strengthened by excluding finitely many other examples.

The independent domination number and domination number of a graph may differ greatly: note that $i(K_{m,m})=m$ and $\gamma (K_{m,m})=2$. Barefoot, Harary, and Jones [1] suggested studying the difference between $i(G)$ and $\gamma (G)$ in cubic graphs (see also [2]). They showed that the difference can be about $n/20$ for 2-connected cubic graphs and conjectured that it is bounded for 3-connected cubic graphs. Kostochka [7] disproved that by constructing 3-connected cubic graphs with $130k$ vertices where the difference is at least $k$.

The definition of $i(G)$ yields $\gamma (G)\le i(G) \le \alpha (G)$, where $\alpha (G)$ is the maximum number of pairwise nonadjacent vertices. It is easy to show that if $G$ is regular, then $\alpha (G) \le n/2$, with equality only when $G$ is bipartite. Also, note that $\gamma (G) \ge n/(r+1)$ for an $n$-vertex $r$-regular graph. Thus the difference between $\gamma (G)$ and $i(G)$ is at most $\frac{r-1}{2r+2}n$ for $r$-regular graphs. Goddard, Henning, Lyle, and Southey [5] asked whether a stronger bound than the resulting $n/4$ holds when $r=3$ and a connectivity condition is imposed.

Question 1.1

[5] Does $i(G)-\gamma (G) \le n/16$ hold whenever $G$ is an $n$-vertex 3-connected cubic graph with $n\ge 12$?

Equality is known to hold on two infinite families of examples [5]. Later, a conjecture was posed for the ratio $i(G)/\gamma (G)$.

Conjecture 1.2

(Henning and Southey [6]) If $G$ is a connected cubic graph with sufficiently many vertices, then $i(G)/\gamma (G) \le 6/5$.

In [5] it was shown that $i(G)/\gamma (G) \le 3/2$ for connected cubic graphs $G$, with equality if and only if $G=K_{3,3}$. In [6], it was shown that $i(G)/\gamma (G)\le 4/3$ for connected cubic graphs other than $K_{3,3}$, with equality if and only if $G$ is the cartesian product of $C_5$ and $K_2$.

In this note we provide an infinite family of counterexamples to the conjecture of [6]. For $k\ge 1$, we construct a 2-connected cubic graph $H_k$ with $14k$ vertices such that $i(H_k)=5k$ and $\gamma (H_k)=4k$. These graphs also show that Question 1.1 requires 3-connectedness. However, the first graph $H_1$ is 3-connected, showing that a positive answer to Question 1.1 at least requires restricting to $n\ge 16$. The family also suggests the question of finding the sharpest bound on $i(G)/\gamma (G)$ for cubic graphs that has only finitely many exceptions.

Question 1.3

Does $i(G)/\gamma (G)\le 5/4$ hold whenever $G$ is an $n$-vertex cubic graph with sufficiently many vertices?

2 Counterexamples

We first describe our construction.

Construction 2.1

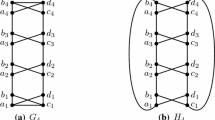
Construct a graph $F$ from the 14-cycle on vertices $x,a^1,\ldots ,a^6,y,b^6,\ldots ,b^1$ in order by adding the chords $a^jb^j$ for $j\in \{1,2,5,6\}$ and $\{a^4b^3,a^3b^4\}$ (see Fig. 1). Given $k$ disjoint copies $F_{1},\ldots ,F_{k}$ of $F$, with $x_i$ and $y_i$ being the copies of $x$ and $y$ in $F_i$, form $H_k$ by adding the edges of the form $y_{i-1}x_i$ (with indices taken modulo $k$).

When $k=1$, the indices $i-1$ and $i$ are congruent modulo $k$, and the construction just adds the edge $yx$ to $F$. The resulting graph $H_1$ is 3-connected. For $k\ge 2$, $H_k$ has connectivity 2. Always $H_k$ has $14k$ vertices and is cubic.

Fig. 1

The graph $F$

Theorem 2.2

$i(H_k)=5k$ and $\gamma (H_k)=4k$.

Proof

First, we prove $\gamma (H_k)=4k$. Since $\{a^1, b^3, b^4, a^6\}$ is a dominating set in $F$, we have $\gamma (H_k) \le 4k$. If $\gamma (H_k) < 4k$, then $H_k$ has a dominating set $S$ such that $|S \cap V(F_i)| \le 3$ for some $i$. Since each vertex dominates only four vertices, both $x_i$ and $y_i$ are dominated by vertices of $S$ outside $F_i$ (which do not exist when $k=1$), and each vertex of $S$ in $F_i$ dominates four vertices not in $\{x_i,y_i\}$. This requires using the copies of $a^2,b^2,a^5,b^5$ in $F_i$ to dominate the copies of $a^1,b^1,a^6,b^6$, which contradicts $|S\cap V(F_i)|\le 3$.

Next, we prove $i(H_k)=5k$. Since $\{a^1,a^4,a^6,b^2,b^4\}$ is an independent dominating set in $F$, we have $i(H_k) \le 5k$. If $i(H_k) < 5k$, then $H_k$ has an independent dominating set $S$ such that $|S \cap V(F_i)| \le 4$ for some $i$. Within the copy $F_i$ of $F$, let $X$ be the set of copies of $\{x,a^1,a^2,a^3,b^1,b^2,b^3\}$, and let $Y$ be the set of copies of $\{a^4,a^5,a^6,b^4,b^5,b^6,y\}$. Indeed, for clarity we keep these names as in Fig. 1, without subscripts.

The only vertices of $X$ that can be dominated by vertices outside $X$ are $x$, $a^3$, and $b^3$. Hence if $|X\cap S|\le 1$, then one vertex must dominate $\{a^1,a^2,b^1,b^2\}$, which is impossible. Since the subgraphs of $F_i$ induced by $X$ and $Y$ are isomorphic, we conclude $|X \cap S| = |Y\cap S|=2$.

Since $S$ cannot contain $\{a^2,b^2\}$ or $\{a^5,b^5\}$, it must contain a vertex in $\{a^3\!,b^3\!,a^4\!,b^4\}$. By symmetry, we may assume $a^4\in S$, and then $a^3,b^3\notin S$. Dominating $b^4$ now requires $b^4$ or $b^5$ in $S$, which leaves no vertex available to dominate $a^6$, since $|Y\cap S|=2$. $\square$