1 Introduction

One of the fundamental goals in machine learning research is to construct models that possess a comprehensive understanding of the world. In the realm of supervised machine learning, two prominent methodologies have emerged: generative approaches and discriminative approaches, which give rise to generative models and discriminative models, respectively. Generative models, relying on joint distributions, capture a broader spectrum of data information and exhibit greater universality, whereas discriminative models focus on conditional distributions. Over the past few decades, significant efforts have been directed toward the exploration of generative models for image generation. Notable approaches include the utilization of generative adversarial networks (GANs) [1,2,3,4], variational autoencoder (VAE) [5,6,7], PixelCNN [8, 9], or diffusion models [10,11,12]. The encoder and decoder modules of autoencoder (AE) and VAE network architectures have found extensive application in various neural network frameworks. Additionally, the investigation of the variational lower bound serves as a typical implementation of optimal transport theory, and advancements in this aspect hold the potential to propel the development of optimal transport theory. Among these models, research on VAE models is regarded as more foundational and significant than others [6, 7, 15, 32].

From a modeling perspective, the VAE follows an autoencoder-like architecture consisting of an encoder and a decoder [13]. The objective is to not only achieve effective reconstruction of the input but also generate a latent representation that is meaningful and informative [14]. In the vanilla VAE, the approximate posterior is restricted to be a multivariate Gaussian with a diagonal covariance structure. However, this modeling approach suffers from non-identifiable. To address this issue, we sample from a more flexible distribution, specifically a mixture of Gaussians, which allows for a richer latent space representation. By incorporating a Gaussian mixture model (GMM) [15], comprising multiple Gaussian distributions, the model’s marginal distribution over observed variables better captures the data characteristics. The effectiveness of Gaussian mixture VAE (GMVAE) has been demonstrated in various existing works. DLGMM [16] employs a mixture of Gaussian distribution as the approximate posterior for VAE, while VaDE [17] replaces the single Gaussian prior of VAE with a mixture of Gaussians, making it suitable for clustering tasks. Similarly, GMVAE [18] assumes a multimodal prior distribution to model complex data. Lee et al. [19] apply variational inference and a mixture of Gaussian prior optimized using the expectation–maximization (EM) algorithm for meta-learning. Additionally, Bai et al. [20] adopt a Gaussian mixture VAE and incorporate a contrastive loss to capture latent correlations for classification. Other works, such as Figueroa et al. [21] for semi-supervised learning, Collier et al. [22] for unsupervised clustering with continuous relaxation of discrete variables, Yang et al. [23]for handling complex spread in deep latent space using graph embedding, and Abdulaziz et al. [24] employing GMVAE with auxiliary loss functions, have also utilized GMVAE for various applications. In this paper, we focus on the generative manner, aiming to improve image synthesis performance with GMVAE. To the best of our knowledge, while some methods combine these approaches, there are distinctions in our specific modeling approach, resulting in superior results compared to existing methods.

In the quest to discover encoding functions that disentangle [25] high-level concepts from each other, the consciousness prior is regarded as one among several tools to guide the learner toward better high-level representations [26]. In the context of VAE-based models, the objective is to capture factors in the latent space through independent variables in the representation, which can be valuable for various downstream tasks. A notable attempt in this direction is the \( \beta \)-VAE [27], which introduced a regularizer hyperparameter, \( \beta \), limit the capacity of the latent channel and exert implicit pressure for independence in the learned posterior. Theoretical analysis of \(\beta \)-VAE based on the information bottleneck principle [28] was provided by Burgess et al. [29]. Hu et al. explored that constraining mean variable alone can achieve better disentanglement and reconstruction performance and introduced mean constraint VAE [30]. Other models, such as FactorVAE [31], \(\beta \)-TCVAE [32], and InfoVAE [33], adopted different regularization approaches, including mutual information reweighting and Hilbert–Schmidt independence criterion (HSIC) [34], to encourage disentanglement and independence between latent variables. Drawing inspiration from the work of Esmaeili et al. [35], who employed a factorized decomposition to encourage independence between groups of latent variables, we apply a similar approach to our loss function. While a deep hierarchy of latent stochastic variables can lead to a more expressive model, no direct connection has been established between disentangling sub-Gaussian distributions within a GMM and introducing the total correlation (TC) term. In our approach, by incorporating the TC term, we establish inter-dependencies among the sub-Gaussian distributions after the hierarchical decomposition. This enables the decoupling of several components within the sub-Gaussian distributions, and we add an extra regularization term to prevent posterior collapse.

Fig. 1
figure 1

Variational autoencoder network architecture with Gaussian mixture prior

Full size image

Another challenging issue in the latent space of Gaussian mixture models is the overlapping and hard-to-classify nature of different sub-distributions. Existing loss functions are insufficient to address this problem effectively. Geometrically, minimizing the variances of sub-Gaussian distributions and maximizing the distances between different sub-Gaussian distributions can effectively tackle this issue, aligning with the principles of Fisher discriminant analysis. The geometric interpretation and optimization framework of Fisher distance have been extensively studied by experts in the field [36]. Building upon this, we establish a theoretical relationship between Fisher distance and Gaussian mixture models. By introducing the Fisher term, our aim is to constrain the distances between samples, thereby maximizing within-class differences and minimizing between-class distances. Through comprehensive experiments and an ablation study, we demonstrate the effectiveness of incorporating the Fisher term.

In summary, our contributions are as follows:

  • Our first contribution is to utilize a more powerful representation model, the Gaussian mixture model (GMM), for fitting the ground truth distribution, and derives ELBO from the Bayesian equation. We enhance the expressiveness of the latent space by constructing a one-sample-one-GM approach, in contrast to the one-sample-one-standard Gaussian distribution in the vanilla VAE. However, validated by experiments, our model is more effective. Furthermore, we also found that the distribution of the coefficient vectors depends on the dimensionality of the latent variables, which results in different distributions of coefficient vectors needing to be chosen for different datasets as well as tasks.

  • Our second contribution is to introduce the decoupling of the total correlation (TC) term into the Gaussian mixture model, which results in the decoupling of individual Gaussian components. We apply the total correlation term to Gaussian mixture distributions, enabling the decoupling of individual sub-Gaussian distributions. In the case of complex latent variables, such as 2 or higher for the dimension of the latent variables, this technique can also be used for hierarchical disentanglement to achieve improved fidelity and diversity.

  • Our third contribution is to address the challenge of hard-to-classify samples. We use the Fisher discriminant as a regularization term. This method helps to minimize within-class distance and maximize between-class distance, which improves clustering quality.

Our experiments and ablation study with various datasets demonstrate the model’s improved performance.

2 Theory and methods

2.1 Gaussian mixture prior

A Gaussian mixture model (GMM) can be seen as a combination of T individual Gaussian models, providing enhanced expressive capabilities by leveraging various probability distributions. Let \({\varvec{z}} = \left( {\varvec{z}}_{1}, {\varvec{z}}_{2},\ldots , {\varvec{z}}_{T} \right) \) denote the set of sub-Gaussian distributions, where \({\varvec{z}}_{i} \sim {\mathcal {N}}(\varvec{\mu }_{i}, \varvec{\sigma }_{i})\). The weighting factor for each sub-Gaussian distribution is \({\varvec{w}} = \left( w_{1}, w_{2},\ldots , w_{T}\right) \), where \(w_{i} \in {\mathbb {R}}\). The calculation method for the latent variable x is as follows:

$$\begin{aligned} x = \sum _{i=1}^{T} w_{i} {\varvec{z}}_{i} = {\varvec{w}}^{T} {\varvec{z}} \end{aligned}$$
(1)

At this moment, the latent variable follows a Gaussian mixture distribution.

In standard VAE, the posterior distribution is combined with a parameter-free isotropic Gaussian prior. The training process involves optimizing two losses simultaneously: the KL divergence and the reconstruction loss. However, calculating the KL divergence between two Gaussian mixture models poses a significant challenge.

Our modeling approach differs from that of Nat et al. [18]. In their experiments, the global data sample is modeled as a Gaussian mixture model, with individual samples belonging to one of the sub-Gaussian distribution spaces. However, their modeling approach is inaccurate, as individual samples still follow a certain Gaussian distribution. In contrast, our model calculates the corresponding K sub-Gaussian distributions and their coefficients from a single sample, yielding a weighted Gaussian mixture distribution. Theoretically, employing more complex modeling techniques leads to improved representation, and the generated data align more closely with real data. Our experiments demonstrate that the images generated by our proposed method are clearer and more distinguishable than those generated by other models.

Fig. 2
figure 2

Probabilistic graphic model for the Gaussian mixture variational autoencoder (GMVAE) showing the generative model (left) and the variational family (right)

Full size image

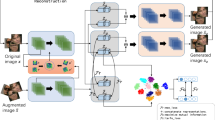
The generation and inference processes of the GMVAE generative model, as depicted in Fig. 1, are trained using the variational inference objective, specifically the evidence lower bound (ELBO), expressed as follows:

$$\begin{aligned} {\mathcal {L}}_\textrm{ELBO}={\mathbb {E}}_{q} \left[ \log \frac{p({\varvec{y}}, {\varvec{x}}, {\varvec{w}}, {\varvec{z}})}{q({\varvec{x}}, {\varvec{w}}, {\varvec{z}} | {\varvec{y}})}\right] . \end{aligned}$$
(2)

where generative model \( p({\varvec{y}}, {\varvec{x}}, {\varvec{w}} , {\varvec{z}})\!=\! p({\varvec{w}}) p({\varvec{z}}) p({\varvec{x}} | {\varvec{w}} , {\varvec{z}}) p({\varvec{y}} | {\varvec{x}}) \), cognition model \( q({\varvec{x}}, {\varvec{w}}, {\varvec{z}}|{\varvec{y}})= q({\varvec{x}} | {\varvec{y}}) q({\varvec{w}} | {\varvec{y}}) q({\varvec{z}} | {\varvec{x}}, {\varvec{w}}) \).

Considering the factorization of the probabilistic graphic model and the nature of logarithmic computation, the ELBO of the GMVAE-generated model can be decomposed as:

$$\begin{aligned} {\mathcal {L}}_\textrm{E L B O}&=\int q({\varvec{x}},{\varvec{w}},{\varvec{z}}|{\varvec{y}})\log \frac{ p({\varvec{w}})}{q({\varvec{w}}|{\varvec{y}})}\cdot \frac{ p({\varvec{z}})}{q({\varvec{z}}|{\varvec{x}},{\varvec{w}})}\nonumber \\&\quad \cdot \frac{p({\varvec{x}}|{\varvec{w}},{\varvec{z}})}{q({\varvec{x}}|{\varvec{y}})} \cdot p({\varvec{y}}|{\varvec{x}}) \textrm{d}q({\varvec{x}},{\varvec{w}},{\varvec{z}}|{\varvec{y}})\nonumber \nonumber \\&=-\underbrace{KL(q({\varvec{w}}|{\varvec{y}})||p({\varvec{w}}))}_{w - \textrm{prior}}\nonumber \\ {}&\quad -\underbrace{{\mathbb {E}}_{q({\varvec{x}}|{\varvec{y}})q({\varvec{w}}|{\varvec{y}})}[KL(q({\varvec{z}}|{\varvec{x}},{\varvec{w}})||p({\varvec{z}}))]}_{z - \textrm{prior}} \nonumber \\&\quad -\underbrace{{\mathbb {E}}_{q({\varvec{w}}|{\varvec{y}})q({\varvec{z}}|{\varvec{x}},{\varvec{w}})}[KL(q({\varvec{x}}|{\varvec{y}})||p({\varvec{x}}|{\varvec{w}},{\varvec{z}}))]}_{\textrm{conditional} \; \textrm{prior}}\nonumber \\ {}&\quad +\underbrace{{\mathbb {E}}_{q({\varvec{x}}|{\varvec{y}})}[\log p({\varvec{y}}|{\varvec{x}})]}_{\textrm{reconstruction} \; \textrm{term}} \end{aligned}$$
(3)

Subsequently, we can identify four sub-terms within the ELBO: w-prior, z-prior, conditional prior, and reconstruction term. The w-prior and z-prior terms impose constraints on the sub-Gaussian distributions and their corresponding coefficients, respectively. These terms aim to align the sub-Gaussian distributions as closely as possible with the standard Gaussian distribution, thereby bringing the Gaussian mixture model closer to the true underlying distribution in the latent space. The conditional prior term ensures that the distribution obtained by sampling from the ground truth aligns as closely as possible with the distribution obtained by sampling from the latent space. Lastly, the reconstruction term evaluates the faithfulness of the model by measuring the proximity of the generated data to the ground truth data. The objective is to generate data that closely resembles the real data, thus enhancing the fidelity of the generative process.

  1. 1.

    W-prior : The weight coefficients of the sub-Gaussian obey different distributions, and the w-prior is calculated differently.

    • Assuming that w follows a Gaussian distribution, the w-prior term is expressed as KL divergence, and the model is denoted as HGMVAE-G.

    • Assuming that w is uniformly distributed, the degeneracy of the w-prior term is the information entropy, and the model is denoted as HGMVAE-U.

  2. 2.

    Z-prior : Unlike GMVAE [18], our approach decomposes the z-prior by introducing a total correlation term. It makes each sub-Gaussian distribution be independent from others, decouple from the latent space, and has stronger controllable generative ability. See the next section for decomposition in detail.

  3. 3.

    Conditional prior : Conditional prior restricts that the latent variables computed from the samples are similar to those obtained by sampling from the mixed Gaussian distribution. In this paper, the KL divergence of the mixed Gaussian model can be expressed as a weighted sum of the KL divergence of the sub-Gaussian distribution, expressed by the formula:

    $$\begin{aligned}&{\mathbb {E}}_{q(w|y)q(z|x,w)}[KL(q(x|y)||p(x|w,z))]\nonumber \\&\quad = \sum _{i} \sum _{j} w_{i} {\hat{w}}_{j} KL({\mathcal {N}}(\varvec{\mu _{i}}, \varvec{\Sigma _{i}}), {\mathcal {N}}(\varvec{{\hat{\mu }}_{j}}, \varvec{{\hat{\Sigma }}_{j}}) ) \end{aligned}$$
    (4)

    \(\varvec{\mu _{i}}\), \(\varvec{\Sigma _{i}}\) denotes the mean and variance calculated from the sample, and \(w_{i}\) denotes the mixing coefficient of the sub-Gaussian distribution in the mixed Gaussian model.

  4. 4.

    Reconstruction term : The computation of the reconstruction term differs depending on the appliance domain. If the downstream task is to generate the data of 0-1 black and white image, the reconstruction term can use the binary cross-entropy loss function. If the generated image is a grayscale or color image, the reconstruction term can use the mean square error (MSE) loss function.

2.2 Methods of disentanglement

In order to make the distributions in GMVAE and their variables disentangleable, we introduce the total correlation (TC) term, which is inspired by hierarchically factorized VAE [35]. For z-prior term,

$$\begin{aligned}&-KL({q({\varvec{z}}|{\varvec{x}}, {\varvec{w}})} ||{p({\varvec{z}})} )\nonumber \\&\quad =-{\mathbb {E}}_{q({\varvec{z}}|{\varvec{x}}, {\varvec{w}})}\frac{{q({\varvec{z}}|{\varvec{x}}, {\varvec{w}})}}{{p({\varvec{z}})}}\nonumber \\&\quad =-{\mathbb {E}}_{q({\varvec{z}}|{\varvec{x}}, {\varvec{w}})} \left[ \log \frac{{q({\varvec{z}}|{\varvec{x}}, {\varvec{w}})} }{\prod _{k} q({\varvec{z}}_{k}|{\varvec{x}}, {\varvec{w}})} +\log \frac{\prod _{k} q({\varvec{x}}_{k}|y)}{\prod _{k} p({\varvec{z}}_{k})}\right. \nonumber \\&\qquad \left. +\log \frac{\prod _{k} p({\varvec{z}}_{k})}{{p({\varvec{z}})}} \right] \nonumber \\&\quad ={\mathbb {E}}_{q({\varvec{z}}|{\varvec{x}}, {\varvec{w}})} \underbrace{ \left[ \log \frac{{p({\varvec{z}})}}{\prod _{k} p({\varvec{z}}_{k})} - \log \frac{{q({\varvec{z}}|{\varvec{x}},{\varvec{w}})} }{\prod _{k} q({\varvec{z}}_{k}|{\varvec{x}}, {\varvec{w}})} \right] }_{A}\nonumber \\&\qquad - \underbrace{\sum _{k} KL\left( q({\varvec{z}}_{k}|{\varvec{x}}, {\varvec{w}})|p({\varvec{z}}_{k}) \right) }_{B} \end{aligned}$$
(5)

In the above equation, \({\varvec{z}} = ( {\varvec{z}}_{1}, \ldots , {\varvec{z}}_{k} )\), where \({\varvec{z}}_{i} \) denotes the sub-latent variables sampled from the sub-Gaussian distribution, and \({\varvec{z}}\) denotes the matrix consisting of the sub-latent variables.

we can decompose it into two sub-components A and B. Term A matches the total correlation between variables in the inference model relative to the total correlation in the generative model. The total correlation can be calculated by the following equation:

$$\begin{aligned} T C({\varvec{z}})= & {} {\mathbb {E}}_{q_{\phi }({\varvec{z}})}\left[ \log \frac{q_{\phi }({\varvec{z}})}{\prod _{k} q_{\phi }\left( {\varvec{z}}_{k}\right) }\right] \nonumber \\= & {} {\text {KL}}\left( q_{\phi }({\varvec{z}}) \Vert \prod _{k} q_{\phi }\left( {\varvec{z}}_{k}\right) \right) \end{aligned}$$
(6)

which introduces disentanglement mechanism naturally. Term B minimizes the KL divergence between the inference marginal and prior marginal for each distribution of GMM \( {\varvec{z}}_{k} \), which is formally identical to Eq. 5.

In cases with complex latent variables, such as when the dimension of the latent variables is 2, the variable of distribution \( {\varvec{z}}_{k} \) contains sub-variables \( {\varvec{z}}_{k,i} \), which means \( {\varvec{z}}_{k} = \left( {\varvec{z}}_{k,1} , \ldots ,{\varvec{z}}_{k,d}\right) \), and we can recursively decompose the KL on the marginals \( {\varvec{z}}_{k} \).

$$\begin{aligned}&-KL\left( q({\varvec{z}}_{k}|{\varvec{x}}, {\varvec{w}})| p({\varvec{z}}_{k}) \right) \nonumber \\&\quad = {\mathbb {E}}_{q({\varvec{z}}|{\varvec{x}}, {\varvec{w}})} \underbrace{ \left[ \log \frac{{p({\varvec{z}}_{k})}}{\prod _{k} p({\varvec{z}}_{k,d})} - \log \frac{{q({\varvec{z}}_{k}|{\varvec{x}}, {\varvec{w}})} }{\prod _{d} q({\varvec{z}}_{k,d}|{\varvec{x}}, {\varvec{w}})} \right] }_{C}\nonumber \\ {}&\qquad - \underbrace{\sum _{d} KL\left( q({\varvec{z}}_{k,d}|{\varvec{x}},{\varvec{w}})| p({\varvec{z}}_{k,d}) \right) }_{D} \end{aligned}$$
(7)

Although Hierarchical KL decomposition has already appeared in hierarchically factorized VAE [35], our use case is not quite the same. Equation 5 makes the individual sub-Gaussian distributions of the mixed Gaussian model statistically independent of each other by introducing a TC term, and Eq. 7 makes the individual components of the sub-Gaussian distributions independent from each other by introducing a total correlation term. If \({\varvec{z}}_{k,d}\) is sufficiently complex, which means \({\varvec{z}}_{k,d} = ({\varvec{z}}_{k,d, 1} \ldots {\varvec{z}}_{k,d, e} )\), we can still continue the hierarchical decomposition similar to hierarchically factorized VAE [35]. But this operation imposes a greater computational cost.

2.3 Fisher term for regularization

In Nat’s experiment [18], each value of \({{\textbf {w}}}\) corresponds to a specific style of the digit, indicating that different sub-Gaussian distributions control different styles. To ensure that each feature is as independent as possible during sampling, it is desirable for samples of the same style to be close to each other and samples of different styles to be far away from each other. This implies that the within-class distance variance should be minimized for samples within the same sub-Gaussian distribution, while the between-class distance should be maximized.

Consequently, the objective becomes one of minimizing the between-class distance and maximizing the within-class distance, aligning with the principles of Fisher discriminant analysis. Building upon this idea, we adopt a latent space consisting of K classes, corresponding to K sub-Gaussian distributions in this paper. Each sub-Gaussian distribution follows \({\mathcal {N}}(w_{i} \varvec{\mu }_{i}, w_{i}^{2} \varvec{\Sigma }_{i})\), where \(w_{i}\) represents the mixture weight of each sub-Gaussian distribution, and \(\varvec{\mu }_{i}\) and \(\varvec{\Sigma }_{i}\) denote the mean and variance of the sub-Gaussian distribution, respectively.

Let \(n_{i}\) be the number of samples sampled from each sub-Gaussian distribution, denoted as \(z_{i,j}\) for the i-th class and the j-th sample. By constructing the samples set \(D=\{z_{i,j}\}\), where the total number of samples is \(N=\sum _{k} n_{i}\), we can proceed to define the between-class covariance matrix \({\varvec{S}}_{B}\) and the within-class covariance matrix \({\varvec{S}}_{W}\).

First, within-class distance \({\varvec{S}}_{k} \in {\mathbb {R}}\) is defined as:

$$\begin{aligned} \begin{aligned} {\varvec{S}}_{k}&= \sum _{n_{i}} ({\varvec{z}}_{i} - w_{i}\varvec{\mu }_{i})({\varvec{z}}_{i} - w_{i}\varvec{\mu }_{i})^{T} \\&= n_{i} w_{i}^{2} \varvec{\Sigma }_{i} \end{aligned} \end{aligned}$$
(8)

Within-class covariance matrix \(S_{W}\) is defined as the sum of the covariance matrices of each class:

$$\begin{aligned} {\varvec{S}}_{W} = \sum _{k} {\varvec{S}}_{k} \end{aligned}$$
(9)

Thus, the definition of the between-class covariance matrix \({\varvec{S}}_{B}\) is obtained as:

$$\begin{aligned} {\varvec{S}}_{B} = \sum _{k=1}^{K} n_{k} (w_{k}\varvec{\mu }_{k} - {\varvec{m}})(w_{k}\varvec{\mu }_{k} - {\varvec{m}})^{T} \end{aligned}$$
(10)

In the training process of this paper, the global mean of the data after processing is 0 using normalization. In the implementation, a weak assumption is introduced: the global mean vector \({\varvec{m}} = {\varvec{0}}\). Then, the between-class covariance matrix \({\varvec{S}}_{B}\) can be written as:

$$\begin{aligned} {\varvec{S}}_{B} = \sum _{k=1}^{K} n_{k} w_{k}^{2} \varvec{\mu }_{k}\varvec{\mu }_{k}^{T} \end{aligned}$$
(11)

We want to maximize the between-class variance and minimize the within-class variance, so we can define the Fisher regularization term \(F_\textrm{reg}\) as:

$$\begin{aligned} tr({\varvec{S}}_{W}^{-1}{\varvec{S}}_{B}) = tr \left( \left( \sum _{k=1}^{K} n_{k} w_{k}^{2} \varvec{\Sigma }_{i} \right) ^{-1} \left( \sum _{k=1}^{K} n_{k} w_{k}^{2} \varvec{\mu }_{k}\varvec{\mu }_{k}^{T}\right) \right) \end{aligned}$$
(12)

Assuming that the number of samples sampled from each sub-Gaussian distribution is the same, i.e., \(n_1=n_2=\cdots =n_k\). The calculation of the Fisher regularization term could be simplified as follows:

$$\begin{aligned} F_\textrm{reg} = tr \left( \left( \sum _{k=1}^{K} w_{k}^{2} \varvec{\Sigma }_{i} \right) ^{-1} \left( \sum _{k=1}^{K} w_{k}^{2} \varvec{\mu }_{k}\varvec{\mu }_{k}^{T}\right) \right) \end{aligned}$$
(13)

So, the total loss can be written as:

$$\begin{aligned} {\mathcal {L}}&=\underbrace{-K L(q({\varvec{w}} \mid y) \Vert p({\varvec{w}}))}_{{\varvec{w}}- \text{ prior } }\nonumber \\ {}&\quad -\underbrace{{\mathbb {E}}_{q(x \mid y) q({\varvec{w}} \mid y)}[K L(q({\varvec{z}} \mid x, {\varvec{w}}) \Vert p({\varvec{z}}))]}_{{\varvec{z}}- \text{ prior } } \nonumber \\&-{\mathbb {E}}_{q(x \mid y)} \underbrace{\left[ \log \frac{p(x \mid {\varvec{w}}, {\varvec{z}})}{\prod _{k} p\left( x_{k} \mid {\varvec{w}}, {\varvec{z}}\right) }-\log \frac{q(x \mid y)}{\prod _{k} q\left( x_{k} \mid y\right) }\right] }_{A}\nonumber \\&-\sum _{k} \underbrace{K L\left( q\left( x_{k} \mid y\right) \Vert p\left( x_{k} \mid {\varvec{w}}, {\varvec{z}}\right) \right) }_{B}\nonumber \\&\quad +\underbrace{{\mathbb {E}}_{q(x \mid y)}[\log p(y \mid x)]}_{\text{ reconstruction } \text{ term } } +F_{reg} \end{aligned}$$
(14)

3 Experiments and evaluations

In this section, we validate the effectiveness of our HGMVAE model on several downstream clustering (3.1), classification (3.2) and generation (3.3) tasks. The conventional VAE typically employs fully connected neural networks to compute the latent variables, which can result in over-fitting and a larger number of data parameters. To address this, we utilize convolutional neural networks (CNNs) in our network architecture. Our CNN model consists of five convolutional layers with a kernel size of \(3\times 3\), followed by two fully connected layers. Notably, we exclude fully connected neural networks and pooling layers in order to retain the essential information of the data. The network is trained using stochastic gradient descent (SGD) optimization, minimizing the KL divergence cost, and initialized with the network parameters from the VAE. Despite the simplicity of our model, it demonstrates excellent performance on the datasets used in this paper. To ensure reliable results, all experiments were conducted 10 times with the same network structure, and the quantitative experimental results were obtained by averaging the outcomes.

3.1 Clustering results

3.1.1 Setup

For our clustering experiments, we primarily utilize the MNIST [37] dataset. We evaluate the performance using three metrics: Silhouette Coefficient (SC) [38], Calinski Harabasz Index (CH) [39], and Davies Bouldin Index (DB) [40]. The SC measures the similarity between samples within the same category and the dissimilarity between samples of different categories. A value closer to 1 indicates high similarity within categories and significant dissimilarity between categories. The CH Index assesses the clustering quality based on the within-class covariance (within-cluster variance) and between-class covariance (between-cluster variance). A higher value signifies smaller within-class covariance, larger between-class covariance, and better clustering performance. The DB Index evaluates the clustering by considering both the within-class distance (within-cluster distance) and between-class distance (between-cluster distance). A smaller value indicates smaller within-class distances and larger between-class distances, reflecting improved clustering results.

3.1.2 Visualization of learned embeddings

We compare our model of different z-prior with GMVAE [18]. The results are presented in Table 1, where the best-performing model is indicated in bold. Across different latent space dimensions, the proposed model in this paper outperforms the GMVAE model.

Table 1 The clustering results on the MNIST dataset
Full size table

In analyzing unsupervised clustering, the behavior of different models across varying latent dimensions can be seen in Fig. 3. Results indicate that clustering with weight coefficients following a Gaussian distribution outperforms when latent variable dimensions are less than 16, while clustering with weight coefficients following the uniform distribution is better for dimensions greater than or equal to 16. This can be explained by the fact that in lower dimensionalities, encoding processes lose more information for different latent variables, creating different importance levels. Conversely, in higher dimensionalities, the information contained in latent variables is relatively consistent, resulting in similar importance levels and learned weight distributions that obey the uniform distribution.

Fig. 3
figure 3

Experimental results of GMVAE, HGMVAE-G, and HGMVAE-U for clustering in latent dimensions of 2, 4, 8, 16, 32, 64, and 128, respectively. From left to right are Silhouette Coefficient (SC), Calinski Harabasz Index (CH), and Davies Bouldin Index (DB), respectively

Full size image

The clustering performance of models with various dimensions on the MNIST dataset is displayed in Fig. 3. The figure reveals that dimension 8 yields the most favorable clustering outcomes. In terms of information encoding, a latent variable with too short dimension results in a loss of information and worsens clustering performance. On the contrary, a latent variable with too long dimension introduces excessive noise and also deteriorates clustering performance. Conducting comparative experiments on the dataset can help identify the optimal latent variable dimensions. To facilitate a clearer observation of the clustering effect in latent space, we present a visualization of the clusters on MNIST in Fig. 4.

Fig. 4
figure 4

Latent space of 10-class dataset with full labels projected by t-SNE [41]

Full size image

3.2 Classification results

Based on our clustering task, we find that clustering is most effective when using 8 dimensions for the latent variables. In our experimentation with the CIFAR10 and MINIST datasets, we train for 10 epochs using 8 dimensions for the latent variables, a learning rate of 0.001, and the AdamW optimizer. We use SVM as our classifier and then compare the impact of the latent variables obtained from different VAE variants in the classification task.

Table 2 The results of classification task on MNIST and CIFAR10 datasets
Full size table

The evaluation metric employed in this paper is classification accuracy. On the CIFAR10 test dataset, HGMVAE_G exhibited an improvement of 1.8% and 3.6% over VAE and GMVAE, respectively. On the MNIST test dataset, both HGMVAE_G and HGMVAE_U outperformed other models in accuracy.

3.3 Generation results

3.3.1 Setup

The most important metric for evaluating the generated task is to calculate the similarity between the generated image and the original image. In this paper, we use four different evaluation metrics. we include four metrics: Fréchet Inception Distance (FID), Structural Similarity (SSIM), Multi-Scale Structural Similarity (MS-SSIM), and Learned Perceptual Image Patch Similarity (LPIPS). FID is primarily used to measure the difference between generated images and real images. SSIM and MS-SSIM are used to measure the structural similarity between two images. SSIM is a single-scale metric, while MS-SSIM considers multiple scales. LPIPS is a deep learning-based metric for assessing the perceptual difference between images. It is used to evaluate the perceptual quality of images. We validate on four datasets: 3D Chair [42], CelebA [43], MNIST [37], and Fashion MNIST [44].

Table 3 shows the generation performance obtained by these baselines; in most cases, our model is the best.

3.3.2 Visualization results

The results are obtained by training 10 epochs with the dimensions of the latent variables chosen as 128, the learning rate chosen as 0.001, and the optimizer chosen as AdamW. Figure 5a shows the fidelity of every two rows. Figure 5b shows gradual change in 2-D latent space, including changes of gender, hair color, hair length, background color, smile angle, and face orientation.

Table 3 Reconstruction performance comparison
Full size table
Fig. 5
figure 5

a Image reconstructions on MNIST. Every two lines represents a reconstruction, the original image is above, while the generated image from ours is below. b Latent manifold on CelebA. Give four images at corners to generate a transformation process between them

Full size image

In order to validate whether a generative model learns disentangled representations, we test its ability to recognize independent components underlying the data. In digit dataset (Fig. 6a), it represents as keeping content unchanged and varying angle, handwritten stroke, width, and thickness of digits. In CelebA (Fig. 6b), it characterized by transformations of size, style of legs or back, material, azimuth, etc.

Fig. 6
figure 6

Latent traversals on MNIST and 3D Chair

Full size image

3.4 Ablation study

We conducted ablation experiments on the clustering and generation tasks using the proposed model in this paper. Our experiments compared different w-prior terms and Fisher regularization terms to determine their impact on performance.

Based on the results presented in Tables 1, 2, and 3, we find that using a more robust Gaussian mixture model for modeling the hidden space can lead to superior performance. However, different distributions of the prior terms also have different effects on performance. Specifically, our results in Tables 4 and  5 show that the one-sample-one-GMM modeling approach outperforms the approach using the Gaussian distribution.

Furthermore, we investigate the impact of the Fisher regularization term on our experiments. We find that incorporating this term makes sub-Gaussian distributions more independent, improving clustering performance. On the generation task, our model without the regularization term has a similar performance as GMVAE, but incorporating the regularization term results in substantial improvements in metrics. For example, on the 3D Chair dataset, HGMVAE-G w/o \(F_\textrm{reg}\) shows a 59.84% improvement in FID, HGMVAE-U w/o \(F_\textrm{reg}\) shows a 65.76% improvement in FID compared to HGMVAE-G, and HGMVAE-U w/o \(F_\textrm{reg}\) shows an increase in FID.

Table 4 Ablation experiment on clustering
Full size table
Table 5 Ablation experiment on generation
Full size table

4 Conclusion

In this paper, we introduce the hierarchical disentanglement in Gaussian mixture variational autoencoder (HGMVAE) as a novel approach for disentangled representation learning tasks. HGMVAE combines the learning of Gaussian mixture latent spaces and the hierarchical disentanglement of feature and label embeddings. Not only does HGMVAE achieve better performance, but it also provides insights into unsupervised clustering and model interpretability. However, it is important to acknowledge that the modeling of the latent space as a Gaussian mixture model and the hierarchical disentanglement of the variational lower bound lead to increased computational costs compared to standard VAEs. Despite this limitation, the benefits and advancements brought about by HGMVAE outweigh these challenges.