1 Introduction

Due to the quick development of advanced information, cloud computing, and Internet of Things (IoT) applications, protection, and individual data security have got extraordinary mindfulness. The main difficulties within the validation frameworks include codes, individual recognizable Proof Identification Numbers (PINs), and passwords. Refined frameworks of individual security can be used for better confirmation and identification. In this way, biometric traits are utilized in different validation, check, and recognizable proof applications. The essential capacity of these biometric frameworks incorporates selecting biometrics for certain people. After that, features are extracted and stored in datasets. Biometric schemes for the security of physiological traits of people, like face, iris, and fingerprint traits, are turning into a broad reality. The issue is that the clients use biometrics forever and cannot change them. It is recommended that irreversible transforms are applied to prevent biometrics from being stolen. To improve the security of fingerprint recognition, different features and algorithms have been proposed.

Generally, passwords and encryption keys are simply known to the client, yet can be utilized without the client's allowance. Accordingly, secrecy can not be achieved. In addition, biometrics like face, voice, and fingerprint can be recorded and abused without the client’s allowance. Therefore, these biometrics can be stolen, forever. Moreover, the stolen biometrics can be used in a cross-coordinating scenario [1].

To overcome the above-mentioned issues, the cancelable biometrics can be used. In a cancelable biometric framework, basic hashing functions or encryption schemes can be used to strengthen the protection and security of the framework. However, the hash functions are susceptible to minor changes in the information interaction. Practically, all biometric changes as indicated by environmental conditions may affect the obtained hash functions. For example, face and iris biometrics are exceptionally affected by light contrast. So, in practice, these functions cannot be used, directly.

In simple biometric encryption schemes, biometric traits are encrypted at the transmitter and decrypted at the receiver to allow authentication or verification using decrypted biometrics. Unfortunately, this strategy allows hacking scenarios as the decrypted biometrics may be stolen. On the other hand, the concept of cancelable biometrics depends on verification or authentication with encrypted or deformed biometrics. This trend of cancelable biometrics prevents cross-matching as a cancelable template can be generated for each application. In addition, it is infeasible for the attackers to try to get the original biometrics from the cancelable templates [2].

The main contributions of this paper can be summarized as follows:

  1. 1.

    Different types of chaotic maps are investigated and compared for biometric encryption.

  2. 2.

    A bio-convolving scheme is investigated, and new biometric encryption schemes are proposed.

  3. 3.

    The suggested encryption schemes are implemented in a cancelable biometric framework.

The contents of this paper are organized as follows. Section 2 gives the related work. Section 3 gives the chaotic map description. Section 4 introduces a scheme for biometric encryption based on convolution kernels. Section 5 introduces the description of the chaos-based cancelable biometric recognition system, its architecture and the authentication metrics. Section 6 gives the simulation results and discussion. Finally, Sect. 7 gives the concluding remarks.

2 Related work

Several strategies for producing cancelable biometric templates were produced in [3] to overcome the problem of cross-matching between biometric databases. These strategies work on fingerprint images to generate multiple cancelable templates. In essence, a user can use biometric identifiers as needed by issuing a new transformation key. The identifiers can be cancelled and replaced, when attacked. These strategies were applied on face and fingerprint biometrics. The biometric templates can be changed in the signal or feature domain. In [4], an alignment-free scheme to produce cancelable fingerprint biometrics was presented. This scheme is based on a circular curtailed convolution algorithm, which is one-way in nature. It can protect the biometric templates without the possibility to retrieve them from the convolution outcomes. This scheme achieves improvement in the ability to generate cancelable templates and the diversity of these templates.

In [5], the authors tried to overcome the problems of security, and trustiness of biometric templates generated from their scheme. This scheme is dependent on Double Random Phase Encoding (DRPE) and cepstral analysis. In the merged biometric template for each person, four biometrics are combined through Discrete Cosine Transform (DCT) compression. To guarantee security, the authors encrypt the unified biometric templates with the DRPE algorithm. The ability to generate cancelable templates is warranted by changing the random phase sequences of the DRPE algorithm. The compression is performed for all four biometrics by maintaining the most significant coefficients in the DCT domain. In the biometric recognition phase, the unified biometric templates are decrypted, and then a cepstral analysis scheme is applied for biometric verification.

In [6], the authors proposed a fingerprint- and finger-vein-based cancelable multi-biometric scheme. This scheme provides template authentication and verification. It merges the minutia-based feature set of fingerprints and the image-based feature set of finger-veins. In [7], the authors studied biometric recognition based on a pore feature-based scheme. This scheme discovers pores in the input fingerprint images with a Convolutional Neural Network (CNN) model. Then, a patch CNN-based descriptor is estimated for each uncovered pore. This high-resolution fingerprint recognition scheme achieves EERs of 2.91% and 0.57% on partial DBI and complete DBII fingerprints for the standard Poly UHRF dataset. In [8], the authors presented a scheme for fingerprint recognition via deep learning using CNNs. In this scheme, fingerprint recognition was conducted on few available samples.

In [9], the authors provided a comprehensive review and insightful analysis of different types of biometric recognition schemes using deep learning. A comprehensive review of all schemes was presented, including network architectures, training data, and strategies. Both face, fingerprint, iris, palm print, ear, voice, signature, and gait recognition were considered in this paper. In [10], a cancelable fingerprint recognition scheme that depends on multiple spiral curves and fuzzy principles was presented. The fuzzy commitment scheme was used to perform encryption of minutiae features. This scheme achieved an EER of 1.17%. The authors of [11] stated that one of the advantages of cancelable biometrics is to save privacy. In order to save privacy, cancelable biometric transformations should be non-invertible. No information about the original biometric templates should be revealed from the cancelable templates. Also, the authors of [11] presented new cancelable biometric schemes based on bio-hashing. Those schemes depend on non-invertible transforms to protect privacy of users.

In [12], the authors presented a feature-based method for generating cancelable templates from 2D face images. The authors have used five public databases in their proposed scheme and used Speeded-Up Robust Features (SURF) and Scale-Invariant Feature Transform (SIFT) for feature extraction. The authors of [13] presented a merging scheme for aligning fingerprint images in the training set, followed by a learning descriptor for all pore patches using a patch matching model based on a CNN. The scheme in [14] presented a new feature descriptor for fake iris detection. This descriptor exploits the relationship between the center pixel and its hexa neighbor. A hexagonal shape using the six-neighbor approach is preferable to the rectangular structure due to its higher symmetry, consistent connectivity, and efficient use of space. The authors of [15] proposed some ideas to improve the bio-hashing scheme. This improved bio-hashing scheme was used to maintain a very low error rate, when nobody steals the hash key, and to reach a good performance when an attacker steals the hash key. The authors in [16] introduced a cancelable biometric recognition scheme based on producing secret keys for cryptographic methods. The authors of [17] proposed a scheme that encrypts the biometric templates, or training images, by convolving them with random convolution kernels. The authors used the seed to generate the random convolution kernels, which are utilized as the Personal Identification Numbers (PINs). The random kernels are saved and used in the authentication process.

In [18], a new architecture for template generation in the context of situation awareness systems in real and virtual applications was presented. The authors of this paper presented a cancelable biometric template generation algorithm using random biometric fusion, and random projection. This random cross-folding scheme generates cancelable biometric templates from multiple biometric traits.

In this paper, we investigate the efficiency of chaotic maps for the generation of cancelable biometric templates. In addition, the effect of chaotic map parameters on the cancelable biometric system is investigated. First, we investigate different types of chaotic maps to be used for the encryption of the biometric templates. Then, we discuss the effect of the kernel size.

3 Chaotic maps

Implementation of chaos-based cryptography depends on chaotic maps. A function whose domain (input) space and range (output) space are chaotic is called a chaotic map. Chaotic maps represent a class of dynamic systems in which time is discrete rather than being continuous. They exhibit a chaotic behavior for specific parameter values. In the next subsections, we present a brief description of some chaotic maps used in this paper.

3.1 Logistic map

Logistic map is a nonlinear dynamic map. It is one of the simple and popular chaotic maps [19]. The logistic map equation is as follows:

$$ X_{n + 1} = rX_{n} (1 - X_{n} ) $$
(1)

where Xn is a value between 0 and 1, n is the iteration index, and r is a positive number between 0 and 4.

  • Bifurcation

This property is referenced as qualitative bifurcation transition from regular behavior to chaotic behavior. It is achieved by changing the control parameter. The bifurcation diagram of the logistic map is shown in Fig. 1. This diagram contains three regions. The convergence region is at \(r \in [0,{\kern 1pt} 3]\). The bifurcation region is at \(r \in [3,{\kern 1pt} 3.57]\), where the phenomenon of period-doubling bifurcation occurs. The chaos region is at \(r \in [3.57,4],\) where there is a chaotic behavior.

  • Lyapunov Exponent

Fig. 1
figure 1

Logistic map bifurcation diagram for \(r \in [0,4]\), X0 = 0.02

Full size image

Lyapunov exponent λ reveals the nature of a chaotic system. It is used as a quantitative metric for the sensitivity to initial conditions. For example, for a discrete system represented as Xn+1 = f(Xn) with an orbit beginning with X0, the Lyapunov exponent can be characterized as follows [20,21,22]:

$$ \lambda { }\left( {X_{0} } \right){ } = { }\mathop {\lim }\limits_{n \to \infty } \frac{1}{n}\mathop \sum \limits_{{i = 1{ }}}^{\infty } \ln \left| {f^{\prime}\left( {X_{i} } \right)} \right| $$
(2)

where f′ is the derivative of f. If λ is above 0, the system is chaotic as the evolution is sensitive to initial conditions. If λ is under 0, the system is not chaotic. If λ is 0, the system is stable, and this represents a steady-state mode. The largest λ defined by Eq. (2) is the Maximal Lyapunov Exponent (MLE). It defines the concept of predictability for a chaotic system.

When r is between 0 and 4, we can plot the Lyapunov exponent of the logistic map with Eq. (2), as shown in Fig. 2. From Fig. 2, we observe that all Lyapunov exponents are equal to 0 or less. The orbit is attracted to a fixed or stable point. When \(r \in [3.57,{\kern 1pt} 4]\), the Lyapunov exponents are larger than zero, leading to a chaotic behavior. The MLE of the logistic map is 0.6785 at r = 4.

Fig. 2
figure 2

Logistic map Lyapunov exponent

Full size image

3.2 Modified logistic map

The modified logistic chaotic map is a development of the classical logistic map given by Eq. (1), where two polynomial terms \((1 - X_{n - 1} )\), and \((1.2 - 2 \times X_{n - 1} )^{2}\) are added to the logistic map equation to enlarge the range of the parameter r. The modified logistic map is defined as follows [23]:

$$ X_{n} = \, r \times X_{n - 1} \times (1 - X_{n - 1} ) \times (1 - X_{n - 1} ) \times (1.2 - 2 \times X_{n - 1} ) \times (1.2 - 2 \times X_{n - 1} ) $$
(3)

where Xn is a value between zero and one, n is the iteration index, and r is a number between 0 and 13.8.

  • Bifurcation

Figure 3 illustrates the bifurcation diagram of the modified logistic map. This chart contains three regions. When \(r \in [0,{\kern 1pt} 3.4]\), this refers to the convergence region. When \(r \in [3.4,5.2]\), this refers to the bifurcation region. Finally, for the chaos region, \(r \in [5.2,13.8]\).

  • Lyapunov exponent

Fig. 3
figure 3

Modified logistic map bifurcation diagram at r \(\in\) [0,13.8], and X0 = 0.02

Full size image

We can plot the Lyapunov exponent of the modified logistic map as shown in Fig. 4. It is clear that when \(r \in [0,{\kern 1pt} 5.2]\), Lyapunov exponent is less than or equal to 0. When \(r \in [5.2,{\kern 1pt} 13.8]\), the Lyapunov exponents are positive, and the dynamic behavior is chaotic. The MLE of the modified logistic map is 1.0317 at r = 13.8. It is higher than the MLE of the classical logistic map.

Fig. 4
figure 4

Lyapunov exponent of the modified logistic map

Full size image

3.3 Classical quadratic map

An essential example of a chaotic system is the quadratic map. The classical quadratic map equation is given by [23]:

$$ X_{n + 1} = r - aX_{n}^{2} $$
(4)

where r is a parameter of the chaotic map, a is constant and n is the iteration index.

  • Bifurcation

Figure 5 shows the bifurcation diagram of the quadratic map. This diagram has three regions. The convergence region is at \(r \in [0,{\kern 1pt} 0.74]\). The bifurcation region is at \(r \in [0.74,1.5]\). The chaos region is at \(r \in [1.5,{\kern 1pt} 2]\).

  • Lyapunov exponent

Fig. 5
figure 5

Classical quadratic map bifurcation diagram

Full size image

Figure 6 shows the Lyapunov exponent of the quadratic map. It is clear that when \(r \in [0,{\kern 1pt} 1.5]\), all Lyapunov exponents are equal to or less than 0. When \(r \in [1.5,{\kern 1pt} 2]\), the Lyapunov exponents are above 0, and hence the behavior is chaotic. The MLE of the quadratic map is 0.6720.

Fig. 6
figure 6

Classical quadratic map Lyapunov exponent

Full size image

3.4 Proposed quadratic maps

The proposed quadratic maps general equation is:

$$ X_{n + 1} = \left( {r + \left( {1 - aX_{n} } \right)^{2} } \right) \bmod 1 $$
(5)

We supplant −(Xn)2 in Eq. (4) with the term (1 − aXn)2 and take the modulo 1 division. For three unique values of a = 2, 4, and 8, we analyze the proposed quadratic maps to illustrate the cycle state, bifurcation region, and Lyapunov exponent. Table 1 summarizes the characteristics of all chaotic maps. It reveals the values of both chaotic parameter r and MLE.

Table 1 Comparison between classical and proposed quadratic maps
Full size table

Figures 7, 8, and 9 show the bifurcation diagrams of the proposed quadratic maps 1, 2, and 3. It is shown that the proposed chaotic quadratic map 3 has a wider range of r that can be used for encryption. Figures 10, 11, and 12 reveal the Lyapunov exponent for quadratic maps 1, 2, and 3. The Lyapunov exponent for quadratic map 3 has positive values for all values of r except for r = {0.11, 1.11,….}. Hence, the MLE of the proposed quadratic map 3 is 3.4709, which is larger than those of the chaotic maps 1 and 2.

Fig. 7
figure 7

Bifurcation diagram of the quadratic map 1

Full size image
Fig. 8
figure 8

Bifurcation diagram of the quadratic map 2

Full size image
Fig. 9
figure 9

Bifurcation diagram of the quadratic map 3

Full size image
Fig. 10
figure 10

Lyapunov exponent of the quadratic map 1

Full size image
Fig. 11
figure 11

Lyapunov exponent of the quadratic map 2

Full size image
Fig. 12
figure 12

Lyapunov exponent of the quadratic map 3

Full size image

4 Encryption based on convolution kernels

The proposed encryption scheme is implemented through convolution with a random kernel generated using a key related to the plain image [24]. First, the convolution kernel is generated with one of the chaotic maps discussed above. The encryption process is performed through convolution operation between the random kernel and the fingerprint image.

5 Chaos-based cancelable biometric system

To maintain the users’ biometrics from hackers and to guarantee the ability to generate cancelable templates, the biometrics need to be encrypted. So, in the case of theft or loss, we can obtain a different encrypted biometric template from the same original biometric pattern. Chaos-based image encryption is very proper for biometric template encryption, as the chaotic maps are very sensitive to initial conditions. By making a small change in the initial conditions of the chaotic map, this radically changes the obtained encrypted biometric that can be reused in the same application. If the cancelable biometrics are stolen, they can be re-issued. In the following subsection, we explain, in detail, the architecture of the cancelable biometric system.

5.1 Architecture

The cancelable biometric system is divided into two phases: the enrollment phase and the authentication phase, as shown in Figs. 13 and 14. In the enrollment phase shown in Fig. 13, a fingerprint capturing device is used to generate the fingerprint images [25]. These images are then convolved with a random convolution kernel. In our scheme, the kernel is generated by a PIN generated by the user. To generate the random convolution kernel, the PIN is used as the initial condition. This random convolution kernel is convolved with the training images to generate the encrypted training templates.

Fig. 13
figure 13

Enrollment stage for cancelable biometric templates

Full size image
Fig. 14
figure 14

Authentication stage for cancelable biometric templates

Full size image

The resulting encrypted training templates can be put away on a card and used afterwards to verify the users’ IDs. If the card is lost or stolen, it is possible to create an alternate wrapping kernel to generate different encoded biometric templates. If the attacker attempts to use the stolen card to reconstruct the users’ biometrics, he or she needs to know the circumvention kernel used in the recording stage. In order for the hackers to retrieve the original model, image decoding must be performed, which is incredibly hard to perform without knowing the client’s PIN and the encryption scheme [17]. Consequently, this is viewed as a significant degree of safety for biometric templates.

In the authentication phase shown in Fig. 14, the user presents an encrypted fingerprint in the same way as in the enrollment phase. The test images are correlated with stored templates. Distributions are generated for the correlation scores in genuine and imposter tests. Hence, a threshold is determined for the approval process for users.

5.2 Authentication metrics

To ensure the similarity between a test encrypted fingerprint and an encrypted biometric template in the dataset, the correlation score is used. The higher the correlation value is, the higher the similarity between patterns. If the individual correlation score is higher than a specific threshold, admittance to the system is confirmed. The scores of unapproved users ought to be consistently lower than those of approved users [26].

Because of various reasons in biometric frameworks, some arrangement mistakes may happen. For example, unapproved templates may create scores higher than those of some approved ones.

The threshold can be chosen to ensure that all unapproved scores do not exceed a predetermined threshold. Hence, the system does not acknowledge any templates, wrongly. In addition, approved templates with scores lower than the predetermined threshold are mistakenly rejected. Hence, we can choose the threshold, so that no authorized pattern is rejected, wrongly. In this case, some unapproved subjects are wrongly recognized. Generally, in a biometric verification system, test information contains approved and unapproved patterns. Scores for each of the approved and unapproved examples will be circulated somehow or another around a mean of the distribution. The mean score of approved templates is higher than that of unapproved templates.

Hence, the tools that can be utilized to check the obtained scores are the Probability of True Distribution (PTD) and the Probability of False Distribution (PFD) of correlation scores obtained in the validation stage. The PTD is the probability of correlation between authorized fingerprints and the encoded biometric templates in the database, while the PFD (unapproved designs) is the probability of correlation between an unauthorized fingerprint and those stored in the database. We allow admittance to the system if the new fingerprint score is higher than the predetermined threshold with a certain probability of error. The probability of correct detection can be easily obtained from the probability of error, and we can obtain a better system performance at lower error probabilities.

6 Simulation results

Our simulations experiments have been implemented on 20 different fingerprints for 20 persons as shown in Fig. 15 [27]. Each fingerprint is of size 300 × 300 pixels. We use the quadratic and logistic chaotic maps with keys related to the plain images. These keys are used to generate the random convolution kernels (see Fig. 16). The initial conditions of these chaotic maps are changed according to the PIN each user presents. Finally, we compare all chaotic maps.

Fig. 15
figure 15

Training fingerprints [27]

Full size image
Fig. 16
figure 16

Corresponding kernel for each fingerprint

Full size image

In the enrollment phase, the user inserts his or her own PIN, and this produces equivalent kernels that are convolved with the training images. The resulting 20 encrypted biometric templates are stored in the database, see Fig. 17.

  • Probability of True Distribution (PTD) and Probability of False Distribution (PFD)

Fig. 17
figure 17

Encrypted training fingerprints with corresponding convolution kernels

Full size image

In the authentication phase, we use two fingerprints for testing. One of them belongs to authorized users, and the other belongs to unauthorized users. In both cases, the test user gives a PIN and produces a random wrap kernel. Hence, we obtain two encoded fingerprints for the test. We assume that the unauthorized person knows the correct PIN for an authorized user to test the system security.

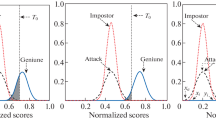
We obtain correlation values between the two encrypted fingerprints and the 20 stored encrypted biometric templates. The PTD and PFD are ploted for the cancelable biometric systems for all chaotic maps to determine the error threshold and probability (see Figs. 18, 19, 20, 21, 22, 23). The intersection of the two curves determines the threshold value according to which we can define whether the user is authorized or not.

Fig. 18
figure 18

PTD and PFD using logistic map for convolution kernel generation

Full size image
Fig. 19
figure 19

PTD and PFD using modified logistic map for convolution kernel generation

Full size image
Fig. 20
figure 20

PTD and PFD using classical quadratic map for convolution kernel generation

Full size image
Fig. 21
figure 21

PTD and PFD using quadratic map 1 for convolution kernel generation

Full size image
Fig. 22
figure 22

PTD and PFD using quadratic map 2 for convolution kernel generation

Full size image
Fig. 23
figure 23

PTD and PFD using quadratic map 3 for convolution kernel generation

Full size image

We examine the proposed quadratic chaotic map 3, because it has a wide range of the parameter r, extended to infinity. Hence, there is no restriction on the PIN chosen by the user. Finally, we compare all chaotic maps. The different sizes of the kernels are illustrated in Table 2.

Table 2 Kernel size
Full size table

In the enrollment phase, the user inserts his or her own PIN, and this creates the corresponding kernel, which is convolved with the fingerprint. In the authentication phase, we use two fingerprints for evaluation. One is for an approved person, and the other is for an unapproved person. In the two cases, the test person embeds the PIN and produces the random convolution kernel. Hence, two encoded test fingerprints can be obtained. The unapproved user is assumed to know the correct PIN for one of the approved users to test the level of security of our system. We get the correlation between the two encrypted fingerprints and the 20 stored encrypted biometric templates for each kernel size.

  • True Acceptance Distribution (TAD) and False Acceptance Distribution (FAD)

We plot the TAD and the FAD as shown in Figs. 24, 25, 26, 27, 28, and 29. The intersection between the two curves determines the threshold value to approve user access.

  • Kernel size effect

Fig. 24
figure 24

TAD and FAD using Z1 kernel

Full size image
Fig. 25
figure 25

TAD FAD using Z2 kernel

Full size image
Fig. 26
figure 26

TAD and FAD using Z3 kernel

Full size image
Fig. 27
figure 27

TAD and FAD using Z4 kernel

Full size image
Fig. 28
figure 28

TAD and FAD using Z5 kernel

Full size image
Fig. 29
figure 29

TAD and FAD using Z6 kernel

Full size image

We study the effect of the kernel size in the enrollment phase, the authentication time, and the threshold value, as shown in Table 3.

Table 3 Kernel size effect
Full size table

As we see from Table 3, for a large kernel size, the threshold value becomes large or close to 1. This case is not preferred since the difference between the correlation distributions of the authorized, and unauthorized scores is very small. As the kernel size is decreased, the threshold value is also decreased until reaching 0.59 for the smallest kernel size of 8 × 8. This means that the distance between the distributions of the correlation for authorized and unauthorized fingerprints is large enough for the system to decide and reject the unauthorized users. The enrollment time, which is used to store the cancelable biometric fingerprints, is decreased as the kernel size is decreased, because the convolution is performed by sliding the kernel over the fingerprint image. As the kernel size is increased, the number of multiplication and addition operations is increased, and then the enrollment time is increased.

  • Chaotic map effect

Now, we study the effect of all chaotic maps we developed in this paper on the threshold value. The EER is used to predetermine the threshold value for the acceptance or rejection of users. The lower the EER value is, the higher the accuracy of the biometric system. As shown in Table 4, the threshold value with all chaotic maps decreased as the kernel size is decreased. However, the difference in the threshold values between all chaotic maps is very small. The reason is that convolving the training fingerprints with any random convolution kernel generated from any chaotic map does not modify the correlation output, significantly. As a result, the authentication reliability is preserved. In addition, different cancelable biometric templates can be created from the same biometric by altering the convolution kernels simply.

  • Performance comparison of different chaotic maps

Table 4 Chaotic map effect
Full size table

We study the effect of the different chaotic maps according to the mean value of the authorized patterns, the mean value of the unauthorized patterns, the value of the threshold, the probability of error, and the authentication time as shown in Table 5. The probability of error is changed according to the chaotic map. The proposed quadratic map 3 achieves the smallest value of error probability among all chaotic maps, with 3.861%. The mean values of the authorized/unauthorized patterns and the authentication times per user are nearly the same for all chaotic maps. The difference in the threshold values between all chaotic maps is very small, since convolving the training images with arbitrary convolution kernels produced from different maps does not modify the subsequent correlation output, significantly. Accordingly, the authentication accuracy is kept high. In addition, by altering the PIN for every user, different cancelable biometric templates can be produced from similar biometrics. This is guaranteed through altering the underlying state of the chaotic map and henceforth altering the convolution kernel.

  • Comparison with Recent Related Studies

Table 5 Chaotic map effect
Full size table

Table 6 provides a comparison between the proposed system that depends on enhanced quadratic map 3 and some other cancelable biometric systems (Sandhya et al. [15], Dahia and Segundo [17], Xu et al. [19], Anand et al. [7]). The results in Table 6 show superior performance with the enhanced quadratic map 3 with good EER values and a small processing burden.

Table 6 Comparison of the EER values for the proposed system with enhanced quadratic map 3 and some other related works
Full size table

7 Conclusion

Encryption and hashing schemes are regularly used to secure biometric templates. There are two issues with these strategies. First, the encoded biometrics need to be decoded for recognition. If the biometrics are decoded, this gives a chance for hacking attempts. Another problem is that minor changes in biometrics affect hash functions, severely. Hence, these functions, in practice, could not be used, directly. The concept of cancelable biometrics is introduced in this paper as a solution for these two problems. We presented a method to produce encrypted biometric templates that can be altered using different convolution kernels generated by different chaotic maps. The utilization of scrambled data in biometric systems allows the implementation of the verification process straightforwardly through a correlation test. Even if the attacker succeeds in stealing the encrypted biometric templates, he needs a deconvolution process with a random kernel generated through a certain key. The effect of the chaotic map on the threshold value, error probability, authentication time, and other parameters has been studied. Finally, a comparison between all the chaotic maps used in this paper show that the utilization of the proposed quadratic map 3 in the cancelable biometric system leads to the smallest error probability among all systems with different chaotic maps. Hence, the cancelable biometric system using the proposed quadratic map 3 has the best performance.