A robust non-rigid point set registration method based on inhomogeneous Gaussian mixture models

Abstract

In this paper, we propose a novel robust non-rigid point set registration method adopting a new probability model called inhomogeneous Gaussian mixture models (IGMM), where we regard one point set as the centroids of a Gaussian mixture model and the other point set as the data. The IGMM is defined by applying local features and Gaussian mixture models. Considering the local relationship among neighboring points is stable, a neighborhood structural descriptor, named as local shape context, is first presented. On the basis of local descriptors, we can obtain a measure of compatibility between local features in the point sets. Then, the similarity of the local structure of point neighborhoods can be calculated on the basis of the matching scores. Each Gaussian mixture component is assigned a different weight depending on the feature similarity, which differs from the traditional Gaussian mixture model where each Gaussian mixture component has the same weight. The proposed IGMM makes point pairs with more similar features have bigger probability to formulate a match, while in algorithms based on GMMs, all point pairs have the same probability to construct correspondence points. Finally, we support our claims through regularization theory and formulate registration as a likelihood maximization problem, which is solved by updating transformation parameters and outlier ratios using the expectation maximization algorithm. Extensive comparison and evaluation experiments on synthetic point-sets datasets demonstrate that the proposed approach is robust and achieves superior performance in the presence of non-rigid deformation, noise, outliers and occlusion. In addition, a number of experiments on real images reveal that our proposed algorithm is more applicable than state-of-the-art algorithms.

1 Introduction

Point set registration is frequently encountered in computer vision, pattern recognition and image analysis [1,2,3], with various applications, such as 3D reconstruction [4], object recognition [5], image retrieval [6], image registration [7,8,9,10]. Generally, the registration problem can be broadly classified as rigid and non-rigid registration. Rigid registration under affine or projective transformation only involves a small number of transformation parameters. The rigid registration problem is relatively easy to solve and has been widely studied [11]. On the contrary, the non-rigid case is more challenging since the underlying non-rigid transformation is usually complicated and difficult to model. However, the non-rigid problem occurs ubiquitously in real-world tasks, such as medical image registration, hand-written character recognition and shape recognition [12]. Recently, a variety of methods have been put forward to tackle non-rigid problems. In this paper, non-rigid registration problems primarily focus on four cases of degradation of point sets including deformation, noise, outliers, and occlusion. The deformation of the input data denotes that the shape of the point set is distorted, and noisy data means the feature points cannot be matched accurately. Outliers and occlusion indicate that there are some points without correspondences in the corresponding point set.

Point set registration algorithms can be divided into three categories, including methods based on transformation parameters estimation, feature-based registration methods and methods combining transformation parameter estimation with feature comparison. In algorithms based on transformation parameter estimation, the correspondence relationship between point sets is first assumed, which turns the registration problem into an optimization problem with the transformation parameter as unknowns. The iterative closest point (ICP) [13] algorithm is one of the most well-known algorithms owing to its simplicity and low computation complexity, which applies the nearest-neighbor distance criterion to the arrangement of correspondences with binary values. However, the ICP method requires an adequately close initialization between the two point sets to be matched. To overcome the limitations of ICP, Chui and Rangarajan [14] proposed a robust point set registration method named the thin-plate spline robust point matching (TPS-RPM), where the deterministic annealing and a soft assignment technique were combined to evaluate a candidate transformation and improve correspondence estimation. The core of TPS-RPM is modeling a transformation as a thin-plate spline, so the algorithm is more robust compared to ICP. However, the joint estimation of correspondences and transformation increases the algorithm complexity. In [15], a kernel correlation (KC) technique for point set registration is presented, where the matching problem is defined as a search for the maximum kernel correlation configuration between the given two point sets. Adopting the idea of kernel correlation, Jian et al. [16] treat each of the point sets as Gaussians mixture models (GMM) and the point set registration problem is translated into a problem of aligning the two mixtures. A closed-form expression for the ${L_2}$ distance between these two Gaussian mixtures is obtained to solve the registration problem. These articles [17,18,19] extended this method to an asymmetric Gaussian representation, mixture of asymmetric Gaussian models to reflect the density of the two point sets. The distribution of point sets satisfies asymmetric Gaussian model. The vector field consensus (VFC) algorithm [20, 21] is an efficient algorithm for establishing robust point correspondences between two point sets. The method simultaneously generates a smoothly interpolated vector field and estimates the consensus set by an iterative EM algorithm. The coherent point drift (CPD) [22] algorithm is another efficient method based on GMM, where model points and target points are considered as GMM centroids and data points, respectively. The core idea of CPD is that GMM centroids move with one accord as a group to preserve the topological characteristics of the point set. However, for this algorithm, an applicable outlier ratio should be given in advance, which limits its applicability. To overcome the problem, Yuan Gao et al. [23] proposed a robust and outlier-adaptive method for non-rigid point registration with no need for setting the appropriate outlier ratio which is formulated in Expectation Maximization (EM) framework and updated in time of iteration. Matching algorithms mentioned above are all based on the estimation of transformation parameters. These methods only consider the global structure of point sets ignoring the local feature.

Fig. 1

Local shape context descriptor. a Diagram of log-polar histogram bins used in computing the shape contexts. b The local shape context of point ${x_m}$. There are 12 bins for angle and 5 bins for distance

In feature-based registration methods, the correspondences between point sets are found by comparing the extracted features of points in the point set. This method is popular in the field of medical imaging and computer vision. For example, Belongie et al. introduced the concept of the shape context (SC) [24] which is assigned to each point and describes the relative spatial distribution of the neighboring points of each point using a histogram. Yefeng Zheng and David Doermann [25] presented the robust point matching-preserving local neighborhood structures (RPM-LNS) technique and formulated the point set registration problem as an optimization solution with the goal to preserve local neighborhood structures. There is other related point set registration work including the probabilistic relaxation labeling algorithms, generalized in [26,27,28,29], and the graph matching method for constructing feature correspondences [30]. However, a drawback encountered by most feature-based matching algorithms is to establish point correspondence just considering local shape features without the global feature.

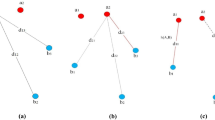
The algorithm combining feature-based registration and transformation parameter estimation gradually becomes an important research topic. Recently, Ma et al. [31, 32] introduced a new point matching algorithm based on SC. They use SC as the feature descriptor to update the correspondence iteratively, and a robust ${L_2}$-Minimizing Estimate $({L_2} E)$ estimator is applied to estimate transformation parameters. Wang et al.[33] proposed context-aware Gaussian fields (CA-LapGF) to solve point set registration problems. The CA-LapGF combines shape context with Laplacian Regularized Gaussian Fields (LapGF) to estimate the most likely correspondence and the transformation parameters between point sets iteratively. In this paper, applying GMM, we combine feature-based registration and transformation parameters estimation to render point set registration more robust in the presence of large degree of degradations of point sets. Considering that the local relationship among neighboring points is more stable under non-rigid transformations, we use local shape context which is demonstrated in Fig. 1 to exploit the feature similarity (the features of one point in one point set is similar to the features of a point in another point set) between two point sets, and then define different weights for each Gaussian mixture component based on the quantification of the similarity between the estimated local shape features to generate Inhomogeneous Gaussian mixture models (IGMM) for the two point sets. Finally, we formulate the registration task as solving a likelihood maximization problem, which is solved by updating transformation parameters and the outlier ratio under an EM-type algorithm.

The rest of the paper is organized as follows: in Sect. 2, we describe the Inhomogeneous Gaussian mixture models formulation of solving point set registration. In Sects. 3 and 4, we demonstrate the performance of our method through extensive evaluation on both synthetic data and real-world data, respectively. In Sect. 5, we discuss our conclusions from the performed experiments, and reason about limitations and future work.

2 Inhomogeneous Gaussian mixture models formulation

The article [22] proposed the coherent point drift (CPD) algorithm, and it is considered to be the state-of-the-art approach for solving non-rigid point set registration. CPD treats the first point set as the GMM centroids and the second point set corresponds to the data, and fits the centroids to the data by maximizing the likelihood. This algorithm obtains good results in the presence of deformation of the point set shape, noise in the point locations, outliers, and occlusion, but the drawback of CPD is that the outlier ratio has to be specified on beforehand. This piece of extra input outlier ratio severely limits the applicability of CPD because the outlier ratio of these two point sets is difficult to predict before registration. Besides, in the CPD algorithm, all points of one point set coherently move to another point set with one accord. Considering that corresponding point pairs have similar features, we define that more similar point pairs have larger probability to drift together, which can improve the efficiency of the algorithms and accelerate algorithm convergence. To avoid the limitation of the CPD algorithm and make our algorithm more robust to degradations, we construct an IGMM based on local shape context, and input a random outlier ratio in the EM framework so that the outlier ratio can successfully be optimized in an iterative fashion. According to the local shape context descriptor, the feature similarity between the two point sets can be obtained. We regard the feature similarity of local shape context as prior information that guides the IGMM iteratively.

2.1 Feature similarity based on local shape context

Shape context, as an effective descriptor of the point set, represents the spatial distribution of the other neighbor points relative to the reference point in a point set. In non-rigid deformations, the local relationship among neighboring points is well preserved, which motivates us to introduce the concept of local topological characteristics defined in point sets. Our method efficiently demonstrates that local topology can expedite the matching process. Suppose there are two point sets, let the two point sets be the template point set $X = \left\{ {{x_1},{x_2}, \ldots ,{x_M}} \right\} \in {{\mathbb {R}}^{M \times D}}$ and the target point set $Y = \left\{ {{y_1},{y_2}, \ldots ,{y_N}} \right\} \in {{\mathbb {R}}^{N \times D}}$, where M and N denote the number of points in each point set, respectively, and D is the dimension of the points. From Fig. 1 we can get the local shape context of a random point ${x_m}$. Firstly, we compute the Euclidean distance of any point pair in point set X. There are $M \times (M-1)/2$ point pairs, so we can get $M \times (M-1)/2$ values about the Euclidean distance. Then we choose the median distance from these $M \times (M-1)/2$ values. Finally, we select a random point ${x_m}$ from point set X as original point and regard the median value of all Euclidean distances as the radius of a circle. The obtained circle is called the neighborhood of the point ${x_m}$. To make the problem tractable, log distance and polar angle bins are used to capture the coarse location information [24]. The bins are uniform in log-polar space, where we use 5 bins for log distance and 12 bins for polar angle. In the diagram, the distance is defined as zero in the origin and incremented by one unit for points in the outer bin from 0 to 5, where 0 and 5 indicate the shortest and the longest Euclidean distance, respectively. And the angle increases by one radian in the direction of a counterclockwise from positive x-axis of the local coordinate system [26]. In log-polar space, the uniform bins guide the descriptor to be more sensitive to neighboring points than to points far away. Then a histogram comprised of the remaining neighboring points in each bin is introduced and evaluated as the local shape context of point ${x_m}$ which is given as follows:

$$\begin{aligned} \begin{array}{c} {h_m}({k_d},{k_\theta }) = \# \{ {x_i} \ne {x_m}|{x_i} \in {X_{{x_m}}},({x_i} - {x_m}) \in \\ bin({k_d},{k_\theta })\}, \end{array} \end{aligned}$$

(1)

where ${X_{{x_m}}}$ denotes the neighborhood of the point ${x_m}$, and ${x_i}$ is a random point from ${X_{{x_m}}}$. $({k_d},{k_\theta })$ is the index of a bin, estimated from the quantized log radial point-pair distance and polar angle measure.

Considering a point ${x_m}$ and a point ${y_n}$ from the template point set and the target point set, respectively, let ${C_{mn}}$ denote the matching cost of these two points which is defined as follows [24]:

$$\begin{aligned} {C_{mn}} \equiv C({x_m},{y_n}) = \frac{1}{2}\sum \limits _{{k_d}} {\sum \limits _{{k_\theta }} {\frac{{{{[{h_m}({k_d},{k_\theta }) - {h_n}({k_d},{k_\theta })]}^2}}}{{{h_m}({k_d},{k_\theta }) + {h_n}({k_d},{k_\theta })}}} }, \end{aligned}$$

(2)

where ${h_m}({k_d},{k_\theta })$, ${h_n}({k_d},{k_\theta })$ denote the histogram values for the bin $({k_d},{k_\theta })$ at ${x_m}$ and ${y_n}$, respectively. The probability measure of correspondence $({x_m},{y_n})$ can be computed by [27]:

$$\begin{aligned} {\Gamma _{mn}} = \exp ( - {C_{mn}}/{\alpha ^2}), \end{aligned}$$

(3)

where $\alpha$ is defined to adjust the reliability of the probability measures. ${\Gamma _{mn}}$ can be utilized to describe the feature similarity between point ${x_m}$ and point ${y_n}$. The larger the value of ${\Gamma _{mn}}$, ${x_m}$ is more similar to ${y_n}$.

2.2 Construction of inhomogeneous Gaussian mixture models

The basic idea of point set registration using IGMM is to encode local shape context in a GMM framework. In this subsection, we treat the points in point set Y as n centroids of the IGMM and fit Y to the data point set X. The purpose of point set registration is to learn the transformation model T: $X = T(Y)$. The transformation which can be demonstrated by $T\left( {Y|f} \right) = Y + f\left( Y \right)$ is built using the Gaussian radial basis function (GRBF) technique and regarded as the sum of the initial location and a displacement function f (where f is a set of transformation parameters). The IGMM probability density function of a random data point ${x_m}(i = 1,2,\ldots ,M)$ is defined as follows:

$$\begin{aligned} p({x_m}) = \sum \limits _{n = 1}^N {{v_{mn}}p({x_m}|n)}, \end{aligned}$$

(4)

where $p({x_m}|n) = \frac{1}{{{{(2\pi {\sigma ^2})}^{D/2}}}}{e^{ - \frac{{{{\left\| {{x_m} - {y_n} - f({y_n})} \right\| }^2}}}{{2{\sigma ^2}}}}}$ is the probability of the nth Gauss distribution of ${x_m}$ at the relative position of ${y_n}$, and $\sigma$ denotes the Gauss bandwidth. Here, ${v_{mn}}(m = 1,2,\ldots ,M;n = 1,2,\ldots ,N)$ denotes the nth mixture coefficient for the mth data point. In contrast to GMM, where ${v_{mn}}$ is uniform for all Gaussian models, ${v_{mn}}$ in IGMM is inhomogeneous, which is estimated based on feature similarity of the two point sets. The feature similarity is calculated using the local shape context. Here, if one GMM centroid represented by ${y_n}$ resembles the data point ${x_m}$ in feature space, we give a larger weight to this GMM component in order to make a correct correspondence. If these two points have more similar features, they will easily form a correct matching point pair. Therefore the feature similarity can lead the spatial motion to the correct registration. For a given random data point ${x_m}$, using Eqs. 2 and 3, its nth GMM coefficient ${v_{mn}}$ can be defined as follows:

$$\begin{aligned} {v_{mn}} = \frac{{{\Gamma _{mn}}}}{{\sum \limits _{o = 1}^N {{\Gamma _{mo}}} }}, \end{aligned}$$

(5)

where ${\Gamma _{mo}}$ denotes the feature similarity measure of point ${x_m}$ and point ${y_o}$. Here, a random data point ${x_m}$ will have N different coefficients ${v_{mn}}(m = 1,2,\ldots ,M;n$ $= 1,2,\ldots ,N)$ which satisfies $\sum \nolimits _{n = 1}^N {{v_{mn}}} = 1$, ${v_{mn}} \ge 0$. A data point has more chance to construct a match with one GMM centroid represented by a model point with larger coefficient. Applying the feature similarity to construct the GMM coefficients, an IGMM strategy is formed, which can accelerate algorithm convergence and obtain robust registration results.

Taking the noise and outliers into account, an extra uniform distribution $p({x_m}|N + 1) = 1/M$ is added to the IGMM. We denote noise and outliers ratio as $\gamma$, so the weight of IGMM is $1 - \gamma$. Consequently, the IGMM probability density function takes the form:

$$\begin{aligned} p({x_m}|f,\gamma ,\sigma ) = (1 - \gamma )\sum \limits _{n = 1}^N {{v_{mn}}p({x_m}|n)} + \gamma p({x_m}|N + 1).\nonumber \\ \end{aligned}$$

(6)

Considering the data points are independent and satisfy the consistent distribution, the joint probability distribution of the whole data set X, namely, the likelihood function, is given by:

$$\begin{aligned} \varPhi (X|Y,f,\gamma ,\sigma ) = \mathop \prod \limits _{m = 1}^M p({x_m}|f,\gamma ,\sigma ). \end{aligned}$$

(7)

In order to enforce the smoothness of the GRBF, we define the prior over f in the Tikhonov regularization framework [14] as

$$\begin{aligned} p(f) = {e^{ - \frac{\lambda }{2}\left\| f \right\| _\mathcal{H}^2}}, \end{aligned}$$

(8)

where $\left\| f \right\| _\mathcal{H}^2$ denotes the norm of f(y) in the Reproduction Kernel Hilbert Space (RKHS). We choose the optimal form of f , which can be represented as the linear combination of kernels [23]

$$\begin{aligned} f(z) = \sum \limits _{n = 1}^N {{w_n}\mathcal{R}} (z,{y_n}) = \mathcal{R}W, \end{aligned}$$

(9)

where $\mathcal{R}$ is a $N \times N$ kernel matrix with ${\mathcal{R}_{ns}} = {e^{ - \frac{1}{2}\frac{{{{\left\| {{y_n} - {y_s}} \right\| }^2}}}{{{\beta ^2}}}}}$, $n,s = 1,2,\ldots ,N$, and $\beta$ is an adjustment parameter. $W = ({w_1},{w_2},\ldots ,{w_N})$ is a coefficient set.

Combining with the smoothness constraint, we can define the negative log likelihood function as:

$$\begin{aligned} \mathrm{E}(\varTheta )= & {} - ln\varPhi (X|Y,f,\gamma ,\sigma ) + \frac{\lambda }{2}\left\| f \right\| _\mathcal{H}^2\nonumber \\= & {} - \sum \limits _{m = 1}^M {ln((1 - \gamma )\sum \limits _{n = 1}^N {{v_{mn}}p({x_m}|n)} + \gamma p({x_m}|N + 1)} )\nonumber \\&+ \frac{\lambda }{2}\left\| f \right\| _\mathcal{H}^2, \end{aligned}$$

(10)

where ${\varTheta } = \{ f,\gamma ,\sigma \}$ includes a set of unknown parameters, and $\lambda$ is a trade-off parameter. These parameters are estimated by solving the maximum a posteriori (MAP) problem, which is equivalent to minimizing the negative log likelihood function in Eq. 10.

2.3 The EM algorithm

The well-known EM algorithm [8] provides a framework for dealing with this MAP problem. It consists of two steps: an expectation step (E-step) and a maximization step (M-step). In the E-step, we compute the posteriori probability of the mixture components using the Bayes theorem and the fixed parameters, while the M-step updates the values of parameters based on the current estimate of the posteriori probability by minimizing the following objective function:

$$\begin{aligned} Q(\varTheta )= & {} \frac{D}{2}\ln {\sigma ^2}\sum \limits _{m = 1}^M {\sum \limits _{n = 1}^N {{p^{\mathrm{old}}}(n|{x_m},\varTheta )} } \nonumber \\&+\, \frac{1}{{2{\sigma ^2}}}\sum \limits _{m = 1}^M {\sum \limits _{n = 1}^N {\left[ {{p^{\mathrm{old}}}(n|{x_m},\varTheta ){{\left\| {{x_m} - {y_n} - f({y_n})} \right\| }^2}} \right] } } \nonumber \\&- \ln (1 - \gamma )\sum \limits _{m = 1}^M {\sum \limits _{n = 1}^N {{p^{\mathrm{old}}}(n|{x_m},\varTheta )} } \nonumber \\&- \ln \gamma \sum \limits _{m = 1}^M {{p^{\mathrm{old}}}(N + 1|{x_m},\varTheta )} + \frac{\lambda }{2}\left\| f \right\| _\mathcal{H}^2, \end{aligned}$$

(11)

where some terms independent of $\varTheta = \{ f,\gamma ,\sigma \}$ are omitted.

E-step: Denote $P = {[{p^{\mathrm{old}}}(n|{x_m},\varTheta )]_{N \times M}}$, where the posteriori probability of the mixture components can be computed applying the Bayes theorem:

$$\begin{aligned} {p^{\mathrm{old}}}(n|{x_m},\varTheta ) = \frac{{(1 - \gamma ) \times \frac{{{v_{mn}}}}{{(2\pi {\sigma ^2})}^{\frac{D}{2}}}{e^{ - \frac{{{{\left\| {{x_m} - {y_n} - f({y_n})} \right\| }^2}}}{{2{\sigma ^2}}}}}}}{(1 - \gamma )\sum \nolimits _{l = 1}^N {{v_{ml}}p({x_m}|l) + \gamma /M}} \end{aligned}$$

(12)

The posteriori probability for the outliers and noise is defined as follows:

$$\begin{aligned} {p^{\mathrm{old}}}(N + 1|{x_m},\varTheta )= & {} 1 - \sum \nolimits _{n = 1}^N {{p^{\mathrm{old}}}(n|{x_m},\varTheta )} \nonumber \\= & {} \frac{\gamma }{{M(1 - \gamma )\sum \nolimits _{l = 1}^N {{v_{ml}}p({x_m}|l) + \gamma } }}\nonumber \\ \end{aligned}$$

(13)

The posteriori probability ${p^{\mathrm{old}}}(n|{x_m},\varTheta )$ is a soft matching determination, and it indicates to what degree the point ${y_n}$ corresponds to point ${x_m}$.

M-step: We revise the parameter $\varTheta = \{ f,\gamma ,\sigma \}$ by minimizing the objective function Eq. 10. Taking partial derivative of $Q(\varTheta )$ with respect to $\sigma$ and setting it to zero, we can obtain

$$\begin{aligned} {\sigma ^2} = \frac{{\sum \nolimits _{m = 1}^M {\sum \nolimits _{n = 1}^N {{p^{\mathrm{old}}}(n|{x_m},\varTheta ){{\left\| {{x_m} - {y_n} - f({y_n})} \right\| }^2}} } }}{{D\sum \nolimits _{m = 1}^M {\sum \nolimits _{n = 1}^N {{p^{\mathrm{old}}}(n|{x_m},\varTheta )} } }}. \end{aligned}$$

(14)

Similarly, taking $\frac{{\partial Q(\varTheta )}}{{\partial \gamma }} = 0$, we can get

$$\begin{aligned} \gamma = \frac{{\sum \nolimits _{m = 1}^M {{p^{\mathrm{old}}}(N + 1|{x_m},\varTheta )} }}{{\sum \nolimits _{m = 1}^M {{p^{\mathrm{old}}}(N + 1|{x_m},\varTheta )} + \sum \nolimits _{m = 1}^M {\sum \nolimits _{n = 1}^N {{p^{\mathrm{old}}}(n|{x_m},\varTheta )} } }}. \end{aligned}$$

(15)

To solve the minimization with respect to f, we apply Eq. 9 to rewrite the objective function as:

$$\begin{aligned} Q(\varTheta )= & {} \frac{D}{2}\ln {\sigma ^2}\sum \limits _{m = 1}^M {\sum \limits _{n = 1}^N {{p^{\mathrm{old}}}(n|{x_m},\varTheta )} }\nonumber \\&+\, \frac{1}{{2{\sigma ^2}}}\sum \limits _{m = 1}^M {\sum \limits _{n = 1}^N {\left[ {{p^{\mathrm{old}}}(n|{x_m},\varTheta ){{\left\| {{x_m} - {y_n} - f({y_n})} \right\| }^2}} \right] } } \nonumber \\&- \ln (1 - \gamma )\sum \limits _{m = 1}^M {\sum \limits _{n = 1}^N {{p^{\mathrm{old}}}(n|{x_m},\varTheta )} } \nonumber \\&- \ln \gamma \sum \limits _{m = 1}^M {{p^{\mathrm{old}}}(N + 1|{x_m},\varTheta )} + \frac{\lambda }{2}tr({W^T}\mathcal{R}W). \end{aligned}$$

(16)

Let $\frac{{\partial Q(\varTheta )}}{{\partial \mathcal{R}}} = 0$ and $\mathcal{R}$ can be obtained from

$$\begin{aligned} (\mathcal{R} + \lambda {\sigma ^2}{(diag(P\mathbf 1 ))^{ - 1}})W = {(diag(P\mathbf 1 ))^{ - 1}}PX - Y,\nonumber \\ \end{aligned}$$

(17)

where $P = {[{p^{\mathrm{old}}}(n|{x_m},\varTheta )]_{N \times M}}$, and 1 is a column vector of all ones.

The proposed algorithm runs E-step and M-step iteratively until ${\delta ^2}< \delta _{final}^2$, which is summarized in Algorithm 1.

In our algorithm, all the parameters are set on the basis of the experimental evaluations. The parameter $\alpha$ is utilized to adjust the reliability of the probability measures, which controls the weight of Gauss components and is set to 1. The GRBF parameter $\beta$ defines the model of the non-rigid transformation, and we empirically set $\beta$ to 1. The parameter $\lambda$ plays an important role in controlling smoothness regularization, and $\lambda$ is empirically set to 8. The parameter $\delta _{final}^2$ is set to ${10^{ - 8}}$.

3 Experiments and analysis on synthetic data

In this section, to evaluate the performance of our proposed algorithm with respect to deformation, noise, outliers and occlusion, we compare our approach with six state-of-the-art algorithms: GMMReg [16], AGMReg [18, 19], CPD [22], SC-TPS [24], RPM-L2E [32], and CA-LapGF [33] on the Chui−Rangarajan synthetic data set as done in [14] and the 3D face data as employed in [22]. The experiments are conducted in MATLAB R2014a, and tested on a Pentium Core I7-6700 CPU with 8GB RAM.

3.1 Results on 2D point set registration

The 2D data set includes two different shape models: a fish and a Chinese character shape. The fish shape consists of 96 points, and the Chinese character is a more complicated model consisting of 108 points. For each model, four groups of data sets are designed to assess the performance of registration methods in face of deformation, noise, outliers and occlusion. When evaluating the robustness to test, the transformation model is based on Gaussian radial basis functions (GRBF), whose coefficients are satisfied with a Gaussian distribution with zero mean and standard deviation that ranges from 0.02 to 0.08. In the noise test, the positional noise is defined as Gaussian noise with zero mean and standard deviation ranges from 0 to 0.05. Both outliers and occlusion test cases denote that some points of one set have no corresponding point in the other point set. The outlier and occlusion rate ranges from 0 to 2 and 0 to 0.5, respectively. For the fish and Chinese character shape, 100 samples are generated in each degradation level and there are 4000 samples in the aggregate.

We estimate the registration error to evaluate the performance of registration methods. The registration error is defined as the mean squared distance between the corresponding points after the registration, which is given as follows:

$$\begin{aligned} \hbox {Error} = \sqrt{\frac{1}{{{N_{\mathrm{total}}}}}\sum \limits _{k = 1}^{{N_{\mathrm{total}}}} {{{({x_k} - T({y_k}))}^2}} }, \end{aligned}$$

(18)

where ${N_{\mathrm{total}}}$ denotes the total number of true correspondences, and ${x_k}$ corresponds to ${y_k}$ in the ground truth.

Fig. 2

Registration examples on the fish point set. Notice that we align the target point set (blue circles) onto the template point set (red ‘+’). The leftmost column is the template point set and target point set. From the second column to the rightmost column, the registration results of GMMReg, RPM-L2E, CPD, AGMReg, CA-LapGF, SC-TPS and our method, respectively. From top row to bottom row: the deformation (0.08), noise (0.05), outliers (2) and occlusion (0.5), respectively

Fig. 3

Comparison of registration methods on the fish point set under different degradation circumstances. a, e Deformation test. b, f Noise test. c, g Outlier test. d, h Occlusion test

3.1.1 Non-rigid fish point set registration

The registration results on the fish point set are illustrated in Fig. 2, in face of the largest degree of degradations, such as deformation level to 0.08, noise level to 0.05, outlier ratio to 2 and occlusion ratio to 0.5. From Fig. 2 we can see the GMMReg algorithm and our proposed method perform well for non-rigid deformation. There is no winner when the target point set is disturbed by the largest variance Gaussian noise. The AGMReg method performs best in face of outliers, followed by our proposed method. In the occlusion test, our method gets superior registration results.

To further explore the performance of registration methods, quantitative comparative experiments on the fish dataset under four degradation scenarios were conducted. We use error bars of the registration results of all the 100 samples to assess the registration performance of all algorithms. The error bars depict the mean and standard deviation of the registration errors. We summarize the experimental results in Fig. 3. According to Fig. 3a, we can see that our method performs best due to adopting the robust local features. Figure 3b shows the registration performance when adding Gaussian noise, all algorithms except AGMReg can achieve quite satisfactory results, and the proposed method gets the best registration results. Figure 3c depicts the performance for the fish dataset with outliers. The best performance is obtained by AGMReg, followed by our algorithm. Figure 3d shows the registration results in the presence of increasing levels of occlusion. Our algorithm and CA-LapGF perform better due to applying local features. Figure 3e–h separately denotes the average time consumed by the registration methods at different levels of deformation, noise, outliers and occlusion. We can see GMMReg and CA-LapGF spend more time in all four groups of tests; in the meanwhile, the CPD algorithm costs less time, however, performed worse, see Fig. 3c.

Fig. 4

Registration examples on the Chinese character point set. Notice that we align the target point set (blue circles) onto the template point set (red ‘+’). The leftmost column is the template point set and target point set. From the second column to the rightmost column, the registration results of GMMReg, RPM-L2E, CPD, AGMReg, CA-LapGF, SC-TPS and our method, respectively. From top row to bottom row: the deformation (0.08), noise (0.05), outliers (2) and occlusion (0.5), respectively

Fig. 5

Comparison of registration methods on the Chinese character point set under different degradation circumstances. a, e Deformation test. b, f Noise test. c, g Outlier test. d, h Occlusion test

In summary, the registration rate of all methods decreases with the degree of degradation increasing. Our algorithm performs more desirably in general because of having applied robust features to construct the IGMM. GMMReg performs well in the deformation, noise and occlusion tests, but it cannot capture the true distributions of the point sets with outliers. The AGMReg method performs best in the outlier test; however, it performs much poorer in the other three tests and its registration rate fluctuates strongly. Because it is not sufficient to assign point sets only capturing global distributions without considering the local structure of the point set. The CA-LapGF uses features and Laplacian Regularized Gaussian Fields (LapGF) to solve the point set registration, and it performs well in the outlier and occlusion tests; however, it costs much more time. The CPD method achieves good performance in deformation, noise and occlusion tests and spends less time than others, but the sensitivity to outliers makes it perform poorly in the outliers test. Our method is more time-consuming than CPD, that is because we apply local feature similarity to construct the IGMM. In addition, we iteratively estimate the outlier ratio, which allows the proposed algorithm to obtain better results than the CPD method in the outliers test. The SC-TPS and RPM-L2E algorithms consistently perform well in the presence of deformation, noise and occlusion because of the robustness of shape context; however, they are vulnerable to outliers. In general, our method obtains better registration results in all degradation experiments.

3.1.2 Non-rigid the Chinese character point set registration

The experimental results on the Chinese character point set are shown in Fig. 4 which shows four test modes, with varying levels of degradation applied. We set the deformation degree to 0.08, noise level to 0.05, outlier ratio to 2 and occlusion ratio to 0.5. Different from the fish shape, points of the Chinese character are far away from each other, that is to say, it is not well clustered. In the deformation test, GMMReg, AGMReg and our method perform better than the other four algorithms. Noise is a challenge for all methods, and none of the competing methods obtain satisfactory registration results when the noise ratio is very large. The AGMReg algorithm performs best, followed by our method and RPM-L2E; however, when there are missing points in the target point set, our method outperforms the other tested approaches.

Fig. 6

Registration examples on the 3D face point set. Notice that we align the target point set (blue circles) onto the template point set (red ‘+’). The leftmost column is the template point set and target point set. From the second column to the rightmost column, the registration results of GMMREG, RPM-L2E, CPD, AGMReg, CA-LapGF, SC-TPS and our method, respectively. From top row to bottom row: the deformation, noise, outliers and occlusion, respectively

In the following experiments, we test the performance of the registration methods on the Chinese character under four degradation scenarios, where we generated 100 samples for each degradation level. The quantitative evaluation results are depicted in Fig. 5. In Figure 5a, we can see that the average error of all approaches gets larger as the deformation level is increasing. The error of our algorithm increases much slower than the others. Figure 5b shows that all algorithms except AGMReg can get a good registration performance with the noise level ranging from 0 to 0.05. Our proposed method performs slightly better than SC-TPS, RPM-L2E, CA-LapGF and GMMReg. Figure 5c evaluates the registration performance of all algorithms against outliers. The AGMReg algorithm gets best experimental results, followed by our method. In Fig. 5d, all algorithms besides AGMReg can get satisfactory results under occlusion scenarios, and our proposed method performs best. From Fig. 5e–h, we show the average time consumed by the registration methods under different degradation. Due to more points and more complicated structure relative to fish shape, the time consumed on the Chinese character point set registration increases faster than on the fish dataset. GMMReg and CA-LapGF need more time to accomplish the registration; however, the CPD algorithm costs the least time.

Table 1 Average time consumed of registration methods

Relatively speaking, our proposed algorithm performs much better under these large degradations. The GMMReg, SC-TPS, RPM-L2E and CPD perform well in deformation, noise and occlusion tests; however, none of them can get good registration results with respect to outliers. When the target point set contains outliers, the distribution of point sets is asymmetrical, so the GMMReg is inapplicable in this case. Both SC-TPS and RPM-L2E unite shape context to achieve the registration, but they are not robust to outliers. The CPD algorithm cannot perform better in the outliers scenarios due to the unknown outlier ratio. In contrast, the AGMReg approach performs best in the case of outliers, but gets poorer results in the other three degradations. CA-LapGF performs well under noise, outliers and occlusion; however, it is sensitive to the deformation of the point sets. In addition, CA-LapGF is much more time-consuming under all experiments. In general, our proposed algorithm obtains better assignments over all degradations in the experiments.

In summary, the overall trend of error bars on the Chinese character is similar to the results of the fish set registration, especially in the aspect of the noise experiment. However, the registration errors of all tested methods decrease slightly faster compared to the fish point set, because the Chinese character point set is not well clustered, and its structure is more complex.

Fig. 7

Examples of the Oxford affine covariant regions datasets. From a–h, there are bark, bike, boat, graf, trees, leuven, ubc and wall, respectively. Each sequence has five image pairs from 1 and 2 to 1 and 6

3.2 Results on 3D face point set registration

We test the registration methods on the 3D face point set in this experiment. The 3D face data set includes two point sets, and there is a non-rigid deformation between these two point sets (template point set and target point set). Each 3D face data set consists of 392 points. We construct three point pairs with respect to noise, outliers and occlusion on basis of the original 3D face data structure, respectively. In the noise test, we added positional noise to the coordinate of each point from target point set. In the outlier test and occlusion test, we randomly increase and reduce points in the target point set, respectively. Figure 6 shows experimental results of several registration methods. GMMReg, AGMReg and our proposed approach outperform other methods in the deformation scenario. In the noise test, our algorithm and CPD obtain better registration results. The AGMReg approach gives the best assignment with respect to outliers, followed by our method. When the target point set contains missing points, the proposed algorithm performs better than the other tested approaches. Table 1 gives the average time consumed of all registration algorithms. In Table 1, one can see our proposed approach is more time-consuming than SC-TPS and CPD; however, in general, the proposed method is acceptant and available to deal with 3D point set registration.

Fig. 8

The matching results of our proposed method on the 1st and 6th frame of eight sequence of images. a bark (44 out of 100), b bike (184 out of 200), c boat (71 out of 75), d graf (45 out of 55), e trees (184 out of 200), f leuven (184 out of 200), g ubc (168 out of 200) and h wall (30 out of 30)

4 Experiments and analysis on real-world image data

In this section, we evaluate the proposed approach via eight groups of real-world images. These images are from the Oxford affine covariant data sets provided by Mikolajczyk et al. [34], which are bark, bike, boat, graf, trees, leuven, ubc and wall sequences, respectively, and shown in Fig. 6. Each sequence contains six frames of images. The registration image pairs are constructed from the 1st frame to the 2nd, 3rd, 4th, 5th, 6th frame. There is varying amounts of blur, and light, and difference in the ratio of JPEG compression, scale, and rotation between the image pairs. The degree of degradations is gradually increasing as the increasing of the frame. To construct the template and target point sets, we firstly extract the SIFT [35] feature points from each image pairs and then combine the BBF (Best bin first) algorithm [36] with the Random sample consensus (RANSAC) strategy [37] to construct initial correspondences. Finally, we randomly select some points from these initial correspondences. In bike, trees, leuven, and ubc tests, the template and target point set include 200 points, respectively. In bark, boat, graf, and wall tests, we randomly choose 100, 75, 55, and 30 points, respectively. (The selected number of points is based on the number of initial correspondences.)

We select the largest degradation between image pairs, that is to say, the 1st and 6th frame images of each sequence, to verify the applicability and robustness of our proposed method. The matching results are depicted in Fig. 7. We can see our proposed algorithm is available to real-word images registration. We next assign the 1st frame to other five frames to test the performance of the registration methods. The SC-TPS, GMMReg and AGMReg algorithm perform much poorer on our data sets so that we cannot properly depict the curve of registration error. The constructed template and target point sets are employed to test RPM-L2E, CA-LapGF, CPD and the proposed method. The performance of the registration algorithms are displayed in Fig. 8. According to the experimental result, we can see that the CA-LapGF algorithm obtains poorer results on the eight group of datasets, and our proposed algorithm performs a slightly better than CPD and RPM-L2E in most cases. In the bark and boat test, the registration error of all methods is much larger due to varying scale and rotation between image pairs. Because there are larger change of viewpoint in the graf datasets, registration approaches cannot obtain better results. However, on the wall dataset with varying viewpoint, the registration error is lower due to the structure of the wall dataset. According to the bikes and trees test, we can see that registration methods are robust to blur in the images. Figure 9e, g shows that when there are varying light conditions and degrees of JPEG compression between the image pairs, our proposed algorithm still performs well. The proposed approach outperforms other methods on most tested image pairs.

Fig. 9

Average registration error of RPM-L2E, CPD, CA-LapGF and our method on the Oxford affine covariant regions datasets. a bark, b bike, c boat, d graf, e trees, f leuven, g ubc and h wall

5 Conclusion and future work

In this paper, we propose a robust non-rigid point set registration method based on Inhomogeneous Gaussian mixture models (IGMM), which differs from many traditional registration methods based on the Gaussian model. First, since the local relationship among neighboring points is mostly well preserved under non-rigid transformations, we apply a robust neighborhood structural descriptor, local shape context to describe the two point sets, and compute the matching scores of local descriptors. Then, we calculate the feature similarity on the basis of the matching measure. According to the feature similarity, each Gaussian mixture component is assigned a different weight, which can more easily make correspondence points form a assignment, while many traditional registration methods are based on the Gaussian model using a single weight parameter. Finally, we presented the necessary proofs in the domain of regularization theory and formulated the problem as a likelihood maximization problem, which we solve by updating transformation parameters and the outlier ratio using the EM algorithm. Extensive experimental results on synthetic and real-world image data sets illustrate that our proposed method outperforms several state-the-art algorithms.

However, there are also some noticeable aspects to expand this work in the future. We utilize the local shape context to define the weight of each Gaussian mixture component, the process is always iterated, so the proposed algorithm is slightly time-consuming. Therefore, it would be interesting to improve the computation efficiency of our proposed method in the future.