1 Introduction

Since its introduction by Veach and Guibas [23], the multiple importance sampling (MIS) technique has been widely used in computer graphics, particularly in rendering. MIS is based on combining several sampling techniques into a single estimator. Veach proved that from the several MIS techniques he presented, the balance heuristic, which he showed is the same as the classic Monte Carlo estimator using a mixture of techniques, is optimal in the sense of minimum variance. He used an equal count of samples for each technique, and the balance heuristic was almost exclusively used thereafter as a mixture of distributions with equal weights.

The use of different counts of samples in the balance heuristic has been raised so far in very few papers. This might be because Veach himself discouraged this possibility in his thesis (Theorem 9.5 [22]). He shows that the variance of the balance heuristic with an equal number of samples is less than or equal to n times the variance of any other MIS estimator with the same number of samples distributed in any other way. But observe that, even for the most simple case of \(n=2\), we could theoretically improve by up to 100%. However, the sampling costs were not considered in the theorem.

The question whether a count of samples other than equal count can improve the MIS variance appears in few papers. Lu et al. [16] use a Taylor second order approximation around the weight 1/2 for environment map illumination computation, combining the techniques of sampling the BRDF and the environment map. Yu-Chi Lai et al. [15] used adaptive weights in combination with population Monte Carlo. In Csonka et al. [4], the cost of sampling was also taken into consideration when minimizing the variance of the combination of stochastic iteration and bidirectional path tracing. However, none of these papers exploits that the balance heuristic is a mixture of distributions. Havran and Sbert [11] exploited this fact to study the optimal combination for the particular case of a product of functions. We advance on their work in many aspects, by showing that their study can be extended to any function, by shedding light on the relationship between the linear combination of estimators and MIS, and by providing proofs for it. Recently, Sbert et al. [20] analyzed the variances of one-sample and multi-sample MIS.

As for adaptive schemes inspired by MIS, the review article by Owen and Zhou [18] surveys the principles in mixture and multiple importance sampling at that time. More recently, Douc et al. [5] derived sufficient convergence conditions for adaptive mixtures and also iterative formulae for the optimal weights [6]. Cornuet et al. [3] present optimal recycling of past simulations in iterative adaptive MIS algorithms (applied to final gathering by Tokuyoshi et al. [21]). This work was extended by Marin et al. [17]. Elvira et al. [7] proposed the use of the gradient to accelerate convergence. A recent work by Hachisuka et al. [9] uses Markov Chain Monte Carlo to distribute different numbers of samples among the different techniques.

Our work differs from the adaptive MIS schemes above. We will obtain for Monte Carlo integration of general functions with a balance heuristic a mathematical expression that the different weights have to fulfill for optimality, and the heuristic technique to compute the weights close to the optimal ones. In other words, we give a recipe of how many samples to take according to each strategy to minimize variance. We also take into account the cost of each sampling technique. As we cannot isolate the weights in the resulting formula, we outline a procedure to obtain their optimal values. As this procedure is combinatorial on the number of techniques used, we introduce a sound heuristic approximation based on the optimal linear combination of two or more estimators with known variance, supposing that all estimators are unbiased. We also show the relationship of the MIS technique with the linear combination of the independent techniques, and that the minimum variance for MIS is upper bounded by the variance of the minimum variance technique.

2 Importance sampling

In this section, we recall first the idea of importance sampling and then we study the linear combination of estimators. The reader can consult classic references on Monte Carlo such as [12, 19].

2.1 Monte Carlo integration and importance sampling

Suppose we have to solve the definite integral of a function f(x) on domain D, \(I= \int _D f(x) \mathrm{d}x\). We factor \(f(x)=\frac{f(x)}{ p(x)} p(x) \), where \(p(x) \ne 0\) when \(f(x) \ne 0\)

$$\begin{aligned} I= \int _D f(x) \mathrm{d}x = \int _D \frac{f(x)}{ p(x)} p(x) \mathrm{d}x. \end{aligned}$$
(1)

If \(p(x) \ge 0\) and \(\int _D p(x) \mathrm{d}x =1\), then p(x) can be considered as a probability density function (abbreviated pdf), and the integral Eq. 1 is then the expected value of the random variable \(\frac{f(x)}{ p(x)}\) with pdf p(x). An unbiased primary estimator \(I_1\) for the mean (which is the value of integral I) of this random variable is:

$$\begin{aligned} I \approx I_1 = \frac{f(x_1)}{ p(x_1)}, \end{aligned}$$
(2)

where \(x_1\) is obtained sampling the pdf p(x), and the unbiasedness means that the expected value of this estimator is the value of the integral, that is, \(E[I_1] = I\). The variance of this estimator, \(V[I_1]\), is given by

$$\begin{aligned} V[I_1]= & {} E\left[ \left( \frac{f(x)}{ p(x)}\right) ^2\right] - E^2\left[ \frac{f(x)}{ p(x)}\right] \nonumber \\= & {} \int _D \big (\frac{f(x)}{ p(x)} \big )^2 p(x) \mathrm{d}x - \int _D \frac{f(x)}{ p(x)} p(x) \mathrm{d}x \nonumber \\= & {} \int _D \frac{f(x)^2}{ p(x)}\mathrm{d}x - I^2. \end{aligned}$$
(3)

Averaging N independent primary estimators (obtained by sampling N independent values \(x_1,x_2,\ldots ,x_N\) from p(x)), we obtain a new unbiased estimator (secondary estimator) \(I_N\)

$$\begin{aligned} I \approx I_N = \frac{1}{N}\sum _k \frac{f(x_k)}{ p(x_k)} \end{aligned}$$
(4)

with variance

$$\begin{aligned} V[I_N] = \frac{1}{N} V[I_1] = \frac{1}{N} \left( \int _D \frac{f(x)^2}{ p(x)}\mathrm{d}x - I^2 \right) . \end{aligned}$$
(5)

Obviously, \(V[I_1]\) depends upon p(x), or the pdf, that we are using. The minimum variance corresponds to \(p(x) = \frac{\mid f(x)\mid }{I}\), which is the absolute value of the normalized integrand function [12]. As the value of I is unknown, a heuristic rule is to take a pdf that mimics the integrand. This is known as importance sampling.

2.2 Linear combination of estimators

Suppose we have M independent primary unbiased estimators \(\{ {I_{i,1}}\}\) of \(I = \int f(x) \mathrm{d}x\) , \(1 \le i \le M, E\left[ {I_{i,1}}\right] =I\), and want to distribute N samples among them, assigning \(n_i\) samples to each of them, \(\sum _{i=1}^{M} n_i = N\). Any convex combination of \(\{ {I_{i,n_i}}\}\), \(\sum _{i=1}^{M} w_i {I_{i,n_i}}\), \(w_i \ge 0\), \(\sum _{i=1}^{M} w_i = 1\), is also an unbiased estimator of I, i.e., by the properties of the expected value, \(E\left[ \sum _{i=1}^{M} w_i {I_{i,n_i}}\right] = \sum _{i=1}^{M} w_i E\left[ {I_{i,n_i}}\right] = I\). And by the properties of variance, its variance is:

$$\begin{aligned} v=V\left[ \sum _{i=1}^{M} w_i {I_{i,n_i}}\right] = \sum _{i=1}^{M} \frac{w_i^2}{n_i} V\left[ {I_{i,1}}\right] . \end{aligned}$$
(6)

2.2.1 Fixed weights

When we fix the \(w_i\) values, then using Lagrange multipliers we can obtain the values \(n_i\) for minimum variance. We derivate the following objective function, where \(\sum _{i=1}^{M} n_i = N\) is the constraint and \(v_i=V[ {I_{i,1}}]\):

$$\begin{aligned} {\varLambda }\left( n, \lambda \right) = \sum _{i=1}^{M} \frac{w_i^2}{n_i} v_i + \lambda \left( \sum _{i=1}^{M} n_i - N\right) , \end{aligned}$$
(7)

and we obtain the optimal values

$$\begin{aligned} n_i=\frac{N \cdot w_i \cdot \sqrt{v_i}}{\sum _{k=1}^M w_k \sqrt{v_k}}, \end{aligned}$$
(8)

and optimal variance

$$\begin{aligned} \sum _{k=1}^M w_k^2 \frac{v_k}{n_k}{=} \sum _{k=1}^M w_k \frac{\sqrt{v_k}\left( \sum _{l} w_l \sqrt{v_l}\right) }{N} {=} \frac{\left( \sum _{k=1}^M w_k \sqrt{v_k}\right) ^2 }{N}.\nonumber \\ \end{aligned}$$
(9)

If we find the weights \(w_i\) that minimize Eq. 9, the only, trivial solution, is that all variances are equal, \(v=v_k=v_i\) for any i and k, with variance value v / N.

2.2.2 Fixed number of samples

If the \(n_k\) values are known, using Lagrange multipliers with constraint \(\sum _{i=1}^M w_i = 1\) and objective function

$$\begin{aligned} {\varLambda }\left( w, \lambda \right) = \sum _{i=1}^{M} \frac{w_i^2}{n_i} v_i + \lambda \left( \sum _{i=1}^{M} w_i - 1\right) , \end{aligned}$$
(10)

we find that the optimal combination is:

$$\begin{aligned} w_k=\frac{\frac{n_k}{v_k}}{\sum _{k=1}^M \frac{n_k}{v_k}}. \end{aligned}$$
(11)

Observe that in general, for M estimators, \(\sum _{k=1}^M \frac{n_k}{v_k}\) is the inverse of the harmonic mean (defined as

\(H(\{x_i\}) = \frac{M}{\sum _{i=1}^M 1/x_i}\)) of the \(\frac{n_k}{v_k}\) values times M, as the harmonic mean \(H(\{\frac{v_k}{n_k}\})\) is equal to:

$$\begin{aligned} H\left( \left\{ v_k/n_k\right\} \right) =\frac{M}{\sum _{k=1}^M \frac{n_k}{v_k}}. \end{aligned}$$
(12)

Thus, for optimal weights \(w_k\) we get the formula:

$$\begin{aligned} w_k=\frac{H\left( \left\{ \frac{v_k}{n_k}\right\} \right) n_k}{M v_k}. \end{aligned}$$
(13)

Using these values in Eq. 6, we obtain the minimum value for the variance:

$$\begin{aligned} v_{min}= & {} \sum _{k=1}^M w_k^2 \frac{v_k}{n_k} = \sum _{k=1}^M \frac{\left( H\left( \left\{ \frac{v_k}{n_k}\right\} \right) \right) ^2 n^2_k}{M^2 v^2_k} \frac{v_k}{n_k}\nonumber \\= & {} \frac{\left( H\left( \left\{ \frac{v_k}{n_k}\right\} \right) \right) ^2}{M} \sum _{k=1}^M \frac{1}{M}\frac{n_k}{v_k} \nonumber \\= & {} \frac{\left( H\left( \left\{ \frac{v_k}{n_k}\right\} \right) \right) ^2}{M} \frac{1}{H\left( \left\{ \frac{v_k}{n_k}\right\} \right) }=\frac{H\left( \left\{ \frac{v_k}{n_k}\right\} \right) }{M}. \end{aligned}$$
(14)

See Graybill and Deal [8] for the two estimators case. We can minimize Eq. 14 for a fixed budget of samples, i.e., \(\sum _{k=1}^M n_k =N\) fixed, but the result is simply to sample only the estimator with less variance.

Let us consider now two particular cases. The first is when the count of samples is equal for all estimators, i.e., \(n_k =N/M\). In this case, the variance in Eq. 14 becomes

$$\begin{aligned} \frac{H\left( \left\{ \frac{v_k}{n_k}\right\} \right) }{M} = \frac{H\left( \left\{ M v_k/N\right\} \right) }{M} = \frac{H\left( \left\{ v_k\right\} \right) }{N}. \end{aligned}$$
(15)

The second is when the count of samples is inversely proportional to the variance of each estimator, i.e., \( n_k = \frac{H(\{v_k\})N}{M v_k}\). In that case, the variance in Eq. 14 becomes

$$\begin{aligned} \frac{H\left( \left\{ \frac{v_k}{n_k}\right\} \right) }{M}=\frac{H(\left\{ M v_k^2/H\left( \left\{ v_k\right\} \right) N\right\} )}{M} = \frac{H\left( \left\{ v_k^2\right\} \right) }{H\left( \left\{ v_k\right\} \right) N}. \end{aligned}$$
(16)

But from power mean monotonicity in the exponent [13], we can obtain that \(\frac{H(\{v_k^2\})}{H(\{v_k\}) } \le H(\{v_k\})\), as \(H(\{v_k\})\) corresponds to a power mean with exponent \(-1\) while \(\sqrt{H(\{v_k^2\})}\) to exponent \(-2\). Thus, the strategy of distributing the count of samples inversely proportional to the variance of each estimator is always better than the strategy of assigning an equal count of samples.

If we optimize at the same time \(w_k\) and \(n_k\), there is only the trivial solution when for all k, \(v_k =v\).

The conclusions so far are that if you have a fixed weighted combination, use Eq. 8. If you have a fixed count of samples for each estimator, use Eq. 11. If you know in advance which is the most efficient estimator, then just sample this one. If not, you can use batches of samples to estimate the variance of the different estimators and then combine them using Eq. 11.

3 Multiple importance sampling with optimal weights

Veach and Guibas [23] introduced the multiple importance sampling estimator, which makes it possible to combine different sampling techniques in a novel way. The optimal heuristic MIS case was when the weights were proportional to the count of samples, a technique they named the balance heuristic. Given M sampling techniques (i.e., pdfs) \(p_k(x)\), if we sample \(n_k\) samples from each, \(\sum _{k=1}^M n_k =N\), the balance heuristic estimate for \(I=\int f(x) \mathrm{d}x\) is given by the sum

$$\begin{aligned} F= \frac{1}{N} \sum _{l=1}^N\frac{f(x_{l})}{\sum _{k=1}^M \alpha _k p_k(x_{l})}\mathrm {,~with}~~~\alpha _k =\frac{n_k}{N}. \end{aligned}$$
(17)

As Veach observed (see Veach’s thesis [22], section 9.2.2.1), the balance heuristic estimate corresponds to a standard Monte Carlo importance sampling estimator, where the pdf p(x) is given by a mixture of distributions:

$$\begin{aligned}&p(x) = \sum _{k=1}^M \alpha _k p_k (x), \mathrm {with}~~~ \alpha _k \ge 0,~\sum _{k=1}^M \alpha _k = 1,\nonumber \\&\int p_k(x) \mathrm{d}x = 1, ~~p_k(x) \ge 0, ~~\forall k \in \{1,M\}. \end{aligned}$$
(18)

This corresponds to the estimator: \(F (x)= f(x)/p(x)\) where x is distributed according to p(x).

We will analyze next the variance of the balance heuristic, or equivalently, the variance when using as the importance sampling function a mixture of distributions. Our interest is in obtaining the weights \(\alpha _k\) that give the minimum variance. These weights determine the count of samples to be taken for each technique.

3.1 Optimal weights for equal sample cost

Observe that \(\mu = I = \int f(x)\mathrm{d}x\) is the expected value of \(F(x)=\frac{f(x)}{\sum _{k=1}^M \alpha _k p_k(x)}\) according to pdf p(x) \(p(x)=\sum _{k=1}^M \alpha _k p_k(x)\), i.e., \(\mu =E[F (x)]\). Observe also that F(x) depends on \(\{ \alpha _k \}\). Also, for all M sampling strategies,

$$\begin{aligned} \mu _k = \int \frac{f(x) p_k(x)}{\sum _{l=1}^M \alpha _l p_l(x)} \mathrm{d}x = E_k [F (x)] \end{aligned}$$
(19)

is the expected value of F(x) according to \(p_k(x)\). Observe that \(\mu = \sum _{k=1}^M \alpha _k \mu _k\).

The variance V[F(x)] can be written in several ways:

$$\begin{aligned} V[F(x)]= & {} E[F ^2(x)]-(E[F (x)])^2\nonumber \\= & {} \int \left( \frac{f(x)}{\sum _{k=1}^M \alpha _k p_k(x)} \right) ^{2} \left( \sum _{k=1}^M \alpha _k p_k(x) \right) \mathrm{d}x{-} \mu ^2 \nonumber \\= & {} \int \frac{f(x)^2}{ \sum _{k=1}^M \alpha _k p_k (x)} \mathrm{d}x - \mu ^2 \nonumber \\= & {} \sum _{k=1}^M \alpha _k \int \left( \frac{f(x)}{ \sum _{k=1}^M \alpha _k p_k (x)} \right) ^2 p_k (x) \mathrm{d}x - \mu ^2 \nonumber \\= & {} \sum _{k=1}^M \alpha _k E_k[F ^2(x)] - \mu ^2 \nonumber \\= & {} \sum _{k=1}^M \alpha _k (V_k[F (x)] + \mu _k^2) - \mu ^2, \end{aligned}$$
(20)

where by \(V_k[F (x)]\) we mean the variance of F(x) when sampling according to \(p_k(x)\):

$$\begin{aligned} V_k[F (x)]= & {} E_k\left[ F^2(x)\right] -(E_k[F (x)])^2 \nonumber \\= & {} \int \left( \frac{f(x)}{\sum _{l=1}^M \alpha _l p_l(x)}\right) ^2p_k(x) \mathrm{d}x - \mu _k^2.\\ \nonumber \end{aligned}$$
(21)

We want to find now the set of \(\{ \alpha _k \}\) that minimizes the variance of the estimator F(x), subject to the constraint \(\sum _{k=1}^M \alpha _k = 1\). We will use the Lagrange multipliers method. The Lagrangian function is \({\varLambda }(\alpha , \lambda ) = V[F(x)] + \lambda (\sum _{k=1}^M \alpha _k -1)\). Thus, for all j from 1 to M:

$$\begin{aligned} \frac{\partial {\varLambda }\left( \alpha ,\lambda \right) }{\partial \alpha _j}= & {} \frac{\partial \left( V\left[ F (x)\right] + \lambda \left( \sum _{k=1}^M \alpha _k -1\right) \right) }{\partial \alpha _j} \nonumber \\= & {} \frac{\partial V\left[ F (x)\right] }{\partial \alpha _j} + \lambda = 0. \end{aligned}$$
(22)

We have

(23)

Thus,

$$\begin{aligned} \lambda = E_j \left[ F^2 (x) \right] . \end{aligned}$$
(24)

This means that the optimal combination of \(\alpha _k\) is reached when all \(\lambda \) values are equal, i.e., when for all i, j

$$\begin{aligned} E_i \left[ F^2 (x) \right] = E_j \left[ F^2 (x) \right] . \end{aligned}$$
(25)

Using Eq. 20, the minimum variance is:

$$\begin{aligned} V\left[ F(x)\right]= & {} \sum _{k=1}^M \alpha _k E_k[F ^2(x)] - \mu ^2 \nonumber \\= & {} \sum _{k=1}^M \alpha _k \lambda - \mu ^2 = \lambda - \mu ^2. \end{aligned}$$
(26)

On the other hand, Eq. 26 gives us the value of \(\lambda \):

$$\begin{aligned} \lambda = V\left[ F(x)\right] + \mu ^2 = E \left[ F^2 (x)\right] . \end{aligned}$$
(27)

Thus, for all j,

$$\begin{aligned} E_j \left[ F^2 (x) \right] = E \left[ F^2 (x)\right] . \end{aligned}$$
(28)

Equation 25 (or equivalently Eq. 28) gives the necessary condition for \(\{ \alpha _k \}\) to be a critical point. Douc et al. [6] stated, in the context of population Monte Carlo, the convexity of the variance; thus, this critical point has to be a global minimum.

3.1.1 Discussion

The Lagrange multiplier method works by trying to equate the gradients of the function to be minimized, which in our case are \(\frac{\partial V[F (x)]}{\partial \alpha _j} = - E_j[F^2(x)]\), with the gradient of the constraint \(\frac{\partial \sum _{j=1}^M \alpha _j-1}{\partial \alpha _j}\), which is constant; thus, in our case it tries to equate all the gradients \(E_j[F^2(x)]\). These gradients can equate within the domain, where for all j, \(\alpha _j > 0\), in which case Eq. 28 holds for all j, and there is a local (and global) minimum, or otherwise there is no local minimum within the domain, and the global minimum is at the border, when for some j, \(\alpha _j = 0\). In that latter case, the gradients which correspond to \(\alpha _j > 0\) still equate and obey Eq. 28. This is because we can consider the problem reduced to the nonzero \(\alpha _j\), which thus has a global minimum within the reduced domain and thus obeys Eq. 28. See Fig. 1a, b for the case \(M=2\).

Observe also from Fig. 1 that the convexity of variance V[F(x)] ensures that its minimum will be always less or equal than the minimum of the variances of the independent techniques. This makes valuable any strategy to approximate the minimum.

Fig. 1
figure 1

At the left, the minimum is taken within the domain \(\alpha _1+\alpha _2=1\). At the right, no local minimum exists within the domain, and the global minimum is taken at the border. \(v_1,v_2\) are the variances for each technique in turn, in Eq. 35

Full size image

3.1.2 Combinatorial strategy

A strategy to approximate the optimal \(\alpha _k\) values in general would run along the following lines. First, for each j, sample \(n_j\) samples from \(p_j(x)\). In this way, we can estimate, for all combinations of \(\alpha _k\) and with the same samples, the \(\lambda \) values in Eq. 24, using the estimator

$$\begin{aligned} E_j \left[ F^2(x)\right] \approx \frac{1}{n_j} \sum _{l=1}^{n_j} F^2(x^{j}_l), \end{aligned}$$
(29)

where

$$\begin{aligned} F(x^{j}_l) = \frac{f(x^{j}_l)}{\sum _{k=1}^M \alpha _{k} p_k(x^{j}_l)}. \end{aligned}$$
(30)

The optimal \(\alpha _k\) values would be the ones that make all these values the most similar. Observe that for each j you need to take the \(n_j\) samples only once. This strategy could be organized by taking batches of samples to improve on the \(\{\alpha _k\}\) gradually.

3.2 Optimal weights for non-equal sample cost

The optimal \(\alpha _k\) values considered before do not take into account the different sampling costs for each pdf \(p_k(x)\). Let \(c_k\) be the cost for one sample from technique k. The average cost per sample is then \(\bar{c} = \sum _{k=1}^M c_k \alpha _k \). The optimal \(\alpha _k\) values will come now from minimizing the inverse of efficiency, which is defined as cost times variance, subject to the constraint \(\sum _{k=1}^M \alpha _k= 1\), i.e., \({\varLambda }(\alpha , \lambda ) = \bar{c} V[F (x)]+ \lambda (\sum _{k=1}^M \alpha _k -1)\). Using again the Lagrange multiplier method, we obtain for all j,

$$\begin{aligned} \lambda = \bar{c} E_j [F^2(x)] -c_j V[F(x)] \end{aligned}$$
(31)

By multiplying Eq. 31 by \(\alpha _j\) and summing over j, and using Eq. 20, we can obtain the value of \(\lambda \):

$$\begin{aligned} \lambda = \sum _{j=1}^M \alpha _j \lambda= & {} \sum _{j=1}^M \left( \bar{c} \alpha _j E_j [F^2(x)] - \alpha _j c_j V[F(x)] \right) \nonumber \\= & {} \bar{c} E[F^2(x)] - \bar{c} V[F(x)] = \bar{c} \mu ^2. \end{aligned}$$
(32)

As \(\lambda = \bar{c} \mu ^2 = \bar{c} (E[F^2(x)] - V[F(x)])\) we can write Eq. 31 as

$$\begin{aligned} \bar{c} E[F^2(x)] = \bar{c} E_j [F^2(x)] + (\bar{c}-c_j) V[F(x)]. \end{aligned}$$
(33)

When all costs are equal, \(\bar{c} = c_j\) for all j, Eq. 33 reduces to Eq. 28.

To minimize the variance for a given cost budget and thus to maximize the efficiency for all j, the right-hand side for different index j in Eq. 31 have to be the same. Observe expected values appearing in Eq. 31 can be estimated in the same way as before for Eq. 24, by sampling \(n_j\) samples for all j from \(p_j(x)\) pdf. We can include the cost in a batching strategy to approximate the optimal \(\alpha _k\) weights.

3.3 Heuristic for weights

The question arises now whether, without recourse to the brute force batching procedure or to some slow iterative strategy, there is some heuristic that would give suboptimal values. We outline the adaptive algorithm in Appendix C in the supplementary material. We have seen in Sect. 2.2 that in the linear case, the strategy of distributing the samples inversely proportional to the variance of each estimator is always better than the strategy of assigning an equal count of samples to each estimator. Thus, we will consider the \(\alpha _k\) values inversely proportional to the variances of the estimators taking as pdf each \(p_k(x)\) in turn, respectively; that is, we compute \(\alpha _k\) as follows:

$$\begin{aligned} \alpha _k=\frac{H(\{v_k\})}{M v_k}, \end{aligned}$$
(34)

where \(v_k\), introduced in Sect. 2.2, is the variance of the estimator of I, \(\frac{f(x)}{p_k(x)}\), when doing importance sampling according to \(p_k(x)\), i.e.,

$$\begin{aligned} v_k = {\int \frac{f^2(x)}{p_k(x)} \mathrm{d}x - I^2}. \end{aligned}$$
(35)

Here we considered the estimators to be unbiased. This happens for estimator k if, whenever \(f(x)\ne 0\), then \(p_k(x) \ne 0\). As a particular case, if we take \(f(x) = {\varPi }_k p_k(x)\), then all the estimators are unbiased. Observe from Eq. 34 that the less the variance of a technique is, the more we sample from that technique, remember from Eq. 17 that the count of samples is proportional to \(\alpha _k\). Trivially, for any pair \(\{ k,j \}\), if \(v_k\ne 0,v_j \ne 0\), then \(\alpha _k/\alpha _j=v_k/v_j\). Thus, if all \(v_k\) are equal, so are all \(\alpha _k\).

Let us examine the limiting case, when a variance \(v_k\) is zero. For this to happen, \(p_k(x)= f(x)/I\), as then doing importance sampling with pdf \(p_k(x)\) the integrand will be constant, and variance \(v_k\) will be zero. In that case, no other variance can be zero (supposing \(p_i(x) \ne p_j(x)\) for \(i \ne j\)) and taking the limits in Eq. 34 for \(v_k \rightarrow 0\), \(\alpha _k = 1\), \(\alpha _{j\ne k} = 0\).

The other limiting case, when some variance(s) \(v_m\) are high with respect to the other ones, taking the limits in Eq. 34 for \(v_m \rightarrow \infty \) we obtain \(\alpha _m = 0\).

3.3.1 Comparing bounds for equal count of sampling and new heuristic

We show here that we can find tighter bounds for our heuristic than for equal count of samples. We start from the inequality between weighted harmonic and arithmetic means [2]. For any two sets of positive values \(\{ b_k\}\) and \(\{\alpha _k\}\) (\(\sum _{k=1}^M\alpha _k=1\)), it holds that:

$$\begin{aligned} \frac{1}{\sum _k \frac{\alpha _k}{b_k}} \le \sum _k \alpha _k b_k, \end{aligned}$$
(36)

Then, taking \(b_k = \frac{f^2(x)}{p_k (x)}\), we get:

$$\begin{aligned} \frac{1}{ \sum _{k=1}^M \frac{\alpha _k}{{\frac{f^2(x)}{p_k (x)}}}} \le \sum _{k=1}^M \alpha _k \frac{f^2(x)}{p_k (x)}. \end{aligned}$$
(37)

And using the expression for the variance Eq. 20, we obtain the bound for V[F(x)]:

$$\begin{aligned} V[F(x)]= & {} \int \frac{1}{ \sum _{k=1}^M \frac{\alpha _k}{{\frac{f^2(x)}{p_k (x)}}}} \mathrm{d}x -\mu ^2 \nonumber \\\le & {} \sum _{k=1}^M \alpha _k \left( \int \frac{f^2(x)}{p_k (x)} \mathrm{d}x - \mu ^2\right) = \sum _{k=1}^M \alpha _k v_k. \end{aligned}$$
(38)

A first observation is that, by the rearrangement inequality [10], given a fixed set \(\alpha _k\), the minimum bound in Eq. 38 will be obtained when the \(\alpha _k\) and the \(v_k\) are paired in inverse order, i.e., \(\alpha _i \le \alpha _j \Leftrightarrow v_i \ge v_j\), i.e., \(\alpha _k\) is decreasing on \(v_k\).

For equal count of samples, \(\alpha _k = 1/M\) for all k in Eq. 38, we have that \(\sum _{k=1}^M \alpha _k v_k = \frac{1}{M} \sum _{k=1}^M v_k\), i.e., the arithmetic mean of \(\{v_k\}\).

For the new heuristic, \(\alpha _k=\frac{H(\{v_k\})}{M v_k}\), \(\sum _{k=1}^M \alpha _k v_k = \sum _{k=1}^M \frac{H(\{v_i\})}{M v_k} v_k = H(\{v_k\})\), harmonic mean of \(\{v_k\}\).

As the harmonic mean is always less than or equal the arithmetic mean, i.e.,

$$\begin{aligned} H(\{v_k\}) \le \frac{1}{M} \sum _{k=1}^M v_k \end{aligned}$$
(39)

we can guarantee that using \(\alpha _k \propto \frac{1}{v_k}\) we have always a lower bound for the variance than using \(\alpha _k = \frac{1}{M}\).

The question about how much better is the bound using \(\alpha _k \propto \frac{1}{v_k}\) than using \(\alpha _k = \frac{1}{M}\) is the same as the one about how much distance there is between harmonic and arithmetic mean. Both means are equal if and only if all values \(\{v_k\}\) are equal. And the more unequal the \(\{v_k\}\) values are, the more dissimilar are the means. Observe that, by the properties of harmonic mean, \(H(\{v_k\}) \le M \text{ min }_k \{v_k\}\) while the behavior of arithmetic mean is driven by \(\text{ max }_k \{v_k\}\). The bigger the difference between \(\text{ max }_k \{v_k\}\) and \(\text{ min }_k \{v_k\}\), the bigger the difference between the means.

Observe finally that although we can guarantee a lower bound, we cannot guarantee that using the new heuristic we always obtain a better result. As an example, consider the trivial case \(f(x) \propto \sum _{k=1}^M\alpha _k p_k(x)\), with \(p(x)= \sum _{k=1}^M\alpha _k p_k(x)\), where \(V[F(x)]=0\), while with the new heuristic \(V[F(x)]>0\).

3.3.2 Extension of the new heuristic to include cost of sampling

If we want to include the cost \(c_k\) of importance sampling, it seems natural to extend the heuristic in Eq. 35:

$$\begin{aligned} \alpha _k \propto \frac{1}{c_k \left( {\int \frac{f^2(x)}{p_k(x)} \mathrm{d}x - I^2}\right) } \end{aligned}$$
(40)

and thus

$$\begin{aligned} \alpha _k=\frac{H(\{c_k v_k\})}{M c_k v_k}. \end{aligned}$$
(41)

As the variances are not usually known in advance, they have to be estimated using some batch of samples.

4 Linear combination versus MIS

The question arises about which kind of combination to use when we have several techniques at hand, either linear combination in Sect. 2.2 or MIS in Sect. 3. If some techniques are biased, such as in reusing paths techniques [1], linear combination of estimators will be biased. But if it holds that when \(f(x) > 0\) then \(p(x) >0\), MIS will produce an unbiased estimator. If all techniques are unbiased, we can use both kinds of estimators. We know from Sect. 2.2 that the variance for the linear combination of unbiased estimators is greater or equal than \({\min }_k\{v_k\}\). On the other hand, we have seen in the discussion in Sect. 3.1 that the minimum MIS variance will be always less or equal than \({\min }_k\{v_k\}\). Using MIS pays off if we have a good strategy to approximate this minimum. Also, when for all k, \(v_k >0\), using the MIS estimator to estimate \(f(x) \propto \sum _{k=1}^M\alpha _k p_k(x)\) we can obtain zero variance with \(p(x) \propto f(x)\), while it is not possible with linear combination.

Let us see a relationship between the variances for MIS estimator and linear combination of estimators. Observe that the second member of the inequality Eq. 38 is the variance of the linear combination of estimators when the weights are taken as proportional to the count of samples. Effectively, given the M estimators each with variance \(v_k\) and \(n_k\) samples, by taking in Eq. 6 \(w_k=\alpha _k = n_k/N\), where \(N=\sum _{k=1}^M n_k\),

$$\begin{aligned} \frac{1}{N^2} \sum _{k=1}^M n_k^2 \frac{v_k}{n_k} = \frac{1}{N} \sum _{k=1}^M \alpha _k v_k, \end{aligned}$$
(42)

which normalized to \(N=1\) becomes \(\sum _{k=1}^M\alpha _k v_k\). Thus, Eq. 38 tells us that the variance of MIS estimator using the values \(\{ \alpha _k \}\) is less than the variance of the linear combination of estimators when the weights are proportional to the count of samples, i.e., \(w_k=\alpha _k\).

5 Results

We have tested the proposed MIS algorithm on one- and two-dimensional functions. We keep the analysis as simple as possible and restrict numerical evaluation to the implementation of the environment map illumination.

Fig. 2
figure 2

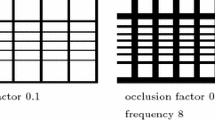
Four out of eight occlusion masks used in our tests as textures put on a sphere (white windows in the texture have approximately the same area when mapped on the sphere surface located around the object). The black color corresponds to the occluded part of the texture, and the white color represents the un-occluded part of the texture through which a 3D object is lit from infinity from the environment map

Full size image

5.1 Simple functions in \(R^1\)

In domain \(R^1\), we show an example with a general function \(f(x)=x^2\sin ^2 (x) + (3 x + 1) \cos ^2(x)\) sampled by three independent functions \(p_1(x)=\frac{x+1}{2.692} \), \(p_2(x)=\frac{x^2-x/\pi +1}{3.203}\), and \(p_3(x)=\sin (x)\) with domain \(\langle 1/3\pi , 2/3\pi \rangle \). The functions depiction, the detailed computation of variance and efficiency is in Appendix A in the supplementary material. The maximum theoretical gain in the efficiency improvement for equal costs of sampling from the three functions is +265%, when compared to the equal count and equal cost of sampling. For C++ implementation with sampling batches, we get an efficiency improvement of +224% for 500 samples taken.

For unequal cost of sampling, the gain in efficiency can drop or increase in dependence on the actual cost of sampling. We show here the decrease in gain from +265% for unequal sample cost (\(c_1=1\), \(c_2=1.6\), \(c_3=1.07\)) to +151%, since sampling according to \(p_2(x)\) is the most efficient. For C++ implementation with sampling batches, the relative efficiency improvement is +120% for 500 samples taken.

5.2 Analytical test in \(R^2\)

The first test in \(R^2\) is the analytical derivation of formulas in Mathematica and corresponds to the illumination of an object with a Lafortune–Phong BRDF model with an environment map simplified to the function \(R(\theta ,\phi )=\cos (\theta )\) assuming full visibility, described in Appendix B in the supplementary material. For this setting, the maximum theoretical gain in efficiency of the adaptive algorithm is by +138% for equal costs of sampling from both functions. For uneven sampling costs, where the ratio 1:4.8 was measured from C++ implementation of the algorithm when the environment map is represented by a 1 MPixel image (the cost of sampling from the environment map is 4.8 times less than the cost of sampling from the BRDF), the maximum theoretical gain achieved in sampling efficiency is +702%.

5.3 Numerical test in \(R^2\)

The second test in \(R^2\) was numerical and implemented in C++ for environment map illumination using a broad range of BRDF values. The computed images were ray traced (primary and shadow rays) and sampling is computed independently for each pixel with a different set of random numbers. To make sampling more difficult, we used the occlusion grid around the object, unlike [11], where the full visibility was considered. The occlusion grid is a sphere positioned with center in the object and texture defining the occlusion geometry. For the sake of getting the visual results across the whole image, the occlusion sphere is not visible from the camera and it is used only for shadow rays.

Environment maps. We collected 58 environment maps (EM) represented by HDR images. First we normalized all EMs to unit power and then we computed the variance of the normalized EM. We selected 25 EM with different variance providing the whole range of variance values in 6 magnitudes. The 25 EM were then used for the initial rendering of images as described above.

BRDF setting. For the BRDF, we used the physically corrected Lafortune–Phong BRDF model [14] that allows for analytical importance sampling. It was used 4 times with a fixed setting over the whole object and once with the BRDF varying over the geometry. The first setting of the BRDF model was: \(\rho _\mathrm{d}=0.5, \rho _\mathrm{s}=0.5, n=1\). The second setting of the BRDF model was: \(\rho _\mathrm{d}=0.5, \rho _\mathrm{s}=0.5, n=10\). The third setting of the BRDF model was: \(\rho _\mathrm{d}=0.1, \rho _\mathrm{s}=0.9, n=10\). The fourth setting of the BRDF model was: \(\rho _\mathrm{d}=0.1, \rho _\mathrm{s}=0.9, n=100\). The fifth setting of the BRDF was varying the BRDF model over the surface by changing the exponent and ratio between diffuse albedo \(\rho _\mathrm{d}\) and specular albedo \(\rho _s\) along a texture square, while the total albedo of the BRDF is set to one (i.e., \(\rho _\mathrm{s}+\rho _\mathrm{d}=1\)). The diffuse albedo \(\rho _{\mathrm {diff}}\) is interpolated in axis y on a square by function \(\rho _{\mathrm {diff}}(y) = (1-y)^2\) for range \(y \in \langle 0, 1\rangle \), while the specular albedo is \(\rho _{\mathrm {spec}}=1-\rho _{\mathrm {diff}}\). For the specular exponent, we use the mapping in texture for coordinate \(x \in \langle 0, 1\rangle \) by formula \(n(x) = 10 + 90 x^{\frac{1}{4}}\) that gives the range \(\langle 10, 100\rangle \).

Geometry and Viewpoint. We used a sphere as geometry viewed from two view points, which allowed to show substantial differences in BRDF variation.

Occluder setting. To set the occlusion grid, we used three different occlusion factors (0.1, 0.2, and 0.3) and four different frequencies for our tests (\(4\times 4\), \(6\times 6\), \(8\times 8\), and \(10\times 10\) blocking grid on the sphere), in total 12 occluder grid settings. Due to the lack of space we show here only 4 occluders in Fig. 2.

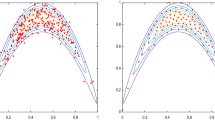
We used 2 combinations viewpoints for a single object, 5 different settings of BRDF, in total 25 EM and 12 occlusion grids. We have used all \(2\times 5\times 25\times 12=3000\) test cases and rendered them with BRDF.\(\cos (\theta )\) sampling and EM sampling, using 100 samples per pixel. We then selected 8 representative cases with different noise in pairs of images rendered by the two methods to show the properties of the sampling algorithms. The images computed for 1000 samples for 8 test scenes are shown in Fig. 3. The variances of the EMs for the 8 representative cases are given in Table 1.

Fig. 3
figure 3

Rendered images for 200 samples per pixel for the 8 representative cases and MIS with balance heuristic \(\alpha _1=\alpha _2=0.5\)

Full size image
Table 1 Setting of the 8 test scenes used with scene identification (first column), identification of BRDF setting for images computed (second column), variance computed from the environment map used after the normalization to unit power (third column), (1) image MSE for sampling from the environment map (fourth column), (2) image MSE for sampling from BRDF.\(\cos (\theta )\) (fifth column), and the ratio of the two previous columns (sixth column). The resolution of the environment maps used varied from 1024\(\times \)512 to 4096\(\times \)2048
Full size table

Testing methodology. We have tested the methods for moderate count of samples from 100 to 1500 to get visible differences in noise and evaluated the mean square error (MSE corresponding to variance, averaged over all pixels). The reference images were computed with 400,000 samples by the balanced heuristic with fixed weights \(\alpha =0.5\). The MSE results are summarized in Table 1 as log–log graphs. For adaptive sampling algorithms, we have set the number of samples in the pilot stage to 20% for which half of samples were taken according to the BRDF and the second half according to the EM. The computation was then organized in eight additional stages, each 10% of all samples. At the end of each stage, it was decided how to distribute samples in the next one using in Eqs. 34 and 41.

Fig. 4
figure 4

Scene 1 to 8, graphs with MSE for all 9 sampling methods in terms of MSE for 100,200,500,1000,1500 samples. The axis x is the number of samples, axis y shows MSE, both axes have logarithmic scale. The convention for importance sampling (IS) methods in graphs is: 1—environment map IS, 2—BRDF.\(\cos {\theta }\) IS, 3—optimal linear combination between environment map IS and BRDF.\(\cos {\theta }\) IS (Eq. 13), 4—balance heuristic with equal weights \(\alpha _1=\alpha _2=0.5\), 5—adaptive balance heuristic by Lu et al. [16], 6—balance heuristic with heuristic weights (Eq. 34), 7—balance heuristic with unequal weights, combinatorial search, minimal variance of Eq. 17 for each pixel, 8—optimal balance heuristic MIS scheme (Eq. 24), 9—balance heuristic MIS with heuristic weights and considering cost (Eq. 41, the total cost the same as for the balance heuristic with equal weights)

Full size image

Our adaptive sampling algorithm decreases the variance both against standard MIS with an equal count of samples and also against the technique by Lu et al. [16]. We computed two combinatorial solutions given a fixed count of N samples for a range of \(\alpha \in \langle 0.1, 0.9\rangle \). This corresponds to the need for a pilot sampling stage with 20% of the samples. The first one minimizes the variance from N samples using Eq. 17 by searching for the best \(\alpha \). The second one finds the optimal value of \(\alpha \) to equalize \(\lambda \) values in Eq. 24 using N samples.

To comment in detail on the results for all 8 test scenes is difficult. Our balance heuristic with heuristic weights was always better than standard balance heuristic with equal weights and mostly better than the algorithm by Lu et al. [16]. The selected test cases have a wide range of initial MSE values. The combinatorial algorithms that are the best in theory are not always better than adaptive ones. A reason is that the evaluation is carried out pixel by pixel and we compute the averages of MSE for the whole image.

The computation overhead of our technique with batches, needed to adapt the samples distribution during the computation, was less than 2% in all cases; the computation of variances and means in the sampling scheme together with computing the distribution of samples in the next stage of sampling presents a negligible overhead. The cost of sampling from the BRDF and the EM was almost equal in our tests (\(\mathrm{cost}_{\mathrm{BRDF}} = 0.8 \mathrm{cost}_{\mathrm{EM}}\)), as we stored the precomputed lights to an array in preprocessing and randomized their selection during sampling. The equal cost of sampling from both strategies is the worst case for our scheme, but still we achieve an improvement over equally distributed samples (fixed \(\alpha =0.5\)). Without storing precomputed light to array then \(\mathrm{cost}_{\mathrm{EM}} = 4.8 \mathrm{cost}_{\mathrm{BRDF}}\) achieved even higher efficiency improvement.

5.4 Discussion and limitations

Other adaptive sampling schemes with MIS are possible, but our proposed scheme requires little additional memory and almost no computational overhead, and it is accurate with respect to the presented theory. The improvement of sampling efficiency for other applications of this sampling scheme is potentially even higher if the sampling costs between the functions differ.

The proposed adaptive technique requires to estimate the variances. This is only a small cost overhead, although to estimate them reliably a low count of samples such as 10 or 20 cannot be used. This is the same as in Lu et al. [16], where the minimum number of samples in the pilot stage was set to 64, or as in other adaptive techniques [3, 5, 17]. The charts show that the crossover points where the adaptive methods start to be more efficient vary widely between 100 and 1500 samples, for scenes 5 and 7 crossover points are past 1500 samples (Fig. 4).

6 Conclusion and future work

In this paper, we have analyzed the multiple importance sampling estimator with the balance heuristic weights. Exploiting that the balance heuristic is importance sampling with a mixture of densities, we have given mathematical expressions for the variance of the MIS estimator, for the optimal weights, i.e., the distribution of sampling that optimizes the variance, a batch procedure to approximate them, and finally a heuristic formula to approximate directly the optimal weights. We have also considered the cost of sampling in our formulation, when we optimize the efficiency of the estimator. We have demonstrated our algorithm with numerical experiments on functions in \(R^1\) and in \(R^2\) for a problem of local illumination computation of a 3D object covered by a spatially varying BRDF and lit by an environment map with the presence of occluders. We have shown more than doubling of the sampling efficiency to the standard non-adaptive MIS algorithm for an equal sample cost for \(R^1\) case and various improvements for the \(R^2\) case. As a future work, our proposed sampling method could be tested in other rendering algorithms, for example, in many-light methods.