Adaptive compression of animated meshes by exploiting orthogonal iterations

Abstract

We introduce a novel approach to support fast and efficient lossy compression of arbitrary animation sequences ideally suited for real-time scenarios, such as streaming and content creation applications, where input is not known a priori and is dynamically generated. The presented method exploits temporal coherence by altering the principal component analysis (PCA) procedure from a batch- to an adaptive-basis aiming to simultaneously support three important objectives: fast compression times, reduced memory requirements and high-quality reproduction results. A dynamic compression pipeline is presented that can efficiently approximate the k-largest PCA bases based on the previous iteration (frame block) at a significantly lower complexity than directly computing the singular value decomposition. To avoid errors when a fixed number of basis vectors are used for all frame blocks, a flexible solution that automatically identifies the optimal subspace size for each one is also offered. An extensive experimental study is finally offered, showing that the proposed methods are superior in terms of performance as compared to several direct PCA-based schemes while, at the same time, achieves plausible reconstruction output despite the constraints posed by arbitrarily complex animated scenarios.

1 Introduction

Fig. 1

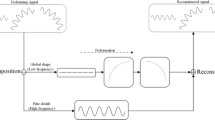
Overview of our animation compression method. Assuming sequential arrival of the animation data (top), the dictionary is dynamically updated for each cluster (block of 10 frames) by employing adaptive orthogonal iterations (AOI). The reconstructed results of the Handstand animation confirm that AOI achieves similar quality in 25$\times$ faster times when compared to a direct SVD-based solution (bottom)

With the rapid advances in high-performance computing, scanning operations and content creation tools, the output data are expanding rapidly generating massive datasets. While this can be mitigated by applying compression techniques to the data being archived or transferred, the tremendous computing resources required bring tough challenges to be solved. Recently, there has been increasing interest on acquiring, processing, storing and transmitting 3D animated meshes facilitating several real-time applications (e.g., Microsoft Holoportation, an immersive telepresence system).

Throughout the years, numerous approaches have been proposed improving more or less some of the key animation compression characteristics [16]: encoding–decoding requirements, reconstruction quality and compression rates. Without loss of generality, these methods can be classified either as local- or global-based, depending on the frame window analysis taken for compressing the animation sequence. The main benefit of the global approaches is an improved compression rate by analyzing the overall motion coherence, whereas the local ones focus on local frame-to-frame transitions allowing low-latency streaming.

Skinning as well as principal component analysis (PCA) can be considered as the most well-known global methods for providing efficient compact representations of rigid and highly deformable animations, respectively. Though a large variety of different strategies have been introduced in both skinning [8] and PCA [16], all of them suffer from excessive computational requirements, strongly dependent on the geometry size and the total animation length. While for non-interactive applications, where animation is known a priori, the compression choice can easily be determined solely based on the underlying motion, new challenges rise when attempting to support unknown arriving geometry (see Fig. 2).

In this work, we introduce a novel out-of-core adaptive approach capable of approximating efficiently the PCA-based dictionary at a significantly lower computational complexity than directly applying singular value decomposition (SVD) as illustrated in Fig. 1. Inspired by the observation that only small deformation variations will normally occur between consecutive poses [32], we split the animation sequence into uniform frame blocks and perform subspace tracking by processing each incoming block at a time. By exploiting temporal coherence, we are capable of efficiently estimating the dictionary of the current frame batch using as input the precomputed dictionary of the previous batch [4]. To this end, we present a general iterative method to perform orthonormalization by exploring several orthogonal iterations variants [24]. In cases of high motion change between frame blocks, the optimal subspace size k can be automatically and dynamically adjusted to consistently reconstruct each incoming block of animation data. Our method can be successfully applied in cases where the animated data are handled as separate geometry clusters [22] as well as for exploiting both spatial [1] and temporal correlations [27]. An extensive experimental evaluation study on a wide range of animations considering a large spectrum of settings and configurations is finally offered showing the notable improvements in processing times (up to 60$\times$) as compared to prior art without sacrificing the final reconstruction quality.

2 Related work

Animation compression schemes aim to provide a compact representation of the original animation, without affecting the perceived amount of distortion during reconstruction. Assuming constant connectivity (which can be encoded in an extremely efficient way [16], the sequence consists of a geometric evolution of the vertices of the initial mesh over time. A straightforward approach for compressing the animated geometry can be derived by applying one of the numerous available static mesh compression methods [3, 13, 14, 18, 25] to each one of the individual frames. Although such an approach would result in an efficient exploitation of the spatial coherence, it completely ignores the temporal one, missing a crucial factor to achieve higher compression ratios [9].

A large variety of animation compression algorithms has been introduced the last few years in the literature [16]. One can classify them into two core groups according to whether the time coherence is locally or globally analyzed. Despite the computationally fast behavior of the local approaches (e.g., wavelets  [19] and predictive coding methods  [23]), for the remainder of this paper we will focus on global compression schemes (Fig. 2).

Fig. 2

Selected snapshots of (left) flag, (middle) ocean and (right) airflow dynamic simulations [12]

PCA-based approaches. Generally, these can be classified according to where PCA is used to exploit spatial and/or temporal coherence of the input data, the matrix representation of the sequence’s geometry. Alexa and Müller [1] were the first to employ PCA to fit a low-dimension subspace to the animation dataset and express each frame as a linear combination of the largest eigenvectors (EigenShapes) that spans the selected subspace. By exploiting temporal coherence, Karni and Gotsman [9] advanced this method by performing linear prediction coding on the extracted spatial PCA coefficients. Luo et al. have further achieved better compression ratio and computation times by aggregating similar frames into temporal clusters and compress them separately [15]. Contrary to the streaming nature of our method, in this approach the frames belonging to the same cluster may not be contiguous.

Conversely, several authors [22, 27] suggested to apply PCA on the temporal space (EigenTrajectories); the main benefit is that it involves the decomposition of a smaller covariance matrix, since the number of frames is usually less than the number of vertices. To capture more efficiently local similarity characteristics, the authors in [2, 20, 22] suggested segmenting the mesh into deformation-aware clusters, which are then compressed independently. An adaptive compression allocation procedure is also offered, assigning more PCA coefficients to clusters that undergo extreme deformations [2]. To achieve better compression ratio, several algorithms were introduced to code (i) the PCA bases via principal components [22] and non-least squares optimal linear/accelerated movement [28] as well as (ii) the PCA coefficients by local predictor coding schemes such as the parallelogram rule [27], neighborhood average and radial basis functions [29] and Laplacian coordinates  [26]. These methods can enhance their final approximation by representing the residual motion compensation errors via temporal DCT-based (discrete cosine transform) [17] or PCA-based corrections [11]. Before storing or transmitting, quantization (uniformly [7] or not [28]) is finally performed to encode the floating point data. Figure 3 provides a generic diagram summarizing the stage flow which one may follow during a PCA-based compression pipeline.

Subspace tracking approaches. Unfortunately, computing SVD (the standard direct approach to estimate PCA), can be extremely memory-demanding and time-consuming for large-scale animation problems (specifically, $O(m^3)$ for a matrix of $m\times m$ size). On the other hand, subspace tracking algorithms are fast alternatives relying on the execution of iterative schemes for evaluating the desired eigenvectors per incoming block of floating point data [4]. These alternatives schemes can be classified into low ($O(mk^2)$) and high ($O(m^2k)$) complexity, where $k(\ll m)$ denotes the number of principal eigenvectors. The best performance among the high complexity class is achieved by the Lanczos Iterations (LI) [33], while the primary representative of the other class is based on the Orthogonal Iterations (OI) [24]. Although the LI method requires less iterations for evaluating the subspace of a symmetric matrix, the complexity of each one is $O(m^2k)$. On the other hand, the OI alternative can result in very fast solutions when the initial input subspace is close to the subspace of interest, as well as the size of the subspace remains at small levels [21]. The effectiveness of OI is attributed to the fact that both matrix multiplications and QR factorizations have been highly optimized for maximum efficiency on modern serial and parallel architectures. These properties make the OI approach more attractive for real-time applications. To the best of our knowledge, subspace tracking algorithms have never been applied to the animation compression problem, despite their wide success on a large range of filtering applications.

Fig. 3

High-level PCA-based compression framework. We revise accordingly the PCA computation stage providing notable speed benefits without altering the general pipeline

Fig. 4

Our adaptive animation compression pipeline. Temporal, and optionally spatial, clustering is initially employed to support the encoding of sequentially arriving animation frames (left). For each incoming block of frames, the dictionary is estimated by readjusting the subspaces computed at the previous block via adaptive orthogonal iterations (middle). High-quality reconstructions are finally computed by efficiently combining the estimated dictionary and feature vectors (right)

3 Overview of our method

Apart from the high-quality reconstruction output when compressing skeletal (skinning-based) and highly deformable objects (PCA-based), these methods assume that (i) all frames of the animation sequence are already known to the encoder, an unsuitable requirement for interactive scenarios; (ii) the maximum animation length lasts a few seconds (assuming real-time rendering at 30fps); as well as (iii) the geometry size is upper-bounded to a fixed number of triangles, avoiding memory overflows and performance delays.

We introduce a general, fast and lossy compression approach suited when the animated data are either dynamically produced or too large to fit into main memory at once. From a high-level point of view, the basic structure of our framework is very similar to that of the aforementioned methods, altering only the encoding stage from offline to online, leaving the rest unchanged including connectivity compression, geometry clustering, dictionary coding and quantization (see Fig. 3). In this work, the animation sequence is divided into an uniform block of frames corresponding to disjoint temporal intervals, which are then encoded independently one from another by performing adaptive (online) PCA-based compression (in either the spatial or the temporal domain). Assuming low dictionary variance between successive frame blocks, we successfully apply subspace tracking via adaptive orthogonal iterations (AOIs) significantly reducing the processing requirements needed if the conventional PCA schemes are alternatively utilized. When quality consistency of reconstructions is of utmost importance, the optimal subspace size k can dynamically be adjusted in an iterative manner. The entire pipeline is illustrated in Fig. 4 and discussed in further detail in the following sections.

3.1 Preliminaries on PCA-based compression

The central idea of principal component analysis is to reduce the dimensionality of a dataset $\mathbf {D}$ consisting of a large number of interrelated variables without sacrificing the variation present in the dataset. This is achieved by transforming to a new set of variables, the principal components, which are uncorrelated, and which are ordered so that the first few retain most of the variation present in all of the original variables [5].

The input is a series of f consecutive static, point or triangular, meshes $\mathcal {P}_1, \ldots , \mathcal {P}_f$, namely poses. Each pose $\mathcal {P}_i$ with n vertices can be represented by two different sets $\mathcal {P}_i=\left( \mathcal {V}_i,\mathcal {F}_i\right)$ corresponding to the vertices $\mathcal {V}_i$ and the indexed faces $\mathcal {F}_i$. In our case, all poses have the same connectivity $\mathcal {F}_i=\mathcal {F}$, yet different geometry $\mathcal {V}_i$. So, the animation data matrix $\mathbf {D}$ can be defined as:

$$\begin{aligned} \mathbf {D} = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \mathbf {p}_{11},&{}\mathbf {p}_{12},&{}\ldots ,&{}\mathbf {p}_{1j},&{}\ldots ,&{}\mathbf {p}_{1n}\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ \mathbf {p}_{f1},&{}\mathbf {p}_{f2},&{}\ldots ,&{}\mathbf {p}_{fj},&{}\ldots ,&{}\mathbf {p}_{fn}\\ \end{array}\right] \in ~\mathfrak {R}^{3f\times n}, \end{aligned}$$

(1)

where $\mathbf {p}_{ij} = \left[ x_{ij}, y_{ij}, z_{ij}\right] ^\mathrm{T}$ are the x, y, z Euclidean coordinates of the vertex position $\mathbf {p}_{j}$ in pose $\mathcal {P}_i$.

The classic PCA-based approaches provide efficient representations in either the spatial [1] or the temporal space [22] by suggesting to evaluate the autocorrelation matrix $\mathbf {A}$ in the domain with the smaller size:

$$\begin{aligned} \mathbf {A}&= {\left\{ \begin{array}{ll} \frac{1}{e}\cdot \mathbf {D}\mathbf {D}^\mathrm{T}\in ~\mathfrak {R}^{e\times e} &{} \mathbf{if } \,{f} \ll {n} \quad (\mathrm{temporal})\\ \frac{1}{n}\cdot \mathbf {D}^\mathrm{T}\mathbf {D}\in ~\mathfrak {R}^{n\times n} &{} \mathbf{otherwise }\, (\mathrm{spatial}) \end{array}\right. }, \end{aligned}$$

(2)

where $e=3f$. For the sake of simplicity, we will focus on the temporal case. After constructing the autocorrelation matrix (Eq. (2)), the direct SVD is applied to $\mathbf {A}$ leading to a factorization of the form:

$$\begin{aligned} \mathbf {A}&= \mathbf {U}\varvec{\varSigma }\mathbf {U}^\mathrm{T} \end{aligned}$$

(3)

where $\mathbf {U}=\left[ \mathbf {u}_{1},\ldots ,\mathbf {u}_{e}\right]$, $\mathbf {u}_{i}\in ~\mathfrak {R}^{e\times 1}$ and $\mathbf {U}^\mathrm{T}$ are called the left- and right-singular vectors, respectively. The matrix $\varvec{\varSigma }=\mathrm{diag}(\lambda _{i}),~\lambda _{i}\in \mathfrak {R}$ contains the singular values of $\mathbf {A}$: $\lambda _{i}\ge \lambda _{j}>0,~\forall i>j\ge r=\mathrm{rank}(\mathbf {A})$. The encoding is performed by projecting the trajectories of each vertex to the subspace dictionary defined by the k-eigenvectors $\mathbf {E} = \left[ \mathbf {u}_{1},\ldots ,\mathbf {u}_{k}\right] \in \mathfrak {R}^{e\times k}$ that correspond to the k-largest eigenvalues $[\lambda _{1}$, $\ldots ,\lambda _{k}]$, creating a feature vectors matrix $\mathbf {F}$:

$$\begin{aligned} \mathbf {F} = \mathbf {E}^\mathrm{T}\mathbf {D}\in \mathfrak {R}^{k\times n},~\text {where}~k\le r. \end{aligned}$$

(4)

The compressed frames are finally decoded by multiplying the feature vectors with the dictionary:

$$\begin{aligned} \hat{\mathbf {D}} = \mathbf {E}\mathbf {F}\in ~\mathfrak {R}^{e\times n} \end{aligned}$$

(5)

3.2 Adaptive processing via direct SVD

The most computational and memory-demanding operation of the previously described compression method is the SVD-based dictionary estimation. However, assuming that the dynamic data are processed in sequential manner (because it is either generated or streamed), a naive encoding solution is to temporally cluster the animation [15] into consecutive subsequences $\{\mathcal {S}_1,\mathcal {S}_2,\ldots \}$ of frame block sizes $\{d_1,d_2,\ldots \}$ and then directly perform SVD on each subsequence $\mathcal {S}_i=\{\mathcal {P}_{y+1},\ldots ,\mathcal {P}_{y+d_i}\}$, $y=\sum _{j=1}^{i-1}d_j$. For simplicity reasons, we subdivide the time space into uniform batches: $d_i=d,\forall i>0$. In mathematical terms, the animation matrix $\mathbf {D}$ can be rewritten as a concatenation of sub-matrices $\mathbf {D}_i$ which we assume that are available sequentially:

$$\begin{aligned} \mathbf {D}&= \left[ \right. \mathbf {D}^\mathrm{T}_1\ \mathbf {D}^\mathrm{T}_2\ \ldots \ \left. \right] ^\mathrm{T},~\text {where}\nonumber \\ \mathbf {D}_i&=\left[ \begin{array}{c@{\quad }c@{\quad }c} \mathbf {p}_{(i-1)d+1,1},&{}\ldots ,&{}\mathbf {p}_{(i-1)d+1,n}\\ \vdots &{}\ddots &{}\vdots \\ \mathbf {p}_{id,1},&{}\ldots ,&{}\mathbf {p}_{id,n}\\ \end{array}\right] \in \mathfrak {R}^{3d\times n} \end{aligned}$$

(6)

3.3 Adaptive processing via orthogonal iterations

By exploiting subspace tracking, we introduce an efficient way to adaptively estimate the dictionary at a lower cost as compared to the direct evaluation of SVD for each incoming sequence $\mathcal {S}_i$. In this section, we initially present the orthogonal iteration method (Sect. 3.3.1) followed by the analytic description of our adaptive scheme to the animation compression problem, capable of readjusting the dictionary of previous subsequence $\mathcal {S}_{i-1}$ in an iterative way. More specifically, we offer two alternative adaptive orthogonal iteration (AOI) schemes: the Bandwidth-consistent (BAOI) that allows the user to determine the compression efficiency by keeping fixed the dictionary size for the entire animation (Sect. 3.3.2) as well as the Quality-consistent (QAOI) that identifies the optimal subspace size required for achieving an user-defined acceptable reconstruction quality goal (Sect. 3.3.3).

3.3.1 Orthogonal iterations (OIs)

The orthogonal iterations [24] is an iterative procedure that can be applied to compute the singular vectors corresponding to the k dominant singular values of a symmetric, nonnegative definite matrix and can be summarized in the following lemma [5]:

Lemma 1

Consider a symmetric, positive definite matrix $\mathbf {M}\in \mathfrak {R}^{n\times n}$ with $\lambda _j>0$ and $\mathbf {u}_j,~1\le j\le n$ be its nonzero singular values and corresponding singular vectors, respectively. Consider the sequence of matrices $\left\{ \mathbf {E}(t)\right\} \in \mathfrak {R}^{n\times k}$, defined in the iteration t as

$$\begin{aligned} \mathbf {E}(t) = \mathbf{o }\_\mathbf{norm } (\mathbf {M}\mathbf {E}(t-1)~),~t=1,2,\ldots \end{aligned}$$

(7)

where o_norm function stands for the orthonormalization procedure. Then, provided that the initial matrix $\mathbf {E}^\mathrm{T}(0)$ is not singular results at $\lim _{t\rightarrow \infty }\mathbf {E}(t) = \left[ \mathbf {u}_1,\ldots , \mathbf {u}_k \right]$.Note that the convergence rate of this function depends on the $\sigma _{k}=| \lambda _{k}/\lambda _{k+1}|$ factor.

3.3.2 Bandwidth-consistent AOI (BAOI)

In order to derive a low complexity compression scheme, we exploit the two attractive properties of the OI: (i) computational efficiency as well as (ii) fast convergence when the initialization is close to the subspace of interest. To this end, we suggest executing a single orthogonal iteration per incoming subsequence $\mathcal {S}_{i}$ using as initial input the subspace $\mathbf {E}_{i-1}$ that corresponds to the previous subsequence $\mathcal {S}_{i-1}$. More specifically, when we acquire the data block $\mathbf {D}_i$, we can replace $\mathbf {M}$ in Eq. (7) with the symmetric data autocorrelation matrix $\mathbf {A}_i$, leading to the following method for estimating the subspace of interest $\mathbf {E}_{i} = \mathbf{o }\_\mathbf{norm } (\mathbf {A}_i\mathbf {E}_{i-1})$. Depending on the choice of $\mathbf {A}_i$, we can obtain alternative subspace tracking methods. The simplest and most efficient selection is the block estimate of the autocorrelation matrix,

$$\begin{aligned} \mathbf {A}_i&= \mathbf {D}_i\mathbf {D}^\mathrm{T}_i+\delta \cdot \mathbf {I}_{3d} \end{aligned}$$

(8)

where $\delta$ is a small scalar value that is used to ensure that $\mathbf {A}_i$ is nonnegative definite and $\mathbf {I}_s$ is the identity matrix of size s.

A common way to increase the estimation accuracy of the presented scheme is by executing more than one orthogonal iterations $t_{\max }$ per incoming block of animated data $\mathbf {D}_i$, using a fixed matrix $\mathbf {A}_i$. Contrary to the direct SVD approach, our method can benefit from the convergence properties of OI by substituting the matrix $\mathbf {A}_i$ with $\mathbf {A}^z_i$, where $z>1$. This action increases the convergence speed of the method from $\sigma _{k}$ to $\sigma _{k}^z$. Taking into account these observations, we can conclude in Algorithm 1.

To preserve orthonormality and initialize the subspace to the direct SVD subspace, it is important that the initial estimate $\mathbf {E}_{1}$ is orthonormal. For that reason, the initial subspace is estimated by applying direct SVD via Eq. (3), while the following subspaces $i=2,\ldots$ are adjusted using Algorithm 1. A summary of the proposed technique is highlighted with pink in Algorithm 3.

3.3.3 Quality-consistent AOI (QAOI)

So far we have been assumed that a fixed, either insufficient or redundant, number k of components per frame block is used, neglecting the fact that the motion behavior may significantly vary during the whole animation sequence. To this end, we present a dynamic scheme that automatically identifies the optimal subspace size $k_i$ for “error consistently” compressing each incoming frame block $\mathcal {S}_i$ based on the previous subspace size $k_{i-1}$ and two user-defined low- and high-quality thresholds $\epsilon _{low},\epsilon _{high}$ (instead of adjusting $t_{\max }$), thus allowing the user to easily trade reconstruction quality with speedup. The idea is to repeatedly increase or decrease $k_{i-1}$ factor with the number of iterations t, i.e., $k_{i}=k_{i-1} \pm t,$ with $k_0=k$, until the value of an error metric e(t) lies within the goal quality range $\left( \epsilon _{low},\epsilon _{high}\right)$. Note that if we, instead, split the animation into non-uniform frame blocks (while keeping the subspace size fixed), it will potentially introduce unnecessary delays attributed to the packetization of a large number of frames.

In practical scenarios, it is reasonable to assume that the feature vectors $\mathbf {F}_i$ of each block $\mathbf {D}_i$ reside in subspaces $\mathbf {E}_i$ of different sizes. The subspace size $k_{i}$ of the incoming data block $\mathbf {D}_{i}=\left[ \mathbf {d}_{i_1}, \ldots , \mathbf {d}_{i_n}\right] ,\ \mathbf {d}_{i_j} \in \mathfrak {R}^{3d\times 1}$, should be carefully selected so that the relevant animation data block characteristics are identified with the minimum loss of information. To quantify the loss of information at each iteration t, we suggest using the $l_2$-norm of the following mean residual error $\mathbf {r}(t) = \sum ^{n}_{j=1}\left( \mathbf {d}_{i_j} - \mathbf {E}(t)\mathbf {E}^\mathrm{T}(t)\mathbf {d}_{i_j}\right)$. When moving from a high to low motion complexity, the incoming frame block $\mathcal {S}_{i}$ requires less than $k_{i-1}$ principal eigenvectors to be sufficiently reconstructed. In this case, the subspace size $k_{i}$ is iteratively decreased by 1 by simply selecting the first $k_{i-1}-1$ columns of $\mathbf {E}(t)$ until the goal quality is achieved $\left\| \mathbf {r}(t)\right\| _2 > \epsilon _{low}$. On the other hand, inspired by the incremental PCA, we can simply add one normalized column in the estimated subspace $\mathbf {E}(t) = \left[ \mathbf {E}(t)\cdot ( \mathbf {r}(t)/\left\| \mathbf {r}(t)\right\| _2)\right]$ and then perform the orthonormalization stage. The proposed dynamic scheme can be easily integrated in Algorithm 3 (see blue color) by replacing Algorithm 1 with 2.

Orthonormalization. There are a number of different choices that can be used for the orthonormalization of the estimated subspace. The most widely adopted are the Householder Reflections (HR), Gram-Schmidt (GS) and Modified  Gram-Schmidt (MGS) methods [6]. While all variants exhibit different properties related to the numerical stability and computational complexity, without loss of generality, we used HR for the orthonormalization stage.

Table 1 Extensive comparison in terms of quality and performance of the SVD and BAOI for a variety of compression configuration setups in a highly motion-divergent collection of dynamic sequences

4 Results and discussion

We present an experimental analysis of our subspace tracking approach as compared to the direct application of PCA in an adaptive setup focusing on encoding performance and decoding robustness (Sect. 4.2) of different animation sequences under a broad set of configuration parameters (Sect. 4.1). A short discussion is finally offered describing on how to select a compression variant from the given repertoire (Sect. 4.3).

4.1 Simulation setup

To provide an objective comparison between the tested solutions, we follow the general pipeline stages described in Section 3 and illustrated in Fig. 4 using a series of 3D dynamic point clouds and triangular meshes with fixed connectivity, that represent a wide range of rigid and highly deformable motions (see Table 1 and video).We assume that the animation poses are not known ahead in time and are generated and processed sequentially. To that end, we divide the animation into uniform blocks of consecutive frames or namely subsequences $\{\mathcal {S}_i\}$ (Sect. 3.2) that are processed individually. In addition, our framework supports also the segmentation and processing of spatial clusters allowing a parallel adaptive implementation of very dense animated meshes. METIS [10], an efficient topological partitioning approach was used that uniformly partitions a mesh based on its connectivity. For each data block, compact representations can be computed by approximating the k-largest PCA bases in spatial or temporal space via

SVD::

Jacobi singular value decomposition (Sect. 3.2). Note that experiments were also tested with the truncated SVD resulting to similar observations.

BAOI $^z(t_{\max })$::

bandwidth-consistent adaptive orthogonal iterations on the $\mathbf {A}^z$ matrix (Sect. 3.3.2). Note that the default values for BAOI parameters are $z=1,t_{\max }=1$ unless specified otherwise, meaning that BAOI corresponds to BAOI$^1(1)$.

QAOI $\left( \epsilon _{low},\epsilon _{high}\right)$::

quality-consistent adaptive orthogonal iterations (Sect. 3.3.3) until goal reconstruction quality resides between $\left( \epsilon _{low}\epsilon _{high}\right)$.

IPCA::

Incremental PCA. It identifies the best subspace size for achieving a user-defined quality.

For simplicity reasons, uniform quantization [7] is performed on the generated dictionary ($q_d = 14 bits$) and feature vectors ($q_f = 12 bits$).

Encoding performance. We measure the performance in terms of milliseconds (ms) for executing only the dictionary estimation process (without including the initialization SVD step), since the rest stages remain the same for all variants under study (see Fig. 4). The experiments were performed on an Intel Core i7 4790 @3.6GHz CPU with 8GB RAM.

Reconstruction quality. The evaluation of the distortion amount between the original and reconstructed animation is traditionally performed by vertex-based error metrics such as the well-established KG error metric [9] which is defined as $\mathbf {KG}=100 \cdot \frac{||\mathbf {D}-\hat{\mathbf {D}}||_F}{||\mathbf {D}-E(\mathbf {D})||_F},$ where $||\cdot ||_F$ denotes the Frobenius norm and $E(\mathbf {D})$ is a matrix whose columns consist of the average vertex positions for all frames. On the other hand, STED error metric has been shown to correlate well with perceived distortion by measuring spatiotemporal edge differences [30]. The overall error is evaluated as a hypotenuse of two parts: spatial $\mathbf {E_S}$ and temporal $\mathbf {E_T}$ errors using a weighting constant w to relate them $\mathbf {STED}$ $=\sqrt{\mathbf {E_S}^2 + w^2\cdot \mathbf {E_T}^2}.$ In this work, we have used both metrics to measure distortion related to absolute via KG (Figs. 1, 6, 7, 8, 10) as well as relative changes via STED (Table 1 and video) of the vertex positions.

Compression efficiency. Data rate is measured in bits per vertex per frame (bpvf) encapsulating the mesh connectivity, the feature vectors matrix and the dictionary coefficients required for reconstructing the original dataset at the decoder.

4.2 Experimental study

Impact of spatiotemporal correlations. Figure 5 illustrates a reconstructed frame using two state-of-the-art static mesh compression approaches, MBL [13] and OD3GC [18], as compared to the SVD and BAOI approaches. Observe that the exploitation of PCA significantly outperforms the application of static compression approaches on a frame-to-frame basis in terms of both reconstruction accuracy and execution time.

Fig. 5

Comparison of PCA-based approaches with static mesh compression methods at Samba animation sequence

Impact of frame block size (d). Figure 6 illustrates how altering the time subdivision length $d=\{50,250\}$ affects the reconstruction accuracy as well as the total processing time when encoding, under a wide compression ratio range (bpvf $=2,\ldots ,12$), the Flag animation sequence that consists of 1000 frames. First of all, it is highly evident how the reconstruction quality of BAOI converges to the one of the SVD when the number of OI is slightly increased. Furthermore, the block size d should be carefully selected when focusing on the final reconstruction quality since updating the dictionaries less ($d=250$) or more ($d=50$) frequently does not guarantee better approximation output. In terms of performance, we observe the superiority of BAOI for all sizes when compared to the SVD method even when more than two OIs are employed. Note that while updating the dictionaries less frequently ($d=250$) results to a higher performance gain (21$\times$–52$\times$), the total encoding time in each case is proportionally higher (following a linear behavior) than the one performed with a smaller block size ($d=50$). Similar conclusions can also be derived from Table 1 (Temporal Space).

Fig. 6

Approximation and performance evaluation for the Flag animation sequence for different compression ratios using various frame block sizes

Impact of iterations/multiplications ($t_{\max },z$). Figure 6 as well as Table 1 shows how the BAOI closes the gap and finally reaches, in high precision, the levels of reconstruction quality (in both KG and STED metrics) derived by the SVD when increasing the number of OI for a wide range of compression configurations and animations. We further observe that the speedup of BAOI is exponentially decreased when moving to higher OI. As we expected, BAOI$^z$ is faster than BAOI($t_{\max }$) when $t_{\max }=z>$ 1, since a matrix multiplication requires less computations time than performing one OI. Heatmap visualizations are also offered showing the distortion alleviation when one extra OI is used (Fig. 7).

Fig. 7

Heatmap visualization differences of KG between SVD and BAOI for Tablecloth (top), Flag (middle) and Camel Collapse poses (bottom). Insets highlight how the severe approximation artifacts are mitigated using one extra OI

Fig. 8

Approximation as well as time and compression ratio (in brackets) for various k using different spatial clusterings on the Handstand animation

Impact of partitioning (c): Figure 8 shows the impact on compression quality and performance when uniform geometry clustering the Handstand animation into $c=\{40,100\}$ parts. First of all, it is clearly shown that the more components mesh is partitioned into, the less distortion artifacts arise (see also spatial space scenarios in Table 1). However, this comes at the cost of sacrificing compression efficiency, since we store the same number of features ($k=\{3,\ldots ,7\}$) for more sub-meshes. On the other hand, it should be noted that processing small independent parts reduces significantly the computational complexity of the reconstruction, allowing at the same time a parallel compression implementation (not performed here). Last but not least, the segmentation must not reach high levels in order to maintain the performance gain of BAOI.

Fig. 9

QAOI (top) and BAOI (bottom) produce high-quality visual reproduction despite the extreme temporal incoherence between frame blocks in two particle simulations

Impact of frame incoherence: Figure 9 shows the rich reconstruction quality when QAOI and BAOI ($d=200$) are employed, respectively, on highly inconsistent point cloud animation generated from (a) the transient analysis of the particles behavior in a patient-specific 3D lung model reconstructed from CT scans ($f=215$) [12] and (b) morphing from one letter into another forming the word “2017” ($f=600$). Despite the high motion variance of animated particles, performing dictionary updates with QAOI and BAOI do not impose any noticeable perceptual visual error, generating in the end plausible global illuminated image results with a huge performance speedup (up to 18.64$\times$) as compared to the direct SVD approach.

Impact of error thresholds ($\epsilon _{low},\epsilon _{high}$). Figure 8 shows that the QAOI scheme allows the user to determine the reconstruction quality (by altering the error bounds) of the Handstand animation, but by deteriorating the compression efficiency and slightly increasing the execution time as compared to the BAOI approach. However, it still achieves up to 10$\times$ lower execution times as compared to the SVD approach. Similar conclusions are also drawn from Fig. 10 by observing the per frame normalized square error of the reconstructed Tablecloth animation ($f=240,d=40,k=6$). While BAOI scheme exhibits the fastest execution time and the best compression efficiency, it suffers from high variability in the reconstruction error. On the other hand, QAOI provides a stable reconstruction accuracy (almost identical when compared to the IPCA) that can easily be adjusted by the defined thresholds. However, this comes with a slight increase in the execution time (more OI) as well as a significant increase in the final compression rate (dynamic k).

Fig. 10

Observe how fast QAOI reaches the levels of reconstruction quality of IPCA for the entire Tablecloth animation

4.3 Discussion and limitations

The thorough experimental study on a vast collection of 3D dynamic meshes that represent a wide range of animations (ranging from rigid motions to complex simulations, see Table 1 and video) showed that the subspace tracking approaches allow the robust estimation of dictionaries at significantly lower execution times compared to the direct SVD implementations. In general, the BAOI scheme focuses on fast-streaming scenarios, while QAOI approach aims at providing progressively high reconstruction accuracy. Despite the superiority of BAOI when compared to the direct SVD, the initial subspace size should be carefully selected in order to simultaneously achieve the highest reconstruction quality and fastest compression times (Fig. 6). Experiments showed that plausible reconstructed animations can be generated by employing either $t_{\max }=1$ and $z=2$ or $t_{\max }=2$. The execution of more $t_{\max },z$ increases the computational complexity without affecting noticeably the reconstruction quality (Fig. 6). Finally, the approximation artifacts that occur in a single frame block may slightly increased and propagated when moving to the subsequent ones (Fig. 9). To address the latter issue, we suggest to either re-initialize the subspace of interest using the SVD or execute an QAOI update, when the decoded meshes are detected to drift too far from the original ones.

5 Conclusions

We have introduced two novel approaches to support fast and efficient compression of fully dynamic scenarios with an undefined motion pattern and unknown topology modification behavior. In the heart of our pipeline lies an adaptive PCA-based dictionary estimation stage designed to simultaneously maintain three important criteria: fast encoding times, plausible decoding results and out-of-core behavior. While this stage is general and independent of the underlying compression framework, an extensive analysis has demonstrated the performance superiority of our online variant compared to prior compression solutions, while the reconstruction quality is maintained in high level of detail. Despite the tremendous progress on the landscape of the dynamic compression field, we believe that our approach provides a novel insight at a key area with renewed research interest, where high potential for novel improvements such as dynamic clustering [15, 31] is feasible in the near future.