Extended surface distance for local evaluation of 3D medical image segmentations

Abstract

The evaluation of 3D medical image segmentation quality requires a reliable detailed comparison of a reference segmentation with an automatic segmentation. It should be able to measure the quality accurately and, thus, to reveal problematic regions. While several (global) measures, providing a single quality value, are available, the only widely used local measure is the Surface Distance (i.e., point-to-surface distance). This measure, however, has significant drawbacks such as asymmetry and underestimation in distant and differently formed regions. Other available measures have limited suitability for 3D medical segmentation evaluation. We present a more reliable distance measure for assessing and analyzing local differences between automatic and reference (i.e., ground truth) 3D segmentations. We identify and overcome Surface Distance drawbacks, esp. in regions with larger dissimilarities. We evaluated our approach on four real medical image datasets. The results indicate that our measure provides more accurate local distance values.

1 Introduction

Evaluating 3D medical image segmentations is important for the development of high-quality automatic segmentation algorithms. Although sophisticated algorithms have been developed (e.g., using deformable M-Reps [23] or statistical shape models [12, 15, 17, 21]), wrongly segmented regions still occur in difficult cases. Algorithm evaluation compares reference (i.e., ground truth) and automatic segmentations, which can be in form of meshes (see Fig. 1). Local (per vertex) quality analysis may reveal regions of bad segmentation within the anatomical structure. This, in turn, indicates the need for local algorithm improvement such as local appearance model adjustment. However, the detailed evaluation on a local level is currently not precise enough.

Fig. 1

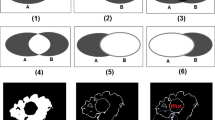
The widely used surface distance (SD) compared to our extended surface distance (ESD). The measures are used for the local comparison of a (ground truth) reference segmentation mesh and an automatic segmentation mesh of a 3D medical image. The SD is asymmetric and underestimates the distances. The new measure shows better results

The mostly used local measure is the so-called surface distance (SD) (i.e., point-to-surface distance, see also Sect. 3). Although other evaluation methods exist (see Sect. 2), the SD is the most versatile measure since it has no general restrictions. We investigated possible measurement error cases of the SD (see Sect. 3). It has several drawbacks, which we discovered (see Sect. 4). For example, it may provide low distance values underestimating the difference of the meshes, especially in locally distant parts of the mesh (see Fig. 1 within the red rectangles). This drawback can be serious in 3D medical image segmentation, as such cases can occur in pathological organs.

We developed an extended surface distance (ESD), which overcomes the problems of the SD. It provides more accurate results in more distant organ areas and reduces the asymmetry. We evaluated the new measure on liver, nervus facialis, semicircular canals and cochlea datasets (see Sect. 5). It indicates the robustness and flexibility of our measure.

The accompanying program for exploration of segmentation quality (i.e., mesh comparison) using our measure is provided at: http://www.gris.tu-darmstadt.de/research/vissearch/projects/esd/. As we work with meshes, our approach can be applied to other domains, such as 3D reconstruction.

2 Related work

Several distance measures are used in medical image segmentation evaluation [11] and in mesh comparison [9]. Distance measures can be divided into global and local. Global measures provide a single distance value. Local measures determine values per mesh vertex. We focus on local measures and global measures transformable into local.

2.1 Transformability of global measures

Many global measures are based on the SD, e.g., [1, 9]. They aggregate (maximum or average) the local SD values. Their basis SD can be used for local mesh comparing. We base our work on it.

Volume comparing measures include the Volumetric Overlap Error [27] and the Relative Volume Difference [11]. They measure a ratio of the shared part to the non-shared parts of the two meshes. They could possibly be calculated for smaller regions, but they cannot be transformed to a local per vertex measure.

Other global measures focus on curvature and form differences of the meshes using, e.g., normal fields [7] or the energy metric [13]. The result can only be compared per mesh and not per vertex.

2.2 General local measures

Medical image segmentation often employs 2D measures for comparing 2D slices of the segmented 3D structures [6, 8, 26, 32]. However, this depends on the slicing and disregards intra-slice dependencies. Therefore, they are not suitable for our case.

In 3D mesh comparison, ray casting-based measures [6, 25] calculate a relative error by casting rays from inside or outside the mesh. These measures are highly dependent on the form of the meshes. For example, the radial distance [6] is suitable only for sphere-like form meshes. The distance by Strecha et al. [25] casts rays from rather randomly chosen points. These rays disregard surface orientation, thus are problematic in distant and differently formed regions.

Local measures based on a surface parametrization relate surface points with the same parameters, e.g., The Fréchet distance [29]. The distance can then be measured between related points. A consistent parametrization depends on the mesh form. For every case, a different suitable parametrization method is needed. This excludes parametrizations for our measure, since we need a robust and flexible measure for varying object forms.

2.3 Local measures based on correspondence

Various local distance measurements rely on matching two surface points of both meshes. This problem is related to finding point-to-point mesh correspondences [28]. So, we also review correspondence methods.

Often a dense point correspondence is computed from several corresponding feature points, which must be known in advance [28]. Kraevoy et al. [16] require user-defined basic corresponding points. A fully automatic method is not present. Cates et al. [5] move particles along the surface for finding corresponding points. It is restricted to smooth surfaces allowing for free particle movement.

Another concept is to deform one mesh into the other, so that the points lying on top of each other can be marked as corresponding. However, one cannot allow arbitrary surface deformations. Therefore, non-rigid registrations often focused only on small local deformations [4]. Other methods use additional registered scan data for global deformation [10, 19], which are unavailable to us.

Other methods include shape context [3] and spin images [14]. A corresponding point is detected by matching point neighborhood descriptions, e.g., [20]. However, these methods cannot measure the distance between dissimilar regions, as no similar neighborhoods exist in these regions. Analogously, many other methods are not suitable for our purpose [22, 24, 30, 31].

We note that correspondence is a difficult problem, which is solved mainly for specific cases, where it may provide very good results. However, it is difficult to identify one algorithm for arbitrary comparisons irrespective of the specific case (see also the discussion in Sect. 5.4). Therefore, we do not consider it for our problem.

3 Problematic cases of the surface distance

We describe the three main and two combined error cases of the SD, which we identified during our work. The order of the three main cases expresses their severity, with case-3 being the most severe. We explain the error cases on two meshes $M^1$ (orange) and $M^2$ (blue) in a 2D view for easier understanding (see Fig. 2a).

We show the SD as a distance vector pointing from one vertex on one surface to its nearest vertex on the other surface. We show the SD for the blue surface $M^2$ in Fig. 2b and the SD for the orange surface $M^1$ in Fig. 2c. The distance vectors pointing into the same direction of the surface normal of the vertex are colored in dark green, while the others are colored in light green. Note that we only show the vertices and distance vectors for the interesting part of the example and omit the rest.

In the examples, the SD is calculated by taking a discrete amount of vertices of the two surfaces (e.g., the vertices of a mesh). The distance of each vertex $v^1_i \in M^1$ is determined by its nearest vertex in $M^2$ (see Fig. 2). Note, the exact SD considers every possible point of the surface represented by the mesh. Taking a discrete amount of vertices provides a good approximation for meshes with dense vertex coverage.

Fig. 2

Example meshes and SD distance vectors. a Vertices on the surfaces $M^1$ and $M^2$. b SD distance vectors of $M^2$ (from blue vertices). c SD distance vectors of $M^1$ (from orange vertices)

Case-1: Wrong distance in one comparison direction This problem of the SD results from the strong asymmetry (see $P^1$ in Fig. 2). The distance vectors are correct in one of the two directions: from the blue to the orange surface. But, we see that the distance vectors are erroneous from the orange surface in the same region.

Case-2: Nearest vertex in an unrelated region This error occurs when the nearest vertex is found in a region representing a “semantically” different part of the other mesh (see $P^2$ in Fig. 2). The distance vectors from the blue surface are pointing to the wrong side of the other surface.

Case-3: Wrong distance in both comparison directions The error of case-3 is shown in $P^3$ (see Fig. 2). Since the surfaces differ only in the direction of the deformation (inward and outward), we can expect that the distance vectors connect these regions. However, the distance vectors from both sides only point to the border of the deformations. Note that in this case the distance vectors of both meshes are wrong in the erroneous region.

Case-2 errors overlaying case-3 or case-1 errors It is possible that case-2 errors overlay case-3 or case-1 errors (see $P^4$ and $P^5$ in Fig. 2). The distance vectors from the blue surface $M^2$ show an erroneous behavior of case-2 (pointing to an unrelated region). Case-2 error of $P^4$ (formed like $P^3$) overlays the case-3 error in this region. Analogously, $P^5$ is formed like $P^1$. In $P^5$, the errors of case-2 overlay the errors of case-1. These overlaying errors imply that we have to solve the errors of case-2 before identifying the residual errors.

4 Methodology

We now describe our algorithm for calculating the new distance measure. It is based on the surface distance (SD), therefore, we refer to it as extended surface distance (ESD). We first present assumptions and the notations used in the paper. We then explain the concepts used in our algorithm. The algorithm is explained step-by-step in the last subsection. We also provide a detailed pseudocode of the algorithm and a program enabling to analyze the results quantitatively and visually. Both are available at http://www.gris.tu-darmstadt.de/research/vissearch/projects/esd/.

4.1 Assumptions

Our assumptions stem from the 3D medical image segmentation quality assessment.

We assume two triangular meshes: a reference mesh (RS, i.e., ground truth) and an automatic segmentation (AS). They can be either a direct output of the algorithm (e.g., result of statistical shape model) or can be a result of a pre-processing of the volumetric data. We pose no constraints on mesh size and the number of mesh faces. The two meshes can differ in these properties. We assume that point correspondences between the RS and AS meshes are unknown.

Depending on the used segmentation method the resulting meshes have several favorable properties, which we assume: mesh closeness and 2-manifoldness as well as spatial alignment. These properties can also be established by pre-processing, e.g., 3D-registration [18].

4.2 Notations

We assume a comparison of two meshes $M^1$ and $M^2$. For clarifying that several calculations are done for both comparison directions $M^1 \rightarrow M^2$ and $M^2 \rightarrow M^1$ we also use the notation $M^a$ and $M^b$ with $\forall a,b \in \{1,2\}$ and $a \ne b$.

The vertices of $M^a$ can lie inside or outside $M^b$. $v_i^a \in M^a$ is an inner vertex if the vertex lies inside the surface of $M^b$. Otherwise, $v_i^a$ is outside. Every vertex $v_k^a$ connected to $v_i^a$ via an edge is in the set of neighbors $nb(v_i^a)$. We define a region $R^a$ as a set of vertices $R^a = \bigcup {v^a_i \in M^a}$. A region pair $P_i$ is a tuple $(R^1_i,R^2_i)$ with $R^1_i \subset M^1$ and $R^2_i \subset M^2$

A vertex $v_i^a$ has exactly one distance vector $\mathbf {d}(v_i^a)$ targeting a vertex $v_j^b \in M^b$. Several distance vectors can end in the same vertex $v_j^b$. The vertex’s distance value is the Euclidean length of its distance vector.

4.3 Concepts

The input for our algorithm are two meshes $M^1$ and $M^2$ (e.g., automatic and reference segmentations).

In our approach, we identify and correct cases in which the Surface Distance (SD) measure is erroneous (see Sect. 3). The identification uses the results of initial SD calculation. It uses concepts of Surface-Vertex-Sets, uncovered vertices, erroneous region, and region pairs. We explain them before we detail on the algorithm.

The SD distance vectors of a vertex $v_i^a \in M^a$ are calculated as a vector pointing from $v_i^a$ to the nearest vertex of $M^b$. A more dense vertex distribution on the surface of the meshes lead to more accurate results. Therefore, we introduce the surface-vertex-sets.

A surface-vertex-set $M^{Ea}$ is a set of vertices lying on the surface of $M^a$. $M^{Ea}$ includes original vertices of $M^a$ and additional (subdivision) vertices. The calculation is described in Sect. 4.4 Stage 1. These dense vertex sets are needed for identification of uncovered vertices (see Fig. 4).

Uncovered vertices in mesh $M^a$ are vertices with no distance vectors pointing to them from mesh $M^b$. Figure 3 shows the uncovered vertices of our example as red dots. The uncovered vertices can only be correctly determined if enough distance vectors cover the surface of one mesh. We show this problem in Fig. 4. Therefore, we always calculate the distance vectors between a surface-vertex-set $M^{Ea}$ and an original mesh $M^a$. The uncovered vertices result from the SD asymmetry and thus indicate SD errors.

Fig. 3

Uncovered vertices: not targeted by any distance vector. a Uncovered vertices of $M^1$ (red points). b Uncovered vertices of $M^2$ (red points)

Fig. 4

The need for surface sets $M^{E}$ for vertex coverage. $M^{E1} \rightarrow M^2$: enough distance vectors cover the surface. a $M^1 \rightarrow M^2$. b $M^{E1} \rightarrow M^2$

Erroneous region is a region $R^a_i \subset M^a$ composed of erroneous vertices, i.e., an error case of the SD (see Sect. 3).

Region pair $P_i = (R^1_i,R^2_i)$ is composed of two regions $R^1_i \subset M^1$ and $R^2_i \subset M^2$, which are related. (see Fig. 2, $P^1$–$P^5$). We need to identify all region pairs $P_i$ for correcting the erroneous distance vectors of the SD.

4.4 Algorithm for distance calculation

We describe our algorithm for the computation of the extended distance measure. It consists of 4 stages.

• S1: Calculation of the surface-vertex-sets $M^{E1}$ and $M^{E2}$.

• S2: Construction of region pairs and limitation of distance vectors within a region pair.

• S3: Classification of erroneous vertices.

• S4: Final correction of distance vectors.

Stage 1: Calculation of surface-vertex-sets We calculate surface-vertex-sets $M^{E1},M^{E2}$, and the initial SD.

The surface-vertex-sets are constructed by iteratively subdividing mesh triangles. A triangle is divided into 4 triangles. We use the same scheme as Aspert et al. [1], because it leads to well distributed vertices. The surface-vertex-set $M^{Ea}$ consists of all vertices of $M^a$ and all additionally obtained vertices from the subdivision steps.

The number of subdivision iterations depends on the area of the triangle. Each triangle is subdivided until its area is smaller than a defined threshold. We propose a threshold heuristic: we set the threshold to one quarter of the smaller average triangle area of the two meshes. This threshold assures at least one iteration for most triangles.

Afterwards, we compute the SD from a mesh to a surface-vertex-set and vice versa: $M^a \rightarrow M^{Eb}, M^{Ea} \rightarrow M^b$.

Stage 2: Construction of region pairs This stage constructs region pairs $P_i = (R_i^1,R_i^2)$ using identification of uncovered vertices and regions. As case-2 errors cause that vertices are covered by an erroneous distance vector, we need to filter them out first.

The distance vectors not fulfilling the following criteria are filtered out. Note that these criteria are conservative, which means that the erroneous case-2 distance vectors are filtered out correctly but a few correct distance vectors could also be included. Actually, this does not cause problems since the correct distance vectors within differently formed regions are recognized as correct in the next stage. The criteria are:

• 1. A distance vector has to point from an inner vertex to an outer vertex or vice versa.

• 2. The surface normals of the start and end vertex of a distance vector should be similarly oriented (the angle between them is less than 90 degree).

• 3. A distance vector should not intersect any surface, since the distance vectors of the SD should mark the shortest connection between two vertices.

Then the uncovered vertices are identified as defined in Sect. 4.3. We construct regions $R_i^a$ on each mesh separately: neighboring uncovered vertices form a region. We differentiate between inner and outer vertices, leading to inner and outer regions. A region pair always consists of an inner region on one mesh and an outer region on the other mesh.

We then construct region pairs $P_i$. For each region $R_i^a \subset M^a$ we need to find its counterpart $R_i^b \subset M^b, \forall a,b \in \{1,2\}, a \ne b$. If an uncovered vertex $v_i^a \in R_i^a$ has a (non case-2 erroneous) distance vector, the end vertex $v_j^b$ is a part of the searched region $R_i^b$ (see Fig. 5a). If $v_j^b$ has a neighbor $v_k^b$ which belongs to a erroneous region $R_k^b$, then $R_k^b$ and the vertex $v_j^b$ is merged to the searched region $R_i^b$. This is done iteratively until no neigbouring error vertices exist. The resulting region pairs are highlighted in Fig. 5b.

Fig. 5

Stage 2 identifies region pairs and corrects case-2 errors. a Distance vectors of uncovered vertices, except out-filtered case-2 errors. b Resulting regions pairs and reoriented distance vectors

We now need to correct the filtered out case-2 erroneous vertices/regions. The distance vectors of vertices $v_i^a \in R_i^a \in P_i$ are reoriented, so that they target the nearest vertex in the counterpart region $v_i^b \in R_i^b \in P_i$ (see Fig. 5b). This solves case-2 errors overlaying case-1 or case-3 errors.

Stage 3: Classification of erroneous vertices We now classify the errors of every region pair $P_i = (R_i^1,R_i^2)$ for their correction in Stage 4. As case-2 errors were already eliminated in stage 2, we need to distinguish only case-1 and case-3 errors. Case-3 errors are identified as residual erroneous vertices after case-1 identification.

We first identify case-1 errors (i.e., erroneous in one comparison direction). These can be easily identified, because correct distance vectors are present in one of the two regions $R_i^1 \in P_i$ or $R_i^2 \in P_i$. We have to identify which region $R_i^a$ ( $a \in \{1,2\}$) of the region pair $P_i$ is the erroneous one. The other region $R_i^b$ has correct distance vectors. These vectors can then be used for correcting the case-1 errors in the erroneous region (see Stage 4).

The erroneous region is identified by counting the number of uncovered vertices. Erroneous regions have less uncovered vertices, since correct distance vectors always cover more vertices of the surface than erroneous distance vectors (see Fig. 6). We count the erroneous vertices of the surface-vertex-sets $M^{Ea}$ and $M^{Eb}$, because they have similar number of vertices across region pairs. Original meshes $M^a$ and $M^b$ can differ much in the number of vertices. As shown in Figure 6 in $P^3$, region pairs of case-3 error can have the same count of erroneous vertices, in which case we can simply choose one of the two regions (we take the region in $M^2$) as erroneous, as both are erroneous and will be identified as case-3 in the following.

Fig. 6

Stage 3: The vertices in the erroneous regions (red boxes) of every region pair are classified

The vertices of the erroneous region $R_i^a \in P_i$ are classified as follows (see Fig. 6 ):

• 1. The vertex is covered by at least one distance vector from an uncovered vertex $\rightarrow$ case-1 error.

• 2. The vertex is only covered by distance vectors of covered vertices. This vertex is correct, so it is not classified.

• 3. The vertex is not covered at all $\rightarrow$ case-3 error.

Stage 4: Final correction of distance vectors We now correct the distance vectors. We first correct the case-1 errors. This correction is used for the later correction of case-3 errors. Note that case-2 was corrected in stage 2.

The case-1 erroneous vertices are in the erroneous region $R_i^a \in P_i$. The other region $R_i^b \in P_i$ has correct distance vectors. We will now use the correct distance vectors of $R_i^b$ for the reorientation of the distance vectors of $R_i^a$. The classification in stage 2 required that every vertex $v_i^a \in R_i^a$ of case-1 error has one or more uncovered $v_i^b \in R_i^b$, whose distance vector targets $v_i^a$. One of these correct distance vectors targeting $v_i^a$ should be mirrored by $v_i^a$. We reorient the distance vector of $v_i^a$ so that it points to the furthest vertex of all the vertices $v_i^b$, as defined above. By choosing the furthest vertex we rather slightly overestimate the distance—leading to a locally maximal distance. Figure 7a shows the result.

Fig. 7

In Stage 4 distance vectors of case-1 and case-3 erroneous vertices are reoriented. a case-1 distance vectors are reoriented by mirroring correct distance vectors. b case-3 distance vectors are reoriented with the help of rays cast between the erroneous regions. Black arrows are corrected by rays. Green arrows are corrected by final case-1 adaption

We can now correct the possible residual case-3 errors in $P_i$. In contrast to case-1 errors, the case-3 errors are located on both regions of the region pair $P_i$. We denote the case-3 error regions as $R_k^a \subset R_i^a \in P_i$ and $R_k^b \subset R_i^b \in P_i$. We already identified the case-3 erroneous vertices of $R_k^a$ within $R_i^a$ as these are the vertices classified as case-3 in stage 3, but we now also need to identify the case-3 erroneous vertices of $R_k^b$ within the counterpart $R_i^b$.

We use the case-1 correction for the identification of $R_k^b$, as these are closely related (see Fig. 7a, $P^3$ and $P^4$). The distance vectors of $v_i^a \in R_i^a$ of the former case-1 error vertices now target the case-3 erroneous region $R_k^b$ within $R_i^b$.

The specific case-3 erroneous region $R^a_k$ is defined as all neighboring vertices classified as case-3 in $R^a_i$. We identify its counterpart case-3 error region $R^b_k$. Every vertex of $R^b_i$ which is pointing to one of the former case-1 error vertices surrounding $R^a_k$ is now labeled as a candidate vertex, i.e., a candidate for the searched region $R^b_k$.

We now have to identify which candidate vertices of $R_i^b$ are related to $R_k^a$ and, therefore, are a part of $R^b_k$. For this identification we use a ray casting approach as case-3 regions can contain arbitrarily dissimilar deformations.

We first identify the direction of the rays: we compute the centroid of $R^a_k$ and the centroid of all candidate vertices which are target vertices of a distance vector of the former case-1 error vertices neighbored to $R^a_k$. Our ray direction vector points from the first to the second centroid. We cast a ray from each vertex of $R^a_k$ in this direction. The nearest candidate vertex of each ray belongs to $R^b_k$.

As a last step in case-3 region identification, we need to adapt some of former case-1 error vertices surrounding $R^a_k$, because these are pointing to $R^b_k$ and possibly also belong to case-3. If a surrounding vertex of $R^a_k$ is only covered by vertices of $R^b_k$, then it is only covered by case-3 erroneous vertices and, therefore, belongs to $R^a_k$. Otherwise, if the vertex is also covered by a vertex outside of $R^b_k$, then the distance vector has to be adapted, so that it targets the furthest covering vertex, outside of $R^b_k$.

The final reorientation of the distance vectors uses additional ray cast between both regions $R^a_k$ and $R^b_k$. The rays are aligned as before: every vertex of $R^a_k$ and $R^b_k$ casts a ray. The nearest vertex to the ray on the other region is the end vertex of vertex distance vector (see Fig. 7b).

5 Evaluation and discussion

We evaluate our approach on several real medical segmentation datasets. We compare automatic with ground truth segmentations. The focus of our evaluation is on the assessment of the quality measurement using our distance measure and using the SD. Note, we do not focus on getting best segmentation results, as this is the subject of segmentation algorithm development.

We first describe the datasets and then show the qualitative and quantitative evaluation. Finally, we discuss the advantages and limitations of our approach.

5.1 Data description

We evaluated four datasets consisting of 20 livers, 42 nervus facialis, 42 semicircular canals and 20 cochleas. The real-world medical image data were extracted from CT scans. The liver segmentation algorithm is [15] and the segmentation of the other datasets was done using [2].

Table 1 Dataset properties

We evaluate various datasets to show the versatility of our approach. The new distance measure is independent of the mesh size and number of vertices and faces (see Table 1). It is able to evaluate the organs of different sizes. The cochleas are very small, while the livers are rather large. They also differ in other proprieties, as the Nervus facialis are of genus 0 and the Semicircular canals are of genus 3. The livers have different genera within the dataset (some livers include tubular structures inside the organ)

5.2 Qualitative evaluation

We assess how well the measure identifies regions of bad/good segmentation quality. We visually inspected the local distances on both automatic and reference segmentations for every comparison. Owing to space limitations, we present one example of each data set.

One important benefit of the new measure is its symmetry. Symmetry enables to spot problems on both automatic (AS) and reference (RS) segmentations. The SD was not symmetric and thus it was not possible to detect all segmentation errors by analyzing the results on one mesh. In contrast, the new distance measure recognizes regions of bad segmentation that were either only identified on one of the two meshes or could not be identified with the SD at all (see Figs. 1 and 8).

Fig. 8

Qualitative comparison of SD (left) and ESD (right) for segmentation evaluation (middle). a Cochlea SD shows a region with highly underestimated distance values on both meshes. b Semicircular Canals. c Nervus Facialis. b, c High asymmetry of SD values. ESD shows more accurate information on both meshes even in these difficult examples

As an example, we look at the Semicircular canals and the Nervus facialis (see Fig. 8b, c). Both have two large erroneous regions (see red box). Here, one region is erroneously measured in the AS and the other region is erroneously measured in the RS. Thus, for several erroneous regions the correct distance values can be scattered across both meshes. This means that there is no single mesh, which identifies correct distances on all regions. The ESD is able to detect correct distances for all regions on both meshes.

The Liver (see Fig. 1) and the Cochlea (see Fig. 8a) examples show errors that are even more severe than the symmetry problem. Both examples have one large region (see red box), in which the SD underestimates the difference on both meshes. Therefore, the correct information is not available anywhere. The new distance measure indicates better and more plausible results, even on these very difficult and badly segmented examples.

5.3 Quantitative evaluation

We quantitatively evaluate the new distance measure. This evaluation is difficult as there are no ground truth distances available. This is because the difference of meshes is not well defined, so that a ground truth could only be constructed with a similarity measure itself. Despite a thorough review of literature, we could not find a methodology for assessing the quality of a distance measure in medical image segmentations. Therefore, we propose a quality assessment method which uses a symmetric global measure for the comparison of the local measures.

We transform the two input meshes $M^1$ and $M^2$ to the deformed meshes $M^{D1}$ and $M^{D2}$ by moving each vertex of the mesh to the target vertex of its distance vector (see Fig. 9). The target vertices of the distance vectors of $M^1$ are on the surface of $M^2$. Therefore, if the distance vectors are good, the deformed mesh $M^{D1}$ should be very similar to the original mesh $M^2$. We measure this similarity using symmetric Hausdorff Distance. The lower this global distance the better the distance measure (SD or ESD) performs. We note that this method does not replace ground truth distances. Nevertheless, it provides a quality indicator. Figure 10 shows the results for all datasets.

Fig. 9

Mesh transformation for quantitative evaluation

Fig. 10

Quality of the SD and the ESD for four real datasets. Low mean—better distance quality. Low standard deviation—robustness. ESD shows better results

• Accuracy The mean value close to zero indicates high accuracy. Our measure has lower mean values for each direction in all datasets. ESD is more accurate than SD.

• Reliability and robustness Low standard deviation indicates robustness (i.e., low measure quality variation). ESD has lower standard deviations then SD, thus ESD has lower variability and higher reliability.

• Asymmetry The asymmetry of the distance measures can be assessed by looking at the difference between the first comparison $M^1 \leftrightarrow M^{D2}$ and the second comparison $M^2 \leftrightarrow M^{D1}$. Symmetric measures would have no differences. The SD is much more asymmetric than ours as it has larger differences.

5.4 Discussion

We presented the ESD for comparing two meshes resulting from medical image segmentations. Our new distance measure overcomes the shortcomings of the widely used SD. It provides more accurate and more symmetric distance values. The new measure does not need any user interaction or parameter setting. It can deal with various anatomical structures. It, however, has several limitations. We now discuss the main aspects of our approach: the assumptions and specifics of our algorithm. We discuss the relationship of our approach to finding correspondences. Finally, we touch upon the evaluation and runtime of our approach.

Our algorithm has several assumptions on the input data. The input meshes should be closed 2-manifolds and should be spatially aligned. These properties can already be ensured by the results of 3D medical image segmentation algorithms. Alternatively, these properties can also be established by pre-processing. This, however, can introduce approximations errors. Therefore, mesh comparison measures (like the ESD) can be dependent on the quality and accuracy of the surface representation as mesh.

Although our measure provides generally better results than the SD, it can still slightly overestimate the distance values in the differently formed regions (due to the concept of local maxima). This characteristic, however, ensures a clear indication, where large differences exist. An underestimation could lead to false implications of segmentation quality.

The problems of local distance measurement and the identification of point-to-point correspondences are related. However, the correspondence is generally very difficult to solve for arbitrarily formed meshes [28]. The algorithms for calculating correspondences often focus on specific cases. Therefore, they are also more restrictive concerning the preconditions and are less flexible and robust concerning the input meshes. Correspondence algorithms are mostly restricted to input meshes which fulfill assumptions about the form and semantic coherence. We aimed for a more general solution. In our case, the input meshes can have arbitrary formed surfaces and topologies, when our basic assumptions are met. Moreover, our algorithm also does not need any parameter setting for different sizes and types of meshes. In case a well-suited correspondence finding algorithm is available for a particular case at hand, this might be used by imaging experts in this case. This could, however, reduce comparability of result quality across organs.

The evaluation of our approach on real data indicates that the new measure provides more expressive and more reliable results than the SD. It also reduces asymmetry problems. Thereby it allows for visual inspection of the results solely on one of the two meshes. This reduces the evaluation burden for larger datasets. Nevertheless, We note that these results are only indicative, as there is no established methodology for evaluating distance measures, as in our case.

Our work primarily concentrated on the improvement of comparison quality. Nevertheless, we also assessed the runtime on the example datasets (ca. 2k–23k faces). We used a computer with an Intel(R) Core(TM) i7-3930K Processor. Without parallelization, the calculation took 7–16 sec.

6 Conclusions and future work

We introduced an Extended Surface Distance (ESD) for the evaluation of medical image segmentations. The new measure improves the drawbacks of the widely used Surface Distance (SD). It offers better distance accuracy and reliability as well as it reduces asymmetry.

The ESD is developed for a local evaluation, as it delivers local meaningful distance values on each vertex of both meshes. Therefore, the primary usage of our measure is the visual inspection of the differences of two meshes. Nevertheless, the local difference values can also be aggregated over the whole mesh leading to a global similarity value. This global measure can be used together with other established global measures of medical image segmentation.

We evaluated our measure on several real 3D medical image segmentations. The new measure detects regions of bad segmentation quality, which would otherwise be hidden. Therefore, medical experts can gain more insight into segmentation quality by analyzing the local distances on any of the two compared meshes.

In the future, we will address the issues stated in Sect. 5.4 and try to ease the assumptions by integrating pre-processing steps. We will also investigate the use of our measure for other applications such as 3D reconstruction.