A fast modal space transform for robust nonrigid shape retrieval

Abstract

Nonrigid or deformable 3D objects are common in many application domains. Retrieval of such objects in large databases based on shape similarity is still a challenging problem. In this paper, we take advantages of functional operators as characterizations of shape deformation, and further propose a framework to design novel shape signatures for encoding nonrigid geometries. Our approach constructs a context-aware integral kernel operator on a manifold, then applies modal analysis to map this operator into a low-frequency functional representation, called fast functional transform, and finally computes its spectrum as the shape signature. In a nutshell, our method is fast, isometry-invariant, discriminative, smooth and numerically stable with respect to multiple types of perturbations. Experimental results demonstrate that our new shape signature for nonrigid objects can outperform all methods participating in the nonrigid track of the SHREC’11 contest. It is also the second best performing method in the real human model track of SHREC’14.

1 Introduction

Content-based 3D object retrieval facilitates the search for desired objects within a large 3D object repository. It has become increasingly popular due to the rapid development of 3D scanning technologies and the emergence of large 3D object databases. Content-based object retrieval is useful in many application domains, including CAD/CAM, medicine, molecular biology, 3D computer games and virtual worlds.

Since many 3D object models, such as avatars, creatures and biomedical objects, can take various types of deformations, it is much desired for an object retrieval technique to be able to recognize deformed versions of an object. Nonetheless, nonrigid object retrieval is a very challenging task because a deformed object may not be visually similar to the original one any more. In the following, we summarize a few criteria for measuring the performance of nonrigid object retrieval techniques.

• Isometry invariance There exist a large variety of nonrigid deformations. In theory, one can always work out a deformation that transforms one object into another completely different object. Therefore, it is very important to define a subclass of deformations that usually do not alter the identity of an object, and then develop nonrigid object retrieval methods that are invariant or at least insensitive to this subclass of deformations. In the literature, isometric deformations are commonly adopted for this purpose.

• Discrimination power In most retrieval techniques, an object is represented with a relatively short shape descriptor or signature. It is important for the shape descriptor or signature to encode the intrinsic characteristics of an object while discarding unimportant details so that it can distinguish two different objects even when they are visually very similar, and accurately measure the degree of dissimilarity between them. Such a capability makes it possible for a retrieval technique to return a ranked list of objects with decreasing similarity with a query object.

• Efficiency Computation of shape signatures or descriptors contains offline and online stages. Many methods often requires significant amount of time to process a single mesh in offline stage, which prohibits their use in large database (say if a PC takes 10 min to process a mesh, it would take tens of years to process an entire database in size of a million). In online stage, comparison of shape is also often time critical, such that signature-based approaches are still favored over shape matching approaches in a typical retrieval system.

• Smoothness and stability Although isometric modeling provides a state-of-the-art theoretical base for nonrigid object retrieval, numerical stability of isometry-invariant shape descriptors or signatures has not been sufficiently explored. It is much desired that a shape descriptor only changes slightly when a small amount of non-isometric deformation is introduced to the original object. Likewise, it is also desired that the shape descriptor is stable when other types of defects, such as noise and holes, are introduced to the original object. Stable shape descriptors and signatures give rise to robust retrieval results. Mathematical definitions with respect to the smoothness of shape perturbations and the stability of descriptors are still missing.

In addition to the above four criteria, there exist other considerations, including extensibility, applicability and complexity of implementation (e.g., parameter free).

1.1 Related work

Among extensive work on 3D object retrieval, most techniques are devoted to rigid objects and are based on extrinsic geometry such as Euclidean distance, curvatures and snapshots of 3D canonical views. Nevertheless, nonrigid models have gained increasing popularity. Their extrinsic geometry often varies under nonrigid deformations. Isometric shape deformation was initially addressed in [13], where researchers began to consider bending invariant or insensitive 3D shape recognition. Recently, more extensive classes of invariance have been studied, such as elastic deformations [19] and affine transformations [33].

To our knowledge, two major classes of approaches are proposed for nonrigid shape retrieval during the last decade. The first class includes all local feature-based approaches (such as earlier work  [17, 29, 40, 48]). Inspired by the success of the SIFT feature descriptor in image retrieval, researchers proposed local descriptors, such as meshSIFT [29], MeshHOG [48], covariance descriptor [43], and descriptors based on the spectral graph wavelet transform [23], for representing features on mesh surfaces. ShapeGoogle [8] emphasizes the robustness of association and classification, especially for objects with missing parts and topological noises. It integrates the local heat kernel signature (HKS) [40] with the bag-of-word framework [21]. By extracting isometrically invariant dense point descriptors and quantizing them into binary codes, shapes are registered for efficient indexing, comparison and association. A more recent method [15] also endeavors to characterize 3D surfaces by measuring the likelihood of points in the 3D space being local centers of radial symmetry at selected scales. It could be useful in domain-specific 3D object retrieval, where the scale is known.

The second class emphasizes coarser-scale or global shape of a 3D nonrigid model. The skeleton-based method (e.g., [2]) encodes the geometric and topological information in the form of a skeleton graph and uses graph matching to retrieve similar skeletons. An approach for matching 3D objects in the presence of nonrigid transformations and partially similar models is presented in [42], which uses 3D curves extracted around feature points to represent surfaces. Another method based on distributions of diffusion distances has been proposed in [9] for matching nonrigid shapes. Techniques, such as histograms, D2 distributions [36] and spatial pyramids [22], are also popular in designing descriptors in respect of coarse-scale shapes. Some of them are “context-aware”: the term “context-aware” refers to dependencies between geometric characteristics not within each other’s immediate neighborhoods, distinguishing itself from “bag-of-words” approaches that focus on local geometric neighborhoods. Laga et al. [20] model the context of a shape part as a set of walks in the graph of specific length originating from the part’s node. In particular, they construct a context-aware similarity measure by relating their model of contexts to semantic correspondences. In our paper, we merely consider the context as a purely geometric property, aka the context of a point given a shape domain, and therefore, do not intend to recognize functionalities of shape parts. As other global shape descriptors, we do not generate an exact signature for contexts, yet our proposed signature is sensitive to any changes of such geometric contexts.

Among those methods concerning global shapes, spectrum-based techniques became popular in recent years. Shape-DNA [35] proposes to use the spectrum of the Laplace–Beltrami operator as an isometry-invariant shape descriptor. Another similar method, SD-GDM [38] proposes to compute a singular value decomposition (spectrum) for the geodesic distance matrix, which seems to outperform shape-DNA [24]. However, compared to shape-DNA, matrix assembly in SD-GDM requires all-pairs geodesic distances, which are computationally prohibitive to obtain even with the latest developments in fast geodesic distance computation [47], and a uniform mesh decimation is typically employed in practice to speed up this process. Utilizing spectral analysis is often effective for extracting isometric information. For example, spectral multidimensional scaling [1] has used the spectral projection of geodesic distances for better MDS embedding of data points. An efficient method for computing a robust spectrum-based shape descriptor insensitive to noises and small topological changes is presented in [46], which achieves efficiency and robustness by performing a modal space transform. This paper is an extended version of [46].

Local features, such as SIFT [28] and its variants, have been successfully adopted in image retrieval. However, in the context of 3D nonrigid shape retrieval, local feature-based methods have often been outperformed by shape descriptors emphasizing coarser-scale shapes. The reason for this phenomenon is twofold. First, pixel values captured by a camera are related to high-frequency surface properties, such as textures, of real scenes and objects. Given such high-frequency signals, it is possible for a local feature descriptor to encode sufficiently discriminative visual information for recognition or retrieval tasks. Second, 3D scanning techniques are not as mature as digital photography. Even when a 3D surface does have high-frequency details, such as pores and wrinkles on skin, it is unlikely for them to be accurately captured by a 3D scanner. Very often, such high-frequency details are buried in noises. Therefore, high-frequency geometry over a 3D surface tend to be inaccurate and unreliable (see [31] for related discussions).

Content-based multimedia retrieval is known as a problem-/scenario-dependent task. If one is interested in retrieving objects that share similar parts with the query object, methods based on point signatures should be more useful. However, if one is interested in finding globally similar nonrigid objects with potentially different poses and deformations, a global shape signature can more effectively prune the list of candidates. Even when a state-of-the-art point signature, such as the one in [23], is used in global shape retrieval, a spatial aggregation and matching scheme, such as histogram matching and spatial pyramid matching, still needs to be employed. Inevitably, such aggregation partially loses relative spatial information among point features. On the other hand, a global signature is capable of encoding the complete geometric shape up to an invariant class, and thus is a more powerful global shape representation. Therefore, global and local shape signatures are complementary to each other.

1.2 Overview and contributions

In this paper, we analyze functional operators over modal space and further introduce spectrum-based shape signatures to encode the shape of a nonrigid model. The basic idea underlying our shape signature is to compute the spectrum of the newly proposed functional operator, which is constructed from an intrinsic, context-aware integral kernel operator by projecting it to the linear space spanned by low-frequency modes defined over an object surface, while the integral kernel operator is itself based on a modal-based pairwise distance. The resulting transformation matrix can be analytically written in a succinct form. Our method is isometry-invariant and stable with respect to noise, holes and non-isometric deformations. The implementation of our shape signature is based on linear FEM. The signature itself can be efficiently computed for meshes in a wide range of resolutions and topologies.

The main contribution of this paper is the introduction of a substantially improved global shape signature, which has been experimentally validated to meet most of the aforementioned criteria. Our experiments demonstrate that our new shape signature for nonrigid objects can outperform all methods participating in the nonrigid track of the SHREC 2011 contest [24], including the best performing method. In particular, our method achieves obviously higher precision than all other methods when recall is above 50 %. Comparisons were performed on two representative datasets, the dataset used in the nonrigid track of SHREC’11 and a more challenging one created by ourselves. We have also tested our method on the more recent SHREC 2014 dataset for the retrieval of nonrigid human models [31], which have two tracks (synthetic and real). Our method is among the best performing methods in the real human model track.

The rest of the paper is organized as follows. In Sect. 2, we discuss the fundamental mathematics behind our signature design. In Sect. 3, we discuss our numerical implementation. In Sect. 4, we present experimental results to validate our shape signature. Section 5 concludes our paper.

2 Our approach

2.1 Laplace–Beltrami operator

Shape-DNA [35] exploits eigenvalues to achieve an impressive shape retrieval performance, while there are a number of other methods, such as [36, 40], utilizing eigenvectors. All these methods compute the spectrum of the Laplace–Beltrami operator $\Delta _M$, where $M$ is the underlying manifold embedded in the 3D Euclidean space as a surface, by solving the following eigenvalue problem,

$$\begin{aligned} -\Delta _M u=\lambda u. \end{aligned}$$

(1)

The Laplace–Beltrami operator is a generalized operator for functions defined on Riemannian manifolds. By solving the above equation, we obtain a complete set of modal bases $\{\phi _i\}_{i=0}^{\infty }$ over a manifold, where each $\phi _i$ corresponds to a normalized eigenvector with eigenvalue $\lambda _i$ in an ascending order.

Table 1 Differences between integral kernel operators before and after modal space restriction

2.2 Functional operator

The eigenvectors of Laplace–Beltrami operator intrinsically span a low-frequency functional space $\Phi$ which is useful in modal analysis. For example, in [30], the authors construct intrinsic flexible maps between two shapes by solving for a linear transform matrix between their modal spaces $\Phi _1\mapsto \Phi _2$ subject to certain constraints.

We instead focus on intrinsic functional transforms, i.e., maps between $\Phi$ and itself. Of course, Laplace–Beltrami operator is itself a functional transform that maps $\phi _i\mapsto - \lambda _i \phi _i$, which is isometry-invariant. We in this section introduce a new set of functional transforms whose spectra are more robust than the spectrum of the Laplace–Beltrami operator.

Given a symmetric function, $k(\cdot ,\cdot )$, let us consider the following integral kernel operator,

$$\begin{aligned} \mathcal {K}f(y)=\int _Mk(x,y)f(x)\mathrm {d}x. \end{aligned}$$

(2)

If $k(\cdot ,\cdot )$ is isometry-invariant, the spectrum of $\mathcal K$ is also isometry-invariant. For example, in the nonrigid track of the 2011 3D shape retrieval contest (SHREC’11) [24], the retrieval performance of SD-GDM [38], a method based on geodesic distance matrices (GDM), is ranked first. It outperforms shape-DNA. GDMs are in fact a class of integral kernel operators. If we set $k(x,y)$ as the geodesic distance between $x$ and $y$, the spectrum of $\mathcal K$ is the mathematically precise form of SD-GDM and is provable isometry-invariant. More importantly, we show in Appendix 6 that an integral kernel operator defines a family of “smooth” deformations, and the total deviation of the spectral signature of the integral kernel operator is finitely bounded under $\epsilon$-deformation no matter how many dimensions the signature has. Such a property is important for spectral signatures, as their performance should improve rather than degrade with an increasing number of eigenvalues. A theoretical justification for the use of integral kernel operators is as follows. If the intended invariant class (typically larger than the isometric class) of shape perturbations is the family of deformations characterized by an integral kernel operator $\mathcal K$ whose perturbed kernel $\mathcal K_{\epsilon }$ ¹ admits certain spatial smoothness condition, the distance measure based on its spectral signature with a varying number of dimensions stably changes with respect to the amount of perturbation. That is to say, in nonrigid shape retrieval, integral kernel operators can typically tolerate a larger class of smooth deformations than isometric deformations.

The major contribution of our approach is instead of naively computing a transform matrix in the complexity of the original geometry (i.e., pairwise values $k(x_i,x_j)$ for all $x_i,x_j\in M$), we restrict the kernel to modal space $\Phi$ (i.e., applying the kernel to functions in $\Phi$, the space spanned by the lower eigenvectors, and then projecting the solution back into $\Phi$). We can write the transform matrix as

$$\begin{aligned} \widetilde{K} = \Phi ^T \mathcal {K} \Phi , \end{aligned}$$

(3)

where $\Phi = [\phi _0,\phi _1,\ldots ,\phi _m,\ldots ]$.

It is worth noting that this restriction is not a simple efficient approximation, the functional transforms before and after restriction are different in the numerical aspects. Precisely speaking, the original functional space before restriction is a vector space endowed with an inner product; while the functional space $\Phi$ in restriction is an infinite-dimensional separable Hilbert space (and is numerically approximated by truncated lower eigenvectors, which converge in a weak sense) spanned by the modes. These two vector spaces are endowed with the same inner product structure in the limit. However, their numerical convergence properties are different. Table 1 summarizes their differences.

There exists a theoretical issue when we work with integral kernel operators numerically without modal restriction: numerical convergence is only guaranteed in the weak sense, while the underlying representation is pointwise. Thus the numerically estimated eigenvector of an operator may converge, but it is not guaranteed for the estimation to converge pointwise to the true eigenvector as the resolution of the mesh goes to the infinity. On the other hand, by restricting the functions of interest in the modal space, we make them have required smoothness that implicitly guarantee pointwise convergence. In our experiments (see comparison of BiHDM and R-BiHDM in Sect. 4.2), it has been observed that spectra computed by modal space restriction can better tolerate manifold deformations, and outperform the spectrum of a pairwise kernel in retrieval tasks.

2.3 Distance map using modes

Computing the geodesic distance matrix is very computationally expensive for large meshes. We choose to compute (squared) biharmonic distance [26] instead because it exhibits multiple nice properties while being more efficient to compute, and can be restricted in modal space analytically in a succinct way.

In the continuous case, the (squared) biharmonic distance is defined as follows,

$$\begin{aligned} d^2(x,y)=\sum _{i=1}^{\infty }\dfrac{(\phi _i(x)-\phi _i(y))^2}{\lambda _i^2}, \end{aligned}$$

(4)

where $\phi _i$ and $\lambda _i$ are the eigenfunctions and eigenvalues (resp.) of the semi-positive definite Laplace–Beltrami operator, $-\Delta \phi _i(x)=\lambda _i\phi _i(x)$, where $0= \lambda _0<\lambda _1\le \lambda _2\le \cdots$ and $\int _M\left| \phi _i \right| ^2=1$. The distance is a metric, and is smooth, locally isotropic, globally “shape aware”, isometry-invariant, insensitive to noise and small topology changes, parameter free, and practical to compute on a discrete mesh. In [26], these two types of distances have been extensively compared in detail. Biharmonic distance provides a nice trade-off between being nearly geodesic for small distances and global shape-awareness for large distances.

2.4 Functional biharmonic distance map

Combining previous two sections together, i.e., let $k(x,y)=d^2(x,y)$, we formulate $\widetilde{K}$ explicitly as follows.

$$\begin{aligned} \mathcal {K}\phi _0(y)= & {} \sum \limits _{i=1}^{\infty }\int \nolimits _M\dfrac{(\phi _i(x)-\phi _i(y))^2}{\lambda _i^2}\phi _0(x)\mathrm {d}x\\= & {} \dfrac{1}{\sqrt{A}}\sum \limits _{i=1}^{\infty }\dfrac{1}{\lambda _i^2}+\sqrt{A}\sum \limits _{i=1}^{\infty }\dfrac{\phi _i^2(y)}{\lambda _i^2} \end{aligned}$$

where $A$ is the total area of $M$, and note $\phi _0 = 1/\sqrt{A}$. Let $\left<\cdot ,\cdot \right>$ be the standard inner product of $L^2$ functions, we have

$$\begin{aligned} \begin{aligned} a_0 =&\left<\phi _0, \mathcal K \phi _0\right> = \sum _{i=1}^{\infty }\dfrac{2}{\lambda _i^2}, \\ a_j =&\left<\phi _j, \mathcal K \phi _0\right> = \sqrt{A}\int _M\sum _{i=1}^{\infty }\dfrac{\phi _i^2}{\lambda _i^2}\phi _j\quad j>0. \end{aligned} \end{aligned}$$

(5)

We also have

$$\begin{aligned} \mathcal {K}\phi _j(y)= & {} \sum \limits _{i=1}^{\infty }\int \limits _M\dfrac{(\phi _i(x)-\phi _i(y))^2}{\lambda _i^2}\phi _j(x)\mathrm {d}x\\= & {} \int _M\sum \limits _{i=1}^{\infty }\dfrac{\phi _i^2}{\lambda _i^2}\phi _j-\dfrac{2\phi _j(y)}{\lambda _j^2}\quad j>0, \end{aligned}$$

where $\left<\phi _0,\mathcal K \phi _j\right> = a_j$ and $\left<\phi _i,\mathcal K\phi _j\right> = -\dfrac{2}{\lambda _j^2}\delta _{ij}$. Thus we have obtained the projected matrix $\widetilde{K}$, called reduced biharmonic distance matrix (R-BiHDM),

$$\begin{aligned} \widetilde{K} = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} a_0&{}a_1&{}a_2&{}\ldots \\ a_1&{}-2/\lambda _1^2&{}&{}\\ a_2&{}&{}-2/\lambda _2^2&{}\\ \vdots &{}&{}&{}\ddots &{}\\ \end{array}\right] . \end{aligned}$$

(6)

The above matrix is infinite. We first define $\widetilde{K}_{m,n}$ be an $(n+1)\times (n+1)$ matrix

$$\begin{aligned} \widetilde{K}_{m,n} = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} a_0^{(m)}&{}a_1^{(m)}&{}a_2^{(m)}&{}\ldots &{}a_n^{(m)}\\ a_1^{(m)}&{}\frac{-2}{(\lambda _1^{(m)})^2}&{}&{}0\\ a_2^{(m)}&{}&{}\frac{-2}{(\lambda _2^{(m)})^2}&{}0\\ \vdots &{}&{}&{}\ddots &{}\vdots \\ a_n^{(m)}&{}0&{}0&{}\ldots &{}\frac{-2}{(\lambda _n^{(m)})^2} \end{array}\right] , \end{aligned}$$

(7)

which is formed by the following two steps: (i) take the first $n+1$ rows and first $n+1$ columns of $\widetilde{K}$; (ii) set $\lambda _i^{(m)}:=\lambda _i$ for $i\le m$ and $\lambda _i^{(m)} := \infty$ if $i>m$ in Eq. (7), thus when calculating each $a_j^{(m)}$ in this truncated matrix $\widetilde{K}_{m,n}$, every infinite summation in (5) is approximated by the first $m$ terms. The spectrum of $\widetilde{K}_{m,n}$ can converge in two ways:

$$\begin{aligned} \text{ BiHDM: } \lim _{m\rightarrow \infty } \text{ spectrum }(\lim _{n\rightarrow \infty } \widetilde{K}_{m,n}), \end{aligned}$$

(8)

and

$$\begin{aligned} \text{ R-BiHDM: } \lim _{m\rightarrow \infty } \text{ spectrum }(\widetilde{K}_{m,m}). \end{aligned}$$

(9)

The first scheme corresponds to the case where no modal space restriction is used. That is, $n\rightarrow \infty$ already before the spectrum is estimated. The second scheme is our method based on modal space restriction. The spectra under these two schemes are different asymptotically. For a finite $m$, BiHDM computes the spectrum of $\widetilde{K}_{m,\infty }$, which still includes the high-frequency components in the first row and the first column, i.e., $a_j^{(m)}\ne 0$ for $j>m$. On the other hand, R-BiHDM computes the spectrum of $\widetilde{K}_{m,m}$ without any high-frequency components. In general, the scheme with high-frequency components removed is not guaranteed to outperform the one without. But we remark that our proposed signature has a close connection with the traditional Fourier descriptor [49], where coefficients corresponding to low-frequency components of a contour signal are used for constructing informative shape signatures. Since high-frequency components are more likely to be contaminated with noises, which are typically high-frequency signals themselves, high-frequency components are less reliable in characterizing geometric shapes. Our approach extends a similar spirit to integral kernel operators on a manifold: the “low-frequency representation” of an integral kernel operator is more useful and reliable in characterizing its shape domains.

We call $\widetilde{K}_{m} := \widetilde{K}_{m,m}$ empirical R-BiHDM. As $m \rightarrow \infty$, the largest tens of eigenvalues of $\widetilde{K}_{m}$ enjoy a fast convergence rate. Figure 7 shows the maximum error of the first 30 eigenvalues versus $m$, the number of eigenpairs of the Laplace–Beltrami operator. It has been observed that the asymptotic eigenvalues converge linearly.

Theorem 2.1

(Spectral convergence of empirical R-BiHDM) If $M$ is a two-dimensional Riemannian manifold and is compact, then $\sum \nolimits _{i=1}^{\infty } \frac{\phi _{i}^2}{\lambda _i^2}$ is bounded both pointwise and in the form of the $L_2$ norm. Furthermore, the leading eigenvalues of $\widetilde{K}_m$ converge to that of $\widetilde{K}$ as $m\rightarrow \infty$.

Proof

See Appendix 7 for a proof with a more general condition.

Note that $\mathrm {tr}(\widetilde{K}) = 0$. We denote all eigenvalues of $\widetilde{K}$ in a magnitude descending order as $\{\mu _j\}_{j=0}^L$. We have observed that $\mu _0>0$ and $\mu _j<0\quad \forall j>0$. (Such matrix has a single positive eigenvalue, and the rest are negative. See [3] and references therein) Hence a scale-invariant spectrum can be defined as

$$\begin{aligned} \bar{\mu }_j = \left| {\mu _j}/{\mu _0} \right| . \end{aligned}$$

(10)

Our shape signature is defined as a vector $S= [\bar{\mu }_1, \bar{\mu }_2, \ldots ,$ $\bar{\mu }_L]^T$, which in theory is also isometric invariant. In practice, we select $L$ ranging from 10–30, and $m> \max \{60, 2L\}$.

To compare two shape signatures, $S^p$ and $S^q$, one can reference the dissimilarity measures in [38]. In particular, let us mention two useful ones here, mean normalized Manhattan distance,

$$\begin{aligned} D_1=\sum _{j=1}^L\left| \dfrac{S_j^p-S_j^q}{S_j^p+S_j^q} \right| , \end{aligned}$$

which is used in SD-GDM, and normalized Euclidean distance

$$\begin{aligned} D_2^2=\sum _{j=1}^L{\dfrac{(S_j^p-S_j^q)^2}{S_j^p S_j^q}}, \end{aligned}$$

(11)

which performs slightly better for our approach by experiments.

Computational efficiency A clear advantage of working with functionally transformed biharmonic distance is significantly reduced size and complexity of the kernel matrix. The computation of the original kernel matrix (either geodesics or biharmonic distance) has a much higher complexity, $O(Cn^2)$, than that of the reduced one (6), whose complexity is $O(nm)$. Here $n$ is the number of sample points on the surface, $m\ll n$, and $C$ is the time for computing a distance between two sample points, e.g., $C=O(m)$ for biharmonic distance. Also, computing the eigenvalues of the original kernel matrix could be even more expensive because it is usually a large-scale $n \times n$ dense matrix, while computing the eigenvalues of the reduced one takes much less time.

3 Implementation

To compute the eigenspace of the Laplace–Beltrami operator on a manifold, we use finite elements [50] to formulate the eigenfunction space as in [35]. Although solving PDEs with FEM is sampling invariant, mesh quality during discretization is an important factor affecting numerical accuracy. Fortunately, there is already considerable amount of work [5, 12] in mesh generation, repairing and quality improvement. Our method only assumes that the mesh is properly refined to at least a few thousand triangles and has no (near) degenerated faces. In our implementation, we use Neumann boundary condition whenever a mesh has boundaries.

Table 2 Timings for constructing shape signatures or descriptors

Following the standard setup of FEM, we need to solve the following sparse symmetric generalized eigenvalue problem that has efficient solvers, such as IRAM [4] and Krylov–Schur [39],

$$\begin{aligned} L\mathbf {u}=\lambda D\mathbf {u}, \end{aligned}$$

where $L$ is the stiff matrix and $D$ is the mass matrix. They are defined as follows. $L_{ij} = \int _M \nabla \varphi _i\cdot \nabla \varphi _j$, and $\qquad D_{ij} = \int _M \varphi _i\varphi _j$, where $L_{ij}$ and $D_{ij}$ are analytically calculated from the geometry of the elements, and $\varphi _i$ is chosen to be a piecewise polynomial in each element. See Appendix 8 for a detailed implementation of linear and cubic triangular FEMs.

Once $L$ and $D$ have been assembled, the inner products between two functions $f$ and $g$, discretely represented by finite elements over a mesh domain, are given as

$$\begin{aligned} \int _Mfg= & {} \sum ^N_{i,j=1}D_{ij}f_ig_j,\quad \int _M \nabla f\cdot \nabla g = \sum ^N_{i,j=1}L_{ij}f_ig_j, \\ \int _Mf^2g= & {} \sum ^N_{i,j=1}f^2_iD_{ij}g_j\quad \mathrm{or}\quad \sum ^N_{i,j=1}f_iD_{ij}f_jg_j. \end{aligned}$$

Once eigenfunctions of the Laplace–Beltrami operator have been computed, we are able to use the above equations to compute $a_i$ in (6).

4 Experimental results

4.1 Efficiency

Efficiency is usually important for shape retrieval techniques to be practical on large datasets. Computational intensity is a major limitation of methods based on optimization, geodesic computation, and per-node-based quantization. In contrast, our approach can always compute shape signatures in an efficient manner. Because our approach is directly based on computing lower eigenvalues/eigenvectors of Laplace–Beltrami operator and requires very little extra cost of assembly R-BiHDM [see Eq. (6)] and solving for its eigenvalues. The eigensolver of Laplace–Beltrami operator contains a sparse direct preconditioner in complexity $O(n^2)$ and a dimensional-free iterative eigensolver in complexity $O(n)$.

On an Intel Core2 Duo CPU E8400@3.00 GHz, running times required for the methods used in the subsequent Sect. 4.2 are reported in Table 2. Such running times are based on our implementation of R-BiHDM and SD-GDM [38],² and the original authors’ implementation of meshSIFT [29].³

It is seen from the timing table that, computations of SD-GDM and meshSIFT are expensive even for a mesh with only thousands vertices and grow super linearly, while our method is much faster at the same resolutions (see timing of model “abstract”). Some of more recent leading performance methods, such as ShapeGoogle [8], Supervised DL [27] and ISPM [22, 23], also suffer from the prohibitive long running time [27, 31].

4.2 Signature-based retrieval

We have tested the nonrigid shape retrieval performance of our method on two representative datasets. One is provided by the nonrigid track of SHREC’11 [24] (Fig. 1), which has 600 watertight triangle meshes that were derived from 30 original models. The second dataset mixes the nonrigid dataset from SHREC’11 with a dataset custom built by ourselves. The SHREC’11 nonrigid track dataset serves as a background dataset. The custom-built dataset contains 200 deformed meshes derived from 4 biped models, 3 dinosaur models and 3 quadruped models (Fig. 2a) and 40 background meshes (other biped, dinosaur and quadruped models, see Fig. 2b). The second dataset was designed to be more challenging and practical than the first one because it contains multiple similar meshes from each category of models, such as bipeds, dinosaurs and quadrupeds. Distinguishing similar models from the same category requires a retrieval technique to be more discriminative and stable. In the second dataset, we have performed retrieval tests on the 200 deformed meshes in a repository with a total of 840 (200 + 40 + 600) meshes.⁴

We applied the same evaluation methodology of the SHREC’11 contest to evaluate our method. It is based on the precision–recall curve and five quantitative measures: nearest neighbor (NN), first tier (FT), second tier (ST), E-measure (E), and discounted cumulative gain (DCG). We refer to [37] for detailed definitions. In our method, we use normalized Euclidean distance to measure similarity among R-BiHDM signatures [see Eq. (10)].

Fig. 1

30 classes of nonrigid models in the nonrigid track of SHREC’11

Fig. 2

Examples from our second dataset

We have compared the retrieval performance of our method with that of Shape-DNA (OrigM-n12-norm1) [35], meshSIFT [29], and SD-GDM [38]. These are the best state-of-art performing methods in the nonrigid track of the SHREC’11 contest.⁵ The parameters in these methods were set empirically to produce best performance. We also compare our method, i.e., R-BiHDM, with pairwise biharmonic distance matrix (BiHDM) and report its performance. Detailed comparison results on the SHREC’11 nonrigid track dataset are shown in Table 3 and Fig. 3a. Detailed comparison results on the second dataset are shown in Table 4 and Fig. 3b.

Table 3 Retrieval performance evaluated using five standard measures on the SHREC’11 dataset

Fig. 3

Precision–recall curves of R-BiHDM, BiHDM, SD-GDM and shape-DNA on two retrieval tasks

According to the statistics, our method achieves better performance than all of these methods on both datasets. In particular, our method has obvious improvements in the 1-tier precision. And according to the PR curves, our method achieves higher precision when recall is above 50 %. Furthermore, the retrieval performance is stable when the number of chosen eigenvalues ranges from 15 to 30. The changes of NN, ST, E and DCG measures are not larger than 0.5 % (absolutely) on both datasets, while the changes of 1-tier precisions on the original SHREC’11 dataset and the second dataset are smaller than 2 and 1 %, respectively. The best performance is achieved when $L=23$ on both datasets simultaneously, further indicating that different datasets could share the same parameter setting. The primary goal of ShapeGoogle [8] is to achieve a high level of robustness in the presence of partial shapes and topological noises. However, it does not address the identical problem as ours. In our experiments (based on implementation provided by authors), its retrieval performance on our two datasets is not comparable to the performance of our method.

Note that the performance gap between our method and the other methods becomes larger on the second dataset. As discussed earlier, the second dataset is more challenging with similar shape instances from the same categories. The results indicate that our method exhibits more discriminative power on datasets with very similar shape instances.

Table 4 Retrieval performance evaluated using five standard measures on the second dataset

4.3 Nonrigid retrieval of human models

We have also tested our proposed signature on the SHREC’14 nonrigid dataset for retrieving human models. There are two tracks, one uses synthetic data, and the other uses real data built from point clouds. These two datasets exhibit substantially different properties. The synthetic dataset consists of 15 different human models, each with its own unique body shape, which is determined by a parametric model. The real dataset is composed of 400 meshes, made up of 40 human subjects in 10 different poses. This real dataset is noisy and inaccurate in that certain body features cannot be accurately captured and human poses cannot be precisely controlled. As a participating method, detailed performance statistics of our method have been reported as the R-BiHDM-s method in [31] and more recently in [27], from which we only quote relevant results in this paper (Table 5).

Table 5 Comparison with different retrieval methods in terms of mean average precision (mAP, in %) on the SHREC’14 Human Model datasets (selected results from [27])

On the synthetic dataset, our method does not perform as well as others which gather statistics from local features. This is perhaps because our proposed signature is a geometric descriptor that captures smooth and global deformations. It has no intention to distinguish between different types of localized deformation, such as pose-driven muscle deformation. Overall, this dataset is relatively easy because a simplistic baseline method, such as the total area of a mesh, can already achieve decent performance [31].

The real dataset is much more challenging than the synthetic one. The performance of our proposed signature is ranked second. The only participating method that outperforms ours is supervised DL, which is a supervised data-driven method that requires an extra labeled dataset to train the model. Because of this, supervised methods have clear advantages over unsupervised ones, such as ours, in terms of retrieval performance. Nevertheless, our method achieves the best performance among unsupervised methods, including unsupervised DL (the unsupervised version of supervised DL), and even performs better than HAPT, another participating method that requires parameter optimization w.r.t. working datasets [31].

4.4 Continuity and stability

Continuity analysis examines the range or level of shape deformation that a descriptor can capture. Ideally, retrieved objects should be ranked according to their similarity to the query. Note that retrieval performance on a relatively small nonrigid dataset (typically with hundreds of objects) can often be sensitive to particular attributes of the dataset [31], such as the mesh resolution and total surface areas that are largely uninteresting regarding a benchmark study. As a complementary qualitative example, we show our shape signature has a good performance with respect to varied 2D shapes. Compared to 3D shapes, 2D shapes have less geometric features (where we empirically choose less dimensions for shape signatures in experiments) and their boundary can be very noisy, hence global shapes play a key role in similarity-based retrieval. We gathered the dataset of 2D contour shapes⁶ used in [44], which contains four subsets (fighter planes, vehicles and two subsets of MPEG-7 CE Shape-1 Part-B, 590 images in total). We used existing software to triangulate these contour shapes, have them cleaned as connected manifold meshes with at least 6k vertices. Then we performed query-based shape retrieval. Note that class labels of these 2D shapes were not used. A comparative example between our method and shape-DNA [35] is given in Fig. 4, which shows a ranked list of retrieved shapes when the first shape is used as the query shape. It is observed from such results that our method is able to retrieve shapes according to their global shapes, and the similarity between the query shape and a retrieved shape in the ranked list continuously decreases when we move towards the end of the list.

As for stability analysis, we will show the stability of shape retrieval results when the query shape undergoes deformations. Here we show by examples (Fig. 5) that in addition to deformations, our method is also stable when noise and small holes are added to the shape instances. In our experiments, varying degrees of zero mean white noise (0.1–0.5 average edge length) were added to vertex positions along their normal direction and a certain percentage (1–3 %) of faces was removed from the query meshes. The retrieval results turned out to be even more stable than those under deformations.

Fig. 4

The result of a query (the first shape) in a 2D shape dataset, which contains similar shapes under several types of deformations, including bending, torsion, and partial scaling

4.5 Isospectral vs isometric

Shape-DNA is known to be identical on isospectral manifolds, which is a family theoretically larger than isometrics. In fact, it has already been proven that one cannot “hear the shape of drum”. There are many examples of isospectral manifolds which are not isometric. The first example was given in 1964, and later mathematicians proposed several general construction techniques [41] to find non-isometric isospectral manifolds in two and three dimensions. Perhaps the simplest non-isometric isospectral shapes are GWW prisms [16] (Fig. 6). Shape-DNA has self-intersections in the spectral space when a shape undergoes non-isometric shape deformations, therefore may not be sufficiently discriminative near those intersections. In contrast, spectra of the reduced biharmonic distance matrices are clearly different for those non-isometric but isospectral pairs [10]. It is of interest to ask if it indicates an isometry that two 2D/3D manifolds have identical R-BiHDM, i.e., not only their $\lambda _i$, but also $a_j$ in Eq. (5) are the same.

Fig. 5

Stability test (the first shape is the query). Our retrieval results remain stable even when the meshes are corrupted with noise and holes. (Set $L=23$, $m=60$)

Fig. 6

Shape-DNA and R-BiHDM spectra computed with linear FEM for GWW prisms ($\sim$1k vertices)

4.6 Limitations

Our method has a few limitations that need further investigation. Although it has strength in identifying global nonrigid shapes, how to enhance our method for retrieving meaningful partial shapes still remains unknown. Furthermore, it assumes the surface, which is a 2D manifold, is connected. It is unclear how to extend our method for matching and retrieving complicated models with many disconnected parts.

5 Conclusions

In this paper, we have first given a brief introduction to existing methods for nonrigid 3D shape retrieval. Our method uses biharmonic distance to construct a context-aware integral kernel operator on a manifold, then applies modal space restriction to project this operator into a low-frequency representation, and finally computes its spectrum. Our method is simple to implement, isometry-invariant, discriminative, and numerically stable with respect to multiple types of perturbations. Our current implementation is based on FEM. We have evaluated our proposed method on representative datasets, including both the nonrigid track of SHREC’11 and the nonrigid human track of SHREC’14. Evaluation results demonstrate that our shape signature is highly effective in nonrigid shape retrieval.

Appendices

Appendix A: Error bounds under deformation

In this section, we investigate error bounds of the spectral signature of integral kernel operators in the presence of “smooth” manifold deformations using perturbation theory [14, 18]. The general result, intuitively speaking, is that the total deviation of a spectral signature with an arbitrary number of dimensions is finitely bounded under smooth deformations. Given a general matrix $A$ and a perturbation parameter $\epsilon$ within a neighborhood of zero, the perturbed matrix is written as $A+\epsilon B$, where $B$ is an arbitrary matrix. In this situation, each eigenvalue or eigenvectors of $A+\epsilon B$ admits an expansion in fractional powers of $\epsilon$, and the zeroth order term of this expansion is an eigenvalue or eigenvector of the unperturbed matrix $A$ (Lidskii theorem, 1965 [25]). This is a well-known result in regular perturbation theory. In particular, one can actually derive a Lipschitz condition number for this continuity:

Theorem 6.1

(A special case of Lidskii theorem [18]) Assuming $\mu (\epsilon )$ is an eigenvalue of the perturbed matrix $A+\epsilon B$ for a sufficiently small $\epsilon$, it admits a first-order expansion

$$\begin{aligned} \mu (\epsilon ) = \mu + \left\| \Phi ^T B\Phi \right\| _{\max } \epsilon + o(\epsilon ), \end{aligned}$$

where $\Phi$ is the eigenvector of $A$ corresponding to eigenvalue $\mu$, $A$ and $B$ are conjugated matrices, $\left\| \cdot \right\| _{\max }$ represents the largest singular value. The first-order coefficient $\left\| \Phi ^T B\Phi \right\| _{\max }$ is called the Lipschitz condition number.

For the rest of this section, $A$ is called characterization, and $B$ is called perturbation. The Lipschitz condition number characterizes the total amount of deviation in a signature with respect to a certain amount of perturbation. In the ideal case of isometric perturbation, where $A$ is isometric and $B$ is zero, the Lipschitz condition number is degenerated. Let $M$ and $M'$ be two compact manifold domains, and $H$ and $H'$ be the spaces of bounded and continuous linear functionals defined on $M$ and $M'$. In the current context, we consider $M'$ as a “gently” deformed version of $M$. We assume that implicitly there exists a matching (or registration) between these two domains such that it induces a mapping between $H$ and $H'$, which is a closed and densely defined operator $\mathcal D$ from $H$ to $H'$. The characterization of this mapping is a self-adjoint operator $\mathcal O$. Suppose $\mathcal O'(\epsilon )$ has a first-order approximate perturbed (infinitely dimensional) matrix representation $A + \epsilon B$ with respect to an underlying domain deformation $\mathcal D_{\epsilon }$.

Definition 6.1

(Perturbated $(\alpha ,p)$ -smoothness) Consider a perturbated matrix $A + \epsilon B$ with a spectral family $\{\mu _i(\epsilon )\}$ admitting first-order expansions: $\mu _i(\epsilon ) = \mu _i + \left| \phi _i^T B\phi _i \right| \epsilon + o(\epsilon )$. $A + \epsilon B$ is perturbated $(\alpha ,p)$-smooth if

$$\begin{aligned} \left\| A^{-\frac{\alpha }{2}}B^pA^{-\frac{\alpha }{2}} \right\| _1=: \sum \limits _{i=1}^{\infty }\left| \mu _i \right| ^{-\alpha }\left\| \phi _i^T B\phi _i \right\| ^p < C(\alpha , p), \end{aligned}$$

for some $\alpha \ge 0$ and $p> 0$, where $\left\| \cdot \right\| _1$ is Schatten p-norms.

Perturbed smoothness actually admits a substantially larger class of deformations of practical interest. It allows the characterization to be varied with respect to the domain deformation, but it bounds the amount of deviation.

Theorem 6.2

(Error bound of spectral signature) Consider a discrepancy function for a pair of original and perturbed spectra

$$\begin{aligned} d_n(\mu ,\mu ';\alpha , p) :=\sum _{i=1}^n\left| \mu _i \right| ^{-\alpha }\left| \mu _i-\mu _i' \right| ^p, \end{aligned}$$

and two Hilbert spaces $H$ and $H'$ admitting a perturbation path $\mathcal D_{\epsilon }$ for $\epsilon \in [0,1]$. If the perturbation path is uniformly perturbed $(\alpha , p)$-smooth with a bound $C(\alpha ,p)$ with respect to a characterization operator $\mathcal O(\epsilon )$, and order preserving, aka $\mu _i\ge \mu _j\iff \mu _i'\ge \mu _j'$ for any $i,j$, we have

$$\begin{aligned} d_n(\mu ,\mu ';\alpha , p)\le \kappa ^{-\alpha } C(\alpha , p), \quad \forall n \end{aligned}$$

where $\kappa = \max \limits _{i}\{\left| \frac{\mu _i}{\mu _{i+1}} \right| ,\left| \frac{\mu _{i+1}}{\mu _i} \right| \}$.

Proof

(Sketch) Take the integral w.r.t $\epsilon$: $\mu _i'-\mu _i=\int _0^1 \mathrm {d}\mu _i(\epsilon )$ and use the condition of perturbated $(\alpha ,p)$-smoothness (Definition 6.1). $\square$

Integral kernel operator Experimental evidences suggest that distance maps/matrices, more generally, integral operators, could be a useful source for shape descriptor construction, and are potentially better than differential operators (e.g., LBO). As a rigorous treatment justifying the capability of integral kernel operators, we establish another definition for the smoothness of perturbations:

Definition 6.2

($\alpha$ -Hölder class of perturbed kernel) Consider integral kernel operator $k_{\epsilon }(\cdot ,\cdot )$ with perturbation parameter $\epsilon$, and define the perturbed kernel

$$\begin{aligned} \gamma _{\epsilon }(x,y; k) = \frac{1}{\epsilon } (k_{\epsilon }(\tilde{x},\tilde{y})-k(x,y)), \end{aligned}$$

where $(\tilde{x},\tilde{y})\in M'(\epsilon )$ is the perturbed version of $(x,y)\in M$. Let $d_M$ be the geodesic distance on $M$. If there exists $C>0$ such that

$$\begin{aligned} \left| \gamma _{\epsilon }(x,y; k) - \gamma _{\epsilon }(x,z; k) \right| \le C_{\alpha } \cdot d_M(y,z)^{\alpha }, \end{aligned}$$

and

$$\begin{aligned} \left| \gamma _{\epsilon }(x,y; k) \right| \le C_{\alpha }, \end{aligned}$$

$\forall x\in M$ and any $\epsilon >0$ in a sufficiently small neighborhood of zero.

Remark

If $k(\cdot ,\cdot ) = d_M(\cdot ,\cdot )$, the infimum of bound $C_{\alpha }$ that makes $k_{\epsilon }$’s perturbed kernel belong to $\alpha$-Hölder class, aka

$$\begin{aligned} C_{\alpha }^* := \sup _{x,y,z,\epsilon } \left\{ \dfrac{\left| \gamma _{\epsilon }(x,y; k) - \gamma _{\epsilon }(x,z; k) \right| }{d_M^{\alpha }(\cdot ,\cdot )}, \left| \gamma _{\epsilon }(x,y; k) \right| \right\} , \end{aligned}$$

is a “natural” quantity indicator of deformations.

In the sequel, we connect $\alpha$-Hölder class of perturbed kernel with perturbed smoothness.

Theorem 6.3

(Main result) Given an integral kernel operator $\mathcal K$ as described in Sect. 2.2, we assume the distance map is in accordance with the geodesics of power $q$, aka, there exist positive constants $C_1$, $C_2$ and some $\delta \ge 0$ such that

$$\begin{aligned} C_1/n^{1+q+\delta } \le \lambda _n(k) \le C_2/n^{1+q},\quad \forall n, \end{aligned}$$

(12)

for some integer $q\ge 1$.

If its perturbed kernels with respect to a class of deformations, i.e., $\gamma _{\epsilon }(\cdot ,\cdot ; k)$, are of $\varepsilon$-Hölder class (Definition 6.2) for some $1\ge \varepsilon > 0$, $\mathcal K$ or the transformed operator $\widetilde{\mathcal K} = \Phi ^T \mathcal K \Phi$ (Sect. 2.2, Eq. 3), as a characterization of the deformed manifold $M'(\epsilon )$, is perturbed $(\alpha ,p)$-smooth (Definition 6.1) as long as

$$\begin{aligned} \left( \frac{1}{2} + \varepsilon \right) p > (1+q+\delta )\alpha + 1. \end{aligned}$$

Thus, spectral signatures (with an arbitrary number of dimensions) of both $\mathcal K$ and $\widetilde{\mathcal K}$ have finite error bounds under smooth manifold deformations (Theorem 6.2).

Proof

For a general Hilbert–Schmidt operator $k$ satisfying uniformly $\varepsilon$-Hölder condition, it has already been shown in [34] that the decay rate of eigenvalues of $k(x,y)$ is at least $O(n^{-1/2-\varepsilon })$. And if $k$ is positive definite, the decay rate is improved to at least $O(n^{-{1}-\varepsilon })$. It immediately follows that for $\varepsilon > \frac{1}{2}$, $\varepsilon$-Hölder continuous kernel $\gamma _{\epsilon }$ is perturbed $(0,1)$-smooth.

For $\alpha >0$, we require the eigenvalues of the characterization kernel that have lower bounds on its decay rate. It is generally not true, for example if $k(x,y)=d_M(x,y)^2$, the resulting Gram matrix has a finite number of nonzero eigenvalues if sample points are uniformly drawn from the Euclidean space. But it is typically tangible, as preliminary work has shown examples where condition (12) holds when $k(x,y)=d_M(x,y)$ (e.g., see [7, 11] examples). Then following the main result on Hölder condition and the decay of eigenvalues [34], one has $\dfrac{\left| \lambda _n(\gamma _{\epsilon }) \right| ^p}{\left| \lambda _n(k) \right| ^{\alpha }}\sim O(n^{-(\frac{1}{2} +\varepsilon )p+\alpha (1+q+\delta )})$.

Appendix B: Spectral convergence of R-BiHDM

Since we know eigenvalues of the Laplace–Beltrami operator follow $\lambda _m \sim \frac{4\pi }{A} m$ for surfaces (Weyl-asymptotic growth of eigenvalue [45]), we can therefore deduce the convergence of a spectral sequence under weak assumptions. Note $\left\| \cdot \right\|$ always denotes the $L_2$-norm of a vector, a function or a matrix, by default.

Lemma 1

Let $A\in \mathbb {C}^{n\times n}$ be an Hermitian matrix, and let $(\hat{\lambda },\hat{x})$ be the computed approximation of an eigenvalue/eigenvector pair $(\lambda ,x)$ of $A$. By defining the residual

$$\begin{aligned} \hat{r} = A \hat{x} - \hat{\lambda }\hat{x}, \hat{x} \ne 0, \end{aligned}$$

it follows that

$$\begin{aligned} \min _{\lambda _i\in \sigma (A)} \left| \hat{\lambda }- \lambda _i \right| \le \dfrac{\left\| \hat{r} \right\| _2}{\left\| \hat{x} \right\| _2}. \end{aligned}$$

Proof

See [32] page 195. $\square$

Theorem 7.1

(Spectral convergence) Let $\widetilde{K}_{m}$ be an $(m+1)\times (m+1)$ square matrix formed by the following steps: (i) take the first $m+1$ rows and first $m+1$ columns of $\widetilde{K}$; (ii) when calculating each $a_j$ in this truncated matrix, every infinite summation in (5) is approximated by the first $m$ terms. Set $\mu _i^{(m)}$ be the $i$-th eigenvalue of $\widetilde{K}_m$, for $i\le m+1$ and $\mu _i{(m)}=0$, for any $i> m+1$. Let $f_m = \sqrt{A}\sum _{i=1}^m\phi _i^2/\lambda _i^2$ converge (pointwisely) to $f$. If $f$ is bounded and square integrable, i.e., eigenpairs $\{(\lambda _i, \phi _i)\}_{i=1}^\infty$ satisfy

$$\begin{aligned} \sum _{i=1}^\infty \dfrac{\left\| \phi _i^2 \right\| ^2}{\lambda _i^4} < \infty , \end{aligned}$$

(13)

it then follows that for any $i$,

$$\begin{aligned} \mu _i^{(m)}\rightarrow \mu _i,\quad \text{ as } m\rightarrow \infty . \end{aligned}$$

Proof

By definition, we have $\widetilde{K}_{m+n} - \widetilde{K}_{m-1}=$

$$\begin{aligned} \sum _{k=m}^{m+n} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \frac{2}{\lambda ^2_k}&{}\frac{C_{k,1}}{\lambda _k^2}&{}\ldots &{}\frac{C_{k,m-1}}{\lambda _k^2}&{} 0&{}\ldots &{}a^{(m+n)}_k&{}\ldots \\ \frac{C_{k,1}}{\lambda _k^2}&{}0\\ \vdots &{}&{}\ddots &{}&{}\\ \frac{C_{k,m-1}}{\lambda _k^2}&{}&{}&{}0\\ 0&{}&{}&{}&{}0\\ \vdots &{}&{}&{}&{}&{}\ddots \\ a^{(m+n)}_k&{}&{}&{}&{}&{}&{}-\frac{2}{\lambda ^2_k}\\ \vdots &{}&{}&{}&{}&{}&{}&{}\ddots \end{array}\right] , \end{aligned}$$

where extra rows and columns of zeros are padded to $\widetilde{K}_{m-1}$, and

$$\begin{aligned} C_{m,j} = \sqrt{A}\int _M \phi _m^2\phi _j, \end{aligned}$$

which is the Fourier coefficient of $\sqrt{A}\phi _m^2$ w.r.t series $\{\phi _j\}_{j=1}^{m-1}$. By Bessel’s inequality we have $1+\sum _{j=1}^{m-1}C_{m,j}^2\le A\left\| \phi _m^2 \right\| ^2$, and we also have

$$\begin{aligned} \sum _{k=m}^{m+n}\left| a^{(m+n)}_k \right| ^2\le & {} \sum _{k=m}^{\infty }\left| \int _Mf_{m+n}\phi _k \right| ^2\\\le & {} \left\| f_{m+n} -f \right\| ^2 + \sum _{k=m}^{\infty }\left| \int _M f\phi _k \right| ^2. \end{aligned}$$

By assumptions about $f$ and the norm convergence of Fourier series (as shown for example in [1]), we know that $\left\| f_{m+n} -f \right\| ^2\rightarrow 0$ and $\sum _{k=m}^{\infty }\left| \int _M f\phi _k \right| ^2\rightarrow 0$ as $m\rightarrow \infty$. Since the $L_2$-norm of a matrix is less than its Frobenius norm, we have

$$\begin{aligned}&\!\!\! \left\| \widetilde{K}_{m+n} - \widetilde{K}_{m-1} \right\| ^2_2\\&\quad \le \sum _{k=m}^{m+n}\left( \frac{2}{\lambda _k^4} (4+\sum _{j=1}^{m-1}C^2_{k,j}) + 2\left| a^{(m+n)}_k \right| ^2\right) \\&\quad \le \sum _{k=m}^{m+n}\left( \frac{2}{\lambda _k^4}(3+A\left\| \phi _k^2 \right\| ^2) + 2\left| a^{(m+n)}_k \right| ^2\right) \rightarrow 0 \end{aligned}$$

as $m\rightarrow \infty$. By Lemma 1, we have

$$\begin{aligned} \left| \mu _i^{(m+n)}-\mu _i^{(m-1)} \right|\le & {} \dfrac{\left\| (\widetilde{K}_{m+n} - \widetilde{K}_{m-1})u_i^{(m+n)} \right\| }{\left\| u^{(m+n)}_i \right\| }\\\le & {} \left\| \widetilde{K}_{m+n} - \widetilde{K}_{m-1} \right\| _2 \end{aligned}$$

for any $i<m$, where $u^{(m)}_i$ is the eigenvector associated with $\mu ^{(m)}_i$ of $\widetilde{K}_{m}$. $\{\mu _i^{(m)}\}_{m=1}^{\infty }$ is a Cauchy sequence, that converges. $\square$

Note that the condition, i.e., Eq. (13), used in the spectral convergence theorem is rather weak. Observe that for two-dimensional Riemannian manifold $M$, $f(x)$ is given by the green function $G(x,y)$ with $f(x):=G(x,x)$. If $M$ is a compact manifold (without boundary), it satisfies that $G(x,y)$ is bounded [6], hence $f(x)$ is also bounded for any $x\in M$. So is $\left\| f \right\| ^2$ (square integrable). An experimental validation is also provided in Fig. 7.

Fig. 7

A experimental validation: convergence of the first 30 eigenvalues of an R-BiHDM

Appendix C: Matrices for linear and cubic FEM

Fig. 8

Node configuration of linear and cubic FEM

Table 6 The four matrices of integrals on the unit triangle for linear FEM

Table 7 The four matrices of integrals on the unit triangle for cubic FEM

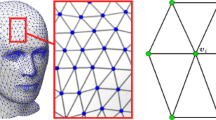
Here we provide elementary matrices used in linear and cubic FEM. Every FEM has its own set of nodes. There is a finite element associated with every node. The finite element at a specific node is a piecewise polynomial basis function whose value is equal to 1 at the node and 0 at all other nodes. The support of a basis function includes all triangle faces surrounding the node corresponding to the basis function. Consider a triangle face in a mesh with two node configurations shown in Fig. 8. These node configurations are defined for linear and cubic FEM, respectively. Each node in either configuration is associated with a piecewise linear or cubic polynomial basis function. If we focus on a triangle face, an arbitrary bivariate polynomial over the triangle face can be defined as a linear combination of the basis functions associated with the nodes either inside or on the edges of the triangle. This polynomial can interpolate arbitrary prescribed values at the nodes. It reduces to a univariate polynomial along each triangle edge. The two polynomials defined over two adjacent triangles agree with each other along their shared triangle edge. The stiff and mass matrices used in FEM are given as follows.

$$\begin{aligned} L_{ij}(T)= & {} \frac{1}{a(T)}\left( \sum _{k=1}^3 l_k^2(T)J_k\left( t_i,t_j\right) \right) , \quad i,j\in N(T)\\ D_{ij}(T)= & {} a(T)J_4\left( t_i,t_j\right) , \quad i,j\in N(T)\\ L_{ij}(T)= & {} D_{ij}(T) = 0, \quad i,j\not \in N(T) \end{aligned}$$

and

$$\begin{aligned} L = \sum _{T} L(T), \quad D = \sum _{T} D(T), \end{aligned}$$

where $T$ denotes a triangle face, $N(T)$ denotes the set of incidence nodes on $T$, $t_i$ denotes the local index (used for $T$) of the $i$-th node used in the FEM, $l_k(T)$ $(k=1,2,3)$ denotes the length of the $k$-th edge of $T$, $a(T)$ denotes the area of $T$, and $J_k(t_i,t_j)$ denotes the entry with indices $(t_i,t_j)$ of the matrix $J_k$. $J_k$ $(k=1,2,3,4)$ for linear and cubic FEM are given in Tables 6 and 7, respectively. Details on the construction of $J_k$ can be found in [50]. Note that these matrices are assembled triangle-wise rather than element-wise in a typical implementation.