Comparative study of modelling flows in porous media for engineering applications using finite volume and artificial neural network methods

Abstract

A neural solution methodology, using a feed-forward and a convolutional neural networks, is presented for general tensor elliptic pressure equation with discontinuous coefficients. The methodology is applicable for solving single-phase flow in porous medium, which is traditionally solved using numerical schemes like finite-volume methods. The neural solution to elliptic pressure equation is based on machine learning algorithms and could serve as a more effective alternative to finite volume schemes like two-point or multi-point discretization schemes (TPFA or MPFA) for faster and more accurate solution of elliptic pressure equation. Series of 1D and 2D test cases, where the results of Neural solutions are compared to numerical solutions obtained using two-point schemes with range of heterogeneities, are also presented to demonstrate general applicability and accuracy of the Neural solution method.

1 Introduction

Subsurface reservoirs generally have a complex description in terms of both geometry and geology. Typical reservoir grid block sizes are of the order of tens of meters, while rock properties are measured below the centimeter scale. This poses a continuing challenge to modeling and simulation of reservoirs since fine-scale effects often have a profound impact on flow patterns on larger scales. Resolving all pertinent scales and their interaction is therefore imperative to give reliable qualitative and quantitative simulation results.

Rapid variation in permeability is common in oil reservoirs where permeability coefficients can jump by several orders of magnitude. Continuity of normal flux and pressure at local physical interfaces between grid blocks with strong discontinuities in permeability are fundamental laws that must be built into the discrete approximation of the pressure equation. Finite volume methods are a class of discretization schemes that have proven highly successful in approximating the solution of a wide variety of conservation laws. The primary advantages of these methods are improved numerical robustness through discrete maximum (minimum) principles, applicability on very general unstructured grids, and the intrinsic local conservation properties of the resulting schemes. In last two decades “flux-continuous control volume distributed (CVD) finite-volume schemes" for determining the discrete pressure and velocity fields in subsurface reservoirs [2] and [14]. Schemes of this type are also called as multi-point flux approximation schemes or MPFA [9]. Other schemes that preserve flux continuity have also been developed using mixed methods [1] and discontinuous galerkin methods [29]. Numerical convergence of these schemes on structured and unstructured grids has also been presented in [14, 3] and [21].

When applying these schemes to strongly anisotropic heterogeneous media, they can fail to satisfy a maximum principle (as with other Finite-element and finite-volume methods) and result in loss of solution monotonicity for high anisotropy ratios causing spurious oscillations in the numerical pressure solution [16]. In recent years, with the advances in machine learning and the development of deep learning algorithms, researchers have started to apply deep learning methods to solve a variety of mathematical and engineering problems. For example, researchers have tried to solve ordinary differential equations using neural networks [26] and develop a deep learning framework for solving partial differential equations [10] as well. More to that, Neural networks have also been used for solving steady state and turbulent flow problems [4, 28], and deep learning methods have been applied for solving poro-elastic problems in porous media [27]. Some researchers have also started using the power of deep learning techniques, like RNN-LSTM type models [23], for history matching and forecasting of hydrocarbon flows in heterogeneous porous media. Neural networks have also been introduced permeability upscaling and homogenization [7]

Machine learning approaches have been applied to find models of heat conduction problem [31], which is similar to flow in porous media solving elliptic equation. The work was presented for a one-dimensional heat conduction problem which involves a system of Partial Differential Equations (PDEs). The training data is generated by solving numerically. Nonlinear heat transfer via conduction with a complex geometry using machine learning has been presented by [32], where the ANN technique is adopted to deal with the geometry complexity and nonlinear aspects of the thermal model. Researcher [33] have developed an ANN model for predicting the behaviour of non-linear flow in porous media by taking pressure gradient into account. Particle diameter, density, shape and porosity has been identified as the influencing factors which were taken as input parameters. The generated ANN model is developed by using a huge experimental data set which is found to be better to predict the flow behaviour over previous empirical relations. Heat and mass transfer investigation on the flow impingement of a hybrid nanofluid over a cylindrical shaped structure embedded with porous media has also been conduced by [34] using machine learning approaches.

In this paper we aim to use the power of artificial neural networks to solve elliptic pressure equation with discontinuous coefficients. A neural solution methodology is presented using a feed-forward and a convolutions neural network for solving the elliptic partial differential equation. The method presented in this paper could serve as a more effective alternative to finite-volume and other numerical schemes. This paper also presents the challenges associated with solving elliptic PDE with discontinuous coefficients using finite-volume method and demonstrates with help of test cases the superiority of neural solution methods.

This paper is organized as follows: Flow equations and general problem description is presented in Sect. 2. Numerical solution methodology using Two-Point Flux and Multi-Point Flux approximation along with its limitations is presented in Sect. 3. Neural solution of elliptic PDE using feed forward neural networks is presented in Sect. 4. Improved solution methodology using convolution neural networks is presented in Sect. 5. Section 6 presents results and conclusions follow in Sect. 7.

2 Flow equation and problem description

2.1 Cartesian tensor

The problem is to find the pressure p satisfying

$$\begin{aligned} -\int _{\Omega }\nabla \cdot \mathbf {K}(x,y)\nabla p\,d\tau = \int _{\Omega }q\,d \tau = \mathbf {M} \end{aligned}$$

(1)

over an arbitrary domain $\Omega$, subjected to suitable (Neumann/Dirichlet) boundary conditions on boundary $\partial \Omega$. The right hand side term $\mathbf {M}$ represents a specified flow rate and $\nabla = (\partial _{x}, \partial _{y})$. Matrix $\mathbf {K}$ can be a diagonal or full cartesian tensor with general form

$$\begin{aligned} \mathbf {K} = \left( \begin{array}{cc} K_{11} &{} K_{12} \\ K_{12} &{} K_{22} \\ \end{array} \right) \end{aligned}$$

(2)

The full tensor pressure equation is assumed to be elliptic such that

$$\begin{aligned} K_{12}^{2}\le K_{11}K_{22} \end{aligned}$$

(3)

The tensor can be discontinuous across internal boundaries of $\Omega$. The boundary conditions imposed here are Dirichlet and Neumann. The pressure is specified at at-least one point in the domain for incompressible flow. For reservoir simulation, Neumann boundary conditions on $\partial \Omega$ require zero flux on solid walls such that $(\mathbf {K}\nabla p)\cdot \hat{n} = 0$, where $\hat{n}$ is the outward normal vector to $\partial {\Omega }$.

2.2 General tensor equation

The pressure equation is defined above with respect to the physical tensor in the initial classical Cartesian coordinate system. Now we proceed to a general curvilinear coordinate system that is defined with respect to a uniform dimensionless transform space with a $(\xi , \eta )$ coordinate system. Choosing $\Omega _{p}$ to represent an arbitrary control volume comprised of surfaces that are tangential to constant $(\xi , \eta )$ respectively, equation 1 is integrated over $\Omega _ {p}$ via the Gauss divergence theorem to yield

$$\begin{aligned} -\oint _{\partial \Omega _{p}} \mathbf {K}\nabla (p)\cdot \hat{n}\,ds = \mathbf {M} \end{aligned}$$

(4)

where $\partial \Omega _{p}$ is the boundary of $\Omega _{p}$ and $\hat{n}$ is the unit outward normal. Spatial derivatives are computed using

$$\begin{aligned} p_{x} = \frac{J(p,y)}{J(x,y)}, \quad p_{y} = \frac{J(x,p)}{J(x,y)}, \end{aligned}$$

(5)

where $J(x,y)= x_{\xi }y_{\eta }-x_{\eta }y_{\xi }$ is the Jacobian. Resolving the x, y components of velocity along the unit normals to the curvilinear coordinates $(\xi , \eta )$, e.g., for $\xi =$ constant, $\hat{\mathbf {n}}\,ds = (y_{\eta },-x_{\eta })\,d\eta$ gives rise to the general tensor flux components

$$\begin{aligned} F = -\int (T_{11}p_{\xi }+T_{12}p_{\eta })\,d\eta , \quad G = -\int (T_{12}p_{\xi }+T_{22}p_{\eta })\,d\xi , \end{aligned}$$

(6)

where general tensor $\mathbf {T}$ has elements defined by

$$\begin{aligned} T_{11}= & {} (K_{11}y_{\eta }^2+K_{22}x_{\eta }^2-2K_{12}x_{\eta }y_{\eta })/J,\nonumber \\ T_{22}= & {} (K_{11}y_{\xi }^2+K_{22}x_{\xi }-2K_{12}x_{\xi }y_{\xi })/J, \nonumber \\ T_{12}= & {} (K_{12}(x_{\xi }y_{\eta }+x_{\eta }y_{\xi })-(K_{11}y_{\eta }y_{\xi }+K_{22}x_{\eta }x_{\xi }))/J \end{aligned}$$

(7)

and the closed integral can be written as

$$\begin{aligned} \iint _{\Omega _{p}}\frac{(\partial _{\xi }\tilde{F}+\partial _{\eta }\tilde{G})}{J}J\,d\xi d\eta = \triangle _{\xi }F + \triangle _{\eta }G = m \end{aligned}$$

(8)

where e.g. $\triangle _{\xi }F$ is the difference in net flux with respect to $\xi$ and $\tilde{F} = T_{11}p_{\xi }+T_{12}p_{\eta }$, $\tilde{G} = T_{12}p_{\xi }+T_{22}p_{\eta }$. Thus any scheme applicable to a full tensor also applies to non-K-Orthogonal grids. Note that $T_{11},T_{22}\ge 0$ and ellipticity of $\mathbf {T}$ follows from equations 3 and 7. Full tensors can arise from upscaling, and local orientation of the grid and permeability field. For example by equation 7, a diagonal anisotropic Cartesian tensor leads to a full tensor on a curvilinear orthogonal¹ grid ([16]).

2.3 Boundary conditions

The two most common kinds of boundary conditions used in reservoir simulators to solve equation 1, are Dirichlet and Neumann Boundary Conditions. The Dirichlet boundary condition requires the specification of pressure at the reservoir boundaries or wells. Typically, this involves specifying flowing bottom hole pressure at a well and a constant pressure at physical boundaries of reservoir. The Neumann boundary condition requires specification of flow rates at reservoir boundaries. Typically, it involves specifying flow rates at wells and no-flow across physical boundaries of reservoir.

3 Numerical schemes for solving general tensor pressure equation

Conventional reservoir simulation employs a standard five-point cell-centred stencil in 2D (seven in 3D) for approximating the discrete diagonal tensor pressure (not full tensor) equation, Fig. 1. Continuity of flux and pressure is readily incorporated into the standard discretization by approximating the interface coefficients with a harmonic average of neighboring grid block permeabilities. Unfortunately, for an arbitrary heterogeneous domain the assumption of a diagonal tensor is not always valid at the grid block scale.

Fig. 1

Depiction of Five-Point Stencil on the left and a Nine-Point Stencil on the right for 2D case

In general a full tensor equation arises whenever the computational grid is nonaligned with the principal axes of the local tensor field. A full tensor can occur when representing cross bedding, modeling any anisotropic medium that is non-aligned with the computational grid, using non K-orthogonal [12, 13] or unstructured grids as well as upscaling rock properties from fine scale diagonal tensor simulation to the 12 grid block scale. Consequently, a standard five-point diagonal tensor simulator will suffer from an inconsistent O(1) error in flux when applied to cases involving these major features. Accurate approximation of the full-tensor pressure equation requires nine-point support in two dimension (19 or 27 in 3-D), Fig. 1. The nine point formulation is possibly the most reliable method to counter grid-orientation effect and widen the simulator range of applicability to general non-orthogonal grids and full-tensors [14,15,16, 18, 19].

Fig. 2

One dimensional Cell centered and Cell face pressures

3.1 Two-point flux approximation (TPFA) Scheme

We begin with classical cell centered formulation in one dimension where pressures and permeabilities are defined with respect to cell centres. In this case equation 1 reduces to

$$\begin{aligned} -\int \left( K(x)\,p'_{x}\right) '_{x}dx = m \end{aligned}$$

(9)

Integration of the equation 9 over the cell i (referring to Fig. 2) results in the discrete difference of fluxes

$$\begin{aligned} F_{i+\frac{1}{2}} - F_{i-\frac{1}{2}} = m \end{aligned}$$

(10)

where m is possible specified local flow rate, $F_{i+\frac{1}{2}} =-K\,\dfrac{\partial p_{i+\frac{1}{2}}}{\partial x}$ and the derivative remains to be defined. If the coefficient $\mathbf{K}$ is sufficiently smoothly varying it is possible to use linear interpolation between the centers of cells i and $i+1$ and approximates the flux by

$$\begin{aligned} F_{i+\frac{1}{2}} = -K_{i+\frac{1}{2}}\frac{p_{i+1}-p_{i}}{x_{i+1}-x_{i}} \end{aligned}$$

(11)

where $K_{i+\frac{1}{2}}$ is a suitable average of the adjacent cell centered permeabilities. However if $\mathbf{K}$ is discontinuous then (since normal flux and pressure are continuous) the pressure gradient is discontinuous and linear interpolation is not valid across the cell faces. Continuous pressure and normal flux are incorporated in the cell centered approximation by introducing a mean pressure $p_{f}$ at a cell face dividing neighboring cells Fig. 2. Equating the resulting one sided flux approximation at the cell face results in

$$\begin{aligned} -K_{r}\frac{p_{r}-p_{f}}{\Delta x_{r}} = -K_{l}\frac{p_{f}-p_{l}}{\Delta x_{l}} = -F_{f}\frac{p_{r}-p_{l}}{\Delta x} \end{aligned}$$

(12)

which ensures flux continuity. From equation 12 cell face pressure is given by

$$\begin{aligned} p_{f} = \dfrac{\dfrac{p_{l}K_{l}}{\Delta x_{l}}+ \dfrac{p_{r}K_{r}}{\Delta x_{r}}}{\dfrac{K_{l}}{\Delta x_{l}}+ \dfrac{K_{r}}{\Delta x_{r}}} \end{aligned}$$

(13)

which is back-substituted into the discrete flux equation 11 to yield the classical cell face flux approximation

$$\begin{aligned} F_f = -2K_{r}K_{l}\frac{p_{r}-p_{l}}{K_{r}\Delta x_{l}+K_{l}\Delta x_{r}} \end{aligned}$$

(14)

As in one dimension pressures and permeabilities have a cell-wise distribution and cells act as control volumes. The equivalent two-dimensional discontinuous diagonal tensor five-point scheme on rectangular grid is derived by introduction of interface pressures and a sub-cell triangular support, see Fig. 3. As in one dimension cell face pressures are eliminated in the flux continuity conditions to yield the classical five point scheme with harmonic mean coefficients in two dimensions, further details of the scheme can be found in [12, 13]. The support for the classical five-point scheme is shown in Fig. 3, and shows that introduction of cell face pressures ($p_{f}=(p_{N},p_{S},p_{E},p_{W},)$) enables the normal velocity and pressure to be point-wise continuous at the cell faces.

Fig. 3

Imposing continuity between the grid blocks in a five-point scheme. Cell-centered five-point support on a cartesian grid

3.2 Multi-point flux approximation (MPFA) scheme

Two-point flux approximation method only take into account neighbouring grid cells and deals with only isotropic permeability. To get a generalized discretization for anisotropic permeablities and general polyhedral grids, multipoint flux-approximation method or (MPFA) uses more than two points to approximate the flux across each inter-cell face, typically it uses a stencil similar to a 9-point scheme, resulting in a 9 diagnoals in 2D and 27 diagnoals in 3D for the global assembly matrix. A lot of literature and details on MPFA method have been published, see [14,15,16, 18, 19].

For the standard MPFA - O method each face in the grid is subdivided into a set of subfaces, one subface per node that makes up the face, see Fig. 4. The inner product of the local-flux mimetic method gives exact result for linear flow and is block diagonal with respect to the faces corresponding to each node of the cell, but it is not symmetric. The block-diagonal property makes it possible to reduce the system into a cell-centered discretisation for the cell pressures. This naturally leads to a method for calculating the MPFA transmissibilities. The MPFA-O scheme is consistent on grids that are not necessarily K-orthogonal.

Fig. 4

Full tensor pressure support with standard MPFA scheme

3.3 Limitations of TPFA and MPFA schemes for elliptic pressure eqn

The two-point flux approximation method (TFPA) is convergent if and only if grid cells are Cartesian or parallelogram in 2D and parallelepiped in 3D, otherwise, also known as a $\mathbf{K}$-orthogonal grids. Cartesian grids are $\mathbf{K}$-orthogonal with respect to diagonal permeability tensor but not with respect to full permeability tensor, see Fig. 5. Therefore, a major limitation of TFPA method is that if its used to solve the elliptic pressure equation on a non $\mathbf{K}$-orthogonal grid it results in wrong results due to grid-orientation effects. MPFA method, on the other hand, is more suitable for such non $\mathbf{K}$-orthogonal grids and gives a more accurate solution, see Fig. 6, which shows how permeability anisotropy impacts the pressure propagation between sources and sinks leading to wrong results.

Fig. 5

The grid on the left is a cartesian type grid with grid lines aligned with principal coordinate axes. The grid on the right is a plot of K-orthogonal grid

Fig. 6

Figure showing comparative simulation results, on a cartesian grid with high anisotropy, between TPFA and MPFA methods

Although, MPFA methods give correct results for non-K-orthogonal and full permeability tensor, they result in non-monotonic solution when applied to highly an-isotropic permeability tensors [14, 17]. A variety of modified MPFA schemes have been developed by many authors to correct for non-monotonic behavior but still some challenges exist for highly complex cases. An example of such a case where standard MPFA method fail to yield accurate solution is shown in Fig. 7, which shows non-monotonic behavior of the pressure solution in presence of very high anisotropy, for more details please see reference [17].

Fig. 7

Figure showing comparative simulation results, on a Cartesian grid with high anisotropy, between TPFA and MPFA methods

4 Neural solution method

Machine learning is a field of mathematics and computer science for artificial intelligence that analyzes algorithms that solve various problems without giving “precise” instructions. These algorithms can be loosely classified into supervised and non-supervised learning, however in this paper the focus is on the former. Each time a machine solves a particular problem from a given input, some relevant feedback is obtained about its output by comparing it to a "true" result. At first epochs the computer is untrained and the errors are high, however, with time it manages to learn by re-selecting a set of parameters automatically for more accurate results.

Artificial Neural Network is a very renowned type of machine learning algorithms that is used for many difficult problems such as applications for image and language processing, forecasting, risk assessment, market research, etc. The idea behind machine learning algorithms is trying to recognize an underlying relationship between some input and its output vectors. This is done by mimicking the phenomenon inside the brain where nerve cells (called neurons) create intricate relationships of varying strength between one another that resembles a net, thus such algorithm earned its name as a "neural network". ANN is known for being an universal function approximator - this means that it may, in theory, given sufficient amount of data that is processed for a specific problem and fed accordingly, imitate any possible relationship (where there is one).

There are two types of problems ANN can deal with: classification and regression. Classification usually outputs some kind of probability estimate of a defined occurrence, whereas regression outputs values of a function at a certain input. The main focus in this paper is on the latter, however it is extremely important to understand the part that is usually taught in classification approach - Logistic Regression (LR). This is because LR is in a way a building block of NN as it defines what a neuron is.

Using one LR approach will only yield strictly monotonous solutions (either increasing in value or decreasing), however if two or more LRs are used on the same input - they can be added to construct almost any shape imaginable much like Fourier series. The main idea idea behind basic feed-forward ANN is - stacking LR approach multiple times and repeatedly feeding modified input spaces into sequential modifiers. However, the weights are guided to produce a wanted output (called target) using back-propagation and optimization algorithms. If weights are not optimal - the output of the ANN is far from a target by some error calculated by a cost function (e.g. Mean Square Error). This cost function has to be minimized by weights (e.g. using Gradient Descent algorithm) so that the error would be as small as possible. A lot of minimization algorithms make use of cost function gradient which is very computationally expensive to compute, so a back-propagation algorithm is usually used [5] to approximate the gradient.

4.1 Neural solutions to elliptic pressure equation - using convolutional neural network

The inspiration behind this work was drawn from Physically Informed Neural Network (PINN) [30] approach with an implementation of convolutions for solving the elliptic pressure equation. This is due to inherent limitation of a simple feed forward neural networks failing to obtain a good quality numerical solution and the problem being more focused on spacial derivatives.

Implementation of neural network, which would replicate TPFA results for the elliptic pressure equation is done for 1D problems before moving on to more complex 2D problems. Assuming the isotropic permeability domain that is aligned with the rectangular grid, the Poisson’s equation becomes:

$$\begin{aligned} \frac{d^{2}p(x)}{dx^{2}}\cdot k(x) = 0 \end{aligned}$$

(15)

where p(x) is the FVM approximation obtained from (TPFA or MPFA) type formulation. In 1D case, $\mathbf {K} = \left( \begin{array}{cc} K_{11} \end{array} \right)$, so the whole permeability domain can be described by a singlevariate function $\mathbf {K}=k(x)$. The main objective is to set up the neural network, given as, NN(x) such that the solution would converge on the numerical one:

$$\begin{aligned} NN(x) = p(x) \end{aligned}$$

(16)

Substituting equation 16 into equation 15 the expression becomes:

$$\begin{aligned} \frac{d^{2}NN(x)}{dx^{2}}\cdot k(x) = 0 \end{aligned}$$

(17)

for some specifically defined boundary conditions, as source (1) and sink (0), at the both ends of the domain given as: $(p(0) = P_{0}$ and $p(1) = P_{1})$.

Loss function is constructed in such a way so that it mimics the Darcy’s law. Two separate loss functions with differing weights are constructed, one of which is only for learning the numerical FVM stencil and the another is a typical data driven loss function, see equation 18.

$$\begin{aligned} Loss = \left( \frac{d^{2}NN(x)}{dx^{2}}\cdot k(x)\right) ^{2} \end{aligned}$$

(18)

The loss function could be subsequently written using the FVM stencil shown in equation 19 as:

$$\begin{aligned} \begin{gathered} Loss =\left( \frac{2k(x_{i})k(x_{i+1})}{k(x_{i})+k(x_{i+1})}(NN(x_{i+1})-NN(x_{i})) \right. \\ \left. - \frac{2k(x_{i-1})k(x_{i})}{k(x_{i-1})+k(x_{i})}(NN(x_{i})-NN(x_{i-1})) \right) ^2 \end{gathered} \end{aligned}$$

(19)

The most straightforward way of implementing boundary conditions is by putting them directly inside of the loss function, given as:

$$\begin{aligned} \begin{gathered} Loss =\left( \frac{2k(x_{i})k(x_{i+1})}{k(x_{i})+k(x_{i+1})}(NN(x_{i+1})-NN(x_{i})) \right. \\ \left. - \frac{2k(x_{i-1})k(x_{i})}{k(x_{i-1})+k(x_{i})}(NN(x_{i})-NN(x_{i-1})) \right) ^2 \\ +(NN(0) - P_{0})^{2} +(NN(1) -P_{1})^{2} \end{gathered} \end{aligned}$$

(20)

Where the last term of 20 corresponds to the boundary condition. But the implementation of BCs within the loss function results in unstable solutions. To avoid instabilities in the neural solution the BCs are implemented as a function that would represent the pressure distribution, say g(x). Since neural network could approximate any function, g(x) could be arranged in such a way that it would always satisfy the left and right boundary conditions on one dimensional domain, shown in equation 21.

$$\begin{aligned} g(x) = P_{0} + (x^{2} - x)\cdot NN(x) + x(P_{1} -P_{0}) \end{aligned}$$

(21)

such that at $x =0,\, g(0) = P_{0}$ and at $x =1,\, g(1) = P_{1}$. With the boundary conditions implemented the resulting loss function becomes as shown in equation 22.

$$\begin{aligned} \begin{gathered} Loss =\left( \frac{2k(x_{i})k(x_{i+1})}{k(x_{i})+k(x_{i+1})}(g(x_{i+1})-g(x_{i})) \right. \\ \left. - \frac{2k(x_{i-1})k(x_{i})}{k(x_{i-1})+k(x_{i})}(g(x_{i})-g(x_{i-1})) \right) ^2 \end{gathered} \end{aligned}$$

(22)

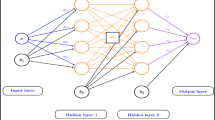
Input for an elementary 1D PINN is usually a single neuron that represents any real ${x}$-coordinate, where the output is also a single neuron that returns a pressure value at that particular ${x}$-coordinate. This is great as the neural network can evaluate the pressure distribution at any point of the 1-D domain, where numerical methods would find it difficult for a given discretization, thus being not as flexible in that regard. Another point to note is the implementation of the boundary conditions. Here Dirichlet BCs are implemented, which define some fixed pressure values at the ends of the domain. A very simple architecture with only one dense layer out of 32 neurons is used, see Fig. 8.

Fig. 8

Architecture of a simple feed forward network with one dense layer consisting out of 32 hidden neurons (1:32:1). This network was used for the classic PINN formulation for the elliptic pressure equations in 1D

Although this type of network architecture works well, it has one limitation that this network could only be trained with one permeability distribution at a time. To overcome this challenge the input neurons are treated as discrete coordinates themselves, rather than having one single input neuron for coordinate insertion. That way it is possible to have an input slot for every permeability value of the discretized domain. The network would also produce an output of the same size (equal to the disrcretization node count $n_{x}$).

Gaussian noise glossed over with moving mean algorithm is used to generate several realizations of complex input permeability domains k(x). The new architecture of the neural network could now be drawn and is shown in Fig. 9.

Fig. 9

Architecture of a bit more complex feed forward network with two dense layers both consisting out of 32 hidden neurons $(n_x:32:32:n_x)$. This model was used for feeding the network permeabilities at each discretized point in the domain while getting the pressure values as an output

To further improve the performance of the network additional convolutional layers are added to the network, see Fig. 10. Convolution operation can be thought as evaluation of permeability change at every point, which act as a derivative analog. This meant that the network could learn from shapes and edges rather then intricately interconnected raw data.

Fig. 10

Architecture of a convolutional neural network (CNN) used with two convolutional layers that triple the channels for feature extraction, two max pooling layers after each convolution for reduction of the amount of neurons by two and two dense layers for loss minimization

5 Results

Once the neural network is constructed it requires to be tested for validation. In this section we will show series of test in 1D and 2D to validate the neural solution method. The results are also compared with numerical solution obtained via finite volume method. Finally, convergence results are also presented as means to validate the neural solutions for 2D cases, where successive refinement of the problem are used to compare neural solution against the numerical solution to demonstrate error convergence.

5.1 1D case

In this subsection the results are presented for a few 1D test cases using the convolutional neural network described in section above for solving the elliptic pressure equation. The test case includes a permeability distribution in 1D described by Gaussian noise. The results generally show a very good agreement between the FVM and NN results, see Fig. 11.

Fig. 11

Permeability distribution with hills and valleys with a corresponding 1-D pressure solution from FVM and NN showing very good correlation. This is an example of a solution at around the mean error value of 0.01

However, there are a few exeptional cases where NN fails to accurately capture the physical pressure solution of FVM, resulting in a somewhat trivial shape with a considerable amount of noise. The worst case error wise is demonstrated in Fig. 12.

Fig. 12

Test case with the highest error where NN has trouble capturing the solution of FVM accurately, due to the strong changes in permeability distribution

Finally, we present some statistics involving training and testing to show that the loss function is minimized and that there only a small number of cases with a relatively larger error between the FVM and NN solutions, see Fig. 14. Out of 5 million trials only a handful of them had “significantly" large loss. After identifying the worst cases, they were analyzed on how were they different from the whole population. It would seem that NN had a difficult time dealing with permeability domains with sharps fronts (see Fig. 13) as well as unexpected deviations from the overall permeability trajectories (highlighted with a circle in Fig. 13). Difficult cases usually also contain a higher number of peaks/valleys (sometimes 5 at a time as in Fig. 13), not only being more likely to create the aforementioned sharp fronts, but also making it considerably more difficult to properly estimate the pressure solution. In these particular cases even FVM produces a somewhat flat pressure line with small deviations, which are hard to pick up by the NN, because of the diminishing error and the vast quantity of simpler cases. This is all speculation based on the observations.

Fig. 13

One of the most difficult permeability domains on which NN produced pressure solutions with higher errors. Sharp front and inconsistencies in value are highlighted with orange circles, where the numbering refers to the amount of peaks/valleys the curve has. These qualities are hypothesized to be something that differentiate poor NN solutions from the well-behaved ones

Fig. 14

a This histogram shows how much of the training samples every bin of squared errors received. The X-axis actually goes up to  0.311 (this highest error pressure solution example presented in Fig. 14), but the frequencies become vanishingly small quite soon. b This graph shows every squared error of every trial. Since most of the errors are clumped at around the 0.005, we see a high density at the bottom of the graph. The red line indicates the level of the errors that are higher

5.2 2D case

The main focus in this section is to observe the ability of CNN to deal with a strong heterogeneity of the domain which is commonly present in real world problems. Since CNN approach produced satisfactory results in 1D case, the work is now carried out to a 2D domain for further investigation. Similarly to 1D case, the following results are achieved by training CNN on the FVM’s generated data on a highly heterogeneous domain made by Gaussian noise and moving-mean algorithms (see Fig. 15).

Fig. 15

A highly heterogeneous permeability space generated by Gaussian noise function coupled with moving-mean algorithm. It somewhat resembles the permeability structure of what can be found in various porous media including Earth subsurface

While these domains are unpredictable, they do have a certain frequency analog to them - a general idea of a number of wave-like structures being repeated across the domain. This is one of the hyper-parameters that can be somewhat controlled while generating such permeability domains. The aforementioned waves have ever-changing amplitudes and even frequencies, which make this problem even more difficult. It is fair to say, that there are more types of domains to be considered in the future, like cracked surfaces, non-circular heterogeneity and layering, however this paper focuses only on high heterogeneity. The permeability domain for a 2D case is set to range from 1 to 10, creating more interesting solutions to showcase.

The first Fig. 16 depicts the overall pressure distribution. In these graphs the main point is to notice that CNN manages to deal with large areas of uniformity in permeability data and understand what overall "color" should the graph undertake. Upper images correspond to FVM solutions and the lower ones are the outputs of CNN, having respective underlying permeability domains. These are more trivial solutions, whereas Fig. 17 depicts how well CNN distributes pressure values along more complicated domains. There is a noticeable correspondence between the FVM solution variation and the analogous shift of colours in the CNN images. This shows the NN ability to replicate finer details on top of aforementioned overall pressure distribution.

Fig. 16

Graph depicting CNN ability to deal with overall distribution of u on a highly heterogeneous permeability domain. a–c Solutions using FVM d–f Solutions using CNN

Fig. 17

Graph depicting CNN ability to deal with some challenging distributions of u on a highly heterogeneous permeability domain. a–c Solutions using FVM d)–f Solutions using CNN

The obvious issue is that the noise contamination is most severe with these cases in its amplitude and the amount. Some stochastic jumps in value break the desired uniformity of the solution as well as the conservation of the flux which can be reduced by implementing smoothing functions. While this approach would decrease the error of the solution, overall it is not desirable as the standard smoothing functions do not take into account the underlying permeability domain. In theory, this could be reduced by implementing deeper network structures and more sophisticated network architectures.

Fig. 18

a This histogram illustrates the density of the 2D training samples at certain MSE values. b This graph shows every MSE value of every 2D trial. The red line indicates the mean MSE value which is at the very bottom of the graph

From the error profile of 2D case it can be seen, that increasing dimensionality of the problem leads to the error histogram being more skewed and its peak considerably skinnier (see Figs. 14a and 18 (a)). These results show that for 1D case it was relatively easier to maintain roughly the same error throughout the possible instances of the problem, whereas, in 2D case it can be observed that there is a clear subsection of cases that have lower error, while the error dispersion is overall higher. These results show that it could be expected that the neural network model may lead to larger error in higher dimensions and might require further improvements to contain the errors.

The mean error is still relatively low and sits at some very low values (see Fig. 14 (b)). Figure 19 shows the solution and spacial error distribution of a case with mean error.

Fig. 19

2D pressure solution from FVM and NN showing a good correlation alongside the corresponding permeability distribution and the absolute error distribution. This is an example of a solution at around the mean of MSE value of 0.00085

5.3 Neural convergence results

Convergence of the NN method can be investigated by solving the same elliptic equation on different refinement grids. This is implemented by generating hundred thousand 32x32, 16x16, 8x8 and 4x4 grid permeabilities and along their FVM solutions by reducing the resolution 2, 4 and 8 fold. The NN model is trained only on the 32x32 grid. Since the network has $32\times 32=1024$ input neurons, the lower resolution permeabilities are augmented to a 32x32 grid by repeating the values in matrix. An example of an augmentation by a double is shown in equation 23.

$$\begin{aligned} \begin{matrix} 1 &{} 2 \\ 3 &{} 4 \end{matrix} \rightarrow \begin{matrix} 1 &{} 1 &{} 2 &{} 2 \\ 1 &{} 1 &{} 2 &{} 2 \\ 3 &{} 3 &{} 4 &{} 4 \\ 3 &{} 3 &{} 4 &{} 4 \end{matrix} \end{aligned}$$

(23)

This way MSE can be calculated on for each 32x32, 16x16, 8x8 and 4x4 cases (now augmented to a 32x32 grid). A log-log graph (see Fig. 20) is produced with two a straight lines - orange depicts an overall trend line, where the green one is only fitted on 16x16, 8x8 and 4x4 permeability grids. This is because 32x32 case will always have a significantly lower error as the network was trained on it. Figure 20 shows that error is reducing with refinement and that NN method is working, which builds confidence in the scheme.

Fig. 20

Convergence graph for the 2D NN solutions

6 Comparative analysis

6.1 Computational efficiency

While it is true, that in a reservoir simulation context, the pressure equation is usually coupled to the saturation/component concentration equation (which is then solved at each time step), the focus of this paper is on the solution of the pressure step, as it takes large computational effort, from numerical solution point of view. Solving coupled system, pressure and saturation, is most certainly to be investigated in future work. Although the neural network constructed in this research work focuses on simplicity and scalability, it will be further improved to handle more challenging cases in future research work.

Other researchers have also worked on solving Darcy flow problem using neural networks [6]. Their methodology uses a special network architecture like residual layers that are enhanced with Fourier transformations and point-wise convolutions to obtain a resolution invariant method. This allows any arbitrarily sized image to be processed by the neural network, making the neural methodology much less task specific.

Exploring the sensitivity of computational efficiency concerning the number of layers and grid blocks is important, because our neural network’s architecture actually varies depending on the resolution. For example, cases presented here use at most $32\times 32=1024$ grid blocks requiring 1024 neurons as input, whereas practical models usually comprise of resolution in the order of $128\times 128$ and would require 16 times more neurons. We address computational efficiency of our method in this paper by including a simple study of comparative computation time with a traditional FVM done. FVM has a lot of different implementations, which could impact its computational efficiency, in this paper we have used the FVM implementation presented in [8]. Lot of factors can effect the efficiency like simple choice of programming language, libraries used and the programming competence of the authors themselves. Other factors, which may also impact computational efficiency include CPU parameters versus GPU, since the neural network could be trained using GPU, but not parallelized, where as for FVM - it is other way around. In this comparative analysis we have used a computer with Intel(R) Core(TM) i9-10900KF CPU @ 3.70GHz 3.70 GHz.

Fig. 21

A bar plot concerned with the computation time comparison between FVM and CNN methods across different problem grid sizes

Figure  21 illustrates that with the number of grid cells increase, the computation time for both methods becomes exponentially more expensive. It is worth noting that when using smaller grids, the FVM is actually faster than the suggested neural network, however, it is not the case with larger problems, where CNN outperforms FVM in terms of time efficiency Fig.  22.

Fig. 22

A plot concerned with the training time of CNN with different problem grid node counts. Blue dots are the actual measured data, whereas orange curve is a fitted line to better visualise the exponential growth in training times required by the neural operator

Figure  21 presents all information related to network training times across varying grid sizes. So it happens, that bigger networks are able to produce much better results at the cost of being large and hard to train, whereas smaller networks reach their accuracy limit swiftly and stops improving soon after. To give all networks a fair chance to compete timewise, the results provided in Fig. 21 are gathered by training each network until their error does not decrease after 100 iterations since the last minimum error value. This means, that the data presented in Fig. 21 is not of the networks that would produce the best results, as those provided in Sect. 5, but such that they could be comparable to one another. Results shown in Fig. 21 show that as the number of domain nodes grows, the computational resources needed for CNN training increase exponentially.

6.2 Comparison with analytical solution

When demonstrating the convergence of the method, MPFA numerical result were used as an approximation for the analytical solution. As to compensate for that, we provide a homogeneous domain case, where the analytical solution in 2D is known to be linear. A comparison between the exactly computed analytical solution and CNN is provided in Fig. 23.

Fig. 23

CNN comparison with analytical solutions on homogeneous domain

Analytical comparison shows that the neural network mostly produces very accurate results, however, nearing permeability boundary values 1 and 50, the errors tended to accumulate. The rightmost orange part is quite commonly observed in neural network training, when the network lacks the knowledge about what is happening with never seen input values. For example, at early stage of training a fully connected network to learn a simple sin(x) function in range $[0,2\pi ]$, it will usually be more neglectful towards the ends of the interval. After $2\pi$ the values diverge from sine function as does the CNN with the permeability values it never seen. Some challenges are seen in analytical comparison for lower homogeneous permeability value, corresponding to the leftmost right part of the curve in Fig. 23. Analytical results show that it is unusually hard for the neural network to deal with relatively small permeability values closer to sources and sinks. Relatively low means both low in accordance to its surroundings as well as in the working interval [1, 50]. We hypothesize this, because relatively permeability values about sources and sinks are responsible for creating solutions addressed in subsection 5.2 in Fig. 16. Even though the CNN manages to occasionally train on such data (and produce pretty consistent and accurate results), it seems that in homogeneous domain at relatively low permeability makes this fault very noticeable. This requires further investigation and will be addressed in upcoming research, as it is only a hypothesis.

6.3 Anisotropy

As mentioned in the beginning of this paper, MPFA methods leads to oscillatory outcomes in scenarios where the anisotropy is particularly pronounced. The primary focus of this paper, however, is to work with highly heterogeneous porous domains and to maintain its purity with regards to this aspect only, so there was no rush to introduce other aggravating specifics as anisotropy. nevertheless, this remains a highly relevant issue, which has been quite extensively tackled in a recently published paper [20]. Their findings demonstrate that neural networks, in general, have a tendency to evade oscillatory behavior, which is one of the motivations behind utilizing such NN methods.

7 Summary

In this paper the details of constructing a Neural Network for tackling elliptic pressure equation for single-phase flow in porous media with discontinuous coefficients is presented, refereed to as Neural operator for elliptic PDE. Firstly, numerical solution to elliptic pressure equation with discontinuous coefficients is presented using standard two-point (TFPA) and multi-point flux (MPFA) approaches. Pros and cons of each of the approach is discussed. Numerical solutions are used to generated training data sets for Neural Network approach proposed in the paper. Next an approach is presented where the Neural operator network is developed using a Convolutional Neural Network with hidden layers, and is trained using back-propagation using the training data-set generated from numerical approaches. Most results are good and are obtained for simpler cases where as for some more complex rare cases - network fails to generate satisfactory solutions. Paper also presents a number of one and two dimensional cases using the Neural solutions for a range of elliptic PDE problems with discontinuous coefficients. Series of tests are performed on cases involving varying degree of fine scale permeability heterogeneity. Mean square error is used to optimize network performance with a help of a large training data-set comprising of over 5 million realizations of permeability and pressure distribution in one and two dimensions. Finally, convergence results are also presented where error between neural solution and numerical solution method is compared for successive refinements. It can be concluded from the results presented in this paper that CNN based neural networks are capable of solving simple to complex problems involving elliptic pressure equation with discontinuous coefficients.