Probabilistic medical image imputation via deep adversarial learning

Abstract

The ability to impute missing images from a sequence of medical images plays an important role in enabling the detection, diagnosis and treatment of disease. Motivated by this, in this manuscript we propose a novel, probabilistic deep-learning algorithm for imputing images. Within this approach, given a sequence of contrast enhanced CT images, we train a generative adversarial network (GAN) to learn the underlying probabilistic relation between these images. Thereafter, given all but one member from a sequence, we infer the probability distribution of the missing image using Bayesian inference. We make the inference problem computationally tractable by mapping it to the low-dimensional latent space of the GAN. Thereafter, we use Markov Chain Monte Carlo (MCMC) techniques to learn and sample the inferred distribution. Moreover, we propose a novel style loss unique to contrast-enhanced computed tomography (CECT) imaging to improve the texture of the generated images, and apply these techniques to infer missing CECT images of renal masses collected during an IRB-approved retrospective study. In doing so, we demonstrate how the ability to infer the probability distribution of the missing image, as opposed to a single image recovery, can be used by the end-user to quantify the reliability of the imputed results.

1 Introduction

Medical image data acquired from ultrasound, X-rays (CT), MR and other types of imaging modalities is routinely used in detecting, diagnosing and planning treatment for myriad diseases. The problem of missing data is ubiquitous in medical imaging. Missing image data can be in the form of missing images in a sequence of images, missing regions within a single image, or artifacts like blurring, which degrade the image significantly. In all these cases, missing data leads to the loss in utility of the images, and an accompanying loss in the accuracy of detection, diagnosis, and treatment planning for a disease.

Missing or lost data can be attributed to many reasons. In some cases patients may be initially scanned under one protocol, while the final management of the disease might require additional, or more thorough, scans. However, this may not be feasible due to the patient’s inability to tolerate additional scans, logistical issues such as visits to a tertiary care center, and restrictions imposed by the insurance provider. In addition to this, the authors in [1] refer to missing image data as the “leaky” radiological pipeline, and lament the fact that the transition from analog to digital imaging and the advent of standards like PACS and DICOM has not eliminated this problem. They point to several causes for missing image data that include incompatibility between different vendors of medical imaging equipment, saturation of the bandwidth of a device, and collateral damage during events like server errors. In all these cases, a portion of image data is missing which renders useless the portion that is collected, or diminishes its value.

Image imputation refers to the task of recovering the missing/corrupted part of an image from the part that is available/not corrupted. This task has typically relied on problem-specific computer vision algorithms. In contrast, the advent of new deep learning algorithms has made it possible to develop techniques that could work well across a wide range of image imputation tasks [2, 3]. Further, by relying on statistical versions of these techniques, it is possible to not only impute the missing image data, but also provide quantitative measures of confidence in the imputed solution. This additional information can allow the clinician to make an informed decision about how much to trust the imputed data when making their final decision. This principle, that is, using novel statistical deep learning techniques to impute imaging data, and to provide a measure of confidence in the imputation, forms the main thrust of work described in this manuscript. While the techniques developed in this manuscript can be applied to a wide range of image imputation tasks, we focus on the task of imputing missing contrast enhanced CT (CECT) images of renal tumors.

Over 90% of renal tumors are asymptomatic and are identified incidentally in 27–50% of all patients that are imaged. While all imaging modalities have their strengths and limitations, the widespread use of CECT imaging has lead to the increased detection of kidney cancers. CECT images are generated by injecting an intravenous contrast agent into the subject and then imaging during four distinct time-points. These are the pre-contrast, corticomedullary, nephrographic, and excretory time-points. The four phases correspond to different phases in the enhancement and therefore characterize the masses with reference to their vascularity (quantity of neovascularity), and washout (quality of the neovascularity). Tumor vasculature (tumor neoangiogenesis) is characterized by disorganized branching and shunting and various degrees of leakiness. When a radiologist assesses these, they are looking at both in relation to the adjacent normal tissue. In addition, a qualitative diagnosis of the tumor is often based on the combination of analyzing different tissue densities, change in density, vascularity and washout, and its margins with adjacent normal tissue. Therefore, a conventional diagnosis on whether a tumor is benign or malignant is based on the qualitative visual inspection of the four CECT phase images. More recently, techniques such as radiomics or machine learning that rely on quantitative evaluation of these images, are also being considered for this task. Further, once a decision has been made to treat or resect the renal mass, these images are used by the surgeon to plan the surgery. The results presented in this present study are an initial attempt to recover missing images. In future studies, these will be evaluated to determine whether they reveal the diagnostic markers that radiologists are looking for.

The loss of any one or more CECT phase images due to any of the reasons discussed above negatively impacts the management of renal masses. It leads to less accurate diagnosis of malignant masses and adversely effects surgical planning in cases where surgical intervention is necessary. According to [4] images from at least three CECT phases are required to characterize a renal mass. We note that the problem of missing CECT images is significant. For example, from 2011 to 2017 the Keck school Medicine at USC curated CECT images from 735 patients. However, out of these, images for all four phases are available for only 453 patients. That is for  40% of the patients at least one image is missing. Given that Keck school is a tertiary care center, the proportion of missing images is small. For other smaller/secondary centers this percentage is substantially higher.

In this manuscript, we address the problem of imputing missing CECT images by developing a statistical deep-learning based technique. Our technique uses the information encoded in a set of complete CECT images (a set that includes all four time-points) to train a generative adversarial network (GAN) [5], whose generator learns this distribution, and can be used to efficiently sample from it. This generator is then used to represent the prior in a Bayesian inference problem, whose goal is to infer the distribution of the CECT image corresponding to a missing time-point, given the CECT images at all other time-points. Using the GAN allows us to encode the complex information available through the sample set as a prior in the inference problem. It also allows us to formulate the inference problem in the latent space of the GAN, whose dimension is much smaller than that of the image itself. This dimension reduction in turn allows us to use methods like Markov Chain Monte Carlo (MCMC) [6] to efficiently sample from the posterior distribution. Once the MCMC chain attains its equilibrium, it is used to compute the desired statistics of the posterior distribution for the missing image. This includes quantities such as the most likely image, and the pixel-wise mean and standard deviation. We note that statistics like standard deviation provide a quantitative measure of the uncertainty in the prediction, and may be used to determine the confidence in the prediction.

We are not aware of any prior work that attempts to impute missing images within a sequence of CECT images acquired at different time-points. However, in the broader field of medical image imputation, there is significant work that has demonstrated effectiveness of modern machine learning algorithms for different imaging modalities [2, 3, 7, 8]. There are also several applications that utilize image-to-image algorithms that are inspired by GANs. These include algorithms like the CycleGAN, StarGAN and CollaGAN [9,10,11]. In most instances these algorithms are utilized in applications where medical images from a given domain (say T1 or T2 MR images) are translated to another domain (say FLAIR image). We note that these algorithms are significantly different from the one described in this paper, since for a given input image they produce a single output image. More specifically, they do not solve a statistical inference problem and therefore are not able to quantify the distribution of likely answers.

Recently, Wasserstein GANs have shown promise in efficiently solving statistical inference problems in physics and computer vision [12, 13]. This work builds upon those ideas and applies them to real-world medical applications. More recently, the augmented CycleGAN architecture has also been used to accomplish this task, however to our knowledge this approach has not been applied to imputing medical images [14]. Indeed, its application to the problem described in this manuscript will be an interesting area for future work.

The format of the remainder of this manuscript is as follows. In Sect. 2, we describe the new image imputation algorithm and the two candidate GAN architectures that are used in this study. The code and dataset are available online¹. In Sect. 3, we apply this algorithm to generate missing CECT images for four subjects across four different time-points and validate its performance. This includes qualitative comparison with the true images, and quantitative comparison of metrics associated with the texture of the images. It also includes an analysis of the uncertainty predicted by the algorithm and a demonstration of how it may be used in clinical practise. We end with conclusions in Sect. 4.

2 Methods

2.1 Overall algorithm

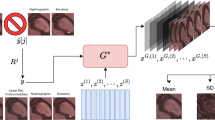
Let $x_i \in \Omega _{x_i} \subset {\mathbb {R}}^{N_x}, i=1,\ldots ,4$, denote CECT images, each with $N_x$ pixels, corresponding to the four distinct time points. Let $x = [x_1, x_2,x_3,x_4]$, be a composite image that includes images from all four time-points. Further, let ${\mathcal {S}} \equiv \{x^{(1)}, \ldots , x^{(N)} \}$, be a collection of N such composite images. These samples are drawn from an underlying distribution $p_X$, which is assumed unknown.

In the first stage of our algorithm (see Fig. 1), the set ${\mathcal {S}}$ is used to train the generator G of a Wasserstein GAN (WGAN) [15, 16] which maps a $N_z-$dimensional latent space vector $z\in \Omega _z \subset {\mathbb {R}}^{N_z}$ to x. The dimension of the latent space $N_z \ll N_x$, and the samples z are drawn from an uncorrelated Gaussian distribution ($p_Z$) with zero mean a unit variance.

For a fully trained WGAN with infinite capacity the push-forward of $p_Z$ by G is weakly equivalent to $p_X$. That is for any continuous, bounded function l(x),

$$\begin{aligned} \mathbb {E}_{x \sim p_X}[l(x)] = \mathbb {E}_{z \sim p_Z}[l(G(z))], \end{aligned}$$

(1)

which implies that all moment-based statistics, such as the mean and variance, will be equal. Thus, sampling x from $p_X$ is (statistically) equivalent to sampling z from $p_Z$ and passing each sample through the fully-trained generator. We will use this relation later in this section.

Next, consider the restriction operator $R_i(x)$, which acts on x and deletes the CECT image corresponding to the $i-$th time-point. We assume that we observe a noisy version of this restricted set of images. That is, we observe,

$$\begin{aligned} y = R_i(x) + \eta , \end{aligned}$$

(2)

where $\eta \sim p_\eta$ is assumed to be an uncorrelated Gaussian with zero mean and variance $\sigma$. The problem we wish to solve is: given this noisy, restricted version of the CECT image sequence, and the prior knowledge encoded in the set ${\mathcal {S}}$, determine the CECT image corresponding to the missing time-point i.

To solve this problem we rely on Bayesian inference, which provides a suitable framework to solve ill-posed (inverse) problems and quantifying the underlying uncertainty [17]. We proceed by first defining a prior distribution $p_\mathrm{prior}$ for the field x to be inferred, before making the measurement/observation y. This distribution is typically constructed based on domain knowledge, snapshots and/or known constraints on x. Next, the restriction operator $R_i$ is used in conjunction with the measurement noise to define the likelihood distribution $p_{Y\mid X}(y\mid x):= p_\eta (y-R_i(x))$. This distribution captures the inherent uncertainty and loss of information in the measurement about the inferred field. Finally, we use Bayes’ rule to obtain an expression for the posterior probability of the composite image x, given the measurement y

$$\begin{aligned} p_{X \mid Y}(x \mid y)=\,\, & {} p_{Y \mid X}(y \mid x) p_\mathrm{prior}(x)/{\mathbb {Z}} \nonumber \\=\,\, & {} p_\eta ( y - R_i(x) ) p_X(x) / {\mathbb {Z}}, \end{aligned}$$

(3)

where ${\mathbb {Z}}$ is the evidence term which ensures that the integral of the the probability density is unity.

There are two fundamental challenges in using this formula to infer the posterior distribution $p_{X \mid Y}$. (1) The dimension of x is large and therefore methods like MCMC cannot be easily used to learn the posterior distribution. For example, in the problems studied in Sect. 3, this dimension is $4 \times 100 \times 100 = 40,000$ and most existing MCMC methods work well only for dimension of ${\mathcal {O}}(100)$. (2) $p_X$ is not known explicitly; rather it is known only through the set ${\mathcal {S}}$. Thus it is difficult to construct a prior distribution that captures this information. We address these challenges using the set ${\mathcal {S}}$ to train a WGAN and mapping the expression for the posterior to the latent space of the WGAN. We accomplish this below by utilizing (1) and (3).

The expectation of any continuous bounded function l(x) over the posterior density is given by

$$\begin{aligned} \mathbb {E}_{x \sim p_{X \mid Y}}[l(x)]=\,\, & {} \mathbb {E}_{x \sim p_{X}}[l(x) p_\eta ( y - R_i(x) ) / {\mathbb {Z}} ] \nonumber \\=\,\, & {} \mathbb {E}_{x \sim p_{X}}[m(x)] \nonumber \\=\,\, & {} \mathbb {E}_{z \sim p_{Z}}[m(G(z))] \nonumber \\=\,\, & {} \mathbb {E}_{z \sim p_{Z}}[l(G(z)) p_\eta ( y - R_i(G(z)) ) / {\mathbb {Z}} ] \nonumber \\=\,\, & {} \mathbb {E}_{z \sim p_{Z \mid Y}}[l(G(z))]. \end{aligned}$$

(4)

In the first line of the equation above, we have used the definition of $p_{X \mid Y}$ (3). The second line follows by defining $m(x) \equiv l(x) p_\eta ( y - R_i(x) ) / {\mathbb {Z}}$. The third line follows from the weak equivalence statement for a WGAN (1). The fourth line follows from the definition of m(x). The fifth line makes use of the definition of the posterior density in the latent space, that is,

$$\begin{aligned} p_{Z \mid Y}(z \mid y)\equiv & {} p_\eta ( y - R_i(G(z)) ) p_Z(z) / {\mathbb {Z}}. \end{aligned}$$

(5)

Equating the left hand side and the final expression on the right hand side of (4), we have

$$\begin{aligned} \mathbb {E}_{x \sim p_{X \mid Y}}[l(x)] = \mathbb {E}_{z \sim p_{Z \mid Y}}[l(G(z))]. \end{aligned}$$

(6)

Here $p_{Z \mid Y}$ is the posterior distribution in the latent space of the WGAN and is given by (5).

The pair of equations (5) and (6) allow us to compute statistics of the posterior distribution in a computationally tractable way. We use the expression in (5) to train a MCMC algorithm whose stationary point yields samples that are drawn from an approximation of $p_{Z \mid Y}$. This constitutes the second stage of our algorithm, and is described in some detail in “Appendix A”. Once this is done, we use (6) to approximate any statistic of the posterior using the samples from the Markov chain trained in Stage 2. That is,

$$\begin{aligned} \mathbb {E}_{x \sim p_{X \mid Y}}[l(x)] \approx \frac{1}{N_\mathrm{samp}} \sum _{i = 1}^{N_\mathrm{samp}} l(G(z)). \end{aligned}$$

(7)

This is the third and final stage of our algorithm. The overall algorithm is depicted pictorially in Fig. 1.

Fig. 1

Schematic diagram of algorithm

2.2 Enhancements to the WGAN

A unique characteristic of CECT images is the presence of fine-scale features which cannot be captured simply by training the WGAN model using standard adversarial loss. Since this fine-scale structure is crucial in making important diagnostic decisions, it is desirable to have a model which can learn these features. For this, we propose a novel style-based loss in addition to standard adversarial loss for learning the true prior density. Similar to previous works on deep style transfer and texture synthesis [18,19,20] we propose to use a Gramm matrix-based style loss. However, unlike these works, we do not rely on a pre-trained classification network (VGG-16) to build the Gramm matrix. Instead we rely on the features extracted from certain layers of the discriminator (or critic) D of the GAN to build the Gramm matrix. In other words, the discriminator serves the dual purpose of a critic for real versus fake image classification and a feature extractor for style transfer.

Specifically, we define the Gramm matrix as ${{\mathcal {G}}_{ij}}^l = \sum _{k} {{\mathcal {F}}_{ik}}^l{{\mathcal {F}}_{jk}}^l$, where ${\mathcal {F}_{ik}}^l$ is the activation of $i^\mathrm{th}$ filter in layer l of the discriminator at location j. We then define the style loss by minimizing the Gramm matrices of a batch of real and fake samples.

$$\begin{aligned} {\mathcal {L}}_\mathrm{style} = \sum _{l=1}^{b} \lambda _l \mid {{\mathcal {G}}_{ij}}^l \mathrm{(real)} - {{\mathcal {G}}_{ij}}^l \mathrm{(fake)}\mid ^2 \end{aligned}$$

(8)

where $\lambda _l$ is the relative weight of style loss for each layer. We use the first 3 layers to compute the style loss ($b=3$) with $\lambda _l$=10. The total loss is the sum of adversarial and style losses. Finally, to introduce the very fine-scale speckle pattern seen in the training data, we adapt recent ideas from state-of-the-art StyleGAN architectures [21] and inject a fixed amount of Gaussian noise (with zero mean and identity covariance matrix) in the final layer of the generator. We refer to the WGAN with style loss and noise as the ”enhanced” formulation. The architecture of the WGAN used in this work is described in “Appendix B”.

3 Results and discussion

3.1 CECT image data

The patient population includes renal masses diagnosed on abdominal CECT scans with pathological diagnoses confirmed after resection at our institution. Patients were identified by retrospective query of a prospectively maintained surgical database of consecutive radical or partial nephrectomies between May 2007 and September 2018. Pathologic evaluation was performed by specialized genitourinary pathologists. Patients with no evaluable preoperative imaging a year prior to nephrectomy were excluded. Only patients with all 4 time-points of the CECT study were included. Our final data cohort included 372 patients. For further details on the cohort the reader is referred to our prior publications [22, 23] in which a subset of these images was used for classifying malignant lesions.

Three-dimensional regions of interest of the renal masses were manually segmented by two senior radiologists using Synapse 3D software (Fujifilm, Lexington, MA). Images were coregistered by using the normalized mutual information cost function implemented in the Statistical Parametric Mapping software package (Wellcome Centre for Human Neuroimaging). Tessellated 3-D models of the tumor were created from segmented voxels using a custom MATLAB (MathWorks) code. From this registered volume of CECT images at multiple time-points, scans containing the largest axial cross-section of the tumor volume were extracted and used to train the WGAN as described below.

We remark that each institution has different protocols, with the measurement of three-four phases being the most common. However, one of the phases may be missing or be technically inadequate, for instance due to patient motion (happens 3–5% of times). In addition, depending on where and how the scan was performed, the scan may be obtained in mid-phase. In the present study, we work with a four phase setup and assume one of the phases is missing. In a follow up study, we will look at additional missing phases or nonstandard phases, and how our methodology can be extended to work in such a scenario.

CT images in our dataset are created using the Hounsfield units, which are a non-dimensional measure of the attenuation coefficient of a tissue relative to water. A Hounsfield unit of 0 corresponds to water, while fat has a value of around − 100 and cancellous bone of around 350. To present the GAN with normalized data, we have converted images from this scale to another scale which varies between − 1 and + 1 through a linear transformation. In this scale − 1 corresponds to − 200 Hounsfield units and + 1 corresponds to 300 Hounsfield units. Any values outside this range are clipped to − 1 and + 1 respectively.

Each image has a dimension of $100 \times 100$, with a scale of 0.9765 mm per pixel in the horizontal and vertical directions. Given that it takes at least 5-6 pixels to resolve any feature, the proposed method can be expected to work on renal masses of size between 0.5 and 9.8 cm.

3.2 Results of image imputation

Using the set of images described above, we train a Wasserstein GAN with Gradient Penalty (WGAN) [16], to learn the underlying distribution of the composite images. The dimension of the latent space of the WGAN is 100, which is a factor of 400 smaller than the dimension of the composite image. The architecture of the WGAN is described in “Appendix B”.

We use the trained WGAN to recover missing CECT images. We select a sequence of CECT images for a subject not included in the training set, and delete the image corresponding to one of the four time-points. Then using the algorithm described in Sect. 2 and depicted in Fig. 1, we generate a Markov chain to sample from the approximate posterior density. As described in “Appendix A”, the length of the chain is suitably chosen to ensure that is has sufficiently converged and is well-mixed. Using the samples in the Markov chain, we infer important posterior statistics about the missing image. These include (a) the most likely guess of the missing image, that is the maximum a-posteriori (MAP) estimate, (b) the pixel-wise mean of the image, and (c) the pixel-wise standard deviation (SD). This process is repeated for each of the four time-points, and then for four different subjects. The subjects are chosen such that the corresponding renal tumors represent the observed diversity in the size and shape of the tumor.

Fig. 2

True images, imputed images and their statistics for Subject 1

Fig. 3

True images, imputed images and their statistics for Subject 2

Fig. 4

True images, imputed images and their statistics for Subject 3

Fig. 5

True images, imputed images and their statistics for Subject 4

The results of the image imputation algorithm are shown in Figs. 2, 3, 4 and 5, where each figure corresponds to one of the four subjects. In each figure, the columns represent the four time-points of the CECT images. The first row contains the true images, while the other rows contain the results of the image imputation algorithms. In these rows, the images in the first column are obtained by assuming that the true image for the pre-contrast time-point is missing and needs to be imputed, while those for all the other time-points are available. Similarly, images in the second/third/fourth column are obtained assuming that the true images for the corticomedullary/nephrographic/excretory time-points are to be imputed by making use of the images at other time-points. Thus each figure captures the ability of the algorithm to impute images for the four distinct CECT time-points. In the second and third rows of Figs. 2 , 3, 4 and 5 we have shown the MAP estimate (the best guess of the imputed image) produced using the standard WGAN algorithm and the enhanced WGAN algorithm, respectively. In the fourth row we have shown the pixel-wise standard deviations evaluated using the enhanced WGAN. In “Appendix A” we have described our approach of ensuring that the MCMC results have converged.

There are several observations to be made here. The MAP estimate from both the standard and enhanced WGAN correctly predict the changes in the overall intensity across the different time-points. That is, the time-points in the order of increasing intensity are: pre-contrast, nephrographic, corticomedullary and excretory. Both the MAP estimates also correctly recognize that the segmented shape of the tumor does not change from one time-point to another.

The texture produced by the standard WGAN is not consistent with the texture observed in the true images. In particular, we observe swirling patterns of brightness in the images imputed using the standard WGAN, that are absent from the true images. Further, the true images contain pixel-to-pixel variations in intensity that are also not seen in the images using the standard WGAN. On the other hand, the enhanced WGAN (enhanced by style loss and noise) displays a texture that is much closer to that of the true images.

3.3 Validation of the texture of the imputed images

Assessing the difference between the texture of true and imputed images visually is difficult, and is subject to inter-observer variability and bias. Statistical methods of assessing texture that consider the spatial relationship of pixels within a given neighborhood are well suited for this task. Among these, the neighborhood-based texture assessment techniques that include the grey-level co-occurrence matrix (GLCM), grey-level difference matrix (GLDM), grey-level run-length matrix (GLRLM) and grey-level size zone matrix (GLSZM), are popular [24]. Each of these matrices are obtained by transforming the original image, so as to highlight some of its texture-based features. GLCM is sensitive to how combinations of discretised grey-levels of neighbouring pixels are distributed along different image directions. GLDM is similar to GLCM, however it works with differences in grey-levels rather than the grey-levels themselves. Like the GLCM, GLRLM is also sensitive to the distribution of discretised grey-levels in an image. However, whereas GLCM is sensitive to the occurrence of the same grey-levels within neighbouring pixels, GLRLM is sensitive to run lengths. A run length is defined as the length of a consecutive sequence of pixels with the same grey-level along a given direction. The grey-level size zone matrix (GLSZM) contains a count of the number of zones of linked pixels. Pixels are defined as ”linked” when the neighbouring pixel has the identical discretised grey-level value.

Once these matrices are computed we may compute scalar metrics that highlight their degree of heterogeneity. For this purpose, in this study we compute the entropy of these matrices. That is

$$\begin{aligned} H(X) = - \sum _{i} \rho _X(i) \log _2(\rho _X(i)), \end{aligned}$$

(9)

where X denotes an image or its corresponding grey-level matrix, and $\rho _X(i)$ is the probability of attaining the intensity i at any pixel.

In Fig. 6 we have shown the normalized difference in entropy between features derived from true and imputed images. In this figure, each bar represents the mean value of this difference over the 16 images, and the whiskers represent the standard deviation. Further, ”HIST” refers to the entropy of the original images (imputed and true) before applying any transformations, and the other labels refer to the four matrices described above. In each case, except HIST, the difference in the average entropy of the imputed and true images is smaller for the enhanced WGAN formulation when compared with the standard WGAN. Further, we evaluated the mean (± std. dev.) SSIM metric across all 4 patients and all 4 phases as, Standard GAN: $0.6961 \pm 0.1287$, and Enhanced GAN: $0.7496 \pm 0.1763$, which is clearly higher for the enhanced GAN. This validates the improved visual quality of this formulation observed in Figs. 2, 3, 4 and 5.

Fig. 6

Normalized difference in the entropic metrics for the true and imputed images for 4 subjects across 4 time-points

3.4 Utility of estimating standard deviation

One of the advantages of the method described in this paper is ability to produce multiple samples drawn from the posterior distribution, instead of producing just a single, most likely sample. These samples can be used to compute statistics that shed light on the quality of the imputed image. To highlight this, in each of the Figs. 2, 3, 4 and 5, we have also plotted the estimated pixel-wise standard deviation in the imputed images. These images provide us with a spatial map of the degree of uncertainty in the imputed results. When observing these images a few things stand out. First, the standard deviation, and therefore the uncertainty is largest at the tumor boundaries indicating that the location of the tumor boundary in the imputed image may be incorrect by about 1–2 pixels. Second, the standard deviation, and hence the uncertainty is largest for the nephrographic time-point, followed by the corticomedullary, the excretory and the pre-contrast time-points.

Fig. 7

Average estimated standard deviation versus the normalized $L_2$ error for the standard and enhanced WGAN formulations. Subject 1, $\bigcirc$; Subject 2, $\square$; Subject 3, $\star$; Subject 4, $\diamond$. Standard GAN, Red; Enhanced GAN, Blue

It is of interest to determine how the standard deviation computed by our algorithm correlates with true error of the most likely (MAP) imputed image. If the two are found to be positively correlated, we may use the standard deviation as a measure of the error in the MAP of the imputed image, and therefore provide the end-user of the algorithm with an estimate of the likely error. This correlation is examined in Fig. 7, where we have plotted the normalized $l_2$ error versus the average (over all pixels) of the computed standard deviation for each of the 16 images (4 subjects across four time-points). We have done this for the both the standard and the enhanced WGAN formulations. In both cases, we observe a positive correlation between the standard deviation and the normalized error. For the standard formulation the correlation coefficient is 0.79, while for the enhanced formulation it is 0.62. We believe that this positive correlation will be useful in estimating the reliability of imputed images when the proposed approach is applied in a clinical setting.

4 Conclusion

In this manuscript we have developed a method for imputing missing medical images that utilizes a WGAN to represent the prior distribution in Bayesian inference, and have applied it for imputing missing CECT images of renal masses. We have also developed a novel architecture for the generator of the WGAN which is driven by a style loss and Gaussian noise to accurately model the fine-scale features of the CECT images. A distinguishing feature of our method is its ability to learn the entire distribution of missing images and to sample from this distribution. This allows us to compute statistics like pixel-wise standard deviation in addition to the most likely guess for the missing image. We have shown that these statistics can be used to quantify the uncertainty in the imputed images, and provide the end-user quantitative estimates of the reliability of the proposed algorithm.

Appendices

Appendix A Convergence of MCMC algorithm

MCMC algorithms are known to suffer from challenges when used in high-dimensional spaces, where the mass of the target density is typically concentrated in narrow regions on a lower dimensional manifold [25]. To fully explore the regions of interest, the requirements on the length of the Markov chains [26] can make the algorithm computationally infeasible. Thus, posing the inference problem on the lower-dimensional latent space can alleviate this issue.

A number of diagnostic tools are available to analyse the convergence of the MCMC algorithm, and thus determine the termination length of the generated Markov chains. We direct interested readers to [27] for a summary of such techniques. In the present work, we use the Gelman-Rubin diagnostic [28] which estimates the convergence by considering multiple Markov chains and evaluating the between-chains and within-chains variances.

We consider M chains of length N, each of which is generated by the MCMC algorithm from different random initial points. Let $\mu _m$ and $\sigma _m^2$ denote the sample mean and variance of the mth chain, and $\mu$ denote the overall mean across all chains, i.e., $\mu = \sum _{m=1}^M \mu _m/M$. Then, we estimate the within-chain variance W, the between-chain variance B and the pooled variance $\widehat{V}$ as

$$\begin{aligned} \begin{aligned} W&= \frac{1}{M} \sum _{m=1}^M \sigma _m^2, \quad B = \frac{N}{M-1}\sum _{m=1}^M(\mu _m - \mu )^2,\\ \widehat{V}&= \frac{N-1}{N} W + \frac{B}{N}. \end{aligned} \end{aligned}$$

(A1)

Finally, we evaluate the potential scale reduction factor $\widehat{R} = \sqrt{\widehat{V}/W}$. Assuming that the initial points of the chains were sampled from an over-dispersed distribution compared to the target distribution, $\widehat{V}$ is expected to overestimate the variance of the target distribution, while W underestimates it. Thus, the closer that value of $\widehat{R}$ is to 1, the more assured we are about the convergence of the chains.

To demonstrate the utility of this tool, we consider the chains generated to impute the missing images at the 4 time-points for Subject 1. At each time-point, we use $M=4$ chains for each of the lengths N = 256 K, 512 K, 1024 K. Since the chains are generated for latent variable $z \in {\mathbb {R}}^{N_z}$, we obtain a vector $\widehat{R} \in {\mathbb {R}}^{N_z}$ for each configuration. To simplify the analysis, we condense this vector to a scalar by considering the dimensional mean ± standard deviation of $\widehat{R}$, which is listed in Table 1. Note that these scalar value moves closer to 1 as N increases, indicating convergence. In practice, a value of $\widehat{R} < 1.2$ is considered as a good termination threshold. To balance the convergence of the chains and the associated computational cost, we use $N=1024$ K for all results presented in this work.

Table 1 $\widehat{R}$ values of Markov chains in z used to impute the images at the four time-points for Subject 1

Appendix B Architecture and hyper-parameters

Table 2 Generator architecture

Table 3 Discriminator architecture

We use the axial slice of the 3000 CECT images for training. The WGAN-GP models, whose architectures are described in Tables 2 and 3, are trained with the gradient penalty parameter set to 10. We use the ADAM optimizer with learning rate of $2 \times 10^{-4}$ and momentum parameters $\beta _1 = 0.0, \beta _2 = 0.9$. We perform 5 gradient updates of critic per gradient update of generator and train both networks in TensorFlow with a batch size of 64. For posterior inference we sample Markov chain using Hamiltonian Monte Carlo (HMC) with No-U Turn Sampler (NUTS) [29] and implement it in TensorFlow Probability [30]. We use initial step size of 1.0 for HMC and adapt it following [31] based on the target acceptance probability. A burn-in period of 50% is used for all HMC simulations. These hyper-parameters are chosen to ensure the convergence of the chains.