1 Introduction

The surfactant is an organic chemical material which consists of a hydrophobic tail and a hydrophilic head. This special structure of the surfactant leads to the high concentration of surfactant on two-phase interface. In our daily life, the soap and liquid detergent are common surfactant. In industrial fields, the surfactant is usually used to control the interfacial dynamics because the existence of surfactant will affect the surface tension. To construct mathematical models of two-phase surfactant system, the volume-of-fluid [1], level-set [2, 3], and immersed boundary methods [4, 5] have been considered by many researchers. In actual physical problems, the topological changes of interface, such as coalescence and separation, are very common. To naturally capture the interfacial changes, the phase-field method is a good way.

The well-known pioneering research of phase-field surfactant model can be traced back to Laradji et al. [6], where the authors used two phase-field functions to represent the surfactant and two-phase fluids. This famous model belongs to a Cahn–Hilliard (CH)-type model which consists of two fourth-order nonlinear partial differential equations (PDE), a main advantage of CH type phase-field model is the property of mass conservation. Because of this property, the CH model has been extensively applied in incompressible two-phase flow simulations [7,8,9,10,11]. Based on the CH type binary surfactant model, Kim [12] performed the simulations using a Crank–Nicolson temporal discretization. Gu et al. [13] developed an energy stable time-marching scheme using the well-known convex splitting approach [14,15,16]. Recently, the energy quadratization (IEQ) [17, 18] and scalar auxiliary variable (SAV) [19,20,21] methods are two popular ways to develop the linear and energy stable time-marching schemes. For the applications of IEQ and SAV on phase-field surfactant problems, please refer to [22,23,24].

As mentioned above, the numerical computations of CH type models may be tedious because the fourth-order characteristics. Comparing with the CH type models, the Allen–Cahn (AC)-type models are easier because they only contains two-order nonlinear PDEs. However, the AC-type models cannot satisfy the mass conservation. To fix this shortcoming, the conservative Allen–Cahn (CAC) model was proposed [25,26,27], where a nonlocal Lagrange multiplier was introduced to achieve the mass conservation. In recent years, the CAC model has been studied in many simulations of two-phase systems [28,29,30].

In this work, we propose a CAC type two-phase surfactant model, where two nonlocal Lagrange multipliers are defined to satisfy the mass conservation. In the present model, the Lagrange multipliers are only related to the nonlinear and coupling terms and they can be treated explicitly; thus, the numerical implementation will be efficient. Some details can be found in Sect. 4. The energy dissipation law is a basic property of most phase-field problems. To construct energy dissipation-preserving numerical schemes with respect to original variables, we adopt a time-dependent auxiliary variable (new Lagrange multiplier). Meanwhile, the stabilization technique [31] is used to enhance the stability in computation. The main merits of this work are: (i) The CAC-type surfactant model is easier than the CH type in numerical computation, (ii) All nonlinear and coupling terms are treated as source terms; thus, the schemes are highly efficient, (iii) The energy dissipation law and mass conservation of our proposed schemes can be easily proved. The present work aims to develop efficient and energy-dissipation preserving schemes for a CAC type two-phase surfactant model using a new Lagrange multiplier approach.

The outline of the rest part is as follows. In Sect. 2, the original equations of CAC-type surfactant system are introduced. Using a time-dependent auxiliary variable, we transform the original model into equivalent form in Sect. 2. We propose efficient and energy dissipation-preserving temporal schemes in Sect. 3. In Sect. 4, various benchmark problems are investigated to validate the proposed schemes. The conclusions are given in Sect. 5.

2 Original model

Let \(\varOmega\) be a smooth, bounded, and connected domain in \({\mathbb R}^d\), where \(d = 2\) or 3 represents the spatial dimension. We consider the following CAC-type two-phase surfactant model

$$\begin{aligned} \psi _t= & {} -M_2\left( \frac{\delta E(\phi ,\psi )}{\delta \psi } - q_\psi \right) , \end{aligned}$$
(1)
$$\begin{aligned} \phi _t= & {} -M_1\left( \frac{\delta E(\phi ,\psi )}{\delta \phi } - q_\phi \right) , \end{aligned}$$
(2)

where the subscript t represents the partial derivative with respect to time t, the positive constants \(M_1\) and \(M_2\) are the mobilities, \(\phi\) is a marker function which is used to distinguish two materials, the value of \(\phi\) is close to 1 in one phase and \(-1\) in another phase, \(\psi\) represents the local concentration of surfactant, which reaches the maximum value \(\psi _s\) at the interface \(\phi = 0\). Here, the total energy \(E(\phi ,\psi )\) is given by

$$\begin{aligned} E(\phi ,\psi )&= \int \limits _\varOmega \left[ \frac{1}{2}|\nabla \phi |^2 + F(\phi ) + \frac{1}{2}|\nabla \psi |^2 + G(\psi ) \right. \nonumber \\&\quad \left. - \theta \psi |\nabla \phi |^2 + \frac{\alpha }{2}\psi \phi ^2 \right] d\mathbf{x}, \end{aligned}$$
(3)

where the nonlinear potentials are \(F(\phi ) = (\phi ^2-1)^2/4\epsilon ^2\) and \(G(\psi ) = \psi ^2(\psi -\psi _s)^2/4\eta ^2\). The small positive parameters \(\epsilon\) and \(\eta\) are related to the thickness of interface of \(\phi\) and \(\psi\). In this work, we take \(\psi _s = 1\). In Eqs. (1) and (2), the variational derivatives of \(E(\phi ,\psi )\) with respect to \(\psi\) and \(\phi\) are given as

$$\begin{aligned} \frac{\delta E(\phi ,\psi )}{\delta \psi }= & {} -\varDelta \psi + G'(\psi ) - \theta |\nabla \phi |^2 + \frac{\alpha }{2}\phi ^2, \\ \frac{\delta E(\phi ,\psi )}{\delta \phi }= & {} -\varDelta \phi + F'(\phi ) + 2\theta \nabla \cdot (\psi \nabla \phi ) + \alpha \psi \phi . \end{aligned}$$

In the definition of total energy, Eq. (3), \(F(\phi )\) and \(G(\psi )\) describe the phase separation of \(\phi\) and \(\psi\), respectively. On the contrary, \(|\nabla \phi |^2/2\) and \(|\nabla \psi |^2/2\) contribute to the phase mixing of \(\phi\) and \(\psi\), respectively. The coupling term \(\alpha \psi \phi ^2/2\) keeps the same solubility of surfactant in two phases. Another coupling term \(- \theta \psi |\nabla \phi |^2\) ensures the accumulation of surfactant at the interface.

Two Lagrange multipliers \(q_\psi\) and \(q_\phi\) are used to ensure the mass conservations of \(\phi\) and \(\psi\), respectively. The definitions are given to be

$$\begin{aligned} q_\psi\,= & \,\frac{1}{|\varOmega |}\int \limits _\varOmega \left[ G'(\psi ) + \frac{\alpha }{2}\phi ^2 - \theta |\nabla \phi |^2\right] {\text{d}}\mathbf{x},\\ q_\phi\,= & \,\frac{1}{|\varOmega |}\int \limits _\varOmega \left[ F'(\phi ) + \alpha \psi \phi + 2\theta \nabla \cdot (\psi \nabla \phi )\right] {\text{d}}\mathbf{x}, \end{aligned}$$

where \(|\varOmega |\) is the total volume of domain. Using the integration by parts and appropriate boundary conditions (periodic or zero Neumann), we note that the last term on the right-hand side of the expression of \(q_\phi\) will be zero. For the purpose of mass conservation, this term is unnecessary. In the Sect. 4, we will explicitly treat all nonlinear and coupling terms. The definition of \(2\theta \nabla \cdot (\psi \nabla \phi )\) in the expression of \(q_\phi\) not only affects the results but also simplifies the estimations of discrete energy dissipation laws. Let us define the \(L^2\)-inner product of two functional as \((f,g) = \int _\varOmega (f\cdot g)~{\text{d}}\mathbf{x}\) and the \(L^2\)-norm of f is \(\Vert f\Vert ^2 = (f,f)\). To close Eqs. (1) and (2), we consider the periodic or homogeneous Neumann boundary conditions, i.e., \(\nabla \phi \cdot \mathbf{n} = \nabla \psi \cdot \mathbf{n} = 0\) on the boundary \(\partial \varOmega\), where \(\mathbf{n}\) is the outward unit normal vector to \(\partial \varOmega\). By taking the inner product of Eqs. (1) and (2) with \(\mathbf{1}\) and using the integration by parts, we have

$$\begin{aligned}&\int \limits _\varOmega \phi _t ~{\text{d}}\mathbf{x} = \frac{{\text{d}}}{{\text{d}}t}\int \limits _\varOmega \phi ~{\text{d}}\mathbf{x} = 0, \end{aligned}$$
(4)
$$\begin{aligned}&\int \limits _\varOmega \psi _t ~{\text{d}}\mathbf{x} = \frac{{\text{d}}}{{\text{d}}t}\int \limits _\varOmega \psi ~{\text{d}}\mathbf{x} = 0, \end{aligned}$$
(5)

which indicates that the system satisfies the property of mass conservation. Furthermore, Eqs. (1) and (2) dissipate the energy functional, Eq. (3). To show this, we multiply Eq. (1) by \(-\psi _t\) and take the integral operation, we get

$$\begin{aligned} -\frac{1}{M_2}\Vert \psi _t\Vert ^2&= \frac{{\text{d}}}{{\text{d}}t}\int \limits _\varOmega \left[ \frac{1}{2}|\nabla \psi |^2 + G(\psi )\right] {\text{d}}\mathbf{x} \nonumber \\&\quad + \frac{\alpha }{2}(\phi ^2,\psi _t) -\theta (|\nabla \phi |^2,\psi _t) - q_\psi (\psi _t,\mathbf{1}). \end{aligned}$$
(6)

Then we multiply Eq. (2) by \(-\phi _t\) and take the integral operation, we get

$$\begin{aligned}-\frac{1}{M_1}\Vert \phi _t\Vert ^2 & = \frac{\text{d}}{\text{d}t}\int\limits_\varOmega \left[ \frac{1}{2}|\nabla \phi |^2 + F(\phi )\right] d\mathbf{x} \nonumber \\&\quad - \theta \frac{\text{d}}{\text{d}t}\int\limits_\varOmega \psi |\nabla \phi |^2 ~\text{d}\mathbf{x} + \theta (|\nabla \phi |^2,\psi _t) \nonumber \\&\quad + \frac{\alpha }{2}\frac{\text{d}}{\text{d}t}\int\limits_\varOmega \psi \phi ^2 ~\text{d}\mathbf{x} \nonumber \\&\quad - \frac{\alpha }{2}(\phi ^2,\psi _t) - q_\phi (\phi _t,\mathbf{1}). \end{aligned}$$
(7)

By combining Eqs. (6) and (7), we get the following energy dissipation law

$$\begin{aligned}&\frac{{\text{ d }}}{{\text{ d }}t}\int \limits _\varOmega \left[ \frac{1}{2}|\nabla \phi |^2 + F(\phi ) + \frac{1}{2}|\nabla \psi |^2 + G(\psi ) \right] {\text{d}}\mathbf{x} \nonumber \\&\quad -\theta \frac{{\text{ d }}}{{\text{ d }}t}\int \limits _\varOmega \psi |\nabla \phi |^2 ~{\text{d}}\mathbf{x} \nonumber \\&\quad + \frac{\alpha }{2}\frac{{\text{ d }}}{{\text{ d }}t}\int \limits _\varOmega \psi \phi ^2 ~{\text{d}}\mathbf{x} \nonumber \\&\qquad = -\frac{1}{M_1}\Vert \phi _t\Vert ^2 - \frac{1}{M_2}\Vert \psi _t\Vert ^2 \le 0. \end{aligned}$$
(8)

3 Equivalent model

The basic idea of time-dependent auxiliary variable-type method is to transfer the original equations to be the equivalent equations by introducing a scalar variable which is the function of time t. Based on the transformed forms, one can construct first- and second-order time-accurate linear methods and the energy estimation is easy to perform. Some details can be founded in the next section. Herein, we consider a time-dependent auxiliary variable U which satisfies \(U = 1\) in time-continuous case. We define \(W(\phi ,\psi ) = F(\phi )+G(\psi )+\frac{\alpha }{2}\psi \phi ^2 -\theta \psi |\nabla \phi |^2\), then Eqs. (1) and (2) can be recast to be

$$\begin{aligned} \psi _t&= -M_2\left[ -\varDelta \psi + U H_2 - U q_\psi \right] , \end{aligned}$$
(9)
$$\begin{aligned} \phi _t&= -M_1\left[ -\varDelta \phi + U H_1 - U q_\phi \right] , \end{aligned}$$
(10)
$$\begin{aligned} \frac{{\text{ d }}(W(\phi ,\psi ),\mathbf{1})}{{\text{ d }}t}&\,=\, U \int \limits _\varOmega \left[ F'(\phi )\phi _t + G'(\psi )\psi _t + \frac{\alpha }{2}\phi ^2\psi _t + \alpha \psi \phi \phi _t \right. \nonumber \\&\quad \left. - \theta |\nabla \phi |^2\psi _t + 2\theta \nabla \cdot (\psi \nabla \phi )\phi _t \right] {\text{d}}\mathbf{x}, \end{aligned}$$
(11)

where the periodic or homogeneous Neumann boundary conditions, i.e., \(\nabla \phi \cdot \mathbf{n}|_{\partial \varOmega } = \nabla \psi \cdot \mathbf{n}|_{\partial \varOmega } = 0\) are used. And

$$\begin{aligned} H_1\,= & \, F'(\phi ) + \alpha \psi \phi + 2\theta \nabla \cdot (\psi \nabla \phi ),\\ H_2\,= & \,G'(\psi ) + \frac{\alpha }{2}\phi ^2 - \theta |\nabla \phi |^2. \end{aligned}$$

Here, U is a time-dependent auxiliary variable which takes the constant value 1 all along. Therefore, Eqs. (9) and (10) are indeed equivalent to the original equations, Eqs. (1) and (2). Because we introduce an extra variable U, Eq. (11) is used to construct the evolutional equation of U. Moreover, Eq. (11) is an ordinary differential equation (ODE) of U, thus we do not need to add extra boundary conditions. It it obvious that the equivalent equations, Eqs. (9) and (10) still satisfy the mass conservations. To show the energy dissipation law, we first multiply Eq. (9) by \(-\psi _t\) and take the integral operation, we get

$$\begin{aligned} -\frac{1}{M_2}\Vert \psi _t\Vert ^2 = \frac{{\text{ d }}}{{\text{ d }}t}\int \limits _\varOmega \frac{1}{2}|\nabla \psi |^2 ~{\text{d}}\mathbf{x} + (U H_2, \psi _t) - U q_\psi (\psi _t,\mathbf{1}). \end{aligned}$$
(12)

By multiplying Eq. (10) by \(-\phi _t\) and taking the integral operation, we get

$$\begin{aligned} -\frac{1}{M_1}\Vert \phi _t\Vert ^2 = \frac{{\text{ d }}}{{\text{ d }}t}\int \limits _\varOmega \frac{1}{2}|\nabla \phi |^2 ~{\text{d}}\mathbf{x} + (U H_1, \phi _t) - U q_\phi (\phi _t,\mathbf{1}). \end{aligned}$$
(13)

By multiplying \(-1\) on Eq. (11) and combining with Eqs. (12) and (13), we have the desired energy law

$$\begin{aligned}&\frac{{\text{ d }}}{{\text{ d }}t}(W(\phi ,\psi ),\mathbf{1}) + \frac{{\text{ d }}}{{\text{ d }}t}\int \limits _\varOmega \left[ \frac{1}{2}|\nabla \phi |^2 + \frac{1}{2}|\nabla \psi |^2 \right] {\text{d}}\mathbf{x} \nonumber \\&= -\frac{1}{M_1}\Vert \phi _t\Vert ^2 - \frac{1}{M_2}\Vert \psi _t\Vert ^2 \le 0. \end{aligned}$$
(14)

Here, we notice \(W(\phi ,\psi )\) represents all nonlinear terms in original energy functional, the above relation is indeed equivalent to the original energy dissipation law. Using the equivalent equations, we will propose energy dissipation-preserving first- and second-order time-accurate methods in the next section.

4 Time-marching schemes

We define \(f^n\) be the approximation of \(f(\mathbf{x},t)\) at \(t = n\delta t\), where \(\delta t\) is the time step.

4.1 First-order time-accurate scheme (1st-S)

Using the implicit Euler approximation, the first-order time-accurate method is

$$\begin{aligned}&\frac{\psi ^{n+1}-\psi ^n}{\delta t} \nonumber \\&\quad = -M_2\left[ -\varDelta \psi ^{n+1} + U^{n+1} H^n_2 - U^{n+1} q^{n}_{\psi } + \frac{S_{\psi }}{\eta ^2}(\psi ^{n+1}-\psi ^n)\right] , \end{aligned}$$
(15)
$$\begin{aligned}&\frac{\phi ^{n+1}-\phi ^n}{\delta t} \nonumber \\&\quad = -M_1\left[ -\varDelta \phi ^{n+1} + U^{n+1} H^n_1 - U^{n+1} q^{n}_{\phi } + \frac{S_\phi }{\epsilon ^2}(\phi ^{n+1}-\phi ^n) \right] , \end{aligned}$$
(16)
$$\begin{aligned}&\frac{(W(\phi ^{n+1},\psi ^{n+1})-W(\phi ^n,\psi ^n),\mathbf{1})}{\delta t} = U^{n+1}\int \limits _\varOmega \left[ F'(\phi ^n)\frac{\phi ^{n+1}-\phi ^n}{\delta t} \right. \nonumber \\&\quad \left. + G'(\psi ^n)\frac{\psi ^{n+1}-\psi ^n}{\delta t} + \frac{\alpha }{2}(\phi ^n)^2\frac{\psi ^{n+1}-\psi ^n}{\delta t} + \alpha \psi ^n\phi ^n\frac{\phi ^{n+1}-\phi ^n}{\delta t} \right. \nonumber \\&\quad \left. -\theta |\nabla \phi ^n|^2 \frac{\psi ^{n+1}-\psi ^n}{\delta t} + 2\theta \nabla \cdot (\psi ^n\nabla \phi ^n)\frac{\phi ^{n+1}-\phi ^n}{\delta t} \right] {\text{d}}\mathbf{x}, \end{aligned}$$
(17)

where the last terms in Eqs. (15) and (16) play the role of stabilization, \(S_\psi\) and \(S_\phi\) are positive constants and

$$\begin{aligned} H^n_1 \,= & \, F'(\phi ^n) + \alpha \psi ^n\phi ^n + 2\theta \nabla \cdot (\psi ^n\phi ^n), \\ H^n_2 \,= & \, G'(\psi ^n) + \frac{\alpha }{2}(\phi ^n)^2 - \theta |\nabla \phi ^n|^2,\\ q^n_\psi\,= & \, \frac{1}{|\varOmega |}\int \limits _\varOmega \left[ G'(\psi ^n)+ \frac{\alpha }{2}(\phi ^n)^2 - \theta |\nabla \phi ^n|^2\right] {\text{d}}\mathbf{x},\\ q^n_\phi\,= &\,\frac{1}{|\varOmega |}\int \limits _\varOmega \left[ F'(\phi ^n) + \alpha \psi ^n\phi ^n + 2\theta \nabla \cdot (\psi ^n\phi ^n) \right] {\text{d}}\mathbf{x}. \end{aligned}$$

Here, the periodic or zero Neumann boundary conditions, i.e., \(\nabla \phi ^{n+1}\cdot \mathbf{n}|_{\partial \varOmega } = \nabla \psi ^{n+1}\cdot \mathbf{n}|_{\partial \varOmega } = 0\) are considered. To show the mass conservations of the proposed method, Eqs. (15)–(17), we first rewrite Eq. (15) to be

$$\begin{aligned} \left( \frac{1}{\delta t}+\frac{M_2S_\psi }{\eta ^2}\right) (\psi ^{n+1}-\psi ^n) = M_2\varDelta \psi ^{n+1} - M_2U^{n+1}(H^n_2 - q^n_\psi ). \end{aligned}$$

By taking the inner product of the above equation with \(\mathbf{1}\) and using the divergence theorem, we have

$$\begin{aligned}&\left( \frac{1}{\delta t}+\frac{M_2S_\psi }{\eta ^2}\right) (\psi ^{n+1}-\psi ^n,\mathbf{1}) = M_2 \\&\qquad \int \limits _{\partial \varOmega } \mathbf{n}\cdot \nabla \psi ^{n+1}~ {\text{d}}\mathbf{s} - M_2U^{n+1}(H^n_2 - q^n_\psi ,\mathbf{1}) = 0, \end{aligned}$$

which indicates \((\psi ^{n+1}-\psi ^n,\mathbf{1}) = 0\) because \(\left( \frac{1}{\delta t}+\frac{M_2S_\psi }{\eta ^2}\right) > 0\).

Using the same way, we can obtain \((\phi ^{n+1}-\phi ^n,\mathbf{1}) = 0\) from Eq. (16). Thus, we claim the proposed first-order time-accurate scheme satisfies the mass conservations. To show the energy dissipation law in a time-discretized version, we multiply Eq. (15) by \(-(\psi ^{n+1}-\psi ^n)\) and take the integral operation, we have

$$\begin{aligned} -\frac{1}{\delta t M_2}\Vert \psi ^{n+1}-\psi ^n\Vert ^2&= \frac{1}{2}(\Vert \nabla \psi ^{n+1}\Vert ^2 - \Vert \nabla \psi ^n\Vert ^2 + \Vert \nabla \psi ^{n+1}-\nabla \psi ^n\Vert ^2) \nonumber \\& \quad + (U^{n+1} H^n_2, \psi ^{n+1}-\psi ^n) - U^{n+1}q^n_{\psi }(\psi ^{n+1}-\psi ^n,\mathbf{1}) \nonumber \\&\quad + \frac{S_\psi }{\eta ^2}\Vert \psi ^{n+1}-\psi ^n\Vert ^2. \end{aligned}$$
(18)

By multiplying Eq. (16) by \(-(\phi ^{n+1}-\phi ^n)\) and taking the integral operation, we have

$$\begin{aligned} -\frac{1}{\delta t M_1}\Vert \phi ^{n+1}-\phi ^n\Vert ^2&= \frac{1}{2}(\Vert \nabla \phi ^{n+1}\Vert ^2 - \Vert \nabla \phi ^n\Vert ^2 + \Vert \nabla \phi ^{n+1}-\nabla \phi ^n\Vert ^2) \nonumber \\&\quad + (U^{n+1} H^n_1, \phi ^{n+1}-\phi ^n) - U^{n+1}q^n_\phi (\phi ^{n+1}-\phi ^n,\mathbf{1})\nonumber \\&\quad+ \frac{S_\phi }{\epsilon ^2}\Vert \phi ^{n+1}-\phi ^n\Vert ^2. \end{aligned}$$
(19)

By multiplying \(-1\) on Eq. (17) and combining Eqs. (18) and (19), we obtain the following time-discretized energy dissipation law

$$\begin{aligned}&(W(\phi ^{n+1},\psi ^{n+1})-W(\phi ^n,\psi ^n),\mathbf{1}) \nonumber \\&\quad + \frac{1}{2}(\Vert \nabla \phi ^{n+1}\Vert ^2-\Vert \nabla \phi ^n\Vert ^2) \nonumber \\&\quad +\frac{1}{2}(\Vert \nabla \psi ^{n+1}\Vert ^2 - \Vert \nabla \psi ^n\Vert ^2) \nonumber \\&= -\left( \frac{1}{\delta t M_1}+ \frac{S_\phi }{\epsilon ^2}\right) \Vert \phi ^{n+1}-\phi ^n\Vert ^2 \nonumber \\&\quad - \frac{1}{2}\Vert \nabla \phi ^{n+1}-\nabla \phi ^n\Vert ^2 -\left( \frac{1}{\delta t M_2}+\frac{S_\psi }{\eta ^2}\right) \Vert \psi ^{n+1}-\psi ^n\Vert ^2 \nonumber \\ &\quad-\frac{1}{2}\Vert \nabla \psi ^{n+1}-\nabla \psi ^n\Vert ^2 \le 0. \end{aligned}$$
(20)

4.2 Efficient algorithm for 1st-S

As we can observe, Eqs. (15)–(17) are weakly coupled due to the existence of \(U^{n+1}\). To decouple the computation, we describe the following efficient algorithm. First, let \(\psi ^{n+1} = \psi ^{n+1}_1 + U^{n+1}\psi ^{n+1}_2\) and \(\phi ^{n+1} = \phi ^{n+1}_1 + U^{n+1}\phi ^{n+1}_2\), then Eqs. (15)–(17) are recast to be

$$\begin{aligned}&\frac{\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2-\psi ^n}{\delta t} \nonumber \\&\quad = -M_2\left[ -\varDelta (\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2)+U^{n+1}H^n_2-U^{n+1}q^n_\psi \right. \nonumber \\&\left. \quad+\frac{S_\psi }{\eta ^2}(\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2-\psi ^n)\right] , \end{aligned}$$
(21)
$$\begin{aligned}&\frac{\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2-\phi ^n}{\delta t} \nonumber \\&\quad = -M1\left[ -\varDelta (\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2)+U^{n+1}H^n_1-U^{n+1}q^n_\phi \right. \nonumber \\&\left. \quad +\frac{S_\phi }{\epsilon ^2}(\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2-\phi ^n)\right] , \end{aligned}$$
(22)
$$\begin{aligned}&(W(\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2,\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2)-W(\phi ^n,\psi ^n),\mathbf{1})\nonumber \\&\quad = U^{n+1}\int \limits _\varOmega \left[ F'(\phi ^n)(\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2-\phi ^n)+G'(\psi ^n)(\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2-\psi ^n)\right. \nonumber \\&\quad \left. +\frac{\alpha }{2}(\phi ^n)^2(\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2-\psi ^n)+\alpha \psi ^n\phi ^n(\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2-\phi ^n)\right. \nonumber \\&\quad \left. -\theta |\nabla \phi ^n|^2(\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2-\psi ^n) \right. \nonumber \\&\quad \left. + 2\theta \nabla \cdot (\psi ^n\nabla \phi ^n)(\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2-\phi ^n)\right] {\text{d}}\mathbf{x},~~~~~~ \end{aligned}$$
(23)

Because \(\psi ^{n+1}_1\) and \(\psi ^{n+1}_2\) are independent, we can split Eq. (21) into

$$\begin{aligned} \frac{\psi ^{n+1}_1-\psi ^n}{\delta t}&= M_2\varDelta \psi ^{n+1}_1 - \frac{M_2S_\psi }{\eta ^2}(\psi ^{n+1}_1-\psi ^n), \end{aligned}$$
(24)
$$\begin{aligned} \frac{\psi ^{n+1}_2}{\delta t}&= M_2\varDelta \psi ^{n+1}_2 - M_2\left( H^n_2-q^n_\psi +\frac{S_\psi }{\eta ^2}\psi ^{n+1}_2\right) . \end{aligned}$$
(25)

Similarly, we can split Eq. (22) into

$$\begin{aligned} \frac{\phi ^{n+1}_1-\phi ^n}{\delta t}&= M_1\varDelta \phi ^{n+1}_1 - \frac{M_1S_\phi }{\epsilon ^2}(\phi ^{n+1}_1-\phi ^n), \end{aligned}$$
(26)
$$\begin{aligned} \frac{\phi ^{n+1}_2}{\delta t}&= M_1\varDelta \phi ^{n+1}_2 - M_1\left( H^n_1-q^n_\phi +\frac{S_\phi }{\epsilon ^2}\phi ^{n+1}_2\right) . \end{aligned}$$
(27)

Here, the periodic or zero Neumann boundary conditions, i.e., \(\nabla \phi ^{n+1}_1\cdot \mathbf{n}|_{\partial \varOmega } = \nabla \phi ^{n+1}_2\cdot \mathbf{n}|_{\partial \varOmega } = \nabla \psi ^{n+1}_1\cdot \mathbf{n}|_{\partial \varOmega } = \nabla \psi ^{n+1}_2\cdot \mathbf{n}|_{\partial \varOmega } = 0\) are considered. It can be observed that the computations of \(\psi ^{n+1}_1\) and \(\psi ^{n+1}_2\), \(\phi ^{n+1}_1\) and \(\phi ^{n+1}_2\) are fully decoupled. In each time iteration, we solve four linear elliptic equations with constant coefficients in a step-by-step manner, thus the computation is highly efficient. With the computed \(\psi ^{n+1}_1\), \(\psi ^{n+1}_2\), \(\phi ^{n+1}_1\), and \(\phi ^{n+1}_2\), we can update \(U^{n+1}\) from Eq. (23). Because Eq. (23) is a nonlinearly algebraic equation with respect to \(U^{n+1}\), the Newton’s iteration with a proper initial assumption \(U^{n+1} = 1\) usually works well.

4.3 Second-order time-accurate method (2nd-S)

Using the BDF2 approximation, we can develop the following second-order time-accurate method

$$\begin{aligned}&\frac{3\psi ^{n+1}-4\psi ^n+\psi ^{n-1}}{2\delta t} \nonumber \\&\quad = -M_2\left[ -\varDelta \psi ^{n+1}+U^{n+1}H^*_2 - U^{n+1}q^*_\psi + \frac{S_\psi }{\eta ^2}(\psi ^{n+1}-\psi ^*)\right] ,~~~~~ \end{aligned}$$
(28)
$$\begin{aligned}&\frac{3\phi ^{n+1}-4\phi ^n+\phi ^{n-1}}{2\delta t} \nonumber \\&\quad = -M\left[ -\varDelta \phi ^{n+1}+U^{n+1}H^*_1-U^{n+1}q^*_\phi + \frac{S_\phi }{\epsilon ^2}(\phi ^{n+1}-\phi ^*)\right] , \end{aligned}$$
(29)
$$\begin{aligned}&\frac{(3W(\phi ^{n+1},\psi ^{n+1})-4W(\phi ^n,\psi ^n)+W(\phi ^{n-1},\psi ^{n-1}),\mathbf{1})}{2\delta t} \nonumber \\&\quad =U^{n+1}\int \limits _\varOmega \left[ F'(\phi ^*)\frac{3\phi ^{n+1}-4\phi ^n+\phi ^{n-1}}{2\delta t}+G'(\psi ^*)\frac{3\psi ^{n+1}-4\psi ^n+\psi ^{n-1}}{2\delta t} \right. \nonumber \\& \left. \quad +\frac{\alpha }{2}\phi ^*\frac{3\psi ^{n+1}-4\psi ^n+\psi ^{n-1}}{2\delta t} + \alpha \psi ^*\phi ^*\frac{3\phi ^{n+1}-4\phi ^n+\phi ^{n-1}}{2\delta t} \right. \nonumber \\& \left. \quad-\theta |\nabla \phi ^*|^2\frac{3\psi ^{n+1}-4\psi ^n+\psi ^{n-1}}{2\delta t} \right. \nonumber \\& \left. \quad+ 2\theta \nabla \cdot (\psi ^*\nabla \phi ^*)\frac{3\phi ^{n+1}-4\phi ^n+\phi ^{n-1}}{2\delta t}\right] {\text{d}}\mathbf{x}, \end{aligned}$$
(30)

where \(\phi ^* = 2\phi ^n - \phi ^{n-1}\) and \(\psi ^* = 2\psi ^n - \psi ^{n-1}\) are the extrapolations from the previous information. The periodic or homogeneous Neumann boundary conditions, i.e., \(\nabla \phi ^{n+1}\cdot \mathbf{n}|_{\partial \varOmega } = \nabla \psi ^{n+1}\cdot \mathbf{n}|_{\partial \varOmega } = 0\) are used. We claim that the above method satisfies the mass conservations with the preconditions \(\psi ^{1} = \psi ^0\) and \(\phi ^{1} = \phi ^0\) which have been obtained from the first-order scheme. To show this, we first consider the case \(n = 1\) and rewrite Eq. (28) to be

$$\begin{aligned} \left( \frac{3}{2\delta t} + \frac{M_2S_\psi }{\eta ^2}\right) (\psi ^2-\psi ^1) = M_2\varDelta \psi ^2 - M_2U^2(H^*_2-q^*_\psi ). \end{aligned}$$

By taking the inner product of the above equation with \(\mathbf{1}\) and using the divergence theorem, we have

$$\begin{aligned}&\left( \frac{3}{2\delta t} + \frac{M_2S_\psi }{\eta ^2}\right) (\psi ^2-\psi ^1,\mathbf{1}) \\&\quad = M_2\int \limits _{\partial \varOmega } \mathbf{n}\cdot \nabla \psi ^2 ~{\text{d}}\mathbf{s} - M_2U^2(H^*_2-q^*_\psi ,\mathbf{1}) = 0, \end{aligned}$$

which indicates \((\psi ^2 - \psi ^1, \mathbf{1}) = 0\) because \(\left( \frac{3}{2\delta t} + \frac{M_2S_\psi }{\eta ^2}\right) > 0\). By the recurrence relation, we have \((\psi ^{n+1}-\psi ^n,\mathbf{1}) = 0\). In a similar way, we can obtain \((\phi ^{n+1}-\phi ^n,\mathbf{1}) = 0\) from Eq. (29). Thus, we have proved that the second-order time-accurate method still satisfies the mass conservations. Next, we will prove that Eqs. (28)–(30) dissipate the following time-discretized energy

$$\begin{aligned}&\tilde{E}(\phi ^{n+1},\phi ^n,\psi ^{n+1},\psi ^n) \nonumber \\&\quad = \frac{1}{2}(3W(\phi ^{n+1},\psi ^{n+1})-W(\phi ^n,\psi ^n),\mathbf{1}) \nonumber \\&\quad + \frac{1}{4}(\Vert \nabla \phi ^{n+1}\Vert ^2+\Vert 2\nabla \phi ^{n+1}-\nabla \phi ^n\Vert ^2) \nonumber \\&\quad + \frac{1}{4}(\Vert \nabla \psi ^{n+1}\Vert ^2+\Vert 2\nabla \psi ^{n+1}-\nabla \psi ^n\Vert ^2)\nonumber \\&\quad + \frac{S_\phi }{2\epsilon ^2}\Vert \phi ^{n+1}-\phi ^n\Vert ^2 + \frac{S_\psi }{2\eta ^2}\Vert \psi ^{n+1}-\psi ^n\Vert ^2, \end{aligned}$$
(31)

By multiplying Eq. (28) by \(-(3\psi ^{n+1}-4\psi ^n+\psi ^{n-1})\) and taking the integral operation, we have

$$\begin{aligned}&-\frac{1}{2\delta t M_2}\Vert 3\psi ^{n+1}-4\psi ^n+\psi ^{n-1}\Vert ^2 \nonumber \\&\quad = \frac{1}{2}(\Vert \nabla \psi ^{n+1}\Vert ^2-\Vert \nabla \psi ^n\Vert ^2 \nonumber \\&\qquad +\Vert 2\nabla \psi ^{n+1}-\nabla \psi ^n\Vert ^2 -\Vert 2\nabla \psi ^n-\nabla \psi ^{n-1}\Vert ^2 \nonumber \\&\qquad +\Vert \nabla \psi ^{n+1}-2\nabla \psi ^n+\nabla \psi ^{n-1}\Vert ^2)\nonumber \\&\qquad +(U^{n+1}H^*_2,3\psi ^{n+1}-4\psi ^n+\psi ^{n-1}) \nonumber \\&\qquad - U^{n+1}q^*_\psi (3\psi ^{n+1}-3\psi ^n-(\psi ^n-\psi ^{n-1}),\mathbf{1})\nonumber \\&\qquad +\frac{S_\psi }{\eta ^2}( \Vert \psi ^{n+1}-\psi ^n\Vert ^2 \nonumber \\&\qquad -\Vert \psi ^n-\psi ^{n-1}\Vert ^2 + 2\Vert \psi ^{n+1}-2\psi ^n+\psi ^{n-1}\Vert ^2 ), \end{aligned}$$
(32)

By multiplying Eq. (29) by \(-(3\phi ^{n+1}-4\phi ^n+\phi ^{n-1})\) and taking the integral operation, we have

$$\begin{aligned}&-\frac{1}{2\delta t M_1}\Vert 3\phi ^{n+1}-4\phi ^n+\phi ^{n-1}\Vert ^2 \nonumber \\&\quad = \frac{1}{2}(\Vert \nabla \phi ^{n+1}\Vert ^2-\Vert \nabla \phi ^n\Vert ^2 \nonumber \\&\qquad +\Vert 2\nabla \phi ^{n+1}-\nabla \phi ^n\Vert ^2 -\Vert 2\nabla \phi ^n-\nabla \phi ^{n-1}\Vert ^2 \nonumber \\&\qquad +\Vert \nabla \phi ^{n+1}-2\nabla \phi ^n+\nabla \phi ^{n-1}\Vert ^2)\nonumber \\&\qquad +(U^{n+1}H^*_1,3\phi ^{n+1}-4\phi ^n+\phi ^{n-1}) \nonumber \\&\qquad - U^{n+1}q^*_\phi (3\phi ^{n+1}-3\phi ^n-(\phi ^n-\phi ^{n-1}),\mathbf{1})\nonumber \\&\qquad +\frac{S_\phi }{\epsilon ^2}( \Vert \phi ^{n+1}-\phi ^n\Vert ^2 \nonumber \\&\qquad -\Vert \phi ^n-\phi ^{n-1}\Vert ^2 + 2\Vert \phi ^{n+1}-2\phi ^n+\phi ^{n-1}\Vert ^2 ), \end{aligned}$$
(33)

By multiplying \(-1\) on Eq. (30) and combining Eqs. (32) and (33) together, we obtain the following time-discretized energy law

$$\begin{aligned}&\frac{1}{2}(3W(\phi ^{n+1},\psi ^{n+1})-W(\phi ^n,\psi ^n),\mathbf{1}) \nonumber \\&\qquad - \frac{1}{2}(3W(\phi ^n,\psi ^n)-W(\phi ^{n-1},\psi ^{n-1}),\mathbf{1})\nonumber \\&\qquad +\frac{1}{4}(\Vert \nabla \phi ^{n+1}\Vert ^2+\Vert 2\nabla \phi ^{n+1} -\nabla \phi ^n\Vert ^2-\Vert \nabla \phi ^n\Vert ^2-\Vert 2\nabla \phi ^n-\nabla \phi ^{n-1}\Vert ^2)\nonumber \\&\qquad +\frac{1}{4}(\Vert \nabla \psi ^{n+1}\Vert ^2+\Vert 2\nabla \psi ^{n+1}-\nabla \psi ^n\Vert ^2 -\Vert \nabla \psi ^n\Vert ^2-\Vert 2\nabla \psi ^n-\nabla \psi ^{n-1}\Vert ^2) +\frac{S_\phi }{2\epsilon ^2}( \Vert \phi ^{n+1}-\phi ^n\Vert ^2 -\Vert \phi ^n-\phi ^{n-1}\Vert ^2 ) \nonumber \\&\qquad + \frac{S_\psi }{2\eta ^2}( \Vert \psi ^{n+1}-\psi ^n\Vert ^2 -\Vert \psi ^n-\psi ^{n-1}\Vert ^2 )\nonumber \\& \quad = -\frac{1}{4\delta t M_1}\Vert 3\phi ^{n+1}-4\phi ^n+\phi ^{n-1}\Vert ^2 -\frac{1}{4\delta t M_2}\Vert 3\psi ^{n+1}-4\psi ^n+\psi ^{n-1}\Vert ^2\nonumber \\&\qquad -\frac{1}{4}\Vert \nabla \phi ^{n+1}-2\nabla \phi ^n+\nabla \phi ^{n-1}\Vert ^2 - \frac{1}{4}\Vert \nabla \psi ^{n+1}-2\nabla \psi ^n+\nabla \psi ^{n-1}\Vert ^2 \nonumber \\&\qquad - \frac{S_\phi }{\epsilon ^2}\Vert \phi ^{n+1}-2\phi ^n+\phi ^{n-1}\Vert ^2 -\frac{S_\psi }{\eta ^2}\Vert \psi ^{n+1}-2\psi ^n+\psi ^{n-1}\Vert ^2 \le 0, \end{aligned}$$
(34)

which is a second-order approximation of original energy law. For example, we observe

$$\begin{aligned}&\frac{(3W(\phi ^{n+1},\psi ^{n+1})-4W(\phi ^n,\psi ^n)+W(\phi ^{n-1},\psi ^{n-1}),\mathbf{1})}{2\delta t} \nonumber \\&\quad \cong \frac{{\text{ d }}}{{\text{ d }}t}(W(\phi (\cdot ,t^{n+1}),\psi (\cdot ,t^{n+1})),\mathbf{1}) + O(\delta t^2), \end{aligned}$$
(35)
$$\begin{aligned}&\left( \frac{\Vert \nabla \phi ^{n+1}\Vert ^2+\Vert 2\nabla \phi ^{n+1}-\nabla \phi ^{n+1}\Vert ^2}{2\delta t}\right) \nonumber \\&- \left( \frac{\Vert \nabla \phi ^{n}\Vert ^2+\Vert 2\nabla \phi ^{n}-\nabla \phi ^{n-1}\Vert ^2}{2\delta t}\right) \nonumber \\&\quad \cong \left( \frac{\Vert \nabla \phi ^{n+2}\Vert ^2-\Vert \nabla \phi ^n\Vert ^2}{2\delta t}\right) + O(\delta t^2) \nonumber \\&\quad \cong \frac{{\text{ d }}}{{\text{ d }}t}\Vert \nabla \phi (\cdot ,t^{n+1})\Vert ^2 + O(\delta t^2), \end{aligned}$$
(36)
$$\begin{aligned}&\quad \left( \frac{\Vert \nabla \psi ^{n+1}\Vert ^2+\Vert 2\nabla \psi ^{n+1}-\nabla \psi ^{n+1}\Vert ^2}{2\delta t}\right) \nonumber \\&- \left( \frac{\Vert \nabla \psi ^{n}\Vert ^2+\Vert 2\nabla \psi ^{n}-\nabla \psi ^{n-1}\Vert ^2}{2\delta t}\right) \nonumber \\&\cong \left( \frac{\Vert \nabla \psi ^{n+2}\Vert ^2-\Vert \nabla \psi ^n\Vert ^2}{2\delta t}\right) \nonumber \\&+ O(\delta t^2)\cong \frac{{\text{ d }}}{{\text{ d }}t}\Vert \nabla \psi (\cdot ,t^{n+1})\Vert ^2 + O(\delta t^2), \end{aligned}$$
(37)
$$\begin{aligned}&\left( \frac{\Vert \phi ^{n+1}-\phi ^n\Vert ^2 - \Vert \phi ^n-\phi ^{n-1}\Vert ^2}{\delta t} \right) \cong O(\delta t^2), \end{aligned}$$
(38)
$$\begin{aligned}&\left( \frac{\Vert \psi ^{n+1}-\psi ^n\Vert ^2 - \Vert \psi ^n-\psi ^{n-1}\Vert ^2}{\delta t} \right) \cong O(\delta t^2). \end{aligned}$$
(39)

Remark 4.1

In Sect.4.1, we presented the first-order time-accurate scheme and estimated its energy dissipation law with respect to the following discrete energy

$$\begin{aligned} E(\phi ^n,\psi ^n) = W(\phi ^n,\psi ^n) + \frac{1}{2}\Vert \nabla \phi ^n\Vert ^2 + \frac{1}{2}\Vert \nabla \psi ^n\Vert ^2. \end{aligned}$$
(40)

It should be noted that the above discrete energy is a first-order approximation of original and time-continuous energy \(E(\phi ,\psi )\). In Sect. 4.4, we presented the second-order time-accurate scheme and proved the discrete energy dissipation law with respect to a discrete energy (Eq. (31)). We note that Eq. (31) is a pseudo energy because it contains variables at different time levels. This issue always exits for the BDF2-based temporally second-order scheme of phase-field models, please refer to [14, 17, 20, 21, 32,33,34] for more details. However, Eq. (31) is still a second-order approximation of original and time-continuous energy \(E(\phi ,\psi )\). For a desired numerical method, we aim to obtain discrete results which are appropriate approximations of continuous problems. Because Eqs. (40) and (31) are both approximations of \(E(\phi ,\psi )\) with different orders, thus inequalities (20) and (34) can be identified as appropriate discrete energy dissipation laws.

4.4 Efficient algorithm for 2nd-S

We define \(\psi ^{n+1} = \psi ^{n+1}_1 + U^{n+1}\psi ^{n+1}_2\) and \(\phi ^{n+1} = \phi ^{n+1}_1 + U^{n+1}\phi ^{n+1}_2\), then Eqs. (28)–(30) can be recast to be

$$\begin{aligned}&\frac{3(\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2)-4\psi ^n+\psi ^{n-1}}{2\delta t} \nonumber \\&\quad =-M_2\left[ -\varDelta (\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2)\right. \nonumber \\&\left. \quad + U^{n+1}H^*_2 - U^{n+1}q^*_\psi + \frac{S_\psi }{\eta ^2}(\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2-\psi ^*)\right] , \end{aligned}$$
(41)
$$\begin{aligned}&\frac{3(\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2)-4\phi ^n+\phi ^{n-1}}{2\delta t} \nonumber \\&\quad = -M_1\left[ -\varDelta (\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2)\right. \nonumber \\&\left. \quad + U^{n+1}H^*_1 - U^{n+1}q^*_\phi + \frac{S_\phi }{\epsilon ^2}(\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2-\phi ^*)\right] , \end{aligned}$$
(42)
$$\begin{aligned}&(3W(\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2,\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2)-4W(\phi ^n,\psi ^n)+W(\phi ^{n-1},\psi ^{n-1}),\mathbf{1})\nonumber \\&\quad = U^{n+1}\int \limits _\varOmega \left[ F'(\phi ^*)(3(\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2)-4\phi ^n+\phi ^{n-1})\right. \nonumber \\&\left. \quad +G'(\psi ^*)(3(\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2)-4\psi ^n+\psi ^{n-1}) \right. \nonumber \\&\left. \quad +\frac{\alpha }{2}\phi ^*(3(\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2)\right. \nonumber \\&\left. \quad -4\psi ^n+\psi ^{n-1}) + \alpha \psi ^*\phi ^*(3(\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2)-4\phi ^n+\phi ^{n-1})\right. \nonumber \\&\left. \quad -\theta |\nabla \phi ^*|^2(3(\psi ^{n+1}_1+U^{n+1}\psi ^{n+1}_2)-4\psi ^n+\psi ^{n-1})\right. \nonumber \\&\left. \quad +2\theta \nabla \cdot (\psi ^*\nabla \phi ^*) \right. \nonumber \\&\quad \left. (3(\phi ^{n+1}_1+U^{n+1}\phi ^{n+1}_2)-4\phi ^n+\phi ^{n-1})\right] {\text{d}}\mathbf{x}, \end{aligned}$$
(43)

Since \(\psi ^{n+1}_1\) and \(\psi ^{n+1}_2\) are independent, we can split Eq. (41) to be

$$\begin{aligned}&\frac{3\psi ^{n+1}_1-4\psi ^n+\psi ^{n-1}}{2\delta t} = M_2\varDelta \psi ^{n+1}_1 - \frac{M_2S_\psi }{\eta ^2}(\psi ^{n+1}_1-\psi ^*), \end{aligned}$$
(44)
$$\begin{aligned}&\frac{3\psi ^{n+1}_2}{2\delta t} = M_2\varDelta \psi ^{n+1}_2 - M_2\left( H^*_2-q^*_\psi +\frac{S_\psi }{\eta ^2}\psi ^{n+1}_2\right) . \end{aligned}$$
(45)

Similarly, we can split Eq. (42) to be

$$\begin{aligned}&\frac{3\phi ^{n+1}_1-4\phi ^n+\phi ^{n-1}}{2\delta t} = M_1\varDelta \phi ^{n+1}_1 - \frac{M_1S_\phi }{\epsilon ^2}(\phi ^{n+1}_1-\phi ^*), \end{aligned}$$
(46)
$$\begin{aligned}&\frac{3\phi ^{n+1}_2}{2\delta t} \nonumber \\&\quad = M_1\varDelta \phi ^{n+1}_2 - M_1\left( H^*_1-q^*_\phi +\frac{S_\phi }{\epsilon ^2}\phi ^{n+1}_2\right) . \end{aligned}$$
(47)

Here, the periodic or homogeneous Neumann boundary conditions, i.e., \(\nabla \phi ^{n+1}_1\cdot \mathbf{n}|_{\partial \varOmega } = \nabla \phi ^{n+1}_2\cdot \mathbf{n}|_{\partial \varOmega } = \nabla \psi ^{n+1}_1\cdot \mathbf{n}|_{\partial \varOmega } = \nabla \psi ^{n+1}_2\cdot \mathbf{n}|_{\partial \varOmega } = 0\) are considered. In each time iteration, only four linear elliptic equations with constant coefficients need to be solved. With the computed \(\psi ^{n+1}_1\), \(\psi ^{n+1}_2\), \(\phi ^{n+1}_1\), and \(\phi ^{n+1}_2\), we can update \(U^{n+1}\) by solving Eq. (43) with Newton’s iteration.

Remark 4.2

In the proposed methods, two stabilization parameters \(S_\phi\) and \(S_\psi\) were introduced to perform the stabilization. We admit that the discrete version of energy dissipation law (energy stability) can be proved with \(S_\phi = S_\psi = 0\). However, the energy stability is just a physical property and can not guarantee the stability of numerical solution. In linear methods, the explicit treatments of nonlinear terms will increase the stiffness of schemes when we use large time steps. The incorrect calculations of \(\phi\) and \(\psi\) also lead to the nondissipative behaviour of discrete energy. To a certain extent, the implicit parts containing in the stabilization terms reduce the bad effect caused by the explicit nonlinear terms. Because the nonlinear terms contain \((\cdot )/\epsilon ^2\) and \((\cdot )/\eta ^2\), we need to choose \(S_\phi /\epsilon ^2\) and \(S_\psi /\eta ^2\) to control these parts. In Sect. 5, the numerical results indicate that \(S_\phi = S_\psi = 2\) plays an essential role to preserve the energy dissipation property even if a relatively large time step is used. Furthermore, extensive recent works [21, 35,36,37] also displayed the necessity of stabilization terms on the linear auxiliary variable-type approaches. Although \(S_\phi /\epsilon ^2\) and \(S_\psi /\eta ^2\) are not negligible, the whole terms \(\frac{S_\phi }{\epsilon ^2}(\phi ^{n+1}-\phi ^*)\) and \(\frac{S_\psi }{\eta ^2}(\psi ^{n+1}-\psi ^*)\) only bring up extra splitting errors which are of the order \(S_\phi \delta t^2\phi _{tt}(\cdot )\) and \(S_\psi \delta t^2\psi _{tt}(\cdot )\) that are comparable with the errors introduced by the extrapolations of the explicit nonlinear terms [35, 37]. Moreover, Eqs. (17) and (30) are only used to compute the time-dependent auxiliary variable U, they are not evolutional equations of \(W(\phi ,\psi )\). With the computed \(\phi ^{n+1}\), \(\psi ^{n+1}\), \(\phi ^n\), and \(\psi ^n\), we directly obtain \(W(\phi ^{n+1},\psi ^{n+1})\) and \(W(\phi ^n,\psi ^n)\) from their definition in time-continuous version. Therefore, the discrete energy functionals ( Eqs. (40) and (31) ) consist of original variables (i.e., \(\phi\) and \(\psi\)) and they are both appropriate approximations of continuous energy \(E(\phi ,\psi )\). In Sect. 5, we plot the evolutions of discrete pseudo energy (Eq. (31)) and discrete version of original energy with \(S_\phi = S_\psi = 2\). The results indicate that the pseudo and original energy curves are almost consistent.

Remark 4.3

In the 1st-S and 2nd-S, we observe that only four linear elliptic type equations need to be computed in one time iteration, thus any fast and accurate numerical methods can be used. Moreover, the unique solvability of linear elliptic type equations can be easily obtained using Lax–Milgram theorem, please refer to [31] for some details. For the nonlinear algebraic equation with respect to \(U^{n+1}\), we can use Newton’s iteration with 1 as initial assumption. Note that the exact solution of U is 1, thus the Newton’s iteration generally converges to desired result. As reported in [34], the convergence and error estimations of numerical schemes based on a new Lagrange multiplier approach are still open questions and we will further consider them in a separate work. In the present study, we only focus on the implementation of efficient and energy dissipation-preserving time-marching schemes. The numerical examples in Sect. 5 will indicate that the proposed schemes work well for the CAC type binary surfactant system.

Remark 4.4

In this section, we proposed temporally first- and second-order accurate schemes for the CAC surfactant model. Comparing with the discrete pseudo energy dissipation law based on the second-order accurate scheme, the solutions of first-order accurate scheme dissipate the discrete version of original energy (i.e., the discrete energy only contains the variables at the same time level). However, the second-order accurate scheme usually leads to better computational accuracy and convergence. The numerical tests shown in Sect. 5 indicate this.

5 Numerical validations

In this section, we perform various 2D and 3D computational examples to validate the proposed time-marching schemes. The finite difference method is adopted to discretize the space and efficient linear multigrid algorithm [38] is used to speed up the convergence. The computational domain for 2D and 3D problems are \(\varOmega = (0,2\pi )\times (0,2\pi )\) and \(\varOmega = (0,2\pi )\times (0,2\pi )\times (0,\pi )\), respectively. Without specific needs, we use the spatial mesh size \(128\times 128\) and \(128\times 128\times 64\) for 2D and 3D tests, respectively. The following parameters are considered

$$\begin{aligned} M_1= & {} M_2 = 0.01, ~\alpha = 0.001, ~\theta = 0.001, \\ \epsilon= & {} 0.05, ~\eta = 0.01, ~S_\phi = S_\psi = 2. \end{aligned}$$

5.1 Accuracy tests

To validate the proposed first-order scheme (1st-S) and second-order scheme (2nd-S) have the corresponding temporal accuracy, we consider the following initial conditions

$$\begin{aligned} \phi (x,y,0)&= \tanh \left( \frac{0.4\pi - \sqrt{(x-0.6\pi )^2+(y-\pi )^2}}{\sqrt{2}\epsilon } \right) \nonumber \\&\quad + \tanh \left( \frac{0.15\pi - \sqrt{(x-1.15\pi )^2+(y-1.2\pi )^2}}{\sqrt{2}\epsilon } \right) + 1, \end{aligned}$$
(48)
$$\begin{aligned} \psi (x,y,0)&= 0.2. \end{aligned}$$
(49)

Because the analytical solution is hard to find in general, we define the numerical reference solutions using a finer time step \(\delta \tilde{t} = 2.4096\)e-5. The increasingly coarser time steps \(\delta t = 5\delta \tilde{t}, ~10\delta \tilde{t}, ~20\delta \tilde{t}, ~40\delta \tilde{t}, ~80\delta \tilde{t}\), and \(160\delta \tilde{t}\) are used to perform the simulations until \(t = 0.1234\). Tables 1 and 2 illustrate the \(L^2\)-errors and convergence rates with respect to 1st-S and 2nd-S, respectively. As we can observed, the proposed schemes indeed have the desired first- and second-order temporal accuracy.

Table 1 1st-S: \(L^2\)-errors and convergence rates of \(\phi\) and \(\psi\) with various time steps
Full size table
Table 2 2nd-S: \(L^2\)-errors and convergence rates of \(\phi\) and \(\psi\) with various time steps
Full size table

5.2 Energy dissipation law and mass conservations

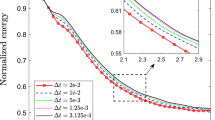
To validate the proposed schemes satisfy the properties of energy dissipation and mass conservations, we consider the evolution of two droplets with different sizes. The initial conditions in Sect. 5.1 are considered. The increasingly coarser time steps \(\delta t = 0.01, ~0.05, ~0.1, ~0.2\) and 0.4 are used. All simulations are performed until \(t = 100\). The snapshots obtained by a smaller time step \(\delta t = 0.01\) are shown in Fig. 1, two initially separated droplets merge together to form a bigger one. In this process, the shrinking of interfacial length will dissipate the total energy. Figure 2a and b displays the temporal evolutions of normalized energy with respect to the 1st-S and 2nd-S, respectively. Although both schemes dissipate the total energy at each time step, the 2nd-S speeds up the convergence of energy curve. In Fig. 3a and b, we also plot the evolutions of total mass of \(\phi\) and \(\psi\), where the definitions of total mass are as follow

$$\begin{aligned} V^n_\phi\,= & \, h^2\sum \limits ^{N_x}_{i=1}\sum \limits ^{N_y}_{j=1} \left( \frac{1+\phi ^n_{ij}}{2} \right) ,\\ V^n_\psi\,= & \, h^2\sum \limits ^{N_x}_{i=1}\sum \limits ^{N_y}_{j=1} \psi ^n_{ij}, \end{aligned}$$

where \(h = 2\pi /128\) is the grid size, \(N_x\) and \(N_y\) are the numbers of mesh grids along x- and y-directions, respectively. It can be observed that both schemes satisfy the mass conservations. In Fig. 4, we plot the temporal evolutions of auxiliary variable U with respect to different time steps. As we can see, U converges to desired result 1 with the refinement of time step. The results indicate that a smaller time step is necessary to obtain an accurate solution.

Fig. 1
figure 1

The snapshots of \(\phi\) and \(\psi\) at \(t = 0, ~3, ~15\), and 100 from (a)–(d)

Full size image
Fig. 2
figure 2

Evolutions of normalized energy obtained by a 1st-S and b 2nd-S

Full size image
Fig. 3
figure 3

Evolutions of total mass obtained by a 1st-S and b 2nd-S

Full size image
Fig. 4
figure 4

Temporal evolutions of auxiliary variable U with respect to different time steps

Full size image

We note that the discrete energy dissipation law (energy stability) still holds for the case of \(S_\phi = S_\psi = 0\) (i.e., the stabilization terms are absent). However, the energy stability does not guarantee the stability of numerical solutions. When we use a relatively large time step, the stabilization terms play important roles to suppress the effect of explicit nonlinear terms. In Fig. 5a, we plot the evolutions of normalized energy with respect to \(S_\phi = S_\psi = 0\) and different time steps. We observe that the energy curve does not follow the dissipative property when \(\delta t = 0.2\) is used. By comparing the results shown in Figs. 5a and 2b, we find that the energy curves are non-increasing when we use \(S_\phi = S_\psi = 2\). Moreover, Fig. 5b displays the evolutions of discrete version of original energy (Eq. (40)) and pseudo energy (Eq. (31)) with \(S_\phi = S_\psi = 2\). As we can see, the energy curves are approximately consistent.

Fig. 5
figure 5

Evolutions of energy curves. Here, a shows the normalized energy with respect to \(S_\phi = S_\psi = 0\) and different time steps; b plots the discrete original and pseudo energy with \(S_\phi = S_\psi = 2\)

Full size image

5.3 Effect of surfactant

In a surfactant-laden two-phase system, the interfacial dynamics will be influenced by the existence of surfactant. If the effect of surfactant is weak, the dominance of interfacial intension will drive the interface to coalesce. On the contrary, the dominant effect of surfactant will makes the interface be separated since the tension is weaken. Here, we consider two initially separated droplets

$$\begin{aligned} \phi (x,y,0)&= \tanh \left( \frac{0.4\pi - \sqrt{(x-0.6\pi )^2+(y-0.83\pi )^2}}{\sqrt{2}\epsilon } \right) \nonumber \\ +&\quad \tanh \left( \frac{0.4\pi - \sqrt{(x-1.4\pi )^2+(y-1.17\pi )^2}}{\sqrt{2}\epsilon } \right) + 1, \end{aligned}$$
(50)
$$\begin{aligned} \psi (x,y,0)&= \bar{\psi }. \end{aligned}$$
(51)

We first perform the simulation with \(\alpha = \theta = 0.001\) and \(\bar{\psi } = 0.2\) until \(t = 100\). The results in Fig. 6 show that two droplet merge with each other to form a bigger droplet. Then, we increase the effect of surfactant using \(\alpha = \theta = 0.3\) and \(\bar{\psi } = 0.8\). From the results in Fig. 7, we can observe that two droplets keep separated all along. The energy curves and total mass for two cases are plotted in Figs. 8 and 9, respectively. Although the interfacial evolutions are different, both cases dissipate the total energy and satisfy the mass conservations.

Fig. 6
figure 6

The snapshots of \(\phi\) and \(\psi\) with \(\alpha = \theta = 0.001\) and \(\bar{\psi } = 0.2\). The subfigures a–f are at \(t = 4, ~10, ~20, ~30, ~60, ~100\)

Full size image
Fig. 7
figure 7

The snapshots of \(\phi\) and \(\psi\) with \(\alpha = \theta = 0.3\) and \(\bar{\psi } = 0.8\). The subfigures a–f are at \(t = 4, ~10, ~20, ~30, ~60, ~100\)

Full size image
Fig. 8
figure 8

Energy curves of two surfactant-laden droplets with respect to a \(\alpha = \theta = 0.001\), \(\bar{\psi } = 0.2\) and b \(\alpha = \theta = 0.3\), \(\bar{\psi } = 0.8\)

Full size image
Fig. 9
figure 9

Total mass with respect to a \(\alpha = \theta = 0.001\), \(\bar{\psi } = 0.2\) and b \(\alpha = \theta = 0.3\), \(\bar{\psi } = 0.8\)

Full size image

5.4 Surfactant-laden coarsening dynamics

The coarsening dynamics is an important benchmark problem for the CH or AC type models. The initial concentration of \(\phi\) plays an obvious role in pattern formation. Please refer to previous works for this phenomenon [12, 22, 29]. In this subsection, we investigate the surfactant-laden coarsening dynamics in 2D space by using the following initial conditions

$$\begin{aligned} \phi (x,y,0)\,= \, \bar{\phi } + 0.001\text{ rand }(x,y), \end{aligned}$$
(52)
$$\begin{aligned} \psi (x,y,0)\,= \, 0.2 + 0.001\text{ rand }(x,y), \end{aligned}$$
(53)

where \(\text{ rand }(x,y)\) is the random number between \(-1\) to 1. Here, we take \(\bar{\phi } = 0\) and 0.3 to perform the simulations until \(t = 300\). The snapshots with respect to \(\bar{\phi } = 0\) and 0.3 are plotted in Figs. 10 and 11, respectively. As we can observed, the structures of pattern are obviously affected by the initial concentrations of \(\phi\). Due to the effect of nonlinear coupling between \(\phi\) and \(\psi\), the surfactant always accumulates at the interface. The normalized energy curves shown in Fig. 12 indicate the energy becomes flat if the evolution goes to steady state.

Fig. 10
figure 10

The snapshots of \(\phi\) and \(\psi\) with \(\bar{\phi } = 0\). The subfigures a–h are at \(t = 4, ~10, ~20, ~40, ~70, ~96, ~140, ~300\)

Full size image
Fig. 11
figure 11

The snapshots of \(\phi\) and \(\psi\) with \(\bar{\phi } = 0.3\). The subfigures a–h are at \(t = 4, ~10, ~20, ~40, ~70, ~96, ~140, ~300\)

Full size image
Fig. 12
figure 12

Normalized energy curves in 2D space with respect to \(\bar{\phi } = 0\) and 0.3

Full size image

Next, we consider the coarsening phenomenon in 3D space using the following initial conditions

$$\begin{aligned} \phi (x,y,z,0)\,= \, \bar{\phi } + 0.01\text{ rand }(x,y,z), \end{aligned}$$
(54)
$$\begin{aligned} \psi (x,y,z,0)\,=\, 0.2 + 0.01\text{ rand }(x,y,z). \end{aligned}$$
(55)

The simulations are performed until \(t = 50\). The results with respect to \(\bar{\phi } = 0\) and 0.3 are shown in Figs. 13 and 14. Figure 15 displays the snapshots of interfaces of \(\phi\) (green) and \(\psi\) (yellow). The normalized energy curves plotted in Fig. 16 show that the total energy is non-increasing in time.

Fig. 13
figure 13

The snapshots of coarsening dynamics in 3D space with \(\bar{\phi } = 0\). The subfigures from the top to bottom are at \(t = 4, ~8, ~15\), and 50

Full size image
Fig. 14
figure 14

The snapshots of coarsening dynamics in 3D space with \(\bar{\phi } = 0.3\). The subfigures from the top to bottom are at \(t = 4, ~8, ~15\), and 50

Full size image
Fig. 15
figure 15

The snapshots of interfaces of \(\phi\) (green) and \(\psi\) (yellow). The subfigures from the top to bottom are at \(t = 4, ~8, ~15\), and 50

Full size image
Fig. 16
figure 16

Normalized energy curves in 3D space with respect to \(\bar{\phi } = 0\) and 0.3

Full size image

6 Conclusion

We proposed a easier two-phase surfactant model which consists of two CAC type evolutional equations and developed its efficient numerical methods. By introducing a time-dependent auxiliary variable, we transformed the original equations into equivalent forms. Using the equivalent forms, we proposed first- and second-order time-accurate methods and explicitly treated all nonlinear terms. A practical splitting algorithm was adopted to decouple the auxiliary variable and phase-field variables. Thus, the proposed time-marching schemes were highly efficient because we only need to computed four linear elliptic type equations. The numerical tests indicated that the proposed schemes indeed had first- and second-order temporal accuracy and satisfied the energy dissipation law and mass conservations at numerical level. We also investigated the effect of surfactant on interfacial evolution and the effect of initial concentration on phase separation. In a upcoming work, we will extend the proposed method to a hydrodynamics coupled CAC type surfactant system, i.e., the surfactant model is solved using the present method. As for the Navier–Stokes equation, an time-dependent auxiliary variable can be introduced to treat the nonlinear advection term. To close the system, the extra governing equation can be easily defined by taking the time derivative to the kinetic energy. The implementation is similar with the procedure proposed in the present work. Moreover, the proposed time-discretized scheme can be applied to simulate binary surfactant system on curved surfaces [39] using the surface finite element method [40, 41].