1 Introduction

Wavelets, recognized as good-localized functions, are an influential instrument used in signal and image processing, computer science, quantum mechanics, communications and various further areas of science. The wavelets methods allow the improvement of very quick algorithms and give accurate solutions when compared to the normally used algorithms. Some wavelet methods such as Haar wavelets [1,2,3,4,5,6,7,8,9,10], Legendre wavelets [11,12,13,14,15,16], Chebyshev wavelets [17,18,19,20,21,22,23,24,25,26,27,28] and Gegenbauer wavelets [29,30,31,32,33,34,35,36,37,38,39] are given special attention in the literature.

Many real-life problems are related to nonlinear models occurring in various fields of science and engineering, especially in plasma physics, plasma wave, chemical physics, fluid mechanics, and solid-state physics. They can be expressed in terms of nonlinear partial differential equations. Nonlinear equations also include surface waves in compressible liquids, acoustic waves in a harmonic crystal, and hydromagnetic waves in cold plasma [47]. Nonlinear partial differential equation of the important physical model called the modified w-equation is expressed as follows:

$$ {u_t} - {u_{xxt}} + (w + 1){u^2}{u_x} - w{u_x}{u_{xx}} - u{u_{xxx}} = 0,\quad a < x < b, $$
(1)

have been solved by the suggested method for \(w = 2\) and \(w = 3.\) When \(w = 2\), Eq. (1) is transformed to

$$ {u_t} - {u_{xxt}} + 3{u^2}{u_x} - 2{u_x}{u_{xx}} - u{u_{xxx}} = 0, $$
(2)

and called as modified Camassa–Holm (mCH) equation. If initial condition is taken as \(u(x,0) = - 2{\operatorname{sech}^2}\left( \frac{x}{2} \right)\), the exact solution of Eq. (2) is [40]

\(u(x,t) = - 2{\operatorname{sech}^2}\left( {\frac{x}{2} - t} \right).\)

When \(w = 3\), Eq. (1) is transformed to

$$ {u_t} - {u_{xxt}} + 4{u^2}{u_x} - 3{u_x}{u_{xx}} - u{u_{xxx}} = 0, $$
(3)

and called as modified Degasperis–Procesi (mDP) equation. If initial condition is taken as \(u(x,\,0) = - \frac{15}{8}\sec {h^2}\left( \frac{x}{2} \right)\), the exact solution of Eq. (3) is [40]

\(u(x,0) = - \frac{15}{8}{\operatorname{sech}^2}\left( {\frac{x}{2} - \frac{5t}{4}} \right).\)

For nonlinear partial differential equation in

\(\dot u(x,t) = F(u,u^{\prime},u^{\prime\prime},\,...\,,{u^{(r)}}),\)the quasilinearization method gives a sequence of repetition for linear partial differential equations:

$$ {\dot u_{s + 1}}(x,t) = F({u_s},{u^{\prime}_s},{u^{\prime\prime}_s},\,...\,,u_s^{(r)}) + \sum\limits_{i = 0}^r {\left( {u_{s + 1}^{(i)} - u_s^{(i)}} \right)} \,{F_{u_s^{(i)}}}({u_s},{u^{\prime}_s},{u^{\prime\prime}_s},\,...\,,u_s^{(r)}), $$
(4)

where \({F_{u_s^{(i)}}}({u_s},{u^{\prime}_s},{u^{\prime\prime}_s},\,...\,,u_s^{(r)}) = \frac{\partial }{{\partial u_s^{(i)}}}\left( {F({u_s},{{u^{\prime}}_s},{{u^{\prime\prime}}_s},\,...\,,u_s^{(r)})} \right)\), \( \dot u(x,t) = \frac{\partial u(x,t)}{{\partial t}}\), \( u^{\prime}(x,t) = \frac{\partial u(x,t)}{{\partial x}}\) and \({u_0}(x,t)\) is selected as any function that provides boundary and initial conditions [41].

In this study, integration of the Jacobi polynomial \(P_m^{(\alpha ,\beta )}(x)\) from − 1 to x has been found, the general procedures for obtaining operational matrices of integration of Jacobi wavelets have been introduced and operational matrix of rth integration of Jacobi wavelets and two theorems about error analysis of presented method have been given for the first time in this study. Presented technique is built on the approach to the solution of problem by the truncated Jacobi wavelet series. System of algebraic equations is attained by handling the Chebyshev collocation points. If system of algebraic equations is solved, unknown coefficients of the Jacobi wavelet series may be obtained. Therefore, implicit shape of the approximate solutions of nonlinear partial differential equations can be found using Jacobi wavelet series with the obtained coefficients. This process can be performed to the modified Camassa–Holm and Degasperis–Procesi equations by utilization of quasilinearization technique. Approximate results indicated that the Jacobi wavelet collocation method has a quite superior accuracy even at a minor number of grid points.

2 Jacobi polynomials

For m ∈ Z+, Jacobi polynomials of degree \(m\) are defined as \(P_m^{(\alpha ,\beta )}(x)\) where \(\alpha > - 1\) and \(\beta > - 1\) on the range [− 1, 1]. Recurrence formulae of their may be given as:

$$ P_0^{(\alpha ,\beta )}(x) = 1,\quad P_1^{(\alpha ,\beta )}(x) = \frac{1}{2}(\alpha + \beta + 2)x + \frac{1}{2}(\alpha - \beta ), $$
$$ P_{m + 1}^{(\alpha ,\beta )}(x) = (a_m^{(\alpha ,\beta )}\,x + b_m^{(\alpha ,\beta )})P_m^{(\alpha ,\beta )}(x) - c_m^{(\alpha ,\beta )}P_{m - 1}^{(\alpha ,\beta )}(x),\quad m \geqslant 1 $$
(5)

where

\(a_m^{(\alpha ,\beta )} = \frac{(2m + \alpha + \beta + 1)(2m + \alpha + \beta + 2)}{{2(m + 1)(m + \alpha + \beta + 1)}},\)

\(b_m^{(\alpha ,\beta )} = \frac{{(2m + \alpha + \beta + 1)({\alpha^2} - {\beta^2})}}{2(m + 1)(m + \alpha + \beta + 1)(2m + \alpha + \beta )},\)

\(c_m^{(\alpha ,\beta )} = \frac{(2m + \alpha + \beta + 2)(m + \alpha )(m + \beta )}{{(m + 1)(m + \alpha + \beta + 1)(2m + \alpha + \beta )}}.\)

The generating function for Jacobi polynomials are given as:

$$ {2^{\alpha + \beta }}{R^{ - 1}}{(1 - t + R)^{ - \alpha }}{(1 + t + R)^{ - \beta }} = \sum\limits_{m = 0}^\infty {P_m^{(\alpha ,\beta )}(x)\,\,{t^m}} , $$

where \(R = {(1 - 2xt + {t^2})^{{\raise0.5ex\hbox{$\scriptstyle 1$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle 2$}}}}\). Some relations of Jacobi polynomials can be given as [42]:

$$ \frac{{\text{d}}}{{{\text{d}}x}}(P_m^{(\alpha ,\beta )}(x)) = \frac{1}{2}(m + \alpha + \beta + 1)P_{m - 1}^{(\alpha + 1,\beta + 1)}(x), $$
(6)
$$ \begin{aligned}& (m + \alpha + \beta + 1)P_{m - 1}^{(\alpha + 1,\beta + 1)}(x)\\ &\quad = (m + \alpha )P_{m - 1}^{(\alpha ,\beta + 1)}(x) + (m + \beta )P_{m - 1}^{(\alpha + 1,\beta )}(x), \end{aligned} $$
$$ (2m + \alpha + \beta )P_m^{(\alpha - 1,\beta )}(x) = (m + \alpha + \beta )P_m^{(\alpha ,\beta )}(x) - (m + \beta )P_{m - 1}^{(\alpha ,\beta )}(x), $$
(7)
$$ (2m + \alpha + \beta )P_m^{(\alpha ,\beta - 1)}(x) = (m + \alpha + \beta )P_m^{(\alpha ,\beta )}(x) + (m + \alpha )P_{m - 1}^{(\alpha ,\beta )}(x), $$
(8)
$$ P_m^{(\alpha ,\beta )}( - x) = {( - 1)^m}P_m^{(\beta ,\alpha )}(x), $$
$$ P_m^{(\alpha ,\beta )}(1) = \frac{\Gamma (m + \alpha + 1)}{{m!\,\Gamma (\alpha + 1)}}, $$
$$ P_m^{(\alpha ,\beta )}( - 1) = \frac{{{{( - 1)}^m}\Gamma (m + \beta + 1)}}{m!\,\Gamma (\beta + 1)}, $$
$$ \frac{{\text{d}}}{{{\text{d}}x}}\left[ {{{(1 - x)}^{\alpha + 1}}{{(1 + x)}^{\beta + 1}}P_{m + 1}^{(\alpha + 1,\beta + 1)}(x)} \right] = 2m{(1 - x)^\alpha }{(1 + x)^\beta }P_m^{(\alpha ,\beta )}(x), $$
$$ 2m\int {{{(1 - x)}^\alpha }{{(1 + x)}^\beta }P_m^{(\alpha ,\beta )}(x)\,\,{\text{d}}x = } {(1 - x)^{\alpha + 1}}{(1 + x)^{\beta + 1}}P_{m + 1}^{(\alpha + 1,\beta + 1)}(x). $$

The following relation can be obtained by integration of the Jacobi polynomial \(P_m^{(\alpha ,\beta )}(x)\) from − 1 to x:

$$ \begin{array}{l} \int\limits_{ - 1}^x {P_m^{(\alpha ,\beta )}(t)} \,{\rm{d}}t = \left. {\frac{2}{{(m + \lambda - 1)}}\left[ {P_{m + 1}^{(\alpha - 1,\beta - 1)}(t)} \right]} \right|_{ - 1}^x\\ = \left. {\frac{2}{{(m + \lambda - 1)}}\left[ {\frac{{(m + \lambda - 1)}}{{(2m + \lambda )}}P_{m + 1}^{(\alpha ,\beta - 1)}(t) - \frac{{(m + \beta )}}{{(2m + \lambda )}}P_m^{(\alpha ,\beta - 1)}(t)} \right]\,} \right|_{ - 1}^x\\ = \,\frac{2}{{(m + \lambda - 1)}}\left[ {\frac{{(m + \lambda - 1)}}{{(2m + \lambda )}}\left( {\frac{{(m + \lambda )}}{{(2m + \lambda + 1)}}P_{m + 1}^{(\alpha ,\beta )}(t) + \frac{{(m + \alpha + 1)}}{{(2m + \lambda + 1)}}P_m^{(\alpha ,\beta )}(t)} \right)} \right.\\ - \left. {\left. {\frac{{(m + \beta )}}{{(2m + \lambda )}}\left( {\frac{{(m + \lambda - 1)}}{{(2m + \lambda - 1)}}P_m^{(\alpha ,\beta )}(t) + \frac{{(m + \alpha )}}{{(2m + \lambda - 1)}}P_{m - 1}^{(\alpha ,\beta )}(t)} \right)} \right]} \right|_{ - 1}^x\\ = \,2\left\{ {\frac{{(m + \lambda )}}{{(2m + \lambda + 1)(2m + \lambda )}}P_{m + 1}^{(\alpha ,\beta )}(x) + \frac{{(\alpha - \beta )}}{{(2m + \lambda + 1)(2m + \lambda - 1)}}P_m^{(\alpha ,\beta )}(x)} \right.\\ \left. {\,\,\,\, - \frac{{(m + \alpha )(m + \beta )}}{{(2m + \lambda )(2m + \lambda - 1)(m + \lambda - 1)}}P_{m - 1}^{(\alpha ,\beta )}(x)} \right\} - \,2\left\{ {\frac{{(m + \lambda )}}{{(2m + \lambda + 1)(2m + \lambda )}}P_{m + 1}^{(\alpha ,\beta )}( - 1)} \right.\\ \left. { + \frac{{(\alpha - \beta )}}{{(2m + \lambda + 1)(2m + \lambda - 1)}}P_m^{(\alpha ,\beta )}( - 1) - \frac{{(m + \alpha )(m + \beta )}}{{(2m + \lambda )(2m + \lambda - 1)(m + \lambda - 1)}}P_{m - 1}^{(\alpha ,\beta )}( - 1)} \right\},\quad \,m \ge 1 \end{array} $$

where \(\lambda = \alpha + \beta + 1\).

Jacobi polynomials are orthogonal polynomials according to the weight function \(w(x) = {(1 - x)^\alpha }{(1 + x)^\beta }\) on the range [− 1, 1] as [42]:

$$ \int\limits_{ - 1}^1 {{{(1 - x)}^\alpha }{{(1 + x)}^\beta }} P_n^{(\alpha ,\beta )}(x)P_m^{(\alpha ,\beta )}(x)\,{\text{d}}x = \left\{ \begin{gathered} L_m^{(\alpha ,\beta )},\,\,\,\,\,\,\,\,\,m = n \hfill \\ \,\,\,\,0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m \ne n \hfill \\ \end{gathered} \right. $$

where

$$ L_m^{(\alpha ,\beta )} = \frac{{{2^{\alpha + \beta + 1}}\Gamma (m + \alpha + 1)\Gamma (m + \beta + 1)}}{(2m + \alpha + \beta + 1)\,m!\,\Gamma (m + \alpha + \beta + 1)} $$

is the normalizing factor.

3 Jacobi wavelet method

Wavelets are composed of functions family generated by dilation (or contraction) and translation of a single function named the mother wavelet. a and b are named the as dilation parameter and translation parameter. If translation and dilation parameters change continuously, continuous wavelets family may be obtained as follows [43]:

$$ {\psi_{a,b}}(x) = {\left| a \right|^{1/2}}\psi \left( {\frac{x - b}{a}} \right),\quad a,b \in R,\quad a \ne 0. $$
(9)

Jacobi wavelets are written as

$${\psi_{nm}}(x) = \psi (k,n,m,x). $$

where k = 0, 1, 2, …, n = 1, 2, …, 2k, degree of the Jacobi polynomial is shown as m, \( \alpha ,\beta > - 1\) are parameters and x ∈ [0,1). Jacobi wavelets can be defined as:

$$ \psi_{nm}(x) = \left\{ \begin{gathered} \frac{{{2^{\frac{k + 1}{2}}}}}{{\sqrt {L_m^{(\alpha ,\beta )}} }}P_m^{(\alpha ,\beta )}({2^{k + 1}}x - 2n + 1),\,\,\,\,\,\,\,\,\frac{n - 1}{{2^k}} \leqslant x < \frac{n}{{2^k}},\mathop {}\limits \hfill \\ 0\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{otherwise}} \hfill \\ \end{gathered} \right. $$
(10)

where \( P_m^{(\alpha ,\beta )}({2^{k + 1}}x - 2n + 1)\) is the Jacobi polynomial whose degree is m and it is orthogonal polynomial according to the weight function

$$ \begin{aligned} {w_n}(x) &= w({2^{k + 1}}x - 2n + 1) \\ &= {(1 - ({2^{k + 1}}x - 2n + 1))^\alpha }{(1 + ({2^{k + 1}}x - 2n + 1))^\beta } \end{aligned} $$

on interval \( 0 \leqslant x \leqslant 1\). Any finite interval \( a \leqslant y \leqslant b\) can be converted into the simple range \( 0 \leqslant x \leqslant 1\) by transformation of variable given as \( y = (b - a)x + a\).

Any function \( f(x) \in L_w^2[0,1][0,1]\) can be extended as:

$$ f(x) = \sum\limits_{n = 1}^{2^k} {\sum\limits_{m = 0}^\infty {{f_{nm}}{\psi_{nm}}(x)} } , $$
(11)

where

$$ {f_{nm}} = \left\langle {f(x),{\psi_{nm}}(x)} \right\rangle . $$
(12)

\( \left\langle {\,.\,,\,.\,} \right\rangle \) indicates the dot product according to weight function \( {w_n}(x)\) in Eq. (12).

Truncated series of Eq. (11) may be given as:

$$ f(x) \cong \sum\limits_{n = 1}^{2^k} {\sum\limits_{m = 0}^{M - 1} {{f_{nm}}{\psi_{nm}}(x)} } = {{\mathbf{C}}^{\mathbf{T}}}\,{\mathbf{\Psi (}}x{\mathbf{)}}, $$
(13)

where \( {\mathbf{\Psi (}}x{\mathbf{)}}\) and \({\mathbf{C}}\) are \( {2^k}M \times 1\) dimensional columns vectors assumed as:

$$ {{\mathbf{C}}^{\mathbf{T}}} = [{f_{10}},\,\,{f_{11}},\,\,...,\,\,{f_{1M - 1}},\,\,{f_{20}},\,\,...,\,\,{f_{2M - 1}},\,\,...,\,\,{f_{{2^k}0}},\,\,...,\,\,{f_{{2^k}M - 1}}\,\,], $$
$$ {\mathbf{\Psi (}}x{\mathbf{)}} = {[{\psi_{10}},\,\,{\psi_{11}},\,\,...,\,\,{\psi_{1M - 1}},\,\,{\psi_{20}},\,\,...,\,\,{\psi_{2M - 1}},\,\,...,\,\,{\psi_{{2^k}0}},\,\,...,\,\,{\psi_{{2^k}M - 1}}\,\,]^T}. $$
(14)

If the function \({\psi_{nm}}(x)\) in Eq. (10) is integrated, it may be shown as follows:

$$ {p_{nm}}(x) = \int\limits_0^x {{\psi_{nm}}(s){\text{d}}s} . $$
(15)

The following equations may be obtained by calculating \( {p_{nm}}(x)\) for \( m = 0,\)\( m = 1\) and \( m > 1\):

$$ {p_{n0}}(x) = \left\{ \begin{gathered} 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \leqslant x < \frac{n - 1}{{2^k}} \hfill \\ \frac{2(\beta + 1)}{{\lambda + 1}}{\psi_{n0}}(u) + \frac{2}{\lambda + 1}\sqrt {\frac{{L_1^{(\alpha ,\beta )}}}{{L_0^{(\alpha ,\beta )}}}} {\psi_{n1}}(u),\,\,\,\,\,\,\,\,\,\,\frac{n - 1}{{2^k}} \leqslant x < \frac{n}{{2^k}} \hfill \\ 2, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{n}{{2^k}} \leqslant x < 1 \hfill \\ \end{gathered} \right. $$
$$ {p_{n1}}(x) = \left\{ \begin{array}{l} 0,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 0 \le x < \frac{{n - 1}}{{{2^k}}}\\ - 2\left\{ {\frac{{(\lambda + 1)}}{{(\lambda + 3)(\lambda + 2)}}P_2^{(\alpha ,\beta )}( - 1) + \frac{{(\alpha - \beta )}}{{(\lambda + 3)(\lambda + 1)}}P_1^{(\alpha ,\beta )}( - 1)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_1^{(\alpha ,\beta )}}}} {\psi _{n0}}(u)\,\,\\ + \frac{{2(\alpha - \beta )}}{{(\lambda + 3)(\lambda + 1)}}{\psi _{n1}}(u)\,\,\, + \frac{{2(\lambda + 1)}}{{(\lambda + 3)(\lambda + 2)}}\sqrt {\frac{{L_2^{(\alpha ,\beta )}}}{{L_1^{(\alpha ,\beta )}}}} {\psi _{n2}}(u),\quad \quad \quad \quad \quad \quad \frac{{n - 1}}{{{2^k}}} \le x < \frac{n}{{{2^k}}}\\ 2\left\{ {\frac{{(\lambda + 1)}}{{(\lambda + 3)(\lambda + 2)}}\left( {P_2^{(\alpha ,\beta )}(1) - P_2^{(\alpha ,\beta )}( - 1)} \right) + \frac{{(\alpha - \beta )}}{{(\lambda + 3)(\lambda + 1)}}\left( {P_1^{(\alpha ,\beta )}(1) - P_1^{(\alpha ,\beta )}( - 1)} \right)} \right.\\ \left. { - \frac{{(\alpha + 1)(\beta + 1)}}{{(\lambda + 2)(\lambda + 1)\lambda }}\left( {P_0^{(\alpha ,\beta )}(1) - P_0^{(\alpha ,\beta )}( - 1)} \right)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_1^{(\alpha ,\beta )}}}} {\psi _{n0}}(u),\quad \quad \quad \quad \quad \quad \frac{n}{{{2^k}}} \le x < 1 \end{array} \right. $$
$$ {p_{nm}}(x) = \left\{ \begin{array}{l} 0,\mathop {}\limits_{\mathop {}\limits_{} } \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \le x < \frac{{n - 1}}{{{2^k}}}\\ - \,2\left\{ {\frac{{(m + \lambda )}}{{(2m + \lambda + 1)(2m + \lambda )}}P_{m + 1}^{(\alpha ,\beta )}( - 1) + \frac{{(\alpha - \beta )}}{{(2m + \lambda + 1)(2m + \lambda - 1)}}P_m^{(\alpha ,\beta )}( - 1)} \right.\\ \,\left. { - \frac{{(m + \alpha )(m + \beta )}}{{(2m + \lambda )(2m + \lambda - 1)(m + \lambda - 1)}}P_{m - 1}^{(\alpha ,\beta )}( - 1)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_m^{(\alpha ,\beta )}}}} {\psi _{n0}}(u)\\ - \frac{{2(m + \beta )(m + \alpha )}}{{(2m + \lambda )(2m + \lambda - 1)(m + \lambda - 1)}}\sqrt {\frac{{L_{m - 1}^{(\alpha ,\beta )}}}{{L_m^{(\alpha ,\beta )}}}} {\psi _{nm - 1}}(u) + \frac{{2(\alpha - \beta )}}{{(2m + \lambda + 1)(2m + \lambda - 1)}}{\psi _{nm}}(u)\,\,\\ + \frac{{2(m + \lambda )}}{{(2m + \lambda + 1)(2m + \lambda )}}\sqrt {\frac{{L_{m + 1}^{(\alpha ,\beta )}}}{{L_m^{(\alpha ,\beta )}}}} {\psi _{nm + 1}}(u),\frac{{n - 1}}{{{2^k}}} \le x < \frac{n}{{{2^k}}}\\ 2\left\{ {\frac{{(m + \lambda )}}{{(2m + \lambda + 1)(2m + \lambda )}}\left( {P_{m + 1}^{(\alpha ,\beta )}(1) - P_{m + 1}^{(\alpha ,\beta )}( - 1)} \right) + \frac{{(\alpha - \beta )}}{{(2m + \lambda + 1)(2m + \lambda - 1)}}\left( {P_m^{(\alpha ,\beta )}(1) - P_m^{(\alpha ,\beta )}( - 1)} \right)} \right.\\ \left. {\, - \frac{{(m + \alpha )(m + \beta )}}{{(2m + \lambda )(2m + \lambda - 1)(m + \lambda - 1)}}\left( {P_{m - 1}^{(\alpha ,\beta )}(1) - P_{m - 1}^{(\alpha ,\beta )}( - 1)} \right)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_m^{(\alpha ,\beta )}}}} {\psi _{n0}}(u),\,\frac{n}{{{2^k}}} \le x < 1 \end{array} \right. $$

where \( \lambda = \alpha + \beta + 1\) and u = 2k+1x−2n + 1. If \( {\mathbf{\Psi (}}x{\mathbf{)}}\) column vector is integrated, the following matrix representation may be obtained:

$$ \int\limits_0^x {{\mathbf{\Psi (}}s{\mathbf{)}}{\text{d}}s} \, = {[{p_{10}},\,\,{p_{11}},\,\,...,\,\,{p_{1M - 1}},\,\,{p_{20}},\,\,...,\,\,{p_{2M - 1}},\,\,...,\,\,{p_{{2^k}0}},\,\,...,\,\,{p_{{2^k}M - 1}}\,\,]^T} = {{\mathbf{P}}_{\mathbf{1}}}\,{{{\varvec{\Psi}}}_{\mathbf{1}}}{\mathbf{(}}x{\mathbf{)}}, $$
(16)

where

$$ {{{\varvec{\Psi}}}_{\mathbf{1}}}{\mathbf{(}}x{\mathbf{)}} = {[{\psi_{10}},\,\,{\psi_{11}},\,\,...,\,\,{\psi_{1M}},\,\,{\psi_{20}},\,\,...,\,\,{\psi_{2M}},\,\,...,\,\,{\psi_{{2^k}0}},\,\,...,\,\,{\psi_{{2^k}M}}\,\,]^T}, $$
$$ {{\mathbf{L}}_{\mathbf{1}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{2(\beta - 1)}}{{\lambda + 1}}}&{\frac{2}{{\lambda + 1}}\sqrt {\frac{{L_1^{(\alpha ,\beta )}}}{{L_0^{(\alpha ,\beta )}}}} }&0&0& \cdots &0&0&0\\ { - 2\left\{ {\frac{{(\lambda + 1)}}{{(\lambda + 3)(\lambda + 2)}}P_2^{(\alpha ,\beta )}( - 1) + \frac{{(\alpha - \beta )}}{{(\lambda + 3)(\lambda + 1)}}P_1^{(\alpha ,\beta )}( - 1)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_1^{(\alpha ,\beta )}}}} }&{\frac{{2(\alpha - \beta )}}{{(\lambda + 3)(\lambda + 1)}}}&{\frac{{2(\lambda + 1)}}{{(\lambda + 3)(\lambda + 2)}}\sqrt {\frac{{L_2^{(\alpha ,\beta )}}}{{L_1^{(\alpha ,\beta )}}}} }&0& \cdots &0&0&0\\ \begin{array}{l} - \,2\left\{ {\frac{{(\lambda + 2)}}{{(\lambda + 5)(\lambda + 4)}}P_3^{(\alpha ,\beta )}( - 1) + \frac{{(\alpha - \beta )}}{{(\lambda + 5)(\lambda + 3)}}P_2^{(\alpha ,\beta )}( - 1)} \right.\\ \,\,\,\,\,\,\,\left. { - \,\,\frac{{(\alpha + 2)(\beta + 2)}}{{(\lambda + 4)(\lambda + 3)(\lambda + 1)}}P_1^{(\alpha ,\beta )}( - 1)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_2^{(\alpha ,\beta )}}}} \end{array}&{\frac{{ - 2(\beta + 2)(\alpha + 2)}}{{(\lambda + 4)(\lambda + 3)(\lambda + 1)}}\sqrt {\frac{{L_1^{(\alpha ,\beta )}}}{{L_2^{(\alpha ,\beta )}}}} }&{\frac{{2(\alpha - \beta )}}{{(\lambda + 5)(\lambda + 3)}}}&{\frac{{2(\lambda + 2)}}{{(\lambda + 5)(\lambda + 4)}}\sqrt {\frac{{L_3^{(\alpha ,\beta )}}}{{L_2^{(\alpha ,\beta )}}}} }& \cdots &0&0&0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ \begin{array}{l} - \,2\left\{ {\frac{{(M + \lambda - 1)}}{{(2M + \lambda - 1)(2M + \lambda - 2)}}P_M^{(\alpha ,\beta )}( - 1) + \frac{{(\alpha - \beta )}}{{(2M + \lambda - 1)(2M + \lambda - 3)}}P_{M - 1}^{(\alpha ,\beta )}( - 1)} \right.\\ \,\,\,\,\,\,\,\left. { - \,\,\,\frac{{(M + \alpha - 1)(M + \beta - 1)}}{{(2M + \lambda - 2)(2M + \lambda - 3)(M + \lambda - 2)}}P_{M - 2}^{(\alpha ,\beta )}( - 1)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_{M - 1}^{(\alpha ,\beta )}}}} \end{array}&0&0&0& \cdots &{\frac{{ - 2(M + \beta - 1)\,(M + \alpha - 1)}}{{(2M + \lambda - 2)(2M + \lambda - 3)(M + \lambda - 2)}}\sqrt {\frac{{L_{M - 2}^{(\alpha ,\beta )}}}{{L_{M - 1}^{(\alpha ,\beta )}}}} }&{\frac{{2(\alpha - \beta )}}{{(2M + \lambda - 1)(2M + \lambda - 3)}}}&{\frac{{2(M + \lambda - 1)}}{{(2M + \lambda - 1)(2M + \lambda - 2)}}\sqrt {\frac{{L_M^{(\alpha ,\beta )}}}{{L_{M - 1}^{(\alpha ,\beta )}}}} } \end{array}} \right] $$
$$ {{\mathbf{F}}_{\mathbf{1}}} = \left[ {\begin{array}{*{20}{c}} 2&{\mathop 0\limits_{} }& \cdots &0\\ \begin{array}{l} 2\left\{ {\frac{{(\lambda + 1)}}{{(\lambda + 3)(\lambda + 2)}}\left( {P_2^{(\alpha ,\beta )}(1) - P_2^{(\alpha ,\beta )}( - 1)} \right) + \frac{{(\alpha - \beta )}}{{(\lambda + 3)(\lambda + 1)}}\left( {P_1^{(\alpha ,\beta )}(1) - P_1^{(\alpha ,\beta )}( - 1)} \right)} \right.\\ \left. {\,\,\,\, - \frac{{(\alpha + 1)(\beta + 1)}}{{(\lambda + 2)(\lambda + 1)\lambda }}\left( {P_0^{(\alpha ,\beta )}(1) - P_0^{(\alpha ,\beta )}( - 1)} \right)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_1^{(\alpha ,\beta )}}}} {\psi _{n0}}(u) \end{array}&0& \cdots &0\\ \vdots & \vdots & \ddots &0\\ \begin{array}{l} 2\left\{ {\frac{{(M + \lambda )}}{{(2M + \lambda + 1)(2M + \lambda )}}\left( {P_{M + 1}^{(\alpha ,\beta )}(1) - P_{M + 1}^{(\alpha ,\beta )}( - 1)} \right) + \frac{{(\alpha - \beta )}}{{(2M + \lambda + 1)(2M + \lambda - 1)}}\left( {P_M^{(\alpha ,\beta )}(1) - P_M^{(\alpha ,\beta )}( - 1)} \right)} \right.\\ \,\,\,\,\,\,\,\left. {\, - \frac{{(M + \alpha )(M + \beta )}}{{(2M + \lambda )(2M + \lambda - 1)(M + \lambda - 1)}}\left( {P_{M - 1}^{(\alpha ,\beta )}(1) - P_{M - 1}^{(\alpha ,\beta )}( - 1)} \right)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_{M - 1}^{(\alpha ,\beta )}}}} {\psi _{n0}}(u) \end{array}&0& \cdots &0 \end{array}} \right] $$

\( {{\mathbf{P}}_{\mathbf{1}}} = \frac{1}{{{2^{k + 1}}}}\left[ {\begin{array}{*{20}{c}} {{{\mathbf{L}}_{\mathbf{1}}}}&{{{\mathbf{F}}_{\mathbf{1}}}}&{{{\mathbf{F}}_{\mathbf{1}}}}& \cdots &{{{\mathbf{F}}_{\mathbf{1}}}}&{{{\mathbf{F}}_{\mathbf{1}}}} \\ {\mathbf{0}}&{{{\mathbf{L}}_{\mathbf{1}}}}&{{{\mathbf{F}}_{\mathbf{1}}}}& \cdots &{{{\mathbf{F}}_{\mathbf{1}}}}&{{{\mathbf{F}}_{\mathbf{1}}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ {\mathbf{0}}&{\mathbf{0}}&{\mathbf{0}}& \cdots &{{{\mathbf{L}}_{\mathbf{1}}}}&{{{\mathbf{F}}_{\mathbf{1}}}} \\ {\mathbf{0}}&{\mathbf{0}}&{\mathbf{0}}& \cdots &{\mathbf{0}}&{{{\mathbf{L}}_{\mathbf{1}}}} \end{array}} \right]\)

If the vector \( {\mathbf{\Psi (}}x{\mathbf{)}}\) is integrated two times, matrix representation of integration may be denoted as:

$$ \int\limits_0^x {\int\limits_0^{x_1} {{\mathbf{\Psi (}}s{\mathbf{)}}{\text{d}}s} } {\text{d}}{x_1} = \int\limits_0^x {{{\mathbf{P}}_{\mathbf{1}}}\,{{{\varvec{\Psi}}}_{\mathbf{1}}}{\mathbf{(}}{x_{\mathbf{1}}}{\mathbf{)}}} {\text{d}}{x_1} = {{\mathbf{P}}_{\mathbf{1}}}\int\limits_0^x {{{{\varvec{\Psi}}}_{\mathbf{1}}}{\mathbf{(}}{x_{\mathbf{1}}}{\mathbf{)}}{\text{d}}{x_1}} = {{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{{\varvec{\Psi}}}_{\mathbf{2}}}{\mathbf{(}}x{\mathbf{)}} \ne {\mathbf{P}}_{\mathbf{1}}^{\mathbf{2}}{\mathbf{\Psi (}}x{\mathbf{)}}. $$

The rth integration of the vector \( {\mathbf{\Psi (}}x{\mathbf{)}}\) may be denoted as:where

$$ \int\limits_0^x {\int\limits_0^{x_1} {\int\limits_0^{x_2} \cdots } } \int\limits_0^{{x_{r - 1}}} {{\mathbf{\Psi (}}s{\mathbf{)}}} \,{\text{d}}s{\text{d}}{x_{r - 1}}{\text{d}}{x_{r - 2}} \cdots {\text{d}}{x_1} = {{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}} \cdots {{\mathbf{P}}_{\mathbf{r}}}\,{{{\varvec{\Psi}}}_{\mathbf{r}}}{\mathbf{(}}x{\mathbf{)}} \ne {\mathbf{P}}_{\mathbf{1}}^{\mathbf{r}}{\mathbf{\Psi (}}x{\mathbf{)}}, $$
$$ {{{\varvec{\Psi}}}_{\mathbf{r}}}{\mathbf{(}}x{\mathbf{)}} = {[{\psi_{10}},\,\,{\psi_{11}},\,\,...,\,\,{\psi_{1M + r - 1}},\,\,{\psi_{20}},\,\,...\,,\,\,{\psi_{2M + r - 1}},\,\,...\,,\,\,{\psi_{{2^k}0}},\,\,...\,,\,\,{\psi_{{2^k}M + r - 1}}\,\,]^T}. $$
(17)

\( {{\mathbf{L}}_{\mathbf{r}}}\,\,{\text{and }}\,{{\mathbf{F}}_{\mathbf{r}}}\,\,\) are \( (M + r - 1) \times (M + r)\) dimension matrices, \( \,{{\mathbf{P}}_{{\mathbf{r}}\,}}\) is a \( {2^k}(M + r - 1) \times {2^k}(M + r)\) dimension matrix and the matrices \(\,{{\mathbf{P}}_{{\mathbf{r}}\,}}\), \( {{\mathbf{L}}_{\mathbf{r}}}\,\,{\text{and }}\,{{\mathbf{F}}_{\mathbf{r}}}\,\,\) have the following form:

\( {{\mathbf{P}}_{\mathbf{r}}} = \frac{1}{{{2^{k + 1}}}}\left[ {\begin{array}{*{20}{c}} {{{\mathbf{L}}_{\mathbf{r}}}}&{{{\mathbf{F}}_{\mathbf{r}}}}&{{{\mathbf{F}}_{\mathbf{r}}}}& \cdots &{{{\mathbf{F}}_{\mathbf{r}}}}&{{{\mathbf{F}}_{\mathbf{r}}}} \\ {\mathbf{0}}&{{{\mathbf{L}}_{\mathbf{r}}}}&{{{\mathbf{F}}_{\mathbf{r}}}}& \cdots &{{{\mathbf{F}}_{\mathbf{r}}}}&{{{\mathbf{F}}_{\mathbf{r}}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ {\mathbf{0}}&{\mathbf{0}}&{\mathbf{0}}& \cdots &{{{\mathbf{L}}_{\mathbf{r}}}}&{{{\mathbf{F}}_{\mathbf{r}}}} \\ {\mathbf{0}}&{\mathbf{0}}&{\mathbf{0}}& \cdots &{\mathbf{0}}&{{{\mathbf{L}}_{\mathbf{r}}}} \end{array}} \right]\)

$$ {{\mathbf{F}}_{\mathbf{r}}} = \left[ {\begin{array}{*{20}{l}} 2&0& \cdots &0\\ \begin{array}{l} 2\left\{ {\frac{{(\lambda + 1)}}{{(\lambda + 3)(\lambda + 2)}}\left( {P_2^{(\alpha ,\beta )}(1) - P_2^{(\alpha ,\beta )}( - 1)} \right) + \frac{{(\alpha - \beta )}}{{(\lambda + 3)(\lambda + 1)}}\left( {P_1^{(\alpha ,\beta )}(1) - P_1^{(\alpha ,\beta )}( - 1)} \right)} \right.\\ \left. { - \frac{{(\alpha + 1)(\beta + 1)}}{{(\lambda + 2)(\lambda + 1)\lambda }}\left( {P_0^{(\alpha ,\beta )}(1) - P_0^{(\alpha ,\beta )}( - 1)} \right)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_1^{(\alpha ,\beta )}}}} {\psi _{n0}}(u) \end{array}&0& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ \begin{array}{l} 2\left\{ {\frac{{(M + \lambda )}}{{(2M + \lambda + 1)(2M + \lambda )}}\left( {P_{M + 1}^{(\alpha ,\beta )}(1) - P_{M + 1}^{(\alpha ,\beta )}( - 1)} \right) + \frac{{(\alpha - \beta )}}{{(2M + \lambda + 1)(2M + \lambda - 1)}}\left( {P_M^{(\alpha ,\beta )}(1) - P_M^{(\alpha ,\beta )}( - 1)} \right)} \right.\\ \,\,\,\,\,\,\,\left. { - \frac{{(M + \alpha )(M + \beta )}}{{(2M + \lambda )(2M + \lambda - 1)(M + \lambda - 1)}}\left( {P_{M - 1}^{(\alpha ,\beta )}(1) - P_{M - 1}^{(\alpha ,\beta )}( - 1)} \right)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_{M - 1}^{(\alpha ,\beta )}}}} {\psi _{n0}}(u) \end{array}&0& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ \begin{array}{l} 2\left\{ {\frac{{(M + r + \lambda - 1)}}{{(2M + 2r + \lambda - 1)(2M + 2r + \lambda - 2)}}\left( {P_{M + r}^{(\alpha ,\beta )}(1) - P_{M + r}^{(\alpha ,\beta )}( - 1)} \right) + \frac{{(\alpha - \beta )}}{{(2M + 2r + \lambda - 1)(2M + 2r + \lambda - 3)}}\left( {P_{M + r - 1}^{(\alpha ,\beta )}(1) - P_{M + r - 1}^{(\alpha ,\beta )}( - 1)} \right)} \right.\\ \,\,\,\,\,\,\,\left. {\, - \frac{{(M + r + \alpha - 1)(M + r + \beta - 1)}}{{(2M + 2r + \lambda - 2)(2M + 2r + \lambda - 3)(M + r + \lambda - 2)}}\left( {P_{M + r - 2}^{(\alpha ,\beta )}(1) - P_{M + r - 2}^{(\alpha ,\beta )}( - 1)} \right)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_{M + r - 2}^{(\alpha ,\beta )}}}} {\psi _{n0}}(u) \end{array}&0& \cdots &0 \end{array}} \right] $$

\( {{\mathbf{L}}_{\mathbf{r}}} = \left[ {\begin{array}{*{20}{l}} {\frac{{2(\beta - 1)}}{{\lambda + 1}}}&{\frac{2}{{\lambda + 1}}\sqrt {\frac{{L_1^{(\alpha ,\beta )}}}{{L_0^{(\alpha ,\beta )}}}} }&0& \cdots &0&0&0\\ { - 2\left\{ {\frac{{(\lambda + 1)}}{{(\lambda + 3)(\lambda + 2)}}P_2^{(\alpha ,\beta )}( - 1)\,\, + \,\,\frac{{(\alpha - \beta )}}{{(\lambda + 3)(\lambda + 1)}}P_1^{(\alpha ,\beta )}( - 1)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_1^{(\alpha ,\beta )}}}\mathop {}\limits_{\mathop {}\limits_{} } } }&{\frac{{2(\alpha - \beta )}}{{(\lambda + 3)(\lambda + 1)}}}&{\frac{{2(\lambda + 1)}}{{(\lambda + 3)(\lambda + 2)}}\sqrt {\frac{{L_2^{(\alpha ,\beta )}}}{{L_1^{(\alpha ,\beta )}}}} }& \cdots &0&0&0\\ \begin{array}{l} - \,2\left\{ {\frac{{(\lambda + 2)}}{{(\lambda + 5)(\lambda + 4)}}P_3^{(\alpha ,\beta )}( - 1)\,\, + \,\,\frac{{(\alpha - \beta )}}{{(\lambda + 5)(\lambda + 3)}}P_2^{(\alpha ,\beta )}( - 1)\mathop {}\limits_{}^{\mathop {}\limits^{} } } \right.\\ \,\left. { - \,\,\,\frac{{(\alpha + 2)(\beta + 2)}}{{(\lambda + 4)(\lambda + 3)(\lambda + 1)}}P_1^{(\alpha ,\beta )}( - 1)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_2^{(\alpha ,\beta )}}}} \end{array}&{\frac{{ - 2(\beta + 2)(\alpha + 2)}}{{(\lambda + 4)(\lambda + 3)(\lambda + 1)}}\sqrt {\frac{{L_1^{(\alpha ,\beta )}}}{{L_2^{(\alpha ,\beta )}}}} }&{\frac{{2(\alpha - \beta )}}{{(\lambda + 5)(\lambda + 3)}}}& \cdots &0&0&0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ \begin{array}{l} - \,2\left\{ {\frac{{(M + r + \lambda - 1)}}{{(2M + 2r + \lambda - 1)(2M + 2r + \lambda - 2)}}P_{M + r}^{(\alpha ,\beta )}( - 1)\,\, + \,\,\frac{{(\alpha - \beta )}}{{(2M + 2r + \lambda - 1)(2m + 2r + \lambda - 3)}}P_{M + r - 1}^{(\alpha ,\beta )}( - 1)} \right.\\ \,\,\,\,\,\,\,\left. { - \,\,\frac{{(M + r + \alpha - 1)(M + r + \beta - 1)}}{{(2M + 2r + \lambda - 2)(2M + 2r + \lambda - 3)(M + r + \lambda - 2)}}P_{m - 1}^{(\alpha ,\beta )}( - 1)} \right\}\sqrt {\frac{{L_0^{(\alpha ,\beta )}}}{{L_{M + r - 2}^{(\alpha ,\beta )}}}} \end{array}&0&0& \cdots &{\,\,\frac{{ - 2(M + r + \beta - 2)\,(M + r + \alpha - 2)}}{{(2M + 2r + \lambda - 4)(2M + 2r + \lambda - 5)(M + r + \lambda - 3)}}\sqrt {\frac{{L_{M + r - 3}^{(\alpha ,\beta )}}}{{L_{M + r - 2}^{(\alpha ,\beta )}}}} }&{\frac{{2\,(\alpha - \beta )}}{{(2M + 2r + \lambda - 3)\,(2M + 2r + \lambda - 5)}}}&{\frac{{2(M + r + \lambda - 2)}}{{(2M + 2r + \lambda - 3)\,(2M + 2r + \lambda - 4)}}\sqrt {\frac{{L_{M + r - 1}^{(\alpha ,\beta )}}}{{L_{M + r - 2}^{(\alpha ,\beta )}}}} } \end{array}} \right] \)

4 Jacobi wavelet collocation method for the mCH and mDP equations

Consider nonlinear partial differential equations in Eq. (1) with boundary and initial conditions:

$$ u(x,0) = f(x),\,\,\,\,u(0,t) = {g_0}(t),\,\,\,\,u(1,t) = {g_1}(t),\,\,\,\,{u_x}(0,t) = {g_2}(t). $$
(18)

We presume that \( {\dot u^{(3)}}(x,t)\) may be extended like truncated Jacobi wavelets series as:

$$ {\dot u^{(3)}}(x,t) = \sum\limits_{n = 1}^{\,{2^k}} {\,\sum\limits_{m = 0}^{M - 1} {{f_{nm}}{\psi_{nm}}(x)} } = {{\mathbf{C}}^{\mathbf{T}}}{\mathbf{\Psi (}}x{\mathbf{)}}, $$
(19)

where “ ” and “(3)” imply differentiation according to \( t\) and \(x\). If Eq. (19) is integrated according to \( t\) from \( {t_s}\) to \( t\) and three times according to \( x\) from \( 0\) to \( x\), we can find the following equations:

$$ {u^{(3)}}(x,t) = {u^{(3)}}(x,{t_s}) + (t - {t_s}){{\mathbf{C}}^{\mathbf{T}}}{\mathbf{\Psi (}}x{\mathbf{)}}, $$
(20)
$$ {u^{(2)}}(x,t) = {u^{(2)}}(x,{t_s}) + {u^{(2)}}(0,t) - {u^{(2)}}(0,{t_s}) + (t - {t_s}){{\mathbf{C}}^{\mathbf{T}}}{{\mathbf{P}}_{\mathbf{1}}}{{{\varvec{\Psi}}}_{\mathbf{1}}}{\mathbf{(}}x{\mathbf{)}}, $$
(21)
$$ {\dot u^{(2)}}(x,t) = {\dot u^{(2)}}(0,t) + {{\mathbf{C}}^{\mathbf{T}}}{{\mathbf{P}}_{\mathbf{1}}}{{{\varvec{\Psi}}}_{\mathbf{1}}}{\mathbf{(}}x{\mathbf{)}}, $$
(22)
$$ {u_x}(x,t) = {u_x}(x,{t_s}) + {u_x}(0,t) - {u_x}(0,{t_s})\, + x({u^{(2)}}(0,t) - {u^{(2)}}(0,{t_s})) + (t - {t_s}){{\mathbf{C}}^{\mathbf{T}}}{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{{\varvec{\Psi}}}_{\mathbf{2}}}{\mathbf{(}}x{\mathbf{)}}, $$
(23)
$$ \begin{gathered} u(x,t) = u(x,{t_s}) + u(0,t) - u(0,{t_s})\, + x({u_x}(0,t) - {u_x}(0,{t_s})) + \frac{{x^2}}{2}({u^{(2)}}(0,t) - {u^{(2)}}(0,{t_s})) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + (t - {t_s}){{\mathbf{C}}^{\mathbf{T}}}{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{{\varvec{\Psi}}}_{\mathbf{3}}}{\mathbf{(}}x{\mathbf{)}}, \hfill \\ \end{gathered} $$
(24)
$$ {u_t}(x,t) = {u_t}(0,t)\, + x{u_{xt}}(0,t) + \frac{{x^2}}{2}{\dot u^{(2)}}(0,t) + {{\mathbf{C}}^{\mathbf{T}}}{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{{\varvec{\Psi}}}_{\mathbf{3}}}{\mathbf{(}}x{\mathbf{)}}. $$
(25)

By substituting boundary and initial conditions into Eq. (18), the following equation may be obtained:

$$ \begin{gathered} \frac{1}{2}({u^{(2)}}(0,t) - {u^{(2)}}(0,{t_s})) = {g_1}(t) - {g_1}({t_s}) - ({g_2}(t) - {g_2}({t_s})) - ({g_0}(t) - {g_0}({t_s})) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - (t - {t_s}){{\mathbf{C}}^{\mathbf{T}}}{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{{\varvec{\Psi}}}_{\mathbf{3}}}{\mathbf{(}}1{\mathbf{)}}. \hfill \\ \end{gathered} $$
(26)

If Eqs. (18) and (26) are replaced into Eqs. (20–25), we can obtain the following equations:

$$ {u^{(3)}}(x,t) = (t - {t_s}){{\mathbf{C}}^{\mathbf{T}}}{\mathbf{\Psi (}}x{\mathbf{)}} + {u^{(3)}}(x,{t_s}), $$
(27)
$$ \begin{gathered} {u^{(2)}}(x,t) = {u^{(2)}}(x,{t_s}) + (t - {t_s}){{\mathbf{C}}^{\mathbf{T}}}\left[ {{{\mathbf{P}}_{\mathbf{1}}}{{{\varvec{\Psi}}}_{\mathbf{1}}}{\mathbf{(}}x{\mathbf{)}} - 2{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{{\varvec{\Psi}}}_{\mathbf{3}}}{\mathbf{(}}1{\mathbf{)}}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 2({g_2}(t) - {g_2}({t_s}))\, - 2({g_0}(t) - {g_0}({t_s})) + 2({g_1}(t) - {g_1}({t_s}))\,, \hfill \\ \end{gathered} $$
(28)
$$ {\dot u^{(2)}}(x,t) = {{\mathbf{C}}^{\mathbf{T}}}\left[ {{{\mathbf{P}}_{\mathbf{1}}}{{{\varvec{\Psi}}}_{\mathbf{1}}}{\mathbf{(}}x{\mathbf{)}} - 2{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{{\varvec{\Psi}}}_{\mathbf{3}}}{\mathbf{(}}1{\mathbf{)}}} \right]\, - 2{g^{\prime}_2}(t)\, - 2{g^{\prime}_0}(t) + 2{g^{\prime}_1}(t)\,, $$
(29)
$$ \begin{aligned} {u_x}(x,t) =& {u_x}(x,{t_s}) + (t - {t_s}){{\mathbf{C}}^{\mathbf{T}}}\\ &\left[ {{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{{\varvec{\Psi}}}_{\mathbf{2}}}{\mathbf{(}}x{\mathbf{)}} - 2x{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{{\varvec{\Psi}}}_{\mathbf{3}}}{\mathbf{(}}1{\mathbf{)}}} \right]\\ & - (1 - 2x)({g_2}(t) - {g_2}({t_s}))\, - 2x({g_0}(t) \\ &- {g_0}({t_s})) + 2x({g_1}(t) - {g_1}({t_s})), \end{aligned} $$
(30)
$$ \begin{aligned} u(x,t) = & u(x,{t_s}) + (t - {t_s}){{\mathbf{C}}^{\mathbf{T}}}\\ &\left[ {{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{{\varvec{\Psi}}}_{\mathbf{3}}}{\mathbf{(}}x{\mathbf{)}} - {x^2}{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{{\varvec{\Psi}}}_{\mathbf{3}}}{\mathbf{(}}1{\mathbf{)}}} \right] \\ & + (x - {x^2})({g_2}(t) - {g_2}({t_s})\,)\, + (1 - {x^2})({g_0}(t) \\ &- {g_0}({t_s})) + {x^2}({g_1}(t) - {g_1}({t_s}))\,, \end{aligned} $$
(31)
$$ \begin{aligned} {u_t}(x,t) = &{{\mathbf{C}}^{\mathbf{T}}}\left[ {{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{{\varvec{\Psi}}}_{\mathbf{3}}}{\mathbf{(}}x{\mathbf{)}} - {x^2}{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{{\varvec{\Psi}}}_{\mathbf{3}}}{\mathbf{(}}1{\mathbf{)}}} \right]\\ & + (x - {x^2}){g^{\prime}_2}(t) + (1 - {x^2}){g^{\prime}_0}(t) + {x^2}){g^{\prime}_1}(t). \end{aligned} $$
(32)

Using quasilinearization technique, Eq. (1) can be transformed into the sequence of linear differential equations. Nonlinear terms in Eq. (1) may be written as:

$$ \begin{aligned} &{({u^2}(x,t){\mkern 1mu} {u_x}(x,t))^{l + 1}} \cong {\mkern 1mu} 2{u^l}(x,t){\mkern 1mu} u_x^l(x,t){u^{l + 1}}(x,t){\mkern 1mu} \\ &\quad+ {u^{{l^2}}}(x,t){\mkern 1mu} u_x^{l + 1}(x,t) - 2{u^{{l^2}}}(x,t){\mkern 1mu} u_x^l(x,t) \end{aligned} $$
(33)
$$ \begin{aligned}& {({u_x}(x,t)\,{u_{xx}}(x,t))^{l + 1}} \cong \,u_x^{l + 1}(x,t)\,u_{xx}^l(x,t) \\ &\quad+ u_x^l(x,t)\,u_{xx}^{l + 1}(x,t) - u_x^l(x,t)\,u_{xx}^l(x,t) \end{aligned} $$
(34)
$$ \begin{aligned} & {(u(x,t)\,{u_{xxx}}(x,t))^{l + 1}} \cong \,u^{l + 1}(x,t)\,u_{xxx}^l(x,t) \\ &\quad+ u^l(x,t)\,u_{xxx}^{l + 1}(x,t) - u^l(x,t)\,u_{xxx}^l(x,t). \end{aligned} $$
(35)

By replacing Eqs. (33), (34) and (35) into Eq. (1), transformed equation is found as:

$$ \begin{aligned} & u_t^{l + 1}(x,t) - \,u_{xxt}^{l + 1}(x,t) + \left( {2(w + 1){u^l}(x,t)\,u_x^l(x,t) - u_{xxx}^l(x,t)} \right)\,{u^{l + 1}}(x,t)\, \\ & \quad + \left( {(w + 1){{\left( {{u^l}(x,t)} \right)}^2} - wu_{xx}^l(x,t)} \right)\,u_x^{l + 1}(x,t)\, - wu_x^l(x,t)u_{xx}^{l + 1}(x,t) - {u^l}(x,t)u_{xxx}^{l + 1}(x,t) \\ & \quad = 2(w + 1){\left( {u^l(x,t)} \right)^2}u_x^l(x,t) - wu_x^l(x,t)u_{xx}^l(x,t) - {u^l}(x,t)\,u_{xxx}^l(x,t) \\ \end{aligned} $$
(36)

where \( l = 0,1,2,\,...\) and it is called index of quasilinearization technique. \( {u^0}(x,t)\) which provides boundary and initial conditions is taken as

$$ {u^0}(x,t) = u(x,{t_s}) + (x - {x^2})({g_2}(t) - {g_2}({t_s})\,)\, + (1 - {x^2})({g_0}(t) - {g_0}({t_s})) + {x^2}({g_1}(t) - {g_1}({t_s})), $$
(37)

which satisfies initial/boundary conditions. Substituting Eqs. (27–32) into Eq. (36), we obtain the following equation:

$$\begin{array}{l} \Delta t\,{{\bf{C}}^{\bf{T}}}\left[ \begin{array}{l} \left( {\frac{1}{{\Delta t}} + 2(w + 1){u^l}(x,t)\,u_x^l(x,t) - u_{xxx}^l(x,t)} \right){{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{\mathbf{\Psi}} _{\mathbf{3}}}(x) + \left( {(w + 1){{\left( {{u^l}(x,t)} \right)}^2} - wu_{xx}^l(x,t)} \right){{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{\Psi}} _2}(x)\\ - \left( {1 + wu_x^l(x,t)} \right)\,{{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{\Psi}} _{\mathbf{1}}}(x) - {u^l}(x,t)\,{mathbf{\Psi}} (x)\\ + \left( {\frac{{2 - {x^2}}}{{\Delta t}} + {x^2}\left( {2(w + 1){u^l}(x,t)\,u_x^l(x,t) - u_{xxx}^l(x,t)} \right) - 2x\left( {(w + 1){{\left( {{u^l}(x,t)} \right)}^2} - wu_{xx}^l(x,t)} \right) + 2wu_x^l(x,t)} \right){{\mathbf{P}}_{\mathbf{1}}}{{\mathbf{P}}_{\mathbf{2}}}{{\mathbf{P}}_{\mathbf{3}}}{{\mathbf{\Psi}} _1}(1) \end{array} \right]\\ = 2(w + 1){\left( {{u^l}(x,t)} \right)^2}u_x^l(x,t) - wu_x^l(x,t)\,u_{xx}^l(x,t) - {u^l}(x,t)\,u_{xxx}^l(x,t)\\ - \left( {2(w + 1){u^l}(x,t)\,u_x^l(x,t) - u_{xxx}^l(x,t)} \right)\,\,\left( {{u^l}(x,{t_s}) + (x - {x^2})\left( {{g_2}(t) - {g_2}({t_s})} \right) + (1 - {x^2})\,\left( {{g_0}(t) - {g_0}({t_s})} \right) + {x^2}\left( {{g_1}(t) - {g_1}({t_s})} \right)} \right)\,\\ - \left( {(w + 1){{\left( {{u^l}(x,t)} \right)}^2} - wu_{xx}^l(x,t)} \right)\left( {u_x^l(x,{t_s}) + (1 - 2x)\left( {{g_2}(t) - {g_2}({t_s})} \right) - 2x)\,\left( {{g_0}(t) - {g_0}({t_s})} \right) + 2x\left( {{g_1}(t) - {g_1}({t_s})} \right)} \right)\\ + wu_x^l(x,t)\left( {u_{xx}^l(x,{t_s}) - 2\left( {{g_2}(t) - {g_2}({t_s})} \right) - 2\,\left( {{g_0}(t) - {g_0}({t_s})} \right) + 2\left( {{g_1}(t) - {g_1}({t_s})} \right)} \right) + {u^l}(x,t)u_{xxx}^l(x,{t_s})\,\\ + ({x^2} - x - 2)g_2^\prime (t)\, + ({x^2} - 3)g_0^\prime (t) + (2 - {x^2})g_1^\prime (t)\,\,\,\,\, \end{array}$$
(38)

where \( \Delta t = t - {t_s}\).

The collocation points may be selected as \({2^{k + 1}}{x_{ni}} - 2n + 1 = \cos \frac{((M + 1) - i)\pi }{{(M + 1)}}\) or

$$ {x_{ni}} = \frac{1}{{{2^{k + 1}}}}\left( {2n - 1 + \cos \frac{((M + 1) - i)\pi }{{(M + 1)}}} \right),\quad i = 1,\,\,2,\,\,...,\,M\quad n = 1,\,\,2,\,\,...,\,\,{2^k}. $$
(39)

Replacing the collocation points \( x \to {x_{ni}}\) and time variable \( t \to {t_{s + 1}}\) into Eq. (38), vectors \( {\mathbf{\Psi (}}{x_{{\mathbf{ni}}}}{\mathbf{)}}\),\( {{{\varvec{\Psi}}}_{\mathbf{1}}}{\mathbf{(}}{x_{{\mathbf{ni}}}}{\mathbf{)}}\) and \( {{{\varvec{\Psi}}}_{\mathbf{r}}}{\mathbf{(}}{x_{{\mathbf{ni}}}}{\mathbf{)}}\) may be achieved. We can find system of algebraic equations from Eq. (38) whose matrix notation may be written as:

$$ {{\mathbf{C}}^{\mathbf{T}}}{\mathbf{U}} = {\mathbf{B}}, $$
(40)

where \( {\mathbf{B}}\) and \({\mathbf{C}}\) are \( {2^k}M \times 1\) dimensional vectors, \( {\mathbf{U}}\) is a \( {2^k}M \times {2^k}M\) dimensional matrix. If system of algebraic equations in Eq. (40) is solved, we may achieve the coefficients of Jacobi wavelet series in Eq. (31) which provides Eq. (1) and initial/ boundary conditions in Eq. (18).

5 Convergence analysis

In this part, convergence and error analysis of the Jacobi wavelet series expansion of a function \( f(x)\) are studied.

Lemma 1

If the Jacobi wavelet series expansion of a continuous function \( f(x)\) converges uniformly, then Jacobi wavelet series expansion converges to the function \( f(x)\).

Proof

For Jacobi wavelet, proof may be shown similar way in [20]

Theorem 1

A function \(f(x) \in {{\text{C}}^r}\left[ {0,1} \right]\) with the \( \left| {{f^{(r + 1)}}(x)} \right| < U\) may be expanded as an infinite sum of Jacobi wavelets series which converges uniformly to \( f(x)\), that is,

$$ f(x) = \sum\limits_{n = 1}^{2^k} {\sum\limits_{m = 0}^\infty {{c_{nm}}{\psi_{nm}}(x)} } . $$

Proof

The following equation can be found from the inner product in Eq. (12):

$$ {c_{nm}} = \int\limits_0^1 {f(x){\phi_{nm}}(x){w_k}(x){\text{d}}x = \frac{{{2^{\frac{k + 1}{2}}}}}{{\sqrt {L_m^{(\alpha ,\beta )}} }}} \int\limits_{\frac{n - 1}{{2^k}}}^{\frac{n}{{2^k}}} {f(x)} P_m^{(\alpha ,\beta )}({2^{k + 1}}x - 2n + 1)\,w({2^{k + 1}}x - 2n + 1)\,\,{\text{d}}x. $$

By substituting \( {2^{k + 1}}x - 2n + 1 = t\) and successive integration by parts in the above equation, it yields

$$ \begin{gathered} {c_{nm}} = \frac{{{2^{ - \,\frac{k + 1}{2}}}}}{{\sqrt {L_m^{(\alpha ,\beta )}} }}\int\limits_{ - 1}^1 {f\left( {\frac{t + 2n - 1}{{{2^{k + 1}}}}} \right)} P_m^{(\alpha ,\beta )}(t)\,{(1 - t)^\alpha }{(1 + t)^\beta }{\text{d}}t \hfill \\ \,\,\,\,\,\,\,\,\, = \frac{{{2^{ - \,\frac{3}{2}(k + 1)}}}}{{2m\sqrt {L_m^{(\alpha ,\beta )}} }}\int\limits_{ - 1}^1 {f^{\prime}\left( {\frac{t + 2n - 1}{{{2^{k + 1}}}}} \right)} P_{m - 1}^{(\alpha + 1,\beta + 1)}(t)\,{(1 - t)^{\alpha + 1}}{(1 + t)^{\beta + 1}}\,{\text{d}}t \hfill \\ \,\,\,\,\,\,\,\,\,\, = \cdots \mathop {}\limits \hfill \\ \,\,\,\,\,\,\,\,\, = \frac{{{2^{ - \,\frac{(2r + 3)(k + 1)}{2}}}}}{{{2^{r + 1}}m(m - 1)\,...\,(m - r)\sqrt {L_m^{(\alpha ,\beta )}} }}\int\limits_{ - 1}^1 {{f^{(r + 1)}}\left( {\frac{t + 2n - 1}{{{2^{k + 1}}}}} \right)} P_{m - r - 1}^{(\alpha + r + 1,\beta + r + 1)}(t)\,{(1 - t)^{\alpha + r + 1}}{(1 + t)^{\beta + r + 1}}\,{\text{d}}t. \hfill \\ \end{gathered} $$

By applying Cauchy–Schwarz inequality, above equation can be written as:

$$ \begin{aligned} {c_{nm}} \leqslant & \frac{{{2^{\,\frac{ - (2r + 3)(k + 1)}{2}\, - \,\,r\,\, - \,1}}}}{{m(m - 1)\,...\,(m - r)\sqrt {L_m^{(\alpha ,\beta )}} }}\\ &{\left( {\int\limits_{ - 1}^1 {{{\left( {{f^{(r + 1)}}\left( {\frac{t + 2n - 1}{{{2^{k + 1}}}}} \right)} \right)}^2}{{(1 - t)}^{\alpha + r + 1}}{{(1 + t)}^{\beta + r + 1}}{\text{d}}t} } \right)^\frac{1}{2}}\,\\ &{\left( {\int\limits_{ - 1}^1 {{{\left( {P_{m - r - 1}^{(\alpha + r + 1,\beta + r + 1)}(t)} \right)}^2}\,{{(1 - t)}^{\alpha + r + 1}}{{(1 + t)}^{\beta + r + 1}}\,{\text{d}}t} } \right)^\frac{1}{2}}. \end{aligned} $$

Thus, we get

$$ \begin{gathered} \left| {{c_{nm}}} \right| \leqslant \frac{{{2^{\,\frac{ - (2r + 3)(k + 1)}{2} - r - 1}}\,\,U}}{{m(m - 1)\,...\,(m - r)\sqrt {L_m^{(\alpha ,\beta )}} }}\sqrt {L_0^{(\alpha + r + 1,\beta + r + 1)}} \sqrt {L_{m - r - 1}^{(\alpha + r + 1,\beta + r + 1)}} \hfill \\ \leqslant \frac{{{2^{\,\frac{ - (2r + 3)(k + 2) + \alpha + \beta + 3}{2}}}\,\,U}}{m(m - 1)\,...\,(m - r)}\sqrt {\frac{\Gamma (r + \alpha + 2)\Gamma (r + \beta + 2)}{{\Gamma (2r + \alpha + \beta + 4)}}} . \hfill \\ \end{gathered} $$

Since \( n \leqslant {2^k}\), for \( m > r\), we obtain

$$\left| {{c_{nm}}} \right| \leqslant \frac{{{2^{\,\frac{ - (4r + 3) + \alpha + \beta }{2}}}\,\,U}}{{{n^{\frac{(2r + 3)}{2}}}m(m - 1)\,...\,(m - r)}}\sqrt {\frac{\Gamma (r + \alpha + 2)\Gamma (r + \beta + 2)}{{\Gamma (2r + \alpha + \beta + 4)}}} . $$

If \( m = r\), it can be shown

$$ {c_{nm}} \leqslant \frac{{{2^{\,\frac{ - (2m + 1)(k + 1)}{2}\,}}}}{{{2^m}m\,!\sqrt {L_m^{(\alpha ,\beta )}} }}\int\limits_{ - 1}^1 {{f^{(m)}}\left( {\frac{t + 2n - 1}{{{2^{k + 1}}}}} \right){{(1 - t)}^{\alpha + m}}{{(1 + t)}^{\beta + m}}{\text{d}}t} . $$

Thus, we get

$$ \left| {{c_{nm}}} \right| \leqslant \frac{{{2^{\,\frac{ - (4m + 1)}{2}\,}}}}{{{n^{\frac{2m + 1}{2}}}m\,!\,\,\sqrt {L_m^{(\alpha ,\beta )}} }}L_0^{(\alpha + m,\beta + m)}\mathop {\max }\limits_{0 \leqslant x \leqslant 1} {f^{(m)}}(x). $$

It is referred in [43] that for \( m = 0\), \(\left\{ {{\phi_{n0}}} \right\}_{n = 1}^{2^k}\) construct an orthogonal system build by Haar scaling function according to the weight function \(\omega (x)\), so \(\sum\limits_{n = 1}^{2^k} {{c_{n0}}{\psi_{n0}}(x)} \) is convergent. Hence, we have

$$ \left| {\sum\limits_{n = 1}^{2^k} {\sum\limits_{m = 0}^\infty {{c_{nm}}{\psi_{nm}}(x)} } } \right| \leqslant \left| {\sum\limits_{n = 1}^{2^k} {{c_{n0}}{\psi_{n0}}(x)} } \right| + \sum\limits_{n = 1}^{2^k} {\sum\limits_{m = 1}^\infty {\left| {{c_{nm}}} \right|\,\,\left| {{\psi_{nm}}(x)} \right|} } \leqslant \left| {\sum\limits_{n = 1}^{2^k} {{c_{n0}}{\psi_{n0}}(x)} } \right| + \sum\limits_{n = 1}^{2^k} {\sum\limits_{m = 1}^\infty {\left| {{c_{nm}}} \right|} < \infty } . $$

Thus, with the help of Lemma 1, the series \(\sum\limits_{n = 1}^{2^k} {\sum\limits_{m = 0}^\infty {{c_{nm}}{\psi_{nm}}(x)} } \) converges to \(f(x)\) uniformly.

Theorem 2

Let \(f(x) \in {{\text{C}}^r}\left[ {0,1} \right]\) with the \( \left| {{f^{(r + 1)}}(x)} \right| < U\) be a continuous function, then accuracy estimation is obtained as:

$$ \left\| {f(x) - {{\mathbf{C}}^{\mathbf{T}}}{{\varvec{\Psi}}}} \right\|_2^2\, \leqslant \,\,\frac{{{U^2}\Gamma (r + \alpha + 2)\Gamma (r + \beta + 2)}}{{{2^{4r + 4 - \alpha - \beta }}\Gamma (2r + \alpha + \beta + 4)}}\frac{1}{(r + 1)(2r + 1)}\frac{1}{{{{(M - r)}^{2r + 1}}}}\left[ {1 - \frac{1}{{{2^{2k(r + 1)}}}}} \right]. $$

Proof

We have

$$ \begin{gathered} \left\| {f(x) - {{\mathbf{C}}^{\mathbf{T}}}{{\varvec{\Psi}}}} \right\|_2^2 = {\int\limits_0^1 {\left[ {f(x) - \sum\limits_{n = 1}^{2^k} {\sum\limits_{m = 0}^{M - 1} {{c_{nm}}{\phi_{nm}}(x)} } } \right]}^2}{w_n}(x)\,\,dx \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\int\limits_0^1 {\left[ {\sum\limits_{n = 1}^{2^k} {\sum\limits_{m = 0}^\infty {{c_{nm}}{\phi_{nm}}(x) - \sum\limits_{n = 1}^{2^k} {\sum\limits_{m = 0}^{M - 1} {{c_{nm}}{\phi_{nm}}(x)} } } } } \right]}^2}{w_n}(x)\,\,dx\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\int\limits_0^1 {\left[ {\sum\limits_{n = 1}^{2^k} {\sum\limits_{m = M}^\infty {{c_{nm}}{\phi_{nm}}(x)} } } \right]}^2}{w_n}(x)\,\,dx = \sum\limits_{n = 1}^{2^k} {\sum\limits_{m = M}^\infty {c_{nm}^2} } . \hfill \\ \end{gathered} $$

By substituting the relation \( c_{nm}^2\) in the above equation, desired result is obtained as:

$$ \begin{gathered} \left\| {f(x) - {{\mathbf{C}}^{\mathbf{T}}}{{\varvec{\Psi}}}} \right\|_2^2 \leqslant \,\,\frac{{{U^2}\Gamma (r + \alpha + 2)\Gamma (r + \beta + 2)}}{{{2^{4r + 3 - \alpha - \beta }}\Gamma (2r + \alpha + \beta + 4)}}\left[ {\sum\limits_{n = 1}^{2^k} {\,\sum\limits_{m = M}^\infty {\,\,\frac{1}{{{n^{2r + 3}}{{\left( {m(m - 1)\,...\,(m - r)} \right)}^2}}}} } } \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathop {}\limits \, \leqslant \,\,\frac{{{U^2}\Gamma (r + \alpha + 2)\Gamma (r + \beta + 2)}}{{{2^{4r + 3 - \alpha - \beta }}\Gamma (2r + \alpha + \beta + 4)}}\left[ {\int_1^{2^k} {\frac{dt}{{{t^{2r + 3}}}}} \,\,\int_M^\infty {\frac{dt}{{{{(t - r)}^{2(r + 1)}}}}} } \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \leqslant \frac{{{U^2}\Gamma (r + \alpha + 2)\Gamma (r + \beta + 2)}}{{{2^{4r + 3 - \alpha - \beta }}\Gamma (2r + \alpha + \beta + 4)}}\frac{1}{2(r + 2)(2r + 1)}\frac{1}{{{{(M - r)}^{2r + 1}}}}\left[ {1 - \frac{1}{{{2^{2k(r + 1)}}}}} \right]. \hfill \\ \end{gathered} $$

6 Numerical results

The modified Camassa–Holm and modified Degasperis–Procesi equations are solved to show the effectiveness and the applicability of Jacobi wavelet collocation method. Approximate results of proposed method are compared with analytical and numerical results in the literature.

Example 1

Consider Eq. (1) for \( w = 2\), modified Camassa–Holm (mCH) equation may be obtained as:

$$ {u_t} - {u_{xxt}} + 3{u^2}{u_x} - 2{u_x}{u_{xx}} - u{u_{xxx}} = 0,\,\,\,\,\,\,\,\,a < x < b, $$

with the initial condition \(u(x,0) = - 2{\operatorname{sech}^2}\left( \frac{x}{2} \right)\) and boundary conditions:

\( u(a,t) = - 2{\operatorname{sech}^2}\left( {\frac{a}{2} - t} \right),\quad u(b,t) = - 2{\operatorname{sech}^2}\left( {\frac{b}{2} - t} \right),\quad {u_x}(a,t) = 2{\operatorname{sech}^2}\left( {\frac{a}{2} - t} \right)\,\tanh \left( {\frac{a}{2} - t} \right)\).

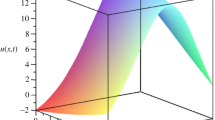
Substituting boundary and initial conditions into Eq. (38) and solving system of algebraic equations in Eq. (40), we may find vector \({\mathbf{C}}\), whose components give us coefficients of Jacobi wavelet series. By substituting \({\mathbf{C}}\) in Eq. (31), we have obtained approximate solution of mCH equation that provides initial and boundary conditions. Graphics of the exact solution, approximate solutions and absolute errors of Example 1 are shown in Figs. 1, 2, 3, 4, 5 and 6 when \(\alpha = 0,\beta = 0,M = 71,\,\,k = 0\) and \( \Delta t = 0.001\) for various values of \( t\) in the interval \( \left[ { - 10,\,10} \right]\). In Table 1, absolute errors can be shown for different values of \( M\) and \( k\) when α = 0, β = 0, ∆t = 0.001, t = 0.1, and various values of x in the interval [−15,15]. It can be seen from Table 1 that the Jacobi wavelet collocation-based algorithm produces stable and converging solution by increasing the level of resolution of the Jacobi wavelet \( k\). Absolute errors of Example 1 have been given in Table 2 to compare presented results with earlier results in the interval \( \left[ { - 15,\,15} \right]\). Graphics of the approximate and exact solutions of Example 1 have been given Fig. 2 [45], Fig. 3 [46] and Fig. 4.2 [47]. As can be seen in Tables 1 and 2 and Figs. 1, 2, 3, 4, 5 and 6, it is clear that suggested method provides more accurate results if we compare the tables and graphics in [44,45,46,47].

Fig. 1
figure 1

Exact solution of Example 1

Full size image
Fig. 2
figure 2

Approximate solution of Example 1

Full size image
Fig. 3
figure 3

Absolute errors of Example 1 at \( t = 0.05\)

Full size image
Fig. 4
figure 4

Absolute errors of Example 1 at \( t = 0.1\)

Full size image
Fig. 5
figure 5

Absolute errors of Example 1 at \( t = 0.2\)

Full size image
Fig. 6
figure 6

Absolute errors of Example 1 at \( t = 0.5\)

Full size image
Table 1 Absolute errors of Example 1 for various values of x
Full size table
Table 2 Comparison with absolute errors of offered method and existing methods in the literature at different time levels for mCH equation
Full size table

Example 2

Consider Eq. (1) for \( w = 3\), modified Degasperis–Procesi (mDP) equation may be obtained as:

$$ {u_t} - {u_{xxt}} + 4{u^2}{u_x} - 3{u_x}{u_{xx}} - u{u_{xxx}} = 0,\,\,\,\,\,\,\,\,a < x < b, $$

with the initial condition \( u(x,0) = - \frac{15}{8}{\operatorname{sech}^2}(\frac{x}{2})\) and boundary conditions

$$ u(a,t) = - \frac{15}{8}{\operatorname{sech}^2}(\frac{a}{2} - \frac{5t}{4}),\,\,\,\,\,u(b,t) = - \frac{15}{8}{\operatorname{sech}^2}(\frac{b}{2} - \frac{5t}{4}),\,\,\,\,\,{u_x}(a,t) = \frac{15}{8}{\operatorname{sech}^2}(\frac{a}{2} - \frac{5t}{4})\,\tanh (\frac{a}{2} - \frac{5t}{4}). $$

Substituting boundary and initial conditions into Eq. (38) and solving system of algebraic equations in Eq. (40), we may find vector \({\mathbf{C}}\), whose components give us coefficients of Jacobi wavelet series. By substituting \( {\mathbf{C}}\) in Eq. (31), we have obtained approximate solution of mDP equation that provides boundary and initial conditions. Graphics of the absolute errors, approximate solution and exact solution of Example 2 are shown in Figs. 7, 8, 9, 10, 11 and 12 when \( \alpha = 0,\beta = 0,M = 71,\,\,k = 0\) and \( \Delta t = 0.001\) for various values of \( t\) in the interval \( \left[ { - 10,\,10} \right]\). Like in the Example 1, absolute errors can be shown in Table 3 for different values of \( M\) and \( k\) when α = 0, β = 0, ∆t = 0.001, t = 0.1 and various values of in the interval. It can be seen from Table 3 that the Jacobi wavelet collocation-based algorithm produces stable and converging solution by increasing the level of resolution of the Jacobi wavelet \( k\). Absolute errors of Example 2 have been given in Table 4 to compare presented results with earlier results in the interval \( \left[ { - 15,\,15} \right]\). Graphics of the exact solution and approximate solution of Example 2 have been given in Fig. 4 [45], Fig. 4 [46] and Fig. 4.4 [47]. As can be seen in Tables 3 and 4 and Figs. 7, 8, 9, 10, 11 and 12, it is clear that suggested method provides more accurate results if we compare the tables and graphics in [44,45,46,47].

Fig. 7
figure 7

Exact solution of Example 2

Full size image
Fig. 8
figure 8

Approximate solution of Example 2

Full size image
Fig. 9
figure 9

Absolute errors of Example 2 at \( t = 0.05\)

Full size image
Fig. 10
figure 10

Absolute errors of Example 2 at \( t = 0.1\)

Full size image
Fig. 11
figure 11

Absolute errors of Example 2 at \( t = 0.2\)

Full size image
Fig. 12
figure 12

Absolute errors of Example 2 at \( t = 0.5\)

Full size image
Table 3 Absolute errors of Example 2 for various values of x
Full size table
Table 4 Comparison with absolute errors of offered method and existing methods in the literature at different time levels for mDP equation
Full size table

7 Discussions and conclusion

Jacobi wavelets are general form of the Legendre, first-kind Chebyshev, second-kind Chebyshev and Gegenbauer wavelets. For Jacobi wavelet collocation method, matrix representation, called as operational matrices, of rth integration of Jacobi wavelets have been introduced and convergence analysis of offered method has been also investigated in present study. Suggested method has been applied to find approximate solutions of the nonlinear modified Camassa–Holm and Degasperis–Procesi equations linearized using quasilinearization technique. The advantage of this method is that it transforms problems into matrix products. Therefore, present method can be easily applied to obtain solutions of physical and engineering problems and its application is simple. When the Jacobi wavelets collocation method is applied to obtain approximate solutions of engineering problems using a small number of grids it has given convergent results. Algebraic equation systems depend on the number of grids so using a small number of grids reduces the size of equation systems. In Tables 1, 2, 3 and 4, convergence of the proposed method, even in the case of a small number of grid points, is observed. Comparison of the absolute errors given in Tables 1, 2, 3 and 4 and Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 show that suggested method is superior to the results in [44,45,46,47] and offered method give highly accurate solution for the examples.

This study is applied to obtain approximate solutions of one-space dimensional problems. However, this method can also be applied for two- and three-dimensional problems as well.