Fractional Jacobi Galerkin spectral schemes for multi-dimensional time fractional advection–diffusion–reaction equations

Abstract

One of the ongoing issues with time fractional diffusion models is the design of efficient high-order numerical schemes for the solutions of limited regularity. We construct in this paper two efficient Galerkin spectral algorithms for solving multi-dimensional time fractional advection–diffusion–reaction equations with constant and variable coefficients. The model solution is discretized in time with a spectral expansion of fractional-order Jacobi orthogonal functions. For the space discretization, the proposed schemes accommodate high-order Jacobi Galerkin spectral discretization. The numerical schemes do not require imposition of artificial smoothness assumptions in time direction as is required for most methods based on polynomial interpolation. We illustrate the flexibility of the algorithms by comparing the standard Jacobi and the fractional Jacobi spectral methods for three numerical examples. The numerical results indicate that the global character of the fractional Jacobi functions makes them well-suited to time fractional diffusion equations because they naturally take the irregular behavior of the solution into account and thus preserve the singularity of the solution.

1 Introduction

Many mathematical models for scientific and engineering applications involve fractional-order derivatives. The time fractional partial differential equations are proposed to improve the modeling accuracy in depicting the anomalous diffusion process, successfully capturing power-law frequency dependence [30], adequately modeling various types of viscoelastic damping [13], properly simulating the unsteady flow of a fractional Maxwell fluid [41] and Oldroyd-B fluid [18]. These models rely on fractional-order derivatives to represent the observed sublinear or superlinear growth of the variance of the variable of interest. The former corresponds to subdiffusion and the latter to superdiffusion. Subdiffusion is modeled by a fractional time derivative and characterized by temporally non-local transport (i.e. memory effects). Superdiffusion is modeled by a fractional diffusion term and typically characterized by spatially non-local transport (i.e. large displacements). As such, they can be used to represent memory effects and long-range dispersion processes.

The application of time fractional diffusion models to realistic problems strongly depends on the numerical methods available to solve the model equation. Hendy and Zaky [26] developed an efficient finite difference/Legendre Galerkin method to solve a coupled system of nonlinear multi-term time-space fractional diffusion equations. They obtained optimal error estimates introducing a new generalized discrete form of the fractional Grönwall inequality which enabled them to overcome the difficulties caused by the sum of Caputo time-fractional derivatives and the positivity of the reaction term over the nonuniform time mesh. Gao and Sun [19] constructed a compact difference scheme to solve the fractional sub-diffusion equations using the $L_{1}$ scheme for the time-fractional derivative and fourth-order accuracy compact approximation for spatial direction. Zhao et al. [52] established two fully-discrete approximate schemes with unconditional stability for the time-fractional diffusion equation based on spatial conforming and nonconforming mixed finite element methods combined with classical $L_{1}$ time stepping method. For the first time in literature, Zaky et al. [50] proposed semi-implicit spectral approximations for nonlinear Caputo time- and Riesz space-fractional diffusion equations with both smooth and non-smooth solutions. Mustapha and Mclean [36] developed and analysed the discontinuous Galerkin method to solve the fractional diffusion and wave equations, and obtained superconvergence results. Sousa [40] proposed a high order explicit finite difference method for fractional advection diffusion equations. Hendy [24] constructed a fully implicit difference method for the numerical solution of those equations. The scheme was built on the idea of separating the current state and the prehistory function such that the prehistory function was approximated by means of an appropriate interpolation–extrapolation operator. Abbaszadeh and Dehghan [2] developed a numerical scheme based on fast and efficient meshless local Petrov–Galerkin method for solving the fractional fourth-order partial differential equation on computational domains with complex shape. Abbaszadeh and Dehghan [1] proposed meshless upwind local radial basis function-finite difference technique to simulate the time– fractional distributed–order advection–diffusion equation. Li et al. [31] presented two-grid algorithms based on expanded mixed finite element method for solving two-dimensional semilinear time fractional reaction–diffusion equations. Gu and Sun [20] constructed a meshless method for solving three-dimensional time fractional diffusion equation with variable-order derivatives. Jin [28] considered a finite element method to solve time fractional diffusion equation with non-smooth initial data, and established optimal error estimates. Most of the aforementioned methods relied on the finite difference method to discretize the time fractional derivative. Moreover, most of the known methods work well on fractional differential equations with smooth solutions or solutions with relatively good regularities.

Another approach to design an accurate numerical scheme is to discretize these non-local differential operators with global numerical methods [3, 17, 23, 46,47,48]. Hence, the non-local behaviour of the solution can be taken into account and the computational cost is not substantially increased when moving from a first-order to a fractional-order diffusion model [4, 5, 15, 44, 45]. In a series of papers Bhrawy et al. developed spectral tau [7, 8, 43] and collocation methods [9, 12] for solving various types of fractional differential equations. Unlike the classical differential equations, solutions to time-fractional partial differential are generally non-smooth. Up to now, few numerical methods have been proposed for fractional differential equations with non-smooth solutions, such as the use of nonuniform grids (see e.g. [25]), the nonpolynomial/singular basis (see e.g. [10, 11, 49]), and Lubich’s correction method (see e.g. [51]). It was pointed out by Diethelm et al. [14] that the approximation of the function $f(t)=t^\alpha$ on [0, h] by any linear polynomial is at best $O(h^\alpha )$. But the order of approximation $O(h^\alpha )$ of $t^\alpha$ on [0, h] is also achieved by the constant polynomial 0. That is: using a linear polynomial to approximate $t^\alpha$ on [0, h] does not give an essentially better result than using a constant polynomial. In a similar way one can show that using polynomials of higher degree does not improve the situation: the order of approximation of $t^\alpha$ on [0, h] is still only $O(h^\alpha )$. The purpose of this paper is to extend our approaches in [21, 22] introducing two efficient fractional Galerkin spectral algorithms for solving multi-dimensional time fractional advection–diffusion–reaction equations with constant and variable coefficients with non smooth solutions. The model solution is discretized in time with a spectral expansion of fractional Jacobi functions (FJFs). For the space discretization, the proposed schemes accommodate high-order Jacobi Galerkin spectral discretization. The numerical schemes do not require imposition of artificial smoothness assumptions in time direction because they naturally take the irregular behavior of the solution into account and thus preserve the singularity of the solution.

The rest of the paper is organized as follows. In the next section, we briefly review some basic properties of fractional integrals and derivatives, and recall relevant properties of the Jacobi polynomials. In Sect. 3, the fractional Jacobi functions and their fractional differentiation are presented. In Sect. 4, a time-space discretization for the time fractional advection–diffusion–reaction equations with constant coefficients is constructed. In Sect. 5, we consider the numerical solution of the one-dimensional time fractional advection–diffusion–reaction equations with variable coefficients. In Sect. 6, we consider the numerical solution of the two-dimensional case with constant coefficients. In Sect. 7, the variable coefficients case is considered. In Sect. 8, various numerical tests exhibiting the efficiency of our numerical schemes are presented. We end the paper with some concluding remarks in Sect. 9.

2 Preliminaries

In this section, we recall some basic properties of fractional integrals and derivatives, and briefly review some relevant properties of the Jacobi polynomials. All of these properties can be found in [37, 39].

2.1 Fractional integrals and derivatives

For $\nu >0$, the fractional integrals of order $\nu$ is defined by

$$\begin{aligned} {}_{0}I_x^{\nu } u(x)= \frac{1}{\Gamma (\nu )} \int _{0}^{x} \frac{u(z)}{(x-z)^{1-\nu }} \mathrm {d}z, \end{aligned}$$

(2.1)

where $\Gamma (x)$ is the gamma function. Let n be the positive integer satisfying $n-1\le \nu <n$, then the Riemann–Liouville and the Caputo fractional derivatives of order $\nu$ are defined, respectively, as

$$\begin{aligned}&{}_{0}^{RL}D_x^{\nu } u(x)= \frac{\mathrm {d}^n}{\mathrm {d}x^n}{}_{0}I_x^{n-\nu } u(x)\nonumber \\&\quad = \frac{1}{\Gamma (n-\nu )} \frac{\mathrm {d}^n}{\mathrm {d}x^n} \int _{0}^{x} \frac{u(z)}{(x-z)^{\nu +1-n}} \mathrm {d}z, \end{aligned}$$

(2.2)

$$\begin{aligned}&{}_{0}^{C}D_x^{\nu } u(x)= {}_{0}I_x^{n-\nu } f^{(n)}(x)\nonumber \\&\quad =\frac{1}{\Gamma (n-\nu )} \int _{0}^{x} \frac{f^{(n)}(z)}{(x-z)^{\nu +1-n}} \mathrm {d}z. \end{aligned}$$

(2.3)

For any absolutely integrable function u(x), an important property of Riemann–Liouville fractional derivatives is

$$\begin{aligned} {}_{0}^{RL}D_x^{\nu }\{{}_{0}I_x^{\nu }u(x)\} = u(x), \end{aligned}$$

(2.4)

where this equation holds in the almost everywhere sense.

The following lemma gives the relation between Riemann–Liouville and Caputo fractional derivatives.

Lemma 1

We have

$$\begin{aligned} {}_{0}^{RL}D_x^{\nu } u(x)= {} {}_{0}^{C}D_x^{\nu } u(x) + \sum _{j=0}^{n-1} \frac{f^{(j)}(0)}{\Gamma (j+1-\nu )}x^{j-\nu }. \end{aligned}$$

(2.5)

2.2 Jacobi polynomials and their properties

Let $J_n^{(\alpha ,\beta )}(x)$ denote the Jacobi polynomial of degree n, which is explicitly defined by

$$\begin{aligned} J^{(\alpha ,\beta )}_{n}{(x)}=\sum \limits _{k=0}^{n }E_k^{(\alpha ,\beta ,n)} \left( {\frac{{x + 1}}{2}} \right) ^{k}, \end{aligned}$$

(2.6)

where

$$\begin{aligned} E_k^{(\alpha ,\beta ,n)}=\frac{(-1)^{n-k}\Gamma {(1+n+\beta )}\Gamma {(k+\alpha +n+\beta +1)}}{\Gamma (k+\beta +1)k!\Gamma (n+\alpha +\beta +1)(n-k)!}, \end{aligned}$$

(2.7)

then we see that $J_n^{(\alpha ,\beta )}(x)$ are always polynomials in x for $\alpha ,\ \beta \in \mathbb {R}$. The classical Jacobi polynomials are correspond to the parameters $\alpha ,\beta >-1$. Let $\omega ^{(\alpha ,\beta )}(x)=(1-x)^{\alpha }(1+x)^{\beta }$ be the Jacobi weight function and let $I=(-1,1)$, then we define the inner product and the associated norm by

$$\begin{aligned} (u,v)_{\omega ^{(\alpha ,\beta )}}= & {} \int _{I} \omega ^{(\alpha ,\beta )}(x) u(x) v(x) \mathrm {d}x, \quad \Vert u \Vert _{\omega ^{(\alpha ,\beta )}}\nonumber \\&= (u, u)_{\omega ^{(\alpha ,\beta )}}^{ \frac{1}{2} }. \end{aligned}$$

(2.8)

For notational simplicity, we will drop the subscript $\omega ^{(\alpha ,\beta )}$ from $(u,v)_{\omega ^{(\alpha ,\beta )}}$ and $\Vert u \Vert _{\omega ^{(\alpha ,\beta )}}$ when $\alpha =\beta =0$. Moreover, we denote by $L_{\omega ^{(\alpha ,\beta )}}^{2}(I)$ the space of functions such that $\Vert u\Vert _{\omega ^{(\alpha ,\beta )}} < \infty$. It is well known that the Jacobi polynomials are orthogonal with respect to $\omega ^{(\alpha ,\beta )}(x)$ and

$$\begin{aligned} (J_n^{(\alpha ,\beta )},J_m^{(\alpha ,\beta )} )_{\omega ^{(\alpha ,\beta )}} = h_n^{(\alpha ,\beta )}\delta _{mn}, \end{aligned}$$

(2.9)

where $\delta _{n,m}$ is the Kronecker delta and

$$\begin{aligned} h_n^{(\alpha ,\beta )}=\frac{2^{\alpha +\beta +1}}{2n+\alpha +\beta +1}\frac{\Gamma (n+\alpha +1)\Gamma (n+\beta +1)}{\Gamma (n+\alpha +\beta +1)\Gamma (n+1)}. \end{aligned}$$

(2.10)

In practical computations, it is convenient to compute the Jacobi polynomials by using the three-term recurrence relation

$$\begin{aligned} J_{n+1}^{(\alpha ,\beta )}(x) = \left( a_n^{\alpha ,\beta } x + b_n^{\alpha ,\beta }\right) J_{n}^{(\alpha ,\beta )}(x) - c_n^{\alpha ,\beta } J_{n-1}^{(\alpha ,\beta )}(x), \end{aligned}$$

(2.11)

where

$$\begin{aligned} \begin{aligned} a_n^{\alpha ,\beta }&= \frac{(2n+\alpha +\beta +1)(2n+\alpha +\beta +2)}{2(n+1)(n+\alpha +\beta +1)}, b_n^{\alpha ,\beta }\\&=\frac{(\alpha ^2-\beta ^2)(2n+\alpha +\beta +1)}{2(n+1)(n+\alpha +\beta +1)(2n+\alpha +\beta )}, c_n^{\alpha ,\beta }\\&=\frac{(n+\alpha )(n+\beta )(2n+\alpha +\beta +2)}{(n+1)(n+\alpha +\beta +1)(2n+\alpha +\beta )}, \end{aligned} \end{aligned}$$

(2.12)

with the two initial Jacobi polynomials given by

$$\begin{aligned} J_{0}^{(\alpha ,\beta )}(x) = 1, \quad J_{1}^{(\alpha ,\beta )}(x) = \frac{\alpha +\beta +2}{2}x + \frac{\alpha -\beta }{2}. \end{aligned}$$

(2.13)

For bounding some approximation error of Jacobi polynomials, we need the following nonuniformly-weighted Sobolev space, namely

$$\begin{aligned}&H_{{\chi ^{(\alpha ,\beta )}}, * }^m ( - 1,1) \\&:= \left\{ {v\ :\ \partial _x^k v \in L_{\chi ^{(\alpha +k,\beta +k)}}^2 ( - 1,1),\ 0 \le k \le m} \right\} , \end{aligned}$$

equipped with the inner product and the norm

$$\begin{aligned}& \left( {u,v} \right) _{m,{\chi ^{(\alpha ,\beta )}}, * }= {} \sum \limits _{k = 0}^m {\left( {\partial _x^k u,\partial _x^k v} \right) _{\chi ^{(\alpha +k ,\beta +k )}} },\\&\quad \quad \left\| u \right\| _{m,{\chi ^{(\alpha ,\beta )}}, * } = \left( {u,u} \right) _{m,{\chi ^{(\alpha ,\beta )}}, * }^{\frac{1}{2}} . \end{aligned}$$

Lemma 2

Let $u \in H_{{\chi ^{(\alpha ,\beta )}}, * }^m ( - 1,1)$ for some $m \ge 1$ and $\phi \in \mathcal {P}_{N}$. Then for the Jacobi-Gauss and Jacobi–Gauss–Radau integration, we have

$$\begin{aligned}&\left| {(u,\phi )_{\chi ^{(\alpha ,\beta )}} - (u,\phi )_{N,\chi ^{(\alpha ,\beta )}} } \right| \nonumber \\&\quad \le CN^{ - m} \left\| {\partial _x^m u} \right\| _{\chi ^{(\alpha +m ,\beta +m )}} \left\| \phi \right\| _{\chi ^{(\alpha ,\beta )}}, \end{aligned}$$

(2.14)

and for the Jacobi Gauss–Lobatto integration, we have

$$\begin{aligned}&\left| {(u,\phi )_{\chi ^{(\alpha ,\beta )}} - (u,\phi )_{N,\chi ^{(\alpha ,\beta )}} } \right| \nonumber \\&\quad \le CN^{ - m} \left\| {\partial _x^m u} \right\| _{\chi ^{(\alpha +m-1 ,\beta +m-1 )}} \left\| \phi \right\| _{\chi ^{(\alpha ,\beta )}}. \end{aligned}$$

(2.15)

In practical computations, it is convenient to compute the Jacobi polynomials on the interval $[0,\mathscr {L}]$. Hence, we rescale the interval $[-1,1]$ onto $[0,\mathscr {L}]$ by the linear map $z=\dfrac{2x}{\mathscr {L}}-1$. The set of Jacobi polynomials $J^{(\alpha ,\beta )}_{\mathscr {L},i}(x)$ which are defined on $[0,\mathscr {L}]$ are generated by:

$$\begin{aligned} \quad J^{(\alpha ,\beta )}_{\mathscr {L},i+1}(x)= & {} \left( \hat{a}_i^{\alpha ,\beta } x-\hat{b}_i^{\alpha ,\beta }\right) J^{(\alpha ,\beta )}_{\mathscr {L},i}(x)\\&\quad -c_i^{\alpha ,\beta } J^{(\alpha ,\beta )}_{\mathscr {L},i-1}(x),\quad i\ge 1, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \hat{a}_i^{\alpha ,\beta }=&\frac{(2 i+\alpha +\beta +1)(2 i+\alpha +\beta +2)}{\mathscr {L}(i+1)(i+\alpha +\beta +1)},\\ \hat{b}_i^{\alpha ,\beta }=&\frac{(2 i+\alpha +\beta +1)(2 i^2+(1+\beta )(\alpha +\beta )+2 i(\alpha +\beta +1))}{(i+1)(i+\alpha +\beta +1)(2 i+\alpha +\beta )}. \end{aligned} \end{aligned}$$

The endpoint values of the shifted Jacobi polynomials are given as

$$\begin{aligned} \begin{aligned}&J_{\mathscr {L},i}^{(\alpha ,\beta )} (0)= ( - 1)^i \frac{{\Gamma (1+i + \beta )}}{{\Gamma (1+\beta )i!}} ,\quad J_{\mathscr {L},i}^{(\alpha ,\beta )} (\mathscr {L}) \\&= \frac{{\Gamma (1+i + \alpha )}}{{\Gamma (1+\alpha )i!}}, \end{aligned} \end{aligned}$$

(2.16)

which will be of important use later. They satisfy the following orthogonality relation

$$\begin{aligned} \int _{0}^{\mathscr {L}} J^{(\alpha ,\beta )}_{\mathscr {L},j}(x)J^{(\alpha ,\beta )}_{\mathscr {L},i}(x) w^{(\alpha ,\beta )}_\mathscr {L}(x)\mathrm{d}x = \delta _{ji} h^{(\alpha ,\beta )}_{\mathscr {L},i}, \end{aligned}$$

(2.17)

where $w^{(\alpha ,\beta )}_\mathscr {L}(x)=x^\beta (\mathscr {L}-x)^\alpha$ is the weight function, and

$$\begin{aligned} h^{(\alpha ,\beta )}_{\mathscr {L},i}= \dfrac{\mathscr {L}^{1+\alpha +\beta }\Gamma (i+1+\alpha )\Gamma (i+1+\beta )}{(2 i+1+\alpha +\beta ) i!\Gamma (i+1+\alpha +\beta )}. \end{aligned}$$

(2.18)

The following lemma will be of essential use in establishing our main results.

Lemma 3

(see [16]) The q times repeated differentiation of$J_{\mathscr {L},j}^{(\alpha ,\beta )}(x)$ are given explicitly by

$$\begin{aligned} D^{q} J_{\mathscr {L},j}^{(\alpha ,\beta )}(x)=\sum _{i=0}^{j-q}\mathcal {A}_{q}(j,i,\alpha ,\beta )J_{\mathscr {L},i}^{(\alpha ,\beta )}(x),\qquad q \in \mathbb {N}^+, \end{aligned}$$

(2.19)

where

$$\begin{aligned} \begin{aligned} \mathcal {A}_{q}(j,i,\alpha ,\beta )=& \frac{(j+)_{q}(j+\lambda +q)_{i} (q+i+\alpha +1)_{j-i-q}\ \Gamma (i+\lambda )}{\mathscr {L}^{q}(j-q-i)!\ \Gamma (2i+\lambda )}\\& \times \, _{3}F_{2} \begin{pmatrix} q-j+i, & q+j+i+\lambda , & i+\alpha +1 & \\ & & & 1 \\ q+i+\alpha +1, & \qquad 1+2i+\lambda \end{pmatrix} ,\end{aligned} \end{aligned}$$

(2.20)

where $\lambda = \alpha + \beta + 1$, $(\cdot )_i$ is the Pochhammer symbol, and for the definition of generalized hypergeometric functions and special $_3 F_2$, see [32].

3 Fractional-order Jacobi functions

In this section, we first introduce some basic properties of fractional-order Jacobi functions [11, 49]. Then, we construct the fractional derivative for the fractional-order Jacobi functions. The fractional-order Jacobi functions are the eigenfunctions of the singular Sturm–Liouville problem

$$\begin{aligned}&\partial _{t}\left( \lambda ^{-1}(1-t^{\lambda })^{\alpha +1}t^{\lambda \beta +1}\partial _{t}V(t)\right) \nonumber \\&\quad +\lambda n (n+\alpha +\beta +1)(1-t^{\lambda })^{\alpha }t^{\lambda \beta +\lambda -1}V(t)=0,\ t\in [0,1], \end{aligned}$$

(3.1)

and they are given explicitly by

$$\begin{aligned} J_{i}^{(\alpha ,\beta ,\lambda )}(t)=J_{1,i}^{(\alpha ,\beta )}(t^{\lambda }) =\sum _{k=0}^{i}a_{i,k} t^{k\lambda },\ \lambda \in (0,1], \end{aligned}$$

(3.2)

where

$$\begin{aligned} a_{i,k}= & {} (-1)^{i-k}\frac{\Gamma (i+\beta +1)\Gamma (i+k+\alpha +\beta +1)}{\Gamma (k+\beta +1)\Gamma (i+\alpha +\beta +1)(i-k)!k!} \end{aligned}$$

(3.3)

$$\begin{aligned}J_{i}^{(\alpha ,\beta ,\lambda )}(0)&=(-1)^i\frac{\Gamma (i+\beta +1)}{\Gamma (\beta +1)i!},\quad J_{i}^{(\alpha ,\beta ,\lambda )}(1)\nonumber \\&=\frac{\Gamma (i+\alpha +1)}{\Gamma (\alpha +1)i!}, \end{aligned}$$

(3.4)

and satisfy the following recurrence relations

$$\begin{aligned} (i+\alpha +1)J_{i}^{(\alpha ,\beta ,\lambda )}(t)&-(i+1)J_{i+1}^{(\alpha ,\beta ,\lambda )}(t)\nonumber \\&=(2i+\alpha +\beta +2)(1-t^{\lambda })J_{i}^{(\alpha +1,\beta ,\lambda )}(t). \end{aligned}$$

(3.5)

$$\begin{aligned}&J_{i}^{(\alpha ,\beta -1,\lambda )}(t)-J_{i}^{(\alpha -1,\beta ,\lambda )}(t)\nonumber \\&=J_{i-1}^{(\alpha ,\beta ,\lambda )}(t). \end{aligned}$$

(3.6)

$$\begin{aligned} (i+\alpha +\beta )J_{i}^{(\alpha ,\beta ,\lambda )}(t)= & {} (i+\beta )J_{i}^{(\alpha ,\beta -1,\lambda )}(t)\nonumber \\&\quad +(i+\alpha )J_{i}^{(\alpha -1,\beta ,\lambda )}(t). \end{aligned}$$

(3.7)

$$\begin{aligned}&\partial _{t}J_{i}^{(\alpha ,\beta ,\lambda )}(t)\nonumber \\&=\lambda (i+\alpha +\beta +1)t^{\lambda -1}J_{i-1}^{(\alpha +1,\beta +1,\lambda )}(t). \end{aligned}$$

(3.8)

$$\begin{aligned}& J_{i}^{(\alpha ,\beta ,\lambda )}(t)=\\&\frac{(\alpha +\beta +2i-1)\{\alpha ^2-\beta ^2+ (2t^\lambda -1)(\alpha +\beta +2i)(\alpha +\beta +2i-2)\}}{2i(\alpha +\beta +i)(\alpha +\beta +2i-2)} J_{i-1}^{(\alpha ,\beta ,\lambda )}(t)\\&-\frac{(\alpha +i-1)(\beta +i-1)(\alpha +\beta +2i)}{i(\alpha +\beta +i)(\alpha +\beta +2i-2)} J_{i-2}^{(\alpha ,\beta ,\lambda )}(t)\qquad \qquad \qquad i=2,3,\ldots , \end{aligned}$$

(3.9)

where

$$\begin{aligned}&J_{0}^{(\alpha ,\beta ,\lambda )}(t)=1\quad \mathrm{and} \quad J_{1}^{(\alpha ,\beta ,\lambda )}(t)=\frac{\alpha +\beta +2}{2}(2t^\lambda -1)\\&+\frac{\alpha -\beta }{2}. \end{aligned}$$

Let $\ w^{(\alpha ,\beta ,\lambda )}(t)=\lambda t^{(\beta +1)\lambda -1} (1-t^\lambda )^\alpha$. Thanks to (2.17), then the fractional-order Jacobi functions form a complete $L^{2}_{w^{(\alpha ,\beta ,\lambda )}}[0,1]$-orthogonal system, that is,

$$\begin{aligned} \int _{0}^{1} J_{j}^{(\alpha ,\beta ,\lambda )}(t)J_{k}^{(\alpha ,\beta ,\lambda )}(t) w^{(\alpha ,\beta ,\lambda )}(t)\mathrm{d}t = \delta _{jk} h^{(\alpha ,\beta )}_{1,i}. \end{aligned}$$

(3.10)

Remark 1

We note that if $t_i,\ 1\le i\le N$ are the roots of the shifted Jacobi polynomials $J_{\mathscr {L},i}^{(\alpha ,\beta )}(t)$, then $t_i^{\frac{1}{\lambda }},\ 1\le i\le N$ are the roots of the shifted fractional-order Jacobi functions $J_{i}^{(\alpha ,\beta ,\lambda )}(t)$.

Remark 2

The FJFs comprise an unlimited number of orthogonal functions, including the shifted fractional-order Gegenbauer functions $C^{\alpha }_{\lambda ,i}(x)$, the shifted fractional-order Chebyshev functions of the first kind $T_{\lambda ,i}(x)$, the shifted fractional-order Legendre functions $P_{\lambda ,i}(x)$ [29], the shifted Chebyshev functions of the second kind $U_{\lambda ,i}(x)$, the shifted fractional-order Chebyshev functions of third and fourth kinds $V_{\lambda ,i}(x)$ and $W_{\lambda ,i}(x)$. These orthogonal functions are interrelated with the FJFs by the following relations:

$$\begin{aligned} \begin{aligned} C^{\alpha }_{\lambda ,i}(x)&=\frac{i!\ \Gamma \left( \alpha +\frac{1}{2}\right) }{\Gamma \left( i+\alpha +\frac{1}{2}\right) } J^{\left( \alpha -\frac{1}{2},\beta -\frac{1}{2},\lambda \right) }_i{(x)},\qquad T_{\lambda ,i}(x)\\&=\frac{i!\ \Gamma (\frac{1}{2})}{\Gamma \left( i+\frac{1}{2}\right) }J^{\left( -\frac{1}{2},-\frac{1}{2},\lambda \right) }_i{(x)},\\ J_{\lambda ,i}(x)&=J^{(0,0,\lambda )}_i{(x)},\qquad \qquad \qquad \qquad \qquad \ U_{\lambda ,i}(x)\\&=\frac{(i+1)!\ \Gamma (\frac{1}{2})}{\Gamma \left( i+\frac{3}{2}\right) }J^{\left( \frac{1}{2},\frac{1}{2},\lambda \right) }_i{(x)},\\ V_{\lambda ,i}(x)&=\frac{(2i)!!}{(2i-1)!!}J^{\left( \frac{1}{2},-\frac{1}{2},\lambda \right) }_i{(x)},\qquad W_{\lambda ,i}(x)\\&=\frac{(2i)!!}{(2i-1)!!}J^{\left( -\frac{1}{2},\frac{1}{2},\lambda \right) }_i{(x)}. \end{aligned} \end{aligned}$$

(3.11)

Lemma 4

(see [11]) The fractional derivative of order $\nu$, $0< \nu <1$ in the Caputo sense for the shifted fractional Jacobi polynomials is given by

$$\begin{aligned} {}_0^CD_t^{\nu }J^{(\alpha ,\beta ,\lambda )}_i(x)=\sum \limits _{j=0}^{\infty }S_{\nu }(i,j,\alpha ,\beta )J^{(\alpha ,\beta ,\lambda )}_j(x), \end{aligned}$$

(3.12)

where

$$\begin{aligned} \begin{aligned} S_{\nu }(i,j,\alpha ,\beta )=&\sum \limits _{k=1}^{i}a_{i,k} \frac{ \Gamma (\lambda k+1) \Gamma (\alpha +1)}{h_j \Gamma (\lambda k-\nu +1)}\ \\&\times \sum \limits _{s=0}^{j}a_{j,s}\frac{ \Gamma (1+k+s+\beta -\frac{\nu }{\lambda })}{\Gamma (2+k+s+\alpha +\beta -\frac{\nu }{\lambda }) }. \end{aligned} \end{aligned}$$

Lemma 5

(see, [49]) Let $\mathcal {F}_N^{(\alpha ,\beta ,\lambda )}$ be the set of fractional-order Jacobi functions of degree N, $u(x)=v(( {\frac{{1 + x}}{2}})^{\frac{1}{\lambda }}) \in H_{{\chi ^{(\alpha ,\beta )}}, * }^m ( - 1,1)$ for some $m \ge 1$ and $\phi (x)=\varphi (( {\frac{{1 + x}}{2}})^{\frac{1}{\lambda }}) \in \mathcal {F}^{(\alpha ,\beta ,\lambda )}_{N}$. Then for the fractional Jacobi-Gauss and the fractional Jacobi-Gauss–Radau integration, we have

$$\begin{aligned} \begin{aligned}&\left| {(v,\varphi _{\chi ^{(\alpha ,\beta ,\lambda )}} - (v,\varphi )_{N,\chi ^{(\alpha ,\beta ,\lambda )}} } \right| \\&\le CN^{ - m} \left\| {\partial _x^m u} \right\| _{\chi ^{(\alpha +m ,\beta +m )}} \left\| \phi \right\| _{\chi ^{(\alpha ,\beta )}}, \end{aligned} \end{aligned}$$

(3.13)

and for the fractional Jacobi Gauss–Lobatto integration, we have

$$\begin{aligned} \begin{aligned}&\left| {(v,\varphi _{\chi ^{(\alpha ,\beta ,\lambda )}} - (v,\varphi )_{N,\chi ^{(\alpha ,\beta ,\lambda )}} } \right| \\&\le CN^{ - m} \left\| {\partial _x^m u} \right\| _{\chi ^{(\alpha +m-1 ,\beta +m -1)}} \left\| \phi \right\| _{\chi ^{(\alpha ,\beta )}}. \end{aligned} \end{aligned}$$

(3.14)

4 Fractional Galerkin method for the one-dimensional case

One of the standard techniques for solving linear time-fractional partial differential equations with constant coefficients is the Galerkin method. In this section, we derive a time-space discretization for the following time fractional advection–diffusion–reaction equation with constant coefficients based on the Galerkin method with fractional Jacobi and Jacobi expansions in both time and space, respectively.

$$\begin{aligned} \begin{aligned} {}_0^CD_t^{\nu } u - \tau _0 \frac{{\partial ^2 u}}{{\partial x^2 }} -\tau _1 \frac{{\partial u}}{{\partial x}} + \tau _2 u = f(x,t), \ (x,t) \in \Omega := \Lambda \times I, \end{aligned} \end{aligned}$$

(4.1)

with the homogeneous initial-boundary conditions

$$\begin{aligned} \begin{aligned}&u(x,0)=0 ,\ \text {in}\ \Lambda ,\\&u(x,t)=0,\ \text {on}\ \partial \Lambda \times I, \end{aligned} \end{aligned}$$

(4.2)

where $\Lambda =(0,\mathscr {L})$ denotes a bounded domain with its boundary $\partial \Lambda$, and $I=(0,1]$ is the time interval. We plug in an ansatz for the solution into (4.1)–(4.2) and require the residual of the projection onto the space spanned by the test functions to vanish.

Let $\mathcal {F}_M^{(\alpha ,\beta ,\lambda )}(I)$ be the space of fractional functions in time and $P_N (\Lambda )$ be the set of polynomials of degree N in space, and since we consider $u(x,0) \equiv 0$ as well as $u(\partial \Lambda ,t) \equiv 0$, then we choose appropriate basis for the time ansatz from

$$\begin{aligned} P_M^t (I) = \left\{ {y \in \mathcal {F}_M^{(\alpha ,\beta ,\lambda )}(I)\left| {y(0) = 0} \right. } \right\} , \end{aligned}$$

(4.3)

as well as for space

$$\begin{aligned} P_N^s (\Lambda ) = \left\{ {y \in P_N (\Lambda )\left| {y(0) = y(\mathscr {L}) = 0} \right. } \right\} . \end{aligned}$$

(4.4)

For the sake of convenience, we define

$$\begin{aligned} \begin{aligned} S_{L}:&= P_N (\Lambda ) \otimes \mathcal {F}_M^{(\alpha ,\beta ,\lambda )}(I),\\ W_L:&= P_N^s (\Lambda ) \otimes P_M^t (I), \end{aligned} \end{aligned}$$

(4.5)

where the multiindex $L=(N,M)$. Finally, we introduce the following notation for the integrals involved in the Jacobi–Galerkin spectral formulation of the model equations.

$$\begin{aligned} \begin{aligned} \left\langle { \left\langle {\left\langle \cdot \right\rangle } \right\rangle } \right\rangle&\equiv \int _0^{\mathscr {L}} \int _0^{\mathscr {L}} {\int _0^{1} { \cdot \ w_{\mathscr {L}}^{(\alpha ,\beta )}(x)\ w_{\mathscr {L}}^{(\alpha ,\beta )}(y)\ w^{(\alpha ,\beta ,\lambda )}(t) \ \mathrm{d}x\ \mathrm{d}y\ \mathrm{d}t}},\\ \left\langle {\left\langle \cdot \right\rangle } \right\rangle&\equiv \int _0^{\mathscr {L}} {\int _0^{1} { \cdot \ w_{\mathscr {L}}^{(\alpha ,\beta )}(x)\ w^{(\alpha ,\beta ,\lambda )}(t) \ \mathrm{d}x\ \mathrm{d}t}},\\ \left\langle \cdot \right\rangle _x&\equiv \int _0^{\mathscr {L}} { \cdot \ w_{\mathscr {L}}^{(\alpha ,\beta )}(x)\ \mathrm{d}x},\\ \left\langle \cdot \right\rangle _t&\equiv \int _0^{1} { \cdot \ w^{(\alpha ,\beta ,\lambda )}(t)\ \mathrm{d}t}. \end{aligned} \end{aligned}$$

(4.6)

The discrete solution is expressed in terms of a matrix of unknown coefficients $\mathcal {U}_{ij}$ as follows:

$$\begin{aligned} u(x,t)\backsimeq \hat{u}(x,t)= \sum _{i=0}^{N-2}\sum _{j=0}^{M-1}\phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) \mathcal {U}_{ij} \psi^{(\alpha ,\beta ,\lambda )}_{j}(t), \end{aligned}$$

(4.7)

where $\phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) \in P_N^s (\Lambda )$ and $\psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \in P_M^t (I)$. Then the Galerkin problem is given by finding $\hat{u} \in W_L$ such that

$$\begin{aligned} \begin{aligned}&\left\langle {\left\langle \hat{v} {}_0^CD_t^{\nu } \hat{u} \right\rangle } \right\rangle -\tau _0 \left\langle {\left\langle \hat{v} \partial ^{2}_{x} \hat{u} \right\rangle } \right\rangle -\tau _1 \left\langle {\left\langle \hat{v} \partial _{x}\hat{u} \right\rangle } \right\rangle +\tau _2 \left\langle {\left\langle \hat{u} \hat{v} \right\rangle } \right\rangle \\&= \left\langle {\left\langle f \hat{v} \right\rangle } \right\rangle ,\ \forall \hat{v}\in W_L, \end{aligned} \end{aligned}$$

(4.8)

The linear system obtained from (4.8) depends on the choice of the basis functions $\phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x)$ and $\psi^{(\alpha ,\beta ,\lambda )}_{j}(t)$ of $W_L$. By carefully selecting an appropriate basis for both space and time, we can make sure that the resulting system is sparse, that allowing us to invert it easily. Therefore, we look for basis functions as a linear combination of the shifted Jacobi functions and FJFs, namely,

$$\begin{aligned} \begin{aligned} \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x)&=J_{\mathscr {L},i}^{(\alpha ,\beta )}(x) +\epsilon _i J_{\mathscr {L},i+1}^{(\alpha ,\beta )}(x) +\varepsilon _i J_{\mathscr {L},i+2}^{(\alpha ,\beta )}(x),\\ \psi^{(\alpha ,\beta ,\lambda )}_{j}(t)&=J_{j}^{(\alpha ,\beta ,\lambda )}(t) +\rho _j J_{j+1}^{(\alpha ,\beta ,\lambda )}(t), \end{aligned} \end{aligned}$$

(4.9)

where the parameters $\left\{ \epsilon _i,\ \varepsilon _i \right\}$ and $\left\{ \rho _j \right\}$ are chosen to satisfy the homogeneous initial and Dirichlet boundary conditions. Even though this choice of modal basis functions might seem arbitrary, it can be verified that these polynomials constitute a suitable basis that allows easy evaluation of the involved derivatives in combination with (2.19) and (3.12).

Lemma 6

For all $i\ge 0$, there exists a unique set of $\left\{ \epsilon _i,\ \varepsilon _i,\ \rho _i \right\}$ such that

$$\begin{aligned} \begin{aligned} \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x)&=J_{\mathscr {L},i}^{(\alpha ,\beta )}(x) +\epsilon _i J_{\mathscr {L},i+1}^{(\alpha ,\beta )}(x) +\varepsilon _i J_{\mathscr {L},i+2}^{(\alpha ,\beta )}(x),\\ \psi^{(\alpha ,\beta ,\lambda )}_{i}(t)&=J_{i}^{(\alpha ,\beta ,\lambda )}(t) +\rho _i J_{i+1}^{(\alpha ,\beta ,\lambda )}(t), \end{aligned} \end{aligned}$$

(4.10)

verify the boundary conditions in (4.2).

Proof

Since $\phi^{(\alpha ,\beta )}_{\mathscr {L},i}(0)= \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(\mathscr {L})=0$ and from (2.16), we have the following system

$$\begin{aligned} \begin{aligned} -\epsilon _i \frac{(i+\beta +1)}{(i+1)}+\varepsilon _i\frac{(i+\beta +1)(i+\beta +2)}{(i+1)(i+2)}=-1, \end{aligned} \end{aligned}$$

(4.11)

$$\begin{aligned} \begin{aligned} \epsilon _i \frac{(i+\alpha +1)}{(i+1)}+\varepsilon _i\frac{(i+\alpha +1)(i+\alpha +2)}{(i+1)(i+2)}=-1. \end{aligned} \end{aligned}$$

(4.12)

Hence $\epsilon _i$ and $\varepsilon _i$ can be uniquely determined to give

$$\begin{aligned} \begin{aligned}&\epsilon _i= -\frac{(i+1)(\beta -\alpha )(2i+\alpha +\beta +3)}{(i+\alpha +1)(i+\beta +1)(2i+\alpha +\beta +4)},\\&\varepsilon _i=-\frac{(i+1)(i+2)(2i+\alpha +\beta +2)}{(i+\alpha +1)(i+\beta +1)(2i+\alpha +\beta +4)}. \end{aligned} \end{aligned}$$

(4.13)

Also, since $\psi^{(\alpha ,\beta ,\lambda )}_{j}(0)=0$ and from (3.4), we have that

$$\begin{aligned} \begin{aligned} \rho _j \frac{(j+\beta +1)}{(j+1)}=1, \end{aligned} \end{aligned}$$

(4.14)

Hence $\rho _j$ can be uniquely determined to give

$$\begin{aligned} \begin{aligned}&\rho _j=\frac{(j+1)}{(j+\beta +1) }. \end{aligned} \end{aligned}$$

(4.15)

$\square$

It is obvious that the two sets of basis functions $\phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) \in P_{N+2}^s (\Lambda )$ and $\psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \in P_{M+1}^t (I)$ are linearly independent. Therefore, by dimension argument, we have

$$\begin{aligned} \begin{aligned}&P_M^t (I) = \text {span} \left\{ \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) : j=0,\ 1,\ 2, \ldots ,\ M-1 \right\} ,\\&P_N^s (\Lambda ) = \text {span} \left\{ \phi^{(\alpha ,\beta )}_{\mathscr {L},j}(x) : j=0,\ 1,\ 2, \ldots ,\ N-2 \right\} . \end{aligned} \end{aligned}$$

(4.16)

It is clear that the Galerkin formulation of (4.8) is equivalent to the following discretization

$$\begin{aligned} \begin{aligned}&&\left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) {}_0^CD_t^{\nu } \hat{u}(x,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle \\&\quad -\tau _0 \left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) \partial ^2_{x} \hat{u}(x,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle \\&&\ -\tau _1 \left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) \partial _{x} \hat{u}(x,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle \\&&+\tau _2 \left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) \hat{u}(x,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle \\&&= \left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) f(x,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle , \end{aligned} \end{aligned}$$

(4.17)

for $0\le i\le N-2$ and $0\le j\le M-1$. To simplify the presentation, we shall always assume that the indices i and r vary between 0 and $N-2$ and that the indices j and s vary between 0 and $M-1$. Further, we assume that a repeated index is summed over. The above discretization can be expressed in the matrix form:

$$\begin{aligned} \begin{aligned}&\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}\phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _x \mathcal {U}_{ij} \left\langle {}_0^CD_t^{\nu } \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _t\\ {}&-\tau _0 \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d}^2 \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x^2} \right\rangle _x \mathcal {U}_{ij} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _t\\&-\tau _1 \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d} \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x} \right\rangle _x \mathcal {U}_{ij} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _t\\ {}&+\tau _2 \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _x \mathcal {U}_{ij} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _t\\ {}&\qquad \qquad = \left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) f(x,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle , \end{aligned} \end{aligned}$$

(4.18)

which can be written compactly in the form

$$\begin{aligned} \mathcal {A} \mathcal {U} \mathcal {D}_{\nu }- \tau _0\mathcal {B} \mathcal {U} \mathcal {E} -\tau _1 \mathcal {C} \mathcal {U} \mathcal {E}+\tau _2 \mathcal {A} \mathcal {U} \mathcal {E}= \mathcal {F}, \end{aligned}$$

(4.19)

where

$$\begin{aligned} \begin{aligned}&\mathcal {A}=\left( \mathcal {A}_{ir} \right) _{0\leqslant i,r\leqslant N-2}=\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}\phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _x,\\&\mathcal {D}_{\nu }=\left( \mathcal {D}_{js}^{\nu } \right) _{0\leqslant j,s\leqslant M-1}= \left\langle {}_0^CD_t^{\nu } \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _t,\\&\mathcal {B}=\left( \mathcal {B}_{ir} \right) _{0\leqslant i,r\leqslant N-2}=\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d}^2 \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x^2} \right\rangle _x,\\&\mathcal {E}=\left( \mathcal {E}_{js} \right) _{0\leqslant j,s\leqslant M-1}=\left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _t,\\&\mathcal {C}=\left( \mathcal {C}_{ir} \right) _{0\leqslant i,r\leqslant N-2}=\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d} \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x} \right\rangle _x,\\&\mathcal {F}=\left( \mathcal {F}_{js} \right) _{0\leqslant i\leqslant N-2,\ 0\leqslant j\leqslant M-1}\\&=\left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) f(x,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle , \end{aligned} \end{aligned}$$

(4.20)

$\mathcal {U}=\left( \mathcal {U}_{ij} \right) _{0\leqslant i\leqslant N-2,\ 0\leqslant j\leqslant M-1}$ is the matrix of unknown coefficients, and reaction matrix. To solve (4.19), we recast it in a more convenient form using the Kronecker product (represented by $\otimes$).

If we consider the matrices $\mathbf {F} \in \mathbb {R}^{n,m}$ and $\mathbf {G} \in \mathbb {R}^{q,p}$, then the Kronecker product of $\mathcal {F}$ and $\mathcal {G}$ is defined as the matrix

$$\begin{aligned} \mathbf {F}\otimes \mathbf {G}=\left( \begin{array}{cccc} f_{11}\mathbf {G} &{} f_{12}\mathbf {G} &{} \cdots &{} f_{1m}\mathbf {G} \\ f_{21}\mathbf {G} &{} f_{22}\mathbf {G} &{} \cdots &{} f_{2m}\mathbf {G} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ f_{n1}\mathbf {G} &{} f_{n2}\mathbf {G} &{} \cdots &{} f_{nm}\mathbf {G} \\ \end{array} \right) \in \mathbb {R}^{nq,mp} . \end{aligned}$$

Let $f_i \in \mathbb {R}^{n}$ denote the columns of $\mathcal {F}\in \mathbb {R}^{n,m}$ so that $\mathcal {F}= \left[ f_1, \ldots , f_m \right]$. Then $\text {vec}(\mathcal {F})$ is defined to be the nm-vector formed by stacking the columns of $\mathcal {F}$ on top of one another, i.e.,

$$\begin{aligned} \text {vec}(\mathcal {F}) = \left[ \begin{array}{l} f_1 \\ \vdots \\ f_m \\ \end{array} \right] \in \mathbb {R}^{nm}. \end{aligned}$$

The Kronecker product and the $\text {vec}$ operator have the following useful property which will be used in the following discussions. For any three matrices $\mathcal {F}$, $\mathcal {G}$ and $\mathbf{H}$ we define the matrix product $\mathcal {F} \mathcal {G} \mathbf{H}$ to be

$$\begin{aligned} \text {vec}(\mathcal {F}\mathcal {G}{} \mathbf{H} ) = \left( \mathbf{H ^T \otimes \mathcal {F}} \right) \text {vec}(\mathcal {G}), \end{aligned}$$

where ${}^T$ denotes the transpose.

Accordingly the set of discrete equations (4.19) may be put in the following matrix form:

$$\begin{aligned}&&\left( \mathcal {D}_{\nu }^T \otimes \mathcal {A}-\tau _0 \mathcal {E}^T \otimes \mathcal {B}-\tau _1 \mathcal {E}^T \otimes \mathcal {C}+\tau _2 \mathcal {E}^T \otimes \mathcal {A} \right) \text {vec}(\mathcal {U})\nonumber \\&&=\text {vec}(\mathcal {F}). \end{aligned}$$

(4.21)

Theorem 1

The nonzero elements $\mathcal {A}_{ir},\ \mathcal {B}_{ir},\ \mathcal {C}_{ir},\ \mathcal {D}^{\nu }_{js}$ and $\mathcal {E}_{js}$ are given by

$$\begin{aligned} \begin{aligned}&\mathcal {A}_{ii}=h^{(\alpha ,\beta )}_{\mathscr {L},i}+\epsilon ^{2}_ih^{(\alpha ,\beta )}_{\mathscr {L},i+1} +\varepsilon ^2_{i}h^{(\alpha ,\beta )}_{\mathscr {L},i+2},\\&\mathcal {A}_{i+1,i}=\mathcal {A}_{i,i+1}=\epsilon _ih^{(\alpha ,\beta )}_{\mathscr {L},i+1}+\varepsilon _i\epsilon _{i+1}h^{(\alpha ,\beta )}_{\mathscr {L},i+2},\\&\mathcal {A}_{i+2,i}=\mathcal {A}_{i,i+2}=\varepsilon _ih^{(\alpha ,\beta )}_{\mathscr {L},i+2}, \end{aligned} \end{aligned}$$

(4.22)

$$\begin{aligned} \begin{aligned} \mathcal {B}_{ii}=&\varepsilon _{i}\mathcal {A}_{2}(i+2,i,\alpha ,\beta )h^{(\alpha ,\beta )}_{\mathscr {L},i}, \\ \mathcal {B}_{ir}=&O_{2}(r,i,\alpha ,\beta )h^{(\alpha ,\beta )}_{\mathscr {L},i} +O_{2}(r,i+1,\alpha ,\beta )\epsilon _{i}h^{(\alpha ,\beta )}_{\mathscr {L},i+1}\\&+O_{2}(r,i+2,\alpha ,\beta )\varepsilon _{i}h^{(\alpha ,\beta )}_{\mathscr {L},i+2},\quad r=i+n,\quad n\ge 1, \end{aligned} \end{aligned}$$

(4.23)

$$\begin{aligned} \begin{aligned} \mathcal {C}_{i+1,i}=&\varepsilon _i\mathcal {A}_{1}(i+2,i+1,\alpha ,\beta )h^{(\alpha ,\beta )}_{\mathscr {L},i+1},\\ \mathcal {C}_{ii}=&\left( \epsilon _i\mathcal {A}_{1}(i+1,i,\alpha ,\beta )+\varepsilon _i\mathcal {A}_{1}(i+2,i,\alpha ,\beta )\right) h^{(\alpha ,\beta )}_{\mathscr {L},i}\\&+\epsilon _i\varepsilon _i\mathcal {A}_{1}(i+2,i+1,\alpha ,\beta )h^{(\alpha ,\beta )}_{\mathscr {L},i+1}, \\ \mathcal {C}_{ir}=&O_{1}(r,i,\alpha ,\beta )h^{(\alpha ,\beta )}_{\mathscr {L},i} +O_{1}(r,i+1,\alpha ,\beta )\epsilon _{i}h^{(\alpha ,\beta )}_{\mathscr {L},i+1}\\&\qquad +O_{1}(r,i+2,\alpha ,\beta )\varepsilon _{i}h^{(\alpha ,\beta )}_{\mathscr {L},i+2},\quad r=i+n,\quad n\ge 1, \end{aligned} \end{aligned}$$

(4.24)

$$\begin{aligned} \begin{aligned} \mathcal {D}^{\nu }_{js}=&\left( S_{\nu }(s,j,\alpha ,\beta )+\rho _{s}S_{\nu }(s+1,j,\alpha ,\beta )\right) h^{(\alpha ,\beta )}_{1,j}\\&+\rho _{j}\left( S_{\nu }(s,j+1,\alpha ,\beta \right. )\\&\left. +\rho _{s}S_{\nu }(s+1,j+1,\alpha ,\beta )\right) h^{(\alpha ,\beta )}_{1,j+1}, \end{aligned} \end{aligned}$$

(4.25)

$$\begin{aligned} \begin{aligned}&\mathcal {E}_{jj}=h^{(\alpha ,\beta )}_{1,j}+\rho ^2_{j}h^{(\alpha ,\beta )}_{1,j+1},\\&\mathcal {E}_{j+1,j}=\mathcal {E}_{j,j+1}=\rho _{j}h^{(\alpha ,\beta )}_{1,j+1}, \end{aligned} \end{aligned}$$

(4.26)

where

$$\begin{aligned} \begin{aligned} O_{\sigma }(r,i,\alpha ,\beta )=&\,\mathcal {A}_{\sigma }(r,i,\alpha ,\beta ) +\epsilon _{r}\mathcal {A}_{\sigma }(r+1,i,\alpha ,\beta )\\&\quad +\varepsilon _r\mathcal {A}_{\sigma }(r+2,i,\alpha ,\beta ), \end{aligned} \end{aligned}$$

(4.27)

and $h^{(\alpha ,\beta )}_{\mathscr {L},i}$ is given by (2.18).

Proof

From (4.10), we have

$$\begin{aligned} \begin{aligned} \mathcal {A}_{ir}&=\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}\phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _x\\&=\left\langle {\left( J_{\mathscr {L},i}^{(\alpha ,\beta )}(x) +\epsilon _i J_{\mathscr {L},i+1}^{(\alpha ,\beta )}(x) +\varepsilon _i J_{\mathscr {L},i+2}^{(\alpha ,\beta )}(x)\right) \left( J_{\mathscr {L},r}^{(\alpha ,\beta )}(x)+\epsilon _r J_{\mathscr {L},r+1}^{(\alpha ,\beta )}(x) +\varepsilon _r J_{\mathscr {L},r+2}^{(\alpha ,\beta )}(x)\right) } \right\rangle _x. \end{aligned} \end{aligned}$$

(4.28)

Using the orthogonality relation (2.17), we obtain

$$\begin{aligned} \begin{aligned}&\mathcal {A}_{ii}=h^{(\alpha ,\beta )}_{\mathscr {L},i}+\epsilon ^{2}_ih^{(\alpha ,\beta )}_{\mathscr {L},i+1} +\varepsilon ^2_{i}h^{(\alpha ,\beta )}_{\mathscr {L},i+2},\\&\mathcal {A}_{i+1,i}=\mathcal {A}_{i,i+1}=\epsilon _ih^{(\alpha ,\beta )}_{\mathscr {L},i+1}+\varepsilon _i\epsilon _{i+1}h^{(\alpha ,\beta )}_{\mathscr {L},i+2},\\&\mathcal {A}_{i+2,i}=\mathcal {A}_{i,i+2}=\varepsilon _ih^{(\alpha ,\beta )}_{\mathscr {L},i+2}. \end{aligned} \end{aligned}$$

(4.29)

$\square$

Note. It is worthy to be noted here that the nonzero entries of the other matrices $\mathcal {B},\ \mathcal {C},\ \mathcal {D}^{\nu }$ and $\mathcal {E}$ can be obtained similarly.

5 Fractional Galerkin method with numerical integration for the one-dimensional case

The pure fractional-order Jacobi–Galerkin method presented in the previous section lead to efficient spectral algorithms for linear time-fractional partial differential equation with constant coefficients. However, it is not feasible for problems with variable coefficients for which the integration is often not possible. Therefore, for the linear time-fractional partial differential equations with variable coefficients, we have to resort to numerical integration [6]. In this way, we obtain the modified scheme (5.3), which we term the fractional Galerkin with numerical integration scheme.

In this section, we consider the numerical solution of the following one-dimensional time-fractional partial differential equations with variable coefficients:

$$\begin{aligned} \begin{aligned} {}_0^CD_t^{\nu }u- \tau _0(x) \frac{{\partial ^2 u}}{{\partial x^2 }}-\tau _1(x) \frac{{\partial u}}{{\partial x}} + \tau _2(x) u = f(x,t),\quad (x,t) \in \Omega , \end{aligned} \end{aligned}$$

(5.1)

with homogeneous initial and Dirichlet boundary conditions. The fractional-order Jacobi–Galerkin method for (5.1) is to find $\hat{u} \in W_L$ such that

$$\begin{aligned} \begin{aligned} \left\langle {\left\langle \hat{v} {}_0^CD_t^{\nu } \hat{u} \right\rangle } \right\rangle _{N,M}-&\left\langle {\left\langle \tau _0(x) \hat{v} \partial ^{2}_{x} \hat{u} \right\rangle } \right\rangle _{N,M}- \left\langle {\left\langle \tau _1(x) \hat{v} \partial _{x}\hat{u} \right\rangle } \right\rangle _{N,M}\\&\quad +\left\langle {\left\langle \tau _2(x) \hat{u} \hat{v} \right\rangle } \right\rangle _{N,M}\\&= \left\langle {\left\langle f \hat{v} \right\rangle } \right\rangle _{N,M},\ \forall \hat{v}\in W_L, \end{aligned} \end{aligned}$$

(5.2)

with $\left\langle {\left\langle \cdot \right\rangle } \right\rangle _{N,M}$ being the discrete inner product relative to the Jacobi–Gauss quadrature and fractional Jacobi–Gauss quadrature in both space and time, respectively. Equation (5.2) implies

$$\begin{aligned} \begin{aligned}&\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}\phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _{x,N} \mathcal {U}_{ij} \left\langle {}_0^CD_t^{\nu }\psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _{t,M}\\&- \left\langle \tau _0(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d}^2 \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x^2} \right\rangle _{x,N} \mathcal {U}_{ij} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _{t,M}\\&- \left\langle \tau _1(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d} \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x} \right\rangle _{x,N} \mathcal {U}_{ij} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _{t,M} \\&+ \left\langle \tau _2(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _{x,N} \mathcal {U}_{ij} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _{t,M}\\ {}& = \left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) f(x,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle _{N,M}. \end{aligned} \end{aligned}$$

(5.3)

where $\left\langle \cdot \right\rangle _{t,M}$, $\left\langle \cdot \right\rangle _{x,N}$ and $\left\langle {\left\langle \cdot \right\rangle } \right\rangle _{N,M}$ are the discrete approximations of the integrals in (4.6) with the fractional Jacobi–Gauss quadrature in time, Jacobi–Gauss quadrature in space and both of them in both space and time, respectively.

Let us denote

$$\begin{aligned} \begin{aligned}&\widetilde{\mathcal {B}}=\left( \widetilde{\mathcal {B}}_{ir} \right) ,\ \widetilde{\mathcal {C}} =\left( \widetilde{ \mathcal {C}}_{ir} \right) ,\ \widetilde{\mathbf{R }}=\left( \widetilde{\mathbf{R }}_{ir} \right) ,\ \widetilde{\mathcal {F}}=\left( \widetilde{\mathcal {F}}_{ij} \right) ,\ \end{aligned} \end{aligned}$$

(5.4)

where

$$\begin{aligned} \begin{aligned} \widetilde{\mathcal {B}}_{ir}&= \left\langle \tau _0(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d}^2 \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x^2} \right\rangle _{x,N}\quad \widetilde{\mathcal {C}}_{ir}\\&=\left\langle \tau _1(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d} \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x} \right\rangle _{x,N},\\ \widetilde{\mathbf{R }}_{ir}&=\left\langle \tau _2(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i}\phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _{x,N},\quad \widetilde{\mathcal {F}}_{ij}\\&=\left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) f(x,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle _{N,M}, \end{aligned} \end{aligned}$$

(5.5)

then, the linear system (5.3) becomes

$$\begin{aligned} \left( \mathcal {D}_{\nu }^T \otimes \mathcal {A}- \mathcal {E}^T \otimes \widetilde{\mathcal {B}}+ \mathcal {E}^T \otimes \widetilde{\mathcal {C}}+ \mathcal {E}^T \otimes \widetilde{\mathbf{R }} \right) \text {vec}(\mathcal {U})=\text {vec}(\widetilde{\mathcal {F}}). \end{aligned}$$

(5.6)

6 Fractional Galerkin method for the two-dimensional case

The two-dimensional fractional Galerkin method is significantly more complex than the one-dimensional version. In this section, we consider the numerical solution of the two-dimensional time fractional advection–diffusion–reaction equations in the form:

$$\begin{aligned} \begin{aligned}&{}_0^CD_t^{\nu }u - \delta _0 \frac{{\partial ^2 u}}{{\partial x^2 }} - \delta _1 \frac{{\partial ^2 u}}{{\partial y^2 }} - \delta _2\frac{{\partial u}}{{\partial x}} - \delta _3 \frac{{\partial u}}{{\partial y}} + \delta _4 u \\&= f(x,y,t),\quad (x,y,t) \in \Lambda ^2 \times I, \end{aligned} \end{aligned}$$

(6.1)

with homogeneous initial and Dirichlet boundary conditions, where $\Lambda ^2=\Lambda \times \Lambda$. The two-dimensional Galerkin approximation may be written as

$$\begin{aligned} u(x,y,t)\simeq \hat{u}(x,y,t)= & {} \sum _{i=0}^{N-2}\sum _{i'=0}^{N-2}\sum _{j=0}^{M-1} \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i'}(y)\nonumber \\&\widehat{ \mathcal {U}}_{ii'j} \psi^{(\alpha ,\beta ,\lambda )}_{j}(t). \end{aligned}$$

(6.2)

Then the fractional-order Jacobi–Galerkin scheme (4.18) in the two-dimensional case is equivalent to

$$\begin{aligned} \begin{aligned}&\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}\phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _x \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'}\phi^{(\alpha ,\beta )}_{\mathscr {L},r'} \right\rangle _y \widehat{ \mathcal {U}}_{ii'j} \left\langle {}_0^CD_t^{\nu }\psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{\mathcal {T},s} \right\rangle _t\\&\qquad \qquad -\delta _0 \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d}^2 \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x^2} \right\rangle _x \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'} \phi^{(\alpha ,\beta )}_{\mathscr {L},r'} \right\rangle _y \widehat{ \mathcal {U}}_{ii'j} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _t\\&\qquad \qquad -\delta _1 \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _x \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'} \frac{d^2 \phi^{(\alpha ,\beta )}_{\mathscr {L},r'}}{dy^2} \right\rangle _y \widehat{ \mathcal {U}}_{ii'j} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _t\\&\qquad \qquad -\delta _2 \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d} \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x} \right\rangle _x \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'} \phi^{(\alpha ,\beta )}_{\mathscr {L},r'} \right\rangle _y \widehat{ \mathcal {U}}_{ii'j} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _t\\&\qquad \qquad -\delta _3 \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _x \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'} \frac{d \phi^{(\alpha ,\beta )}_{\mathscr {L},r'}}{dy} \right\rangle _y \widehat{ \mathcal {U}}_{ii'j} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _t\\&\qquad \qquad +\delta _4 \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _x \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'} \phi^{(\alpha ,\beta )}_{\mathscr {L},r'} \right\rangle _y \widehat{ \mathcal {U}}_{ii'j} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _t\\&\qquad \qquad = \left\langle { \left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i'}(y) f(x,y,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle } \right\rangle . \end{aligned} \end{aligned}$$

(6.3)

Let us denote

$$\begin{aligned} \begin{aligned}&\widehat{ \mathcal {U}}=[ \overline{\mathcal {U}}_0, \overline{\mathcal {U}}_1,\ldots , \overline{\mathcal {U}}_{M-1}],\\&\overline{\mathcal {U}}_{i}=[ \overline{\mathcal {U}}_{i,0}, \overline{\mathcal {U}}_{i,1},\ldots , \overline{\mathcal {U}}_{i,N-2}]^T,\\&\overline{\mathcal {U}}_{i,i'}=[\widehat{ \mathcal {U}}_{i,i',0},\widehat{ \mathcal {U}}_{i,i',1},\ldots ,\widehat{ \mathcal {U}}_{i,i',N-2}]^{T}, \end{aligned} \end{aligned}$$

(6.4)

and

$$\begin{aligned} \begin{aligned}&\widehat{ \mathcal {F}}=[ \overline{\mathcal {F}}_0, \overline{\mathcal {F}}_1,\ldots , \overline{\mathcal {F}}_{M-1}],\\&\overline{\mathcal {F}}_{i}=[ \overline{\mathcal {F}}_{i,0}, \overline{\mathcal {F}}_{i,1},\ldots , \overline{\mathcal {F}}_{i,N-2}]^T,\\&\overline{\mathcal {F}}_{i,i'}=[\widehat{ \mathcal {F}}_{i,i',0},\widehat{ \mathcal {F}}_{i,i',1},\ldots ,\widehat{ \mathcal {F}}_{i,i',N-2}]^{T}, \end{aligned} \end{aligned}$$

(6.5)

where $\widehat{ \mathcal {U}}$ is the matrix of unknown coefficients and $\widehat{ \mathcal {F}}$ is the reaction matrix whose entries are $\mathcal {F}_{ii'j}=\left\langle { \left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i'}(y) f(x,y,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle } \right\rangle$. The fractional-order Jacobi-Galerkin discretization (6.3) is equivalent to the following matrix equation

$$\begin{aligned} \begin{aligned}&\left( \mathcal {A}\otimes \mathcal {A} \right) \widehat{ \mathcal {U}} \mathcal {D}_{\nu }- \delta _0\left( \mathcal {B}\otimes \mathcal {A} \right) \widehat{ \mathcal {U}} \mathcal {E}\\&- \delta _1\left( \mathcal {A}\otimes \mathcal {B} \right) \widehat{ \mathcal {U}} \mathcal {E} - \delta _2\left( \mathcal {C}\otimes \mathcal {A} \right) \widehat{ \mathcal {U}} \mathcal {E}\\&- \delta _3\left( \mathcal {A}\otimes \mathcal {C} \right) \widehat{ \mathcal {U}} \mathcal {E}\\&+ \delta _4\left( \mathcal {A}\otimes \mathcal {A} \right) \widehat{ \mathcal {U}} \mathcal {E} = \widehat{ \mathcal {F}}. \end{aligned} \end{aligned}$$

(6.6)

To solve (6.6), we recast it in a more convenient form using the Kronecker product. We can express the set of discrete equations (6.6) in the following matrix form

$$\begin{aligned} \begin{aligned}&\left( \mathcal {D}_{\nu }^T\otimes \mathcal {A}\otimes \mathcal {A} - \delta _0 \mathcal {E}^T \otimes \mathcal {B}\otimes \mathcal {A} - \delta _1\right. \\&\quad \left. \mathcal {E}^T \otimes \mathcal {A}\otimes \mathcal {B} - \delta _2 \mathcal {E}^T \otimes \mathcal {C}\otimes \mathcal {A} \right. \\&\qquad \qquad \left. - \delta _3 \mathcal {E}^T \otimes \mathcal {A}\otimes \mathcal {C} + \delta _4 \mathcal {E}^T \otimes \mathcal {A}\otimes \mathcal {A} \right) \text {vec}( \widehat{ \mathcal {U}})\\&=\text {vec}(\widehat{ \mathcal {F}}). \end{aligned} \end{aligned}$$

(6.7)

This linear system can be solved by using a suitable iterative method to obtain the numerical solution (6.2). In our implementation, this system has been solved using the Mathematica function FindRoot with zero initial approximation.

7 Fractional Galerkin method with numerical integration for the two-dimensional case

Without any lose of generality, we consider the two-dimensional time-fractional partial differential equation with variable coefficients supplemented by homogeneous initial and boundary conditions, namely

$$\begin{aligned} \begin{aligned}&{}_0^CD_t^{\nu }u - \delta _0 (x)\frac{{\partial ^2 u}}{{\partial x^2 }} - \delta _1 (x)\frac{{\partial ^2 u}}{{\partial y^2 }} - \delta _2 (x)\frac{{\partial u}}{{\partial x}} \\&\quad - \delta _3 (x)\frac{{\partial u}}{{\partial y}} + \delta _4 (x)u = f(x,y,t),(x,y,t) \in \Lambda ^2 \times I, \end{aligned} \end{aligned}$$

(7.1)

with the initial condition

$$\begin{aligned} \begin{aligned} u(x,y,0)=0,\quad (x,y) \in \Lambda ^2, \end{aligned} \end{aligned}$$

(7.2)

and the homogeneous Dirichlet boundary condition

$$\begin{aligned} \begin{aligned} u(x,y,t)&=0, \quad (x,y,t) \in \partial \Lambda ^2 \times I. \end{aligned} \end{aligned}$$

(7.3)

We can always modify the right-hand side to take care of the nonhomogeneous initial and boundary conditions. We will utilize (6.2) to establish the fractional-order Jacobi-Galerkin method with numerical integration for (7.1). Hence the fractional-order Jacobi–Galerkin scheme (5.3) in the two-dimensional case is equivalent to

$$\begin{aligned} \begin{aligned}&\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}\phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _{x,N} \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'}\phi^{(\alpha ,\beta )}_{\mathscr {L},r'} \right\rangle _{y,N} \widehat{ \mathcal {U}}_{ii'j} \left\langle {}_0^CD_t^{\nu } \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _{t,M}\\&- \left\langle \delta _0(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d}^2 \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x^2} \right\rangle _{x,N} \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'} \phi^{(\alpha ,\beta )}_{\mathscr {L},r'} \right\rangle _{y,N} \widehat{ \mathcal {U}}_{ii'j} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _{t,M}\\&-\left\langle \delta _1(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _{x,N} \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'} \frac{\mathrm{d}^2 \phi^{(\alpha ,\beta )}_{\mathscr {L},r'}}{\mathrm{d}y^2} \right\rangle _{y,N} \widehat{ \mathcal {U}}_{ii'j} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _{t,M}\\&- \left\langle \delta _2(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \frac{\mathrm{d} \phi^{(\alpha ,\beta )}_{\mathscr {L},r}}{\mathrm{d}x} \right\rangle _{x,N} \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'} \phi^{(\alpha ,\beta )}_{\mathscr {L},r'} \right\rangle _{y,N} \widehat{ \mathcal {U}}_{ii'j} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _{t,M}\\&-\left\langle \delta _3(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _{x,N} \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'} \frac{d \phi^{(\alpha ,\beta )}_{\mathscr {L},r'}}{dy} \right\rangle _{y,N} \widehat{ \mathcal {U}}_{ii'j} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _{t,M}\\&+\left\langle \delta _4 (x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _{x,N} \left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i'} \phi^{(\alpha ,\beta )}_{\mathscr {L},r'} \right\rangle _{y,N} \widehat{ \mathcal {U}}_{ii'j} \left\langle \psi^{(\alpha ,\beta ,\lambda )}_{j} \psi^{(\alpha ,\beta ,\lambda )}_{s} \right\rangle _{t,M}\\&= \left\langle { \left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i'}(y) f(x,y,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle } \right\rangle _{N,N,M}. \end{aligned} \end{aligned}$$

(7.4)

Let us denote

$$\begin{aligned} \begin{aligned}&\widetilde{\mathcal {G}}_{ir}= \left\langle \delta _0(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _{x,N} ,\quad \widetilde{\mathbf{H }}_{ir}= \left\langle \delta _1(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i} \phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _{x,N}\\&\widetilde{\mathbf{R }}_{ir}= \left\langle \delta _2 (x)\phi^{(\alpha ,\beta )}_{\mathscr {L},i} \phi^{(\alpha ,\beta )}_{\mathscr {L},r} \right\rangle _{x,N}, \end{aligned} \end{aligned}$$

(7.5)

and

$$\begin{aligned} \begin{aligned}&\widetilde{\mathcal {F}}=[ \underline{\mathcal {F}}_0, \underline{\mathcal {F}}_1,\ldots , \underline{\mathcal {F}}_{M-1}],\\&\underline{\mathcal {F}}_{i}=[ \underline{\mathcal {F}}_{i,0}, \underline{\mathcal {F}}_{i,1},\ldots , \underline{\mathcal {F}}_{i,N-2}]^T,\\&\underline{\mathcal {F}}_{i,i'}=[\widetilde{ \mathcal {F}}_{i,i',0},\widetilde{ \mathcal {F}}_{i,i',1},\ldots ,\widetilde{ \mathcal {F}}_{i,i',N-2}]^{T}, \end{aligned} \end{aligned}$$

(7.6)

where

$$\begin{aligned} \begin{aligned} \mathcal {F}_{ii'j}&=\left\langle { \left\langle {\left\langle \phi^{(\alpha ,\beta )}_{\mathscr {L},i}(x) \phi^{(\alpha ,\beta )}_{\mathscr {L},i'}(y) f(x,y,t) \psi^{(\alpha ,\beta ,\lambda )}_{j}(t) \right\rangle } \right\rangle } \right\rangle _{N,N,M}. \end{aligned} \end{aligned}$$

(7.7)

Then using the same notation introduced in (5.5) and (4.20), the fractional-order Jacobi–Galerkin discretization (7.4) is equivalent to the following matrix equation

$$\begin{aligned} \begin{aligned} \left( \mathcal {A}\otimes \mathcal {A} \right) \widehat{ \mathcal {U}} \mathcal {D}_{\nu }-&\left( \widetilde{\mathcal {B}}\otimes \mathcal {A} \right) \widehat{ \mathcal {U}} \mathcal {E} - \left( \widetilde{\mathcal {G}}\otimes \mathcal {B} \right) \widehat{ \mathcal {U}} \mathcal {E} + \left( \widetilde{\mathcal {C}}\otimes \mathcal {A} \right) \widehat{ \mathcal {U}}\mathcal {E}\\&+\left( \widetilde{\mathbf{H }}\otimes \mathcal {C} \right) \widehat{ \mathcal {U}} \mathcal {E} +\left( \widetilde{\mathbf{R }}\otimes \mathcal {A} \right) \widehat{ \mathcal {U}} \mathcal {E} = \widetilde{\mathcal {F}}. \end{aligned} \end{aligned}$$

(7.8)

To solve (6.6), we recast it in a more convenient form using the Kronecker product. We can express the set of discrete equations (6.6) in the following matrix form

$$\begin{aligned} \begin{aligned} \widetilde{\mathbf{M }}\ \text {vec}( \widehat{ \mathcal {U}})=&\left( \mathcal {D}_{\nu }^T \otimes \mathcal {A}\otimes \mathcal {A} - \mathcal {E}^T \otimes \widetilde{\mathcal {B}}\otimes \mathcal {A} - \mathcal {E}^T \otimes \widetilde{\mathcal {G}}\otimes \mathcal {B} + \mathcal {E}^T \otimes \widetilde{\mathcal {C}}\otimes \mathcal {A} \right. \\&\left. + \mathcal {E}^T \otimes \widetilde{\mathbf{H }}\otimes \mathcal {C} +\mathcal {E}^T \otimes \widetilde{\mathbf{R }}\otimes \mathcal {A} \right) \text {vec}( \widehat{ \mathcal {U}})=\text {vec}(\widetilde{\mathcal {F}}). \end{aligned} \end{aligned}$$

(7.9)

This system has the same method of solution like that of (6.2). We now describe how problems with nonhomogeneous initial-boundary conditions can be efficiently transformed into problems with homogeneous initial-boundary conditions. We proceed as follows: Setting

$$\begin{aligned} u(x,t)=\tilde{u}(x,t)+u_e(x,t), \end{aligned}$$

(7.10)

where $\tilde{u}$ is an auxiliary unknown function satisfying the modified problem

$$\begin{aligned} \begin{aligned}&{}_0^CD_t^{\nu }\tilde{u}(x,t) - \tau _0 \partial ^{2}_{x} \tilde{u}(x,t)-\tau _1 \partial _{x} \tilde{u}(x,t)\\&+\tau _2 \tilde{u}(x,t)=f^*(x,t), \ (x,t) \in \Omega , \end{aligned} \end{aligned}$$

(7.11)

subject to the homogeneous initial-boundary conditions

$$\begin{aligned} \begin{aligned}&\tilde{u}(x,0)=0 ,\ x\in [0,\mathscr {L}],\\&\tilde{u}(0,t)=\tilde{u}(\mathscr {L},t)=0,\ t\in [0,1], \end{aligned} \end{aligned}$$

(7.12)

where

$$\begin{aligned} \begin{aligned} f^*(x,t)&=f(x,t)- {}_0^CD_t^{\nu }u_e(x,t) + \tau _0 \partial ^{2}_{x} u_e(x,t)\\&\quad +\tau _1 \partial _{x} u_e(x,t)-\tau _2 u_e(x,t), \end{aligned} \end{aligned}$$

(7.13)

while $u_e(x,t)$ is an arbitrary function satisfying the original nonhomogeneous boundary conditions.

8 Numerical results and comparisons

In this section, three numerical examples are outlined to demonstrate the pertinence and proficiency of the novel technique. The calculations are executed by utilizing Mathematica of Version 9, and all counts are completed in a PC of CPU Intel(R) Core(TM) i3-2350M 2 Duo CPU 2.30 GHz, 6.00 GB of RAM.

The distinction between the measured value of approximate solution and its actual value (absolute error), is given by

$$\begin{aligned} \begin{aligned} E(x,t)=|u(x,t)-\hat{u}(x,t)|, \end{aligned} \end{aligned}$$

(8.1)

where u(x, t) and $\hat{u}(x,t)$ are the exact solution and the numerical solution at the point (x, t), respectively. Moreover, the maximum absolute error (MAE) is given by

$$\begin{aligned} \begin{aligned} \text {MAEs}=\text {Max}\{E(x,t):\forall (x,t)\in [0,\mathcal {L}]\times [0,\mathcal {T}]\} = L_{\infty }, \end{aligned} \end{aligned}$$

(8.2)

and

$$\begin{aligned} \begin{aligned} L_{2}&=\sqrt{\sum \limits _{i=0}^{N-2} (u(x_{G ,\mathscr {L},i}^{(\alpha ,\beta )},t)-\hat{u}(x_{G ,\mathscr {L},i}^{(\alpha ,\beta )},t))^2}, \end{aligned} \end{aligned}$$

(8.3)

also we can denote to the root mean square (RMS) error by

$$\begin{aligned} \begin{aligned} \mathrm{RMS}=\sqrt{\frac{\sum \limits _{i=0}^{N-2} (u(x_{G ,\mathscr {L},i}^{(\alpha ,\beta )},t)-\hat{u}(x_{G ,\mathscr {L},i}^{(\alpha ,\beta )},t))^2}{(N-1)}}, \end{aligned} \end{aligned}$$

(8.4)

Example 1

We consider the one-dimensional fractional-order advection diffusion equation with constant coefficients [33]:

$$\begin{aligned} {}^C_0D^{\nu }_t u-10 \frac{{\partial ^2 u}}{{\partial x^2 }} +4 \frac{{\partial u}}{{\partial x}} =f(x,t) ,\quad x\in (0,2 \pi ),\ t\in (0,1],\ \nu \in (0,1), \end{aligned}$$

(8.5)

with the initial condition:

$$\begin{aligned} u(x,0)=0,\quad x\in (0,2 \pi ), \end{aligned}$$

(8.6)

and the boundary conditions:

$$\begin{aligned} u(0,t)=u(2 \pi ,t)=t^{\gamma },\quad t\in (0,1],\ \gamma \ge \nu . \end{aligned}$$

(8.7)

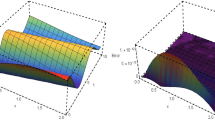
The exact solution of the above problem is $u(x,t)=t^{\gamma } \cos (x)$. The source function is given by $f(x,t)=\frac{\Gamma (\gamma +1)}{\Gamma (\gamma -\nu +1)}t^{\gamma -\nu } \cos (x)+t^{\gamma }(10\cos (x)-4\sin (x))$. In Tables 1 and 2, we present the $L_{\infty },\ L_{2}$ errors and the RMS of errors when $t=0.2,\ 0.4,\ 0.6,\ 0.8,\ 1,$ $\alpha =\beta =0$ and $N=M=16$ for two different values of $\nu +3=\gamma =3.2$ and $\nu +3=\gamma =3.6$, respectively. For $\nu +3=\gamma =3.6$, $\lambda =0.6,\ \alpha =\beta =\frac{1}{2}$ and $N=M=16$ the space-time graphs of the approximate solution and its absolute error function are illustrated in Fig. 1. The numerical results show high accuracy of the fractional Jacobi Galerkin method for the sufficiently smooth solution. For the non-smooth case, where $\nu =\gamma =\lambda =\frac{1}{2}$, the $L_{\infty }$- errors are considered in Table 3. This results show also that the method is flexible for the non-smooth solutions.

Table 1 Comparison of the errors for Example 1 with $\nu =\lambda =0.2$ and $\gamma =3.2$

Table 2 Comparison of the errors for Example 1 with $\nu =\lambda =0.6$ and $\gamma =3.6$

Table 3 The $L_{\infty }$- errors for Example 1 versus N and M at various values of $\alpha ,\ \beta$ and $\nu =\gamma =\lambda =\frac{1}{2}$

Fig. 1

The space-time graphs of the approximate solution (left) and its absolute error function (right) for Example 1 with $\nu =\lambda =0.6,\ \alpha =\beta =\frac{1}{2},$ $\gamma =3.6$ and $N=M=16$

Example 2

Consider the one-dimensional fractional diffusion equation [27, 34, 35, 38]:

$$\begin{aligned} {}^C_0D^{\nu }_t u=\frac{1}{2} x^2 \frac{{\partial ^2 u}}{{\partial x^2 }} ,\quad 0<x\le 1,\ 0<t\le 1,\ 0<\nu \le 1, \end{aligned}$$

(8.8)

with the initial condition:

$$\begin{aligned} u(x,0)=x^2, \end{aligned}$$

(8.9)

and the boundary conditions:

$$\begin{aligned} u(0,t)=0,\qquad u(1,t)=e^t. \end{aligned}$$

(8.10)

When $\nu =1$, the exact solution of this problem is

$$\begin{aligned} u(x,t)=x^2e^t. \end{aligned}$$

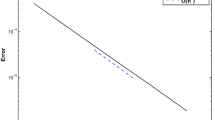
Taking $\nu =\lambda =0.75,\ \nu =\lambda =0.9,$ $N=M=4$ and $\alpha =\beta =-\frac{1}{2}$, in Tables 4 and 5, we compare our results with those obtained by using the Adomian decomposition method (ADM) [35], variational iteration method (VIM) [34], Sinc-Legendre collocation method (S-LCM) [38], Gegenbauer spectral method (GSM) [27], and fractional-order Jacobi Tau method (F-OJTM) [11]. It should be noted that only the fourth-order term of the ADM was used in evaluating the approximate solutions for Tables 4 and 5. In Table 6, it clearly appears that our method is more accurate than VIM, S-LCM, and GSM, and the obtained results are in good agreement with the exact solution. Moreover, in Fig. 2, the convergence rate of the fractional Galerkin method presented is displayed based on MAEs for different values of M and N.

Fig. 2

The $L^\infty$- errors for Example 2 versus $N=M$ with $\alpha =-\beta =\frac{1}{2}$ and $\nu =\lambda =1$

Table 4 Comparison of the numerical solutions with the other methods for Example 2 at $\nu =\lambda =0.75$ and $N=M=4$

Table 5 Comparison of the numerical solutions with the other methods for Example 2 at $\nu =\lambda =0.9$ and $N=M=4$

Table 6 The absolute errors with $\nu =\lambda =1$ for Example 2

Example 3

We consider the exact solution $u(x,y,t)=\cos (x)\cos (y)t^{\nu +2}$ for the two-dimensional time fractional advection–diffusion–reaction equation (6.1)-(7.1) on the domain,   $0<x\le \pi ,\ 0<y\le \pi ,\ 0<t\le 1$. The initial and boundary conditions can be extracted using the exact solution.

Constant coefficients problem:

$$\begin{aligned} {}^C_0D^{\nu }_t u= \frac{{\partial ^2 u}}{{\partial x^2 }}+\frac{{\partial ^2 u}}{{\partial y^2 }}+f(x,y,t),\ 0<x\le \pi ,\ 0<y\le \pi ,\ 0<t\le 1, \ 0<\nu \le 1, \end{aligned}$$

(8.11)

where the source term

$$\begin{aligned} f(x,y,t)=\cos (x)\cos (y)\left( \frac{\Gamma (\nu +3)}{2}t^2+2 t^{\nu +2}\right) . \end{aligned}$$

This problem has been studied in [42]. In [42], the problem has been discretized by a fourth-order compact finite difference approximation in the spatial directions and by an alternating direction implicit (ADI) approximation in the temporal direction. In Table 7, we compare the MAEs using our scheme at $\alpha =\beta =\frac{1}{2}$ and those achieved using the Compact ADI method [42] for various choices of $\nu$. The space graph of absolute errors at $\alpha =\beta =0$ and $\nu =\lambda =0.9$ for different values of t with $N = M=10$ of the approximate solution is displayed in Fig. 3.

Table 7 Comparison of our scheme with the compact ADI method [42] at $\nu =\frac{1}{3},\ \frac{1}{2}$ and $\frac{3}{4}$ for the constant coefficients problem of Example 3

Fig. 3

The space-time graph of the absolute errors at various choices of t with $\nu =\lambda =0.9,\ N=M=10$ and $\alpha =\beta =0$ for the constant coefficients problem in Example 3

Variable coefficients problem:

$$\begin{aligned} {}^C_0D^{\nu }_t u-x^2 \frac{{\partial ^2 u}}{{\partial x^2 }}+y^2\frac{{\partial ^2 u}}{{\partial y^2 }}=f(x,y,t),0<x\le \pi ,\ 0<y\le \pi ,\ 0<t\le 1, \ 0<\nu \le 1, \end{aligned}$$

(8.12)

where the source term

$$\begin{aligned} f(x,y,t)=x^2 t^{\nu +2} \cos (x) \cos (y)-y^2 t^{\nu +2} \cos (x) \cos (y)-\frac{\pi t^2 \csc (\pi \nu ) \cos (x) \cos (y)}{2 \Gamma (-\nu -2)}. \end{aligned}$$

In Table 8, we present MAEs obtained by our method, with $\alpha =\beta =0$ and $\nu =0.25$ at different values of t and $N=M$. The numerical results presented in this table show that the results are very accurate for small values of $N=M$. Figure 4 demonstrates that the absolute errors of $\hat{u}(x,y,t_i)$ are very small for even the small number of grid points taken.

Table 8 The MAEs for problem (8.12) with $\nu = 0.25$ and different values of t and $N=M$

Fig. 4

The space-time graphs of the absolute error functions at various choices of t with $\nu =\lambda =-0.5,\ N=M=10$ and $\alpha =\beta =-\frac{1}{2}$ for the variable coefficients problem of Example 3

9 Concluding remarks

In this paper, we have introduced a non-polynomial spectral Galerkin schemes for certain class of time fractional partial differential equations. We have constructed two efficient Galerkin spectral algorithms for solving multi-dimensional time fractional advection–diffusion–reaction equations with constant and variable coefficients. The model solution has discretized in time with a spectral expansion of fractional Jacobi functions. For the space discretization, the proposed schemes have accommodated high-order Jacobi Galerkin spectral discretization. We have illustrated the flexibility of the algorithms by comparing the fractional Jacobi Galerkin schemes with the methods proposed in [27, 34, 35, 38] for three numerical examples. The numerical results have indicated that the global character of the FJFs makes them well-suited to time fractional diffusion equations because they naturally take the irregular behavior of the solution into account and thus preserve the singularity of the solution.