Pull-in and freestanding instability of actuated functionally graded nanobeams including surface and stiffening effects

Abstract

Because of fasttechnological development, electrostatic nanoactuator devices like nanosensors, nanoswitches, and nanoresonators are highly considered by scientific community. Thus, this article presents a new solution technique in solving highly nonlinear integro-differential equation governing electrically actuated nanobeams made of functionally graded material. The modified couple stress theory and Gurtin–Murdoch surface elasticity theory are coupled together to capture the size effects of the nanoscale thin beam in the context of Euler–Bernoulli beam theory. For accurate modelling, all the material properties of the bulk and surface continuums of the FG nanoactuator are varied continuously in thickness direction according to power law. The nonlinearity arising from the electrostatic actuation, fringing field, mid-plane stretching effect, axial residual stress, Casimir dispersion, and van der Waals forces are considered in mathematical formulation. The nonlinear nonclassical equilibrium equation of FG nanobeam-based actuators and associated boundary conditions are exactly derived using Hamilton principle. The new solution methodology is combined from three phases. The first phase applies Galerkin method to get an integro-algebraic equation. The second one employs particle swarm optimization method to approximate the integral terms (i.e. electrostatic force, fringing field, and intermolecular forces) to non-integral cubic algebraic equation. Then, solved the system easily in last phase. The resulting algebraic model provides means for obtaining critical deflection, pull-in voltage, detachment length, minimum gap, and freestanding effects. A reasonable agreement is found between the results obtained from the present method and those in the available literature. A parametric study is performed to investigate the effects of the gradient index, material length scale parameter, surface energy, intermolecular forces, initial gap, and beam length on the pull-in response and freestanding phenomena of fully clamped and cantilever FG nanoactuators.

1 Introduction

Recent advances in the application of nanotechnology have resulted in the manufacture of nanoelectromechanical devices. The attractiveness of them is due to their excellent and distinctive mechanical and electrical properties, Ebrahimi and Hosseini [21]. Recently, FGMs are employed in micro/nano-electro-mechanical system (MEMS/NEMS) and atomic force microscopes (AFMs) to achieve high sensitivity and desired performance, [23, 24]. Electrostatic micro/nano-actuator devices like nanosensors, nanoswitches, and nanoresonators are widely used and can be modeled as nanobeam structures, Younis [81]. These devices usually comprise a conductive deformable body suspended above a rigid grounded body, Batra et al. [13]. When the applied voltage between the two bodies reaches an upper limit, called “pull-in voltage”, they eventually collapse due to interaction between electrostatic and elastic forces. Accurate estimate of the pull-in voltage is crucial in the design of micro/nano-actuator devices. For a switching device, the designer exploits pull-in phenomenon to optimize device’s performance while for a micro-resonator, the designer avoids this phenomenon to achieve stable motion.

Rotation in continuum solid mechanics is divided into two kinds; one is independent called micro-polar rotation, which represents one sort of microstructure effects, and the other is the anti-symmetric part of displacement gradient field, called local rotation. In fact, the local rotation, at a point of the continuum, represents a constraint on the displacements at this point that induces an additional couple stress and, consequently, contributes on the strain energy density of the continuum. In the present study, the local-rotation is captured using the modified couple stress theory (MCST), Yang et al. [78]. For nanoscale structures, the surface is regarded as a membrane with a negligible thickness, [31, 32], where the atoms’ arrangements and material properties differ from those of the bulk material. For nanostructures with higher ratio of surface layer volume to the bulk volume, surface energy effect becomes effective and cannot be ignored, Miller and Shenoy [43], and Shenoy [68].

Therefore, a nonclassical couple stress continuum model considering the effect of surface energy is proposed. In the present study, modified couple-stress theory and surface elasticity theory are exploited to develop an integrated model to investigate simultaneously the effects of microstructure local rotation and surface energy on the response of nano-devices. Using different beam theories in conjunction with combined influence of microstructure and surface energy, static and dynamic analyses of micro/nanoscale beams and plates have been investigated by some researchers, i.e. Gao and Mahmoud [29], Gao [28], Gao and Zhang [30], Shaat et al. [63], Zhang and Gao [86], Wang et al. [75], Attia and Mahmoud [5, 6], Attia et al. [10], and Shanab et al. [66, 67, 65].

In this regard, various experimental [12, 34], analytical [11, 55, 60, 59], [61, 14, 42, 47], and numerical [8, 2, 4, 6, 7, 55, 64, 88] investigations have been conducted on the pull-in instability behavior of micro/nano-beams subjected to electrostatic loadings. Numerical methods including finite difference method (FDM) [51, 55, 62], finite element method (FEM) [33, 45], differential quadrature method (DQM) [33, 74], [80], [4], and reduced order model (ROD) [14, 44, 54, 82] can predict the pull-in voltage with a very high degree of accuracy; however, these methods are computationally intensive.

Closed and semi-analytical expressions for pull-in voltages of micro/nano-actuators are very helpful since they save time and complex computational work required by numerical methods. Several researchers have provided closed-form expressions for the calculation of pull-in voltage [11, 42, 55]. Osterberg and Senturia [46] and Pamidighantam et al. [48] assumed a lumped spring mass model to obtain a closed-form expression for the pull-in voltage of microstructures such as beams/plates with different end conditions. Based on a lumped two degrees of freedom model, Bochobza-Degani and Nemirovsky [15] presented an analytical solution for calculating the pull-in parameters of electrostatic actuators. Baghani [11] presented an analytical solution for size-dependent response of cantilever micro-beams based on the MCST using the modified variational iteration method. Rokni et al. [55] derived analytical closed-form solutions in explicit forms for electrostatically actuated cantilever and fully clamped micro-beams based on the MCST. However, the solution of this approach is nontrivial. On the other hand, including nonlinearity caused by fringing field and/or intermolecular forces much complicates this approach. In Bhojawala and Vakharia [14], a closed-form for static pull-in voltage of fully clamped electrostatically actuated microbeam was derived as an explicit function of mid-plane stretching, axial load, fringing field, Casimir force, and finite conductivity. This closed form is invalid if other effects such as couple stress, surface residual stress, surface elasticity, van der Waals force, and/or material gradation are included. Miandoab et al. [42] predicted the static pull-in voltage of clamped-free, clamped–clamped and curved nanobeams based on the MCST, by transforming governing equations to a single degree of freedom model using Galerkin method and Genetic Algorithm to approximate the integral form of electrostatic force to non-integral form. However, this closed form does not account for fringing field or intermolecular forces.

In general, intermolecular forces are negligible for MEMS, where the separation distance is of the order of micron, but they play a significant role for NEMS, where the gap reduces to the nanoscale. Ramezani et al. [53, 52] obtained closed-form solutions for the pull-in parameters of cantilever nanoswitches subjected to intermolecular, electrostatic, and fringing forces using the Green’s function. They estimated the detachment length and the minimum initial gap of freestanding nanocantilevers. Radi et al. [49, 50] investigated the pull-in instability of nanocantilevers actuated by electrostatic force and subject to Casimir or van der Waals forces by using the Green’s function. This approach provided accurate predictions for the pull-in parameters of a freestanding nanoactuator. However, they did not consider the influences of microstructure, surface elasticity, and surface residual stresses parameters, which are important when the physical dimensions of structures descend to nanoscale. The influence of the surface energy on the pull-in instability of nanocantilevers under the electrostatic, fringing forces, and Casimir intermolecular attraction was investigated by Farrokhabadi et al. [26]. They employed the Duan–Rach method of determined coefficients and included the contribution of the surface energy on the free end boundary conditions, which have been ignored by almost other researchers.

Recently, Dehghan et al. [17] investigated the wave propagation analysis of fluid-conveying magneto-electro-elastic nanotube incorporating nanoscale effect by using nonlocal elasticity theory of Eringen. Ebrahimi and Hosseini [20] studied analytically nonlinear vibration and dynamic instability of nonlocal nanobeams under thermo‑magneto‑mechanical loads by using Galerkin method and multiple scales method. Sahmani et al. [58] developed analytical solution for vibrational response of postbuckled laminated FG graphene platelet-reinforced composite nonlocal strain gradient nanobeams. Ebrahimi et al. [22] studied bending of magneto‑electro‑elastic analysis of piezoelectric–flexoelectric nonlocal nanobeams rested on silica aerogel foundation. Ebrahimi and Hosseini [21] presented effect of residual surface stress on nonlinear dynamics and instability of double-walled nanobeams by using nonlinear Mathieu–Hill equation. Wu and Liu [76] studied nonlinear thermo‑mechanical response of temperature‑dependent FG sandwich nonlocal strain gradient nanobeams with geometric imperfection. Xie et al. [77] investigated nonlinear secondary resonance of FG porous silicon nanobeams under periodic hard excitations based on surface elasticity theory. For more details, many recent studies in the literature on the static and dynamic response of nanobeams and nanoplates in the context of the nonlocal elasticity theory, nonlocal strain gradient theory, or modified couple stress theory have been developed, i.e. Fattahi et al. [27], Thanh et al. [71], Fan et al. [25], Ma et al. [40], Sahmani and Safaei [57], Trinh et al. [73], Yi et al. [79], Yuan et al. [85, 83, 84], Zhang and Liu [87], Lyu et al. [39], Liu et al. [38] and Liu and Lyu [37].

From the prementioned literature, it is noticed that the availability of closed-form or analytical model expressions for static pull-in instability analysis is still limited. These closed-form models mostly suffer from increased complexity and they may involve complicated mathematical operations. Therefore, the objective of the present paper was to propose a generalized closed-form expression for the size-dependent pull-in voltage of electro-mechanical FG nanobeams as well as the critical parameters of freestanding nanoactuator. The mathematical model is derived utilizing Hamilton principle taking into account the simultaneous effects of material length scale parameter, surface elasticity, and surface residual stress as well as nonlinearity raised by mid-plane stretching effect, axial residual stress, and van der Waals, Casimir, and electrostatic forces including fringing field under static condition in conjunction with Euler–Bernoulli beam theory. Power law distribution is employed to describe the material distribution of bulk and surface continuums through thickness and consequently the physical neutral axis is considered. Application of Galerkin method transforms the highly nonlinear integro-differential governing equation into a highly nonlinear integro-algebraic equation. The main idea behind the proposed closed-form solution is to replace appropriately the integral-terms in this equation by non-integral algebraic functions with undetermined coefficients. Particle Swarm Optimization (PSO) method is utilized to determine these coefficients such that they minimize the error between integral- and non-integral forms. Based on the resulting algebraic equation, generalized simple closed forms for the pull-in voltage and freestanding parameters are derived.

Accordingly, the present paper was organized as follows: in Sect. 2, the size-dependent governing equation and associated boundary conditions are derived. Section 3 presents the proposed solution method and its accuracy is verified by comparing the obtained results with other reported literature in Sect. 4. Section 5 presents an extensive parametric study to explore the effects of various material and geometrical parameters on the pull-in response as well as proposed expressions for permissible detachment length, minimum gap, and pull-in parameter parameters. Finally, Sect. 6 presents conclusion including key findings.

2 Theoretical formulation

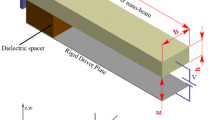
An electrostatically actuated FG nanobeam is depicted in a rectangular coordinate system as illustrated in Fig. 1. The beam has length $L$ with a uniform rectangular cross section of width $b$ and thickness $h$. The initial gap separating the nanobeam from the substrate is $d$. The effective material properties ${\mathcal{P}}$ of the FG nanobeam that vary continuously along the thickness are described according to the following power law:

$${\mathcal{P}}\left( z \right) = \left( {{\mathcal{P}}_{U} - {\mathcal{P}}_{L} } \right)\left( {\frac{1}{2} + \frac{{z_{{\text{m}}} }}{h}} \right)^{k} + {\mathcal{P}}_{L} , - \frac{h}{2} \le z_{{\text{m}}} \le \frac{h}{2} ,$$

(1)

where subscripts ${\mathcal{P}}_{U}$ and ${\mathcal{P}}_{L}$ are the material properties of the two constituents at the upper $\left( {z = h/2} \right)$ and lower $\left( {z = - h/2} \right)$ surfaces of the nanobeam, respectively, and $k$ is a non–negative number (power law index), which controls the material variation profile through the thickness of the beam,where neutral surface reference can be evaluated by

$$\tilde{z} = \frac{{\mathop \smallint \nolimits_{A} z_{{\text{m}}} \left[ {\lambda \left( {z_{{\text{m}}} } \right) + 2\mu \left( {z_{m} } \right)} \right]{\text{d}}A}}{{\mathop \smallint \nolimits_{A} \left[ {\lambda \left( {z_{{\text{m}}} } \right) + 2\mu \left( {z_{m} } \right)} \right]{\text{d}}A}}, \tilde{z} = z_{{\text{m}}} - h_{0} .$$

(2)

Fig. 1

Schematic of an FGM nanobeam subjected to an electrostatic force

Taking the physical neutral surface as a reference, the effective material properties take the following form:

$${\mathcal{P}}\left( z \right) = {\mathcal{P}}_{L} + \left( {{\mathcal{P}}_{U} - {\mathcal{P}}_{L} } \right)\left( {\frac{1}{2} + \frac{{\tilde{z} + h_{0} }}{h}} \right)^{k} .$$

(3)

From this equation, it is seen that ${\mathcal{P}} = {\mathcal{P}}_{L}$, when $\tilde{z} = - \left( {0.5h + h_{0} } \right)$ and ${\mathcal{P}} = {\mathcal{P}}_{U}$ when $\tilde{z} = \left( {0.5h - h_{0} } \right)$. Young’s modulus ($E\left( z \right)$), Poisson’s ratio ($\nu \left( z \right)$), mass density ($\rho \left( z \right)$), microstructure material length scale ($l\left( z \right)$) of the bulk, surface Lamé constants ($\lambda^{{\text{s}}} \left( z \right)$ and $\mu^{{\text{s}}} \left( z \right)$), surface residual stress (${\tau }^{\mathrm{s}}(z)$), and surface mass density ($\rho^{{\text{s}}} \left( z \right)$) can be expressed by power law gradation function, Eq. (3).

The displacement field based on the Euler–Bernoulli beam theory is expressed as

$$u_{x} \left( {x,z,t} \right){ } = u\left( {x,t} \right) - \tilde{z}w^{\prime}\left( {x,t} \right),{ }u_{y} \left( {x,z,t} \right) = 0,{ }u_{z} \left( {x,z,t} \right) = w\left( {x,t} \right),$$

(4)

where $u$ and $w$ are the axial and lateral displacements of any point $\left( {x,z} \right)$ on the mid-plane and $t$ denotes time.

Based on Euler–Bernoulli beam theory in conjunction with the modified couple stress theory (MCST) presented by Yang et al. [78], the non-zero components of the infinitesimal strain vector ($\varepsilon_{ij}$), rotation vector ($\theta_{i}$), and the symmetric curvature tensor ($\chi_{ij}$), respectively, can be obtained as [5, 9, 66]

$$\varepsilon_{xx} = u^{\prime} - \tilde{z}w^{\prime\prime},$$

(5)

$$\theta_{y} = - w^{\prime},$$

(6)

$$\chi_{xy} = \chi_{yx} = - \frac{1}{2}w^{\prime\prime},$$

(7)

where the prime dash refers to the derivative with respect to the coordinate $x$ and dot represents to the derivative with respect to the time $t$. Assuming a linear elastic behavior of the nanobeam, the bulk constitutive equations of the FG nanobeam can be expressed in terms of displacements as follows [5]:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\sigma_{yy} = \sigma_{zz} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\left[ {\lambda \left( z \right) + 2\mu \left( z \right)} \right]\left( {u^{\prime} - \tilde{z}w^{\prime\prime}} \right) } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\lambda \left( z \right)\left( {u^{\prime} - \tilde{z}w^{\prime\prime}} \right)} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\} ,$$

(8)

$$\begin{array}{*{20}c} {m_{xy} = m_{yx} = - \mu \left( z \right)l^{2} \left( z \right) w^{\prime\prime}{,}} \\ \end{array}$$

(9)

where the other components are zero. $\sigma_{ij}$ and $m_{ij}$ are the force-stress component and the deviatoric part of the symmetric couple stress tensor, respectively. $\mu \left( z \right)$ and $\lambda \left( z \right)$ are the Lamé constants in classical elasticity, $l\left( z \right)$ refers to the material length scale parameter which is spatially dependent according to Eq. (3), and $\delta_{ij}$ denotes the Kronecker delta.

The surface energy effects are incorporated into the developed size-dependent model based on Gurtin–Murdoch surface elasticity theory [32], in which the surface constitutive relations of the FG micro/nanoscale beam can be formulated as, [3, 5]

$$\left\{ {\begin{array}{*{20}c} {\tau_{xx}^{{{\text{s}} \pm }} } \\ {\begin{array}{*{20}c} {\tau_{nx}^{{{\text{s}} \pm }} } \\ \end{array} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\tau_{{\text{s}}}^{ \pm } + E_{s}^{ \pm } \left( {u^{\prime} - \tilde{z}w^{\prime\prime}} \right) } \\ {\begin{array}{*{20}c} {\tau_{{\text{s}}}^{ \pm } u_{n,x} = \tau_{{\text{s}}}^{ \pm } n_{z} w^{\prime}} \\ \end{array} } \\ \end{array} } \right\},$$

(10)

where $E_{{\text{s}}}^{ \pm }$ is the surface elastic modulus, i.e. $E_{{\text{s}}}^{ \pm } = \lambda_{{\text{s}}}^{ \pm } + 2\mu_{{\text{s}}}^{ \pm }$, where $\lambda_{{\text{s}}}^{ \pm } {\text{and }}\mu_{{\text{s}}}^{ \pm }$ are the surface Lamé constants, $\tau_{s}^{ \pm }$ is the surface residual stress, and $n_{z}$ represents the z-component of the outward unit normal ${\varvec{n}}$ to the beam lateral surface. Here, the indices “ + ” and “−” represent the upper and lower surfaces of the nanobeam, respectively. The stresses of the surface layers must satisfy the equilibrium equations of Gurtin–Murdoch model; thus the normal component of the Cauchy stress $\sigma_{xx}$ (Eq. (8)) is modified into [3, 5, 41]:

$$\sigma_{xx} = \left[ {\lambda \left( z \right) + 2\mu \left( z \right)} \right]\left( {u^{\prime} - \tilde{z}w^{\prime\prime}} \right) + \frac{\nu \left( z \right)}{{1 - \nu \left( z \right)}}\left[ {\left( {\frac{1}{2}\Delta \tau_{{\text{s}}} + f\left( z \right)\overline{\tau }_{{\text{s}}} } \right)w^{\prime\prime}} \right],$$

(11)

in which $f\left( z \right) = - \left[ {2\left( \frac{z}{h} \right)^{3} - \frac{3z}{{2h}}} \right]$, $\overline{\tau }_{{\text{s}}} = \tau_{{\text{s}}}^{ + } + \tau_{{\text{s}}}^{ - }$ and $\Delta \tau_{{\text{s}}} = \tau_{{\text{s}}}^{ + } - \tau_{{\text{s}}}^{ - }$.

Hamilton’s principle is employed to derive the governing equations and corresponding boundary conditions for the static analysis of FG nanobeams as following:

$$\mathop \int \limits_{{t_{1} }}^{{t_{2} }} \left( {\delta {\mathcal{U}} + \left[ {\delta {\text{W}}_{{\text{q}}} + \delta {\text{W}}_{{\text{s}}} + \delta {\text{W}}_{{\text{r}}} } \right]} \right){\text{d}}t$$

(12)

The first variation of the total strain energy of FG nanobeam can be obtained as follows:

$$\begin{aligned} \delta {\mathcal{U}} & = \frac{1}{2}\delta \mathop \int \limits_{0}^{L} \mathop \int \limits_{A} \left( {\sigma_{ij} \varepsilon_{ij} + m_{ij} \chi_{ij} } \right){\text{d}}A{\text{d}}x + \frac{1}{2}\delta \mathop \int \limits_{0}^{L} \mathop {\oint }\limits_{\partial A} \tau_{ij}^{s} \varepsilon_{ij} {\text{d}}S {\text{d}}x \\ & = \frac{1}{2}\delta \mathop \int \limits_{0}^{L} \left\{ {\mathop \int \limits_{A} \left( {\sigma_{xx} \varepsilon_{xx} + 2m_{xy} \chi_{xy} } \right){\text{d}}A + \mathop {\oint }\limits_{\partial A} \left( {\tau_{xx}^{{\text{s}}} \varepsilon_{xx} + 2\tau_{nx}^{{\text{s}}} \varepsilon_{nx} } \right){\text{d}}S} \right\}{\text{d}}x \\ \end{aligned}$$

(13)

in which $\varepsilon_{nx} = 0.5w^{\prime}n_{z}$. Substituting Eqs. (5, 7, 9, 10), Eq. (13) can be obtained in terms of the stress resultants as follows:

$$\delta {\mathcal{U}} = \mathop \int \limits_{L} \left\{ {\left[ {N_{xx} + N_{xx}^{{\text{s}}} + \frac{1}{2}{\mathcal{T}}_{11} w^{\prime\prime} - \frac{1}{2}{\mathcal{C}}_{P1} } \right]\delta u^{\prime} - \left[ {M_{xx} + Y_{xy} + M_{xx}^{{\text{s}}} - \frac{1}{2}{\mathcal{P}}_{A1} - \frac{1}{2}{\mathcal{T}}_{11} u^{\prime}} \right]\delta w^{\prime\prime} + \left[ {{\mathcal{S}}_{P} w^{\prime}} \right]\delta w^{\prime}} \right\}{\text{d}}x ,$$

(14)

where the forces and moments resultants are expressed as

$$\left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {M_{xx} } \\ \end{array} } \right\} \equiv \mathop \int \limits_{A} \left\{ {\begin{array}{*{20}c} 1 \\ {\tilde{z}} \\ \end{array} } \right\}\sigma_{xx} {\text{d}}A = \left\{ {\begin{array}{*{20}c} {A_{xx} } \\ {B_{xx} } \\ \end{array} } \right\}u^{\prime} - \left\{ {\begin{array}{*{20}c} {B_{xx} - {\mathcal{T}}_{11} } \\ {D_{xx} - {\mathcal{T}}_{22} } \\ \end{array} } \right\}w^{\prime\prime},$$

(15a)

$$\left\{ {\begin{array}{*{20}c} {N_{xx}^{{\text{s}}} } \\ {M_{xx}^{{\text{s}}} } \\ \end{array} } \right\} \equiv \mathop {\oint }\limits_{\partial A} \left\{ {\begin{array}{*{20}c} 1 \\ {\tilde{z}} \\ \end{array} } \right\}\tau_{xx}^{s} {\text{d}}S = \left\{ {\begin{array}{*{20}c} {{\mathcal{C}}_{P1} } \\ {{\mathcal{P}}_{A1} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {{\mathcal{C}}_{P2} } \\ {{\mathcal{P}}_{A2} } \\ \end{array} } \right\}u^{\prime} - \left\{ {\begin{array}{*{20}c} {{\mathcal{P}}_{A2} } \\ {I_{P} } \\ \end{array} } \right\}w^{\prime\prime},$$

(15b)

$$Y_{xy} \equiv \mathop \int \limits_{A} m_{xy} {\text{d}}A = - S_{xy} w^{\prime\prime},$$

(15c)

in which,

$$\left\{ {\begin{array}{*{20}c} {A_{xx} } & {B_{xx} } & {D_{xx} } \\ \end{array} } \right\} = \mathop \int \limits_{A} \overline{E}\left( z \right)\left\{ {\begin{array}{*{20}c} 1 & {\tilde{z}} & {\tilde{z}^{2} } \\ \end{array} } \right\}{\text{d}}A, \overline{E}\left( z \right) = \frac{E\left( z \right)}{{\left( {1 - \nu \left( z \right)^{2} } \right)}} {\text{if}} b \ge 5h \;{\text{else }}\;\overline{E}\left( z \right) = E\left( z \right),$$

(16a)

$$S_{xy} = \mathop \int \limits_{A} \mu \left( z \right)l\left( z \right)^{2} {\text{d}}A, \mu \left( z \right) = \frac{E\left( z \right)}{{2\left( {1 + \nu \left( z \right)} \right)}},$$

(16b)

$$\left\{ {\begin{array}{*{20}c} {{\mathcal{C}}_{P1} } & {{\mathcal{P}}_{A1} } & {{\mathcal{S}}_{P} } \\ \end{array} } \right\} = \mathop {\oint }\limits_{\partial A} \tau_{s} \left( z \right)\left\{ {\begin{array}{*{20}c} 1 & {\tilde{z}} & {n_{z}^{2} } \\ \end{array} } \right\}{\text{d}}S,$$

(16c)

$$\left\{ {\begin{array}{*{20}c} {{\mathcal{C}}_{P2} } & {{\mathcal{P}}_{A2} } & {I_{P} } \\ \end{array} } \right\} = \mathop {\oint }\limits_{\partial A} E_{{\text{s}}} \left( z \right)\left\{ {\begin{array}{*{20}c} 1 & {\tilde{z}} & {\tilde{z}^{2} } \\ \end{array} } \right\}{\text{d}}S,$$

(1d)

$$\left\{ {\begin{array}{*{20}c} {{\mathcal{T}}_{11} } & {{\mathcal{T}}_{22} } \\ \end{array} } \right\} = \mathop \int \limits_{A} f_{\tau } \left\{ {\begin{array}{*{20}c} 1 & {\tilde{z}} \\ \end{array} } \right\}{\text{d}}A, f_{\tau } = \frac{\nu \left( z \right)}{{1 - \nu \left( z \right)}}\left[ {\left( {\frac{1}{2}\Delta \tau_{{\text{s}}} + f\left( z \right)\overline{\tau }_{s} } \right)} \right].$$

(16e)

The virtual work done by the electrostatic and intermolecular forces ($\delta {\text{W}}_{{\text{q}}}$) is

$$\delta {\text{W}}_{{\text{q}}} = \mathop \int \limits_{0}^{L} \left[ {q_{{\text{e}}} + q_{{{\text{vdW}}}} + q_{{\text{C}}} } \right]\delta w{\text{d}}x.$$

(17)

The electrostatic force $q_{{\text{e}}}$ per unit length of the nanobeam including the first-order fringing field correction can be defined as [53, 52, 69]

$$q_{{\text{e}}} = \frac{{\varepsilon_{0} bv^{2} }}{{2\left[ {d - w} \right]^{2} }} + \frac{{0.65\varepsilon_{0} v^{2} }}{{2\left[ {d - w} \right]}},$$

(18)

in which, $\varepsilon_{0} = 8.854 \times 10^{ - 12} {\text{C}}^{2} {\text{N}}^{ - 1} {\text{m}}^{ - 2}$ denotes the vacuum permittivity, $v$ is the voltage applied on the system, and $d$ represents the initial distance between the nanobridge and fixed substrate. When the width of the nanobeam is much larger than the gap between beam and substrate (i.e. $b \gg d$), the effect of fringing field can be neglected. For nanobeams with the width in order of the initial gap, effect of fringing field is important and neglecting this phenomenon underestimates the electrostatic load and overestimates the pull-in voltage of the nanobeam, Rahaeifard et al. [51]. Regarding the interatomic forces $q_{{{\text{int}}}}$, two interaction regimes can be considered; the first one belongs to the small separation sizes (typically below several tens of nanometers, Soroush et al. [69] and [1] that vdW force ($q_{{{\text{vdW}}}}$) dominates. The second one accomplished with the large separation sizes (typically above several tens of nanometers, Soroush et al. [69] and Abdi et al. [1] that Casimir force ($q_{{{\text{Cas}}}}$) dominates. These interatomic forces per unit length of the nanobeam are given by

$$q_{{{\text{vdW}}}} = \frac{{{\text{A}}_{{\text{H}}} b}}{{6\pi \left( {d - w} \right)^{3} }} {\text{and}} q_{{{\text{Cas}}}} = \frac{{b\pi^{2} h_{{\text{P}}} \overline{C}}}{{240\left( {d - w} \right)^{4} }},$$

(19)

where ${\text{A}}_{{\text{H}}} = \left( { 0.4 {\text{up}} {\text{to}} 4} \right) \times 10^{ - 19} {\text{J}}$ is the Hamaker constant, $h_{{\text{P}}} = 1.055 \times 10^{ - 34} {\text{Js}}$ denotes the reduced Planck’s constant divided by $2\pi$, and $\overline{C} = 2.998 \times 10^{8} {\text{m}}/{\text{s}}$ is the light speed.

In the case of FG nanobeams with immovable boundary conditions, the virtual work due to midplane stretching of the nanobeam ($\delta {\text{W}}_{{\text{s}}}$) and residual stress ($\delta {\text{W}}_{{\text{r}}}$) is, respectively, given by

$$\delta W_{{\text{s}}} = \delta \left( { - N_{{\text{r}}} \mathop \int \limits_{0}^{L} w^{^{\prime}2} {\text{d}}x} \right) ,$$

(20)

$$\delta {\text{W}}_{r} = - \frac{1}{8}{\text{K}}_{a} \delta \left( {\mathop \int \limits_{0}^{L} w^{{\prime}{2}} dx} \right)^{2} , {\text{K}}_{a} = \mathop \int \limits_{A} \frac{{\overline{E}\left( z \right)}}{L}dA$$

(21)

where the axial force $N_{{\text{r}}} = s_{{\text{r}}} bh$, in which the effective residual stress $s_{{\text{r}}} = \left( {1 - \nu } \right)s_{0}$; otherwise, $s_{{\text{r}}} = s_{0}$ for narrow beams (b < 5 h), where $s_{0}$ is the initial biaxial residual stress in the beam, Rokni et al. [55]. For the case of cantilever nanobeams, $\delta {\text{W}}_{{\text{s}}}$ and $\delta {\text{W}}_{{\text{s}}}$ are set to zero. Substituting Eqs. (14), (17), (20), and (21) into Eq. (13), and integrating by parts, results in the following size-dependent nonlinear governing equations of motion in terms of displacements,

$$\delta u: \left( {A_{xx} + {\mathcal{C}}_{P2} } \right)u^{\prime\prime} - \left( {{\mathbf{\mathcal{B}}} + \frac{1}{2}{\mathcal{T}}_{11} } \right)w^{\prime\prime\prime} = 0,$$

(22a)

$$\delta w: - {\mathbf{\mathcal{D}}}w^{{\prime\prime\prime\prime}} + \left( {{\mathbf{\mathcal{B}}} + \frac{1}{2}{\mathcal{T}}_{11} } \right)u^{\prime\prime\prime} + \left[ {{\mathcal{S}}_{{\text{P}}} + N_{{\text{r}}} + \frac{1}{2}K_{{\text{a}}} \left( {\mathop \int \limits_{0}^{L} w^{{\prime}{2}} {\text{d}}x} \right)} \right]w^{\prime\prime} + q_{{\text{e}}} + q_{{{\text{vdW}}}} + q_{{{\text{Cas}}}} = 0 ,$$

(22b)

subject to the following boundary conditions at $x = 0$ and $x = L$.

$${\text{Either}} \, u = \tilde{u} {\text{or }}\;\left( {A_{xx} + {\mathcal{C}}_{{{\text{P}}2}} } \right)u^{\prime} - \left( {{\mathbf{\mathcal{B}}} + \frac{1}{2}{\mathcal{T}}_{11} } \right)w^{\prime\prime} + \frac{1}{2}{\mathcal{C}}_{{{\text{P}}1}} = 0,$$

(23a)

$${\text{Either}} w = \tilde{w} {\text{or }}\;{\mathbf{\mathcal{D}}}w^{\prime\prime\prime} - \left( {{\mathbf{\mathcal{B}}} + \frac{1}{2}{\mathcal{T}}_{11} } \right)u^{\prime\prime} - \left( {{\mathcal{S}}_{{\text{P}}} + N_{{\text{r}}} + \frac{1}{2}K_{a} \mathop \int \limits_{0}^{L} w^{^{\prime}2} {\text{d}}x} \right)w^{\prime} = 0,$$

(23b)

$${\text{Either}} w^{\prime} = \widetilde{{w^{\prime}}} {\text{or }} \left( {{\mathbf{\mathcal{B}}} + \frac{1}{2}{\mathcal{T}}_{11} } \right)u^{\prime} - {\mathbf{\mathcal{D}}}w^{\prime\prime} + \frac{1}{2}{\mathcal{P}}_{{{\text{A}}1}} = 0,$$

(23c)

where

$${\mathbf{\mathcal{D}}} = D_{xx} - {\mathcal{T}}_{22} + S_{xy} + I_{{\text{P}}} \, {\text{and}} \, {\mathbf{\mathcal{B}}} = B_{xx} - {\mathcal{T}}_{11} + {\mathcal{P}}_{{{\text{A}}2}} .$$

Substitution of Eq. (22a) into Eq. (22b) yields Eq. (22b) in terms of the transverse displacement only as follows:

$$\left[ {{\mathbf{\mathcal{D}}} - \frac{1}{{A_{xx} + {\mathcal{C}}_{{{\text{P}}2}} }}\left( {{\mathbf{\mathcal{B}}} + \frac{1}{2}{\mathcal{T}}_{11} } \right)^{2} } \right]w^{{\prime\prime\prime\prime}} - \left[ {{\mathcal{S}}_{{\text{P}}} + N_{r} + \frac{1}{2}K_{a} \left( {\mathop \int \limits_{0}^{L} w^{{\prime}{2}} dx} \right)} \right]w^{\prime\prime} = q_{e} + q_{{{\text{vdW}}}} + q_{{{\text{Cas}}}} .$$

(24)

For convenience, introducing the nondimensional variables $\hat{x} = x/L$ and $\hat{w} = w/d$ in Eq. (24), multiplying the result by $L^{4} /E_{L} Id$ and dropping the hats, we obtain the following nondimensional governing equation:

$${\overline{\mathbb{D}}}w^{{\prime\prime\prime\prime}} - \left[ {{\overline{\mathcal{S}}}_{{\text{P}}} + \overline{N}_{{\text{r}}} + \overline{K}_{{\text{a}}} \left( {\mathop \int \limits_{0}^{1} w^{^{\prime}2} {\text{d}}x} \right)} \right]w^{\prime\prime} = V^{2} \left[ {\frac{1}{{\left( {1 - w} \right)^{2} }} + \frac{{c_{{\text{f}}} }}{{\left( {1 - w} \right)}}} \right] + \frac{{c_{{{\text{vdW}}}} }}{{\left( {1 - w} \right)^{3} }} + \frac{{c_{{{\text{Cas}}}} }}{{\left( {1 - w} \right)^{4} }}.$$

(25)

Further, the nondimensional boundary conditions are obtained as

$${\text{Clamped }}\left( {\text{C}} \right): w = 0 {\text{and}} w^{\prime} = 0,$$

(26a)

$${\text{Simply supported }}\left( {\text{S}} \right):w = 0 {\text{and}} - {\mathbf{\overline{\mathcal{D}}}}w^{\prime\prime} + {\overline{\mathcal{P}}}_{{{\text{A}}1}} = 0 ,$$

(26b)

$${\text{Free }}\left( {\text{F}} \right):\user2{ } - { }{\overline{\mathbb{D}}}w^{\prime\prime\prime} + \left( {{ }{\overline{\mathcal{S}}}_{{{\text{P}}1}} + \overline{N}_{{\text{r}}} + \overline{K}_{{\text{a}}} \mathop \int \limits_{0}^{1} w^{^{\prime}2} {\text{d}}x} \right) w^{\prime} = 0 {\text{and}} - {\overline{\mathbb{D}}}w^{\prime\prime} + {\overline{\mathbb{K}}} = 0.$$

(26c)

The dimensionless coefficients appear in Eqs. (25) and (26a–26c) and are defined as

$$\left\{ {\begin{array}{*{20}c} {{\mathbb{D}} = {\mathbf{\mathcal{D}}} - \frac{1}{{A_{xx} + {\mathcal{C}}_{{{\text{P}}2}} }}\left( {{\mathbf{\mathcal{B}}} + \frac{1}{2}{\mathcal{T}}_{11} } \right)^{2} } \\ {{\mathbb{K}} = \frac{1}{2}\left[ {{\mathcal{P}}_{{{\text{A}}1}} - \frac{{{\mathcal{C}}_{{{\text{P}}1}} }}{{A_{xx} + {\mathcal{C}}_{{{\text{P}}2}} }}\left( {{\mathbf{\mathcal{B}}} + \frac{1}{2}{\mathcal{T}}_{11} } \right)} \right]} \\ {\left\{ {\begin{array}{*{20}c} V & {c_{f} } & {c_{{{\text{vdW}}}} } & {c_{{{\text{Cas}}}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\sqrt {\frac{{\varepsilon_{0} bL^{4} }}{{2E_{L} Id^{3} }}} {\text{v}}} & {\frac{0.65d}{b}} & {\frac{{bL^{4} {\text{A}}_{H} }}{{6\pi E_{L} Id^{4} }}} & {\frac{{\pi^{2} bL^{4} h_{P} \overline{c}}}{{240E_{L} Id^{5} }}} \\ \end{array} } \right\}} \\ {\left\{ {\begin{array}{*{20}c} {{\mathbf{\overline{\mathcal{D}}}}} & {{\overline{\mathbb{D}}}} & {{\overline{\mathbb{K}}}} & {\overline{N}_{r} } & {\overline{K}_{a} } & {{\overline{\mathcal{S}}}_{{\text{P}}} } & { {\overline{\mathcal{P}}}_{{{\text{A}}1}} } \\ \end{array} } \right\} = \frac{1}{{E_{L} I}}\left\{ {\begin{array}{*{20}c} {\mathbf{\mathcal{D}}} & {\mathbb{D}} & {\frac{{E_{L} I}}{d}{\mathbb{K}}} & {L^{2} N_{{\text{r}}} } & {\frac{{Ld^{2} }}{2}K_{{\text{a}}} } & {L^{2} {\mathcal{S}}_{{\text{P}}} } & {L^{2} {\overline{\mathcal{P}}}_{{{\text{A}}1}} } \\ \end{array} } \right\}} \\ \end{array} } \right..$$

(27)

3 Analytical approach

3.1 Pull-in closed form

To derive a closed-form solution to Eqs. (25, 26a–26c), the normalized displacement of the FG micro/nanobeam $w\left( x \right)$ is approximated as

$$w\left( x \right) \cong u \varphi \left( x \right),$$

(28)

where $\varphi \left( x \right)$ is deflection shape function satisfying the boundary conditions and $u$ denotes a scaling of the displacement function such that Eq. (25) is satisfied. Note that $\varphi \left( x \right)$ is normalized such that $\max \left( {\left| {\varphi \left( x \right)} \right|} \right) = 1$ and hence $u$ describes the mid-point and tip deflections of, respectively, clamped–clamped and clamped-free FG nanobeams.

The deflection shape function $\varphi \left( x \right)$ is given in Table 1 for fully clamped and clamped-free nanobeams.

Table 1 Trial shape function $\varphi \left( x \right)$ for the clamped–clamped and clamped-free FG nanobeams and associated integrals (Eq. (30))

Substitution of Eq. (28) into Eq. (25) and multiplying the result by $\varphi \left( x \right)$, then integrating with respect to $x$ between 0,1 yields

$$\begin{aligned} \left( {i_{04} {\overline{\mathbb{D}}} - i_{02} \left( {{\overline{\mathcal{S}}}_{{\text{P}}} + \overline{N}_{{\text{r}}} } \right)} \right)u - i_{02} i_{11} \overline{K}_{a} u^{3} & = V^{2} \mathop \int \limits_{0}^{1} \left[ {\frac{1}{{\left( {1 - u\varphi \left( x \right)} \right)^{2} }} + \frac{{c_{f} }}{{\left( {1 - u\varphi \left( x \right)} \right)}}} \right]\varphi \left( x \right){\text{d}}x \\ & \; + \mathop \int \limits_{0}^{1} \left[ {\frac{{c_{{{\text{vdW}}}} }}{{\left( {1 - u\varphi \left( x \right)} \right)^{3} }} + \frac{{c_{{{\text{Cas}}}} }}{{\left( {1 - u\varphi \left( x \right)} \right)^{4} }}} \right]\varphi \left( x \right){\text{d}}x , \\ \end{aligned}$$

(29)

where

$$\left\{ {\begin{array}{*{20}c} {i_{02} } & {i_{04} } & {i_{11} } \\ \end{array} } \right\} = \mathop \int \limits_{0}^{1} \left\{ {\begin{array}{*{20}c} {\varphi \varphi^{\prime\prime}} & {\varphi \varphi^{{\prime\prime\prime\prime}} } & {\varphi^{{\prime}{2}} } \\ \end{array} } \right\} {\text{d}}x.$$

(30)

In this study, the integral forms of the electrostatic and intermolecular forces in the right-hand side of Eq. (29) are approximated in the form of algebraic functions of $u$ as follows:

$$\mathop \int \limits_{0}^{1} \left[ {\frac{1}{{\left( {1 - u\varphi \left( x \right)} \right)^{2} }} + \frac{{c_{{\text{f}}} }}{{\left( {1 - u\varphi \left( x \right)} \right)}}} \right]\varphi \left( x \right){\text{d}}x \cong \frac{{a_{0} }}{{\left( {1 - a_{1} u} \right)^{{a_{2} }} }},$$

(31)

$$\mathop \int \limits_{0}^{1} \frac{\varphi \left( x \right)}{{\left( {1 - u\varphi \left( x \right)} \right)^{3} }}{\text{d}}x \cong b_{3} u^{3} + b_{2} u^{2} + b_{1} u + b_{0} ,$$

(32a)

$$\mathop \int \limits_{0}^{1} \frac{\varphi \left( x \right)}{{\left( {1 - u\varphi \left( x \right)} \right)^{4} }}{\text{d}}x \cong c_{3} u^{3} + c_{2} u^{2} + c_{1} u + c_{0} .$$

(32b)

At specific values of $u$ in the range $0 \le u \le 0.5$, the values of the integrals in the left-hand sides of Eqs. (31, 32a, 32b) can be accurately computed. Then, the least squares method is applied to determine the coefficients in the right-hand sides of Eqs. (32a, 32b). However, such classical method is not applicable for Eq. (31).

Particle Swarm Optimization (PSO) is a powerful evolutionary technique for many optimization applications due to its high performance and flexibility. PSO was first developed by Kennedy and Eberhart [35]. PSO shares many similarities with evolutionary computation techniques such as Genetic Algorithms (GA). In PSO, the process is initialized with a population of random solutions and continuing searching for optima by updating generations. However, unlike GA, PSO has no evolution operators, such as mutation and crossover. PSO has been successfully applied in many research and application areas, Eberhart et al. [19]. It is demonstrated that, compared with other methods, PSO gets better results in a faster and cheaper way. Therefore, in the present study, a PSO algorithm is used to approximate the coefficients in the right-hand side of Eq. (31). For this equation, the coefficients are determined to minimize an objective function defined as the sum of squares of the difference of the two sides at the chosen values of $u$.

Substitution of Eqs. (31, 32a, 32b) in Eq. (29), reduces to

$$A_{1} u + A_{3} u^{3} = V^{2} \frac{{a_{0} }}{{\left( {1 - a_{1} u} \right)^{{a_{2} }} }} + \left( {k_{3} u^{3} + k_{2} u^{2} + k_{1} u + k_{0} } \right),$$

(33)

where

$$\left\{ {\begin{array}{*{20}c} {A_{1} } & {A_{3} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {i_{04} {\overline{\mathbb{D}}} - i_{02} \left( {{\overline{\mathcal{S}}}_{{\text{P}}} + \overline{N}_{r} } \right)} & { - i_{02} i_{11} \overline{K}_{a} } \\ \end{array} } \right\} ,$$

(34)

$$k_{i} = \left\{ {\begin{array}{*{20}c} {c_{{{\text{vdW}}}} b_{i} } & {\text{for vdW force}} \\ {c_{{{\text{Cas}}}} c_{i} } & {\text{for Casimir force}} \\ \end{array} } \right., i = 0,1, 2, 3 .$$

(35)

Notice that the coefficients in the left-hand side of Eq. (33) are dependent on mechanical parameters ${\overline{\mathbb{D}}}, {\overline{\mathcal{S}}}_{{\text{P}}} ,\overline{N}_{{\text{r}}} ,$ and $\overline{K}_{{\text{a}}}$. In the right-hand side, the first term corresponds to the electrostatic force including fringing field, while the last term corresponds to the intermolecular forces.

Equation (33) represents an implicit algebraic equation of the deflection amplitude $u$ and applied voltage $V$. Differentiating Eq. (33) with respect to $u$ yields

$$A_{1} + 3A_{3} u^{2} = V^{2} \frac{{a_{0} }}{{\left( {1 - a_{1} u} \right)^{{a_{2} }} }}\frac{{a_{1} a_{2} }}{{\left( {1 - a_{1} u} \right) }} + 2V\frac{{{\text{d}}V}}{{{\text{d}}u}}\frac{{a_{0} }}{{\left( {1 - a_{1} u} \right)^{{a_{2} }} }} + \left( {3k_{3} u^{2} + 2k_{2} u + k_{1} } \right) .$$

(36)

Multiplying Eq. (36) by $\left( {1 - a_{1} u} \right)$ and subtracting the result from Eq. (33) and since the mathematical condition of pull-in phenomena is ${\text{d}}V{\text{/d}}u = 0$, the pull-in deflection $u_{{{\text{pi}}}}$ must satisfy the following relation:

$$C_{0} u_{{{\text{pi}}}}^{3} + C_{1} u_{{{\text{pi}}}}^{2} + C_{2} u_{{{\text{pi}}}} + C_{3} = 0$$

(37)

where

$$\left\{ {\begin{array}{*{20}c} {C_{0} } \\ {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {a_{1} \left( {3 + a_{2} } \right)A_{3} - a_{1} k_{3} \left( {a_{2} + 3} \right)} \\ { - 3A_{3} - (a_{1} a_{2} k_{2} - 3k_{3} + 2k_{2} a_{1} )} \\ {a_{1} \left( {a_{2} + 1} \right)A_{1} - \left( {k_{1} a_{1} + a_{2} a_{1} k_{1} - 2k_{2} } \right)} \\ { - A_{1} - \left( {a_{1} a_{2} k_{0} - k_{1} } \right)} \\ \end{array} } \right\}.$$

(38)

Equation (37) is a cubic algebraic equation in the pull-in deflection${ u}_{\mathrm{pi}}$. Once ${u}_{\mathrm{pi}}$ is obtained, the pull-in voltage ${V}_{\mathrm{pi}}$ is computed from Eq. (33). The integration parameters $i_{02}$, $i_{11}$ and $i_{04}$ defined in Eq. (30) as well as the used shape functions $\varphi \left( x \right)$ are reported in Table 1 for the C–C and C–F nanobeams. On the other hand, the approximation parameters ($a_{0} , a_{1}$, $a_{2}$ in Eq. (31)) are dependent on $c_{{\text{f}}}$ and are computed using PSO. Table 2 reports these parameters at some values of $c_{{\text{f}}}$. The case of $c_{{\text{f}}} = 0$ corresponds to $b \gg d$, where the fringing field effect is neglected.

Table 2 Coefficients of approximation ($a_{0}$, $a_{1}$, $a_{2}$) in Eq. (31) for various fringing field parameters $c_{{\text{f}}}$

3.2 Freestanding closed form

When considering a nanosystem, it is worth noting that one of the most important parameters is its freestanding behavior. In the absence of electrostatic force (applied voltage), interatomic Casimir and van der Waals forces may tend the nanobeam to undergo a primary displacement, i.e. the movable electrode falls on the fixed electrode, and thus the nanobeam may behave unstably. Such effect can induce undesired adhesion in freestanding during the fabrication and operation procedures of such systems, which should be considered when either the gap distance between the movable electrode and the field one is small or the length of the nanobeam is greater than a certain magnitude, Farrokhabadi et al. [26]. In this regard, modeling of intermolecular interatomic Casimir and van der Waals force-induced instability is crucial for investigating the performance of nanoactuators made of FGMs.

When the nanoactuator becomes freestanding, the voltage difference between the nanobeam and the substrate vanishes. Accordingly, the smallest amount of intermolecular force that causes the movable electrode to fall on the fixed electrode in the absence of electrostatic force is called critical intermolecular force. Behavior of a freestanding nanoactuator is a special case of the present study. Setting the applied voltage $V = 0$ in Eqs. (33) yields

$$c_{{{\text{vdW}}}} = \frac{{A_{1} u + A_{3} u^{3} }}{{b_{3} u^{3} + b_{2} u^{2} + b_{1} u + b_{0} }},$$

(39)

$$c_{{{\text{Cas}}}} = \frac{{A_{1} u + A_{3} u^{3} }}{{c_{3} u^{3} + c_{2} u^{2} + c_{1} u + c_{0} }},$$

(40)

where $A_{1} ,A_{3}$ are defined by Eq. (34) and coefficients $b_{i}$, $c_{i}$, $i = 0,1,2,3$ are given in Table 3 for C–C and C–F nanobeams.

Table 3 Coefficients of approximation in Eqs. (32a, 32b): approximation of $\mathop \smallint \limits_{0}^{1} \frac{1}{{\left( {1 - u\varphi } \right)^{r} }}\varphi {\text{d}}x$

Let the critical parameters of Eqs. (39, 40) be, respectively ($u_{{{\text{vdW}}}}^{*} ,c_{{{\text{vdW}}}}^{*} { }){\text{ and }}$ ($u_{{{\text{Cas}}}}^{*} ,$ $c_{{{\text{Cas}}}}^{*} )$. Once the critical intermolecular parameters $c_{{{\text{vdW}}}}^{*} { }$ and $c_{{{\text{Cas}}}}^{*}$ are determined, the definitions of $c_{{{\text{vdW}}}}$ and $c_{{{\text{Cas}}}}$ in Eq. (27) can be used to compute the permissible maximum length (called the detachment length) and minimum initial gap and of the of freestanding nanobeams as follows:

$${\text{The detachment length}}: L_{{{\text{Cas}}}}^{*} = d^{5/4} \sqrt[4]{{ \frac{{20E_{1} h^{3} }}{{\pi^{2} h_{P} \overline{c}}} c_{{{\text{Cas}}}}^{*} }}{\text{ and}} \, L_{{{\text{vdW}}}}^{*} = d \sqrt[4]{{\frac{{\pi E_{1} h^{3} }}{{2{\text{A}}_{H} }}c_{{{\text{vdW}}}}^{*} }},$$

(41)

$${\text{Minimum gap}}:{ }d_{{{\text{Cas}}}}^{*} = L^{4/5} \sqrt[5]{{\frac{{\pi^{2} h_{P} \overline{c}}}{{20E_{1} h^{3} c_{{{\text{Cas}}}}^{*} }}}}{\text{ and }}d_{{{\text{vdW}}}}^{*} = L \sqrt[4]{{\frac{{2{\text{A}}_{H} }}{{\pi E_{1} h^{3} c_{{{\text{vdW}}}}^{*} }}}}.$$

(42)

4 Model validation

4.1 Proposed approximation in Eqs. (31, 32a, 32b)

As mentioned in Sect. 3, the basic idea to get the proposed closed-form approximations is to replace the integral forms representing electrostatic, fringing, and intermolecular forces in Eq. (29) by non-integral algebraic functions. For the purpose of validation of these approximations introduced in Eqs. (31, 32a, 32b), the integral and non-integral forms are computed at different values of the maximum deflection, $u$, as presented in Figs. 2 and 3 for the C–C and C–F cases. Figure 2 shows the accuracy of the PSO approximation given in Eq. (31) for the terms of electrostatic and fringing (with $d/b = 1$) forces, while Fig. 3 corresponds to Eqs. (32a, 32b) that associates with approximations of van der Waals and Casimir forces. The maximum relative errors $E_{{\text{r}}}^{\infty }$ are reported in Table 4 for the proposed approximations, where the error is the difference between the exact integral values and the corresponding algebraic functions in Eqs. (31, 32a, 32b).

Fig. 2

Exact and PSO approximation of the integral function in Eq. (31)

Fig. 3

Exact and pproximation of the integral function in Eqs. (32a, 32b)

Table 4 Maximum relative error $E_{r}^{\infty }$ in the proposed PSO approximation given in Eqs. (31, 32a, 32b)

4.2 Validation of pull-in voltage

To validate the present analytical closed-form approach for predicting the static pull-in phenomenon, the static pull-in voltage of microcantilevers with different geometric and material properties are obtained and compared with some available analytical and numerical results in Table 5. For clamped–clamped nanobeams with different geometric, material properties and axial residual stresses, the static pull-in voltages obtained using the proposed closed-form are compared with similar ones available in literature in Table 6. Based on the results of Tables 5 and 6, the accuracy of present analytical closed-form approach can be observed. It should be noted that for comparison in the above validations, the nanobeams are assumed homogeneous, i.e. $k=0$, and are modeled based on the classical elasticity theory (CT), i.e. all the nonclassical surface and microstructure parameters are set to zero. Also, the effects of fringing field and intermolecular van der Waals and Casimir forces are neglected.

Table 5 Comparison of static pull-in voltage of homogeneous microcantilevers obtained from the present closed-form method with data from the literature based on the classical analysis ($E$ = 169 GPa, $\nu$ = 0.06)

Table 6 Comparison of static pull-in voltage of homogeneous clamped–clamped nanobeams obtained from the present method with data from the literature based on the classical analysis

To validate the present closed-form model in the presence of microstructure effect, homogeneous cantilever microactuators are considered and modeled based on the modified couple stress theory (MCST), i.e. all the surface parameters are set to zero. For the aim of comparison, the influences of fringing field and intermolecular forces are neglected in this validation. The geometrical and material parameters used in Rahaeifard et al. [51] and Rokni et al. [55] are $E$ =169.2 GPa, $\nu$=0.239, $b$=50 µm, $h$=2.94 µm, and $d$=1.05 µm. The obtained results of the static pull-in voltage for different beam lengths and microstructure material length scale parameters are displayed in Table 7 and compared with corresponding values reported in Rokni et al. [55] based on a closed-form solution and Rahaeifard et al. [51] where a numerical approach was used.

Table 7 Comparison of the static pull-in voltage (volts) of homogeneous cantilever microactuators based on the MCST

Next, the proposed closed-form solution is validated by investigating the pull-in characteristics of a micro/nanocantilever including the effects of fringing field and intermolecular forces. The obtained results are compared with Radi et al. [49], who modeled a micro/nanocantilever actuated by electrostatic force including fringing field and subject to Casimir or van der Waals forces based on the classical continuum mechanics (CL). Rather than determining the pull-in parameters, they estimated lower and upper bounds of the parameters, namely the pull-in voltage parameter ($\beta_{l}$ and $\beta_{u}$) and the normalized tip displacement ($u_{l}$ and $u_{u}$). For comparison with Radi et al. [49], Eq. (25) is reduced to account for a classical cantilever nanobeam by setting ${\overline{\mathcal{S}}}_{{\text{P}}} = \overline{N}_{{\text{r}}} = \overline{K}_{{\text{a}}} = 0 , {\overline{\mathbb{D}}} = 1$, and defining the pull-in voltage parameter $\beta = V^{2}$; thus the governing equation becomes

$$\frac{{{\text{d}}^{4} w}}{{{\text{d}}x^{4} }} = \beta \left[ {\frac{1}{{\left( {1 - w} \right)^{2} }} + \frac{{c_{{\text{f}}} }}{{\left( {1 - w} \right)}}} \right] + \frac{{c_{{{\text{vdW}}}} }}{{\left( {1 - w} \right)^{3} }} + \frac{{c_{{{\text{Cas}}}} }}{{\left( {1 - w} \right)^{4} }}.$$

(43)

Results are reported in Table 8 for some specific values of the initial gap-to-width ratio $d/b$, which controls the fringing field effects and for various values of the coefficients $c_{{{\text{vdW}}}}$ and $c_{{{\text{Cas}}}}$. In this table, the normalized pull-in tip displacement and pull-in voltage are displayed, respectively, as $u$ and $\beta$, determined by the present closed-form approach and by lower and upper bounds $\left( {u_{l} , u_{u} } \right)$ and $\left( {\beta_{l} , \beta_{u} } \right)$ reported in Radi et al. [49]. It is noticed that excellent agreement is observed, since almost of the parameter values computed by the present closed-form PSO-based approach lie within the lower and upper bounds computed in Radi et al. [49]. Note that negative values of $\beta = V^{2}$ appearing in Table 8 imply sudden occurrence of the pull-in instability as no real solution can be obtained for the tip displacement and that at these situations the intermolecular forces exceed their critical values.

Table 8 Comparison of the static normalized pull-in tip deflection $u$ and pull-in voltage parameter $\beta = V^{2}$ with the corresponding lower and upper values $\left( {u_{l} ,u_{u} } \right)$ and $\left( {\beta_{l} ,\beta_{u} } \right)$ obtained by Radi et al. [49] of a homogeneous cantilever microactuator based on the classical analysis

4.3 Validation of freestanding behavior

To determine the critical points of the intermolecular parameters $c_{{{\text{vdW}}}}$ and $c_{{{\text{Cas}}}}$ based on Eqs. (39) and (40), respectively, they are plotted in Fig. 4 based on the classical elasticity theory for a cantilever nanobeam. For the purpose of comparison with Duan et al. [18], the material is assumed to be homogeneous$, k = 0$. The critical points on the curves of Eqs. (39 and 40) are, respectively, $\left( {u_{{{\text{vdW}}}}^{*} , c_{{{\text{vdW}}}}^{*} } \right)$ = (0.34, 1.204) and $\left( {u_{{{\text{Cas}}}}^{*} , c_{{{\text{Cas}}}}^{*} } \right)$ = (0.27, 0.9372) as displayed in the figure. Based on the classical elasticity theory (CT), Duan et al. [18] reported that for a homogeneous cantilever $u_{{{\text{Cas}}}}^{*}$ = 0.269401 and $c_{{{\text{Cas}}}}^{*}$ = 0.932616, which agree well with the corresponding values displayed in Fig. 4. Also, Radi et al. [49] have reported lower and upper bounds for $c_{{{\text{vdW}}}}^{*}$ as [1.1967, 1.2171], $u_{{{\text{vdW}}}}^{*}$ as [0.3350, 0.3423] and $c_{{{\text{Cas}}}}^{*} { }$ as [0.9326, 0.9492], $u_{{{\text{Cas}}}}^{*}$ as [0.2694, 0.2756], which agree well with the present predicted critical values.

Fig. 4

Variation of intermolecular parameters $c_{{{\text{vdW}}}}$ and $c_{{{\text{Cas}}}}$ versus the normalized maximum deflection $u$ for the freestanding analysis of cantilever homogeneous nanobeams based on classical analysis

5 Parametric studies

In this section, selected numerical results are presented to demonstrate the capability of the developed closed-form approach to investigate the influences of incorporating surface energy and microstructure theories on the pull-in instability and freestanding behavior of electrically actuated clamped–clamped (C–C) and clamped–free (C–F) FG nanobeams. To demonstrate the influence of couple stress and surface energy simultaneously together or individually, four various analyses are considered: (1) the classical theory (CT), based on the classical continuum mechanics theory, where all surface and microstructure parameters are set to zero: (2) analysis based on the modified couple stress theory only (MCST): (3) analysis based on surface elasticity theory only (SET), and (4) fully nonclassical analysis incorporating the simultaneous effects of surface energy and modified couple stress (CSSE). Also, effects of fringing field and the intermolecular Casimir and van der Waals forces are simultaneously included.

Throughout the following analyses, consider an FG beam possessing the material properties given in Table 9, assuming a material length scale parameter ratio $l_{L} /l_{U} = 1.5$. The geometrical parameters of the beam are $h = 3l_{U}$, $L = 40h$, $b = 5h$, and $d = 0.6h$; otherwise, other values of the material or geometrical parameters are defined. Further, Poisson’s effect is included in this parametric study and $N_{{\text{r}}} = 0$. Due to the assumption in Eq. (28) that $w\left( x \right) \cong u \varphi \left( x \right),$ where $\varphi \left( x \right)$ is deflection shape function satisfying the classical boundary conditions, the proposed closed-form does not account for the nonclassical boundary conditions. In fact, nonclassical boundary conditions occur only at a free end due nonzero surface residual stress $\tau^{{\text{s}}}$ as can be seen from Eq. (26c) since ${\overline{\mathcal{S}}}_{{{\text{P}}1}} = {\overline{\mathbb{K}}} = 0$ if $\tau^{{\text{s}}} = 0.$

Table 9 Material properties of the functionally graded nanobeam constituents

5.1 Effect of the material composition

To understand the effect of the material composition on the pull-in instability of the nanobeam, the distribution of bulk Young's modulus through thickness $E\left( z \right)$ for various values of the gradient index $k$ is plotted in Fig. 5. Note first that at upper edge of the beam ($z = h/2$), the material is pure ceramic. As the value of $k$ increases, the constitution of ceramic in the material decreases and results in lower Young's modulus distribution, i.e. as $k$ tends to $\infty$, the material becomes pure metal. Since the beam stiffness depends mainly on Young's modulus, one can expect that increasing $k$ would result in reducing the beam stiffness. However, incorporation of micro/nanoscale effects (couple stress and surface energy) adds important contributions to the stiffness of the beam as can be seen in the coefficients of the governing equation (Sect. 2).

Fig. 5

Distribution of bulk Young's modulus through the thickness for different gradient index k values (Eq. (1))

First, the effect of the gradient index on the pull-in voltage of a nanobeam is investigated taking into consideration the influence of MCST. The variations of the pull-in voltage with the gradient index $k$ are shown in Fig. 6a for a clamped–clamped nanobeam and in Fig. 6b for a cantilever nanobeam, according to CT and MCST with and without fringing field effect.

Fig. 6

Variation of the pull-in voltage of FG nanobeams versus the gradient index incorporating intermolecular forces based on the CL and MCST with and without fringing field ($l_{U} = 65 {\text{nm}}$), a clamped–clamped and b cantilever FG nanobeams

Some numerical values of the pull-in voltage at different gradient indices are provided in Table 10. From these results, one can conclude that increasing the gradient index decreases the pull-in voltage of the nanobeam. Compared with CT, MCST results in increasing the beam bending rigidity. Therefore, the microstructure size-dependent effect provides a hardening behavior that enhances the elastic resistance of the nanobeam and accordingly requires higher applied voltage before the instability occurs. Also, including fringing field acts as additional electrostatic force that increases the nanobeam deflection and results in lower pull-in voltage. These results also demonstrate that, for the same material geometric parameters, pull-in voltages for nanocantilevers are lower than those of clamped–clamped nanobeams.

Table 10 Pull-in voltages (volt) for the clamped–clamped and cantilever FG nanobeams at different gradient indices incorporating CT and MCST with and without fringing field

Next, the effect of the surface energy (surface elasticity and surface residual stress) is explored in the presence of Poisson’s effect and intermolecular forces. The variations of the pull-in voltage versus the gradient index for CT, SET, MCST, and CSSE are shown in Fig. 7a for a clamped–clamped FG nanobeam. For a fixed value of the gradient index $\left( {k = 3} \right)$, Eq. (33) is used to plot the variation of normalized maximum deflection $\left( u \right)$ versus the applied voltage in Fig. 7b.

Fig. 7

Pull-in behavior of a clamped–clamped FG nanobeam with and without fringing field for CT, SET, MCST, and CSSE analyses ($l_{U} = 65 {\text{nm}}$), a variation of the pull-in voltage versus the gradient index and b variation of normalized maximum deflection versus the applied voltage at $k = 3$

A further interesting study is obtained by repeating the previous case study by just changing the material length scale parameter of the upper surface of the beam (ceramic) from $l_{U} = 65 {\text{nm}}$ to $l_{U} = 10 {\text{nm}}$, keeping $h = 3l_{U}$,$L = 40\;h,\; b = 5\;h$ and $d = 0.6\;h$. Thus, in this study not only the effect of the couple stress is reduced but also the dimensions of the beam are decreases and consequently the influence of intermolecular forces can be significantly observed. Results are drawn in Fig. 8. Comparing Fig. 8 with Fig. 7, the following conclusions can be derived. First, due to the smaller size of the beam, less electrostatic force is required to cause instability and hence much low pull-in voltages are observed. Second, the effect of surface energy is more significant which can be interpreted due to the increase of the surface to volume ratio. Finally, at no applied voltage, one can observe nonzero deflection in Fig. 8b compared with zero deflection in Fig. 7b. Furthermore, as the initial gap between the nanobeam and substrate becomes sufficiently small, the induced intermolecular forces cannot be neglected. These intermolecular forces induce the beam deflection even at no applied voltage. More details about influence of intermolecular forces will be considered in the following subsections.

Fig. 8

Pull-in behavior of a clamped–clamped FG nanobeam with and without fringing field for CT, SET, MCST, and CSSE analyses ($l_{U} = 10 {\text{nm}}$) a variation of the pull-in voltage with the gradient index and b variation of normalized maximum deflection with the applied voltage at $k = 3$

5.2 Effect of the intermolecular forces

To clearly investigate the influence of the intermolecular forces on the pull-in voltage of actuated FG nanobeams, the nonclassical effects due to surface energy and microstructure are not incorporated, i.e. classical elasticity theory (CT) is employed. The variations of pull-in voltage versus the gradient index with and without the effects of Casimir or/and van der Waals forces are shown in Fig. 9. The dimensions of the beam are taken as $h = 10 {\text{nm}}$, $L/h = 50$, and $b/h = 5$. Results for a clamped–clamped FG nanobeam with initial gap-to-thickness ratio $d/h = 1.2$ are plotted in Fig. 9a, whereas Fig. 9b shows results for an FG nanocantilever with $d/h = 2.6$. These results reveal that the intermolecular forces significantly reduce the pull-in voltage. Such behavior is due to that these forces increase the beam deflection and consequently the pull-in instability occurs at lower applied voltage. Next, the effect of the initial gap-to-thickness ratio on the pull-in voltage with and without the intermolecular forces is demonstrated in Fig. 10 and Table 11 at $k = 1$. It is observed that the pull-in voltage significantly decreases with the decrease of $d/h$ and that a critical value of the initial gap ($d^{*}$) exists, at which the pull-in instability occurs in the absence of any applied voltage. These situations are shown in Tables 12, 13 by symbol “-”. For the geometrical and material parameters considered here, it can be observed that these critical values are $\left[ {d^{*} /h} \right]_{{{\text{vdW}}}} = 0.65$, $\left[ {d^{*} /h} \right]_{{{\text{Cas}}}} = 1.1$ for the clamped–clamped FG nanobeam and $\left[ {d^{*} /h} \right]_{{{\text{vdW}}}} = 1.6$, $\left[ {d^{*} /h} \right]_{{{\text{Cas}}}} = 2.3$ for the FG nanocantilever.

Fig. 9

Variation of the pull-in voltage versus the gradient index based on the classical elasticity theory with and without the Casimir and van der Waals forces, a clamped–clamped b cantilever nanobeams

Fig. 10

Variation of the pull-in voltage versus the initial gap-to-thickness ratio $d/h$ based on the classical elasticity theory with and without the Casimir and van der Waals forces ($k = 1$), a clamped–clamped, b cantilever nanobeams

Table 11 Pull-in voltage (volt) at different gap-to-thickness ratios $d/h$ for clamped–clamped and cantilever FG nanobeams based on the classical elasticity theory with and without (WO) the intermolecular forces ($k = 1$)

Table 12 Minimum gap (nm) due to Casimir or van der Waals force at different beam lengths for clamped–clamped and cantilever nanobeams ($k = 0$, $b = h = 10\;{\text{nm}}$)

Table 13 Detachment length (μm) due to Casimir or van der Waals force at different initial gaps for clamped–clamped and cantilever nanobeams ($k = 0$, $b = h = 10\;{\text{nm}}$)

5.3 Freestanding nanoactuator analysis

The detachment length $L^{*}$ of a nanobeam and the minimum initial gap $d^{*}$ are basic design parameters for NEMS. An actuator nanobeam with specified initial gap $d$ and length $L > L^{*}$ would collapse onto the substrate due to the intermolecular forces even in the absence of any applied voltage. If the length of the nanobeam is fixed, one can calculate the minimum gap $d^{*}$ between the beam and the substrate to ensure that the nanobeam does not adhere to the substrate without applying a voltage due to the intermolecular forces. Therefore, it is very important for the designers to estimate the critical dimensions, i.e. minimum feasible gap and maximum detachment length, for the freestanding actuated FG beam to prevent collapse or adhesion due to intermolecular forces. As mentioned in Sect. 3.2, the critical points of Eqs. (39, 40) have to be computed first. Based on the values $c_{{{\text{vdW}}}}^{*}$ and $c_{{{\text{Cas}}}}^{*}$, the freestanding parameters can be determined using Eqs. (41, 42). Equations (39) and (40) are plotted in Fig. 11 based on the classical elasticity and modified couple stress theories for clamped–clamped and cantilever FG nanobeams. The critical points $\left( {u_{{{\text{vdW}}}}^{*} , c_{{{\text{vdW}}}}^{*} } \right)$ and $\left( {u_{{{\text{Cas}}}}^{*} , c_{{{\text{Cas}}}}^{*} } \right)$ on the curves of Eqs. (39 and 40), respectively, are displayed in the figure. It is observed that, for both clamped–clamped and cantilever nanobeams, introducing the microstructure effect considerably increases the critical intermolecular parameters $c_{{{\text{vdW}}}}^{*}$ and $c_{{{\text{Cas}}}}^{*}$ but does not affect the critical normalized maximum deflections $\left( {u_{{{\text{Cas}}}}^{*} , c_{{{\text{Cas}}}}^{*} } \right)$. In addition, the predicted critical parameters under the effect of Casimir force are higher than those under the effect of van der Waals force.

Fig. 11

Variation of intermolecular parameters $c_{{{\text{vdW}}}}$ and $c_{{{\text{Cas}}}}$ versus the normalized maximum deflection for the freestanding analysis ($k = 0$), a clamped–clamped (neglecting mid-stretching) and b cantilever homogeneous nanobeams

Next, the critical intermolecular forces $F_{{{\text{vdW}}}}^{*}$ and $F_{{{\text{Cas}}}}^{*}$ are plotted versus the beam length $L$ and initial gap $d$ in Fig. 12. These forces are defined as

$$F_{{{\text{vdW}}}}^{*} = \frac{{c_{{{\text{vdW}}}}^{*} }}{{\left( {1 - u_{{{\text{vdW}}}}^{*} } \right)^{3} }} {\text{and}} \, F_{{{\text{Cas}}}}^{*} = \frac{{c_{{{\text{Cas}}}}^{*} }}{{\left( {1 - u_{{{\text{Cas}}}}^{*} } \right)^{4} }}.$$

Fig. 12

Variation of critical intermolecular forces versus beam length and initial gap length based on CT and MCST analysis for different gradient indices of clamped–clamped FG nanoactuator ($h = 10 {\text{nm}}, b = 5h, l_{U} = 0.5h, l_{B} = 0.75h$), a critical van der Waals and b critical Casimir force

It is observed from Fig. 12 that for a clamped–clamped FG nanobeam, the critical values of both van der Waals and Casimir forces are independent on either the beam length or the initial gap. However, these critical values depend on the material distribution (gradient index) and the microstructure material length scale parameter. Also, it can be noticed that as the stiffness of the beam increases either by decreasing $k$ or including the couple stress effect, larger force is required to cause instability.

In Fig. 13, the minimum gap required to prevent instability of the nanoactuator due to intermolecular Casimir and van der Waals forces is plotted versus beam length in the range of 1–20 µm and thickness in the range of 6–30 nm, considering CT, MCST, and SET analyses. It is observed that, compared with MCST and SET, the classical theory CT overestimates the minimum gap which in turn lead to unexpected damage during device operation. Tables 12 and 13 tabulate the values of the minimum gap and detachment length of actuated clamped–clamped and cantilever nanobeams due to the influence of Casimir or van der Waals force based for classical and MCST analyses.

Fig. 13

Variation of minimum gap for a van der Walls and b Casimir forces versus beam length and thickness for CT and MCST and SET analyses of a clamped–clamped FG nanoactuator, ($k = 0, b = 50{\text{nm}}, l_{U} = 5{\text{nm}})$, a due to van der Waals force only and b due to Casimir force only

Tables 12 and 13 tabulate the values of the minimum gap and detachment length of actuated clamped–clamped and cantilever nanobeams due to the influence of Casimir or van der Waals force based for classical and MCST analyses.

6 Conclusions

A novel, simple, and accurate closed-form solution is derived for computing the size-dependent pull-in voltage of clamped–clamped and cantilever electrically actuated FG nanobeams using a Particle Swarm Optimization (PSO) algorithm. The mathematical model of the problem is presented using the size-dependent Euler–Bernoulli beam hypothesis accounting for surface energy and microstructure effects. In the present model, the modified couple-stress theory and Gurtin–Murdoch surface elasticity model are employed to, respectively, determine the effect of microstructure local rotational degree of freedom and surface energy effect on the pull-in behavior of FG micro/nanobeam. The model accounts for the simultaneous effect of intermolecular Casimir and van der Waals forces, fringing field, mid-plane stretching, and axial residual stress. All properties of the bulk material and surface layers of the FG beam are supposed to vary across the thickness direction according to power-law. The governing equation and boundary conditions are exactly derived employing Hamilton principle accounting for the position of physical neutral axis of the mentioned FG nanobeam.

Using Galerkin method, the governing equation is reduced to an algebraic-integral equation, then a PSO method is utilized to approximate the integral forms of the fringing field, electrostatic, and intermolecular Casimir and van der Waals forces to non-integral forms. Finally, a general closed form solution of the pull-in voltage is obtained. Also, the proposed method leads to an accurate prediction of the detachment length and minimum initial gap of the freestanding nanoactuator. The main conclusions that can be extracted from the numerical results are outlined as follows:

• 1. Different coefficients of the non-integral forms for electrostatic force, fringing field effect, and intermolecular Casimir and van der Waals forces are extracted using PSO and tabulated (Tables 2, 3).

• 2. A single nonlinear algebraic equation (Eq. (33)) is derived for the relation between the applied voltage and the maximum normalized deflection of the FG nanoactuator. This equation is very helpful for understanding the instability behavior under the mutual nonlinear effects of mechanical, electrostatic, and intermolecular forces. Based on this equation, the closed-form expressions for pull-in voltage and freestanding parameters are easily derived. Besides being simple, the accuracy of the closed-form expression for pull-in voltage of micro/nanobeams with clamped–clamped and clamped-free boundary conditions as well as the detachment length and minimum gap of the freestanding nanoactuator are verified by comparing the present results with those in published literature and good agreement is found.

• 3. The presence of surface energy effects (surface elasticity and surface residual stress) leads to a higher pull-in voltage compared with that of classical theory due to the stiffening effect of surface modulus. The effects of surface energy become considerable when the beam reduced to nanoscale. Comparison between CT, MCST, SET, and CSSE demonstrates that the nonclassical analyses predict higher pull-in voltage due to the stiffness effect, which becomes stronger in CSSE than SET and MCST.

• 4. For both classical and nonclassical analyses, increasing the gradient index shows a significant reduction in the pull-in voltage. This is attributed to the softening effect as the gradient index increases, since we assume that the constitution of ceramic in the material decreases with increasing k.

• 5. The coupled effects of fringing field and intermolecular Casimir and van der Waals forces distinctly decrease the pull-in voltage. If the contribution of these effects is neglected, the pull-in voltage may be considerably overestimated leading to unexpected damage during device operation. Therefore, the present investigation may be very helpful for assuring the safe operation of MEMS and NEMS actuators. As the initial gap decreases, the influence of the intermolecular forces become more significant and the nanobeam may collapse at no applied voltage.

• 6. The proposed method is used to determine the critical dimensions of the freestanding FG nanoactuators, i.e. minimum initial gap and detachment length. It is observed that the critical intermolecular forces are independent of the beam length and the initial gap. Increasing the gradient index, smaller forces are required to cause pull-in. In addition, neglecting the nonclassical effects overestimates the minimum gap which may result in unexpected damage of the actuator if it is designed based on classical theory.

This present model and the proposed analytical solution can be used as an efficient accurate tool for predicting the influences of the material and geometrical parameters on the size-dependent static pull-in instability and freestanding behavior of FG nanobeams for their design and optimization which may need a large number of simulations.